多项式各种运算的速算法和多项式方程
多项式的运算

多项式的运算在数学的广袤天地中,多项式是一个非常重要的概念,而多项式的运算更是我们解决众多数学问题的有力工具。
首先,咱们来聊聊什么是多项式。
简单说,多项式就是由几个单项式相加或相减组成的式子。
比如 3x + 2y 5 就是一个多项式,其中 3x、2y 和-5 就是单项式。
多项式的运算主要包括加法、减法、乘法和除法。
咱们一个一个来看。
多项式的加法和减法相对来说比较直观。
在进行加法或减法运算时,我们只需要将同类项(就是所含字母相同,并且相同字母的指数也相同的项)进行合并就可以了。
比如说,计算(2x²+ 3x 1) +(x² 2x+ 5) ,先把同类项找出来,2x²和 x²是同类项,3x 和-2x 是同类项,-1 和 5 是同类项。
然后分别把同类项相加,得到 3x²+ x + 4 。
减法也是同样的道理,比如计算(4x² 3x + 2) (2x²+ x 1) ,还是先找同类项,然后同类项相减,得到 2x² 4x + 3 。
接下来是多项式的乘法。
这就稍微有点复杂了,但只要掌握好方法,也不难。
比如说计算(x + 2)(x 3) ,我们可以使用“ FOIL 法则”,也就是先把第一个括号里的 x 乘以第二个括号里的每一项,得到 x² 3x ,再把第一个括号里的 2 乘以第二个括号里的每一项,得到 2x 6 ,最后把这两个结果相加,得到 x² x 6 。
如果是更复杂一点的多项式相乘,比如(2x + 3)(x² 2x + 1) ,那就先把第一个多项式的每一项分别乘以第二个多项式的每一项,然后合并同类项。
2x 乘以 x²得到 2x³,2x 乘以-2x 得到-4x²,2x 乘以1 得到 2x ;3 乘以 x²得到 3x²,3 乘以-2x 得到-6x ,3 乘以 1 得到3 。
多项式运算与多项式因式分解

总结与展望
回顾多项式运算与 多项式因式分解的 基础知识
多项式运算包括加减乘除
等运算,多项式因式分解
是将多项式拆解成不可约
的因式
总结解决多项式运 算问题的方法和技 巧
递推法、质因数分解等方
法可以帮助解决多项式运
算中的问题
展望多项式运算在未 来的应用前景
多项式运算在人工智能、 大数据分析等领域有着广 泛的应用前景,未来将继 续发挥重要作用
乘法
应用分配律和乘 法公式展开式子
除法
根据长除法或因 式定理简化式子
减法
多项式相同次数 的式提取 法
找出所有项的最 高公因式
三项一次式 分解法
分解成两个一次 式相乘
待定系数法
设定未知数确定 系数
配方法
应用二项式平方 公式或公式法配
对
多项式运算与因式分解对比
多项式运算
多项式的高级因式分解
完全平方法
完全平方公式、 完全立方公式等
实例演练
应用所学知识解 决问题
选取合适的 因式分解方
法
根据题目特点灵 活选择
特殊类型多项式的因式分解
01 完全平方差公式
应用范围及示例
02 立方差公式
具体应用与实例分析
03 三角函数的因式分解
推导过程及应用案例
多项式因式分解在实际问题中的应用
基于代数式的计算 操作符号为加减乘除 简化复杂的代数式
多项式因式分解
根据公因式提取或特定方 法分解 拆分成简化的因式 用于化简及求解方程
共同点
都是对代数式进行操作 能够简化问题、方便计算
不同点
运算着重于计算结果 因式分解着重于式子形式 的变换
多项式因式分解步骤
多项式运算掌握多项式的加减乘除运算

多项式运算掌握多项式的加减乘除运算多项式运算:掌握多项式的加减乘除运算在代数学中,多项式是由一系列称为“项”的代数式构成的。
每个项由一个系数与一个或多个变量的乘积组成。
多项式运算是代数学中非常重要的一部分,通过加减乘除等运算,可以对多项式进行各种计算和化简。
在本文中,我将为您介绍多项式的加减乘除运算,帮助您全面掌握这一重要概念。
一、多项式的加法运算多项式的加法运算是将两个或多个具有相同变量幂次的项相加得到一个新的多项式。
在进行多项式的加法运算时,需要按照变量的幂次进行合并,相同幂次的项进行系数相加。
例如,给定两个多项式:P(x) = 3x^2 + 2x + 1Q(x) = 2x^2 + 4x + 3将两个多项式相加,得到:P(x) + Q(x) = (3x^2 + 2x + 1) + (2x^2 + 4x + 3)= 3x^2 + 2x^2 + 2x + 4x + 1 + 3= 5x^2 + 6x + 4通过以上例子,我们可以看出,多项式的加法运算就是将相同幂次的项合并,并将其系数相加得到新的多项式。
二、多项式的减法运算多项式的减法运算是将两个多项式相减得到一个新的多项式。
减法运算可以看作加法运算的逆运算,只需将第二个多项式的所有项的系数取相反数,再进行加法运算即可。
例如,给定两个多项式:P(x) = 3x^2 + 2x + 1Q(x) = 2x^2 + 4x + 3将第一个多项式减去第二个多项式,得到:P(x) - Q(x) = (3x^2 + 2x + 1) - (2x^2 + 4x + 3)= 3x^2 - 2x^2 + 2x - 4x + 1 - 3= x^2 - 2x - 2通过以上例子,我们可以看出,多项式的减法运算可以转化为加法运算,并将第二个多项式的所有项的系数取相反数。
三、多项式的乘法运算多项式的乘法运算是将两个多项式相乘得到一个新的多项式。
在进行多项式的乘法运算时,需要对每一项进行相乘,并将相同幂次的项合并。
奥数解题窍门多项式运算技巧

奥数解题窍门多项式运算技巧多项式是奥数中重要的概念和技巧之一。
在解题过程中,灵活运用多项式运算技巧可以帮助我们简化问题、提高解题效率。
下面将介绍一些奥数解题中常用的多项式运算技巧。
技巧一:多项式的加减运算在多项式的加减运算中,我们要根据多项式的指数规律进行合并和简化。
例如,对于多项式$ax^n+bx^n+...+c$,我们可以合并同类项,即将指数相同的项合并在一起,如$ax^n+bx^n=(a+b)x^n$。
此外,我们还可以根据交换律和结合律进行运算的重组,以便更好地简化和计算多项式。
技巧二:多项式的乘法运算在多项式的乘法运算中,我们可以使用分配律和合并同类项的方法来简化计算。
例如,对于多项式$(x+a)(x+b)$,我们可以使用分配律进行展开,得到$x^2+ax+bx+ab$,然后根据合并同类项的原则,将指数相同的项合并在一起,即可简化为$x^2+(a+b)x+ab$。
技巧三:多项式的除法运算多项式的除法运算可以通过长除法的方式进行。
我们首先要确定被除式和除式的次数,然后逐步进行除法运算,得出商和余数。
例如,对于多项式$ax^n+bx^{n-1}+...+c$和除式$dx^m+ex^{m-1}+...+f$,我们可以按照长除法的步骤进行运算,得出商和余数。
技巧四:多项式的简化与因式分解在奥数中,我们常常需要将多项式进行简化,或将其进行因式分解。
简化多项式可以帮助我们更清晰地理解问题的本质;而因式分解则可以帮助我们寻找多项式的根和解。
例如,对于多项式$x^2+2xy+y^2$,我们可以运用完全平方公式进行因式分解,得到$(x+y)^2$。
技巧五:多项式的代入与求解在多项式中,我们可以将一些数值代入到变量中,以求得多项式的具体值。
这可以帮助我们验证多项式的正确性,并在具体问题中求解。
例如,对于多项式$2x^3+3x^2-5x+1$,如果我们代入$x=2$,即可求得多项式的值为$2(2^3)+3(2^2)-5(2)+1=17$。
多项式的加减乘除四则运算
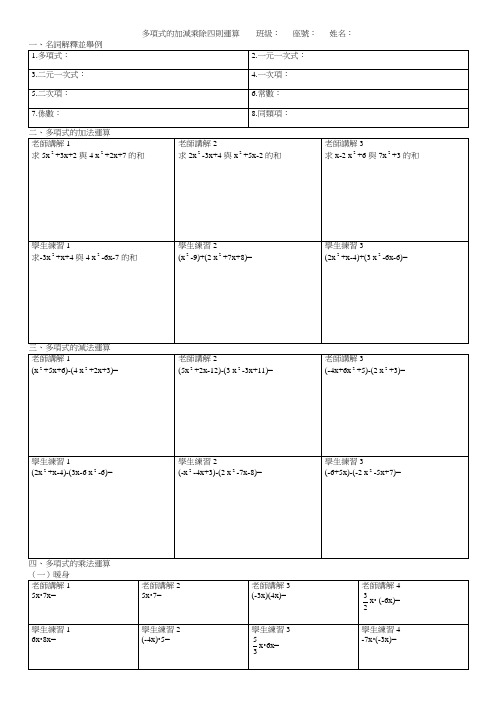
多項式的加減乘除四則運算班級:座號:姓名:
五、多項式的除法運算
四、十字交乘法(三項式) 班級:座號:姓名:
2
2. x2項的係數「不是1」的十字交乘法
二、完全平方數:背1~20的平方
三、平方根的定義
四、利用方格紙畫圖,作出面積是2 平方單位、5 平方單位、18平方單位的正方形-----介紹無理數
五、非完全平方數的平方根:根號引入的必須
六、利用方格紙畫圖,作出1、2、3、4、5、……. 、n
七、正數、零、負數的平方根
(一)正數:
(二)零:
(三)負數:
八、利用標準分解式計算平方根
九、十分逼近法:求無理數的近似值
十、電算器求平方根
一元二次方程式班級:座號:姓名:
5. a x2+bx+c=0,a和b 和c是常數(、十字交乘法)
6. 綜合題
7. 應用問題。
多项式的加减法运算

多项式的加减法运算多项式是数学中的一个重要概念,它是由各种项组成的代数表达式。
每个项包含一个系数和一个变量的幂次。
在代数运算中,多项式的加减法是基本而重要的运算,本文将详细介绍多项式的加减法运算的方法和步骤。
多项式的表示形式为:P(x) = a1x^n + a2x^(n-1) + a3x^(n-2) + ... + anx^0其中,P(x)表示多项式,ai表示各项的系数,n表示最高次幂,x表示变量。
一、多项式的加法运算多项式的加法运算是指将两个或多个多项式相加得到一个新的多项式。
进行多项式的加法运算时,需要注意以下步骤:1. 将相同幂次的项进行合并:将各项系数相加,并保持变量的幂次不变。
例如,考虑以下两个多项式的加法运算:P(x) = 3x^3 + 2x^2 + x + 5Q(x) = 2x^3 + 4x^2 - 3x + 7对应的幂次项分别为:3x^3 + 2x^2 + x + 52x^3 + 4x^2 - 3x + 7将相同幂次的项进行合并,得到新的多项式:5x^3 + 6x^2 - 2x + 122. 如果有多个多项式需要相加,只需重复步骤1,将相同幂次的项进行合并,最后得到一个新的多项式。
二、多项式的减法运算多项式的减法运算是指将一个多项式减去另一个多项式得到一个新的多项式。
进行多项式的减法运算时,需要注意以下步骤:1. 转化为加法运算:将减法运算转化为加法运算,即通过取反操作将减号变成加号。
例如,考虑以下两个多项式的减法运算:P(x) = 3x^3 + 2x^2 + x + 5Q(x) = 2x^3 + 4x^2 - 3x + 7将减法转化为加法:P(x) - Q(x) = P(x) + (-Q(x))2. 取反操作:将减去的多项式中各项的系数取反。
例如,对于多项式Q(x)中的各项,取反后得到:-Q(x) = -2x^3 - 4x^2 + 3x - 73. 将取反后的多项式与原多项式进行加法运算。
初中代数学习辅导:多项式的四则运算

初中代数学习辅导:多项式的四则运算
个多项式的次数
2多项式的值
任何一个多项式,就是一个用加、减、乘、乘方运算把已知数和未知数连接起来的式子
3多项式的恒等
对于两个一元多项式f(x)、g(x)来说,当未知数x同取任一个数值a时,如果它们所得的值都是相等的,即f(a)=g(a),那么,这两个多项式就称为是恒等的记为f(x)==g(x),或简记为f(x)=g(x)
性质1如果f(x)==g(x),那么,对于任一个数值a,都有
f(a)=g(a)
性质2如果f(x)==g(x),那么,这两个多项式的个同类项系数就一定对应相等
4一元多项式的根
一般地,能够使多项式f(x)的值等于0的未知数x的值,叫做多项式f(x)的根
多项式的加、减法,乘法
1多项式的加、减法
2多项式的乘法
单项式相乘,用它们系数作为积的系数,对于相同的字母因式,则连同它的指数作为积的一个因式
3多项式的乘法外语学习网
多项式与多项式相乘,先用一个多项式等每一项乘以另一个多项式的各项,再把所得的积相加
常用乘法公式
公式I平方差公式
(a+b)(a-b)=a^2-b^2
两个数的和与这两个数的差的积等于这两个数的平方差。
多项式的加减法

多项式的加减法多项式是代数学中的重要概念,它是由数和字母的乘积按照特定规则组成的代数表达式。
在代数学中,多项式的加减法是一项基本操作,掌握多项式的加减法对于解决各种数学问题具有重要意义。
本文将介绍多项式的加减法的基本原理和运算方法,以及一些实际应用。
一、多项式的加法多项式的加法是指将同类项相加得到一个新的多项式。
同类项是具有相同指数的项,例如2x^2和3x^2就是同类项。
多项式加法的基本原理是对应同类项的系数相加得到新的系数。
例如,考虑以下两个多项式的加法:3x^2 + 4x + 2 和 2x^2 + 5x + 1。
首先,对应同类项的系数相加,3x^2 + 2x^2 = 5x^2;4x + 5x = 9x;2 + 1 = 3。
将得到的系数组合在一起,得到新的多项式:5x^2 + 9x + 3。
二、多项式的减法多项式的减法是指用减去的多项式减去被减去的多项式,得到一个新的多项式。
和加法类似,多项式减法也要对应同类项的系数相减。
例如,考虑以下两个多项式的减法:4x^3 + 6x^2 + 2x - 1 和 2x^3 +3x^2 - 5x + 1。
首先,对应同类项的系数相减,4x^3 - 2x^3 = 2x^3;6x^2 - 3x^2 =3x^2;2x + 5x = 7x;-1 - 1 = -2。
将得到的系数组合在一起,得到新的多项式:2x^3 + 3x^2 + 7x - 2。
三、多项式的加减法综合运用多项式的加减法可以在解决各种数学问题中起到重要的作用,下面通过几个例子来说明。
例1:假设小明有一些苹果和橘子,表示苹果的多项式为3x + 2,表示橘子的多项式为4x - 1。
问小明共有多少水果?解:将两个多项式相加,(3x + 2) + (4x - 1) = 7x + 1。
根据新的多项式,小明共有7x + 1个水果。
例2:某高中学生参加了数学竞赛,得分规则为答对一道题得5x^2 + 3x + 2分,答错一道题扣除2x^2 - 4x - 1分。
高中数学多项式方程解题方法

高中数学多项式方程解题方法一、一元多项式方程的解法在高中数学中,我们经常会遇到一元多项式方程,即只含有一个未知数的多项式方程。
解一元多项式方程的方法有很多种,下面我将介绍其中几种常用的方法。
1.1 因式分解法当方程可以进行因式分解时,我们可以通过因式分解来求解方程。
例如,考虑如下方程:x^2 - 5x + 6 = 0我们可以将其因式分解为:(x - 2)(x - 3) = 0从而得到方程的解为 x = 2 或 x = 3。
因式分解法适用于方程的系数比较简单的情况,能够快速求解方程。
1.2 完全平方公式法当方程可以写成完全平方的形式时,我们可以利用完全平方公式来求解方程。
例如,考虑如下方程:x^2 - 6x + 9 = 0由于方程可以写成 (x - 3)^2 = 0 的形式,根据完全平方公式,我们知道方程的解为 x = 3。
完全平方公式法适用于方程的系数较为复杂,但方程可以写成完全平方形式的情况。
1.3 二次方程求根公式法对于一元二次方程 ax^2 + bx + c = 0,我们可以利用二次方程求根公式来求解方程。
二次方程求根公式为:x = (-b ± √(b^2 - 4ac)) / (2a)例如,考虑如下方程:2x^2 - 5x + 2 = 0根据二次方程求根公式,我们可以得到方程的解为 x = 1 或 x = 0.5。
二次方程求根公式法适用于一元二次方程的解法,可以求解任意一元二次方程。
二、多元多项式方程的解法除了一元多项式方程,我们还会遇到多元多项式方程,即含有多个未知数的多项式方程。
解多元多项式方程的方法也有很多种,下面我将介绍其中几种常用的方法。
2.1 消元法消元法是解多元多项式方程的常用方法之一。
通过逐步消去未知数的方法,将方程化简为只含有一个未知数的方程,从而求解方程。
例如,考虑如下方程组:2x + 3y = 74x - 5y = 1我们可以通过消元法将方程组化简为:2x + 3y = 78x - 10y = 2然后再通过加减法或代入法求解方程组。
初中数学 多项式方程的解如何计算

初中数学多项式方程的解如何计算计算多项式方程的解可以使用不同的方法,具体方法取决于方程的次数和系数的类型。
以下是一些常见的方法:1. 一次方程的解:一次方程是次数为1的多项式方程,具有形式ax + b = 0。
解一次方程时,我们可以通过移项将方程转化为形如x = c的形式,其中c是一个实数。
2. 二次方程的解:二次方程是次数为2的多项式方程,具有形式ax^2 + bx + c = 0。
对于二次方程,我们可以使用求根公式或配方法来解。
- 求根公式法:二次方程的解可以使用二次方程公式x = (-b ± √(b^2 - 4ac))/(2a)来计算,其中a、b、c是方程的系数。
- 配方法:对于无法直接使用求根公式的二次方程,我们可以使用配方法将其转化为一个可以因式分解的形式,然后求解因子等于零的方程。
3. 高次多项式方程的解:对于高次多项式方程,解的计算会更加复杂。
以下是一些常见的方法:- 因式分解法:如果多项式可以进行因式分解,我们可以将方程转化为每个因子等于零的形式,然后求解每个因子等于零的方程,得到方程的解。
- 零点定理和综合除法:零点定理告诉我们,如果一个多项式方程有有理数解r,那么它可以被(x-r)整除。
我们可以使用综合除法来将多项式除以(x-r),然后继续求解得到的商式。
- 迭代法和数值方法:对于高次多项式方程或复杂的多项式方程,我们可以使用迭代法或数值方法来近似求解。
这些方法通过逐步逼近方程的解,直到满足所需的精度。
以上是解多项式方程的一些常见方法,具体选择哪种方法取决于方程的特点和要求的精度。
在学习过程中,学生可以根据方程的类型和要求选择适当的方法来计算方程的解。
多项式的乘法和除法运算

多项式的乘法和除法运算在代数学中,多项式是由常数和变量以及它们的乘积和幂次组成的表达式。
多项式的乘法和除法运算是代数学中重要的基本操作之一,它们在数学和实际问题中都有广泛的应用。
本文将介绍多项式的乘法和除法运算方法及其相关概念。
一、多项式的乘法运算多项式的乘法运算是指对两个或多个多项式进行相乘的操作。
一般来说,多项式的乘法运算可以通过对每一项进行乘法运算,并将结果相加得到。
例如,我们考虑两个多项式的乘法运算:P(x) = a₀xⁿ + a₁xⁿ⁻¹ + ... + aₙQ(x) = b₀xᵐ + b₁xᵐ⁻¹ + ... + bₙ其中,a₀、a₁、...、aₙ和b₀、b₁、...、bₙ是常数系数,x是变量,n和m是乘法项的幂次。
要进行多项式的乘法运算,我们可以按照下列步骤进行:1. 将P(x)和Q(x)中的每一项进行乘法运算:P(x) * Q(x) = (a₀xⁿ + a₁xⁿ⁻¹ + ... + aₙ) * (b₀xᵐ + b₁xᵐ⁻¹ + ... + bₙ) = a₀b₀xⁿ⁺ᵐ + (a₀b₁ + a₁b₀)xⁿ⁺ᵐ⁻¹ + ...+ (a₀bₙ + a₁bₙ⁻¹ + ... + aₙb₀)xⁿ⁻¹ + (a₁bₙ⁻¹ + ... +aₙb₁)xⁿ + aₙbₙ2. 将乘法运算得到的每一项按照幂次的降序排列,得到最终结果。
需要注意的是,在乘法运算过程中,要注意对幂次相同的项进行合并,以简化最终结果。
例如,如果P(x)和Q(x)中有相同幂次的项,要将它们相加合并。
二、多项式的除法运算多项式的除法运算是指对两个多项式进行相除的操作。
一般来说,多项式的除法运算可以通过将被除式除以除式,从而得到商式和余式。
例如,我们考虑两个多项式的除法运算:P(x) = a₀xⁿ + a₁xⁿ⁻¹ + ... + aₙQ(x) = b₀xᵐ + b₁xᵐ⁻¹ + ... + bₙ其中,a₀、a₁、...、aₙ和b₀、b₁、...、bₙ是常数系数,x是变量,n和m是除法项的幂次。
数学中的多项式运算

数学中的多项式运算数学中的多项式运算是一种基础而重要的运算方法,它在代数学和数学分析中都有广泛的应用。
多项式是由常数和变量的乘积组成的代数表达式,它是数学中的一种基本概念。
多项式的定义很简单,它由一系列项组成,每一项由一个常数和一个变量的乘积构成。
例如,多项式2x^2 + 3x + 1就是一个由三个项组成的多项式,其中2、3和1是常数,x是变量。
在多项式运算中,最基本的运算是加法和乘法。
加法运算是将两个多项式相加,乘法运算是将两个多项式相乘。
下面我们来详细讨论这两种运算。
1. 加法运算多项式的加法运算很简单,只需要将相同次数的项相加即可。
例如,考虑多项式2x^2 + 3x + 1和4x^2 + 2x + 5的相加运算,我们只需要将相同次数的项相加即可,得到6x^2 + 5x + 6。
在多项式的加法运算中,我们可以利用结合律和交换律来简化计算。
结合律指的是加法运算中,项的顺序可以任意调整,而结果不变。
交换律指的是加法运算中,项的顺序可以任意交换,而结果不变。
这两个性质使得多项式的加法运算更加简便。
2. 乘法运算多项式的乘法运算相对来说稍微复杂一些。
乘法运算需要将两个多项式的每一项相乘,并将结果相加。
例如,考虑多项式2x^2 + 3x + 1和4x^2 + 2x + 5的相乘运算,我们需要将每一项相乘,并将结果相加,得到8x^4 + 16x^3 + 4x^2 + 15x + 5。
在多项式的乘法运算中,我们可以利用分配律来简化计算。
分配律指的是乘法运算中,一个多项式乘以另一个多项式的和,等于这个多项式分别乘以另一个多项式的每一项,并将结果相加。
这个性质使得多项式的乘法运算更加方便。
除了加法和乘法运算,多项式还有其他一些重要的运算。
例如,多项式的减法运算可以通过将减数的每一项取相反数,然后进行加法运算来实现。
多项式的除法运算可以通过长除法的方法来实现。
此外,多项式还有一些特殊的形式和性质。
例如,多项式的次数指的是多项式中最高次项的次数。
多项式的运算与应用

2x3 2x2 6x x2 2x 5 x2 x 3
x 2 餘式
課本頁次:65
乙、多項式的四則運算
(三)多項式的除法(長除法)
f (x) 2x3 3x2 8x 5 除以 g(x) x2 x 3
an為f(x)的首項係數(或領導係數)
課本頁次:60
甲、多項式的基本觀念
(一)多項式的定義
f x an xn an1xn1 a1x a0
(3)項: anxn﹐an1xn1﹐…﹐a1x﹐a0分別為此多項式的 n次項﹐n1次項﹐…﹐1次項﹐常數項﹒
(4)整係數多項式: an﹐an1﹐…﹐a1﹐a0都是整數 (或有理數﹑實數)的多項式 f(x)
稱為整係數(或有理係數﹑實係數)多項式
課本頁次:60
甲、多項式的基本觀念
(一)多項式的定義
f x an xn an1xn1 a1x a0
(5)多項式的值: f(x)中的 x 代表 特定數值 a時,
稱 f(a)為f(x)在 x=a 的值
(6)常數多項式: 只有一個非零常數項a0時﹐ 稱為零次多項式。如:3﹐ 2 0也是一個多項式﹐稱為零多項式 不規定它的次數
課本頁次:62
例2 已知f(x) = 3x3 + 4x 5﹐g(x) = x2 3x +1﹐求
(2) f(x) - g(x)﹐
並整理成降次排列的多項式﹒
解:
直式算法:(缺項補0) 分離係數法:(缺項補0)
同次項的位置上下對齊 略去文字符號x
3x3 +0x2 +4x 5
-)
x2 3x +1
多项式的加减运算

多项式的加减运算多项式是学习数学中的重要概念之一,它在代数学和数值分析等领域中应用广泛。
在这篇文章中,我们将重点讨论多项式的加减运算,探究其规则和方法。
一、多项式的定义和表示形式在开始讨论多项式的加减运算之前,我们先来回顾一下多项式的定义和表示形式。
一个多项式包含若干项的代数和,每一项都由系数与指数的乘积组成。
一般表示为:P(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0其中,P(x)表示多项式,ai表示系数,xi表示未知数,n表示多项式的次数。
二、多项式的加法运算多项式的加法运算是指将两个多项式相加,合并相同次数的项,对应系数相加的过程。
具体步骤如下:1. 对应次数的项进行系数相加。
2. 如果某个多项式中没有与另一个多项式对应次数的项,则保留原有的项。
3. 最后化简得到新的多项式。
例如,考虑以下两个多项式的加法运算:P(x) = 2x3 - 5x2 + 3x + 1Q(x) = -3x3 + 4x - 2按照上述步骤进行计算,我们可以得到它们的相加结果为:P(x) + Q(x) = -1x3 - 5x2 + 7x - 1三、多项式的减法运算多项式的减法运算是指将一个多项式减去另一个多项式,合并相同次数的项,对应系数相减的过程。
具体步骤如下:1. 对应次数的项进行系数相减。
2. 如果某个多项式中没有与另一个多项式对应次数的项,则保留原有的项。
3. 最后化简得到新的多项式。
举个例子,考虑以下两个多项式的减法运算:P(x) = 2x3 - 5x2 + 3x + 1Q(x) = -3x3 + 4x - 2按照上述步骤进行计算,我们可以得到它们的相减结果为:P(x) - Q(x) = 5x3 - 5x2 - 1x + 3四、多项式的加减混合运算在实际问题中,我们常常会遇到多项式的加减混合运算。
这时,我们需要按照以下步骤进行计算:1. 先进行多项式的加法运算。
2. 再进行多项式的减法运算。
多项式的加法和减法运算

多项式的加法和减法运算多项式是数学中常见的一种表达形式,它由一系列的同一变量的次幂项和系数相加或相乘而成。
多项式的加法和减法运算是我们在代数学习过程中经常会遇到的基本操作。
本文将围绕多项式的加法和减法运算展开论述。
一、多项式的定义和表示方式多项式是由若干项组成的代数和,其中每一项可以是常数、变量、常数与变量的乘积。
多项式的一般形式如下:P(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0其中,P(x)表示多项式,a_n, a_{n-1}, ..., a_1, a_0是常数项,x是变量,n是多项式的次数。
多项式中的每一项可以看作是一个幂函数,系数a表示该幂函数的比例关系。
二、多项式的加法运算多项式的加法运算是将两个或多个多项式进行相加,根据每一项次数相同的原则,最后得到一个新的多项式。
具体步骤如下:1. 将相同次数的项进行相加,保持次数不变,得到新的项;2. 若有次数相同的项系数为零,可以省略该项;3. 将所有不同次数的项合并,得到最简形式的多项式。
示例:已知多项式A(x)=3x^2 + 2x + 1,B(x)=-2x^2 + x + 2,计算A(x) + B(x)。
解:按照多项式加法的规则,将相同次数的项进行相加:A(x) + B(x) = (3x^2 + 2x + 1) + (-2x^2 + x + 2)= (3x^2 - 2x^2) + (2x + x) + (1 + 2)= x^2 + 3x + 3因此,A(x) + B(x) = x^2 + 3x + 3。
三、多项式的减法运算多项式的减法运算是将一个多项式减去另一个多项式,同样根据每一项次数相同的原则,最后得到一个新的多项式。
具体步骤如下:1. 将减数中的每一项系数取相反数;2. 将得到的相反数减法式与另一个多项式按照多项式加法的规则进行相加。
示例:已知多项式C(x)=x^3 - 2x^2 + 1,D(x)=2x^2 - x + 2,计算C(x) - D(x)。
多项式的基本运算

多项式的基本运算
汇报人:XX
目录
CONTENTS
01 多项式的加法
02 多项式的减法
03 多项式的乘法
04 多项式的除法
05 多项式的混合运算
多项式的加法
相同次数的项相加
定义:将多项式中相同次数的项进行相加,得到的结果仍为多项式。
规则:按照次数从低到高的顺序,依次进行加法运算。
举例:多项式2x^2 + 3x + 4与多项式3x^2 + 2x + 1相加,得到的结果为5x^2 + 5x + 5。
多项式与多项式相乘
定义:两个多项 式相乘,将一个 多项式的每一项 与另一个多项式 的每一项相乘, 合并同类项
举
例
:
$(x+1)(x+2) =
x^2 + 3x + 2$
展开过程:按照 乘法分配律展开, 注意符号的运算
注意事项:合并 同类项时,注意 符号的运算
多项式的除法
单项式除以多项式
单击此处添加标题
括号内的运算先进行
括号内的运算具有最高优先级 先进行括号内的运算可以避免混淆和错误 括号内的运算顺序是固定的,不受其他因素的影响 在多项式的混合运算中,括号内的运算必须先进行
运算顺序的注意事项
先进行乘除运算,再进行加减运算 括号内的内容优先进行运算 幂运算优先于乘除运算,与加减运算同级 需要注意运算的优先级,避免出现计算错误
添加标题
原因:乘法和除法运算的优先级高于加法和减法运算,遵循数学运算的基本规则。
添加标题
举例:对于多项式 2x^2 + 3x*y + 4x - y^2,先进行乘法运算 x*y 和 x*4,得到 3x*y 和 4x,再进 行加法和减法运算,得到最终结果。
人教版八年级数学上册多项式的乘法与多项式的因式分解

人教版八年级数学上册多项式的乘法与多项式的因式分解多项式是数学中常见的代数表达式形式之一,它由若干项的代数式按照加法或减法连接而成。
在八年级数学上册中,我们将研究多项式的乘法和多项式的因式分解。
1. 多项式的乘法多项式的乘法是指将两个或多个多项式相乘得到一个新的多项式。
我们可以将多项式的乘法分为以下几个步骤:1. 将每一个多项式中的每一项按照乘法法则展开。
2. 将所有的展开式按照对应的幂和系数进行整理,并合并同类项。
3. 化简合并同类项后的表达式,得到最终的乘积多项式。
例如,我们可以用以下步骤计算多项式的乘积:(2x + 3)(x - 4)展开式为:2x^2 - 8x + 3x - 12合并同类项得到:2x^2 - 5x - 12通过上述步骤,我们可以得到两个多项式相乘的结果。
2. 多项式的因式分解多项式的因式分解是指将一个多项式拆分为几个乘积形式的因式的过程。
通过因式分解,我们可以将多项式表示为若干个因子的乘积形式,从而更好地理解和处理多项式。
对于一个多项式的因式分解,我们可以使用以下常见的方法:1. 公因式提取:当多项式中的每一项都有一个相同的因子时,我们可以将该因子提取出来,得到公因式。
2. 利用分配律:当多项式中存在公因式后,我们可以使用分配律将公因式分别与其他的项相乘。
3. 特殊因式:有些多项式具有特殊的因式形式,如平方差公式、立方差公式等,可以利用这些特殊因式进行因式分解。
通过以上的因式分解方法,我们可以将一个多项式分解为多个乘积形式的因式。
总结起来,八年级数学上册中的多项式的乘法和因式分解是我们研究的重点内容。
通过掌握多项式的乘法和因式分解的基本原理和方法,我们可以更好地解决与多项式相关的数学问题。
参考资料:- 人教版八年级数学上册教材。
多项式的计算

第1章多项式的计算1.1 一维多项式求值1.功能计算多项式p(x)=a n-1x n-1+a n-2x n-2+…+a1x+a0在指定点x处的函数值。
2.方法说明首先将多项式表述成如下嵌套形式:p(x)=(…((a n-1x+a n-2)x+a n-3)x+…+a1)x+a0然后从里往外一层一层地进行计算。
其递推计算公式如下:u n-1=a n-1u k=u k+1x+a k,k=n-2,…,1,0最后得到的u0即是多项式值p(x)。
3.函数语句与形参说明4.函数程序(文件名:1plyv.c)double plyv(a,n,x)int n;double x,a[];{ int i;double u;u=a[n-1];for (i=n-2; i>=0; i--)u=u*x+a[i];return(u);}5.例计算多项式p (x )=2x 6-5x 5+3x 4+x 3-7x 2+7x -20在x =±0.9,±1.1,±1.3处的函数值。
主函数程序(文件名:1plyv0.c )如下:#include "stdio.h" #include "1plyv.c" main() { int i ;static double a[7]={-20.0,7.0,-7.0,1.0,3.0,-5.0,2.0}; static double x[6]={0.9,-0.9,1.1,-1.1,1.3,-1.3}; printf("\n");for (i=0; i<=5; i++)printf("x(%d)=%5.2lf p(%d)=%13.7e\n", i ,x[i],i ,plyv(a ,7,x[i])); printf("\n"); }运行结果为:x(0)= 0.90 p(0)=-1.856227e+01 x(1)=-0.90 p(1)=-2.671537e+01 x(2)= 1.10 p(2)=-1.955613e+01 x(3)=-1.10 p(3)=-2.151303e+01 x(4)= 1.30 p(4)=-2.087573e+01 x(5)=-1.30 p(5)=-6.340432e+001.2 一维多项式多组求值1.功能利用系数预处理法对多项式p (x )=a n -1x n -1+a n -2x n -2+…+a 1x +a 0进行多组求值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多项式各种运算的速算法和多项式方程【摘要】本节主要写数与多项式相关运算的统一关系,把数的各种运算和数的各种方程的求根方法应用到多项式中来。
多项式的各种算式及方程式是不定数的式子, 而数的各种算式及方程式就是当x=10时,且系数是一位数的定数式子。
因而运算一一相关统一。
如二元一次多项式方程组的解法,不仅有加减消元法,同样也有代入消元法;一元二次多项式方程的解法,不仅有公式法,同样还有配方法,十字乘法等。
多项式的乘方开方运算及多项式方程,这是教科书上没有的,因此本节可以充实教科文,使多项式的计算领域得以拓展而完善。
【关键词】科学速算法多项式各种运算多项式方程充实教科文拓展完善多项式的各种运算,教科书上只有加减法和乘除法,而乘方也按乘法一样计算,其速算法不像数的各种运算的速算法研究那么热,甚至几乎没有谈及。
在乘法运算中,教科书上都是通过一一展开,然后合并同类项,算法相当繁琐,并且两个因式的项数多了,就很难计算。
多项式的开方运算和多项式方程,教科书上一片空白。
中小学数学教材第八册《整式的运算》,这一章写整式的加减法、乘除法(及分解因式),没有写乘方开方,更没有写多项式方程。
多项式的加减法和乘除法除了教科书上所写的方法之外,有没有更简捷的算法?多项式能不能开方?多项式方程能不能求解?这些都是本文要研究的问题。
(1)多项式加减法的快速运算;(2)多项式乘除法的快速运算;(3)多项式的乘方及开方的快速运算;(4)多项式方程的求解方法。
多项式的速算法也像数的速算法一样,采取同级(类)项科学速算法;多项式方程也像数的方程解法一样求解。
1.多项式的加减速算法例1:已知:f(x)=-6x 7+5x 6-11x 4+3x 2-10x+6ɡ(x)=-4x 5-6x 4+7x 3-9x+5H(x)=-7x 6-5x 4+2x 3-6x 2+13x-9求:f(x)-ɡ(x)+H(x)解:将次数最高的f(x)所缺的项0x 5、0x 3补上,并按升幂排列或降幂排列,然后将-ɡ(x)、H(x)和f(x)的同级(类)项对齐地写在一起,算式如下:f(x)=-6x 7+5x 6+0x 5-11x 4+0x 3+3x 2-10x+6-ɡ(x)=--4x 5+6x 4-7x 3 +9x-5H(x)=+7x 6 -5x 4+2x 3-6x 2+13x-9∴f(x)-ɡ(x)+H(x) =-6x 7+12x 6-4x 5-10x 4-5x 3-3x 2+12x-8(左右相加)把减法转化为加法运算就比较简捷。
练习1(1)已知:f(x)=-9x 8+5x 6-3x 3+2x 2-4g(x)=4x 9-6x 7+4x 6-3x 5-2x 2H(x)=-15x 7-7x 6+5x 4-x+6I(x)=x 8-x 7+3x 5+7x 4-2x-5求f(x) -g(x)-H(x)+I(x)例2:已知:f(x)=-5x 6+11x 5+7x 2-9ɡ(x)=-8x 8+4x 7-10x 5+12x 4+2x 3-6H(x)=-7x 9+6x 7-13x 6+5x 2-11x+7求:f(x)-ɡ(x)-H(x)2.多项式乘除法的快速运算多项式的乘法,教科书上一般是将一个因式的每一项去乘以另一个因式的各项,然后将所得的结果合并同类项,这样不仅算式太繁,而且寻找同类项要花费很多时间,运算速度太慢,又很容易出现差错。
同类项其实就是同级项,懂得这一原理,就可应用同级项理论进行计算,这样不仅式子简单,而且速度很快,准确度也很高。
例2:计算:(-4x 3+2x 2+5x-6)(4x 2-3x+4)解:算式如下〖TP1.TIF;%40%40,BP〗〖KH-*1〗∴(-4x 3+2x 2+5x-6)(4x 2-3x+4)=-16x 5+20x 4-2x 3-31x 2+38x-24以上计算就相当于将一个因式升幂排列而另一个因式降幂排列,然后通过移动对项积和差来求x的各次系数(例4)例3:已知:f(x)=7x 8+13x 7-25x 6+32x 5-x 4+21x 3+57x 2-96x+100g(x)= 6x 7-36x 6+78x 5-15x 4-123x 3-78x 2+34x-39求:f (x)·g(x)解:f (x)和g(x)表成如下式f (x)=(78 137 -256 325 -14 213 572 -961 100。
)g (x) =( 67 -366 785 -154 -1233 -782 341 -39。
) ①f (x)·g(x)的各同级项系数,像例2一样应用涨缩中心对称积和法则计算如下:〖TP2.TIF;%60%60,BP〗〖LL〗〖TP002.TIF;%60%60,BP〗〖KH-*1〗∴f (x)·g(x) =42x 15 -174x 14 -72x 13 +2001x 12-4164x 11 +888x 10 +1327x 9-2792x 8+4457x 7-12385x 6-691x 5+6615x 4-3693x 3-13287x 2+7144x-3900这一题如按传统的计算方法是先展开,然后合并同类项,则展开后总共就有72项,因而寻找同类项要花费很多时间,而且容易出错,其缺点是没有直接的把各同类项的系数罗列在一起,而造成的计算准度。
现在采取同级项方法进行运算,速度大大提高了。
像两数相乘一样,两个多项式相乘,其系数也具有顺逆移动对项性。
多项式相乘其系数具有这一特性,叫作升降幂排列移动对项积和差求系数法。
例4:已知:f (x) = 9x 9 -6x 7 + 12x 6-3x 4 + 26x 3-15g(x) = 7x 8 + 5x 7 -13x 5-2x 2 + 6x-8这两个多项式都缺项,所缺的项系数都为零。
解:将f (x)和g(x)的系数表成如下升降幂排列的形式〖TP3.TIF;%50%50,BP〗〖KH-*1〗上面两式系数对项积和差就为x 9的系数。
因此,f (x)·g(x)的各同类项系数,应用升降幂排列移动对项积和差求法如下:〖TP4.TIF;%60%60,BP〗〖KH-*1〗∴ f (x)·g(x) =63x 17 +45x 16 -42x 15 -63x 14 +60x 13 +57x 12 -7x 11 +184x 10 -21x 9-503x 8+45x 7-90x 6+125x 5+180x 4-208x 3+30x 2-90x+120例5: 计算:(3x 2+2x-7)(2x 3-5x 2+3x+2)解:〖XC5.TIF;%50%50〗∴(3x 2+2x-7)(2x 3-5x 2+3x+2)=6x 5-11x 4-15x 3+47x 2-17x-14上面三种算法我们都可以直接的把各同类项系数之积有序地写在一起,运算起来非常方便。
例6:已知:f (x)=14x 8+13x 7-58x 6+132x 5-324x 4+450x 3-325x 2+120x-100∴f 3(x)的27次项=-10929x 27 -8460x 27 +1134x 27 +9072x 27 =-9183x 27f 3(x)的26次项算式如下〖XC11.TIF;%35%40〗带点项的平方和连线项的乘积之和的3倍=3[(3x 13 ) 2· 14 〖TX-〗+(7x 12 ) 25〖TX-〗· x 2+(0x 11 ) 2·x 4+( 12 〖TX-〗x 10 ) 2· x 6+(x 9) 2·6x 8+(6x 8) 2· 12 〖TX-〗x 10 +(0x 7) 2·7x 12 ]=3×259x 26 =777x 26〖XC12.TIF;%35%40〗上连线项的乘积之和的6倍与3x 13 的积=3x 13 (7x 12 ·9x+0x 11 ·5〖TX-〗x 2+ 12 〖TX-〗x 10 · 13 〖TX-〗x 3+ 21 〖TX-〗x 9·x 4+6x 8·17x 5+0x 7· 11 〖TX-〗x 6)×6=3x 13 ·300x 13 ×6=5400x 26下连线项的乘积之和的6倍与7x 12 的积=7x 12 (0x 11 · 13 〖TX-〗x 3+ 12 〖TX-〗x 10 ·x 4+ 21 〖TX-〗x 9·17x 5+6x 8· 11 〖TX-〗x 6)×6 =7x 12 ·4〖TX-〗3〖TX-〗5〖TX-〗x 14 ×6=-18270x 26 〖XC13.TIF;%32%40〗上连线项的乘积之和的6倍与0x 11 的积+下连线项的乘积之和的6倍与x 10 的积=0x 11 ( 12 〖TX-〗x 10 ·17x 5+ 21 〖TX-〗x 9·11x 6+6x 8·0x 7)×6+ 12 〖TX-〗x 10 ( 21 〖TX-〗x 9·0x 7)×6=0∴f 3(x)的26次项=777x 26 +5400x 26 -18270x 26 =-12093x 26立方同级项展开公式,就是由上面方法求得。
例4:已知:f (x) =-2x 4+5x 3+7x 2-12x+3求:f 3(x)解:五位数的立方共有[3(位数-1)+1]级,即共13级。
同样道理四次多项式的立方项数共有(3×次数+1)项,即共13项。
计算时只需应用立方同级项展开公式前七级就可以了,后六级和前六级是对称的。
计算时(2〖TX-〗、5、7、 12 〖TX-〗、3)分别代表前六级(a b c d e )和后六级(e d c b a ),由同级项展开公式,得(这时f = g = 0)〖XC14.TIF;%40%40〗〖XC15.TIF;%40%40〗∴f 3 (x) =-8x 12 +60x 11 -66x 10 -439x 9+987x 8+663x 7-3068x 6+1458x 5+2331x 4-3105x 3+1485x 2-324x+27数的运算法则和公式都适用于多项式的运算,这是它们的共同点。
其不同点是相邻的两个级数之间,数的运算存在进位,多项式的运算不存在进位。
练习41、在例3中求f 3(x)的28次项和25次项2、已知f(x)=x 8-3x 7+5x 6-7x 5-6x 4+8x 3-3x 2+2x-5求f 3(x)2、多项式的开方①多项式的开平方例1:已知: f (x)=169x 10 -546x 9+2339x 8-2832x 7+4535x 6+1084x 5-1961x 4-1310x 3+130x 2+224x+49 求:〖KF(〗f(x)〖KF)〗解:和平方根的求法一样,算式如下〖XC16.TIF;%35%35〗∴〖KF(〗f (x)〖KF)〗= 13x 5 -21x 4 + 73x 3 + 9x 2 -16x -7f (x)无论指数多高,项数多大,只要它是一个多项式的完全平方,应用这种方法,就可以把f (x)的开平方式求出来。
