相似三角形知识点及典型例题
九年级数学相似三角形典型例题

九年级数学相似三角形典型例题一、利用相似三角形的判定定理证明相似例1:已知:在△ABC和△DEF中,∠A = ∠D = 60°,AB = 4,AC = 8,DE = 2,DF = 4。
求证:△ABC∽△DEF。
解析:1. 我们看相似三角形的判定定理。
对于两个三角形,如果它们的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
2. 在本题中:计算公式,公式。
并且已知∠A = ∠D = 60°。
因为公式且∠A = ∠D,所以根据相似三角形判定定理中的“两边对应成比例且夹角相等的两个三角形相似”,可以得出△ABC∽△DEF。
二、相似三角形性质的应用(求边长)例2:已知△ABC∽△A'B'C',相似比为公式,若AB = 6,则A'B'的长为多少?解析:1. 因为相似三角形对应边成比例。
设A'B' = 公式。
已知相似比公式。
2. 又已知公式,AB = 6,所以公式。
通过交叉相乘可得:公式。
即公式,解得公式,所以A'B'的长为9。
三、利用相似三角形解决实际问题(测量高度)例3:在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,求这棵大树的高度。
解析:1. 因为在同一时刻,太阳光下不同物体的高度和影长成正比。
设大树的高度为公式米。
可以得到两个相似三角形,一个是由小强及其影子构成,另一个是由大树及其影子构成。
2. 根据相似三角形的性质,对应边成比例。
则公式。
交叉相乘可得:公式。
计算得公式,解得公式米。
所以这棵大树的高度是9.6米。
九下 相似三角形4种判定方法 知识点+模型+例题+练习 (非常好 分类全面)

①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥l 2∥l 3。
则,,,…AB BC DE EF AB AC DE DF BC AC EFDF===②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
○4推论:如果一条直线平行于三角形的一条边,截其它两边(或其延长线),那么所截得的三角形与原三角形相似.推论○4的基本图形有三种情况,如图其符号语言:∵DE ∥BC ,∴△ABC ∽△ADE ;知识点二、相似三角形的判定判定定理1:两角对应相等,两三角形相似.符号语言:拓展延伸: (1)有一组锐角对应相等的两个直角三角形相似。
(2)顶角或底角对应相等的两个等腰三角形相似。
例题1.如图,直线DE 分别与△ABC 的边AB 、AC 的反向延长线相交于D 、E ,由ED ∥BC 可以推出AD AEBD CE=吗?请说明理由。
(用两种方法说明)例题2.(射影定理)已知:如图,在△ABC 中,∠BAC=90°,AD ⊥BC 于D.求证:(1)2AB BD BC =⋅;(2)2AD BD CD =⋅;(3)CB CD AC ⋅=2例题3.如图,AD 是Rt ΔABC 斜边BC 上的高,DE ⊥DF ,且DE 和DF 分别交AB 、AC 于E 、F.则BDBEAD AF =例题精讲AEDBCABCD吗?说说你的理由.例题4.如图,在平行四边形ABCD 中,已知过点B 作BE ⊥CD 于E,连接AE ,F 为AE 上一点,且∠BFE=∠C(1) 求证:△ABF ∽△EAD ;(2)若AB=4,∠BAE=30°,求AE 的长;3分之8倍根号3 (3)在(1)(2)条件下,若AD=3,求BF 的长。
2分之3倍根号3 随练: 一、选择题1.如图,△ABC 经平移得到△DEF ,AC 、DE 交于点G ,则图中共有相似三角形( )D A . 3对 B . 4对 C . 5对 D . 6对2.如图,已知DE ∥BC ,EF ∥AB ,则下列比例式中错误的是( )CADCBEF G F E DCBA。
中考数学《相似三角形》知识点及练习题

相似三角形一. 知识梳理1.平行线分线段成比例定理定理:两条直线被三条平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
2.相似三角形定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。
相似比:相似三角形对应边的比叫做相似比。
3.相似三角形的判定平行法:平行于三角形一边的直线和其他两边相交,所得的三角形与原三角形相似。
两角法:两角分别相等的两个三角形相似。
边角法:两边成比例且夹角相等的两个三角形相似。
三边法:三边对应成比例的两个三角形相似。
4.相似三角形的性质①相似三角形的对应角相等,对应边成比例;②相似三角形对应边上高的比,对应边上中线的比与对应角平分线的比都等于相似比;③相似三角形周长的比等于相似比;④相似三角形面积的比等于相似比的平方。
5.位似图形定义:如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心。
这时的相似比又叫位似比6. 黄金分割:点C 把线段AB 分成两条线段AC 和BC,如果ACBC AB AC =,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比. 1:618.0215:≈-=AB AC 二.课后作业1.下列图形中不一定属于相似形的是( )A.两个圆B.两个等边三角形C.两个正方形D.两个矩形2.如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )A. 1∶16B. 1∶4C. 1∶6D. 1∶23.已知△ABC ∽△DEF ,且AB:DE=1:2,则△ABC 的周长与△DEF 的周长之比( )A.1:2B.1:4C.2:1D.4:14.如图,给出下列条件:其中,不能单独判定△ABC∽△ACD 的条件为( )A.∠B=∠ACDB.∠ADC=∠ACBC.AC CD =AB BCD.AC AD =AB AC5.如图,DE ∥BC ,且AD=2,BD=5,则△ADE 与△ABC 的相似比为( )A.2:5B.5:2C.2:7D.7:26.如图,在△ABC 中,DE ∥BC ,AD=2,AE=3,BD=4,则AC=( ) A.7 B.8 C.9 D.10 E A D CB A BC DE7.已知△ABC ∽△DEF ,且它们的周长之比为1:2,那么它们的相似比为 。
相似三角形经典题型

相似三角形经典题型一、相似三角形的判定定理相关题型1. 题目已知在△ABC和△A'B'C'中,∠A = 50°,AB = 3cm,AC = 4cm,∠A'= 50°,A'B'= 6cm,A'C' = 8cm。
判断这两个三角形是否相似。
解析根据相似三角形的判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
在△ABC和△A'B'C'中,(AB)/(A'B')=(3)/(6)=(1)/(2),(AC)/(A'C')=(4)/(8)=(1)/(2),且∠A = ∠A' = 50°。
所以△ABC∽△A'B'C'。
2. 题目如图,在四边形ABCD中,∠B = ∠ACD,AB = 6,BC = 4,AC = 5,CD=(7)/(2),求AD的长。
解析因为∠B = ∠ACD,且(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),(AC)/(AD)未知。
又因为(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),不满足三边对应成比例。
但是由∠B = ∠ACD,(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),可以尝试证明△ABC和△ACD相似。
因为∠B = ∠ACD,(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),这里我们重新计算(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)是错误的,应该是(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(BC)/(CD)所以△ABC∽△DCA。
相似三角形的性质与判定(知识点+例题)

海豚教育个性化简案学生姓名:年级:科目:授课日期:月日上课时间:时分------ 时分合计:小时教学目标1.掌握两个三角形相似的判定条件(三个角对应相等,三条边的比对应相等,则两个三角形相似);2.会运用“两个三角形相似的判定条件”和“三角形相似的预备定理”解决简单的问题;3.掌握两个直角三角形相似的判定条件,并能解决简单的问题.重难点导航1. 解决相似三角形相似的应用并会探索;2. 由已知条件寻找相似三角形.教学简案:一、真题演练二、个性化教案三、个性化作业四、错题汇编授课教师评价:□ 准时上课:无迟到和早退现象(今日学生课堂表□ 今天所学知识点全部掌握:教师任意抽查一知识点,学生能完全掌握现符合共项)□ 上课态度认真:上课期间认真听讲,无任何不配合老师的情况(大写)□ 海豚作业完成达标:全部按时按量完成所布置的作业,无少做漏做现象审核人签字:学生签字:教师签字:备注:请交至行政前台处登记、存档保留,隔日无效(可另附教案内页)大写:壹贰叁肆签章:海豚教育个性化教案(真题演练)1.(2013•舟山)若一次函数y=ax+b (a≠0)的图象与x 轴的交点坐标为(-2,0),则抛物线y=ax 2+bx 的对称轴为( )A .直线x=1B .直线x=-2C .直线x=-1D .直线x=-42.(2010•天津)已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列结论:①b 2-4ac >0; ②abc >0; ④9a+3b+c ③8a+c >0; <0其中,正确结论的个数是( )A .1B .2C .3D .43. (2011•扬州)如图,已知函数xy 3=与y=ax 2+bx (a >0,b >0)的图象交于点P .点P 的纵坐标为1.则关于x 的方程032=++xbx ax 的解为 .海豚教育个性化教案相似三角形的性质与判定知识点一:相似三角形的定义及性质1.定义:三个角对应相等、三条边对应成比例的两个三角形叫做相似三角形。
(完整版)相似三角形基本知识点+经典例题(完美打印版)

相似三角形知识点与经典题型知识点1 有关相似形的概念(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多 边形.相似多边形对应边长度的比叫做相似比(相似系数).知识点2 比例线段的相关概念(1)如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。
(2)在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注:①比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:ad c b=.②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c 叫比例内项, a 、c 叫比例前项,b 、d 叫比例后项,d 叫第四比例项,如果b=c ,即 a b b d =::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
(3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB.即AC BC AB AC ==简记为:12长短==全长注:黄金三角形:顶角是360的等腰三角形。
黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质(注意性质立的条件:分母不能为0)(1) 基本性质:①bc ad d c b a =⇔=::;②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb db a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 (3)反比性质(把比的前项、后项交换): a c b d b da c=⇔=.(4)合、分比性质:a c abcd b d b d±±=⇔=.注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=dc dc b a b a c cd a a b d c b a 等等.(5)等比性质:如果)0(≠++++====n f d b nm f e d c b a ΛΛ,那么b an f d b m e c a =++++++++ΛΛ.注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:ba f db ec a f ed c b a fe d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . 知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE ∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或注:①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边......与原三角形三边......对应成比例.②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例. 已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等.注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
初中相似三角形基本知识点和经典例题

初中相似三角形基本知识点和经典例题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初三相似三角形知识点与经典题型知识点1 有关相似形的概念(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多 边形.相似多边形对应边长度的比叫做相似比(相似系数).知识点2 比例线段的相关概念(1)如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。
(2)在四条线段dc b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注:①比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:a d c b =.②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c 叫比例内项, a 、c 叫比例前项,b 、d 叫比例后项,d 叫第四比例项,如果b=c ,即 a b b d =::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
(3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB.即12AC BC AB AC ==简记为:长短=全长注:黄金三角形:顶角是360的等腰三角形。
黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质(注意性质立的条件:分母不能为0)(1) 基本性质:①bc ad d c b a =⇔=::;②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除 了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb d b a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 (3)反比性质(把比的前项、后项交换): a c b db d a c=⇔=.(4)合、分比性质:a c a b c db d b d±±=⇔=.注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a 等等.(5)等比性质:如果)0(≠++++====n f d b nm f e d c b a ,那么b an f d b m e c a =++++++++ .注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零. ③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . 知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE ∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或 注:①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边......与原三角形....三边..对应成比例. ②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. 此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,已知AD ∥BE ∥CF,B可得AB DE AB DE BC EF BC EF AB BC BC EF AC DF AB DE AC DF DE EF=====或或或或等.注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
(完整word版)九年级数学相似三角形知识点及习题

相似三角形要点一、本章的两套定理第一套(比例的有关性质): b a n d b m c a n d b n m d c b a =++++++⇒≠+++=== :)0(等比性质 涉及概念:①第四比例项②比例中项③比的前项、后项,比的内项、外项④黄金分割等。
二、有关知识点:1.相似三角形定义: 对应角相等,对应边成比例的三角形,叫做相似三角形。
2.相似三角形的表示方法:用符号“∽”表示,读作“相似于”。
3.相似三角形的相似比: 相似三角形的对应边的比叫做相似比。
4.相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
5.相似三角形的判定定理:(1)三角形相似的判定方法与全等的判定方法的联系列表如下:类型斜三角形 直角三角形 全等三角形的判定 SASSSS AAS (ASA ) HL 相似三角形的判定 两边对应成比例夹角相等 三边对应成比例 两角对应相等一条直角边与斜边对应成比例 从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理,这就是我们数学中的用类比的方法,在旧知识的基础上找出新知识并从中探究新知识掌握的方法。
6.直角三角形相似:(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
7.相似三角形的性质定理:(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
8.相似三角形的传递性 如果△ABC ∽△A 1B 1C 1,△A 1B 1C 1∽△A 2B 2C 2,那么△ABC ∽A 2B 2C 2三、注意1、相似三角形的基本定理,它是相似三角形的一个判定定理,也是后面学习的相似三角形的判定定理的基础,这个定理确定了相似三角形的两个基本图形“A ”型和“ X ”型。
(完整版)相似三角形知识点及典型例题,推荐文档

相似三角形知识点及典型例题知识点归纳:1、三角形相似的判定方法(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
简述为:两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
简述为:两边对应成比例且夹角相等,两三角形相似。
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
简述为:三边对应成比例,两三角形相似。
(6)判定直角三角形相似的方法:①以上各种判定均适用。
②如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
③直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
#直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下: (1)(AD)2=BD·DC, (2)(AB)2=BD·BC , (3)(AC)2=CD·BC 。
注:由上述射影定理还可以证明勾股定理。
即(AB)2+(AC)2=(BC)2。
典型例题:例1 如图,已知等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ‖AB ,BG 分别交AD ,AC 于E 、 F ,求证:BE 2=EF·EG证明:如图,连结EC ,∵AB =AC ,AD ⊥BC ,∴∠ABC =∠ACB ,AD 垂直平分BC∴BE =EC ,∠1=∠2,∴∠ABC-∠1=∠ACB-∠2,即∠3=∠4,又CG ∥AB ,∴∠G =∠3,∴∠4=∠G又∵∠CEG =∠CEF ,∴△CEF ∽△GEC ,∴EG CE =CEEF∴EC 2=EG· EF ,故EB 2=EF·EG 【解题技巧点拨】本题必须综合运用等腰三角形的三线合一的性质,线段的垂直平分线的性质和相似三角形的基本图形来得到证明.而其中利用线段的垂直平分线的性质得到BE=EC ,把原来处在同一条直线上的三条线段BE ,EF ,EC 转换到相似三角形的基本图形中是证明本题的关键。
相似三角形的判定+性质+经典例题分析

相似形一一、比例性质1.基本性质:bc ad dcb a =⇔=两外项的积等于两内项积 2.反比性质:cda b d c b a =⇔= 把比的前项、后项交换3.合比性质:ddc b b ad c b a ±=±⇒=分子加减分母;分母不变 .4.等比性质:分子分母分别相加;比值不变.如果)0(≠++++====n f d b nmf e d c b a ;那么b a n f d b m ec a =++++++++ . 谈重点:1此性质的证明运用了“设k 法” ;这种方法是有关比例计算;变形中一种常用方法.2应用等比性质时;要考虑到分母是否为零.3可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数;再利用等比性质也成立.5.黄金分割:错误!内容 错误!尺规作图作一条线段的黄金分割点经典例题回顾:例题1.已知a 、b 、c 是非零实数;且k cb a dd a b c d c a b d c b a =++=++=++=++;求k 的值.例题2.已知111x y x y+=+;求y x x y +的值..板块二、新课讲解知识点一、相似形的概念概念:具有相同形状的图形叫相似图形. 谈重点:⑴相似图形强调图形形状相同;与它们的位置、颜色、大小无关. ⑵相似图形不仅仅指平面图形;也包括立体图形相似的情况.⑶我们可以这样理解相似形:两个图形相似;其中一个图形可以看作是由另一个图形放大或缩小得到的. ⑷若两个图形形状与大小都相同;这时是相似图形的一种特例——全等形.知识点二、平行线分线段成比例定理①定理:三条平行线截两条直线;所得的对应线段成比例;如图:l 1∥l 2∥l 3..则,,,…AB BC DE EF AB AC DE DF BC AC EFDF===②推论:平行于三角形一边的直线截其他两边或两边的延长线所得的对应线段成比例..③定理:如果一条直线截三角形的两边或两边的延长线所得的对应线段成比例;那么这条直线平行于三角形的第三边..错误!推论:如果一条直线平行于三角形的一条边;截其它两边或其延长线;那么所截得的三角形与原三角形相似.推论错误!的基本图形有三种情况;如图其符号语言:∵DE ∥BC;∴△ABC ∽△ADE ;知识点三、相似三角形的判定判定定理1:两角对应相等;两三角形相似. 符号语言:拓展延伸:1有一组锐角对应相等的两个直角三角形相似.. 2顶角或底角对应相等的两个等腰三角形相似..重难点高效突破例题1.如图;直线DE 分别与△ABC 的边AB 、AC 的反向延长线相交于D 、E;由ED ∥BC 可以推出AD AEBD CE=吗 请说明理由..用两种方法说明例题2.射影定理已知:如图;在△ABC 中;∠BAC=90°;AD ⊥BC 于D.求证:12AB BD BC =⋅;22AD BD CD =⋅;3CB CD AC ⋅=2例题3.如图;AD 是Rt ΔABC 斜边BC 上的高;DE ⊥DF;且DE 和DF 分别交AB 、AC 于E 、F.则BDBEAD AF =吗 说说你的理由.例题精讲AEDBCAB CD例题4.如图;在平行四边形ABCD 中;已知过点B 作BE ⊥CD 于E;连接AE;F 为AE 上一点;且∠BFE=∠C(1) 求证:△ABF ∽△EAD ;(2) 若AB=4;∠BAE=30°;求AE 的长; (3) 在12条件下;若AD=3;求BF 的长..即时训练 一、选择题1.如图;△ABC 经平移得到△DEF;AC 、DE 交于点G;则图中共有相似三角形 A . 3对 B . 4对 C . 5对 D . 6对2.如图;已知DE ∥BC;EF ∥AB;则下列比例式中错误的是 A .AC AE AB AD = B . FB EA CF CE = C . BD AD BC DE = D . CB CF AB EF =.3.在矩形ABCD 中;E 、F 分别是CD 、BC 上的点;若∠AEF=90°;则一定有 A .ΔADE ∽ΔAEF B.ΔECF ∽ΔAEF C.ΔADE ∽ΔECF D.ΔAEF ∽ΔABF4、如图;直线l 1∥l 2;AF ∶FB=2∶3;BC ∶CD=2∶1;则AE ∶EC 是 A.5∶2 B.4∶1 C.2∶1 D.3∶2ADCBEF GFEDCBA1题图 2题图 3题图 4题图5.如图;E 是平行四边形ABCD 的边BC 的延长线上的一点;连结AE 交CD 于F;则图中共有相似三角形 A.1对 B.2对 C.3对 D.4对5题图 6题图 7题图 8题图6.ΔABC 中;DE ∥BC;且AD ∶DB=2∶1;那么DE ∶BC 等于 A.2∶1 B.1∶2 C.2∶3 D.3∶27.如图;P 是Rt ΔABC 的斜边BC 上异于B 、C 的一点;过点P 做直线截ΔABC;使截得的三角形与ΔABC 相似;满足这样条件的直线共有 A.1条 B.2条 C.3条 D.4条8.如图;已知DE ∥BC;EF ∥AB;则下列比例式中错误的是 A.AC AE AB AD = B.FB EA CF CE = C.BDAD BC DE = D.CB CFAB EF =9.下列说法:其中正确的是①所有的等腰三角形都相似;②所有的等边三角形都相似; ③所有等腰直角三角形都相似;④所有的直角三角形都相似. A.①② B.③④ C.①④ D.②③ 二、解答题1、如图;ΔABC 中;BD 是角平分线;过D 作DE ∥AB 交BC 于点E;AB=5cm;BE=3cm;求EC 的长.2.如图;在梯形ABCD 中;AD ⊥BC;∠BAD=90°;对角线BD ⊥DC. 1ΔABC 与ΔDCB 相似吗 请说明理由. 2如果AD=4;BC=9;求BD 的长.3.已知:如图;在正方形ABCD 中;P 是BC 上的点;且BP=3PC; Q 是CD 的中点.ΔADQ 与ΔQCP 是否相似 为什么4.如图;已知AD 为△ABC 的角平分线;AD 的垂直平分线交BC 的延长线于点E;交AB 与F;试判定△BAE 与△ACE 是否相似;并说明理由..5.如图;在矩形ABCD 中;AB=5cm;BC=10cm;动点P 在AB 边上由A 向B 作匀速运动;1分钟可到达B 点;动点Q 在BC 边上由B 向C 作匀速运动;1分钟可到达C 点;若P 、Q 两点同时出发;问经过多长时间;恰好有PQ ⊥BDA BEFQ P DC B AABC DDABCDABCEA BCD E6.已知:如图所示;D 是AC 上一点;BE ∥AC;AE 分别交BD 、BC 于点F 、G;∠1=∠2.则BF 是FG 、EF 的比例中项吗 请说明理由.7.如图;CD 是Rt ΔABC 的斜边AB 上的高;∠BAC 的平分线分别交BC 、CD 于点E 、F. AC •AE=AF •AB 吗 说明理由.相似形二板块二、新课讲解知识点1.相似三角形的判定判定定理2:两边对应成比例且夹角相等;两三角形相似.判定定理3:三边对应成比例;两三角形相似.知识点2.直角三角形相似的判定 在直角三角形中;斜边和一条直角边对应成比例;两直角三角形相似.知识点3. 相似三角形中的基本图形AB C D EA 型;X 型 交错型 旋转型 母子形重难点高效突破例题1.如图在4×4的正方形方格中;△ABC 和△DEF 的顶点都在长为1的小正方形顶点上.1填空:∠ABC=______;BC=_______. 2判定△ABC 与△DEF 是否相似 并说明理由..例题2. 如图;在△ABC 中;已知BD 、CE 是△ABC 的高;求证:△ADE ∽△ABC..例题3.如图;已知AB ⊥BD;CD ⊥BD;AB=6cm;CD=4cm;BD=14cm;点P 在BD 上由B 点向D 点移动;当BP 等于多少时;△ABP 与△CPD 相似例题4.已知:如图;在△ABC 中;∠C =90°;P 是AB 上一点;且点P 不与点A 重合;过点P 作PE ⊥AB 交AC 于E ;点E 不与点C 重合;若AB =10;AC =8;设AP =x ;四边形PECB 的周长为y ;求y 与x 的函数关系式.例题精讲A BCD EABDCP例题5.在三角形ABC 中;AB=AC;AD ⊥BC 于点D;DE ⊥AC 于点E;M 为DE 的中点;AM 与BE 相交于点N;延长AM 交BC 于点G;AD 与BE 相交于点F; 求证:1DE AD =CECD;(2)△BCE ∽△ADM ; 3AM ⊥BE.随堂演练 A 组1.下列命题中正确的是①三边对应成比例的两个三角形相似 ②二边对应成比例且一个角对应相等的两个三角形相似 ③一个锐角对应相等的两个直角三角形相似 ④一个角对应相等的两个等腰三角形相似 A 、①③ B 、①④ C 、①②④ D 、①③④2.如图;D 、E 分别是AB 、AC 上两点;CD 与BE 相交于点O;下列条件中不能使ΔABE 和ΔACD 相似的是A. ∠B=∠CB. ∠ADC=∠AEBC. BE=CD;AB=ACD. AD ∶AC=AE ∶AB3.如图;在正方形网格上有6个斜三角形:①ΔABC;②ΔBCD;③ΔBDE;④ΔBFG;⑤ΔFGH;⑥ΔEFK.其中②~⑥中;与三角形①相似的是A ②③④B ③④⑤C ④⑤⑥D ②③⑥ 4.如图;DE 与BC 不平行;当ACAB= 时;ΔABC 与ΔADE 相似.. 5.如图;平行四边形 ABCD 中;AB=10;AD=6;E 是AD 的中点;在AB 上取一点F;使△CBF•∽△CDE;则BF 的长是 .A .5B .8.2C .6.4D .1.8M N F ABCDEG3题图 4题图 5题图5.如图;四边形ABCD 是平行四边形;AE ⊥BC 于E;AF ⊥CD 于F.1ΔABE 与ΔADF 相似吗 说明理由. 2ΔAEF 与ΔABC 相似吗 说说你的理由.6.已知:如图;在正方形ABCD 中;P 是BC 上的点;且BP=3PC;Q 是CD 的中点.ΔADQ 与ΔQCP 是否相似 为什么7.如图;在正方形ABCD 中;E 为AD 的中点;EF ⊥EC 交AB 于F;连接FC (),AE AB >△AEF ∽△EFC 吗若相似;请证明;若不相似;请说明理由..若ABCD 为矩形呢板块三、课后作业1.如图;正方形ABCD 中;点E;F 分别为AB;BC 的中点;AF 与DE 相交于点O;则AODO等于 . A .13 B .255C .23D .122.如图;直线EF 交AB 、AC 于点F 、E;交BC 的延长线于点D;AC ⊥BC;已知AB CD=DE AC ⋅⋅;求证:AE CE=DE EF ⋅⋅6.已知D 是BC 边延长线上的一点;BC =3CD ;DF 交AC 边于E 点;且AE =2EC .试求AF 与FB 的比.7.已知:如图;在△ABC 中;∠BAC =90°;AH ⊥BC 于H ;以AB 和AC 为边在Rt △ABC 外作等边△ABD 和△ACE ;试判断△BDH 与△AEH 是否相似;并说明理由.相似三角形的性质及其应用板块二、新课讲解知识要点:相似三角形的性质①相似三角形的对应角相等;对应边成比例.②相似三角形对应高的比;对应中线的比和对应角平分线的比都等于相似比. ③相似三角形周长的比等于相似比.④相似三角形面积的比等于相似比的平方.FABCDE重难点高效突破 例题1.1两个相似三角形的面积比为21:s s ;与它们对应高之比21:h h 之间的关系为_______ 2如图;已知D E ∥BC;CD 和BE 相交于O;若16:9:=∆∆COB ABC S S ;则AD:DB=_________3如图;已知AB ∥CD;BO:OC=1:4;点E 、F 分别是OC;OD 的中点;则EF:AB 的值为 4如图;已知DE ∥FG ∥BC;且AD:FD:FB=1:2:3;则) (S ::FBCG DFGE =∆四边形四边形S S ABCA.1:9:36B.1:4:9C.1:8:27D.1:8:36(5)梯形ABCD 中;AD ∥BC;AD<BC;AC 、BD 交于点O;若ABCD OAB S S ∆∆=256;则△AOD 与△BOC 的周长之比为__________..例题2.如图;在△ABC 中;DE ∥BC;且S △ADE :S 四边形BCED =1:2;BC =26..求DE 的长..例题3. 如图所示;已知DE ∥BC;且与△ABC 的边CA 、BA 的延长线分别相交于点D 、E;F 、G 分别在边AB 、AC 上;且AF :FB=AG :GC;求证:△AFG ∽△AED..A BCD E BC D E A O 2题图3题图 C E FOBA D 4题图B G FE D A C 5题图 CA ’ DD ’ C ’B ’ B A OBC DA例题4. 如图;矩形EFGH 内接于△ABC;AD ⊥BC 于点D;交EH 于点M;BC =20㎝;AM =8㎝; S △ABC =100㎝2..求矩形EFGH 的面积..例题5.△ABC 中;D 为AB 上一点;若∠ABC=∠ACD;AD=8㎝;DB=6㎝;求AC 的长..例题6.已知;如图△ABC 中;∠BAC=900;AB=AC=1;D 为BC 上一动点不与B;C 重合;∠ADE=45°(1)求证△ABD ∽△DCE(2)设BD=x;AE=y;求y 与x 的函数关系式 3若△ADE 为等腰直角三角形时;求AE 的长例题7、如图;在等腰梯形ABCD 中;AD ∥BC;AD=3㎝;BC=7㎝;∠B=60°;P 为下底BC 上一点不与B 、C 重合;连结AP;过P 点作PE 交DC 于E;使得∠APE=∠B.ABCD EF MH GPABCD1求证:△ABP ∽△PCE ; 2求等腰梯形的腰AB 的长;3在底边BC 上是否存在一点P;使得DE ∶EC=5∶3;如果存在;求出BP 的长;如果不存在;请说明理由.随堂演练A 组1.两个相似三角形的面积比为4:9;那么它们周长的比为__________.2.若x :y :z=3:5:7;3x +2y -4z =9则x +y +z 的值为____________. 3.如图;∠APD =90°;AP =PB =BC =CD;则下列结论成立的是 A .ΔPAB ∽ΔPCA B.ΔPAB ∽ΔPDA C .ΔABC ∽ΔDBA D.ΔABC ∽ΔDCA第3题4.如图;D 、E 分别是△ABC 的边AB 、AC 上的点;∠1=∠B;AE =EC =4;BC =10;AB =12;则△ADE 的周长为_______5.某学生利用树影测松树的高度;他在某一时刻测得1.5米长的竹竿影长0.9米;但当他马上测松树高度时;因松树靠近一幢高楼;影子不是全部在地面上;有一部分影子落在墙上;他测得留在地面部分的影长是2.4米;留在墙上部分的影高是1.5米;则松树的高度为________米6.如图;C 为线段AB 上的一点;△ACM 、△CBN 都是等边三角形;若AC =3;BC =2;则△MCD 与60°AE第7题图PD CBABCDMN 第6题 ADE 1BC第4题△BND 的面积比为 ..7.如图;在梯形ABCD 中;AD ∥BC;AC 、BD 交于O 点;S △AOD :S △COB =1:9;则S △DOC :S △BOC =板块三、课后作业1.已知:如图;△ABC 中;∠A =36°;AB =AC ;BD 是角平分线. 1求证:AD 2=CD ·AC ; 2若AC =a ;求AD .2.已知:如图;□ABCD 中;E 是BC 边上一点;且AE BD EC BE ,,21相交于F 点. 1求△BEF 的周长与△AFD 的周长之比;2若△BEF 的面积S △BEF =6cm 2;求△AFD 的面积S △AFD .3.已知:如图;Rt △ABC 中;AC =4;BC =3;DE ∥AB .1当△CDE 的面积与四边形DABE 的面积相等时;求CD 的长; 2当△CDE 的周长与四边形DABE 的周长相等时;求CD 的长.。
相似三角形的性质及判定知识点总结+经典题型总结(学生版)

一、相似的有关概念1.相似形具有相同形状的图形叫做相似形.相似形仅是形状相同,大小不一定相同.相似图形之间的互相变换称为相似变换. 2.相似图形的特性两个相似图形的对应边成比例,对应角相等. 3.相似比两个相似图形的对应角相等,对应边成比例.二、相似三角形的概念1.相似三角形的定义对应角相等,对应边成比例的三角形叫做相似三角形.如图,ABC △与A B C '''△相似,记作ABC A B C '''△∽△,符号∽读作“相似于”.2.相似比相似三角形对应边的比叫做相似比.全等三角形的相似比是1.“全等三角形”一定是“相似形”,“相似形”不一定是“全等形”.三、相似三角形的性质1.相似三角形的对应角相等A 'B 'C 'CB A中考要求知识点睛相似三角形的性质及判定2.相似三角形的对应边成比例ABC △与A B C '''△相似,则有AB BC ACk A B B C A C===''''''(k 为相似比).3.相似三角形的对应边上的中线,高线和对应角的平分线成比例,都等于相似比.如图1,ABC △与A B C '''△相似,AM 是ABC △中BC 边上的中线,A M ''是A B C '''△中B C ''边上的中线,则有AB BC AC AM k A B B C A C A M ====''''''''(k 为相似比).图1如图2,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AH k A B B C A C A H ====''''''''(k 为相似比).图2如图3,ABC △与A B C '''△相似,AD 是ABC △中BAC ∠的角平分线,A D ''是A B C '''△中B A C '''∠的角平分线,则有AB BC AC ADk A B B C A C A D ====''''''''(k 为相似比).图34.相似三角形周长的比等于相似比. 如图4,ABC △与A B C '''△相似,则有AB BC ACk===(k 为相似比).应用比例的等比性质有A 'B 'C 'CB AM 'MA 'B 'C 'C BAH 'H AB C C 'B 'A 'D 'D A 'B 'C B AAB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++. 图45.相似三角形面积的比等于相似比的平方.如图5,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AH k A B B C A C A H ====''''''''(k 为相似比).进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△.图5四、相似三角形的判定1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可简单说成:两角对应相等,两个三角形相似.3.如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似. 4.如果一个三角形的三条边与另一个三角形的你对应成比例,那么这两个三角形相似.可简单地说成:三边对应成比例,两个三角形相似.5.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.6.直角三角形被斜边上的高分成的两个直角三角形相似(常用但要证明)7.如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等,那么这两个等腰三角形相似;如果它们的腰和底对应成比例,那么这两个等腰三角形也相似.五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有“三点定形法”. 1.横向定型法欲证AB BCBE BF =,横向观察,比例式中的分子的两条线段是AB 和BC ,三个字母A B C ,,恰为ABC △的顶点;分母的两条线段是BE 和BF ,三个字母B E F ,,恰为BEF △的三个顶点.因此只需证ABC EBF △∽△.A 'B 'C 'CB AH 'H AB C C 'B 'A '欲证AB DEBC EF=,纵向观察,比例式左边的比AB 和BC 中的三个字母A B C ,,恰为ABC △的顶点;右边的比两条线段是DE 和EF 中的三个字母D E F ,,恰为DEF △的三个顶点.因此只需证ABC DEF △∽△. 3.中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况,此时可考虑运用等线,等比或等积进行变换后,再考虑运用三点定形法寻找相似三角形.这种方法就是等量代换法.在证明比例式时,常用到中间比.比例中项式的证明,通常涉及到与公共边有关的相似问题。
相似三角形典型例题
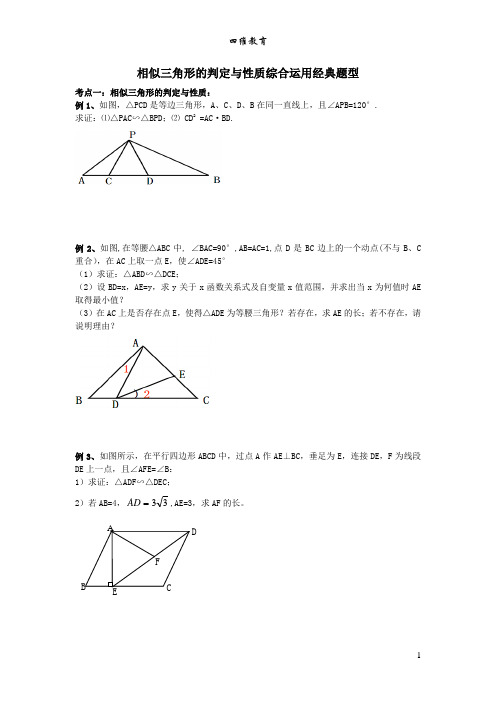
相似三角形的判定与性质综合运用经典题型考点一:相似三角形的判定与性质:例1、如图,△PCD 是等边三角形,A 、C 、D 、B 在同一直线上,且∠APB=120°.求证:⑴△PAC ∽△BPD ;⑵ CD 2 =AC ·BD.例2、如图,在等腰△ABC 中, ∠BAC=90°,AB=AC=1,点D 是BC 边上的一个动点(不与B 、C 重合),在AC 上取一点E ,使∠ADE=45°(1)求证:△ABD ∽△DCE ;(2)设BD=x ,AE=y ,求y 关于x 函数关系式及自变量x 值范围,并求出当x 为何值时AE 取得最小值?(3)在AC 上是否存在点E ,使得△ADE 为等腰三角形?若存在,求AE 的长;若不存在,请说明理由?例3、如图所示,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线段DE 上一点,且∠AFE=∠B :1)求证:△ADF ∽△DEC ;2)若AB=4,33 AD ,AE=3,求AF 的长。
A BC DE F考点二:射影定理:例4、如图,在Rt ΔABC 中,∠ACB=90°,CD ⊥AB 于D ,CD=4cm,AD=8cm,求AC 、BC 及BD 的长。
例5、如图,已知正方形ABCD ,E 是AB 的中点,F 是AD 上的一点,且AF=14AD ,EG ⊥CF 于点G ,(1)求证:△AEF ∽△BCE ; (2)试说明:EG 2=CG ·FG.例6、已知:如图所示的一张矩形纸片ABCD (AD>AB ),将纸片折叠一次,使点A 与点C 重合,再展开,折痕EF 交AD 边于E ,交BC 边于F ,分别连结AF 和CE .(1)求证:四边形AFCE 是菱形;(2)若AE=10cm ,△ABF 的面积为24cm 2,求△ABF 的周长;(3)在线段AC 上是否存在一点P ,使得2AE 2=AC ·AP ?若存在,请说明点P 的位置,并予以证明;若不存在,请说明理由.A B C D E FG考点三:相似之共线线段的比例问题:例7、已知如图,P 为平行四边形ABCD 的对角线AC 上一点,过P 的直线与AD 、BC 、CD 的延长线、AB 的延长线分别相交于点E 、F 、G 、H. 求证:PGPH PF PE例8、如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于点E ,交BA 的延长线于点F .(1)求证:PC 2=PE •PF ;(2)若菱形边长为8,PE=2,EF=6,求FB 的长.例9、如图,CD 是Rt △ABC 斜边上的高,E 为AC 的中点,ED 交CB 的延长线于F . 求证:BD •CF=CD •DF .例10、如图:已知在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD=CE ,直线CD 与AE 相交于点F .(1)求证:DC=AE ;(2)求证:AD 2=DC •DF .例11、如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.(1)找出与△ABH相似的三角形,并证明;(2)若E是BC中点,BC=2AB,AB=2,求EM的长.例12、如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD 相交于点N.求证:(1)AE=CG;(2)AN•DN=CN•MN.例13、如图,在Rt△ABC中,CD是斜边AB上的高,点M在CD上,DH⊥BM且与AC的延长线交于点E.求证:(1)△AED∽△CBM;(2)AE•CM=AC•CD.例14、如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.(1)求证:FD2=FB•FC;(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.例15、如图,四边形ABCD、CDEF、EFGH都是正方形.(1)⊿ACF与⊿ACG相似吗?说说你的理由.(2)求∠1+∠2的度数.考点四:相似三角形的实际应用:例16、如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.(1)若这个矩形是正方形,那么边长是多少?(2)若这个矩形的长PQ是宽PN的2倍,则边长是多少?例17、已知左,右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m。
九年级相似三角形知识点总结及例题讲解

相似三角形基本知识知识点一:放缩与相似1.图形的放大或缩小,称为图形的放缩运动。
2.把形状相同的两个图形说成是相似的图形,或者就说是相似性。
注意:⑴相似图形强调图形形状相同,与它们的位置、颜色、大小无关。
⑵相似图形不仅仅指平面图形,也包括立体图形相似的情况。
⑶我们可以这样理解相似形:两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到的.⑷若两个图形形状与大小都相同,这时是相似图形的一种特例一一全等形.3.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例。
注意:X两个相似的女边形是全等形时,他们的对应边的长度的比值是1.知识点二:比例线段有关概念及性质(1)有关概念1、比:选用同一长度单位量得两条线段。
a、b的长度分别是m、n,那么就说这两条线段的比是8 :b=m:na _ m(或厂T)2、比的前项,比的后项:两条线段的比a: b中。
a叫做比的前项,b叫做比的后项。
说明:求两条线段的比时,对这两条线段要用同一单位长度。
3、比例:两个比相等的式子叫做比例,如厂7Λ _ C4、比例外项:在比例厂7 (或a:b=c: d)中a、d叫做比例外项。
« _ C5、比例内项:在比例厂7(或8:b=C: d)中b、C叫做比例内项。
α _ c6、第四比例项:在比例丁万(或a: b二c:d)中,d叫a、b、C的第四比例项。
d _b7、比例中项:如果比例中两个比例内项相等,即比例为厂万(或a:b=b:C时,我们把b叫做a和d的比例中项。
8、比例线段:对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即-=-(或a: b=c: d),那么,这四条线段叫做成比例线段,简称比例线段。
(注总:在求线段比时,线段单位b d 要统一,单位不统一应先化成同一单位)(2)比例性质1.基本性质:— = — <=> Cld = beb d(两外项的积等于两内项积)a Cb dFd GC (把比的前项、后项交换)2.反比性质:3•更比性质(交换比例的内项或外项):-=^(交换内项)C a(交换外项)b d b a侗时交换内外项)C a4.合比性质:?=匚=P =仝L(分子加(减)分母,分母不变)b d b d■注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项.后项之间b _ a _ d _ C发生同样和差变化比例仍成立.⅛∣:- = -^ " C .b d a_b _c_d.a + b c + d5•等比性质:(分子分母分别相加,比值不变•)a Ce m Zt f G …a+ c + e + ・・• + 〃】a如果—=—=—= ・・・ =—(b + d + / +・-• + n ≠ 0),那么---------------------- =—.b Clf n/? + 〃 + /+ ・• + 〃/?注意:⑴此性质的证明运用r “设£法”,这种方法是有关比例汁算,变形中一种常用方法.(2)应用等比性质时.要考虑到分母是否为零・(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立. 知识点三:黄金分割Λ C RCD定义:在线段AB上,点C把线段/1B分成两条线段AC和BC (AC> BC),如果—=—•即AC⅛A AB AC BxBC,那么称线段AB彼点C黄金分割,点C叫做线段SB的黄金分割点,SC与AB的比叫做黄金√5-1比。
第27章相似三角形知识点总结及典型题目精选全文完整版

可编辑修改精选全文完整版相似三角形知识点总结1. 比例线段的有关概念:b、d叫后项,d叫第四比例项,如果b=c,那么b叫做a、d的比例中项。
把线段AB分成两条线段AC和BC,使AC2=AB·BC,叫做把线段AB黄金分割,C叫做线段AB的黄金分割点。
2. 比例性质:3. 平行线分线段成比例定理:①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l1∥l2∥l3。
②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
4. 相似三角形的判定:①两角对应相等,两个三角形相似②两边对应成比例且夹角相等,两三角形相似③三边对应成比例,两三角形相似④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角形相似⑤平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似⑥直角三角形被斜边上的高分成的两个直角三角形和原三角形相似5. 相似三角形的性质①相似三角形的对应角相等②相似三角形的对应边成比例③相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比 ④相似三角形周长的比等于相似比⑤相似三角形面积的比等于相似比的平方一.选择题:1、下列各组数中,成比例的是( )A .-7,-5,14,5B .-6,-8,3,4C .3,5,9,12D .2,3,6,122、如果x:(x+y)=3:5,那么x:y =( )A. B. C. D. 3、如图,F 是平行四边形ABCD 对角线BD 上的点,BF ∶FD=1∶3,则BE ∶EC=( ) A 、21 B 、31 C 、32 D 、41 4、下列说法中,错误的是( )(A )两个全等三角形一定是相似形 (B )两个等腰三角形一定相似 (C )两个等边三角形一定相似 (D )两个等腰直角三角形一定相似5、如图,RtΔABC 中,∠C=90°,D 是AC 边上一点,AB =5,AC =4,若ΔABC∽ΔBDC,则CD = . A .2 B .32 C .43 D .94二、填空题6、已知a =4,b =9,c 是a b 、的比例中项,则c = .7、如图,要使ΔABC∽ΔACD,需补充的条件是 .(只要写出一种)8、如图,小东设计两个直角,来测量河宽DE ,他量得AD =2m ,BD =3m ,CE =9m ,则河宽DE 为ABCD(第7题)238332589、一公园占地面积约为8000002m ,若按比例尺1∶2000缩小后,其面积约为 2m .10、如图,点P 是R tΔABC 斜边AB 上的任意一点(A 、B 两点除外)过点P 作一条直线,使截得的三角形与RtΔABC 相似,这样的直线可以作 条. 三、解答题11、如图18—95,AB 是斜靠在墙壁上的长梯,梯脚B 距墙80cm ,梯上点D 距墙70cm ,BD 长55cm .求梯子的长.12、如图,已知AC⊥AB,BD⊥AB,AO =78cm ,BO =42cm ,CD =159cm ,求CO 和DO .13、如图,在正方形网格上有111C B A ∆∽222A C B ∆,这两个三角形相似吗?如果相似,求出222111A C B A C B ∆∆和的面积比.CBAP(第10题)14、已知:如图,在△ABC 中,点D 、E 、F 分别在AC 、AB 、BC 边上,且四边形CDEF 是正方形,AC =3,BC =2,求△ADE、△EFB、△ACB 的周长之比和面积之比.15、如图所示,梯形ABCD 中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB 上确定点P 的位置,使得以P,A,D 为顶点的三角形与以P,B,C 为顶点的三角形相似.16、如图,□ABCD 中,:2:3AE EB =,DE 交AC 于F . (1)求AEF ∆与CDF ∆周长之比;(2)如果CDF ∆的面积为220cm ,求AEF ∆的面积.PAB DCABECDF。
九年级数学相似三角形知识点总结及例题讲解

1. 平行线分线段成比例定理
例.
已知 l 1∥ l 2∥ l 3,
A Dl
B El
: 三条平行线截两条直线
1 2
, 所得的 对应线段成比 .
C
Fl
可得 AB
DE AB 或
DE 等.
BC EF AC DF
2. 推论 : 平行于三角形一边的直线截其它两边
3
( 或两边的延长线 ) 所得的对应线段成比例 .
注意 :(1) 此性质的证明运用了“设 k 法” ,这种方法是有关比例计算,变形中一种常用方法.
(2) 应用等比性质时,要考虑到分母是否为零.
(3)
可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.
知识点三:黄金分割
1) 定义 :在线段 AB 上,点 C 把线段 AB 分成两条线段 AC 和 BC(AC>BC ),如果 AC AB
ad bc
(两外项的积等于两内项积)
2. 反比性质:
ac bd
bd a c ( 把比的前项、后项交换 )
3. 更比性质 ( 交换比例的内项或外项 ) :
ac bd
a b ,(交换内项 ) cd d c ,(交换外项 ) ba d b .(同时交换内外项 ) ca
4. 合比性质
a
:
c
bd
ab b
cd (分子加(减)分母 , 分母不变)
例 4、矩形 ABCD 中, BC=3AB , E、F,是 BC 边的三等分点,连结 AE 、 AF 、AC ,问图中是否存在非全 等的相似三角形?请证明你的结论。
二、如何应用相似三角形证明比例式和乘积式
例 5、△ ABC 中,在 AC 上截取 AD ,在 CB 延长线上截取 BE ,使 AD=BE ,求证: DF AC=BC FE
相似三角形基本知识点+经典例题(完美打印版)

相似三角形基本知识点+经典例题(完美打印版)相似三角形基本知识点+经典例题一、相似三角形的定义和性质相似三角形是指具有相同形状但大小不同的三角形。
它们的对应角度相等,对应边长成比例。
以下是相似三角形的基本知识点和性质:1. 相似三角形的定义:如果两个三角形对应角相等,且对应边成比例,则它们是相似三角形。
2. 相似三角形的性质:a. 对应角相等:两个相似三角形的对应角是相等的。
b. 对应边成比例:两个相似三角形的对应边的比值相等。
3. 相似三角形的判定条件:a. AA判定:如果两个三角形的两对对应角相等,则它们是相似三角形。
b. AAA判定:如果两个三角形的对应角相等,则它们是相似三角形。
二、相似三角形的比例关系相似三角形的对应边长之间存在一定的比例关系。
如果两个三角形是相似的,则对应边的比值相等。
以∆ABC∼∆DEF为例,A与D为对应顶角,AB与DE、BC与EF、AC与DF分别为对应边长。
则有以下比例关系:AB/DE = BC/EF = AC/DF三、相似三角形的应用相似三角形在几何学中有广泛的应用,下面通过一些经典例题来进一步了解相似三角形的应用。
例题一:已知∆ABC与∆DBC是相似三角形,AB = 3cm, BC = 4cm, AC = 5cm, DB = 2cm,求DC的长度。
解析:根据相似三角形的性质,可以得到以下比例关系:AB/DB = AC/DC3/2 = 5/DCDC = 10/5 = 2cm因此,DC的长度为2cm。
例题二:在平行四边形ABCD中,∠B的度数是∠D的度数的2倍。
若AB= 10cm,BC = 15cm,求AD的长度。
解析:由于ABCD是平行四边形,所以∠B = ∠D。
根据题目条件可得:∠B = 2∠D∠B + ∠D = 180°(平行四边形的内角和为180°)将∠B代入上式得:2∠D + ∠D = 180°3∠D = 180°∠D = 60°由相似三角形的性质可得AB/AD = BC/CD,代入已知值可得:10/AD = 15/CD将CD表示为AD的式子,并代入已知条件可得:10/AD = 15/(2AD)10AD = 30AD = 3cm因此,AD的长度为3cm。
相似三角形(含练习有答案、例题和知识点)

第27章:相似一、基础知识(一).比例1.第四比例项、比例中项、比例线段;2.比例性质:(1)基本性质:bc ad d c b a =⇔= ac b c bb a =⇔=2 (2)合比定理:d dc b b ad c b a ±=±⇒= (3)等比定理:)0.(≠+++=++++++⇒==n d b ban d b m c a n m d c b a3.黄金分割:如图,若AB PB PA ⋅=2,则点P 为线段AB 的黄金分割点.4.平行线分线段成比例定理(二)相似1.定义:我们把具有相同形状的图形称为相似形.2.相似多边形的特性:相似多边的对应边成比例,对应角相等.3.相似三角形的判定● (1)平行于三角形一边的直线与其它两边相交,所构成的三角形与原三角形相似。
● (2)如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
● (3)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
● (4)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
4.相似三角形的性质● (1)对应边的比相等,对应角相等. ● (2)相似三角形的周长比等于相似比.● (3)相似三角形的面积比等于相似比的平方.● (4)相似三角形的对应边上的高、中线、角平分线的比等于相似比. 5.三角形中位线定义:连接三角形两边中点的线段 叫做三角形的中位线. 三角形中位线性质: 三角形的中位线平行于第三边,并且等于它的一半。
6.梯形的中位线定义:梯形两腰中点连线叫做梯形的中位线.梯形的中位线性质: 梯形的中位线平行于两底并且等于两底和的一半. 7.相似三角形的应用:1、利用三角形相似,可证明角相等;线段成比例(或等积式); 2、利用三角形相似,求线段的长等3、利用三角形相似,可以解决一些不能直接测量的物体的长度。
如求河的宽度、求建筑物的高度等。
(三)位似:位似:如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形。
相似三角形经典练习题及答案

相似三角形经典练习题及答案一、选择题1、若两个相似三角形的面积之比为 1∶4,则它们的周长之比为()A 1∶2B 1∶4C 1∶5D 1∶16答案:A解析:相似三角形面积的比等于相似比的平方,相似三角形周长的比等于相似比。
因为两个相似三角形的面积之比为 1∶4,所以相似比为 1∶2,那么它们的周长之比为 1∶2。
2、如图,在△ABC 中,点 D、E 分别在边 AB、AC 上,DE∥BC,若 AD∶DB = 1∶2,则下列结论中正确的是()A AE∶EC = 1∶2B AE∶EC = 1∶3 C DE∶BC = 1∶2 DDE∶BC = 1∶3答案:B解析:因为 DE∥BC,所以△ADE∽△ABC。
因为 AD∶DB =1∶2,所以 AD∶AB = 1∶3。
因为相似三角形对应边成比例,所以AE∶AC = AD∶AB = 1∶3,所以 AE∶EC = 1∶2。
3、已知△ABC∽△A'B'C',相似比为 3∶4,△ABC 的周长为 6,则△A'B'C'的周长为()A 8B 7C 9D 10答案:A解析:因为相似三角形周长的比等于相似比,所以△ABC 与△A'B'C'的周长之比为3∶4。
设△A'B'C'的周长为x,则6∶x =3∶4,解得 x = 8。
4、如图,在△ABC 中,D、E 分别是 AB、AC 上的点,且DE∥BC,如果 AD = 2cm,DB = 1cm,AE = 15cm,则 EC =()A 05cmB 1cmC 15cmD 3cm答案:B解析:因为 DE∥BC,所以△ADE∽△ABC,所以 AD∶AB =AE∶AC。
因为 AD = 2cm,DB = 1cm,所以 AB = 3cm。
所以 2∶3= 15∶(15 + EC),解得 EC = 1cm。
5、下列各组图形一定相似的是()A 两个直角三角形B 两个等边三角形C 两个菱形D 两个矩形答案:B解析:等边三角形的三个角都相等,都是 60°,所以两个等边三角形一定相似。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形知识点及典型例题知识点归纳:1、三角形相似的判定方法(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
简述为:两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
简述为:两边对应成比例且夹角相等,两三角形相似。
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
简述为:三边对应成比例,两三角形相似。
(6)判定直角三角形相似的方法:①以上各种判定均适用。
②如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
③直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
#直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(AD)2=BD·DC,(2)(AB)2=BD·BC ,(3)(AC)2=CD·BC 。
注:由上述射影定理还可以证明勾股定理。
即(AB)2+(AC)2=(BC)2。
典型例题:例1 如图,已知等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ‖AB ,BG 分别交AD ,AC 于E 、 F ,求证:BE2=EF·EG 证明:如图,连结EC ,∵AB =AC ,AD ⊥BC , ∴∠ABC =∠ACB ,AD 垂直平分BC ∴BE =EC ,∠1=∠2,∴∠ABC-∠1=∠ACB-∠2, 即∠3=∠4,又CG ∥AB ,∴∠G =∠3,∴∠4=∠G又∵∠CEG =∠CEF ,∴△CEF ∽△GEC ,∴EG CE =CE EF∴EC 2=EG· EF,故EB 2=EF·EG 【解题技巧点拨】本题必须综合运用等腰三角形的三线合一的性质,线段的垂直平分线的性质和相似三角形的基本图形来得到证明.而其中利用线段的垂直平分线的性质得到BE=EC ,把原来处在同一条直线上的三条线段BE ,EF ,EC 转换到相似三角形的基本图形中是证明本题的关键。
例2 已知:如图,AD 是Rt △ABC 斜BC 上的高,E 是AC 的中点,ED 与AB 的延长线相交于F ,求证:BA FB =AC FD证法一:如图,在Rt △ABC 中,∵∠BAC =Rt ∠,AD ⊥BC , ∴∠3=∠C ,又E 是Rt △ADC 的斜边AC 上的中点,∴ED=21AC =EC ,∴∠2=∠C ,又∠1=∠2,∴∠1=∠3, ∴∠DFB =∠AFD ,∴△DFB ∽△AFD ,∴FD FB =AD BD(1)又AD 是Rt △ABC 的斜边BC 上的高,∴Rt △ABD ∽Rt △CAD ,∴AD BD =AC BA(2) 由(1)(2)两式得FD FB =AC BA ,故BA FB =AC FD证法二:过点A 作AG ∥EF 交CB 延长线于点G ,则BA FB =AG FD(1)∵E 是AC 的中点,ED ∥AC ,∴D 是GC 的中点,又AD ⊥GC ,∴AD 是线段GC 的垂直平分线,∴AG =AC (2)由(1)(2)两式得:BA FB =AC FD,证毕。
【解题技巧点拨】本题证法中,通过连续两次证明三角形相似,得到相应的比例式,然后通过中间比“AD BD”过渡,使问题得证,证法二中是运用平行线分线段成比例定理的推论,三角形的中位线的判定,线段的垂直平分线的判定与性质使问题得证.一、如何证明三角形相似例1、如图:点G 在平行四边形ABCD 的边DC 的延长线上,AG 交BC 、BD 于点E 、F ,则△AGD ∽ ∽ 。
例2、已知△ABC 中,AB=AC ,∠A=36°,BD 是角平分线, 求证:△ABC ∽△BCD例3:已知,如图,D 为△ABC 内一点连结ED 、AD ,以BC 为边在△ABC 外作 ∠CBE=∠ABD ,∠BCE=∠BAD 求证:△DBE ∽△ABC例4、矩形ABCD 中,BC=3AB ,E 、F ,是BC 边的三等分点,连结AE 、AF 、AC ,问图中是否存在非全等的相似三角形?请证明你的结论。
二、如何应用相似三角形证明比例式和乘积式例5、△ABC 中,在AC 上截取AD ,在CB 延长线上截取BE ,使AD=BE ,求证:DF •AC=BC •FE例6:已知:如图,在△ABC 中,∠BAC=900,M 是BC 的中点,DM ⊥BC 于点E ,交BA 的延长线于点D 。
求证:(1)MA 2=MD •ME ;(2)MD MEADAE =22例7:如图△ABC 中,AD 为中线,CF 为任一直线,CF 交AD 于E ,交AB 于F ,求证:AE :ED=2AF :FB 。
三、如何用相似三角形证明两角相等、两线平行和线段相等。
ABCDEM12A B C D E FG1234A B C DAB CDEF K A B C D E F例8:已知:如图E 、F 分别是正方形ABCD 的边AB 和AD 上的点,且31==AD AF AB EB 。
求证:∠AEF=∠FBD例9、在平行四边形ABCD 内,AR 、BR 、CP 、DP 各为四角的平分线, 求证:SQ ∥AB ,RP ∥BC例10、已知A 、C 、E 和B 、F 、D 分别是∠O 的两边上的点,且AB ∥ED ,BC ∥FE ,求证:AF ∥CD例11、直角三角形ABC 中,∠ACB=90°,BCDE 是正方形,AE 交BC 于F ,FG ∥AC 交AB 于G ,求证:FC=FG例12、Rt △ABC 锐角C 的平分线交AB 于E ,交斜边上的高AD 于O ,过O 引BC 的平行线交AB 于F ,求证:AE=BFAB C DE FG A B C DS P RQ OA B C D EFABCDEFO 123A BC DF G E课后作业一、填空题1.已知:在△ABC 中,P 是AB 上一点,连结 CP ,当满足条件∠ACP=____或∠APC= _____或 AC 2=______时, △ACP ∽△ABC .2.两个相似三角形周长之比为4∶9,面积之和为291,则面积分别是____________。
3.如图,DEFG 是Rt △ABC 的内接正方形,若CF =8,DG =42,则BE =__________。
4.如图,直角梯形 ABCD 中,AD ‖BC ,AD ⊥CD ,AC ⊥AB ,已知AD =4,BC =9,则 AC =____________。
5.△ABC 中,AB =15,AC =9,点D 是AC 上的点,且AD=3,E 在AB 上,△ADE 与△ABC 相似,则AE 的长等于_____________。
6.如图,在正方形网格上画有梯形ABCD ,则∠BDC 的度数为______________。
7.△ABC 中,AB =AC ,∠A =36°,BC =1,BD 平分∠ABC 交于D ,则BD =_______,AD =______,设AB =x,则关于x 的方程是______________.8.如图,已知D 是等边△ABC 的BC 边上一点,把△ABC 向下折叠,折痕为MN ,使点A 落在点D 处,若BD ∶DC =2∶3,则AM ∶MN=_________________。
二、选择题9.如图,在正△ABC 中,D 、E 分别在AC 、AB 上,且31AC AD ,AE=BE ,则有() A .△AED ∽△BEDB .△AED ∽△CBDC .△AED ∽△ABDD .△BAD ∽△BCD10.如图,在△ABC 中,D 为AC 边上一点,∠DBC =∠A ,BC=6,AC =3,则CD 的长为( ) A.1B.23 C.2 D.25 11.如图,□ABCD 中,G 是 BC 延长线上一点,AG 与 BD 交于点E ,与DC 交于点F ,则图中相似三角形共有( ) A .3对 B .4对 C .5对 D .6对12. P 是Rt △ABC 的斜边BC 上异于B 、C 的一点,过点P 作直线截△ABC ,使截得的三角形与△ABC 相似,满足这样条件的直线共有( ) A .1条 B.2条 C .3条 D .4条13.如图,在直角梯形 ABCD 中,AB =7,AD =2,BC=3,若在 AB 上取一点P ,使以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似,这样的P点有()A.1个B.2个C.3个D.4个三、解答下列各题14.如图,长方形ABCD中,AB=5,BC=10,点P从A点出发,沿AB作匀速运动,1分钟可以到达B点,点Q从B点出发,沿BC作匀速直线运动,1分钟可到C点,现在点P点Q同时分别从A点、B点出发,经过多少时间,线段PQ恰与线段BD垂直?15.已知:如图,正方形DEFG内接于Rt△ABC,EF在斜边BC上,EH⊥AB于H.求证:(1)△ADG≌△HED;(2)EF2=BE·FC(答案)例1分析:关键在找“角相等”,除已知条件中已明确给出的以外,还应结合具体的图形,利用公共角、对顶角及由平行线产生的一系列相等的角。
本例除公共角∠G外,由BC∥AD可得∠1=∠2,所以△AGD∽△EGC。
再∠1=∠2(对顶角),由AB∥DG可得∠4=∠G,所以△EGC∽△EAB。
例2分析:证明相似三角形应先找相等的角,显然∠C是公共角,而另一组相等的角则可以通过计算来求得。
借助于计算也是一种常用的方法。
证明:∵∠A=36°,△ABC是等腰三角形,∴∠ABC=∠C=72°又BD平分∠ABC,则∠DBC=36°在△ABC和△BCD中,∠C为公共角,∠A=∠DBC=36°∴△ABC∽△BCD例3分析:由已知条件∠ABD=∠CBE,∠DBC公用。
所以∠DBE=∠ABC,要证的△DBE和△ABC,有一对角相等,要证两个三角形相似,或者再找一对角相等,或者找夹这个角的两边对应成比例。
从已知条件中可看到△CBE∽△ABD,这样既有相等的角,又有成比例的线段,问题就可以得到解决。
证明:在△CBE和△ABD中,∠CBE=∠ABD, ∠BCE=∠BAD∴△CBE∽△ABD∴BCAB=BEBD即:BCBE=ABBD△DBE和△ABC中,∠CBE=∠ABD, ∠DBC公用∴∠CBE+∠DBC=∠ABD+∠DBC∴∠DBE=∠ABC且BCBE=ABBD∴△DBE∽△ABC例4分析:本题要找出相似三角形,那么如何寻找相似三角形呢?下面我们来看一看相似三角形的几种基本图形:(1)如图:称为“平行线型”的相似三角形(2)如图:其中∠1=∠2,则△ADE∽△ABC称为“相交线型”的相似三角形。
