理论力学课件力偶
合集下载
理论力学B第二章力偶

若:作用在刚体上 作用在刚体上
{F , F2 ,⋯, Fn} 1
{FR}
则: n MO (FR ) = ∑MO (F ) i
i=1
A C B E D
§2-1
力矩 (moment of a force)
二.力对轴之矩(moment of a force about an axis) 力对轴之矩
z Fz F o d F Fxy Fxy
(B)
N
1、研究OA杆 、研究 杆
2、研究AB杆 、研究 杆
例:已知 AB=2a BD=a,不计摩擦。求:当θ=π/2, BD=a,不计摩擦 不计摩擦。 /2, /3时 系统平衡力偶M 应满足的关系。 π/3时,系统平衡力偶M1 、M2 应满足的关系。
M2
B C D B D C
θ
A
M1
A
θ=π/2时: M1 = 5M2 /2时
方向
§2-3、力偶系作用下刚体的平衡
(Equilibrium of Rigid Bodies Applied by a System of Couples)
平衡的充分必要条件
{ M 1 , M 2 ,⋯ , M n } = { M
R
} = {0}
x y z
即:MR = ∑Mi = 0
i=1
n
∑M ∑M ∑M
{F , F ' } ≠ {FR }
性质二 力偶可在其作用面内任意移动(或移到 力偶可在其作用面内任意移动(
另一平行平面),而不改变对刚体的作用 另一平行平面),而不改变对刚体的作用 ),
⇔
⇔
§2-2
2、力偶的性质
力偶 (Couples)
三、力偶的等效条件和性质
{F , F2 ,⋯, Fn} 1
{FR}
则: n MO (FR ) = ∑MO (F ) i
i=1
A C B E D
§2-1
力矩 (moment of a force)
二.力对轴之矩(moment of a force about an axis) 力对轴之矩
z Fz F o d F Fxy Fxy
(B)
N
1、研究OA杆 、研究 杆
2、研究AB杆 、研究 杆
例:已知 AB=2a BD=a,不计摩擦。求:当θ=π/2, BD=a,不计摩擦 不计摩擦。 /2, /3时 系统平衡力偶M 应满足的关系。 π/3时,系统平衡力偶M1 、M2 应满足的关系。
M2
B C D B D C
θ
A
M1
A
θ=π/2时: M1 = 5M2 /2时
方向
§2-3、力偶系作用下刚体的平衡
(Equilibrium of Rigid Bodies Applied by a System of Couples)
平衡的充分必要条件
{ M 1 , M 2 ,⋯ , M n } = { M
R
} = {0}
x y z
即:MR = ∑Mi = 0
i=1
n
∑M ∑M ∑M
{F , F ' } ≠ {FR }
性质二 力偶可在其作用面内任意移动(或移到 力偶可在其作用面内任意移动(
另一平行平面),而不改变对刚体的作用 另一平行平面),而不改变对刚体的作用 ),
⇔
⇔
§2-2
2、力偶的性质
力偶 (Couples)
三、力偶的等效条件和性质
第二章平面汇交力系及平面力偶系

一、几何法合成(作图法)
1、两力的合成方法——平行四边形法则。
2、多个力的合成。方法——力多边形法 则(依据平行四边形法则)。将汇交
力系各力平行移至首尾相接,起点至
第
终点连线为合力。
一 章
静 力 学 基 础
理论力学教学课件
第一节 平面汇交力系的合成
一、几何法(作图法)
F1
R12
O
F2
F3
R123
同理 :Ry= F1y+ F2y+ F3y
R FX 2 Fy 2
第二节 平面汇交力系合成的解析法
例 用 解 析 法 求 三 力 的 合 力 。 已 知 F1=100N ,
F2=200N,F3=300N 。
F1
45°
O
F2
解:F1X=F1COS45°=71N F1y=F1sin45°=71N F2X=F2=200N
静 力
自行封闭。
学 基
础
第二节 平面汇交力系的合成与 平衡的解析法
一、解析法合成(计算 ) 1、力在直角坐标轴上的投影
y
a’
A
αF
B
b’
oa
b
x
ab:F在x轴上的投影(Fx). a’b’:F在y轴上的投影(Fy)。
Fx=ab=Fsinα
第
一
Fy=a’ b’= - Fcosα
章
静 力 学 基 础
第二节 平面汇交力系合成的解析法
解:据平衡方程:ΣFx=0 ΣFy=0
ΣFy=-P- FD cos30°-FCBsin30°=0 FCB=-74.6 KN (BC杆受压) ΣF x=-FAB - FD sin30°FCBcos30°=0 FAB =54.6 KN (AB杆受拉)
1、两力的合成方法——平行四边形法则。
2、多个力的合成。方法——力多边形法 则(依据平行四边形法则)。将汇交
力系各力平行移至首尾相接,起点至
第
终点连线为合力。
一 章
静 力 学 基 础
理论力学教学课件
第一节 平面汇交力系的合成
一、几何法(作图法)
F1
R12
O
F2
F3
R123
同理 :Ry= F1y+ F2y+ F3y
R FX 2 Fy 2
第二节 平面汇交力系合成的解析法
例 用 解 析 法 求 三 力 的 合 力 。 已 知 F1=100N ,
F2=200N,F3=300N 。
F1
45°
O
F2
解:F1X=F1COS45°=71N F1y=F1sin45°=71N F2X=F2=200N
静 力
自行封闭。
学 基
础
第二节 平面汇交力系的合成与 平衡的解析法
一、解析法合成(计算 ) 1、力在直角坐标轴上的投影
y
a’
A
αF
B
b’
oa
b
x
ab:F在x轴上的投影(Fx). a’b’:F在y轴上的投影(Fy)。
Fx=ab=Fsinα
第
一
Fy=a’ b’= - Fcosα
章
静 力 学 基 础
第二节 平面汇交力系合成的解析法
解:据平衡方程:ΣFx=0 ΣFy=0
ΣFy=-P- FD cos30°-FCBsin30°=0 FCB=-74.6 KN (BC杆受压) ΣF x=-FAB - FD sin30°FCBcos30°=0 FAB =54.6 KN (AB杆受拉)
理论力学13力偶与力偶矩

习题: P.29 1-15、1-16
2020/4/30
19
谢谢大家!
2020/4/30
20
理论力学
主讲
广东海洋大学寸金学院
庞雪飞
2020/4/30
1
1.3 力偶与力偶矩
F =-F′
F' F
2020/4/30
2
F =-F′
■力偶的定义
F
两个大小相等、
作用线不重合的反
向平行力组成的力
系称为力偶
F′
(couple)。
2020/4/30
3
力偶中两个力的作
用线所确定的平面称 为力偶的作用面
(acting plane of a couple),二力作用线 之间的垂直距离d称 为力偶臂(couple arm)。
x
黑版手书计算上例。
2020/4/30
17
练习
如图汽缸盖上4个相同的 孔,每个孔的切削力偶矩大 小为M1=M2=M3=M4=15 N.m。
求工件的总切削力偶矩
解:根据 M Mi 可得
M2
M1
M4
M3
M M 1 M 2 M 3 M 4
415 60N .m 负号表示合力偶矩的转向为顺时针方向
2020/4/30
8
d1 M=F0×d1=F×d
平面问题
由于力偶的作用面总是与力系所在的平面 重合,力偶矩由矢量变成代数量
M = Fd
正负号用来区别 转向,通常规定: 逆时针为正 顺时针为负
+–
这里的逆时针或顺时针转向是指物体在力偶的作用下转
动202的0/4/方30 向。
10
■力偶是最简单的力系之一
工程力学 04力偶系.ppt

Theoretical Mechanics
§3-1、力对点之矩矢
(3)力对点之矩矢的基本性质 作用于刚体上的二力对刚体产生的绕一点的转动效应, 可以用该点的一个矩矢来度量,这个矩矢等于二力分别 对该点之矩矢的矢量和。
即 MO =MO (F1 )+MO (F2 )
推广:力系(F1,F2,- - -,Fn)对刚体产生的绕一点的
(2)力F与z轴相交
2019年11月10日星期日
理论力学
Theoretical Mechanics
§3-2、力对轴之矩
5.力对任意l 轴(方向l°)之矩
Ml (F) MA(F)l
A为l 轴上任意一点
z
F
M A(F)
r l轴
y
对任意l 轴之矩的几何意义
A
l x
定理:力对点的矩矢在通过该点的任意轴上的投影等于这力
§3-1、力对点之矩矢
力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
一.平面力系中力对点之矩(代数量)
简称力矩
1.现象
2.定义 M0 F F d
F
o 力矩中心
d 力臂
力矩作用面
两个要素:
大小:力F与力臂的乘积 方向:转动方向
2019年11月10日星期日
同理:
Mx(F)= Fz y Fy z
My(F ) = Fx z Fz x
2019年11月10日星期日
理论力学
Theoretical Mechanics
§3-2、力对轴之矩 空间力对点的矩与空间力对轴的矩的关系(力矩关系定理):
Mo (F )x yFz zFy M x (F )
§3-1、力对点之矩矢
(3)力对点之矩矢的基本性质 作用于刚体上的二力对刚体产生的绕一点的转动效应, 可以用该点的一个矩矢来度量,这个矩矢等于二力分别 对该点之矩矢的矢量和。
即 MO =MO (F1 )+MO (F2 )
推广:力系(F1,F2,- - -,Fn)对刚体产生的绕一点的
(2)力F与z轴相交
2019年11月10日星期日
理论力学
Theoretical Mechanics
§3-2、力对轴之矩
5.力对任意l 轴(方向l°)之矩
Ml (F) MA(F)l
A为l 轴上任意一点
z
F
M A(F)
r l轴
y
对任意l 轴之矩的几何意义
A
l x
定理:力对点的矩矢在通过该点的任意轴上的投影等于这力
§3-1、力对点之矩矢
力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
一.平面力系中力对点之矩(代数量)
简称力矩
1.现象
2.定义 M0 F F d
F
o 力矩中心
d 力臂
力矩作用面
两个要素:
大小:力F与力臂的乘积 方向:转动方向
2019年11月10日星期日
同理:
Mx(F)= Fz y Fy z
My(F ) = Fx z Fz x
2019年11月10日星期日
理论力学
Theoretical Mechanics
§3-2、力对轴之矩 空间力对点的矩与空间力对轴的矩的关系(力矩关系定理):
Mo (F )x yFz zFy M x (F )
力矩和力偶PPT课件

3、力矩 的计算公式
MO(F) = ± F ·r
F ——力的大小
O点—— 矩心;
r ——力臂
力臂 r
F
第6页,共34页。
●力矩的转向
●力矩的转向 (正负号±)
—— 规定:力使物体绕矩心作逆时针方向转动,
力矩取正号,反之取负号。
逆时针 +
r
顺时针 -
第7页,共34页。
思考 ? 公式:MO(F) = ± F ·r
任务 二: 实例 --- 练习册P15 2 - 70
力矩的计算公式: (根据力矩的定义)
MO(F) = ±F ·r
r
r= L MO(F) = + F ·r
= F ·L
r= 0
r = L ·sina
MO(F) = 0
MO(F)= +F ·r
= F ·L ·sina
力的作用线通过矩心时, 力臂 r = 0
--- 其大小、转向 与矩心的选择有关。 2)力偶矩 M = ± Fd
--- 其大小、转向与矩心无关。
r
第21页,共34页。
力的平移定理
F Od
F' F
Od
F' M Od
F''
M = + Fd = MO(F)
平移定理:作用于刚体上的力,可平移到刚体上的任一点, 但必须附加一力偶,其附加力偶矩等于原力对平移点的 力矩 。
分析单手用丝锥攻螺纹
动画
第24页,共34页。
§2-3 平衡方程及应用
1、平衡方程的定义、意义。
2、力在坐标轴上的投影。 3、建立平衡方程,求出未知力。
第25页,共34页。
一、平面受力时的解析表示法
理论力学第3章-力偶系

例 3-1 图示机构,各杆自重不计,在两力偶作用下处于平 衡。已知:M1 = 100 N · m,O1A = 40 cm,O2B = 60 cm。 试求力偶矩M2的大小。 B A FB F B FA
30 o
B
O1
B
A FA M2
M1 FO1 O1 A M1
M
2
O2
O2
FO2
解:取O1A杆为研究对象,受力如图所示,
若两个力偶对刚体的作用效应相同,则称这二力 偶等效。
两力偶的等效条件 :力偶矩矢相等,即
M1 M2
(3-2) FR'
B'
证明:
A'
FR F1 FR F'
A B
FR' F1'
F
力偶(FR,FR' ) 代了原力偶(F,F' ) 并与原力偶等效。
A'
FR
FR'
B'
D F' C
比较(F,F')和(FR,FR')可得 M(F,F')=2△ABD=M(FR,FR') =2 △ABC
合力偶矩矢的大小和方向余弦为
M ( M x )2 ( M y )2 ( M z )2 (280)2 1602 (800)2 862.55 kN m
M cos( M , i )
280 0.3246 M 862.55 My 160 cos( M , j ) 0.1855 M 862.55
1 3 200 280kN m 5 5 4 M y M y M 1 y M 2 y 0 200 160kN m 5 2 M z M z M1z M 2 z 400 5 0 800kN m 5 M x M x M1x M 2 x 400 5
理论力学课件第2章 力偶

解: AB、BC杆为二力杆,取滑轮B (或点B),画受力图.建图示 坐标系
F
x
0
F B A F 1 co s 6 0 F 2 co s 3 0 0
F
y
0 F F co s 3 0 F co s 6 0 0 BC 1 2
F1 F 2 P
F B A 7 . 321 kN F BC 2 7 . 3 2 kN
l
§2-2 平面力偶
课堂练习 下面哪个图中的力系与图 (a)等效?
10N
9N· m
15N
0.4m
3N· m
15N 0.6m (A)
0.4m
0.6m 10N (a)
5N
0.6m (B)
5N
7.5N
0.3m
0.4m
7.5N 0.6m (C)
合力的大小为: 方向为:
FR FR x FR y
2
2
Fix cos( FR , i ) FR
Fiy cos( FR , j ) FR
作用点为力的汇交点.
四、平面汇交力系的平衡方程
平衡条件 平衡方程
FR 0
Fx 0
Fy
0
例2-1 已知: P 20 kN, R 0.6 m, h 0.08 m 求:
第 二 章 平面汇交力系与平面力偶系
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩 2. 合力矩定理
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩(力矩)
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩(力矩)
z
B O 矩心 O
理论力学:力偶系

ND
M2
A
2020/12/9
M1 BDND sin
M 2 ADND
M1
BD AD
M2
sin
M2
A NA
22
理论力学
§2-3 空间一般力系简化
z
F1
F2 F3
o
y
x Fi Fn
•空间一般力系(general noncoplanar force system ): 力作用线在空间任意分布的力系
? 问题: {F1, F2,, Fn} {FR , MO}
F' F
F
MO MO(F) MO(F') rA F rB F '
B rBA
A d
F’
rB
rA
O
rA F rB (F ) (rA rB ) F rBA F
M dF
M
注:力偶矩矢量垂直于力偶所在的平 面,其大小和方向与取矩点无关。
B rBA
F’
F A
2020/12/9
16
理论力学
MO
{F1, F2,, Fn} {F1', F2 ', , Fn ', M1, M2, , Mn} {FR , MO}
FR 一个作用在O点上的力, MO 一个作用在刚体上的力偶
n
n
•主矢 FR Fi Fi '
i1
i1
(与简化点无关)
•主矩
n
n
MO Mi ri Fi
i 1
i 1
(与简化点有关)
n
根据牛顿第二定律有 ma Fi FR
n
i1
结论:力系中 Fi 是反映其作用效应的物理量之一
M2
A
2020/12/9
M1 BDND sin
M 2 ADND
M1
BD AD
M2
sin
M2
A NA
22
理论力学
§2-3 空间一般力系简化
z
F1
F2 F3
o
y
x Fi Fn
•空间一般力系(general noncoplanar force system ): 力作用线在空间任意分布的力系
? 问题: {F1, F2,, Fn} {FR , MO}
F' F
F
MO MO(F) MO(F') rA F rB F '
B rBA
A d
F’
rB
rA
O
rA F rB (F ) (rA rB ) F rBA F
M dF
M
注:力偶矩矢量垂直于力偶所在的平 面,其大小和方向与取矩点无关。
B rBA
F’
F A
2020/12/9
16
理论力学
MO
{F1, F2,, Fn} {F1', F2 ', , Fn ', M1, M2, , Mn} {FR , MO}
FR 一个作用在O点上的力, MO 一个作用在刚体上的力偶
n
n
•主矢 FR Fi Fi '
i1
i1
(与简化点无关)
•主矩
n
n
MO Mi ri Fi
i 1
i 1
(与简化点有关)
n
根据牛顿第二定律有 ma Fi FR
n
i1
结论:力系中 Fi 是反映其作用效应的物理量之一
力偶系教学课件PPT

M x (F ) Fzb Fb sin M y (F ) Fza Fa sin
M z (F ) Fy a Fxb
Fb cos sin Fa cos cos
MO(F) Mx(F) i M y(F) j Mz(F)k
Fbsin i Fa sin j (Fb cos sin Fa cos cos ) k
合成结果:
M Mi
平衡条件:
Mi = 0
例 题 2 已知:a, M
求:A、 C 处约束反力。
M
B
a
解:(1)取AB为研究对象
M 0, M FA 2a 0
FA
FB
2 2a
M
(2)取BC为研究对象
FC
FB
FB
2 2a
M
A
a
C
a
FB
M
FA
A
B B
FB
C
FC
若将此力偶移至BC构件上,再求A、C处约束反力。在
例 题 3 已知: F 、 a、b、c
求: 力F 对OA轴之矩 解:(1)计算 MO(F)
i jk MO(F) r F 0 b 0
00F Fbi
(2)利用力矩关系
z
O
b x
MOA (F ) MO (F ) cos
Fab a2 b2 c2
AF
c ay
例题4
已知: OA=OB=OC =b, OA⊥OB⊥OC. 求:力 F 对OA 边的中点D之矩在AC方向的投影。
“+ ”—— 使物体逆时针转时力矩为正; “-” —— 使物体顺时针转时力矩为负。
§3-1 平面力对点之矩的概念和计算
2.合力矩定理
平面汇交力系合力对于平面内一点之矩等于所有各分力对于 该点之矩的代数和。
M z (F ) Fy a Fxb
Fb cos sin Fa cos cos
MO(F) Mx(F) i M y(F) j Mz(F)k
Fbsin i Fa sin j (Fb cos sin Fa cos cos ) k
合成结果:
M Mi
平衡条件:
Mi = 0
例 题 2 已知:a, M
求:A、 C 处约束反力。
M
B
a
解:(1)取AB为研究对象
M 0, M FA 2a 0
FA
FB
2 2a
M
(2)取BC为研究对象
FC
FB
FB
2 2a
M
A
a
C
a
FB
M
FA
A
B B
FB
C
FC
若将此力偶移至BC构件上,再求A、C处约束反力。在
例 题 3 已知: F 、 a、b、c
求: 力F 对OA轴之矩 解:(1)计算 MO(F)
i jk MO(F) r F 0 b 0
00F Fbi
(2)利用力矩关系
z
O
b x
MOA (F ) MO (F ) cos
Fab a2 b2 c2
AF
c ay
例题4
已知: OA=OB=OC =b, OA⊥OB⊥OC. 求:力 F 对OA 边的中点D之矩在AC方向的投影。
“+ ”—— 使物体逆时针转时力矩为正; “-” —— 使物体顺时针转时力矩为负。
§3-1 平面力对点之矩的概念和计算
2.合力矩定理
平面汇交力系合力对于平面内一点之矩等于所有各分力对于 该点之矩的代数和。
理论力学2—平面汇交力系与平面力偶系.ppt

M
i 1
n
i
0
思考题1
刚体上A、B、C、D四点组成一个平行四边形,如在其 四个顶点作用有四个力,此四力沿四个边恰好组成封闭 的力多边形,如图所示。此刚体是否平衡?
F1
B
A
F4
D
F2
C
F3
思考题2
从力偶理论知道,一力不能与力偶平衡。图示轮子上的 力P为什么能与M平衡呢?
M
O R
FO
P
[例3] 在一钻床上水平放置工件,在工件上同时钻四个等直径 的孔,每个钻头的力偶矩为 m1 m2 m3 m4 15Nm ,求工件的
2. 合力矩定理与力矩的解析表达式
(1) 合力矩定理
平面汇交力系的合力对于平面内任一点之矩等于 所有各分力对于该点之矩的代数和。
M O (F R ) M O (F i )
i 1
n
y
Fy
A
O x y
F
q
(2) 力矩的解析表达式
M O ( F ) xF sin q yF cos q xFy yFx
2. 同平面内力偶的等效定理定理
定理:在同平面内的两个力偶,如果力偶矩相等,则两力偶彼 此等效。 推论: (1) 任一力偶可以在它的作用面内 任意移转,而不改变它对刚体的作 用。因此,力偶对刚体的作用与力 偶在其作用面内的位置无关。 (2) 只要保持力偶矩的大小和力偶 的转向不变,可以同时改变力偶中 力的大小和力偶臂的长短,而不改 变力偶对刚体的作用。
Fi 0
在平衡的情形下,力多边形中最后一力的 终点与第一力的起点重合,此时的力多边形称 为封闭的力多边形。于是,平面汇交力系平衡 的必要与充分条件是:该力系的力多边形自行 封闭,这是平衡的几何条件。
02-4.3 平面力对点的矩和平面力偶(课件)

面称为力矩作用面
• O到力的作用线的垂直距 离 h称为力臂
•力F 使物体绕O点的转动效果,完全 由两个要素决定: a. 大小:力F与力臂h的乘积 F·h b. 转向:使物体绕O点转动方向
用数学式子来表示:
MO (F ) F h
F
O
h
平面力对点之矩是一个代数量, 它的绝对值等于力的大小与力臂 的乘积,它的正负:力使物体绕 矩心逆时针转向时为正,反之为 负.常用单位N.m或kN.m
3平面力对点的矩和平面力偶平面汇交力系和平面力偶系3力偶由两个大小相等等值方向相反反向不共线的平行力组成的力系称为力偶记作力偶和力一样是力学中的一个基本要素
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(1)平面力对点的矩
3、平面力对点的矩和平面力偶
• O称为矩心 • O与力矢量的首尾确定的平
力偶矩是平面力偶作用的唯一度量
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
ቤተ መጻሕፍቲ ባይዱ
平面汇交力系和平面力偶系
(2)合力矩定理与力矩的解析表达式
MO(FR ) MO (Fi )
合力矩定理:平面汇交力系的合力对平面内任一点的矩等于各分力对该点 的矩的代数和。
该结论适用于任何存在合力的力系!
y
力矩的解析表达式:
MO(F) MO(Fy ) MO(Fx ) x F sin θ y F cos θ xFy yFx
M F d 2 AABC
两个要素 a. 大小:力与力偶臂乘积
b. 转向:作用面内的转动方向
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(5)同平面内力偶的等效定理
定理:在同一平面内的两个力偶,如果力偶矩相等,则两力偶彼此相等。 推论(1):力偶可在其作用面内任意移转,而不改变它对刚体的作用。力偶对 刚体的作用与力偶在其作用面内的位置无关。 推论(2):只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力 的大小与力偶臂的长短,对刚体的作用效果不变。
• O到力的作用线的垂直距 离 h称为力臂
•力F 使物体绕O点的转动效果,完全 由两个要素决定: a. 大小:力F与力臂h的乘积 F·h b. 转向:使物体绕O点转动方向
用数学式子来表示:
MO (F ) F h
F
O
h
平面力对点之矩是一个代数量, 它的绝对值等于力的大小与力臂 的乘积,它的正负:力使物体绕 矩心逆时针转向时为正,反之为 负.常用单位N.m或kN.m
3平面力对点的矩和平面力偶平面汇交力系和平面力偶系3力偶由两个大小相等等值方向相反反向不共线的平行力组成的力系称为力偶记作力偶和力一样是力学中的一个基本要素
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(1)平面力对点的矩
3、平面力对点的矩和平面力偶
• O称为矩心 • O与力矢量的首尾确定的平
力偶矩是平面力偶作用的唯一度量
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
ቤተ መጻሕፍቲ ባይዱ
平面汇交力系和平面力偶系
(2)合力矩定理与力矩的解析表达式
MO(FR ) MO (Fi )
合力矩定理:平面汇交力系的合力对平面内任一点的矩等于各分力对该点 的矩的代数和。
该结论适用于任何存在合力的力系!
y
力矩的解析表达式:
MO(F) MO(Fy ) MO(Fx ) x F sin θ y F cos θ xFy yFx
M F d 2 AABC
两个要素 a. 大小:力与力偶臂乘积
b. 转向:作用面内的转动方向
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(5)同平面内力偶的等效定理
定理:在同一平面内的两个力偶,如果力偶矩相等,则两力偶彼此相等。 推论(1):力偶可在其作用面内任意移转,而不改变它对刚体的作用。力偶对 刚体的作用与力偶在其作用面内的位置无关。 推论(2):只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力 的大小与力偶臂的长短,对刚体的作用效果不变。
理论力学__第3章__力偶理论

图
3.3
3.1 力对点之矩
有
M O ( F R ) = rA o × F R = rA o × ( ∑ Fi )
∑ (r =∑ M
=
Ao O
× Fi ) ( Fi )
(3.5)
可见,汇交力系的合力对任一点之矩矢等于各分力对 汇交力系的合力对任一点之矩矢等于各分力对 同一点之矩矢的矢量和,称为汇交力系合力矩定理 汇交力系合力矩定理。 同一点之矩矢的矢量和 汇交力系合力矩定理
3.2 力对轴之矩
设有通过坐标原点O 的任一轴 ζ,其单位矢量ζ0,ζ轴在坐标 系Oxyz中的方向余弦为 l 、m、 n,如图3.7所示。应用力矩关系 定理求得力F 对于ζ轴的矩为
3.1 力对点之矩
1.平面力系中力对点之矩 1.平面力系中力对点之矩 人们从实践中知道力除了 能使物体移动外,还能使物体 转动。而力矩的概念是人们在 使用杠杆、滑轮、绞盘等简单 机械搬运或提升重物时逐渐形 成的。下面以用扳手拧螺帽为 例说明力矩的概念(图3.1)。
图
3.1
3.1 力对点之矩
实践表明,作用在扳手上 A 点的力 F 能使扳手 绕O 点(即绕通过 O 点并垂直于图面的轴)发生转动。 而这种转动效应不仅与力 F 的大小成正比,而且与力 的作用线到 O 点的垂直距离 h 成正比,亦即与乘积 成正比。另外,力 F 使扳手绕 O 点转动的方向不同, F ⋅h 作用效果也不同。因此,规定 冠以适当的正负 F ⋅h 号作为力 F 使物体绕 O 点发生转动效应的度量,称 点之矩。用符号MO(F)表示,即 为力 F 对 O 点之矩 力
M z ( F ) = M O ( Fxy ) = ± Fxy h
(3.7)
3.2 力对轴之矩
理论力学课件 力偶、力系简化
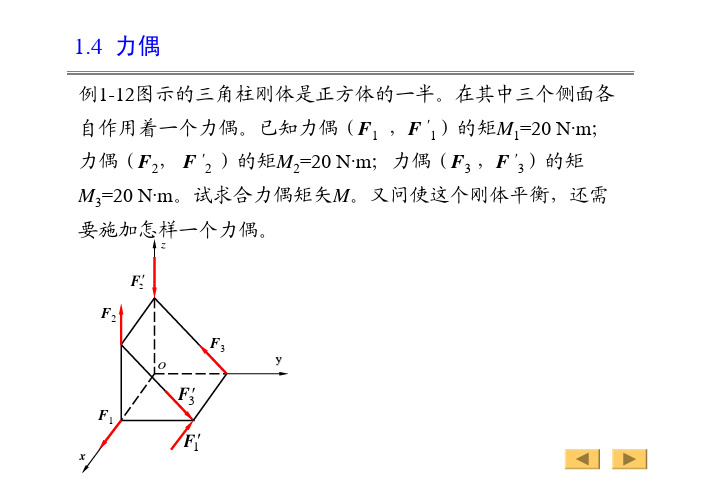
Fy
M = 0.5 kN ⋅ m
M
合力的大小
O
FR′ = (∑ X )2 + (∑Y )2 = 4.662 kN
y
x
Fx C
A
B
合力的方向
α
=
arctan
∑Y ∑X
= arctan 0.768 4.598
= 9.35°
M
FR′
O
α
x C
1.5 力系的简化
3、该力系的最后合成结果。
FvR′
⋅
v M
=
一、力平移定理
B
F=
A
F″ B A
F′
F=
F′ MB
A
定理:作用在刚体上点A的力F平行移到任 一点B,但必须同时附加一个力偶,这个附加 力偶的矩等于原来的力F对新作用点B的矩。
1.5 力系的简化
B
F=
A
F′ MB
A
1、力的平移定理揭示,当力和力偶互相垂直
一个力和力—力偶系统等效
v F
⋅
v M
=
0
⇔
F1 FR
zA r1 rC O
F2 C
B r2
y
x
思考:平行力系同时旋转个角度, 平行力系中心变不变?
不变;平行力系中心只和力 系的大小和作用点有关,与 方向无关.
1.6 重心、平行分布力
F1 FR zA r1 rC O
F2 C
B r2
y
对O点应用合力矩定理.
rv1
×
v F1
+
rv2
×
v F2
=
rvC
0
力和力偶矩矢量互相垂直,最后合成结果是一个合力FR。
理论力学-力偶系PPT课件

力偶系在物理实验中的应用
扭摆实验
扭摆实验是一种用于研究力矩和角动量守恒的经典实验。在实验 中,通过测量不同质量的物体在相同力矩作用下的转动周期,可 以验证力矩与转动惯量的关系,从而进一步理解力偶系的概念。
扭摆实验中,力偶系的作用是提供稳定的力矩,使得物体能够进 行稳定的摆动。通过调整力矩的大小,可以观察到摆动周期的变 化,从而验证力矩对转动惯量的影响。
车辆动力学中的力偶系
总结词
影响车辆性能的关键因素
详细描述
在车辆动力学中,力偶系对车辆的性 能产生重要影响。例如,在汽车悬挂 系统和转向系统中,力偶系的设计直 接关系到车辆的操控性能、行驶稳定 性以及乘坐舒适性。
04
力偶系与刚体平衡
刚体的平衡条件
刚体的平衡条件是合外力为零,即所有外力的矢量 和为零。
06
力偶系理论的发展与展望
力偶系理论的现代发展
计算机技术的引入
利用计算机进行数值模拟和计算,提高了力偶系理 论的计算效率和精度。
非线性力偶系的研究
随着对非线性现象的深入了解,非线性力偶系的研 究逐渐成为热点。
多物理场耦合的力偶系研究
考虑多个物理场之间的相互作用,研究多物理场耦 合下的力偶系特性。
03
力偶系在工程中的应用
机械系统中的力偶系
总结词
重要组成部分
详细描述
在机械系统中,力偶系是实现各种运 动和操作的关键因素。例如,在齿轮 传动、链传动等机械系统中,力偶系 的作用是实现扭矩的传递和转换。
建筑结构中的力偶系
总结词
稳定性与安全性的保障
详细描述
在建筑结构中,力偶系是维持结构稳定性和安全性的重要因 素。通过合理设计梁、柱等结构件的力偶系,可以确保建筑 在承受各种载荷时仍能保持稳定。
扭摆实验
扭摆实验是一种用于研究力矩和角动量守恒的经典实验。在实验 中,通过测量不同质量的物体在相同力矩作用下的转动周期,可 以验证力矩与转动惯量的关系,从而进一步理解力偶系的概念。
扭摆实验中,力偶系的作用是提供稳定的力矩,使得物体能够进 行稳定的摆动。通过调整力矩的大小,可以观察到摆动周期的变 化,从而验证力矩对转动惯量的影响。
车辆动力学中的力偶系
总结词
影响车辆性能的关键因素
详细描述
在车辆动力学中,力偶系对车辆的性 能产生重要影响。例如,在汽车悬挂 系统和转向系统中,力偶系的设计直 接关系到车辆的操控性能、行驶稳定 性以及乘坐舒适性。
04
力偶系与刚体平衡
刚体的平衡条件
刚体的平衡条件是合外力为零,即所有外力的矢量 和为零。
06
力偶系理论的发展与展望
力偶系理论的现代发展
计算机技术的引入
利用计算机进行数值模拟和计算,提高了力偶系理 论的计算效率和精度。
非线性力偶系的研究
随着对非线性现象的深入了解,非线性力偶系的研 究逐渐成为热点。
多物理场耦合的力偶系研究
考虑多个物理场之间的相互作用,研究多物理场耦 合下的力偶系特性。
03
力偶系在工程中的应用
机械系统中的力偶系
总结词
重要组成部分
详细描述
在机械系统中,力偶系是实现各种运 动和操作的关键因素。例如,在齿轮 传动、链传动等机械系统中,力偶系 的作用是实现扭矩的传递和转换。
建筑结构中的力偶系
总结词
稳定性与安全性的保障
详细描述
在建筑结构中,力偶系是维持结构稳定性和安全性的重要因 素。通过合理设计梁、柱等结构件的力偶系,可以确保建筑 在承受各种载荷时仍能保持稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合力偶矩等于各分力偶矩的代数和。
M Mi
§2-2 平面力偶
5. 平面力偶系的平衡条件 平面力偶系平衡的必要和充分条件是:所有
各力偶矩的代数和等于零。
Mi 0
注意:力偶只能由力偶来平衡!!
§2-2 平面力偶
例题 3
如图所示,工件上作用有三个 力偶, M1=M2=10N·m, M3=20N·m,l=200mm. 计算 两个螺拴A,B处的光滑水平 约束反力。
§2-1 平面汇交力系
一、平面汇交力系合成的几何法--力多边形规则
FR1 F1 F2
FR 2
FR 1
FR 3
3
F
i 1
i
11
FR1 F1 F2 3
FR2 FR1 FR3 Fi i 1
.. . .. . .. .
n
FR FRn1 Fn Fi i 1
2.欲将轮子拉过障碍物,水平拉力 F至 少多大?
3.力
F沿什么方向拉动轮子最省力,及此时力
多F 大??
解: 1.取碾子,画受力图. 用几何法,按比例画封闭力四边形
θ arccos R h 30 R
FA 11.4kN
FB sin θ F
FB 10kN
FA FB cos θ P 用解析法如何求解?
解: 用解析法
F Rx F ix F1 c o s 3 0 F 2 c o s 6 0 F3 c o s 4 5 F 4 c o s 4 5 1 2 9 .3 N F Ry F iy F1 sin 3 0 F 2 sin 6 0 F3 sin 4 5 F 4 sin 4 5 1 1 2 .3 N
§2-2 平面力偶
3. 平面内的等效力偶
下面的变化不会改变力偶的作用效果:
F
F
F'
F
F'
F'
在平面内移动 在平面内转动
改变力的大小以及力偶臂 d的 大小,但是保持两者的乘积 Fd 不变.
§2-2 平面力偶
表示力偶的常用图形符号
F
M M
F'
§2-2 平面力偶
4. 平面力偶系的合成 平面内的任意个力偶可以合成为一个合力偶,
FR
F2 Rx
F2 Ry
171.3N
F cos θ Rx 0.7548
FR F cos β Ry 0.6556 F
R
θ 40.99 , β 49.01
例2-4 已知:系统如图,不计杆、轮自重,忽略滑轮大小, P=20kN;
求:系统平衡时,杆AB,BC受力.
解: AB、BC杆为二力杆,取滑轮B (或点B),画受力图.建图示
1. 力对点的矩(力矩)
z
B F
Od
r
y
A
B
F
O
d
r
A
x
r Radius Vector 矢径
矢量:MO F r F
大小: MO (F ) r F
r F r F sin ~ r 和 F 的夹角
§2-2 平面力对点之矩的概念和计算
2 Varignon 定理 (合力矩定理)
坐标系
Fx 0 FBA F1 cos 60 F2 cos 30 0
Fy 0 F F cos30 F cos60 0
BC
1
2
F F P
1
2
F 7.321kN BA
F 27.32kN BC
例2-5 已知: F=3kN, l=1500mm, h=200mm,忽略自重; 求:平衡时,压块C对工件与地面的压力,AB杆受力.
Fix FR
作用点为力的汇交点.
F2 Rx
F2 Ry
cos( FR
,
j)
Fiy FR
四、平面汇交力系的平衡方程
平衡条件
FR 0
平衡方程
Fx 0
Fy 0
例2-1
已知: P 20kN, R 0.6m, h 0.08m
求:
1.水平拉力 F 5时kN,轮子对地面及障碍物的压力?
平面汇交力系的合力对平面内 任意一点的矩等于各分力对该点之 矩的代数和。
Pierre Varignon 法国数学家 1654~1722
§2-2 平面力对点之矩的概念和计算
2 Varignon 定理 (合力矩定理)
MO (F ) MO (F1) MO (F 2 ) ...... MO (F n )
q
A
B
l
§2-2 平面力对点之矩的概念和计算
[解] 1. 计算合力的大小 FR a,研究对象; b,取微元体
c,选定坐标轴或者力矩正向(重要),向下为正,逆时针
为正
A x
qx
FR
q
B
l dx
qx
qx l
dFx
q
x l
dx
FR
l
0 dFx
lx q dx 0l
qx2 xl 2l
第三次课
第二章 平面力系
第 二 章 平面力系 §2-1 平面汇交力系合成与平衡的几何法 平面汇交力系合成与平衡的解析法
汇交力系:若所有力的作用线交于一点,则该力系称为汇 交力系。
第 二 章 平面力系
§2-1 平面汇交力系合成与平衡的几何法 1、平面汇交力系合成的几何法——力多边形规则 2、平面汇交力系平衡的几何条件
A M1 M3 M2
B
l
§2-2 平面力偶
[解] 选择工件作为研究对象 注意:力偶只能由力偶来平衡!!
A M1 M3 M2
l l
FA
B
A
M1 M3 M2B NhomakorabeaFBFA FB
M 0 FAl M1 M 2 M3 0
FA
M1
M2 l
M3
10 10 20 200N
§2-1 平面汇交力系合成与平衡的几何法
力的多边形规则:
共点力系可以合成为一个力,合 力作用在力系的公共作用点,它等 于这些力的矢量和,并可由这力系 的力多边形的封闭边表示。
二、平面汇交力系平衡的几何条件
平衡条件 Fi 0
平面汇交力系平衡的必要和充分条件是:
该力系的力多边形自行封闭.
2 Cx
2h
Fy 0 F C B s in F C y 0
FCy 1.5kN
作业2:习题2-4, 2-5
第 二 章 平面汇交力系与平面力偶系
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩 2. 合力矩定理
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩(力矩)
小结
1、汇交力系的合力 (1)几何法求合力
力多边形法则
(2)解析法求合力
FR FR2x FR2y 0
cos(FR , i) FRx / FR cos(FR , j) FRy / FR
第 二 章 平面汇交力系与平面力偶系
小结
2、汇交力系的合力平衡条件
汇交力系平衡的几何条件:
力多边形自行封闭
汇交力系平衡的解析条件:
FR FR2x FR2y 0
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩(力矩)
z
矩心 O
B F
O
O d d : 力臂 y
矩心 O
A
B F
d d : 力臂
A
x
MO (F ) Fd 2AOAB
单位 : N m 或 kN m
符号 绕矩心旋转: 逆时针 “+” 顺时针 “-”
§2-2 平面力对点之矩的概念和计算
力对刚体的作用效应:
位移 转动
力矢量 力矩
§2-2 平面力对点之矩的概念和计算
例题 1 求力 F 对点 O 和 A 的矩
F
a
B
b
O
A
a
§2-2 平面力对点之矩的概念和计算
[解]
F
a
MO F F d
是否容易计算力臂 d ?
B
d
b
O
A
a
§2-2 平面力对点之矩的概念和计算
[解]
MO F M O Fx M O Fy
0.2
§2-2 平面力偶
课堂练习 下面哪个图中的力系与图 (a)等效?
10N
9N·m
3N·m
15N
0.4m
0.4m
0.4m
0.6m
15N 10N
0.6m (A)
(a)
5N
7.5N
0.6m
(B) 5N
0.3m
0.4m
0.4m
7.5N
0.6m
(C)
5N
0.6m
5N
(D)
7.5N·m
第 二 章 平面汇交力系与平面力偶系
F
a Fy
Fxb Fya
F sina b F cosa a
Fx
B
M AF M AFx M A Fy
b
Fxb 0
F sina b
O
A
a
§2-2 平面力对点之矩的概念和计算
例题 2
三角形分布载荷作用在水平梁AB上,如图所示,最大载 荷集度为q ,梁长l , 试求该力系的合力。
h
ql 2 3
FR
M Mi
§2-2 平面力偶
5. 平面力偶系的平衡条件 平面力偶系平衡的必要和充分条件是:所有
各力偶矩的代数和等于零。
Mi 0
注意:力偶只能由力偶来平衡!!
§2-2 平面力偶
例题 3
如图所示,工件上作用有三个 力偶, M1=M2=10N·m, M3=20N·m,l=200mm. 计算 两个螺拴A,B处的光滑水平 约束反力。
§2-1 平面汇交力系
一、平面汇交力系合成的几何法--力多边形规则
FR1 F1 F2
FR 2
FR 1
FR 3
3
F
i 1
i
11
FR1 F1 F2 3
FR2 FR1 FR3 Fi i 1
.. . .. . .. .
n
FR FRn1 Fn Fi i 1
2.欲将轮子拉过障碍物,水平拉力 F至 少多大?
3.力
F沿什么方向拉动轮子最省力,及此时力
多F 大??
解: 1.取碾子,画受力图. 用几何法,按比例画封闭力四边形
θ arccos R h 30 R
FA 11.4kN
FB sin θ F
FB 10kN
FA FB cos θ P 用解析法如何求解?
解: 用解析法
F Rx F ix F1 c o s 3 0 F 2 c o s 6 0 F3 c o s 4 5 F 4 c o s 4 5 1 2 9 .3 N F Ry F iy F1 sin 3 0 F 2 sin 6 0 F3 sin 4 5 F 4 sin 4 5 1 1 2 .3 N
§2-2 平面力偶
3. 平面内的等效力偶
下面的变化不会改变力偶的作用效果:
F
F
F'
F
F'
F'
在平面内移动 在平面内转动
改变力的大小以及力偶臂 d的 大小,但是保持两者的乘积 Fd 不变.
§2-2 平面力偶
表示力偶的常用图形符号
F
M M
F'
§2-2 平面力偶
4. 平面力偶系的合成 平面内的任意个力偶可以合成为一个合力偶,
FR
F2 Rx
F2 Ry
171.3N
F cos θ Rx 0.7548
FR F cos β Ry 0.6556 F
R
θ 40.99 , β 49.01
例2-4 已知:系统如图,不计杆、轮自重,忽略滑轮大小, P=20kN;
求:系统平衡时,杆AB,BC受力.
解: AB、BC杆为二力杆,取滑轮B (或点B),画受力图.建图示
1. 力对点的矩(力矩)
z
B F
Od
r
y
A
B
F
O
d
r
A
x
r Radius Vector 矢径
矢量:MO F r F
大小: MO (F ) r F
r F r F sin ~ r 和 F 的夹角
§2-2 平面力对点之矩的概念和计算
2 Varignon 定理 (合力矩定理)
坐标系
Fx 0 FBA F1 cos 60 F2 cos 30 0
Fy 0 F F cos30 F cos60 0
BC
1
2
F F P
1
2
F 7.321kN BA
F 27.32kN BC
例2-5 已知: F=3kN, l=1500mm, h=200mm,忽略自重; 求:平衡时,压块C对工件与地面的压力,AB杆受力.
Fix FR
作用点为力的汇交点.
F2 Rx
F2 Ry
cos( FR
,
j)
Fiy FR
四、平面汇交力系的平衡方程
平衡条件
FR 0
平衡方程
Fx 0
Fy 0
例2-1
已知: P 20kN, R 0.6m, h 0.08m
求:
1.水平拉力 F 5时kN,轮子对地面及障碍物的压力?
平面汇交力系的合力对平面内 任意一点的矩等于各分力对该点之 矩的代数和。
Pierre Varignon 法国数学家 1654~1722
§2-2 平面力对点之矩的概念和计算
2 Varignon 定理 (合力矩定理)
MO (F ) MO (F1) MO (F 2 ) ...... MO (F n )
q
A
B
l
§2-2 平面力对点之矩的概念和计算
[解] 1. 计算合力的大小 FR a,研究对象; b,取微元体
c,选定坐标轴或者力矩正向(重要),向下为正,逆时针
为正
A x
qx
FR
q
B
l dx
qx
qx l
dFx
q
x l
dx
FR
l
0 dFx
lx q dx 0l
qx2 xl 2l
第三次课
第二章 平面力系
第 二 章 平面力系 §2-1 平面汇交力系合成与平衡的几何法 平面汇交力系合成与平衡的解析法
汇交力系:若所有力的作用线交于一点,则该力系称为汇 交力系。
第 二 章 平面力系
§2-1 平面汇交力系合成与平衡的几何法 1、平面汇交力系合成的几何法——力多边形规则 2、平面汇交力系平衡的几何条件
A M1 M3 M2
B
l
§2-2 平面力偶
[解] 选择工件作为研究对象 注意:力偶只能由力偶来平衡!!
A M1 M3 M2
l l
FA
B
A
M1 M3 M2B NhomakorabeaFBFA FB
M 0 FAl M1 M 2 M3 0
FA
M1
M2 l
M3
10 10 20 200N
§2-1 平面汇交力系合成与平衡的几何法
力的多边形规则:
共点力系可以合成为一个力,合 力作用在力系的公共作用点,它等 于这些力的矢量和,并可由这力系 的力多边形的封闭边表示。
二、平面汇交力系平衡的几何条件
平衡条件 Fi 0
平面汇交力系平衡的必要和充分条件是:
该力系的力多边形自行封闭.
2 Cx
2h
Fy 0 F C B s in F C y 0
FCy 1.5kN
作业2:习题2-4, 2-5
第 二 章 平面汇交力系与平面力偶系
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩 2. 合力矩定理
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩(力矩)
小结
1、汇交力系的合力 (1)几何法求合力
力多边形法则
(2)解析法求合力
FR FR2x FR2y 0
cos(FR , i) FRx / FR cos(FR , j) FRy / FR
第 二 章 平面汇交力系与平面力偶系
小结
2、汇交力系的合力平衡条件
汇交力系平衡的几何条件:
力多边形自行封闭
汇交力系平衡的解析条件:
FR FR2x FR2y 0
§2-2 平面力对点之矩的概念和计算
1. 力对点的矩(力矩)
z
矩心 O
B F
O
O d d : 力臂 y
矩心 O
A
B F
d d : 力臂
A
x
MO (F ) Fd 2AOAB
单位 : N m 或 kN m
符号 绕矩心旋转: 逆时针 “+” 顺时针 “-”
§2-2 平面力对点之矩的概念和计算
力对刚体的作用效应:
位移 转动
力矢量 力矩
§2-2 平面力对点之矩的概念和计算
例题 1 求力 F 对点 O 和 A 的矩
F
a
B
b
O
A
a
§2-2 平面力对点之矩的概念和计算
[解]
F
a
MO F F d
是否容易计算力臂 d ?
B
d
b
O
A
a
§2-2 平面力对点之矩的概念和计算
[解]
MO F M O Fx M O Fy
0.2
§2-2 平面力偶
课堂练习 下面哪个图中的力系与图 (a)等效?
10N
9N·m
3N·m
15N
0.4m
0.4m
0.4m
0.6m
15N 10N
0.6m (A)
(a)
5N
7.5N
0.6m
(B) 5N
0.3m
0.4m
0.4m
7.5N
0.6m
(C)
5N
0.6m
5N
(D)
7.5N·m
第 二 章 平面汇交力系与平面力偶系
F
a Fy
Fxb Fya
F sina b F cosa a
Fx
B
M AF M AFx M A Fy
b
Fxb 0
F sina b
O
A
a
§2-2 平面力对点之矩的概念和计算
例题 2
三角形分布载荷作用在水平梁AB上,如图所示,最大载 荷集度为q ,梁长l , 试求该力系的合力。
h
ql 2 3
FR
