(完整版)电力系统分析大作业matlab三机九节点潮流计算报告

合集下载

三机九节点潮流暂态MATLAB仿真

三机九节点潮流暂态MATLAB仿真院系: 自动化学院专业:电力系统及其自动化学号: 姓名: 时间: 1 研究对象1.1 三机九节点系统模型100MW35MVar7239j0.0585j0.06250.0119 + j0.10080.0085 + j0.072B/2 = j0.1045B/2 = j0.0745230/13.818/23018kV13.8kV8230kV230kVB/2 = j0.179B/2 = j0.088B/2 = j0.1530.010 + j0.0850.032 + j0.161 56125MW90MW50MVar30MVarB/2 = j0.079230kV40.017 + j0.0790.039 + j0.170j0.057616.5/23016.5kV1图1.1 WSCC-9系统模型图1.1是一个三机九节点的系统阻抗图，图中给出的阻抗参数都是以100MVA为基准的标幺值。

该图中包括三台发电机，三台双绕组变压器，九条母线(节点)和三个负荷。

本文将对该系统的动态过程进行相应的仿真分析。

1.2 系统参数1.2.1 节点参数按照节点类型，9个节点分为，给出已知参数如下表:表1.1 节点已知参数节点类型电压幅值电压角度发电机有功发电机无功负荷有功负荷无功1 Vθ 1.040 0 0.7160 0.2705 0 02 PV 1.025 1.6300 0.0665 0 03 PV 1.025 0.8500 -0.1086 0 04 PQ 0 05 PQ 1.2500 0.50006 PQ 0.9000 0.30007 PQ 0 08 PQ 1(0000 0.35009 PQ 0 0上表中发电机有功、无功出力和负荷的有功无功功率均为以100MVA为基准时的标幺值。

1.2.2 支路参数表1.2 支路参数首节点末节点电阻电抗电纳一半4 5 0.0100 0.0850 0.08804 6 0.0170 0.0920 0.07905 7 0.0320 0.1610 0.15306 9 0.0390 0.1700 0.17907 8 0.0085 0.0720 0.07458 9 0.0119 0.1008 0.10451 4 0.0000 0.0576 0.00002 7 0.0000 0.0625 0.00003 9 0.0000 0.0586 0.0000上表中所有的参数均为标幺值，对于变压器支路。

电力系统三节点潮流算例

for m=1:8
for n=1:8
JJ(m,n)=H(m,n);
end
end
for m=1:8
for n=1:6
JJ(m,n+8)=N(m,n);
end
end
for m=1:6
for n=1:8
%雅克比i不等于j
for m=1:8
for n=1:9
Ai(n)=U(n)*(G(m+1,n)*sin(a(m+1)-a(n))-B(m+1,n)*cos(a(m+1)-a(n)));
end
H(m,m)=U(m+1)*U(m+1)*B(m+1,m+1)+U(m+1)*sum(Ai);
format long
A=[1 4 0 0.0576 0;
2 7 0 0.0625 0;
3 9 0 0.0586 0;
4 5 0.01 0.085 0.088;
4 6 0.017 0.092 0.079;
5 7 0.032 0.161 0.153;
6 9 0.039 0.17 0.179;
end
end
z=inv(y);
line=z(:,4);
If=u(4)/z(4,4);
for m=1:9
uu(m)=u(m)-line(m)*If;
end
for m=1:9
hang=A(m,:);
Y=zeros(2,2);
if hang(1)>3 && hang (2)>3
L(m,n)=-U(m+3)*U(n+3)*(G(m+3,n+3)*sin(a(m+3)-a(n+3))-B(m+3,n+3)*cos(a(m+3)-a(n+3)));

matlab三机九节点电力系统仿真（带程序）

matlab三机九节点电力系统仿真（带程序）三机九节点电力系统暂态仿真学院：专业：学号：姓名：授课教师：一、摘要电力系统仿真计算己经成为电力系统设计、运行与控制中不可缺少的手段。

通过设置不同故障类型、不同故障地点运用仿真技术可以对电力系统的暂态稳定进行分析。

本文采用IEEE 3机9节点的经典多机模型，基于隐式梯形积分法对系统发生三相金属性短路故障进行仿真，分析系统在这种情况下的暂态稳定。

发电机模型采用经典的二阶模型;负荷采用恒定阻抗负荷。

在Matlab2010上编写程序进行调试和运行。

电力系统是由不同类型的发电机组、多种电力负荷、不同电压等级的电力网络等组成的十分庞大复杂的动力学系统。

其暂态过渡过程不仅包括电磁方面的过渡过程，而且还有机电方面的过渡过程。

由此可见，电力系统的数学模型是一个强非线性的高维状态方程组。

在动态稳定仿真中使用简单的电力系统模型，通过仿真计算分析说明，此仿真方法可以进行简单的电力系统暂态分析，对提高电力系统暂态稳定具有重要意义。

二、案例本次课程主要应用P. M. Anderson and A. A. Fouad 编写的《Power System Control and Stability 》一书中所引用的Western System Coordinated Council (WSCC)三机九节点系统模型。

系统电路结构拓扑图如下：0.0625j 0.0586j 0.0576j 18/230230/13.816.5/23018KV230KV 230KV230KV13.8KV 16.5KV112233456789A负荷负荷B负荷C 0.00850.072j +/20.0745B j =/20.1045B j =/20.153B j =/20.179B j =/20.088B j =/20.079B j =0.01190.1008j +0.0320.161j +0.0100.085j +0.0390.170j +0.0170.092j +图2-1 3机9节点系统系统数据其中，节点数据如下：节点号有无负载类型电压相角有功负荷无功负荷有功出力无功出力电压基准期望电压N=[1 0 3 1.0400 0.00 0.00 0.00 71.60 27.00 16.50 1.0402 0 2 1.0250 0.00 0.00 0.00 163.00 6.70 18.00 1.0253 0 2 1.0250 0.00 0.00 0.00 85.00 -10.90 13.80 1.0254 0 0 1.0000 0.00 0.00 0.00 0.00 0.00 230.00 1.0265 1 0 1.0000 0.00 125.00 50.00 0.00 0.00 0.00 0.9966 1 0 1.0000 0.00 90.00 30.00 0.00 0.00 0.00 1.0137 0 0 1.0000 0.00 0.00 0.00 0.00 0.00 230.00 1.0268 1 0 1.0000 0.00 100.00 35.00 0.00 0.00 0.00 1.0169 0 0 1.0000 0.00 0.00 0.00 0.00 0.00 230.00 1.032]; %支路数据% 从到电阻电抗容纳类型变比B=[1 4 0.0 0.0576 0.0 1 12 7 0.0 0.0625 0.0 1 13 9 0.0 0.0586 0.0 1 14 5 0.010 0.085 0.176 0 04 6 0.017 0.092 0.158 0 05 7 0.032 0.161 0.306 0 06 9 0.039 0.170 0.358 0 07 8 0.0085 0.072 0.149 0 08 9 0.0119 0.1008 0.209 0 0];发电机数据如下：% 发电机母线Xd Xd' Td0' Xq Xq' Tq0’Tj XfGe=[ 1 1 0.1460 0.0608 8.96 0.0969 0.0969 0 47.28 0.05762 2 0.8958 0.1198 6.00 0.8645 0.1969 0.535 12.80 0.06253 3 1.3125 0.1813 8.59 1.2578 0.2500 0.600 6.02 0.0585];三、仿真框图在仿真之前，首先，应明确仿真的所要到达的结果，即仿真目标:本此仿真的结果主要是得到发电机攻角、转速随时间变化的值，包括故障前、故障中、故障后。

牛拉法潮流计算程序（附3机9节点结果对比）

摘要电力系统潮流计算是研究电力系统稳态运行的一种重要方法,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态,包括各母线的电压、线路的功率分布以及功率损耗等等。

潮流计算主要用于电网规划和静态安全分析，它可为扩建电力网络，以达到规划周期内所需要的输电能力提供依据；也可以对预想事故进行模拟和分析，校核预想事故下的电力系统安全性。

本文简单介绍了牛顿-拉夫逊潮流计算的原理、模型与算法，然后用具体的实例，利用MATLAB对牛顿-拉夫逊法的算法进行了验证。

关键词：电力系统潮流计算牛顿-拉夫逊法 MATLAB一、牛拉法的数学模型对一个N 节点的电力网路，列写节点电压方程，即I =Y V(1.1)式中，I 为节点注入电流列相量，Y 为节点导纳矩阵，V 为节点电压列相量。

由于异地测量的两个电流缺少时间同步信息，以注入功率替换注入电流作为已知量。

即***1+niij j ij j i i i Y V V I V Q P ∙∙===∑(1.2)其中,Y ij =G ij +j B ij ，带入上式，得到有功功率和无功功率方程 P i =V i V j G ij cos θij +B ij sin θij n j =1 (1.3)Q i =V i V j G ij sin θij −B ij cos θij n j =1(1.4)大部分情况下，已知PQ ，求解V θ。

考虑到电网的功率平衡，至少选择一台发电机来平衡全网有功功率，即至少有一个平衡节点，常选择调频或出线较多的发电机作为平衡节点。

具有无功补偿的母线能保持电压幅值恒定，这类节点可作为PV 节点。

潮流计算中节点分类总结如下：已知电力系统有m 个PQ 节点，r 个PV 节点和1个平衡节点，则可以提取m+r 个有功功率方程和m 个无功功率方程，从而求解出m+r 个θ和m 个V ，其余节点的有功和无功可通过式（1.3）、（1.4）求得，这样就完成了潮流计算。

(完整word版)基于Matlab计算程序的电力系统运行分析

课程设计课程名称：电力系统分析设计题目：基于Matlab计算程序的电力系统运行分析学院：电力工程学院专业：电气工程自动化年级：学生姓名：指导教师：日期：教务处制目录前言··1第一章参数计算··2一、目标电网接线图··2二、电网模型的建立··3第二章潮流计算··6一．系统参数的设置··6二．程序的调试··7三、对运行结果的分析··13第三章短路故障的分析计算··15一、三相短路··15二、不对称短路··16三、由上面表对运行结果的分析及在短路中的一些问题··21心得体会··26参考文献··27前言电力系统潮流计算是电力系统分析中的一种最基本的计算，是对复杂电力系统正常和故障条件下稳态运行状态的计算。

潮流计算的目标是求取电力系统在给定运行状态的计算。

即节点电压和功率分布，用以检查系统各元件是否过负荷.各点电压是否满足要求，功率的分布和分配是否合理以及功率损耗等。

对现有电力系统的运行和扩建，对新的电力系统进行规划设计以及对电力系统进行静态和暂态稳定分析都是以潮流计算为基础。

潮流计算结果可用如电力系统稳态研究，安全估计或最优潮流等对潮流计算的模型和方法有直接影响。

在电力系统中可能发生的各种故障中，危害最大且发生概率较高的首推短路故障。

产生短路故障的主要原因是电力设备绝缘损坏。

短路故障分为三相短路、两相短路、单相接地短路及两相接地短路。

其中三相短路时三相电流仍然对称，其余三类短路统成为不对称短路。

短路故障大多数发生在架空输电线路。

电力系统设计与运行时，要采取适当的措施降低短路故障的发生概率。

短路计算可以为设备的选择提供原始数据。

第一章参数计算一、目标电网接线图系统参数表1. 线路参数表线路编号线路型号线路长度（km）线路电阻{Ω/km}线路正序电抗{Ω/km}线路容纳之半{S/km}4-5LGJ-240/301130.0470.41.78×610-4-6LGJ-120/701200.074 1.47×610-说明：线路零序电抗为正序电抗3倍。

电力系统分析潮流实验报告

南昌大学实验报告学生姓名：学号：专业班级：实验类型：□验证□综合■设计□创新实验日期：实验成绩：电力系统潮流计算实验一、实验目的：本实验通过对电力系统潮流计算的计算机程序的编制与调试，获得对复杂电力系统进行潮流计算的计算机程序，使系统潮流计算能够由计算机自行完成，即根据已知的电力网的数学模型（节点导纳矩阵）及各节点参数，由计算程序运行完成该电力系统的潮流计算。

通过实验教学加深学生对复杂电力系统潮流计算计算方法的理解，学会运用电力系统的数学模型，掌握潮流计算的过程及其特点，熟悉各种常用应用软件，熟悉硬件设备的使用方法，加强编制调试计算机程序的能力，提高工程计算的能力，学习如何将理论知识和实际工程问题结合起来。

二、实验内容：编制调试电力系统潮流计算的计算机程序。

程序要求根据已知的电力网的数学模型（节点导纳矩阵）及各节点参数，完成该电力系统的潮流计算，要求计算出节点电压、功率等参数。

1、在各种潮流计算的算法中选择一种，按照计算方法编制程序。

2、将事先编制好的电力系统潮流计算的计算程序原代码由自备移动存储设备导入计算机。

3、在相应的编程环境下对程序进行组织调试。

4、应用计算例题验证程序的计算效果。

三、实验程序：function [e,f,p,q]=flow_out(g,b,kind,e,f)%计算潮流后efpq的终值s=flow(g,b,kind,e,f);k=0;while max(abs(s))>10^-5J=J_out(g,b,kind,e,f);J_ni=inv(J);dv=J_ni*s;l=length(dv)/2;for i=1:le(i)=e(i)-dv(2*i-1);f(i)=f(i)-dv(2*i);ends=flow(g,b,kind,e,f);endl=length(e);for i=1:ls1=0;s2=0;for j=1:ls1=s1+g(i,j)*e(j)-b(i,j)*f(j);s2=s2+g(i,j)*f(j)+b(i,j)*e(j);endp(i)=e(i)*s1+f(i)*s2;q(i)=f(i)*s1-e(i)*s2;endfunction s=flow(g,b,kind,e,f)%计算当前ef与规定的pqv的差值l=length(e);s=zeros(2*l-2,1);for i=1:(l-1)s1=0;s2=0;for j=1:ls1=s1+g(i,j)*e(j)-b(i,j)*f(j);s2=s2+g(i,j)*f(j)+b(i,j)*e(j);ends(2*i-1)=kind(2,i)-e(i)*s1-f(i)*s2;if kind(1,i)==1s(2*i)=kind(3,i)-f(i)*s1+e(i)*s2;elses(2*i)=kind(3,i)^2-f(i)^2-e(i)^2;endendfunction J=J_out(g,b,kind,e,f)%计算节点的雅克比矩阵l=length(e);J=zeros(2*l-2,2*l-2);for i=1:(l-1);if kind(1,i)==1s=PQ_out(g,b,e,f,i);for j=1:(2*l-2)J(2*i-1,j)=s(1,j);J(2*i,j)=s(2,j);endelses=PV_out(g,b,e,f,i);for j=1:(2*l-2)J(2*i-1,j)=s(1,j);J(2*i,j)=s(2,j);endendendfunction pq=PQ_out(g,b,e,f,i)%计算pq节点的雅克比矩阵l=length(e);pq=zeros(2,2*l-2);for j=1:(l-1)if j==is=0;for k=1:ls=s-(g(i,k)*e(k)-b(i,k)*f(k));endpq(1,2*i-1)=s-g(i,i)*e(i)-b(i,i)*f(i); s=0;for k=1:ls=s-(g(i,k)*f(k)+b(i,k)*e(k));endpq(1,2*i)=s+b(i,i)*e(i)-g(i,i)*f(i);s=0;for k=1:ls=s+(g(i,k)*f(k)+b(i,k)*e(k));endpq(2,2*i-1)=s+b(i,i)*e(i)-g(i,i)*f(i); s=0;for k=1:ls=s-(g(i,k)*e(k)-b(i,k)*f(k));endpq(2,2*i)=s+g(i,i)*e(i)+b(i,i)*f(i);elsepq(1,2*j-1)=-(g(i,j)*e(i)+b(i,j)*f(i)); pq(1,2*j)=b(i,j)*e(i)-g(i,j)*f(i);pq(2,2*j)=-pq(1,2*j-1);pq(2,2*j-1)=pq(1,2*j);endendfunction pv=PV_out(g,b,e,f,i)%计算pv节点的雅克比矩阵l=length(e);pv=zeros(2,2*l-2);for j=1:(l-1)if j==is=0;for k=1:ls=s-(g(i,k)*e(k)-b(i,k)*f(k));endpv(1,2*i-1)=s-g(i,i)*e(i)-b(i,i)*f(i); s=0;for k=1:ls=s-(g(i,k)*f(k)+b(i,k)*e(k));endpv(1,2*i)=s+b(i,i)*e(i)-g(i,i)*f(i);pv(2,2*i-1)=-2*e(i);pv(2,2*i)=-2*f(i);elsepv(1,2*j-1)=-(g(i,j)*e(i)+b(i,j)*f(i)); pv(1,2*j)=b(i,j)*e(i)-g(i,j)*f(i);endend%数据输入g=[1.042093 -0.588235 0 -0.453858-0.588235 1.069005 0 -0.4807690 0 0 0-0.453858 -0.480769 0 0.9344627];b=[-8.242876 2.352941 3.666667 1.8910742.352941 -4.727377 0 2.4038463.666667 0 -3.333333 01.8910742.40385 0 4.26159];e=[1 1 1.1 1.05];f=[0 0 0 0];kind=[1 1 2 0-0.3 -0.55 0.5 1.05-0.18 -0.13 1.1 0];[e,f,p,q]=flow_out(g,b,kind,e,f);ef四、例题及运行结果在上图所示的简单电力系统中，系统中节点1、2为PQ节点，节点3为PV节点，节点4为平衡节点，已给定P1s+jQ1s=-0.30-j0.18 P2s+jQ2s=-0.55-j0.13 P3s=0.5 V3s=1.10 V4s=1.05∠0°容许误差ε=10-5节点导纳矩阵：各节点电压：节点 e f v ζ1.0.984637 -0.008596 0.984675 -0.5001722.0.958690 -0.108387 0.964798 -6.4503063. 1.092415 0.128955 1.100000 6.7323474. 1.050000 0.000000 1.050000 0.000000各节点功率：节点P Q1-0.300000 -0.1800002–0.550000 -0.13000030.500000 -0.55130540.367883 0.264698结果：五、思考讨论题1.潮流计算有几种方法？简述各种算法的优缺点。

matlab3机九节点潮流计算

matlab3机九节点潮流计算
由于本人是AI语言模型，无法进行具体的matlab3机九节点潮流计算，以下是一般性的matlab潮流计算步骤，供参考：
1. 构建潮流计算模型，包括发电机、负荷、变压器、线路等元件的参数和拓扑结构。

2. 设计潮流计算算法，一般采用迭代法，如牛顿-拉夫逊法等。

3. 初始化潮流计算，将节点电压和相角初值赋予各节点。

4. 迭代计算，根据节点电压和相角的初值和元件参数，计算各节点电压和相角的变化量，并更新节点电压和相角。

5. 判断精度是否满足要求，若满足则输出结果，否则继续迭代计算。

6. 结束潮流计算。

在具体实现时，需要根据九节点的具体参数和拓扑结构进行修改和优化。

(完整word版)基于MATLAB进行潮流计算

基于MATLAB进行潮流计算学生：王仕龙2011148213指导老师：李咸善摘要：电力系统潮流计算方法有两类，即手算潮流和计算机潮流计算。

手算潮流主要借助于形成简化的等值电路来实现，这种方法尤其适用于规模不大的辐射型电力潮流计算。

计算机潮流计算的实现有两种途径：其一是编程实现网络方程的迭代求解；其二是借助与电力系统分析仿真软件，搭建系统模型来完成潮流计算。

MATLAB具有强大的矩阵运算功能，同时其具有电力系统仿真平台也为直观地实现潮流计算提供了更便捷的手段[1]。

本文是基于MATLAB软件，采用极坐标形式牛顿─拉夫逊法进行潮流计算，为其他形式的潮流计算有借鉴的作用。

关键词：电力系统；计算机潮流计算；MATLAB ；牛顿─拉夫逊法Abstract:The power flow calculation method has two kinds,which are the hand calculation of tidal current and computer power flow calculation.Hand calculation tidal current is mainly realized by means of the formation of simplified equivalent circuit.This method is especially suitable for small scale radiation power flow calculation.There are two ways to realize the computer power flow calculation.The first one is through the programming iteration for solving network equation,the second one is with the help of analysis of power system simulation software to build the system model complete the power flow calculation.The software of MATLAB has strong matrix function,.At the same time,It’s power system simulation platform provides a more convenient means to realize power flow calculation intuitively[1].This paper is based on the software of MATLAB to calculate the power flow calculation by adopting the form of Newton-Raphson method of power flow calculation of polar coordinates.And it can be the role of reference of other forms of power flow calculation.Key words: power system computer; power flow calculation;MATLAB;Newton-Raphson1.计算原理电力系统潮流是指系统中所有运行参数的总体，包括各个母线电压的大小和相位，各个发电机和负荷的功率及电流，以及各个变压器和线路等元件所通过的功率,电流和其中的损耗。

matlab实验电力系统潮流计算

matlab实验电力系统潮流计算电力系统潮流计算是电力系统运行分析的基础，它通过计算电力系统中各节点的电压幅值和相角，以及各支路的功率和电流，来研究电力系统的稳态工作状态。

本文将介绍潮流计算的原理及其在电力系统中的应用。

潮流计算的基本原理是基于电力系统节点间的功率平衡方程，即节点注入功率等于节点负荷消耗功率加上节点发电机注入功率和节点之间传输输电功率的代数和。

潮流计算通常分为直流潮流计算和交流潮流计算两种方法。

直流潮流计算是指忽略电流相位差的计算方法。

在直流潮流计算中，电力系统的节点电压幅值和相角可以用复数来表示，节点注入功率和节点负荷消耗功率也采用复功率的形式。

直流潮流计算的基本方程为：P+iQ = V*(Gcosθ+Bsinθ)其中，P和Q分别表示节点注入有功功率和无功功率，V表示节点电压幅值，θ表示节点电压相角，G和B分别表示节点导纳矩阵的实部和虚部。

交流潮流计算考虑了电流相位差的影响，是更为准确的潮流计算方法。

交流潮流计算通常采用牛顿-拉夫逊法（Newton-Raphson method）进行迭代求解。

该方法以功率不平衡最小为目标，通过迭代计算更新节点电压幅值和相角，直到收敛为止。

潮流计算在电力系统运行和规划中具有重要的应用价值。

首先，潮流计算可以用来评估电力系统的稳态工作状态，包括节点电压幅值和相角、支路功率和电流等信息。

通过分析潮流计算结果，可以发现电力系统中潜在的潮流瓶颈和潮流分布情况，为电网调度和运行提供参考依据。

其次，潮流计算可以用来优化电力系统的运行和规划。

通过分析潮流计算结果，可以确定潮流分布不均衡的节点和支路，进而优化电力系统的输电和变电容量配置，提高电力系统的可靠性、经济性和稳定性。

此外，潮流计算还可用于电力系统的故障分析和重构，对于故障点的电压幅值、相角以及故障后的支路功率和电流进行分析，有助于电力系统故障的定位和恢复。

总的来说，电力系统潮流计算是电力系统运行分析的重要工具，通过计算电力系统中各节点的电压幅值和相角，以及各支路的功率和电流，可以评估电力系统的稳态工作状态，优化电力系统的运行和规划，实现电力系统的安全、稳定和高效运行。

matlab实验电力系统潮流计算

实验一电力系统潮流计算一、一元非线性方程求解例1-1 试求非线性方程 )(x f =0 的解。

解：（1）取一个合理的初值)0(x 作为方程)(x f =0的解，如果正好0)()0(=x f ，则方程的解*x =)0(x 。

否则做下一步。

（2）取)0()0(x x ∆+为第一次修正值。

)0(x ∆充分小，将)()0()0(x x f ∆+在)0(x 附近展开成泰勒级数，并且将的高次项略去，取其线性部分，得到)()0()0(x x f ∆+≈)0()0()0()()(x x f x f ∆'+=0 （1-1）上式表明，在)0(x 处把非线性方程0)(=x f 线性化，变成求)0(x 附近修正量)0(x ∆的线性方程，这个方程也称为修正方程式。

从而可求得)()()0()0()0(x f x f x'-=∆ （1-2）所以，可以确定第一次修正值)0()0()1(x x x ∆+=。

若0)()1(=x f ，则)1(*x x =。

（3）若0)()1(≠x f ，则用步骤（2）阐述的方法由)1(x 确定出第二次修正值)2(x。

如此迭代下去，在第)1(+k 次迭代时，)1(+k x应为)()()1(k k k xxx∆+=+=)()()()()(k k k x f x f x'- （1-3）式中k 为迭代次数。

如果ε<+)()1(k x f （ε是预设的一个小的正数，如510-=ε），则方程的解)1(*+=k xx ，迭代停止。

例1-2 应用牛顿—拉夫逊法求解非线性方程0122)(23=-+-=x x x x f解：设初始近似解0.2)0(=x，首先根据（1-1）计算)()0(x f10)()0(-=x f然后计算)()0(x f '5)()0(='x f根据（1-2）式计算)0(x ∆2510)()()0()0()0(=--='-=∆x f x f x再根据（1-3）式计算)1(x ∆422)0()0()1(=+=∆+=x x x重复以上计算直到5)1(10)(-+<k x f ，得到的计算过程量和结果见表1-1。

牛拉法潮流计算程序(附3机9节点结果对比)

本文简单介绍了牛顿-拉夫逊潮流计算的原理、模型与算法，然后用具体的实例，利用MATLAB对牛顿-拉夫逊法的算法进行了验证。

由于异地测量的两个电流缺少时间同步信息，以注入功率替换注入电流作为已知量。

即***1+niij j ij j i i i Y V V I V Q P ••===∑(1.2)其中,Y ij =G ij +jB ij ，带入上式，得到有功功率和无功功率方程 P i =V i ∑V j (G ij cos θij +B ij sin θij )n j=1 (1.3)Q i =V i ∑Vj (G ij sin θij −B ij cos θij )n j=1 (1.4)大部分情况下，已知PQ ，求解V θ。

考虑到电网的功率平衡，至少选择一台发电机来平衡全网有功功率，即至少有一个平衡节点，常选择调频或出线较多的发电机作为平衡节点。

具有无功补偿的母线能保持电压幅值恒定，这类节点可作为PV 节点。

3机9节点潮流、短路仿真计算课程设计总结

3机9节点潮流、短路仿真计算课程设计总结以3机9节点潮流、短路仿真计算课程设计总结为标题的文章概述：本次课程设计主要涉及到3机9节点潮流和短路仿真计算。

通过对电力系统进行潮流计算和短路仿真，可以了解系统的电压、电流等重要参数，为系统的稳定运行提供参考。

本文将对本次课程设计的过程、结果和总结进行详细介绍。

一、潮流计算潮流计算是电力系统中常用的一种计算方法，用于确定系统中各节点的电压、电流等参数。

在本次课程设计中，我们使用了3台发电机和9个节点的电力系统进行潮流计算。

1.1 数据准备在进行潮流计算之前，需要准备系统的基本数据，包括发电机的有功功率、无功功率和电压，各节点的负荷功率和电压等信息。

通过收集和整理这些数据，我们可以建立电力系统的节点和支路信息。

1.2 潮流计算方法潮流计算可以使用不同的方法，如高斯-赛德尔迭代法、牛顿-拉夫逊法等。

在本次课程设计中，我们选择了高斯-赛德尔迭代法进行潮流计算。

该方法通过迭代计算各节点的电压和电流，直到满足收敛条件为止。

1.3 结果分析经过潮流计算，我们得到了系统中各节点的电压、电流等参数。

通过分析这些结果，我们可以了解系统中的电力流动情况，判断系统是否存在潮流过载、电压偏差等问题，并采取相应的措施进行调整和优化。

二、短路仿真计算短路仿真计算是针对系统发生故障时的一种计算方法，用于确定短路电流的大小和分布情况。

在本次课程设计中，我们使用了相同的3机9节点电力系统进行短路仿真计算。

2.1 短路故障类型短路故障可以分为对称短路和非对称短路两种类型。

对称短路是指系统中的故障电流对称分布，非对称短路则是指故障电流非对称分布。

在本次课程设计中，我们分别考虑了对称短路和非对称短路的情况。

2.2 短路电流计算方法短路电流的计算可以使用不同的方法，如阻抗法、对称分量法等。

在本次课程设计中，我们选择了阻抗法进行短路电流的计算。

该方法通过计算系统中各节点的阻抗和电压，确定短路电流的大小和分布情况。

基于MATLAB电力系统潮流计算和分析

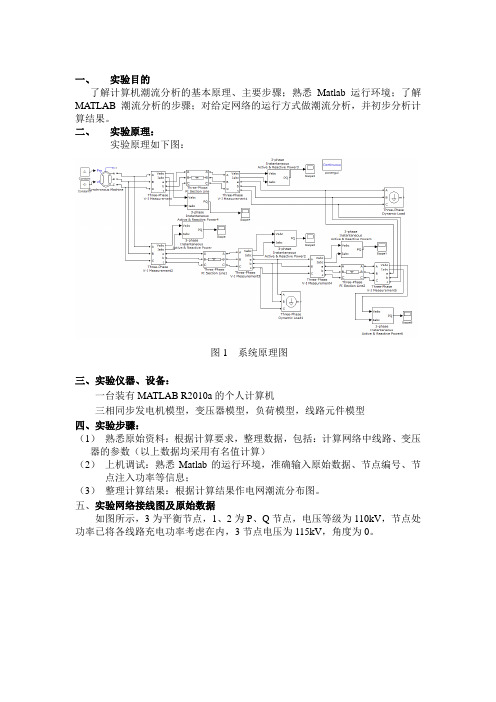
一、实验目的了解计算机潮流分析的基本原理、主要步骤；熟悉Matlab运行环境；了解MATLAB潮流分析的步骤；对给定网络的运行方式做潮流分析，并初步分析计算结果。

二、实验原理：实验原理如下图：图1 系统原理图三、实验仪器、设备：一台装有MATLAB R2010a的个人计算机三相同步发电机模型，变压器模型，负荷模型，线路元件模型四、实验步骤：（1）熟悉原始资料：根据计算要求，整理数据，包括：计算网络中线路、变压器的参数（以上数据均采用有名值计算）（2）上机调试：熟悉Matlab的运行环境，准确输入原始数据、节点编号、节点注入功率等信息；（3）整理计算结果：根据计算结果作电网潮流分布图。

五、实验网络接线图及原始数据如图所示，3为平衡节点，1、2为P、Q节点，电压等级为110kV，节点处功率已将各线路充电功率考虑在内，3节点电压为115kV，角度为0。

原始数据各参数是以其自身额定功率和额定电压为基准的标幺值。

发电机参数 Pn=100MV·A,Un=10.5KV ,fn=50Hz, 变压器参数采用Y-Y 连接方式 T1的参数 Pn=100MV·A,fn=50Hz,一次绕组：U1=10.5KV ,R1=0.002，L1=0，二次绕组：U2=121KV ，R2=0.002，L2=0.015， Rm=5000，Lm=5000 T2的参数 Pn=100MV·A,fn=50Hz,一次绕组：U1=10.5KV ,R1=0.002，L1=0，二次绕组：U2=121KV ，R2=0.002，L2=0.03，25+j18MV A3225+j18MVA32Rm=5000，Lm=5000线路参数L23:R*=0.08,X*=0.30,Y*=0.5L31:R*=0.10,X*=0.35,Y*=0L12:R*=0.04,X*=0.25,Y*=0.5六、实验数据记录及处理：从各个Scope中可以看到输电线π型等值电路两端的有功与无功功率的波形，具体操作方法是从Workspace中读出记录的数据（如图三、图四），数据有多组，取其平均值，分别得到各输电线π型等值电路两端的有功和无功功率。

matlab三机九节点电力系统仿真(带程序)

GenE(1,i)=abs(N(i,4)*exp(1i*N(i,5))+1i*gen(i,3)/10000*conj(((N(i,8)/100+1i*N(i,9)/100)/(N(i,4)*exp(1i*N(i,5))))));
GEgj(1,i)=angle(N(i,4)*exp(1i*N(i,5))+1i*gen(i,3)/10000*conj(((N(i,8)/100+1i*N(i,9)/100)/(N(i,4)*exp(1i*N(i,5))))));
稳态情况下有，机械功率Pme=Pe
四、求解运动方程
发电机的运动方程可以写成常微分方程组：
其中Pmi为第i个机组故障前稳态的电磁功率。在本次仿真中Djωi为零，即阻尼为零。仿真开始，t=0Βιβλιοθήκη 引入故障，0.083s后切除故障。
求解运动方程后得到曲线如下：
五、结果分析
上图分别显示了各台发电机的转子角与时间的关系曲线，显示了发电机转速差的曲线，和、的曲线，由图可以看到，最大角差为，出现在处，无论是还是第二个摇摆都不大于第一个摇摆，可见系统是稳定的。
一、潮流计算
由于本文以三机九节点为模型，假定节点一为参考节点，这样就有2两个发电机的PV节点，6个PQ节点，未知量为8个节点(包括2个PV节点和6个PQ节点)的电压相角，还有6个节点(PQ节点)的电压幅值。
可以先求出Y矩阵
图4-1 Y矩阵
然后，我们列写方程，也就是利用各个节点的有功、无功功率的平衡关系，列写14个功率平衡方程。这样就能使用牛顿一拉夫逊算法来求解这14个非线性方程。
%支路数据
%从到电阻电抗容纳类型变比
B=[1 4 0.0 0.0576 0.0 1 1

电力系统潮流计算实验报告

１1．手算过程已知：节点1：PQ 节点， s(1)= -0.5000-j0.3500 节点2：PV 节点， p(2)=0.4000 v(2)=1.0500 节点3：平衡节点，U(3)=1.0000∠0.0000 网络的连接图：0.0500+j0.2000 1 0.0500+j0.2000231）计算节点导纳矩阵由2000.00500.012j Z 71.418.112j y ;2000.00500.013j Z71.418.113j y ;导纳矩阵中的各元素：42.936.271.418.171.418.1131211j j j y y Y ;71.418.11212j y Y ; 71.418.11313j y Y; 21Y 71.418.11212j y Y ; 71.418.12122j y Y;002323j y Y;31Y 71.418.11313j y Y; 32Y 002323j y Y;71.418.13133j y Y;形成导纳矩阵BY ：71.418.10071.418.10071.418.171.418.171.418.171.418.142.936.2j j j j j j j j j Y B2）计算各PQ、PV 节点功率的不平衡量，及PV 节点电压的不平衡量：取:000.0000.1)0(1)0(1)0(1j jf e U000.0000.1)0(2)0(2)0(2j jf e U节点3是平衡节点，保持000.0000.1333j jf e U为定值。

nj j jij jij ijij jij i ieB fG f fB eG e P1)0()0()0()0()0()0()0(；２nj j jij jij ijij jij i ie B fG e f B eG f Q 1)0()0()0()0()0()0()0(；);(2)0(2)0(2)0(iiif e U)0.142.90.036.2(0.0)0.042.90.136.2(0.1)0(1P)0.171.40.018.1(0.0)0.071.40.118.1(0.1 )0.171.40.018.1(0.0)0.071.40.118.1(0.1 0.0 ；)0.142.90.036.2(0.1)0.042.90.136.2(0.0)0(1Q)0.171.40.018.1(0.1)0.071.40.118.1(0.0 )0.171.40.018.1(0.1)0.071.40.118.1(0.0 0.0 ；)0.171.40.018.1(0.0)0.071.40.118.1(0.1)0(2P)0.171.40.018.1(0.0)0.071.40.118.1(0.1 )0.00.00.00.0(0.0)0.10.00.10.0(0.1 0.0 ；101)(222)0(22)0(22)0(2f e U；于是：;)0()0(iiiP P P ;)0()0(iiiQQ Q);(2)0(2)0(22)0(iiiif e UU5.00.05.0)0(11)0(1P P P ;35.00.035.0)0(11)0(1QQ Q;4.00.04.0)0(22)0(2P P P ;1025.0)01(05.1)(2222)0(22)0(2222)0(2f e UU3）计算雅可比矩阵中各元素雅可比矩阵的各个元素分别为：３ji ij ji ij j i ij j i ij ji ij j i ij e U S f U R e Q L f Q J e P N f P H 22;;; 又： nj j jij jij i jij jij i ieB fG f fB eG e P1)0()0()0()0()0()0()0(； nj j jij jij ijij jij iieB fG e fB eG f Q 1)0()0()0()0()0()0()0(；);(2)0(2)0(2)0(iiif e U)0(1P )0(111)0(111)0(1)0(111)0(111)0(1e Bf G f f B e G e)0(212)0(212)0(1)0(212)0(212)0(1e B fG f f B e G e313313)0(1313313)0(1e Bf G f f B e G e ；)()()0(111)0(111)0(1)0(111)0(111)0(1)0(1e Bf Ge f B e G f Q)()()0(212)0(212)0(1)0(212)0(212)0(1e Bf G e f B e G f)()(313313)0(1313313)0(1e Bf G e f B e G f；)0(2P )0(121)0(121)0(2)0(121)0(121)0(2e Bf G f f B e G e)0(222)0(222)0(2)0(222)0(222)0(2eB fG f fBeG e323323)0(2323323)0(2e Bf G f f B e G e ；)(2)0(22)0(22)0(2f e U42.90.171.40.171.4313)0(212)0(1)0(1)0(11e B e Bf P H ； 36.20.118.10.118.10.136.222313)0(212)0(111)0(1)0(1)0(11 e G e G e G e P N 36.20.118.10.118.1313)0(212)0(1)0(1)0(11 e G e G f Q J４42.90.171.40.171.40.142.922313)0(212)0(111)0(1)0(1)0(11 e B e B e B e Q L 71.40.171.4)0(112)0(2)0(1)0(12 e B f P H ； 18.10.118.1)0(112)0(2)0(1)0(12 e G e P N ； 18.10.118.1)0(112)0(2)0(1)0(12 e G f Q J ；71.40.171.4)0(112)0(2)0(1)0(12 e B e Q L ； 71.40.171.4)0(221)0(1)0(2)0(21 e B f P H ； 11.40.111.4)0(221)0(1)0(2)0(21 e G e P N ； 0)0(12)0(2)0(21 f U R ； 0)0(12)0(2)0(21 e U S ； 71.40.10.00.171.4323)0(121)0(2)0(2)0(22 e B e B f P H ； 18.10.10.00.118.10.118.122323)0(121)0(222)0(2)0(2)0(22 e G e G e G e P N ；02)0(2)0(22)0(2)0(22 f f U R ； 0.20.122)0(2)0(22)0(2)0(22 e e U S ；得到K=0时的雅可比矩阵：0.200018.171.418.171.471.418.142.936.218.171.436.242.9)0(J4）建立修正方程组：５)0(2)0(2)0(1)0(10.200011.4959.1011.4959.10959.1011.4918.2122.811.4959.1022.8918.210975.04.035.08.0e f e f 解得：04875.001828.00504.00176.0)0(2)0(2)0(1)0(1e f e f 因为 )0()0()1(iiie e e ； )0()0()1(iiif f f ；所以 9782.00218.00.1)0(1)0(1)1(1e e e ； 0158.00158.00)0(1)0(1)1(1f f f ；05125.105125.00.1)0(2)0(2)1(2e e e ；05085.005085.00)0(2)0(2)1(2f f f ；5）运用各节点电压的新值进行下一次迭代：即取: 0158.09782.0)1(1)1(1)1(1j jf e U05085.005125.1)1(2)1(2)1(2j jf e U节点3时平衡节点，保持000.0000.1333j jf e U为定值。

三机九节点潮流计算

clc;clear;close all;n1=9;n2=9;B1=load('b1.txt','ascii');B2=load('b2.txt','ascii');m=0;r=0;for i=1:n1if B1(i,8)==1m=m+1;endendr=n1-m-1;e=B1(1:n1,2);f=B1(1:n1,3);ps=B1(1:n1,4)-B1(1:n1,6);qs=B1(1:n1,5)-B1(1:n1,7);Y=zeros(n1);for j=1:n2p=B2(j,2);q=B2(j,3);J=zeros(2*n1);Y(p,q)=-1./((B2(j,4)+1i*B2(j,5))*B2(j,7));Y(q,p)=Y(p,q);Y(p,p)=Y(p,p)+1/(B2(j,4)+1i*B2(j,5))+1i*B2(j,6);Y(q,q)=Y(q,q)+1/((B2(j,4)+1i*B2(j,5))*B2(j,7)^2)+1i*B2(j,6);end%导纳矩阵YH1=zeros(n1);N1=zeros(n1);J1=zeros(n1);L1=zeros(n1);G=real(Y);B=imag(Y);dp(1:(n1-1))=1;dq(1:m)=1;dx(1:(2*m+r))=1;while(abs(max(dp)>=1.0e-5)||abs(max(dq)>=1.0e-5)||abs(max(dx(1:(m+r)))>=1.0e-5)||abs(max(dx((m +r+1):(2*m+r)).*e(1:m))>=1.0e-5))for i=1:n1for j=1:n1si(i,j)=sin(f(i)-f(j));co(i,j)=cos(f(i)-f(j));if i==jH1(i,j)=e(i)^2*B(i,i)+qs(i);N1(i,j)=-e(i)^2*G(i,i)-ps(i);J1(i,j)=e(i)^2*G(i,i)-ps(i);L1(i,j)=e(i)^2*B(i,i)-qs(i);elseH1(i,j)=-e(i)*e(j)*(G(i,j)*si(i,j)-B(i,j)*co(i,j));N1(i,j)=-e(i)*e(j)*(G(i,j)*co(i,j)+B(i,j)*si(i,j));J1(i,j)=e(i)*e(j)*(G(i,j)*co(i,j)+B(i,j)*si(i,j));L1(i,j)=-e(i)*e(j)*(G(i,j)*si(i,j)-B(i,j)*co(i,j));endendendH=H1(2:n1,2:n1);N=N1(2:n1,r+2:n1);J=J1(r+2:n1,2:n1);L=L1(r+2:n1,r+2:n1);J=[H N;J L];%雅克比矩阵Jfor i=2:n1a(i)=0;b(i)=0;for j=1:n1a(i)=a(i)+e(j)*(G(i,j)*co(i,j)+B(i,j)*si(i,j));if i>=(r+2)b(i)=b(i)+e(j)*(G(i,j)*si(i,j)-B(i,j)*co(i,j));endenddp(i-1)=ps(i)-e(i)*a(i);if i>=(r+2)dq(i-(r+1))=qs(i)-e(i)*b(i);endendF=[dp';dq'];dx=-J\F;f(2:n1)=f(2:n1)+dx(1:(m+r));e1=e((r+2):n1)+dx((m+r+1):(2*m+r)).*e((r+2):n1); e2=e(1:(r+1));e=[e2;e1];enddisp('各节点电压');disp('e=');disp(e');disp('单位：度f=');disp(f'*180/3.1415926)%求出各节点电压幅值及相角a=0;for i=1:n1a=a+conj(Y(1,i))*(e(i)*cos(f(i))-1i*e(i)*sin(f(i))); enda=a*(e(1)*cos(f(1))+1i*e(1)*sin(f(1)));disp('平衡节点P+jQ=');disp(a);disp('输电线路有功无功:');for i=1:n2p=B2(i,2);q=B2(i,3);s1(p,q)=e(p)^2*(-1i*B2(i,6))+(e(p)*cos(f(p))+1i*e(p)*sin(f(p)))*(e(p)*cos(f(p))-1i*e(p)*sin(f(p))-e( q)*cos(f(q))+1i*e(q)*sin(f(q)))*conj(-Y(q,p));s1(q,p)=e(q)^2*(-1i*B2(i,6))+(e(q)*cos(f(q))+1i*e(q)*sin(f(q)))*(e(q)*cos(f(q))-1i*e(q)*sin(f(q))-e( p)*cos(f(p))+1i*e(p)*sin(f(p)))*conj(-Y(q,p));fprintf('S%d%d=',p,q);disp(s1(p,q));fprintf('S%d%d=',q,p);disp(s1(q,p));end%初值计算for j=1:n1s(j)=0;for i=1:n1s(j)=s(j)+conj(Y(j,i))*(e(i)*cos(f(i))-1i*e(i)*sin(f(i)));ends(j)=s(j)*(e(j)*cos(f(j))+1i*e(j)*sin(f(j)));endY1=conj(-s)./(e'.^2);%负荷等值导纳disp('各节点等值导纳');disp('Y1=');disp(Y1);disp('各节点功率');disp('S=');disp(s);Ra=[0 0 0];X_d=[0.0608 0.1198 0.1813];Xq=[0.0969 0.8645 1.2578];%Xq=X_d;%不计凸极效应v=e.*cos(f)+1i*e.*sin(f);for i=1:3I(i)=conj(s(i)/(e(i)*cos(f(i))+1i*e(i)*sin(f(i))));EQ(i)=e(i)*cos(f(i))+1i*e(i)*sin(f(i))+(Ra(i)+1i*Xq(i))*I(i);EQx(i)=real(EQ(i));EQy(i)=imag(EQ(i));delta(i)=atan(EQy(i)/EQx(i));enddisp('各发电机的暂态电动势，功角和输入机械功率初值');disp('delta=');disp(delta*180/3.1415926);for i=1:3Vx(i)=e(i)*cos(f(i));Vy(i)=e(i)*sin(f(i));Vdq=[sin(delta(i)) -cos(delta(i));cos(delta(i)) sin(delta(i))]*[Vx(i);Vy(i)];Vd(i)=Vdq(1);Vq(i)=Vdq(2);Ix(i)=real(I(i));Iy(i)=imag(I(i));Idq=[sin(delta(i)) -cos(delta(i));cos(delta(i)) sin(delta(i))]*[Ix(i);Iy(i)];Id(i)=Idq(1);Iq(i)=Idq(2);E_q(i)=Vq(i)+Ra(i)*Iq(i)+X_d(i)*Id(i);enddisp('E_q=');disp(E_q);for i=1:3Pm(i)=real(s(i))+(Ix(i)^2+Iy(i)^2)*Ra(i); enddisp('Pm=');disp(Pm);。

相关主题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

电力系统分析大作业一、设计题目本次设计题目选自课本第五章例5-8,美国西部联合电网WSCC系统的简化三机九节点系统，例题中已经给出了潮流结果，计算结果可以与之对照。

取ε=0.00001 。

二、计算步骤第一步，为了方便编程，修改节点的序号，将平衡节点放在最后。

如下图：第二步，这样得出的系统参数如下表所示：第三步，形成节点导纳矩阵。

92132 7 45683第四步，设定初值：01)0(6)0(5)0(4)0(3)0(2)0(1∠======••••••U U U U U U ；0)0(8)0(7==Q Q ，0)0(8)0(7==θθ。

第五步，计算失配功率)0(1P ∆=0，)0(2P ∆=-1.25，)0(3P ∆=-0.9，)0(4P ∆=0，)0(5P ∆=-1，)0(6P ∆=0，)0(7P ∆=1.63， )0(8P ∆=0.85；)0(1Q ∆=0.8614，)0(2Q ∆=-0.2590，)0(3Q ∆=-0.0420，)0(4Q ∆=0.6275，)0(5Q ∆=-0.1710， )0(6Q ∆=0.7101。

显然，5108614.0|},max {|-=>=∆∆εi i Q P 。

第六步，形成雅克比矩阵（阶数为14×14）第七步，解修正方程，得到：=∆)0(1θ-0.0371，=∆)0(2θ-0.0668，=∆)0(3θ-0.0628，=∆)0(4θ0.0732，=∆)0(5θ0.0191，=∆)0(6θ0.0422，=∆)0(7θ0.1726，=∆)0(8θ0.0908；=∆)0(1U 0.0334，=∆)0(2U 0.0084，=∆)0(3U 0.0223，=∆)0(4U 0.0372，=∆)0(5U 0.0266，=∆)0(6U 0.0400。

从而=)1(1θ-0.0371，=)1(2θ-0.0668，=)1(3θ-0.0628，=)1(4θ0.0732，=)1(5θ0.0191，=)1(6θ0.0422，=)1(7θ0.1726，=)1(8θ0.0908；=)1(1U 1.0334，=)1(1U 1.0084，=)1(1U 1.0223，=)1(1U 1.0372，=)1(1U 1.0266，=)1(1U 1.0400。

然后转入下一次迭代。

经三次迭代后5510101845.0|},max {|--=<⨯=∆∆εi i Q P 。

迭代过程中节点电压变化情况如下表：迭代收敛后各节点的电压和功率：最后得出迭代收敛后各支路的功率和功率损耗：三、源程序及注释由于计算流程比较简单，所以编写程序过程中没有采用模块化的形式，直接按顺序一步步进行。

disp('【节点数:】');[n1]=xlsread('input.xls','A3:A3')%节点数disp('【支路数:】');[n]=xlsread('input.xls','B3:B3')%支路数disp('【精度:】');Accuracy=xlsread('input.xls','B4:B4')%精度[branch]=xlsread('input.xls','E4:K12');[node]=xlsread('input.xls','M4:S12');Data_B1=branch;%支路参数Data_B2=node;%节点参数T1=zeros(n,2);T2=zeros(n1,3);i=sqrt(-1);format shortfor j=1:nT1(j,1)=Data_B1(j,3)+Data_B1(j,4)*1i;T1(j,2)=Data_B1(j,5)*1i;endfor j=1:n1T2(j,1)=Data_B2(j,1)+Data_B2(j,2)*1i;T2(j,2)=Data_B2(j,3)+Data_B2(j,4)*1i; endB1=zeros(n,6);B2=zeros(n1,5);for j=1:nB1(j,1)=Data_B1(j,1);B1(j,2)=Data_B1(j,2);B1(j,3)=T1(j,1);B1(j,4)=T1(j,2);B1(j,5)=Data_B1(j,6);B1(j,6)=Data_B1(j,7);endfor j=1:n1B2(j,1)=T2(j,1);B2(j,2)=T2(j,2);B2(j,3)=Data_B2(j,5);B2(j,4)=Data_B2(j,6);B2(j,5)=Data_B2(j,7);enddisp('【支路参数矩阵:】');B1 %显示支路参数矩阵disp('【节点参数矩阵:】');B2 %显示节点参数矩阵% 以上为从excel中导入初值的程序Y=zeros(n1);for i=1:nif B1(i,6)==0 %不含变压器的支路p=B1(i,1);q=B1(i,2);Y(p,q)=Y(p,q)-1/B1(i,3);Y(q,p)=Y(p,q);Y(p,p)=Y(p,p)+1/B1(i,3)+0.5*B1(i,4); Y(q,q)=Y(q,q)+1/B1(i,3)+0.5*B1(i,4);else%含有变压器的支路p=B1(i,1);q=B1(i,2);Y(p,q)=Y(p,q)-1/(B1(i,3)*B1(i,5));Y(q,p)=Y(p,q);Y(p,p)=Y(p,p)+1/B1(i,3);Y(q,q)=Y(q,q)+1/(B1(i,5)^2*B1(i,3));endenddisp('【导纳矩阵:】');Y %显示导纳矩阵m=0;for i=1:n1if B2(i,5)==2m=m+1;endendm %PQ节点个数l=0;for i=1:n1if B2(i,5)==1l=l+1;endendl %PV节点个数Mismatch_power=zeros(l+m*2,1);for i=1:n1-1Pj=0;for j=1:n1Pj=Pj+(B2(i,3)*B2(j,3)*(real(Y(i,j))*cos(B2(i,4)-B2(j,4))+imag(Y(i,j) )*sin(B2(i,4)-B2(j,4))));endMismatch_power(i,1)=real(B2(i,1))-real(B2(i,2))-Pj;endfor k=n1:(l+m*2)Qj=0;for j=1:n1Qj=Qj+B2((k-n1+1),3)*B2(j,3)*(real(Y((k-n1+1),j))*sin(B2((k-n1+1),4)-B2(j,4))-imag(Y((k-n1+1),j))*cos(B2((k-n1+1),4)-B2(j,4)));endMismatch_power(k,1)=imag(B2((k-n1+1),1))-imag(B2((k-n1+1),2))-Qj;end% Mismatch_power %计算失配功率times=0;while(max(Mismatch_power)>Accuracy)for i=1:(n1-1)Pj=0;for j=1:n1Pj=Pj+B2(i,3)*B2(j,3)*(real(Y(i,j))*cos(B2(i,4)-B2(j,4))+imag(Y(i,j)) *sin(B2(i,4)-B2(j,4)));endMismatch_power(i,1)=real(B2(i,1))-real(B2(i,2))-Pj;endfor k=n1:(l+m*2)Qj=0;for j=1:n1Qj=Qj+B2((k-n1+1),3)*B2(j,3)*(real(Y((k-n1+1),j))*sin(B2((k-n1+1),4)-B2(j,4))-imag(Y((k-n1+1),j))*cos(B2((k-n1+1),4)-B2(j,4)));endMismatch_power(k,1)=imag(B2((k-n1+1),1))-imag(B2((k-n1+1),2))-Qj;enddisp('【当前迭代次数:】');timesdisp('【失配功率:】');Mismatch_powerJacobian=zeros(l+m*2);%雅克比矩阵7*7%————————————————————————————————————Hfor i=1:(n1-1)for j=1:(n1-1)if i==jP_H=0;for k=1:n1P_H=P_H+B2(i,3)*B2(k,3)*(real(Y(i,k))*sin(B2(i,4)-B2(k,4))-imag(Y(i,k ))*cos(B2(i,4)-B2(k,4)));endJacobian(i,i)=P_H-B2(i,3)*B2(i,3)*(0-imag(Y(i,i)));elseJacobian(i,j)=0-B2(i,3)*B2(j,3)*(real(Y(i,j))*sin(B2(i,4)-B2(j,4))-im ag(Y(i,j))*cos(B2(i,4)-B2(j,4)));endendend%————————————————————————————————————Nfor i=1:(n1-1)for j=1:mif i==jP_N=0;for k=1:n1P_N=P_N+B2(k,3)*(real(Y(i,k))*cos(B2(i,4)-B2(k,4))+imag(Y(i,k))*sin(B 2(i,4)-B2(k,4)));endJacobian(i,n1-1+i)=0-B2(i,3)*real(Y(i,i))-P_N;elseJacobian(i,n1-1+j)=0-B2(i,3)*(real(Y(i,j))*cos(B2(i,4)-B2(j,4))+imag( Y(i,j))*sin(B2(i,4)-B2(j,4)));endendend%————————————————————————————————————Kfor i=1:mfor j=1:(n1-1)if i==jP_K=0;for k=1:n1P_K=P_K+B2(i,3)*B2(k,3)*(real(Y(i,k))*cos(B2(i,4)-B2(k,4))+imag(Y(i,k ))*sin(B2(i,4)-B2(k,4)));endJacobian(n1-1+i,i)=0+B2(i,3)*B2(i,3)*real(Y(i,i))-P_K;elseJacobian(n1-1+i,j)=B2(i,3)*B2(j,3)*(real(Y(i,j))*cos(B2(i,4)-B2(j,4)) +imag(Y(i,j))*sin(B2(i,4)-B2(j,4)));endendend%————————————————————————————————————Lfor i=1:mfor j=1:mif i==jP_L=0;for k=1:n1P_L=P_L+B2(k,3)*(real(Y(i,k))*sin(B2(i,4)-B2(k,4))-imag(Y(i,k))*cos(B2(i,4)-B2(k,4)));endJacobian(n1-1+i,n1-1+i)=0-P_L+B2(i,3)*imag(Y(i,i));elseJacobian(n1-1+i,n1-1+j)=0-B2(i,3)*(real(Y(i,j))*sin(B2(i,4)-B2(j,4))-imag(Y(i,j))*cos(B2(i,4)-B2(j,4)));endendendS=zeros(l+m*2,1); %初始化电压角度变化量S=inv(Jacobian)*(0-Mismatch_power); %求解修正方程S=(Jacobian)\(0-Mismatch_power); %求解修正方程for i=1:(n1-1) %角度初值加变化量B2(i,4)=B2(i,4)+S(i,1);endfor i=1:m %电压初值加变化量B2(i,3)=B2(i,3)+S(n1-1+i,1);enddisp('【雅克比矩阵:】');Jacobian %显示雅克比矩阵% S=inv(Jacobian)times=times+1;endtimes=times-1;disp('【共计迭代次数:】');times %显示迭代次数U_It=zeros(n1,1); %初始化电压向量for i=1:n1U_It(i,1)=B2(i,3)*cos(B2(i,4))+B2(i,3)*sin(B2(i,4))*1j;endangle_It=zeros(n1,1); %将电压角度的弧度值转为角度值for i=1:n1angle_It(i,1)=B2(i,4)*180/pi;endNode_S_It=U_It.*(conj(Y)*conj(U_It)); %求解节点功率disp('【迭代收敛后各节点的电压幅值:】');Node_U_It=abs(U_It) %显示迭代收敛后各节点的电压幅值disp('【迭代收敛后各节点的电压角度:】');angle_It %显示迭代收敛后各节点的电压角度disp('【迭代收敛后各节点的功率:】');Node_S_It %显示迭代收敛后各节点的功率Branch_It=zeros(n,10);for i=1:n;if B1(i,6)==0; %不带变压器支路m=B1(i,1); %得到支路号n=B1(i,2);Branch_It(i,1)=m; %显示支路号Branch_It(i,2)=n;a=U_It(m,1)*(conj(U_It(m,1))*conj(B1(i,4))*0.5+(conj(U_It(m,1))-conj( U_It(n,1)))/conj(B1(i,3)));Branch_It(i,3)=real(a); %显示PijBranch_It(i,4)=imag(a); %显示Qijb=U_It(m,1)*B1(i,4)*0.5+(U_It(m,1)-U_It(n,1))/B1(i,3);Branch_It(i,5)=sqrt(real(b)^2+imag(b)^2); %显示Iijc=U_It(n,1)*(conj(U_It(n,1))*conj(B1(i,4))*0.5+(conj(U_It(n,1))-conj( U_It(m,1)))/conj(B1(i,3)));Branch_It(i,6)=real(c); %显示PjiBranch_It(i,7)=imag(c); %显示Qjid=U_It(n,1)*B1(i,4)*0.5+(U_It(n,1)-U_It(m,1))/B1(i,3);Branch_It(i,8)=sqrt(real(d)^2+imag(d)^2); %显示Ijie=a+c;Branch_It(i,9)=real(e); %显示线路损耗有功分量Branch_It(i,10)=imag(e); %显示线路损耗无功分量else%带变压器支路(同以上内容)m=B1(i,1);n=B1(i,2);Branch_It(i,1)=m;Branch_It(i,2)=n;a=U_It(m,1)*(conj(U_It(m,1))/conj(B1(i,3))-conj(U_It(n,1))*conj(1/(B1 (i,5)*B1(i,3))));Branch_It(i,3)=real(a);Branch_It(i,4)=imag(a);b=U_It(m,1)*(B1(i,5)-1)/B1(i,3)/B1(i,5)+(U_It(m,1)-U_It(n,1))/(B1(i,5 )*B1(i,3));Branch_It(i,5)=sqrt(real(b)^2+imag(b)^2);c=U_It(n,1)*(conj(U_It(n,1))/(conj(B1(i,5)*B1(i,5)*B1(i,3)))-conj(U_I t(m,1))*conj(1/(B1(i,5)*B1(i,3))));Branch_It(i,6)=real(c);Branch_It(i,7)=imag(c);d=U_It(n,1)*(1-B1(i,5))/B1(i,5)/B1(i,5)/B1(i,3)+(U_It(n,1)-U_It(m,1)) /B1(i,5)/B1(i,3);Branch_It(i,8)=sqrt(real(d)^2+imag(d)^2);e=a+c;Branch_It(i,9)=real(e);Branch_It(i,10)=imag(e);endenddisp('【迭代收敛后各支路的功率和功率损耗:】');Branch_It %显示迭代收敛后各支路的功率和功率损耗% %—————————————————————————————向Excel表中输出数据% Node_S_It_Real=real(Node_S_It);% Node_S_It_imag=imag(Node_S_It);% xlswrite('output.xls',Node_U_It,1,'B3');% xlswrite('output.xls',angle_It,1,'C3');% xlswrite('output.xls',Node_S_It_Real,1,'D3');% xlswrite('output.xls',Node_S_It_imag,1,'E3');% xlswrite('output.xls',Branch_It,1,'G3');程序中还有将数据从Excel表格中读入输出的xlsread和xlswrite功能，直接将数据输入到Excel表格中，可以省略将数据写在程序中或者一一输入的步骤，适用于任何节点的电力系统潮流计算。