第2章 动量和角动量
2-5-角动量-角动量守恒定律

力矩,等于力的作用点
对该点的位矢与力的矢
积,即
M
r
F
M 的方向垂直于r和F所决定的
平面,指向用右手法则确定。
M x yFz zFy
在直角坐标系中,表示式为 M y zFx xFz
3
第2章 运动定律与力学中的守恒定律
M z xFy yFx
2–5 角动量 角动量守恒定律
2 质点的角动量定理
例2.16 在光滑的水平桌面上,放有质量为M的木块, 木块与一弹簧相连,弹簧的另一端固定在O点,弹簧
的劲度系数为k,设有一质量为m的子弹以初速 v0
垂直于OA射向M并嵌在木块内.弹簧原长 l0 ,子弹击
中木块后,木块M运动到B点时刻,弹簧长度变为l,
此时OB垂直于OA,求在B点时,木块的运动速v2度 .
解 击中瞬间,在水平 面内,子弹与木块组成 的系统沿 v0方向动量守 恒,即有
mv0 (m M )v1 6 第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量守恒定律
2-5-角动量-角动量守恒定律
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量守恒定律
v L
rv
pv
rr
r xi
r yj
r zk
pr
r pxi
r py j
r pzk
rr
pr
(
ypz
zpy
r )i
( zpx
xpz
)
r j
( xp y
ypx
r )k
Z
rr
rr rr
tr
Mdt 叫冲量矩 t0
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量守恒定律
2-5角动量 角动量守恒定律

例:一个人站在转台(质量为M,半径为R)的边
缘,质量为m ,当人沿转台边缘行走一周时,人和转台
相对地面各转过了多少角度?
解:取人和转台为一系统,对整个系统而言,M 0
系统的角动量守恒。
取地面为参照系,人相对地面转动的角速度为 1,
转台相对地面转动的角速度为 2 ,人相对转台转动的
角速度为 。
(mR2 )1
12 v0
7l
由角动量定理
M dL d(I) dI
dt dt
dt
即
mgr cos d ( 1 ml2 mr2 ) 2mr dr
dt 12
dt
考虑到 t
dr g cost 7lg cos(12v0 t)
dt 2
24 v0
7l
§2.5角动量 角动量守恒定律 第2章 运动定律与力学中的守恒定律
§2.5角动量 角动量守恒定律 第2章 运动定律与力学中的守恒定律
2.5.L2 质r点的p角动量定dp理
F,
dL ?
dL
d
(r
dt
p)
r dp
dt
dr
p
dt
dr v,
dt
v p 0
dt dL
dt r dp
r
F
dt
dt
dt
M
dL
作用于质点的合力对参考点 O 的力矩 ,等于质点对该点 O 的角
得 LdL m2 gR3 cosd
L LdL m2gR3
cosd
0
0
L mR 3 2 (2g sin )1 2
L mR 2
( 2g sin )1 2
R
§2.5角动量 角动量守恒定律 第2章 运动定律与力学中的守恒定律
动量角动量

= 1.2×10 -22 kg · m · s ×
-22
-1
剩余核反冲动量 大小和方向
方向
以
标识
间的夹角
。
。
118 º 6 ’
mb
ma
空车质量 m10
引例
静
两人先后跳上 车后,车的速度。 车后,车的速度。
vb
va
水平光滑
选车和跳离地后的人为质点系。 选车和跳离地后的人为质点系。 无外力作用, 系统在水平方向 ( X )无外力作用,系统动量守恒。 无外力作用 系统动量守恒。 设第一人跳上车后的车速为
定律说明
系统总动量不变,但系统内各质点动量可相互转移。 系统总动量不变,但系统内各质点动量可相互转移。 只要满足守恒条件,系统始末总动量不变,不管过程细节。 只要满足守恒条件,系统始末总动量不变,不管过程细节。 系统受合力在某一坐标分量为零,总动量在该坐标分量守恒。 系统受合力在某一坐标分量为零,总动量在该坐标分量守恒。 时 恒量 时 恒量 时 恒量
0 时,
则
0
L
r p
恒矢量
简易演示 角动量守恒的一种简易的定性演示
先使小球获得某一速率绕 O 转动 可直观看出
变短时, 变短时, 小球速率变快。 小球速率变快。
若设法进行测量, 若设法进行测量,可发现
两边乘 然后缓慢下拉 软绳
,即角动量守恒
卫星的运动
抛物线
11.2 km < v1 < 16.7 km/s
动量的SI制单位是 动量的SI制单位是 SI 动量 P = m v 千克 • 米 / 秒 ( kg • m • s -1 )
线动量,以区别以后讲到的角动量。 又称 线动量,以区别以后讲到的角动量。
02_动量角动量3

瞬时功率:
A dA P lim dt t 0 t dA F dr F v P dt dt
i 1
i 1
b A lim Fi ri F dr
n r 0 i 1
F1
F2
a
b A F dr a
a
r1
1
2
功和能
合力的功:
A
L
F dr F1 F2 Fn dr
动量与角动量
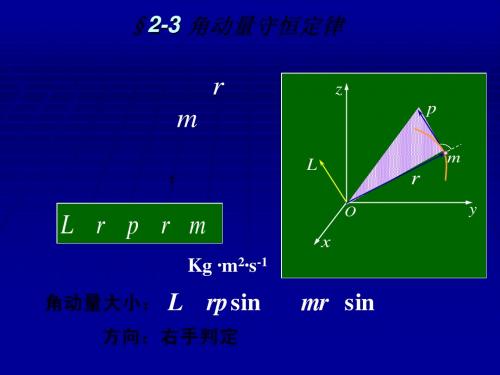
一、质点的角动量 angular momentum
定义:
L r P r mv
——质点对O点的 角动量
L
z
O
x
mv
y
L rmv sin L Lx i Ly j Lz k
单位:kg · m2· s-1
动量与角动量
地球在椭圆的一个焦点上,则
(1)卫星的动量是否守恒? (2)卫星的角动量是否守恒?
m
(3)卫星的动能是否守恒?
(4)开普勒面积定律的实质是什么?
动量与角动量
Example 质量为 m 小球系在绳子的一端,绳穿过铅 直套管,使小球限制在一光滑水平面上运动。先使小 球一速度 v0 绕管心作半径为 r0 的圆周运动,然后向下 拉绳子,使小球运动半径变为 r1 。求小球的速度.
• 对质点系
dLi F2 M i外 M i内 dt f2 dLi (M i外 M i内 ) f1 d t i i d( L) dL F 1 M外 m1 dt dt t t0 M 外 dt L L0 t ——外力矩的冲量矩 M d t 外
物理学概念知识:动量定理和动量角动量定理

物理学概念知识:动量定理和动量角动量定理动量定理和动量角动量定理是物理学中非常基本的两个概念。
它们的内容涉及到我们对物体运动规律的认识,不仅有助于我们更好地理解物理学知识,还可以应用于现实生活中的一些问题。
下面,我们将分别介绍这两个概念及其应用。
一、动量定理动量定理是描述物体运动过程中动量变化的一个基本定理。
它指出:在总外力作用下,物体的动量就会发生变化,这种变化的大小跟作用力和时间的乘积成正比。
这个定理的表达方式为:Δp=Ft其中,Δp表示物体动量的变化量,F表示物体所受的总外力,t 表示外力作用的时间。
式子的意义是:在总外力作用下,物体动量的变化量等于总外力作用时间的乘积。
重物移动时,如果外力越大,或者作用时间越长,那么物体的动量就会发生更大的变化。
从而可以更快地推动物体运动起来。
同样,如果要让运动中的物体停下来,也可以利用动量定理的知识。
通过对物体施加一个与它的运动方向相反的恒定力,也就是反向加速度,可以让物体的动量逐渐减小,直到物体停下来。
二、动量角动量定理动量角动量定理是物理学中另一个基本的概念。
它是通过描述物体绕某一点旋转的行为,来了解物体运动过程中动量变化的定理。
它指出:在物体绕某一点旋转时,物体的角动量就会发生变化,这种变化的大小跟作用力矩和时间的乘积成正比。
这个定理的表达方式为:ΔL=Mt其中,ΔL表示物体角动量的变化量,M表示作用力矩,t表示外力作用的时间。
式子的意义是:在物体绕某一点旋转时,物体角动量的变化量等于力矩作用时间的乘积。
个陀螺时,如果外力越大,或者作用时间越长,那么陀螺的角动量也会发生更大的变化。
从而可以更快地让陀螺旋转。
同样,如果要让旋转中的陀螺停下来,也可以利用动量角动量定理的知识。
通过对陀螺施加一个与它的旋转方向相反的外力矩,也就是反向加速度矩,可以让陀螺的角动量逐渐减小,直到陀螺停下来。
总之,动量定理和动量角动量定理是物理学中非常重要的两个概念。
它们既可以帮助我们更好地理解物理学知识,也可以用于实际生活中的问题解决。
大学物理动量角动量

三、质点的角动量定理
L=r×pቤተ መጻሕፍቲ ባይዱ
dL dr dp = × p+r × dt dt dt
r × F =r ×
dP dt
0
υ
dL M = dt
注意: 注意: 1. M, L 必须对同一点 必须对同一点 2. M —合外力矩 合外力矩 3.惯性系成立 惯性系成立
∫t
t2
1
M dt =
∫L d L = L2 L1
M外 = 0 L总 = 常 量 矢
角动量守恒定律
M i = ri × ( Fi + ∑ f ij )
i≠ j
d 注意: M = ∑ ri × Fi = ( ∑ Li ) 注意: dt i i
F外
d P总 = dt
1.内力矩不改变质点系的总 内力矩不改变质点系的总 角动量, 角动量,但可以改变各质点 的角动量。 2. M = ∑ M i 必须对同一点。 必须对同一点。
∫v dv = u ∫M
0
v
M
0
dM M
M0 v = v0 + uln M
Fdt = (v u)dm vdm
u
= udm
它给火箭的推动力 指向前进方向
F ' = F > 0
dm dM F = u <0 =u dt dt
§3 质心运动定理 一 质心
N个粒子系统,可定义质量中心 个粒子系统, 个粒子系统
z mi
rc
ri
y
rc =
∑m r
i =1 N
N
i i
∑m
i =1
=
∑m r
i =1
N
i i
x
2第二章-动量和角动量
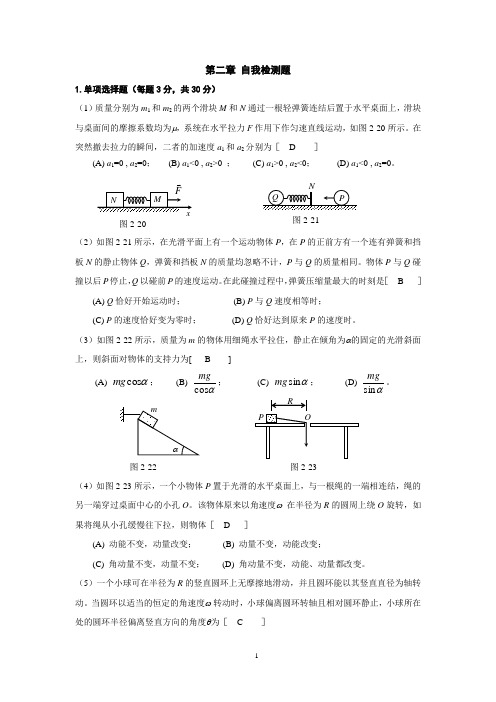
第二章 自我检测题1.单项选择题(每题3分,共30分)(1)质量分别为m 1和m 2的两个滑块M 和N 通过一根轻弹簧连结后置于水平桌面上,滑块与桌面间的摩擦系数均为μ,系统在水平拉力F 作用下作匀速直线运动,如图2-20所示。
在突然撤去拉力的瞬间,二者的加速度a 1和a 2分别为[ D ](A) a 1=0 , a 2=0; (B) a 1<0 , a 2>0 ; (C) a 1>0 , a 2<0; (D) a 1<0 , a 2=0。
(2)如图2-21所示,在光滑平面上有一个运动物体P ,在P 的正前方有一个连有弹簧和挡板N 的静止物体Q ,弹簧和挡板N 的质量均忽略不计,P 与Q 的质量相同。
物体P 与Q 碰撞以后P 停止,Q 以碰前P 的速度运动。
在此碰撞过程中,弹簧压缩量最大的时刻是[ B ] (A) Q 恰好开始运动时; (B) P 与Q 速度相等时; (C) P 的速度恰好变为零时; (D) Q 恰好达到原来P 的速度时。
(3)如图2-22所示,质量为m 的物体用细绳水平拉住,静止在倾角为α的固定的光滑斜面上,则斜面对物体的支持力为[ B ](A) αcos mg ; (B) αcos mg ; (C) αsin mg ; (D) αsin mg。
(4)如图2-23所示,一个小物体P 置于光滑的水平桌面上,与一根绳的一端相连结,绳的另一端穿过桌面中心的小孔O 。
该物体原来以角速度ω 在半径为R 的圆周上绕O 旋转,如果将绳从小孔缓慢往下拉,则物体[ D ](A) 动能不变,动量改变; (B) 动量不变,动能改变; (C) 角动量不变,动量不变; (D) 角动量不变,动能、动量都改变。
(5)一个小球可在半径为R 的竖直圆环上无摩擦地滑动,并且圆环能以其竖直直径为轴转动。
当圆环以适当的恒定的角速度ω 转动时,小球偏离圆环转轴且相对圆环静止,小球所在处的圆环半径偏离竖直方向的角度θ为[ C ]图2-20图2-21图2-22图2-23(A) 2π=θ; (B) g R 2tan arc ωθ=;(C) 2arccosωθR g=; (D) 需由小珠的质量m 决定。
第二章角动量分解

o
x
dx
x
解: 如图,距O点为x,长为dx的质元dm m 的质量 dm dx
其所受阻力矩
M xdmg
l dM x(dm g) mg L 1
l
x
0
xdx
2
mgL
o
dx x
三、质点角动量守恒定律
若外力对某个固定点O的力矩为零时,即 M 0 , 则对同一固定点O的角动量不变,即 L L0
【补充例】质点的圆周运动 (对圆心的)角动量:
L
m
v
【补充例】 行星在绕太阳公转时的椭圆轨 道运动对定点(太阳)的角动量: L
大小: L mvr sin
L r p m(r v)
voBiblioteka rθ方向:垂直于轨道平面
【补充例】 一质量为m、长为L的均匀细棒, 可在水平桌面上绕通过其一端的竖直固定轴转 动,已知细棒与桌面的摩擦因素为 ,求棒转动 时受到的摩擦力矩的大小。
2.何时M 为零? a. F 0 b.力的作用线与轴相交 c.受到有心力作用
注意:
3.如果力 F 的方向始终指向一个固定点,则该力就称为
有心力,该固定点称为这个力的力心。 受到有心力作用的物体,相对于力心,其所受力矩为零。
【补充例】一质量为m的质点沿着一条空间曲线运 动,该曲线在直角坐标下的矢径为:
r a cost i b sint j
其中a、b、 皆为常数,求该质点对原点的角动量。
d r 解: v a sin t i b cos t j d r v dt a sin t i b cos tj
第动量与角动量课件

证角动量守恒定律的正确性。
04
第动量与角动量的应用
第动量与角动量在日常生活中的应用
体育活动
在投掷、击打、跑步等体育活动 中,动量和角动量起着关键作用 ,例如棒球运动员利用角动量原
理转动身体来增加投球速度。
舞蹈和杂技
舞者可以利用角动量来保持旋转, 杂技演员可以利用动量和角动量完 成高难度动作。
交通工具
一个封闭系统,在没有外力矩作用的 情况下,其角动量保持不变。
作用在物体上的力矩,使物体产生旋 转运动。
角动量
一个物体绕某点旋转的动量,等于物 体质量、速度和旋转半径的乘积。
角动量守恒定律的适用范围
适用于封闭系统
角动量守恒定律仅适用于系统边界不随时间变化的封闭系统。
适用于无外力矩作用的情况
只有在没有外力矩作用的情况下,角动量才能保持守恒。
骑自行车、滑冰和驾驶汽车时,动 量和角动量影响平衡和运动轨迹, 例如转弯时自行车利用角动量保持 稳定。
第动量与角动量在科学研究中的应用
物理实验
在研究碰撞、摩擦、旋转等物理 现象时,动量和角动量是重要的 物理量,帮助科学家理解和描述
自然界的运动规律。
天文学
行星和卫星的运动中涉及到角动 量守恒,有助于科学家研究天体
第动量守恒定律的适用范围
01
第动量守恒定律适用于 宏观低速的物理系统, 如物体、质点等。
02
第动量守恒定律不适用 于微观高速的物理系统 ,如原子、粒子等。
03
第动量守恒定律适用于 不受外力作用的封闭系 统,如弹性碰撞、非弹 性碰撞等。
04
第动量守恒定律不适用 于受到外力作用的开放 系统,如摩擦力、重力 等。
运动规律和宇宙演化。
第二章角动量

定义冲量矩:
tb
ta
b Mdt dL Lb La
a
角动量定理的另一形式 在惯性参考系中,质点所受合外力在其任一运动过程 中对任一固定点的冲量矩等于质点对该点的角动量在 该过程中的增量。
1. r 为物体相对于指定参考点的位矢,所以求物体所受 的力矩时必须先指明参考点,相对于不同的参考点,对 应的位矢 r 不同。物体所受的力矩不同。
L
L mrvsin L0
S
L mrvsin L0
开普勒第二定律
L
F
v r
m
dr
L mvr sin
m dr r sin
dt 1 r dr sin dS 2 2m 2m dt dt
dr r dr r 三角形面积
t2 t1
F dt m v 2 m v1
角动量定理(冲量矩与角动量)
t2 t1
L2 M dt L1 d L L 2 L1
动量守恒:某一时间间隔内, 角动量守恒:对固定参考点而 质点系所受外力矢量和始终 言,质点受到的合力矩始终为 为零,… 零,…
dt
L r mv
2 2 mab k mab cos t k mab sin t k
【补充例】质量为 m 的质点,某时刻的位置如图, y 速度为 v 6 j 受力为 F 2 j (4,3) 求:该时刻质点对 0点的角动量 L ? (SI)
o
x
dx
x
解: 如图,距O点为x,长为dx的质元dm m 的质量 dm dx
其所受阻力矩
M xdmg
第2章-2-动量-角动量守恒定律2019

3
4 105
(2)
I
Fdt
00.003
400
4 105 3
t
dt
400t
4105t 2 23
0.003
0.6 N s
0
(3) I mv 0
m I 0.6 0.002kg 2g v 300
2.质点系的动量定理
设有 n 个质点构成一个系统
(2)系统内所有质点的动量都必须对同一个惯性参考 系而言。 (3)若系统所受合外力不为零,但是合外力在某一方 向上的分量为零,则系统在该方向上的总动量守恒。
Fix 0 Px mivix 常量
(4)当外力作用远小于内力作用时,可近似认为系统 的总动量守恒。(如:碰撞,打击,爆炸等过程)
称为“冲量矩”
质点系的角动量定理的推导:
m1
m2
质点系的角动量定理:
质点系对某一参考点的角动量随时间的变化率等于 质点所受的所有外力对同一参考点力矩的矢量和。
质点系角动量定理的积分式:
t2
t1
Mdt
L2
L1
作用于质点系的冲量矩等于质点系在作用时间内
的角动量的增量 。
质点系的z轴的角动量定理:
第 i 个质点: 质量mi
内力 fi
初速度 末速度
外力
vviio
Fi
由质点动量定理:
Fi
i
fi
t
to
Fi
fi
dt mivi
mi vio
t
to Fi fi dt mivi mi vio
大学物理上第2章2-动量--角动量 守恒定律

动量守恒的分量式:
Px mivix 常量 Py miviy 常量 Pz miviz 常量
动量守恒定律是物理学中最重要、最普遍的规律 之一,它不仅适合宏观物体,同样也适合微观领域。
力矩 ( Moment of Force /Torque )
j)
2.质点系的动量定理
设有 n 个质点构成一个系统
第 i 个质点: 质量mi
Fi
内力 fi
初速度 末速度
外力
vviio
Fi
i
由质点动量定理:
fi
t
to
Fi
fi
dt mivi
mi vio
t
to Fi fi dt mi vi mivio
车辆超速容易 引发交通事故
结论: 物体的运动状态不仅取决于速度,而且与物 体的质量有关。
动量(Momentum) :运动质点的质量与
速度的乘p 积。mv
单位:kg·m·s-1
由n个质点所构成的质点系的动量:
p
n
pi
n
mivi
i1
i1
2-2-2 动量定理
1.质点的动量定理
冲量:作用力与作用时间的乘积
⑴ 恒力的冲量:
I F (t2 t1)
⑵ 变力的冲量:
I
t2
F
(t)
dt
t1
单位:N·s
⑶ 平均力的冲量:
牛顿运动定律:
F
第二章 角动量守恒定律
v r
证毕
如图,两个质量相等的人分别抓住轻绳的两端。 例2. 如图,两个质量相等的人分别抓住轻绳的两端。 设开始时两人在同一高度上,此时左边的人从静止 设开始时两人在同一高度上 此时左边的人从静止 同一高度 开始往上爬,右边的人抓住绳子不动, 开始往上爬,右边的人抓住绳子不动,如不计滑轮 的摩擦,问哪个人先到达滑轮? 的摩擦,问哪个人先到达滑轮?如果两人的质量不 等,情况又如何? 情况又如何? 解: 以O点为参考点 点为参考点 系统:人、绳子、滑轮 系统: 绳子、
角动量守恒定律是自然界的一条普遍 定律,它有着广泛的应用。
例1、证明开普勒第二定律:行星和太阳之间的连线 、证明开普勒第二定律: 在相等时间内扫过的椭圆面积相等 。 证明
v 1v v dS = r ×dr 2
v dr
v v dS 1 v dr 1 v v = r × = r ×v dt 2 dt 2 v dS 1 v v 1 v = r ×mv = L 有心力作用下角动量守恒 dt 2m 2m
质点系的角动量 设各质点对O点的位矢分别为 设各质点对 点的位矢分别为
v L
v v v r1 , r2 , L, rn
γ
v LA
A
v v v 动量分别为 p1 , p2 , L, pn
n v n v v v L = ∑Li = ∑(ri × pi ) i =1 i =1
O
2-3-2 力矩
v v v v v dL d(r × p) dr v v dp = = × p+ r × dt dt dt dt v v v dr v v v dp 式中 × p = v× p = 0 =F dt dt dt
z
M = rF sin α
大学物理2-5 角动量 角动量守恒定律

A1 2 = Ek2 E k1
2–5 角动量 角动量守恒定律 5 一对作用力和反作用力的功
m1,m2组成一个封闭系统 在dt 时间内
m 1
r 1
f1
dr 1
dr2 dr1 m1 f1 r1 o r2 r21 f2 m2
m2 r2
f2 dr2
dA = f1 dr1 + f2 dr2
Z注意:不能先求合力,再求合力的功;只能先求每个力 注意:不能先求合力,再求合力的功; 注意 的功,再对这些功求和. 的功,2章 运动定律与力学中的守恒定律 第 再对这些功求和.
2–5 角动量 角动量守恒定律 5
质点系动能定理 质点系动能定理
A外 + A内非 + A内保 = Ek2 Ek1
质点系总动能的增量等于外力的功与质点系内保 守力的功和质点系内非保守力的功三者之和. 守力的功和质点系内非保守力的功三者之和.
注意
内力可以改变质点系的动能, 内力可以改变质点系的动能,但 内力不能改变质点系的总动量
第2章 运动定律与力学中的守恒定律
2–5 角动量 角动量守恒定律 5
功能原理
A内保 = E p = ( E p 2 E p1 )
Ep表示势能总和
A外 + A内非 = ( Ek2 Ek1 ) + ( Ep2 Ep1 )
的方向符合右手法则. L 的方向符合右手法则
第2章 运动定律与力学中的守恒定律
= 90
mv
直角坐标系中角 动量的分量表示
Lx = ypz zpy Ly = zpx xpz
Lz = xpy ypx
2–5 角动量 角动量守恒定律 5
第2章 动量和角动量

L
质点的动量p和 矢径r不互相垂直
L
O
m r
2
p
O
90
0
r
90 0
p
m
d
L pr mvr mr
L pd pr sin mvr sin 2 mr sin
用叉积定义
角动量
v
L
m r
p
r
方向用右手螺旋法规定 角动量方向
一、质点的动量定理
1、动量 (描述质点运动状态,矢量)
P=m v
大小:mv 单位:kgm/s
方向:速度的方向 量纲:MLT-1
2、冲量 (力的作用对时间的积累,矢量) I 方向:速度变化的方向 单位:Ns
(1) 常力的冲量
量纲:MLT-1
I Ft
(2) 变力的冲量
F1 t1
F2 t 2
Mv ( M dM )(v dv) dM(v u) Mv vdM Mdv dMdv vdM udM
Mdv udM 0 v M dM M0 v v0 u ln dv u M v0 M0 M
§3.5 质心**
n 个质点组成质点系的质量中心
Fz dt
t1
t2
4、质点的动量定理的应用
例:逆风行舟 f u
m
v
p1
p
p2
例1、质量为2.5g的乒乓球以
10 m/s 的速率飞来,被板推
v2 30o 45o n
挡后,又以 20 m/s 的速率飞
出。设两速度在垂直于板面 的同一平面内,且它们与板 面法线的夹角分别为 45o 和
力学动量与角动量

力学动量与角动量在物理学中,力学动量和角动量是两个重要的概念。
它们描述了物体或系统的运动特性,并且在许多物理问题的分析中起着至关重要的作用。
本文将深入探讨力学动量和角动量的定义、性质以及在力学中的应用。
一、力学动量力学动量是描述物体线性运动状态的物理量。
它由物体的质量和速度决定,可以用数学公式p = mv来表示,其中p表示动量,m表示质量,v表示速度。
动量的单位是千克·米/秒(kg·m/s),在国际单位制中被广泛采用。
动量具有一些重要的性质。
首先,动量是矢量量,具有大小和方向。
其次,根据牛顿第一定律(惯性定律),一个物体的动量在不受外力作用的情况下保持恒定。
第三,根据牛顿第二定律(力学定律),物体所受外力等于动量的变化率,即F = dp/dt,其中F表示力,t表示时间。
力学动量在力学中具有重要的应用。
例如,在碰撞问题中,动量守恒定律指出,碰撞前后物体的总动量保持不变。
这个定律帮助我们理解物体碰撞时的运动情况。
此外,在运动过程中,动量变化率可以帮助我们分析物体所受的力和物体的运动轨迹。
二、角动量角动量是描述物体旋转运动状态的物理量。
它由物体的质量、速度和距离旋转轴的距离决定,可以用公式L = Iω表示,其中L表示角动量,I表示质量关于旋转轴的转动惯量,ω表示角速度。
角动量的单位是千克·米^2/秒(kg·m^2/s^2)。
角动量也具有一些重要的性质。
与动量类似,角动量也是矢量量,具有大小和方向。
在没有外力矩作用的情况下,角动量守恒,即角动量的大小和方向保持不变。
对于刚体的旋转运动,由于质量分布的不同,转动惯量会有所变化,从而影响角动量的大小。
角动量在力学中也有广泛的应用。
例如,在天体力学中,角动量守恒定律有助于我们研究行星和卫星的运动。
此外,在旋转体的稳定性分析、陀螺仪的原理以及核物理中的粒子自旋等问题中,角动量也发挥着重要的作用。
三、力学动量与角动量的关系力学动量和角动量之间存在一定的联系。
动量和角动量

动量和角动量
•牛顿第二定律——外力的作用,质点产生加速度,运动
状态发生变化。
•力作用需要持续一段时间,即力对时间的累积会产生什 么效果。
5-1 冲量和动量定理
定义:物体的质量与速度的乘积叫做物体的动量
P mv
•动量是矢量,大小为 mv,方向就是速度的方向; • 表征了物体的运动状态
Fdt
冲量(力的作用对时间的积累,矢量)
t2 I = Fdt
单位:N· s 说明
t1
•冲量是表征力持续作用一段时间的累积效应; • 矢量: 大小和方向;
F为恒力时,
I Fdt=P I F t P
P F t
F作用时间很短时,可用力的平均值来代替。
最后简写右 边总动量为:
P Pi mii
i i
P0 Pi 0 mii 0
i i
则,质点系的动量定理为
t2
F外dt P P0
t1
作用于质点系上的 合外力的冲量等于 质点系动量的增量 (矢量式)
5-3 动量守恒定律
一、内容
2 y 2
I
I I 6.14 10 Ns
2 x
tg
Iy
Ix
0.1148
6.54
为 I 与x方向的夹角。
5-2 质点系的动量定理
一、质点系 N个质点组成的系统-- 研究对象 内力 internal force 质点系
系统内部各质点间的相互作用力
特点:成对出现;大小相等方向相反
在给定的时间间隔内,外力作用在质点上的冲量,等于 该质点在此时间内动量的增量——动量定理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 动量和角动量思考题2-1 在什么情况下,力的冲量和力的方向相同?答:冲量是矢量,元冲量的方向总是与力的方向相同.至于在一段较长时间内,力的冲量等于这段时间内各无穷小时间间隔元冲量的矢量和,因此,力的冲量方向决定于这段时间诸元冲量矢量和的方向,不一定和某时刻力的方向相同.当在一段时间内,各无穷小时间间隔元冲量方向都相同时,则这段时间内力的冲量和力的方向相同.另外冲量和平均力的方向总是一致的.2-2 用细线把一重球悬挂起来,球下系一同样的细线,用力拉球下细线并逐渐加大力量,哪段细线先断?为什么?如用较大力量突然拉球下细线,哪段细线先断?为什么?答:无论何种拉法,细线之所以断,是因其所受拉力大于它所能承受的极限张力.缓慢的加大力量拉球下细线时,拉力通过重球均匀的作用于球上方的细线,而上方的细线除受拉力外,还受球对对它的作用力(大小等于球的重力).因此在逐渐加大拉力的过程中,球上方细线中的张力因先达到极限而被拉断.用较大力量突然拉下面细线,意味着作用力较大而作用时间较短,该拉力就是冲力.冲力通过细线首先作用于重球,但由于重球质量很大,动量改变极小,在冲力尚未通过重球的位移传给球上之细线前,球下细线所受冲力已大于其所能承受的极限,因此先断.2-3 棒球运动员在接球时为何要戴厚而软的手套?篮球运动员接急球时往往持球缩手,这是为什么?答:这样做是为了增加手与球的作用时间,从而减小球对手的冲力。
2-4 跳伞运动员临着陆时用力向下拉降落伞,这是为什么?答,人用力向下拉降落伞时,降落伞对人可以产生一个向上的作用力,以致可达到减少人着陆的速度,减轻地面对人的冲力.2-5 悬浮在空气中的气球下面吊有软梯,有一人站在上面.最初软梯和人均处于静止,后来人开始向上爬,问气球是否运动?将怎样运动?答:取人、气球和软梯为系统来分析.当人相对软梯静止时,系统所受重力和浮力的合力为零,垂直方向上,系统的动量为零并守恒,系统的质心将保持原有的静止状态不变.当人沿软梯往上爬时,人与软梯间的相互作用力是内力,而内力不改变系统的总动量,系统所受合外力仍为零,系统的质心位置仍保持不变,总动量也不变所以,根据动量守恒定律可知,当人沿软梯往上爬时,气球和软梯将向下运动.2-6 能否利用装在小船上的风扇搧动空气使小船前进?答:假定风扇固定在小船上.当船上的风扇持续地向船尾搧动空气时,风扇同时也受到了空气的反作用力.该反作用力是向着船头、通过风扇作用于船身的.根据动量定理可知,该力持续作用于船身的效果,使船向前运动的动量获得增量.若该作用力大于船向前运动时所受的阻力,小船就可向前运动.若将风扇转向船头搧动空气,则将使小船后退.2-7 物体m被放在斜面M上,如把m与M看成一个系统,在下列几种情形下,系统的水平方向分动量是否守恒?⑴ m与M间无摩擦,而M与地面向有摩擦;⑵ m与M间有摩擦,而M与地面间无摩擦;⑶ 两处都没有摩擦;⑷ 两处都有摩擦.答:(1)对于系统而言,地面摩擦力是水平方向的外力,它的存在,系统的水平方向分动量不守恒.(2)不论滑动还是不滑动,m与M间的摩擦力都是系统的内力,它不改变系统的动量.对系统,无水平方向的外力,因而系统的水平方向动量守恒.(3)对系统,水平方向无外力,水平方向系统的分动量守恒.(4)不动,显然动量为零且不变.如下滑,水平方向摩擦力为外力,系统水平方向分动量不守恒.2-8 有人说:“质心是质量集中之处,因此在质心处必定要有质量”,这话对吗?答:这话不对.质心是表征物体系统质量分布的一个几何点.质心的位置在平均意义上表示质量分布的中心,质心所在处不一定有质量分布.例如:质量均匀分布的细圆环,其质心在环心,但质量却均匀分布于细圆环上.2-9 物体的质心和重心有何区别?答:物体的质心和重心是两个不同的概念.重心是地球对物体各部分引力的合力(即重力)的作用点.不受重力,也就无所谓重心,在失重环境中,重心自然失去意义,而质心是有意义的.对于地球体积不太大的物体,重心和质心的位置可认为是重合的.2-10 质量为和的两个小孩,在光滑水平冰面上用绳彼此拉对方.开始时静止,相距为,问他们将在何处相遇?答:有质心定理可知,两人在他们的共同质心处相遇。
即在处相遇。
2-11试分析下面的叙述是否正确?⑴作用于质点的力不为零,质点所受的力矩也总不为零.答,不是.作用于质点的力不为零,质点所受的力矩是不一定不为零.因为力矩是位矢和力的矢积,所以,作用于质点的力不为零,质点所受的力矩是不一定不为零.⑵一定质量的质点,在运动中某时刻的加速度一经确定,则质点所受的合力就可以确定了.同时,作用于质点的力矩也可以确定了.答.错误.一定质量的质点在运动中某时刻的加速度一经确定,则质点所受的合力就可以确定了,但是作用于质点的力矩却不能确定.因为作用于质点的力矩与力相对空间点或轴有关,不同的空间定点或轴,力矩不同.⑶作用于质点系的外力矢量和为零,外力矩之和也为零.答:作用于质点系的外力矢量和为零,外力矩之和不一定为零.因为,外力矩和力相对空间点的位矢有关,外力矩不一定为零.⑷质点系的动量为零,则质点系的角动量也为零;质点系的角动量为零,则质点系的动量也为零.答:错误.角动量不但与动量有关,还与动量相对空间点(和轴)的位置有关,所以质点系的动量为零,质点系的角动量不一定零;质点系的角动量为零,质点系的动量也不一定零⑸质点作圆周运动必受到力矩的作用;质点作直线运动必定不受力矩作用.答,错误.质点做匀速圆周运动,质点可以不受力矩作用.质点做直线运动所受的力矩与所选的定点有关.如果定点不在原点,则质点所受的力矩不为零.2-12 作匀速直线运动的物体有没有角动量?动量是否守恒?角动量是否守恒?答:要确定其是对空间点的位置,则角动量就可以确定.例如直线运动的物体对直线外一点的角动量就不为零。
匀速直线运动的物体的速度的大小、方向均不变,所以其动量守恒。
匀速直线运动的物体对空间某一定点的角动量为一常量,故其角动量亦守恒。
2-13 在匀速圆周运动中,质点的动量是否守恒?角动量呢?答:在匀速圆周运动中,质点的速度大小不变但方向始终在变,具有向心加速度,质点受到的合外力不为零,因此它的动量不守恒.在匀速圆周运动中,由于质点所受到的合外力指向圆心,合外力对圆心的力矩为零,因此.质点对圆心的角动量守恒.作匀速圆周运动的质点,对除圆心外的其他点的角动量是不守恒的.2-14 质点的动量与角动量守恒的条件各是什么?质点的动量与角动量能否同时守恒?答:质点动量守恒的条件是:质点所受到的合力为零;角动量守恒的条件是:质点在运动过程中所受到的合力对某参考点的合力矩为零.动量和角动量是两个从不同角度描述物体运动规律的物理量.动量守恒和角动量守恒是两个彼此独立的基本规律,不能相互替代.就某个具体物理过程而言,质点的动量守恒而角动量可以不守恒,或者反之;但也可以同时守恒,或者都不守恒.例如:在惯性系中作匀速直线运动的一个质点,其动量守恒;对空间除直线轨迹外的任一参考点有确定的角动量,对该点的角动量也守恒.2-15 质点在有心力场中的运动具有什么性质?答:有心力的方向始终指向或背离一个给定点,即力心.若质点在运动过程中仅受有心力的作用,则因有心力对力心的力矩为零,质点对力心的角动量守恒;又由于有心力是保守力,可以引进势能的概念,因此在有心力场中运动时,系统机械能也守恒.习题2-1 某飞船的返回舱质量,在着陆前先后采用引伞、减速伞和主伞进行减速.已知弹出引伞时返回舱的下落速度,在前16s内,下落速度降为.求在此过程中:⑴ 返回舱所受重力的冲量;⑵返回舱所受合力的冲量及平均冲力;⑶返回舱所受阻力的冲量.解:动量、冲量和力都是矢量,本题只考虑简单的—维问题,物体只在竖直方向受力和运动,设竖直向下为正方向。
⑴在此回收阶段,返回舱离地面仅约10 km,所受重力G可视为恒力,根据恒力的冲量的定义,则返回舱所受重力的冲量为方向竖直向下⑵ 根据动量定理,返回舱所受合力的冲量为方向竖直向上返回舱所受的平均冲力为方向竖直向上⑶ 因,则返回舱所受阻力的冲量为方向竖直向上2-2 某物体上有一变力F作用,它随时间变化的关系如下:在0.1s 内,F均匀地由0增加到20N;又在以后0.2s内,F保持不变;再经0.1s,F又从20N均匀地减少到0.⑴ 画出F- t图;⑵求这段时间内力的冲量及力的平均值;⑶如果物体的质量为3 kg,开始速度为1m/s,且与力的方向一致,问在力刚变为0时,物体的速度为多大?解:⑴⑵ 根据定积分的定义,用计算面积的方法,可得这段时间内力的冲量为力的平均值为⑶ 根据动量定理,有所以2-3 力作用在质量为10 kg的物体上,式中的单位为秒().若物体原来静止,求:⑴ 4 s时力对物体的冲量以及物体的动量和速度的变化;⑵为了使此力的冲量为,此力应在这物体上作用多长时间.解:⑴ 由冲量的定义式,得沿x轴正向根据动量定理,物体的动量为沿x轴正向物体原来静止,故速度的变化为沿x轴正向⑵ 由题意知解得2-4 一颗子弹由枪口射出时速率为,当子弹在枪筒内被加速时,它所受的合力为(a,b为常数),其中t的单位为秒().⑴假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需的时间;⑵求子弹所受的冲量;⑶求子弹的质量.解:⑴子弹走完枪筒全长所需的时间,由题意,得,所以⑵子弹所受的冲量将t=代入,得⑶ 由动量定理可求得子弹的质量2-5 在光滑水平面上,一质量为m的质点以角速度沿半径为R的圆周作匀速圆周运动.试分别根据冲量的定义式和动量定理,求从0到的过程中外力的冲量.解:由题意知,质点的运动方程为可得所受力为由冲量定义式,可得从0到的过程中,其速度由变为,根据动量定理得2-6 假如一质量为50 kg的人,在操作时不慎从高空竖直跌落下来,由于安全带的保护,最终使他被悬挂起来.已知此时人离原处的距离为2.0m,安全带弹性缓冲作用时间为0.50s.求安全带对人的平均冲力.解:以人为研究对象,分两个阶段进行讨论.在自由落体运动过程中,人跌落至2.0m处时的速度为在缓冲过程中.人受重力和安全带冲力的作用,根据动量定理,有其中,所以安全带对人的平均冲力大小为2-7 一架以的速率水平飞行的飞机,与一只身长为、质量为的飞鸟相碰.设碰撞后飞鸟的尸体与飞机具有相同的速度,而原来飞鸟对于地面的速率很小,可以略去不计.试估计飞鸟对飞机的冲击力(碰撞时间可用飞鸟身长被飞机速率相除来估算).解以飞鸟为研究对象,取飞机运动方向为x轴正向.由动量定理得式中为飞机对鸟的平均冲力,而身长为20 cm的飞鸟与飞机碰撞时间约为,此代入上式可得鸟对飞机的平均冲力为式中负号表示飞机受到的冲力与其飞行方向相反.2-8一质量均匀的柔软绳竖直悬挂着,绳的下端刚好触到水平桌面.如果把绳的上端放开,绳将落在桌面上.试证明:在绳下落过程中的任意时刻,作用于桌面上的压力等于已落到桌面上绳的重量的3倍.证明:取如图所示坐标,设柔绳总长为L,总质量为M.将柔绳视为质点系,t 时刻已有x长的柔绳落至桌面,随后时间内将有质量为()的柔绳(质点)以的速率碰到桌面而停止,它的动量变变化率为:根据动量定理,桌面对柔绳的冲力为:柔绳对桌面的冲力′即:又 , 所以而已落到桌面上的柔绳的重量为所以作用于桌面上的压力N为2-9 质量为M的人手里拿着一个质量为m的物体,此人用与水平面成角的速率向前跳去.当他达到最高点时,他将物体以相对于人为u的水平速率向后抛出.问:由于人抛出物体,他跳跃的距离增加了多少?(假设人可视为质点)解:取如图所示坐标.把人与物视为一系统,当人跳跃到最高点处,在向左抛物的过程中.满足动量守恒,故有式中为人抛物后相对地面的水平速率,为抛出物对地面的水平速率.得的水平速率的增量为而人从最高点到地面的运动时间为所以,人跳跃后增加的距离2-10 一静止的物体炸裂成三块,其中两块具有相等的质量,且以相同速率30m/s沿相互垂直的方向飞开,第三块的质量恰好等于前两块质量之和,求第三块的速度.解:物体的动量原等于零。
