北师大版七年级上册 比较线段的长短
北师大版七年级上册数学比较线段的长短课件

拓展延伸:在直线l上取A、B、C三点,使AB=4cm,BC=3cm. 如果点O是线段AC的中点,那么线段OB的长度是多少?
解:若点C在点B的右侧,如图所示:
因为:AB=4cm,BC=3cm
l
A
OB
C
所以:AC = AB + BC = 4 + 3 = 7 (cm)
因为:点O是线段AC的中点
所以:OA OC 1 AC 1 7 3.5(cm)
因为:点O是线段AC的中点
所以: OA 1 AC 1 1 0.5(cm)
2
2
所以: OB = AB−OA = 4 − 0.5 = 3.5 (cm)
1.(单选题)“把曲折的河道改直,就能缩短距离”,其中
蕴含的数学到理是(
)
A
C
AB
CD
3.(单选题)如图C为线段AB的中点,D在线段CB上,线段
3、用圆规在射线AP上截取MB=a.线段AB 就是所求作的线段。
a
M
BP
线段中点的概念:பைடு நூலகம்
A
M
B
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点。
点M是AB中点
AM
=
BM
1 AB
2
AB=2AM AB=2BM
例2 在直线l上顺次截取A,B,C三点,AB=4cm,BC=3cm 如果O是线段AC的中点, 求线段OB的长。
DA=8,线段DB=4,则线段CD长度为(
A、1
B、2
C、3
B
)
D、4
A
CD B
本节课你的收获是什么?
公理线段
比较线段的 长短
两点间距离定 义
北师大版七年级上册比较线段的长短(课件)

探索&交流
绿地里本没有路,走的人多了… …
根据生活经验,容易发现: 两点之间的所有连线中,线段最短.
探索&交流
这一事实可以简述为:两点之间线段最短. 我们把两点之间线段的长度,叫做这两点之间的距离.
探索&交流
将笔直的铁轨向两个方向无限延长形成了直线。直线没有端点。
例题欣赏 ☞
例题&解析
例1.如图,现实生活中有部分行人选择横穿马路而不走天桥
第四章 基本平面图形
2 比较线段的长短
北师大版七年级数学上册
学习&目标
1.借助具体情境,了解“两点之间的所有连线中,线段最短”的性质. 2.能借助直尺、圆规等工具比较两条线段的长短. 3.能用尺规作一条线段等于已知线段.
情境&导入
回顾:什么叫线段?射线和直线?它们之间的联系和区分是什么?
知识点一 线段的基本事实 为什么大家都喜欢走捷径呢?
AB A′ B′ C′
知识点四 线段的中点
探索&交流
若点M把线段AB分成相等的两条线段AM和BM, 则点M叫线段AB的
中点.
A
M
B
AM =
BM =
1 2
AB
探索&交流
2.对线段的中点的认识: (1)线段的中点是线段上的点,且把线段分成相等 的两条线段; (2)一条线段的中点有且只有一个; (3)如图,若M是AB的中点,则①AM=BM= AB; ②AB=2AM=2BM;③AM+BM=AB且AM=BM.反过来也成立.
哪支铅笔长?
探索&交流
窗框相邻的两条边哪条边长?
探索&交流
探索&交流
思考:请同学们思考并回答下面的问题:
《比较线段的长短》教案-北师版数学七年级上册

(实际生活经验的小视频引入引发学生的兴趣,根据学生的生活经验东知道中间的路线最短,教师要提出疑问,你能用数学道理来解释吗?这节课我们一起来探究一下,引出下一个问题)二、探究学习如右图,从A地到C地有四条道路,那条路最近?你发现了什么规律?结论:线段的性质两点之间的所有连线中,线段最短。
简述为两点之间线段最短。
两点之间线段的长度叫做两点之间的距离。
学以致用:刚才的视频说明的数学道理你知道了么?请同学回答。
三、合作学习:活动一:请两位学生比身高,让学生说明理由。
教师引入你能比较两条线段的长短吗?动动手,小组合作:各小组拿着你们手中的绳子与其他同学的进行比较,看看谁的长,谁的短?并且思考怎样比较两条线段的长短?学生思考并回答结论:1.把其中的一条线段移到另一条线段上去,将其中的一个端点重合在一起加以比较,这种方法叫做叠合法。
2.用刻度尺量出它们的长度,再进行比较,这种方法叫做度量法。
3.说明:如果两条线段相差很大,直接视察就可以进行比较了。
学以致用:怎样比较下面两棵树的高矮?怎样比较两根铅笔的长短?怎样比较窗框相邻两边的长?( ) ( ) ( )活动二:1.什么是尺规作图?2.小组合作交流,试一试用尺规做一条线段等于已知直线。
尺规作图 :只用没有刻度的直尺和圆规画图称为尺规作图教师引导学生:作一条线段等于已知线段如图,已知线段AB,用尺规作一条线段等于已知线段AB.作图规律如下:(1)作射线A′C′(如图所示);(2)用圆规在射线A ′C ′上截取A ′B ′=AB.线段A ′B ′就是所求作的线段.活动三:想一想,折一折,怎样找到你手上绳子的中点位置?点M 把线段AB 分成相等的两条线段AM 与BM, 点M 叫做线段AB 的中点.表达式:如果点M 是线段AB 的中点, 那么AM=BM= ( 21) AB. 或者AB=2AM=2BM 练习:如图示:点C 为AB 的中点,AC=3cm ,则BC=() cm ,AB=()cm 。
北师大版数学七年级上册比较线段的长短课件

Pn
B
必做题:课本112页随堂练习1、2题
习题4.2 第2、3题 选做题:
1、利用尺规作图,设计一个美丽的图案。 2、在同一条直线上取出A、B、C三点使AB =4cm,BC=3cm,如果O是线段AC的中点, M是BC的中点,求线段OM的长度。
两点之间的线段,叫做两点之间的距离。( × ) 注:线段——图形
两点间的距离——长度——数值
议一议
下图中哪棵树高?哪根铅笔长? 窗框相邻两条边哪条边长?
(1)
(2)
(3)
注意:一个端点重合
叠合法: “形”
A
B (1)如果点B在线段CD上,
C
D
记作AB<CD
A
B (2)如果点B在线段CD的延
C
D 长线上, 记作AB>CD
A
M
B
2.如图:点C是线段AB的中点,
(1)若AC=2cm,则BC=___2___cm
(2)若AC=2cm,则AB=___4___cm
(3)若AB=4cm,则BC=__2____cm
A
C
B
∵点C是线段AB的中点(已知)
∴BABCCB==A2CA12A=CB==121222c12m××24(=中=42c点cmm的(中(中定点点义的的) 定定义义))
a
解:
A
M
BC
尺规作图注意事项: 线段AB即为所求. 1、要说明作图结果;
2、保留作图痕迹。
如图点M把线段AB分成相等的两条 线段AM与BM,点M叫做线段AB的中点。
A
M
B
线段中点的符号表示:
∵点M是线段AB的中点(已知) ∴AM=BM= 1 AB (中点的定义)
北师大版七年级上册数学 比较线段的长短 课件
议一议
哪棵树更高?哪支铅笔更长?窗框相邻两边
哪边更长?
实质上
就是怎样比较两条线段的长短?
思考:
要比较两根铅笔的长短,你有几
种方法?
1.可以用尺子分别量两支铅笔的长度,然后比较。
——度量法.
2.可以将两支铅笔叠合在一起,就可以比较出来。
——叠合法.
线段的大小比较
第一种方法是:度量法,
即用一把刻度尺量出两条线段的长度,
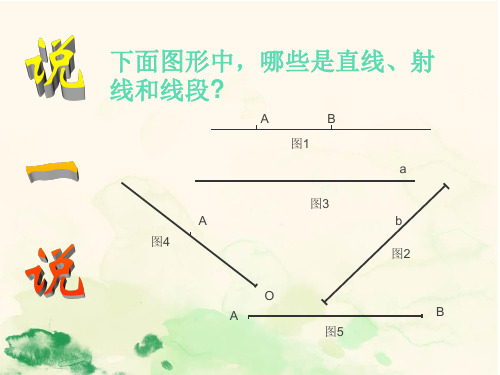
下面图形中,哪些是直线、射
线和线段?
A
B
图1
a
图3
A
b
图4
图2
O
B
A
图5
线段、射线、直线的本质区别
射线
直线
是:_____没有端点,_____只有
线段
一个端点,_____有两个端点。
线段、射线、直线中,只有、
线段
____才可以比较长短.
A
B
直线的基本性质(公理):
经过两点有且只有一条直线.
简述为:
再进行比较。
3.1cm
4.1cm
0
1
2
3
4
5
6
7
8
线段的大小比较
第二种方法是:叠合法
将线段重叠在一起,使一个端点重合,
再进行比较.
叠合法
方法归纳:
比较线段长短的方法有:
1、度量法.
2、叠合法.
注意:
用度量法是从数的方面去比较大小,
而叠合法是从形的方面去比较大小。
重点知识:
你知道什么是尺规作图吗?
B
A
截取A'B'=AB.
(3)线段A'B'为所求作的线段.
北师大版数学七年级上册4.2 比较线段的长短教案

2 比较线段的长短●情景导入 同学们请看大屏幕,认识他们吗?我们目测一下他们的身高,发现姚明高一些.那要是让潘长江老师站到二楼上,姚明站在地面上呢? 如果我们用线段来表示人的身高,又如何比较线段的长短呢?从而引入课题.【教学与建议】教学:把现实生活中的比高矮问题抽象成线段比较长短问题,激发学生解决问题的热情.建议:重点让学生明白两条线段长短的比较方法.●置疑导入 师:如图,从A 村到B 村有四条道路可供选择,你愿意选第几条道路?说出你的理由. 生:走第②条路.因为这条路是直路,感觉它最近.师:虽说条条大路通罗马,但我们都希望走条近路.那么怎样找出最近的路呢?你是怎样得出结论的? 【教学与建议】教学:利用生活中熟悉的情境,极大地激发学生的学习热情.建议:在学生操作时,教师要引导学生进行思考、分析.*命题角度1 利用两点之间线段最短解决问题根据两点之间的所有连线中,线段最短,解决实际问题.【例1】在春季运动会上,七年级的同学想举行一次拔河比赛,他们想从两条大绳中挑出一条最长的绳子,请你为他们选择一种合适的方法是(A)A .把两条大绳的一端对齐,然后拉直两条大绳,另一端在外面的即为长绳B .把两条绳子重合,观察另一端的情况C .把两条绳子接在一起D .没有办法挑选【例2】为抄近路践踏草坪是一种不文明现象,如图是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是(C)A.经过两点有一条直线,并且只有一条直线B .两条直线相交只有一个交点C .两点之间的所有连线中,线段最短D .两点之间线段的长度,叫做这两点之间的距离【例3】把一条弯曲的河道改直,可以缩短航程,这样做的根据是__两点之间线段最短__. *命题角度2 比较线段的长短比较线段长度常用的方法有两种:(1)度量法;(2)叠合法. 【例4】用度量法可得下列线段中最长的是(B)A BC D *命题角度3 线段中点的概念辨析中点具备两个特点:①点在线段上;②把线段分成相等的两条线段,这两者缺一不可. 【例5】如图,B 是线段AD 的中点,C 是BD 上一点,则下列结论中错误的是(C)A .BC =AB -CD B .BC =AC -BDC .BC =12 (AD -CD ) D .BC =12AD -CD【例6】已知线段AB 和点P ,如果P A +PB =AB ,且P A =PB ,则(A) A .点P 为AB 中点 B .点P 在线段AB 的延长线上C .点P 在线段AB 外D .无法确定 *命题角度4 求线段的长度求线段长度,通常借助线段中点的性质和线段的比进行线段长度的变换进行求解.【例7】如图,长度为12 cm 的线段AB 的中点为M ,C 为线段MB 上一点,且MC ∶CB =1∶2,则线段AC 的长度为(A)A .8 cmB .6 cmC .4 cmD .2 cm【例8】如图,B ,C 两点把线段AD 分成长度比为2∶3∶4的三部分,点E 是线段AD 的中点,EC =2 cm ,求:(1)AD 的长; (2)AB ∶BE .解:(1)因为AB ∶BC ∶CD =2∶3∶4,点E 是线段AD 的中点,所以CD =49 AD ,ED =12AD ,所以EC =ED-CD =12 AD -49 AD =2,解得AD =36 cm ;(2)由(1)知,AD =36 cm ,易得AB =36×29 =8(cm),BC =36×39=12(cm),BE =BC -EC =12-2=10(cm).所以AB ∶BE =8∶10=4∶5.高效课堂 教学设计1.借助情境了解“两点之间线段最短”的性质. 2.能借助尺、规等工具比较两条线段的大小. 3.能用圆规作一条线段等于已知线段.线段长短的两种比较方法:线段中点的概念及表示方法;线段的和、差、倍、分关系.叠合法比较两条线段大小;会画一条线段等于已知线段.活动一:创设情境 导入新课(课件:公园曲桥、河道改直的图片)把弯曲的河道改直就可以缩短航程.在公园的河面上修建曲折的桥,就能增加观光的路程,你知道这其中的道理吗?怎样比较两个同学的高矮?你有哪些方法?活动二:实践探究 交流新知 【探究1】 线段公理问题:(多媒体投影P 110图4-6)学生通过观察,实际操作,容易得出线段AC 最短.【归纳】两点之间的所有连线中,线段最短.这一事实可以简述为:两点之间线段最短.我们把两点之间线段的长度,叫做这两点之间的距离.【探究2】 线段的比较多媒体展示P 110“议一议”【归纳】如果直接观察难以判断,我们可以有两种方法进行比较:一种方法是用刻度尺量出它们的长度,再进行比较,即度量法;另一种方法是把其中的一条线段移到另一条线段上去,将其中的一个端点重合在一起加以比较,即叠合法.活动三:开放训练 应用举例【例1】(教材P 111例题)如图,已知线段AB ,用尺规作一条线段等于已知线段AB . 【方法指导】学生通过操作,掌握作一条线段等于已知线段的方法.解:作图步骤如下:(1)作射线A ′C ′(如图所示);(2)用圆规在射线A ′C ′上截取A ′B ′=AB . 线段A ′B ′就是所求作的线段.【例2】(1)如图,点M 把线段AB 分成相等的两条线段AM 与BM ,点M 叫做线段AB 的中点.这时AM =BM =12 AB (或AB =2AM =2BM ).(2)在直线l 上顺次取A ,B ,C 三点,使得AB =4 cm ,BC =3 cm.如果点O 是线段AC 的中点,那么线段OB 的长度是多少?【方法指导】学生画图加以分析,与同伴进行交流,进一步掌握线段中点的性质. 解:如图所示:OB =4-4+32=0.5(cm).活动四:随堂练习1.如图,在我国“西气东输”的过程中,从A 城市往B 城市架设管道,有三条路可供选择,在不考虑其他因素的情况下,架设管道的最短路线是__①__,依据是__两点之间线段最短__.2.已知线段AB =6 cm ,在直线AB 上取点C ,使BC =3 cm ,则线段AC 的长是__9或3__cm. 3.教材第112页上方的“随堂练习”第1题. 解:可用刻度尺量出折线AB 各段线段的长度,再量出线段A ′B ′的长度.将折线AB 各段线段的长度和与A ′B ′的长度作比较,也可用尺规作图法将AB 的每段长度移到线段A ′B ′上,再做判断.4.教材第112页上方的“随堂练习”第2题.解:5.已知线段AB =6,点C 在直线AB 上,BC =4,D 是AC 的中点,那么A ,D 两点间的距离是多少? 解:5或1.活动五:课堂小结与作业学生活动:通过这节课的学习,你掌握了哪些新知识?还有哪些疑问?教学说明:教师引导学生回顾线段的公理,线段的比较,线段的中点等知识,让学生大胆发言,积极与同伴交流,进行知识的提炼和归纳.作业:课本P 112习题4.2中的T 2、T 3、T 4本节课的内容是比较线段的长短,这涉及线段的度量和比较,是几何中的一个基本问题.在教学过程中,把身边的数学材料引入课堂,从而使原来枯燥无味的讲解转变为生动活泼的学习活动,调动了学生学习的积极性,加深了学生对几何知识的理解,从而达到了很好的教学效果,同时也培养了学生分析问题、解决问题、应用数学知识的能力.。
北师大版七年级上4.2比较线段的长短

北师大版七年级上4.2比较线段的长短知识点总结1、线段的性质:两点之间,线段最短。
2、两点之间的距离:两点之间线段的长度叫做两点之间的距离。
3、比较线段长短的方法:(1)目测法;(2)度量法;(3)叠合法4、线段的中点:在线段上,到线段两个端点距离相等的点叫做线段的中点。
5、尺规作图:用没有刻度的直尺和圆规作图6、用尺规作线段:(1)作一条线段等于已知线段;(2)作一条线段等于已知线段的二倍;(3)作一条线段等于已知线段的和或差。
其方法是相同的,都是先画一条射线,然后用圆规在射线上截取即可,注意保留作图痕迹,画完图形后写出总结“某某线段即为所求作的线段”。
尺规作图的定义:仅用圆规和没有刻度的直尺作图的方法叫做尺规作图.要点诠释:(1)只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.(2)直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上面画刻度.(3)圆规可以开至无限宽,但上面也不能有刻度.它只可以拉开成之前构造过的长度.2.线段的中点:如下图,若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.3. 用尺规作线段或比较线段(1)作一条线段等于已知线段:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a.要点诠释:几何中连结两点,即画出以这两点为端点的线段.(2)线段的比较:叠合比较法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.如下图:要点诠释:线段的比较方法除了叠合比较法外,还可以用度量比较法.如图所示,在一条笔直公路a的两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村的距离之和最小,问汽车站C的位置应如何确定?【答案与解析】解:如图,连接AB与直线a交于点C,这个点C的位置就是符合条件的汽车站的位置.【总结升华】“两点之间线段最短”在实际生活中有广泛的应用,此类问题要与线段的性质联系起来,这里线段最短是指线段的长度最短,连接两点的线段的长度叫做两点间的距离,线段是图形,线段长度是数值.举一反三:【变式】(1)如图1所示,把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?(2)如图2,公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比,这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理.【答案】解:(1)河道的长度变小了.(2)由于“两点之间,线段最短”,这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.思维导图教学设计一、教材分析:1、教材的地位和作用本节课是教材第五章《平面图形及其位置关系》的第二节,是平面图形的重要的基础知识。
(名师整理)最新北师大版数学7年级上册第4章第2节《比较线段的长短》精品课件

学习了本课后,你有哪些收获和感想? 告诉大家好吗?
1、线段的基本性质:两点之间线段最短。 两点之间的距离:两点之间线段的长度。
2、尺规作图:作一条线段等于已知线段。 3、线段的两种比较方法:叠合法和度量法。 4、线段的中点的概念及表示方法。
光读书不思考也许能使平庸之辈知识 丰富,但它决不能使他们头脑清醒。
_______________________________
两点之间线段最短
问题⑴在它们追食的过程中哪个跑得更远? 你是怎样比较的?
问题⑵ 如何比较两支铅笔的长短?
问题⑶如何比较两名同学的身高呢?
怎样比较两条线段的长短呢?
度量法:用刻度尺量出它们的长度再进行 比较,此种方法称之为“度量法”.
叠合法:把它们放在同一条直线上,将其 中的一个端点重合在一起加以比较,此种 方法称之为“叠合法”.
—— 约·诺里斯
如何比较两条线段的长短
尺规作图
尺规 作图
作一条线段等于已知线段
已知:线段AB. 求作:线段A’ B’,使A’ B’=AB.
作法与示范:
作
法
A
B
示
范
(1)作射线A’C’ ;
(2) 以点A’圆心,
以AB的长为半径 画弧,
交射线A’ C’于点B’,
A’
A’B’ 就是所求作的线段.
A’
C’
B’
1.请你用尺规作图画线段DE等 于已知线段AB.
2、已知线段a、b,你能作一条线段c, 使c=2a吗?线段d=2a+b又应该怎么画?
线段中点
如图,点M把线段AB分成相等的两 条线段AM与BM,点M叫做线段 AB的中点.
这时AM=BM=
1 2
2024年秋北师大七年级数学上册4.1.2 比较线段的长短(课件)

b. a
b
2a
b A 2a-b B
探究新知
知识点 4 线段的中点
A
MB
在一张纸上画一条线段,折叠纸片,使线段的端 点重合,折痕与线段的交点处于线段的什么位置?
探究新知
A
MB
如图,点M 把线段 AB 分成相等的两条线段AM 与BM, 点 M 叫做线段AB 的中点.类似地,还有线段的三等分点、 四等分点等.
相等的线段?
小提示:在可打开角度 的最大范围内,圆规可 截取任意长度,相当于 可以移动的“小木棍”.
探究新知
讨论 你们平时是如何比较两个同学的身高的?你能从 比身高的方法中得到启示来比较两条线段的长短吗?
探究新知
比较两个同学高矮的方法:
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较.
——度量法.
想一想 如图:从A地到 C 地有四条道路,哪条路最 近?在图上标出.D NhomakorabeaE
F
A
C
B
探究新知
D
E
F
A
C
B
经过比较,我们可以得到一个关于线段的基本事实: 两点之间的所有连线中,线段最短. 这一事实可以简述:两点之间,线段最短. 连接两点间的线段的长度,叫做 这两点的距离.
你能举出这条性质在生活中的应用吗?
探究新知
议一议 如图,这是 A,B 两地之间的公路,在公路工程 改造计划时,为使 A,B 两地行程最短,应如何 设计线路?请在图中画出,并说明理由.
B. A.
两点之间线段最短.
探究新知 想一想 把原来弯曲的河道改直,A,B 两地间的河道长 度有什么变化?
A,B 两地间的河 道长度变短.
A
4.2 比较线段的长短 北师版数学七年级上册课件

目录
讲贰 授 新 知
当叁 堂 训 练
课肆 堂 小 结
壹 新课导入
1.如何表示一条线段?它有哪些特点?
用线段的两个端点字母表示或者一个小写字母表示, 向两端不延伸,可度量. 2.把弯曲的河道改直就可以缩短航程.在公园的河面 上修建曲折的桥,就能增加观光的路程,你知道这其 中的道理吗?怎样比较两个同学的高矮?你有哪些方 法?
2.若点B在线段AC上,AB=6cm,BC=10cm,P、Q分别是AB、BC的
中点,则线段PQ的长为( D )
A.3cm
B.5cm
C.6cm
D.8cm
3.已知线段AB=6cm,在直线AB上画线段BC,使BC=2cm,
则线段AC的长为( D )
A.4cm
B.8cm
C.6cm
D.8cm或4cm
4.如图,从学校A到书店B有①②共2条路线,最短的是①号路线,
知识点二:比较线段的长短
A
B
⑤若端点B落在CD外
则得到线段AB大于线段CD,可记作:AB >CD
二、度量法:用刻度尺分别量出线段AB和线段CD
的长度,再将长度进行比较.
例2.如图,用圆规比较两条线段AB和A′B′的长短, 其中正确的是( C ) A.A′B′>AB B.A′B′=AB C.A′B′<AB D.没有刻度尺,无法确定
你会作一条线段等于已知线段吗? 4.什么是线段的中点?有哪些数量关系?
基础题:1.课后习题 第 1,2,3题。 提高题:2.请学有余力的同学采取合理的方式,搜集 整理与本节课有关的“好题”,被选中的同学下节课 为全班展示。
谢谢
贰 讲授新知
知识点一:线段的基本事实 如图,从A地到C地有四条道路,哪条路最近?
比较线段的长短北师大版数学初一上册教案

比较线段的长短北师大版数学初一上册教案教案一:教学内容:比较线段的长短教学目标:1. 学生能够通过视觉比较线段的长短。
2. 学生能够用数学符号表示线段的长短关系。
教学重点:比较线段的长短教学难点:用数学符号表示线段的长短关系教学准备:纸、铅笔、直尺教学过程:Step 1 导入新知1. 引导学生观察教室中的不同物体,并比较它们的大小。
2. 提出问题:你是如何判断不同物体的大小的?3. 引导学生发现,我们可以通过直观观察来判断物体的大小。
4. 引导学生思考,线段的长短也可以通过直观观察来判断吗?Step 2 学习新知1. 引导学生观察两条线段AB和CD,并比较它们的长短。
2. 引导学生发现,线段AB的长度大于线段CD,可以表示为AB > CD。
3. 通过类似的比较,引导学生记住其他符号,如“小于”<、“等于”=等。
Step 3 练习巩固1. 让学生用纸和铅笔画出两条线段,并通过比较判断线段的长短关系。
2. 让学生互相交流和比较自己画的线段的长短,用数学符号表示出来。
3. 提供更多的练习题,让学生通过比较线段的长度并用数学符号表示出来。
Step 4 拓展应用1. 张贴一些图片,让学生比较不同线段的长度,并用数学符号表示出来。
2. 教师出示一些实际生活中的例子,让学生比较不同物体的长度并用数学符号表示出来。
3. 让学生用线段比较法判断图形的大小关系,并用数学符号表示出来。
教学反思:本节课通过直观观察线段的长短,引导学生理解和掌握了比较线段的方法,并能够用数学符号表示线段的长短关系。
通过练习巩固和应用拓展,提高了学生对线段比较的能力和应用能力。
北师大版七年级上册数学4.2《比较线段的长短》【课件】 (共19张PPT)

∵ 点D是线段BC的中点, ∴ CD = B12C = 1.5厘米 ∴ AD = AC + CD = 3 + 1.5 = 4.5厘米
小结: 本节课你学习哪些知识?
∵ 点O是线段AC的中点 ∴ OC= 1AC = 3.5cm
∴ OB= OC2-BC = 3.5-3 = 0.5(cm). 答:线段OB的长为0.5cm。
1、以下图形能比较大小的是〔 C 〕 A、直线与线段 B、直线与射线 C、两条线段
D、射线与线段
2、判断: 假设AM=BM,那么M为线段AB的中点。
D
E
F
A
C
B
问题二 从教室A地到图书馆B,总有少数同学不走人行道而横穿草坪,
这是为什么呢?
因为人行道是弯曲的,距离远,而横穿草坪所走的路是直的,距离最短。
经过上面的探究,你发现了什么? 两点之间的所有连线中,线段最短。简述为: 两点之间线段最短。 两点之间线段的长度叫做这两点之间的距离。
以下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条 边长?你是怎么比较的?
如果点M是线段AB的中点, ∵ 点M是线段AB的中点
1
那么AM=BM= AB。 ∴ AM = BM = A2B
或者AB=2AM=2BM
例:在直线l上顺次取出A、B、C三点,使AB=4cm, BC=3cm,如果O是线段AC的中点,求线段OB的长度?
解:∵ AB=4cm BC=3cm ∴ AC=AB+BC=7cm
第四单元 · 课题二
比较线段的长短
【学习目标】
1、了解线段的性质及“两点之间的距离〞、比较两条线段的长短。 2、线段中点的定义和运用。 3、能用尺规作一条线段等于线段。
复习: 1.线段、射线、直线的定义及特征。 2.线段、射线、直线中____可以度量长度,所以只有____才可以比较长短。
比较线段的长短课件北师大版数学七年级上册

C
B
合作探究
如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B
地的最短道路?如果能,请你在图上画出最短路线.
A
结论:两点之间的所有连线中,线段最短.
• B
认识概念
上述结论可以简述为:
两点之间,线段最短.
我们把两点之间线段的长度,叫做:
这两点之间的距离.
典例剖析
如图,从甲地到乙地有四条道路,其中最短的路线是
【解】设AB=2x,则BC=3x,CD=4x,
由线段的和差,得AD=AB+BC+CD=9x.
由E为AD的中点,得ED= AD= x.
由线段的和差得,CE=DE-CD= x-4x= =2.
解得x=4.所以AD=9x=36(cm).
【类型三】线段中点的性质应用
【例】在直线L上依次取三点M,N,P, 已知MN=5,NP=3, Q是线段MN的
应用探究
【类型一】根据线段的中点求线段的长
【例】如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是
线段AC、BC的中点.
(1)求线段MN的长;
(2)根据(1)中的计算过程和结果,设AB=a,其它条件不变,你能猜出
MN的长度吗?请用简洁的话表达你发现的规律.
1
2
【解析】 (1)先根据M、N分别是线段AC、BC的中点得出MC= AC,
在C、D之间,
点D_____,
重合
在CD的延长线上,
那么AB____
< CD.
那么AB=CD.
> CD.
那么AB ___
典例剖析
例 如图,已知线段AB,用尺规作一条线段等于已知线段AB.
北师大版七年级数学上册《比较线段的长短》课件(共13张PPT)

2、随堂练习 :2
3、如图,从到有4条道
路,为了节约时间,你
会选择
条路。
如图是一个四边形,现在 取各边的中点并连接成四 边形,想一想得到的四边 形与原四边形,哪一个的 周长大?如是在各边任意 取一点呢?
H A E
B
F
D G C
师生交流、小结作业
1、两点之间的距离是指_____. 2、两点之间, _____最短. 3、线段的长短比较有_____法和_____法,具
猫狗追食物动画 >>
结论:
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
看看谁有办法
1、想一想:小狗跑得远?还是小猫跑得远?你是怎
么比较的? (独立思考、小组交流)
情境2:老师在本班找两个个子差别不大的学 生,问大家谁高?你是怎比较的?
师生交流并小结
小结:1、目测法 2、度量法 3、叠合 法
在纸上画一条线段,你能动手折出线段的 中点吗?
1、你能用圆规作一条线段等于已知线段吗? (教师指导,和学生一起动手,并规范描述)
用圆规作一条线段等于已知线段
三步骤: 1、画射线 2、度量已知线段 3、移到射线上
自我检测,及时反馈
1、已知线段 a,b,你能作一条线段c,使 c= 2a+b 吗?(学生完成)
谢谢观赏
You made my day!
我们,还在路上……
方法之一: 方法之二:
线段长短比较(目测法) 线段长短比较(测量法)
方法之三:
线段长短比较(叠?
答:圆规
1、随堂练习 1
2、
如图,点M在线段AB上,请你比较 线段A M与线段 B M的大小.(用两
北师大版(2024新版)七年级数学上册第四章课件:4.1 课时2 比较线段的长短

探究新知
比较下图哪棵树高?哪支铅笔长?窗框相邻的两条边 哪条边长?你是怎么比较的?
直接观察
直接观察难以判断
探究新知
可以将铅笔的一端重合,再进行比较; 窗框无法移动,可以测量这两条边的长度进行比较; 也可以用一根绳子作为中介去比较.
探究新知
思考:怎样比较两条线段的长短呢?
截取A'B' =AB.
B'
C'
线段A'B'就是所求作的线段.
典型例题
例1 比较折线AB和线段A'B'的长短,你有什么方法?需要 什么工具?
分析:用圆规将折线段的每一小段卡住,将其依次移到 线段A'B'上. 答:可以利用圆规进行比较,折线AB比较长.
探究新知
思考:在一张纸上画一条线段,折叠纸片,使线段的端点 重合,折痕与线段的交点处于线段的什么位置?
A
MB
探究新知
A
MB
如图,点M 把线段AB分成相等的两条线段AM 与BM,
点M 叫做线段AB 的中点.
这时AM =BM=12AB或AB=2AM =2BM.
注意: 线段的中点只有一个,且一定在该线段上.
典型例题
例2 在直线 l 上顺次取A,B,C三点,使得AB=4 cm,
BC=3 cm,如果点O是线段AC的中点,那么线段OB的
课堂练习
2. 如图所示,直线MN表示一条铁路,铁路两旁各有一点A 和B,表示两个工厂.要在铁路上建一货站,使它到两厂距 离之和最短,这个货站应建在何处?
分析:在M上任选一点P,它到A,B 的距离即线段PA与PB的长,结合两 点之间线段最短可求.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
议一议
下图中哪棵树高?哪支铅笔长?窗框相邻的两条边 哪条边长?你是怎么比较的?与同伴进行交流.
01 2 3 4 5 6 7 8
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
七年级数学北师版·上册
第四章 基本平面图形
比较线段的长短
教学目标
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
如图,从A地到B地有四条道路,除它们外能否 再修一条从A地到B地的最短道路?如果能,请你在 图上画出最短路线.
A•
•
B
发现:两点之间的所有连线中,线段最短
新知探究
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
1.了解“两点之间线段最短”的性质以及两点间距 离的概念. 2.理解线段中点的概念及表示方法.(难点) 3.能借助直尺、圆规等工具比较两条线段的长短 (重点、难点)
情景导入
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
例1 如图所示,直线MN表示一条铁路,铁路两旁各 有一点A和B,表示两个工厂.要在铁路上建一货站, 使它到两厂距离之和最短,这个货站应建在何处?
P P [解析] 在MN上任选一点P,它到A,B的距离即线段PA 与PB的长,结合两点之间线段最短可求.
解:连接AB,交MN于点P,则这个货站应建在点P处.
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
例2 如图,已知线段AB,用尺规作一条线 段等于已知线段AB.
解:作图步骤如下:
(1)作射线A'C';
(2)用圆规在射线A'C'上截 取A'B'=AB.
A
B
(3)线段A'B'为所求作的线段. A'
B' C'
新知探究
如图,已知线段a,b,求作线段AB=2a+b.
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
归纳总结
(1)两点之间的距离的概念描述的是数量,而 不是图形,指的是连接两点的线段的长度,而不 是线段本身.
(2)在解决选择位置、求最短距离等问题时, 通常转化为“两点之间线段最短”.
01 2 3 4 5 6 7 8
新知探究
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shuxue/ 美术课件:/kejian/meis hu/ 物理课件:/kejian/wuli/ 生物课件:/kejian/shengwu/ 历史课件:/kejian/lishi/
归纳总结
上述发现可以总结为: 两点之间,线段最短
我们把两点之间线段的长度,叫做这 两点之间的距离.
新知探究
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
小明
小明家
我要到学校可以 怎么走呀?哪一 条路最近呀?
邮局
商店
学校
新知探究
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuwen/ 英语课件:/kejian/yingyu/ 科学课件:/kejian/kexue/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
