华罗庚金杯赛初一初赛试题及答案
第十六届华罗庚金杯少年数学邀请赛初赛试卷初一组1

第十六届华罗庚金杯少年数学邀请赛初赛试卷(初一组 )(时间: 2011 年 3 月 19 日 10: 00~11:00)一、选择题 (每题 10 分。
以下每题的四个选项中,仅有一个是正确的。
请将表示正确答案的英文字母写在每题的圆括号内。
)1.船在江中顺流航行与逆水航行的速度之比为 7:2,那么它在两港间来回一次的均匀速度与顺水速度之比为 ()。
(A)7(B)9(C)2(D)4。
141499AP2. 如右图所示,三角形 ABC 的面积为 1cm2。
AP 垂直 B 的均分C线 BP 于 P。
则与三角形 PBC 的面积相等的长方形是 ()。
B0.5cm0.5cm0.5cm0.5cm0.9cm 1.0cm 1.1cm 1.2cm(A)(B)(C)(D)3. 设 a,B 是常数,不等式x1>0 的解集为 x<1,则对于 x 的不等式 bx a>0 a b5的解集是 ()。
(A) x> 1(B) x<1(C) x>1(D) x<1。
55554. 右图所示的五角星是用螺栓将两头打有孔的 5 根木条连结组成的图形,它的形状不稳固。
假如在木条交错点打孔加装螺栓的方法使其形状稳固,那么至少需要增添 ()个螺栓。
(A)1(B)2(C)3(D)4 。
5.对四堆石子进行以下“操作”:每次同意从每堆中各拿掉同样个数的石子,或从任一堆中拿出一些石子放入另一堆中。
若四堆石子的个数分别为 2011,2010,2009,2008,则按上述方式进行若干次“操作”后,四堆石子的个数可能是()。
(A)0,0,0,1(B)0,0,0,2(C)0,0,0,3(D)0,0,0,4。
6.对于 0 x 100,用[x] 表示不超出 x 的最大整数,则 [x] [ 5x]的不一样取值的个数3为()。
(A) 267 (B) 266 (C) 234 (D) 233 。
二、填空题(每题 10 分,满分 40 分)7. 对整数按以下方法进行加密;每个数字的数字变为与7 乘积的个位数字,再把每个数位上的数字 a 变为 10 a。
华罗庚金杯赛初一初赛试题及答案

华罗庚金杯赛初一初赛试题及答案文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-1.代数和的个位数字是().(A)7(B)8 (C)9(D)02.已知则下列不等式成立的是().3.在数轴上,点A和点B分别表示数a和b,且在原点O的两侧.若AO=2OB,则a+b=().4.如右图所示,三角形ABC是直角三角形,∠ABC=60度.若在直线AC或BC上取一点P,使得三角形PAB为等腰三角形,那么这样的点P的个数为().(A)4(B)5(C)6(D)75.如右图,乙是主河流甲的支流,水流流向如箭头所示.主流和支流的水流速度相等,船在主流和支流中的静水速度也相等.已知AC=CD,船从A处经C开往B处需用6小时,从B经C到D需用8小时,从D经C到B需用5小时.则船从B经C 到A,再从A经C到D需用()小时.6.甲、乙、丙、丁四种商品的单价分别为2元, 3元, 5元和7元.现从中选购了6件共花费了36元.如果至少选购了3种商品,则买了()件丁商品.(A)1(B)2(C)3(D)4二、填空题(每小题10分,共40分)7.如右图,在平行四边形ABCD中,AB=2AB.点O为平行四边形内一点,它到直线AB, BC, CD的距离分别为a,b,c,且它到AD和CD的距离相等,则2a-b+c=.8.如右图所示,韩梅家的左右两侧各摆了3盆花.韩梅每次按照以下规则往家中搬一盆花:先选择左侧还是右侧,然后搬该侧离家最近的.要把所有的花搬到家里,共有种不同的搬花顺序.9.如右图,在等腰梯形ABCD中, AB//CD, AB=6, CD=14, ∠AEC=90度, CE=CB,则10.已知四位数x是完全平方数,将其4个数字各加1后得到的四位数仍然是完全平方数,则x=.。
初中竞赛数学第十届“华罗庚金杯”少年数学邀请赛初一第一试(含答案)

第十九届“华罗庚金杯”少年数学邀请赛试题初一年级 第一试(时间:2018年4月9日上午10:00—11:30)一、选择题:(每小题6分,共60分)1、已知a 、b 都是有理数,且|a|=a ,|b|≠b ,则ab=( )(A )负数; (B )正数; (C )负数或零; (D )非负数2、如图,数轴上每个刻度为1个单位长,点A 对应的数为a ,B 对应的数为b ,且b-2a=7,那么数轴上原点的位置在( )(A )A 点; (B )B 点; (C )C 点; (D )D 点。
3、下列说法正确的是( )(A )-a 的相反数是a; (B )-a 的倒数是-1a; (C )-a 的绝对值是a; (D )-a 2一定是负数; 4、大于353-⎛⎫ ⎪⎝⎭而不大于(-3)2的整数总共有( ) (A )12个; (B )13个; (C )14个; (D )15个。
5、有8个编号分别是①至⑧的球,其中有6个球一样重,另外两个球都轻1克,为了找出这两面三刀个球,用天平称了3次:第一次:①+②比③+④重;第二次:⑤+⑥比⑦+⑧轻;第三次:①+③+⑤与②+④+⑧一样重,则两个轻球的编号分别为( )(A )①③; (B )②④; (C )⑥⑧; (D )④⑤。
6、如图,AB ∥CD 则下列等式成立的是( ) (A )B F D E G ∠+∠+∠=∠+∠ (B )E F G B D ∠+∠+∠=∠+∠(C )F G D E B ∠+∠+∠=∠+∠ (D )B E F D G ∠+∠+∠=∠+∠7、点P 为线段MN 上任意一点,点Q 为NP 的中点,若MQ=6,则MP+MN 为( )(A )8. (B )10。
(C )12 (D )不确定8、已知p+2q=0,(q ≠0),则123p p p q q q-+-+-=( )(A )4; (B )6; (C )3; (D )4或6。
9.若abcd 表示一个四位数,且ab dc =,如1331,2552,则abcd 称为四位对称数,将这样的四作画数由小到大排列起来,第12个四位对称数是( )(A )2442 (B )2112 (C )2332 (D )222210、若A 、B 、C 、D 、E 五名运动员进行乒乓球单循环赛(即每两人赛一场),比赛进行一段时间后,进行过的场次数与队员的对照统计表如下:A C B那么与E (A )A 和B (B )B 和C (C )A 和C (D )A 和D二、填空题:(每小题6分,共90分)11、请将2、2、11、11这四个数用加减乘除四则运算以及括号组成结果为24的算式(每个数有且只能用一次): 。
第22届“华杯赛”初赛试卷初一组试卷

第二十二届华罗庚金杯少年数学邀请赛初赛试卷(初一组)初赛试卷(初一组) (时间: 2017年12月10日10:00—11:00) 一、选择题(每小题10分, 共60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1. 若(121 3.125)121x -⨯÷的值为 3.38-(精确到0.01), 则整数x 为( ). (A )30- (B )31- (C )32- (D )33-2. 已知当x m =时, 代数式3263x x ++的值为11, 则当1x m =时, 代数式32431x x --的值为( ). (A )11- (B )11 (C )0 (D )4-3. 如图所示, 在四边形ABCD 中, BC CD DA ==, DC BC ⊥, 150D ∠=o , 则ABC ∠=( ). (A )75o (B )70o (C )65o (D )60o4. 将不大于2017的整数2017, 2016, 2015, L , 1, 0, 1-, 2-, L 中的相邻三个整数乘积依次排成一列201720162015⨯⨯, 201620152014⨯⨯,……210⨯⨯, 10(1)⨯⨯-, 0(1)(2)⨯-⨯-, L , 记这列数的前n 个数的和为n S , 则当n S 取得最大值时, n 的取值有( )个. (A )1(B )2(C )3(D )45. 将有理数8584, 8887-, 8483, 8786-, 8685两两相乘得到10个积, 将10个积从大到小顺序排列, 排在第5个的积是有理数( )的乘积.(A )8483和8887- (B )8685和8887-装订线B ACD 150o第二十二届华罗庚金杯少年数学邀请赛初赛试卷(初一组)M G F E D C B A(C )8584和8786- (D )8685和8786-6. 已知x , y , m 满足等式1||12x m +=-, ||11y m +=+, 且m 是整数, 则22x y m ++的值是( ).(A )0 (B )12 (C )14 (D )2二、填空题(每小题 10 分, 满分40分). 7. 小明在网上超市购买一件商品, 可以享受原价88折的会员优惠价, 同时网站正在做每满100元减20元的促销活动(每满100元减20元是指, 每个100元少付20元.例如商品价格268元, 含有2个100元, 应少付40元, 实际付款228元).超市规定促销优惠和会员优惠不能同时使用.计算后, 小明发现这件商品的促销优惠价格要比会员价低90元, 那么它的原价为元.8. 放在同一个储藏室会发生爆炸的两种化工产品需用不同的储藏室来存放;不会发生爆炸的可以放在一个储藏室.下图中的10个点表示十种不同的化工产品, 放在同一个储藏室会发生爆炸的两种化工产品对应的两点之间用线连接表示, 否则不用线连接.为了保证这十种化工产品的安全, 至少要用个储藏室.9. 如图, 正方形ABCD 和正方形CEFG 的面积分别为4平方厘米和36平方厘米, 90DCG ∠=o , M 是BF 的中点.则三角形DMG 的面积为平方厘米.10. 从自然数1至2017中选出一个数n , 使得余下的2016个数的和除以2003的余数与n 除以2003的余数相同, 则n =.。
第七届“华罗庚金杯”少年数学邀请赛(初赛试题与解答)

第七届“华罗庚金杯”少年数学邀请赛(初赛试题)1.把1999分成两个质数的和,有多少种方法。
2.澳门人口43万,90%居住在半岛上,半岛面积7平方千米,求半岛上平均每平方千米有多少万人?(取两位小数)3.某人去年买一种股票,当年下跌了20%,今年应上涨百分之几,才能保持原值。
4.某个月里有三个星期日的日期为偶数,请推算出这个月的15日是星期几?5.火树银花楼七层,层层红灯倍加增,共有红灯三八一,试问四层几红灯?6.左下图是由9个等边三角形拼成的图形,已知中间最小的等边三角形的边长是1,求这个六边形的周长是多少?7.一个正六边形的苗圃,用平行于苗圃边缘的直线,把它分成许多相等的正三角形,在三角形的顶点上都栽种上树苗,已知苗圃的最外面一圈栽有90棵,请问苗圃中共栽树苗多少棵?8.甲、乙、丙三所小学人数的总和为1999,已知甲校学生人数的两倍,乙校学生人数减3,丙校学生人数加4都是相等的。
问甲、乙、丙各校学生人数是多少?9.小明爷爷的年龄是一个两位数,将此两位数的数字交换得到的数就是小明爸爸的年龄,他俩年龄之差是小明年龄的4倍,求小明的年龄?10.用10块长7厘米,宽5厘米,高3厘米的长方体积木拼成一个长方体,问这个长方体的表面积最小是多少?11.时钟的时针和分针在6点钟恰好反向成一条直线,问下一次反向成一条直线是什么时间?(准确到秒)第七届“华罗庚金杯”少年数学邀请赛初赛试题解答1、答案:1种。
解:在所有的质数中,只有2是偶数,其它都是奇数。
1999是奇数,不可能分成两个奇质数的和,一定是一奇一偶的情形。
(1999=2+1997)此题有唯一的解。
注:本题的实质是考察在质数中只有一个是偶数,另外奇数分成两个整数的和只能是一个是奇数,另一个是偶数,懂得了这个道理,问题便迎刃而解。
2、答案:5.53万人。
解:先求半岛上共有多少万人:43×90%=38.7(万人)再求平均每平方千米的人数是多少? 38.7÷7≈5.53(万人)综合算式:43×90%÷7≈5.53(万人)注:本题是一道简单的应用题,只是要求我们计算时要准确、迅速。
初一华杯赛考试题及答案

初一华杯赛考试题及答案一、选择题(每题3分,共30分)1. 已知a、b、c是三个不同的自然数,且a+b+c=6,那么a、b、c中至少有一个是偶数,说法正确吗?A. 正确B. 错误C. 不确定答案:A2. 一个数的平方是36,这个数是多少?A. 6B. -6C. 6或-6答案:C3. 一个两位数,十位上的数字是x,个位上的数字是y,这个两位数可以表示为:A. 10x+yB. 10y+xC. x+y答案:A4. 一个数的相反数是-5,这个数是:A. 5B. -5C. 0答案:A5. 一个数的绝对值是5,这个数是:A. 5B. -5C. 5或-5答案:C6. 一个数的倒数是1/3,这个数是:A. 3B. 1/3C. 3或1/3答案:A7. 一个数的平方是25,这个数是:A. 5B. -5C. 5或-5答案:C8. 一个数的立方是-8,这个数是:A. -2B. 2C. -2或2答案:A9. 一个数的绝对值是3,这个数是:A. 3B. -3C. 3或-3答案:C10. 一个数的相反数是2,这个数是:A. 2B. -2C. 0答案:B二、填空题(每题3分,共30分)11. 一个数的平方是49,这个数是______。
答案:7或-712. 一个数的立方是-27,这个数是______。
答案:-313. 一个数的倒数是2,这个数是______。
答案:1/214. 一个数的绝对值是4,这个数是______。
答案:4或-415. 一个两位数,十位上的数字是3,个位上的数字是4,这个两位数是______。
答案:3416. 一个数的相反数是-3,这个数是______。
答案:317. 一个数的平方是16,这个数是______。
答案:4或-418. 一个数的立方是64,这个数是______。
答案:419. 一个数的绝对值是2,这个数是______。
答案:2或-220. 一个数的相反数是1,这个数是______。
答案:-1三、解答题(每题10分,共40分)21. 已知a、b、c是三个不同的自然数,且a+b+c=12,求a、b、c的可能取值。
第十七届华罗庚金杯少年数学邀请赛初赛试卷(初一组笔试版)

第十七届华罗庚金杯少年数学邀请赛初赛试卷(初一组笔试版)〔吋间:2012年3月17曰10:00-11:00 〕一、选择题(每小题10分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内)1.平面上四个点,任意三个点都不在一条直线上,在连接这四个点的六条线段所形成的图形中,最少可以形成〔〕个三角形.(A)3 (B)4 (C) 6 (D) 82.在右图所示的三位数加法算式中,每个字母代表非零数字,不同的字母代表不同的数字,则和“”的最小值是〔〕.(A)459 〔B〕457 (C)456 (D) 4533.内角都小于180度的七边形的内角至少有〔〕个钝角.(A)6 〔B〕5 (C) 4 (D)34.四支排球队进行单循环比赛,即每两队都要赛-场,且只赛一场.如果一场比赛的比分是3:0或3:1,则胜队得3分,负队得0分;如杲比分是3:2,则胜队得2分,负队得1分.如杲比赛后各队得分恰好是四个连续的自然数,那么笫一名的得分是〔〕分.(A)3 〔B〕4 (C) 5 (D) 65.如图所示,M为平行四边形ABCD中BC边上一点,BM:MC=2:3.己知三角形CMN的面积为45 cm2.则平行四边形ABCD的面积为〔〕cm2.(A)30 (B)45(C)90(D)1006.如果正整数x与y使得的值为质数:那么x+y共有〔〕种可能的值.(A) 1 (B) 2 (C)3 (D)4二、填空题〈每小题10分,满分40分)7.计算:1.2345 ×0.2345 ×2.469-123455-1.2345 X 0.23452=________.8.己知关于x的一元一次方程7x+(3+x)=k+bx方程有非零解,且这个方程的解是方程7x+(3+x) = k-bx解的1/3,那么b的值为_______.9.己知甲、乙两车分别从A、B两地同吋出发,且在A,B地住返来回勻速行驶.若两车笫一次相遇后,甲车继续行驶4小吋到达B,而乙车只行驶了1小吋就到达A,则两车笫15次相遇(在A,B两地相遇次数不计)吋,它们行驶了______小吋.10.设a、b、c代表三个不同的非零数字,由它们组成一个最大的三位数和一个最小的三位数,记这两个三位数的差为m,且m的数字和恰好整除m,则所有不同的m的值之和为_______.(A)30 〔B〕45 (C)90 (D) 100第十七届全国华罗庚金杯少年数学邀请赛初赛试题(初一组笔试版)答案―、迭择题(每小题10分,满分60分)二、填空题〈每小题10分,满分40分)。
华杯赛初一组试题及答案

华杯赛初一组试题及答案一、选择题(每题5分,共40分)1. 下列哪个数是最小的正整数?A. 0B. 1C. 2D. 3答案:B2. 一个等腰三角形的两个底角相等,如果其中一个底角是45度,那么顶角是多少度?A. 45度B. 90度C. 135度D. 180度答案:B3. 如果一个数的平方等于36,那么这个数是多少?A. 6B. ±6C. 36D. ±36答案:B4. 一个长方体的长、宽、高分别是a、b、c,那么它的体积是多少?A. abcB. ab + bc + acC. a + b + cD. a/b + b/c + c/a答案:A5. 下列哪个分数是最简分数?A. 3/4B. 4/6C. 5/8D. 7/9答案:D6. 一个圆的半径是r,那么它的面积是多少?A. πrB. πr^2C. 2πrD. 2πr^2答案:B7. 如果一个数x满足方程x^2 - 5x + 6 = 0,那么x的值是多少?A. 2B. 3C. 2或3D. 以上都不是答案:C8. 一个等差数列的首项是a1,公差是d,那么它的第n项是多少?A. a1 + (n-1)dB. a1 - (n-1)dC. a1 + ndD. a1 - nd答案:A二、填空题(每题5分,共30分)9. 一个数的相反数是-5,那么这个数是______。
10. 一个数的绝对值是8,那么这个数可以是______或______。
答案:8或-811. 一个等腰直角三角形的斜边长是10,那么它的直角边长是______。
答案:5√212. 一个数列的前三项是1,2,3,如果每一项都是前一项的两倍,那么第10项是______。
答案:2^9 = 51213. 一个圆的周长是2πr,如果周长是12π,那么半径r是______。
14. 一个长方体的长、宽、高分别是2,3,4,那么它的表面积是______。
答案:5215. 一个数列的前三项是1,3,5,如果每一项都比前一项多2,那么第n项是______。
(整理)第二十一届华罗庚金杯少年数学邀请赛初赛试卷初一组带答案

第二十一届华罗庚金杯少年数学邀请赛初赛试卷(初一组)一、选择题(每小题10 分,共60 分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1.代数和-1⨯2008+2⨯2007-3⨯2006+4⨯2005+L -1003⨯1006+1004⨯1005的个位数字是()A.7B.8C.9D.0【答案】B【解析】只需考察每个组合的个位数的乘积,发现这2015 个的组合中,个位数的乘积每十个一循环,观察这个循环中的乘积和:-1⨯ 8+2 ⨯ 7 -3⨯ 6+4 ⨯ 5 -5⨯ 4 + 6 ⨯ 3 - 7 ⨯ 2 +8⨯1 - 9 ⨯ 0 + 0 ⨯ 9=0 ,因此每个循环的个位数和为0,观察最后循环外的几个数的乘积和:-1⨯ 8+2 ⨯ 7 -3⨯ 6+4 ⨯ 5=8 。
因此最后得到的个位数为82.已知-1<a<b<0,则下列不等式成立的是()A. a<a3 <ab2 <abB. a<ab2 <ab<a3C. a<ab<ab2 <a3D. a3<ab2 <a<ab【答案】A【解析】a,a3 ,ab2 ,ab 中易知只有ab >0,故ab 最大,排除B,C;另外由于-1 <a < 0 得a2 < 1 ,即a <a3 ,排除D,所以选A3.在数轴上,点A 和点B 分别表示数a 和b ,且在原点O 的两则,若a -b =2016 ,AO =2BO ,则a +b =()A.6048B. -6048C. ±672D.0【答案】C【解析】由a -b = 2016 且A,B 在O 点两侧以及a= 2 b 知a, b的解有两种可能性:i. a >0,b<0则可解得a =2⨯ 2016 = 1344 ,b =-1⨯ 2016 =-672 ,a +b =672 3 34.如右图所示,三角形ABC 是直角三角形,∠ABC =60o ,若在直线AC 或BC 上取一点P ,使得三角形PAB 为等腰三角形,那么这样的点P 的个数为()A.4B.5C.6D.7【答案】C【解析】考察不同的等腰三角形的顶角:若P 为顶角,则P 必位于AB 的中垂线上,而AB 中垂线与直线AC,AB 的交点有两个,故这样的等腰三角形有2 个;若A 为顶角,则AB 为其中一条腰,将线段AB 绕A 点旋转,与直线AC,AB 的交点有三个,但是由于∠ABC = 60︒,此旋转后的直线与BC 延长线的交点与以P 为顶点的一个三角形重合,故这样不同的等腰三角形有2 个;若B 为顶角,同样AB 为其中一条腰,将线段AB 绕B 点旋转,与直线AC,AB 的交点同样有三个,同样与P 为顶点的一个三角形重合,故不同的三角形只有2 个;综上这样的点P 的个数为6 个。
初一华罗庚杯第19届a卷试题及答案

初一华罗庚杯第19届a卷试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的?A. 2 + 2 = 5B. 3 + 3 = 5C. 4 + 4 = 7D. 5 + 5 = 10答案:D2. 如果一个数的平方是9,那么这个数是:A. 3B. -3C. 3或-3D. 无法确定答案:C3. 一个长方体的长、宽、高分别为2cm、3cm、4cm,那么它的体积是:A. 12cm³B. 24cm³C. 36cm³D. 48cm³答案:C4. 下列哪个分数是最简分数?A. 4/8B. 5/10C. 3/9D. 2/4答案:C5. 一个圆的直径是14cm,那么它的半径是:A. 7cmB. 14cmC. 28cmD. 无法确定答案:A6. 一个数的立方是27,那么这个数是:A. 3B. -3C. 3或-3D. 无法确定答案:A7. 一个三角形的三个内角之和是:A. 90度B. 180度C. 360度D. 无法确定答案:B8. 下列哪个选项是正确的?A. 2的平方根是2B. 4的平方根是2C. 5的平方根是5D. 3的平方根是3答案:B9. 如果一个数的绝对值是5,那么这个数是:A. 5B. -5C. 5或-5D. 无法确定答案:C10. 一个数的倒数是1/2,那么这个数是:A. 2B. 1/2C. -2D. -1/2答案:A二、填空题(每题4分,共20分)11. 一个数的平方是16,这个数是______。
答案:4或-412. 一个数的立方是-8,这个数是______。
答案:-213. 一个数的绝对值是3,这个数是______。
答案:3或-314. 一个数的倒数是2,这个数是______。
答案:1/215. 一个数的平方根是4,这个数是______。
答案:16或-16三、解答题(每题10分,共50分)16. 计算下列表达式的值:(3 + 5) × 2 - 4答案:(3 + 5) × 2 - 4 = 16 - 4 = 1217. 一个长方体的长是5cm,宽是4cm,高是3cm,求它的体积。
(完整版)第11-17届初一华杯赛试题及答案
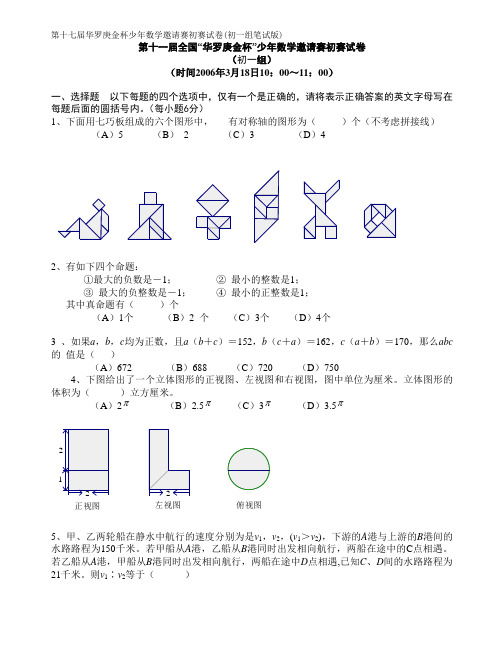
二、A组填空题
7.4/9设AB=2r则{πr^2/2-[π(r/3)^2/2+π(2r/3)^2/2]}/ (πr^2/2)=1-(1/9+4/9)=4/9
8.1.98原式=[2^2/(1×3)]×[3^2/(2×4)] ×[4^2/(3×5)] ×[5^2/(4×6)] ×[6^2/(5×7)] ×……×[98^2/(97×99)] ×[99^2/(98×100)]=2×99/100=1.98
(A) (B) (C) (D)
6、有一串数:1,22,,33,44,……,20042004,20052005,20062006。大明从左往右依次计算前面1003个数的末位数字之和,并且记为a,小光计算余下的1003个数的末位数字之和,并且记为b,则a-b=()。
(A)-3(B)3(C)-5(D)5
二、A组填空题(每小题8分)
4、下图给出了一个立体图形的正视图、左视图和右视图,图中单位为厘米。立体图形的体积为()立方厘米。
(A)2 (B)2.5 (C)3 (D)3.5
5、甲、乙两轮船在静水中航行的速度分别为是v1,v2,(v1>v2),下游的A港与上游的B港间的水路路程为150千米。若甲船从A港,乙船从B港同时出发相向航行,两船在途中的C点相遇。若乙船从A港,甲船从B港同时出发相向航行,两船在途中D点相遇,已知C、D间的水路路程为21千米。则v1∶v2等于()
2006
中,汉字“第、十、一、届、华、杯、赛”代表1~9中的9个数字,不同的汉字代表不同的数字,恰使得加法算式成立。则不同的填法共有;三位数华杯赛的最大可能值为。
第十九届“华杯赛”初赛初一组试题B与答案

只有 5 个整数解,实数 a 的最大值是
(A) 4
(C) 0
(D) 3
二、填空题 (每小题 10 分, 满分 40 分)
7、沿着下图的实线走,从 A 点到 B 点的最短线路共有 种。
8、 用七块棱长为 1 cm 的小正方块堆成一立体, 其俯视图如右图所示, 则 共有 种不同的堆法(经旋转能重合的算一种堆法) .
(A) a b
(B) a b
(C) a ) 。
(D) b
2、在十进制记数法中,数 416 535 的位数是( (A)32 (B)33
2
(C)34
(D)35
3、已知 a 1 (ab2) 0 ,那么
1 1 1 1 的值是 ( a 2014 b 2014 ab a 1b 1 a 2b 2
9 、 已 知 有 理 数 m, n 满 足 m3 n3 99 mn 333 , 其 中 mn 0 。 m n 的 值 是 .
10、正方体的各个顶点上分别写着整数 1 至 8,各条棱上分别写着其两个顶点上 的数的差的绝对值,那么 12 条棱上至少可以出现 个互不相同的数。
第 2 页
共 2 页
第十九届华罗庚金杯少年数学邀请赛 初赛试题答案(初一 B 组)
一、选择题(每小题 10 分,满分 60 分)
题号 答案 1 D 2 D 3 B 4 D 5 A 6 D
二、填空题(每小题 10 分,满分 40 分)
题号 答案 7 35 8 5 9 -66 或 33 10 3
第 1 页
共 1 页
第十九届华罗庚金杯少年数学邀请赛
初赛试卷(初一 B 组)
一、 选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
第十五届“华杯赛”初一组初赛试题答案

a b 9 , b c 20 , c a 11.
进而
a 2 b 2 c 2 ab bc ca
1 = [( a b) 2 (b c) 2 (c a) 2 ] 2 1 = (81 400 121) 301. 2
6. 乘积为 240 的不同的五个整数的平均值最大是 ( (A) 【答案】D. 【解答】假设 240 a b c d e , a b c d e .
{3, 4, 1, 1, 20}小. 故最多有一个负数, 设为 a .
这个负数 a 一定是 1 . 否则, 用 a 乘以最大的整数, 满足五个数都不相同. 现在根据 240 分解的特点, 证明 240 (1) 1 2 3 40 为和最大的分解.
设 a 1, b 1 , 则 240 c d e , c, d , e 1 . 我 们 用 一 个 性 质 : 如 果
7 千米, 到达对岸 AD 最少要用 13
小时.
图 A-8
【答案】0.4 小时. 【解答】 连接 AC, 见图 A-9. 由勾股定理容易求得 AC=5 千米. 又因为 52 +122 132 , 所以三角形 ACD 是直角 三角形, ACD 90 . 要乘游艇由点 C 出发, 行进速度为每 小时 11
个. 【答案】3. 【解答】若数 a 是奇数, 则
a 1 a 1 a . 2 2
如果 a 是 4 的倍数, 则
a a a 1 1 . 4 4
2 2
2
2
一个偶数如果能表示成两个平方数的差, 则这两个数一定同时为奇数或者偶数. 而两个奇数(偶数)的平方差一定是 4 的倍数, 因为 2002, 2006, 2010 不是 4 的 倍数, 故不能表示成两个平方数的差. 10. 如图 A-8, 某风景区的沿湖公路 AB=3 千米, BC=4 千米, CD=12 千米, AD=13 千米, 其中 AB BC , 图中阴影是草地, 其余是水面. 那么乘游艇由点 C 出发, 行进速度为每小时 11
2016年华罗庚金杯赛初一初赛试题及答案

第二十一届华罗庚金杯少年数学邀请赛初赛试卷(初一组)(时间:2015年12月12I]10:00—11:00)一、选择题(每小题10分,共60分,以下每题的四个选项中,仅仃一个毡正确的,请将表示正确答案的英文字母写在每题的I则括号内.)1,代数和-1X2008--2X2007-3X2006+4X2OO5+----1003x100641004x1005的个位数字是().(A)7CB)K CO9(D)02,已知-1<^<人父0.则F列不等式成汇的是().(A)a<u1'<ub2<ah(B)a<ab2<ab<(C)a<ab<ah2<u y(D)a3<ab2<a<cth3.在数轴上,4T和点/,分别表小数日和a IL在取点。
的两侧.若|订一占二2016.AO=2BO.[[\\(t+h=().(A)6048(B)—6048(C)±672(D)04.如力图所示,-:角形加右拈直角三角形,乙4出「=60口.若在i工线.或”上取-点儿使刊,一角形〃月一为等腰-关吟一那么达抨K 的点尸的个数为().\(A)4(B)5(C)6(D)7ifi I')1★2奴小时(D)二、填空题(每小题10分,共40分)5.如右图,乙是主河流甲的支流,水流流向如箭头所示.匕流和支流的水流速度相等,船在匕流和支流中的静水 (B)12-r6.甲、乙、内、「四种商品的单价分别为2元,3元,5元和7元,现从中选购里,共有种不同的搬花顺邙.全平方数,则彳=需用5小时.则船从B 经C 到4再从/经C 到力需用(件共花费「36元一如果至少选购「3种而品,则买了)件丁商品.7.如右图,在平行四边形丽Z )中,AB =2AD.点OC/9=14,ZAEC'=90Q ,(E =CB ,则10已知四位数工是完全平片数,将其4个数字各加1后得到的四位数仍然是方 速度也相等一已知船从/处经「•开往出处需川6小时.从B 经「到D 需用&小时,从I )经('到X 为平行四边形内一点,它到直战出九仅二(力的距 离分别为短氏一“它到仞和CD 的距离相等,则品如右图所小、韩梅家的花右两侧各摆了3盆花.韩梅每次按照以下规则往家中搬盆花:先选择左侧还是 右侧,然后搬该侧离家最近的.要把所有的花撤到家 如右图,在等腰梯形片肌笫中.AB//CD,加?=6(A)7(B)8(C)9(D)0a 和b,且在原点O 的两侧.若AO=2OB,则a+b=().4.如右图所示,三角形ABC 是直角三角形,口ABC=60度.若在直线(A)4(B)5(C)6(D)7 5.如右图,乙是主河流甲的支流度相等,船在主流和支流中的静水速度也相等 需用6小时,从B 经C 到D 需用8小时A,再从A 经C 到D 需用()小时.1.代数和的个位数字是().,那么这样的点P 的个数为().PAB 为等腰三角形AC 或BC 上取一点P,使得三角形水流流向如箭头所示.主流和支流的水流速.已知AC=CD,船从A 处经C 开往B 处从D 经C 到B 需用5小时.则船从B 经C 到2.已知则下列不等式成立的是().3.在数轴上,点A 和点B 分别表示数2元,3元,5元和7元.现从中选购了6.甲、乙、丙、丁四种商品的单价分别为件共花费了36元.如果至少选购了3种商品,则买了()件丁商品.(A)1(B)2(C)3(D)4二、填空题(每小题10分,共40分)7.如右图,□□□□□□ABCD中,AB=2AB.点O为平行四边形内一点,它到直线AB, BC,CD□□□□□□a,b,c,且它到AD和CD的距离相等,则2a-b+c=.8.如右图所示,韩梅家的左右两侧各摆了3盆花.韩梅每次按照以下规则往家中搬一盆花:先选择左侧还是右侧,然后搬该侧离家最近的.要把所有的花搬到家里,共有种不同的搬花顺序.9.如右图,□□□□□ABCD中,AB//CD,AB=6,CD=14,1AEC=90度,CE=CB,则10.已知四位数x是完全平方数,将其4个数字各加1□□□□□□□□□□□□平方数,则x=.第二十一届华罗庚金杯少年数学邀请赛初赛试卷(初一组)一.选择理t每小理1。
历届华罗庚金杯赛试题与答案(初中)

图4
8.0,1,2,3,4,5,6 这七个数字填在圆圈和方格内,每个数字恰好出现一次,组成有
一位数和两位数的整数算式.问填在方格里的数是几?
○×○ = □ = ○÷○
9.甲、乙、丙、丁与小强五位同学一起比赛象棋,每两人都要比赛一盘.到现在为止,甲已经赛了 4 盘, 乙赛了 3 盘,丙赛了 2 盘,丁赛了 l 盘.问小强赛了几盘? 10.有三堆棋子,每堆棋子一样多,并且都只有黑、白两色棋子.第一堆里的黑子和第二堆里的白子一样
6、6 7、29 8、8 点 11 分 9、19 10、0 16、40 17、 2.718281 18、10 19、108
复赛简略答案 1、85 2、392 3、37.5 4、5000 5、5 11、8/9 12、8 点 32 分 13、162 14、84
6、2.5
7、0.2
பைடு நூலகம்
8、12
9、2
10、4/9
25 20
4.在一条公路上,每隔一百千米有一个仓库,共有五个仓库.一号仓库存有 10 吨货物,
二号仓库存有 20 吨货物,五号仓库存有 40 吨货物,其余两个仓库是空的。现在想把所
30
有的货物集中存放在一个仓库里,如果每吨货物运输一千米需要 0.5 元的运费,那么最少
图3
要花多少运费才行?
5.有一个数,除以 3 的余数是 2,除以 4 的余数是 1,问这个数除以 12 的余数是几?
图6
棋子放在空盒内,再把盒子重新排了一下.小明回来仔细察看了一番,没有发现
有人动过这些盒子和棋子.问共有多少个盒子? 12.如图,把 1.2、3.7、6.5、2.9、4.6 分别填在五个○内.再在每个□中填上和
它相连的三个○种的数的平均值,再把三个□中的数的平均数填在△中,找一个
华罗庚金杯少年数学邀请赛初赛试卷(初中组)试题

第十五届华罗庚金杯少年数学邀请赛初赛试卷(初中组)试题(时间:2010年3月13日10:00~11:00)一、选择题:(每小题10分,满分60分。
以下每题的四个选项中,仅有一个是正确的,请将表 示正确答案的英文字母写在每题的圆括号内)1. 如果x ,y 满足2x +3y =15,6x +13y =41,则x +2y 的值是 。
(A) 5 (B) 7 (C) 215(D) 9 。
2. -2和2对应的点将数轴分成3段,如果数轴上任意n 个不同的点中至少有3个在其中之ㄧ段, 那么n 的最小值是 。
(A) 5 (B) 6 (C) 7 (D) 8 。
3. 用甲乙两种饮料按照x :y (重量比)混合配制成一种新饮料,原来两种饮料成本是:甲每500 克5元,乙每500克4元。
现甲成本上升10%,乙下降10%,而新饮料成本恰好保持不变, 则x :y = 。
(A) 4:5 (B) 3:4 (C) 2:3 (D) 1:2 。
4. 满足 || x -1 |-| x ||-| x -1 +| x |=1的x 的值是 。
(A) 0 (B) ±41 (C) 43 (D) ±43。
5. 一个立方体的每一个面都写有一个自然数,并且相对的两个面内的两数之和 都相等,右图是这个立方体的平面展开图,若20、0、9的对面分别写的是 a 、b 、c ,则a 2+b 2+c 2-ab -bc -ca 的值为 。
(A) 481 (B) 301 (C) 602 (D) 962 。
2096. 乘积为-240的不同五个整数的平均值最大是 。
(A) 517(B) 518 (C) 7 (D) 9 。
二、 填空题:(每小题10分,满分40分) 7. 如果x +y +z =a ,x1+y 1+z1=0,那么x 2+y 2+z 2的值为 a 2 。
8. 如图,甲,乙两人分别从A 、B 两地同时出发去往C 地,在距离C 地2500米处甲追上乙;若乙提前10分钟出发,则在距离C 地1000米处甲追上乙。
第十二届全国“华罗庚金杯”少年数学邀请赛初赛试题(初一组)

第十二届全国“华罗庚金杯”少年数学邀请赛初赛试题(初一组)(时间:2007年3月24日10:00——11:00)一、选择题(每小题10分)以下每题的的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.1.算式1)1(22)1(1)1(132+-⨯--⨯-+--等于( ).(A )2- (B )1- (C )1 (D )22.新制作的渗水防滑地板是形状完全相同的长方形。
如图1,三块这样 的地板可以拼成一个大的长方形。
如果大长方形的周长为150厘米, 则一块渗水防滑地板的面积是( )平方厘米.(A )450 (B )600 (C )900 (D )1350 图13.如果一个多项式的各项次数都相同,则称该多项式为齐次多项式。
例如:32322y xyz xy x +++是3次齐次多项式。
若23223z xy y x m ++是齐次多项式,则m 等于( ).(A )1 (B )2 (C )3 (D )44.若x y y x -=+,则有( ).(A )y >0,x <0 (B )y <0,x >0(C )y <0,x <0 (D )x =0, y ≥0或y =0, x ≤05.设b a >0,dc>0,有如下四个结论: (1)如果ad >bc ,则必定有b a >d c. (2)如果ad >bc ,则必定有b a <d c. (3)如果ad <bc ,则必定有b a <d c. (4)如果ad <bc ,则必定有b a >dc.其中正确结论的个数是( ).(A )0 (B )1 (C )2 (D )36.已知a 是整数,则以下四个代数式中,不可能得整数值的是( ).(A )523+a (B )32a - (C )613+a (D )725-a二、填空题(每小题10分).7.如图2,空心圆柱底面圆环的外径和内径之比为2∶1,若保持内径不 变,外径扩大成内径的3倍,则扩大后的空心圆柱的体积是原来的体 积的 倍.图28.如图3是某车间的1-12月份的产量图表,记月份为n ,1至5月份的产量为20+an , 6至12月份的产量为b n -2. 则ab 等于 .图39.相同的正方块码放在桌面上,从正面看,如图4;从侧面看,如图5,则正方块最多有 个,最少有 个.10.甲种签字笔每支3.5元,乙种签字笔每支2.65元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华罗庚金杯赛初一初赛
试题及答案
文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-
1.代数和的个位数字是().
(A)7?(B)8 (C)9?(D)0
2.已知则下列不等式成立的是().
3.在数轴上,?点A和点B分别表示数a和b,?且在原点O的两侧.若AO=2OB,?则a+b=().
4.如右图所示,?三角形ABC是直角三角形,∠ABC=60度.若在直线AC或BC上取一点P,?使得三角形PAB为等腰三角形,那么这样的点P的个数为().
(A)4(B)5(C)6(D)7
5.如右图,?乙是主河流甲的支流,?水流流向如箭头所示.?主流和支流的水流速度相等,?船在主流和支流中的静水速度也相等.?已知AC=CD,?船从A处经C开往B处需用6小时,?从B经C到D需用8小时,?从D经C到B需用5小时.?则船从B经C到A,?再从A经C到D需用()小时.
6.甲、乙、丙、丁四种商品的单价分别为2元, 3元, 5元和7元.?现从中选购了6件共花费了36元.?如果至少选购了3种商品,?则买了()件丁商品.
(A)1?(B)2?(C)3?(D)4
二、填空题(每小题10?分,?共40分)
7.如右图,?在平行四边形ABCD中,AB=2AB.点O为平行四边形内一点,?它到直线AB, BC, CD的距离分别为a,?b,?c,?且它到AD和CD的距离相等,则2a-
b+c=.
8.如右图所示,?韩梅家的左右两侧各摆了3盆花.韩梅每次按照以下规则往家中搬一盆花:先选择左侧还是右侧,?然后搬该侧离家最近的.?要把所有的花搬到家里,?共有种不同的搬花顺序.
9.如右图,在等腰梯形ABCD中, AB//CD, AB=6, CD=14, ∠AEC=90度,
CE=CB,?则
10.已知四位数x是完全平方数,?将其4个数字各加1后得到的四位数仍然是完全平方数,?则x=.。
