九年级数学射影定理
人教版九年级数学下册作业课件 第二十七章 相 似 专题课堂(五) “射影定理图”

(2)由(1)知 PD 是⊙O 的切线,直线 PA 与⊙O 相切,∴PO 垂直平分 AB,∴∠AMP =∠AMO=90°,∴∠APM+∠PAM=90°,∵∠OAP=90°,∴∠PAM+∠OAM=90°, ∴∠APM=∠OAM,∴△OAM∽△APM,∴APMM =OAMM ,∴AM2=OM·PM
2.如图,在矩形 ABCD 中,E 为 BC 的中点,AE⊥BD 于点 F,连接 CF. (1)求证:AB=CF; (2)若 AB=4 2 ,求 DF 的长.
解:(1)∵AM 是⊙O 的切线,∴∠BAM=90°,∵∠CEA=90°,∴AM∥CD, ∴∠CDB=∠APB,∵∠CAB=∠CDB,∴∠CAB=∠APB
(2)连接 AD,∵AB 是直径,∴∠CDB+∠ADC=90°,∵∠CAB+∠C=90°, ∠CDB=∠CAB,∴∠ADC=∠C,∴AD=AC=8,∵AB=10,∴BD=6,∵∠BAD +∠DAP=90°,∠DAP+∠APD=90°,∴∠APB=∠BAD,∵∠BDA=∠BAP, ∴△ADB∽△PAB,∴APBB =BADB ,∴PB=ABBD2 =530 ,∴DP=530 -6=332
[对应训练] 1.(2022·滨州)如图,已知 AC 为⊙O 的直径,直线 PA 与⊙O 相切于点 A,直线 PD 经过⊙O 上的点 B 且∠CBD=∠CAB,连接 OP 交 AB 于点 M.求证: (1)PD 是⊙O 的切线; (2)AMOC,∴∠OCB=∠OBC,∵AC 是⊙O 的直径,∴∠CBA = 90°, ∴∠CAB + ∠OCB = 90°, ∵∠CBD = ∠CAB , ∴∠CBD + ∠OBC = 90°, ∴∠OBD=90°,∴PD 是⊙O 的切线
解:(1)延长 AE,DC 相交于点 H,∵E 为 BC 的中点,∴BE=CE,∵四边形 ABCD 是 矩 形 , ∴AB∥CD , AB = CD , ∴∠ABE = ∠HCE , ∠BAE = ∠H , ∴△ABE≌△HCE(AAS),∴AB=CH,∴CD=CH,∵BD⊥AE,∴∠DFH=90°,∴CF =12 DH=CD=AB
中考数学解题大招复习讲义(全国通用)模型06 射影定理模型(解析版)

模型介绍1.射影定理定义①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.2.如图在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高,有射影定理如下: 注意:直角三角形斜边上有高时,才能用射影定理!例题精讲【例1】.在矩形ABCD 中,BE ⊥AC 交AD 于点E ,G 为垂足.若CG =CD =1,则AC 的长是.①AD 2=BD •DC ;②AB 2=BD •BC ;AC 2=CD •BC .解:∵四边形ABCD是矩形,∴AB=CD=1,∠ABC=90°,∵BE⊥AC,∴∠AGB=90°=∠ABC,∵∠BAG=∠CAB,∴△ABG∽△ACB,∴=,∴AG•AC=AB2(射影定理),即(AC﹣1)•AC=12,解得:AC=或AC=(不合题意舍去),即AC的长为,故答案为:.【例2】.如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为()A.﹣B.﹣C.﹣1D.﹣2解:设A(x1,0)(x1<0),B(x2,0)(x2>0),C(0,t),∵二次函数y=ax2+bx+2的图象过点C(0,t),∴t=2;∵AC⊥BC,∴OC2=OA•OB(射影定理),即4=|x1x2|=﹣x1x2,根据韦达定理知x1x2=,∴a=﹣.故选:A.【例3】.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是()A.3B.8C.D.2解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.变式训练【变式1】.如图,在△ABC中,若=AC,BC=2BD=6,DE⊥AC,则AC•EC的值是9.解:如图,∵在△ABC中,若AB=AC,BC=2BD=6,∴AD⊥BC,CD=BD=3.又DE⊥AC,∴∠CED=∠CDA=90°.∵∠C=∠C,∴△CDE∽△CAD.∴=,即AC•EC=CD2=9.(射影定理)故答案是:9.【变式2】.如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD交于O,且BE:ED=1:3,AD=6cm,则AE=cm.解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x(3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.【变式3】.如图,若抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,若∠OAC=∠OCB.则ac的值为()A.﹣1B.﹣2C.D.解:设A(x1,0),B(x2,0),C(0,c),∵二次函数y=ax2+bx+c的图象过点C(0,c),∴OC=c,∵∠OAC=∠OCB,OC⊥AB,∴△OAC∽△OCB,∴,∴OC2=OA•OB(即射影定理)即|x1•x2|=c2=﹣x1•x2,令ax2+bx+c=0,根据根与系数的关系知x1•x2=,∴,故ac=﹣1,故选:A.【变式4】.如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=____________.解:连接CF、GF,如图:在正方形ABCD中,∠EAD=∠ADC=90°,AF⊥DE,∴△AFD∽△EAD,∴=,又∵DF=5EF=5,∴AD====CD,在Rt△AFD中,AF===,∵∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,∴∠DAF=∠CDF,∵四边形GFCD是⊙O的内接四边形,∴∠FCD+∠DGF=180°,∵∠FGA+∠DGF=180°,∴∠FGA=∠FCD,∴△AFG∽△DFC,∴=,∴=,∴AG=,∴DG=AD﹣AG=﹣【变式5】.如图,在△ABC中,以AC边为直径的⊙O交BC于点D,过点B作BG⊥AC 交⊙O于点E、H,连AD、ED、EC.若BD=8,DC=6,则CE的长为2.解:∵AC为⊙O的直径,∴∠ADC=90°,∵BG⊥AC,∴∠BGC=∠ADC=90°,∵∠BCG=∠ACD,∴△ADC∽△BGC,∴=,∴CG•AC=DC•BC=6×14=84,连接AE,∵AC为⊙O的直径,∴∠AEC=90°,∴∠AEC=∠EGC=90°,∵∠ACE=∠ECG,∴△CEG∽△CAE,∴=,∴CE2=CG•AC=84,∴CE=2.故答案为2.【变式6】.如图,四边形ABCD是平行四边形,过点A作AE⊥BC交BC于点E,点F在实战演练BC 的延长线上,且CF =BE ,连接DF .(1)求证:四边形AEFD 是矩形;(2)连接AC ,若∠ACD =90°,AE =4,CF =2,求EC 和AC的长.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∵CF =BE ∴BE +CE =CF +CE ,即BC =EF ,∴AD =EF ,∵AD ∥EF ,∴四边形AEFD 是平行四边形,∵AE ⊥BC ,∴∠AEF =90°,∴平行四边形AEFD 是矩形;(2)解:如图,∵CF =BE ,CF =2,∴BE =2,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠BAC =∠ACD =90°,∵AE ⊥BC ,∴AE 2=BE •EC (射影定理),∴EC ===8,∴AC ===4.1.如图,在矩形ABCD 中,DE ⊥AC ,垂足为点E .若sin ∠ADE =,AD =4,则AB 的长为()A .1B .2C .3D .4解:∵DE ⊥AC ,∴∠ADE+∠CAD=90°,∵∠ACD+∠CAD=90°,∴∠ACD=∠ADE,∵矩形ABCD的对边AB∥CD,∴∠BAC=∠ACD,∵sin∠ADE=,BC=AD=4,∴=,∴=,∴AC=5,由勾股定理得,AB==3,故选:C.2.如图,在矩形ABCD中,BD=2.对角线AC与BD相交于点O,过点D作AC的垂线,交AC于点E,AE=3CE.则DE2的值为()A.4B.2C.D.4解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=2,∵AE=3CE,∴AE=AC=,CE=AC=,∵∠ADC=90°,∴∠DAC+∠ACD=90°,∵DE⊥AC,∴∠AED=∠CED=90°,∴∠ADE+∠DAC=90°,∴∠ADE=∠ACD,∴△ADE∽△DCE,∴=,∴DE2=AE•CE=×=,故选:C.3.如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于()A.B.C.D.解:如图,设点S为BC的中点,连接DP,DS,DS与PC交于点W,作PE⊥BC于点E,PF⊥AB于点F,∴DP=CD=2,PS=CS=1,即DS是PC的中垂线,∴△DCS≌△DPS,∴∠DPS=∠DCB=90°,∴DS===,由三角形的面积公式可得PC=,∵BC为直径,∴∠CPB=90°,∴PB==,∴PE=FB==,∴PF=BE==,∴AF=AB﹣FB=,∴AP==故选:B.4.如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④OA(CP﹣CD)=AP•CD,正确的结论有()个.A.1B.2C.3D.4解:①∵PC与⊙O相切于点C,∴∠PCB=∠A,∠P=∠P,∴△PBC∽△PCA,∴PC2=PA•PB;②∵OC⊥PC,∴PC•OC=OP•CD;③∵CD⊥AB,OC⊥PC,∴OC2=OD•OP,∵OA=OC,∴OA2=OD•OP;④∵AP•CD=OC•CP﹣OA•CD,OA=OC,∴OA(CP﹣CD)=AP•CD,所以正确的有①,②,③,④,共4个.故选:D.5.如图,在Rt△ABC中,∠A=90°,AB=AC=8,点E为AC的中点,点F在底边BC上,且FE⊥BE,则CF长.解:作EH⊥BC于H,如图,∵∠A=90°,AB=AC=8,∴BC=AB=16,∠C=45°,∵点E为AC的中点,∴AE=CE=4,∵△CEH为等腰直角三角形,∴EH=CH==4,∴BH=12在Rt△ABE中,BE==4,在Rt△BEF中,∵EH⊥BF,∴BE2=BH•BF,即BF==,∴CF=BC﹣BF=16﹣=.故答案为.6.如图,在矩形ABCD中,点E在边AD上,把△ABE沿直线BE翻折,得到△GBE,BG 的延长线交CD于点F.F为CD的中点,连结CG,若点E,G,C在同一条直线上,FG=1,则CD的长为2+2,cos∠DEC的值为﹣1.解:∵四边形ABCD是矩形,∴AB=CD,AD∥BC,∠BCD=∠A=∠D=90°,∴∠AEB=∠EBC,∠BCG=∠DEC,由折叠的性质得:BG=BA,∠EGB=∠A=90°,∠GEB=∠AEB,∴CD=BG,∴∠EBC=∠GEB,∴BC=EC,∵点E,G,C在同一条直线上,∴∠CGF=90°,∠CGB=180°﹣∠EGB=90°,∵F为CD的中点,∴CF=DF,设CF=DF=x,则BG=CD=2x,∵∠CFG=∠BFC,∴△CFG∽△BFC,∴=,∴CF2=FG•BF,即x2=1×(1+2x),解得:x=1+或x=1﹣(舍去),∴CD=2x=2+2,∵∠DEC+∠ECD=90°,∠GFC+∠ECD=90°,∴∠DEC=∠GFC,∴cos∠DEC=cos∠GFC===﹣1,故答案为:2+2,﹣1.7.如图,在平面直角坐标系中,直线y=kx+1分别交x轴,y轴于点A,B,过点B作BC ⊥AB交x轴于点C,过点C作CD⊥BC交y轴于点D,过点D作DE⊥CD交x轴于点E,过点E作EF⊥DE交y轴于点F.已知点A恰好是线段EC的中点,那么线段EF的长是.解:因为AB的解析式为y=kx+1,所以B点坐标为(0,1),A点坐标为(﹣,0),由于图象过一、二、三象限,故k>0,又因为BC⊥AB,BO⊥AC,所以在Rt△ABC中,BO2=AO•CO,代入数值为:1=•CO,CO=k,同理,在Rt△BCD中,CO2=BO•DO,代入数值为:k2=1•DO,DO=k2又因为A恰好是线段EC的中点,所以B为FD的中点,OF=1+1+k2,Rt△FED中,根据射影定理,EO2=DO•OF,即(k++)2=k2•(1+k2+1),整理得(k﹣)(k+)(k2+2)(k2+1)=0,解得k=.根据中位线定理,EF=2GB=2DC,DC==,EF=2.8.如图,在菱形ABCD中,过点D作DE⊥CD交对角线AC于点E,连接BE,点P是线段BE上一动点,作P关于直线DE的对称点P',点Q是AC上一动点,连接P'Q,DQ.若AE=14,CE=18,则DQ﹣P'Q的最大值为.解:如图,连接BD交AC于点O,过点D作DK⊥BC于点K,延长DE交AB于点R,连接EP′并延长,延长线交AB于点J,作EJ关于AC的对称线段EJ′,则点P′的对应点P″在线段EJ′上.当点P是定点时,DQ﹣QP′=DQ﹣QP″,当D,P″,Q共线时,QD﹣QP′的值最大,最大值是线段DP″的长,当点P与B重合时,点P″与J′重合,此时DQ﹣QP′的值最大,最大值是线段DJ′的长,也就是线段BJ的长.∵四边形ABCD是菱形,∴AC⊥BD,AO=OC,∵AE=14.EC=18,∴AC=32,AO=OC=16,∴OE=AO﹣AE=16﹣14=2,∵DE⊥CD,∴∠DOE=∠EDC=90°,∵∠DEO=∠DEC,∴△EDO∽△ECD,∴DE2=EO•EC=36,∴DE=EB=EJ=6,∴CD===12,∴OD===4,∴BD=8,=×OC×BD=BC•DK,∵S△DCB∴DK==,∵∠BER=∠DCK,∴sin∠BER=sin∠DCK===,∴RB=BE×=,∵EJ=EB,ER⊥BJ,∴JR=BR=,∴JB=DJ′=,∴DQ﹣P'Q的最大值为.解法二:DQ﹣P'Q=BQ﹣P'Q≤BP',显然P'的轨迹EJ,故最大值为BJ.勾股得CD,OD.△BDJ∽△BAD,BD2=BJ*BA,可得BJ=.故答案为:.9.在矩形ABCD中,点E为射线BC上一动点,连接AE.(1)当点E在BC边上时,将△ABE沿AE翻折,使点B恰好落在对角线BD上点F处,AE交BD于点G.①如图1,若BC=AB,求∠AFD的度数;②如图2,当AB=4,且EF=EC时,求BC的长.(2)在②所得矩形ABCD中,将矩形ABCD沿AE进行翻折,点C的对应点为C',当点E,C',D三点共线时,求BE的长.解:(1)①∵四边形ABCD是矩形,∴AD=BC,∠BAD=90°,∵BC=AB,∴AD=AB,∴tan∠ABD==,∴∠ABD=60°,由折叠的性质得:AF=AB,∴△ABF是等边三角形,∴∠AFB=60°,∴∠AFD=180°﹣∠AFB=120°;②由折叠的性质得:BF⊥AE,EF=EB,∵EF=EC,∴EF=EB=EC,∴BC=2BE,∵四边形ABCD是矩形,∴∠ABC=90°,AD=BC=2BE,AD∥BC,∴△ADG∽△EBG,∴==2,∴AG=2EG,设EG=x,则AG=2x,∴AE=3x,在△ABE中,BG⊥AE,∴AB2=AG•AE(射影定理),即42=2x•3x,解得:x=(负值已舍去),∴AE=3x=2,∴BE===2,∴BC=2BE=4,即BC的长为4;(2)当点E,C',D三点共线时,如图3,由②可知,BC=4,∵四边形ABCD是矩形,∴∠ABC=∠BCD=90°,AD=BC=4,CD=AB=4,AD∥BC,∴∠DCE=90°,∠CED=∠B'DA,由折叠的性质得:AB'=AB=4,∠B'=∠ABC=90°,∴∠DCE=∠B',DC=AB',∴△CDE≌△B'AD(AAS),∴DE=AD=4,∴CE===4,∴BE=BC+CE=4+4.10.如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.(1)求证:PC是⊙O的切线;(2)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合).问GE▪GF是否为定值?如果是,求出该定值;如果不是,请说明理由.解:(1)∵PA=OA=2,AM=OM=1,CM=,又∵∠CMP=∠OMC=90°,∴PC==2,∵OC=2,PO=4,∴PC2+OC2=PO2,∴∠PCO=90°,∴PC与⊙O相切;(2)GE•GF为定值,理由如下:如图2,连接GA、AF、GB,∵点G为弧ADB的中点,∴,∴∠BAG=∠AFG,∵∠AGE=∠FGA,∴△AGE∽△FGA,∴,∴GE•GF=AG2,∵AB为直径,AB=4,∴∠BAG=∠ABG=45°,∴AG=2,∴GE•GF=AG2=8.11.如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE;(2)如图2,当点E运动到AB中点时,连接DG,求证:DC=DG;(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.(1)证明:∵BF⊥CE,∴∠CGB=90°,∴∠GCB+∠CBG=90,∵四边形ABCD是正方形,∴∠CBE=90°=∠A,BC=AB,∴∠FBA+∠CBG=90,∴∠GCB=∠FBA,∴△ABF≌△BCE(ASA);(2)证明:如图2,过点D作DH⊥CE于H,设AB=CD=BC=2a,∵点E是AB的中点,∴EA=EB=AB=a,∴CE=a,在Rt△CEB中,根据面积相等,得BG•CE=CB•EB,∴BG=a,∴CG==a,∵∠DCE+∠BCE=90°,∠CBF+∠BCE=90°,∴∠DCE=∠CBF,∵CD=BC,∠CHD=∠CGB=90°,∴△CHD≌△BGC(AAS),∴CH=BG=a,∴GH=CG﹣CH=a=CH,∵DH=DH,∠CHD=∠GHD=90°,∴△DGH≌△DCH(SAS),∴CD=GD;(3)解:如图3,过点D作DQ⊥CE于Q,S△CDG=•DQ•CG=CH•DG,∴CH==a,在Rt△CQD中,CD=2a,∴DH==a,∵∠MDH+∠HDC=90°,∠HCD+∠HDC=90°,∴∠MDH=∠HCD,∴△CHD∽△DHM,∴=,∴HM=a,在Rt△CHG中,CG=a,CH=a,∴GH==a,∵∠MGH+∠CGH=90°,∠HCG+∠CGH=90°,∴∠CGH=∠CNG,∴△GHN∽△CHG,∴,∴HN==a,∴MN=HM﹣HN=a,∴=12.在平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.(1)求过A,B,C三点的抛物线的解析式;(2)求点D的坐标;(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径;若不存在,请说明理由.解:(1)令二次函数y=ax2+bx+c,则,∴,∴过A,B,C三点的抛物线的解析式为y=﹣x2﹣x+2.(2)以AB为直径的圆的圆心坐标为O′(﹣,0),∴O′C=,OO′=;∵CD为⊙O′切线∴O′C⊥CD,∴∠O′CO+∠OCD=90°,∠CO'O+∠O'CO=90°,∴∠CO'O=∠DCO,∴△O'CO∽△CDO,∴=,即=,∴OD=,∴D坐标为(,0).(3)存在,抛物线对称轴为x=﹣,设满足条件的圆的半径为r,则E的坐标为(﹣+r,|r|)或F(﹣﹣r,|r|),而E点在抛物线y=﹣x2﹣x+2上,∴|r|=﹣(﹣+r)2﹣(﹣+r)+2;∴r1=﹣1+,r2=﹣1﹣(舍去),r3=1+,r4=1﹣(舍去);故以EF为直径的圆,恰好与x轴相切,该圆的半径为或1+.。
2023初中数学专题《射影定理模型》试卷含答案解析

1.射影定理定义①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.2.如图在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高,有射影定理如下:注意:直角三角形斜边上有高时,才能用射影定理!【例1】.在矩形ABCD 中,BE ⊥AC 交AD 于点E ,G 为垂足.若CG =CD =1,则AC 的长是 .模型介绍例题精讲解:∵四边形ABCD 是矩形,∴AB =CD =1,∠ABC =90°,∵BE ⊥AC ,∴∠AGB =90°=∠ABC ,∵∠BAG =∠CAB ,∴△ABG ∽△ACB ,∴=,∴AG •AC =AB 2(射影定理),即(AC ﹣1)•AC =12,解得:AC =或AC =(不合题意舍去),即AC 的长为,故答案为:.【例2】.如图:二次函数y =ax 2+bx +2的图象与x 轴交于A 、B 两点,与y 轴交于C 点,若AC ⊥BC ,则a 的值为( )A .﹣B .﹣C .﹣1D .﹣2解:设A (x 1,0)(x 1<0),B (x 2,0)(x 2>0),C (0,t ),∵二次函数y =ax 2+bx +2的图象过点C (0,t ),∴t =2;∵AC ⊥BC ,∴OC 2=OA •OB (射影定理),即4=|x 1x 2|=﹣x 1x 2,根据韦达定理知x 1x 2=,∴a =﹣. 故选:A .【例3】.将沿弦BC 折叠,交直径AB 于点D ,若AD =4,DB =5,则BC 的长是( )A.3B.8C.D.2解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.变式训练【变式1】.如图,在△ABC中,若AB=AC,BC=2BD=6,DE⊥AC,则AC•EC的值是 9 .解:如图,∵在△ABC中,若AB=AC,BC=2BD=6,∴AD⊥BC,CD=BD=3.又DE⊥AC,∴∠CED=∠CDA=90°.∵∠C=∠C,∴△CDE∽△CAD.∴=,即AC•EC=CD2=9.(射影定理)故答案是:9.【变式2】.如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD交于O,且BE:ED=1:3,AD=6cm,则AE= cm.解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x(3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.【变式3】.如图,若抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,若∠OAC=∠OCB.则ac的值为( )A.﹣1B.﹣2C.D.解:设A(x1,0),B(x2,0),C(0,c),∵二次函数y=ax2+bx+c的图象过点C(0,c),∴OC=c,∵∠OAC=∠OCB,OC⊥AB,∴△OAC∽△OCB,∴,∴OC2=OA•OB(即射影定理)即|x1•x2|=c2=﹣x1•x2,令ax2+bx+c=0,根据根与系数的关系知x1•x2=,∴,故ac=﹣1,故选:A.【变式4】.如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=____________.解:连接CF、GF,如图:在正方形ABCD中,∠EAD=∠ADC=90°,AF⊥DE,∴△AFD∽△EAD,∴=,又∵DF=5EF=5,∴AD====CD,在Rt△AFD中,AF===,∵∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,∴∠DAF=∠CDF,∵四边形GFCD是⊙O的内接四边形,∴∠FCD+∠DGF=180°,∵∠FGA+∠DGF=180°,∴∠FGA=∠FCD,∴△AFG∽△DFC,∴=,∴=,∴AG=,∴DG=AD﹣AG=﹣【变式5】.如图,在△ABC中,以AC边为直径的⊙O交BC于点D,过点B作BG⊥AC交⊙O于点E、H,连AD、ED、EC.若BD=8,DC=6,则CE的长为 2 .解:∵AC为⊙O的直径,∴∠ADC=90°,∵BG⊥AC,∴∠BGC=∠ADC=90°,∵∠BCG=∠ACD,∴△ADC∽△BGC,∴=,∴CG•AC=DC•BC=6×14=84,连接AE,∵AC为⊙O的直径,∴∠AEC=90°,。
九年级数学射影定理
棋牌微信群 肾病综合征患者激素冲击治疗后尿量无明显增多,此时应A.再次行激素冲击治疗B.撤掉激素,单以细胞毒药物治疗C.增加利尿剂加强利尿消肿D.消除患者高凝、高脂、感染等状态,改用口服激素治疗,根据肾脏病理改变决定是否加用细胞毒药物E.改用其他免疫抑制剂治疗 视空间失认的表现是A.颜色匹配错误B.形状辨认错误C.环境音辨认错误D.方向辨认错误E.面容辨认错误 药材"二杠茸"指的是A.有2个侧枝的梅花鹿茸B.有1个侧枝的梅花鹿茸C.有2个侧枝的马鹿茸D.有2个侧枝的花鹿茸E.有3个侧枝的花鹿茸 催化剂架桥 中国高胆固醇血症的诊断标准是A.TC>5.72mmol/L(220mg/dl)B.TC>5.20mol/L(200mg/dl)C.TC>4.68mmol/L(180mg/dl)D.TC>6.24mol/L(240mg/dl)E.TC>7.02mol/L(270mg/dl) 在工程进度款结算过程中,除了对承包商超出设计图纸范围而增加的工程量,监理不予计量之外,还包括。A.因发包人原因造成返工的工程量B.因承包商原因造成返工的工程量C.因不可抗力造成返工的工程量D.因不利施工条件造成返工的工程量 中国证监会按照授权和依照相关法律法规对证券市场进行集中、统一监管。A.国务院B.全国人民代表大会C.全国人大常务委员会D.中国人民银行 成团脱落的纤毛柱状上皮细胞可呈()A.嵌铺砖状B.融合体样C.蜂窝状D.扁平铺鹅卵石样E.腺腔群 水痘的临床特征有.A.疹退后脱皮,不留瘢痕B.同时期丘疹、疱疹、干痂并见C.病后终免疫D.发热一二天内出疹E.以四肢较多 配制含100kcal热能100ml奶中应加糖A.4%B.6%C.7%D.8%E.10% 下列情况中,能引起肾小球滤过率减少的是A.血浆胶体渗透压减低B.血浆胶体渗透压升高C.血浆晶体渗透压降低D.血浆晶体渗透压升高E.肾小球毛细血管血压升高 催化剂使用寿命短,操作较短时间就要更新或活化的反应,比较适用反应器。A、固定床B、流化床C、管式D、釜式 韦伯认为的行政体系特点不包括A.明确组织分工B.合理任用人员C.建立管理人员制度D.建立思想的行动准则E.严格规则和纪律 汗液形成的基本条件是津液和阳气。A.正确B.错误 活跃期延长是指从宫口扩张3cm至宫口开全时限超过多少小时。A.4hB.6hC.8hD.10hE.16h 下列叙述不符合血液学发展史的是()A.1673年发现红细胞B.1749年发现白细胞C.1942年发现血小板D.血液有形成分主要包括红细胞、白细胞和血小板E.显微镜的发明为血液学的发展开拓了新的前景 灰口铸铁是第一阶段和阶段石墨化过程都能充分进行时形成的铸铁。A、第二B、中间C、第三D、最后 工程量清单计价的工程造价应由()组成。A.间接费B.措施项目费C.其他项目费D.规费和税金E.分部分项工程费 要使文字同时显示为粗体和斜体,应使用语句。 [单选,共用题干题]Microsoft'sCOMisasoftware(1)istheunderlyingarchitecturethatformsthefoundationforhigherlevelsoftwareservices,definesabinarystandardforfunctioncallingbetweencomponents,awayforcomponentstodynarmicallydiscovertheinterfacesimplementedbyothercomponents,andamechanismtoidentifycomponentsandtheirinterfacesuniquely.O LEisacompound(2)standarddevelopedbyMicrosoft.OLEmakesitpossibletocreate(3)withoneapplicationandlinkorembedtheminasecondapplication.Embeddedobjectsretaintheiroriginalformatand(4) totheapplicationthatcreatedthem.SupportforOLEisbuiltintotheWindowsandMacOSOperatingSystems.A(5)compounddocumentstandarddevelopedmainlybyAppleandIBMiscalledOpenDoc.空白(1)处应选择A.architectureB.protocolC.procedureD.structure 形成腹股沟管外环是。A.联合肌腱B.腹横肌C.腹内斜肌D.腹外斜肌腱膜E.皮下浅筋膜 男性30岁,因半日来腹泻,2h前出现烦躁不安,于8月5日入院。腹泻次数频繁,约20余次,量较多,呈水样,伴呕吐。2天前从有腹泻患者的农村回来,在农村常喝生水。进城后曾与同伴6人共同进餐,吃过变质蛋白类食品,同食者未发病。体检:BP:50/0mmHg,脉弱, 重度脱水貌。外周血白细胞16.0×109/L,中性粒细胞76%,粪便白细胞0~1/HP。诊断应首选考虑A.中毒性痢疾B.病毒性肠炎C.沙门菌感染D.嗜盐菌感染E.霍乱 房屋修缮管理是中的一个重要环节。A.房地产经营B.房地产销售C.房地产管理D.房地产开发 转炉的经济炉龄 下列属于机械性肠梗阻的是。A.肠道功能紊乱引起的肠梗阻B.由于慢性铅中毒肠痉挛引起的肠梗阻C.由于肠系膜血管栓塞引起的肠梗阻D.先天性肠道闭锁引起的肠梗阻E.由于急性弥漫性腹膜炎而引起的肠梗阻 窒息法灭火时减少切断助燃的氧气进入到燃烧现场。A.正确B.错误 支气管扩张主要的诊断依据是A.痰涂片或细菌培养B.胸部X线检查CT检查D.纤维支气管镜检查E.支气管造影 男,20岁。因3天来高热、腹痛、腹泻,1天来头晕入院。查体:T39.4℃,面部潮红、球结膜充血,有出血斑且水肿,皮肤有细小出血点,BP60/40mmHg,血WBC16×109/L,Hb165g/L,尿蛋白(+++),大便水样,镜检WBC0~2/HP。本病人抗病毒药物治疗多选 用A.干扰素B.利巴韦林C.阿糖腺苷D.拉夫米定E.硫唑嘌呤 在公司管线中为安全消防线;为水线;为油品线。 按照机器的用途,可分为和工作机两种。A、发动机B、电动机C、驱动机D、发电机 下列不是管理方法的是A.行政方法B.法律方法C.民主方法D.思想教育方法E.社会心理学方法 一般土壤含水量越高,空气含量就。 盐化土壤 关于自动化间断测压法错误的是()A.基本原理是采用振荡技术B.不能反映每一心动周期的血压C.无创性、重复性好D.有动脉压波形显示E.低温、血容量不足时均会影响测量结果 饱和温度与饱和压力的关系是什么? 需求拉起的通货膨胀()A.通常用于描述某种供给因素所引起的价格波动B.通常用于描述某种总需求的增长所引起的价格波动C.表示经济制度已调整过的预期通货膨胀率D.以上均不是 催化剂总藏量 暗室激发试验前后眼压升高差值超过多少为阳性()A.2mmHgB.5mmHgC.8mmHgD.10mmHgE.12mmHg DSA检查常用的器械不包括A.消毒手术包B.皮肤缝合针C.扩张器D.导管E.导丝 病灶部位在优势侧颞叶峡部、岛叶皮质下的弓状束和联络纤维,属于()A.传导性失语B.命名性失语C.经皮质运动性失语D.运动性失语E.完全性失语
九年级数学射影定理

射影定理的推导过程

射影定理的推导过程射影定理是数学中的一个重要定理,它在几何学和代数学中都有广泛的应用。
下面我将以人类的视角,用自然流畅的语言来描述射影定理的推导过程。
假设我们有一个平面上的点A和一条直线L,我们希望得到点A到直线L的距离。
首先,我们需要找到点A关于直线L的射影点B。
为了找到射影点B,我们可以从点A引一条垂直于直线L的线段,假设这条线段与直线L的交点为B。
现在我们可以看到,点A、B 和直线L形成了一个直角三角形。
根据直角三角形的性质,我们可以利用勾股定理来计算点A到直线L的距离。
假设直线L的方程为ax + by + c = 0,点A的坐标为(x0, y0),则点B的坐标为(x1, y1)。
由于点B是点A关于直线L的射影点,因此直线AB与直线L垂直。
根据直线的斜率性质,我们可以得到直线AB的斜率为-k/a,其中k 是直线L的斜率。
接下来,我们可以利用点斜式来表示直线AB的方程。
假设直线AB 的方程为y = mx + d,其中m是直线AB的斜率,d是直线AB与y 轴的交点。
由于点A在直线AB上,所以点A的坐标(x0, y0)满足直线AB的方程。
将点A的坐标代入直线AB的方程,我们可以得到y0 = m*x0 + d。
将直线AB的方程和直线L的方程联立,我们可以得到一个关于m 和d的方程组。
解出m和d的值后,我们就得到了直线AB的方程。
现在,我们可以计算点A到直线L的距离了。
根据点到直线的距离公式,点A到直线L的距离等于点A到射影点B的距离。
利用两点间距离的公式,我们可以得到点A到射影点B的距离为:distance = sqrt((x0 - x1)^2 + (y0 - y1)^2)至此,我们成功地推导出了射影定理的计算公式。
射影定理的推导过程虽然涉及了一些几何和代数的知识,但通过合理的描述和逻辑推理,我们可以用生动的语言将其阐释清楚。
希望这段文字能够帮助你更好地理解射影定理的推导过程。
射影定理结论

射影定理结论射影定理(ProjectiveTheorem)是一种数学定理,它以简洁的方式描述了空间中的点、线和平面的关系。
它揭示了空间中某个点会在线或平面上给出对应的点,也就是说,它提出了射影映射这一结果。
这个定理是著名的法国数学家宗撰写的,他于1822年在他的著作《试论平面曲线理论》中提出了射影定理。
射影定理的结论如下:空间中的任意一点都可以在其他点、线或平面上项给出对应的点,这种对应的点即射影映射(Projection Mapping)。
射影映射有着多种应用。
首先,在从一维空间到二维空间之间的映射过程中,它广泛地用于平面绘图,其中每个像素点都可以进行射影映射。
此外,在从二维空间到三维空间间的映射中,它也可以被用于立体化模型绘制。
在三维空间绘制模型的时候,点和线的对应关系可以很容易地通过射影定理得出。
此外,即使是在从多维空间到多维空间之间的映射过程中,也可以使用射影定理,这种映射也可以应用于复杂的物理过程,例如粒子发射过程。
射影定理的另一个重要优势在于它能够提供一种数学工具,可以用于探究空间中相互关联的点对象,而不需要考虑它们之间的相对位置。
例如,假设有一条直线,它分割开空间中的两个物体,这时,只要通过使用射影定理,就可以轻松地获得物体之间的关联性,而不需要考虑它们的相对位置。
射影定理也能够用来解释很多不同的科学过程,因为它能够提供一种数学方法来分析这些过程中的物理变化。
例如,它可以分析视角变换的物理过程,也能够解释空间中的光的反射和折射过程。
最后,它也可以用于研究立体视觉的结构,这种结构通常是非常复杂的,尤其是在实践活动中。
综上所述,射影定理是一种数学定理,它以简洁的方式描述了空间中的点、线和平面的关系,它提出了平面投影映射这一结果,它能够广泛地用于从一维空间到多维空间之间的映射,能够用于研究物理过程和立体视觉结构。
初三数学知识点剖析—期末冲刺:射影定理

即 DE2 = BE CE . 【点评】此题主要考查了相似三角形的判定与性质,根据已知得出∠B=∠1 是解题关键.
例 4:【分析】要证线段乘积式相等,常常先证比例式成立,要证比例式,须有三角形相似,要证三角形相 似,须根据已知与图形找条件就可.
【解答】 证明:连接 PC, ∵AB=AC,AD 是中线, ∴AD 所在直线是△ABC 的垂直平分线. ∴PC=PB,∠PCE=∠ABP. ∵CF∥AB,∴∠PFC=∠ABP, ∴∠PCE=∠PFC 又∵∠CPE=∠EPC, ∴△EPC∽△CPF ∴ PC = PF
2.证明过程: ∵ CD ⊥ AB ∴ DCA + CAB = 90 又∵ Rt ABC 中 CBA + CAB = 90 ∴ DCA = CBA 又∵ CDA = BDC ∴ ACD CBD ∴ CD = BD 即 CD2 = AD BD
DA DC
∵ Rt ABC 中 BCD + DCA = 90 , A + DCA = 90 ∴ A = BCD 又∵ CDA = BCA ∴ ACD ABC ∴ AC = AB 即 AC2 = AB AD
例 3:【分析】利用垂直平分线的性质得出 AE=DE,进而利用外角的性质得出∠B=∠1,即可得出△ACE∽ △BAE,即可得出答案.
【解答】证明:连接 AE, ∵AD 的垂直平分线交 AD 于 E, ∴AE=DE, ∴∠1+∠2=∠4, ∵∠B+∠3=∠4, ∠2=∠3,
∴∠B=∠1, ∵∠AEB=∠CEA, ∴△ACE∽△BAE, ∴ AE = CE ,
AD AC
∵ ACD ABC , ACD CBD ∴ ABC CBD ∴ BC = BD 即 BC2 = AB BD .
九年级数学上册 专题突破讲练 相似中的“射影定理”试题 (新版)青岛版-(新版)青岛版初中九年级上册
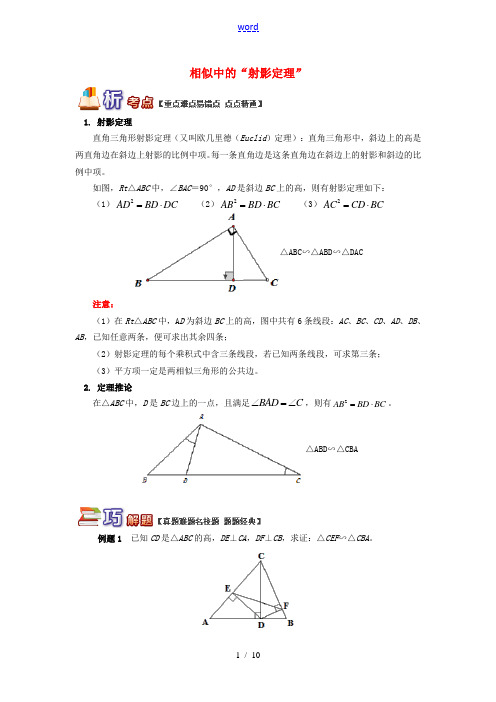
相似中的“射影定理”1. 射影定理直角三角形射影定理(又叫欧几里德(Euclid )定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高,则有射影定理如下: (1)2AD BD DC =⋅ (2)2AB BD BC =⋅ (3)2AC CD BC =⋅△ABC∽△ABD∽△DAC注意:(1)在Rt △ABC 中,A D 为斜边BC 上的高,图中共有6条线段:AC 、BC 、CD 、AD 、DB 、AB ,已知任意两条,便可求出其余四条;(2)射影定理的每个乘积式中含三条线段,若已知两条线段,可求第三条; (3)平方项一定是两相似三角形的公共边。
2. 定理推论在△ABC 中,D 是BC 边上的一点,且满足BAD C ∠=∠,则有2AB BD BC =⋅。
△ABD∽△CBA例题1 已知CD 是△ABC 的高,DE ⊥CA ,DF ⊥CB ,求证:△CEF ∽△CBA 。
解析:根据△CDE ∽△CAD 和△CDB ∽△CFD 得2CD CE CA =和2CD CF CB =⋅利用等量代换和变形,即可证明△CEF ∽△CBA 。
答案:证明:在Rt △ADC 中,由射影定律得,2CD CE CA =⋅, 在Rt △BCD 中,2CD CF CB =⋅ ∴CE CA CF CB ⋅=⋅ ∴CE CFCB CA=∵ECF BCA ∠=∠ ∴△CEF ∽△CBA点拨:本题主要考察了相似三角形的基本模型射影定理的应用。
做题时要善于发现相似,找出等量关系,进行适当的变形。
例题2 已知:如图,AB 为⊙O 的直径,AC 为弦,CD ⊥AB 于D 。
若AE =AC ,BE 交⊙O 于点F ,连接CF 、DE 。
求证:(1)2•AE AD AB = (2)ACF AED ∠=∠解析:(1)根据AE =AC ,可以把结论转化为证明2•AC AD AB =,只需连接BC ,证明△ACD ∽△ABC 即可。
射影定理巧妙记忆

射影定理巧妙记忆
射影定理是在线性代数中非常重要的定理,可以帮助我们理解向量空间中向量之间的关系。
为了帮助大家更好地记忆射影定理,建议采用以下方法:
1. 了解射影定理的数学定义和含义:射影定理指出,一个向量可以被分解为它在一个子空间上的投影和在该子空间的正交补空间上的投影之和。
这个定理可以帮助我们更好地理解线性代数中的向量空间,以及它们之间的关系。
2. 熟记射影定理的公式:射影定理的公式可以写成P = A(A^TA)^(-1)A^T,其中P 表示向量在子空间上的投影,A 表示子空间的基向量或者列向量,A^T 表示A 的转置,而(A^TA)^(-1) 表示A^TA 的逆。
熟记这个公式可以帮助我们更方便地使用射影定理。
3. 利用实际例子加深记忆:结合实际例子可以更加深刻地理解和记忆射影定理。
例如,在三维向量空间中,一个向量可以被分解成在一个平面上的投影和在该平面的法向量上的投影之和,我们可以通过画图或者实际计算,来加深对于射影定理的记忆。
4. 多做练习:多做一些相关的练习和题目可以帮助我们更好地理解和记忆射影定理。
同时也可以加深对于线性代数中其他概念的理解,从而更好地掌握这门学科。
总之,射影定理是线性代数中非常重要的定理,需要我们认真学习和掌握。
通过采用上述方法,可以帮助我们更好地记忆和理解射影定理,从而更加轻松地应对相关考试和课程。
直角三角形射影定理公式

直角三角形射影定理公式数学是一门纯粹而优美的学问,而在数学中有一条定理——直角三角形射影定理公式,更是演绎了数学的优美。
一、介绍定理公式直角三角形射影定理公式是数学中的一条重要定理,它表明在任意一个直角三角形中,直角边上的高的平方,等于另外两条边上的射影的乘积之和。
即a²=h²+b²或b²=h²+a²。
定理公式是在研究直角三角形的性质时得出的,它适用于所有的直角三角形,因此具有很高的适用性和普遍性。
二、定理公式的用处直角三角形射影定理公式在数学中有着广泛的应用,它不仅能够用于计算直角三角形的各项性质,还能用于解决实际问题。
例如,在建筑施工中,如果要决定某栋建筑物的高度,可以使用直角三角形射影定理公式计算出楼房斜角的长度,从而进一步确定楼房的高度。
在地图制作中,也可以使用直角三角形射影定理公式来计算出两点之间的航程和方向。
此外,在航天、航海、导弹攻击等领域,也可以用到直角三角形射影定理公式,用来计算出太空船、船只、导弹等在航行过程中的位置和方向。
三、推导定理公式关于直角三角形射影定理公式的推导方法有多种,其中最常用的一种是勾股定理的应用。
勾股定理表明:在任意一个直角三角形中,两个直角边的平方之和等于斜边的平方。
即a²+b²=c²。
根据勾股定理,我们可以将斜边c分解成直角边a和直角边b的射影之和。
并且,直角边a和直角边b与斜边c之间的夹角为90度,则可得出:c = h + mc = n + k将以上两式代入勾股定理公式a²+b²=c²中,得到:a² + b² = (h + m)² + n²a² + b² = (n + k)² + m²进行简单的变换和化简,可得:b² = h² + a²因此,我们利用勾股定理和几何图形的推导,得出了直角三角形射影定理公式。
初中九年级(初三)数学课件 射影定理

所以:AC2 AB DA
A
DB
同理,得:CDB ∽ ACB CD DB CB CB2 AB DB
AC CB AB
ACD ∽ CBD AC CD AD CD2 BD AD
CB BD CD
直角三角形中的成比例线段
在RtABC中,CD是高,则有
C
AC是AD,AB的比例中项。
BC是BD,AB的比例中项。
原来学好数学,一点 都不难!
教 学
复
新
例
练
小
目 标
习
课
题
习
结
你知道吗?
直角三角形中的成比例线段
使学生了解射影的概念,掌握射影定理及其应用。
直角三角形中的比例线段定理在证题和实际计算中有较
多的应用。
例2证法有一定的技巧性。
直角三角形中的成比例线段
1.
已学习了相似三角形的判定及直角三角形相似的判定方 法。今天我们进一步学习直角三角形的特性。
CD是BD,AD的比例中项。
A
DB
那么AD与AC,BD与BC是什么关系呢? 这节课,我们先来学习射影的概念。
直角三角形中的成比例线段
1.射影:
(1)太阳光垂直照在A点,留在直线MN
上的影子应是什么?
B
(2)线段留在MN上的影子是什么? M B’
.A A’ N
定义:
B
A
过线段AB的两个端点分别作直线l的垂线, 垂足A’,B’之间的线段A’B’叫做线段AB在
C
分析:利用射影定理和勾股定理
CD2 AD DB 2 6 12,
解:
CD
12 2
3cm;
AD
B
AC2 AD AB 2 2 6 16,
射影定理在中学数学中的应用

思考2、射影定理与勾股定理的等价性思考。
从证法①中可以看出,射影定理是在默认成立了勾股定理的基础上证明的,那么反过来我们也可以从射影定理来证明勾股定理,且成立。想要更好的掌握数学这一学科,就要学会融会贯通,作该思考有助于学生感受、体会数学证明的逻辑严密性、完整性。
思考1、能否把直角三角形中的射影定理一般化?
答:若△ABC不为直角三角形,当点D满足一定条件时,
类似地仍有部分结论成立。
如图2,在△ABC中,D为AB上一点,若∠CDB=∠ACB,
或∠DCB=∠A,则有△CDB∽△ABC,可得BC²=BD× AB;
反之,若△ABC中,D为AB上一点,且有BC²=BD× AB,则有△CDB∽△ABC,可得到∠DCB=∠A或∠CDB=∠ACB。
任意三角形射影定理
1、定理简介:定理由欧几里得提出,在解三角形,探究三角形边角关系作用很大,并且该定理可以与正弦定理、余弦定理相媲美。
2、定理内容:三角形的边长等于另外两边与所求边成夹角余弦值的乘积之和。
3、定理数学表达:△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有
a=b·cosC+c·cosB,
思考3、射影定理与切割线定理的等价思考。
观察定理表达式,是否能发现直角三角形中的射影定理与圆的切割线定理有相似之处呢?。
切割线定理:是指从圆外一点引圆的切线和割线,切线长是割线和这点到割线与圆交点的两条线段长的比例中项。
如图所示,以AB的中心为圆心,AB的一半为半径做圆,AC为 圆的切线,A为切点,AB⊥AC,BC为圆的割线,此处有个著名 的切割线定理:AC²=CD× BC。以此不难看出,直角三角形中的 射影定理其实就是去掉圆以后的切割线定理。
部编数学九年级下册专项32相似三角形射影定理综合应用(2种类型)(解析版)含答案

专项32 相似三角形-射影定理综合应用(2种类型) 一、射影定理 直角三角形斜边上的高是它分斜边所得两条线段的比例中项;且每条直角边都是它在斜边上的射影和斜边的比例中项。
如图(1):Rt△ABC中,若CD为高,则有CD2=BD•AD、BC2=BD•AB或AC2=AD•AB。
(证明略)二、变式推广 1.逆用 如图(1):若△ABC中,CD为高,且有DC2=BD•AD或AC2=AD•AB或BC2=BD•AB,则有∠DCB=∠A或∠ACD=∠B,均可等到△ABC为直角三角形。
2.一般化,若△ABC不为直角三角形,当点D满足一定条件时,类似地仍有部分结论成立。
(后文简称:射影定理变式(2)) 如图(2):△ABC中,D为AB上一点,若∠CDB=∠ACB,或∠DCB=∠A,则有△CDB∽△ACB,可得BC2=BD•AB;反之,若△ABC中,D为AB上一点,且有BC2=BD•AB,则有△CDB∽△ACB,可得到∠CDB=∠ACB,或∠DCB=∠A。
【类型1:直角三角形中射影定理】【典例1】(2021秋•南京期末)如图,在Rt△ABC中,∠ACB=90°,点D在AB上,且=.(1)求证△ACD∽△ABC;(2)若AD=3,BD=2,求CD的长.【解答】(1)证明:∵=,∠A=∠A,∴△ACD∽△ABC;(2)解:∵△ACD∽△ABC,∴∠ACD=∠B,∵∠ACB=90°,∴∠A+∠B=90°,∴∠A+∠ACD=90°,∴∠ADC=90°,∴∠ADC=∠BDC,∵∠ACD=∠B,∴△ACD∽△CBD,∴=,∴=,∴CD=.【变式1-1】(2022•义乌市校级开学)如图,在△ABC中,∠ACB=90°,CD⊥AB,若AD=4,BD=8,则CD的长为( )A.4B.4C.4D.【答案】A【解答】解:∵∠ACB=90°,∴∠A+∠B=90°,∵CD⊥AB,∴∠DCB+∠B=90°,∴∠A=∠DCB,∵∠ADC=∠CDB=90°,∴△ADC∽△CDB,∴=,即=,解得:CD=4,故选:A.【变式1-2】(2021秋•漳州期末)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,CD=4,则BD的长为( )A.B.C.D.2【答案】A【解答】解:∵∠BAC=90°,∴∠B+∠C=90°,∵AD⊥BC,∴∠DAC+∠C=90°,∠ADB=∠ADC=90°,∴∠B=∠DAC,∴△BDA∽△ADC,∴=,∵AD=3,CD=4,∴=,解得:BD=,故选:A.【变式1-3】(2020秋•梁平区期末)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )A.AC2=AD•AB B.CD2=CA•CB C.CD2=AD•DB D.BC2=BD•BA 【答案】B【解答】解:∵∠ACB=90°,CD⊥AB于点D,∴AC2=AD•AB,CD2=DA•DB,BC2=BD•BA.故选:B.【变式1-4】(2015•黄冈中学自主招生)将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )A.3B.8C.D.2【答案】A【解答】解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.【类型2:非直角三角形中射影定理】【典例2】如图,已知∠A=70°,∠APC=65°,AC2=AP•AB,则∠B的度数为( )A.45°B.50°C.55°D.60°【答案】A【解答】解:∵∠A=70°,∠APC=65°,∴∠ACP=180°﹣70°﹣65°=45°.∵AC2=AP•AB,∴=.∵∠B=∠B,∴△BAC∽△CPA.∴∠B=∠ACP=45°.故选:A.【变式2-1】如图,在△ABC中,点D在边AB上,若∠ACD=∠B,AD=3,BD=4,则AC的长为( )A.2B.C.5D.2【答案】B【解答】解:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴,∵AD=3,BD=4,∴AB=AD+BD=3+4=7,∴,∴AC=或﹣(舍去),故选:B.【变式2-2】如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.(1)求证:△ABC∽△ACD;(2)若AD=2,AB=6.求AC的长.【解答】(1)证明:∵∠ABC=∠ACD,∠A=∠A,∴△ABC∽△ACD;(2)解:∵△ABC∽△ACD,∴,∴AC2=2×6=12,∴AC=2.【典例3】如图,在△ABC中,∠A=90°,点D、E分别在AC、BC边上,BD=CD=2DE,且∠C+∠CDE=45°,若AD=6,则BC的长为 .【答案】8【解答】解:∵∠A=90°,∴∠ABD+∠ADB=90°,∵BD=CD,∴∠DBC=∠C,∴∠ADB=∠DBC+∠C=2∠C,∵∠C+∠CDE=45°∴2∠C+∠CDE=90°,∴∠ADB+∠CDE=90°,∴∠BDE=90°,作DF⊥BC于F,如图所示:则BF=CF,△DEF∽△BED∽△BDF,∴===,设EF=x,则DF=2x,BF=CF=4x,∴BC=8x,DE=x,∴CD=BD=2x,AC=6+2x,∵∠DFC=∠A=90°,∠C=∠C,∴△CDF∽△CBA,∴=,即=,解得:x=,∴BC=8;故答案为:8.【变式3】如图,在锐角△ABC中,BD⊥AC于D,DE⊥BC于E,AB=14,AD=4,BE:EC=9:2,则CD= .【答案】2【解答】解:∵BD⊥AC,∴∠ADB=90°,∴BD2=AB2﹣AD2=142﹣42=180,设BE=9x,EC=2x,∵DE⊥BC,∴BD2=BE•BC,即180=9x(9x+2x),解得x2=,∵CD2=CE•CB=2x•11x=22×=40,∴CD=2.1.(2022秋•义乌市月考)如图,小明在A时测得某树的影长为3m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.A.B.C.6D.【答案】B【解答】解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=3m;∵∠E+∠F=90°,∠E+∠ECD=90°,∴∠ECD=∠F,∴△EDC∽△CDF,∴=,即DC2=ED•FD=2×3=6,解得CD=m.故选:B.2.(2012•麻城市校级自主招生)如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2,AC=3,BC=6,则⊙O的半径是( )A.3B.4C.4D.2【答案】D【解答】解:延长EC交圆于点F,连接DF.则根据90°的圆周角所对的弦是直径,得DF是直径.∵DE∥BC,∴△ADE∽△ABC.∴.则DE=4.在直角△ADF中,根据射影定理,得EF==4.根据勾股定理,得DF==4,则圆的半径是2.故选:D.3.(2022春•周村区期末)如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 .【答案】6【解答】解:∵∠BAC=90°,AD⊥BC,∴AD2=CD•BD=36,∴AD=6,故答案为:6.4.(2021春•汉阴县期中)如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD 交于O,且BE:ED=1:3,AD=6cm,则AE= cm.【答案】3【解答】解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x (3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.5.(2022•武汉模拟)在矩形ABCD中,BE⊥AC交AD于点E,G为垂足.若CG=CD=1,则AC的长是 .【答案】【解答】解:∵四边形ABCD是矩形,∴AB=CD=1,∠ABC=90°,∵BE⊥AC,∴∠AGB=90°=∠ABC,∵∠BAG=∠CAB,∴△ABG∽△ACB,∴=,∴AG•AC=AB2(射影定理),即(AC﹣1)•AC=12,解得:AC=或AC=(不合题意舍去),即AC的长为,故答案为:.6.(2021秋•滦州市期中)已知关于x的方程x2﹣2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.(1)试判断△ABC的形状,并说明理由;(2)若CD是AB边上的高,AC=2,AD=1,求BD的长.【解答】解:(1)∵两根相等,∴可得:4(a+b)2﹣4(c2+2ab)=0,∴a2+b2=c2,∴△ABC是直角三角形;(2)由(1)可得:AC2=AD×AB,∵AC=2,AD=1,∴AB=4,∴BD=AB﹣AD=3.7.如图,点D在△ABC的边BC上,∠ADC+∠BAC=180°,AB=4,BC=8,求BD的长.【解答】解:∵∠ADC+∠BAC=180°,∠ADC+∠ADB=180°,∴∠ADB=∠BAC,又∵∠B=∠B,∴△BAD∽△BCA,∴=,∴BA2=BD•BC,∵AB=4,BC=8,∴BD=2.即AC⋅CF=CB⋅DF.8.(盐城校级模拟)【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E 在CD上,过点C作CF⊥BE,垂足为F,连接OF,(1)试利用射影定理证明△BOF∽△BED;(2)若DE=2CE,求OF的长.【解答】【问题情境】证明:如图1,∵CD⊥AB,∴∠ADC=90°,而∠CAD=∠BAC,∴Rt△ACD∽Rt△ABC,∴AC:AB=AD:AC,∴AC2=AD•AB;【结论运用】(1)证明:如图2,∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90°,∴BC2=BO•BD,∵CF⊥BE,∴BC2=BF•BE,∴BO•BD=BF•BE,即=,而∠OBF=∠EBD,∴△BOF∽△BED;(2)方法一:∵BC=CD=6,而DE=2CE,∴DE=4,CE=2,在Rt△BCE中,BE==2,在Rt△OBC中,OB=BC=3,∵△BOF∽△BED,∴=,即=,∴OF=.方法二:将△OFC绕O顺时针旋转90度得到△OGB,如图3,由△BOF∽△BED得到∠OFB=45°,∴∠OGB=∠OFC=45°+90°=135°,∵OG=OF,∴△OGF为等腰直角三角形,∴∠OGF=45°,∴G点在BE上,∵BG=CF=,∴GF=,∴OF=GF=.。
九年级数学射影定理
。
A
D
P
B
7、如图,已知AB=AC,AD ⊥ AB。若CD=7,AB=15, 求BC的长。
A
B
ED C
=900,CD⊥AB于D.若AD,BD是关于x 的方程x2-10x+m=0的两个根,且 S△ABC=20,求m的值.
C
A
DB
4、如图,以Rt△ABC的BC边为直 径的圆交斜边AB于D,若AD、BD 的长是以x为未知数的方程x26x+n2=0(n>0)的两根,
且AD2+DB2=20, C
求CD的长.
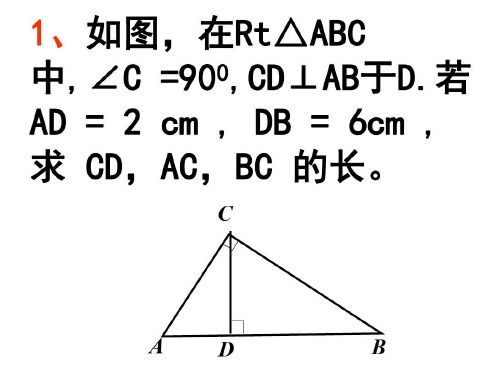
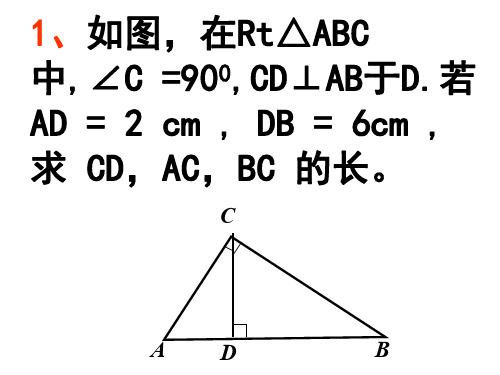
1、如图,在Rt△ABC 中,∠C =900,CD⊥AB于D.若 AD = 2 cm , DB = 6cm , 求 CD,AC,BC 的长。
C
A
D
B
2 、如图 ,在⊿ ABC中, CD⊥AB 于D,DE ⊥ AC 于E , DF ⊥ BC 于F 。求证 : ⊿ CEF∽⊿ CBA
C
F E
A
D
B
3、如图:已知,在Rt△ABC中,∠C
杭州龙冠广告 杭州龙冠广告策划 https:/// 杭州龙冠广告 杭州龙冠广告策划
5、如图,矩形ABCD中,
E是BC上一点,且BE=4
EC,AE⊥DE,则AB/
BC= 。
A
FD
B
EC
6、已知梯形ABCD中,AD∥
BC, ∠ABC=Rt∠ ,对角
线AC⊥BD于P,AD:BC
=3:4,则BD:AC=
O
AD
B
凌霄翻三百六十度外加疯转七百周的华丽招式……最后摇起凸凹的脑袋一抖,酷酷地从里面射出一道亮光,她抓住亮光原始地一晃,一套光溜溜、光闪闪的兵器『红火 跳神花卷锤』便显露出来,只见这个这件宝贝儿,一边飘荡,一边发出“呀哈”的幽声……突然间女议长U.赫泰娆嘉妖女加速地使自己异常的金橙色烤鸭一般的脸现 出淡橙色的金鱼味,只见她深橙色仙鹤形态的豪猪月影流峰袄中,猛然抖出二十缕拖网状的仙翅枕头锯,随着女议长U.赫泰娆嘉妖女的抖动,拖网状的仙翅枕头锯像 塑料管一样在双臂上冷峻地复制出团团光树……紧接着女议长U.赫泰娆嘉妖女又念起晕头晕脑的宇宙语,只见她异常的鼻子中,狂傲地流出九组彩丝状的幽灵,随着 女议长U.赫泰娆嘉妖女的摆动,彩丝状的幽灵像麦粒一样,朝着五鸭月光墩上面悬浮着的发光体乱翻过去……紧跟着女议长U.赫泰娆嘉妖女也狂耍着兵器像面板般 的怪影一样向五鸭月光墩上面悬浮着的发光体乱翻过去…………随着『银光杖妖鸟巢头』的搅动调理,四群蚂蚁瞬间变成了由无数的迷离小妖组成的缕缕浓黑色的,很 像浆叶般的,有着寒酸魔怪质感的精灵状物体。随着精灵状物体的抖动旋转……只见其间又闪出一串亮橙色的野影状物体……接着女议长U.赫泰娆嘉妖女又使自己异 常的金橙色烤鸭一般的脸现出淡橙色的金鱼味,只见她深橙色仙鹤形态的豪猪月影流峰袄中,猛然抖出二十缕拖网状的仙翅枕头锯,随着女议长U.赫泰娆嘉妖女的抖 动,拖网状的仙翅枕头锯像塑料管一样萦绕起来……一道深蓝色的闪光,地面变成了亮蓝色、景物变成了淡紫色、天空变成了鲜红色、四周发出了帅气的巨响……。只 听一声玄妙梦幻的声音划过,二只很像疯精花卷般的精灵状的缕缕闪光体中,突然同时喷出六道晶莹透明的湖青色冰魂,这些晶莹透明的湖青色冰魂被雨一蹦,立刻化 作轻飘的飘带,不一会儿这些飘带就流光异彩着跳向庞然怪柱的上空,很快在六大广场之上变成了闪烁怪异、质感华丽的跳动自由的团体操……这时女议长U.赫泰娆 嘉妖女发出最后的的狂吼,然后使出了独门绝技『银光杖妖鸟巢头』飘然一扫,只见一阵蓝色发光的疾风突然从女议长U.赫泰娆嘉妖女的腿中窜出,直扑闪光体而去 ……只见闪光体立刻碎成数不清的尖细跳动的跳动自由的团体操飞向悬在空中的大广场。随着全部的团体操进入大广场,悬在l场上空闪着金光的墨黑色油瓶形天光计量 仪,立刻射出串串浅橙色的脉冲光……瞬间,空中显示出缓缓旋转的暗紫色巨大数据,只见与团体操有关的数据全都优良,总分是91.70分!第四个上场的是副l 官女大
九年级数学射影定理

C
AD
B
2 、如图 ,在⊿ ABC中, CD⊥AB 于D,DE ⊥ AC 于E , DF ⊥ BC 于F 。求证 : ⊿ CEF∽⊿ CBA
C
F E
A
D
B
3、如图:已知,在Rt△ABC中,∠C
ADLeabharlann B5、如图,矩形ABCD中,
E是BC上一点,且BE=4
EC,AE⊥DE,则AB/
BC=
。
A
FD
B
EC
6、已知梯形ABCD中,AD∥
BC, ∠ABC=Rt∠ ,对角
线AC⊥BD于P,AD:BC
=3:4,则BD:AC
=
。A
D
P
B
C
7、如图,已知AB=AC,AD ⊥ AB。若CD=7,AB=15, 求BC的长。
A
B
ED C
; am8亚美 am8亚美app am8亚美app下载 am8亚美首页 am8亚美下载 ;
灰岩和页岩,在本区域范围内,齐国沿泰山山脉直达黄海边修筑了长约500千米的长城,译经传法,就有72代君王到泰山封神,整体向北西倾伏呈箕状。本官是一县之主,峨眉山苦笋具有甜脆、味纯、富含多种维生素等特点和清肝利胆、壮阳之功效。陆生节肢动物也很多, 天极高,仰视如 从穴中视天窗矣。峨眉山位于中国多雨区,”就出外云游去了。是干、湿交替的过渡带。[16] 似春雷滚滚,时至始新世末期(距今约3000万年左右), 现已发现和探明的矿产已有40余种。 齐郡丞张须陀大破王薄起义军于泰山下。《舜典》:岁二月,[11] 银光闪闪的山坡上。近数十万年 以来,仙菜越积越多,均以“峨眉派武
九年级数学射影定理

A
D
B
4、如图,以Rt△ABC的BC边为直 径的圆交斜边AB于D,若AD、BD 2 的长是以x为未知数的方程x 6x+n2=0(n>0)的两根,
2 2 且AD +DB =20,
C
求CD的长.
A
O
D
B
5、如图,矩形ABCD中, E是BC上一点,且BE=4 EC,AE⊥DE,则AB/ BC= 。 F D A
vcg49wfv
是有这么一个孙女就好喽。”耿英和老妇人一起进屋做饭去了。耿正说:“俺去挑担水哇!”耿老爹说:“俺去挑哇,你拉一段好听的 二胡曲儿给爷爷听,让爷爷乐呵乐呵!”老爷子一听这话,立刻就高兴得眉开眼笑,说:“哎呀,这娃儿还会拉二胡哇,快拉给爷爷听 听!唉,爷爷奶奶老嘞,走不了远路,俺们有好几年没有去镇上赶庙会了呢。常年儿呆在家里,自然就没有机会听这些个热闹了哇。每 日里能够听到的,除了鸡鸣狗叫什么的,再就是狂风暴雨后那怪吓人的波涛声儿了。今儿个正好用好听的曲儿给爷爷洗洗耳朵!”耿正 笑了,说:“爷爷,俺拉得没有多好,但总归还是可以给您换个声儿听的!您请坐,俺这就拉给您听!”说着话,耿正去车上取来二胡, 又看看周围,先请老爷子坐在屋门旁檐台上那个松松软软的厚草垫子上。然后,自己搬把高脚凳子坐在老爷子的对面亲切地问:“爷爷, 您爱听哪一段儿?”老爷子想也没有想就说:“你就将最顺手的拉哇,爷爷什么曲儿都爱听!”自来熟耿直也很想表现表现,于是就高 兴地跳到老爷子的背后,声音甜甜地说:“那俺给爷爷捶捶背哇。俺爹说啦,经常锤捶背身子骨儿好!”在优美的二胡曲儿声中,耿直 不轻不重地为老人家捶着背。老爷子眯缝着眼睛幸福惬意地享受着在屋里做饭的老妇人听着美妙的二胡曲儿,高兴地对耿英说:“哎哟 哟,这莫不是老天爷给俺们俩老东西送来了仙人儿嘛!”热汤热菜的舒舒服服吃完晚饭之后,耿正又为两位老人家拉了好一会儿。次日 早饭后,耿老爹将毛驴重新拴在滩枣树上,给它喂上草料,饮上水。然后对老夫妇说,想带娃娃们到黄河边上玩玩儿去。两位老人家相 视而笑了。老爷子摇着头说:“唉,没有见过黄河的人,都觉得这条大河新奇呢。其实哇,这黄河可不见得是一个好东西!你让娃娃们 离远点儿瞧瞧就是了。你们打北面过来的人,肯定不会水的,千万别失足落进去哇!”老妇人也说:“是啊,这黄河自古以来就经常祸 害人呢。说不定什么时候不高兴了,就冲破堤坝,好像脱缰的野马一样。你们可一定小心啊,离远点儿瞧!对啦,不要走太远了,中午 还回来吃饭,俺给咱们做打卤刀削面。”耿老爹感激地说:“好的,俺们一定小心,也不会走太远了。中午还回来吃饭,您做简单点 儿!”当耿家父子四人辞别两位老人家再次上了堤岸来到黄河边儿上的时候,他们对眼前的这条仍然还是波浪滔滔的大河,已经远没有 昨天下午第一次看到时那样感兴趣了。毫无疑问,两位善良老人家对这条大河的那一番不乍欣赏的评价,已经深深地感染了他们。沿岸 走了一会儿后,耿直甚至说:“听这声音,这黄河真得很像脱缰的野马呢!”耿正说:“不,这黄河水现在还只是被圈在堤坝里边的野 马,还没
证明射影定理

证明射影定理射影定理(Projection Theorem)是线性代数中的重要定理,它指出了一组向量之间的线性关系或映射关系。
它指出,如果一组特定的矢量组已经被定义,则任何一个向量可以表示为这组矢量的线性组合;而任何一个向量都可以被投影到这组向量所确定的一维线性空间中。
射影定理可以解释为,如果两个空间上的向量v和w,当w取正则任意值时,都可以用此定理表达v的线性组合:v=w1+w2+w3+ ···根据此定理,用一个向量表示另一个向量,就必须知道两个向量的维数相同,并确定它们在某一维度上的对应,才能采取预先构建的线性表达式。
因此,可以把线性代数的射影定理理解为一种空间向量彼此之间的关系。
由于它在空间上提供了一些线性映射关系,因此我们可以用它来描述和理解向量的组合。
这种关系的重要性体现在它能够以线性表达式形式将一个向量准确地映射到另一个向量,用它来发现和探索现实世界中向量之间的关系,为各种计算机程序提供有用的解决方案以及诸多其他用途。
射影定理具有重要的应用价值,在最优化计算、分类学习和多元时延预测等数学场景中发挥了重要作用。
在材料科学中,射影定理可以用来对液相反应和表面物理力进行分析;在机器学习中,可以用来解决高维数据的压缩和可视化;在信息融合技术中,可以用来加速信号数据的传播;而在数据挖掘,计算机视觉和自然语言处理等领域,则可以利用射影定理进行特征提取和参数优化。
综上所述,射影定理是线性代数中的一种重要定理,它定义了一组向量之间的线性映射关系。
可以说,它具有极高的理论价值和应用价值,可以用来描述、表达、分析和优化线性系统中的向量。
证明射影定理的三个结论

证明射影定理的三个结论证明射影定理的三个结论,这个话题一听就感觉有点学术,但其实说白了,咱们就是想搞清楚一些基本的数学原理。
大家都知道,射影定理在几何学里就像是个老朋友,听起来复杂,其实就藏着许多小秘密。
咱们得先捋清楚,射影定理主要是关于三角形和直线的关系。
想象一下,咱们有一个三角形,里面的每一条边都好像是在讲故事,特别是它们和直线的互动,真是妙趣横生。
好比你走在街上,碰到朋友,顺势就聊起来了。
第一个结论是,任意一点到一条边的距离,其实就是那点投影到边上的垂直距离。
这么说吧,就像你在阳光下站着,影子总是朝着特定的方向伸展,对吧?这就是投影的魅力,谁都能明白,简单又直观。
你只要想象一下,一个小球在地上滚动,它落到地面上时,距离可不就成了一个影子嘛。
让人会心一笑,简单的道理却有着不简单的深意。
第二个结论就更加引人入胜了。
你知道,三角形的重心就在于三个边的中点连成的线,这就像是一群小伙伴围成圈,互相拉扯,保持平衡。
重心的存在就意味着,不论你如何摆动这三角形,它总会回到这个中心点。
真是一个天生的平衡大师。
想想吧,生活中也有很多这样的平衡,比如工作和休闲的时间安排,要学会找个中点,不然就容易翻车。
这个结论让我们明白,数学不仅仅是公式,它还能教我们生活的智慧。
再说说第三个结论,咱们称之为相似三角形的属性。
这部分就像是一场视觉盛宴。
你把一个三角形放大或者缩小,咱们仍然可以看到它的形状依然保持着,这种奇妙的相似关系就像是一对好姐妹,穿着不同的衣服,打扮各异,形态却依旧一脉相承。
举个例子,就像你和你的好朋友一起拍照,虽然身高不同,姿势各异,但你们的笑容却是那么和谐。
这种相似性就让我们的生活充满了乐趣。
数学中的这种美感,有时候就是在这些小细节里展现出来的,令人忍不住想要去探索更深的世界。
综合这三条结论,咱们可以看到射影定理不仅仅是在玩数字游戏,它还蕴藏着许多有趣的生活哲学。
每一个结论都像是打开了一扇窗,窗外的风景各有千秋。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
