最新北师大版五年级数学下册长方体(一)专题
北师大版五年级下册长方体

⑵哪个面的长是36cm、宽是10cm?
2.下面的长方体都是由棱长为1cm的小正方体搭成 的,它们的长、宽、高各是多少?
长= 4 cm 宽= 2 cm 高= 2 cm
长= 2 cm 宽= 2 cm 高= 5 cm
长= 3 cm 宽= 3 cm 高= 3 cm
下图是长方体的长、宽、高
4 厘 米
6厘米想象ຫໍສະໝຸດ 1、长方体的左面的面积是多少平 方厘米?
2、哪个面的面积是36平方 厘米?
方体; 3、把你的发现与组员说一说,并用自己的方法证明
你的发现; 4、最后完成表格。
高 宽
长
相交于一个顶点的三条棱的长度 分别叫做长方体的长、宽、高。
高 宽
长
高 宽
长
高 宽
长
高 宽
长
高 宽
长
长=宽=高
正方体
正方体是特殊的长方体
高 宽
长
棱
棱 棱
1.右图是一个长方体盒子。(上、下两面近似认为 一致,单位:cm)
北师大版 五年级下册 第二单元 长方体(一)
我们已经学过这些图形,你能说 出它们的名称吗?
生活中哪些物体的形状是长方体或正方体?
生活中哪些物体的形状是长方体或正方体?
面
顶点
棱
长方体 面
顶点
棱
正方体
小组合作 探究发现
要求: 1、用学具拼成一个长方体; 2、以同桌为单位,围绕下发的表格上的内容观察长
【北师大版】五年级数学下册--第二单元《长方体(一)》--知识点+思维导图+针对性训练
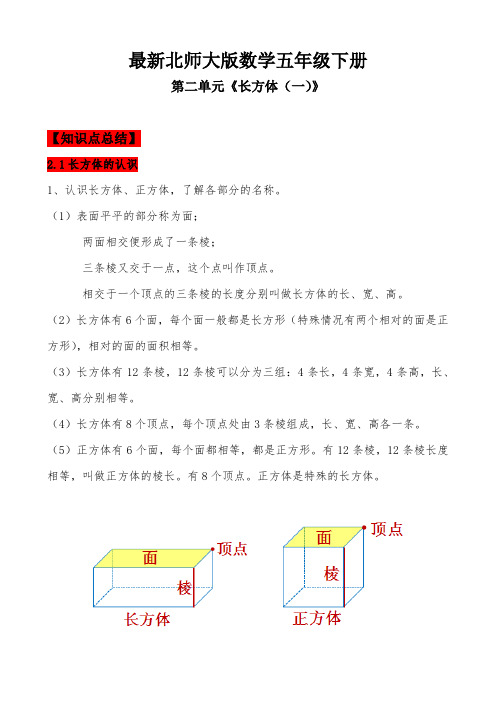
最新北师大版数学五年级下册第二单元《长方体(一)》【知识点总结】2.1长方体的认识1、认识长方体、正方体,了解各部分的名称。
(1)表面平平的部分称为面;两面相交便形成了一条棱;三条棱又交于一点,这个点叫作顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
(2)长方体有6个面,每个面一般都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。
(3)长方体有12条棱,12条棱可以分为三组:4条长,4条宽,4条高,长、宽、高分别相等。
(4)长方体有8个顶点,每个顶点处由3条棱组成,长、宽、高各一条。
(5)正方体有6个面,每个面都相等,都是正方形。
有12条棱,12条棱长度相等,叫做正方体的棱长。
有8个顶点。
正方体是特殊的长方体。
2、长方体、正方体各自的特点。
3、长方体的棱长总和=(长+宽+高)×4,或者是长×4+宽×4+高×4正方体的棱长总和=棱长×122.2展开与折叠正方体的展开图,一共11种。
第一类,中间四连方,两侧各一个,共六种。
第二类,中间三连方,两侧各有一、二个,共三种。
第三类,中间二连方,两侧各有二个,只有一种。
第四类,两排各三个,只有一种。
注意:“田”字型与“凹”字型的是错误的。
2.3长方体的表面积1、表面积的意义:是指六个面的面积之和。
2、长方体表面积的计算方法:长方体上面(或下面)的面积=长×宽长方体前面(或后面)的面积=长×高长方体左面(或右面)的面积=宽×高长方体的表面积=长×宽×2+长×高×2 +宽×高×2,用字母表示为:S长 = a×b×2+ a×h×2 +b×h×2或者,长方体的表面积=(长×宽+长×高 +宽×高)×2,用字母表示为:S长 = (a×b+ a×h +b×h)×23、正方体表面积的计算方法:正方体每个面的面积=棱长×棱长。
北师大版数学5年级下册 第2单元(长方体一)常考易错题B卷(含答案)

第二单元长方体(一)-五年级数学下册易错点汇总及优选易错题B卷本单元知识点易错汇总:1.长方体的6个面有时不都是长方形。
2.长方体的长发生变化,这个长方体的左面和右面的大小不变。
3.在长方体中,同一方向的4条棱互相平行。
4.长方体的高=棱长总和÷4-(长+宽)。
5.判断图形折叠后能否围成正方体,除了要具备6个相同的正方形外,还要考虑折叠时6个面是否重复。
6.正方体的棱长扩大到原来的n倍,表面积就扩大到原来的n2倍。
7.用几个相同的正方体拼成一个长方体后,有几个接合处,表面积就减少(接合处的个数×2)个面的面积。
8.在实际生活中,并不是所有的长方体形状的物体都有6个面,如长方体形状的鱼缸、游泳池等只有5个面,长方体形状的烟囱、通风管等只有4个面。
9.相同个数的小正方体摆放的方式不同,露在外面的面的个数一般也不同。
(时间:60分钟,总分:100分)一.选择题(满分16分,每小题2分)1.下图中不可能围成正方体的是()A.B.C.D.2.一个正方体的6个面分别写着1、2、3、4、5、6六个数字,下图是从三个不同角度所看到的图形,这个正方体正确的展开图是()A.B.C.D.3.图中能表示长方体和正方体关系的是()A.B.C.D.4.下面()可以折叠成正方体A.B.C.D.5.一个长方体只有两个相对的面是正方形,这个长方体有()条棱长度相等.A.4B.6C.8D.126.把一个棱长为1米的正方体切成两个完全相同的长方体,表面积将增加多少平方米?( )A.0.5B.1C.27.一个长26cm、宽18cm,高0.6cm的长方体物体,它可能是()A.黑板擦B.橡皮C.数学书8.装修工人把三块玻璃拼在一起装饰墙面,求三块玻璃的总面积,下列等式成立的是() A.535254(555)324⨯+⨯+⨯=++⨯⨯⨯B.535254(324)5⨯+⨯+⨯=++⨯C.5352545324⨯+⨯+⨯=⨯⨯⨯D.535254(555)(324)⨯+⨯+⨯=++⨯++二.填空题(满分16分,每小题2分)9.在一个长方体中,相交于同一顶点的三条棱长之和是30厘米,则这个长方体的棱长总和是厘米.10.将五本长15厘米,宽10厘米,厚4厘米的新华字典包在一起,至少需要平方厘米的包装纸。
北师大版五年级数学下册4.4 长方体的体积(1)(优质课件)

第1个长方体 第2个长方体 第3个长方体
返回
长方体的体积(1)
同组交流。
把你的想法在小组中交流下,看一看能得 到什么结论?
返回
长方体的体积(1)
长方体的体积 = 长×宽×高 V =a×b×h =abh
返回
长方体的体积(1)
如何计算正方体的体积?与同伴交流下你的 想法。
同学们,你还有其他的摆法吗?
返回
长方体的体积(1)
4.冷藏车厢的内部长3m、宽2.2m、高2m,它的 容积是多少?
容积表示能容纳物体的体积, 所以车厢内部的体积就是冷 藏车厢的容积。
V = abh =3×2.2×2 =13.2(m³)
答:它的容积是13.2m³。
返回
长方体的体积(1)
5.妈妈要寄一个包裹给我的外婆,这个包裹的 体积应该怎样计算呢?
返回
长方体的体积(1)
长方体的体积可能与什么有关?观察下面各 图,想一想。
宽、高不变,长变短了, 体积变小了……
长方体的体积与长、宽、 高都有关系。
返回
长方体的体积(1)
猜一猜,做一做。
长方体的体积与长、宽、高有什么关系?用一些相同的小正 方体(棱长为1cm)摆出3个不同的长方体,记录它们的长、 宽、高完成下表,验证你的猜想。
曹操的次子曹丕做了皇帝后,常想借口除掉曹植。一次,他 为难曹植,命令曹植在走七步路的时间内作出一首诗,并要以兄 弟为题,但诗内不许出现兄弟二字,不然就要被处死。曹植被迫 答应。七步还没走完,曹植的诗已吟出来了:煮豆燃豆箕,豆在 釜中泣。本是同根生,相煎何太急!曹丕听后,又惭愧又心酸, 只得罢休。后来,曹丕对曹植的监视迫害并未减少,曾经六次变 更其爵位,使其三次迁徙封地。
【典型例题系列】五年级数学下册典型例题系列之第二单元长方体(一)的表面积提高部分(原卷版)北师大版

五年级数学下册典型例题系列之第二单元长方体(一)的表面积提高部分(原卷版)编者的话:《五年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题和专项练习两大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
本专题是第二单元长方体(一)的表面积提高部分。
本部分内容考察长方体和正方体的表面积的增减变化及不规则立体图形的表面积,考点和题型难度稍大,建议作为本章核心内容选择性进行讲解,一共划分为十个考点,欢迎使用。
【考点一】正方体表面积的增减变化:切片问题。
【方法点拨】1.表面积的增减变化问题主要有三种,一种是切片问题,表面积会相应增加,一种是拼接问题,表面积会相应减少,一种是高的变化引起的表面积变化。
2.切片问题,即切一刀多两个切面,沿着不同的方向切,多出的表面积一般是不一样的,但正方体比较特殊,它的表面积的增减变化都是都是正方形在进行变化,相对比较简单。
3.刀数×2=切面个数。
【典型例题】把一个棱长是2cm的正方体切成两个完全一样的长方体后,表面积比原来增加了()平方厘米,每个小长方体的表面积是()平方厘米。
【对应练习1】一个正方体的棱长是4厘米,把它切成两个完全相同的长方体后,表面积增大()平方厘米,每个长方体的表面积是()平方厘米,两个长方体的表面积和是()平方厘米。
【对应练习2】把一个棱长是5分米的正方体木块锯成两个完全一样的长方体,表面积比原来增加了()平方分米,每个小长方体的表面积是()平方分米。
【对应练习3】一个正方体的表面积是20平方厘米,将它切成8个一样大小的小正方体,每个小正方体的表面积是多少平方厘米?【对应练习4】一个正方体形状的木块,棱长为1m,沿着水平方向将它锯成3片,每片又按任意尺寸锯成4条,每条再按任意尺寸锯成5小块,共得到大大小小的长方体60块,如图所示。
北师大版五年级数学下册第二单元 长方体 (一)第4课时 长方体的表面积

【教材P17 T6】
6. 如图,包装一个长方体纸盒,选择下面哪种尺寸的包
装纸比较合适?与同伴交流你的想法。(单位:cm)
①
②
29×8
2
30×18
8
分析:包装纸的大小需要满
2 10 2 足长大于等于24cm,宽大于
10
等于12cm这个条件。
课堂小结
通过这节课的学习, 你有什么收获?
5
下
3左 5
前上 后 3
右 5
3
3
7
7
怎样计算这个长方体包装盒的表面积? 想一想,填一填。
前、后两面的 面积和
左、右两面的 面积和
上、下两面的 面积和
7×3×2 = 42(cm2) 5×3×2 = 30(cm2) 7×5×2 = 70(cm2)
长方体表面积 42+30+70=142(cm2)
想一想,长方体表面积的 计算方法是什么?
长方体表面积= 长×宽×2+宽×高×2+长×高×2 =(长×宽+宽×高+长×高)×2
怎样计算正方体的表面积?想一想,说一说。
正方体6个面的面积都相等,先 计算一个面的面积,再乘6。
正方体的表面积=棱长×棱长×6
练一练
【教材P17 T1】
1. 在下面的长方体展开图上,先把相对的面涂上相同
的颜色,再标出每个面的长和宽。(单位:cm)
需要多大面积的玻璃?
5个面
35×35×5=6125(cm2) 答:至少需要6125平方厘米的玻璃。
【教材P17 T5】
5. 淘气的房间长3.5m、宽3m、高3m。除去门窗4.5m2, 房间的墙壁和房顶都贴上墙纸,这个房间至少需要 多大面积的墙纸? 5个面
2021年小学数学第二单元《长方体》—五年级下册章节复习精编讲义(思维导图+知识讲解+达标训练)北师大版,含解析
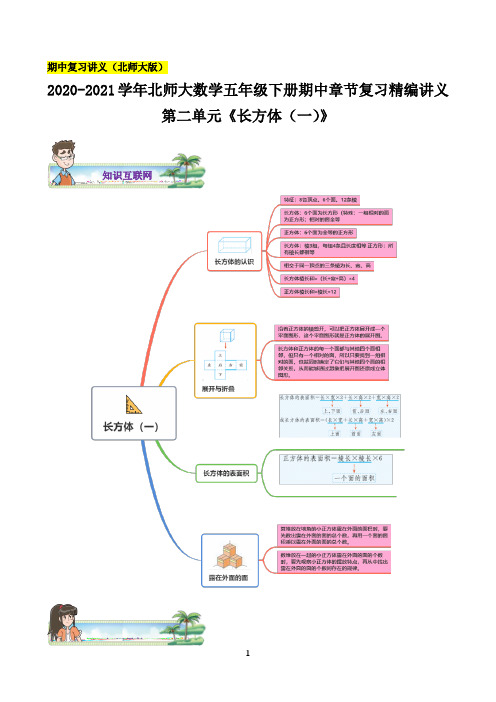
期中复习讲义(北师大版)2020-2021学年北师大数学五年级下册期中章节复习精编讲义第二单元《长方体(一)》知识互联网知识导航知识点一:长方体的认识1 长方体和正方体的各部分名称:在长方体或正方体中,围成的长方形或正方形叫作长方体或正方体的面;面和面相交的边叫作棱;棱和棱相交的点叫作顶点。
2 长方体和正方体的特征3 长方体和正方体的异同点4 长方体和正方体的关系:正方体可以看成是长、宽、高都相等的特殊的长方体5 长方体和正方体特征的应用:判断所给图形能否组成长方体,可以根据长方体的特征一组一组地进行寻找,看看能否找到3组相对应的面。
知识点二:展开与折叠1 正方体展开图的特点(1)沿着正方体的棱剪开,可以把正方体展开成一个平面图形,这个平面图形就是正方体的展开图。
在展开图中,正方体的6个面是相连的,相对的面完全隔开。
(2)将展开图沿虚线(折痕)向内折,能重新折叠成正方体。
(3)正方体的展开图是由6个大小、形状完全相同的正方形组成的组合图形。
(4)正方体的展开图,可分四个类型错误!“一四一”型:中间四个正方形相连,两侧各一个错误!“二三一”型:中间三个正方形相连,两侧分别是两个和一个错误!“二二二”型:中间两个正方形相连,两侧各两个错误!“三三”型:两侧各三个2 长方体展开图的特点:长方体相对的面大小、形状完全相同,并且相对的面完全隔开;长方体上、下两个面的面积相等,长和宽分别是长方体的长和宽;前、后两个面的面积相等,长和宽分别是长方体的长和高;左、右两个面的面积相等,长和宽分别是长方体的宽和高。
3长方体和正方体与展开图之间的对应关系(1)长方体和正方体的每一个面都与其他四个面相邻,但只有一个相对的面,所以只要找到一组相对的面,也就同时确定了它们与其他四个面的相邻关系,从而能够通过想象把展开图还原成立体图形。
(2)判断一个图形折叠后相对应的面,可以根据长方体、正方体展开图的特点,先确定一个面为下面,再想象折叠的过程,从而找出相对的面,也可以用实物折一折,直观地找一找。
五年级下册数学课件第3课时 长方体的表面积 北师大版

正方体的表面积呢? ①长方体展开后是由6个长方形组成,或者是由4个长方形和2个正方形组成的。
(1)请说说长方体它有哪些特征? 同学们对长方体、正方体有了比较深的认识,也会计算每个面的面积,那么长方体的表面积怎样计算呢?这节课我们就来学习这方面的知识。 先把6个面的长、宽测出来,再把6个面的面积求出来后相加。 谁能说说将长方体、正方体展开后各有什么特点? 做一个长54cm、宽50cm、高95cm的洗衣机包装箱,至少需要多大面积的硬纸板? 做一个长54cm、宽50cm、高95cm的洗衣机包装箱,至少需要多大面积的硬纸板? 同学们对长方体、正方体有了比较深的认识,也会计算每个面的面积,那么长方体的表面积怎样计算呢?这节课我们就来学习这方面的知识。
小结:
长方体的表面积=(上面的面积+前面的面积+左面的面 积)×2。 或上面的面积×2+前面的面积×2+左面的面积×2=长方 体的表面积。 正方体的表面积=面我们学习了长方体、正方体的认识,谁能说说长方体、正方体各有什么特征?
在下面的长方体展开图上,先把相对的面涂上相同的颜色,再标出每个面的长和宽。
做一个长54cm、宽50cm、高95cm的洗衣机包装箱,至少需要多大面积的硬纸板?
(1)请说说长方体它有哪些特征?
正方体:8×8×6=384(cm2)
先把6个面的长、宽测出来,再把6个面的面积求出来后相加。
②长方体中相对的面完全相等。
先把6个面的长、宽测出来,再把6个面的面积求出来后相加。
(3)长方体和正方体都有6个面,我们把长方体或正方体6个面的总面积,叫做它的表面积。
2.表面积的计算方法。
前面我们学习了长方体、正方体的认识,谁能说说长方体、正方体各有什么特征?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新北师大版五年级数学下册长方体(一)专题
棱长计算专题练习(1)
长方体:已知棱长求棱长总和
用铁丝焊一个长12cm,宽9cm,高6cm的长方体框架,至少需要多少厘米长的铁丝?(8分)
学校有一幢长方体形状的教学楼(如图)。
为了庆祝建党90周年,现准备买彩灯装饰教学楼除地面外的边。
那么,学校至少需要买多长的彩灯?(10分)
用一根绳子捆扎一种礼品盒(如图),结头处的绳子长15cm。
这根绳子共多少厘米?(8分)
用一根彩带捆扎一种礼盒(如图),如果结头处的彩带长30cm,求这根彩带的长度?(8分)
把两个同样的长方体盒子(如下图)叠在一起,在外面用纸包起来,并扎上包装袋,包装带长(结头不计)
多少厘米?(10分)
做一个长7米、宽1米、高3米的长方形灯箱框架,需要多少米长的铁条?(8分)
长方体:已知棱长总和求棱长
一个长方体游泳池,长50米,宽20米,深2米,沿着这个游泳池游一圈,共游了多少米?(8分)
一个长方体的棱长总和是48厘米,底面周长是18厘米,求高是多少厘米?(10分)
把一根长72厘米的铁丝做成一个长方体框架,已知长和宽分别做成8厘米和5厘米。
高要做成多少厘米才能刚好把铁丝用完?(10分)
一个长方体框架,棱长总和为128厘米,长是高的2倍,宽是8厘米,它的高是多少厘米?(10分)
表面积计算专题练习(2)
1、要制一个长方体油箱,长4分米,宽3分米,高6分米,一共需要多少铁皮?
2、做一个无盖的铁箱,长1米,宽5分米,高8分米,至少需要多少平方米的铁皮?
3、做20个棱长为30厘米的小正方体纸箱,至少需要多少平方米硬纸?
4、要做一个棱长是45厘米的鱼缸,至少需要多少平方厘米的玻璃?
5、用3个棱长是1厘米的正方体拼成一个长方体,这个长方体的表面积是多少平方厘米?
6、把一个长6厘米、宽5厘米、高4厘米的长方体截成两个完全一样的长方体后,这两个长方体的表面积之和最大是多少平方厘米?
7、一只底面是正方形的长方体铁箱,如果把它的侧面展开,正好得到一个边长为40厘米的正方形。
这只铁箱的表面积是多少平方厘米?
8、把三根相同的长方体木料拼成一个大长方体,每根长10厘米、宽5厘米、高2厘米。
怎样才能使拼成
的长方体表面积最大,最大是多少平方厘米?
5、一间教室长8米、宽6米,高3米,现在要用涂料粉刷它的四壁和顶棚。
如果扣除门、窗和黑板24平
方米,求要粉刷的面积有多大?如果每平方米用涂料0.15千克,一共需要多少千克涂料?
6、水泥厂要制作10根长方体铁皮通风管,管口是边长30厘米的正方形,管子长2米。
共需多少平方米
铁皮?
7、一个长方体游泳池,长20米,宽15米,深2米,现要将它的每个面先抹上水泥,再贴上边长4分米
瓷砖,需要这样的瓷砖多少块?如果每平方米用水泥5千克,要用去多少水泥
8、一种长方体铁皮烟囱,底面是边长3分米的正方形,高4米,制这样一节烟囱至少要用铁皮多少平方米?
9、一个正方体木块,若把它切成3个完全相等的长方体后,表面积增加了80平方厘米,这个正方本木块原来的表面积是多少平方厘米?
10、一个长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,它的表面积是多少平方厘米?。
