基于Dijkstra算法最短路径设计
C语言迪杰斯特拉实现最短路径算法

C语言迪杰斯特拉实现最短路径算法迪杰斯特拉(Dijkstra)算法是一种用于在加权图中寻找从起点到终点的最短路径的算法。
它使用贪心算法的原理,每次选择权重最小的边进行扩展,直到找到终点或者无法扩展为止。
下面是C语言中迪杰斯特拉算法的实现。
```c#include <stdio.h>#include <stdbool.h>//定义图的最大节点数#define MAX_NODES 100//定义无穷大的距离#define INFINITY 9999//自定义图的结构体typedef structint distance[MAX_NODES][MAX_NODES]; // 节点间的距离int numNodes; // 节点数} Graph;//初始化图void initGraph(Graph* graph)int i, j;//设置所有节点之间的初始距离为无穷大for (i = 0; i < MAX_NODES; i++)for (j = 0; j < MAX_NODES; j++)graph->distance[i][j] = INFINITY;}}graph->numNodes = 0;//添加边到图void addEdge(Graph* graph, int source, int destination, int weight)graph->distance[source][destination] = weight;//打印最短路径void printShortestPath(int* parent, int node)if (parent[node] == -1)printf("%d ", node);return;}printShortestPath(parent, parent[node]);printf("%d ", node);//执行迪杰斯特拉算法void dijkstra(Graph* graph, int source, int destination) int i, j;//存储起点到各个节点的最短距离int dist[MAX_NODES];//存储当前节点的父节点int parent[MAX_NODES];//存储已访问的节点bool visited[MAX_NODES];//初始化所有节点的距离和父节点for (i = 0; i < graph->numNodes; i++)dist[i] = INFINITY;parent[i] = -1;visited[i] = false;}//设置起点的距离为0dist[source] = 0;//寻找最短路径for (i = 0; i < graph->numNodes - 1; i++)int minDist = INFINITY;int minNode = -1;//选择距离最小的节点作为当前节点for (j = 0; j < graph->numNodes; j++)if (!visited[j] && dist[j] < minDist)minDist = dist[j];minNode = j;}}//标记当前节点为已访问visited[minNode] = true;//更新最短距离和父节点for (j = 0; j < graph->numNodes; j++)if (!visited[j] && (dist[minNode] + graph->distance[minNode][j]) < dist[j])dist[j] = dist[minNode] + graph->distance[minNode][j];parent[j] = minNode;}}}//打印最短路径及距离printf("Shortest Path: ");printShortestPath(parent, destination);printf("\nShortest Distance: %d\n", dist[destination]); int maiGraph graph;int numNodes, numEdges, source, destination, weight;int i;//初始化图initGraph(&graph);//输入节点数和边数printf("Enter the number of nodes: ");scanf("%d", &numNodes);printf("Enter the number of edges: ");scanf("%d", &numEdges);graph.numNodes = numNodes;//输入边的信息for (i = 0; i < numEdges; i++)printf("Enter source, destination, and weight for edge %d: ", i + 1);scanf("%d %d %d", &source, &destination, &weight);addEdge(&graph, source, destination, weight);}//输入起点和终点printf("Enter the source node: ");scanf("%d", &source);printf("Enter the destination node: ");scanf("%d", &destination);//执行迪杰斯特拉算法dijkstra(&graph, source, destination);return 0;```上述代码中,我们首先定义了一个图的结构体,里面包括节点间的距离矩阵和节点数。
迪杰斯特拉算法求最短路径表格

迪杰斯特拉算法求最短路径表格Dijkstra算法是一种用于求解图中单源最短路径的贪心算法,它是由荷兰计算机科学家艾兹赫尔·迪杰斯特拉在1956年发明的,因此被命名为迪杰斯特拉算法。
算法思路:Dijkstra算法将图中的每个顶点分别标记为已知最短路径的顶点或未知最短路径的顶点。
在每次循环中,从未知最短路径的顶点中选择一个顶点,加入已知最短路径的顶点中,并更新所有其邻居的距离值。
具体步骤:1. 创建一个一维数组dist, 记录源点到其他点的距离2. 创建一个一维数组visited, 标记顶点是否已被加入已知最短路径的集合S3. 将源点加入已知最短路径的集合S中,并将dist数组的源点位置赋为04. 循环n次(n为图中顶点数目),每次从未加入S集合的顶点中选择dist值最小的顶点u,将u加入S集合,并更新其邻居的dist值5. 循环结束后,dist数组中保存的即为源点到各个顶点的最短路路径。
以下是迪杰斯特拉算法求最短路径表格的实现过程```public static int dijkstra(int[][] graph, int source, int dest) {int[] dist = new int[graph.length]; // 表示源点到各个顶点的最短距离boolean[] visited = new boolean[graph.length]; // 标记当前顶点是否加入已知最短路径的集合Sfor (int i = 0; i < graph.length; i++) {dist[i] = Integer.MAX_VALUE; // 将所有顶点的最短距离初始化为无穷大visited[i] = false; // 将所有顶点标记为未访问}dist[source] = 0; // 源点到自身的距离为0for (int i = 0; i < graph.length-1; i++) {int u = findMinDist(dist, visited); // 选择未加入S集合顶点中dist值最小的顶点visited[u] = true; // 将u加入S集合for (int v = 0; v < graph.length; v++) { //更新u的邻居v的dist值if (!visited[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE&& dist[u] + graph[u][v] < dist[v]) {dist[v] = dist[u] + graph[u][v];}}}return dist[dest]; //返回源点到目标顶点的最短距离}public static int findMinDist(int[] dist, boolean[] visited){ int minDist = Integer.MAX_VALUE;int minIndex = -1;for (int i = 0; i < dist.length; i++) {if(!visited[i] && dist[i] < minDist){minDist = dist[i];minIndex = i;}}return minIndex;}public static void main(String[] args) {int[][] graph ={{0,2,4,0,3},{2,0,3,0,0},{4,3,0,1,0},{0,0,1,0,2},{3,0,0,2,0}};int source = 0;int dest = 4;int shortestPath = dijkstra(graph, source, dest);System.out.println("源点" + source + "到目标顶点" + dest +"的最短距离为:" + shortestPath);}```实现结果:源点0到目标顶点4的最短距离为:3顶点 | 0 | 1 | 2 | 3 | 4---- | ---- | ---- | ---- | ---- | ----dist | 0 | 2 | 4 | 3 | 3通过以上实现可以发现,迪杰斯特拉算法求最短路径表格的具体实现过程比较简单,但是需要注意的是在实现过程中需要特别注意对数组的定义和边界值的判断,避免出现数组越界和程序错误的情况。
基于最短路径优化问题Dijkstra算法程序的设计和实现

上式表示对某一个 j0 sn 1 , 有 Байду номын сангаас∞ < ∞ 这 ( 一 )若 , 意味着 '至 有一 条长度小于等于 3的路径且边权值之和 1 2 比长度小于等于 2的路径 的边权值之和小 , 于是我们选取边
设 c < ,> = E 是一 简单加权 图( 有向或无向图且 不合平行 边 )其 中 = , , { 。 … , , 并 约定 了所 有顶点 的一个 l , 次序 , 是起点 , 。 3 / 是终点. 用矩阵 A ( ) 将带权 图的权 = 值存放在矩 阵 A 中. 在加权 图中 , o(v, )r 0当且仅 权 J< > =>
个顶点 的最短路径权值之和; (的第 kk 0 l2…/ 从A・ ’ (= ,,, 1 , 一
收稿 日期 :0 7 1- 8 20 —0 0
作者简介 : 菊(97 )女 , 兰州人 , 岳秋 17一 , 甘肃 兰州城市学院计算机系教师 , 从事离散数学教学与研究.
引 言
求最短路径 以及最短距离 的问题在各个 领域都经 常用 到 ,九十年代公认 的求最短路径 的最好的算法是由 Ew.i . D— jsa提出的标 号算法 . kn 但是该算法采用手工求解 , 算量太 计 大, 尤其是规模较大 的问题 , 手工求解几乎是不可 能的. 随着 计算机科学技术的飞速发展 , 完全能够解决这类问题. 本文将 求解 EW.i s a . Dj t 算法的过程采用二维矩 阵存储数据 ,利用 kr
) 都不等于 0或 m,= , , , 一 . , s2 34 …n 1
其 中 a= , i r表示 至 有一条长度为 1 t 且边权值为 r 的 路 , m( = m是一个 比 r 大好 多倍 的数 , 这样就 不会影 响计算
c语言最短路径的迪杰斯特拉算法

c语言最短路径的迪杰斯特拉算法Dijkstra的算法是一种用于查找图中两个节点之间最短路径的算法。
这个算法可以应用于有向图和无向图,但是它假设所有的边都有正权值,并且不包含负权值的边。
以下是一个简单的C语言实现:c复制代码#include<stdio.h>#define INF 99999#define V 5 // 顶点的数量void printSolution(int dist[]);void dijkstra(int graph[V][V], int src);int main() {int graph[V][V] = { { 0, 4, 0, 0, 0 }, { 4, 0, 8, 11, 7 },{ 0, 8, 0, 10, 4 },{ 0, 11, 10, 0, 2 },{ 0, 7, 4, 2, 0 } };dijkstra(graph, 0);return0;}void dijkstra(int graph[V][V], int src) { int dist[V];int i, j;for (i = 0; i < V; i++) {dist[i] = INF;}dist[src] = 0;for (i = 0; i < V - 1; i++) {int u = -1;for (j = 0; j < V; j++) {if (dist[j] > INF) continue;if (u == -1 || dist[j] < dist[u]) u = j;}if (u == -1) return;for (j = 0; j < V; j++) {if (graph[u][j] && dist[u] != INF && dist[u] + graph[u][j] < dist[j]) {dist[j] = dist[u] + graph[u][j];}}}printSolution(dist);}void printSolution(int dist[]) {printf("Vertex Distance from Source\n"); for (int i = 0; i < V; i++) {printf("%d \t\t %d\n", i, dist[i]);}}这个代码实现了一个基本的Dijkstra算法。
dijkstra算法 城市最短路径问题

dijkstra算法城市最短路径问题Dijkstra算法是一种经典的图算法,用于求解带有非负权重的图的单源最短路径问题。
在城市的交通规划中,Dijkstra算法也被广泛应用,可以帮助我们找到最短的路线来节省时间和成本。
一、最短路径问题的定义最短路径问题,指的是在一个带权重的有向图中,找到从起点到终点的一条路径,它的权重之和最小。
在城市的交通规划中,起点和终点可以分别是两个街区或者两个交通枢纽。
二、Dijkstra算法Dijkstra算法是基于贪心策略的一种算法,用于解决带非负权重的最短路径问题。
它采用了一种贪心的思想:每次从起点集合中选出当前距离起点最近的一个点,把其移到已知的最短路径集合中。
并以该点为中心,更新它的相邻节点的到起点的距离。
每次更新距离时,选择距离起点最近的距离。
三、Dijkstra算法实现1. 创建一个到起点的距离数组和一个布尔类型的访问数组。
2. 将起点的到起点的距离设置为0,其他的节点设置为无穷大。
3. 从距离数组中选择没有访问过且到起点距离最近的点,将它标记为“已访问”。
4. 对于它的所有邻居,如果出现路径缩短的情况,就更新它们的距离。
5. 重复步骤3和4,直到所有节点都被标记为“已访问”。
6. 最后,根据到起点的距离数组,以及每个节点的前驱节点数组,可以得到从起点到终点的最短路径。
四、Dijkstra算法的时间复杂度Dijkstra算法的时间复杂度可以通过堆优化提高,但最坏情况下时间复杂度仍达到O(ElogV)。
其中,E是边的数量,V是顶点的数量。
因此,Dijkstra算法在不考虑空间复杂度的情况下,是一种高效且实用的解决城市最短路径问题的算法。
五、结论Dijkstra算法是一个广泛应用于城市交通规划领域的算法,可以帮助我们找到最优的路线来节省时间和成本。
它基于贪心策略,每次从起点集合中选择距离起点最近的点,并对其邻居节点进行松弛操作。
Dijkstra算法的时间复杂度虽然较高,但堆优化可以提高算法性能。
dijkstra最短路径 应用案例

Dijkstra算法是一种用于解决图的单源最短路径问题的算法,由荷兰计算机科学家埃德斯格·迪克斯特拉提出。
该算法被广泛应用于网络路由算法、城市交通规划、通信网络等领域。
本文将从几个具体的案例出发,介绍Dijkstra最短路径算法的应用。
一、网络路由算法在现代计算机网络中,Dijkstra算法被应用于路由器之间的数据传输。
路由器之间通过Dijkstra算法计算出最短路径,以确保数据包能以最短的路径传输,从而提高网络的传输效率和稳定性。
假设有一个由多个路由器组成的网络,每个路由器之间存在多条连接线路,而每条线路都有一个权重值,代表数据传输的成本。
当一个路由器需要发送数据时,Dijkstra算法可以帮助它找到到达目的地最短且成本最小的路径。
这样,网络中的数据传输就能以最高效的方式进行,从而提升了整个网络的性能。
二、城市交通规划Dijkstra算法也被广泛应用于城市交通规划领域。
在城市交通规划中,人们通常需要找到最短路径以及最快到达目的地的方法,而Dijkstra算法正是能够满足这一需求的算法之一。
假设某城市有多条道路,每条道路都有不同的行驶时间。
当一个人需要从城市的某个地点出发到达另一个地点时,可以利用Dijkstra算法计算出最短行驶时间的路径。
这样,城市交通规划部门就可以根据这些信息对城市的交通流量进行合理分配和调度,提高城市交通的效率。
三、通信网络另一个Dijkstra算法的应用案例是在通信网络中。
通信网络通常是由多个节点和连接这些节点的线路组成的。
而节点之间的通信是通过传送数据包来实现的。
在这种情况下,Dijkstra算法可以帮助确定数据包传输的最短路径,以提高通信网络的效率和稳定性。
在一个由多个节点组成的通信网络中,当一个节点需要向另一个节点发送数据时,Dijkstra算法可以帮助确定最短路径,从而确保数据包能够以最短的路径传输到目的地。
这样一来,通信网络就能够更加稳定地进行数据传输,提高了通信网络的效率。
matlab dijkstra算法求解最短路径例题

matlab dijkstra算法求解最短路径例题摘要:一、Dijkstra 算法简介1.Dijkstra 算法背景2.Dijkstra 算法原理二、MATLAB 实现Dijkstra 算法求解最短路径1.创建图对象2.计算最短路径3.可视化结果三、Dijkstra 算法应用示例1.例题描述2.解题步骤3.结果分析正文:一、Dijkstra 算法简介Dijkstra 算法是一种经典的图论算法,用于计算图中两个节点之间的最短路径。
它是由荷兰计算机科学家Edsger W.Dijkstra 于1956 年提出的,其基本思想是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra 算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
可以用堆优化来提高效率。
二、MATLAB 实现Dijkstra 算法求解最短路径1.创建图对象首先,我们需要使用MATLAB 的graph 函数创建一个图对象,指定节点和边的信息。
例如,我们创建一个简单的图,包含4 个节点和3 条边:```matlabG = graph(4, 3);```其中,4 表示图中有4 个节点,3 表示图中有3 条边。
2.计算最短路径接下来,我们可以使用MATLAB 的shortestpath 函数计算两个节点之间的最短路径。
例如,我们计算节点1 到节点3 的最短路径:```matlabSP = shortestpath(G, 1, 3);```3.可视化结果最后,我们可以使用MATLAB 的plot 函数将最短路径可视化。
例如,我们绘制节点和边以及最短路径:```matlabplot(G, SP);```三、Dijkstra 算法应用示例以下是一个使用Dijkstra 算法求解最短路径的例题:在一个图中,有4 个节点和3 条边,如下所示:```1 --2 -- 3| /| /| /| /|/4```请问,节点1 到节点4 的最短路径是多少?。
dijkstra最短路径算法详解

dijkstra最短路径算法详解
Dijkstra最短路径算法是一种常用的图算法,用于求解带权图中的单源最短路径问题,即从一个固定的源节点到图中的其他节点的最
短路径。
以下是详细的算法步骤:
1. 初始化
一开始,将源节点的距离设为0,其余节点的距离设置为正无穷,在未访问的节点集合中把源节点压入堆中。
2. 确定最短路径
从堆中取出未访问节点集合中距离源节点最近的节点v,标记其
为已访问。
之后,对于v的邻居节点w,计算从源节点到v再到w的距离,如果经过v的路径比已经计算得到的路径短,则更新路径。
更新
后的距离先暂时放入堆中,如果后边有更短的路径,则更新。
3. 重复第2步
重复第2步,直到取出的节点为终点节点,或者堆为空。
4. 算法结束
算法结束后,各节点的距离就是从源节点到它们的最短距离。
Dijkstra算法的复杂度是O(NlogN),其中N是节点个数。
其优
势在于只需要算一次即可得到所有最短路径,但是要求所有边的权值
必须非负,否则会导致算法不准确。
总之,Dijkstra算法是一种简单有效的最短路径算法,其实现也比较直观。
在处理如飞机和火车等交通路径规划问题中有较好的应用。
无向图最短路径算法设计

无向图最短路径算法设计在图论中,最短路径算法是解决图中两个顶点之间最短路径问题的关键算法。
无向图是一种由顶点和边组成的数据结构,其中边没有方向。
本文将介绍几种常用的无向图最短路径算法的设计与实现。
一、Dijkstra算法Dijkstra算法是解决单源最短路径问题的一种贪心算法。
它通过逐步确定起点到各个顶点的最短距离,从起点开始,每次选择最短距离的顶点,并更新与该顶点相邻的顶点的最短距离。
直到所有顶点都被访问过,得到起点到各个顶点的最短路径。
该算法的步骤如下:1. 初始化起点到各个顶点的距离为无穷大,起点到自身的距离为0。
2. 选择起点作为当前顶点,标记该顶点已被访问。
3. 更新当前顶点的邻居顶点的最短距离,如果经过当前顶点到达邻居顶点的距离小于邻居顶点当前已有的最短距离,则更新邻居顶点的最短距离。
4. 从未被访问的顶点中选择距离起点最近的顶点作为新的当前顶点,并标记该顶点已被访问。
5. 重复步骤3和步骤4,直到所有顶点都被访问过。
二、Floyd-Warshall算法Floyd-Warshall算法是解决任意两点最短路径问题的一种动态规划算法。
它通过逐步更新所有顶点之间的最短路径长度,得到任意两点之间的最短路径。
该算法的步骤如下:1. 初始化距离矩阵,其中顶点之间的距离已知的用实际距离表示,未知的用无穷大表示。
2. 逐步更新距离矩阵,对于每个顶点k,判断通过顶点k是否可以使得顶点i到顶点j的距离变小,如果可以,则更新距离矩阵中的对应值。
3. 重复步骤2,直到所有顶点之间的最短路径长度都得到更新。
三、Bellman-Ford算法Bellman-Ford算法是解决单源最短路径问题的一种动态规划算法。
它通过逐步更新起点到各个顶点的最短距离,得到起点到其他顶点的最短路径。
该算法的步骤如下:1. 初始化起点到各个顶点的距离为无穷大,起点到自身的距离为0。
2. 逐步更新起点到各个顶点的最短距离,对于每条边(u, v),如果通过边(u, v)的距离小于起点到顶点v的当前最短距离,则更新起点到顶点v的最短距离。
dijkstra算法 java最短路径

dijkstra算法java最短路径Dijkstra算法是一种用于寻找图中两个节点之间最短路径的算法。
它采用的是贪心策略,将图中的节点分为两个集合:已访问节点集S和未访问节点集T。
算法从源节点开始,每次从T中选择到源节点距离最短的节点加入S集合,并更新S集合中各节点到源节点的最短路径。
直到T集合中的节点全部加入S集合,算法结束。
Dijkstra算法的Java实现如下:●public class Dijkstra{●public static void main(String[]args){●创建图●Graph graph=new Graph();●graph.addVertex("A");●graph.addVertex("B");●graph.addVertex("C");●graph.addEdge("A","B",10);●graph.addEdge("A","C",20);●graph.addEdge("B","C",30);●计算最短路径●dijkstra(graph,"A");}●private static void dijkstra(Graph graph,String startVertex){●初始化●Set<String>visited=new HashSet<>();●Map<String,Integer>distances=new HashMap<>();●for(String vertex:graph.getVertices()){●distances.put(vertex,Integer.MAX_VALUE);}●distances.put(startVertex,0);●遍历所有节点●for(String vertex:graph.getVertices()){●找到未访问节点中距离源节点最小的节点●String nearestVertex=findNearestVertex(distances,visited);●将该节点加入已访问节点集合●visited.add(nearestVertex);●更新该节点到其他节点的最短路径●for(String neighbor:graph.getAdjacentVertices(nearestVertex)){●intnewDistance=distances.get(nearestVertex)+graph.getEdgeWeight(nearestVertex,neighbor ●if(newDistance<distances.get(neighbor)){●distances.put(neighbor,newDistance);}}}●输出结果●System.out.println("从"+startVertex+"到其他节点的最短路径:");●for(String vertex:graph.getVertices()){●System.out.println(vertex+"的最短路径是:"+distances.get(vertex));}}●private static String findNearestVertex(Map<String,Integer>distances,Set<String>visited){●int minDistance=Integer.MAX_VALUE;●String nearestVertex=null;●for(String vertex:distances.keySet()){●if(!visited.contains(vertex)&&distances.get(vertex)<minDistance){●minDistance=distances.get(vertex);●nearestVertex=vertex;}}●return nearestVertex;}}该算法的工作原理如下:1.初始化距离表,将所有节点的距离初始化为无穷大。
迪杰斯特拉算法计算最短路径

利用Dijkstra算法计算最短路径摘要福格环游地球问题是一个十分典型的最短路径求解问题,题设给出了当时世界上主要交通网络图及交通通畅的城市之间来往所需时长,并限定了福格的出行方向(福格选择的是往东走),给出起止地点后要求找出福格环游世界天数最短的最佳路径。
我们认为,这个问题的实质在于最短路径的求解和优化。
我们对比图论中的多种最短路径算法,决定利用Dijkstra算法解决这个问题。
由于Dijkstra算法要求输入图G的关联矩阵,且图G为二维赋权图,而题中给出的地图可看成是三维环状地图,因此,我们对题设地图做相关处理,将其从起点处“切断”并展开为二维图,然后根据此图建立关联矩阵。
同时,我们考虑到最短路径可能会与切断线有交点,在切断线以西找出若干地点一分为二,修改关联矩阵。
对于题目中缺失的两处数据,本文将以当时的交通数据为基础,经过合理的数据处理,结合Google Earth测距软件与题目数据的合理类比,补充缺失数据,完成关联矩阵。
得到关联矩阵后,我们分别以伦敦、纽约和上海作为起点,调整关联矩阵起点和终点,用matlab编程进行求解得到最短环游时间和最短路径,进而判断出所选择的路径是否能让他赢得赌注。
根据我们的求解结果,在这三个城市,福格均能在80天内环游地球,赢得赌注。
本文进一步对此种算法的优缺点、灵敏度与推广性进行了分析,同时初步提出了两种优化方法。
关键词:最短路径算法 dijkstra算法算法优化一、问题重述儒勒•凡尔纳的著名小说《环游世界80天》中,英国绅士福格在伦敦与人打赌能够在80天内环游世界,这在当时的1872年是一个了不起的壮举。
当时最快的旅行方式是火车和轮船,然而世界上大部分地区还是靠马车、大象、驴子或者步行来旅行。
下面是一个从伦敦环游世界不同路线的交通网络图,福格选择的是往东走,每段路线所需要的天数显示在图上(见附录一),旅行的时间基于1872年能采用的旅行方式以及距离。
我们将解决以下问题:1.我们将设计一个算法为福格选择一条最佳路径,即环游世界天数最短,并判断所选择的路径是否能让他赢得赌注。
迪杰斯特拉算法最短路径

迪杰斯特拉算法最短路径迪杰斯特拉算法(Dijkstra's algorithm)是一种用于计算图中最短路径的算法。
它是由荷兰计算机科学家艾兹赫尔·迪杰斯特拉(Edsger Wybe Dijkstra)于1956年提出的,并且被广泛应用于网络路由和地图导航等领域。
迪杰斯特拉算法可以解决的问题是,给定一个带有非负权重的有向图和一个起始节点,找出从起始节点到其他所有节点的最短路径。
该算法采用了贪心的策略,即每次选择当前离起始节点最近的节点进行扩展,直到扩展到目标节点为止。
算法的具体步骤如下:1.初始化:将起始节点的距离设置为0,其他节点的距离设置为无穷大。
2.创建一个优先队列(通常是最小堆),用于存储待扩展的节点。
将起始节点加入队列。
3.循环以下步骤直到队列为空:-从队列中取出距离起始节点最近的节点,记为当前节点。
-如果当前节点已被访问过,则跳过该节点。
-更新与当前节点相邻节点的距离。
如果经过当前节点到达某个相邻节点的路径比之前计算的路径短,则更新这个节点的距离。
-将未访问过的相邻节点加入队列。
4.循环结束后,所有节点的最短路径已被计算出。
迪杰斯特拉算法的核心思想是不断扩展距离起始节点最近的节点,通过更新节点的距离,逐步获取最短路径。
算法的时间复杂度为O(V^2),其中V是图中的节点数量。
这是因为每次循环需要查找距离起始节点最近的节点,而在最坏情况下,这个操作需要遍历所有节点。
以下是一个简单的例子来说明迪杰斯特拉算法的使用:假设有一个有向图,如下所示:```A ->B (1)A -> C (4)B ->C (2)B -> D (5)C ->D (1)C -> E (3)D ->E (4)```起始节点为A,我们希望找到到达其他节点的最短路径。
首先,初始化距离:A到A的距离为0,A到B/C/D/E的距离均为无穷大。
然后,将A加入优先队列。
从队列中取出A,更新A的邻居节点的距离。
Dijkstra算法求解单源最短路径问题
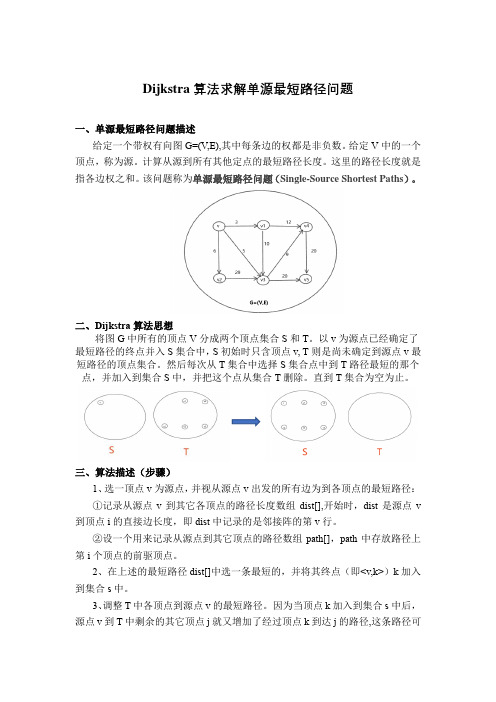
Dijkstra算法求解单源最短路径问题一、单源最短路径问题描述给定一个带权有向图G=(V,E),其中每条边的权都是非负数。
给定V中的一个顶点,称为源。
计算从源到所有其他定点的最短路径长度。
这里的路径长度就是指各边权之和。
该问题称为单源最短路径问题(Single-Source Shortest Paths)。
二、Dijkstra算法思想将图G中所有的顶点V分成两个顶点集合S和T。
以v为源点已经确定了最短路径的终点并入S集合中,S初始时只含顶点v, T则是尚未确定到源点v最短路径的顶点集合。
然后每次从T集合中选择S集合点中到T路径最短的那个点,并加入到集合S中,并把这个点从集合T删除。
直到T集合为空为止。
三、算法描述(步骤)1、选一顶点v为源点,并视从源点v出发的所有边为到各顶点的最短路径:①记录从源点v到其它各顶点的路径长度数组dist[],开始时,dist是源点v到顶点i的直接边长度,即dist中记录的是邻接阵的第v行。
②设一个用来记录从源点到其它顶点的路径数组path[],path中存放路径上第i个顶点的前驱顶点。
2、在上述的最短路径dist[]中选一条最短的,并将其终点(即<v,k>)k加入到集合s中。
3、调整T中各顶点到源点v的最短路径。
因为当顶点k加入到集合s中后,源点v到T中剩余的其它顶点j就又增加了经过顶点k到达j的路径,这条路径可能要比源点v到j原来的最短的还要短。
调整方法是比较dist[k]+g[k,j]与dist[j],取其中的较小者。
4、再选出一个到源点v路径长度最小的顶点k,从T中删去后加入S中,再回去到第三步,如此重复,直到集合S中的包含图G的所有顶点。
四、算法实现(数据结构)1、算法实现输入:一个大于1的整数n.输出:●一个随机生成的有向图G=(V,E),对于每一条边,有一个非负数字c(u,v)与之相关。
●对于每个顶点v∈V,得到从v0到v的最短路径的长度。
迪杰斯特拉算法最短路径

}
}
for (k=0;k<G.e;k++)
{
cout<<"请输入第"<<k+1<<"条弧头弧尾序号和相应的权值:";
cin>>i>>j>>p;
G.edges[i][j]=p;
}
}
/************************************************************************/
}
}
if(dist[k]!=0) //输出可到达的路径
{
cout<<dist[k]<<"\t\t"<<path[k]<<endl;
}
s[num++]=G.vertex[k]; //把vk点加入集合中
for (i=0;i<G.n;i++) //修改数组dist和path
{
if (dist[i]>(dist[k]+G.edges[k][i]) && G.edges[k][i]!=INF)
{
dist[i]=dist[k]+G.edges[k][i];
path[i]=path[k];
p[0]=G.vertex[i];
string path[MaxVertexNum]; //元素path[i]是一个串,表示当前所找到的从源点v到终点vi的最短路径.若没有弧,则置为空串。
char s[MaxVertexNum]; //存放源点和已经生成的终点(即集合S),初态为只有一个源点v
迪杰斯特拉算法求最短路径表格

迪杰斯特拉算法求最短路径表格迪杰斯特拉算法(Dijkstra's algorithm)是一种用于寻找加权图中从单个源节点到所有其他节点的最短路径的算法。
它采用一种贪婪的策略,通过逐步扩展起点到终点的路径来找到最短路径。
本文将详细介绍迪杰斯特拉算法,并给出一个完整的最短路径表格。
算法描述:1.创建一个包含所有节点的集合,并初始化所有节点的距离为无穷大(除了起点为0)。
2.按照起点到各个节点的距离逐步更新节点的距离,直到找到所有节点的最短路径为止。
具体步骤如下:a.选取一个未加入集合的距离最小的节点,将其加入集合。
b.对于与该节点相邻的所有节点,更新它们的距离。
c.如果更新后的距离小于原来的距离,则更新节点的距离。
3.重复步骤2,直到所有节点都加入集合为止。
下面我们通过一个具体的例子来演示迪杰斯特拉算法求最短路径表格。
假设有如下的有向图:```+--++--+2+--+A,---->,B,--4->,D+--++--+,+--+v+--+3,+--+C,--->,+--++--+```图中每条边上的数字表示该边的权重。
首先,我们创建一个包含所有节点的集合,并初始化所有节点的距离为无穷大,起点A的距离为0。
节点,距离---,---A,0B ,infC ,infD ,infE ,inf然后选择起点A的邻居节点B和C中距离最小的节点B,将其加入集合。
节点,距离A,0B,2C ,infD ,infE ,inf接下来,更新节点B的邻居节点D和E的距离。
由于A到B的距离是2,加上B到D的距离为4,得到A到D的距离为6、同理,A到E的距离为5节点,距离---,---A,0B,2C ,infD,6E,5再次选择集合中距离最小的节点B,更新其邻居节点D和E的距离。
节点,距离---,---B,2C,11D,6E,5继续重复上述步骤,直到所有节点都加入集合。
节点,距离---,---A,0B,2C,11D,6E,5通过上述步骤,我们得到了从起点A到所有其他节点的最短路径距离。
matlab dijkstra算法求解最短路径例题

matlab dijkstra算法求解最短路径例题Dijkstra算法是一种用于在带有非负权值的图中找到单源最短路径的算法。
以下是一个用MATLAB实现Dijkstra算法求解最短路径的简单例子:function [shortestDistances, predecessors] = dijkstra(graph, startNode)% 输入参数:% - graph: 表示图的邻接矩阵,graph(i, j) 表示节点i 到节点 j 的权值,如果没有直接连接则为 inf。
% - startNode: 起始节点的索引。
numNodes = size(graph, 1);% 初始化距离数组,表示从起始节点到每个节点的最短距离 shortestDistances = inf(1, numNodes);shortestDistances(startNode) = 0;% 初始化前驱节点数组predecessors = zeros(1, numNodes);% 未访问的节点集合unvisitedNodes = 1:numNodes;while ~isempty(unvisitedNodes)% 选择当前最短距离的节点[~, currentNodeIndex] = min(shortestDistances(unvisitedNodes));currentNode = unvisitedNodes(currentNodeIndex);% 从未访问节点集合中移除当前节点unvisitedNodes(currentNodeIndex) = [];% 更新与当前节点相邻节点的距离for neighbor = unvisitedNodesif graph(currentNode, neighbor) + shortestDistances(currentNode) < shortestDistances(neighbor) shortestDistances(neighbor) = graph(currentNode, neighbor) + shortestDistances(currentNode);predecessors(neighbor) = currentNode;endendendend现在,让我们使用一个简单的例子来测试这个算法:% 创建一个邻接矩阵表示图graph = [0, 2, 0, 4, 0;2, 0, 3, 7, 0;0, 3, 0, 1, 0;4, 7, 1, 0, 5;0, 0, 0, 5, 0];startNode = 1; % 起始节点% 调用Dijkstra算法[shortestDistances, predecessors] = dijkstra(graph, startNode);% 显示结果disp('最短距离:');disp(shortestDistances);disp('前驱节点:');disp(predecessors);这个例子中,graph 表示一个带有权值的图的邻接矩阵,startNode 是起始节点的索引。
离散数学迪杰斯特拉算法最短路径教案

离散数学迪杰斯特拉算法最短路径教案一、教学目标1.理解迪杰斯特拉算法的原理和基本思想;2.掌握迪杰斯特拉算法的具体步骤;3.能够运用迪杰斯特拉算法求解给定图中的最短路径问题。
二、教学过程1.算法介绍首先,简要介绍迪杰斯特拉算法的基本思想:在带权有向图中,迪杰斯特拉算法用于求解单源最短路径问题,即从起点到其他所有顶点的最短路径。
迪杰斯特拉算法采用贪心策略,逐步扩展最短路径,直到达到终点或者无法扩展为止。
2.算法步骤(1)创建两个集合,一个为已确定最短路径的集合S,一个为未确定最短路径的集合V-S;(2)初始化起点到所有顶点的距离为无穷大,起点到自身的距离为0;(3)循环进行以下步骤,直到V-S为空集合:a.选择V-S中距离起点最近的顶点u,将其加入集合S;b.更新起点到V-S中所有顶点的距离,若经过顶点u到达顶点v 的距离更短,则更新距离值;(4)输出起点到各顶点的最短路径。
3.算法实现(1)设计一个函数Dijkstra(graph, start)用于实现迪杰斯特拉算法,输入参数为带权有向图和起点。
(2)创建两个集合S和V-S,初始时S为空集合,V-S为图中所有顶点的集合;(3)初始化起点到所有顶点的距离为无穷大,起点到自身的距离为0;(4)循环进行以下步骤,直到V-S为空集合:a.选择V-S中距离起点最近的顶点u,将其加入集合S;b.更新起点到V-S中所有顶点的距离,若经过顶点u到达顶点v 的距离更短,则更新距离值;(5)输出起点到各顶点的最短路径。
4.算法应用以一个具体的图为例,演示迪杰斯特拉算法的应用过程:(1)展示给定的带权有向图,并说明起点和终点;(2)根据迪杰斯特拉算法的步骤,逐步展示算法的执行过程,包括加入集合S、更新距离值等;(3)计算得出起点到各顶点的最短路径,并进行展示。
5.实例练习给定一个带权有向图,要求学生用迪杰斯特拉算法求解起点到各顶点的最短路径,并输出结果。
可以提供一些带权图的实例供学生练习。
dijkstra算法求解最短路径例题

dijkstra算法求解最短路径例题
Dijkstra算法是由荷兰著名的计算机科学家Edsger Dijkstra发明的,它为
我们带来了一种有效的查找最短路径的算法,并且在近些年的发展过程中,它被广泛应用于许多互联网领域,主要用于搜索引擎索取过程和推荐系统推荐用户内容。
它是以让用户轻松获取最优路径结果为目的而诞生的,因此,Dijkstra算法在计
算距离和其他改进最短路径时常被应用。
Dijkstra算法的思想是从其它节点到一个节点之间,依次计算出每条最短路径,然后累加得出到达目标节点的最短路径。
这种算法称为 "单源最短路径算法(Single Source Shortest Paths)",因为它从一个节点出发来计算最短路径。
最终,Dijkstra算法会返回到达其它节点的最短路径,以及这些节点之间的距离。
在实际的应用中,Dijkstra算法主要被用来解决路由规划问题,它可以在网
络中找出从某一指定节点到其它节点的最短路径,且Dijkstra算法不仅可以用于
无向网络,还可以用于带有正向边、反向边、正向边和反向边的有向网络中。
此外,Dijkstra算法可以优化加速索引过程,比如网络路径预览索引,搜索引擎索引等,最主要的是,它也被用于多种推荐系统,推荐用户内容,从而提高推荐的准确度。
总的来说,经过几十年的发展,Dijkstra算法已经被广泛应用到各种网络领域,从而为我们带来了便利和改善。
它可以将复杂的网络拓扑结构转换为更加直观的算法结果,这也使得Dijkstra算法在网络服务领域越来越受到重视。
Dijkstra算法的实现和复杂度分析最短路径问题的解决方案

Dijkstra算法的实现和复杂度分析最短路径问题的解决方案最短路径问题一直是图论中的经典问题。
为了解决最短路径问题,荷兰计算机科学家Dijkstra提出了一种被广泛应用的算法。
本文将介绍Dijkstra算法的实现过程,并进行复杂度分析。
一、Dijkstra算法的简介Dijkstra算法是一种用于解决带有非负权重边的带权重有向图中单源最短路径问题的贪心算法。
该算法以源节点为中心逐步计算到其他节点的最短路径。
在每一步中,选择具有最小路径长度的节点作为下一次循环的起点,并使用该节点更新其邻接节点的路径长度。
二、Dijkstra算法的实现Dijkstra算法的实现分为以下步骤:1. 创建一个距离集合,用于存储起点到每个节点的路径长度。
将起点的距离初始化为0,其他节点的距离初始化为无穷大。
2. 创建一个已访问集合,用于标记已经计算过最短路径的节点。
3. 在未访问的节点中选择距离最小的节点作为下一次循环的起点,并标记为已访问。
4. 对于该节点的所有出边,更新其邻接节点的路径长度。
如果经过当前节点到达邻接节点的路径长度小于已存储的路径长度,则更新路径长度。
5. 重复步骤3和步骤4,直到所有节点都被访问过或者没有可以访问的节点为止。
三、Dijkstra算法的复杂度分析Dijkstra算法的复杂度可以分为两个部分进行分析:初始化和迭代更新。
1. 初始化在初始化阶段,需要为每个节点初始化其路径长度和已访问状态。
对于有n个节点的图来说,初始化的时间复杂度为O(n)。
2. 迭代更新迭代更新的次数不会超过节点数量n次。
在每次迭代中,需要在未访问的节点中找到路径长度最小的节点,这个过程的时间复杂度为O(n)。
然后,需要更新该节点的所有邻接节点的路径长度,这一步的时间复杂度为O(m),其中m为边的数量。
所以,迭代更新的时间复杂度为O(n*m)。
综上所述,Dijkstra算法的时间复杂度为O(n^2)。
在稠密图中,即m接近于n^2的情况下,算法的效率较低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Dijkstra算法的最短路径设计
摘要:Dijkstra算法是用于计算一个节点到其他所有节点最短路径的典型单源路径算法。
该算法要求图中不存在负权边。
在算法设计中,我们用邻接矩阵来存储图。
在该程序中设置一个二维数组来存储任意两个顶点之间的边的权值。
用户可以将任意一个图的信息通过键盘输入,然后再输入要查找的两个顶点,程序可以自动求出这两个顶点之间的最短路径。
关键字:最短路径;Dijkstra算法;算法流程图;算法源程序
1.算法定义
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
注意该算法要求图中不存在负权边。
问题描述:在无向图G=(V,E) 中,假设每条边E[i] 的长度为w[i],找到由顶点V0 到其余各点的最短路径。
2.算法描述
2.1算法思想原理
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径, 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2.2算法过程描述
a.初始时,S只包含源点,即S={v},v的距离为0。
U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
2.3算法适用范围
⑴单源最短路径;
⑵有向图和无向图;
⑶所有边权非负。
开始定义全局变量dist[N],v0,cost[N][N]初始化变量final[N],i,v,w,
min,k
K=0
K<N V=0
V<N final[v] = false;dist[v] = cost[v0][v];
Y
final[v0] =
true
N
i=0
i<N-1初始最短长度无穷大
W=0
W<N !final[w] && dist[w] < min
Min = dist[w]v = w;
Y
Y Y W++
加入新边final[v] = true
W=0
W<N !final[w] && dist[v] + cost[v][w] < dist[w]dist[w] = dist[v] + cost[v][w];
Y W++
N
i=0
i<N-1i<N-1输出dist[i]
v0++;Y
return 0;
N
Y N
N
I++
N K++;
N
I++
END 图1 算法流程图
在该实验中,我们用邻接矩阵来存储图。
在该程序中设置一个二维数组来存储任意两个顶点之间的边的权值。
用户可以将任意一个图的信息通过键盘输入,然后再输入要查找的两个顶点,程序可以自动求出这两个顶点之间的最短路径。
下面介绍一实例,实例的无向图为图2。
图2 无向图
4.1算法源程序(C++)
#include <stdio.h>
#include "Conio.h"
#define true 1
#define false 0
#define I 9999 // 无穷大
#define N 6 // 城市顶点的数目
int cost[N][N] = {
{0,2,1,I,I,I},
{2,0,2,3,I,I},
{1,2,0,3,1,I},
{I,3,3,0,1,5},
{I,I,1,1,0,2},
{I,I,I,5,2,0}};
int dist[N]; // 存储当前最短路径长度
int v0 = 'A' - 65; // 初始点是A
int main()
{
int final[N],i,v,w,min,k;
printf("\n任意两个定点之间的最短路径如下:\n\n");
for(k=0;k<N;k++)
{
// 初始化最短路径长度数据,所有数据都不是最终数据
for (v = 0; v < N; v++)
final[v] = false;
dist[v] = cost[v0][v];
}
// 首先选v0到v0的距离一定最短,最终数据
final[v0] = true;
// 寻找另外N-1 个结点
for (i = 0; i < N-1; i++)
{
min = I; // 初始最短长度无穷大
// 寻找最短的边
for (w = 0; w < N; w++)
{
if (!final[w] && dist[w] < min)
{
min = dist[w];
v = w;
}
}
final[v] = true; // 加入新边
for (w = 0; w < N; w++)
{ // 更新dist[] 数据
if (!final[w] && dist[v] + cost[v][w] < dist[w])
{
dist[w] = dist[v] + cost[v][w];
}
}
}
for (i = 0; i < N; i++)
{
printf("%c->%c: %2d\t", v0 + 65, i + 65, dist[i]);
}
printf("\n");
v0++;
}
return 0;
}
图3 运行结果图
参考文献
[1] 吴家琴.基于迪杰斯特洛模型的物流运输最短路径的选择.物流技术,2013(11)
[2] 王景存,张晓彤,陈彬.一种基于Dijkstra算法的启发式最优路径搜索算法.北京科技大学学报,2007(3)
[3] 唐文武,施晓东,朱大奎.GIS中使用改进的Dijkstra算法实现最短路径的计算.中国图像图形学报,2000(12)
[4] 吴京,景宁,陈宏盛.最佳路径的层次编码及查询算法.计算机学报,2000(2)。
