课程设计 单源点最短路径算法的实现
单源最短路径Dijkstra算法

单源最短路径算法设计问题描述:一个带有权值的有向图G=(V,E) ,其中每条边的权是一个非负实数。
另外,还给定V 中的一个源点。
现在我们要计算从源到所有其他各顶点通路的权值和最小值,继承做单源最短路径问题。
输入:顶点个数权值输出:最短路径及权值算法描述:Dijkstra提出按各顶点与源点v间的路径长度的递增次序,生成到各顶点的最短路径的算法。
既先求出长度最短的一条最短路径,再参照它求出长度次短的一条最短路径,依次类推,直到从源点v 到其它各顶点的最短路径全部求出为止。
算法设计:将图G中所有的顶点V分成两个顶点集合S和T。
以v为源点已经确定了最短路径的终点并入S集合中,S初始时只含顶点v ,T则是尚未确定到源点v最短路径的顶点集合。
然后每次从T集合中选择S集合点中到T路径最短的那个点,并加入到集合S中,并把这个点从集合T删除。
直到T集合为空为止1、选一顶点v为源点,并视从源点v出发的所有边为到各顶点的最短路径(确定数据结构:因为求的是最短路径,所以①就要用一个记录从源点v到其它各顶点的路径长度数组dist[],开始时,dist是源点v到顶点i的直接边长度,即dist中记录的是邻接阵的第v行。
②设一个用来记录从源点到其它顶点的路径数组path[],path中存放路径上第i个顶点的前驱顶点)。
2、在上述的最短路径dist[]中选一条最短的,并将其终点(即<v,k>)k加入到集合s中。
3、调整T中各顶点到源点v的最短路径。
因为当顶点k加入到集合s中后,源点v到T中剩余的其它顶点j就又增加了经过顶点k到达j的路径,这条路径可能要比源点v到j 原来的最短的还要短。
调整方法是比较dist[k]+g[k,j]与dist[j],取其中的较小者。
4、再选出一个到源点v路径长度最小的顶点k,从T中删去后加入S中,再回去到第三步,如此重复,直到集合S中的包含图G的所有顶点。
举例:初始情况第一次松弛,选取A顶点第二次松弛,C的估算距离最小,选取C顶点:第三次松弛,E的估算距离最小,选取E:第四次松弛,B的估算距离最小,选取B:第五次松弛:(最后一个点,完成程序:1 #include <iostream>2 #include <cstdio>3 #include <vector>4 #include <queue>5using namespace std;67#define maxn 110 //最大顶点个数8int n; //顶点个数910struct arcnode //边结点11 {12int vertex; //与表头结点相邻的顶点编号13int weight; //连接两顶点的边的权值14 arcnode * next; //指向下一相邻接点15 arcnode() {}16 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}17 };1819struct vernode //顶点结点,为每一条邻接表的表头结点20 {21int vex; //当前定点编号22 arcnode * firarc; //与该顶点相连的第一个顶点组成的边23 }Ver[maxn];2425void Init() //建立图的邻接表需要先初始化,建立顶点结点26 {27for(int i = 1; i <= n; i++)28 {29 Ver[i].vex = i;30 Ver[i].firarc = NULL;31 }32 }3334void Insert(int a, int b, int w) //尾插法,插入以a为起点,b为终点,权为w的边,效率不如头插,但是可以去重边35 {36 arcnode * q = new arcnode(b, w);37if(Ver[a].firarc == NULL)38 Ver[a].firarc = q;39else40 {41 arcnode * p = Ver[a].firarc;42if(p->vertex == b)43 {44if(p->weight > w)45 p->weight = w;46return ;47 }48while(p->next != NULL)49 {50if(p->next->vertex == b)51 {52if(p->next->weight > w)53 p->next->weight = w;54return ;55 }56 p = p->next;57 }58 p->next = q;59 }60 }61void Insert2(int a, int b, int w) //头插法,效率更高,但不能去重边62 {63 arcnode * q = new arcnode(b, w);64if(Ver[a].firarc == NULL)65 Ver[a].firarc = q;66else67 {68 arcnode * p = Ver[a].firarc;69 q->next = p;70 Ver[a].firarc = q;71 }72 }73struct node //顶点节点,保存id和到源顶点的估算距离,优先队列需要的类型74 {75int id; //源顶点id和估算距离76int w;77 friend bool operator<(node a, node b) //因要实现最小堆,按升序排列,因而需要重载运算符,重定义优先级,以小为先78 {79return a.w > b.w;80 }81 };8283#define INF 0xfffff //权值上限84int parent[maxn]; //每个顶点的父亲节点,可以用于还原最短路径树85bool visited[maxn]; //用于判断顶点是否已经在最短路径树中,或者说是否已找到最短路径86 node d[maxn]; //源点到每个顶点估算距离,最后结果为源点到所有顶点的最短路。
单源顶点最短路径问题设计报告

软件工程设计报告题目:单源顶点最短路径问题设计报告科系:计算机科学与技术班级:姓名:学号:设计报告分析:报告内容分为四大部分:1)课程设计的需求和规格说明:包括描述问题,简述题目要解决的问题是什么;规定软件做什么;原题条件不足时补全。
2)设计:(概要设计和详细设计)设计思想:存储结构(题目中限定的要复述);主要算法基本思想。
不要画框图。
设计表示:每个函数声明和规格说明;列出每个函数所调用和被调用的函数,也可以通过调用关系图表达。
实现注释:各项功能的实现程度;在完成基本要求的基础上还实现了什么功能。
3)调试报告:调试过程中遇到的主要问题是如何解决的;对设计和编码的回顾讨论和分析;时间复杂度、空间复杂度分析;改进设想;经验和体会等。
4)附录:源程序清单和结果:源程序要加注释,除原有的注释外还可以再用笔加一些必要的注释。
如果题目规定了测试数据,则结果要包含这些测试数据和运行输出结果,当然还要包含其它测试数据及其运行输出(有时需要多组数据)。
报告正文:1、[问题描述]用邻接矩阵cost[n][n]表示一个有向网,若cost[i][j]=0,则表示顶点i和j为同一个顶点;若cost[i][j]=∞,则表示顶点i和j无边;若cost[i][j]=W ij,则表示顶点i和j有边,其权值为W ij。
试求出从有向网的某一顶点(称源点)出发到其余各顶点的最短路径。
2、[基本要求]程序能够求出源点到其余各顶点间的一条最短路径。
1.需求与规格说明对用邻接矩阵表示的有向图,从某一顶点出发(称为源点)到该图其它各顶点(称为终点)有无路径?最短路径是什么?路径长为多少?问题要求写一个程序从有向网中的某一顶点出发找出该顶点到其余各顶点的最短路径。
对邻接矩阵cost[n][n]中的每一个元素只能有三种情况:①当i=j时,cost[i][j]=0;②当顶点i和j无边时,cost[i][j]=∞;③当顶点i和j有边,且其权值为W ij时,cost[i][j]=W ij。
单源最短路径

单源最短路径问题[Dijkstra实现]一、问题带权有向图G(E,V), 找出从给定源顶点s到其它顶点v的权最小路径。
“最短路径” = 最小权二、问题求解:求1到5的最短路径值?三、执行过程:如果大家对这个问题的要求还不是很明白的话那么我再带着大家走一遍:第一次:从1-->2:10 此时从1-->3没有路径所有是无穷大1-->4:30 1-->5:100那么我们发现这一组组最小的是10也就是2这一点,所以我们再把2这一点加到集合里面来,那么2这一点就可以当作一个桥来用,第二次:此时我们再从1à3就可以通过1-->2-->3:60其他的1-->4:301-->5:100 可以发现此时最小的应该是3,所以我们再把3这一点加入到这个集合里面来,如此重复的去做这些事情,到最后可以发现1à5的最短路径应该是60(1-->4-->3-->5)四、Dijkstra伪代码:int dijkstra(int s,int t) {初始化S={空集}d[s] = 0; 其余d值为正无穷大while (NOT t in S){取出不在S中的最小的d[i];for (所有不在S中且与i相邻的点j)if (d[j] > d[i] + cost[i][j]) d[j] = d[i] + cost[i][j]; ( “松弛”操作” )S = S + {i}; //把i点添加到集合S里}return d[t];}为何松弛操作:也就是说如果1-->3这点的值为dist[3]>dist[2]+map[2][3]那么dist[3]=dits[2]+map[2][3]五、代码实现:#include <iostream>using namespace std;#define MAX 9999999#define LEN 210int map[LEN][LEN]; //某点到某点两点间的的距离int dist[LEN]; //记录当前点到源点的最短路径长度int mark[LEN]; //加入进来的点的集合//初始化map为正无穷大void init(){int i,j;for(i=0;i<LEN;i++){for(j=0;j<LEN;j++){map[i][j]=MAX;}}//n:多少条路start:起始点void myDijstra(int n,int start){int i,j,min,k;for(i=1;i<=n;i++){mark[i]=0;//没有点加入dist[i]=map[start][i];//初始}mark[start]=1;//把起始点加进来dist[start]=0;for(i=1;i<=n;i++){min=MAX;for(j=1;j<=n;j++){if(!mark[j] && dist[j]<min){ //取出不在mark里的最小的dist[i] min=dist[j];k=j;//标记}}if(min==MAX)break;mark[k]=1;//把K加进来//做松弛操作for(j=1;j<=n;j++){if(!mark[j] && dist[j]>dist[k]+map[k][j]){dist[j]=dist[k]+map[k][j];}}}}int main(){int i,j,n,line;int a,b,d;cin>>n>>line; //输入点和边for(i=0;i<line;i++){cin>>a>>b>>d; //输入各边的权值if(map[a][b]>d){map[a][b]=map[b][a]=d;}}myDijstra(n,1);//调用方法//输出1到5的最短路径cout<<dist[5]<<endl;return 0;}Dijkstra算法(单源最短路径)单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。
课程设计 单源点最短路径算法的实现

数据结构课程设计设计说明书单源点最短路径算法的实现学生姓名学号班级成绩指导教师数学与计算机科学学院2015年 1 月 2 日数据结构课程设计评阅书课程设计任务书2014—2015学年第1学期专业:学号:姓名:课程设计名称:数据结构课程设计设计题目:单源点最短路径算法的实现完成期限:自 2014 年 12 月 22 日至 2015 年 1 月 2 日共 2 周设计内容及要求:最短路径问题已经被应用到GIS、GPS等信息管理系统中,为人们生活带来了很大便利。
它属于图结构问题,其解决方法也有不少(如Dijkstra、A-star)。
单源点最短路径问题解决的是既定起点的情况下,寻求该点到图中其它顶点的最短路径。
请用C/C++语言的结构体、指针、数据结构等基础知识,编写程序实现图的结构定义、图的存储,以及求解单源点最短路径。
设计过程以及写作要求如下:(1)要针对本题目,认真研究所设计的内容,用简明扼要的语言描述课题,给出课题的基本内容及要求;(2)根据数据结构的相关知识给出实现建立任意m个顶点n条边的图算法、按照用户给定的源点和目标点,求出它们间的最短路径(打印出来)算法的基本策略及思路;(3)给出较为详尽数据结构与算法,算法可以用流程图、伪代码等描述手段进行描述;(4)给出一个完整的算法实现的C/C++程序,算法中的各子算法要力求用函数来实现;(5)对编写的程序要进行详尽的测试分析;(6)对本课题的设计工作要进行一个完整深刻的总结。
最终设计成果形式为:1、设计软件一套;2、撰写一份课程设计说明书一份,打印并装订成册。
指导教师(签字):教研室主任(签字):批准日期:年月日摘要本系统以VC++作为软件开发环境,C语言作为程序开发语言,邻接矩阵作为存储结构,设计与实现了最短路径运算。
该系统实现了有向图的存储、最短路径的运算等主要功能。
依照该系统可以解决生活中许多问题,比如交通路线的选择,工程时间的预算等等,让人们可以做出合理的选择。
单源最短路径dijkstra算法c语言

单源最短路径dijkstra算法c语言单源最短路径问题是图论中的经典问题之一,指的是在图中给定一个起始节点,求出该节点到其余所有节点之间的最短路径的算法。
其中,Dijkstra 算法是一种常用且高效的解决方案,可以在有向图或无向图中找到起始节点到其余所有节点的最短路径。
本文将逐步介绍Dijkstra算法的思想、原理以及C语言实现。
一、Dijkstra算法的思想和原理Dijkstra算法的思想基于贪心算法,通过逐步扩展当前已知路径长度最短的节点来逐步构建最短路径。
算法维护一个集合S,初始时集合S只包含起始节点。
然后,选择起始节点到集合S之外的节点的路径中长度最小的节点加入到集合S中,并更新其他节点的路径长度。
具体来说,算法分为以下几个步骤:1. 初始化:设置起始节点的路径长度为0,其他节点的路径长度为无穷大。
2. 选择最小节点:从集合S之外的节点中选择当前路径长度最短的节点加入到集合S中。
3. 更新路径长度:对于新加入的节点,更新与其相邻节点的路径长度(即加入新节点后的路径长度可能更小)。
4. 重复步骤2和3,直到集合S包含所有节点。
二、Dijkstra算法的C语言实现下面我们将逐步讲解如何用C语言实现Dijkstra算法。
1. 数据结构准备首先,我们需要准备一些数据结构来表示图。
我们可以使用邻接矩阵或邻接表来表示图。
这里,我们选择使用邻接矩阵的方式来表示权重。
我们需要定义一个二维数组来表示图的边权重,以及一个一维数组来表示起始节点到各个节点的路径长度。
c#define MAX_NODES 100int graph[MAX_NODES][MAX_NODES];int dist[MAX_NODES];2. 初始化在使用Dijkstra算法之前,我们需要对数据进行初始化,包括路径长度、边权重等信息。
cvoid initialize(int start_node, int num_nodes) {for (int i = 0; i < num_nodes; i++) {dist[i] = INT_MAX; 将所有节点的路径长度初始化为无穷大}dist[start_node] = 0; 起始节点到自身的路径长度为0初始化边权重for (int i = 0; i < num_nodes; i++) {for (int j = 0; j < num_nodes; j++) {if (i == j) {graph[i][j] = 0; 自身到自身的边权重为0} else {graph[i][j] = INT_MAX; 其他边权重初始化为无穷大}}}}3. 主要算法接下来是Dijkstra算法的主要逻辑。
算法-单源点最短路径-Dijkstra算法

实验单源点最短路径一、实验目的1、深入理解贪心策略的基本思想。
2、能正确采用贪心策略设计相应的算法,解决实际问题。
3、掌握贪心算法时间空间复杂度分析,以及问题复杂性分析方法二、实验内容单源最短路径三、设计分析单源点最短路径Dijkstra算法是解单源点最短路径的一个贪心算法。
其基本思想是,设置顶点集合S并不断地做贪心选择来扩充这个集合。
一个顶点属于集合当且仅当从源点到该顶点的最短路径长度已知。
初始时,S中仅含有源。
设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短路径特殊长度。
Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist做必要的修改。
一旦S包括了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
存在一个带权有向图。
四、算法描述及程序#include "stdafx.h"#include "iostream"using namespace std;#define N 5#define MAX 1000int edge1[7] = { 1, 1, 1, 2, 3, 4, 4 };int edge2[7] = { 2, 5, 4, 3, 5, 3, 5 };int length[7] = { 10, 100, 30, 50, 10, 20, 60 };int c[N][N];template<class T>void Dijkstra(int n, int v, T dist[], int prev[]){bool s[MAX];for (int i = 1; i <= n; i++){dist[i] = c[v][i];if (dist[i] == MAX)prev[i] = 0;elseprev[i] = v;}dist[v] = 0;s[v] = true;for (int i = 1; i<n; i++){int temp = MAX;int u = v;for (int j = 1; j <= n; j++){int temp = MAX;int u = v;for (int j = 1; j <= n; j++)if ((!s[j]) && (dist[j]<temp)){u = j;temp = dist[j];}s[u] = true;for (int j = 1; j <= n; j++){if ((!s[j]) && (c[u][j] < MAX)){T newdist = dist[u] + c[u][j];if (newdist < dist[j]){dist[j] = newdist;prev[j] = u;}}}}}}int main(){int v;for (int i = 1; i < N + 1; i++)for (int j = 1; j < N + 1; j++){}for (int i = 0; i < 7; i++){int m = edge1[i];int n = edge2[i];int Length = length[i];c[m][n] = Length;}int dist[N + 1], prev[N + 1];cout << endl << "可通行的路径:" << endl<<endl;for (int i = 1; i < N + 1; i++){for (int j = 1; j < N + 1; j++){if (c[i][j] < MAX){cout << i << "--" << j <<'\t' <<"距离为:";cout << c[i][j] << endl;}}cout << "从" << i << "无法到达其它顶点" << endl << endl;}cout << endl << "请输入源点:";cin >> v;Dijkstra(N, v, dist, prev);cout << "最短路径为:" << endl << endl;for (int i = 1; i < N + 1; i++){if (dist[i]<MAX&&dist[i]>0){cout << v << "-->" << i << "的最短路径为"<<i;for (int n = prev[i]; n != 0;){cout << "<--" << n;n = prev[n];}cout << endl << "长度为" << dist[i] << endl << endl;}elsecout << v << "--" << i << "无最短路径"<<endl<<endl;}return 0;}五、测试与分析六、实验总结与体会1.用算法中数组prev记录的信息求出相应的最短路径;2.计算复杂性:对于一个具有n个顶点和e条边的带权有向图,如果用带权邻接矩阵表示这个图,那么Dijkstra算法的主循环体需要O(n)时间。
单源点最短路径算法的实现 数据结构 课程设计

数据结构课程设计设计说明书数学与计算机科学学院 2014年3月7日单源点最短路径算法的实现学生姓名 学 号班 级成 绩 指导教师课程设计任务书2013 —2014 学年第2 学期专业:学号:姓名:课程设计名称:数据结构课程设计设计题目:单源点最短路径算法的实现完成期限:自2014 年 2 月24 日至2014 年 3 月7 日共 2 周设计依据、要求及主要内容(可另加附页):最短路径算法关键先把已知最短路径顶点集(只有一个源点)和未知的顶点分开,然后依次把未知集合的顶点按照最短路径(特别强调一下是源点到该顶点的路径权重和,不仅仅是指它和父结点之间的权重,一开始就是在没有这个问题弄清楚)加入到已知结点集中。
在加入时可以记录每个顶点的最短路径,也可以在加入完毕后回溯找到每个顶点的最短路径和权重。
针对最短路径问题,在本系统中采用图的相关知识,以解决在实际情况中的最短路径问题,本系统中包括了建立图的存储结构、单源最短问题,这对以上几个问题采用了迪杰斯特拉算法。
并为本系统设置一人性化的系统提示菜单,方便使用者的使用。
本课程设计中主要完成以下内容:1. 建立图的存储结构。
2. 解决单源最短路径问题。
3.实现两个顶点之间的最短路径问题。
基本要求如下:1.程序设计界面友好;2.设计思想阐述清晰;3.算法流程图正确;4.软件测试方案合理、有效。
指导教师(签字):教研室负责人(签字):批准日期:年月日课程设计评阅评语:指导老师签名:年月日摘要本软件以VC++作为开发平台,设计了关于从某个单一原点到任意顶点的一个类似于查询,咨询系统的软件。
它能够准确快速的计算出从某个单一原点到任意顶点的最短路径以及路径长度。
该类软件目前广泛运用于城市交通运输系统,为人们出行带来了方便。
关键字:VC++;最短路径;迪杰斯特拉算法;目录目录 --------------------------------------------------------------------------------------------------------------- - 1 -1、课题描述----------------------------------------------------------------------------------------------------- - 1 -2、问题分析与设计思想------------------------------------------------------------------------------------- - 2 -3、概要设计----------------------------------------------------------------------------------------------------- - 4 -4、详细设计----------------------------------------------------------------------------------------------------- - 6 -4.1建立图的存储结构---------------------------------------------------------------------------------- - 6 -4.2单源最短路径 ---------------------------------------------------------------------------------------- - 6 -5、程序编码----------------------------------------------------------------------------------------------------- - 8 -6、程序调试和测试 ----------------------------------------------------------------------------------------- - 12 -7、总结--------------------------------------------------------------------------------------------------------- - 16 - 参考文献 ------------------------------------------------------------------------------------------------------- - 16 -1、课题描述在城市交通网络日益发达的今天,针对人们出行关心的各种问题,利用计算机软件建立一个交通咨询系统。
单源结点最短路径
L->size--;
return 1;
}
}
int ListGet(SeqList L,int i,DataType *x)
//取顺序表L中第i个元素的值,取到则返回1,否则返回0
{
if(i<0 || i>L.size-1)
{
L->list[j]=L->list[j-1];
}
L->list[i]=x;
L->size++;
return 1;
}
}
int ListDelete(SeqList *L,int i,DataType *x)
//删除顺序表L中位置i上的数据元素并保存到x中
//插入成功返回1,否则返回0
{
int j;
2.子函数AdjMGraphCreate.h
/**图的创建函数**/
#ifndef ADJMGRAPHCREATE_H_INCLUDED
#define ADJMGRAPHCREATE_H_INCLUDED
typedef struct
{
int row; //行下标
int col; //列下标
int weight; //权值
单源结点最短路径
一、题目
单源结点最短路径问题。
二、问题描述
求从有向图的某一结点出发到其余各结点的最短路径。
三、基本要求
(1)有向图采用邻接矩阵表示。
(2)单源结点的最短路径问题采用狄克斯特拉算法。
(3)输出有向图中从源结点到其余各结点的最短路径和最短路径值。
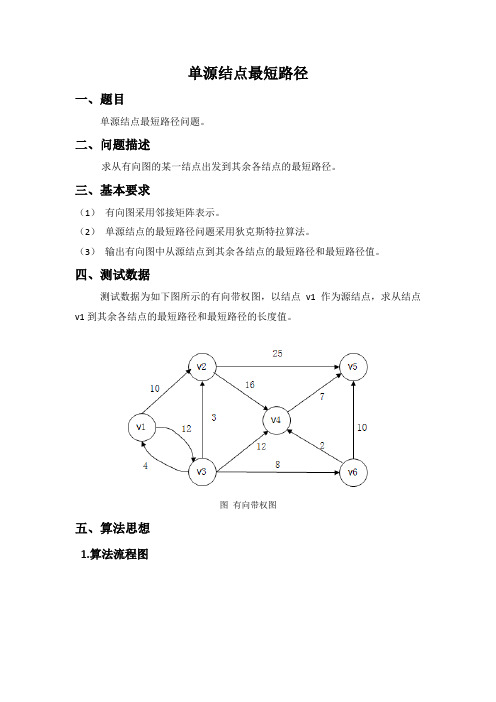
四、测试数据
测试数据为如下图所示的有向带权图,以结点v1作为源结点,求从结点v1到其余各结点的最短路径和最短路径的长度值。
迪杰斯特拉算法求单源最短路径

迪杰斯特拉算法是一种用于求解单源最短路径的经典算法,它被广泛应用于网络路由、电信领域以及各种其他实际问题中。
本文将从以下几个方面详细介绍迪杰斯特拉算法的原理、实现以及应用,以帮助读者深入理解并掌握该算法。
一、迪杰斯特拉算法的原理迪杰斯特拉算法的核心思想是通过逐步确定从起点到其他顶点的最短路径来求解单源最短路径问题。
其具体原理包括以下几个步骤:1. 初始化:将起点到所有其他顶点的距离初始化为无穷大,起点到自身的距离为0,并建立一个空的集合S来存放已确定最短路径的顶点。
2. 选择最近顶点:从未确定最短路径的顶点中选择距离起点最近的顶点u加入集合S。
3. 更新距离:对于顶点集合V-S中的每个顶点v,如果通过顶点u可以找到一条比当前最短路径更短的路径,则更新起点到顶点v的距离。
4. 重复步骤2和步骤3,直到集合S包含所有顶点。
通过上述步骤,迪杰斯特拉算法可以求解出起点到图中所有其他顶点的最短路径。
二、迪杰斯特拉算法的实现迪杰斯特拉算法可以通过多种数据结构来实现,其中最常见的是使用优先队列来存储未确定最短路径的顶点,并通过松弛操作来更新顶点的距离。
下面将介绍一种基于优先队列的迪杰斯特拉算法实现方法:1. 初始化距离数组dist[],其中dist[i]表示起点到顶点i的最短距离,将所有顶点初始化为无穷大,起点初始化为0。
2. 将起点加入优先队列,并将其距离更新为0。
3. 循环执行以下步骤直到优先队列为空:(1)从优先队列中取出距离起点最近的顶点u。
(2)遍历顶点u的所有邻接顶点v,对于每个邻接顶点v,如果通过顶点u可以找到一条更短的路径,则更新顶点v的距离,并将其加入优先队列。
通过上述实现,我们可以得到起点到所有其他顶点的最短路径。
三、迪杰斯特拉算法的应用迪杰斯特拉算法在实际应用中有着广泛的应用场景,其中最典型的应用包括网络路由、电信领域以及地图路径规划等。
1. 网络路由:在计算机网络中,迪杰斯特拉算法被用于寻找最短路径,以确保数据包以最短的路径到达目的地,提高网络传输效率。
单源最短路径问题实验报告

单源最短路径问题实验报告
单源最短路径问题是计算机科学中极其重要的问题之一,它能够找出
两个节点之间的最短路径。
本次实验我们采用迪杰斯特拉算法来求解
单源最短路径问题。
首先,我们采用邻接矩阵法来表示一个有向无权图G=(V,E),其中V
表示点集,E表示边集。
图G中有V个节点,并且每条边都有一个权重。
接下来,我们采用迪杰斯特拉算法来求解单源最短路径问题,具体算
法流程如下:
1. 初始化:初始化源点作为起点,且此数据源点距离自身节点权值为0,其他节点距离起点权值为无穷大。
2. 迭代:选择与当前节点最近的一个邻接点,计算它到其余每个节点
的距离,如果当前节点到其余每个节点的距离大于当前节点的距离,
则更新距离。
3. 结束:直到当前点求出的路径最短路径逐渐稳定下来,即可求出最
短路径的结果,结束算法。
本次实验我们编写一个程序,将算法流程实现在计算中,并对该程序
运行时钟,来衡量算法的效果。
该程序运行内容是它从零到最后,使
用迪杰斯特拉算法求解一个特定的单源最短路径问题,整个过程消耗
的时间是17ms。
通过本次实验,我们验证了迪杰斯特拉算法在求解单源最短路径问题
时的有效性,同时也了解了它的运行效率。
在实际应用中,此算法的
运行效率将会有很大的启示作用。
综上所述,本次实验采用了迪杰斯特拉算法求解单源最短路径问题,充分证明了此算法的有效性,也证明了它的运行效率。
是一种有效的算法,可以用于实际应用中。
单源最短路径

实验四:单源最短路径一.问题描述给定带权图G和源点V,对图进行遍历并求从V到G中其余各顶点的最短路径。
二.输入及结果输入:带全图G的各个顶点及各边的权值。
输出:Dijkstra算法的结果(用矩阵表示),并给出各最短路径长度。
三.需求分析1图的深度优先搜索①数组visited[i]用来表示顶点V[i]是否被访问过。
②递归调用函数2图的广度优先搜索①队列操作的相关函数②数组visited[i]用来表示顶点V[i]是否被访问过。
3单源最短路径①需要一个辅助变量D,它的每个分量D[i]表示当前所找到的从始点V到每个终点V[i]的最短路径长度。
它的初态为:若从V到V[i]有弧,则D[i]为弧上的权值;否则置D[i]为INFINITY。
②需要二元数组P[v][w],值为1,则W是V0到V当前球的最短路径上的顶点。
③需要Final[v],值为1当且仅当已经求得V0到V的最短路径。
④用带权的邻接矩阵来表示带权有向图,arcs[i][j]表示弧<vi,vj>上的权值。
⑤函数Locate来确定顶点对应的数组编号。
四.算法描述1图的深度优先搜索深度优先搜索可以从图中的某个顶点V出发,访问此顶点,然后依次从V的未被访问过的邻接点出发深度优先遍历图,直至所有和V有路径相通的顶点都被访问,若此时还有未被访问过的节点,则重复上述过程,开始深度搜索。
2图的广度优先搜索从图中某顶点V出发,在访问了V之后一次访问V的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问他们的邻接点,并使“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问”,直至图中所有被已访问的顶点的邻接点都被访问到。
若此时图中尚有顶点未被访问,则另选图中未被访问的结点作为起始点,重复上述过程,直至图中所有顶点都被访问。
其中要用到队列的有关算法。
3单源最短路径①记S为已经找到的从源点出发的最短路径的点的集合,它的初始状态为空集。
那么,从V出发到图上其余各顶点V[i]可能达到的最短路径的初始值为D[i]=arcs[Locate Vex(G,V)][i].②选择Vj使得:D[j]=Min{D[i] :vi S} ,Vj就是当前求得的一条从V出发的最短路径的终点。
单源最短路径算法(Dijkstra算法)

设图G=(V,E)是一个有向图,它的每一条边(U,V)都有一个非负权W(U,V),在G中指定一个结点V0,要求从V0到G的每一个结点Vj的最短路径找出来(或指出不存在)。
由于源结点V0是给定的,所谓称为单源最短路径。
【Dijkstra算法思想】把所有结点分为两组。
第一组:包含已确定最短路径的结点。
第二组:包含尚未确定最短路径的结点。
按最短路径长度递增的顺序把第二组的结点加到第一组中去,直到V0可达的所有结点都包含于第一组中。
在这个过程中,总保持从V0到第一组各结点的最短路径长度都不大于从V0到第二组任何结点的路径长度。
【单源最短路径算法实例】现有一张县城的城镇地图,图中的顶点为城镇,无向边代表两个城镇间的连通关系,边上的权为公路造价,县城所在的城镇为v0。
由于该县经济比较落后,因此公路建设只能从县城开始规划。
规划的要求是所有可到达县城的城镇必须建设一条通往县城的汽车线路,该线路的工程总造价必须最少。
【输入】第一行一个整数v,代表城镇数,县城编号为1。
第二行是一个整数e,表示有向边数。
以下e行,每行为两个城镇编号和它们之间的公路造价。
【输出】 v-1行,每行为两个城市的序号,表明这两个城市间建一条公路。
【输入样例】6101 2 101 5 191 6 212 3 52 4 62 6 113 4 64 5 184 6 145 6 33 【输出样例】原图从第1点出发的最短路径1 22 32 41 51 6program dijkstra_example;constvmax=100;typepath=record {此记录类型用于记录每一个结点与v0的距离和其父结点} length:integer;pre:0..vmax;end;varw:array[1..vmax,1..vmax] of integer;dist:array[1..vmax] of path;v,e,u,i,j,x,y:integer;procedure init;beginassign(input,'dijkstra.in');reset(input);assign(output,'dijkstra.out');rewrite(output);readln(v);readln(e);for i:=1 to v dofor j:=1 to v doif i<>jthen w[i,j]:=maxint{maxint只是一个较大的数的意思,实际应用于应该根据题目中给出的取值范围赋予一个充else w[i,j]:=0;for i:=1 to e dobeginread(x,y);readln(w[x,y]);w[y,x]:=w[x,y];end;end;procedure dijkstra(v0:integer);varmin:integer;beginw[v0,v0]:=1; {v0首先进入第一组}for i:=1 to v dobegindist[i].length:=w[v0,i]; {计算每个结点的距离值}if dist[i].length<>maxintthen dist[i].pre:=v0 {如和v0直接有路,则置前驱结点为v0} else dist[i].pre:=0;end;repeatmin:=maxint;u:=0;for i:=1 to v do {找最短距离}if (w[i,i]=0) and (dist[i].length<min)then beginu:=i;min:=dist[i].length;end;then beginw[u,u]:=1;for i:=1 to v do {重新计算其他结点的距离值}if (w[i,i]=0) and (dist[i].length>dist[u].length+w[u,i]) then begindist[i].length:=dist[u].length+w[u,i];dist[i].pre:=u;end;end;until u=0;end;begininit;v0:=1;dijkstra(v0);for i:=1 to v dobeginif (i<>v0) and (dist[i].length<>maxint)then write(dist[i].pre,' ',i);end;close(input);close(output);end.。
单源最短路径c语言代码

单源最短路径c语言代码以下是Dijkstra算法的C语言代码实现,用于求解单源最短路径:```。
#include <stdio.h>。
#include <limits.h>。
#define V 6 // 图中顶点数。
//定义一个宏,用于查找尚未处理的最短路径的节点。
#define minDistance(dist, visited) \。
({ int min = INT_MAX, index; \。
for (int i = 0; i < V; i++) \。
if (!visited[i] && dist[i] <= min) \。
min = dist[i], index = i; \。
index; })。
void dijkstra(int graph[V][V], int src) 。
int dist[V]; // 存储从源点到各顶点的距离。
bool visited[V]; // 标记顶点是否被处理。
for (int i = 0; i < V; i++) 。
dist[i] = INT_MAX;。
visited[i] = false;。
}。
dist[src] = 0;。
for (int i = 0; i < V - 1; i++) 。
int u = minDistance(dist, visited);。
visited[u] = true;。
for (int j = 0; j < V; j++) 。
if (!visited[j] && graph[u][j] && dist[u] != INT_MAX &&。
dist[u] + graph[u][j] < dist[j])。
dist[j] = dist[u] + graph[u][j];。
}。
}。
printf("顶点距离源点的距离\n");。
算法设计与分析 单点源最短路径

单点源最短路径问题问题:已知一个赋权有向图G=(V,E ,w),求由G 中某个指定的顶点v 0出发到其它各个顶点的最短路径。
一个加权有向图对于一般的单点源最短路径问题,我们采用逐条构造最短路径的办法,用迄今已生成的所有路径长度之和为最小作为贪心准则,因此,每一条单独的路径都必须具有最小长度。
假定已经构造了k 条最短路径,则下面要构造的路径应该是下一条最短长度的最小长度路径。
现在这k 条最短路径的终点之集记为S ,为陈述方便,也将v 0放于S 中。
如果V\S 不是空集,则从v 0到V\S 中顶点的最短路径中应该有一条最短的,比如是v 0到v k+1的最短路径P :P=v 0u 1…u s-1u s v k+1(5.7)显然,P 1=v 0u 1…u s-1u s 应是v 0到u s 的最短路径,因而由S 的定义和选定的贪心准则,u s 应属于S ,同理,路径P 上其它顶点u i 也都在S 中。
所以,由v 0出发的新的最短路径一定是某个已有的最短路径向前延伸一步。
如果用Dist(v i )记从v 0到S 中顶点v i 的最短路径的长度,而图G 中的顶点w 依其属于S 与否分别记之为S(w)=1或S(w)=0,则从4550103530 30 20 15 1020 15 V 0 V 2 V 1 V 4V 5 V 3 路径 长度 (1) v 0v 2 10 (2) v 0v 2v 3 25 (3) v 0v 2v 3v 1 45 (4) v 0v 4 45从v 0到其它各个顶点的最短路v 0出发,新的最短路径的长度应该是 =)(S D )},()({min)(,1)(w u COST u Dist w S u S +==(5.8)满足(5.8)式的顶点w 被选择加入S ,新的最短路径就是从v 0出发到w 的最短路径,而此时的Dist(w)=D(S),S 被更新为}{'w S S ⋃=,后者可以由更新w 的(集合)特征值来实现:S(w)=1(原来S(w)=0).上述算法思想是Dijkstra(迪杰斯特)提出的。
单源点最短路径课程设计

单源点最短路径课程设计一、教学目标本课程的学习目标包括以下三个方面:1.知识目标:学生需要掌握单源点最短路径的概念、算法及其应用。
能够理解并运用迪杰斯特拉算法、贝尔曼-福特算法等解决实际问题。
2.技能目标:学生能够运用所学的算法,独立完成编程实现单源点最短路径的求解。
同时,培养学生的逻辑思维能力、问题解决能力以及团队合作能力。
3.情感态度价值观目标:培养学生对计算机科学和算法的兴趣,使其认识到算法在实际生活中的重要性,培养学生的创新精神和责任感。
二、教学内容本课程的教学内容主要包括以下几个部分:1.单源点最短路径的概念和意义:介绍单源点最短路径的定义、性质以及其在图论中的重要性。
2.迪杰斯特拉算法:讲解迪杰斯特拉算法的原理、步骤和实现,并通过实例让学生了解算法的具体应用。
3.贝尔曼-福特算法:介绍贝尔曼-福特算法的原理、步骤和实现,对比与迪杰斯特拉算法的优缺点。
4.算法优化与扩展:探讨单源点最短路径算法的优化方法,如动态规划、启发式搜索等,并了解其在实际应用中的扩展。
三、教学方法为了提高教学效果,本课程将采用以下教学方法:1.讲授法:教师通过讲解单源点最短路径的概念、算法及其应用,让学生掌握基本知识。
2.案例分析法:通过分析实际案例,让学生了解算法的具体应用,提高学生的应用能力。
3.实验法:安排实验课程,让学生动手编程实现单源点最短路径算法,培养学生的实践能力。
4.讨论法:课堂讨论,引导学生思考算法优化的问题,培养学生的创新思维。
四、教学资源为了支持本课程的教学,我们将准备以下教学资源:1.教材:《图论与算法导论》等图论及算法方面的教材,为学生提供理论支持。
2.参考书:推荐学生阅读图论、算法相关的参考书籍,拓展知识面。
3.多媒体资料:制作课件、教学视频等,以图文并茂的形式展示单源点最短路径的相关概念和算法。
4.实验设备:提供计算机实验室,让学生进行实验课程的学习和实践。
五、教学评估本课程的教学评估将采用多元化方式,全面客观地评价学生的学习成果。
文字描述用bfs算法求单源最短路径的过程

文字描述用bfs算法求单源最短路径的过程BFS(广度优先)算法用于求解单源最短路径问题,其基本过程如下:
1.创建一个队列,并将源点加入队列中。
2. 创建一个数组 dist[],用于存储源点到各个顶点的最短路径长度。
初始化 dist[] 数组,将所有顶点的最短路径长度设置为无穷大,将源点
的最短路径长度设置为0。
3. 创建一个数组 visited[],用于标记顶点是否已经被访问过。
初
始化 visited[] 数组,将所有顶点的标记设置为未访问。
4.开始循环直到队列为空:
a.从队头取出一个顶点v,标记顶点v为已访问。
b.遍历顶点v的邻接顶点:
i. 如果邻接顶点 u 尚未被访问过,则将顶点 u 加入队列中,并更
新顶点 u 的最短路径长度为 dist[v] + 1
c.检查队列中是否还有未访问的顶点,如果有则回到步骤4a。
5. 循环结束后,dist[] 数组中存储的即为源点到各个顶点的最短路
径长度。
6. 如果需要求解最短路径的具体路径,可以使用一个数组 prev[]
来记录每个顶点的前驱顶点,即 prev[u] 表示顶点 u 在最短路径上的前
驱顶点。
通过 prev[] 数组可以回溯出最短路径。
以上步骤即为使用BFS算法求解单源最短路径的过程。
求单源最短路径—Dijkstra算法实验报告

本科学生综合性实验报告项目组长杨滨学号_ 0123707 _成员杨滨专业_软件工程班级 12软件 2班实验项目名称求单源最短路径—Dijkstra算法指导教师及职称_赵晓平讲师___开课学期 13 至_14 学年_一_学期上课时间 2013 年 9 月 1 日学生实验报告三(综合性实验) 学生姓名杨滨 学号 0123707 同组人 实验项目 求单源最短路径——Dijkstra 算法□必修 □选修 □演示性实验 □验证性实验 □操作性实验 □综合性实验 实验地点W101 实验仪器台号 指导教师 赵晓平 实验日期及节次 2013.12.17(二) 12节2013.12.19(一) 89A 节一、实验综述1、实验目的及要求(1)了解求最优化问题的贪心算法,了解贪心法的基本要素,学会如何使用贪心策略设计算法;(2)了解单源最短路径问题,掌握Dijkstra 算法的思想;(3)编写程序,利用Dijkstra 算法实现,求任意两点间的单源最短路径。
实验题:给出如右有向图的边权图,求任意两点间的单源最短路径。
实验要求:认真完成实验题,能正确运行,提交实验报告并上传程序,实验报告要求写出操作步骤、结果、问题、解决方法、体会等。
2、实验仪器、设备或软件计算机、VC++6.0、office 、相关的操作系统等。
√ √二、实验过程(实验步骤、记录、数据、分析)#include<iostream>using namespace std;/*void Graph(int n,bool *inS,int a[6][6],int *d) {inS=new bool[n];inS[0]=0;for(int i=1;i<n;i++)inS[i]=1;a=new int*[n];for(i=0;i<n;i++)a[i]=new int[n];cout<<"input "<<endl;for(i=0;i<n;i++)for(int j=0;j<n;j++)cin>>a[i][j];d=new int[n];for(i=0;i<n;i++)d[i]=a[0][i];}*/int Choose(int n,int *d,bool *s){int i,minpos=-1,min=500;for(i=1;i<n;i++)if(d[i]<min && !s[i]){ min=d[i];minpos=i; }return minpos;}void Dijkstra(int s,int n,bool *inS,int *d,int *path,int a[6][6]) {int k,i,j;for(i=0;i<n;i++){inS[i]=false;d[i]=a[s][i];if(i!=s && d[i]<500) path[i]=s;else path[i]=-1;}inS[s]=true;d[s]=0;for(i=0;i<n-1;i++){k=Choose(n,d,inS);inS[k]=true;for(j=0;j<n;j++)if(!inS[j] && d[k]+a[k][j]<d[j]){ d[j]=d[k]+a[k][j];path[j]=k; } }}void Display(int s,int n,int a[6][6],int *d,int *path) {int t,m;cout<<"a["<<n<<"]["<<n<<"]: "<<endl;for(int i=0;i<n;i++){for(int j=0;j<n;j++)cout<<a[i][j]<<" ";cout<<endl;}cout<<"输入终点: ";cin>>t;cout<<"距离为 d["<<t<<"]: "<<d[t]<<" ";cout<<"路径为: "<<t;while(t!=s){m=path[t];cout<<m;t=m;}cout<<endl;}int main(){int n,*d,*path;//**a,bool *inS;inta[6][6]={0,50,10,500,70,500,500,0,15,500,10,500,20,500,0,15,500,500, 500,20,500,0,35,500,500,500,500,30,0,500,500,500,500,3,500,0};cout<<"Input n: ";cin>>n;inS=new bool[n];/* a=new int*[n];for(i=0;i<n;i++)a[i]=new int[n];cout<<"input "<<endl;for(i=0;i<n;i++)for(int j=0;j<n;j++)cin>>a[i][j];*/path=new int[n];d=new int[n];// Graph(n,inS,a,d);int s=0;Dijkstra(s,n,inS,d,path,a);Display(s,n,a,d,path);return 0;}三、结论1、实验结果2、分析讨论这个实验稍微复杂些,在实现算法时遇到好多问题,首先要实现距离的算法:图中的数等同于下图:1 2 3 4 5 6 然后经过Dijkstra算法分析求出最短路径,1┏0 50 10 ∞70 ∞┓通过这道程序,我明白了:你有了一个算法,2┃∞0 15 ∞ 10 ∞┃要通过程序去实现它非常复杂,以后需要勤3┃20 ∞0 15 ∞∞┃学苦练,加以熟练才能将算法变成程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构课程设计设计说明书单源点最短路径算法的实现学生姓名学号班级成绩指导教师数学与计算机科学学院2015年 1 月 2 日数据结构课程设计评阅书课程设计任务书2014—2015学年第1学期专业:学号:姓名:课程设计名称:数据结构课程设计设计题目:单源点最短路径算法的实现完成期限:自 2014 年 12 月 22 日至 2015 年 1 月 2 日共 2 周设计内容及要求:最短路径问题已经被应用到GIS、GPS等信息管理系统中,为人们生活带来了很大便利。
它属于图结构问题,其解决方法也有不少(如Dijkstra、A-star)。
单源点最短路径问题解决的是既定起点的情况下,寻求该点到图中其它顶点的最短路径。
请用C/C++语言的结构体、指针、数据结构等基础知识,编写程序实现图的结构定义、图的存储,以及求解单源点最短路径。
设计过程以及写作要求如下:(1)要针对本题目,认真研究所设计的内容,用简明扼要的语言描述课题,给出课题的基本内容及要求;(2)根据数据结构的相关知识给出实现建立任意m个顶点n条边的图算法、按照用户给定的源点和目标点,求出它们间的最短路径(打印出来)算法的基本策略及思路;(3)给出较为详尽数据结构与算法,算法可以用流程图、伪代码等描述手段进行描述;(4)给出一个完整的算法实现的C/C++程序,算法中的各子算法要力求用函数来实现;(5)对编写的程序要进行详尽的测试分析;(6)对本课题的设计工作要进行一个完整深刻的总结。
最终设计成果形式为:1、设计软件一套;2、撰写一份课程设计说明书一份,打印并装订成册。
指导教师(签字):教研室主任(签字):批准日期:年月日摘要本系统以VC++作为软件开发环境,C语言作为程序开发语言,邻接矩阵作为存储结构,设计与实现了最短路径运算。
该系统实现了有向图的存储、最短路径的运算等主要功能。
依照该系统可以解决生活中许多问题,比如交通路线的选择,工程时间的预算等等,让人们可以做出合理的选择。
本系统通过分析课题的背景、意义、要求,分别从课题描述、逻辑设计、算法设计、调试与测试等各个方面详细介绍了系统的设计与实现过程,最后对系统的完成情况进行了总结。
界面清晰,操作简单,易于用户接受。
关键词:VC++;邻接矩阵; 最短路径目录1课题描述 (1)2 问题分析与任务定义 (2)2.1问题分析 (2)2.2任务定义 (2)3 算法设计 (3)3.1 图的邻接矩阵的存储结构 (3)3.2 Dijkstra算法思想 (4)4 系统逻辑设计 (5)4.1 主函数流程图如图4.1所示 (5)4.2 Create函数流程图如图4.2所示 (6)4.3 Dijkstra函数流程图如图4.3所示 (8)5 源代码 (11)6 调试与测试 (14)6.1合法数据输入 (14)6.2非法数据输入 (15)总结 (16)参考文献 (17)1课题描述乘车旅行的人大多数都希望找出到目的地尽可能短,花费少的行程,那么如何找出从出发点到目的地的最短路径?由于路径比较多,所以用手工计算起来比较复杂,抽象,因此人们用计算机语言代替手工计算来求得最短路径。
而在计算机语言中迪杰斯拉算法比较常用,简捷,故人们经常借助计算机程序用迪杰斯拉算法求得单源点的最短路径,这样可以广泛的提高效率,而且条理清晰,通俗易懂。
2 问题分析与任务定义2.1问题分析本系统是要解决的是单源点最短路径问题,设计程序,实现最短路径的求法,系统需要达到的主要功能如下:(1) 编写算法能够建立带权图,并能够用Dijkstra算法求该图的最短路径。
(2) 能够选择图上的任意一顶点做为开始节点。
最短路径输出不必采用图形方式,可顶点序列方式输出。
(3) 根据课设题目要求,拟将整体程序分为三大模块。
两个子模块相互独立,没有嵌套调用的情况,在主模块中调用上面两个子模块。
2.2任务定义根据课设题目要求,拟将整体程序分为三大模块。
两个子模块相互独立,没有嵌套调用的情况,在主模块中调用上面两个子模块以下是三个模块的大体分析:(1) 建立有向图的存储结构。
(2) 应用Dijkstra算法求出该有向图的最短路径。
(3) 在主函数中调用两个子函数,完成最短路径的程序设。
3算法设计3.1图的邻接矩阵的存储结构一个图的邻接矩阵表示唯一的。
故在图的邻接矩阵表示中,除了需要用一个二维数组存储顶点之间相邻关系的邻接矩阵外,通常还需要使用一个具有n个元素的一维数组存储顶点信息,其中下标为i的元素存储顶点vi的信息。
本设计是基于类C语言的算法描述,因此,图的邻接矩阵的存储结构定义如下:#define MVNum 50typedef struct {VertexType vexs[MVNum];Adjmatrix arcs[MVNum][MVNum];}Mgraph;在本系统中,以邻接矩阵存储有向图,如图3.1a中有向图G所示,其邻接矩阵为3.2 Dijkstra算法思想(1)Dijkstra算法核心是贪心,实质是按路径长度递增产生诸顶点的最短路径算法。
用自然语言描述如下:初始化S和D,置空最短路径终点集,置初始的最短路径值;S[v1]=TRUE;D[v1]=0;While(S集中的顶点数<n){开始循环,每次求的v1到某个v顶点的最短路径,并将v加到S集中;S[v]=TRUE; 更新当前最短路径及距离。
}(2)Dijkstra算法结束后,通过设置一个数组记录下一个节点的前趋节点,然后通过倒叙的方式输出该最短路径。
4系统逻辑设计4.1主函数流程图如图4.1所示4.2 Create函数流程图如图4.2所示4.3Dijkstra函数流程图如图4.3所示、5 源代码#include<stdio.h>#include<stdlib.h>#define MVNum 50#define Maxint 1111typedef char VertexType; // 定义顶点typedef int Adjmatrix;typedef enum {FALSE,TRUE}boolean;typedef struct { // 图的邻接矩阵VertexType vexs[MVNum]; //顶点向量存放顶点的一维数组Adjmatrix arcs[MVNum][MVNum]; // 邻接矩阵二维数组}MGraph; //定义邻接矩阵结构类型void CreateMGraph(MGraph *G,int m,int n) // 采用数组(邻接矩阵)表示法,构造图G{int i,j,k,w;char a,b;for(i=1;i<=m;i++) //构造顶点向量G->vexs[i]=i;for(i=1;i<=m;i++) //初始化邻接矩阵for(j=1;j<=m;j++)G->arcs[i][j]=Maxint;printf("输入%d条边的i,j及w:\n",n);for(k=1;k<=n;k++) // 构造邻接矩阵{fflush(stdin);scanf("%c,%c,%d",&a,&b,&w); //输入一条边依附的顶点及权值i=a-'a'+1;j=b-'a'+1;G->arcs[i][j]=w; //弧<i,j>的权值}printf("有向图的存储结构建立完成!\n");printf("**********************************\n");}void Dijkstra(MGraph G,int v1,int m)//用Dijkstra算法求G中v1顶点到其余顶点v的最短路径p[v]及带权长度D[v]{int D[MVNum],P[MVNum];int v,i,w,min;boolean S[MVNum];// S以求得最短路径的终点的集合for(v=1;v<=m;v++){S[v]=FALSE;D[v]=G.arcs[v1][v];if(D[v]<Maxint)P[v]=v1;elseP[v]=0;}D[v1]=0;S[v1]=TRUE; // 初始化,v1顶点属于s集//开始主循环,每次求得v1到某个v顶点的最短路径,并加v到s集for(i=2;i<=m;i++) // 其余n-1个顶点{min=Maxint; //当前所知离v1顶点的最近距离for(w=1;w<=m;w++)if(!S[w]&&D[w]<min) // w顶点在v-s中{v=w;min=D[w]; //w顶点离v1顶点更近}S[v]=TRUE;for(w=1;w<=m;w++) //更新当前最短路径及距离if(!S[w]&&(D[v]+G.arcs[v][w]<D[w])) // 修改D[w]和P[w],w属于v-s{D[w]=D[v]+G.arcs[v][w];P[w]=v;}}printf("路径长度-----------路径\n");for(i=1;i<=m;i++){printf("%5d",D[i]);printf("%12c",i-1+'a');v=P[i];while(v!=0){printf("<-%c",v-1+'a');v=P[v];}printf("\n");}}void main(){MGraph G;int m,n,v;char ch;printf("输入所需图的顶点个数和边数m,n:"); scanf("%d,%d",&m,&n);CreateMGraph(&G,m,n);while (v<=m){printf("求最短路径,请输入初始点v:"); fflush(stdin);scanf("%c",&ch);printf("\n");v=ch-'a'+1;Dijkstra(G,v,m);}}6 调试与测试6.1合法数据输入(1)合法数据测试结果如图6.1所示图6.1合法数据测试结果6.2非法数据输入(2)非法数据测试结果如图6.2所示图6.2非法数据测试结果当前任务已达到任务目标,对于n个顶点的有向图,求一个顶点到其他顶点的最短路径的时间为O(n),调整最短路径的循环共执行n-1次,所以,时间复杂度是O(n2)。
