第七章∶图练习题
数据结构章节练习题 - 答案第7章 图

7.1选择题1.对于一个具有n个顶点和e条边的有向图,在用邻接表表示图时,拓扑排序算法时间复杂度为()A)O(n)B)O(n+e)C)O(n*n)D)O(n*n*n)【答案】B2.设无向图的顶点个数为n,则该图最多有()条边。
A)n-1B)n(n-1)/2C)n(n+1)/2【答案】B3.连通分量指的是()A)无向图中的极小连通子图B)无向图中的极大连通子图C)有向图中的极小连通子图D)有向图中的极大连通子图【答案】B4.n个结点的完全有向图含有边的数目()A)n*n B)n(n+1)C)n/2【答案】D5.关键路径是()A)AOE网中从源点到汇点的最长路径B)AOE网中从源点到汇点的最短路径C)AOV网中从源点到汇点的最长路径D)n2D)n*(n-1)D)AOV网中从源点到汇点的最短路径【答案】A6.有向图中一个顶点的度是该顶点的()A)入度B)出度C)入度与出度之和D)(入度+出度)/2【答案】C7.有e条边的无向图,若用邻接表存储,表中有()边结点。
A)e B)2eC)e-1D)2(e-1)【答案】B8.实现图的广度优先搜索算法需使用的辅助数据结构为()A)栈B)队列C)二叉树D)树【答案】B9.实现图的非递归深度优先搜索算法需使用的辅助数据结构为()A)栈B)队列C)二叉树D)树【答案】A10.存储无向图的邻接矩阵一定是一个()A)上三角矩阵B)稀疏矩阵C)对称矩阵D)对角矩阵【答案】C11.在一个有向图中所有顶点的入度之和等于出度之和的()倍A)B)1C)2D)4【答案】B12.在图采用邻接表存储时,求最小生成树的Prim 算法的时间复杂度为(A)O(n)B)O(n+e)C)O(n2)D)O(n3))【答案】B13.下列关于AOE网的叙述中,不正确的是()A)关键活动不按期完成就会影响整个工程的完成时间B)任何一个关键活动提前完成,那么整个工程将会提前完成C)所有的关键活动提前完成,那么整个工程将会提前完成D)某些关键活动提前完成,那么整个工程将会提前完成【答案】B14.具有10个顶点的无向图至少有多少条边才能保证连通()A)9B)10C)11D)12【答案】A15.在含n个顶点和e条边的无向图的邻接矩阵中,零元素的个数为()A)e B)2eC)n2-e D)n2-2e【答案】D7.2填空题1.无向图中所有顶点的度数之和等于所有边数的_____________倍。
数据结构第7章图习题

、单项选择题1.在一个无向图 G 中,所有顶点的度数之和等于所有边数之和的 _________ 倍A .l/2B .1D .42.在一个有向图中, 所有顶点的入度之和等于所有顶点的出度之和的 ________倍A .l/2 C .2D .43.一个具有 n 个顶点的无向图最多包含 _____ 条边。
A .nB .n +1C .n-1D .n(n-1)/24.一个具有 n 个顶点的无向完全图包含 _____ 条边。
A .n(n-l)B .n(n+l)C .n(n-l)/2D .n(n-l)/25.一个具有 n 个顶点的有向完全图包含 _____ 条边。
A .n(n-1)B .n(n+l)C .n(n-l)/2D .n(n+l)/2 6.对于具有 n 个顶点的图,若采用邻接矩阵表示,则该矩阵的大小为A. nB. n><h C .n-17 .无向图的邻接矩阵是一个 ______A .对称矩阵 C .上三角矩阵8.对于一个具有 n 个顶点和 e 条边的无 (有)向图,若采用邻接表表示,则表头 向量的大小为 。
A .n C . 2nD . 2e 9.对于一个具有 n 个顶点和 e 条边的无 (有)向图,若采用邻接表表示,则所有 顶C .2B .1 D . (n-I)也-I)B .零矩阵 D .对角矩阵 B .e点邻接表中的结点总数为_________ 。
B. eC. 2nD. 2e10.在有向图的邻接表中,每个顶点邻接表链接着该顶点所有邻接点。
A .入边B.出边C.入边和出边 D .不是入边也不是出边11.在有向图的逆邻接表中,每个顶点邻接表链接着该顶点所有邻接点。
A .入边B.出边C.入边和出边 D .不是人边也不是出边12.如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是A .完全图B.连通图C.有回路 D .一棵树13.采用邻接表存储的图的深度优先遍历算法类似于二叉树的算法。
数据结构章节练习题2

第七章图一、选择题1.图中有关路径的定义是()。
A.由顶点和相邻顶点序偶构成的边所形成的序列B.由不同顶点所形成的序列C.由不同边所形成的序列D.上述定义都不是2.设无向图的顶点个数为n,则该图最多有()条边。
A.n-1 B.n(n-1)/2 C.n(n+1)/2 D.0 E.n23.一个n个顶点的连通无向图,其边的个数至少为()。
A.n-1 B.n C.n+1 D.nlogn;4.要连通具有n个顶点的有向图,至少需要()条边。
A.n-l B.n C.n+l D.2n5.一个有n个结点的图,最少有(B )个连通分量,最多有(D )个连通分量。
A.0 B.1 C.n-1 D.n6. 下列说法不正确的是()。
A.图的遍历是从给定的源点出发每一个顶点仅被访问一次C.图的深度遍历不适用于有向图B.遍历的基本算法有两种:深度遍历和广度遍历D.图的深度遍历是一个递归过程7.无向图G=(V,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是()。
A.a,b,e,c,d,f B.a,c,f,e,b,d C.a,e,b,c,f,d D.a,e,d,f,c,b8. 在图采用邻接表存储时,求最小生成树的Prim 算法的时间复杂度为( )。
A. O(n)B. O(n+e)C. O(n2)D. O(n3)9. 求解最短路径的Floyd算法的时间复杂度为( )。
A.O(n) B. O(n+c) C. O(n*n)D. O(n*n*n)10.已知有向图G=(V,E),其中V={V1,V2,V3,V4,V5,V6,V7},E={<V1,V2>,<V1,V3>,<V1,V4>,<V2,V5>,<V3,V5>,<V3,V6>,<V4,V6>,<V5,V7>,<V6,V7>},G的拓扑序列是()。
习题第七章图答案

第七章图一、选择题1.图中有关路径的定义是( A )。
【北方交通大学 2001 一、24 (2分)】A.由顶点和相邻顶点序偶构成的边所形成的序列 B.由不同顶点所形成的序列C.由不同边所形成的序列 D.上述定义都不是2.设无向图的顶点个数为n,则该图最多有(B )条边。
A.n-1 B.n(n-1)/2 C. n(n+1)/2 D.0 E.n2【清华大学 1998 一、5 (2分)】【西安电子科技大 1998 一、6 (2分)】【北京航空航天大学 1999 一、7 (2分)】3.一个n个顶点的连通无向图,其边的个数至少为( A )。
【浙江大学 1999 四、4 (4分)】A.n-1 B.n C.n+1 D.nlogn;4.要连通具有n个顶点的有向图,至少需要(B )条边。
【北京航空航天大学 2000 一、6(2分)】A.n-l B.n C.n+l D.2n5.n个结点的完全有向图含有边的数目(D )。
【中山大学 1998 二、9 (2分)】A.n*n B.n(n+1) C.n/2 D.n*(n-l)6.一个有n个结点的图,最少有(B)个连通分量,最多有( D )个连通分量。
A.0 B.1 C.n-1 D.n【北京邮电大学 2000 二、5 (20/8分)】7.在一个无向图中,所有顶点的度数之和等于所有边数(B )倍,在一个有向图中,所有顶点的入度之和等于所有顶点出度之和的( C )倍。
【哈尔滨工业大学 2001 二、3 (2分)】A.1/2 B.2 C.1 D.48.用有向无环图描述表达式(A+B)*((A+B)/A),至少需要顶点的数目为( A)。
【中山大学1999一、14】A.5 B.6 C.8 D.99.下列哪一种图的邻接矩阵是对称矩阵?( B)【北方交通大学 2001 一、11 (2分)】A.有向图 B.无向图 C.AOV网 D.AOE网10. 下列说法不正确的是( C )。
【青岛大学 2002 二、9 (2分)】A.图的遍历是从给定的源点出发每一个顶点仅被访问一次 C.图的深度遍历不适用于有向图B.遍历的基本算法有两种:深度遍历和广度遍历 D.图的深度遍历是一个递归过程11.无向图G=(V,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是( D )。
数据结构课后习题答案第七章
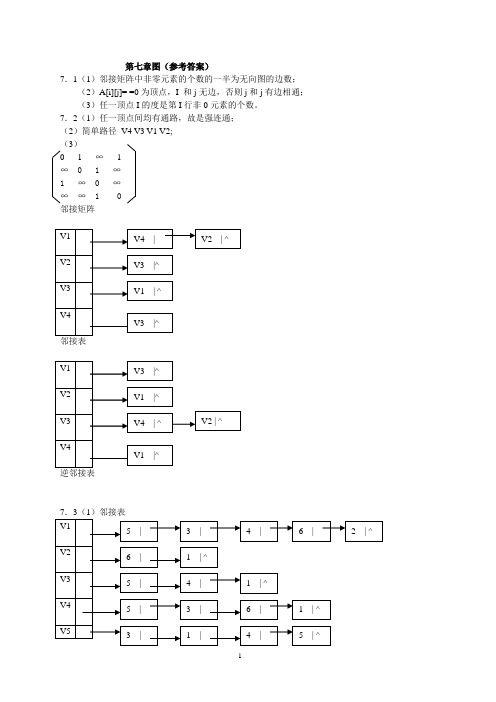
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
第七章图 习题答案

第七章图习题答案基础知识:7.1 在图7.23所示的各无向图中:(1)找出所有的简单环。
(2)哪些图是连通图?对非连通图给出其连通分量。
(3)哪些图是自由树(或森林)?答:(1)所有的简单环:(同一个环可以任一顶点作为起点)(a)1231(b)无(c)1231、2342、12341(d)无(2)连通图:(a)、(c)、(d)是连通图,(b)不是连通图,因为从1到2没有路径。
具体连通分量为:(3)自由树(森林):自由树是指没有确定根的树,无回路的连通图称为自由树:(a)不是自由树,因为有回路。
(b)是自由森林,其两个连通分量为两棵自由树。
(c)不是自由树。
(d)是自由树。
7.2 在图7.24(下图)所示的有向图中:(1) 该图是强连通的吗? 若不是,则给出其强连通分量。
(2) 请给出所有的简单路径及有向环。
(3) 请给出每个顶点的度,入度和出度。
(4) 请给出其邻接表、邻接矩阵及逆邻接表。
答:(1)该图是强连通的,所谓强连通是指有向图中任意顶点都存在到其他各顶点的路径。
(2)简单路径是指在一条路径上只有起点和终点可以相同的路径:有v1v2、v2v3、v3v1、v1v4、v4v3、v1v2v3、v2v3v1、v3v1v2、v1v4v3、v4v3v1、v3v1v4、另包括所有有向环,有向环如下:v1v2v3v1、v1v4v3v1(这两个有向环可以任一顶点作为起点和终点)(3)每个顶点的度、入度和出度:D(v1)=3ID(v1)=1OD(v1)=2D(v2)=2 ID(v2)=1OD(v2)=1D(v3)=3 ID(v3)=2OD(v3)=1D(v4)=2 ID(v4)=1OD(v4)=1(4)邻接表:(注意边表中邻接点域的值是顶点的序号,这里顶点的序号是顶点的下标值-1) vertex firstedge next┌─┬─┐┌─┬─┐┌─┬─┐0│v1│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘1│v2│─→│ 2│∧│├─┼─┤├─┼─┤2│v3│─→│ 0│∧│├─┼─┤├─┼─┤3│v4│─→│ 2│∧│└─┴─┘└─┴─┘逆邻接表:┌─┬─┐┌─┬─┐0│v1│─→│ 2│∧│├─┼─┤├─┼─┤1│v2│─→│ 0│∧│├─┼─┤├─┼─┤┌─┬─┐2│v3│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘3│v4│─→│ 0│∧│└─┴─┘└─┴─┘邻接矩阵:0 1 0 10 0 1 01 0 0 00 0 1 07.3 假设图的顶点是A,B...,请根据下述的邻接矩阵画出相应的无向图或有向图。
一年级数学下册第七单元画图题专项练习题

一年级数学下册第七单元画图题专项练习题1、继续画。
□△□△□△□△__________________________________________ △△▽△△▽△△▽________________________________________2、第一行缺少的是哪个图形,在第二行中圈出。
3、把下面的○和□有规律地涂色。
○○○○○○○○○○○○○○○□□□□□□□□□□□□□□□4、苹果和梨按规律摆放着,有几个水果被毛巾盖着。
想想毛巾下面最少有几个水果。
5、珠子按规律串在一起.想想盒子里有几颗珠子。
6、按规律涂一途。
1237、8、9、10、12、按规律接着涂。
(1)(2)(3)13、请你接着画一画。
(1)(3)14、自己涂出有规律的颜色。
(1)(2)(3)15、找出与其他图形不同的一组图形,并圈出来。
16、找一找,有什么规律?画一画。
17、按规律选一选。
(填序号) (1)(2)18、给小鱼画花纹。
19、按规律选一选。
(填序号) (1)(2)(3)20、按规律画一画,填一填。
(1)(2)21、找规律涂一涂,画一画。
22、按图形的排列规律接着画。
23、自己涂出有规律的颜色。
24、(挑战题)按规律接着画。
25、哪两行的规律相同?在后面的括号里画“√”。
26、找规律,填一填。
遮住了7个珠子,有()个,( )个。
27、第10个灯笼是什么颜色的?在下面圈出来。
机械工程图学习题集加详细答案 第7章

7-5完成被截切圆柱的三面投影。
(2)完成水平和侧面投影
7-5完成被截切圆柱的三面投影。
(3)完成水平和正面投影
7-5完成被截切圆柱的三面投影。
(3)完成水平和正面投影
7-5完成被截切圆柱的三面投影。
(4)完成侧面投影。
7-5完成被截切圆柱的三面投影。
(4)完成水平投影。
7-5完成被截切圆柱的三面投影。
(2)完成水平及侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(2)完成水平及侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(3)完成正面和侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(3)完成正面和侧面投影(注意整理轮廓线)。
7-10完成相贯体(曲面立体与曲面立体)的投影。 (6)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (6)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (7)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (7)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (8)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (8)
7-6完成被截切圆锥的三面投影。
(4)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(5)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(5)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(6)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(6)完成水平和侧面投影。
7-10完成相贯体(曲面立体与曲面立体)的投影。 (1)
机械制图第七章练习题

机械制图常用标准件练习1 回答下列问题 , 并在相应图上分别标出内、外螺纹的尺寸 .(1) a 内、外螺纹旋合时 , 需要、、、、等五要素相同.b 不论内螺纹或是外螺纹 , 螺纹的代号及尺寸均应注在螺纹的径上 ;但管螺纹用标注 .c 标准螺纹的、、都要符合国家标准。
常用的标准螺纹有。
(2) M16-6g 表示螺纹 .M16-5H 表示螺纹 .M16 ╳ 1.5 —— 5g6g 表示螺纹。
M16 ╳ 1.5 —— 6H 表示螺纹。
Tr32 ╳ 12(P6)LH表示为32毫米,为12毫米,线旋螺纹。
B120 ╳ 18(P6)表示为120毫米,为6毫米,线、旋螺纹。
M16 ╳ 1.55是螺纹,其、符合国家标准规定,但不符合国标规定.2 圈出下列各题 (1)-(4) 中的错误并改正。
3解释下列螺纹标记的意义• M24LH-5H-S• M20X1.5-5g6g• Tr32X6LH-7H• B40X14(P7)-8e-L补充。
4 标注代号普通粗牙外螺纹,公称直径 24mm ,单线,右旋,中径、顶径公差带代号6g ,中等旋合长度。
普通螺纹,公称直径 24mm ,螺距 2mm ,单线,左旋,中径、顶径公差带代号分别为 5H 、 6H ,中等旋合长度。
锯齿形螺纹,公称直径 32mm ,螺距 6mm ,双线,右旋,中径公差带代号7h,中等旋合长度。
•用螺纹密封的圆锥内螺纹尺寸代号 1 ,右旋。
•非螺纹密封的管螺纹尺寸代号 1 ,公差等级 A 级,右旋。
•用螺纹密封的圆锥外螺纹尺寸代号1 ,左旋。
5 键联结。
已知齿轮和轴用 A 型普通平键联结,轴、孔直径为20mm ,键长为 20mm 。
要求写出键的规定标记,查表确定键槽的尺寸,画全下列各视图和断面图中所缺漏的图线,并在轴的断面图和齿轮的局部视图中标注轴、孔直径和键槽的尺寸。
6 用规定画法在轴端画出轴承与轴的装配图,并解释滚动轴承代号的含义。
滚动轴承 6205含义:内径尺寸系列轴承类型。
数据结构第7章 图习题

习题7 图7.1 单项选择题1.在一个图中,所有顶点的度数之和等于所有边数的____倍。
A. 1/2B. 1C. 2D. 42.任何一个无向连通图的最小生成树。
A.只有一棵B.有一棵或多棵C.一定有多棵D.可能不存在3.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的____倍。
A. 1/2B. 1C. 2D. 44.一个有n个顶点的无向图最多有____条边。
A. nB. n(n-1)C. n(n-1)/2D. 2n5.具有4个顶点的无向完全图有____条边。
A. 6B. 12C. 16D. 206.具有6个顶点的无向图至少应有____条边才能确保是一个连通图。
A. 5B. 6C. 7D. 87.在一个具有n个顶点的无向图中,要连通全部顶点至少需要____条边。
A. nB. n+1C. n-1D. n/28.对于一个具有n个顶点的无向图,若采用邻接矩阵表示,则该矩阵的大小是____。
A. nB. (n-1)2C. n-1D. n29.对于一个具有n个顶点和e条边的无向图,若采用邻接表表示,则表头向量的大小为_①___;所有邻接表中的接点总数是_②___。
①A. n B. n+1 C. n-1 D. n+e②A. e/2 B. e C.2e D. n+e10.已知一个图如图7.1所示,若从顶点a出发按深度搜索法进行遍历,则可能得到的一种顶点序列为__①__;按宽度搜索法进行遍历,则可能得到的一种顶点序列为__②__。
①A. a,b,e,c,d,f B. e,c,f,e,b,d C. a,e,b,c,f,d D. a,e,d,f,c,bC. a,e,b,c,f,dD. a,c,f,d,e,b图 7.1 一个无向图11.已知一有向图的邻接表存储结构如图7.2所示。
⑴根据有向图的深度优先遍历算法,从顶点v1出发,所得到的顶点序列是____。
A. v1,v2,v3,v5,v4B. v1,v2,v3,v4,v5C. v1,v3,v4,v5,v2D. v1,v4,v3,v5,v2⑵根据有向图的宽度优先遍历算法,从顶点v1出发,所得到的顶点序列是____。
第7章-图练习题及标准答案

第七章 图一、单选题( C )1. 在一个图中,所有顶点的度数之和等于图的边数的 倍。
A .1/2 B. 1 C. 2 D. 42. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的( B )倍。
A .1/2 B. 1 C. 2 D. 4 (B )3. 有8个结点的无向图最多有 条边。
A .14 B. 28 C. 56 D. 112 ( A )一个n 个顶点的连通无向图,其边的个数至少为( )。
A .n-1B .nC .n+1D .nlogn ; ( C )5. 有8个结点的有向完全图有 条边。
A .14 B. 28 C. 56 D. 112 (B )6. 用邻接表表示图进行广度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ( A )7. 用邻接表表示图进行深度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图8. 下面关于求关键路径的说法不正确的是( C )。
A .求关键路径是以拓扑排序为基础的B .一个事件的最早开始时间同以该事件为尾的弧的活动最早开始时间相同C .一个事件的最迟开始时间为以该事件为尾的弧的活动最迟开始时间与该活动的持续时间的差D .关键活动一定位于关键路径上9. 已知图的邻接矩阵如下,根据算法思想,则从顶点0出发,按深度优先遍历的结点序列是( D )A . 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2 C. 0 4 2 3 1 6 5 D. 0 ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡01000111011000010110101100110010001100100110111101 3 42 5 610、设数据结构A=(D,R),其中D={1,2,3,4},R={r},r={<1,2>,<2,3>,<3,4>,<4,1>,<4,2>},则数据结构A是(C )。
第7章 静电场习题

q 4πε 0 r 2
。由此可知,球外空间的场强与气球吹大过程无关。
(3)因为球表面的场强 E 表=
q 4πε 0 R 2
,在球吹大的过程中,R 变大,所以,
球表面的场强随气球的吹大而变小。 通过该立方体各面的 7-7 一个点电荷 q 位于一个边长为 a 的立方体的中心, 电通量是多少? 答:点电荷位于立方体中心时,通过该立方体各面的电通量都相等,并且等 于总通量的 1/6。由高斯定理可知总通量为
ε0
∑q
i
i
E2 4πr 2 =
由此可解得区域 II 的电场强度为
Q1
ε0
E2 =
4πε 0 r 2
Q1
在区域 III,做半径 r﹥R2 的球形高斯面。由于该高斯面内的电荷为 Q1+Q2, 由高斯定理可得
∫∫
S
r 1 r E 3 ⋅ dS =
ε0
∑q
i
i
E3 4πr 2 =
Q1 + Q2
ε0
E3 =
( 方向向上 )
7-5 如图 7-46 所示,长为 l 的细直线 OA 带电线密度为 λ ,求下面两种情 况下在线的延长线上距线的端点 O 点为 b 的 P 点的电场强度: (1) λ 为常量,且 λ >0;(2) λ =kx,k 为大于零的常量,(0≤x≤1)。
P O A x
b
54
第七章 静电场
合力的大小为
F = Fx = 2 F1cosθ = 2 ⋅
1 4πε 0
⋅
2e 2 d x2 + 2
2
⋅
2
x d x + 2
2
=
1
4πε 0 4 x 2 + d 2
初一数学第七章 平面图形认识(二) 第6课时 认识三角形练习题(附答案)

第七章 平面图形认识(二)第6课时 认识三角形一、选择题1.(2011·来宾)已知一个三角形的两边长分别是2和3,则下列数据中,可作为第三边的长的是【 】A .1B .3C . 5D .72.下列哪组数据能构成三角形的三边 【 】A .1cm 、2cm 、3cmB .2cm 、3cm 、4cmC .4cm 、4cm 、9cmD .1cm 、2cm 、4cm3.一个三角形三边长分别为3、4、x ,则x 的取值范围是 【 】A .x >2B .x <5C .3<x <5D .1<x <74.(2012·义乌)三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是 【 】A .2B . 3C . 4D .85.若三角形的三边长分别为3,4,x -1,则x 的取值范围是 【 】A .0<x <8B .2<x <8C .0<x <6D .2<x <66.下列说法中正确的是 【 】A .有且只有一条直线垂直于已知直线B .互相垂直的两条线段一定相交C .从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离D .三角形的高、中线、角平分线都是线段7.三角形的高线是 【 】A .直线B .线段C .射线D .三种情况都可能8.在三角形中,交点一定在三角形内部的有①三角形的三条高线 ②三角形的三条中线 ③三角形的三条角平分线 ④三角形的外角平分线 【 】A .①②③④B .①②③C .①④D .②③9.下列说法中:①三条线段组成的图形叫做三角形;②三角形的角平分线是射线;③三角形的三条高所在的直线相交于一点,这一点不在三角形的内部,就在三角形的外部;④三角形的三条中线相交于一点,且这点一定在三角形的内部.其中正确的有 【 】A .4个B .3个C .2个D .1个10.三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是 【 】A .角平分线B .中位线C .高D .中线二、填空题11.(2012·金华)已知三角形的两边长为4,8,则第三边的长度可以是_________(写出一个即可).12.(2012·柳州)如果三角形的两条边长分别为23cm 和10cm ,第三边与其中一边的长相等,那么第三边的长为_________.12.若一个边长都是整数的三角形周长是15cm ,则满足条件的三角形有_________种.14.小明有两根3cm 、7cm 的木棒,他想以这两根木棒为边做一个等腰三角形,还需再选用一根_________. 长的木棒15.已知:在△ABC 中,AB =3,AC =7,BC 长是正整数,当△ABC 的周长最大时,此时BC 的长为_________.16.如果三角形的三条高的交点落在一个顶点上,那么它的形状是 _________.17.已知BD 是△ABC 的一条中线,△ABD 与△BCD 的周长分别为24,17,则AB -BC 的长是_________.18.如图,AD 、BE 、CF 是ABC ∆的3条中线,若AF =2cm ,则AB =____cm ,若BD =5cm ,则BC =____cm , 若AE =2cm ,则AC =____cm .则ABC ∆的周长是_______cm .F E D C B A 第19题A B C F E D 第20题 第18题19.如图,在△ABC 中,AD 是高,AE 是角平分线,BF 是中线,则∠ =∠ =90o ;∠ =∠ =BAC 21; = =12AC . 20.如图,(1)△ABC 的边BC 上的高是 ;(2)△ADC 的边DC 上的高是 ;(3)△EBC 的边EC 上的高是 ;(4)AB =2cm ,CF =2cm ,△ABC 的面积S =_____ cm 2.三、解答题21.(2013·新疆)等腰三角形的两边长分别为3和6,求这个等腰三角形的周长22.已知a 、b 、c 是△ABC 的三边长,化简|a +b -c |+|a -b -c |23.已知三角形的两边a =3,b =7,第三边是c ,且a <b <c ,求c 的取值范围?24.小亮家离学校1千米,小明家离学校3千米,如果小亮家与小明家相距x 千米,那么求x 的取值范围?25.如图,线段AB =CD ,AB 与CD 相交于•,且∠A •C =60°,CE 是由AB 平移所得,判断AC +BD 与AB 的大小关系?并说明理由。
制图第七章练习题

第七章练习题一、选择题1.关于零件图和装配图,下列说法不正确的是。
A.零件图表达零件的大小、形状及技术要求。
B.装配图是表示装配体及其组成部分的连接、装配关系的图样。
C.零件图和装配都用于指导零件的加工制造和检验。
D.零件图和装配图都是生产上的重要技术资料。
2.关于装配图的画法,下列说法正确的是。
A.装配图中两零件的接触面应画两条线。
B.装配图中的剖面线间隔必须一致。
C.同一零件的剖面线必须同向且间隔一致。
D.装配图中相邻零件的剖面线方向必须一致。
3.关于零件图的视图选择,下面说法正确的是。
A.零件图视图数量及表达方法应根据零件的具体结构特点和复杂程度而定,表达的原则是:完整、简洁、清晰。
B.要表达完整,一个零件至少需要两个视图。
C.视图数量越少越好。
D.零件图应通过剖视图和断面图表达内部结构,不应出现虚线。
4.关于表面粗糙度的标注,下面说法不正确的是。
A.表面粗糙度代号一般注在可见轮廓线、尺寸界线、引出线或它们的延长线上。
B.符号的尖端必须从材料外指向零件表面。
C.可以将使用较多的一种代号统一注在图样右上角,并加注“其余”两字,这时代号和文字大小应为图中代号和文字的倍。
D.粗糙度数字的方向一律向上。
5.下面的说法不正确的是。
A.最大极限尺寸必大于基本尺寸。
B.上偏差必大于下偏差。
C.上偏差或下偏差可为正值,也可以为负或零。
D.公差必为正值。
6.一尺寸的上偏差为+,下偏差为,则其公差为。
A. B. C. D.7. 国家标准的表示符号是以下哪种()。
A、GBB、JBC、QBD、NY8.表面粗糙度代号标注中,用( )时,可不注明参数代号。
A.Ry B.RZ9.装配图中,装配体安装在地基或其他机器上时所需的尺寸是_ ____。
A、特性尺寸B、装配尺寸C、安装尺寸D、外形尺寸10.形位公差符号“◎”表示()。
A.圆度 B.圆柱度 C.位置度 D.同轴度11. 装配图中,装配体安装在地基或其他机器上时所需的尺寸是___ __。
数据结构 习题 第七章 图 答案

第7章图二.判断题部分答案解释如下。
2. 不一定是连通图,可能有若干连通分量 11. 对称矩阵可存储上(下)三角矩阵14.只有有向完全图的邻接矩阵是对称的 16. 邻接矩阵中元素值可以存储权值21. 只有无向连通图才有生成树 22. 最小生成树不唯一,但最小生成树上权值之和相等26. 是自由树,即根结点不确定35. 对有向无环图,拓扑排序成功;否则,图中有环,不能说算法不适合。
42. AOV网是用顶点代表活动,弧表示活动间的优先关系的有向图,叫顶点表示活动的网。
45. 能求出关键路径的AOE网一定是有向无环图46. 只有该关键活动为各关键路径所共有,且减少它尚不能改变关键路径的前提下,才可缩短工期。
48.按着定义,AOE网中关键路径是从“源点”到“汇点”路径长度最长的路径。
自然,关键路径上活动的时间延长多少,整个工程的时间也就随之延长多少。
三.填空题1.有n个顶点,n-1条边的无向连通图2.有向图的极大强连通子图3. 生成树9. 2(n-1) 10. N-1 11. n-1 12. n 13. N-1 14. n15. N16. 3 17. 2(N-1) 18. 度出度 19. 第I列非零元素个数 20.n 2e21.(1)查找顶点的邻接点的过程 (2)O(n+e) (3)O(n+e) (4)访问顶点的顺序不同 (5)队列和栈22. 深度优先 23.宽度优先遍历 24.队列25.因未给出存储结构,答案不唯一。
本题按邻接表存储结构,邻接点按字典序排列。
25题(1) 25题(2) 26.普里姆(prim )算法和克鲁斯卡尔(Kruskal )算法 27.克鲁斯卡尔28.边稠密 边稀疏 29. O(eloge ) 边稀疏 30.O(n 2) O(eloge) 31.(1)(V i ,V j )边上的权值 都大的数 (2)1 负值 (3)为负 边32.(1)n-1 (2)普里姆 (3)最小生成树 33.不存在环 34.递增 负值 35.16036.O(n 2) 37. 50,经过中间顶点④ 38. 75 39.O(n+e )40.(1)活动 (2)活动间的优先关系 (3)事件 (4)活动 边上的权代表活动持续时间41.关键路径 42.(1)某项活动以自己为先决条件 (2)荒谬 (3)死循环 43.(1)零 (2)V k 度减1,若V k 入度己减到零,则V k 顶点入栈 (3)环44.(1)p<>nil (2)visited[v]=true (3)p=g[v].firstarc (4)p=p^.nextarc45.(1)g[0].vexdata=v (2)g[j].firstin (3)g[j].firstin (4)g[i].firstout (5)g[i].firstout (6)p^.vexj (7)g[i].firstout (8)p:=p^.nexti (9)p<>nil (10)p^.vexj=j(11)firstadj(g,v 0) (12)not visited[w] (13)nextadj(g,v 0,w)46.(1)0 (2)j (3)i (4)0 (5)indegree[i]==0 (6)[vex][i] (7)k==1 (8)indegree[i]==047.(1)p^.link:=ch[u ].head (2)ch[u ].head:=p (3)top<>0 (4)j:=top (5)top:=ch[j].count(6)t:=t^.link48.(1)V1 V4 V3 V6 V2 V5(尽管图以邻接表为存储结构,但因没规定邻接点的排列,所以结果是不唯一的。
数据结构第7章图习题

第七章图习题1 单项选择题1、图中有关路径的定义是()。
A、由顶点和相邻顶点序偶构成的边所形成的序列B、由不同顶点所形成的序列C、由不同边所形成的序列D、上述定义都不对2、设无向图的顶点个数为n,则该图最多有()条边。
A、n– 1B、n (n– 1)/2C、n (n+1)/2D、n23、一个n个顶点的连通无向图,其边的个数至少为()。
A、n– 1B、nC、n+1D、n log n4、下面结构中最适于表示稀疏无向图的是()。
A、邻接矩阵B、逆邻接表C、邻接多重表D、十字链表5、下列哪一种图的邻接矩阵是对称矩阵?()A、有向图B、无向图C、AOV网D、AOE网6、当一个有N个顶点的图用邻接矩阵A表示时,顶点V i的度是()。
A、第j列所有元素之和B、第i行所有元素之和C、不确定D、第j列所有元素之和+第i行所有元素之和7、下面哪一方法可以判断出一个有向图是否有环(回路)()。
A、深度优先遍历B、拓扑排序C、求最短路径D、求关键路径8、在图采用邻接表存储时,求最小生成树的Prim 算法的时间复杂度为( )。
A、O(n)B、O(n+e)C、O(n2)D、O(n3)9、求解最短路径的Floyd算法的时间复杂度为( )。
A、O(n)B、O(n+e)C、O(n2)D、O(n3)10、已知有向图G=(V, E),其中V={v1, v2, v3, v4, v5, v6, v7},E={<v1,v2>, <v1,v3>, <v1,v4>, <v2,v5>, <v3,v5>, <v3,v6>, <v4,v6>, <v5,v7>, <v6,v7>}, G的拓扑序列是()。
A、v1,v3,v4,v6,v2,v5,v7B、v1,v3,v2,v6,v4,v5,v7C 、v 1,v ,v 4,v 5,v 2,v 6,v 7D 、v 1,v 2,v 5,v 3,v 4,v 6,v 711、在用邻接表表示图时,拓扑排序算法时间复杂度为( )。
数据结构第7章图习题

第7章图一、单项选择题1.在一个无向图G中,所有顶点的度数之和等于所有边数之和的______倍。
A.l/2 B.1C.2 D.42.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的______倍。
A.l/2 B.1C.2 D.43.一个具有n个顶点的无向图最多包含______条边。
A.n B.n+1C.n-1 D.n(n-1)/24.一个具有n个顶点的无向完全图包含______条边。
A.n(n-l) B.n(n+l)C.n(n-l)/2 D.n(n-l)/25.一个具有n个顶点的有向完全图包含______条边。
A.n(n-1) B.n(n+l)C.n(n-l)/2 D.n(n+l)/26.对于具有n个顶点的图,若采用邻接矩阵表示,则该矩阵的大小为______。
A.nB.n×nC.n-1 D.(n-l)×(n-l)7.无向图的邻接矩阵是一个______。
A.对称矩阵B.零矩阵C.上三角矩阵D.对角矩阵8.对于一个具有n个顶点和e条边的无(有)向图,若采用邻接表表示,则表头向量的大小为______。
A.n B.eC.2n D.2e9.对于一个具有n个顶点和e条边的无(有)向图,若采用邻接表表示,则所有顶点邻接表中的结点总数为______。
A.n B.eC.2n D.2e10.在有向图的邻接表中,每个顶点邻接表链接着该顶点所有______邻接点。
A.入边B.出边C.入边和出边D.不是入边也不是出边11.在有向图的逆邻接表中,每个顶点邻接表链接着该顶点所有______邻接点。
A.入边B.出边C.入边和出边D.不是人边也不是出边12.如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是______。
A.完全图B.连通图C.有回路D.一棵树13.采用邻接表存储的图的深度优先遍历算法类似于二叉树的______算法。
A.先序遍历B.中序遍历C.后序遍历 D.按层遍历14.采用邻接表存储的图的广度优先遍历算法类似于二叉树的______算法。
第7章图历年试题及参考答案(08)

第7章图历年试题及参考答案(08)第7章图(2008年1⽉)9、假设有.向图含n 个顶点及e 条弧,则表⽰该图的邻接表中包含的弧结点个数为()A 、nB 、eC 、2eD 、n ·e10、如图所⽰的有向⽆环图可以得到的不同拓扑序列的个数为()A 、1B 、2C 、3D 、422、已知⼀个有向⽹如图所⽰,从顶点1到顶点4的最短路径长度为___________。
28、已知有向图的邻接表如图所⽰,(1) 写出从顶点A 出发,对该图进⾏⼴度优先搜索遍历的顶点序列;(2) 画出该有向图的逆.邻接表。
(1)(2)33、设有向图邻接表定义如下;typedef struct{VertexNode adjlist[Max VertexNum];int n,e; //图的当前顶点数和弧数} ALGraph;其中顶点表结点VertexNode 边表结点EdegNode 结构为:阅读下列算法f33,并回答问题:(1)已知有向图G 的邻接表如图所⽰, 写出算法f33的输出结果;(2)简述算法f33的功能。
void dfs (ALGraph *G,int v){EdgeNode * p;visited[v]=TRUE;printf("%c",G->adjlist[v].vertex);for(p=(G->adjlist[v]).firstedge; p; p=p->next)if(! visited[p->adjvex])dfs (G, p->adjvex);}void f33(ALGraph *G){int v,w;for(v=0; v n; v ++) {for(w=0;wn; w++)visited[w]= FALSE;printf("%d:",v);dfs(G,v);printf("\n");}}(1)(2)(2008年10⽉)8、在⼀个具有n个顶点的有向图中,所有顶点的出度之和为Dout ,则所有顶点的⼊度之和为()A、DoutB、Dout-1C、Dout+1D、n9、如图所⽰的有向⽆环图可以得到的拓扑序列的个数是()A、3B、4C、5D、610、如图所⽰的带权⽆向图的最⼩⽣成树的权为()A 、 51B 、 52C 、 54D 、 5622、n 个顶点且含有环路的⽆向连通图中,⾄少含有条边。
数据结构第7章 图习题

习题7 图7.1 单项选择题1.在一个图中,所有顶点的度数之和等于所有边数的____倍。
A. 1/2B. 1C. 2D. 42.任何一个无向连通图的最小生成树。
A.只有一棵B.有一棵或多棵C.一定有多棵D.可能不存在3.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的____倍。
A. 1/2B. 1C. 2D. 44.一个有n个顶点的无向图最多有____条边。
A. nB. n(n-1)C. n(n-1)/2D. 2n5.具有4个顶点的无向完全图有____条边。
A. 6B. 12C. 16D. 206.具有6个顶点的无向图至少应有____条边才能确保是一个连通图。
A. 5B. 6C. 7D. 87.在一个具有n个顶点的无向图中,要连通全部顶点至少需要____条边。
A. nB. n+1C. n-1D. n/28.对于一个具有n个顶点的无向图,若采用邻接矩阵表示,则该矩阵的大小是____。
A. nB. (n-1)2C. n-1D. n29.对于一个具有n个顶点和e条边的无向图,若采用邻接表表示,则表头向量的大小为_①___;所有邻接表中的接点总数是_②___。
①A. n B. n+1 C. n-1 D. n+e②A. e/2 B. e C.2e D. n+e10.已知一个图如图7.1所示,若从顶点a出发按深度搜索法进行遍历,则可能得到的一种顶点序列为__①__;按宽度搜索法进行遍历,则可能得到的一种顶点序列为__②__。
①A. a,b,e,c,d,f B. e,c,f,e,b,d C. a,e,b,c,f,d D. a,e,d,f,c,b②A. a,b,c,e,d,f B. a,b,c,e,f,d C. a,e,b,c,f,d D. a,c,f,d,e,b图 7.1 一个无向图11.已知一有向图的邻接表存储结构如图7.2所示。
图7.2 一个有向图的邻接表存储结构⑴根据有向图的深度优先遍历算法,从顶点v1出发,所得到的顶点序列是____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章:图练习题一、选择题1、一个有n个顶点的无向图最多有()条边。
A、nB、n(n-1)C、n(n-1)/2D、2n2、具有6个顶点的无向图至少有()条边才能保证是一个连通图。
A、5B、6C、7D、83、具有n个顶点且每一对不同的顶点之间都有一条边的图被称为()。
A、线性图B、无向完全图C、无向图D、简单图4、具有4个顶点的无向完全图有()条边。
A、6B、12C、16D、205、G是一个非连通无向图,共有28条边,则该图至少有()个顶点A、6B、7C、8D、96、存储稀疏图的数据结构常用的是()。
A、邻接矩阵B、三元组C、邻接表D、十字链表7、对一个具有n个顶点的图,采用邻接矩阵表示则该矩阵的大小为()。
A、nB、(n-1)2C、(n+1)2D、n28、设连通图G的顶点数为n,则G的生成树的边数为()。
A、n-1B、nC、2nD、2n-19、n个顶点的无向图的邻接表中结点总数最多有()个。
A、2nB、nC、n/2D、n(n-1)10、对于一个具有n个顶点和e条边的无向图,若采用邻接表表示,则表向量的大小为(),所有顶点邻接表的结点总数为()。
A、nB、n+1C、n-1D、2nE、e/2F、eG、2eH、n+e11、在有向图的邻接表存储结构中,顶点v在表结点中出现的次数是()。
A、顶点v的度B、顶点v的出度C、顶点v 的入度D、依附于顶点v的边数12、已知一个图,若从顶点a出发进行深度和广度优先搜索遍历,则可能得到的顶点序列分别为()和()(1)A、abecdf B、acfebd C、acebfd D、acfdeb(2)A、abcedf B、abcefd C、abedfc D、acfdeb13、采用邻接表存储的图的深度和广度优先搜索遍历算法类似于二叉树的()和()。
A、中序遍历B、先序遍历C、后序遍历D、层次遍历14、已知一有向图的邻接表存储结构如下图所示,分别根据图的深度和广度优先搜索遍历算法,从顶点v1出发,得到的顶点序列分别为()和()。
A、v1,v2,v3,v4,v5B、v1,v3,v2,v4,v5C、v1,v2,v3,v5,v4D、v1,v4,v3,v5,v215、已知有8个顶点为A,B,C,D,E,F,G,H的无向图,其邻接矩阵存A B C D E F G HA 0 1 0 1 0 0 0 0B 1 0 1 0 1 1 1 0C 0 1 0 1 0 0 0 0D 1 0 1 0 0 0 1 0E 0 1 0 0 0 0 0 1F 0 1 0 0 0 0 1 1G 0 1 0 1 0 1 0 1H 0 0 0 0 1 1 1 0E、ABEHFGDCF、ABEHGFCD16、已知一个图如下,在该图的最小生成树中各边上权值之和为(),在该图的最小生成树中,从v1到v6的路径为()。
A、31B、38C、36D、43E、v1,v3,v6F、v1,v4,v6G、v1,v5,v4,v6H、v1,v4,v3,v617、关键路径是事件结点网络中的()。
A、从源点到汇点的最长路径B、从源点到汇点的最短路径C、最长的回路D、最短的回路18、正确的AOE网必须是(),AOE网中某边权值应当是(),权值为0的边表示()。
(1)A、完全图 B、哈密尔顿图 C、无环图 D、强连通图(2)A、实数 B、正整数 C、正数 D、非负数(3)A、为决策而增加的活动 B、为计算方便而增加的活动 C、表示活动间的时间顺序关系 D、该活动为关键活动19、已知一个图如下,则由该图得到的一种拓扑序列为()。
A、v1,v4,v6,v2,v5,v3B、v1,v2,v3,v4,v5,v6C、v1,v4,v2,v3,v6,v5D、v1,v2,v4,v6,v3,v520、下面结论中正确的是()A、在无向图中,边的条数是顶点度数之和。
B、在图结构中,顶点可以没有任何前驱和后继。
C、在n个顶点的无向图中,若边数大于n-1,则该图必定是连通图D、图的邻接矩阵必定是对称矩阵。
21、下面结论中正确的是()A、若有向图的邻接矩阵中对角线以下元素均为0,则该图的拓扑排序序列必定存在。
B、网络的最小代价生成树是唯一的。
C、在拓扑排序序列中,任意两个相继顶点vi和vj都存在从vi到vj的路径。
D、在有向图中,从一个顶点到另一个顶点的最短路径是唯一的。
22、下面结论不正确的是()。
A、无向图的连通分量是该图的极大连通子图。
B、有向图用邻接矩阵表示容易实现求顶点度数的操作。
C、无向图用邻接矩阵表示,图中的边数等于邻接矩阵元素之和的一半。
D、有向图的邻接矩阵必定不是对称矩阵。
23、下面结论中正确的是()。
A、按深度优先搜索遍历图时,与始点相邻的顶点先于不与始点相邻的顶点访问。
B、一个图按深度优先搜索遍历的结果是唯一的。
C、若有向图G中包含一个环,则G的顶点间不存在拓扑排序。
D、图的拓扑排序序列是唯一的。
24、下面结论中不正确的是()。
A、按广度优先搜索遍历图时,与始点相邻的顶点先于不与始点相邻的顶点访问。
B、一个图按广度优先搜索遍历的结果是唯一的。
C、无向图的邻接表表示法中,表中结点的数目是图中边的条数的2倍。
D、图的多重邻接表表示法中,表中结点数目是图中边的条数。
二、填空题1、n个顶点的连通图至少有()条边。
2、一个无向图有n个顶点和e条边,则所有顶点的度数之和为()。
3、在图形结构中,每个结点的前驱结点和后继结点可以有()。
4、若无向图G的顶点度数的最小值大于或等于()时,G至少有一条回路。
5、设无向图G的顶点数为n,图G最少有()边,最多有()条边。
若G为有向图,有n个顶点,则图G最少有()条边,最多有()条边。
具有n个顶点的无向完全图,边的总数为()条,而有n个顶点的有向完全图,边的总数为()条。
6、在无权图G的邻接矩阵A中,若(vi,vj)或<vi,vj>属于G的边/弧的集合,则对应元素A[i][j]等于(),否则等于()。
7、在无向图G的邻接矩阵A中,若A[i][j]=1,则A[j][i]等于()。
8、已知一个图的邻接矩阵表示,计算第I个顶点的入度方法为()9、在一个图G的邻接表表示中,每个顶点的邻接表中所含的结点数,对于有向图而言等于该顶点的(),而对于无向图而言等于该顶点的()。
10、已知图G的邻接表如下,从顶点v1出发的深度优先搜索遍历序列为(),广度优先序列为()。
11、n个顶点的弱连通有向图G最多有()条弧,最少有()条弧。
12、在n个顶点e条边的连通图中,连通分量个数为()。
13、任何()的有向图,其所有结点都可以排在一个拓扑序列中,拓扑排序的方法是先从图中选一个()为0的结点且输出,然后从图中删除该结点及其(),反复执行,直到所有结点都输出为止。
14、一个连通图的()是一个极小连通子图。
15、在AOE网中,从源点到汇点各活动时间总和最长的路径为()。
三、简答题1、对于一个具有n个顶点的连通无向图,如果它有且只有一个简单回路,此图有几条边?一个具有n个顶点的弱连通图至少有几条边?2、已知某图的邻接表,如何建立该图的邻接矩阵?3、有4个顶点A,B,C,D的无向连通图,按广度和深度搜索遍历结果都为ABCD,画出所有可能的结构图?4、简述无向图和有向图有哪几种存储结构,并说明各种结构在图的不同操作中有什么优越性?5、什么是AOE网的关键路径?6、给出下图邻接矩阵、邻接表和邻接多重表存储结构。
从顶点1出发进行广度个深度优先搜索遍历。
7、对下图,请给出(1)对应的邻接矩阵,并给出v1,v2,v3三个顶点的出度和入度;(2)邻接表和逆邻接表表示;(3)强连通分量。
8、试列出图中全部可能的拓扑排序序列。
答案:1 2 3 4 5 6 7 8C A B AD C D A9 10 11 12 13 14 15 16D AG C DB B D CB B17 18 19 20 21 22 23 24A CDB A B A DC B1 n-1 9 出度数,度数2 2e 10 V1v2v3v6v5v4,v1v2v5v4v3v63 任意多个11 N(n-1),n-14 4 12 等于15 0,n(n-1)/2,0,n(n-1),n(n-1)/2,n(n-1) 13 无环,前驱,所有以它为尾的弧6 1,0 14 生成树7 1 15 关键路径8 求矩阵第I列非零元素之和三、简答题1、(1)n条边(2)n-1条边2、根据邻接表中表向量的大小确定邻接矩阵的行列数;由第I个顶点指向的单链表中结点j来确定邻接矩阵中第I行j列元素为1,其余为0。
3、略4、图的存储结构有邻接矩阵、邻接表、十字链表和邻接多重表。
借助于邻接矩阵容易判断任意两个顶点是否有边/弧相连,并容易求出顶点的度。
对无向图,顶点vi的度是邻接矩阵中第I行或第j列的元素之和;对有向图,第I行的元素之和为顶点vi的出度,第j列的元素之和为顶点vj 的入度。
在无向图的邻接表中,第I个链表中表结点个数恰好为顶点vi的度;而在有向图中,第I个链表中表结点个数只是顶点vi的出度。
利用十字链表容易求得顶点的出度和入度。
邻接多重表适合于对边进行操作,如在遍历时对边作记号或在拓扑排序中对边进行删除。
5、在AOE网中完成工程的最短时间是从开始点到完成点的最长路径的长度,这条路径长度最长的路径叫关键路径。
后面题答案略。
