普通物理学第二版第七章课后习题答案
(完整)物理学教程第二版马文蔚上册课后答案完整版
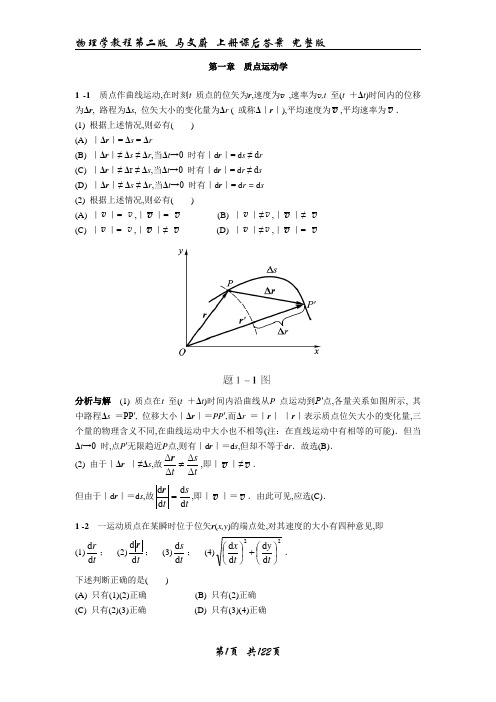
第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( )(A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s(D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s(2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v(C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts t ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故ts t d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;t d d r 表示速度矢量;在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t.下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的(C) 只有(2)是对的 (D) 只有(3)是对的 分析与解td d v 表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;t r d d 在极坐标系中表示径向速率v r (如题1 -2 所述);ts d d 在自然坐标系中表示质点的速率v ;而t d d v 表示加速度的大小而不是切向加速度a t.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -5 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小;(2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx 来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d t x 两式计算.题 1-5 图解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由0d d =tx 得知质点的换向时刻为 s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4s m 48d d -=⋅-==t t x v 2s0.422m.s 36d d -=-==t t x a 1 -6 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求:(1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,(详见题1-1分析).解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为 2412x y -= 这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置.(3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x 其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r 而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r题 1-6 图1 -7 质点的运动方程为23010t t x +-=22015t t y -=式中x ,y 的单位为m,t 的单位为s.试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向.分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向.解 (1) 速度的分量式为t tx x 6010d d +-==v t ty y 4015d d -==v 当t =0 时, v 0x =-10 m·s-1 , v 0y =15 m·s-1 ,则初速度大小为 120200s m 0.18-⋅=+=y x v v v设v 0与x 轴的夹角为α,则23tan 00-==x yαv v α=123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta x x v , 2s m 40d d -⋅-==t a y y v则加速度的大小为222s m 1.72-⋅=+=y x a a a设a 与x 轴的夹角为β,则 32tan -==x y a a β β=-33°41′(或326°19′)1 -8 一升降机以加速度1.22 m·s-2上升,当上升速度为2.44 m·s-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74 m .计算:(1)螺丝从天花板落到底面所需要的时间;(2)螺丝相对升降机外固定柱子的下降距离.分析 在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 =y 1(t )和y 2 =y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解;另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度.升降机厢的高度就是螺丝(或升降机)运动的路程.解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为20121at t y +=v 20221gt t h y -+=v 当螺丝落至底面时,有y 1 =y 2 ,即20202121gt t h at t -+=+v v s 705.02=+=ag h t (2) 螺丝相对升降机外固定柱子下降的距离为 m 716.021202=+-=-=gt t y h d v 解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′=g +a ,螺丝落至底面时,有2)(210t a g h +-= s 705.02=+=ag h t (2) 由于升降机在t 时间内上升的高度为2021at t h +='v 则 m 716.0='-=h h d题 1-8 图1 -9 质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m·s-1 ,求质点的运动方程.分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决.由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =.如a =a (t )或v =v (t ),则可两边直接积分.如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分. 解 由分析知,应有⎰⎰=t t a 0d d 0v v v 得 03314v v +-=t t (1)由 ⎰⎰=txx t x 0d d 0v 得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m·s-1代入(1)、(2)得 v 0=-1 m·s-1, x 0=0.75 m于是可得质点运动方程为75.0121242+-=t t x 1 -10 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a=A -B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程.分析 本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v =a (v )d t 分离变量为t a d )(d =v v 后再两边积分. 解 选取石子下落方向为y 轴正向,下落起点为坐标原点.(1) 由题意知 v v B A ta -==d d (1) 用分离变量法把式(1)改写为 t B A d d =-vv (2) 将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v v v v v 得石子速度 )e 1(Bt B A --=v 由此可知当,t →∞时,B A →v 为一常量,通常称为极限速度或收尾速度. (2) 再由)e 1(d d Bt BA t y --==v 并考虑初始条件有 t BA y t Bt y d )e 1(d 00⎰⎰--= 得石子运动方程)1(e 2-+=-Bt B A t B A y 1 -11 一质点具有恒定加速度a =6i +4j ,式中a 的单位为m·s-2 .在t =0时,其速度为零,位置矢量r 0 =10 m i .求:(1) 在任意时刻的速度和位置矢量;(2) 质点在Oxy 平面上的轨迹方程,并画出轨迹的示意图.题 1-11 图分析 与上两题不同处在于质点作平面曲线运动,根据叠加原理,求解时需根据加速度的两个分量a x 和a y 分别积分,从而得到运动方程r 的两个分量式x (t )和y (t ).由于本题中质点加速度为恒矢量,故两次积分后所得运动方程为固定形式,即20021t a t x x x x ++=v 和20021t a t y y y y ++=v ,两个分运动均为匀变速直线运动.读者不妨自己验证一下. 解 由加速度定义式,根据初始条件t 0 =0时v 0 =0,积分可得⎰⎰⎰+==tt t t 000)d 46(d d j i a vvj i t t 46+=v 又由td d r =v 及初始条件t =0 时,r 0=(10 m)i ,积分可得 ⎰⎰⎰+==tt rr t t t t 00)d 46(d d 0j i r v j i r 222)310(t t ++=由上述结果可得质点运动方程的分量式,即x =10+3t 2y =2t 2消去参数t ,可得运动的轨迹方程3y =2x -20 m 这是一个直线方程.直线斜率32tan d d ===αx y k ,α=33°41′.轨迹如图所示. 1 -12 质点在Oxy 平面内运动,其运动方程为r =2.0t i +(19.0 -2.0t 2 )j ,式中r 的单位为m,t 的单位为s .求:(1)质点的轨迹方程;(2) 在t 1=1.0s 到t 2 =2.0s 时间内的平均速度;(3) t 1 =1.0s时的速度及切向和法向加速度;(4) t =1.0s 时质点所在处轨道的曲率半径ρ.分析 根据运动方程可直接写出其分量式x =x (t )和y =y (t ),从中消去参数t ,即得质点的轨迹方程.平均速度是反映质点在一段时间内位置的变化率,即t ΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v .切向和法向加速度是指在自然坐标下的分矢量a t 和a n ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a t 得到.在求得t 1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ. 解 (1) 由参数方程x =2.0t , y =19.0-2.0t 2消去t 得质点的轨迹方程:y =19.0 -0.50x 2(2) 在t 1 =1.00s 到t 2 =2.0s时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 22222s m 0.4d d d d )(-⋅-=+=ty t x t则t 1 =1.00s时的速度v (t )|t =1s=2.0i -4.0j切向和法向加速度分别为t t y x t t t tt e e e a 222s 1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t =1.0s质点的速度大小为122s m 47.4-⋅=+=y x v v v则m 17.112==na ρv 1 -13 飞机以100 m·s-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问:(1) 此时目标在飞机正下方位置的前面多远? (2) 投放物品时,驾驶员看目标的视线和水平线成何角度?(3) 物品投出2.0s后,它的法向加速度和切向加速度各为多少?题 1-13 图分析 物品空投后作平抛运动.忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动.到达地面目标时,两方向上运动时间是相同的.因此,分别列出其运动方程,运用时间相等的条件,即可求解.此外,平抛物体在运动过程中只存在竖直向下的重力加速度.为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β.由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得.解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x =v t , y =1/2 gt 2飞机水平飞行速度v =100 m·s -1 ,飞机离地面的高度y =100 m,由上述两式可得目标在飞机正下方前的距离m 4522==gy x v(2) 视线和水平线的夹角为o 5.12arctan==xy θ (3) 在任意时刻物品的速度与水平轴的夹角为 vv v gt αx yarctan arctan == 取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为2s m 88.1arctan sin sin -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a t 2s m 62.9arctan cos cos -⋅=⎪⎭⎫ ⎝⎛==v gt g g a n α 1 -14 为迎接香港回归,特技演员柯受良在1997年6月1日驾车飞越黄河壶口,如图所示,柯驾车从跑道东端启动,到达跑道终端时速度大小为1500=v h km 1-⋅,他随即以仰角ο5=α冲出,飞越跨度达57 m ,安全着陆在西岸木桥上,求:题 1-14 图(1) 柯飞车跨越黄河用了多长时间?(2) 若起飞点高出河面10 m ,柯驾车飞行的最高点距河面为几米?(3) 西岸木桥和起飞点的高度差为多少?分析 由题意知,飞车作斜上抛运动,对包含抛体在内的一般曲线运动来说,运用叠加原理是求解此类问题的普适方法,操作程序是:建立一个恰当的直角坐标系,将运动分解为两个相互正交的直线运动,由于在抛体运动中,质点的加速度恒为g ,故两个分运动均为匀变速直线运动或其中一个为匀速直线运动,直接列出相关运动规律方程即可求解,本题可建立图示坐标系,图中m m x y 和分别表示飞车的最大高度和飞跃跨度.解 在图示坐标系中,有t v x )cos (0α= (1)2021sin (gt t v y -=)α (2) gt v v y -=αsin 0 (3)(1) 由式(1),令57m ==x x m ,得飞跃时间37.1cos 0m m ==αv x t s (2)由式(3),令0=y v ,得飞行到最大高度所需时间gv t αsin 0m =’将’m t 代入式(2),得飞行最大高度 67.02sin 220m ==gv y αm 则飞车在最高点时距河面距离为10m +=y h m 67.10= m(3)将37.1m =t s 代入式(2),得西岸木桥位置为y = - 4.22 m“-”号表示木桥在飞车起飞点的下方.讨论 本题也可以水面为坐标系原点,则飞车在 y 方向上的运动方程应为10=y m + 2021)sin (gt t v -α 1 -15 如图所示,从山坡底端将小球抛出,已知该山坡有恒定倾角ο30=α,球的抛射角ο60=β,设球被抛出时的速率v 0 =19.6 m·s-1,忽略空气阻力,问球落在山坡上处离山坡底端的距离为多少?此过程经历多长时间?题 1-15 图分析 求解方法与上题类似,但本题可将运动按两种方式分解,如图(a )和图(b )所示.在图(a )坐标系中,两个分运动均为匀减速直线运动,加速度大小分别为-g αcos 和-g αsin ,看似复杂,但求解本题确较方便,因为落地时有y =0,对应的时间t 和x 的值即为本题所求.在图(b )坐标系中,分运动看似简单,但求解本题还需将落地点P 的坐标y 与x 的关系列出来.解 1 由分析知,在图(a )坐标系中,有20)sin (21)]cos([t g t v x ααβ-+-= (1) 20)cos (21)]sin([t g t v y ααβ-+-= (2)落地时,有y =0,由式(2)解得飞行时间为31.230tan 20==οg v t s将 t 值代入式(1),得1.26322===g v x OP m解 2 由分析知,在图(b )坐标系中,对小球 t v x )cos (0β=(1) 2021)sin (gt t v y -=β(2) 对点P αtan x y ='(3) 由式(1)、(2)可得球的轨道方程为οββ2202cos 2tan v gx x y -=(4) 落地时,应有y y '=,即οοο60cos 260tan 30tan 2202v gx x x -=解之得落地点P 的x 坐标为g v x 332=(5) 则 1.263230cos 20===g v xOP οm联解式(1)和式(5)可得飞行时间31.2=t s讨论 比较两种解法,你对如何灵活运用叠加原理有什么体会?1 -16 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t 时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b ?(3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v 其加速度的切向分量和法向分量分别为 b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为R )(402222bt b a a a a t tn -+=+=v 其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n 20)(arctan arctan v (2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v = (3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为b s s s t 2200v =-= 因此质点运行的圈数为bRR s n π4π220v == 1 -17 一半径为0.50 m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比.在t =2.0s 时测得轮缘一点的速度值为4.0 m·s-1.求:(1) 该轮在t′=0.5s的角速度,轮缘一点的切向加速度和总加速度;(2)该点在2.0s内所转过的角度.分析 首先应该确定角速度的函数关系ω=kt 2.依据角量与线量的关系由特定时刻的速度值可得相应的角速度,从而求出式中的比例系数k ,ω=ω(t )确定后,注意到运动的角量描述与线量描述的相应关系,由运动学中两类问题求解的方法(微分法和积分法),即可得到特定时刻的角加速度、切向加速度和角位移.解 因ωR =v ,由题意ω∝t 2 得比例系数322s rad 2-⋅===Rtt ωk v 所以 22)(t t ωω== 则t ′=0.5s 时的角速度、角加速度和切向加速度分别为12s rad 5.02-⋅='=t ω2s rad 0.24d d -⋅='==t tωα 2s m 0.1-⋅==R αa t总加速度n t t n R ωR αe e a a a 2+=+= ()()2222s m 01.1-⋅=+=R ωR αa 在2.0s内该点所转过的角度rad 33.532d 2d 203202200====-⎰⎰t t t t ωθθ 1 -18 一质点在半径为0.10 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为s.(1) 求在t =2.0s时质点的法向加速度和切向加速度.(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少?(3) t 为多少时,法向加速度和切向加速度的值相等?分析 掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到.解 (1) 由于342t θ+=,则角速度212d d t tθω==.在t =2 s 时,法向加速度和切向加速度的数值分别为 22s 2s m 30.2-=⋅==ωr a t n2s 2s m 80.4d d -=⋅==t ωr a t t (2) 当22212/t n t a a a a +==时,有223n t a a =,即 ()()422212243t r rt = 得 3213=t此时刻的角位置为 rad 15.3423=+=t θ(3) 要使t n a a =,则有()()422212243t r rt = t =0.55s1 -19 一无风的下雨天,一列火车以v 1=20.0 m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v 2 .(设下降的雨滴作匀速运动)题 1-19 图分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得 1o 12s m 36.575tan -⋅==v v 1 -20 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿?分析 这也是一个相对运动的问题.可视雨点为研究对象,地面为静参考系S,汽车为动参考系S′.如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足hl αarctan≥.再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1.题 1-20 图解 由122v v v -='[图(b)],有θθcos sin arctan 221v v v -=α而要使hlαarctan ≥,则 hl θθ≥-cos sin 221v v v ⎪⎭⎫ ⎝⎛+≥θh θl sin cos 21v v 第二章 牛顿定律2 -1 如图(a)所示,质量为m 的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为( )(A) g sin θ (B) g cos θ (C) g tan θ (D) g cot θ分析与解 当物体离开斜面瞬间,斜面对物体的支持力消失为零,物体在绳子拉力F T (其方向仍可认为平行于斜面)和重力作用下产生平行水平面向左的加速度a ,如图(b)所示,由其可解得合外力为mg cot θ,故选(D).求解的关键是正确分析物体刚离开斜面瞬间的物体受力情况和状态特征.2 -2 用水平力F N 把一个物体压着靠在粗糙的竖直墙面上保持静止.当F N 逐渐增大时,物体所受的静摩擦力F f 的大小( )(A) 不为零,但保持不变(B) 随F N 成正比地增大(C) 开始随F N 增大,达到某一最大值后,就保持不变(D) 无法确定分析与解 与滑动摩擦力不同的是,静摩擦力可在零与最大值μF N 范围内取值.当F N 增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态.由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A).2 -3 一段路面水平的公路,转弯处轨道半径为R ,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率( )(A) 不得小于gR μ (B) 必须等于gR μ(C) 不得大于gR μ (D) 还应由汽车的质量m 决定分析与解 由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μF N .由此可算得汽车转弯的最大速率应为v =μRg .因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑.应选(C).2 -4 一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则( )(A) 它的加速度方向永远指向圆心,其速率保持不变(B) 它受到的轨道的作用力的大小不断增加(C) 它受到的合外力大小变化,方向永远指向圆心(D) 它受到的合外力大小不变,其速率不断增加分析与解 由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力F N 作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关.重力的切向分量(m g cos θ) 使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程Rm θmg F N 2sin v =-可判断,随θ 角的不断增大过程,轨道支持力F N 也将不断增大,由此可见应选(B).*2 -5 图(a)示系统置于以a =1/4 g 的加速度上升的升降机内,A 、B 两物体质量相同均为m ,A 所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为( )(A) 5/8 mg (B) 1/2 mg (C) mg (D) 2mg分析与解 本题可考虑对A 、B 两物体加上惯性力后,以电梯这个非惯性参考系进行求解.此时A 、B 两物体受力情况如图(b)所示,图中a ′为A 、B 两物体相对电梯的加速度,m a 为惯性力.对A 、B 两物体应用牛顿第二定律,可解得F T =5/8 mg .故选(A).讨论 对于习题2 -5 这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力.如以地面为惯性参考系求解,则两物体的加速度a A 和a B 均应对地而言,本题中a A 和a B 的大小与方向均不相同.其中a A 应斜向上.对a A 、a B 、a 和a ′之间还要用到相对运动规律,求解过程较繁琐.有兴趣的读者不妨自己尝试一下.2 -6 图示一斜面,倾角为α,底边AB 长为l =2.1 m,质量为m 的物体从题2 -6 图斜面顶端由静止开始向下滑动,斜面的摩擦因数为μ=0.14.试问,当α为何值时,物体在斜面上下滑的时间最短? 其数值为多少?分析 动力学问题一般分为两类:(1) 已知物体受力求其运动情况;(2) 已知物体的运动情况来分析其所受的力.当然,在一个具体题目中,这两类问题并无截然的界限,且都是以加速度作为中介,把动力学方程和运动学规律联系起来.本题关键在列出动力学和运动学方程后,解出倾角与时间的函数关系α=f (t ),然后运用对t 求极值的方法即可得出数值来.解 取沿斜面为坐标轴Ox ,原点O 位于斜面顶点,则由牛顿第二定律有ma αmg μαmg =-cos sin (1)又物体在斜面上作匀变速直线运动,故有()22cos sin 2121cos t αμαg at αl -== 则 ()αμααg l t cos sin cos 2-= (2) 为使下滑的时间最短,可令0d d =αt ,由式(2)有 ()()0sin cos cos cos sin sin =-+--αμαααμαα则可得 μα12tan -=,o 49=α 此时 ()s 99.0cos sin cos 2min =-=αμααg l t 2 -7 工地上有一吊车,将甲、乙两块混凝土预制板吊起送至高空.甲块质量为m 1 =2.00 ×102 kg,乙块质量为m 2 =1.00 ×102 kg .设吊车、框架和钢丝绳的质量不计.试求下述两种情况下,钢丝绳所受的张力以及乙块对甲块的作用力:(1) 两物块以10.0 m·s-2 的加速度上升;(2) 两物块以1.0 m·s-2的加速度上升.从本题的结果,你能体会到起吊重物时必须缓慢加速的道理吗?题2-7 图分析预制板、吊车框架、钢丝等可视为一组物体.处理动力学问题通常采用“隔离体”的方法,分析物体所受的各种作用力,在所选定的惯性系中列出它们各自的动力学方程.根据连接体中物体的多少可列出相应数目的方程式.结合各物体之间的相互作用和联系,可解决物体的运动或相互作用力.解按题意,可分别取吊车(含甲、乙)和乙作为隔离体,画示力图,并取竖直向上为Oy轴正方向(如图所示).当框架以加速度a 上升时,有FT-( m1+m2)g =(m1+m2)a (1)F N2 - m2g =m2a (2) 解上述方程,得FT=(m1+m2)(g +a) (3)F N2=m2(g +a) (4)(1) 当整个装置以加速度a=10 m·s-2上升时,由式(3)可得绳所受张力的值为FT=5.94 ×103 N乙对甲的作用力为F′N2=-F N2=-m2 (g +a)=-1.98 ×103 N(2) 当整个装置以加速度a=1 m·s-2上升时,得绳张力的值为FT=3.24 ×103 N此时,乙对甲的作用力则为F′N2=-1.08 ×103 N由上述计算可见,在起吊相同重量的物体时,由于起吊加速度不同,绳中所受张力也不同,加速度大,绳中张力也大.因此,起吊重物时必须缓慢加速,以确保起吊过程的安全.2 -8如图(a)所示,已知两物体A、B 的质量均为m=3.0kg 物体A 以加速度a =1.0 m·s-2运动,求物体B 与桌面间的摩擦力.(滑轮与连接绳的质量不计)分析该题为连接体问题,同样可用隔离体法求解.分析时应注意到绳中张力大小处处相等是有条件的,即必须在绳的质量和伸长可忽略、滑轮与绳之间的摩擦不计的前提下成立.同时也要注意到张力方向是不同的.解分别对物体和滑轮作受力分析[图(b)].由牛顿定律分别对物体A、B 及滑轮列动力学方程,有m A g-FT=m A a (1)F ′T1 -F f =m B a ′ (2)F ′T -2F T1 =0 (3)考虑到m A =m B =m , F T =F′T , F T1 =F ′T1 ,a ′=2a ,可联立解得物体与桌面的摩擦力()N 2.724f =+-=a m m mg F题 2-8 图讨论 动力学问题的一般解题步骤可分为:(1) 分析题意,确定研究对象,分析受力,选定坐标;(2) 根据物理的定理和定律列出原始方程组;(3) 解方程组,得出文字结果;(4) 核对量纲,再代入数据,计算出结果来.2 -9 质量为m ′的长平板A 以速度v ′在光滑平面上作直线运动,现将质量为m 的木块B 轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板取得共同速度?分析 当木块B 平稳地轻轻放至运动着的平板A 上时,木块的初速度可视为零,由于它与平板之间速度的差异而存在滑动摩擦力,该力将改变它们的运动状态.根据牛顿定律可得到它们各自相对地面的加速度.换以平板为参考系来分析,此时,木块以初速度-v ′(与平板运动速率大小相等、方向相反)作匀减速运动,其加速度为相对加速度,按运动学公式即可解得.该题也可应用第三章所讲述的系统的动能定理来解.将平板与木块作为系统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的共同速度可根据动量定理求得.又因为系统内只有摩擦力作功,根据系统的动能定理,摩擦力的功应等于系统动能的增量.木块相对平板移动的距离即可求出.解1 以地面为参考系,在摩擦力f F =μmg 的作用下,根据牛顿定律分别对木块、平板列出动力学方程f F =μmg =ma 1f F =-f F =m ′a 2a 1 和a 2 分别是木块和木板相对地面参考系的加速度.若以木板为参考系,木块相对平板的加速度a =a 1 +a 2 ,木块相对平板以初速度- v ′作匀减速运动直至最终停止.由运动学规律有。
大学物理课后答案第七章..

第七章 静电场中的导体和电介质一、基本要求1.掌握导体静电平衡的条件及静电平衡时导体电荷的分布规律; 2.学会计算电容器的电容;3.了解介质的极化现象及其微观解释; 4.了解各向同性介质中D 和E 的关系和区别; 5.了解介质中电场的高斯定理; 6.理解电场能量密度的概念.二、基本内容1.导体静电平衡(1)静电平衡条件:导体任一点的电场强度为零(2)导体处于静电平衡时:①导体是等势体,其表面是等势面;②导体表面的场强垂直于导体表面。
(3)导体处于静电平衡时,导体内部处处没有净电荷存在,电荷只能分布在导体的表面上。
2.电容(1)孤立导体的电容 qC V=电容的物理意义是使导体电势升高单位电势所需的电量。
电容是导体的重要属性之一,它反映导体本身具有储存电荷和储存电能的能力。
它的大小仅由导体的几何形状、大小和周围介质决定,与导体是否带电无关. (2)电容器的电容BA V V qC -=q 为构成电容器两极板上所带等量异号电荷的绝对值。
B A V V -为A 、B 两极间电势差。
电容器电容与电容器形状、大小及两极间介质有关,与电容器是否带电无关。
(3)电容器的串并联串联的特点:各电容器的极板上所带电量相等,总电势差为各电容器上电势差之和。
等效电容由121111nC C C C =+++进行计算。
并联的特点:电容器两极板间的电势差相等,不同电容器的电量不等,电容大者电量多。
等效电容为12n C C C C =+++。
(4)计算电容的一般步骤①设两极带电分别为q +和q -,由电荷分布求出两极间电场分布。
②由BA B A V V d -=⋅⎰E l 求两极板间的电势差.③根据电容定义求BA V V qC -=3.电位移矢量D人为引入的辅助物理量,定义0ε=+D E P ,D 既与E 有关,又与P 有关.说明D 不是单纯描述电场,也不是单纯描述电介质的极化,而是同时描述场和电介质的。
定义式无论对各向同性介质,还是各向异性介质都适用.对于各向同性电介质,因为0e χε=P E ,所以0r εεε==D E E 。
大学物理学课后习题7第七章答案

q 6 0
对于边长 a 的正方形,如果它不包含 q
所在的顶点,则 e
q 24 0
,
如果它包含 q 所在顶点则 e 0 .
7.8 均匀带电球壳内半径6cm,外半径10cm,电荷体密度为2×
105 C·m-3求距球心5cm,8cm ,12cm 各点的场强.
解:
高斯定理 当 r 5 cm
均匀分布,其电势U
E
dr
R2
qdr R2 4π 0 r 2
q 4π 0 R
题 7.16 图
(2)外壳接地时,外表面电荷 q 入地,外表面不带电,内表面电荷仍
为 q .所以球壳电势由内球 q 与内表面 q 产生:
U
q 4π 0 R2
q 4π 0 R2
(2)同理
dEQ
1 4π 0
dx
x2
d
2 2
方向如题 7.6 图所示
由于对称性 l dEQx 0 ,即 EQ 只有 y 分量,
∵
dEQy
1 4π 0
dx
x2
d
2 2
d2
x2
d
2 2
EQy
l dEQy
d2 4π 2
l 2
dx
l
3
2
(x2
d
2 2
)
2
l
1由于电荷均匀分布与对称性ab和cd段电荷在o点产生的场强互相抵消取?ddrl?则??ddrq?产生o点e?d如图由于对称性o点场强沿y轴负方向题714图??????cos4dd2220?????rreeyr04???2sin??2sin??r02????2ab电荷在o点产生电势以0??u?????ab200012ln44d4drrxxxxu??????同理cd产生2ln402???u半圆环产生00344??????rru0032142ln2?????????uuuuo715两个平行金属板ab的面积为200cm2a和b之间距离为2cmb板接地如图715所示
普通物理简明教程-胡盘新(第二版)大学物理习题-课后答案

ax =
a=
2
dυ x = −12t dt
2 1 2 2
补充作业1-01-方程求va
a是时间t的一次函数,既是 成正比关系变化,所以能用。
2 1
v − v ( 4 − 6t ) − ( 4 − 6t ) = = −6( t + t ) Δt t −t
2 1
a12 =
a1 + a2 = −6(t2 + t1 ) 2
Chenwq 1
1-2作业-方程求va
1-2. 一质点沿x轴运动,坐标与时间的变化关系为 x=4t-2t 3(SI制),试计算 (1)在最初2s内的平均速度,2s末的瞬时速度; (2)1s末到3s末的位移和平均速度; (3)1s末到3s末的平均加速度。此平均加速度是否可以 用a=(a1+a2)/2计算; (4)3s末的瞬时加速度。 解:(1)最初2s内的平均速度
2 2
2
船的加速度大小
1-10一辆铁路平板车装有货物,在货物与车底板之间的静 摩擦系数为0.25,如果火车以30km/s速度行驶,要使货物 不发生滑动,火车从刹车到完全静止所经过的最短路程是 多少? 解:
2
ax =
当x=s时
dυ x =− dt
h
2 3 2 2
(υ 0 ) = −
2
(l 2 − h )
前
前船接收抛物体前后
得v 前
前增大 中不变 后变小
(M + m)v 前=Mv + m(v + u)
Mv + mu m(u − v ) = =v+ >v M +m ( M + m)
得v 前 = v +
新编基础物理学第二版第七章习题解答

新编基础物理学第⼆版第七章习题解答习题七7-1 氧⽓瓶的容积为32L ,瓶内充满氧⽓时的压强为130atm 。
若每⼩时需⽤1atm 氧⽓体积为400L 。
设使⽤过程中保持温度不变,问当瓶内压强降到10atm 时,使⽤了⼏个⼩时?解已知123130atm,10atm,1atm;p p p === 1232L,V V V ===3400L V =。
质量分别为1m ,2m ,3m ,由题意可得:11m p V RT M = 22mp V RT M =233mp V RT M=所以⼀瓶氧⽓能⽤⼩时数为: ()121233313010329.6(1.0400m m p V p V n m p V -?--====?h)7-2 ⼀氦氖⽓体激光管,⼯作时管内温度是 27C ?。
压强是2.4mmHg ,氦⽓与氖⽓的压强⽐是7:1.求管内氦⽓和氖⽓的分⼦数密度.解:依题意, n n n =+氦氖, 52.41.01310Pa 760p p p =+=氦氖;:7:1p p =氦氖所以552.10.31.01310Pa, 1.01310Pa 760760p p ==氦氖, 根据 p nkT =,得()5223232.1760 1.01310 6.7610(m )1.3810300p n kT --??===氦氦 2139.6610(m )P n kT-==?氖氖7-3 氢分⼦的质量为2410个氢分⼦沿着与墙⾯的法线成?45⾓的⽅向以5110cm s -?的速率撞击在⾯积为22.0cm 的墙⾯上,如果撞击是完全弹性的,试求这些氢分⼦作⽤在墙⾯上的压强.解:单位时间内作⽤在墙⾯上的平均作⽤⼒为:2cos45F N m =?v所以氢分⼦作⽤在墙⾯上的压强为27522342 3.3101010102cos 4522330(Pa)210F m N p S S---====?v7-4 ⼀个能量为1210eV 的宇宙射线粒⼦,射⼊⼀氖管中,氖管中含有氦⽓0.10mol,如果宇宙射线粒⼦的能量全部被氖⽓分⼦所吸收⽽变为热运动能量,问氖⽓的温度升⾼了多少?解: 依题意可得:23121930.1 6.0210 10 1.6102k T -=?? 氖⽓的温度升⾼了771.610 1.2810(K)0.1 6.02 1.5 1.38T --??== 7-5 容器内储有1mol 某种⽓体。
普通物理学教程力学课后答案高等教育出版社刚体力学习题解答

第七章刚体力学习题解答7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.⑴假设转动是匀加速转动,求角加速度。
⑵在此时间内,发动机转了多少转?解:⑴21260/2)12003000(/7.15s rad t===-∆∆πωβ⑵rad 27.152)60/2)(12003000(21039.26222202⨯===∆⨯--πβωωθ对应的转数=42010214.3239.262≈⨯=⨯∆πθ7.1.3 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a dtd dtd -==-+==ωθβω7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立o-xy 坐标系,原点在轴上,x 和y 轴沿水平和铅直向上的方向。
边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足θ=1.2t+t 2 (θ:rad,t:s)。
⑴t=0时,⑵自t=0开始转45º时,⑶转过90º时,A 点的速度和加速度在x 和y 轴上的投影。
解:0.222.1==+==dtd dtd t ωθβω⑴t=0时,s m R v v y x /12.01.02.10,2.1=⨯====ωω2222/2.01.00.2/144.01.0/12.0/sm R a a s m R v a a y y n x =⨯===-=-=-=-=βτ⑵θ=π/4时,由θ=1.2t+t 2,求得t=0.47s,∴ω=1.2+2t=2.14rad/ssm R v s m R v y x /15.02/21.014.245sin /15.02/21.014.245cos =⨯⨯=︒=-=⨯⨯-=︒-=ωω222222222222/182.0)14.20.2(1.0)(45sin 45sin 45sin /465.0)14.20.2(1.0)(45cos 45cos 45cos s m R R R a s m R R R a y x -=-⨯=-︒=︒-︒=-=+⨯-=+︒-=︒-︒-=ωβωβωβωβ⑶θ=π/2时,由θ=1.2t+t 2,求得t=0.7895s,ω=1.2+2t=2.78rad/s2222/77.01.078.2/2.01.00.20/278.01.078.2s m R a s m R a v s m R v y x y x -=⨯-=-=-=⨯-=-==-=⨯-=-=ωβω7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速率ω=10rad/s 逆时针转动,求臂与铅直成45º时门中心G 的速度和加速度。
高中物理(新人教版)必修第二册课后习题:第七章测评(课后习题)【含答案及解析】

第七章测评(时间:75分钟 满分:100分)一、单项选择题(本题共7小题,每小题4分,共28分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2021河北衡水月考)下列说法正确的是( )A.由开普勒第一定律可知,所有行星都在同一椭圆轨道上绕太阳运动B.由F=Gm 1m2r 2可知,当r 趋于零时万有引力趋于无限大C.引力常量G=6.67×10-11N·m 2/kg 2,是由英国物理学家卡文迪什利用扭秤实验测出的D.由开普勒第三定律可知,所有行星轨道半长轴的三次方与公转周期的二次方的比值都相等,即a 3T 2=k ,其中k 与行星有关,所有行星各自绕太阳运行的轨道为椭圆,太阳在椭圆的一个焦点上,所以各行星不在同一椭圆轨道上,故A 错误;万有引力定律的研究对象是质点,当物体间距离趋于零时物体不能被视为质点,万有引力定律不再适用,故B 错误;引力常量G=6.67×10-11N·m 2/kg 2,是由卡文迪什利用扭秤实验测出的,故C 正确;由开普勒第三定律可知,所有绕同一中心天体运行的行星轨道半长轴的三次方与公转周期的二次方的比值都相等,即a 3T 2=k ,其中k 与中心天体有关,与行星无关,故D 错误。
2.(2021山东日照模拟)2020年7月23日,中国首次火星探测任务天问一号探测器发射成功,已知火星的质量约为地球质量的19,火星的半径约为地球半径的12。
下列关于火星探测器的说法正确的是(选项中的宇宙速度均指地球的)( ) A.发射速度只要大于第一宇宙速度即可 B.发射速度只有达到第三宇宙速度才可以C.发射速度应大于第二宇宙速度,小于第三宇宙速度D.火星探测器环绕火星运行的最大速度约为第一宇宙速度的13,可知选项A 、B 错误,选项C 正确;已知m 火=m地9,R 火=R地2,则v 火∶v 地=√Gm火R 火∶√Gm地R 地=√2∶3,选项D 错误。
普通物理学教程 力学 高等教育出版社 最新 第二版 漆安慎、杜婵英主编 课后答案 习题解答

−1 / 2
⑷∫
1
e
1+ ln x x
dx
aw .c om
π /2
第 1 章物理学力学数学 微积分初步习题解答
课后答案网
2
第 1 章物理学力学数学 微积分初步习题解答
解:
∫ sin xdx = − cos x |
0
π
0
2
=1
y
⑸ ∫ (e x + 1 ⑹ ∫ cos 2 xdx ⑺ ∫ 1+1x 2 dx ⑻ ∫ (3 x + sin 2 x)dx x ) dx
6.计算由y=3x和y=x2所围成的平面图形的面积。 解:如图所示,令 3x=x2,得两 y 条曲线交点的 x 坐标:x=0,3. 面积
A = ∫ 3 xdx − ∫ x 2 dx
0 0 3 2 2 1 3
3
3
2 e x 1 ⑷ ∫ 1+ ln x dx = ∫ (1 + ln x ) d (1 + ln x ) = 2 (1 + ln x ) |1 = 1.5 1 1 x 2 2 ⑸ ∫ (e x + 1 x ) dx = (e + ln x ) |1 = e − e + ln 2 1 2
1 0 1/ 2 2 2 解:⑴ ( x |1 − x |1 = ∫ x − 1)dx = ∫ x dx − ∫ dx = 2 3 1 1 1 1 1 2 2 2
3 2
− /2
∫ sin xdx = −1 π∫ sin xdx = 0 π
− /2
0
π /2
-π/2 -
+ 0 π/2
x
4 2 3
−5 3
普通物理学第二版第七章课后习题答案

第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s 估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转[解 答](1)22(30001200)1/601.57(rad /s )t 12ωπβ⨯-⨯===V V(2)222220()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立O-xy 坐标系,原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足21.2t t (:rad,t :s).θθ=+求(1)t=0时,(2)自t=0开始转45o 时,(3)转过90o时,A 点的速度和加速度在x 和y 轴上的投影.[解 答](1) A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==v(2)45θ=o时,由2A 1.2t t ,t 0.47(s)42.14(rad /s)v R πθωω=+==∴==⨯v v v得(3)当90θ=o时,由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速度10rad/s ω=逆时针转动,求臂与铅直45o 时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动,门中心G 的速度、加速度与B 或D点相同。
所以:7.1.6 收割机拔禾轮上面通常装4到6个压板.拔禾轮一边旋转,一边随收割机前进.压板转到下方才发挥作用,一方面把农作物压向切割器,另一方面把切割下来的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反. 已知收割机前进速率为1.2m/s ,拔禾轮直径1.5m ,转速22rev/min,求压板运动到最低点挤压作物的速度.[解 答]取地面为基本参考系,收割机为运动参考系。
普通物理学第二版答案

普通物理学第二版答案【篇一:普通物理学第二版第七章课后习题答案】.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解答]?自?2?24?3600?7.27?10(rad/s)-7-5?公?2?365?24?3600?2.04?10(rad/s)??r?自an???r2?27.1.2 汽车发动机的转速在12s内由1200rev/min增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转?[解答]r(1)?????t?2??(3000?1200)?1/60122?1.57(rad/s)2(2)?2??02?(??)(3000?1200)2?15.7?420(转)222?2639(rad)26392?所以转数=7.1.3 某发动机飞轮在时间间隔t内的角位移为??at?bt?ct34球t时刻的角速度和角加速度.[解答]??at?bt?ct34(?:rad,t:s).23????d?dtd?dt?a?3bt?4ct?6bt?12ct27.1.4 半径为0.1m的圆盘在铅直平面内转动,在圆盘平面内建立o-xy坐标系,原点在轴上.x和y轴沿水平和铅直向上的方向.边缘上一点a当t=0时恰好在x轴上,该点的角坐标满足求(1)t=0时,(2)自t=0开始转45时,(3)转过90时,a点的速度和加速度在x和y轴上的投影.[解答]????1.2t?t(?:rad,t:s).2???1.2t?t??1.2?2t??2?t?0,??1.2,?a?r??j?0.12?j(m/s).(1) ??x?0,?y?0.12(m/s)2ax?an???2yr??0.144(m/s)2ay?r??0.2(m/s)(2)??45?时,?4,得t?0.47(s)??1.2t?t?2由???2.14(rad/s)???va???r?0.15?j?0.15?i??? ij k? 0 0?rcos? rsin?0???aa?dtdtxddtr(??sin??i??cos??j)22?1cos???sin?)?i?(??sin???cos?)?j?r[(??2??0.183?j?0.465?i(m/s)?ax??0.465(m/s),ay??0.183(m/s)22(3)当?2?90?时,由??1.2t?t???va??x?2???r???i??0.278?i(m/s)y2,得t?0.7895(s),??2.78(rad/s)??0.278(m/s),??0(m/s)ax??r???0.2(m/s)7.1.5 钢制炉门由两个各长1.5m的平行臂ab和cd支承,以角速度??10rad/s逆时针转动,求臂与铅直45时门中心g的速度和加速度.[解答]因炉门在铅直面内作平动,门中心g的速度、加速度与b或d点相同。
普通物理学第二版第七章课后习题答案

普通物理学第⼆版第七章课后习题答案第七章刚体⼒学7.1.1 设地球绕⽇作圆周运动.求地球⾃转和公转的⾓速度为多少rad/s?估算地球⾚道上⼀点因地球⾃转具有的线速度和向⼼加速度.估算地⼼因公转⽽具有的线速度和向⼼加速度(⾃⼰搜集所需数据).[解答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.(1)假设转动是匀加速转动,求⾓加速度.(2)在此时间内,发动机转了多少转?[解答](1)22(30001200)1/601.57(rad /s )t 12ωπβ?-?===V V(2)222220()(30001200)302639(rad)2215.7πωωθβ--===?所以转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的⾓位移为球t 时刻的⾓速度和⾓加速度.[解答]7.1.4 半径为0.1m 的圆盘在铅直平⾯内转动,在圆盘平⾯内建⽴O-xy 坐标系,原点在轴上.x 和y 轴沿⽔平和铅直向上的⽅向.边缘上⼀点A 当t=0时恰好在x 轴上,该点的⾓坐标满⾜21.2t t (:rad,t :s).θθ=+求(1)t=0时,(2)⾃t=0开始转45o 时,(3)转过90o 时,A 点的速度和加速度在x 和y 轴上的投影. [解答](1) A ??t 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==v(2)45θ=o 时,由2A1.2t t,t0.47(s)42.14(rad/s)v Rπθωω=+==∴==?vvv得(3)当90θ=o时,由7.1.5 钢制炉门由两个各长1.5m的平⾏臂AB和CD⽀承,以⾓速度10rad/sω=逆时针转动,求臂与铅直45o时门中⼼G的速度和加速度.[解答]因炉门在铅直⾯内作平动,门中⼼G的速度、加速度与B或D点相同。
所以:7.1.6 收割机拔⽲轮上⾯通常装4到6个压板.拔⽲轮⼀边旋转,⼀边随收割机前进.压板转到下⽅才发挥作⽤,⼀⽅⾯把农作物压向切割器,另⼀⽅⾯把切割下来的作物铺放在收割台上,因此要求压板运动到下⽅时相对于作物的速度与收割机前进⽅向相反.已知收割机前进速率为1.2m/s,拔⽲轮直径1.5m,转速22rev/min,求压板运动到最低点挤压作物的速度.[解答]取地⾯为基本参考系,收割机为运动参考系。
普通物理学第二版课后习题答案(全)

第一章 物理学和力学1.1国际单位制中的基本单位是那些?解答,基本量:长度、质量、时间、电流、温度、物质的量、光强度。
基本单位:米(m )、千克(kg )、时间(s )、安培(A )、温度(k )、摩尔(mol )、坎德拉(cd )。
力学中的基本量:长度、质量、时间。
力学中的基本单位:米(m )、千克(kg )、时间(s )。
1.2中学所学习的匀变速直线运动公式为,at 21t v s 20+= 各量单位为时间:s (秒),长度:m (米),若改为以h (小时)和km (公里)作为时间和长度的单位,上述公式如何?若仅时间单位改为h ,如何?若仅0v 单位改为km/h ,又如何?解答,(1)由量纲1LTvdim -=,2LT a dim -=,h/km 6.3h/km 360010h 36001/km 10s /m 33=⨯==--2223232h /km 36006.3h /km 360010)h 36001/(km 10s /m ⨯=⨯==--改为以h (小时)和km (公里)作为时间和长度的单位时,,at 36006.321t v 6.3s 20⨯⨯+=(速度、加速度仍为SI单位下的量值)验证一下:1.0h 3600s t ,4.0m/s a ,s /m 0.2v 20====利用,at 21t v s 20+=计算得:)m (2592720025920000720036004236002s 2=+=⨯⨯+⨯=利用,at 36006.321t v 6.3s 20⨯⨯+=计算得 )km (2.25927259202.71436006.321126.3s 2=+=⨯⨯⨯⨯+⨯⨯=(2). 仅时间单位改为h由量纲1LTv dim -=,2LTadim -=得h /m 3600h/m 3600h 36001/m s /m ===222222h /m 3600h /m 3600)h 36001/(m s /m ===若仅时间单位改为h ,得:,at 360021t v 3600s 220⨯+=验证一下:1.0h 3600s t ,4.0m/s a ,s /m 0.2v 20==== 利用,at 21t v s 20+=计算得:)m (2592720025920000720036004236002s 2=+=⨯⨯+⨯=利用,at 360021t v 3600s 220⨯+=计算得: )m (2592720025920000720014360021123600s 22=+=⨯⨯⨯+⨯⨯= (3). 若仅0v 单位改为km/h由量纲1LTv dim -=,得s/m 6.31h /km ,h /km 6.3)h 36001/(km 10s /m 3===-仅0v 单位改为km/h ,因长度和时间的单位不变,将km/h 换成m/s得,at 21t v 6.31s 20+=验证一下:1.0h 3600s t ,4.0m/s a ,s /m 0.2v 20====利用,at 21t v s 20+=计算得:)m (2592720025920000720036004236002s 2=+=⨯⨯+⨯=利用,at 21t v 6.31s 20+=计算得: )m (25927200259200007200360042136003600/11026.31s 23=+=⨯⨯+⨯⨯⨯=-1.3设汽车行驶时所受阻力f 与汽车的横截面积S 成正比,且与速率v 之平方成正比。
普通物理学第二版习题答案

普通物理学第二版习题答案普通物理学第二版习题答案普通物理学是一门研究物质运动规律的学科,它不仅是理工科学生的必修课,也是培养学生科学思维和解决问题能力的重要课程之一。
在学习普通物理学的过程中,习题是非常重要的一环,通过解习题可以帮助学生巩固知识、加深理解,并培养学生的分析和解决问题的能力。
本文将为大家提供《普通物理学第二版》习题的答案,帮助读者更好地掌握物理学知识。
第一章:运动的描述1. 一辆汽车以10 m/s的速度匀速行驶,经过5秒后,汽车的位移是多少?答案:位移等于速度乘以时间,即位移=速度×时间=10 m/s × 5 s = 50 m。
2. 一个物体以4 m/s的速度向东运动,经过2秒后,它的速度变为8 m/s,方向保持不变。
求物体的加速度。
答案:加速度等于速度的变化量除以时间,即加速度=(8 m/s - 4 m/s)/ 2 s = 2 m/s²。
第二章:牛顿定律和运动学1. 一个质量为2 kg的物体受到一个5 N的力,求物体的加速度。
答案:根据牛顿第二定律,加速度等于力除以质量,即加速度=5 N / 2 kg = 2.5 m/s²。
2. 一个质量为0.5 kg的物体受到一个10 N的力,求物体的加速度。
答案:加速度等于力除以质量,即加速度=10 N / 0.5 kg = 20 m/s²。
第三章:力和运动1. 一个物体受到一个10 N的向上的力和一个5 N的向下的力,求物体的净力和加速度。
答案:净力等于所有力的矢量和,即净力=10 N - 5 N = 5 N。
加速度等于净力除以质量,即加速度=5 N / 质量。
2. 一个物体受到一个20 N的向右的力和一个10 N的向左的力,求物体的净力和加速度。
答案:净力等于所有力的矢量和,即净力=20 N - 10 N = 10 N。
加速度等于净力除以质量,即加速度=10 N / 质量。
第四章:工作和能量1. 一个物体的质量为2 kg,高度为10 m,求物体的重力势能。
普通物理学第二版第七章课后习题答案

普通物理学第二版第七章课后习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转?[解 答](1)22(30001200)1/601.57(rad /s )t12ωπβ⨯-⨯===(2)22222()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立O-xy 坐标系,原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足21.2t t (:rad,t :s).θθ=+求(1)t=0时,(2)自t=0开始转45时,(3)转过90时,A 点的速度和加速度在x 和y 轴上的投影.[解 答](1) A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==(2)45θ=时,由2A 1.2t t ,t 0.47(s)42.14(rad /s)v Rπθωω=+==∴==⨯得(3)当90θ=时,由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速度10rad/s ω=逆时针转动,求臂与铅直45时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动,门中心G 的速度、加速度与B 或D 点相同。
大学物理第二版课后习题答案第七章

习题精解7-1一条无限长直导线在一处弯折成半径为R 的圆弧,如图所示,若已知导线中电流强度为I,试利用比奥—萨伐尔定律求:(1)当圆弧为半圆周时,圆心O 处的磁感应强度;(2)当圆弧为1/4圆周时,圆心O 处的磁感应强度。
解(1)如图所示,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于直线电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据比奥—萨伐尔定律,半圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB Rμπ=方向垂直纸面向内。
半圆弧在O 点产生的磁感应强度为 000220444RIIdl I B R R R Rπμμμπππ===⎰方向垂直纸面向里。
(2)如图(b )所示,同理,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据毕奥—萨伐尔定理,1/4圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB R μπ=方向垂直纸面向内,1/4圆弧电流在O 点产生的磁感应强度为00022204428RIIdl I R B R R Rπμμμπππ===⎰方向垂直纸面向里。
如图所示,有一被折成直角的无限长直导线有20A 电流,P 点在折线的延长线上,设a 为,试求P 点磁感应强度。
解 P 点的磁感应强度可看作由两段载流直导线AB 和BC 所产生的磁场叠加而成。
AB 段在P 点所产生的磁感应强度为零,BC 段在P 点所产生的磁感应强度为 0120(cos cos )4IB r μθθπ=- 式中120,,2r a πθθπ=== 。
所以500(cos cos ) 4.010()42I B T a μπππ=-=⨯ 方向垂直纸面向里。
大学物理习题解答第七章课后习题参考答案

习 题 七7-1 如图所示,O S O S 21=.若在O S 1中放入一折射率为n ,厚度为e 的透明介质片,求O S 1与O S 2之间的光程差.如果1S 和2S 是两个波长为λ的同相位的相干光源,求两光在O 点的相位差.[解] O S1与O S 2的几何路程相等光程差为 ()e n 1-=δ 位相差为 ()e n 122-==∆λπδλπϕ7-2 一束绿光照射到两相距 0.6mm 的双缝上,在距双缝2.5m 处的屏上出现干涉条纹.测得两相邻明条纹中心间的距离为2.27mm ,试求入射光的波长.[解] 由杨氏双缝干涉知 dD x λ=∆ 所以 5448m 10448.55.21060.01027.2733=⨯=⨯⨯⨯=∆=---D xd λÅ7-3 如图所示,在双缝干涉实验中,21SS SS =,用波长为λ的单色光照S ,通过空气后在屏幕E 上形成干涉条纹.已知点P 处为第3级干涉明条纹,求1S 和2S 到点P 的光程差.若整个装置放于某种透明液体中,点P 为第4级干涉明条纹,求该液体的折射率.[解] 1S 和2S 到P 点的光程差满足λλδ312==-=k r r整个装置放置于液体中,1S 和2S 到P 点的光程差满足()λδ412=-=r r nλλ43=n所以得到 33.134==n7-4 如习题7-1图所示,1S 和2S 是两个同相位的相干光源,它们发出波长λ=5000Å的光波,设O 是它们中垂线上的一点,在点1S 与点O 之间插入一折射率n =1.50的薄玻璃,点O 恰为第4级明条纹的中心,求它的厚度e .[解] 在O 点是第4级明条纹的中心光程差 λδ4=-=e ne所以 410414⨯=-=n e λÅ7-5 初位相相同的两相干光源产生的波长为6000Å的光波在空间某点P 相遇产生干涉,其几何路径之差为6102.1-⨯m .如果光线通过的介质分别为空气(11=n )、水(=2n 1.33)或松节油(=3n 1.50)时,点P 的干涉是加强还是减弱.[解] 光在折射率为n 的介质中P 点处光程差为()12r r n -=δ介质为空气时,11=n ,则()λδ2m 102.16121211=⨯=-=-=-r r r r n光程差为半波长的偶数倍,所以P 点处干涉加强. 介质为水时,=2n 1.33,则()m 106.1102.133.1661222--⨯=⨯⨯=-=r r n δ光程差介于两种情况之间,且结果与半波长的奇数倍更接近,所以P 点光强介于明暗条纹中心光强之间,且与暗条纹中心光强更接近.介质为松节油时,=3n 1.50,则()λδ3m 108.1102.15.1661233=⨯=⨯⨯=-=--r r n光程差为半波长的偶数倍,所以P 点处干涉加强.7-6 在双缝干涉实验中,用很薄的云母片(58.1=n )覆盖在双缝的一条上,如图所示.这时屏上零级明纹移到原来第7级明纹位置上.如果入射光波5000Å,试求云母片的厚度(设光线垂直射入云母片).[解] 原来的第7级明纹的位置满足λ721=-r r加上云母片后,光程差满足[]()012121=---=+--e n r r ne e r r所以41003.6158.15000717⨯=-⨯=-=n e λ Å7-7 用单色光源S 照射平行双缝1S 和2S 形成两相干光源.在屏上产生干涉图样,零级明条纹位于点O ,如图所示.若将缝光源S 移到S '位置,问零级明条纹向什么方向移动?若使零级明条纹移回点O ,必须在哪个缝的右边插入一薄云母片才有可能? 若以波长为5890Å的单色光,欲使移动了4个明纹间距的零级明纹移回到点O ,云母片的厚度应为多少? 云母片的折射率为1.58.[解] 零级明纹是光程差为0的位置.移动光源后光线2的光程长了,为仍保持光程差为0,必须让1的光程增加以弥补2的增加,只有在下方1才比2长,所以向下.要回到原点,即通过加片的方法使得1的光程增大,所以在1S 后加.在原点时,两光线的光程差满足()λδ41=-=e n得到 m 1006.4158.1105890414610--⨯=-⨯⨯=-=n e λ7-8 用白光作光源观察杨氏双缝干涉,设缝间距为d ,双缝与屏的距离为D ,试求能观察到的无重叠的可见光(波长范围: 4000~7600Å)光谱的级次.[解] k 级明纹的位置为dD k x λ=k 要使光谱无重叠,必须满足 ()()λm i n 1k λm a x k +≤x x 因此 ()min max 1λλ+≤k k 即 ()140007600+≤k k解得 1.1 ≤k 所以只能看到一级无重叠光谱.7-9 白色平行光垂直照射到间距为m m 0.25=d 的双缝上,在距缝cm 50处放一屏幕,若把白光(4000~7600Å)两极端波长的同级明纹间的距离叫做彩色带的宽度,试求第1级和第5级彩色带的宽度.[解] 每一级的宽度()min max min max λλ-=-=∆dDkx x x 1=k 时,()mm 72.0m 102.710400076001025.010*******21=⨯=⨯-⨯⨯⨯⨯=∆----x 5=k 时,()mm 6.3m 106.310400076001025.010505310325=⨯=⨯-⨯⨯⨯⨯=∆----x7-l0 波长为λ的单色光垂直照射在如图所示的透明薄膜上,薄膜厚度为e .两反射光的光程差是多少?[解]薄膜上下表面的反射光均有半波损失,故没有因半波损失而产生的光程差,因此上下表面反射的光程差为e e n 60.222==δ7-11 白光垂直照射在空气中厚度为71080.3-⨯m 的肥皂膜上,肥皂膜的折射率为1.33,在可见光范围内(4000~7600Å) 哪些波长的光在反射中增强.[解] 光程差 λλδk ne =+=22 所以124-=k neλ 当1=k 时,2021612108.333.1471=-⨯⨯⨯=-λÅ 当2=k 时,同理可得67392=λÅ 当3=k 时,同理可得40433=λÅ所以在可见光范围内波长为4043 Å和6739 Å的光在反射中增强.7-12 在观察肥皂膜的反射光时,表面呈绿色(λ=5000 Å),薄膜表面法线和视线间的夹角为450,试计算薄膜的最小厚度. [解] 两反射光的光程差为λλδk i n n e =+-=2sin 2221221=k 时对应薄膜厚度最小为m 1011.145sin 33.14105000sin 470221022122--⨯=-⨯⨯=-=in n e λ7-13 用波长连续可调的平行光垂直照射覆盖在玻璃板上的油膜,观察到5000 Å和7000 Å这两个波长的光在反射中消失.油的折射率为1.30,玻璃的折射率为1.50.求油膜的厚度.[解] 某一波长的光在反射中消失,表明光在油膜上下表面反射的光干涉相消,故光程差为 ()21222λδ+==k e n对1λ: ()2122112λ+=k e n对2λ: ()2122222λ+=k e n又因1λ与2λ之间没有其他波长的光消失,故1λ与2λ的干涉级数只可能相差一级 故112-=k k 因此575000700012121211===-+λλk k解得 31=k 22=k以31=k 代入得,()m 1073.630.141050007412710211--⨯=⨯⨯⨯=+=n k e λ7-14 波长为5500 Å的黄绿光对人眼和照像底片最敏感,要增大照像机镜头对此光的透射率,可在镜头上镀一层氟化镁 (2MgF )薄膜. 已知氟化镁的折射率为1.38,玻璃的折射率为 1.50,求氟化镁的最小厚度.[解] 要增大波长为λ的光的透射率,则须使反射光干涉减弱.那么,光程差应满足()21222λδ+==k e n当0=k 时,e 最小,为m 1096.938.1410550048102min--⨯=⨯⨯==n e λ7-15 如图所示,用波长为λ的单色光垂直照射折射率为2n 的劈尖.图中各部分折射率的关系是1n <2n <3n ,观察反射光的干涉条纹,从劈尖顶端开始向右数第5条暗纹中心所对应的厚度是多少?[解] 因1n <2n <3n ,故在劈尖上下表面的两反射光无因半波损失引起的附加光程差,干涉暗纹应满足()21222λδ+==k e n因棱边为明纹,故从棱边开始向右数第5条暗纹对应上式中4=k所以()()2225494142412n n n k e λλλ=+⨯=+=7-16 用波长为1λ的单色光垂直照射空气劈尖,从反射光的干涉条纹中观察到劈尖装置的点A 处是暗条纹.若连续改变入射光的波长,直到波长为2λ(2λ>1λ)时,点A 将再变成暗条纹.求点 A 处空气层的厚度. [解] 空气劈尖上暗条纹处满足()21222λλδ+=+=k ne因1=n ,所以()21222λλ+=+k e ,即λk e =2 在A 处 11A 2λk e =,22A 2λk e =同一点,e 相同,又2λ>1λ,故2k <1k ,又因1λ到2λ连续可调,中间无其他波长的光干涉形成暗条纹,故112-=k k因此 122111A 212λλλλλ-==k e7-17 用波长为λ的单色光垂直照射到空气劈尖上,从反射光中观察干涉条纹,距顶点为L 处是暗条纹.使劈尖角θ连续慢慢变大,直到该点再次出现暗条纹为止,劈尖角的改变量θ∆是多少?[解] 空气劈尖干涉暗纹,光程差为 ()21222k λλδ+=+=k e劈尖角为θ时,L 处有 ()212221k 1λλ+=+k e 劈尖角为θθ∆+时,有 ()212222k 2λλ+=+k e因为劈尖角连续改变,即e 连续增大,故2k =1k +1 由上述公式得 ()λ=-12k k 2e e又 θθL L e ==sin 1k ,()()θθθθ∆+=∆+=L L e sin 2k 因此 L2λθ=∆7-18 两块长度为l0cm 的平玻璃片,一端相互接触,另一端用厚度为0.004mm 的纸片隔开形成空气劈尖.以波长为5000Å 的平行光垂直照射,观察反射光的等厚干涉条纹.在全部10cm 长度内呈现多少条明纹?[解] 设平玻璃片长为L ,纸片厚为H ,则形成的空气劈尖角为LH ==θθsin 两相邻明纹间距为 HLl 22sin 2λθλθλ===故总条数为 1610500010004.022103=⨯⨯⨯===--λH l L N7-19 为测量硅片上氧化膜的厚度,常用化学方法将薄膜的一部分腐蚀掉,使之成为劈形(又称为台阶),如图所示.用单色光垂直照射到台阶上,就出现明暗相间的干涉条纹,数出干涉条纹的数目,就可确定氧化硅薄膜的厚度.若用钠光照射,其波长λ=5893Å,在台阶上共看到5条明条纹,求膜的厚度(氧化硅的折射率2n =1.5,硅的折射率为3n =3.42).[解] 因1n <2n < 3n ,故台阶上下表面反射光的光程差为e n 22=δ明条纹满足的条件为 λk e n =22台阶棱边为明纹,因共看到5条明纹,所以4max =k ,由明纹条件得m 1078575.1105893222101022max max--⨯=⨯⨯===n n k e λλ7-20 检查平板的平整度时,在显微镜下观察到的等厚条纹如图所示,条纹的最大畸变量为1.5条纹间距,所用光波波长为546nm ,试描述待测平面的缺陷.[解] 因每一条干涉条纹上对应的空气厚度相同,故在同一条纹上,畸变部分和平行棱边的直线部分所对应的膜厚度相等,本来离棱边越远膜的厚度越大,而现在同一条纹上,远离棱边的畸变部分厚度并不大,这说明畸变部分是凸起的,因最大畸变是为1.5条纹间距,说明最大畸变处膜厚度比非畸变时膜厚度之差e ∆对应的级数差5.1=∆k由劈尖明纹公式 λλk e =+22得 λk e ∆=∆2所以 m 101.421046.55.1277--⨯=⨯⨯=∆=∆λk e7-21 如图所示,A 、B 是两只块规(块规是两端面经过磨平抛光达到相互平行的钢质长方体).A 的长度是标准的,B 是相同规格待校准的.A 、B 放在平台上,用一块样板平玻璃压住.(1)设垂直入射光的波长为λ=5893Å,A 、B 相隔cm 5=d ,T 与A 、 B 间的干涉条纹的间距都是0.55 mm ,试求两块规的长度差.(2)如何判断A 、B 哪一块比较长些?(3)如果T 与A 、B 间的干涉条纹间距分别为0.55 mm 和 0.3 mm ,则说明什么问题?[解] (1) 劈尖干涉,相邻条纹间距l 满足l2sin λα=所以A 、B 两只块规的高度差为m 1068.21055.0210893.51052sin 5372----⨯=⨯⨯⨯⨯⨯===∆l d d h λα (2)因空气劈尖棱边处为暗纹,所以若压平板T ,a 、c 处暗纹位置不变,则B 比A 长,若压T ,b 、d 处暗纹位置不变,则A 比B 长.(3) 设平板T 与A 、B 间形成的劈尖角分别为1α、2α.干涉条纹间距分别为1l 和2l ,则 2sin sin 2211λαα==l l已知1l >2l ,则1α<2α,B 的端面与底面不平行,且d 处向下倾斜.7-22 如图所示的观察牛顿环的装置中,设平球面透镜中心恰好和平玻璃接触,透镜球面的半径cm 400=R ,用某单色光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是cm 30.0(1)求入射光的波长;(2)设图中OA =1.00cm ,求在半径为OA 的范围内可观察到的明环数.[解] (1)牛顿环明环半径公式为()2122k λR k r -=,所以()Rk r 1222k -=λ因中心为暗环,对应第5个明环5=k ,所以()5000104009103.0215222422k =⨯⨯⨯⨯=-⨯=--R r λÅ(2)因为()2122k λR k r -=,所以()5.5010541000.121217222k =⨯⨯⨯+=+≤--λR r k 所以能看到的明环数50个.7-23 用曲率半径为3.00m 的平凸透镜和平板玻璃作牛顿环实验,测得第k 级暗环半径为m m 24.4,第10+k 级暗环的半径为m m 0.6.求所用单色光的波长.[解] 牛顿环暗环半径公式为λkR r =k 故 ()λR k r 1010k +=+因此 ()()323232k 210k 1001.600.3101024.410610⨯=⨯⨯-⨯=-=--+R r r λÅ7-24 用牛顿环实验测单色光的波长.用已知波长为1λ的单色光垂直照射牛顿环装置时,测得第1和第9级暗环的半径之差为1l ;用未知单色光照射时测得第l 和第9级暗环的半径之差为2l .求单色光的波长2λ.[解] 牛顿环暗环半径公式为 λkR r =k对1λ 11λR r = 199λR r = 所以()19119-=-λR r r又 119l r r =-, 故211⨯=λR l 同理得 222⨯=λR l因此 121222λλl l =7-25 一平凸透镜放在平板玻璃上,在反射光中观察牛顿环.当1λ=4500Å时,测得第3级明环的半径为31006.1-⨯m .换用红光,观测到第5级明环的半径为31077.1-⨯m .求透镜曲率半径和红光的波长.[解] 牛顿环明环半径公式为()2122k λR k r -=,对1λ,3=k 时, 25123λR r =对2λ,5=k 时, 29225λR r =由此得 697145001006.191077.15956262123252=⨯⨯⨯⨯⨯==--λλr r Å由25123λR r =得, m 00.110450051006.12521062123=⨯⨯⨯⨯==--λr R7-26 用牛顿环干涉条纹测定凹球面的曲率半径.将已知曲率半径的平凸透镜放在待测的凹球面上,如图所示.在两曲面之间形成空气层,可以观测到环状干涉条纹.测得第4级暗环的半径4r =2.250cm ,已知入射光的波长λ=5893 Å,平凸透镜的曲率半径1R =102.3cm ,求凹球面的曲率半径2R .[解] 牛顿环k 级暗环条件为 ()21222λλ+=+k e 即 λk e =2由几何关系知 ()2111211212k 2e e R e R R r +=--=因为 11R e << ,故 112k 2e R r = 同理 222k 2e R r = 又 21e e e -= 联立上式得2k 1211r k R R λ-= 以 m 023.11=R ,4=k ,m 10589310-⨯=λ,m 10250.224-⨯=r ,代入得cm 8.1022=R7-27 在观察牛顿环干涉条纹的实验中,用图(a )、(b )、(c )所示的装置代替平凸透镜和平玻璃组合.试画出反射光中的干涉条纹(只画暗条纹).[解](a ) (b ) (c )7-28 用波长为λ的单色光源做迈克尔逊干涉仪实验,在移动反光镜2M 的过程中,视场中的干涉条纹移过k 条,求反射镜移动的距离?[解] 设反射镜移过的距离为d ,则光程差改变量为 λδk d ==∆2所以 2λk d =7-29 迈克尔逊干涉仪的一臂中放有长为100.0mm 的玻璃管,其中充有一个大气压空气,用波长为5850Å的光作光源.在把玻璃管抽成真空的过程中,发现视场中有100.0条干涉条纹从某固定点移过.求空气的折射率.[解] 设空气的折射率为n ,在由空气抽成真空的过程中,光程差改变量为()λk e n ∆=-12所以 00029.1100.10021058500.100121310=⨯⨯⨯⨯+=∆+=--e k n λ7-30 在把迈克尔逊干涉仪的可动反射镜移动0.233mm 过程中,数得条纹移动数为792,求所用光的波长.[解] 设反射镜移动距离为d ,则光程差改变 λδk d ∆==∆25884m 10884.579210233.022103=⨯=⨯⨯=∆=--k d λÅ7-31 常用雅敏干涉仪来测定气体在各种温度和压力下的折射率.干涉仪的光路如图所示.S 为光源,L 为正透镜,1G 、2G 为等厚且相互平行的玻璃板.1T 、2T 为等长的两个玻璃管,长度为l .进行测量时,先将1T 、2T 抽空,然后把待测气体徐徐导入一管中,在E123451234512345处观察干涉条纹移动数,即可求得待测气体的折射率.设在测量某气体的折射率时,将气体慢慢放入2T 管中,从开始进气到标准状态时,在E 处共看到有98条干涉条纹移过去.所用的钠光波长λ=5893Å (真空中),l =20cm .求该气体在标准状态下的折射率.[解] 设待测气体在标准状态下的折射率为n ,则在气体导入前后,两条光路中的光程差改变为()λk l n ∆=-1所以00029.110201058939811210=⨯⨯⨯+=∆+=--l k n λ7-32 一单缝宽度4101-⨯=a m ,透镜的焦距m 5.0=f ,若分别用40001=λÅ和76002=λÅ的单色平行光垂直入射,它们的中央明条纹的宽度各是多少?[解] 一级暗纹公式为 λϕ=1sin a 而aλϕϕ==11sin所以 a f f f x λϕϕ===111tan 所以中央明纹的宽度为 af x x λ221==∆对1λ: m 1041011045.02234711---⨯=⨯⨯⨯⨯==∆a f x λ 对2λ: m 106.7101106.75.02234722---⨯=⨯⨯⨯⨯==∆a f x λ7-33 有一单缝宽m m 10.0=a ,在缝后放一焦距cm 50=f 的会聚透镜,用波长λ=5460 Å的平行绿光垂直照射单缝,求位于透镜焦平面处的屏上的中央亮条纹的宽度.如果把此装置浸入水中,并把屏移动到透镜在水中的焦平面上,中央亮条纹的宽度变为多少?设透镜的折射率54.1='n ,水的折射率33.1=n .(提示:透镜在水中的焦距()f nn n n f -'-'=1水) [解] (1) 中央明条纹的宽度为m 1046.51010.01046.51050223372----⨯=⨯⨯⨯⨯⨯==∆a f x λ (2) 在水中,透镜焦距为()f nn n n f -'-'=1水 所以中央明条纹的宽度为()()()()m 1040.1101.033.154.11046.550.0154.12122237---⨯=⨯⨯-⨯⨯⨯-⨯=-'-'==∆a n n f n naf x λλ水7-34 用波长λ=7000Å的平行光垂直照射单缝,缝后放一焦距为70cm 的正透镜,在透镜焦平面处的屏上测得中央亮条纹的宽度为3100.2-⨯m .试计算: (1)单缝的宽度.(2)当用另一单色光照射时,测得中央亮纹的宽度为3105.1-⨯m ,求此光的波长. [解]中央亮条纹宽度为 af x λ2=∆ (1)由上式可得单缝的宽度为 m 109.41021071070224372----⨯=⨯⨯⨯⨯⨯=∆=x f a λ (2)由前式可得光的波长为5250m 1025.510072105.1109.427234=⨯=⨯⨯⨯⨯⨯='∆='----f x a λÅ7-35 用平行光管把某光源发出的单色光变成平行光后垂直照射在宽度为0.308mm 的单缝上.用焦距为12.62cm 的测微目镜测得中央明条纹两侧第5级暗条纹之间的距离为x ∆=2.414mm .求入射光的波长.[解] 单缝衍射暗纹中心到中央亮纹中心距离为 af kx λ= 5=k 时,af x λ55= 两侧第5级暗纹之间的距离为 af x x λ1025==∆ 所以 58921062.121010414.210308.010233=⨯⨯⨯⨯⨯=∆=---f x a λÅ7-36 用波长λ=6328Å的氦-氖激光垂直照射单缝,其夫琅禾费衍射图样的第1级极小的衍射角为50.试求单缝的宽度.[解] 单缝衍射暗纹条件为λϕk a =sin 当 1=k 时,λϕ=sin a所以 ϕλϕλ==sin a 式中 g r a d1805πϕ= 所以 m 1026.7518010328.667--⨯=⨯⨯=πa7-37 在正常照度下,人眼瞳孔的直径约为mm 2,人眼最敏感的波长为5500Å.眼前m m 250 (明视距离)处的点物在视网膜上形成艾里斑的角半径是多少? 明视距离处能够被分辨的两物点的最小距离是多少?(前房液和玻璃状液的折射率33.1=n )[解] (1) 因人眼中玻璃状液体的折射率为n ,所以波长变为nλλ='在视网膜上形成爱里斑的角半径为rad 1052.210233.1105.522.122.122.1437---⨯=⨯⨯⨯⨯=='=nD D λλθ (2) 人眼的最小分辨角 Dλθ22.1min =设在距离L 处能分辨的最小距离为d (l d θ=),则m 104.810250102105.522.122.15337----⨯=⨯⨯⨯⨯⨯==D L d λ7-38 已知天空中两颗星对一望远镜的角距离为61084.4-⨯rad ,设它们发出光的波长为5500Å.望远镜的口径至少要多大才能分辨出这两颗星.[解] 设望远镜孔径为D ,当两星对望远镜的角距离大于其最小分辨角时方可分辨,即Dλ22.11084.46≥⨯-所以 cm 9.131084.4105.522.11084.422.1676=⨯⨯⨯=⨯≥---λD7-39 月球距地面约3.86510⨯km ,设月光按λ=5500Å计算,问月球表面上距离多远的两点才能被直径为5.00m 的天文望远镜所分辨.[解] 设月球上两物点距离为d ,其对望远镜张角大于最小分辨角时,则能分辨该两点即DL d λ22.1≥ 所以 m 8.5100.51086.3105.522.122.187=⨯⨯⨯⨯=≥-D L d λ7-40 用波长为λ=5893Å的钠光垂直照射光栅,测得第2级谱线的衍射角11102'︒=θ,而用待测波长的单色光照射时,测得第一级谱线的衍射角2441'︒=θ.试求光栅常数和待测光的波长.[解] 光栅方程为 ()λϕk b a =+sin 对1λ有 ()11sin λθ=+b a 对2λ有 ()222sin λθ=+b a由上两式得 546410893.51110sin 244sin 2sin sin 27002211=⨯⨯''⨯==-λθθλÅ 将1λ的数值代入得 m 1067.66-⨯=+b a7-4l 一块每毫米刻痕为500条的光栅,用钠黄光正入射,钠黄光中含有两条谱线,其波长分别为5896Å和5890Å.求在第2级光谱中这两条谱线分开的角度.[解] 光栅常数为 m 10250010163--⨯=⨯=+b a 由光栅方程可得 ()122s i nλϕ=+b a ()222sin λϕ='+b a 因此得到 ⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+='-=∆b a b a 21222arcsin 2arcsin λλϕϕϕ6767043.010210890.52arcsin 10210896.52arcsin =⎪⎪⎭⎫⎝⎛⨯⨯⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯⨯=----7-42 一单色平行光投射于衍射光栅,其入射方向与光栅法线夹角为θ,在和法线成︒11和︒53的方向上出现第1级光谱线,并且位于法线的两侧.求θ角的大小.为什么在法线的一侧能观察到第2级谱线,而另一侧却没有?[解](1) 斜入射时,零级主极大在透镜的与入射光线平行的副光轴方向上.530角的衍射光线和入射光线分别在法线两侧,此衍射角应取负值,而110衍射角应取正值,所以两个第一级光谱线对应的方程分别为 ()()λθ-=-+053sin sin b a (1)()()λθ+=++011sin sin b a (2) 因此求得 3039.0sin =θ 07.17=θ(2) 设法线两侧衍射角为900时对应极大的级数分别为k 和k '在与入射光线异侧有 ()()λk b a -=-+0090sin 7.17sin (3) 在与入射光线同侧有 ()()λk b a '=++0090sin 7.17sin (4)由 (1)、(3)式相除,得 4.17.17sin 53sin 7.17sin 90sin 0000≈--=k 由 (2)、(4)式相除,得 64.27.17sin 11sin 7.17sin 90sin 0000≈++='k 由上面结果知,只有与入射光线同侧可观察到第二级谱线.7-43 一衍射光栅,每厘米有200条透光缝,每条透光缝宽为3102-⨯=a cm ,在光栅后放一焦距为m 0.1=f 的凸透镜.现以λ=6000Å单色平行光垂直照射光栅,试求: (1)透光缝的单缝衍射中央明条纹宽度;(2)在该宽度内有哪几个光栅衍射主极大?[解] (1)单缝衍射第一极小满足 λϕ=s i na (1) 中央明纹宽度为m 1061021060.122sin 2tan 2257---⨯=⨯⨯⨯⨯====∆a f f f x λϕϕ (2) 设该范围内主极大最大级数为k ,则()λϕk b a =+sin (2)由 (1)、(2)式有 5.210220010152=⨯⨯⨯=+=--a b a k 所以在此范围内能看到的主极大级数为210±±=,,k ,共5个光栅衍射主极大.7-44 试指出光栅常数()b a +为下述三种情况时,哪些级数的光谱线缺级?(1)光栅常数为狭缝宽度的两倍,即()a b a 2=+; (2)光栅常数为狭缝宽度的三倍,即()a b a 3=+;(3)光栅常数为狭缝宽度的2.5倍,即()a b a 5.2=+.[解] k 级缺级的条件为k aba k '+=() 3,2,1±±±='k (1)()a b a 2=+时,k k '=2,凡2的倍数级都缺级. (2) ()a b a 3=+时,k k '=3,凡3的倍数级都缺级. (3)()a b a 5.2=+时,k k '=5.2,凡5的倍数级都缺级.7-45 波长λ=6000Å的单色光垂直入射到一光栅上,测得第2级主极大的衍射角为︒30,且第3级缺级.(1)光栅常数()b a +是多大?(2)透光缝可能的最小宽度是多少?(3)在屏幕上可能出现的主极大的级次是哪些?[解](1) 由光栅方程得 ()λ230sin 0=+b a所以 m 104.21064430sin 2670--⨯=⨯⨯===+λλb a (2) 当k 级缺级时,满足 k a ba k '+=所以 k kba a '+=当1='k 时,缝宽a 最小,为 m 1083104.276--⨯=⨯=+=k b a a (3) 在屏幕上呈现的主极大的级数由最大级数和缺级情况决定. 因为 ()λφk b a =+sinmax k <4106104.276=⨯⨯=+--λba 因此 m a x k =3又因3=k 缺级,所以在屏上可能出现的级数为 2,1,0±±=k7-46 每厘米刻有400条刻痕的光栅,其透光缝5101-⨯=a m ,用波长为λ=7000Å的光垂直照射在屏幕上可观察到多少条明条纹?[解] 光栅常数 m 105.240010152--⨯=⨯=+b a 因为 ()λϕk b a =+sinmax k <7.35107105.275=⨯⨯=+--λba 因此35max =k 缺级条件 k k k ab a k '='⨯⨯='+=--5.2101105.255所以 凡能被5整除的级数都缺级,共缺级个数为7535=='N 因此,光栅衍射在屏上呈现明条纹总数为 ()5717352=+-⨯=N7-47 以白光(波长范围4000~7600Å)垂直照射光栅,在衍射光谱中,第2级和第3级发生重叠.求第2级被重叠的范围.[解] 最小波长和最大波长分别为4000min =λ Å 7600max =λ Å第3级光谱中,min λ主极大的位置与第2级某一波长λ的主极大位置相同时,开始重叠,由光栅方程可求此波长 ()λϕ2s i n =+b a ()m i n 3s i n λϕ=+b a因此 600040002323min =⨯==λλÅ 故,第2级光谱中被重叠的光谱波长范围为 6000=λÅ~7600 Å7-48 用两米光栅摄谱仪拍摄氢原子光谱,在可见光范围内有四条谱线,如图所示.光栅上每厘米有4000条缝,光栅后的正透镜的焦距为2.00m ,在其焦平面上放一照相底片,求四条谱线在底片上的间距.[解] 光栅常数为 m 105.2400010162--⨯=⨯=+b a ∞对第一条谱线(1=k ),应用光栅方程,为()λϕ=+sin b a 对αH , m 10563.671-⨯=λ,在底片上位置为m 543.0arcsin tan tan 1=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+==b a f f x λϕ 同理可得δγβH H H ,,三条谱线在照像底片上的位置分别为m 396.02=x m 353.03=x m 333.04=x因此 αH 与βH 之间的间距为 7m 14.01=∆x同理可得βH 与γH 之间的间距为 m043.02=∆x γH 与δH 之间的间距为 m 02.03=∆x7-49 用白光照射每毫米50条刻痕的光栅,在距光栅2m 的屏幕上观察到各色光谱,设可见光的上限波长(红光)r λ=7800 Å,下限波长(紫光) v λ=4000 Å,试计算屏幕上第1级光谱的宽度.[解] 第一级谱线满足 ()λϕ=+s i nb a 屏幕上红光谱线的位置为 ba f f x +≈≈r1λϕ 紫光谱线的位置为 ba f f x +≈'≈v2λϕ所以第一级光谱的宽度为()()m 108.310400078001015022103v r 21---⨯=⨯-⨯⨯=-+=-=∆λλb a fx x x7-50 一光源发射红双线在波长λ=6563 Å处,两条谱的波长差λ∆=1.8 Å.有一光栅可以在第1级中把这两条谱线分辨出来,求光栅的最少刻线总数.[解] 光栅的分辨率为 kN R =∆=λλ所以 1.364618.16563=⨯=∆=k N λλ 即光栅最少刻线总数为3647条.7-51 一光栅宽为6cm ,每厘米有6000条刻线,在第三级光谱中,对λ=5000 Å处,可分辨的最小波长间隔是多大?[解] 光栅的总缝数为 3600066000=⨯=N因为光栅的分辨本领为kN =∆λλ046.03600035000=⨯==∆kNλλÅ7-52 一束波长为2.96 Å的X 射线投射到晶体上,所产生的第1级衍射线偏离原入射线方向731'︒,求对应此射线的相邻两原子平面之间的距离.[解] 设掠射角为ϕ,衍射线偏离入射线的角度为θ,则2θϕ=由布拉格方程 λϕk d =sin 2 得相邻两原子平面间距为()52.52731sin296.212sin 2sin 20='⨯⨯===θλϕλk k d Å7-53 以波长为1.10Å的X 射线照射岩盐晶面,测得反射光第1级极大出现在X 射线与晶面的夹角为'3011︒处.问:(1)岩盐晶体的晶格常数d 为多大?(2)当以另一束待测的X 射线照岩盐晶面时,测得反射光第一级极大出现在X 射线与晶面的夹角为'3017︒处,求待测X 射线的波长.[解] (1) 由布拉格方程 λϕk d =sin 2 ,所以 76.25.11sin 210.1sin 20===ϕλk d Å (2) 由布拉格方程得待测X 射线的波长为66.115.17sin 76.22sin 20=⨯⨯==k d ϕλÅ7-54 一束部分偏振光垂直入射于一偏振片上,以入射光为轴旋转偏振片,测得透射光强的最大值是最小值的5倍.求部分偏振光中自然光与线偏振光强度之比.[解] 设该束部分偏振光中自然光光强为0I ,线偏振光光强为I ,透过偏振片后自然光光强变为20I ,因此光强最大时I II +=20max , 光强最小时 20m i n I I =所以22500minmaxI I I I I +== 因此 210=I I7-55 两偏振片A 、B 的透振方向成︒45角,如图所示.入射光是线偏振光,其振动方向和A 的透振方向相同.试求这束光线分别从左边入射和从右边入射时,透射光强之比.[解] 设从左右两边入射时透射光强分别为1I 和2I由马吕斯定律得从左边入射时透射光强为002012145cos I I I == 从右边入射,则00202024145cos 45cos I I I =⋅= 所以入射光从左右两边入射,透射光强之比为1:2:21=I I7-56 三个理想偏振片1P 、2P 、3P 叠放在一起,1P 与3P 的透振方向互相垂直,位于中间的2P 与1P 的透振方向间的夹角为︒30.强度为0I 的自然光垂直入射到1P 上,依次透过1P 、2P 和3P .求通过三个偏振片后的光强.[解] 通过1P 后: 0121I I =通过2P 后: 002128330cos I I I == 通过3P 后: 0022332360cos I I I ==7-57 一束太阳光以某一入射角入射于平面玻璃上,这时反射光为完全偏振光.若透射光的折射角为︒32,试求:(1)太阳光的入射角;(2)这种玻璃的折射率.[解] 因反射光为完全偏振光,所以入射角为布儒斯特角,则 0090=+r i 0000058329090=-=-=r i由布儒斯特定律得 60.158tan tan 00===i n7-58 光从介质1射向介质2时的临界角是︒60.布儒斯特角是多大? [解] 由光的折射定律得 020190sin 60sin n n = 所以2360sin 012==n n 由布儒斯特定律 23tan 120==n n i 由此得 9.400=i7-59 如图所示的各种情况中,以线偏振光或自然光入射于两种介质的界面上.图中0i 为起偏振角, 0i i .试画出折射光线和反射光线并标出它们的偏振状态.[解] 折射光和反射光及其偏振状态如下图7-60 如图(a )所示,一束自然光入射在方解石的表面上,入射光线与光轴成锐角,问有几条光线从方解石透射出来? 如果把方解石切割成等厚的A 、B 两块,并平行地移动一点距离,如图(b )所示,此时光线通过这两块方解石后,有多少条光线射出来? 如果把B 绕入射光线转过一个角度,此时将有几条光线从B 射出来?[答] (1)因入射光不沿光轴方向,也不垂直于光轴,所以在方解石中产生双折射现象,有两条光线透射出来. (2)在A 中为o 光的光线射出来入射到B ,入射面就是B 中o 光的主平面,因此光线通过B 后,只有一条光线射出,同理,在A 中为e 光的光线通过B 后也有一束光线射出,所以从B 中透射出来的仍是两束光.(3)当把B 任意转过一角度时,A 中的o 光和e 透射出来入射到B 中,各自在B 中又发生双折射现象,每条光线在B 中又分为o 光和e 光,因此,总共有四条光线从B 中射出.*7-61 如图所示,一束自然光入射到一方解石晶体上,其光轴垂直于纸面.已知方解石对o 光的折射率o n =1.658,对e 光的折射率为=e n 1.486.(1)如果方解石的厚度为t =1.0 cm ,自然光的入射角︒=45i ,求a ,b 两透射光之间的垂直距离;(2)两透射光的振动方向如何? 哪一束光在晶体中是o 光? 哪一束光在晶体中是e 光?[解](1)由折射定律得:i r n sin sin o o = (1)i r n sin sin e e = (2) 设则,,d BC L AB ==()0e tan tan r r t L -= (3)由于 i ABC =∠,所以 i L d cos = (4)由(1)、(2)、(3)、(4)联立得43.0658.145sin sin sin 000===n i r 002.25=r 48.0486.145sin sin 0e ==r 4.28e =r ()cm 07.02.25tan 4.28tan 0.100=-⨯=Lcm 05.045cos 07.00=⨯=d即a 、b 两光线的垂直距离为cm 05.0.(2)两透射光的振动方向见图.(3)a 为e 光,b 为o 光.*7-62 设方解石对钠黄光 (5893=λÅ)和氦氖激光(63282=λÅ)的主折射率相同,把方解石切割成对上述两光的四分之一波片,其最小厚度各是多少? 6584.1o =n ,4864.1e =n .[解] 设最小厚度分别为1e 和2e ,依题意有()41e o 1λ=-n n e ()42e o 2λ=-n n e所以 ()()m 10565.84864.16584.1410893.5477e 011--⨯=-⨯⨯=-=n n e λ ()()m 10198.94864.16584.1410328.6477e 021--⨯=-⨯⨯=-=n n e λA B C。
普通物理学第二版课后习题答案(全)

�得算计 用利 2 , 2 ta � t 0 v � s 1 h0.1 � s0063 � t , 2s/m0.4 � a ,s / m0.2 � 0 v
2 6.3 , 2 ta � t 0 v �s 1 1
:下一证验
s/m 成换 h/mk 将�变不位单的间时和度长因�h/mk 为改位单 0 v 仅 6.3 s/m � h / mk 1 0063 (/ m k 3 � 0 1 � s / m ,h / mk6.3 � ) h 1 得 得,
2
。误无果成此断判纲量据根。1 为纲量的边两子式出看以可�答解 �否误有果成此断 判纲量据根步初否能你 �1 纲量即数纯为 1 和 、�、 0、 1 01 � 量 质 的 体
9 2� 3�
物 些 某 示 表 p m和2 m、1m、M 中 其 1 1 m 2m m ] ) ( 01 � 1[ 2 ) ( 92 �01 � � M m 3 1m 3 �
1�
TL � v mid
纲量由
h/mk 为改位单 0 v 仅若 .�3� ) m(00272952 � 00002952 � 0027 � 2 1 � 4 � 20063 � � 1 � 2 � 0063 � s 2 1 �得算计 用利 2 , ta 0063 � � t 0 v0063 � s 2 2 1 ) m(00272952 � 00002952 � 0027 � 2 0063 � 4 � � 0063 � 2 � s 1
t2 �
程方迹轨得 t 去消 , 3 � t 2 � y , t 4 � x .① � 解 2
。移位的点质 1=t 至 1-=t 自求.�2� �迹轨的
点质求
.�1� � k 2 � j i e � r 为程方学动运点质 2.1.2 ˆ ˆ t2 e � ˆ t2 � �
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解 答]-527.2710(rad/s)243600πω==⨯⨯自-72 2.0410(rad/s)365243600πω==⨯⨯⨯公 R νω=自22n a RRνω==7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转?[解 答](1)22(30001200)1/601.57(rad /s )t12ωπβ⨯-⨯===(2)22222()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为 34at bt ct θ=+- (:rad,t :s).θ球t 时刻的角速度和角加速度.[解 答]34at bt ct θ=+-23d a 3bt 4ct dt θω==+- 2d 6bt 12ct dt ωβ==-7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立O-xy 坐标系,原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足21.2t t (:rad,t :s).θθ=+求(1)t=0时,(2)自t=0开始转45时,(3)转过90时,A 点的速度和加速度在x 和y 轴上的投影.[解 答]21.2t t 1.22t 2θωβ=+=+=(1) A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==22n a a 0.144(m /s )Ryx ν==-=-2y a R 0.2(m/s )β==(2)45θ=时,由2A 1.2t t ,t 0.47(s)42.14(rad /s)v Rπθωω=+==∴==⨯得ˆˆˆ i j kˆˆ 0 0 0.15j0.15i R cos R sin 0ωθθ==-x y A A 0.15(m /s),015(m /s)d dˆˆa (R sin i R cos j)dt dt νννωθωθ∴=-===-+221222x y dˆˆR(sin i cos j)dtˆˆR[(cos sin )i (sin cos )j ˆˆ0.183j0.465i(m /s )a 0.465(m /s ),a 0.183(m /s )ωθωθωθβθωθβθ-=-+=--+-+=--∴=-=-(3)当90θ=时,由2A x y 2x 22x y 1.2t t ,t 0.7895(s), 2.78(rad /s)2ˆˆv R i 0.278i(m/s)0.278(m /s),0(m /s)a R 0.2(m /s )a 0.77(m /s )Rπθωωννβν=+====-⨯=-∴=-==-=-=-=-得7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速度10rad/s ω=逆时针转动,求臂与铅直45时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动,门中心G 的速度、加速度与B 或D 点相同。
所以:G 222G AB 1.51015(m/s)a AB 1.510150(m/s )νωω=⋅=⨯==⋅=⨯=7.1.6 收割机拔禾轮上面通常装4到6个压板.拔禾轮一边旋转,一边随收割机前进.压板转到下方才发挥作用,一方面把农作物压向切割器,另一方面把切割下来的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反. 已知收割机前进速率为1.2m/s ,拔禾轮直径1.5m ,转速22rev/min,求压板运动到最低点挤压作物的速度.[解 答]取地面为基本参考系,收割机为运动参考系。
ννν∴=+板牵轮取收割机前进的方向为坐标系正方向n D1.20.53(m /s)3020.53(m /s)ˆ0.53i(m /s)πννννν∴-=-+=-⨯+=-∴=∴=-板对地板对轴轴对地板对地板对地7.1.7 飞机沿水平方向飞行,螺旋桨尖端所在半径为150cm ,发动机转速2000rev/min.(1)桨尖相对于飞机的线速率等于多少?(2)若飞机以250km/h 的速率飞行,计算桨尖相对于地面速度的大小,并定性说明桨尖的轨迹.[解 答]取地球为基本参考系,飞机为运动参考系。
(1)研究桨头相对于运动参考系的运动:nR 1.5314.16(m /s)30πνω==⨯=相 (2)研究桨头相对于基本参考系的运动:,(314.16)321.7(m /s)3600νννννν=+⊥∴=+= ⎝绝相牵相牵绝由于桨头同时参与两个运动:匀速直线运动和匀速圆周运动。
故桨头轨迹应是一个圆柱螺旋线。
7.1.8 桑塔纳汽车时速为166km/h.车轮滚动半径为0.26m.自发动机至驱动轮的转速比为0.909.问发动机转速为每分多少转.[解 答]设发动机转速为n 发,驱动轮的转速为n 轮。
由题意:n 0.909,n 0.909n n ==发发轮轮 (1)汽车的速率为316610,60⨯3166102R n 60π⨯=轮轮316610n 2R 60π⨯∴=轮轮 (2)(2)代入(1)3316610n 0.9091.5410(rev /min)2R 60π⨯==⨯发轮7.2.2 在下面两种情况下求直圆锥体的总质量和质心位置.(1)圆锥体为均质;(2)密度为h 的函数:h(1),Lρρρ=-为正常数.[解 答]建立如图坐标O-x,由cdm dv dv dm dv dv x x x x ρρ===⎰⎰⎰⎰⎰⎰ 得:(1)L 20c2(a /L)d 3L 14a L 3x x x ππ==⎰质量 21m v a L 3ρπρ==(2)L200c 200a h ()(1)d 4L L L(h=L )h a 5(1)()d L L x x x x x x x ππρρπ⋅⋅-==--⋅⎰⎰ 质量22000h a L m (1)()d a L L 4x x πρπρπ=-⋅=⎰ 7.2.3 长度为的均质杆,令其竖直地立于光滑的桌面上,然后放开手,由于杆不可能绝对沿铅直方向,故随即到下.求杆子的上端点运动的轨迹(选定坐标系,并求出轨迹的方程式).[解 答]建立坐标系,水平方向为x 轴,竖直方向为y 轴.杆上端坐标为(x,y ),杆受重力、地面对杆竖直向上的支承力,无水平方向力。
由i c F a m =∑外(质心运动定理)质心在杆的中点,沿水平方向质心加速度为零。
开始静止,杆质心无水平方向移动。
由杆在下落每一瞬时的几何关系可得:222(2x)y += 即杆上端运动轨迹方程为:2224x y +=7.3.1 (1)用积分法证明:质量为m 长为的均质细杆对通过中心且与杆垂直的轴线的转动惯量等于21m12.[解 答]建立水平方向o —x 坐标2m dI x dx=2220m1I 2x dx m 12==⎰(2)用积分法证明:质量为m 、半径为R 的均质薄圆盘对通过中心且在盘面内的转动轴的转动惯量为21mR 4.[解 答]3RR222222001m 4m I 2(R x )dx12R 3R ππ=-⎰⎰令x Rsin θ=3222442222204m 4m I (R R sin )R cos d R cos d 3R 3R ππθθθθθππ=-=⎰⎰=222204m 1cos 21()d mR 3R 24πθθπ+=⎰或3R 222204m I (R x )dx,3R π=-⎰利用公式n n n 22221222222u(u a )na (u a )du (u a )du n 1n 1-±±=±±++⎰⎰7.3.2 图示实验用的摆,0.92m =,r 0.08m =,m 4.9kg =,r m 24.5kg =,近似认为圆形部分为均质圆盘,长杆部分为均质细杆.求对过悬点且与摆面垂直的轴线的转动惯量.[解 答] 将摆分为两部分:均匀细杆(1I ),均匀圆柱(2I )则12I I I =+1I =221m L0.14(kg m )32I =22r r1m r m (L r)2++ (用平行轴定理)22.51(kg m )I=0.14+2.51=2.652(kg m ) 7.3.3 在质量为M 半径为R 的均质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量.[解 答]设未挖两个圆孔时大圆盘转动惯量为I 。
如图半径为r 的小圆盘转动惯量为1I 和2I 。
则有x 12I I I I =-- (12I I =)222222211m M R MR 2[r r r ()]22R R 2ππππ=-+ 422212r M(R r )2R =--7.3.5 一转动系统的转动惯量为2I 8.0kg.m =,转速为41.9rad /s ω=,两制动闸瓦对轮的压力都为392N ,闸瓦与轮缘间的摩擦系数为0.4μ=,轮半径为r 0.4m =,从开始制动到静止需要用多少时间?[解 答] zzz M I β=∑z2zzM 15.68(rad /s )I β∴==-∑z 0z z t=41.915.68tt=2.67(s)ωωβ=+-7.3.6 均质杆可绕支点O 转动,当与杆垂直的冲力作用某点A 时,支点O 对杆的作用力并不因此冲力之作用而发生变化,则A 点称为打击中心.设杆长为L ,求打击中心与支点的距离.[解 答]杆不受F 作用时,支点O 对杆的作用力N ,方向竖直向上,大小为杆的重量。
依题意,当杆受力F 时,N 不变。
建立如图坐标系,z 轴垂直纸面向外。
由质心运动定理得:(O x -方向投影)c F ma =(质心在杆中点) (1)由转动定理得:201F OA I mL 3ββ⋅== (2)有角量与线量的关系c 1a L 2β=(3)(1)(2)(3)联立求解21mL 23OA L13L 2ββ==7.3.7 现在用阿特伍德机测滑轮转动惯量.用轻线且尽可能润滑轮轴.两端悬挂重物质量各为1m 0.46kg =,且2m 0.5kg =.滑轮半径为0.05m .自静止始,释放重物后并测得5.0s 内2m 下降0.75m .滑轮转动惯量是多少?[解 答] 分析受力。
建立坐标系,竖直向下为x 轴正方向,水平向左为y 轴正方向。
