MATLAB编程 第六章
合集下载
MATLAB基础教程(第四版) 第6章 MATLAB 编程
命令
说明
disp(A)
显p(‘text’) Format
显示单引号内部的文本串 控制屏幕输出的显示格式
Fprintf x = input('text')
执行格式化的写入到屏幕或者写入到一个文件 显示单引号中的文本，等待用户的键盘输入，并且将输入值存储在x中
x = input('text','s') k=menu('title','option1','option2',...
有变量，就需要考虑使用函数文件。这将避免用变量名“弄乱”工作空间，并将 同时减少内存需求。
(6) 在不使用文本编辑器打开M-文件的情况下，用户可以使用type命令来查看文件的 内容。
2019年9月27日
第7页
MATLAB R2018b 基础教程
脚本文件和编辑器（4/11）
有效使用命令窗口和编辑器/调试器窗口
脚本文件和编辑器（8/11）
使用脚本文件存储数据 可能会有一些应用程序要求用户频繁地访问同一组数据。
如果是这样的话，用户可以将数组中的数据存储在一个脚 本文件之中。
2019年9月27日
第12页
MATLAB R2018b 基础教程
脚本文件和编辑器（9/11）
控制输入和输出
MATLAB为从用户获取输入以及为格式化输出(执行MATLAB命令而获得的结果)提供了许多有用的命令。
2019年9月27日
第5页
MATLAB R2018b 基础教程
脚本文件和编辑器（2/11）
创建和使用脚本文件
2019年9月27日
第6页
MATLAB R2018b 基础教程
Matlab教程第六章
9
例题代码
滚动条代码2 滚动条代码 function sliderEdgeColor_Callback(hObject, eventdata, handles) hsurf=handles.hsurface; newRed=get(hObject,'Value'); currentColor=rand(1,3); currentColor(1)=newRed; set(hsurf,'EdgeColor',currentC数： －－主要用来在图 非常重要的函数：guidata－－主要用来在图 －－ 形用户界面中存储或者获得数据。 形用户界面中存储或者获得数据。 语法：存储数据： 语法：存储数据：guidata(object_handle,data) 获取数据： 获取数据： data=guidata(object_handle) 这里的object_handle若不是图形窗体的句柄， 若不是图形窗体的句柄， 这里的 若不是图形窗体的句柄 则使用object_handle句柄对象的父层次的图 则使用 句柄对象的父层次的图 形窗体对象句柄来保存数据。 形窗体对象句柄来保存数据。
8
例题代码
滚动条代码1 滚动条代码 function sliderEdgeColor_CreateFcn(hObject, eventdata, handles) usewhitebg=1; if usewhitebg set(hObject,'BackgroundColor',[.9 .9 .9]); else set(hObject,'BackgroundColor',get(0,'defaultUicontro lBackgroundColor')); end
《计量经济学》与MATLAB编程-第六章多项式回归与非线性回归
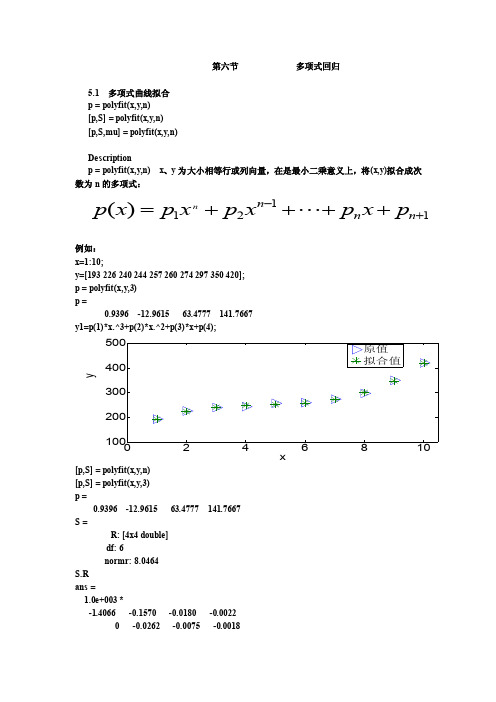
第六节 多项式回归5.1 多项式曲线拟合 p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)Descriptionp = polyfit(x,y,n) x 、y 为大小相等行或列向量，在是最小二乘意义上，将(x,y)拟合成次数为n 的多项式：1121)(+-++++=n n n p x p x p x p x p n例如： x=1:10;y=[193 226 240 244 257 260 274 297 350 420]; p = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667y1=p(1)*x.^3+p(2)*x.^2+p(3)*x+p(4);xy[p,S] = polyfit(x,y,n) [p,S] = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667 S =R: [4x4 double] df: 6normr: 8.0464 S.R ans =1.0e+003 *-1.4066 -0.1570 -0.0180 -0.0022 0 -0.0262 -0.0075 -0.00180 0 -0.0019 -0.00140 0 0 0.0005normr是残差的模，即：norm(y-y1)ans =8.0464[p,S,MU] = polyfit(x,y,n)[p,S,MU] = polyfit(x,y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464MU =5.50003.0277MU是x均值和x的标准差即std(x)S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.0901P它等于：[p,S] = polyfit((x-mean(x))./std(x),y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464>> S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.09015.2 多项式估计y= polyval(p,x)[y,DELT A] = polyval(p,x,S)y= polyval(p,x) 返回给定系数p和变量x值的多项式的预测y = P(1)*x^N + P(2)*x^(N-1) + ... + P(N)*x + P(N+1)x=1:10;y= polyval([3 2],x)y =5 8 11 14 17 20 23 26 29 32[3 2]有两个数，因此为一次多项式，即y=3x+2如：x=1:10;y=[193 226 240 244 257 260 274 297 350 420];p=polyfit(x,3)y1= polyval(p,x)norm(y-y1)ans =8.0464如果是矩阵，则polyval(p,x)为对应x的每一个预测值。
MATLAB第六章
MATLAB第六章第六章代数方程与最优化问题的计算机问题一：求解能转换成多项式方程的联立方程，并检验得出的高精度数值解的精度。
x1 2- x2- 1 = 0(x12- 2)2 + (x2–0.5)2+ 1 = 0【分析】：该题为关于x1,x2的两元联立方程，所以可以由MATLAB符号运算的solve（）函数求解。
如S=solve（enq1, enq2,... enqn）为最简单的调用方式，[x,...]=solve( enq1, enq2,... enqn)为直接得出根。
[x,...]=solve ( enq1, enq2,... enqn，‘x,...’直接得出函数并指定变量)。
该题最后应求出精度。
要利用norm(double())函数求解。
【解答】：（1）求X1，X2的值，输入语句如下：按ENTER键，显示如下：（2）输入如下语句，求精确度：按ENTER键，显示如下：其中高精度为：6.2242e-039，精度非常高，说明这个解是精确的。
题目二：试用图解法求解下面一元方程，并验证得出的结果。
)25sin()(2/)1(2+=++-x e x f x π【分析】：该题需用一元方程的图解法。
在MATLAB 中，需要用ezplot()函数绘制给定隐函数f(x)=0曲线，该方程的曲线和y = 0 线的交点即为方程的解，可以用图形局部放大的方法读出这些交点的x 值。
【解答】：(1)绘制曲线，输入如下语句：按ENTER 键，显示如下图片：由图可知，该方程的实解是多个的。
要用图解法求出根，要对该点附近局部放大，直到曲线穿越0线，且t轴给出的各个标点的数值完全一致，读得此时t轴标度。
如图所示：该点分别为-2.9135 -2.284 -1.6567 -1.0238 -0.4000 0.22284 1.4851（2）验证根，输入如下程序, 语句输入后，显示如下：可见，得出t 的值处的函数值为-0.433*10-3，故可见的出的根是原方程的根。
matlab快速入手第六章PPT课件
例6-1 已知三角形三条边，求周长和面积。
2020/10/13
第2页
条件语句1
if语句 if语句的基本形式为：
if 逻辑表达式 语句 end
每条if语句必须伴随有一条end语句。end语句标志着逻 辑表达式为true时所要执行语句的结束。if和逻辑表达式 (其可以是一个标量、一个矢量或者一个矩阵)之间需要一 个空格。
第9页
switch结构
switch结构的语法是：
switch输入表达式(标量或者字符串) case 值1 语句组1 case 值2 语句组 2 .. otherwise 语句组n end 例 switch的用法。
2020/10/13
第10页
调试MATLAB程序
编辑器/调试器菜单栏包含以下的菜单项： Debug
例 6-5 已知一个向量x=[1.92,0.05,-2.43,-0.02,0.09,0.85,0.06],假设数据在-0.1<x<0.1内的任何一个数值都不是正 确的，并删除这类元素而在数组的结尾处以0代替它们。
2020/10/13
第7页
循环2
break和continue语句
break语句停止循环的执行。 例 continue语句执行循环的下一次迭代。例
2020/10/13
第11页
谢谢您的指导
THANK YOU FOR YOUR GUIDANCE.
感谢阅读！为了方便学习和使用，本文档的内容可以在下载后随意修改，调整和打印。欢迎下载！
汇报人：XXXX 日期：20XX年XX月XX日
2020/10/13
第5页
条件语句4
elseif语句
if语句的一般形式是：
if 逻辑表达式1 语句组1 elseif 逻辑表达式2 语句组2 else 语句组3 end
第6章MATLAB编程精品PPT课件
MATLAB 基础教程
第6 章
6.1.1 创建和使用脚本文件
创建新的M-文件，只需在命令窗口的File菜单中选中New 菜单项，然后选中M-文件。在之后出现的编辑器/调试器窗口 中输入文件，用键盘和编辑器/调试器的Edit菜单创建和编辑文 件。
完成后，从编辑器/调试器的File菜单中选中Save菜单项。 在出现的对话框中，用example1等自我命名的文件名替换系 统所提供的默认名称，并单击Save菜单项。编辑器/调试器将 自动提供扩展名.m，并将文件保存在MATLAB当前目录中。
MATLAB 基础教程
6.1.5 编程风格
第6 章
推荐的脚本文件结构
注释部分
（1） 在第一行中放置程序名和任何关键词。 （2）在第二行中放置创建的日期，以及创建者的姓名。 （3） 每个输入和输出变量的变量名定义。 （4） 程序中调用的每个用户自定义函数名称。
输入部分：放置输入数据和/或输入函数。其允许输入数
保存了文件之后，用户就可以在MATLAB命令窗口中输入 脚本文件名example1以执行程序。用户应该会看到命令窗口 中所显示的结果。
MATLAB 基础教程
第6 章
6.1.2 有效使用脚本文件
(1) 脚本文件名必须满足MATLAB中标识符的命名规则……
(2) 为脚本文件赋予的名称不要与其所计算的变量名称相同。
(3) 为脚本文件赋予的名称要与MATLAB命令或者已有函数的 名称都不相同。
(4) 在交互模式中，脚本文件所创建的所有变量都是全局变量。 用户可以用who来查看之。
(5) 函数文件所创建的变量是该函数的局部变量。用户如果不 必访问脚本文件中的所有变量，就需要考虑使用函数文件。 这将避免用变量名“弄乱”工作空间，并将同时减少内存 需求。
Matlab编程 - 第六章 lingo软件基础
第六章
LINGO软件基础
1
第六章 lingo软件简介 LINGO(linear interactive and general optimiuzer) 的基本含义是交互式的线性和离散化求解器。 最初是由芝加哥大学的Linus Schrage教授于1980年 开发的. 是主要用来求解优化问题的软件。 最大特色：允许优化问题中的决策变量为整数，即可 求解整数规划，而且执行速度快。
x2+2*x4+x5+3*x6>=20; x3+x5+2*x7>=15; @gin(x1);@gin(x2);@gin(x3); @gin(x4);@gin(x5);@gin(x6); @gin(x7);
x3 x5 2 x7 15,
xi 为整数
结论：按第1种模式切5根，第2种模式切5根，第5种 模式切15根，共需切割25根原料钢管。
9
二、LINGO中集 集是一群相联系的对象，这些对象也称为集的成员。 每个集成员可能有一个或多个与之有关联的特征， 这些特征称为属性。 LINGO有两种类型的集：原始集和派生集。 原始集是由一些最基本的对象组成的。 派生集是用一个或多个其它集来定义的。
10
1.定义原始集 sets: setname/member_list /:attribute_list; endsets
Feasible solution found. Total solver iterations: Variable I1 I2
0 Value 2.000000 3.000000
27
4.集循环函数：@for， @sum, @max, @min 用法：(1) @for(setname: expression_list) 对集合setnane的每个元素独立生成expression_list。 (2) @for(setname(i)|logical_condition:expression_list) 对集合setnane中满足logical_condition的成员独立生成 expression_list。 data: 如： x=3,8,5,7,6,-2; sets: enddata niu/1..6/:x,y,z; @ for(niu:y=x^2+2); endsets @for(niu(i)|i#le#3:z(i)=x(i)-3); @for(niu(i)|i#gt#3:z(i)=x(i)^2-2);
LINGO软件基础
1
第六章 lingo软件简介 LINGO(linear interactive and general optimiuzer) 的基本含义是交互式的线性和离散化求解器。 最初是由芝加哥大学的Linus Schrage教授于1980年 开发的. 是主要用来求解优化问题的软件。 最大特色：允许优化问题中的决策变量为整数，即可 求解整数规划，而且执行速度快。
x2+2*x4+x5+3*x6>=20; x3+x5+2*x7>=15; @gin(x1);@gin(x2);@gin(x3); @gin(x4);@gin(x5);@gin(x6); @gin(x7);
x3 x5 2 x7 15,
xi 为整数
结论：按第1种模式切5根，第2种模式切5根，第5种 模式切15根，共需切割25根原料钢管。
9
二、LINGO中集 集是一群相联系的对象，这些对象也称为集的成员。 每个集成员可能有一个或多个与之有关联的特征， 这些特征称为属性。 LINGO有两种类型的集：原始集和派生集。 原始集是由一些最基本的对象组成的。 派生集是用一个或多个其它集来定义的。
10
1.定义原始集 sets: setname/member_list /:attribute_list; endsets
Feasible solution found. Total solver iterations: Variable I1 I2
0 Value 2.000000 3.000000
27
4.集循环函数：@for， @sum, @max, @min 用法：(1) @for(setname: expression_list) 对集合setnane的每个元素独立生成expression_list。 (2) @for(setname(i)|logical_condition:expression_list) 对集合setnane中满足logical_condition的成员独立生成 expression_list。 data: 如： x=3,8,5,7,6,-2; sets: enddata niu/1..6/:x,y,z; @ for(niu:y=x^2+2); endsets @for(niu(i)|i#le#3:z(i)=x(i)-3); @for(niu(i)|i#gt#3:z(i)=x(i)^2-2);
第六章 (2)MATLAB高级图形设计
se因t（此’一u般i_h用aUnsdelreD’a,’tUa存se储rD简a单ta与’,单Va一lu的e数）据
。此时，Value数据就已经存储在句柄值为 ui_handle的对象内。
② 在执行的过程中若要取回该变量，可以通过以下 方式在任一Callback中获取该数据值：
Value=get(‘ui_handle’,’UserData’);
用的有hObject、 eventdata和 handles。
hObject：当前回调函数的图形对象句柄；
eventdata：预留的输入参数；
handles：存放图形窗口中所有图形对象句柄的结 构体，存储了所有在图形界面中的控件、菜单、 坐标轴对象的句柄，可以用于在function之间传 递数据。例如：handles.pushbutton1就是按钮 pushbuton1的句柄，handles.axes1就是axes1 的句柄。
global A;
25
多个回调函数之间变量的传递
方法二：直接通过对象的UserData属性来进行各个
C注al意lb：ack此之方间法的在数操据作存上取简操单作且。方便，但每个对
①象次于首设为仅变复先该V能量杂a必对存时的lu须象取，操e，一先作先的则个前会将句输变的造数柄入量 变 成据值以值 量 很存为下， 值 多储ui程因 就 不_到h序此 会 便一an即被当 。个d可覆同l特e盖一：，定掉对需的，象要对这存存象样储储中对两的，值假
➢string属性是按钮上显示的文字，默认的string属 性与Tag相同。
3．滚动条（Slider） （1）常用属性 滚动条的常用回调函数是callback，当每次单击滚动条
改变当前值时调用该函数。 （2）回调函数 常用属性有value、max、min和SliderStep。
。此时，Value数据就已经存储在句柄值为 ui_handle的对象内。
② 在执行的过程中若要取回该变量，可以通过以下 方式在任一Callback中获取该数据值：
Value=get(‘ui_handle’,’UserData’);
用的有hObject、 eventdata和 handles。
hObject：当前回调函数的图形对象句柄；
eventdata：预留的输入参数；
handles：存放图形窗口中所有图形对象句柄的结 构体，存储了所有在图形界面中的控件、菜单、 坐标轴对象的句柄，可以用于在function之间传 递数据。例如：handles.pushbutton1就是按钮 pushbuton1的句柄，handles.axes1就是axes1 的句柄。
global A;
25
多个回调函数之间变量的传递
方法二：直接通过对象的UserData属性来进行各个
C注al意lb：ack此之方间法的在数操据作存上取简操单作且。方便，但每个对
①象次于首设为仅变复先该V能量杂a必对存时的lu须象取，操e，一先作先的则个前会将句输变的造数柄入量 变 成据值以值 量 很存为下， 值 多储ui程因 就 不_到h序此 会 便一an即被当 。个d可覆同l特e盖一：，定掉对需的，象要对这存存象样储储中对两的，值假
➢string属性是按钮上显示的文字，默认的string属 性与Tag相同。
3．滚动条（Slider） （1）常用属性 滚动条的常用回调函数是callback，当每次单击滚动条
改变当前值时调用该函数。 （2）回调函数 常用属性有value、max、min和SliderStep。
matlab教材第六章
1. Two variables that are functions of the same independent variable, when you wish to emphasize the importance of the independent variable. 2. A single variable that is a function of two independent variables.
paring individual characters for equality and
inequality
All of the relational operators compare the ASCII values of corresponding characters
3.categorizing characters within a string
eval
sscanf
Quiz6.1 P265
1, 4,7,8,10
6.4 additional two-dimensional plots
stem(x,y) stairs(x,y)
bar(x,y)
barh(x,y)
pie(x, explode) compass(x,y)
Plotting functions
Clabel : elevation label
Exm050401 3)Four-dimension plots
1. Quasi four-dimension
2. Cartoon
exm050402
exm050407
Summary
Complex data operation String functions Two- and three-dimensional plots Exercises P283 6.1, 6.10, 6.11
matlab讲义第六章
>> max_rain=max(rains) % 将rains矩阵中的每一列的最大 值列出 max_rain = 328.8000 300.7000 268.3000 210.5000 278.4000 321.5000 >> [max_rain,x]=max(rains) % 将rains矩阵中的每一列的最大 值及其位置列出 max_rain = 328.8000 300.7000 268.3000 210.5000 278.4000 321.5000 x = 2 2 2 2 2 2 >> min_rain=min(rains) % 将rains矩阵中的每一列的最小值 列出 min_rain = 126.8000 148.5000 173.0000 148.4000 194.7000 208.9000
例如： >> rains % rains为一个2x6的矩阵 rains = 126.8 148.5 173.0 148.4 194.7 208.9 328.8 300.7 268.3 210.5 278.4 321.5 >> avg_rain=mean(rains) % 将rains矩阵中的每一列的平均 值列出 avg_rain = 227.8000 224.6000 220.6500 179.4500 236.5500 265.2000 >> avg_rain=mean(avg_rain) % 将上述矩阵中的平均值列出 avg_rain = 225.7083
使用函数须注意几点。函数一定出现在计算等式的 右边，等式左边是代表这个函数的计算值。此外，一个 函数可以被当做另一个函数的引用。 例如，log_x=log(abs(x))其中abs和log皆为内建 函数，其意思是 先计算abs(x)，所得值再代入log函数。 三角函数和双曲线函数的使用，和一般数学式相似， 其语法也很直接易懂。 例如，三角函数有：sin(x), cos(x), tan(x), asin(x), acos(x), atan(x), atan2(y,x)。常用到的 双曲线函数有：sinh(x), cosh(x), tanh(x), asinh(x), acosh(x), atanh(x)。上述函数用法请参考 MATLAB的线上说明或使用手册。
matlab答案第六章
值
figure, plot(alpha3, tan_alpha3, 'k:p');
hold on; %绘精确正切曲线
alpha4=0:75;
tan_Y1=interp1(alpha3, tan_alpha3, alpha4,
'spline'); %3 次样条正切插值
plot(alpha4, tan_Y1,'r-*'); hold on; %绘 3
运行结果：
x=
-1.8060
-0.5373
3.0448
(2) 程序设计：
方法 1：矩阵求逆法
clear all; close all; clc;
A=[5, 1, -1, 0; 1, 0, 3, -1;-1,-1,0, 5; 0,
0, 2, 4];
b=[1; 2; 3; -1];
x=inv(A)*b
运行结果：
第六章
1. 利用 MATLAB 提供的 randn 函数生成符合正
态分布的 10×5 随机矩阵 A，进行如下操作：
(1) A 各列元素的均值和标准方差。
(2) A 的最大元素和最小元素。
(3) 求 A 每行元素的和以及全部元素之和。
(4) 分别对 A 的每列元素按升序、每行元素按
降序排列。
答：
clear all; close all; clc;
141
Yi 187 126 172 125 148 求它的线性拟合曲线。 答： 程序设计： clear all; close all; clc; x=[165, 123, 150, 123, 141]; y=[187, 126, 172, 125, 148]; P=polyfit(x, y, 3) 运行结果： P= 1.0e+003 * -0.0000 0.0013 -0.1779 8.4330 所以它的线性拟合曲线为： P(x)=1.3x2-177.9x+8433 4. 已知多项式 P1(x)=3x+2，P2(x)=5x2−x+2， P3(x)=x2−0.5，求 ： (1) P(x)=P1(x)P2(x)P3(x)。 (2) P(x)=0 的全部根。 (3) 计算 xi=0.2i (i=0,1,2,…,10)各点上的 P(xi)。 答： (1) 程序设计： clear all; close all; clc; P1=[0, 3, 2]; P2=[5, -1, 2]; P3=[1, 0, -0.5]; P=conv(conv(P1, P2), P3) 运行结果： P= 0 15.0000 7.0000 -3.5000 0.5000 -2.0000 -2.0000 所以 P(x)=15x5+7x4-3.5x3+0.5x2-2x-2 (2) 程序设计： r=roots(P) 运行结果： r= 0.7071 0.1000 + 0.6245i 0.1000 - 0.6245i -0.7071 -0.6667 (3) 程序设计： i=0:10; xi=0.2*i; Pxi=polyval(P, xi) 运行结果： Pxi =
MATLAB基础应用案例教程第六章
• (６) ＢａｃｋｇｒｏｕｎｄＣｏｌｏｒ 和 ＥｄｇｅＣｏｌｏｒ 属性 设置文本对象的背景颜色和边框线的颜色，可取值 ｎｏｎｅ ( 默认 值) 或颜色字母。
• (７) ＨｏｒｉｚｏｎｔａｌＡｌｉｇｎｍｅｎｔ 属性设置文本与指 定点的相对位置，可取值 ｌｅｆｔ ( 默认值)、ｃｅｎｔｅｒ 或 ｒｉ ｇｈｔ。
ｍａｌ ( 默认值)、 ｂｏｌｄ、 ｌｉｇｈｔ 或 ｄｅｍｉ。 • (４) ＦｏｎｔＡｎｇｌｅ 属性设置斜体文字模式，取值可以是 ｎｏ
ｒｍａｌ ( 默认值)、 ｉｔａｌｉｃ 或 ｏｂｌｉｑｕｅ。
上一页 下一页 返回
６.１ 二维绘图功能
• (５) Ｒｏｔａｔｉｏｎ 属性设置字体旋转角，取值是数值量，默认 值为 ０，取正值表示逆时针旋转，取负值表示顺时针旋转。
是网格点上的高度矩阵，ｃ用于指定在不同高度下的颜色范围。 • (３) 省略 ｃ 时，ｃ ＝ ｚ，即颜色的设定正比于图形的高度。 • (４) 当ｘ、 ｙ 是向量时，ｘ 的长度必须等于 ｚ 矩阵的列，ｙ 的长
度必须等于必须等于 ｚ 的行，ｘ、 ｙ 向量元素的组合构成网格点的 坐标 (ｘ。ｙ)，ｚ 坐标则取自矩阵ｚ，然后绘制三维曲线。
上一页 下一页 返回
６.１ 二维绘图功能
• ２ 函数图函数 • 语法格式:
• 说明: • (１) ｆｕｎ 必须是 ｍ 文件的函数名或是独立变量为 ｘ 的字符串。 • (２) ｆｐｌｏｔ 函数不能画参数方程和隐函数图形，但在一个图上
可以画多个图形。
上一页 下一页 返回
６.１ 二维绘图功能
• 【例 ６ － １１】 建立函数文件 ｍｙｆｕｎ１ ｍ， 在 [ － １。２] 区间上绘制 ｙ ＝ ｅ２ｘ ＋ ｓｉｎ(３ｘ２ ) 曲线。
有的允许属性。 • ２ 获取图形对象属性
• (７) ＨｏｒｉｚｏｎｔａｌＡｌｉｇｎｍｅｎｔ 属性设置文本与指 定点的相对位置，可取值 ｌｅｆｔ ( 默认值)、ｃｅｎｔｅｒ 或 ｒｉ ｇｈｔ。
ｍａｌ ( 默认值)、 ｂｏｌｄ、 ｌｉｇｈｔ 或 ｄｅｍｉ。 • (４) ＦｏｎｔＡｎｇｌｅ 属性设置斜体文字模式，取值可以是 ｎｏ
ｒｍａｌ ( 默认值)、 ｉｔａｌｉｃ 或 ｏｂｌｉｑｕｅ。
上一页 下一页 返回
６.１ 二维绘图功能
• (５) Ｒｏｔａｔｉｏｎ 属性设置字体旋转角，取值是数值量，默认 值为 ０，取正值表示逆时针旋转，取负值表示顺时针旋转。
是网格点上的高度矩阵，ｃ用于指定在不同高度下的颜色范围。 • (３) 省略 ｃ 时，ｃ ＝ ｚ，即颜色的设定正比于图形的高度。 • (４) 当ｘ、 ｙ 是向量时，ｘ 的长度必须等于 ｚ 矩阵的列，ｙ 的长
度必须等于必须等于 ｚ 的行，ｘ、 ｙ 向量元素的组合构成网格点的 坐标 (ｘ。ｙ)，ｚ 坐标则取自矩阵ｚ，然后绘制三维曲线。
上一页 下一页 返回
６.１ 二维绘图功能
• ２ 函数图函数 • 语法格式:
• 说明: • (１) ｆｕｎ 必须是 ｍ 文件的函数名或是独立变量为 ｘ 的字符串。 • (２) ｆｐｌｏｔ 函数不能画参数方程和隐函数图形，但在一个图上
可以画多个图形。
上一页 下一页 返回
６.１ 二维绘图功能
• 【例 ６ － １１】 建立函数文件 ｍｙｆｕｎ１ ｍ， 在 [ － １。２] 区间上绘制 ｙ ＝ ｅ２ｘ ＋ ｓｉｎ(３ｘ２ ) 曲线。
有的允许属性。 • ２ 获取图形对象属性
MATLAB课件第六章201404
xlabel('Hz') grid on x=x+randn(size(x)); subplot(413),plot(x)
%在信号中加入噪声
title('含随机噪声的信号')
xlabel('序列N'),grid on y=fft(x,number); %对含噪声信号进行512点的傅立叶变换 n=0:length(y)-1; f=fs*n/length(y)
线性拉伸至一个更大的范围，使原本位于该区域的图
像对比度得到增强。
假定原图像表示为g(x,y)，现希望将图像g(x,y)
的范围从[a,b]的灰度拉伸至范围[c,d]。变换形 式如下：
c d c g ( x, y) a c g ( x, y) b a d 0 g ( x, y ) a a g ( x, y ) b b g ( x, y) 255
6.2 信号分析与处理
6.2.1 序列的操作 1. 信号加 x(n)=x1(n)+x2(n) MATLAB实现： x=x1+x2;
2. 信号乘
x(n)=x1(n) x2(n)
MATLAB实现：
x=x1.*x2;
3. 改变比例 y(n)=k*x(n) MATLAB实现： y=k*x; 4. 折叠y(n)=x(-n) MATLAB实现： y=fliplr(x); 5. 抽样和 y
3．实指数序列 n x(n) a n a R 直接实现：n=[ns:nf]; x=a.^n; 4．复指数序列
x(n) e
( j) n
直接实现：n=[ns:nf]; x=exp((sigema+jw)*n); 5．正(余)弦序列 x(n) cos(n ) 直接实现：n=[ns:nf]; x=cos(w*n+sita);
%在信号中加入噪声
title('含随机噪声的信号')
xlabel('序列N'),grid on y=fft(x,number); %对含噪声信号进行512点的傅立叶变换 n=0:length(y)-1; f=fs*n/length(y)
线性拉伸至一个更大的范围，使原本位于该区域的图
像对比度得到增强。
假定原图像表示为g(x,y)，现希望将图像g(x,y)
的范围从[a,b]的灰度拉伸至范围[c,d]。变换形 式如下：
c d c g ( x, y) a c g ( x, y) b a d 0 g ( x, y ) a a g ( x, y ) b b g ( x, y) 255
6.2 信号分析与处理
6.2.1 序列的操作 1. 信号加 x(n)=x1(n)+x2(n) MATLAB实现： x=x1+x2;
2. 信号乘
x(n)=x1(n) x2(n)
MATLAB实现：
x=x1.*x2;
3. 改变比例 y(n)=k*x(n) MATLAB实现： y=k*x; 4. 折叠y(n)=x(-n) MATLAB实现： y=fliplr(x); 5. 抽样和 y
3．实指数序列 n x(n) a n a R 直接实现：n=[ns:nf]; x=a.^n; 4．复指数序列
x(n) e
( j) n
直接实现：n=[ns:nf]; x=exp((sigema+jw)*n); 5．正(余)弦序列 x(n) cos(n ) 直接实现：n=[ns:nf]; x=cos(w*n+sita);
MatLab6
第六章
MATLAB编程
第六章 MATLAB编程
本章主要内容如下：
6.1 6.2 6.3 6.4 MATLAB工作模式 M文件的创建及分类 MATLAB程序控制 串演算函数
MatLab应用
第六章
MATLAB编程
6.1MatLab的工作模式 6.1.1 指令驱动模式 人机交互的命令行方式，即当用户在MatLab 命 令窗口输入单行指令时，MatLab 立即处理这条 指令，并显示结果。 由于MatLab命令窗口只允许一次执行一行上的一 个或几个语句，不能存储，可读性差，当处理复 杂问题和大量数据时很不方便。因此应编辑m文 件。
MatLab应用
第六章
MATLAB编程
a 【例6-3】一数组的元素满足规则： k +2 = ak + ak +1 ,(k=1,2,…)； 且 a1 = a 2 = 1 。现要求该数组中第一个大于10000的元素。
a(1)=1;a(2)=1;i=2; while a(i)<=10000 a(i+1)=a(i-1)+a(i); i=i+1; end; i,a(i),
MatLab应用
第六章
MATLAB编程
6.2.2 M文件的类型 M文件有两类： 脚本式（命令式）文件 函数式文件
MatLab应用
第六章
MATLAB编程
6.2.2.1 M脚本(Scripts)式文件 脚本是最简单的M-文件，它没有入口和出口参数变 量。可以自动执行一系列MATLAB 命令，诸如重复 命令等。 脚本（Scripts）是对工作空间（workspace）中的现有 数据操作，或创建一个新数据，而且脚本所创建的任 一变量在脚本运行完都保留在工作空间中以便进一步 使用。 脚本可以直接在命令窗口用文件名直接调用。 一般用clear、close all等语句开始，可清除掉工作空 间中原有的变量和图形，以避免其他已执行的残留数 据对本程序的影响。
MATLAB编程
第六章 MATLAB编程
本章主要内容如下：
6.1 6.2 6.3 6.4 MATLAB工作模式 M文件的创建及分类 MATLAB程序控制 串演算函数
MatLab应用
第六章
MATLAB编程
6.1MatLab的工作模式 6.1.1 指令驱动模式 人机交互的命令行方式，即当用户在MatLab 命 令窗口输入单行指令时，MatLab 立即处理这条 指令，并显示结果。 由于MatLab命令窗口只允许一次执行一行上的一 个或几个语句，不能存储，可读性差，当处理复 杂问题和大量数据时很不方便。因此应编辑m文 件。
MatLab应用
第六章
MATLAB编程
a 【例6-3】一数组的元素满足规则： k +2 = ak + ak +1 ,(k=1,2,…)； 且 a1 = a 2 = 1 。现要求该数组中第一个大于10000的元素。
a(1)=1;a(2)=1;i=2; while a(i)<=10000 a(i+1)=a(i-1)+a(i); i=i+1; end; i,a(i),
MatLab应用
第六章
MATLAB编程
6.2.2 M文件的类型 M文件有两类： 脚本式（命令式）文件 函数式文件
MatLab应用
第六章
MATLAB编程
6.2.2.1 M脚本(Scripts)式文件 脚本是最简单的M-文件，它没有入口和出口参数变 量。可以自动执行一系列MATLAB 命令，诸如重复 命令等。 脚本（Scripts）是对工作空间（workspace）中的现有 数据操作，或创建一个新数据，而且脚本所创建的任 一变量在脚本运行完都保留在工作空间中以便进一步 使用。 脚本可以直接在命令窗口用文件名直接调用。 一般用clear、close all等语句开始，可清除掉工作空 间中原有的变量和图形，以避免其他已执行的残留数 据对本程序的影响。
Matlab教程Ch6 (多项式及其运算)
>> x=1:0.1:2; >> y=[2.1,3.2,2.1,2.5,3.2,3.5,3.4,4.1,4.7,5.0,4.8]； >> p2=polyfit(x,y,2); p3=polyfit(x,y,3); p7=polyfit(x,y,7); >> x1=1:0.01:2; >> y2=polyval(p2,x1); >> y3=polyval(p3,x1); >> y7=polyval(p7,x1); >> plot(x,y,’rp’,x1,y2,’+’, x1,y3,’k.-’, x1,y7,’g’); >> legend(‘拟合点’，‘二次拟合’，’三次拟合’，’七次 12 拟合’)
25
2018/10/10
1. if语句 if语句的三种基本语法结构 if（关系运算表达式）
选择结构
MATLAB语句 end if（关系运算表达式） MATLAB语句A else MATLAB语句B end if（关系运算表达式a） MATLAB语句A elseif （关系运算表达式b） MATLAB语句B else （关系运算表达式c） … 2018/10/10 26 end
【例】用一个5次多项式在区间[0，2π]内逼近函数sin(x)
X=linspace(0,2*pi,50);Y=sin(X); [P,S]=polyfit(X,Y,5) %得到5次多项式的系数和误差 plot(X,Y,‘r*',X,polyval(P,X))
10
11
例．现有一组实验数据：x的取值是从1到2之间的数，间隔 为0.1，y的取值为2.1, 3.2, 2.1, 2.5, 3.2, 3.5, 3.4,4.1,4.7,5.0,4.8. 要求分别用二次、三次和七次拟合曲线来拟合这组数据， 观察这三组拟合曲线哪个效果更好？
25
2018/10/10
1. if语句 if语句的三种基本语法结构 if（关系运算表达式）
选择结构
MATLAB语句 end if（关系运算表达式） MATLAB语句A else MATLAB语句B end if（关系运算表达式a） MATLAB语句A elseif （关系运算表达式b） MATLAB语句B else （关系运算表达式c） … 2018/10/10 26 end
【例】用一个5次多项式在区间[0，2π]内逼近函数sin(x)
X=linspace(0,2*pi,50);Y=sin(X); [P,S]=polyfit(X,Y,5) %得到5次多项式的系数和误差 plot(X,Y,‘r*',X,polyval(P,X))
10
11
例．现有一组实验数据：x的取值是从1到2之间的数，间隔 为0.1，y的取值为2.1, 3.2, 2.1, 2.5, 3.2, 3.5, 3.4,4.1,4.7,5.0,4.8. 要求分别用二次、三次和七次拟合曲线来拟合这组数据， 观察这三组拟合曲线哪个效果更好？
matlab基础教程教学课件杨德平第6章程序设计
statements
end 说明 每当循环变量variable取expression中的一个值时，就执行循环体 statements一次，直到取完expression中的值。expression常用数组形成 表示。
【例6-4】编写求100！的程序，利用公式k!=(k-1)!×k。 s=1; for k=1:100 s=s*k; end s 运行结果如下： s= 9.3326e+157
表6-3 各种运算符优先级排序
优先级 最高
最低
运算符 （）小括号 ’转置 .^ 数组乘方 ^ 矩阵乘方 逻辑非（not，~） .* 点乘 ./点除 乘法 除法 加减法 冒号 关系操作符（==，~=，>，>=，<，<=） 逻辑与（and，&） 逻辑或、逻辑异或6（/1or，xor，|）
首页
6.2. 顺序语句
and(a,b)
| 或（or）
or(a,b)
6/1
～ 非（not）
not(a,b)
异或(xor)
xor(a,b) 首页
尚 辅 网 shangfuwang
逻辑操作运算法则如下： （1）a&b或and(a,b)：表示a和b作“逻辑与”运算，当a和b全为非零时，运算 结果为1，否则为0； （2）a|b或or(a,b)：表示a和b作“逻辑或”运算，当a和b只要有一个非零，运 算结果为1，否则为0； （3）～a或not(a)：表示对a作“逻辑非”运算，当a是零时，运算结果为1，否 则为0； （4）xor(a,b)：表示a和b作“逻辑异或”运算，当a和b的值一个为零，一个不 为零时运算结果为1，否则为0。
例如，判断当a为偶数时，显示a是偶数，并计算a/2；否则不作任何处理。 If rem(a,2)==0 disp('a is even') b=a/2; end
end 说明 每当循环变量variable取expression中的一个值时，就执行循环体 statements一次，直到取完expression中的值。expression常用数组形成 表示。
【例6-4】编写求100！的程序，利用公式k!=(k-1)!×k。 s=1; for k=1:100 s=s*k; end s 运行结果如下： s= 9.3326e+157
表6-3 各种运算符优先级排序
优先级 最高
最低
运算符 （）小括号 ’转置 .^ 数组乘方 ^ 矩阵乘方 逻辑非（not，~） .* 点乘 ./点除 乘法 除法 加减法 冒号 关系操作符（==，~=，>，>=，<，<=） 逻辑与（and，&） 逻辑或、逻辑异或6（/1or，xor，|）
首页
6.2. 顺序语句
and(a,b)
| 或（or）
or(a,b)
6/1
～ 非（not）
not(a,b)
异或(xor)
xor(a,b) 首页
尚 辅 网 shangfuwang
逻辑操作运算法则如下： （1）a&b或and(a,b)：表示a和b作“逻辑与”运算，当a和b全为非零时，运算 结果为1，否则为0； （2）a|b或or(a,b)：表示a和b作“逻辑或”运算，当a和b只要有一个非零，运 算结果为1，否则为0； （3）～a或not(a)：表示对a作“逻辑非”运算，当a是零时，运算结果为1，否 则为0； （4）xor(a,b)：表示a和b作“逻辑异或”运算，当a和b的值一个为零，一个不 为零时运算结果为1，否则为0。
例如，判断当a为偶数时，显示a是偶数，并计算a/2；否则不作任何处理。 If rem(a,2)==0 disp('a is even') b=a/2; end
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6.1.1 Complex Variable Created automatically when assigned.
6.1.2 Using Complex Numbers with Relational Operators ➢ = ~=
c1 4 3i c2 4 3i
➢ >, <, >=, <=
t = 0 : pi/20 : 4*pi; y = exp (-0.2*t) .* (cos(t) + i * sin(t)); plot (t, real(y), 'b-'); hold on; plot (t, imag(y), 'r-'); title ('\bfPlot of Complex Function vs Time'); xlabel ('\bf\itt'); ylabel ('\bf\ity(t)'); legend ('real','imaginary'); hold off;
8/9/2020
Hangzhou Dianzi University
6
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Function conj (c) real (c) imag (c)
isreal (c)
abs (c) angle (c)
c1 c2 (a1 a2 ) (b1 b2 )i
c1 c2 (a1a2 b1b2 ) (a1b2 b1a2 )i
c1 c2
a1a2 b1b2 a22 b22b1a2 a22a1b2 b22i
8/9/2020
Hangzhou Dianzi University
3
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Returns the angle of the complex number c.
8/9/2020
Hangzhou Dianzi University
7
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Example 6.1 — The Quadratic Equation
Chapter 6 Complex Data, Character Data, and Additional Plot Types
8/9/2020
1
Chapter 6 Complex Data, Character Data, and Additional Plot Types
6.1 Complex Data
8/9/2020
Hangzhou Dianzi University
9
Chapter 6 Complex Data, Character Data, and Additional Plot Types
8/9/2020
Hangzhou Dianzi University
10
Chapter 6 Complex Data, Character Data, and Additional Plot Types
c a bi z
z a2 b2
tan1 b
a
b
.P
a bi
a
.P
z
a bi
8/9/2020
Hangzhou Dianzi University
2
Chapter 6 Complex Data, Character Data, and Additional Plot Types
c1 c2 (a1 a2 ) (b1 b2 )i
8/9/2020
Hangzhou Dianzi University
5
Chapter 6 Complex Data, Character Data, and Additional Plot Types
6.1.3 Complex Functions ➢ Type Conversion Functions ➢ Absolute Value and Angle Functions ➢ Mathematical Functions
8/9/2020
Hangzhou Dianzi University
8
Chapter 6 Complex Data, Character Data, and Additional Plot Types
6.1.4 Plotting Complex Data
y(t) e0.2t (cos t i sin t)
t = 0 : pi/20 : 4*pi; y = exp (-0.2*t) .* (cos(t) + i * sin(t)); plot (t, y); title ('\bfPlot of Complex Function vs Time'); xlabel ('\bf\itt'); ylabel ('\bf\ity (t)'); Warning: Imaginary parts of complex X and/or Y arguments ignored.
Description Computes the complex conjugate of a number c.
Returns the real portion of the complex number c.
Returns the imaginary portion of the complex number c. Returns true (1) if no element of array c has an imaginary component. Returns the magnitude of the complex number c.
c1 4 3i c2 3 8i
abs ( )
8/9/2020
Hangzhou Dianzi University
4
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Good Programming Practice Be careful when using the relational operators with complex numbers. The relational operators >, >=, <, <= only compare the real parts of complex numbers, not their magnitudes.
6.1.2 Using Complex Numbers with Relational Operators ➢ = ~=
c1 4 3i c2 4 3i
➢ >, <, >=, <=
t = 0 : pi/20 : 4*pi; y = exp (-0.2*t) .* (cos(t) + i * sin(t)); plot (t, real(y), 'b-'); hold on; plot (t, imag(y), 'r-'); title ('\bfPlot of Complex Function vs Time'); xlabel ('\bf\itt'); ylabel ('\bf\ity(t)'); legend ('real','imaginary'); hold off;
8/9/2020
Hangzhou Dianzi University
6
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Function conj (c) real (c) imag (c)
isreal (c)
abs (c) angle (c)
c1 c2 (a1 a2 ) (b1 b2 )i
c1 c2 (a1a2 b1b2 ) (a1b2 b1a2 )i
c1 c2
a1a2 b1b2 a22 b22b1a2 a22a1b2 b22i
8/9/2020
Hangzhou Dianzi University
3
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Returns the angle of the complex number c.
8/9/2020
Hangzhou Dianzi University
7
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Example 6.1 — The Quadratic Equation
Chapter 6 Complex Data, Character Data, and Additional Plot Types
8/9/2020
1
Chapter 6 Complex Data, Character Data, and Additional Plot Types
6.1 Complex Data
8/9/2020
Hangzhou Dianzi University
9
Chapter 6 Complex Data, Character Data, and Additional Plot Types
8/9/2020
Hangzhou Dianzi University
10
Chapter 6 Complex Data, Character Data, and Additional Plot Types
c a bi z
z a2 b2
tan1 b
a
b
.P
a bi
a
.P
z
a bi
8/9/2020
Hangzhou Dianzi University
2
Chapter 6 Complex Data, Character Data, and Additional Plot Types
c1 c2 (a1 a2 ) (b1 b2 )i
8/9/2020
Hangzhou Dianzi University
5
Chapter 6 Complex Data, Character Data, and Additional Plot Types
6.1.3 Complex Functions ➢ Type Conversion Functions ➢ Absolute Value and Angle Functions ➢ Mathematical Functions
8/9/2020
Hangzhou Dianzi University
8
Chapter 6 Complex Data, Character Data, and Additional Plot Types
6.1.4 Plotting Complex Data
y(t) e0.2t (cos t i sin t)
t = 0 : pi/20 : 4*pi; y = exp (-0.2*t) .* (cos(t) + i * sin(t)); plot (t, y); title ('\bfPlot of Complex Function vs Time'); xlabel ('\bf\itt'); ylabel ('\bf\ity (t)'); Warning: Imaginary parts of complex X and/or Y arguments ignored.
Description Computes the complex conjugate of a number c.
Returns the real portion of the complex number c.
Returns the imaginary portion of the complex number c. Returns true (1) if no element of array c has an imaginary component. Returns the magnitude of the complex number c.
c1 4 3i c2 3 8i
abs ( )
8/9/2020
Hangzhou Dianzi University
4
Chapter 6 Complex Data, Character Data, and Additional Plot Types
Good Programming Practice Be careful when using the relational operators with complex numbers. The relational operators >, >=, <, <= only compare the real parts of complex numbers, not their magnitudes.