四年级奥数巧数长正方形的个数
数正方形的规律口诀

数正方形的规律口诀
稿子一
嗨,亲爱的小伙伴们!今天咱们来聊聊数正方形的规律口诀哟!
你知道吗,数正方形这事儿啊,其实挺有趣的。
咱们先看看小的正方形,一个一个的,那数起来简单。
可要是好多正方形堆在一起,就得有点小窍门啦。
比如说,先看最小的那种正方形,一个一个地数清楚。
然后呢,再看看由几个小正方形组成的大一点的正方形。
这时候可别着急,眼睛得放亮。
还有哦,要是图形再复杂点,咱们就一层一层地来。
从里往外,或者从外往里,都可以试试。
其实啊,数正方形就像玩游戏,只要耐心点,多观察,就能找到规律。
比如说,横竖格子数一样的时候,那正方形的总数就有个特别的算法。
总之呢,数正方形别怕麻烦,多练几次,你就会发现其中的乐趣啦!怎么样,是不是觉得没那么难啦?
稿子二
嘿,朋友们!咱们来唠唠数正方形的规律口诀呀!
数正方形,刚开始可能会觉得有点晕乎,但是别慌!咱们慢慢来。
你瞧,如果是一个简单的小方格图,那就从最小的开始数呗。
一个一个,可认真啦。
要是遇到那种大一点的方格图,咱们可以先分分类。
比如说,先数单独的小正方形,再数两个小正方形拼成的,然后三个、四个……
有时候啊,你可以想象自己是个探险家,在这个方格的世界里寻找正方形的宝藏。
而且哦,你还可以边数边做记号,这样就不会乱啦。
还有一个小妙招,要是横竖的格子数量一样,那总数就可以通过一个简单的公式算出来。
是不是很神奇?
反正啊,数正方形就是要细心、耐心,多琢磨琢磨,你肯定能数得又快又准!加油哟,相信你没问题的!。
正方形个数计算方法

正方形个数计算方法人们常常在学习或工作中会遇到计算正方形个数的问题,众所周知,正方形是一种具有特殊角的四边形,由四条相等的边构成,四个角都为直角,每条边上的角相互垂直,有时我们需要求出正方形的个数,那么如何计算出正方形的个数呢?本文将带领大家全面了解和掌握正方形个数计算方法。
首先,假如有N个点,要求求出存在N个点构成的正方形的个数,这个问题也是常见的数学概念。
首先,我们需要确定是否存在四点确定一个正方形,即四点要满足以下关系:A(x1,y1)B(x2,y2)C (x3,y3)D(x4,y4),若其中任意三点不共线,且斜率 ABC、BCD、CDA、DAB相等,则满足四点确定一个正方形的条件,且边长是:- AB=√((x1-x2)^2+(y1-y2)^2)BC=√((x2-x3)^2+(y2-y3)^2)CD=√((x3-x4)^2+(y3-y4)^2)DA=√((x4-x1)^2+(y4-y1)^2)其次,求出正方形的个数,可以采用枚举法,即从 N 个点中枚举出四点,当这四点满足正方形的条件时,就算枚举出一个正方形。
当 N 个点中枚举全部的四个点组合时,就可以求出 N 个点组成的正方形的个数。
最后,要再次强调,求出正方形的个数不局限于枚举法,还可以采用组合数计算方法来解决。
比如:N个点组成的正方形的个数为C(N,4)÷4,也就是说,从N个点中枚举出4个点组成的正方形的个数为C(N,4),然后将此值除以4,即可得到N个点构成的正方形的个数。
总结以上,正方形的个数计算方法主要有两种,枚举法和组合数计算法。
其中,枚举法从N个点中枚举出4个点,满足正方形的条件,当我们枚举完全部的组合时,就可以求出N个点构成的正方形的个数;而组合数计算法则是利用公式C(N,4)÷4,其中C(N,4)表示从N个点中枚举出4个点,即可求出N个点构成的正方形的个数。
掌握了正方形个数计算方法,我们在学习和工作中所遇到计算正方形个数的问题,就可以得心应手,轻松解决,为我们节省大量的时间,提高效率。
四年级奥数巧数长正方形的个数

第 4 讲巧数长(正)方形的个数数图形时要有次序、有条理,才能不遗漏、不重复,一般步骤应是:仔细观察,发现规律,应用规律。
长方形是用“点”或者“线”来数的,而正方形是用“块”来数的。
数长方形的公式:长边上的线段和×宽边上的线段和数正方形的公式:1、一个被划分成m×n 的小正方形的长方形中共可以数出的正方形的个数是:m×n+(m-1)×(n-1)+(m-2)×(n-2 )+⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+1×【n-(m-1)】(其中m<n)2 、当m=n时,即一个划分成n×n=n2个小正方形的正方形中,共可以数出正方形的个数是:n2+(n-1)2+⋯⋯⋯⋯⋯⋯⋯⋯+22+12典型例题:1、长方形的构成必须有长和宽,下图中有许多长方形,你能数出它们有多少个?分析与解答:因为长方形的构成与长的线段数有关,也与宽的线段数有关,所以数长方形的个数必须要看长与宽两个因素上图上长有6 条线段,即3+2+1=6(个)宽边上有3 条线段,即2+1=3(个)因此,根据数长方形公式:6×3=18(个)答:上图中共有18 个长方形。
2、下图中共有多少个长方形?分析与解答:这道题比例1 横竖都多了一条线,那么长方形的个数明显增多了,利用公式仍然要数出长边上的线段数和宽边上的线段数即长边上的线段和:4+3+2+1=10 个宽边上的线段和:3+2+1=6个因此根据数长方形公式:10×6=60 个答:上图中共有60 个长方形。
3、下图中共有多少个正方形?分析与解答:我们先来数一数:只含一个正方形的有9个(即3×3=9);含有4个正方形的有4个(即2×2=4);含有9 个正方形的有1个通过刚才的数,我们发现图中正方形的个数为1× 1+2× 2+3×3=1+4+9=14 个,以后我们碰到类似的题目可以用这种方法数出正方形的个数。
人教版四年级数学奥数 数数图形(课件)(共20张PPT)

【例题1】数一数下图中有多少个锐角。
【思路导航】 数角的方法和数线段的方法类似,图中的五条射线相当于线段上的五个点, 因此,要求图中有多少个锐角,可根据公式1+2+3……(总射线数-1)求得: 1+2+3+4=10(个).
【例题2】 数一数下图中有多少个长方形?
【思路导航】 图中的AB边上有线段1+2+3=6条,把AB边上的每一条线段作为长,AD边பைடு நூலகம்的
第12讲 数数图形
小学奥数 四年级
同学们对于图形肯定不陌生,但数学中经常会出现这样的题目: (1)下图中共有几条线段? (2)下图中共有几个长方形?
要正确解答这类问题,就要做到数图形时不重复、不遗漏。这就需要 我们按照一定的顺序去数,并找出它的规律,巧妙地数出图形的个数。数 图形的方法一般有两种:按顺序数和分类数。今天就让我们用数学的方法 巧妙地数图形吧!
实践与应用
【练习5】 P94 数一数,下图中共有多少个长方形?
同学们,图形世界是不是非赏精彩呢?数学的魅力就在于千变万化的图形和数字。通过 这一进,我们对图形有了更深的认识,遇到数图形的问题也能有序、严密地思索,关于数 图形,我们来总结一些最基本的方法吧。
(1)数线段。假设端点有n个(n是整数),那么线段的总条数就是从比n小1的数开始, 一直加到1。
每一条线段作为宽,每一个长配一个宽,就组成一个长方形,所以,图中共有 6×3=18个长方形。 数长方形可以用下面的公式:长边上的线段×短边上的线段=长方形的个数
【例题3】数一数下图中有多少个正方形?(其中每个小方格都是边长为1个 长度单位的正方形)
【思路导航】 边长是1个长度单位的正方形有3×2=6个,边长是2个长度单位的正方形有 2×1=2个。所以,图中正方形的总数为:6+2=8个。 经进一步分析可以发现,一般情况下,如果一个长方形的长被分成m等份, 宽被分成n等份(长和宽的每一份都是相等的)那么正方形的总数为: mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)n.
数正方形的公式口诀

数正方形的公式口诀在初中数学中,我们常常会遇到需要数正方形的问题。
为了更便捷地计算正方形的个数,我们需要掌握几个数正方形的公式口诀。
以下就是数正方形公式口诀的详细介绍:一、以n×n的正方形为例1. 当n为奇数时,正方形的总数为:n² + (n-1)² + (n-3)² + … + 1²2. 当n为偶数时,正方形的总数为:n² + (n-2)² + (n-4)² + … + 2² + (n-1)² + (n-3)² + (n-5)² + … + 1²举例说明,当n=4时,正方形的总数为:4² + 2² + 1² = 21二、以m×n的矩形为例我们将整个矩形拆分成较小的正方形,再统计每种大小的正方形的个数,最终将它们加起来,就能得出总的正方形个数。
下面是一个m×n的矩形的分析列表:1. 大小为1的正方形个数:m×n2. 大小为2的正方形个数:(m-1)×(n-1)3. 大小为3的正方形个数:(m-2)×(n-2)4. 大小为k的正方形个数:(m-k+1)×(n-k+1)那么,矩形中所有正方形的个数为:(m×n + (m-1)×(n-1) + (m-2)×(n-2) + … + 1×1)例如,若矩形为4×3,则所有正方形的个数为:4×3 + 3×2 + 2×1 + 1×0 = 20因此,我们可利用以上公式口诀快速计算出所需的正方形个数,简化计算难度,提高计算速度。
正方形个数的规律公式

正方形个数的规律公式在我们的数学世界里,正方形可是个常见又有趣的图形。
今天,咱们就来好好聊聊关于正方形个数的规律公式。
还记得我之前教过的一个班级,有一次上课,我在黑板上画了一堆小正方形拼成的大图形,然后问同学们:“你们能快速数出这里面有多少个正方形吗?”大家顿时瞪大了眼睛,开始埋头苦数。
结果,答案五花八门,谁也说服不了谁。
这时候,有个聪明的小家伙举手说:“老师,这有没有啥规律呀?”这一问,可把大家的兴趣都勾起来了。
咱们先从简单的情况说起。
假如有一个 1×1 的方格,那里面就只有1 个正方形,这没啥好说的。
如果是 2×2 的方格呢?那可就不止 1 个了,除了单个的 1×1 的小正方形 4 个,还有一个 2×2 的大正方形,所以一共是 5 个正方形。
再看 3×3 的方格,1×1 的小正方形有 9 个,2×2 的正方形有 4 个,3×3 的大正方形有 1 个,加起来一共有 14 个正方形。
这其中的规律到底是啥呢?咱们来好好琢磨琢磨。
通过观察这些数字,你会发现,对于一个 n×n 的方格,正方形的个数可以用这样一个公式来计算:总数 = n² + (n - 1)² + (n - 2)² + …… + 1² 。
就拿刚才说的 3×3 的方格为例,按照这个公式,就是 3² + 2² + 1² =9 + 4 + 1 = 14 ,是不是和咱们数出来的结果一样?这个规律在生活中也有不少用处呢。
比如说,家里铺地砖,你想知道用同样大小的正方形地砖能拼成多少种不同大小的正方形图案,就可以用这个公式来算一算。
再回到之前的课堂上,当我把这个规律公式告诉同学们后,大家都恍然大悟,然后开始兴奋地用这个公式去计算各种不同大小方格中的正方形个数。
看着他们那认真又兴奋的样子,我心里别提多高兴了。
数正方形个数的简便方法

数正方形个数的简便方法数正方形的问题在数学中有着广泛的应用,包括计算几何、组合数学、算法等领域。
本文将介绍数正方形的简便方法,同时讨论该问题在不同领域中的应用。
一、基本概念在介绍数正方形的方法之前,我们先来回顾一下数正方形的基本概念和问题描述。
问题描述:给定一个网格图,其中有若干个正方形格子,要求计算正方形的数量。
例如下图所示的网格图中,红色方框所圈出的格子就是一个正方形。
[Image]基本概念:我们定义一个正方形的边长为k,如果这个正方形的面积为k*k,则称它为一个大小为k的正方形。
根据定义,大小为k的正方形的个数可以表示为:(n-k+1)^2,其中,n表示网格图的大小。
我们可以用一个二元组(i,j)表示一个正方形的左上角,其中,i表示该正方形在竖直方向上的位置,j表示该正方形在水平方向上的位置。
则一个大小为k的正方形就可以用左上角的坐标来表示,即左上角的坐标为(i,j)时,对应的正方形大小为k的正方形。
因此,我们可以枚举所有可能的左上角坐标,然后判断以该坐标为左上角时,能否构成一个大小为k的正方形。
假设网格图的大小为n*n,则总共有\binom{n}{2}个左上角坐标可以枚举。
二、暴力方法我们可以枚举所有可能的左上角坐标(i,j),然后检查以该坐标为左上角时,能否构成一个正方形。
如果可以,则计数器cnt+1。
最终的答案即为cnt的值。
下面是暴力枚举左上角坐标的代码实现:pythondef countSquare(n, mat):cnt = 0for i in range(n):for j in range(n):# 如果该坐标所在的格子是1if mat[i][j] == 1:# 枚举正方形边长for k in range(1, n):# 如果以该坐标为左上角的正方形大小为kif i + k < n and j + k < n and mat[i][j+k] == 1 and mat[i+k][j] == 1 and mat[i+k][j+k] == 1:# 计数器加1cnt += 1return cnt# 测试mat = [[1, 1, 1], [1, 1, 1], [1, 1, 1]]print(countSquare(3, mat))该方法的时间复杂度为O(n^5),显然随着n的大小增加,计算时间会非常长,并且难以应用到大规模数据中。
小学四年级奥数讲义

小学四年级奥数讲义需要牢背的基本概念1、加法中的巧算:加法交换律:a+b=b+a 加法结合律:a+b+c=a+(b+c)减法和加、减混合运算中的巧算:(1)一个数连续减去几个数,等于减去这几个数的和。
相反,一个数减去几个数的和,等于连续减去这几个数。
即 a-b-c=a-(b+c) a-(b+c) =a-b-c(2)在加、减混合运算中,如果算式中没有括号,那么计算时可以带着运算符号“搬家”。
如: a-b+c=a+c-b(3)加、减混合运算中去括号(或添括号)时,如果括号前面是“—”号,那么括号里“—”变“+”,“+”变“-”;如果括号前面是“+”号,那么括号里的符号不变。
如a-(b-c)=a-b+c,a+(b-c)=a+b-c如果两个数的和恰好可以凑成整十、整百、整千……的数,那么其中一个数叫做另一个数的“互补数”。
2、乘法中的巧算:乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律: (a+b)×c=a×c+b×c、 (a-b)×c=a×c-b×c 3、除法中的巧算:(1)除法交换律:a÷b÷c=a÷c÷b(2)根据“被除数和除数同时扩大或缩小相同的倍数,商不变”的规律,进行巧算。
公式:如果a÷b=c 则 (a×n)÷(b×n)=c(a÷n)÷(b÷n)=c n≠0(3)根据“一个数除以两个因数的积等于一个数连续除以这两个因数”的规律,进行巧算。
公式:a÷(b×c)= a÷b÷c(4)根据“一个数除以两个因数的商等于一个数除以第一个因数乘以第二个因数”公式:a÷(b÷c)= a÷b×c(5)除法分配律:(a + b)÷c = a÷c + b÷c a÷c +b÷c=(a + b)÷c4、你知道巧算中有几对好朋友吗?请写出来: 2×5=104×25=100 8×125=1000 16×625=10000 3×37=111 7×11×13=100137037×3=101015、“头同尾合十”:头×(头+1)×100+尾×尾“尾同头合十”:(头×头+尾)×100+尾×尾6、平方差公式: a2-b2=(a+b)×(a-b)7、配对求和,也就是等差数列求和。
数正方体个数技巧口诀

数正方体个数技巧口诀数正方体可不是小事,有时候看着那些几何图形,像是在玩一场密室逃脱游戏一样。
不过,别怕,今天咱们就来聊聊这个数正方体的技巧口诀,让你秒变“数正方体小能手”。
你得懂得咱们的大原则,那就是从大到小,一层一层来。
别急着踩着点数,先看清楚是不是正方体,是不是从小到大都一样规整。
要有耐心,这玩意可不像面条,乱七八糟的。
来来来,我们先从一层说起。
先数一下底下这层有几个正方体,别漏了角落,每个角都要摸得到。
数完第一层,别松懈,得接着上面那层。
有时候它们藏得特别深,就像找老鼠洞里的猫一样,要动动脑子。
还有个秘密技巧,有时候正方体会连着长得像个积木塔,那就一层一层往上数,别心急,慢慢来,就像泡面一样,急不得。
别以为数数就这么简单,有时候还得靠看它们排列,是不是整整齐齐的,像拍马屁一样,齐齐整整才好看。
咦,别忘了有时候还有些混蛋会躲在一些角落,真是像蚂蚁藏在大象脚底下一样,要仔细找找。
别以为眼睛数不过来就得了事,有时候得用个小工具,像放大镜一样,把每个角度都给照个遍,绝对不能偷懒。
还有个绝招,有时候你看那个形状不对,可能它就不是正方体,那就别浪费时间,扔了它,像脏衣服一样,不要留着它占地方。
记得啊,有时候你数着数着会觉得自己眼花,别怕,歇会儿眼不要逞能,眼花了就眼花了,着急也没用。
还有个经验,有时候一边数一边跟自己念叨,“一二三,四五六”,像是唱小曲儿一样,顺手又不费事。
有时候数数还挺像玩游戏,找宝藏似的,一点一点挖,可能还会有惊喜,就像开心果一样,啃啃还挺有味。
最后别忘了,有时候它们会变着花样,藏在一些看不见的地方,那就得狠下心找,别给它们机会,像老鼠过街,人人喊打。
所以啊,数正方体不是一件简单的事,得有耐心有技巧,像解数学题一样,动动脑筋,一点一滴来,别慌张,就能把它们统统揪出来。
正方形数个数的方法

正方形数个数的方法
正方形数是指形如n^2的数,其中n为整数。
求小于等于N的正方形数的个数,可以使用以下方法:
1. 从1开始,计算每个正整数的平方,如果平方数小于等于N,则将数目加1。
2. 也可以使用一种更快的方法来计算正方形数的个数。
首先,可以求出小于等于N的最大完全平方数,设为m^2。
那么小于等于N的正方形数的个数就等于m个。
例如,如果N=25,则最大的完全平方数m^2=16,因此小于等于25的正方形数的个数为16。
3. 如果想要更快地计算正方形数的个数,可以使用以下公式:小于等于N的正方形数的个数等于sqrt(N)的整数部分。
其中,sqrt 表示求平方根的函数。
例如,要计算小于等于25的正方形数的个数,可以使用公式sqrt(25)=5,结果为5个。
无论使用哪种方法,都可以得到小于等于N的正方形数的个数。
四年级奥数第一讲_速算与巧算含答案解析

第一讲 速算与巧算一、 知识点:1. 要认真观察算式中数的特点,算式中运算符号的特点。
2. 掌握基本的运算定律:乘法交换律、乘法结合律、乘法分配律。
3. 掌握速算与巧算的方法:如等差数列求知、凑整、拆数等等。
二、典例剖析:例(1) 19199199919999199999++++分析:运用凑整法来解十分方便,也不容易出错误。
解:原式()()()() =(201)+2001+20001+200001+2000001 -----=20+200+2000+20000+2000005 =2222205 =222215--练一练:898998999899998999998+++++=答案:1111098例(2)10099989796321+-+-++-+分析:暂不看头尾两个数,就会发现中间都是先加后减,并且加数与减数相差1,所以就算这题可以先把中间部分分组凑成若干个1,再与其余部分进行计算。
解:原式100(9998)(9796)(32)1=+-+-++-+100491=++150=练一练:989796959493929190894321+--++--++---++答案:99例(3) 1111111111⨯分析:111,1111121,11111112321⨯=⨯=⨯= 解:1111111111123454321⨯=练一练:2222222222⨯答案:493817284例(4) 1234314243212413+++分析:数字1、2、3、4,在个位、十位、百位、千位上均各出现一次。
解:原式1111222233334444=+++ 1111(1234)=⨯+++ 111110=⨯ 11110=练一练:5678967895789568956795678++++答案:388885例(5) 339340341342343344345++++++分析:这七个数均差1,且个数为7个,所以中间数就是七个数的中位数。
解:原式3427=⨯ 2394=练一练:(445443440439433434)6+++++÷答案:439例(6) 482594115932359⨯+⨯-⨯分析:先改变运算顺序,把4159⨯与32359⨯交换位置,48259⨯与32359⨯都有公共因素59,将48259⨯与32359⨯的差算出再与41159⨯求和。
四年级奥数-----巧数长(正)方形的个数精品资料

第4讲巧数长(正)方形的个数数图形时要有次序、有条理,才能不遗漏、不重复,一般步骤应是:仔细观察,发现规律,应用规律。
长方形是用“点”或者“线”来数的,而正方形是用“块”来数的。
数长方形的公式:长边上的线段和×宽边上的线段和数正方形的公式:1、一个被划分成m×n的小正方形的长方形中共可以数出的正方形的个数是:m×n+(m-1)×(n-1)+(m-2)×(n-2)+…………………………+1×【n-(m-1)】(其中m<n)2、当m=n时,即一个划分成n×n=n2个小正方形的正方形中,共可以数出正方形的个数是:n2+(n-1)2+……………………+22+12典型例题:1、长方形的构成必须有长和宽,下图中有许多长方形,你能数出它们有多少个?分析与解答:因为长方形的构成与长的线段数有关,也与宽的线段数有关,所以数长方形的个数必须要看长与宽两个因素。
上图上长有6条线段,即3+2+1=6(个)宽边上有3条线段,即2+1=3(个)因此,根据数长方形公式:6×3=18(个)答:上图中共有18个长方形。
2、下图中共有多少个长方形?分析与解答:这道题比例1横竖都多了一条线,那么长方形的个数明显增多了,利用公式仍然要数出长边上的线段数和宽边上的线段数即长边上的线段和:4+3+2+1=10个宽边上的线段和:3+2+1=6个因此根据数长方形公式:10×6=60个答:上图中共有60个长方形。
3、下图中共有多少个正方形?分析与解答:我们先来数一数:只含一个正方形的有9个(即3×3=9);含有4个正方形的有4个(即2×2=4);含有9个正方形的有1个。
通过刚才的数,我们发现图中正方形的个数为1×1+2×2+3×3=1+4+9=14个,以后我们碰到类似的题目可以用这种方法数出正方形的个数。
小学奥数:第18讲四年级数学图形的周长和面积教案 ;;
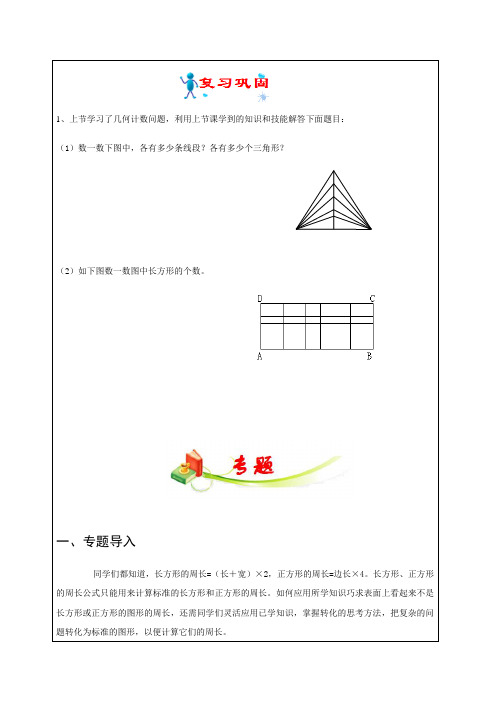
1、上节学习了几何计数问题,利用上节课学到的知识和技能解答下面题目:(1)数一数下图中,各有多少条线段?各有多少个三角形?(2)如下图数一数图中长方形的个数。
一、专题导入同学们都知道,长方形的周长=(长+宽)×2,正方形的周长=边长×4。
长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。
如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长,还需同学们灵活应用已学知识,掌握转化的思考方法,把复杂的问题转化为标准的图形,以便计算它们的周长。
二、专题精讲【例1】有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
分析解答:根据题意,我们可以把每个正方形的边长的一半同时向左、右、上、下平移(如图b),转化成一个大正方形,这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。
因此,所求周长是18×4=72厘米。
【例2 】一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?分析解答:思路导航把截掉的192平方厘米分成A、B、C三块(如图),其中AB的面积是192-4×4=176(平方厘米)。
把A和B移到一起拼成一个宽4厘米的长方形,而此长方形的长就是这块木板剩下部分的周长的一半。
176÷4=44(厘米),现在这块木板的周长是44×2=88(厘米)。
【例3 】已知下图中,甲是正方形,乙是长方形,整个图形的周长是多少?分析解答:从图中可以看出,整个图形的周长由六条线段围成,其中三条横着,三条竖着。
三条横着的线段和是(a+b)×2,三条竖着的线段和是b×2。
所以,整个图形的周长是(a+b)×2+b×2,即2a+4b。
【例4 】下图是边长为4厘米的正方形,求正方形中阴影部分的周长。
数正方形个数的方法

数正方形个数的方法在数学中,正方形是一种特殊的四边形,它的四条边长度相等,四个角都是直角。
在我们日常生活和工作中,经常会遇到需要计算正方形个数的情况,比如在布置房间地板瓷砖、设计花坛、排列货物等。
那么,如何快速准确地数正方形个数呢?下面我将介绍一些方法,希望能对大家有所帮助。
首先,我们可以利用数学知识来计算正方形的个数。
假设一个正方形的边长为a,我们可以将正方形按照边长分成不同的大小,其中边长为a的正方形有1个,边长为a/2的正方形有4个,边长为a/3的正方形有9个,以此类推,边长为a/n的正方形有n^2个。
因此,我们可以通过分解正方形的边长来计算不同大小的正方形个数,最后将它们相加即可得到总的正方形个数。
其次,我们可以利用图形的排列组合来计算正方形的个数。
假设我们有一个n×n的正方形网格,我们可以通过在网格中选择不同大小的正方形来计算总的正方形个数。
具体方法是,我们从1×1的小正方形开始,逐渐增加边长,直到边长等于n。
这样,我们就可以计算出每种边长的正方形个数,然后将它们相加即可得到总的正方形个数。
另外,我们还可以利用计数原理来计算正方形的个数。
假设我们有一个n×n的正方形网格,我们可以通过计数原理来计算正方形的个数。
具体方法是,我们可以从左上角的小正方形开始,逐渐增加边长,直到边长等于n。
这样,我们就可以计算出每种边长的正方形个数,然后将它们相加即可得到总的正方形个数。
总的来说,计算正方形个数的方法有很多种,我们可以根据实际情况选择合适的方法来进行计算。
希望以上方法能够帮助大家更快速、更准确地计算正方形的个数。
如果有更好的方法,也欢迎大家分享交流,共同进步。
谢谢!。
四年级奥数知识点

3、数值原理法.先把加在一起为整十、整百 、整千……的数相加,然后再与其它的数相加 . 4、“基准数”法,基准当几个数比较接近于 某一整数的数相加时,选这个整数为“基准数 ”(要注意把多加的数减去,把少加的数加上 ) 例题精讲
模块一:分组凑整思想 【例 1】 91.8186.789.6270.490.288.891.5
【练习3】 1.1208-569-208 2.283+69-183 3.132-85+68 4.2318+625-1318+375
【练习2】 1.50+52+53+54+51 2.262+266+270+268+264 3.89+94+92+95+93+94+88+96+87 4.381+378+382+383+379 5.1032+1028+1033+1029+1031+1030 6.2451+2452+2446+2453.
【巩固】 2006+200.6+20.06+2.006+ 994+99.4+9.94+0.994=
【例 3】 计算 56.43+12.96+13.57-4.33 -8.96-5.67
模块二、加补凑整思想 【例 5】 (1) 0.999990.99990.9990.990.9 (2)199.819.971.996 (3)999999999.799.79.7 0.7
【巩固】 199.819.971.996
第四讲 体育比赛中的数学问题
一、知识点总结 1.单循环赛:每两个队之间都要比赛一场,无主客场之分。 (通俗的说就是除了不和自己比赛,其他人都要比)
数正方形个数的题目 方法技巧

数正方形个数的题目方法技巧Counting the number of squares in a given figure is an interesting problem that often appears in math competitions and tests. It requires a combination of spatial visualization, pattern recognition, and basic counting skills. The key to solving this problem is to break down the figure into smaller parts and systematically count the number of squares in each part.数正方形个数的问题需要一定的空间想象力、模式识别能力和基本的计数技巧。
关键在于将图形分解成更小的部分,并系统地计算每个部分中正方形的个数。
在解决这个问题时,有几种常见的方法和技巧可以帮助我们更有效地找出所有的正方形。
One approach is to start by identifying the largest square in the figure and then systematically count the smaller squares contained within it. This can be done by visually scanning the figure for the largest square and then counting the number of smaller squares of different sizes that fit within it. It is important to be systematic and methodical in this process to ensure that no squares are missed or double-counted.一种方法是从识别图形中最大的正方形开始,然后系统地计算其中包含的更小正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4讲巧数长(正)方形的个数
数图形时要有次序、有条理,才能不遗漏、不重复,一般步骤应是:仔细观察,发现规律,应用规律。
长方形是用“点”或者“线”来数的,而正方形是用“块”来数的。
数长方形的公式:长边上的线段和×宽边上的线段和
数正方形的公式:1、一个被划分成m×n的小正方形的长方形中共可以数出的正方形的个数是:
m×n+(m-1)×(n-1)+(m-2)×(n-2)+…………………………+1×【n-(m-1)】(其中m<n)
2、当m=n时,即一个划分成n×n=n2个小正方形的正方形中,共可以数出正方形的个数是:n2+(n-1)2+……………………+22+12
典型例题:
1、长方形的构成必须有长和宽,下图中有许多长方形,你能数出它们有多少个?
分析与解答:
因为长方形的构成与长的线段数有关,也与宽的线段数有关,所以数长方形的个数必须要看长与宽两个因素。
上图上长有6条线段,即3+2+1=6(个)宽边上有3条线段,即2+1=3(个)因此,根据数长方形公式:6×3=18(个)
答:上图中共有18个长方形。
2、下图中共有多少个长方形?
分析与解答:
这道题比例1横竖都多了一条线,那么长方形的个数明显增多了,利用公式仍然要数出长边上的线段数和宽边上的线段数即
长边上的线段和:4+3+2+1=10个宽边上的线段和:3+2+1=6个
因此根据数长方形公式:10×6=60个
答:上图中共有60个长方形。
3、下图中共有多少个正方形?
分析与解答:
我们先来数一数:只含一个正方形的有9个(即3×3=9);含有4个正方形的有4个(即2×2=4);含有9个正方形的有1个。
通过刚才的数,我们发现图中正方形的个数为1×1+2×2+3×3=1+4+9=14个,以后我们碰到类似的题目可以用这种方法数出正方形的个数。
4、下图中共有多少个正方形?
分析与解答:
这道题显然与上题不一样,虽然都是由基本小正方形组成,但长和宽里的个数不一样,即小正方形拼接成了一个长方形,那么方法也要有所改变。
先看长边上小正方形的个数,有5个,再看宽边上小正方形的个数,有3个,我们还用数的方法试试,只含有一个小正方形的有3×5=15个,含4个小正方形的有(3-1)×(5-1)=8个,含9个小正方形的有(3-2)×(5-2)=3个,
通过刚才的数,我们发现图中正方形的个数为:
3×5+(3-1)×(5-1)+(3-2)×(5-2)=26个
答:图中共有26个正方形。
5、数一数,下图中共有多少个长方形?
分析与解答:
这道题和前4个题不同,不是横竖规范的分割,这道题意在提醒同学遇到问题不能
思维定式,不能按上面所讲的规律求解,我们可以用枚举法找出个数,灵活解决问题,先给图中每个基本图形编上序号。
再分类数一数:
(1)、6个基本图形中有4个长方形:①、③、④、⑥
(2)、由两个基本图形组成的长方形有3个:②+④、③+⑤、③+④
(3)、由3个基本图形组成的长方形有2个:①+③+⑤、②+④+⑥
(4)、由6个基本图形组成的长方形有1个:①+②+③+④+⑤+⑥
所以上图中共有长方形:4+3+2+1=10个
答:上图中共有10个长方形。
基础练习:
1、下图中共有多少个长方形?
2、下图中共有多少个长方形?
3、下图中共有多少个正方形?
4、下图中共有多少个正方形?
5、下图中共有多少个正方形?
提高练习:
1、数一数图中长方形的个数
2、数一数下图中有多少个正方形?
3、下图中共有多少个正方形?
4、下图中共有多少个正方形?。
