ABAQUS钢筋混凝土损饬塑性模型有限元分析
基于ABAQUS的钢管混凝土柱有限元分析

随着工业 的发 展 和计 算 机仿 真模 拟 技 术 的不 断提 高 , C A E技 术 的应 用 和 研 究 越 来 越 被 关 注 和 重 视 。有 限 元 法 作 为C A E领 域 的 一种 常 用 的 且 较 为 成 熟 的分 析 方 法 , 其 在 建 筑 结构研究 和实际工程应用方 面得到 了普遍 的应用 。A B A Q U S 作 为 一 款 大 型有 限元 分 析 软 件 , 其 塑 性 损 伤 模 型 具 有 非 常 好 的 应 用 前 景 和优 点 。 其 可 对 结 构 的受 荷 到破 坏 进 行 全 过 程 的 模拟分析 , 从 而 获 得 结 构 在不 同 的 受 力 阶 段 的 受 力 状 态 、 变 形 等 。对 于钢筋混 凝土结构 , 运 用该 软件进行非线性分析 , 分析
■建筑 结构
福建建设科技 2 0 1 4 . N o . 5
基于 A B A Q U S的钢 管 混 凝 土柱 有 限 元 分析
王 阳杰 ( 华侨 大学 土木 工程 学 院
[ 摘
福 建 泉州
3 6 2 0 2 1 )
要] A B A Q U S作 为一款 大型有限元分析软件 , 其在 工程结构研 究领域得到 了大量 的应 用。本文基 于混凝土损伤 塑形
N L 2 G E O M参数 。边 界条件非线性 在 A B A Q U S中主要是通过
E mb e d d e d技 术 将 钢筋 单元 埋 人 混凝 土 单 元 中 来 实 现 的 。
3研 究 对 象 及 材 料 本 构 模 型
3 . 1研 究 对 象 本 文 对 两 试 验 圆 形 钢 管 混 凝 土 柱 进 行 模 型 J 。圆柱截
T h e i f n i t e e l e me n t a n a l y s i s o f c o n c r e t e— — i f l l e d t h i n— — wa l l e d s t e e l t u b e c o l u mn s b a s e d o n AB A QU S
ABAQUS混凝土损伤塑性模型的静力性能分析

文章编号 1009-3443(2007D 03-0254-07ABAOUS 混凝土损伤塑性模型的静力性能分析方秦1还毅2张亚栋2陈力2(1.解放军理工大学训练部 江苏南京210007 2.解放军理工大学工程兵工程学院 江苏南京210007D摘要 为评估A A U 有限元软件中混凝土损伤塑性模型分析混凝土材料和构件静力性能的能力 用该模型对混凝土材料单轴 双轴应力状态下力学性能以及构件的抗弯 抗剪性能进行模拟 并与试验结果进行对比分析0结果表明 混凝土损伤塑性模型可以较为精确地模拟单轴受压 单轴受拉 双轴受压以及双轴受拉状态下混凝土材料的力学性能 能较好地反映双轴应力状态下的材料破坏包络线 也能较好地预测钢筋混凝土构件的抗弯和抗剪性能及其破坏特征 但不能很好地描述双轴拉压应力状态下混凝土材料的力学性能 也不能反映材料的体积应变发展变化规律0关键词 A A U混凝土损伤塑性模型 有限元 力学性能 抗弯性能 抗剪性能中图分类号 TU 528.58文献标识码 Al n vesti gati on i n to stati c pr oper ti es of dam aged pl asti ci tym odel for con cr ete i n ABAOUSFANG @zn 1H AN Yz 2ZHANG Yc -dong 2CHEN Lz2(1.Training department PLA Univ .of ci .S Tech . Nanjing 210007 China2.Engineering instit u te of Corps of Engineers PLA Univ .of ci .S Tech . Nanjing 210007 China DA b str act To eva lu ate the capacit y of the d amage d p l asticit y mo d e l for concrete in the finite e l ement soft-W are A A U to ana lyz e the mechanica l properties of concrete materia l an d str u ct u re the mo d e l W as a d opte d to sim ul ate the mechanica l properties of the concrete u n d er u nia X ia l an d b ia X ia l stress con d itions the f l e Xu ra l properties an d shear strength of concrete str u ct u res .The n u merica l res ul ts W ere compare d W ith the test d ata .The res ul ts sho W that the mo d e l co uld sim ul ate the mechanica l properties of concrete materia l u n d er u nia X ia l compression u nia X ia l tension b ia X ia l compression an d b ia X ia l tension con d itions an d that the mo d e l co uld ref l ect the fai lu re enve l ope of concrete materia l u n d er b ia X ia l stress con d ition proper ly .The mo d e l co uld pre d ict the f l e Xu ra l an d shear properties as W e ll as the t y pica l fai lu re mo d es of concrete str u ct u res .~o W ever the mo d e l co uld not pre d ict the mechanica l properties of concrete materia l u n d er b ia X ia l tension an d compression con d ition an d the d eve l opment l a W of the vo lu metric strain of the concrete .K ey W or ds A A U d amage d p l asticit y mo d e l for concrete finite e l ement mechanica l propert y f l e Xu -ra l propert y shear propert y收稿日期 2007-01-17.基金项目 国家自然科学基金重点资助项目(50638030D 国家杰出青年科学基金资助项目(50525825D.作者简介 方秦(1962 D 男 教授 博士生导师 研究方向防护工程 E -mai l fang in e .混凝土作为重要的建筑材料已有百余年的历史 广泛应用于各个领域0目前常采用试验以及数值模拟的方法来研究混凝土结构的力学性能0试验结果比较直观 可靠 但费用高 周期长 受试验条件影响较大0随着计算机技术和有限元数值模拟方法的发展 有限元法已成为研究混凝土结构性能的一种第8卷第3期2007年6月解放军理工大学学报(自然科学版D J o u rna l of PLA Universit y of cience an d Techno l og yV o l .8No.3Ju n.2007重要手段O在混凝土结构的数值分析中9必须考虑混凝土结构组成材料的力学性能O其中9混凝土本构模型对钢筋混凝土结构分析结果有重要影响O在建立混凝土的本构模型时往往基于已有的理论框架9如弹性理论\非线性弹性理论\弹塑性理论\粘弹性\弹粘塑性理论\断裂力学理论\损伤力学理论和内时理论等O由于混凝土材料的复杂性9还没有哪一种理论已被公认可以完全描述混凝土材料的本构关系O混凝土的本构关系主要是表达混凝土在多轴应力作用下的应力}应变关系9应力}应变曲线由上升段和下降应变软化段组成9特别是对下降段9它具有裂缝逐渐扩展9卸载时弹性软化等特点9而非线性弹性\弹塑性理论很难描述这一特性O损伤力学理论既考虑混凝土材料在未受力的初始裂缝的存在9也可反映在受力过程中由于损伤积累而产生的裂缝扩展9从而导致的应变软化O因而近年来不少学者致力于将损伤力学用于混凝土材料9并建立相应的本构关系O2O世纪O年代后期9许多学者采用损伤塑性模型对混凝土的力学性能进行描述和模拟O到目前为止9用损伤塑性模型进行的研究多为对单轴荷载作用下混凝土破坏过程的数值模拟9而多维应力作用下的混凝土破坏机制比较复杂9因此对多维应力作用下混凝土试件的破坏过程的数值模拟至今还不完善9模拟结果相差较大O目前9ANSYS\ADINA\ MARC和ABAOUS等著名的有限元分析软件都有混凝土模型9但是对它们分析混凝土结构的能力却了解不够O1混凝土损伤塑性模型ABAOUS软件中的混凝土损伤塑性模型是使用各向同性损伤弹性结合各向同性拉伸和压缩塑性的模式来表示混凝土的非弹性行为O这是一个基于塑性的连续介质损伤模型O该模型可用于单向加载\循环加载及动态加载等情况9具有较好的收敛性O1.1应变率表达式总的应变率分为弹性应变率和塑性应变率9表达式为E-=E-el+E-pl9(1)其中:E-是总应变率;E-el是弹性应变率;E-pl是塑性应变率O1.2应力}应变关系应力}应变的关系式为6=(1-c)D el O=(E-E pl)=D el=(E-E pl)9(2)其中:D elO是材料的初始(未损伤)弹性刚度;D el为损伤后的弹性刚度;c为刚度损伤变量9O{c{19材料未损坏时9c=O9材料完全损坏时9c=1O1.3屈服条件该模型用有效应力表示的屈服函数的形式为F(69E~pl)=1O(g-3O p+B(E~pl)<6^-max>-7<-6~-max>)-6c(E pl c){O9(3)其中:O和7是与尺寸无关的材料常数;p=-136= 1是有效静压力91为应力不变量;g=32~S=S是Mises等效有效应力;S=p1+6是有效应力张量6的偏分量;6^-max是6的最大特征值;函数B(E~pl)的表达式为B(E~pl)=6c(E~pl c)6t(E~pl t)(1-O)-(1+O)O1.4流动法则塑性损伤模型采用非相关联塑性流动法则:E-pl=/-8G(6)869(4)流动能G为Drucker-Prager 双曲线函数:G=(6tO tam/)2+g~2-p tam/9(5)其中:/为高侧限压力条件下p~g面中测得的膨胀角;6tO为失效时的单轴拉应力;为偏心率9表示该函数接近渐近线的速率(当=O时9G趋向于一条直线)O流动能是连续光滑的9所以流动的方向是唯一的O该函数在高侧限压力条件下9渐近地接近线性Drucker-Prager流动能并在9O 时与静压力轴相交O因为塑性流动是非相关联的9所以用塑性损伤混凝土模型需要求解非对称方程O2混凝土单\双轴受力状态下的计算2O世纪5O年代开始9许多学者对多维应力状态下的混凝土力学性能进行试验研究9其中最为经典的是1969年的Kupfer试验[1]O在试验中采用单轴强度分别为19\31.5及59MPa的3种板式试件9试件尺寸为2OO mm>2OO mm>5O mm9承受平面加载O Kupfer对各组试件在相同的条件下按照不同的应力552第3期方秦9等:ABAOUS混凝土损伤塑性模型的静力性能分析比进行加载直到破坏为止得到了单双轴状态下混凝土材料的应力应变关系和破坏准则,2.1有限元计算模型及计算参数为了精确模拟Kupfer试验混凝土试件的有限元模型尺寸为200mm>200mm>50mm采用三维8节点缩减积分单元C3D8R对模型进行离散单元尺寸为10mm>10mm>10mm整个试件共离散了2000个单元,根据Kupfer试验结果有限元计算参数如表1所示有限元模型如图1所示,表1计算参数Tab.1Computional dataE/Gpa U0/(kg m-3)6co/Mpa6cu/Mpa32.50.2 2 0011.3832.8K c//6u/Mpa6to/Mpa0.10.66671525.6 3.28图1混凝土试块的有限元模型Fig.1Finite element model for concrete specimenE为杨氏模量;U为泊松比;6c0为初始压缩屈服应力;6cu 为最大压缩屈服应力;为偏心率;Kc为屈服常数;/为膨胀角;0为密度;6u为最终压缩屈服应力;6t0为拉伸破坏应力,模拟过程中在垂直和水平两个方向分别对模型试件施加均布应力加载方式以位移控制为主具体实施方法因荷载应力比的不同有所区别,对单轴拉压以及应力比1=1的双轴拉压模拟时采用的加载方式是位移加载可以模拟出试件的应力软化段,而对应力比非1=1的双轴拉压模拟时采用的是应力加载主要考虑到如果同样采用位移加载不能保证在整个模拟过程当中保持初始的应力比这样与真实的试验是不相符的故采用应力加载对该种情况的模拟没有得出试件的应力软化段,以下分析中以拉应力为正U表示应力比,2.2单轴受力状态对混凝土单轴应力状态下数值模拟应力应变曲线与试验曲线如图2所示,图2混凝土单轴应力状态下应力应变曲线Fig.2Stress vs.strain curve of concrete under the u niaxial stress图2中6表示应力;E表示应变,由图可知单轴压缩应力状态下应力应变计算曲线与试验曲线完全重合,单轴拉伸状态下的计算曲线与试验曲线在峰值拉伸强度前也完全重合只是试验曲线未给出峰值后的变化规律,2.3双轴受力状态(1)双轴受压,双轴受压应力状态下应力应变计算曲线与试验曲线对比如图3所示,在对应力比为-1=-0.52的加载进行模拟时采用的是应力控制没有得出该情况下的软化段,由图3可知用混凝土损伤塑性模型来描述混凝土双轴受压状态下的力学性能比较准确;当G为-1=-1时计算极限强度为-38.1Mpa约为单轴抗压强度的1.16倍这与试验值比较吻合;当G为-1=-0.52时计算极限强度与试验值也相差不大,当应变随着应力增大到一定程度以后模拟曲线的应变值逐渐小于试验曲线的应变值;当U为-1=-1时模拟应力峰值点的应变值为1.96> 10-3试验峰值点的应变为2.59>10-3;当U为-1=-0.52时在E1方向模拟应力峰值点的应变值为2.39>10-3试验峰值点的应变为3.00>10-3;652解放军理工大学学报(自然科学版)第8卷图3混凝土双轴受压状态下应力应变曲线Fig.3Stress vs.strain curve of concrete under the bi-axial compressionZ方向也大致如此总的来说模拟结果均比试验结果提前达到应力最大值由此可知模拟结果偏硬(Z)双轴受拉图4是双轴受拉应力状态下数值模拟应力应变曲线与试验曲线的对比在对应力比为1 0.55的加载进行模拟时采用的是应力控制没有得出该情况下的软化段由图4可知双轴拉伸应力状态下的模拟曲线与试验曲线基本吻合如当为1 1时模拟应力峰值点的应变值为6.64> 10-5试验峰值点的应变为6.95>10-5;当o为1 0.55时在1方向模拟应力峰值点的应变值为7.76>10-5试验峰值点的应变为8.04>10-5(3)双轴拉压混凝土双轴拉压应力状态下的数值模拟曲线与试验数据对比如图5所示由该图可知当应力或应变较大时两者开始出现偏差且偏差程度随应力或应变的增大而增大总之双轴拉压应力状态下的数值模拟精度不如单轴和双轴受压~双轴受拉的情况(4)体积应变由试件在双轴受压应力状态下的3个方向的应变1~Z~3得出体积应变AV/V=1-Z-3体积应变与应力的关系曲线如图6所示可见在单轴压缩和双轴压缩情况下体积应变与应力的模拟关系曲线与试验数据的变化规律基本图4混凝土双轴受拉状态下应力应变曲线Fig.4Stress vs.strain curve of concrete under the bi-axial tension一致但是在数值上有较大偏差其原因主要是在加载过程中材料泊松比不是固定不变的尤其是在应变较大时泊松比随着应变的增大而增大许多试验都证明了这一点11*8](5)双轴应力状态下的破坏包络线图7是双轴应力状态下的破坏包络线的数值模拟结果与试验数据的对比情况总体上两者吻合较好图中Os为混凝土抗压强度3混凝土构件抗弯与抗剪性能的计算3.l单向简支板抗弯试验的有限元分析1974年S.C.Jain等人进行了单向简支板的弯曲破坏试验19]单向板的尺寸及钢筋布置如图8所示钢筋面积为1Z5mm Z配筋率为0.7Z%单向板有限元模型尺寸为38.1mm>381mm 两端简支采用三维8节点缩减积分单元CPS8R进行离散单元尺寸为19.Z75mm>76.Z mm有限元模型共离散了10个单元用关键词%REBAR定义钢筋有限元计算参数取值如表Z~3所示有限元模型如图9所示75Z第3期方秦等;ABAGUS混凝土损伤塑性模型的静力性能分析图5混凝土拉压应力应变曲线Fig.5Stress vs.strain curve of concrete under the combined compression and tension图6体积应变与应力的关系曲线Fig.6Volumetric strain vs.stress curve of concrete图7混凝土破坏包络线Fig.7Failure envelope of concrete单向板跨中截面的弯矩与跨中位移关系曲线的数值计算结果与试验结果的对比如图10所示o图中y表示跨中位移~M表示跨中截面单位宽度的弯矩由图10可知数值计算结果与试验结果吻合较好试验中最大弯矩为0-0434N m模拟结果中最大弯矩为0-0430N m两者相差不到1%;试验中单向板产生破坏时的跨中位移为4-0mm模拟结果此时的跨中位移为3-2mm两者相差约20%o该计图8钢筋混凝土单向板Fig.8One-Way reinforced concrete slab算结果与单双轴力学状态下的数值模拟结果一致模拟结果偏硬n o图11~12分别反映了板的受压和受拉损伤程度o由图11可知跨中及其附近截面的靠近上表面的区域出现了一定程度受压损伤;从图12可知板的下表面的大部分区域出现较为严重的受拉损伤这与试验观察的典型弯曲破坏结果一致o852解放军理工大学学报(自然科学版D第8卷表2钢筋混凝土单向板混凝土材料参数Tab.2Material parameter of concrete in one-way rein-f orced concrete slabE/Gpa U O c0/Mpa O cu/Mpa 290.1 24.132e0/(kg m-3)O u/Mpa O t0/Mpa0.12400 2.45 3.32表3钢筋材料参数Tab.3Material parameter of reinf orced steel bar in one-way reinf orced concrete slabE/Gpa0/(kg m-3)D O co/Mpa2007 000.3220图9钢筋混凝土单向板有限元模型Fig.9Finite element model for one-way reinforced concrete slab图10弯矩跨中位移关系曲线Fig.10Moment vs.displacement curve in mid-span of slab图11板的受压损伤程度Fig.11Compressive damage of slab3.2梁抗剪试验的有限元分析1963年,.Bresler等人进行了无腹筋简支梁图12板的受拉损伤程度Fig.12Tensile damage of slab的剪切破坏试验,试验加载及梁的尺寸和钢筋情况如图13所示[10]O图13梁的抗剪试验示意图Fig.13Configuration of shear-resistant test of beam梁的有限元模型尺寸为6400mm 556mm 307mm,两端为简支支承O采用三维节点缩减积分单元C3进行离散,单元尺寸为150mm 150mm 150mm,梁模型共离散了252个单元O钢筋层用四节点缩减积分单元FM34离散,单元尺寸为150mm 150mm,钢筋层共离散了6个单元O有限元计算参数如表4~5所示,有限元模型如图14所示,e d为最大屈服应力时段应变O施加荷载与跨中位移关系曲线的数值计算结果与试验结果的对比,如图15所示O f表示梁跨中施加的荷载O由图15可知,数值计算结果与试验结果吻合较好,梁能够承受的最大荷载试验值为37 .9kN,模拟结果值为376.3kN,两者相差不到1%试验中梁跨中最大位移为25.6mm,模拟结果值为24.2mm,两者相差6%O表试验梁的混凝土材料参数Tab.Material parameter of concrete in t e tested beam E/Gpa D O co/Mpa O cu/Mpa26.0.1 2 .1 37.577e0/(kg m-3)O u/Mpa O t0/Mpa0.12400 3.953 4.136952第3期方秦,等B混凝土损伤塑性模型的静力性能分析表5试验梁的钢筋材料参数Tab.5Material parameter of reinf orced steel bar in the tested beamE/Gpa U O co/Mpa P/(kg-m-3)O cu/Mpa E d 217.8780.3555.037800957.70.1156图14试验梁的有限元模型Fig.14Finite element model for the tested beam图15荷载梁跨中位移的关系曲线Fig.15Load vs.displacement curve in the mid-span of beam图16~17分别反映了有限元模拟梁的受压损伤和受拉损伤程度,由图16可知梁跨中上部和下部混凝土受压损伤状态较轻;由图17可知梁下部的大部分区域均出现了较为严重的受拉损伤与斜拉破坏的试验观察基本一致,图16梁的受压损伤程度Fig.16Compressive damage of beam4结论对ABAOUS有限元软件中混凝土损伤塑性模型模拟材料的力学性能以及试件的抗弯~抗剪能力和破坏特征等进行了较为系统~全面的研究并与Kupfer 等典型的试验数据进行比较分析主要结论有:(1)混凝土损伤塑性模型能较好地模拟单轴受压~单轴受拉双轴受压双轴受拉状态下混凝土材料图17梁的受拉损伤程度Fig.17Tensile damage of beam的力学性能能较好地反映双轴应力状态下的材料破坏包络线;(2)混凝土损伤塑性模型不能很好地描述双轴拉压应力状态下混凝土材料的力学性能也不能反映材料的体积应变发展变化规律模拟计算结果偏硬其主要原因是模拟计算过程中泊松比取定值与实际情况有较大偏差;(3)混凝土损伤塑性模型能较好地预测钢筋混凝土构件的抗弯和抗剪性能及其破坏特征,参考文献:[1]KUpFER H HILSD O RF H K RUSCH H.Behaviorof Concrete Under Bia x ial Stresses[J].American Concrete Institute1969 66(8):656-666.[2]过镇海.混凝土力学性能的试验研究[M].北京:清华大学出版社1996.[3]宋玉普赵国藩李玉君.双轴拉压受力状态下混凝土力学特性的试验研究[J].大连理工大学学报199131(5):579-584.[4]韩海林.钢管混凝土结构[M].北京:科学出版社2000.[5]陈惠发.土木工程材料的本构方程[M].武汉:华中科技大学出版社2001.[6]江见鲸陆新征叶列平.混凝土结构有限元分析[M].北京:清华大学出版社2004.[7]方秦张和平姜锡权.从物理机制角度探讨描述混凝土本构的途径[J].岩石力学与工程学报1999 18(4):484-486.[8]陆新征江见鲸.考虑不同破坏模式的二维混凝土本构模型[J].土木工程学报2003 36(11):70-74.[9]J AI N S C KE N N ED Y J B Y ield criterion for rein-forced concrete slabs[J].J ournal of Structural Divi-sion American Societ y of Civil Engineering1974100(3):631-644.[10]BRESLER R SC O RDELIS A C.Shear strength ofreinforced concrete beams[J].Arerican Concrete In-stitute1963 60(1):51-74.(责任编辑:汤雪峰)062解放军理工大学学报(自然科学版)第8卷ABAQUS混凝土损伤塑性模型的静力性能分析作者:方秦, 还毅, 张亚栋, 陈力, FANG Qin, HUAN Yi, ZHANG Ya-dong, CHEN Li作者单位:方秦,FANG Qin(解放军理工大学,训练部,江苏,南京,210007), 还毅,张亚栋,陈力,HUAN Yi,ZHANG Ya-dong,CHEN Li(解放军理工大学,工程兵工程学院,江苏,南京,210007)刊名:解放军理工大学学报(自然科学版)英文刊名:JOURNAL OF PLA UNIVERSITY OF SCIENCE AND TECHNOLOGY(NATURAL SCIENCE EDITION)年,卷(期):2007,8(3)被引用次数:6次1.宋玉普;赵国藩;李玉君双轴拉压受力状态下混凝土力学特性的试验研究 1991(05)2.过镇海混凝土力学性能的试验研究 19963.KUPFER H;HILSDORF H K;RUSCH H Behavior of Concrete Under Biaxial Stresses 1969(08)4.BRESLER R;SCORDELIS A C Shear strength of reinforced concrete beams 1963(01)5.JAIN S C;KENNEDY J B Yield criterion for reinforced concrete slabs 1974(03)6.陆新征;江见鲸考虑不同破坏模式的二维混凝土本构模型[期刊论文]-土木工程学报 2003(11)7.方秦;张和平;姜锡权从物理机制角度探讨描述混凝土本构的途径[期刊论文]-岩石力学与工程学报 1999(04)8.江见鲸;陆新征;叶列平混凝土结构有限元分析 20049.陈惠发;余天庆土木工程材料的本构方程 200110.韩海林钢管混凝土结构 20001.还毅.方秦.陈力.张亚栋.柳锦春大型地下空间结构地震风险评估方法[期刊论文]-解放军理工大学学报(自然科学版) 2010(4)2.王隼.李平型钢混凝土柱破坏过程数值模拟[期刊论文]-重庆交通大学学报(自然科学版) 2009(6)3.胡少伟南水北调超大钢筒混凝土管道结构安全评估[期刊论文]-水利水运工程学报 2009(4)4.HUAN Yi.FANG Qin.CHEN Li.ZHANG Yadong Evaluation of Blast-Resistant Performance Predicted by Damaged Plasticity Model for Concrete[期刊论文]-天津大学学报(英文版) 2008(6)5.CHEN Li.FANG Qin.ZHANG Yi.ZHANG Yadong Rate-Sensitive Numerical Analysis of Dynamic Responses of Arched Blast Doors Subjected to Blast Loading[期刊论文]-天津大学学报(英文版) 2008(5)6.雷拓.钱江.刘成清混凝土损伤塑性模型应用研究[期刊论文]-结构工程师 2008(2)本文链接:/Periodical_jfjlgdxxb200703011.aspx。
ABAQUS钢筋混凝土有限元分析

ABAQUS钢筋混凝土有限元分析钢筋混凝土作为一种常见的建筑材料,在建筑、交通、水利等领域得到了广泛应用。
然而,钢筋混凝土结构在服役期间会受到多种复杂荷载的作用,导致结构性能退化甚至破坏。
因此,对钢筋混凝土结构进行精确的分析和模拟至关重要。
ABAQUS是一款强大的工程仿真软件,能够模拟各种材料和结构的力学行为。
本文将介绍如何使用ABAQUS 对钢筋混凝土进行有限元分析。
ABAQUS是一款专业的有限元分析软件,它提供了丰富的材料模型库和边界条件设置功能,可以模拟各种复杂结构的力学行为。
ABAQUS具有强大的前后处理功能,用户可以通过直观的界面进行模型构建、材料属性设置、边界条件施加等操作。
同时,ABAQUS还提供了强大的数据分析和可视化工具,方便用户对模拟结果进行详细分析。
钢筋混凝土是由钢筋和混凝土两种材料组成的复合材料。
混凝土是一种抗压强度高、抗拉强度低的材料,而钢筋具有较高的抗拉强度和塑性。
将钢筋嵌入混凝土中,可以提高结构的抗拉强度、抗压强度和韧性。
钢筋混凝土还具有较好的耐久性和防火性能。
在有限元分析中,需要对钢筋混凝土的力学性能进行适当简化。
通常假定混凝土为各向同性材料,钢筋为弹塑性材料。
同时,还应考虑混凝土的裂缝、损伤以及钢筋与混凝土之间的粘结和滑移等因素。
在ABAQUS中,可以对钢筋混凝土结构进行详细的有限元分析。
需要建立合适的计算模型,包括几何模型、材料属性、边界条件和荷载等。
模型建立完成后,可以通过ABAQUS的求解器进行计算,得到各节点位移、应力、应变等结果。
通过对计算结果的分析,可以评价结构的性能和安全性。
例如,可以通过应力和应变分布情况,分析结构的整体和局部稳定性、裂缝分布及扩展等。
还可以观察钢筋与混凝土之间的粘结性能以及评估结构的耐久性。
本文介绍了如何使用ABAQUS对钢筋混凝土进行有限元分析。
通过建立合适的计算模型,设置材料属性和边界条件,以及进行求解计算,可以得到结构的详细应力、应变和位移分布情况。
Abaqus混凝土材料模型解读与参数设置

Abaqus混凝土材料塑性损伤模型浅析与参数设置【壹讲壹插件】欢迎转载,作者:星辰-北极星,QQ群:431603427Abaqus混凝土材料塑性损伤模型浅析与参数设置 (1)第一部分:Abaqus自带混凝土材料的塑性损伤模型 (2)1.1概要 (2)1.2学习笔记 (2)1.3 参数定义与说明 (3)1.3.1材料模型选择:Concrete Damaged Plasticity (3)1.3.2 混凝土塑性参数定义 (3)1.3.3 混凝土损伤参数定义: (4)1.3.4 损伤参数定义与输出损伤之间的关系 (4)1.3.5 输出参数: (4)第二部分:根据GB50010-2010定义材料损伤值 (5)第三部分:星辰-北极星插件介绍:POLARIS-CONCRETE (6)3.1 概要 (6)3.2 插件的主要功能 (6)3.3 插件使用方法: (6)3.3.1 插件界面: (6)3.3.2 生成结果 (7)3.4、算例: (9)3.4.1三维实体简支梁模型说明 (9)3.4.2 计算结果: (9)第一部分:Abaqus自带混凝土材料的塑性损伤模型1.1概要首先我要了解Abaqus内自带的参数模型是怎样的,了解其塑性模型,进而了解其损伤模型,其帮助文档Abaqus Theory Manual 4.5.1 An inelastic constitutive model for concrete讲述的是其非弹性本构,4.5.2 Damaged plasticity model for concrete and other quasi-brittle materials则讲述的塑性损伤模型,同时在Abaqus Analysis User's Manual 22.6 Concrete也讲述了相应的内容。
1.2学习笔记1、混凝土塑性损伤本构模型中的损伤是一标量值,数值范围为(0无损伤~1完全失效[对于混凝土塑性损伤一般不存在]);2、仅适用于脆性材料在中等围压条件(为围压小于轴抗压强度1/4);3、拉压强度可设置成不同数值;4、可实现交变载荷下的刚度恢复;默认条件下,由拉转压刚度恢复,由压转拉刚度不变;5、强度与应变率相关;6、使用的是非相关联流动法则,刚度矩阵为非对称,因此在隐式分析步设置时,需在分析定义other-》Matrix storate-》Unsymmetric。
ABAQUS混凝土塑性损伤模型

4.5.2 混凝土和其它准脆性材料的塑性损伤模型这部分介绍的是ABAQUS提供分析混凝土和其它准脆性材料的混凝土塑性损伤模型。
ABAQUS 材料库中也包括分析混凝的其它模型如基于弥散裂纹方法的土本构模型。
他们分别是在ABAQUS/Standard “An inelastic constitutive model for concrete,” Section 4.5.1, 中的弥散裂纹模型和在ABAQUS/Explicit, “A cracking model for concrete and other brittle materials,” Section 4.5.3中的脆性开裂模型。
混凝土塑性损伤模型主要是用来为分析混凝土结构在循环和动力荷载作用下的提供一个普遍分析模型。
该模型也适用于其它准脆性材料如岩石、砂浆和陶瓷的分析;本节将以混凝土的力学行为来演示本模型的一些特点。
在较低的围压下混凝土表现出脆性性质,主要的失效机制是拉力作用下的开裂失效和压力作用下的压碎。
当围压足够大能够阻止裂纹开裂时脆性就不太明显了。
这种情况下混凝土失效主要表现为微孔洞结构的聚集和坍塌,从而导致混凝土的宏观力学性质表现得像具有强化性质的延性材料那样。
本节介绍的塑性损伤模型并不能有效模拟混凝土在高围压作用下的力学行为。
而只能模拟混凝土和其它脆性材料在与中等围压条件(围压通常小于单轴抗压强度的四分之一或五分之一)下不可逆损伤有关的一些特性。
这些特性在宏观上表现如下:•单拉和单压强度不同,单压强度是单拉强度的10倍甚至更多;•受拉软化,而受压在软化前存在强化;•在循环荷载(压)下存在刚度恢复;•率敏感性,尤其是强度随应变率增加而有较大的提高。
概论混凝土非粘性塑性损伤模型的基本要点介绍如下:应变率分解对率无关的模型附加假定应变率是可以如下分解的:是总应变率,是应变率的弹性部分,是应变率的塑性部分。
应力应变关系应力应变关系为下列弹性标量损伤关系:其中是材料的初始(无损)刚度,是有损刚度,是刚度退化变量其值在0(无损)到1(完全失效)之间变化,与失效机制(开裂和压碎)相关的损伤导致了弹性刚度的退化。
ABAQUS混凝土框架有限元计算分析
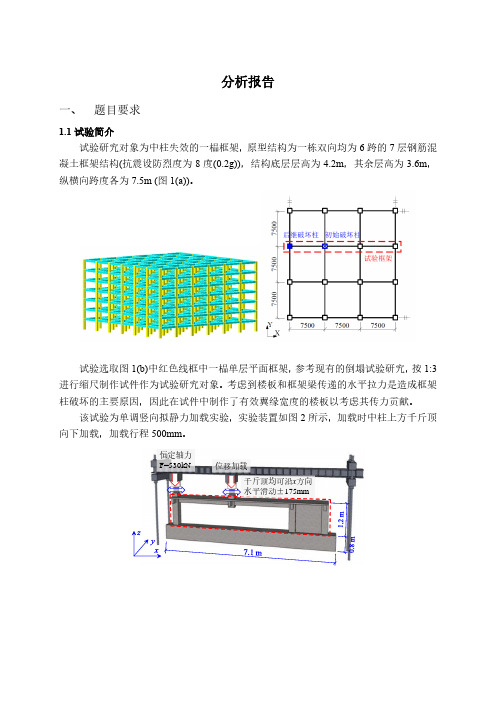
“悬链线”,继续维持该梁一定的承载力。 2.4 加载点荷载-位移曲线
通过计算分析得到的结果,绘制加载点的荷载-位移曲线如下图所示:
荷载/KN
加载点力-位移曲线
120 100
80 60
40
20
0 0
100
200
300
400
500
600
位移/mm
图 2.13 加载点力-位移曲线 通过加载点力-位移曲线可以看到,当位移超过 80mm 后该结构的承载力有所下 降,但下降幅度不大,在 240mm 后荷载保持稳定,值里可以看到梁内塑性铰形成的 “悬链线”机制发挥出来抗倒塌的作用。但是之后还有些许上升,可能是因为计算模 型对于下降段的模拟不够准确所致。
D6
394
519
220
0.3
D10
419
617
219
0.3
D12
625
685
钢筋应力-应变曲线如下图所示:
171
0.3
stress
钢筋应力-应变关系曲线
700
600
500
400
Φ6 300
Φ10 200
Φ12
100
0
0
0.001 0.002 0.003 0.004 0.005 0.006
strain
σ = (1 − ������������)������������������
1 − ������������[1.2 − 0.2 ������5]
������������
=
{1
−
������������(������
������������ − 1)1.7
+
混凝土塑性损伤模型及其ABAQUS子程序开发

模型原理
模型原理
ABAQUS混凝土塑性损伤模型基于应力-应变量关系,通过引入损伤变量来描述 混凝土材料的微观结构变化。该模型假定混凝土是由许多小的弹性体和塑性体组 成的复合材料,当应力超过一定阈值时,塑性体将发生塑性变形。同时,当损伤 积累到一定程度时,混凝土将发生破坏。
模型特点
模型特点
ABAQUS混凝土塑性损伤模型具有以下特点: 1、有限元模拟:该模型能够实现混凝土结构的有限元模拟,从而得到更精确 的应力、应变和损伤分布。
4、进行模拟分析:设置好模拟分析的参数和初始条件,进行混凝土结构的模 拟分析,并得到相应的结果。
参考内容
内容摘要
关键词:混凝土塑性损伤,ABAQUS,用户子程序,有限元分析,材料损伤 在土木工程和材料科学领域,混凝土塑性损伤的研究具有重要的实际意义。 为了更准确地模拟混凝土在加载过程中的塑性行为和损伤演化,本次演示将介绍 如何利用ABAQUS用户子程序进行混凝土塑性损伤模拟。
1、确定混凝土塑性损伤模型的数学表达式:根据前述的屈服准则、塑性势函 数、损伤演化方程和断裂准则等,确定模型的具体数学表达式。
4、断裂准则:描述混凝土达到极限状态时的断裂条件,一般采用应 力失效准则或应变失效准则。
2、编写子程序代码:使用ABAQUS提供的Python API或C++ API等编程接口, 编写实现混凝土塑性损伤模型的子程序代码。其中,需要实现模型的各个组成部 分,如屈服准则、塑性势函数、损伤演化方程等。
一般来说,混凝土塑性损伤模型由以下几部分构成: 1、屈服准则:描述混凝土开始进入塑性变形的应力状态,一般采用米泽斯 (Mises)屈服准则或相关改进型屈服准则。
混凝土塑性损伤模型
2、塑性势函数:描述混凝土在塑性变形过程中的应变软化效应,常用的有德 鲁克-普拉格(Drucker-Prager)模型、摩尔-库仑(Mohr-Coulomb)模型等。
ABAQUS混凝土损伤塑性模型参数标定及验证_刘巍

dt σt ( 1 - d t ) E0
( 3)
在定义受压硬化时, 硬化数据是根据非弹性应 pl ABAQUS 中等效塑性应变 ε 珘 变ε 珘 定义的, c 和非弹 性应变 ε 珘 c 的关系如下 :
pl in ε 珘 珘 c = ε c - in
dc σc ( 1 - d c ) E0
( 4)
ck 珘 单轴受拉应力应变关系及开裂应变 ε t 示意
( 5)
损伤因子 d 为应力状态和单轴损伤变量 d t 和 ( 6)
图1
式中: s t 和 s c 是与应力反向有关的刚度恢复下的应 力状态函数, 它们可根据下面方程定义: s t = 1 - w t r * ( σ11 ) s c = 1 - w c ( 1 - r ( σ11 ) ) 其中 r * ( σ11 ) = H( σ11 ) =
Industrial Construction Vol. 44 ,Supplement, 2014
工业建筑 2014 年第 44 卷增刊 167
1
混凝土损伤塑性模型理论 ABAQUS 中的 CDP 模型是连续的、 基于塑性的
变形特性, 可以用式( 1 ) 、 式( 2 ) 描述。 pl 珘 σ t = ( 1 - d t ) E0 ( ε t - ε t )
pl pl pl pl
( 2) 珘) σ c = ( 1 - d c ) E0 ( ε c - ε 在采用 CDP 模型对钢筋混凝土结构进行模拟 时, 钢筋与混凝土的界面效应 ( 如粘结滑移和锁固 行为) 通过在混凝土模型中引入“拉伸硬化 ” 来模拟 钢筋与混凝土在开裂区的荷载传递作用 。拉伸硬化 ck ABAQUS 的数据是根据开裂应变 ε 珘 t 进 行 定 义 的, 珘 中等效塑性应变 ε 珘 t 和开裂应变 ε t 的关系如下 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ABAQUS钢筋混凝土损饬塑性模型有限元分析
发表时间:2009-10-12 刘劲松刘红军来源:万方数据
钢筋混凝土材料,是一种非匀质的力学性能复杂的建筑材料。
随着计算机和有限元方法的发展,有限元法已经成为研究混凝土结构的一个重要的手段。
由于数值计算具有快速、代价低和易于实现等诸多优点,这种分析方法已经广泛用于实际工程中。
然而,要在有限元软件中尽可能准确地模拟混凝土这种材料,是不容易的,国内外学者提出了基于各种理论的混凝土本构模型。
但是迄今为止,还没有一种理论被公认为可以完全描述混凝土的本构关系。
ABAQUS是大型通用的有限元分析软件,其在非线性分析方面的巨大优势,获得了广大用户的认可,在结构分析领域的应用趋于广泛。
本文把规范建议的混凝土本构关系,应用到损伤塑性模型,对一悬臂梁进行了精细的有限元建模计算和探讨。
1 混凝土损伤塑性模型
ABAQUS在钢筋混凝土分析上有很强的能力。
它提供了三种混凝土本构模型:混凝土损伤塑性模型,混凝土弥散裂缝模型和ABAQUS/Explicit中的混凝土开裂模型。
其中混凝土损伤塑性模型可以用于单向加载、循环加载以及动态加载等场合,它使用非关联多硬化塑性和各向同性损伤弹性相结合的方式描述了混凝土破碎过程中发生的不可恢复的损伤。
这一特性使得损伤塑性模型具有更好的收敛性。
2 模型材料的定义
2.1 混凝土的单轴拉压应力-应变曲线
本模型中选用的混凝土本构关系是《混凝土结构设计规范》所建议的曲线,其应力应变关系可由函数表达式定义。
2.2 钢筋的本构关系
钢筋采用本构关系为强化的二折线模型,无刚度退化。
折线第一上升段的斜率,为钢筋本身的弹性模量,第二上升段为钢筋强化段,此时的斜率大致可取为第一段的1/100。
2.3 损伤的定义
损伤是指在单调加载或重复加载下,材料性质所产生的一种劣化现象,损伤在宏观方面的表现就是(微)裂纹的产生。
材料的损伤状态,可以用损伤因子来描述。
根据前面确定的混凝土非弹性阶段的应力一应变关系。
可求得损伤因子的数值。
2.4混凝土塑性数值的计算
混凝土在单向拉伸,压缩试验中得到的数据,通常是以名义应变和名义应力表示的,为了准确地描述大变形过程中截面积的改变,需要使用真实应变和真实应力,可通过它们之间的换算公式计算。
真实应变是由塑性应变和弹性应变两部分构成的。
在ABAQUS中定义塑性材料参数时,需要使用塑性应变。
3 钢筋混凝土悬臂梁实例分析
3.1 模型设计
该悬臂梁的具体情况如图1所示,梁截面尺寸为200mm×300mm,梁长1500mm;纵筋为HRB335钢筋,箍筋为HPB235钢筋,混凝土强度等级为C30。
混凝土和钢筋的各力学参数均取自《混凝土结构设计规范》的标准值。
图1 悬臂梁配筋详图
3.2 有限元模型及钢筋混凝土参数计算
混凝土和钢筋分别采用C3D8R单元和T3D2单元进行分离式建模,并采用Embedded技术进行自由度耦合。
为了避免梁端因为应力集中导致局部损坏,在梁端设置了一个矩形离散刚片,荷载施加在刚片的参考点上。
受拉主筋的屈服点为335MPa,此时对应的非弹性应变为0。
当应力为355MPa时,塑性应变ε=335/200000+(335-335)/2000-355/200000=0.0099。
为了方便计算,取应力为355时的塑性应变为0.01。
3.3 计算结果
(1)梁端位移控制:在梁端施加向下的50mm的位移,得到的荷载-位移曲线如图2所示。
从图中可以看出,在荷载达到10kN前,构件基本处于弹性阶段,主要是受拉混凝土还未开裂;之后混凝土受拉开裂,拉应力全部由受拉主筋承担。
极限承载力达到了52kN,此时的位移大约是20mm。
钢筋屈服时(意味着梁也屈服了)对应的荷载是43kN,对应的屈服位移是9mm。
图2 荷载-位移曲线
理论计算悬臂梁的屈服荷载,即单筋矩形梁正截面抗弯计算:
混凝土受压区高度x=335×763/(20.1×200)=64(mm)
梁端屈服荷载F=763×335×(300-34-64/2)/1.5=40(kN)
由此可见,有限元结果与理论计算结果相差大约7%,说明模拟结果还是非常可信的。
(2)梁端荷载控制:在梁端施加向下的60kN的荷载。
当受拉主筋屈服的时候对应的荷载为42.8kN,屈服位移为9mm,跟之前的位移控制得出的结论基本完全一致。
说明了对悬臂梁的屈服,梁端的荷载控制加载和位移控制加载是一样的。
这两种方法同样适用。
梁屈服时混凝土的受拉损伤如图3所示。
从图中可以看出,在混凝土受拉区域,根部损伤严重,说明这部分混凝土已经受拉开裂了。
从根部到端部损伤越来越小,而且只出现在受拉区域,这与理论分析完全相符;这说明损伤因子可以形象的反应混凝土的受损情况。
图3 混凝土受拉损伤云图
4 数值计算分析
4.1 粘性系数
在定义混凝土的粘性系数时,粘性系数越大,结构越刚硬,就像越粘稠的液体越难流动一样,粘性系数越小,计算效率很低,很难收敛。
作者通过对粘性系数取0.01、0.005、0.001、0.0005这四种情况的比较,发现当取0.0005和0.001时计算不收敛;取0.01时的荷载位移曲线一直处于上升阶段,说明刚化了结构。
从前面的计算结果来看,取0.005时还是比较好的。
4.2 混凝土受拉损伤
从图4计算结果比较可得,是否考虑混凝土受拉损伤对计算结果影响较大,不考虑损伤时的极限承载力,比考虑损伤时要大10%左右,显然从前面的计算结果可以看出,当考虑损伤时要更为合理,这一特性与混凝土的实际受力是吻合的。
图4 是否考虑混凝土受拉损伤的荷载-位移曲线
5 结束语
通过本文分析,主要得到以下结论:
(1)混凝土损伤塑性模型,以混凝土受压破碎和受拉开裂为准则。
通过该悬臂梁算例,可知此模型在ABAQUS中模拟混凝士材料的非线性关系是行之有效的。
(2)求解混凝土,一般都会碰到计算收敛的问题,参数取值合理是大有帮助的。
对于混凝土的粘性系数、膨胀角等,都值得反复推敲;初始增量步的大小也很重要,模型复杂和受荷载较大的时候,建议尽量取小值,不然计算难以收敛。
(3)ABAQUS提供的Embedded技术,可以方便地解决钢筋与混凝土之间的粘结关系,使建模变得更加的高效和容易实现精细建模,但是它实现不了钢筋的滑移等。
如何用有限元软件方便地模拟钢筋与混凝土之问的关系,需要作进一步深入的研究。
