初中几何最全的模型及证明
完整版)初中数学几何模型大全+经典题型(含答案)

完整版)初中数学几何模型大全+经典题型(含答案)通过将倍长中点相关线段进行旋转变换,可以构造出旋转全等模型。
这种模型的特点是,将相邻等线段所成角的一半旋转后拼接在一起,形成对称全等。
同时,也可以通过将两个等腰三角形或正多边形的夹角进行变化,来构造出模型变形。
如果遇到复杂图形找不到旋转全等,可以先找到两个正多边形或等腰三角形的公共极点,然后围绕公共极点找到两组相邻等线段,分组组成三角形证全等。
幂定理可以用等线段、等比值、等乘积进行代换,从而将两个数之间的比值转换成乘积。
在相似证明中,常用的辅助线是平行线,根据题目条件来确定比值并做出相应的平行线。
题目一:在半圆中,圆心为O,圆上有点C、E,CD垂直于AB,EF垂直于AB,EG垂直于CO。
证明CD等于GF。
题目二:在正方形ABCD内部,点P满足∠PAD=∠PDA=15度。
证明△PBC是正三角形。
题目三:在图中,ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点。
证明A2B2C2D2是正方形。
题目四:在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F。
证明∠DEN=∠F。
题目五:在△ABC中,H为垂心,O为外心,且OM垂直于BC于M。
1)证明AH等于2OM;2)如果∠BAC等于60度,证明AH等于AO。
1.设P为正三角形ABC内任意一点,连接PA,PB,PC,由三角形不等式可得PA+PB>AB。
PB+PC>BC。
PC+PA>CA。
将三式相加得到2PA+2PB+2PC>AB+BC+CA=3,即PA+PB+PC>3/2.又由于P到三角形三边的距离不超过1,所以PA+PB+PC<3,综上可得1.5≤PA+PB+PC<3,即所求不等式成立。
2.设P为正方形ABCD内任意一点,连接PA,PB,PC,PD。
由于正方形四边相等,所以PA+PC=2,PB+PD=2.又由于P到四边的距离不超过1,所以PA+PB+PC+PD<4.将前两式相加得到PA+PB+PC+PD=2(PA+PB)/2+2(PC+PD)/2≥2√(PA·PB)+2√(PC·P D)。
初中数学9大几何模型(证明结论及推导)
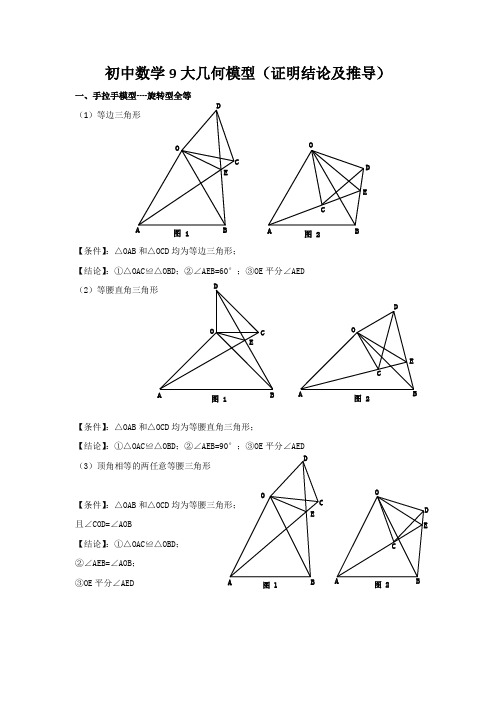
初中数学9大几何模型(证明结论及推导)一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CDO ABCDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中数学几何模型大全

初中数学几何模型大全全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
个角是 30°直角三角形的对称(翻折),翻折成正方 形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型 半角:有一个角含 1/2 角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等 中点旋转:倍长中点相关线段转换成旋转全等问题说明:上图依次是 45°、30°、22.5 15°及有一说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60 度旋60 度,造等边三角形遇90 度旋90 度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180 度,造中心对称说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“ 8 ”字模型可以证明。
共旋转模型模型变形说明:模型变形主要是两个正多边形或者等腰三角形 的夹角的变化,另外是等腰直角三角形与正方形的混 用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
初中数学几何模型大全

初中数学几何模型大全初中数学几何模型大全全等变换:平移:平移是指将平行等线段(平行四边形)沿着相同的方向平移相同的距离。
这种变换可以用来构造平行四边形。
对称:对称变换可以通过角平分线、垂直线或半角来进行。
这种变换可以用来构造对称全等的图形。
旋转:旋转变换是指将相邻等线段绕公共顶点进行旋转。
这种变换可以用来构造旋转全等的图形。
对称全等模型:这种模型是以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型:这种模型是通过翻折构造对称全等的图形。
可以通过上图中的45°、30°、22.5°、15°及有一个角是30°直角三角形的对称来实现。
翻折后可以得到正方形或者等腰直角三角形、等边三角形、对称全等的图形。
旋转全等模型:半角:这种模型是指相邻等线段所成角含1/2角及相邻线段。
通过旋转将另外两个和为二分之一的角拼接在一起,形成对称全等的图形。
自旋转:这种模型是指有一对相邻等线段,需要构造旋转全等。
可以通过遇到60度旋60度,造等边三角形;遇到90度旋90度,造等腰直角;遇到等腰旋顶点,造旋转全等;遇中点旋180度,造中心对称的方法来实现。
共旋转:这种模型是指有两对相邻等线段,直接寻找旋转全等中点。
通过旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
可以通过“8”字模型来证明。
模型变形:这种变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,可以先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:这种模型是指通过两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
初中数学九大几何模型

【结论】:①△OAC^/XOB:):②ZAEB=60° : ®0E 平分NAED【结论】:①△OAC^/XOB:):②ZAEB=90° : ®OE 平分NAED初中数学九大几何模型【条件】:AOAB ^AOCD 均为等腰直角三角形:(3)顶角相等的两任意等腰三角形 【条件】:AOAB ^AOCD 均为等腰三角形; 且 ZCOD=ZAOB【结论】:①△OACq/XOB): ② ZAEB=ZAOB :®OE 平分 NAED模型二:手拉手模型——旋转型相似 (1) 一般情况【条件】:CD/7AB,将2X0CD 旋转至右图的位豈 将八。
旋转至右图的位【结论】:①右图中ZkOCDs△OABT t t AOAC^AOBD: ②延长AC 交BD 于点E,於有ZBEC=ZBQ/\ (2)特殊情况【条件】:CD/7AB, ZA03=90c 【结论】:①右图中ZkOCDs△OABT t t AOAC^AOBD : ② 延长AC 交BD 于点E,必有ZBEC=ZBOA : ③ BD = OD = OB =tanZ0C [):④BD 丄AC : AC OC OA =-ACxBD模型三、对角互补模型(1)全等型-90°【条件】:①ZA0B=ZDCE=90° :②0C 平分NAOB证明提示: ①作垂直,如图2,证明△ CDM^ACEN ②过点C 作CF 丄0C,如图3,证明△ ODC^ZXFEC 楽当ZDCE 的一边交A0的延长线于D 时(如图4)9 以上三个结论:©CD=CE: @0E-0D=j2 0C: S 4⑤连接 AD 、BC.必有AD?+BC2 = AB? +CD 2: 图3【结论】:®CD=CE:②OD+OE=JiOC:(1),皿 =S 场 + S* =三。
芒 ③膈(2)全等型-120°【条件】:®ZA0B=2ZDCE=120° :②OC 平分NA0B【结论】:©CD=CE:②0D+0E=0C:③S.好Sg +证明提示:①可参考“全等型-90° "证法一:②如右下图:在0B上取一点F,使0F=0C,证明ZX0CF为等边三角形。
完整版)初中数学经典几何模型

完整版)初中数学经典几何模型初中数学经典几何模型(模型即套路),是初中数学里的重要部分。
在解决几何证明问题时,我们可以运用这些模型,从而更加高效地解决问题。
人们常说几何很困难,其中一个难点就在于辅助线的运用。
为了更好地运用辅助线,我们需要把握定理和概念,并且刻苦加钻研,找出规律凭经验。
在绘制图形时,我们可以利用角平分线向两边作垂线,或者将图形对折来寻找对称关系。
利用角平分线的平行线,我们可以构造等腰三角形。
同时,我们也可以尝试将角平分线加上垂线,从而将三条线合为一条。
线段垂直平分线时,我们可以将线段向两端延长或缩短来验证线段的倍数与半数关系。
在三角形中,连接两中点可以构造出中位线,同时延长中线也可以等于中线。
对于平行四边形,我们可以找到对称中心等分点。
在梯形中,我们可以利用高线平移一腰来解决问题。
同时,平行移动对角线,补成三角形也是常见的方法。
当证明相似时,我们可以通过比线段,添加平行线来构造相似三角形。
在等积式子比例换时,寻找线段也是很关键的。
直接证明有困难时,我们可以通过等量代换来简化问题。
在计算圆的相关问题时,我们可以利用半径与弦长计算,或者利用勾股定理来计算切线长度。
同时,在判断是否为切线时,我们可以通过半径垂线来进行辨别。
在解决相交圆的问题时,我们需要注意作公共弦。
对于内外相切的两个圆,我们可以通过切点来构造公切线。
同时,我们也可以利用连心线来确定切点。
在绘制图形时,我们需要注意勿改变虚线的位置。
基本作图也是很关键的,我们需要熟练掌握。
在解题时,我们需要多动脑筋,经常总结方法。
同时,我们也需要注意方法的灵活性,不要盲目乱添线。
在选用分析综合方法时,我们需要根据具体情况进行选择。
最重要的是,我们需要虚心勤学,加以苦练,才能在数学上取得更好的成绩。
斜边上作高线,比例中项一大片。
--。
在斜边上作高线,可以得到比例中项一大片。
半径与弦长计算,弦心距来中间站。
--。
通过计算半径和弦长,可以得到弦心距。
(完整版)初中数学——最全:初中数学几何模型.docx
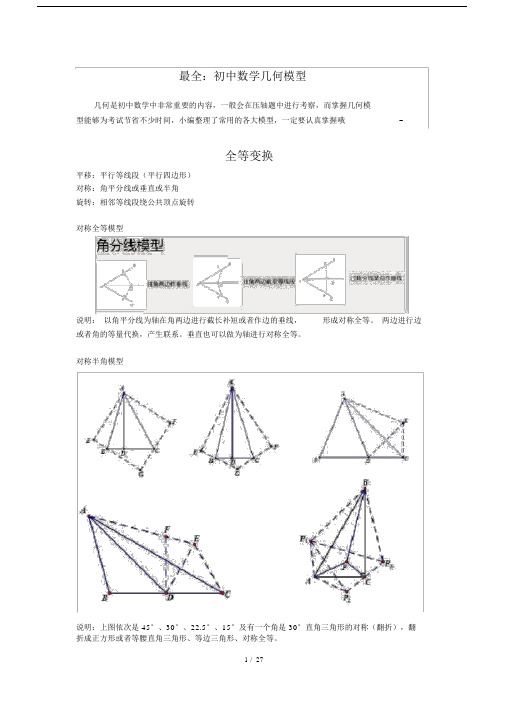
最全:初中数学几何模型几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,小编整理了常用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是 45°、30°、22.5°、15°及有一个角是 30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2 角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇 60 度旋 60 度,造等边三角形;遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等;遇中点旋180 度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
(完整版)初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
八年级几何证明常见模型
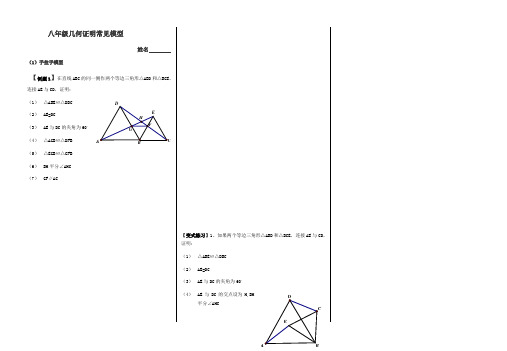
八年级几何证明常见模型(1)手拉手模型【例题1】在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) AE=DC(3) AE 与DC 的夹角为60。
(4) △AGB ≌△DFB (5) △EGB ≌△CFB(6) BH 平分∠AHC(7) GF ∥AC【变式练习】1、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明:(1) △ABE ≌△DBC(2) AE=DC(3) AE 与DC 的夹角为60。
(4) AE 与DC 的交点设为H,BH平分∠AHCA2:如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:(1)△ABE≌△DBC(2)AE=DC(3)AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分∠AHC 【例题2】如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H问:(1)△ADG≌△CDE是否成立?(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分∠AHE?F【变式练习】1:如图两个等腰直角三角形ADC 与EDG ,连接AG,CE,二者相交于H.问 (1)△ADG ≌△CDE 是否成立?(2)AG 是否与CE 相等? (3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分∠AHE ?2:两个等腰三角形ABD 与BCE ,其中AB=BD,CB=EB,∠ABD=∠CBE=a 连接AE 与CD.问(1)△ABE ≌△DBC 是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?A(4)HB 是否平分∠AHC ?【例题3】如图1,AB=AE ,AC=AD ,∠BAE=∠CAD=90°. (1)证明:EC=BD ; (2)证明:EC ⊥BD ;(3)如图2,连接ED ,若N 点为DE 的中点,连接NA 并延长与BC 交于点M ,证明:AM ⊥BC .HABCE【变式练习】1,⊿ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向⊿ABC作等腰Rt⊿ABE和等腰Rt⊿ACF,过点E、F作射线GA的垂线,垂足分别为P、Q。
(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
中考数学:初中数学几何模型大全+经典题型含答案

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
初中数学几何模型归纳

初中数学几何模型归纳1. 直线模型:直线是最基本的几何图形,可以用直线方程y = kx + b 来表示。
其中,k 是斜率,b 是截距。
2. 点模型:点是几何图形中的基本元素,可以用坐标(x, y) 来表示。
3. 线段模型:线段是由两个端点确定的有限长度的直线部分。
线段可以用起点和终点的坐标来表示。
4. 射线模型:射线是由一个端点和一个方向确定的无限延伸的直线部分。
射线可以用起点和方向向量来表示。
5. 角模型:角是由两条射线的公共端点和这两条射线之间的夹角组成的。
角可以用顶点、始边和终边来表示。
6. 三角形模型:三角形是由三条边和三个内角组成的多边形。
三角形可以用三边的长度和三个内角的大小来表示。
7. 四边形模型:四边形是由四条边和四个内角组成的多边形。
四边形可以用四边的长度和四个内角的大小来表示。
8. 圆模型:圆是由一个圆心和一个半径确定的平面上的所有点到圆心的距离都等于半径的图形。
圆可以用圆心和半径来表示。
9. 椭圆模型:椭圆是由两个焦点和一个长轴、短轴确定的平面上的所有点到两个焦点的距离之和等于常数的图形。
椭圆可以用两个焦点和长轴、短轴的长度来表示。
10. 双曲线模型:双曲线是由两个焦点和一个实轴、虚轴确定的平面上的所有点到两个焦点的距离之差等于常数的图形。
双曲线可以用两个焦点和实轴、虚轴的长度来表示。
11. 正多边形模型:正多边形是由相等的边和相等的内角组成的多边形。
正多边形可以用边数和内角度数来表示。
12. 梯形模型:梯形是由一对平行边和一对非平行边组成的四边形。
梯形可以用两对边的长度和夹角来表示。
13. 矩形模型:矩形是由四个直角和两对相等的边组成的四边形。
矩形可以用两对边的长度和夹角来表示。
14. 正方形模型:正方形是特殊的矩形,它的四个边都相等且四个角都是直角。
正方形可以用边长来表示。
15. 三角形面积模型:三角形的面积可以通过底边长度和高来计算,公式为S = (底边长度×高) / 2。
八年级几何证明常见模型

在几何证明中,有一些常见的模型经常被用到。
这些模型涵盖了几何学中的基本概念和性质,帮助我们理解和证明各种几何定理。
本文将介绍几个八年级常见的几何证明模型。
1.直角三角形证明模型直角三角形是指一个角为90度的三角形。
直角三角形的几何证明常用于证明勾股定理,即在一个直角三角形中,两直角边的平方和等于斜边的平方。
例如可以通过构造等辅助角、相似三角形等来证明这一定理。
2.等腰三角形证明模型等腰三角形是指两边相等的三角形。
等腰三角形的几何证明常用于证明等腰三角形的性质,例如等腰三角形的底角相等,等腰三角形的高线经过顶角等。
可以利用等辅助角、对称性等方法来进行证明。
3.平行线证明模型平行线是指在同一个平面内,不相交且不重合的两条直线。
平行线的几何证明常用于证明平行线之间的性质,如对应角相等、内错角相等、外错角相等等。
可以通过构造等辅助线、利用同位角等方法来进行证明。
4.圆证明模型圆是由平面内到一点距离恒定的所有点的集合。
圆的几何证明常用于证明圆的性质,如圆心角是其对应弧的两倍、弧长公式等。
可以通过构造切线、利用角平分线等方法来进行证明。
5.直线与平面证明模型直线与平面的几何证明常用于证明直线与平面之间的性质,如直线与平面的交点个数、直线与平面的夹角等。
可以通过构造垂线、相似三角形等方法来进行证明。
6.多边形证明模型多边形是由若干个边和角组成的图形。
多边形的几何证明常用于证明多边形的性质,如多边形内角和定理、多边形外角和定理等。
可以通过利用相似三角形、构造垂线等方法来进行证明。
以上是八年级几何证明中常见的六个模型。
通过熟练掌握这些模型,可以帮助我们更好地理解和应用各种几何性质和定理,在几何学的学习中取得更好的成绩。
当然,在实际证明过程中,我们也可以灵活运用不同的模型,根据具体问题来选择合适的证明方法。
初中数学几何模型大全+经典题型及答案解析

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
(完整版)初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
初中数学几何经典模型精编版

初中数学几何经典模型精编版几何经典模型在初中数学中占有重要的地位,通过这些模型的学习,可以帮助学生更好地理解几何图形的性质及其变化规律,提高几何思维能力。
下面是初中数学几何经典模型精编版。
一、相似三角形模型1、比例模型:在一个园中,如何取一个点,使得从这个点出发,分别向圆上和圆外伸出两条射线,使得这两条射线的长度之比最大?求出这个比例。
说明:这是相似三角形模型中比例模型的典型问题。
解答:设这个点为P,圆心为O,射线与圆相交于A、B两点,如图所示。
设OP=r,则PA=x,PB=y,由于PA、OP、OB与PB、OP、OA相似,因此有:PA:OP=OP:OB即:x:r=r:y化简得:x:y=r²:(OE²-r²)当x+y最大时,OE=√(r²+xy),代入得x∶y=r²∶(r²+xy),即:x+y=√(r²+xy)=r√(1+(x∶r)·(y∶r)),因此,此时x∶y=r²∶2r²=1∶2。
(注:该问题也可通过悬臂悬链线模型求解)2、面积模型1:已知ABC内接于⊙O,求AO∶OC。
解答:利用相似性质得:AB∶BC=AO∶CO,AB∶AC=AO∶OA即:AB²=AO·OC,AB²=AO²+OC²-2AO·OCcos∠AOC化简得:AO(OC-2r)=(r+AO)(r-AO)因为r>AO,所以有AO∶CO=r-AO∶r+AO3、面积模型2:已知三角形ABC中∠A=60°, AC=2,AB=a,BC=b,则COSB=log[(a²+b²-4)/6],计算 COSB。
解答:应用余弦定理和海龙公式,得:①cosB=(4-b²-a²)/(4a)②S(ABC)=[a²√3]/4③S(ABC)=bhA/2|hA=√(a²-1)∵S(ABC)=S(A′B′C′)∴a′b′/A′B′=(√3a/4)/(a/2)=√3/2设h′是A′B′上的高,由相似关系得:=[S(ABC)/2+√3S(ABC)/2]/2=3S(ABC)/4∵A′B′=a/2,设A′O=x∴B′O^2+AO^2=(a/2)^2;AO+x=b;Hence,x=(b²-a²+1)/2b∴cosB′=2x/a=(b²-a²-1)/ab,∴cosB=log[(a²+b²-4)/6]二、圆1、切线定理:如图,⊙O的两条切线AP、BP(AP>BP),AB的中点为C,OC与BP交于K,求证:AK=KC。
【收藏】初中数学经典几何模型大全

【收藏】初中数学经典几何模型大全
中点模型
【模型1】倍长
1、倍长中线;
2、倍长类中线;
3、中点遇平行延长相交
【模型2】遇多个中点,构造中位线
1、直接连接中点;
2、连对角线取中点再相连
【例】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF 的中点,连接GC、GE.
(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;(2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的数量和位置关系,写出你的猜想;并给予证明;(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.
角平分线模型
【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形
【例】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为 .
手拉手模型
【例】如图,正方形ABCD的边长为6,点O是对角线AC、BD 的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .
邻边相等的对角互补模型
【例】如图,矩形ABCD中,AB=6,AD=5,G为CD中点,DE=DG,FG⊥BE于F,则DF 为 .
半角模型
一线三角模型
弦图模型
最短路径模型
【两点之间线段最短】1、将军饮马
2、费马点【垂线段最短】
【两边之差小于第三边】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
