第2章 随机过程习题及答案
西安交通大学汪荣鑫随机过程第二版课后答案

随机过程习题解答第一章习题解答1.设随机变量X 服从几何分布,即:(),0,1,2,kP X k pqk ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtk k X k f t E ee pq ∞===∑ =()1jt k jtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑(其中 0(1)nnnn n n nx n x x ∞∞∞====+-∑∑∑)令 0()(1)nn S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰同理 2(1)2kkkk k k k k kx k x kx x ∞∞∞∞=====+--∑∑∑∑令2()(1)kk S x k x ∞==+∑ 则211()(1)(1)xkk kk k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为(2) 其期望和方差;(3)证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则 (2)'1()(0)Xp E X fjb∴==(4)若(,)i i X p b Γ 1,2i = 则同理可得:()()i i P X b f t b jt∑=∑-3、设ln (),()(kZ F X E Zk =并求是常数)。
X 是一随机变量,()F x 是其分布函数,且是严格单调的,求以下随机变量的特征函数。
(1)(),(0,)Y aF X b a b =+≠是常数; (2)ln (),()(kZ F X E Z k =并求是常数)。
解(1)11{()}{()}[()]P F x y P x F y F F y y --<=<==(01y ≤≤) ∴00()0111y F y yy y <⎧⎪=≤≤⎨⎪>⎩∴()F x 在区间[0,1]上服从均匀分布()F x ∴的特征函数为11001()(1)jtx jtx jt X e f t e dx e jt jt ===-⎰ (2)ln ()()()[]jtz jt F x Z f t E e E e ===1ln 01jt ye dy ⋅⎰=111jty dy jt =+⎰4、设12n X X X ,,相互独立,且有相同的几何分布,试求1nkk X =∑的分布。
(解答)《随机过程》第二章习题

第二章 Markov 过程 习题解答1、 设}1,{≥n n ξ为相互独立同分布的随机变量序列,其分布为:01}0{,0}1{>-===>==p q P p P n n ξξ定义随机序列}2,{≥n X n 和}2,{≥n Y n 如下:⎪⎪⎩⎪⎪⎨⎧=========----;1,1,3;0,1,2;1,0,1;0,0,01111n nn n n n n nn X ξξξξξξξξ ⎩⎨⎧===-;,1;0,0,01其它n n n Y ξξ试问随机序列}2,{≥n X n 和}2,{≥n Y n 是否为马氏链?如果是的话,请写出其一步转移概率矩阵并研究各个状态的性质。
不是的话,请说明理由。
解:(1)显然,随机序列}2,{≥n X n 的状态空间为}3,2,1,0{=S 。
任意取S i i i j i n ∈-132,,,,, ,由于当i X n =给定时,即1,-n n ξξ的值给定时,就可以确定1+n X 的概率特性,即我们有:}{},,,,{12233111i X j X P i X i X i X i X j X P n n n n n n ========+--+因此}2,{≥n X n 是齐次马氏链,其一步转移概率矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=p qp q p q p qP 0000000 由于01,0>-=>p q p ,画出状态转移图,可知各个状态都相通,且都是非周期的,因此此链是不可约的遍历链。
(也可以利用02>P 判定此链是不可约的遍历链)(2)显然,}2,{≥n Y n 的状态空间为}1,0{=S ,由于:}1,1{}1,1,0{}1,10{23234234=========Y Y P Y Y Y P Y Y Y P}0,1{}0,1,0{}0,10{23234234=========Y Y P Y Y Y P Y Y Y P由}2,{≥n Y n 的定义,可知}1,1,1{}1,1,0{}0,1,1{}0,1,0{}1,0,1{}1,1{12312312312312323===⋃===⋃===⋃⋃===⋃======ξξξξξξξξξξξξξξξY Y}1,1,0,0{}0,1,0,0{}1,1,0{12341234234====⋃========ξξξξξξξξY Y Y}0,0,1{}0,1{12323======ξξξY Y , ∅====}0,1,0{234Y Y Y利用}1,{≥n n ξ是相互独立同分布的随机变量序列及其分布,我们有:322233}1,1{q q p pq Y Y P ++=== 223234}1,1,0{q p pq Y Y Y P +==== 223}0,1{pq Y Y P ===0}0,1,0{234====Y Y Y P即有:22222343}1,10{q p pq qp pq Y Y Y P +++==== 0}0,10{234====Y Y Y P由于01,0>-=>p q p ,因此有}0,10{}1,10{234234===≠===Y Y Y P Y Y Y P根据马氏链的定义可知}2,{≥n Y n 不是马氏链。
随机过程第二章作业及参考答案

第二章 平稳过程2. 设随机过程()sin X t Ut =,其中U 是在[]02π,上均匀分布的随机变量。
试证 (1)若t T ∈,而{}12T = ,,,则(){}12X t t = ,,,是平稳过程; (2)若t T ∈,而[)0T =+∞,,则(){}0X t t ≥,不是平稳过程。
证明:由题意,U 的分布密度为:()10220u f u ππ⎧<<⎪=⎨⎪⎩,,其它数学期望()()[]sin X m t E X t E Ut ==⎡⎤⎣⎦()()2220001111sin sin cos cos 212222ut du ut d ut ut t t t t ππππππππ=⋅==-=--⎰⎰.相关函数()()()()()sin sin X X R R t t E X t X t E Ut U t ττττ=+=+=⋅+⎡⎤⎡⎤⎣⎦⎣⎦,()()()2200111sin sin cos 2cos 222ut u t du ut u u du ππτττππ⎛⎫=⋅+⋅=⋅-+--⎡⎤ ⎪⎣⎦⎝⎭⎰⎰ ()()2220001111cos 2cos sin 2sin 442u t u du u t u t πππττττππττ⎡⎤=-+-=-+-⎡⎤⎢⎥⎣⎦+⎢⎥⎣⎦⎰()()11sin 22sin 2424t t πτπτπτπτ=-+++.(1)若t T ∈,而{}12T = ,,时,()0X m t =,()X R τ只与τ有关,二者均与t 无关,因此,(){}12X t t = ,,,是平稳过程。
(2)若t T ∈,而[)0T =+∞,时,()X m t 可能取到不是常数的值,所取到的值与t 有关,()X R τ取到的值也与t 有关,因此,(){}0X t t ≥,不是平稳过程。
3. 设随机过程()()0cos X t A t ωΦ=+,t -∞<<+∞其中0ω是常数,A 和Φ是独立随机变量。
随机过程课后题答案

第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtkk X k f t E eepq ∞===∑()k jtkk p q e∞==∑ =0()1jt kjtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰202201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则10()()p jtxp bxX b f t ex e dx p ∞--=Γ⎰ 1()0()p p jt b x b x e dx p ∞--=Γ⎰101()()()()(1)p u p p p p p b e u b u jt b x du jt p b jt b jt b∞----==Γ---⎰ 10(())x p p e x dx ∞--Γ=⎰ (2)'1()(0)X p E X f j b∴== 2''221(1)()(0)X p p E X f j b +== 222()()()PD XE X E X b∴===(4) 若(,)i i X p b Γ 1,2i = 则121212()()()()(1)P P X X X X jt f t f t f t b-++==-1212(,)Y X X P P b ∴=+Γ+同理可得:()()iiP X b f t b jt∑=∑-3、设X 是一随机变量,()F x 是其分布函数,且是严格单调的,求以下随机变量的特征函数。
《随机过程及其在金融领域中的应用》习题二答案

0
sin
ux
f
xdx
0
sin
ux
f
xdx
0
0
sin
u
x
f
xdx
sin ux 0
f
x dx
0
令其中一式中的 x t
0
sin
ut
f
t
d
t
0
sin
ux
f
xdx
0
sin ut 0
证明:
X u
eiux f xdx
cos ux i sin ux f xdx
cos ux
f
xdx
i
sin
ux
f
xdx
(a)充分性:
当f
x
f
x时,sin ux
f
x
为奇函数
,
则i
c o vY Y, E Y 2 E Y 2 3 80
故(X,Y)的协方差矩阵为
cov X , X cov Y , X
1
cov X ,Y cov Y ,Y
18 0
0
3 80
4、已知二维随机变量(X,Y)服从联合正态分布,且
dFX
x
e tx f xdx
etxexdx etxdx
(完整版)随机过程习题答案

(完整版)随机过程习题答案随机过程部分习题答案习题22.1 设随机过程b t b Vt t X ),,0(,)(+∞∈+=为常数,)1,0(~N V ,求)(t X 的⼀维概率密度、均值和相关函数。
解因)1,0(~N V,所以1,0==DV EV ,b Vt t X +=)(也服从正态分布,b b tEV b Vt E t X E =+=+=][)]([ 22][)]([t DV t b Vt D t X D ==+=所以),(~)(2t b N t X ,)(t X 的⼀维概率密度为),(,21);(222)(+∞-∞∈=--x ett x f t b x π,),0(+∞∈t均值函数 b t X E t m X ==)]([)(相关函数)])([()]()([),(b Vt b Vs E t X s X E t s R X ++==][22b btV bsV stV E +++=2b st +=2.2 设随机变量Y 具有概率密度)(y f ,令Yt e t X -=)(,0,0>>Y t ,求随机过程)(t X 的⼀维概率密度及),(),(21t t R t EX X 。
解对于任意0>t,Yt e t X -=)(是随机变量Y 的函数是随机变量,根据随机变量函数的分布的求法,}ln {}{})({);(x Yt P x e P x t X P t x F t Y ≤-=≤=≤=-)ln (1}ln {1}ln {tx F t x Y P t x Y P Y --=-≤-=-≥= 对x 求导得)(t X 的⼀维概率密度xtt x f t x f Y 1)ln ();(-=,0>t)(][)]([)(dy y f e eE t X E t m yt tY X相关函数+∞+-+---====0)()(2121)(][][)]()([),(212121dy y f e e E e e E t X t X E t t R t t y t t Y t Y t Y X 2.3 若从0=t 开始每隔21秒抛掷⼀枚均匀的硬币做实验,定义随机过程=时刻抛得反⾯时刻抛得正⾯t t t t t X ,2),cos()(π试求:(1))(t X 的⼀维分布函数),1(),21(x F x F 和;(2))(t X 的⼆维分布函数),;1,21(21x x F ;(3))(t X 的均值)1(),(X X m t m ,⽅差 )1(),(22X Xt σσ。
数字通信原理第二版课后习题答案 第2章

图 2-3RC 高通滤波器
设有一周期信号 x(t)加于一个线性系统的输入端,得到的输出信号为
y(t)= τ [ dx(t ) / dt ] 式中, τ 为常数。试求该线性系统的传输函数 H(f).
6
《通信原理》习题第二章
解:输出信号的傅里叶变换为 Y(f)= τ * j 2π f * X ( f ) ,所以 H(f)=Y(f)/X(f)=j 2π f τ 习题 2.15 功率谱密度为 设有一个 RC 低通滤波器如图 2-7 所示。当输入一个均值为 0、双边
2
4 1 + jω
则能量谱密度
4 16 G(f)= X ( f ) = = 1 + jω 1 + 4π 2 f 2
2
习题 2.4 X(t)= x1 cos 2π t − x2 sin 2π t ,它是一个随机过程,其中 x1 和 x2 是相互统 计独立的高斯随机变量,数学期望均为 0,方差均为 σ 2 。试求:
Rn (τ )
1
Pn ( f )
k 2
0 0
τ
f
图 2-2
习题 2.11
已知一平稳随机过程 X(t)的自相关函数是以 2 为周期的周期性函数:
R(τ ) = 1 − τ , − 1 ≤ τ < 1
试求 X(t)的功率谱密度 PX ( f ) 并画出其曲线。 解:详见例 2-12 习题 2.12 已知一信号 x(t)的双边功率谱密度为
+∞ −∞
j 2π f τ
1 + τ , df = 1 − τ 0,
−1 ≤ τ ≤ 0 0 ≤τ <1 其它
k -k τ e ,k 为常数。 2
习题 2.10
随机过程第一、二章测验题答案(2010)

随机过程测试题一答案每题10分1. 在一汽车工厂中,一辆汽车有两道工序是由机器人完成的。
其一是紧固三只螺栓,其二是焊接两处焊点。
以X 表示由机器人紧固的螺栓不良的数目,以Y 表示由机器人焊接的焊点不良的数目。
据积累资料知),(Y X 具有分布律: Y X 0 1 2 3 0 0.840 0.030 0.020 0.010 1 0.060 0.010 0.008 0.002 20.0100.0050.0040.001(1)求EX ;(2)求]|[j Y X E =,2,1,0=j ;(3)验证 ∑====2}{]|[j j Y P j Y X E EX .解: (1) X 的分布律为 X 0 1 2 3 P0.9100.0450.0320.013148.0=EX .(2) Y 的分布律为 Y 0 1 2 P0.9000.0800.0200=Y 时,X 的条件分布律为X|0=Y 0 123P0.840/0.90.030/0.90.020/0.90.010/0.991]0|[==Y X E ;1=Y 时,X 的条件分布律为X|1=Y 0 123P0.060/0.080.010/0.080.008/0.080.002/0.084.0]1|[==Y X E ;2=Y 时,X 的条件分布律为X|2=Y0 1 2 3P 0.010/0.02 0.005/0.02 0.004/0.02 0.001/0.028.0]2|[==Y X E .(3) EX j Y P j Y X E j ==⨯+⨯+⨯===∑=148.002.08.008.04.09.091}{]|[2.2.设二维随机变量),(Y X 的概率密度为⎩⎨⎧<<=-.,00,),(其他,y x e y x f y(1)求EX;(2)对任意0>y ,求]|[y Y X E =;(3)验证⎰+∞==0)(]|[dy y f y Y X E EX Y .解: (1)当0>x 时, X 的概率密度为x xy xX e dy e dy y x f x f -+∞-+∞===⎰⎰),()(.1)(0===⎰⎰+∞-+∞dx xe dx x xf EX x X .(2) 对任意0>y , Y 的概率密度为y yy yY ye dx e dx y x f y f --===⎰⎰0),()(.⎪⎩⎪⎨⎧<<==.,0,0,1)(),()|(|其他y x y y f y x f y x f Y Y X21)|(]|[0|ydx y xdx y x f x y Y X E yY X ====⎰⎰+∞ (3)EX dy ye y dy y f y Y X E y Y ==Γ=⋅==⎰⎰+∞-+∞1)3(212)(]|[03.写出六种常见分布(退化、二项、泊松、均匀、指数、正态)的特征函数.分布 记号 概率密度或分布律)x (f特征函数)t (ψ退化 {c} 1}{==c X Pict e0-1 b(1,p) .1,0,}{1===-x q p x X P x x q pe it +二项b(n,p) 独立同分布于b(1,p)的n 个r.v.的和..,,1,0,}{1n x q p C x X P x x x n ===-n it q pe )(+泊松 )(P λ.,2,1,0,!}{ ===-x e x x X P xλλ)1(-it e eλ均匀U(a,b))(1)(),(x I ab x f b a -=t a b i e e iatibt )(--标准正态 N(0,1)2221)(x e x f -=π22t e-正态),(N 2σμ222)(21)(σμσπ--=x e x f2)(2t t i eσμ-指数 )(E λ)()(),0(x I e x f x +∞-=λλit-λλ4.关于独立随机变量序列}{n X ,下列哪些命题是正确的. (1)若 ,2,1,||=+∞<k X E k ,则∏∏===nk k nk k EX X E 11;(2) 若 ,2,1,2=+∞<k EX k ,则∑∑===nk k n k n VarX X Var 11)(;(3) 设)(t f k 为k X 的特征函数,)(t f n S 为∑==nk k n X S 1的特征函数,则∏==nk k S t f t f n 1)()(.(4) 设)(t k φ为k X 的矩母函数,)(t n S φ为∑==nk k n X S 1的矩母函数,则∑==nk k S t t n1)()(φφ.解:(4)错,应为 ∏==nk k S t t 1)()(φφ.5.设ηξ,是相互独立,且都为均值0,方差1的随机变量,令t t X ηξ+=)(,求随机过程}0),({≥t t X 的均值函数和相关函数. 解:;0)()()]([)(=+==ηξμtE E t X E t X;1)()()()]([)(222t D t D t D t X D t x +=+=+==ηξηξσ.1)()()()()()]()([),(22ts E E s t tsE E s X t X E s t R x +=+++==ηξηξ6.X (t )=Y cos(t )+Z sin(t ), t >0,Y , Z 相互独立,且 EY =EZ =0,DY =DZ =σ2. 讨论随机过程{X (t ), t >0}的平稳性.解: 0sin cos )]([)(=+==tEZ tEY t X E t X μ;)]()([),(s X t X E s t R X =).cos(sin sin cos cos )()cos sin sin (cos sin sin cos cos 22222s t EZ s t EY s t YZ E s t s t EZ s t EY s t -=⋅+⋅=++⋅+⋅=σ因)(t X μ为常数,),(s t R X 仅与s t -=τ有关,故)}({t X 是宽平稳过程.7.在电报信号)(t X 的传输过程中,信号由不同的电流符号A A -,给出,而电流的发送又有一个任意的持续时间,电流符号的转换是随机的. 设)(t X 在],0(t 时间内的变号次数)(t N 是参数为λ的泊松过程,且可以表示为)()1)(0()(t N X t X -=,又设)0(X 与}0),({≥t t N 独立,且5.0})0({})0({=-===A X P A X P ,求}0),({≥t t X 的均值函数.解:=)]([t X E 0.8.考虑电子管中的电子发射问题,设单位时间内到达阳极的电子数目N 服从参数为λ的泊松分布. 每个电子携带的能量构成一个随机变量序列 ,,21X X 已知}{k X 与N 独立,}{k X 之间互不相关并且具有相同的均值和方差2,σμ==k k DX EX . 单位时间内阳极接收到的能量为∑==Nk kXS 1. 求S 的均值.解:∑∑+∞=====1}{]|[n Nk kn N P n N XE ES∑∑+∞====01}{][n nk k n N P X E ∑+∞===01}{n n N P nEX∑+∞===01}{n n N nP EX λμ=⋅=1EX EN .9.随机过程}0),({≥t t W 称为参数为2σ的维纳过程, 如果 (1) 0)0(=W ;(2),0t s <≤∀))(,0(~)()(2s t N s W t W --σ;(3) ,0v u t s <<<≤∀ 增量)()(s W t W -与)()(u W v W -相互独立.(1)求}0),({≥t t W 的均值函数)]([t W E 和相关函数)]()([s W t W E . (2)}0),({≥t t W 是否为宽平稳过程?证明:(1),0≥∀t ),0(~)(2t N t W σ, 故0)]([)(==t W E t W μ;又,0t s <≤∀))(,0(~)()(2s t N s W t W --σ, 且增量)()(s W t W -与)(s W 相互独立,故)]()([)]())()([()]()([),(s W s W E s W s W t W E s W t W E s t R W +-==s s W D s W E s W t W E 2)]([)]([)]()([σ=+-=从而),min(),(2s t s t R W σ=.(2)由于),(s t R W 与出发时刻),min(s t 有关,因而}0),({≥t t W 不是宽平稳过程.10. 下面四个随机过程中哪些不是宽平稳过程(A) 随机相位正弦波过程:}0),cos()({≥Φ+=t t t X λ,其中),(~ππ-ΦU ,λ是常数. (B) 白噪声序列: },1,0,{ =n X n 是一列两两互不相关(即m n X EX m n ≠=,0)的随机变量序列,且满足2,0σ==n n DX EX . (C) 移动平均序列:},2,1,0,{11 ±±==∑=-+n a X ki in i n ε,其中},2,1,0,{ ±±=n n ε为白噪声序列,k a a a ,,,21 为任意实数.(D) 强度为λ的泊松过程}0),({≥t t N ,其中)(t N 表示到时刻t 为止事件A 发生的次数. 解: D .。
南京大学随机过程练习题附中文解释及答案

8、(3.8)An unbiased die is successively rolled. Let X and Y denote, respectively, the number of rolls necessary to obtain a six and a five. Find (a) E[X], (b) E[X|Y=1] 相继地掷一颗不均匀的骰子。令 X 和 Y 分别记得到一个 6 和一个 5 所必须的抛 掷次数。求(a)E[X],(b)E[X|Y=1]。 重要:E[E[X|Y]]=E[X]
3、(4.32) Each of two switches is either on or off during a day. On day n, each switch will independently be on with probability [1+#of on switches during day n-1]/4. For instance, if both switches are on during day n-1, then each will independently be on during day n with probability3/4. What fraction of days are both switches on? What fractions are both off? 在一天中两个开关或者开或者关。在第 n 天,每个开关独立地处于开的概率是[1+ 第 n-1 天是开的开关数]/4。例如,如果在第 n-1 天两个开关都是开的,那么在第 n 天,每个开关独立地处于开的概率是 3/4。问两个开关都是开的天数的比例是 多少?两个开关都是关的天数的比例是多少?
随机过程答案2

⎪2. (1) 求参数为(p , b )的Γ 分布的特征函数,其概率密度为⎧ b p p (x ) = ⎪ x p -1e -bx , x > 0 b > 0, p 是正整数(2)求其期望和方差。
⎨Γ( p ) ⎪⎩0 x ≤ 0(3)证明对具有相同参数b 的Γ 分布,关于参数 p 具有可加性。
解 (1) 首先,我们知道Γ 函数有下面的性质:Γ(p ) = (p -1)!根据特征函数的定义,有f X (t ) = E [e jtX]= ⎰∞ejtxp (x )dx = ⎰e jtxb p Γ(p ) x p -1e -bx dx= ⎰0bpΓ( p ) -∞ 0x p -1e -(b - jt )x dx =b p 1p -1 -(b - jt )x ∞ b p p - 1 ∞ p -2 -(b - jt )x Γ(p ) - (b - jt ) x e0 + Γ( p ) (b - jt ) ⎰0 x e dx = b p p - 1 ⎰∞ x p -2 e -(b - jt )x dx Γ(p ) (b - jt ) 0 ==b p ( p - 1)! ∞ 0 -(b - jt )x Γ(p ) (b - jt )p -1 ⎰0 x e dx= b p ( p - 1)! = ⎛ b ⎫ Γ(p ) (b - jt )p b - jt ⎪ ⎝ ⎭所以⎛ b ⎫ pf X (t ) = ⎪b - jt ⎝ ⎭(2)根据期望的定义,有∞∞ p]⎰ b ⎰ ∞( )∞b pp -1 -bxb p∞p -bxm X = E [X ] = ⎰-∞ xp x dx = ⎰0 x Γ(p ) x e dx = Γ( p ) ⎰0 x e dx = b p 1 p -bx ∞ b p p ∞p -1 -bxΓ( p ) - b x e 0 + Γ(p ) b ⎰0 xe dx = p ⎰∞ bp -1 -bx = p ⎰∞ ( ) = p b 0 Γ( p ) x 类似的,有e dx p x dx b -∞ bE [X 2= ∞x 2-∞ p (x )dx = ⎰0 2b px Γ(p ) x p -1e -bx dx = p Γ(p ) ⎰0x p +1e -bx dx b p 1 p +1 -bx ∞ b p ( p + 1) ∞ p -bx= Γ( p ) - b x e 0 + Γ(p ) b ⎰0 x e dx= b p Γ( p ) =(p + 1) b 0 x p e -bx dx= (p + 1)p ∞ b pp -1 -bx= ( p + 1)p ∞ ( )b 2⎰0=(p + 1)p b 2Γ(p ) xe dxb 2⎰-∞p x dx所以, X 的方差为D X =E [X 2]- m 2= ( p + 1)p b 2⎛ p ⎫2⎪ b= p b 2⎝ ⎭ (3)p ∞∞ ∞ X -M M M M ∑ ∑ i =1 k =1 i =1 k =1i =1 k =1i =1 k =15. 试证函数 ( ) =e jt (1 - e jnt ) 为一特征函数,并求它所对应的随机变f tn (1 - e jt )量的分布。
第2章-随机过程习题及答案

第2章-随机过程习题及答案第二章随机过程分析1.1 学习指导 1.1.1 要点随机过程分析的要点主要包括随机过程的概念、分布函数、概率密度函数、数字特征、通信系统中常见的几种重要随机过程的统计特性。
1. 随机过程的概念随机过程是一类随时间作随机变化的过程,它不能用确切的时间函数描述。
可从两种不同角度理解:对应不同随机试验结果的时间过程的集合,随机过程是随机变量概念的延伸。
2. 随机过程的分布函数和概率密度函数如果ξ(t )是一个随机过程,则其在时刻t 1取值ξ(t 1)是一个随机变量。
ξ(t 1)小于或等于某一数值x 1的概率为P [ ξ(t 1) ≤ x 1 ],随机过程ξ(t )的一维分布函数为F 1(x 1, t 1) = P [ξ(t 1) ≤ x 1] (2-1)如果F 1(x 1, t 1)的偏导数存在,则ξ(t )的一维概率密度函数为1111111(,)(, ) (2 - 2)?=?F x t f x t x对于任意时刻t 1和t 2,把ξ(t 1) ≤ x 1和ξ(t 2) ≤ x 2同时成立的概率{}212121122(, ; , )(), () (2 - 3)F x x t t P t x t x ξξ=≤≤称为随机过程ξ (t )的二维分布函数。
如果2212122121212(,;,)(,;,) (2 - 4)F x x t t f x x t t x x ?=存在,则称f 2(x 1, x 2; t 1, t 2)为随机过程ξ (t )的二维概率密度函数。
对于任意时刻t 1,t 2,…,t n ,把{}n 12n 12n 1122n n ()(),(),,() (2 - 5)=≤≤≤L L L F x x x t t t P t x t x t x ξξξ,,,;,,,称为随机过程ξ (t )的n 维分布函数。
如果n n 12n 12n n 12n 12n 12n(x )() (2 - 6)?=L L L L L F x x t t t f x x x t t t x x x ,,,;,,,,,,;,,,存在,则称f n (x 1, x 2, …, x n ; t 1, t 2, …, t n )为随机过程ξ (t )的n 维概率密度函数。
随机过程复习题二及其答案

随机过程复习题二及其答案一、选择题1. 随机过程的定义是什么?A. 一系列随机变量的集合B. 一系列确定变量的集合C. 一个随机变量D. 一个确定变量2. 什么是马尔可夫链?A. 一个具有时间序列的随机过程B. 一个具有空间序列的随机过程C. 一个具有独立同分布的随机过程D. 一个具有时间依赖性的随机过程3. 随机过程的期望值定义为:A. \( E[X(t)] \)B. \( E[X] \)C. \( \int_{-\infty}^{\infty} x f(x,t) \, dx \)D. \( \sum_{i=1}^{\infty} x_i p_i \)4. 以下哪个不是随机过程的属性?A. 期望B. 方差C. 协方差D. 导数5. 什么是平稳随机过程?A. 随机过程的期望随时间变化B. 随机过程的方差随时间变化C. 随机过程的统计特性不随时间变化D. 随机过程的协方差随时间变化答案:1. A2. A3. A4. D5. C二、简答题1. 解释什么是遍历定理,并给出其在随机过程分析中的应用。
2. 描述什么是泊松过程,并解释其主要特点。
3. 简述什么是布朗运动,并解释其在金融领域中的应用。
三、计算题1. 给定一个随机过程 \( X(t) \),其期望 \( E[X(t)] = t \),方差 \( Var[X(t)] = t^2 \),计算 \( E[X^2(t)] \)。
2. 假设一个马尔可夫链 \( \{X_n\} \) 有状态空间 \( S = \{1, 2, 3\} \),转移概率矩阵 \( P \) 为:\[P = \begin{bmatrix}0.1 & 0.8 & 0.1 \\0.5 & 0.3 & 0.2 \\0.2 & 0.6 & 0.2\end{bmatrix}\]计算状态 1 在第 3 步的概率。
四、论述题1. 论述随机过程在信号处理中的应用,并举例说明。
(完整版)随机过程习题和答案

一、1.1设二维随机变量(,)的联合概率密度函数为:试求:在时,求。
解:当时,==1.2 设离散型随机变量X服从几何分布:试求的特征函数,并以此求其期望与方差。
解:所以:2.1 袋中红球,每隔单位时间从袋中有一个白球,两个任取一球后放回,对每 对应随机变量一个确定的t⎪⎩⎪⎨⎧=时取得白球如果对时取得红球如果对t e t tt X t 3)(.维分布函数族试求这个随机过程的一2.2 设随机过程,其中是常数,与是相互独立的随机变量,服从区间上的均匀分布,服从瑞利分布,其概率密度为试证明为宽平稳过程。
解:(1)与无关(2),所以(3)只与时间间隔有关,所以为宽平稳过程。
2.3是随机变量,且,其中设随机过程U t U t X 2cos )(=求:,.5)(5)(==U D U E.321)方差函数)协方差函数;()均值函数;((2.4是其中,设有两个随机过程U Ut t Y Ut t X ,)()(32==.5)(=U D 随机变量,且数。
试求它们的互协方差函2.5,试求随机过程是两个随机变量设B At t X B A 3)(,,+=的均值),(+∞-∞=∈T t 相互独若函数和自相关函数B A ,.),()(),2,0(~),4,1(~,21t t R t m U B N A X X 及则且立为多少?3.1一队学生顺次等候体检。
设每人体检所需的时间服从均值为2分钟的指数分布并且与其他人所需时间相互独立,则1小时内平均有多少学生接受过体检?在这1小时内最多有40名学生接受过体检的概率是多少(设学生非常多,医生不会空闲)解:令()N t 表示(0,)t 时间内的体检人数,则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
40300(30)((1)40)!k k P N e k -=≤=∑。
3.2在某公共汽车起点站有两路公共汽车。
乘客乘坐1,2路公共汽车的强度分别为1λ,2λ,当1路公共汽车有1N 人乘坐后出发;2路公共汽车在有2N 人乘坐后出发。
南京大学随机过程练习题附中文解释及答案

南京⼤学随机过程练习题附中⽂解释及答案(以第九版为准)第⼆章Random Variables 随机变量1、(2.16)An airline knows that 5percent of the people making reservations on a certain flight will not show up.Consequently,their policy is to sell 52tickets for a flight that can hold only 50passengers.What is the probability that there will be a seat available for every passenger who shows up?航空公司知道预订航班的⼈有5%最终不来搭乘航班。
因此,他们的政策是对于⼀个能容纳50个旅客的航班售52张票。
问每个出现的旅客都有位置的概率是多少?答:05.0*95.0*52-95.0-15152)()(2、(2.25略变动)Suppose that two teams are playing a series of games,each of which is independently won by team A with probability p and by team B with probability 1-p.The winner of the series is the first team to win i games.If i =4,find the probability that a total of 7games are played.Find the p that maximizes/minimizes this probability.假定两个队玩⼀系列游戏,A 队独⽴地赢的概率是p ,B 队独⽴地赢的概率是1-p 。
随机过程习题解答第1,2章

习题11. 令X(t)为二阶矩存在的随机过程,试证它是宽平稳的当且仅当EX(s)与E[X(s)X(s+t)]都不依赖s.证明:充分性:若X(t)为宽平稳的,则由定义知EX(t)=μ, EX(s)X(s+t)=r(t) 均与s 无关必要性:若EX(s)与EX(s)X(s+t)都与s 无关,说明EX(t)=常数, EX(s)X(s+t)为t 的函数2. 记1U ,...,n U 为在(0,1)中均匀分布的独立随机变量,对0 < t , x < 1定义I( t , x)=⎩⎨⎧>≤,,,,t x t x 01并记X(t)=),(11∑=nk k U t I n ,10≤≤t ,这是1U ,...,n U 的经验分布函数。
试求过程X (t )的均值和协方差函数。
解: EI ()k U t ,= P ()t U k ≤= t , D()),(k U t I = EI ()k U t ,-()2),(kU t EI= t -2t = t(1-t)j k ≠, cov ()),(),(j k U s I U t I ,=EI(t,k U )I(s,j U )-EI(t, k U )EI(s, j U ) = st -st=0k = j , cov ()),(),(j k U s I U t I ,= EI(t,k U )I(s,j U )-st = min(t,s)-stEX(t)=),(11∑=n k k U t EI n =∑=nk tn 11= tcov ())(),(s X t X =()()),(),,(cov 1),(),,(cov 1212j kjk nk k k U s I Ut I n U s I U t I n ∑∑≠=+=[]∑=nk st t s n12),min(1-=()st t s n-),min(13.令1Z ,2Z 为独立的正态分布随机变量,均值为0,方差为2σ,λ为实数,定义过程()t Sin Z t Cos Z t X λλ21+=.试求()t X 的均值函数和协方差函数,它是宽平稳的吗?Solution: ()221,0~,σN Z Z . 02221==EZ EZ .()()221σ==Z D Z D ,()0,21=Z Z Cov ,()0=t EX ,()()()()()[]s Sin Z s Cos Z t Sin Z t Cos Z E s X t X Cov λλλλ2121,+⋅+=[]t C o s S i n Z Z s t S i n C o s Z Z s t S i n S i n Z t C o s C o s Z E λλλλλλλλ12212221+++=()02++=s t S i n S i n s t C o s C o s λλλλσ =()[]λσs t Cos -2(){}t X 为宽平稳过程.4.Poisson 过程()0,≥t t X 满足(i )()00=X ;(ii)对s t >,()()s X t X -服从均值为()s t -λ的Poisson 分布;(iii )过程是有独立增量的.试求其均值函数和协方差函数.它是宽平稳的吗?Solution ()()()()t X t X E t EX λ=-=0,()()t t X D λ= ()()()()()s t s X t EX s X t X Cov λλ⋅-=,()()()()()ts s EX s X s X t X E 22λ-+-= ()()()()ts s EX s X D 220λ-++=()ts s s 22λλλ-+=()t s s λλλ-+=1 显然()t X 不是宽平稳的.5. ()t X 为第4题中的Poisson 过程,记()()()t X t X t y -+=1,试求过程()t y 的均值函数和协方差函数,并研究其平稳性. Solution ()λλ=⋅=1t Ey , ()()λ=t y DCov(y(t),y(s))=Ey(t)y(s)-Ey(t)y(s)=E(x(t+1)-x(t))(x(s+1)-x(s))-λ2(1)若s+1<t, 即s≤t-1,则Cov(y(t),y(s))=0-λ2=-λ2(2)若t<s+1≤t+1, 即t>s>t-1, 则Cov(y(t),y(s))=E[x(t+1)-x(s+1)+x(s+1)-x(t)][x(s+1)-x(t)+x(t)-x(s)] -λ2=E(x(t+1)-x(s+1))(x(s+1)-x(t))+E(x(t+1)-x(s+1))(x(t)-x(s))+E(x(s+1)-x(t))+E(x(s+1)-x(t))(x(t)-x(s))- λ2=λ(s+1-t)= λ-λ(t-s)- λ2(3) 若t<s<t+1Cov(y(t),y(s))= E [x(t+1)-x(s)+x(s)-x(t)] [x(s+1)-x(t+1)+x(t+1)-x(s)]- λ2 =(x(t+1)-x(s))(x(s+1)-x(t+1))+E(x(t+1)-x(s))(x(t+1)-x(s))+E(x(s)-x(t))(x(s+1)-x(t+1))+E(x(s)-x(t))(x(t+1)-x(s))- λ2=0+λ(t+1-s)+0-λ2=λ+λ(t-s)- λ2(4) 若s>t+1 Cov(y(t),y(s))=0-λ2=-λ2由此知,故方差只与t-s有关,与t,s无关故此过程为宽平稳的。
随机过程习题及部分解答(共享).docx

随机过程习题及部分解答习题一1.若随机过程X(/)为X(0 = A?,-oo<r<+oo,式中4为(0, 1)上均匀分布的随机变量,求X(/)的一维概率密度Px(x;t)。
2.设随机过程X(/) = 4cos(初+ 其中振幅A及角频率①均为常数,相位&是在[-兀,刃上服从均匀分布的随机变量,求X(/)的一维分布。
习题二1.若随机过程X(/)为X(t)=At -00 < r < +00 ,式中4为(0,1)上均匀分布的随机变量,求E[xa)],7?xa』2)2.给定一随机过程X(/)和常数Q,试以X(/)的相关函数表示随机过程y(0 = X(/ + a) —X(/)的自相关函数。
3.已知随机过程X(/)的均值阪⑴和协方差函数Cx (爪© , 0(/)是普通函数,试求随机过程丫⑴=X(/) + 0(/)是普通函数,试求随机过程丫⑴=X(/) + 0(/)的均值和协方差函数。
4.设X(t) = A cos at + B sin at,其中A, B是相互独立且服从同一高斯(正态)分布N(0Q2)的随机变量,a为常数,试求X(/)的值与相关函数。
习题三1.试证3.1节均方收敛的性质。
2.证明:若X(t),twT;Y(t),twT均方可微,a0为任意常数,则aX(t) + bY(t) 也是均方可微,且有[aX (?) + b Y(/)]' = aX'(/) + b Y'(/)3.证明:若X⑴,twT均方可微,/X/)是普通的可微函数,则f(Z)X(Z)均方可微且[f(ox(or-/w(o+/(ox,(o4.证明:设X⑴在[a,b]上均方可微,且X0)在[a,切上均方连续,则有X'⑴ dt = X(b) — X(a)J a5•证明,设X(t\t eT =[a,b];Y{t\t eT = [a,b]为两个随机过程,且在T上均方可积,a和0为常数,则有(*b (*b (*bf [aX(/) + 0Y(/)M = a [ Xit)dt + /3\ Y⑴ dtJ a J a J aeb rc rbaX (t)dt = X (t)dt + XQ) dt,aWcWbJ a J a Jc6.求随机微分方程X'(/) + aX ⑴二丫⑴ze[0,+oo]'X(0) = 0的X(t)数学期望E [X(0]。
随机过程试题及答案

随机过程试题及答案一、选择题(每题5分,共20分)1. 下列哪一项是随机过程的典型特征?A. 确定性B. 可预测性C. 无记忆性D. 独立增量性答案:D2. 马尔可夫链的哪一性质表明,系统的未来状态只依赖于当前状态,而与过去状态无关?A. 独立性B. 无记忆性C. 齐次性D. 可逆性答案:B3. 布朗运动是一个连续时间的随机过程,其增量具有什么性质?A. 独立性B. 正态分布C. 独立增量性D. 所有选项都正确答案:D4. 随机过程的平稳性指的是什么?A. 过程的分布随时间不变B. 过程的均值随时间不变C. 过程的方差随时间不变D. 过程的自相关函数随时间不变答案:A二、填空题(每题5分,共20分)1. 如果随机过程的任意时刻的分布函数不随时间变化,则称该随机过程是________。
答案:平稳的2. 随机过程的自相关函数R(t,s)表示在时刻t和时刻s的随机变量的________。
答案:相关性3. 随机游走过程是一类具有________性质的随机过程。
答案:独立增量4. 泊松过程是一种描述在固定时间间隔内随机事件发生次数的随机过程,其特点是事件的发生具有________。
答案:无记忆性三、简答题(每题10分,共30分)1. 简述什么是马尔可夫过程,并给出其数学定义。
答案:马尔可夫过程是一种随机过程,其未来的状态只依赖于当前状态,而与过去状态无关。
数学上,如果对于任意的n,以及任意的时间序列t1, t2, ..., tn,满足P(Xt+1 = x | Xt = x_t, Xt-1 = x_t-1, ..., X1 = x_1) = P(Xt+1 = x | Xt = x_t),则称随机过程{Xt}为马尔可夫过程。
2. 描述布朗运动的三个基本性质。
答案:布朗运动的三个基本性质包括:1) 布朗运动的增量是独立的;2) 布朗运动的增量服从正态分布;3) 布朗运动具有连续的样本路径。
3. 什么是平稳随机过程?请给出其数学定义。
随机信号分析与处理简明教程 第二章习题答案
K = σ 2 [1 − cos 2 ω (t2 − t1 )] = σ 2 sin 2 ω (t2 − t1 ) , t1 ≠ t2 1 − cos ω (t2 − t1 ) ⎤ ⎡ σ2 K = ⎢ ⎥ 1 sin 2 ω (t2 − t1 ) ⎣ − cos ω (t2 − t1 ) ⎦
−1
令 x = [ x1 , x2 ] ,则二维概率密度为:
A
x1
x2
x3
x4
t
T 2T 图2.26 样本函数示意图 3T
解: P[Y (t1 ) = A] = P[ x1 ≥ t1 ] =
∫
T
t1
f X ( x)dx = ∫
T
t1
t 1 dx = 1 − 1 T T
P[Y (t1 ) = 0] = 1 − P[Y (t1 ) = A] =
所以 fY ( y ) =
π 时,求 X (ti ) 的概率密度。 2ω
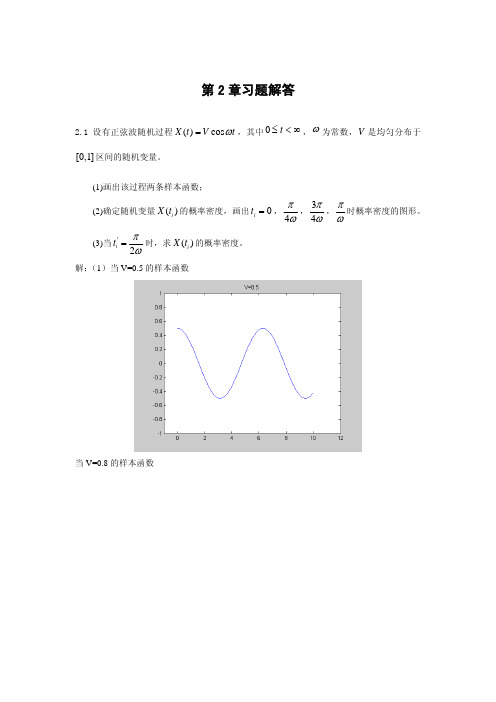
解: (1)当 V=0.5 的样本函数
当 V=0.8 的样本函数
(2)已知 X (t ) = V cos ωt ,求 X (t ) 的概率密度,此时可以把 cos ωt 看作常数。而 V 是均 匀分布于区间[0,1]的随机变量,故 X 是均匀分布于区间[0, cos ωt ]的随机变量。 当 cos ωt > 0 时, f X ( x, t ) = ⎨
t1 T
t1 ⎛ t ⎞ δ ( y ) + ⎜1 − 1 ⎟δ ( y − A) , 0 ≤ t ≤ T T ⎝ T⎠ t − (n − 1)T nT − t δ ( y) + δ ( y − A) T T
推广到其它间隔, f Y ( y ) =
已知 b 为常量, N 为正态随机变量, 其均值为 m, 方差为 σ 。 2.4 设随机过程 X (t ) = b + Nt ,
随机过程习题答案

随机过程习题解答(一)第一讲作业:1、设随机向量的两个分量相互独立,且均服从标准正态分布。
(a)分别写出随机变量和的分布密度(b)试问:与是否独立?说明理由。
解:(a)(b)由于:因此是服从正态分布的二维随机向量,其协方差矩阵为:因此与独立。
2、设和为独立的随机变量,期望和方差分别为和。
(a)试求和的相关系数;(b)与能否不相关?能否有严格线性函数关系?若能,试分别写出条件。
解:(a)利用的独立性,由计算有:(b)当的时候,和线性相关,即3、设是一个实的均值为零,二阶矩存在的随机过程,其相关函数为,且是一个周期为T的函数,即,试求方差函数。
解:由定义,有:4、考察两个谐波随机信号和,其中:式中和为正的常数;是内均匀分布的随机变量,是标准正态分布的随机变量。
(a)求的均值、方差和相关函数;(b)若与独立,求与Y的互相关函数。
解:(a)(b)第二讲作业:P33/2.解:其中为整数,为脉宽从而有一维分布密度:P33/3.解:由周期性及三角关系,有:反函数,因此有一维分布:P35/4. 解:(1) 其中由题意可知,的联合概率密度为:利用变换:,及雅克比行列式:我们有的联合分布密度为:因此有:且V和相互独立独立。
(2)典型样本函数是一条正弦曲线。
(3)给定一时刻,由于独立、服从正态分布,因此也服从正态分布,且所以。
(4)由于:所以因此当时,当时,由(1)中的结论,有:P36/7.证明:(1)(2) 由协方差函数的定义,有:P37/10. 解:(1)当i =j 时;否则令,则有第三讲作业:P111/7.解:(1)是齐次马氏链。
经过次交换后,甲袋中白球数仅仅与次交换后的状态有关,和之前的状态和交换次数无关。
(2)由题意,我们有一步转移矩阵:P111/8.解:(1)由马氏链的马氏性,我们有:(2)由齐次马氏链的性质,有:,(2)因此:P112/9.解:(2)由(1)的结论,当为偶数时,递推可得:;计算有:,递推得到,因此有:P112/11.解:矩阵 的特征多项式为:由此可得特征值为:,及特征向量:,则有:因此有:(1)令矩阵P112/12.解:设一次观察今天及前两天的天气状况,将连续三天的天气状况定义为马氏链的状态,则此问题就是一个马氏链,它有8个状态。
《随机过程》第二章题目与答案

第二章一、填空题1、随机过程若按状态空间与参数集分类可分为__、__、__、__四类.2、__是随机过程{X(t),t∈T}在时刻t的平均值,__是随机过程在时刻t对均值m x(t)的偏离程度,而__和__则反映随机过程{X(t),t∈T}在时刻s和t 时的线性相关度.3、若随机变量x服从(01)分布,即p k=p{x=k}=,k=0,1则其特征函数g(t)=__.4、若随机变量X服从参数为的指数分布,则其特征函数g(t)=__.5、若随机变量X服从退化分布,即p(X=c)=1,其中c为常数,则其特征函数g(t)=__.二、计算题1、已知Γ分布,X~Γ(α,β),若其中α,β>0,试求Γ分布的特征函数.2、设随机变量X服从泊松分布,即p k=p(X=k)=,k=0,1,…,n,求其特征函数.3、设随机过程X(t)=Y+Zt,t>0,其中Y,Z是相互独立的N(0,1)随机变量,求{ X(t),t>0}的一,二维概率密度族.4、设随机过程:0),sin()cos()(>+=t t Z t Y t X θθ,其中Y 、Z 是相互独立的随机变量,且EY=EZ=0,DY=DZ=δ2,求{X(t),t>0}的均值函数、协方差函数和方差函数.5、设随机变量Y 具有概率密度f(y),令)0,0(,)(>>=-Y t t X eYt,求随机过程X(t)的一维概率密度及EX(t),R x (t 1,t 2).6、设随机过程Z t =,t 0,其中X 1,X 2,…,X n 是相互独立的,且服从N(0,)的随机变量,ω1, ω2,…, ωn 是常数,求{Z t ,t}的均值函数m(t)和相关函数R(s,t).参考答案:一、填空题1、离散参数链,连续参数链,随机序列,随机过程2、均值函数m X(t),方差函数D X(t),协方差函数B X(s,t),相关函数R X(s,t)3、q+p4、5、二、解答题1、1、g(t)===其中:Γ(α)=2、g(t)= = ===3、由于X与Z是相互独立的正态随机变量,故其线性组合仍为正态随机变量,要计算{X(t),t>0}的一、二维随机概率密度,只要计算数字特征m x(t),D X(t),即可. m x(t)=E(Y+Zt)=EY+tEZ=0,D X(t)=D(Y+Zt)=DY+t2DZ=1+t2,B X(s,t)=EX(s)X(t)- m x(s) m x(t)=E(Y+Zs)(Y+Zt)=1+st,==,故随机过程{X(t),t>0}的一、二维概率密度分别为f t(x)=exp{-},t>0,f s,t(x1,x2)=.exp{[]}, s,t>0,其中4、由数学期望的性质)sin()cos()]sin()cos([)(=+=+=EZ t EY t t Z t Y E t EX θθθθ又因为Y 、Z 相互独立,故])cos[()()sin()sin()()cos()cos()]sin()cos()][sin()cos([)]()([),(),(σ222θθθθθθθθθs t Z E t s Y E t s t Z t Y s Z s Y E t X s X E t s t s RBxX-=+=++===DX(t)=5、有随机变量函数的概率密度公式知:X(t)的一维概率密度:0,/)/ln ()(/)()()()(>-='='=t tx t x f y x y f x y y f x fX(t)的均值函数和相关函数为:dy e y f E t EX ytYte ⎰∞--==0)()()( dy y f e eeE t X t X E t t R t t y Yt Yt x )(][)]()([),(0)(21212121⎰∞+---===6、m(t)=E(Z t )=E[]=0,R(s,t)=E(Zs )=E===。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 随机过程分析1.1 学习指导 1.1.1 要点随机过程分析的要点主要包括随机过程的概念、分布函数、概率密度函数、数字特征、通信系统中常见的几种重要随机过程的统计特性。
1. 随机过程的概念 随机过程是一类随时间作随机变化的过程,它不能用确切的时间函数描述。
可从两种不同角度理解:对应不同随机试验结果的时间过程的集合,随机过程是随机变量概念的延伸。
2. 随机过程的分布函数和概率密度函数如果ξ(t )是一个随机过程,则其在时刻t 1取值ξ(t 1)是一个随机变量。
ξ(t 1)小于或等于某一数值x 1的概率为P [ ξ(t 1) ≤ x 1 ],随机过程ξ(t )的一维分布函数为F 1(x 1, t 1) = P [ξ(t 1) ≤ x 1] (2-1)如果F 1(x 1, t 1)的偏导数存在,则ξ(t )的一维概率密度函数为1111111(,)(, ) (2 - 2)∂=∂F x t f x t x对于任意时刻t 1和t 2,把ξ(t 1) ≤ x 1和ξ(t 2) ≤ x 2同时成立的概率{}212121122(, ; , )(), () (2 - 3)F x x t t P t x t x ξξ=≤≤称为随机过程ξ (t )的二维分布函数。
如果2212122121212(,;,)(,;,) (2 - 4)F x x t t f x x t t x x ∂=∂⋅∂存在,则称f 2(x 1, x 2; t 1, t 2)为随机过程ξ (t )的二维概率密度函数。
对于任意时刻t 1,t 2,…,t n ,把{}n 12n 12n 1122n n ()(),(),,() (2 - 5)=≤≤≤F x x x t t t P t x t x t x ξξξ,,,;,,,称为随机过程ξ (t )的n 维分布函数。
如果n n 12n 12n n 12n 12n 12n(x )() (2 - 6)∂=∂∂∂F x x t t t f x x x t t t x x x ,,,;,,,,,,;,,,存在,则称f n (x 1, x 2, …, x n ; t 1, t 2, …, t n )为随机过程ξ (t )的n 维概率密度函数。
3. 随机过程的数字特征 随机过程的数字特征主要包括均值、方差、自相关函数、协方差函数和互相关函数。
随机过程ξ (t )在任意给定时刻t 的取值ξ (t )是一个随机变量,其均值为[]1()(, )d (2 - 7)E t xf x t x ξ∞-∞=⎰其中,f 1(x , t )为ξ (t )的概率密度函数。
随机过程ξ (t )的均值是时间的确定函数,记作a (t ),它表示随机过程ξ (t )的n 个样本函数曲线的摆动中心。
随机过程ξ (t )的方差的定义如下:{}2[()][()()] (2 - 8)D t E t a t ξξ=-随机过程ξ (t )的方差常记作σ2(t )。
随机过程ξ (t )的方差的另一个常用的公式为()()()()()()()2222222212[()]2()[()]()=(,)d () (2 - 9)D ξtE ξt a t ξt a t E ξt a t E ξt a t E ξt a t f x t x a t x∞-∞⎡⎤=-+⎡⎤⎣⎦⎣⎦=-+⎡⎤⎣⎦=--⎰也就是说,方差等于均方值与均值平方之差,它表示随机过程在时刻t ,对于均值a (t )的偏离程度。
随机过程ξ (t )的相关函数的定义如下:1212122121212(,)[()()](,;,)d d (2 - 10)R t t E t t x x f x x t t x x ξξ∞∞-∞-∞==⎰⎰式中, ξ (t 1)和ξ (t 2)分别是在t 1和t 2时刻观测得到的随机变量。
R (t 1, t 2)是两个变量t 1和t 2的确定函数。
随机过程ξ (t )的相关函数表示在任意两个时刻上获得的随机变量之间的关联程度。
随机过程ξ (t )的协方差函数的定义如下:{}12112211222121212(,)[()()][()()] [()][()](,;,)d d (2 - 11)B t t E t a t t a t x a t x a t f x x t t x x ξξ∞∞-∞-∞=--=--⎰⎰式中,a (t 1)、a (t 2)分别是在t 1和t 2时刻得到的ξ (t )的均值;f 2 (x 1, x 2; t 1, t 2)是ξ (t )的二维概率密度函数。
B (t 1, t 2) 与R (t 1, t 2)之间有如下关系式:121212(,)(,)()() (2 - 12)B t t R t t a t a t =-若a (t 1) = a (t 2)=0,则B(t 1, t 2) = R(t 1, t 2)。
随机过程ξ (t )和η(t )的互相关函数的定义如下:ξη1212(,)[()()] (2 - 13)R t t E t t ξη=4. 平稳过程及其性质 平稳过程包括严平稳过程(强平稳过程或狭义平稳过程)和广义平稳过程。
如果随机过程ξ(t )的任意有限维分布函数与时间起点无关,也就是说,对于任意的正整数n 和所有实数∆,有n 12n 12n n 12n 12n (,,,,,,)(,,,,,,) (2 - 14)f x x x t t t f x x x t t t ∆∆∆=+++;;则称该随机过程是严格意义下的平稳随机过程,简称严平稳随机过程。
严平稳随机过程的一维分布函数和均值都与时间无关,二维分布函数和自相关函数都只与时间间隔有关。
把对严平稳随机过程的要求降低到仅仅均值与时间无关和自相关函数只与时间间隔有关的随机过程定义为广义平稳随机过程。
严平稳随机过程必定是广义平稳的,反之不一定成立。
平稳随机过程具有各态历经性(遍历性)。
因此,在求解各种统计平均时,无需无限多次的样本,只要获得一次考察,用一次实现的“时间平均”值代替平稳随机过程的“统计平均”值即可,从而使测量和计算大为简化。
平稳过程ξ(t )的功率谱密度与其自相关函数是一付立叶变换对。
据此,可以得到两条结论:平稳过程ξ(t )的功率等于其自相关函数在零点的取值R (0);各态历经过程任一样本函数的功率谱密度等于平稳过程的功率谱密度。
5. 高斯过程高斯过程又被称为正态随机过程。
如果随机过程ξ(t )的任意n 维(n =1, 2, ...)分布均服从正态分布,则称它为正态过程或高斯过程,其n 维正态概率密度函数表示式为()n 12n 12n /2j j k kjk 11j k i1(,,...,; ,,...,)2π1 exp || (2 - 15)2||n n n n j k i f x x x t t t x a x a B B σσσ-===⎡⎤⎛⎫-⎛⎫--=⎢⎥ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∑∑ 其中,数学期望a k = E [ξ(t k )];方差σ2k = E [ξ(t k ) - a k ]2;归一化协方差矩阵行列式[]{}121n j j k k 212n jk j kn1n21()()1||,1b b E t a t a b b B b b b ξξσσ⎡⎤--⎣⎦==如果高斯过程在不同时刻不相关,则它们也是统计独立的。
高斯过程经过线性系统后,其系统输出也是高斯过程。
6. 窄带随机过程如果随机过程ξ(t )的谱密度集中在中心频率f c 附近相对窄的频带范围∆f 内,即满足∆f << f c 的条件,且 f c 远离零频率,则称其为窄带随机过程。
随机过程ξ(t )可以表示为ξc ξξ()()cos[()],()0 (2 - 16)t a t t t a t ξωϕ=+≥其中,a ξ(t )为随机包络;ϕξ(t )为随机相位;ωc 为中心角频率。
显然,a ξ(t )和ϕξ(t )的变化相对于载波产生的相移(ωc t )的变化要缓慢得多。
将窄带随机过程表示式展开为c c s c ()()cos()()sin() (2 - 17)t t t t t ξξωξω=-其中,ξc (t ) = a ξ(t )cos[υξ(t )];ξs (t ) = a ξ(t )sin[υξ(t )]。
ξc (t )和ξs (t )分别被称为同相分量和正交分量。
窄带随机过程ξ(t )的统计特性可以由a ξ(t )和ϕξ(t )或ξc (t )和ξs (t )的统计特性确定。
若ξ(t )的统计特性已知,则a ξ (t )和ϕξ (t )或ξc (t )和ξs (t )的统计特性也随之确定。
由于ξ(t )平稳且均值为零,故对于任意的时间t ,都有E [ξ(t )] = 0 ,所以c s [()]0[()]0 (2 - 18)E t E t ξξ==,若窄带过程ξ(t )是平稳的,则ξc (t )和ξs (t )也是平稳的。
平稳窄带随机过程ξ(t )的自相关函数可以表示为ξc c cs c c c sc c ()()cos()()sin()()cos()()sin() (2-19)R R R R R ττωττωττωττωτ=-=+一个均值为零的窄带平稳高斯过程ξ(t ),它的同相分量ξc (t )和正交分量ξs (t )同样是平稳高斯过程,而且均值为零,方差也相同。
此外,在同一时刻上得到的ξc (t )与ξs (t )是统计独立的。
a ξ服从瑞利(Rayleigh)分布,ϕξ服从均匀分布。
7. 高斯白噪声和带限白噪声电子系统中常见的热噪声近似为白噪声,白噪声的幅值服从高斯分布。
因此,在通信系统中,常用高斯白噪声作为信道中的噪声模型。
白噪声通过一个有限带宽的信道或滤波器后,输出噪声的带宽就是有限的,如果其频谱在信道或滤波器的通带内仍具有白色特性,则称其为带限白噪声。
白噪声n (t )的功率谱密度在所有频率上均为常数,即n () (,) (2 - 20)2n P f f =∈-∞+∞ 或者n 0() (0,) (2 - 21)P f n f =∈+∞其中,n 0为正常数。
式(2 – 20)是白噪声n (t )的双边功率谱密度,式(2 – 21)是其单边功率谱密度。
白噪声n (t )的自相关函数为()() (2 - 22)2n R τδτ=上式表明,白噪声仅在τ = 0时才相关,而在任何两个不同时刻的随机变量都是不相关的。
如果白噪声幅值的概率分布服从高斯分布,则称之为高斯白噪声。
高斯白噪声在任意两个不同时刻上的随机变量之间,不仅是互不相关的,而且还是统计独立的。
带限白噪声一般包括低通白噪声和带通白噪声。
如果白噪声通过理想低通滤波器或理想低通信道时,则其输出的噪声被称为低通白噪声;如果白噪声通过理想带通滤波器或理想带通信道时,则其输出的噪声被称为带通白噪声。
