随机过程习题答案
(完整word版)随机过程试题及答案

1.设随机变量X 服从参数为λ的泊松分布,则X 的特征函数为 。
2.设随机过程X(t)=Acos( t+),-<t<ωΦ∞∞ 其中ω为正常数,A 和Φ是相互独立的随机变量,且A 和Φ服从在区间[]0,1上的均匀分布,则X(t)的数学期望为 。
3.强度为λ的泊松过程的点间间距是相互独立的随机变量,且服从均值为 的同一指数分布。
4.设{}n W ,n 1≥是与泊松过程{}X(t),t 0≥对应的一个等待时间序列,则n W 服从 分布。
5.袋中放有一个白球,两个红球,每隔单位时间从袋中任取一球,取后放回,对每一个确定的t 对应随机变量⎪⎩⎪⎨⎧=时取得白球如果时取得红球如果t t t e tt X ,,3)(,则 这个随机过程的状态空间 。
6.设马氏链的一步转移概率矩阵ij P=(p ),n 步转移矩阵(n)(n)ijP (p )=,二者之间的关系为 。
7.设{}n X ,n 0≥为马氏链,状态空间I ,初始概率i 0p P(X =i)=,绝对概率{}j n p (n)P X j ==,n 步转移概率(n)ij p ,三者之间的关系为 。
8.设}),({0≥t t X 是泊松过程,且对于任意012≥>t t 则{(5)6|(3)4}______P X X ===9.更新方程()()()()0tK t H t K t s dF s =+-⎰解的一般形式为 。
10.记()(),0n EX a t M M t μ=≥→∞-→对一切,当时,t +a 。
二、证明题(本大题共4道小题,每题8分,共32分)P(BC A)=P(B A)P(C AB)。
2.设{X (t ),t ≥0}是独立增量过程, 且X (0)=0, 证明{X (t ),t ≥0}是一个马尔科夫过程。
3.设{}n X ,n 0≥为马尔科夫链,状态空间为I ,则对任意整数n 0,1<n l ≥≤和i,j I ∈,n 步转移概率(n)()(n-)ij ik kjk Ip p p l l ∈=∑ ,称此式为切普曼—科尔莫哥洛夫方程,证明并说明其意义。
随机过程习题和答案

一、1.1设二维随机变量(,)的联合概率密度函数为:试求:在时,求。
解:当时,==1.2 设离散型随机变量X服从几何分布:试求的特征函数,并以此求其期望与方差。
解:所以:2.1 袋中红球,每隔单位时间从袋中有一个白球,两个任取一球后放回,对每 对应随机变量一个确定的t⎪⎩⎪⎨⎧=时取得白球如果对时取得红球如果对t e t tt X t 3)(.维分布函数族试求这个随机过程的一2.2 设随机过程,其中是常数,与是相互独立的随机变量,服从区间上的均匀分布,服从瑞利分布,其概率密度为试证明为宽平稳过程。
解:(1)与无关(2),所以(3)只与时间间隔有关,所以为宽平稳过程。
2.3是随机变量,且,其中设随机过程U t U t X 2cos )(=求:,.5)(5)(==U D U E.321)方差函数)协方差函数;()均值函数;((2.4是其中,设有两个随机过程U Ut t Y Ut t X ,)()(32==.5)(=U D 随机变量,且数。
试求它们的互协方差函2.5,试求随机过程是两个随机变量设B At t X B A 3)(,,+=的均值),(+∞-∞=∈T t 相互独若函数和自相关函数B A ,.),()(),2,0(~),4,1(~,21t t R t m U B N A X X 及则且立为多少?3.1一队学生顺次等候体检。
设每人体检所需的时间服从均值为2分钟的指数分布并且与其他人所需时间相互独立,则1小时内平均有多少学生接受过体检?在这1小时内最多有40名学生接受过体检的概率是多少(设学生非常多,医生不会空闲)解:令()N t 表示(0,)t 时间内的体检人数,则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
40300(30)((1)40)!k k P N e k -=≤=∑。
3.2在某公共汽车起点站有两路公共汽车。
乘客乘坐1,2路公共汽车的强度分别为1λ,2λ,当1路公共汽车有1N 人乘坐后出发;2路公共汽车在有2N 人乘坐后出发。
随机过程课后题答案

第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtkk X k f t E eepq ∞===∑()k jtkk p q e∞==∑ =0()1jt kjtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰202201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则10()()p jtxp bxX b f t ex e dx p ∞--=Γ⎰ 1()0()p p jt b x b x e dx p ∞--=Γ⎰101()()()()(1)p u p p p p p b e u b u jt b x du jt p b jt b jt b∞----==Γ---⎰ 10(())x p p e x dx ∞--Γ=⎰ (2)'1()(0)X p E X f j b∴== 2''221(1)()(0)X p p E X f j b +== 222()()()PD XE X E X b∴===(4) 若(,)i i X p b Γ 1,2i = 则121212()()()()(1)P P X X X X jt f t f t f t b-++==-1212(,)Y X X P P b ∴=+Γ+同理可得:()()iiP X b f t b jt∑=∑-3、设X 是一随机变量,()F x 是其分布函数,且是严格单调的,求以下随机变量的特征函数。
随机过程习题及部分解答【直接打印】

随机过程习题及部分解答习题一1. 若随机过程()(),X t X t At t =-∞<<+∞为,式中A 为(0,1)上均匀分布的随机变量,求X (t )的一维概率密度(;)X P x t 。
2. 设随机过程()cos(),X t A t t R ωθ=+∈,其中振幅A 及角频率ω均为常数,相位θ是在[,]ππ-上服从均匀分布的随机变量,求X (t )的一维分布。
习题二1. 若随机过程X (t )为X (t )=At t -∞<<+∞,式中A 为(0,1)上均匀分布的随机变量,求12[()],(,)X E X t R t t2. 给定一随机过程X (t )和常数a ,试以X (t )的相关函数表示随机过程()()()Y t X t a X t =+-的自相关函数。
3. 已知随机过程X (t )的均值M X (t )和协方差函数12(,),()X C i t t ϕ是普通函数,试求随机过程()()()Y t X t t ϕ=+是普通函数,试求随机过程()()()Y t X t t ϕ=+的均值和协方差函数。
4. 设()cos sin X t A at B at =+,其中A ,B 是相互独立且服从同一高斯(正态)分布2(0,)N σ的随机变量,a 为常数,试求X (t )的值与相关函数。
习题三1. 试证3.1节均方收敛的性质。
2. 证明:若(),;(),X t t T Y t t T ∈∈均方可微,a ,b 为任意常数,则()()aX t bY t +也是均方可微,且有[()()]()()aX t bY t aX t bY t '''+=+3. 证明:若(),X t t T ∈均方可微,()f t 是普通的可微函数,则()()f t X t 均方可微且[()()]()()()()f t X t f t X t f t X t '''=+4. 证明:设()[,]X t a b 在上均方可微,且()[,]X t a b '在上均方连续,则有()()()b aX t dt X b X a '=-⎰5. 证明,设(),[,];(),[,]X t t T a b Y t t T a b ∈=∈=为两个随机过程,且在T 上均方可积,αβ和为常数,则有[()()]()()b b baaaX t Y t dt X t dt Y t dt αβαβ+=+⎰⎰⎰()()(),b c baacaX t dt X t dt X t dt a c b =+⎰⎰⎰≤≤6. 求随机微分方程()()()[0,](0)0X t aX t Y t t X '+=∈+∞⎧⎨=⎩的()X t 数学期望[()]E X t 。
(完整版)随机过程习题答案

(完整版)随机过程习题答案随机过程部分习题答案习题22.1 设随机过程b t b Vt t X ),,0(,)(+∞∈+=为常数,)1,0(~N V ,求)(t X 的⼀维概率密度、均值和相关函数。
解因)1,0(~N V,所以1,0==DV EV ,b Vt t X +=)(也服从正态分布,b b tEV b Vt E t X E =+=+=][)]([ 22][)]([t DV t b Vt D t X D ==+=所以),(~)(2t b N t X ,)(t X 的⼀维概率密度为),(,21);(222)(+∞-∞∈=--x ett x f t b x π,),0(+∞∈t均值函数 b t X E t m X ==)]([)(相关函数)])([()]()([),(b Vt b Vs E t X s X E t s R X ++==][22b btV bsV stV E +++=2b st +=2.2 设随机变量Y 具有概率密度)(y f ,令Yt e t X -=)(,0,0>>Y t ,求随机过程)(t X 的⼀维概率密度及),(),(21t t R t EX X 。
解对于任意0>t,Yt e t X -=)(是随机变量Y 的函数是随机变量,根据随机变量函数的分布的求法,}ln {}{})({);(x Yt P x e P x t X P t x F t Y ≤-=≤=≤=-)ln (1}ln {1}ln {tx F t x Y P t x Y P Y --=-≤-=-≥= 对x 求导得)(t X 的⼀维概率密度xtt x f t x f Y 1)ln ();(-=,0>t)(][)]([)(dy y f e eE t X E t m yt tY X相关函数+∞+-+---====0)()(2121)(][][)]()([),(212121dy y f e e E e e E t X t X E t t R t t y t t Y t Y t Y X 2.3 若从0=t 开始每隔21秒抛掷⼀枚均匀的硬币做实验,定义随机过程=时刻抛得反⾯时刻抛得正⾯t t t t t X ,2),cos()(π试求:(1))(t X 的⼀维分布函数),1(),21(x F x F 和;(2))(t X 的⼆维分布函数),;1,21(21x x F ;(3))(t X 的均值)1(),(X X m t m ,⽅差 )1(),(22X Xt σσ。
随机过程习题和答案

一、1.1设二维随机变量(,)的联合概率密度函数为:试求:在时,求。
解:当时,==1.2 设离散型随机变量X服从几何分布:试求的特征函数,并以此求其期望与方差。
解:所以:2.1 袋中红球,每隔单位时间从袋中有一个白球,两个任取一球后放回,对每 对应随机变量一个确定的t⎪⎩⎪⎨⎧=时取得白球如果对时取得红球如果对t e t tt X t 3)(.维分布函数族试求这个随机过程的一2.2 设随机过程,其中是常数,与是相互独立的随机变量,服从区间上的均匀分布,服从瑞利分布,其概率密度为试证明为宽平稳过程。
解:(1)与无关(2),所以(3)只与时间间隔有关,所以为宽平稳过程。
2.3是随机变量,且,其中设随机过程U t U t X 2cos )(=求:,.5)(5)(==U D U E.321)方差函数)协方差函数;()均值函数;((2.4是其中,设有两个随机过程U Ut t Y Ut t X ,)()(32==.5)(=U D 随机变量,且数。
试求它们的互协方差函2.5,试求随机过程是两个随机变量设B At t X B A 3)(,,+=的均值),(+∞-∞=∈T t 相互独若函数和自相关函数B A ,.),()(),2,0(~),4,1(~,21t t R t m U B N A X X 及则且立为多少?3.1一队学生顺次等候体检。
设每人体检所需的时间服从均值为2分钟的指数分布并且与其他人所需时间相互独立,则1小时内平均有多少学生接受过体检?在这1小时内最多有40名学生接受过体检的概率是多少(设学生非常多,医生不会空闲)解:令()N t 表示(0,)t 时间内的体检人数,则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
40300(30)((1)40)!k k P N e k -=≤=∑。
3.2在某公共汽车起点站有两路公共汽车。
乘客乘坐1,2路公共汽车的强度分别为1λ,2λ,当1路公共汽车有1N 人乘坐后出发;2路公共汽车在有2N 人乘坐后出发。
随机过程习题答案

1 X ( )与 X (1)的联合分布律为 2 1 X( ) 0 1 2 X (1) −1 +2 1 2 0 0 1 2
0, 0, 1 1 , ⇒ F ( x1 , x2 ; ,1) = 2 2 1 , 2 1,
x1 < 0, −∞ < x2 < +∞ x1 ≥ 0, x2 < −1 0 ≤ x1 < 1, x2 ≥ −1 x1 ≥ 1, −1 ≤ x2 < 2 x1 ≥ 1, x2 ≥ 2
假定 Z (t ) = X + Yt , t ∈ R.若已知二维随机变量 例3 σ 12 ( X , Y )的协方差矩阵为 ρσ 1σ 2 的协方差函数.
ρσ 1σ 2 ,试求 Z (t ) 2 σ2
解 CZ (t1 , t2 ) = E[( X + Yt1 − ( µ X + µY t1 ))( X + Yt2 − ( µ X + µY t2 ))] = E[(( X − µ X ) + (Yt1 − µY t1 ))(( X − µ X ) + (Yt2 − µY t2 ))] = E[( X − µ X )( X − µ X )] + t2 E[( X − µ X )(Y − µY )] +t1 E[(Y − µY )( X − µ X )] + t1t2 E[(Y − µY )(Y − µY )]
(3)、令 Z (t ) = aW ( t a 2 ) ⇒ µ Z (t ) = aE[W ( t a 2 )] = 0 C Z (t1 , t 2 ) = E[ aW ( t1 a 2 ) aW ( t2 a 2 )] = a 2 E[W ( t1 a 2 )W ( t2 a 2 )] = a 2σ 2 min{ t1 a 2 , t2 a 2 } = σ 2 min{t1 , t 2 }, t1 , t 2 ≥ 0
《随机过程》课后习题解答
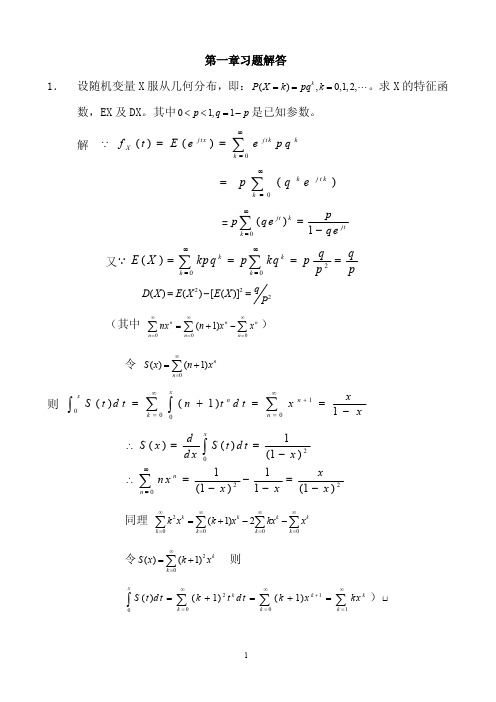
( k 0, 2, n )
1 为一特征函数,并求它所对应的随机变量的分布。 1 t2
n n i
f (t
i 1 k 1
tk )i k
5
=
i 1 k 1
n
n
i k
1 (ti tk )
2
i 1 k 1
n
n
e jti e jti e jti {1 ( jtk )(1 jtk )} n n e jtk e e i k jti = i 1 k 1 e n(1 jtk ) e
1 n n n j ( ti tk ) l ] i k = [e n i 1 k 1 l 1
(2) (3)
其期望和方差; 证明对具有相同的参数的 b 的 分布,关于参数 p 具有可加性。
解 (1)设 X 服从 ( p , b ) 分布,则
f X (t ) e jtx
0
b p p 1 bx x e dx ( p )
bp ( p)
x
0
p 1 ( jt b ) x
i k
1 M 2
0
ti t k } ) ( M 1max{ i , j n
且 f (t ) 连续 f (0) 1 (2) f (t )
f (t ) 为特征函数
1 1 1 1 1 [ ] 2 2 1 t 1 ( jt ) 2 1 jt 1 jt
3
fZ(k)() t (1 )kk! jk (1 jt)(k1)
E (Z k ) 1 (k ) f Z (0) ( 1) k k ! k j
n
(完整版)随机过程习题和答案

一、1.1设二维随机变量(,)的联合概率密度函数为:试求:在时,求。
解:当时,==1.2 设离散型随机变量X服从几何分布:试求的特征函数,并以此求其期望与方差。
解:所以:2.1 袋中红球,每隔单位时间从袋中有一个白球,两个任取一球后放回,对每 对应随机变量一个确定的t⎪⎩⎪⎨⎧=时取得白球如果对时取得红球如果对t e t tt X t 3)(.维分布函数族试求这个随机过程的一2.2 设随机过程,其中是常数,与是相互独立的随机变量,服从区间上的均匀分布,服从瑞利分布,其概率密度为试证明为宽平稳过程。
解:(1)与无关(2),所以(3)只与时间间隔有关,所以为宽平稳过程。
2.3是随机变量,且,其中设随机过程U t U t X 2cos )(=求:,.5)(5)(==U D U E.321)方差函数)协方差函数;()均值函数;((2.4是其中,设有两个随机过程U Ut t Y Ut t X ,)()(32==.5)(=U D 随机变量,且数。
试求它们的互协方差函2.5,试求随机过程是两个随机变量设B At t X B A 3)(,,+=的均值),(+∞-∞=∈T t 相互独若函数和自相关函数B A ,.),()(),2,0(~),4,1(~,21t t R t m U B N A X X 及则且立为多少?3.1一队学生顺次等候体检。
设每人体检所需的时间服从均值为2分钟的指数分布并且与其他人所需时间相互独立,则1小时内平均有多少学生接受过体检?在这1小时内最多有40名学生接受过体检的概率是多少(设学生非常多,医生不会空闲)解:令()N t 表示(0,)t 时间内的体检人数,则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
40300(30)((1)40)!k k P N e k -=≤=∑。
3.2在某公共汽车起点站有两路公共汽车。
乘客乘坐1,2路公共汽车的强度分别为1λ,2λ,当1路公共汽车有1N 人乘坐后出发;2路公共汽车在有2N 人乘坐后出发。
随机过程习题和答案.doc

一、设二维随机变量(,)的联合概率密度函数为:试求:在时,求。
解:当时,==设离散型随机变量X服从几何分布:试求的特征函数,并以此求其期望与方差。
解:所以:袋中有一个白球,两个红球,每隔单位时间从袋中任取一球后放回,对每一个确定的t对应随机变量X(t)t3te如果对如果对t时取得红球t时取得白球试求这个随机过程的一维分布函数族.设随机过程,其中是常数,与是相互独立的随机变量,服从区间上的均匀分布,服从瑞利分布,其概率密度为试证明为宽平稳过程。
解:(1)与无关(2),所以(3)只与时间间隔有关,所以为宽平稳过程。
设随机过程X(t)U cos2t U E(U)5,D(U)5.求:,其中是随机变量,且(1)均值函数;(2)协方差函数;(3)方差函数.设有两个随机过程X(t)Ut2Y(t)Ut3,U随机变量,且D(U)5.,其中是试求它们的互协方差函数。
设A,B,X(t)At3B t T(,)的均值是两个随机变量试求随机过程,函数和自相关函数.A,B,~(1,4),~(0,2),()(,)若相互独立且A N B U则m X t及R X t1t2为多少?一队学生顺次等候体检。
设每人体检所需的时间服从均值为2分钟的指数分布并且与其他人所需时间相互独立,则1小时内平均有多少学生接受过体检在这1小时内最多有40名学生接受过体检的概率是多少(设学生非常多,医生不会空闲)解:令N(t)表示(0,t)时间内的体检人数,则N(t)为参数为30的poisson过程。
以小时为单位。
则E(N(1))30。
40k(30) P(N(1)40)ek!k030。
在某公共汽车起点站有两路公共汽车。
乘客乘坐1,2路公共汽车的强度分别为1,2,当1路公共汽车有N人乘坐后出发;2路公共汽车1在有N2人乘坐后出发。
设在0时刻两路公共汽车同时开始等候乘客到来,求(1)1路公共汽车比2路公共汽车早出发的概率表达式;(2)当N1=N,1=22时,计算上述概率。
随机过程习题答案

解 转移概率如图
一步概率转移矩阵为 二步转移概率矩阵为 4.2 独立地重复抛掷一枚硬币,每次抛掷出现正面的概率为,对于, 令,这些值分别对应于第n-1次和第n次抛掷的结果为(正,正), (正,反),(反,正),(反,反),求马尔可夫链的一步和二步转 移概率矩阵。 解 对应状态为 ,(正,反),(反,正),(反,反) , (不可能事件) (不可能事件) 同理可得下面概率 , , , , , , 一步转移概率矩阵为 二步转移概率矩阵为 4.4设为有限齐次马尔可夫链,其初始分布和转移概率矩阵为
对求导得的一维概率密度 , 均值函数 相关函数 2.3 若从开始每隔秒抛掷一枚均匀的硬币做实验,定义随机过程
试求:(1)的一维分布函数; (2)的二维分布函数; (3)的均值,方差 。 解 (1)时,的分布列为
0
1
P
一维分布函数 时,的分布列为
-1
2
P
一维分布函数 (2)由于相互独立,所以的分布列为
(2)画出状态转移图
因为是有限链,必有正常返态,状态0无周期、正常返,是遍历态;由 于各状态互通,所以1、2也是遍历态,所以是遍历链。 (3)因为该链为遍历链,极限分布就是平稳分布,根据和得方程组 解此方程组得
所以平稳分布为 ,, 4.17 设河流每天的BOD(生物耗氧量)浓度为齐次马尔可夫链,状态空 间是按BOD浓度为极低、低、中、高分别表示的,其一步转移概率矩阵 (以一天为单位)为
-1
2
0
1
二维分布函数 (3)
2.4 设有随机过程,其中为常数,是相互独立且服从正态分布的随机变 量,求随机过程的均值和相关函数。 解 因独立,, 所以, 均值
相关函数 2.5 已知随机过程的均值函数和协方差函数为普通函数,令,求随机过 程均值和协方差函数。 解 均值 协方差
随机过程习题答案

随机过程习题解答(一)第一讲作业:1、设随机向量的两个分量相互独立,且均服从标准正态分布。
(a)分别写出随机变量和的分布密度(b)试问:与是否独立?说明理由。
解:(a)(b)由于:因此是服从正态分布的二维随机向量,其协方差矩阵为:因此与独立。
2、设和为独立的随机变量,期望和方差分别为和。
(a)试求和的相关系数;(b)与能否不相关?能否有严格线性函数关系?若能,试分别写出条件。
解:(a)利用的独立性,由计算有:(b)当的时候,和线性相关,即3、设是一个实的均值为零,二阶矩存在的随机过程,其相关函数为,且是一个周期为T的函数,即,试求方差函数。
解:由定义,有:4、考察两个谐波随机信号和,其中:式中和为正的常数;是内均匀分布的随机变量,是标准正态分布的随机变量。
(a)求的均值、方差和相关函数;(b)若与独立,求与Y的互相关函数。
解:(a)(b)第二讲作业:P33/2.解:其中为整数,为脉宽从而有一维分布密度:P33/3.解:由周期性及三角关系,有:反函数,因此有一维分布:P35/4. 解:(1) 其中由题意可知,的联合概率密度为:利用变换:,及雅克比行列式:我们有的联合分布密度为:因此有:且V和相互独立独立。
(2)典型样本函数是一条正弦曲线。
(3)给定一时刻,由于独立、服从正态分布,因此也服从正态分布,且所以。
(4)由于:所以因此当时,当时,由(1)中的结论,有:P36/7.证明:(1)(2) 由协方差函数的定义,有:P37/10. 解:(1)当i =j 时;否则令,则有第三讲作业:P111/7.解:(1)是齐次马氏链。
经过次交换后,甲袋中白球数仅仅与次交换后的状态有关,和之前的状态和交换次数无关。
(2)由题意,我们有一步转移矩阵:P111/8.解:(1)由马氏链的马氏性,我们有:(2)由齐次马氏链的性质,有:,(2)因此:P112/9.解:(2)由(1)的结论,当为偶数时,递推可得:;计算有:,递推得到,因此有:P112/11.解:矩阵 的特征多项式为:由此可得特征值为:,及特征向量:,则有:因此有:(1)令矩阵P112/12.解:设一次观察今天及前两天的天气状况,将连续三天的天气状况定义为马氏链的状态,则此问题就是一个马氏链,它有8个状态。
随机过程试题及答案

随机过程试题及答案一、选择题(每题5分,共20分)1. 下列哪一项是随机过程的典型特征?A. 确定性B. 可预测性C. 无记忆性D. 独立增量性答案:D2. 马尔可夫链的哪一性质表明,系统的未来状态只依赖于当前状态,而与过去状态无关?A. 独立性B. 无记忆性C. 齐次性D. 可逆性答案:B3. 布朗运动是一个连续时间的随机过程,其增量具有什么性质?A. 独立性B. 正态分布C. 独立增量性D. 所有选项都正确答案:D4. 随机过程的平稳性指的是什么?A. 过程的分布随时间不变B. 过程的均值随时间不变C. 过程的方差随时间不变D. 过程的自相关函数随时间不变答案:A二、填空题(每题5分,共20分)1. 如果随机过程的任意时刻的分布函数不随时间变化,则称该随机过程是________。
答案:平稳的2. 随机过程的自相关函数R(t,s)表示在时刻t和时刻s的随机变量的________。
答案:相关性3. 随机游走过程是一类具有________性质的随机过程。
答案:独立增量4. 泊松过程是一种描述在固定时间间隔内随机事件发生次数的随机过程,其特点是事件的发生具有________。
答案:无记忆性三、简答题(每题10分,共30分)1. 简述什么是马尔可夫过程,并给出其数学定义。
答案:马尔可夫过程是一种随机过程,其未来的状态只依赖于当前状态,而与过去状态无关。
数学上,如果对于任意的n,以及任意的时间序列t1, t2, ..., tn,满足P(Xt+1 = x | Xt = x_t, Xt-1 = x_t-1, ..., X1 = x_1) = P(Xt+1 = x | Xt = x_t),则称随机过程{Xt}为马尔可夫过程。
2. 描述布朗运动的三个基本性质。
答案:布朗运动的三个基本性质包括:1) 布朗运动的增量是独立的;2) 布朗运动的增量服从正态分布;3) 布朗运动具有连续的样本路径。
3. 什么是平稳随机过程?请给出其数学定义。
(完整版)随机过程习题答案

随机过程部分习题答案习题22.1 设随机过程b t b Vt t X ),,0(,)(+∞∈+=为常数,)1,0(~N V ,求)(t X 的一维概率密度、均值和相关函数。
解 因)1,0(~N V,所以1,0==DV EV ,b Vt t X +=)(也服从正态分布,b b tEV b Vt E t X E =+=+=][)]([ 22][)]([t DV t b Vt D t X D ==+=所以),(~)(2t b N t X ,)(t X 的一维概率密度为),(,21);(222)(+∞-∞∈=--x ett x f t b x π,),0(+∞∈t均值函数 b t X E t m X ==)]([)(相关函数)])([()]()([),(b Vt b Vs E t X s X E t s R X ++==][22b btV bsV stV E +++=2b st +=2.2 设随机变量Y 具有概率密度)(y f ,令Yt e t X -=)(,0,0>>Y t ,求随机过程)(t X 的一维概率密度及),(),(21t t R t EX X 。
解 对于任意0>t,Yt e t X -=)(是随机变量Y 的函数是随机变量,根据随机变量函数的分布的求法,}ln {}{})({);(x Yt P x e P x t X P t x F t Y ≤-=≤=≤=-)ln (1}ln {1}ln {tx F t x Y P t x Y P Y --=-≤-=-≥= 对x 求导得)(t X 的一维概率密度xtt x f t x f Y 1)ln ();(-=,0>t均值函数⎰∞+--===0)(][)]([)(dy y f e eE t X E t m yt tY X相关函数⎰+∞+-+---====0)()(2121)(][][)]()([),(212121dy y f e e E e e E t X t X E t t R t t y t t Y t Y t Y X2.3 若从0=t 开始每隔21秒抛掷一枚均匀的硬币做实验,定义随机过程⎩⎨⎧=时刻抛得反面时刻抛得正面t t t t t X ,2),cos()(π 试求:(1))(t X 的一维分布函数),1(),21(x F x F 和;(2))(t X 的二维分布函数),;1,21(21x x F ;(3))(t X 的均值)1(),(X X m t m ,方差 )1(),(22X Xt σσ。
随机过程习题和答案

、1.1设二维随机变量(X , F)的联合概率密度函数为:=—i—[l241-ι>⅛= "k"QTh Xl-JF)1.2 设离散型随机变量X服从几何分布:Hm=(Ip)HPJt=U-试求/的特征函数,并以此求其期望E(X)与方差I K X)¾0 = Efr ir) = ∑e⅛ = *)解:一=⅛α-ri M P=√^∑^α-p)t U O-P) ⅛J1—(I-JI)1—q/(O)=α⅛24(1-小丄0<y<x<l苴它试求:在OJu <■ 1时,求I『F)解:J;240 H)JKfc0<y<l Jj2Jf(I_y)3 0<JF<1P 其它^{θ其它当OJXI 时,Aw)2OT(Xy)y<x<l其它所以:-⅛(0)二丄f PZUr=J Er3-(JEIf)3=^^-^=4PPp2.1袋中有一个白球,两个红球,每隔单位时间从袋中任取一球后放回,对每一个确定的t 对应随机变量x(t^3如果对t时取得红球e t如果对t时取得白球试求这个随机过程的一维分布函数族2.2设随机过程 W 加吨MIF)∙ gZ I叫,其中吗是常数,/与F是相互独立的随机变量,F服从区间(°2刘上的均匀分布,/服从瑞利分布,其概率密度为x>0x≤0试证明Xu)为宽平稳过程。
解:( 1)⑷+F)} q啊诚如+ f)}= 与无关(2)枚F(M 仪加血I(Q/伽说如")汁F(才),f _ t t⅛(Q) =-J PQ ÷g)= -te^t∣Γ÷p ^dt =-2σ1e^i∣Γ=2σ3所以必U)啟0⑴卜"(3)R lM壊M∞¼⅛+Hl∕∞Ψ⅛+y)]}=豺]£{oKs(A +Γ)∞<β(A +Γ)}=2^Jtt 2{α≈(0A + β⅛+ y)-rasfflfc A)I^⅛心’皿叫仏Z L)只与时间间隔有关,所以XU)为宽平稳过程2.3设随机过程 X(t)=Ucos2t,其中U是随机变量,且 E(U)= 5, D(U)= 5.求: (1)均值函数;(2)协方差函数;(3)方差函数2.4设有两个随机过程 X(t)=Ut2, Y(t)=Ut3,其中U是随机变量,且D(U) = 5.试求它们的互协方差函数2.5设代B是两个随机变量,试求随机过程X(t) =At ∙3B,t∙ T =(」:「:)的均值函数和自相关函数若A, B相互独立,且A~ N(1,4), B ~U (0,2),则mχ (t)及Rχ(t1,t2)为多少?3.1 一队学生顺次等候体检。
随机过程习题答案

随机过程复习题一、填空题:1.设}),({0≥t t X 是泊松过程,且对于任意012≥>t t ,)()]()([12123t t t X t X E -=-,则15486}6)5(,4)3(,2)1({-====e X X X P ,618}4)3(|6)5({-===e X X P2. 已知马尔可夫链的状态空间为},,{321=I ,初始分布为),,(412141,⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=43410313131043411)(P 则167)2(12=P ,161}2,2,1{210====X X X P 3.强度λ的泊松过程的协方差函数},min{),(t s t s C X λ= 4.已知平稳过程)(t X 的自相关函数为πττcos )(=X R , 则)]()([)(πωδπωδπω-++=X S5.对于平稳过程X (t)若)()]()([)()(τττX R t X t X E t X t X =+>=+<以概率1成立,则称)(t X 的自相关函数具有各态历经性。
6.已知平稳过程)(t X 的谱密度为23242++=ωωωω)(S ,则)(t X 的均方值=2222- 7. 随机相位过程),cos()(Θω+=t a t X 其中ω,a 为常数,Θ为),(π20上服从均匀分布的随机变量,则0)(>=<t X ,ωττcos 2)()(2a t X t X >=+<8.设马尔可夫链},2,1,0,{ =n X n 的状态空间}1,0{=I ,则一步转移概率矩阵为⎥⎦⎤⎢⎣⎡=9.01.01.09.0P ,初始分布为)31,32()0(=p ,则2X 的分布律为 (2)P = (0.547,0.453),234(1,1,0)________P X X X ====0.099.设...)2,1,0(=n Xn是只有两个状态的齐次马氏链,其n步转移概率矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛-=n n n nD C n P 21311)(,则n n C D ==nn 21,31二、计算与证明:1.设任意相继两天中,雨天转晴天的概率为31,晴天转雨天的概率为21,任一天晴或雨是互为逆事件,以0表示晴天状态,以1表示雨天状态,nX 表示第n 天的状态(0或1)。
随机过程课后试题答案

随机过程课后试题答案1. 题目:简述离散时间马尔可夫链和连续时间马尔可夫链的基本概念和性质。
答案:离散时间马尔可夫链(Discrete-time Markov Chain)是指在时间上的变化是离散的、状态空间是有限或可列无限的马尔可夫链。
其基本概念和性质如下:1.1 基本概念:- 状态空间:马尔可夫链的状态空间是指系统可能处于的状态集合,记作S。
离散时间马尔可夫链的状态空间可以是有限集合或可列无限集合。
- 转移概率:转移概率是指在给定前一个状态的条件下,系统转移到下一个状态的概率。
用P(i, j)表示系统从状态i转移到状态j的概率,其中i和j属于状态空间S。
- 转移概率矩阵:转移概率矩阵P是指表示从任一状态i到任一状态j的转移概率的矩阵。
对于离散时间马尔可夫链,转移概率矩阵是一个方形矩阵,维数与状态空间大小相同。
- 平稳概率分布:对于离散时间马尔可夫链,如果存在一个概率分布π,满足π = πP,其中π是一个行向量,P是转移概率矩阵,则称π为马尔可夫链的平稳概率分布。
1.2 性质:- 马尔可夫性:离散时间马尔可夫链具有马尔可夫性,即将来状态的发展只与当前状态有关,与过去的状态无关。
- 遍历性:若马尔可夫链中任意两个状态之间都存在路径使得概率大于零,则称该马尔可夫链是遍历的。
遍历性保证了马尔可夫链具有长期稳定的性质。
- 正常概率性:对于离散时间马尔可夫链,转移概率矩阵P的元素都是非负的,并且每一行的元素之和等于1。
- 可约性和不可约性:如果一个马尔可夫链中的所有状态彼此之间都是可达的,则称该马尔可夫链是不可约的。
反之,则称它是可约的。
不可约性保证了任意状态之间都可以相互转移。
- 周期性:对于不可约的离散时间马尔可夫链,如果存在某个状态,从该状态出发回到该状态所需的步数的最大公约数大于1,则称该状态是周期的。
若所有状态都是非周期的则称该马尔可夫链是非周期的。
2. 题目:连续时间马尔可夫链的定义和性质有哪些?答案:连续时间马尔可夫链(Continuous-time Markov Chain)是指在时间上的变化是连续的、状态空间是有限或可列无限的马尔可夫链。
随机过程试题及答案

随机过程试题及答案一、单项选择题(每题2分,共10分)1. 随机过程的数学定义中,通常需要满足哪些条件?A. 样本空间、概率测度、随机变量B. 样本空间、概率测度、随机函数C. 样本空间、随机变量、随机函数D. 概率测度、随机变量、随机函数答案:B2. 马尔可夫链的无记忆性指的是什么?A. 过程的未来状态仅依赖于当前状态B. 过程的未来状态仅依赖于过去的状态C. 过程的未来状态依赖于当前和过去的状态D. 过程的未来状态依赖于所有历史状态答案:A3. 在随机过程中,如果一个过程的任何有限维分布都是联合正态的,则称该过程为什么?A. 正态过程B. 高斯过程C. 联合正态过程D. 多元正态过程答案:B4. 以下哪个不是平稳随机过程的性质?A. 一阶矩不随时间变化B. 任意两个不同时间点的协方差仅依赖于时间差C. 过程的均值随时间变化D. 过程的自相关函数仅依赖于时间差答案:C5. 随机过程的谱密度函数与自相关函数之间的关系是什么?A. 互为傅里叶变换B. 互为拉普拉斯变换C. 互为Z变换D. 互为梅林变换答案:A二、填空题(每题3分,共15分)1. 如果随机过程的样本路径是连续的,则称该过程为_________。
答案:连续过程2. 随机过程的样本函数是定义在时间轴上的_________。
答案:随机变量3. 对于一个平稳过程,其自相关函数R(τ)仅依赖于时间差τ,而不依赖于绝对时间t,即R(t1, t2) = R(t1 - t2) = R(τ),其中τ = t2 - t1。
这种性质称为_________。
答案:时间平移不变性4. 随机过程的遍历性是指过程的_________等于其统计平均。
答案:时间平均5. 随机过程的遍历性分为_________遍历性和_________遍历性。
答案:强,弱三、简答题(每题10分,共20分)1. 简述什么是泊松过程,并给出其概率质量函数。
答案:泊松过程是一种描述在固定时间或空间间隔内随机事件发生次数的随机过程。
随机过程课后试题答案

随机过程课后试题答案一、选择题1. 随机过程的基本定义中,样本空间通常表示为:A. 一个集合B. 一个函数集合C. 一个概率空间D. 一个参数集合答案:A2. 若随机过程的样本轨迹几乎是连续的,则该过程是:A. 离散时间随机过程B. 连续时间随机过程C. 泊松过程D. 马尔可夫过程答案:B3. 马尔可夫性质的含义是未来的状态只依赖于当前状态,而与过去的状态无关。
这一性质不适用于:A. 泊松过程B. 布朗运动C. 马尔可夫链D. 所有随机过程答案:D4. 在随机过程中,如果两个随机变量的联合分布可以表示为它们各自的边缘分布的乘积,则这两个随机变量是:A. 独立的B. 相关的C. 正相关的D. 负相关的答案:A5. 随机游走的期望步长是:A. 1B. 2C. 依赖于起始点D. 依赖于步长分布答案:D二、填空题1. 一个随机过程的样本函数是定义在参数集合上的_________函数。
答案:实值或随机2. 在随机过程中,如果给定当前状态,下一状态的条件概率分布仅依赖于当前状态而不依赖于之前的状态,那么该过程是一个_________过程。
答案:马尔可夫3. 随机过程的均值函数(或称数学期望函数)是描述过程长期行为的重要工具,它是一个关于_________的函数。
答案:时间4. 布朗运动是一种连续时间随机过程,其样本轨迹具有_________性质。
答案:无处处可微5. 泊松过程是一种描述事件在时间上随机发生的随机过程,其特点是事件在任意两个不重叠时间区间内发生是_________的。
答案:相互独立三、计算题1. 假设有一个离散时间马尔可夫链,其状态转移矩阵为:\[P = \begin{bmatrix}0.7 & 0.3 \\0.4 & 0.6\end{bmatrix}\]求该马尔可夫链在第二时刻的状态概率分布,给定初始状态概率分布为:\\[\pi_0 = \begin{bmatrix}0.5 \\0.5\end{bmatrix}\]解:首先计算\( P^2 \),即状态转移矩阵的二次幂,然后利用\( \pi_0 \)和\( P^2 \)来计算第二时刻的状态概率分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机过程习题答案
1、已知X(t)和Y(t)是统计独立的平稳随机过程,且它们的均值分别为mx和my,它们的自
相关函数分别为Rx(,)和Ry(,)。
(1)求Z(t)=X(t)Y(t)的自相关函数;(2)求
Z(t)=X(t)+Y(t)
的自相关函数。
答案:
(1) R(,),E,,,,z(t,,)z(t),Ex(t,,)y(t,,)x(t)y(t)z
,,,x(t)y(t)R(),Ex(t,)x(t)Ey(t,)y(t),,,,利用和独立的性质:z,
,R(,)R(,)xy
(2) ,,,,R(,),E,,z(t,,)z(t),E,,x(t,,),y(t,,),x(t),y(t)z
,E,,x(t,,)x(t),x(t,,)y(t),y(t,,)x(t),y(t,,)y(t)
仍然利用x(t)和y(t)互相独立的性质: R(,),R(,),2mm,R(,)zxxyy2、一个RC低通滤波电路如下图所示。
假定输入是均值为0、双边功率谱密度函数为n/20 的高斯白噪声。
(1)求输出信号的自相关函数和功率谱密度函数;(2)求输出信号的一
维概率密度函数。
电流:i(t)
R 电压:x(t) C 电压:y(t)
答案:
Y(s)1H(s),,(1) 该系统的系统函数为 X(s)1,RCs
1H(j,),则频率响应为 1,jRC,
n0()而输入信号x(t)的功率谱密度函数为 ,,PjX2
该系统是一个线性移不变系统,所以输出y(t)的功率谱密度函数为:
n/220P(j,),P(j,)H(j,), YX22,,1,RC,
对求傅里叶反变换,就得到输出的自相关函数: P(j,)Y
,,11/2nj,j,,,0,()()R,Pj,ed,,ed, YY2,,2,,,,,,22,,1,RC,
(2) 线性系统输入为高斯随机过程,则输出也一定是高斯的。
因此,为了求输
出的一维概率密度函数,仅需知道输出随机过程的均值和方差即可。
均值:已知输入均值m=0,则输出均值m=mH(0)=0 xyx
2方差:R(0),Var(Y),m Yy
,1/2n0()(0)因为均值为0,所以方差 VarY,R,d,Y2,2,,,2,,1,RC,
一维PDF:略
3、理想带通滤波器的中心频率为fc、带宽为B,其在通带的频率增益为1。
假定输入是均
值为0、双边功率谱密度函数为n/2的高斯白噪声。
(1)求输出信号的自相关函数和功0
率谱密度函数;(2)求输出信号的平均功率;(3)求输出信号的一维概率密度函数。
答案:类似上一题,仅需注意的是:
f,B,,,f,B1,2(/2)2(/2),,,cc(a) 此处滤波器的频率响应为
Hj,,(),otherwise0,
(b) 平均功率等于功率谱密度函数的积分,也即等于输出信号y(t)的自相关在处,,0
的值,即 R(0)Y
4、设x1(t)与x2(t)为零均值且互不相关的平稳随机过程。
x1(t)通过某个LTI系统所得的输出
为y1(t),x2(t)通过同一个LTI系统的输出为y2(t)。
试证明y1(t)与y2(t)互不相关。
答案:就是要证明y1(t)与y2(t)的协方差为0。
由于x1(t)与x2(t)为零均值,显而易见y1(t)与y2(t)的均值都为0。
所以,我们仅需要证明y1(t)与y2(t)的互相关为0。
设LTI系统的单位冲激响应为h(t),则:
, y(t),x(t,,)h(,)d,11,,,
, y(t),x(t,,)h(,)d,22,,,
所以有:
,,,,,,,Ey(t)y(t),Ex(t,)h()dx(t,v)h(v)dv,,1212,,,,,,,,,,
,,,,,,, ,Ex(t,)x(t,v)h()h(v)ddv 12,,,,,,,,,,
,,,,,Ex(t,,)x(t,v)h(,)h(v)d,dv12,,,,,,
再利用x1(t)与x2(t)互不相关的性质,则有:
,,,,,,,,,从而完成证明。
Ey(t)y(t),Ex(t,,)Ex(t,v)h(,)h(v)d,dv,01212,,,,,,
教材:2.8和2.9题 ,答案略。
