轴扭转计算分解
合集下载
11圆轴扭转变形与刚度计算
§7.5
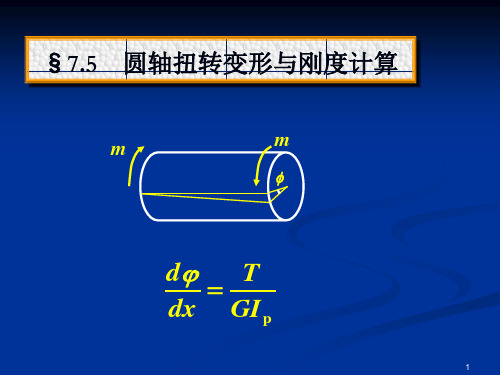
圆轴扭转变形与刚度计算
m m
d T dx GI p
1
一、圆轴扭转变形公式
由
m
m
T ( x )dx 满足平面假设的圆轴: GI p ( x ) l Tl T=Const,等截面圆轴: GI p
GIp-抗扭刚度
d T dx GI p
Ti l i Ti,Ipi在各段内为常数的轴: i 1 GI pi
or
T 180 [ ] GI p max
/ m
等截面圆轴扭转的刚度条件为:
Tmax [ ] (rad/m) GI p
or
Tmax 180 [ ] GI p
/ m
4
【例题1】
传动轴图所示。主动轮A输入功率 PA=36kw , 从 动 轮 B 、 C 、 D 输 出 功 率 分 别 为 PB=PC=11kW , PD=14kW ,轴的转速为 n=300r/min , 许用切应力为[]=50MPa,切变模量为G=80GPa,单 位长度许用扭转角为[]=0.5()/m。试确定: 实心圆截面轴的直径d0;
l
x
12
三、圆轴扭转静不定问题
【例题3】 设有 A 、 B 两个凸缘的圆轴,在扭力矩 m 的作用下发生了变形。这时把一个薄壁圆筒与轴的 凸缘焊接在一起,然后解除m。设轴和圆筒的抗扭 刚度分别是 G1Ip1 和 G2Ip2 ,试求轴内和筒内的扭矩。
m
m
A
B
13
解:由于筒与轴的凸缘焊接在一起,外加扭力矩 m解 除后,圆轴必然力图恢复其扭转变形,而圆筒则阻抗 其恢复。这就使得在轴内和筒内分别出现扭矩T1和T2。 设想用横截面把轴与筒切开,因这时已无外力偶矩作 用,平衡方程为 T1-T2=0 一度静不定问题,应在寻求一个变形协调方程。
圆轴扭转变形与刚度计算
m m
d T dx GI p
1
一、圆轴扭转变形公式
由
m
m
T ( x )dx 满足平面假设的圆轴: GI p ( x ) l Tl T=Const,等截面圆轴: GI p
GIp-抗扭刚度
d T dx GI p
Ti l i Ti,Ipi在各段内为常数的轴: i 1 GI pi
or
T 180 [ ] GI p max
/ m
等截面圆轴扭转的刚度条件为:
Tmax [ ] (rad/m) GI p
or
Tmax 180 [ ] GI p
/ m
4
【例题1】
传动轴图所示。主动轮A输入功率 PA=36kw , 从 动 轮 B 、 C 、 D 输 出 功 率 分 别 为 PB=PC=11kW , PD=14kW ,轴的转速为 n=300r/min , 许用切应力为[]=50MPa,切变模量为G=80GPa,单 位长度许用扭转角为[]=0.5()/m。试确定: 实心圆截面轴的直径d0;
l
x
12
三、圆轴扭转静不定问题
【例题3】 设有 A 、 B 两个凸缘的圆轴,在扭力矩 m 的作用下发生了变形。这时把一个薄壁圆筒与轴的 凸缘焊接在一起,然后解除m。设轴和圆筒的抗扭 刚度分别是 G1Ip1 和 G2Ip2 ,试求轴内和筒内的扭矩。
m
m
A
B
13
解:由于筒与轴的凸缘焊接在一起,外加扭力矩 m解 除后,圆轴必然力图恢复其扭转变形,而圆筒则阻抗 其恢复。这就使得在轴内和筒内分别出现扭矩T1和T2。 设想用横截面把轴与筒切开,因这时已无外力偶矩作 用,平衡方程为 T1-T2=0 一度静不定问题,应在寻求一个变形协调方程。
04. 圆轴的扭转解析

在工厂里当看到一套传动装置时,往往可从轴径的 粗细来判断这一组传动轴中的低速轴和高速轴。
§4-1圆轴扭转时所受外力的分析与计算
一、搅拌轴的三项功能 二、n , P, m 之间的关系(重点)
一、搅拌轴的三项功能
1.传递旋转运动 : 将电动机或减速机输出轴的旋转运动传递给搅拌物 料的桨叶。 2.传递扭转力偶矩: 将轴上端作用的驱动力偶传至轴的下端,用以克服 桨叶旋转时遇到的阻力偶;力偶通过轴传递时,其力偶 矩称为扭矩,扭矩属于内力,其值可借助外力偶矩求出; 3.传递功率: 转轴带动桨叶旋转时要克服流体阻力作功,所需功 率也是从转轴的上端输入后,通过轴传递给浆叶的。
(KN*m)
圆轴传递的功率P和转数n为已知时,用上述公式 即可求出该轴外力矩的大小。由上式可以看出: 如轴的功率P一定,转数n越大,则外力矩越小, 反之,转数越低则外力矩越大。 例如:化工设备厂卷制钢板圆筒用的卷板机,工作时滚轴 所需力矩很大,因为功率受到一定的限制,所以只能减 低滚轴的转数n来增大力矩M。由电动机经过一个三级四 轴减速机带动滚轴,此减速机各轴传递的功率可看成是 一样的。因此,转数n高的轴,力矩M就小,轴径就细一 些;转数低的轴,力矩M就大,轴径就粗.
A
解:1)用截面法把所求
各轴截开:
2)分别求各段轴的扭矩: M M 1+ M B = 0
1 2
= -M =-M
B
B
=-350N.m
C
M M
B D
+ M -M
3
C
+ M = 0
2
=0
M
-M
=-700N.m
M
3
= M
D
= 446N.m
二、扭转内力:(扭矩和扭矩图)(续3)
扭转—扭转轴的应力及强度计算(建筑力学)
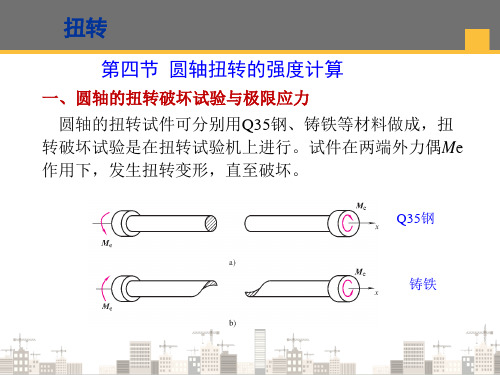
1.5 10 6
MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同,故两轴的最
大切应力相等,即
'max max 51.4MPa
max
Tmax
Tmax
WP
D23 1 4 16
6
16Tmax
16
变形的能力。单位GPa,其数值可由试验测得。
切应变的其单位是 弧度(rad)
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明,圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象,对圆轴内部的变形可做如下假设:扭转
截面(危险截面) 边缘点处。因此,强度条件也可写成 maxFra bibliotekTmax
[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题,即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴,承受的最大扭矩Tmax=1.5kN•m,轴
的直径d1=53mm。求:(1)该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成,扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下,发生扭转变形,直至破坏。
Q35钢
铸铁
MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同,故两轴的最
大切应力相等,即
'max max 51.4MPa
max
Tmax
Tmax
WP
D23 1 4 16
6
16Tmax
16
变形的能力。单位GPa,其数值可由试验测得。
切应变的其单位是 弧度(rad)
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明,圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象,对圆轴内部的变形可做如下假设:扭转
截面(危险截面) 边缘点处。因此,强度条件也可写成 maxFra bibliotekTmax
[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题,即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴,承受的最大扭矩Tmax=1.5kN•m,轴
的直径d1=53mm。求:(1)该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成,扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下,发生扭转变形,直至破坏。
Q35钢
铸铁
轴强度计算公式完整版

#43;C) -Fr×C-Ma=0
RBV=(Fr×C+Fa×d/2)/(b+C)=3790N RCV=Fr-RBV=111N
M′1V=RBV×b=3790×110=416900Nmm M″1V=RCV×C=111×180=19980Nmm
危险截面计算应力:
ca
M ca W
M 2 (T )2
0.1d 3
1
Mpa
危险截面所需直径:
d
3Βιβλιοθήκη M ca0.1 1
3
M 2 (T )2
0.1 1
mm
[σ-1]-许用弯曲应力,按材料查表(15-1) ★ 危险截面的确定:
综合0500 tg12o15 2280 N 2 .求作支反力及弯矩图 H面:
RBH=FtC/(b+C)=10500×180/(110+180) =6520N
RCH=Ft-RBH=10500-6520=3980N
M1H=RBH×b=6520×110=717000Nmm
S S 2
步骤
1. 作轴的受力计算简图,求支反力
2. 求作支反力及弯矩图(MH、MV图) 3. 求作合成弯矩图(M图) 4. 求作扭矩及扭矩图(αT图) 5. 求作当量弯矩及当量弯矩图(Me图) 6. 强度计算(转轴)
⑵ 按疲劳强度条件精确校核计算
Ⅰ计算危险截面弯曲、扭转应力 危险截面:
M
W
T
WT
载荷大直径小 有应力集中处
Ⅱ 计算弯曲、扭转疲劳的安全系数
S
1 K a m
S
1 K a m
Ⅲ 计算危险截面疲劳强度的安全系数
Sca
RBV=(Fr×C+Fa×d/2)/(b+C)=3790N RCV=Fr-RBV=111N
M′1V=RBV×b=3790×110=416900Nmm M″1V=RCV×C=111×180=19980Nmm
危险截面计算应力:
ca
M ca W
M 2 (T )2
0.1d 3
1
Mpa
危险截面所需直径:
d
3Βιβλιοθήκη M ca0.1 1
3
M 2 (T )2
0.1 1
mm
[σ-1]-许用弯曲应力,按材料查表(15-1) ★ 危险截面的确定:
综合0500 tg12o15 2280 N 2 .求作支反力及弯矩图 H面:
RBH=FtC/(b+C)=10500×180/(110+180) =6520N
RCH=Ft-RBH=10500-6520=3980N
M1H=RBH×b=6520×110=717000Nmm
S S 2
步骤
1. 作轴的受力计算简图,求支反力
2. 求作支反力及弯矩图(MH、MV图) 3. 求作合成弯矩图(M图) 4. 求作扭矩及扭矩图(αT图) 5. 求作当量弯矩及当量弯矩图(Me图) 6. 强度计算(转轴)
⑵ 按疲劳强度条件精确校核计算
Ⅰ计算危险截面弯曲、扭转应力 危险截面:
M
W
T
WT
载荷大直径小 有应力集中处
Ⅱ 计算弯曲、扭转疲劳的安全系数
S
1 K a m
S
1 K a m
Ⅲ 计算危险截面疲劳强度的安全系数
Sca
转轴扭转强度、刚度校核

max M n/Wn (1500 103 / 29800 )MPa 50.3MPa<[ ]
传动轴满足强度要求。 2)刚度校核 传动轴的极惯性矩为
IP 0.1D 4 (1 a4 ) {0.1 904[1 (85 / 90)4 ]}mm4 134 10 4 mm4
max 180 M n /(GI P ) (180 1500 103 / 80 103 134 10 4 ) 103/m
当两轴材料、长度相同,它们的重量之比等于横截面面
积之比。设A1、A2分别为空心轴和实心轴的面积,则有
A 1
/
A 2
[
(D
2
d
2)
/
4] /(D 22
/
4)
(90 2
852 )
/
612
0.235
第四节 圆轴扭转时的强度和刚度计算
一、强度计算
为了保证圆轴安全正常地工作,即
max M n/Wn [ ]
(6-12)
例6-4 某传动轴,已知轴的直径d=40mm,转速
n材=料20的0许r/m用i切n,应力 60MPa ,试求此轴可传递的最大功率。
解 (1)确定许可外力偶矩
由扭转强度条件得
M n Wn[ ] (0.2 403 109 60 106 )N m 768N m
最
大力偶矩M =1500N·m,G =80GPa。
(1)试校核其强度及刚度。 (2)若将AB轴改为实心轴,试求其直径。 (3)比较空心轴和实心轴的重量。 解 (1)试校核其强度及刚度。 1) 强度校核 传动轴各截面上的扭矩均为
Mn = M = 1500N·m
传动轴的抗扭截面系数为
Wn 0.2D 3 (1 d 4 ) {0.2 903[1 (85 / 90)4 ]}mm3 29800 mm3 传动轴横截面上的最大切应力为
传动轴满足强度要求。 2)刚度校核 传动轴的极惯性矩为
IP 0.1D 4 (1 a4 ) {0.1 904[1 (85 / 90)4 ]}mm4 134 10 4 mm4
max 180 M n /(GI P ) (180 1500 103 / 80 103 134 10 4 ) 103/m
当两轴材料、长度相同,它们的重量之比等于横截面面
积之比。设A1、A2分别为空心轴和实心轴的面积,则有
A 1
/
A 2
[
(D
2
d
2)
/
4] /(D 22
/
4)
(90 2
852 )
/
612
0.235
第四节 圆轴扭转时的强度和刚度计算
一、强度计算
为了保证圆轴安全正常地工作,即
max M n/Wn [ ]
(6-12)
例6-4 某传动轴,已知轴的直径d=40mm,转速
n材=料20的0许r/m用i切n,应力 60MPa ,试求此轴可传递的最大功率。
解 (1)确定许可外力偶矩
由扭转强度条件得
M n Wn[ ] (0.2 403 109 60 106 )N m 768N m
最
大力偶矩M =1500N·m,G =80GPa。
(1)试校核其强度及刚度。 (2)若将AB轴改为实心轴,试求其直径。 (3)比较空心轴和实心轴的重量。 解 (1)试校核其强度及刚度。 1) 强度校核 传动轴各截面上的扭矩均为
Mn = M = 1500N·m
传动轴的抗扭截面系数为
Wn 0.2D 3 (1 d 4 ) {0.2 903[1 (85 / 90)4 ]}mm3 29800 mm3 传动轴横截面上的最大切应力为
圆轴扭转

空心圆截面:
Wt
D3
16
(1
d4 D4
)
D3
16
(1 4 )
四 等直圆杆扭转时的应力
例题1 已知空心圆截面的扭矩T=1kN·m,D=40mm,d=20mm,求 最大、最小切应力。
解:
max
T
Wt
T
16
D3
(1
d4 D4
)
max min
16 1000
4.按大小比例和正负号,将各段杆的扭矩画在基线两 侧,并在图上标出数值和正负号
例题1 画出图示杆的扭矩图 3kN·m Ⅰ 5kN·m Ⅱ 2kN·m
解: AC段
m 0
AⅠ 3kN·m
CⅡ
T1 T2
3kN·m
B 2kN·m
T1 3 0 T1 3kN m
BC段 m 0
T2 2 0 T2 2kN m
ρ
τdA b dA
O2 T
四 等直圆杆扭转时的应力
4 极惯性矩
【公式3-16;公式3-18】
IP
2dA
A
D
2 2 2 d 0
O
D4
32
D
环形截面:
IP
32
(D4
d4)
d D
极惯性矩单位: m4
四 等直圆杆扭转时的应力
同一截面,扭矩T,极惯性矩IP为常数,因此各点 切应力τ的大小与该点到圆心的距离ρ成正比,方向垂 直于圆的半径,且与扭矩的转向一致
例题3 画出图示杆的扭矩图
4kN·mⅠ 6kN·mⅡ 8kN·mⅢ 6kN·m
圆轴扭转变形与刚计算
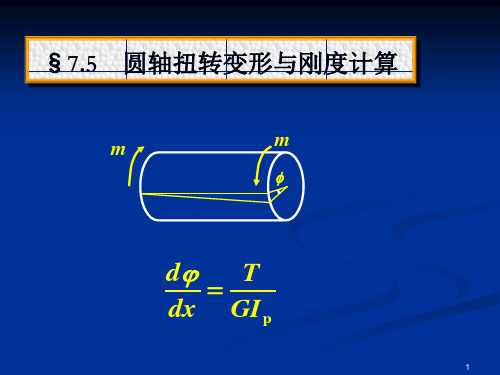
2 dsdx
2G
l
T2
T2
8 2G dsdx
l
8
2G
ds
dx
T为常数的等截面杆
V
T 2l 2GI t
=W=T / 2
式中:
It
4 2 ds
Tl
GI t
27
三、开口薄壁杆的扭转应力
max
3T max
n
hi i 3
i 1
3Tl
n
G hi i 3
i 1
3
1
2
28
【例题5】 如图所示为相同尺寸的闭口钢管和开口 钢管,承受相同的扭矩T。设平均直径为d,壁厚为t,
试比较两者的强度和刚度。
d
t (a)
d
t (b)
29
T 2
Tl
GI t
4 2 I t ds
解:1. 对闭口薄圆环, A d 2 s d ,则
dT
t
t
(a)
(b)
相同的扭矩,由于应力分布不同导致了应力大 小差别。
33
课后练习
思考:
一等直圆杆,当受到轴向拉伸时,杆内会产生 切应变吗?当受到扭转时,杆内会产生正应变吗?
作业:
4-16 4-27 4-32 4-33
34
T1-T2=0
T1
T2
mG2 I p2 G1Ip1 G2 Ip2
T2
2
1
T1
16
§7.6 非圆截面杆的扭转
m
m
农业机械中的方轴
柴油机曲柄的受 扭截面为矩形
圆轴扭转时的强度和刚度计算

A1 / A2 = [π (D 2 − d 2 ) / 4] /(πD 2 2 / 4) = (90 2 − 852 ) / 612 = 0.235
传动轴满足强度要求。 2)刚度校核 传动轴的极惯性矩为
I P = 0.1D 4 (1 − a 4 ) = {0.1 × 90 4 [1 − (85 / 90 ) 4 ]}mm 4 = 134 × 10 4 mm 4 θ max = 180 M n /(πGI P )
= (180 × 1500 × 10 3 / 80 × 10 3 × 134 × 10 4 π ) × 10 3 °/m
= 0.8°/m < [θ ]
传动轴满足刚度要求。 (2)计算实心轴的直径
1)按强度条件设计(设直径为D1)。若实心轴与空心轴强 度相同,当材料相同时,它们的抗扭截面系数应相等,即
W n = πD 13 / 16 = πD 3 (1 Βιβλιοθήκη a 4 ) / 16由此得
D 1 = D3 1 − a 4 = [90 × 3 1 − (85 / 90) 4 ]mm = 53mm
根据扭转刚度条件,可以解决三类问题, 即校核刚度、 设计截面和确定许可载荷 。
例6-5 汽车传动轴AB由45号无缝钢管制成,外径D=90mm,
[ 内径d=85mm,许用切应力 [τ ]=60MPa,θ ] =1.0°/m,工作时最
大力偶矩M =1500N·m,G =80GPa。 (1)试校核其强度及刚度。 (2)若将AB轴改为实心轴,试求其直径。 (3)比较空心轴和实心轴的重量。 解 (1)试校核其强度及刚度。 1) 强度校核 传动轴各截面上的扭矩均为
θ max = 180M n /(πGI P ) ≤ [θ ]
(6-13)
11.轴的扭转

已知传动轴的转速为300r/min, 主动轮 输 主动轮A输 例11.2* 已知传动轴的转速为 入功率为P 入功率为 A=500kW。从动轮 。从动轮B,C,D输出功率 输出功率 分别为 PB =150kW, PC =150kW, PD =200kW. 求作:该轴扭矩图。 求作:该轴扭矩图。 解: (1)计算主、从动轮传递的外力偶矩 )
第 11 章
轴的扭转
11.1
扭转概念及外力偶矩计算
11.1.1 扭转的概念
扭转及变形是一种因转动引起的常见现象。 扭转及变形是一种因转动引起的常见现象。 通过扭转传递功率的构件(转动的杆) 轴:通过扭转传递功率的构件(转动的杆).
m
m
m
m
11.1.2 外力偶矩的计算
已知: 已知:输入输出功率 P (kW) ,转速 n (r/min) . 则:外力偶矩
如图. 用截面法计算扭矩 计算扭矩: 解: 如图 用截面法计算扭矩: T = m = 156N ⋅ m 实心段AC: ① 实心段 :
16 T 156 × 103 τ max1 = = ≈ 24 ( MPa) 3 W p1 6.55 × 10 W p1 =
π
D 3 ≈ 0 .2 × 32 3 = 6 .55 × 10 3 ( mm 3 )
M e = 9550 P / n ( N ⋅ m )
M e dϕ dW = = M eω 证明: 证明:Q P = dt dt
ω = 2π n
∴ P = 2πnM e P ∴ Me = 2π n
P
n
Me
输入功率P以 、转速n以 为单位代入, 输入功率 以kW、转速 以 r/min为单位代入, 为单位代入 那么,外力偶矩M 那么,外力偶矩 e为:
轴的扭转强度计算

非定位轴肩→便于装配→h=(0.5~1)mm
定位轴肩→零件定位→ h =3~5 mm 2.设计轴肩时应注意: (1)轴承定位轴肩(套筒)不能过高 (2)轴长应略短于轮毂宽度 (3)安装标准件轴段直径, (a)滚动轴承 (b)联轴器 (c)密封件 (4)轴肩圆角r 轮毂孔圆角R(倒角C)
轴上有键槽时: 放大轴径:一个键槽:3~5%
二个键槽:7~10%
取标准植
13.3 轴的强度计算
二、轴的弯扭合成强度计算
转轴同时承受扭矩和弯矩,必须按二者组合强度进行计算。通常 把轴当作置于铰链支座上的梁,作用于轴上零件的力作为集中力, 其作用点取为零件轮毂宽度的中点上。具体的计算步骤如下:
①轴和轴上零件要有准确、牢固的工作位置 ②轴上零件装拆、调整方便 ③轴应具有良好的制造工艺性等 ④尽量避免应力集中
13.2 轴的结构设计
二、零件在轴上的固定 1、周向固定 为了传递运动和转矩,防止轴上零件与轴作相对转动。常用的 周向固定方法有键、花键、销、过盈配合、 弹性环联接、成形联接等。
碳钢比合金钢价廉,对应力集中的敏感性比较低,适用于一般要求的轴。 合金钢比碳钢有更高的力学性能和更好的淬火性能,在传递大功率并要求减小 尺寸和质量、要求高的耐磨性,以及处于高温、低温和腐蚀条件下的轴常采用 合金钢。在一般工作温度下(低于200℃),各种碳钢和合金钢的弹性模量均 相差不多,因此相同尺寸的碳钢和合金钢轴的刚度相差不多。
一、轴的扭转强度计算
用于:①只受扭矩或主要承受扭矩的传动轴的强度计算 ②结构设计前按扭矩初估轴的直径dmin
对于圆截面的实心轴,其抗扭强度条件为:
强度条件
T
T WT
9.55 106
0.2d 3
定位轴肩→零件定位→ h =3~5 mm 2.设计轴肩时应注意: (1)轴承定位轴肩(套筒)不能过高 (2)轴长应略短于轮毂宽度 (3)安装标准件轴段直径, (a)滚动轴承 (b)联轴器 (c)密封件 (4)轴肩圆角r 轮毂孔圆角R(倒角C)
轴上有键槽时: 放大轴径:一个键槽:3~5%
二个键槽:7~10%
取标准植
13.3 轴的强度计算
二、轴的弯扭合成强度计算
转轴同时承受扭矩和弯矩,必须按二者组合强度进行计算。通常 把轴当作置于铰链支座上的梁,作用于轴上零件的力作为集中力, 其作用点取为零件轮毂宽度的中点上。具体的计算步骤如下:
①轴和轴上零件要有准确、牢固的工作位置 ②轴上零件装拆、调整方便 ③轴应具有良好的制造工艺性等 ④尽量避免应力集中
13.2 轴的结构设计
二、零件在轴上的固定 1、周向固定 为了传递运动和转矩,防止轴上零件与轴作相对转动。常用的 周向固定方法有键、花键、销、过盈配合、 弹性环联接、成形联接等。
碳钢比合金钢价廉,对应力集中的敏感性比较低,适用于一般要求的轴。 合金钢比碳钢有更高的力学性能和更好的淬火性能,在传递大功率并要求减小 尺寸和质量、要求高的耐磨性,以及处于高温、低温和腐蚀条件下的轴常采用 合金钢。在一般工作温度下(低于200℃),各种碳钢和合金钢的弹性模量均 相差不多,因此相同尺寸的碳钢和合金钢轴的刚度相差不多。
一、轴的扭转强度计算
用于:①只受扭矩或主要承受扭矩的传动轴的强度计算 ②结构设计前按扭矩初估轴的直径dmin
对于圆截面的实心轴,其抗扭强度条件为:
强度条件
T
T WT
9.55 106
0.2d 3
第九节圆轴扭转

结论
横截面: 像刚性平面一样, 只是绕轴线旋转了一个角度。 在此假设的基础上,推倒出的应力与变形计算公式,符 合试验结果,且与弹性力学一致
二、等直圆杆扭转时横截面上的应力:
1. 变形几何关系:
tg
BB' dx
d
dx
d
dx
距圆心为 的任一点处的; 与点到圆心的距离成正比。
d
dx
max
E
T1 WP1
16 1114 π 703 10-9
Pa
16.54MPa
max
H
T2 WP2
16 557 π 503 10-9
Pa
22.69MPa
max
C
T3 WP3
16 185.7 π 353 10-9
Pa
21.98MPa
,
例4 一轴AB传递的功率为 PK 7.5kW
工程上采用空心截面构件:提高强度,节约材料,重量轻, 结构轻便,应用广泛。
四、圆轴扭转时的强度计算
强度条件:
max [ ]
对于等截面圆轴:
Tm a x Wt
[
]
([] 称为许用切应力。)
强度计算三方面:
① 校核强度:
max
Tm a x Wt
[ ]
② 设计截面尺寸:
Wt
Tm a x
[ ]
Wt
实:D3 16 空:1D6(3 1 4)
P1=14kW, P2= P3= P1/2=7 kW
3
n1=n2= 120r/min
D1n1 D3n3
n=3 n1
DD31=n1
Z Z
1 3
=360r/min
2、计算各轴的扭矩
化机基础(力学)_第三章轴扭转
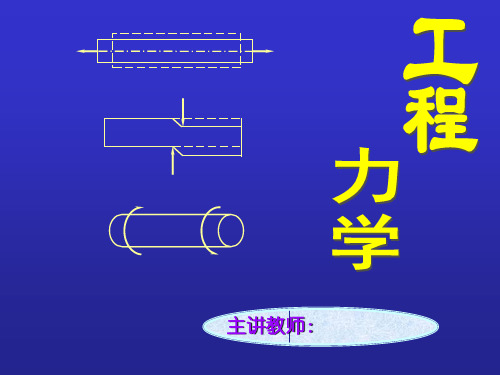
【5.3】一轴以300转/分的转速传递331kW的功率,如 [ ]=40MPa,[ ]=0.5°/m,G=80GPa,求轴的直径。
解:
(1)计算扭矩:
P 331 M e 9550 9550 10537 N m n 300
T M e 10537 m N
(2)设计轴径 T T 由强度条件: max W 3 [ ] t d 16
轴扭转时,横截面上的扭矩T引起切应力 ,故横截面 上各点只有切应力,与该点所在半径垂直,方向与截 面扭矩转向保持一致。
第三节 纯剪切
一、切应力互等定理
围绕横截面上某点取一微小六面体,称为单元体。 y
’
dy x dx z
由平衡条件:
M 0
dy dz dx
'dx dz dy
二、扭矩和扭矩图
1. 研究AB轴各横截面上的内力 me me
1
A me
1 T1-1 1 x 1 T1-1
B
求AB段内的任 一横截面上的内 力:用截面法计 算内力。
m 0
T11 me 0
me
T11 me
注:
1. 内力名称——扭矩T 2. 扭矩正负号规定,利用右手螺旋法则,当拇指背离截 面时,T为正;反之,为负。 不论取截面的哪一侧研究,所得结果的正负号一致。 T1-1 mB mA 1 T1-1
轴:工程上将以扭转变形为主的构件称为轴
第二节
扭转时力偶和内力的计算
一、外力偶矩的计算
作用于轴上的外力偶矩一般不是直接给出的,而是给出 轴的转速n和传递的功率P。
n1 27.5kW 7.5kW A n B
C
n=960r/min
轴的扭转刚度计算(“扭转”相关文档)共6张

Ip=π* 扭转角度=T*l/Байду номын сангаасG*Ip)=3.
扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3.
扭首转先角 将度长=度T单扭*l/位(G化*转Ip为)=米3角.(m) 度=T*l/(G*Ip)=3.82e-5 rad=2.19e-3 deg 扭转刚度Kt=T/扭转角度=4.57 Nm/deg 已知:直径为10mm,长度为300mm,受到扭矩为,求扭转刚度?
轴的扭转刚度计算方法
张志军
几种材料特性举例:
82e-5 rad=2. 首先将长度单位化为米(m) 扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3. 已知:直径为10mm,长度为300mm,受到扭矩为,求扭转刚度? 82e-5 rad=2. 82e-5 rad=2. 扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3.
公式求解:
已知:直径为已10m知m,:长度为直300径mm,为受到1扭0矩m为,m求扭,转刚长度?度为300mm,受到扭矩为,求
82e-5 rad=2.
扭转刚度? 82e-5 rad=2.
扭转角度=T*l/(G*Ip)=3.
首先将长度单位化为米(m) 首先将长度单位化为米(m)
扭转角度=T*l/(G*Ip)=3. 首先将长度单位化为米(m)
扭转角度=T*l/(G*Ip)=3. 已知:直径为10mm,长度为300mm,受到扭矩为,求扭转刚度? 扭转角度=T*l/(G*Ip)=3.
扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3.
扭首转先角 将度长=度T单扭*l/位(G化*转Ip为)=米3角.(m) 度=T*l/(G*Ip)=3.82e-5 rad=2.19e-3 deg 扭转刚度Kt=T/扭转角度=4.57 Nm/deg 已知:直径为10mm,长度为300mm,受到扭矩为,求扭转刚度?
轴的扭转刚度计算方法
张志军
几种材料特性举例:
82e-5 rad=2. 首先将长度单位化为米(m) 扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3. 已知:直径为10mm,长度为300mm,受到扭矩为,求扭转刚度? 82e-5 rad=2. 82e-5 rad=2. 扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3. 扭转角度=T*l/(G*Ip)=3.
公式求解:
已知:直径为已10m知m,:长度为直300径mm,为受到1扭0矩m为,m求扭,转刚长度?度为300mm,受到扭矩为,求
82e-5 rad=2.
扭转刚度? 82e-5 rad=2.
扭转角度=T*l/(G*Ip)=3.
首先将长度单位化为米(m) 首先将长度单位化为米(m)
扭转角度=T*l/(G*Ip)=3. 首先将长度单位化为米(m)
扭转角度=T*l/(G*Ip)=3. 已知:直径为10mm,长度为300mm,受到扭矩为,求扭转刚度? 扭转角度=T*l/(G*Ip)=3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.3.1实心圆轴横截面上的应力
工程中要求对受扭杆件进行强度计算,根据扭矩T确定横截面上各点的切应力。下面用实心圆轴推导切应力在横截面上的分布规律。
1、变形几何关系
取一实心圆轴,在其表面等距离地画上圆周线和纵向线,如图5.9(a)所示,然后在圆轴两端施加一对大小相等、方向相反的扭转力偶矩 ,使圆轴产生扭转变形,如图5.9(b)所示,可观察到圆轴表面上各圆周线的形状、大小和间距均未改变,仅是绕圆轴线作了相对转动;各纵向线均倾斜了一微小角度 。
第5章扭转
5.1 扭转的概念及外力偶矩的计算
5.1.1、扭转的概念
在工程实际中,有很多以扭转变形为主的杆件。例如图示5.1,常用的螺丝刀拧螺钉。
图5.1
图示5.2,用手电钻钻孔,螺丝刀杆和钻头都是受扭的杆件。
图5.2
图示5.3,载重汽车的传动轴。
图5.3
图示5.4,挖掘机的传动轴。
图5.4
图5.5所示,雨蓬由雨蓬梁和雨蓬板组成(图5.5a),雨蓬梁每米的长度上承受由雨蓬板传来均布力矩,根据平衡条件,雨蓬梁嵌固的两端必然产生大小相等、方向相反的反力矩(图5.5b),雨蓬梁处于受扭状态。
(5.1)
式中m----作用在轴上的外力偶矩,单位为 ;
N-----轴传递的功率,单位为 ;
n------轴的转速,单位为r/min。
图5.7
5.2 圆轴扭转时横截面上的内力及扭矩图
5.2.1扭矩
已知受扭圆轴外力偶矩,可以利用截面法求任意横截面的内力。图5.8a为受扭圆轴,设外力偶矩为 ,求距A端为x的任意截面 上的内力。假设在 截面将圆轴截开,取左部分为研究对象(图5.8b),由平衡条件 ,得内力偶矩T和外力偶矩 的关系
图5.10
设半径R,根据平面假设,可以设想扭转时各横截面如同刚性平面一样绕杆轴作相对转动。则由图可知变形后,纵向线段 变为 , 和 的夹角为 (切应变), 对应横截面的圆心角 ,在小变形的条件下可以建立如下关系。
为了研究横截面上任意点的切应变,从圆轴截面内取半径为 的微段,如图5.10(b)所示。同理可得
(5.2)
上式表明,横截面上任意点的切应变同该点到圆心的距离 成正比关系。
2、物理关系
根据剪切胡克定律,在剪切比例极限之内(或弹性范围以内)切应力和切应变成正比关系
将(5–2)式代入上式,得
(5.3)
上式表明,圆轴扭转时,横截面上任意点处的切应力 与该点到圆心的距离 成正比,其分布如图5.11所示,式中 可利用静力方程确定。
塑性材料
脆性材料
例题5.2汽车的主传动轴,由45号钢的无缝钢管制成,外径 ,壁厚 ,工作时的最大扭矩 ,若材料的许用切应力 ,试校核该轴的强度。
解:1、计算抗扭截面系数
主传动轴的内外径之比
抗扭截面系数为
2、计算轴的最大切应力
3、强度校核
主传动轴安全
例题5.3如把上题中的汽车主传动轴改为实心轴,要求它与原来的空心轴强度相同,试确定实心轴的直径,并比较空心轴和实心轴的重量。
图5.5
分析以上受扭杆件的特点,作用于垂直杆轴平面内的力偶使杆引起的变形,称扭转变形。变形后杆件各横截面之间绕杆轴线相对转动了一个角度,称为扭转角,用 表示,如图5.6所示。以扭转变形为主要变形的直杆称为轴。
图5.6
本章着重讨论圆截面杆的扭转应力和变形计算。
5.1.2、外力偶矩的计算
工程中常用的传动轴(图)是通过转动传递动力的构件,其外力偶矩一般不是直接给出的,通常已知轴所传递的功率和轴的转速。根据理论力学中的公式,可导出外力偶矩、功率和转速之间的关系为:
图5.9
根据观察到的现象,由表及里作出如下假设。
⑴变形后,圆轴上所有的横截面均保持为平面,即平面假设;
⑵横截面上的半径仍保持为直线;
⑶各横截面的间距保持不变。
圆轴扭转时,横截面上的切应力非均匀分布,仅依靠静力方程无法求出,必须利用变形条件建立补充方程,即切应力的导出需按解超静定问题的相似步骤进行。
根据上述假设,从圆轴中取相距为 的微段进行研究,如图5.10(a)所示。
5.3.2极惯性矩和抗扭截面系数
极惯性矩 和抗扭截面系数 可按其定义通过积分求得。下面介绍其计算方法。
对于图5.12(a)实心圆轴,可在圆轴截面上距圆心为 处取厚度为 的环形面积作为微面积dA,于是 ,从而可得实心圆截面的极惯性矩为
抗扭截面系数为
如为图(b)空心圆轴,则有
式中 为空心圆轴内外径之比。空心圆轴截面的抗扭截面系数为
极惯性矩 的量纲是长度的四次方,常用的单位为 或 。抗扭截面系数 的
量纲是长度的三次方,常用单位为 或 。
(a)(b)
图5.12
5.4 等直圆轴扭转时的强度计算
5.4.1圆轴扭转强度条件
工程上要求圆轴扭转时的最大切应力不得超过材料的许用切应力 ,即
对于等截面圆轴,表示为
上式称为圆轴扭转强度条件
试验表明,材料扭转许用切应力 和许用拉应力 有如下近似的关系。
例题5.1图示传动轴,转速 ,A轮为主动轮,输入功率 ,B、C、D为从动轮,输出功率分别为 , , ,试求各段扭矩。
解:1、计算外力偶矩
2、分段计算扭矩,设各段扭矩为正,用矢量表示,分别为
(图c)
(图d)
(图e)
, 为负值说明实际方向与假设的相反。
3、作扭矩图
例题5.1图
5.3 等直圆轴扭转时横截面上的切应力
内力偶矩T称为扭矩。
扭矩的正负号规定为:自截面的外法线向截面看,逆时针转向为正,顺时针转向为负。
图5.8
图示5.8的b和c,从同一截面截出的扭矩均为正号。扭矩的单位是 或 。
5.2.2扭矩图
为了清楚地表示扭矩沿轴线变化的规律,以便于确定危险截面,常用与轴线平行的 坐标表示横截面的位置,以与之垂直的坐标表示相应横截面的扭矩,把计算结果按比例绘在图上,正值扭矩画在 轴上方,负值扭矩画在 轴下方。这种图形称为扭矩图。
图5.11
3、静力学关系
根据图5.11所示,横截面上任意点的切应力 和中, 称截面的极惯性矩,代入上式,得
(5.4)
将(5.4)式代入(5.3)式,得到圆轴扭转横截面上任意点切应力公式
(5.5)
当 时,表示圆截面边缘处的切应力最大
(5.6)
式中, 称为抗扭截面系数。它是与截面形状和尺寸有关的量。
解:1、求实心轴的直径,要求强度相同,即实心轴的最大切应力也为 ,即
工程中要求对受扭杆件进行强度计算,根据扭矩T确定横截面上各点的切应力。下面用实心圆轴推导切应力在横截面上的分布规律。
1、变形几何关系
取一实心圆轴,在其表面等距离地画上圆周线和纵向线,如图5.9(a)所示,然后在圆轴两端施加一对大小相等、方向相反的扭转力偶矩 ,使圆轴产生扭转变形,如图5.9(b)所示,可观察到圆轴表面上各圆周线的形状、大小和间距均未改变,仅是绕圆轴线作了相对转动;各纵向线均倾斜了一微小角度 。
第5章扭转
5.1 扭转的概念及外力偶矩的计算
5.1.1、扭转的概念
在工程实际中,有很多以扭转变形为主的杆件。例如图示5.1,常用的螺丝刀拧螺钉。
图5.1
图示5.2,用手电钻钻孔,螺丝刀杆和钻头都是受扭的杆件。
图5.2
图示5.3,载重汽车的传动轴。
图5.3
图示5.4,挖掘机的传动轴。
图5.4
图5.5所示,雨蓬由雨蓬梁和雨蓬板组成(图5.5a),雨蓬梁每米的长度上承受由雨蓬板传来均布力矩,根据平衡条件,雨蓬梁嵌固的两端必然产生大小相等、方向相反的反力矩(图5.5b),雨蓬梁处于受扭状态。
(5.1)
式中m----作用在轴上的外力偶矩,单位为 ;
N-----轴传递的功率,单位为 ;
n------轴的转速,单位为r/min。
图5.7
5.2 圆轴扭转时横截面上的内力及扭矩图
5.2.1扭矩
已知受扭圆轴外力偶矩,可以利用截面法求任意横截面的内力。图5.8a为受扭圆轴,设外力偶矩为 ,求距A端为x的任意截面 上的内力。假设在 截面将圆轴截开,取左部分为研究对象(图5.8b),由平衡条件 ,得内力偶矩T和外力偶矩 的关系
图5.10
设半径R,根据平面假设,可以设想扭转时各横截面如同刚性平面一样绕杆轴作相对转动。则由图可知变形后,纵向线段 变为 , 和 的夹角为 (切应变), 对应横截面的圆心角 ,在小变形的条件下可以建立如下关系。
为了研究横截面上任意点的切应变,从圆轴截面内取半径为 的微段,如图5.10(b)所示。同理可得
(5.2)
上式表明,横截面上任意点的切应变同该点到圆心的距离 成正比关系。
2、物理关系
根据剪切胡克定律,在剪切比例极限之内(或弹性范围以内)切应力和切应变成正比关系
将(5–2)式代入上式,得
(5.3)
上式表明,圆轴扭转时,横截面上任意点处的切应力 与该点到圆心的距离 成正比,其分布如图5.11所示,式中 可利用静力方程确定。
塑性材料
脆性材料
例题5.2汽车的主传动轴,由45号钢的无缝钢管制成,外径 ,壁厚 ,工作时的最大扭矩 ,若材料的许用切应力 ,试校核该轴的强度。
解:1、计算抗扭截面系数
主传动轴的内外径之比
抗扭截面系数为
2、计算轴的最大切应力
3、强度校核
主传动轴安全
例题5.3如把上题中的汽车主传动轴改为实心轴,要求它与原来的空心轴强度相同,试确定实心轴的直径,并比较空心轴和实心轴的重量。
图5.5
分析以上受扭杆件的特点,作用于垂直杆轴平面内的力偶使杆引起的变形,称扭转变形。变形后杆件各横截面之间绕杆轴线相对转动了一个角度,称为扭转角,用 表示,如图5.6所示。以扭转变形为主要变形的直杆称为轴。
图5.6
本章着重讨论圆截面杆的扭转应力和变形计算。
5.1.2、外力偶矩的计算
工程中常用的传动轴(图)是通过转动传递动力的构件,其外力偶矩一般不是直接给出的,通常已知轴所传递的功率和轴的转速。根据理论力学中的公式,可导出外力偶矩、功率和转速之间的关系为:
图5.9
根据观察到的现象,由表及里作出如下假设。
⑴变形后,圆轴上所有的横截面均保持为平面,即平面假设;
⑵横截面上的半径仍保持为直线;
⑶各横截面的间距保持不变。
圆轴扭转时,横截面上的切应力非均匀分布,仅依靠静力方程无法求出,必须利用变形条件建立补充方程,即切应力的导出需按解超静定问题的相似步骤进行。
根据上述假设,从圆轴中取相距为 的微段进行研究,如图5.10(a)所示。
5.3.2极惯性矩和抗扭截面系数
极惯性矩 和抗扭截面系数 可按其定义通过积分求得。下面介绍其计算方法。
对于图5.12(a)实心圆轴,可在圆轴截面上距圆心为 处取厚度为 的环形面积作为微面积dA,于是 ,从而可得实心圆截面的极惯性矩为
抗扭截面系数为
如为图(b)空心圆轴,则有
式中 为空心圆轴内外径之比。空心圆轴截面的抗扭截面系数为
极惯性矩 的量纲是长度的四次方,常用的单位为 或 。抗扭截面系数 的
量纲是长度的三次方,常用单位为 或 。
(a)(b)
图5.12
5.4 等直圆轴扭转时的强度计算
5.4.1圆轴扭转强度条件
工程上要求圆轴扭转时的最大切应力不得超过材料的许用切应力 ,即
对于等截面圆轴,表示为
上式称为圆轴扭转强度条件
试验表明,材料扭转许用切应力 和许用拉应力 有如下近似的关系。
例题5.1图示传动轴,转速 ,A轮为主动轮,输入功率 ,B、C、D为从动轮,输出功率分别为 , , ,试求各段扭矩。
解:1、计算外力偶矩
2、分段计算扭矩,设各段扭矩为正,用矢量表示,分别为
(图c)
(图d)
(图e)
, 为负值说明实际方向与假设的相反。
3、作扭矩图
例题5.1图
5.3 等直圆轴扭转时横截面上的切应力
内力偶矩T称为扭矩。
扭矩的正负号规定为:自截面的外法线向截面看,逆时针转向为正,顺时针转向为负。
图5.8
图示5.8的b和c,从同一截面截出的扭矩均为正号。扭矩的单位是 或 。
5.2.2扭矩图
为了清楚地表示扭矩沿轴线变化的规律,以便于确定危险截面,常用与轴线平行的 坐标表示横截面的位置,以与之垂直的坐标表示相应横截面的扭矩,把计算结果按比例绘在图上,正值扭矩画在 轴上方,负值扭矩画在 轴下方。这种图形称为扭矩图。
图5.11
3、静力学关系
根据图5.11所示,横截面上任意点的切应力 和中, 称截面的极惯性矩,代入上式,得
(5.4)
将(5.4)式代入(5.3)式,得到圆轴扭转横截面上任意点切应力公式
(5.5)
当 时,表示圆截面边缘处的切应力最大
(5.6)
式中, 称为抗扭截面系数。它是与截面形状和尺寸有关的量。
解:1、求实心轴的直径,要求强度相同,即实心轴的最大切应力也为 ,即
