轴的扭转强度计算
轴的强度计算
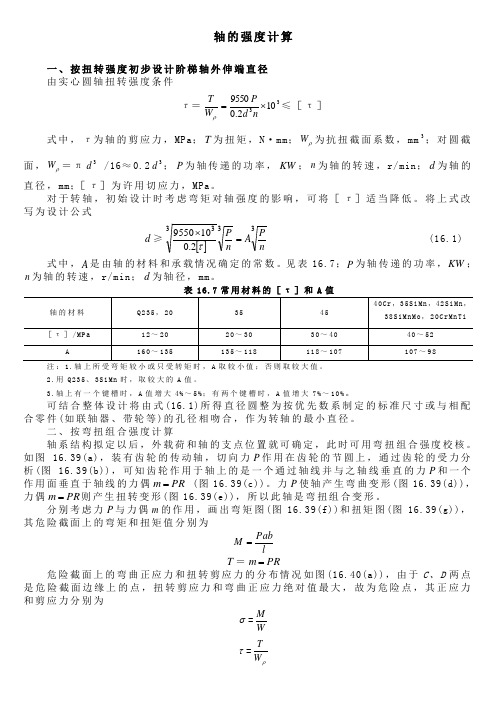
轴的强度计算一、按扭转强度初步设计阶梯轴外伸端直径由实心圆轴扭转强度条件τ=33102.09550⨯=nd P W T ρ≤[τ]式中,τ为轴的剪应力,MPa ;T 为扭矩,N ·mm ;ρW 为抗扭截面系数,mm 3;对圆截面,ρW =π3d /16≈0.23d ;P 为轴传递的功率,KW ;n 为轴的转速,r/min ;d 为轴的直径,mm ;[τ]为许用切应力,MPa 。
对于转轴,初始设计时考虑弯矩对轴强度的影响,可将[τ]适当降低。
将上式改写为设计公式d ≥[]33332.0109550nPA n P =⨯τ (16.1)式中,A 是由轴的材料和承载情况确定的常数。
见表16.7;P 为轴传递的功率,KW ;n 为轴的转速,r/min ;d 为轴径,mm 。
表16.7常用材料的[τ]和A 值轴的材料 Q235,20 35 45 40Cr ,35SiMn ,42SiMn ,38SiMnMo ,20CrMnTi[τ]/MPa12~20 20~30 30~40 40~52 A160~135135~118118~107107~98注:1.轴上所受弯矩较小或只受转矩时,A 取较小值;否则取较大值。
2.用Q235、3SiMn 时,取较大的A 值。
3.轴上有一个键槽时,A 值增大4%~5%;有两个键槽时,A 值增大7%~10%。
可结合整体设计将由式(16.1)所得直径圆整为按优先数系制定的标准尺寸或与相配合零件(如联轴器、带轮等)的孔径相吻合,作为转轴的最小直径。
二、按弯扭组合强度计算轴系结构拟定以后,外载荷和轴的支点位置就可确定,此时可用弯扭组合强度校核。
如图16.39(a),装有齿轮的传动轴,切向力P 作用在齿轮的节圆上,通过齿轮的受力分析(图16.39(b)),可知齿轮作用于轴上的是一个通过轴线并与之轴线垂直的力P 和一个作用面垂直于轴线的力偶PR m = (图16.39(c))。
力P 使轴产生弯曲变形(图16.39(d)),力偶PR m =则产生扭转变形(图16.39(e)),所以此轴是弯扭组合变形。
扭转—扭转轴的应力及强度计算(建筑力学)
MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同,故两轴的最
大切应力相等,即
'max max 51.4MPa
max
Tmax
Tmax
WP
D23 1 4 16
6
16Tmax
16
变形的能力。单位GPa,其数值可由试验测得。
切应变的其单位是 弧度(rad)
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明,圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象,对圆轴内部的变形可做如下假设:扭转
截面(危险截面) 边缘点处。因此,强度条件也可写成 maxFra bibliotekTmax
[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题,即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴,承受的最大扭矩Tmax=1.5kN•m,轴
的直径d1=53mm。求:(1)该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成,扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下,发生扭转变形,直至破坏。
Q35钢
铸铁
轴的强度计算
对于只传递扭转的圆截9.55 10 6 P 0.2d 3n
[ T ]
设计公式为:d 3 9.55106 3 P C 3 P
0.2[ ] n
n
MPa
mm
计算结果为:最小直径! 考虑键槽对轴有削弱,可按以下方式修正轴径:
轴径d>100mm 轴径d≤100mm
有一个键槽 d 增大3% d 增大5%~7%
有两个键槽 d 增大7% d 增大10%~15%
二、按弯扭合成强度计算
一般转轴强度用这 种方法计算,其步 骤如下:
减速器中齿轮轴的受力为典型的弯扭合成。
A
B CD
潘存云教授研制
L1
L2
L3
在完成单级减速器草图设计后,外载荷与支撑 反力的位置即可确定,从而可进行受力分析。
T A
1)轴的弯矩和扭矩分析 水平面受力及弯矩图→
铅垂面受力及弯矩图→ 水平铅垂弯矩合成图→
L1
L2
Fr
L3
Ft
Fa
F’NV1B
C
D
潘存云教授研制
FNV1 FNH1
ω
FNV2 FNH2
FNH1
F’NV1 FNV1
MH
FNH2
MH
Fr
Ma=Fa Fa
r
MV1
FNV2
MV2 M1 M2
扭矩图→
T
2)轴的强度校核
300
140
80
1000
330
150
90
铸钢
400
500
100
50
30
120
70
40
轴的设计实例
a
举例:计算某减速器输出轴危 d
轴强度计算公式完整版

RBV=(Fr×C+Fa×d/2)/(b+C)=3790N RCV=Fr-RBV=111N
M′1V=RBV×b=3790×110=416900Nmm M″1V=RCV×C=111×180=19980Nmm
危险截面计算应力:
ca
M ca W
M 2 (T )2
0.1d 3
1
Mpa
危险截面所需直径:
d
3Βιβλιοθήκη M ca0.1 1
3
M 2 (T )2
0.1 1
mm
[σ-1]-许用弯曲应力,按材料查表(15-1) ★ 危险截面的确定:
综合0500 tg12o15 2280 N 2 .求作支反力及弯矩图 H面:
RBH=FtC/(b+C)=10500×180/(110+180) =6520N
RCH=Ft-RBH=10500-6520=3980N
M1H=RBH×b=6520×110=717000Nmm
S S 2
步骤
1. 作轴的受力计算简图,求支反力
2. 求作支反力及弯矩图(MH、MV图) 3. 求作合成弯矩图(M图) 4. 求作扭矩及扭矩图(αT图) 5. 求作当量弯矩及当量弯矩图(Me图) 6. 强度计算(转轴)
⑵ 按疲劳强度条件精确校核计算
Ⅰ计算危险截面弯曲、扭转应力 危险截面:
M
W
T
WT
载荷大直径小 有应力集中处
Ⅱ 计算弯曲、扭转疲劳的安全系数
S
1 K a m
S
1 K a m
Ⅲ 计算危险截面疲劳强度的安全系数
Sca
第 4 章 圆轴扭转时的强度与刚度计算

基础篇之四第4章 圆轴扭转时的强度与刚度计算杆的两端承受大小相等、方向相反、作用平面垂直于杆件轴线的两个力偶,杆的任意两横截面将绕轴线相对转动,这种受力与变形形式称为扭转(torsion )。
本章主要分析圆轴扭转时横截面上的剪应力以及两相邻横截面的相对扭转角,同时介绍圆轴扭转时的强度与刚度设计方法。
4-1 外加扭力矩、扭矩与扭矩图作用于构件的外扭矩与机器的转速、功率有关。
在传动轴计算中,通常给出传动功率P 和转递n ,则传动轴所受的外加扭力矩M e 可用下式计算:[][]e kw 9549[N m]r /min P M n =⋅其中P 为功率,单位为千瓦(kW );n 为轴的转速,单位为转/分(r/min )。
如功率P 单位用马力(1马力=735.5 N •m/s ),则e []7024[N m][r /min]P M n =⋅马力 外加扭力矩M e 确定后,应用截面法可以确定横截面上的内力—扭矩,圆轴两端受外加扭力矩M e 作用时,横截面上将产生分布剪应力,这些剪应力将组成对横截面中心的合力矩,称为扭矩(twist moment ),用M x 表示。
图4-1 受扭转的圆轴用假想截面m -m 将圆轴截成Ⅰ、Ⅱ两部分,考虑其中任意部分的平衡,有M x -M e = 0由此得到图4-3 剪应力互等M x = M e与轴力正负号约定相似,圆轴上同一处两侧横截面上的扭矩必须具有相同的正负号。
因此约定为:按右手定则确定扭矩矢量,如果横截面上的扭矩矢量方向与截面的外法线方向一致,则扭矩为正;相反为负。
据此,图4-1b 和c 中的同一横截面上的扭矩均为正。
当圆轴上作用有多个外加集中力矩或分布力矩时,进行强度计算时需要知道何处扭矩最大,因而有必要用图形描述横截面上扭矩沿轴线的变化,这种图形称为扭矩图。
绘制扭矩图的方法与过程与轴力图类似,故不赘述。
【例题4-1】 变截面传动轴承受外加扭力矩作用,如图4-2a 所示。
轴扭转计算
第5章扭转5.1 扭转的概念及外力偶矩的计算5.1.1、扭转的概念在工程实际中,有很多以扭转变形为主的杆件。
例如图示5.1,常用的螺丝刀拧螺钉。
图5.1图示5.2,用手电钻钻孔,螺丝刀杆和钻头都是受扭的杆件。
图5.2图示5.3,载重汽车的传动轴。
图5.3图示5.4,挖掘机的传动轴。
图5.4图5.5所示,雨蓬由雨蓬梁和雨蓬板组成(图5.5a),雨蓬梁每米的长度上承受由雨蓬板传来均布力矩,根据平衡条件,雨蓬梁嵌固的两端必然产生大小相等、方向相反的反力矩(图5.5b),雨蓬梁处于受扭状态。
图5.5分析以上受扭杆件的特点,作用于垂直杆轴平面内的力偶使杆引起的变形,称扭转变形。
变形后杆件各横截面之间绕杆轴线相对转动了一个角度,称为扭转角,用 表示,如图5.6所示。
以扭转变形为主要变形的直杆称为轴。
图5.6本章着重讨论圆截面杆的扭转应力和变形计算。
5.1.2、外力偶矩的计算工程中常用的传动轴(图)是通过转动传递动力的构件,其外力偶矩一般不是直接给出的,通常已知轴所传递的功率和轴的转速。
根据理论力学中的公式,可导出外力偶矩、功率和转速之间的关系为:nN m 9550= (5.1) 式中 m----作用在轴上的外力偶矩,单位为m N ⋅;N-----轴传递的功率,单位为kW ;n------轴的转速,单位为r/min 。
图5.75.2 圆轴扭转时横截面上的内力及扭矩图5.2.1 扭矩已知受扭圆轴外力偶矩,可以利用截面法求任意横截面的内力。
图5.8a 为受扭圆轴,设外力偶矩为e M ,求距A 端为x 的任意截面n m -上的内力。
假设在n m -截面将圆轴截开,取左部分为研究对象(图5.8b ),由平衡条件0=∑x M ,得内力偶矩T 和外力偶矩e M 的关系e M T =内力偶矩T 称为扭矩。
扭矩的正负号规定为:自截面的外法线向截面看,逆时针转向为正,顺时针转向为负。
图5.8图示5.8的b 和c ,从同一截面截出的扭矩均为正号。
第三节轴的强度计计算、设计

第三节 轴轴的强度计计算、设计计步骤与与设计实例例一.按抗扭强强度计算小直对于传动轴直径,然后进轴,因只受转进行轴的结构矩,可只按转构设计,并用转矩计算轴的弯扭合成强度的直径;对于度校核。
于转轴,先用用此法估算轴的最 对偿弯实心圆轴扭 对于转轴,也弯矩对轴的强扭转的强度条 τ也可用上式初步强度的影响。
条件为0.2T T W ==步估算轴的直由上式可写二.定,M 截面 式中 T P—— n—— [ τ] d——W T ——d ≥C——由轴的通过9-2式按弯扭组合轴的结构设就可以画出对于一般钢e M W σ=e M =式中,e σ为V 分别为水平面的抗弯截面T——轴传递—轴传递的功—轴的转速(r ——许用扭—轴的最小直—轴的抗弯截=的材料和受载式求出的轴的合强度计算设计完成后,轴出轴的受力简钢制的轴,可e=为当量应力(平面和垂直面面系数(mm 递的工作转矩功率(kW);r/min);扭转切应力;直径,估算时如截面模量。
=载情况所决定表9-4 几的直径d,应按算 轴上零件的位简图,然后就可按第三强度M =MPa);e M 为的弯矩(N·3),W=0.1T 3[]dτ≤ 直径,但必须出计算轴的直,也是轴承受如果该处有一 定的系数,其几种轴用材料按表圆整成标位置也确定下可以进行弯扭理论进行强度1[σ−≤为当量弯矩(mm);T 为;为根3d α据 须把轴的许用直径公式:用扭转切应力 (9-1) 力适当降低,以补受的扭矩,(一个键槽,应(N·mm);将所算的最小小直径增加5%; (9-2) 其值见表9-4.料的[及C ]τ值标准直径,作下来,外加载扭合成强度计度计算。
强度]b b(N·mm);M 为轴传递的转矩据转矩性质而作为转轴的最载荷和支反力计算,其具体度条件为为合成弯矩(矩(N·mm)而定的折合因最小直径。
力作用点也相体步骤如下:应确(N·mm);;W 为轴的危因数。
圆轴扭转时的强度和刚度计算

A1 / A2 = [π (D 2 − d 2 ) / 4] /(πD 2 2 / 4) = (90 2 − 852 ) / 612 = 0.235
传动轴满足强度要求。 2)刚度校核 传动轴的极惯性矩为
I P = 0.1D 4 (1 − a 4 ) = {0.1 × 90 4 [1 − (85 / 90 ) 4 ]}mm 4 = 134 × 10 4 mm 4 θ max = 180 M n /(πGI P )
= (180 × 1500 × 10 3 / 80 × 10 3 × 134 × 10 4 π ) × 10 3 °/m
= 0.8°/m < [θ ]
传动轴满足刚度要求。 (2)计算实心轴的直径
1)按强度条件设计(设直径为D1)。若实心轴与空心轴强 度相同,当材料相同时,它们的抗扭截面系数应相等,即
W n = πD 13 / 16 = πD 3 (1 Βιβλιοθήκη a 4 ) / 16由此得
D 1 = D3 1 − a 4 = [90 × 3 1 − (85 / 90) 4 ]mm = 53mm
根据扭转刚度条件,可以解决三类问题, 即校核刚度、 设计截面和确定许可载荷 。
例6-5 汽车传动轴AB由45号无缝钢管制成,外径D=90mm,
[ 内径d=85mm,许用切应力 [τ ]=60MPa,θ ] =1.0°/m,工作时最
大力偶矩M =1500N·m,G =80GPa。 (1)试校核其强度及刚度。 (2)若将AB轴改为实心轴,试求其直径。 (3)比较空心轴和实心轴的重量。 解 (1)试校核其强度及刚度。 1) 强度校核 传动轴各截面上的扭矩均为
θ max = 180M n /(πGI P ) ≤ [θ ]
(6-13)
材料力学 (扭转)(四章 圆轴扭转时的强度与刚度计算)

Mx 0: T1 MA 0
C
T1 MA 7.03KN.m
22
Mx 0: -T2 MC 0
T2 MC 2.32KN.m
X
(4)讨论现在的设计是否合理。
若将A轮与B轮调换, X 则扭矩图如下:
可见轴内的最大扭矩值减小了。10
T(KN.M)
§3.2 薄壁圆筒扭转
在圆筒表面画 上许多纵向线 与圆周线,形成 许多小方格.
G
剪切胡克定律
G-剪切弹性模量
G E
2(1 )
2021/8/19
17
圆轴扭转时的应力和变形
根据观察到的现象, 经过推理,得出关于圆 轴扭转的基本假设。
m
m
圆轴扭转变形前的横截面,变形后仍保持为平面,
形状和大小不变。且相邻两截面间的距离不变。这就 是圆轴扭转的平面假设。
2021/8/19
18
二. 应力在横截面上的分布
2
而象电动机的主轴,水轮 机的主轴也承受扭转作用, 但这些零件除扭转变形外, 还伴随有其它形式的变形, 属于组合变形。
• 以扭转变形为主要变形形式的构件通常称为轴。 • 工程上应用最广的多为圆截面轴,即圆轴。
2021/8/19
3
• 扭转受力的特点是:
• 在构件的两端作用两个大小相等、方向相反且作 用面垂直于构件轴线的力偶矩。致使构件的任意 两个截面都发生绕构件轴线的相对转动,这种形 式的变形即为扭转变形。
在转矩m作用下,发现圆 周线相对地旋转了一个角 度,但大小、形状和相邻 两圆周线的距离不变。
表明,在圆筒的横截面上没有正应力和径向剪应力。
2021/8/19
11
设圆筒平均半径为r,筒壁厚度为t
因圆筒壁厚很小,可认为剪应力沿
轴的扭转强度计算

定位轴肩→零件定位→ h =3~5 mm 2.设计轴肩时应注意: (1)轴承定位轴肩(套筒)不能过高 (2)轴长应略短于轮毂宽度 (3)安装标准件轴段直径, (a)滚动轴承 (b)联轴器 (c)密封件 (4)轴肩圆角r 轮毂孔圆角R(倒角C)
轴上有键槽时: 放大轴径:一个键槽:3~5%
二个键槽:7~10%
取标准植
13.3 轴的强度计算
二、轴的弯扭合成强度计算
转轴同时承受扭矩和弯矩,必须按二者组合强度进行计算。通常 把轴当作置于铰链支座上的梁,作用于轴上零件的力作为集中力, 其作用点取为零件轮毂宽度的中点上。具体的计算步骤如下:
①轴和轴上零件要有准确、牢固的工作位置 ②轴上零件装拆、调整方便 ③轴应具有良好的制造工艺性等 ④尽量避免应力集中
13.2 轴的结构设计
二、零件在轴上的固定 1、周向固定 为了传递运动和转矩,防止轴上零件与轴作相对转动。常用的 周向固定方法有键、花键、销、过盈配合、 弹性环联接、成形联接等。
碳钢比合金钢价廉,对应力集中的敏感性比较低,适用于一般要求的轴。 合金钢比碳钢有更高的力学性能和更好的淬火性能,在传递大功率并要求减小 尺寸和质量、要求高的耐磨性,以及处于高温、低温和腐蚀条件下的轴常采用 合金钢。在一般工作温度下(低于200℃),各种碳钢和合金钢的弹性模量均 相差不多,因此相同尺寸的碳钢和合金钢轴的刚度相差不多。
一、轴的扭转强度计算
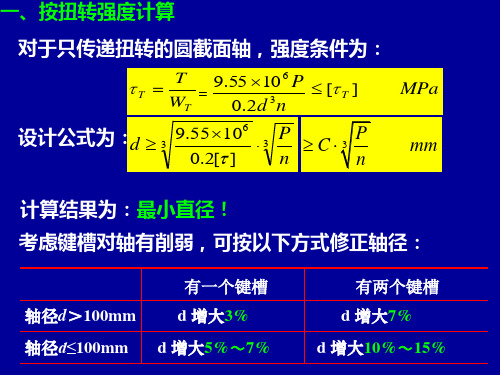
用于:①只受扭矩或主要承受扭矩的传动轴的强度计算 ②结构设计前按扭矩初估轴的直径dmin
对于圆截面的实心轴,其抗扭强度条件为:
强度条件
T
T WT
9.55 106
0.2d 3
扭转强度计算公式

扭转强度计算公式
扭转强度计算公式:m2=2.3KN·m。
扭矩在物理学中就是力矩的大小,等于力和力臂的乘积,国际单位是牛米N·m,剪断应力即物体由于外因(受力、湿度变化等)而变形时,在物体内各部分之间产生相互作用的内力,以抵抗这种外因的作用,并力图使物体从变形后的位置回复到变形前的位置。
力矩表示力对物体作用时所产生的转动效应的物理量。
力和力臂的乘积为力矩。
力矩是矢量。
力对某一点的力矩的大小为该点到力的作用线所引垂线的长度(即力臂)乘以力的大小,其方向则垂直于垂线和力所构成的平面用右手螺旋法则来确定。
力对某一轴线力矩的大小,等于力对轴上任一点的力矩在轴线上的投影。
第四节圆轴扭转时的强度和刚度计算

选择直径、壁厚、长度等作为设计变量。
设计变量
目标函数
约束条件
优化算法
以最大扭矩为目标函数,考虑重量和成本的影响。
强度、刚度、稳定性等为约束条件。
采用遗传算法进行优化,考虑多种方案进行比较和选择。
THANKS
感谢观看
抗扭截面模数是圆轴截面的几何特性,等于圆周上各点的截面模数之和。
剪切弹性模量是衡量圆轴材料抵抗剪切变形能力的参数,等于剪切模量与弹性模量之比。
圆轴扭转的强度计算
02
扭矩的单位
扭矩的单位为牛米(N·m)或千克米(kgf·m)。
扭矩
圆轴扭转时所受的力偶矩为扭矩,用M表示。
扭矩的方向
扭矩的方向垂直于圆轴的轴线。
圆轴扭转的受力分析
强度条件
强度计算公式
强度计算公式说明
圆轴扭转的强度计算公式
选择材料:圆轴的材料为45号钢。
确定许用扭矩:[M] = 50 N·m。
已知圆轴的直径d = 20 mm。
根据强度计算公式
由于Mmax ≤ [M],因此该圆轴满足强度要求。
圆轴扭转的强度计算实例
01
02
03
04
05
圆轴扭转的刚度计算
圆轴扭转时,轴的横截面保持为圆形,且各点的剪切变形相等。
圆轴扭转时,轴的纵向线发生微小的缩短,但各点的缩短量相等。
圆轴扭转的特点
圆轴扭转的基本参数
作用在轴上的扭矩等于作用在轴上所有外力的投影矢量的代数和。
扭矩(M)
极惯性矩(Ip)
抗扭截面模数(Wp)
剪切弹性模量(G)
极惯性矩是衡量圆轴抗扭能力的参数,等于圆周上各点的截面惯性矩之和。
xx年xx月xx日
扭转的强度计算

圆轴扭转时的强度计算
为了保证受扭圆轴安全可靠地工作,必须使圆轴的最大工作剪应力max τ不超过材料的扭转许用切应力[]τ。
因此,圆轴的强度条件为
max []ττ≤
对于等直圆轴,其强度条件为
max []P T W τ≤ (1-1 ) 上式中max T 是扭矩图上绝对值最大的扭矩,最大切应力max τ发生在max T
所在截面的圆周边上。
对于阶梯形变截面圆轴,因为W ρ不是常量,max τ不一定发生在max T
的截面上。
这就要综合考
虑扭矩T 和抗扭截面系数W ρ两者的变化情况来确定max τ。
在静荷载作用下,扭转许用切应力[]τ与许用拉应力[]t σ之间有如下关系: 对塑性材料[]τ=(0.5~0.6[]t σ
对脆性材料[]τ= (0.8~1.0)[]t σ
应用式(1-1)可解决圆轴扭转时的三类强度问题:
(1)强度校核。
已知材料的许用切应力[]τ、截面尺寸、以及所受荷载,直接应用式(1-1)检查构件是否满足强度要求。
(2)选择截面。
已知圆轴所受的荷载及所用材料,可按式(1-1)计算W ρ后,再进一步确定截面直径。
此时式(1-1)改写为
max
[]T W ρτ≥ (1-1a )
(3)确定许可荷载 。
已知构件的材料和尺寸,按强度条件计算出构件所能承担的扭矩max T ,再根据扭矩与外力偶的关系,计算出圆轴所能承担的最大外力偶。
此时式(1-1)改写为
max []T W ρτ≤ (1-1b)。
轴的强度计算

对于一般钢制轴,可用第三强度理论(最大切 应力理论)求出危险截面的当量应力。
按第三强度理论得出的轴的强度条件为:
e
2 b
4 2
[ b ]
弯曲应力:
b
M W
d
M 3/
32
M 0.1d 3
扭切应力:
T T WT 2W
W------抗弯截面系数; WT ----抗扭截面系数;
轴的抗弯和抗扭截面系数
12-2
计算结果为:最小直径! 考虑键槽对轴有削弱,可按以下方式修正轴径:
轴径d>100mm 轴径d≤100mm
有一个键槽 d 增大3% d 增大5%~7%
有两个键槽 d 增大7% d 增大10%~15%
轴的材料
表15-2 常用材料的[τT]值和A0值
Q235-A3, 20 Q275, 35 1Cr18Ni9Ti
80
1000
330
150
90
铸钢
400
500பைடு நூலகம்
100
50
30
120
70
40
折合系数取值:α=
0.3 ----转矩不变; 0.6 ----脉动变化;
1 ----频繁正反转。
设计公式: d 3 Me
mm
0.1[ 1b ]
表15-3 轴的许用弯曲应力
材料
σb
[σ+1b]
[σ0b]
脉400动循环状态下130的
S Sca
S S S S
S
2
S
S
2
S
SS
其中:
SSca----危险截面静强度设计的安全系数;
SS----按屈服强度设计的安全系数; SS=1.2~1.4----高塑性材料的钢轴(σS /σB ≤ 0.6); SS=1.4~1.8----中等塑性材料的钢轴(σS /σB =0.6~0.8);
