清华理论力学课后答案4
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
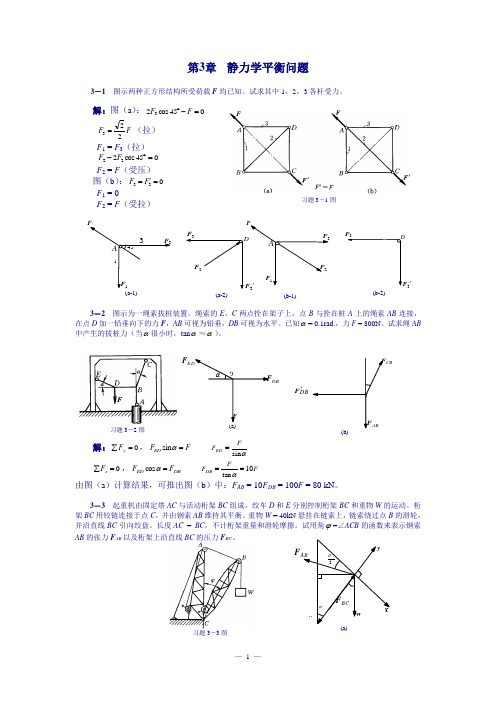
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
理论力学第4版习题答案

理论力学第4版习题答案理论力学是物理学中的一门基础课程,它研究物体运动的规律和力的作用关系。
而理论力学第4版习题是帮助学生巩固和应用所学知识的重要工具。
本文将为读者提供一些理论力学第4版习题的答案,以帮助他们更好地理解和掌握这门学科。
1. 题目:一个质量为m的物体以初速度v0沿着水平面上的直线运动,受到一个与速度成正比的阻力F=-kv作用。
求物体的速度随时间的变化关系。
答案:根据牛顿第二定律,物体的加速度a等于受到的合力F除以质量m。
由于物体只受到阻力和重力两个力的作用,因此有F=mg-kv。
代入牛顿第二定律的公式,得到ma=mg-kv,即m(dv/dt)=mg-kv。
整理后得到mdv/(mg-kv)=dt,两边同时积分得到ln|mg-kv|=-(k/m)t+C,其中C为积分常数。
通过指数函数的性质,可以得到mg-kv=Ae^(-kt/m),其中A为常数。
解出v后,即可得到物体的速度随时间的变化关系。
2. 题目:一个质量为m的物体以初速度v0沿着竖直方向上的直线运动,受到一个与速度平方成正比的阻力F=-kv^2作用。
求物体的速度随时间的变化关系。
答案:同样根据牛顿第二定律,物体的加速度a等于受到的合力F除以质量m。
由于物体只受到阻力和重力两个力的作用,因此有F=mg-kv^2。
代入牛顿第二定律的公式,得到ma=mg-kv^2,即m(dv/dt)=mg-kv^2。
整理后得到mdv/(mg-kv^2)=dt,两边同时积分得到(1/v0-1/v)=kt/m,其中k为常数。
解出v后,即可得到物体的速度随时间的变化关系。
3. 题目:一个质量为m的物体沿着半径为R的圆周上的轨道做匀速圆周运动。
求物体受到的向心力大小和方向。
答案:根据牛顿第二定律,物体的加速度a等于受到的合力F除以质量m。
在圆周运动中,物体受到的合力只有向心力Fc。
由于物体做匀速圆周运动,所以加速度a的大小为v^2/R,其中v为物体的速度。
将这个加速度代入牛顿第二定律的公式,得到Fc=mv^2/R。
理论力学课后答案Word版
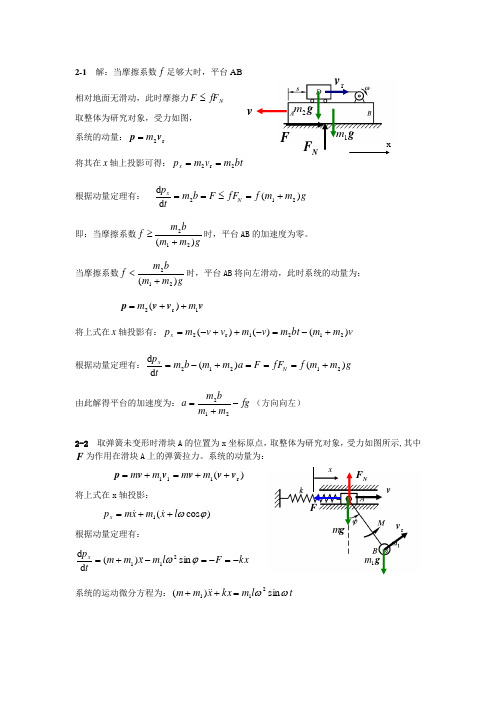
2-1 解:当摩擦系数f 足够大时,平台AB 相对地面无滑动,此时摩擦力N fF F ≤ 取整体为研究对象,受力如图, 系统的动量:r 2v p m =将其在x 轴上投影可得:bt m v m p x 2r 2==根据动量定理有:g m m f fF F b m tp N x)(d d 212+=≤== 即:当摩擦系数gm m bm f )(212+≥时,平台AB 的加速度为零。
当摩擦系数gm m bm f )(212+<时,平台AB 将向左滑动,此时系统的动量为:v v v p 1r 2)(m m ++=将上式在x 轴投影有:v m m bt m v m v v m p x )()()(2121r 2+-=-++-=根据动量定理有:g m m f fF F a m m b m tp N x)()(d d 21212+===+-= 由此解得平台的加速度为:fg m m bm a -+=212(方向向左)2-2 取弹簧未变形时滑块A 的位置为x 坐标原点,取整体为研究对象,受力如图所示,其中F 为作用在滑块A 上的弹簧拉力。
系统的动量为:)(r 111v v v v v p ++=+=m m m m将上式在x 轴投影:)cos (1ϕωl x m xm p x ++= 根据动量定理有:kx F l m xm m tp x-=-=-+=ϕωsin )(d d 211 系统的运动微分方程为:t l m kx x m m ωωsin )(211=++N Fg mg 1mFxvr vvr vN FFg 1mg 2mx2-4 取提起部分为研究对象,受力如图(a)所示,提起部分的质量为vt m ρ=,提起部分的速度为v ,根据点的复合运动可知质点并入的相对速度为r v ,方向向下,大小为v (如图a 所示)。
(a ) (b)根据变质量质点动力学方程有:v vt t t m m t t mρρr r )()(d d )(d d v g F v g F v ++=++= 将上式在y 轴上投影有:)()()()(d d 2r v vgt t F v v g vt t F tvm+-=--=ρρρ 由于0d d =tv,所以由上式可求得:)()(2v vgt t F +=ρ。
【最新试题库含答案】清华理论力学课后答案4

清华理论力学课后答案4篇一:理论力学课后习题答案第4章运动分析基础第4章运动分析基础4-1 小环A套在光滑的钢丝圈上运动,钢丝圈半径为R(如图所示)。
已知小环的初速度为v0,并且在运动过程中小环的速度和加速度成定角θ,且 0 <θ<?,试确定小环2A的运动规律。
22解:asin??a?v,a?v nRsin?R2vdvt1a?dv?acos??v,?dt t2??v00vdtRtan?Rtan?v?ds?v0Rtan?dtRtan??v0tstv0Rtan?ds??0?0Rtan??v0tdtAs?Rtan?lnRtan?Rtan??v0t习题4-1图2??x?3sint?x?4t?2t1.?, 2.?2y?2cos2t?y?3t?1.5t??4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的解:1.由已知得 3x = 4y ? v?5?5t?y?3?3t? ?a??5 ??y??3????4x????4?4t?x(1)为匀减速直线运动,轨迹如图(a),其v、a图像从略。
2.由已知,得arcsinx3?12arccosy242(b)习题4-2图化简得轨迹方程:y?2?x9(2)轨迹如图(b),其v、a图像从略。
4-3 点作圆周运动,孤坐标的原点在O点,顺钟向为孤坐标的正方向,运动方程为s?12?Rt2,式中s以厘米计,t以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y坐标值最大的位置时,求点的加速度在x和y轴上的投影。
解:v?s???Rt,at?v???R,an?v??2Rt2y坐标值最大的位置时:?s? ax?at??R,ay???R22R12?Rt2??22R,?t?1习题4-3图4-4 滑块A,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮以匀角速度ω转动,如图所示。
试求滑块的速度随距离x 的变化规律。
解:设t = 0时AB长度为l0,则t时刻有:r (?t?arcta?arctan)r?l?x2?r2l0x2?r2对时间求导:?r??r2x22xx?r?rx ???xx2?r2???xxx?r224-5 凸轮顶板机构中,偏心凸轮的半径为R,偏心距OC = e,绕轴O以等角速转动,从而带动顶板A作平移。
清华大学版理论力学课后习题答案大全-----第5章点的复合运动分析
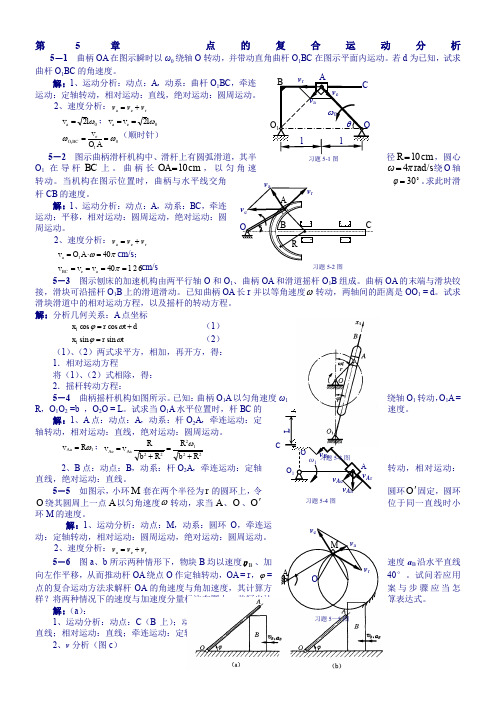
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
理论力学答案完整版(清华大学出版社)1

第一章力和约束 习题解答
1-1 求 图 示 空 间 汇 交 力 系 的 合 力 。 已 知 F1 = 100N , F2 = 200N , F3 = 300N , F4 = 400N ,方向如图示。如果仅改变力 F4 的方向,能否使此力系成为平衡力系?为什么?
解:按合力投影定理计算合力在 x, y, z 轴上的投影: FRx = F1 cosϕ1 + F2 sin γ 2 cosϕ2 − F4 sin2 30o = 111.1 (N); FRy = F2 sin γ 2 sinϕ2 + F3 + F4 sin 30o cos30o
= 601.1 (N); FRz = −F1 sinϕ1 − F2 cosγ 2 sinϕ2 + F4 cos30o
题 1-9(a)图 (b)按三力平衡汇交定理画出整体的受力图,然后依次画出杆 CD、杆 AB、轮 D 的受力图。
题 1-9(b)图
5
(c)折杆 BC 为二力构件,约束力方向一定是沿着 BC 连线。因力偶只能与力偶平衡,所 以,铰链 A 和 B 处的约束力一定互相平行而组成力偶。
题 1-9(c)图 (d)图示结构中,杆 CE 为二力杆,其余杆件的受力按力偶平衡理论确定。
对 x, y, z 轴的力矩和,以及对坐标原点 O 的力矩和。
解:平面 abc 的法向量为 n = 1 i + 1 j + 1 k ,力偶矢为 ab c
M = Mn0 , 其中 i, j,k, n0 依次为 x, y, z, n 方向的单位向
量。力 F 表为 F = Fξ 0
其中ξ 0 为ξ = 1 (a i + b j) − ck 方向的单位向量。
理论力学课后习题及答案解析

理论力学课后习题及答案解析文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-MG129]第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A 点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;将RB向下平移一段距离d,使满足:最后简化为一个力R,大小等于RB。
其几何意义是:R 的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力RA和一个力偶M A,且:如图所示;将RA向右平移一段距离d,使满足:最后简化为一个力R,大小等于RA。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
清华大学版理论力学课后习题答案大全

第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕc o s )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
理论力学第三版课后习题答案

目录第一章质点力学 (2)第二章质点组力学 (56)第三章刚体力学 (74)第四章转动参考系 (105)第五章分析力学 (115)第一章 质点力学1.1 由题可知示意图如题1.1.1图:{{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a . 则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得11021at t s v +=再由此式得()()2121122t t t t t t s a +-=证明完毕.1.2 解 由题可知,以灯塔为坐标原点建立直角坐标如题1.2.1图.题1.2.1图设A 船经过0t 小时向东经过灯塔,则向北行驶的B 船经过⎪⎭⎫ ⎝⎛+2110t 小时经过灯塔任意时刻A 船的坐标()t t x A 15150--=,0=A yB 船坐标0=B x ,⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛+-=t t y B 15211150则AB 船间距离的平方()()222B A B A y y x x d -+-=即()2021515t t d -=201521115⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛++t t()20202211225225675900450⎪⎭⎫ ⎝⎛++++-=t t tt t2d 对时间t 求导()()67590090002+-=t t dtd d AB 船相距最近,即()02=dtdd ,所以h t t 430=- 即午后45分钟时两船相距最近最近距离22min231543154315⎪⎭⎫ ⎝⎛⨯-⨯+⎪⎭⎫ ⎝⎛⨯=s km1.3 解 ()1如题1.3.2图第1.3题图y题1.3.2图由题分析可知,点C 的坐标为⎩⎨⎧=+=ψψϕsin cos cos a y a r x 又由于在∆AOB 中,有ϕψsin 2sin ar =(正弦定理)所以ry r a 2sin 2sin ==ψϕ联立以上各式运用1cos sin 22=+ϕϕ由此可得rya x r a x 22cos cos --=-=ψϕ得12422222222=---++r y a x y a x r y 得22222223y a x r a x y -=-++化简整理可得()()2222222234r a y x y a x -++=-此即为C 点的轨道方程.(2)要求C 点的速度,分别求导⎪⎪⎩⎪⎪⎨⎧=--=2cos sin cos 2cos sin ϕωψψϕωϕωr y r r x 其中ϕω = 又因为ψϕsin 2sin a r =对两边分别求导 故有ψϕωψcos 2cos a r =所以22y x V +=4cos sin cos 2cos sin 2222ϕωψψϕωϕωr r r +⎪⎪⎭⎫ ⎝⎛--= ()ψϕψϕϕψω++=sin cos sin 4cos cos 22r1.4 解 如题1.4.1图所示,A BOCLxθd 第1.4题图OL 绕O 点以匀角速度转动,C 在AB 上滑动,因此C 点有一个垂直杆的速度分量22x d OC v +=⨯=⊥ωωC 点速度dx d d v v v 222sec sec cos +====⊥⊥ωθωθθ 又因为ωθ= 所以C点加速度 θθθω ⋅⋅⋅⋅==tan sec sec 2d dt dv a ()2222222tan sec 2d x d x d +==ωθθω1.5 解 由题可知,变加速度表示为⎪⎭⎫ ⎝⎛-=T t c a 2sin 1π 由加速度的微分形式我们可知dtdv a =代入得dtT t c dv ⎪⎭⎫ ⎝⎛-=2sin 1π 对等式两边同时积分dt T t c dv t v⎰⎰⎪⎭⎫ ⎝⎛-=002sin 1π可得 :D Ttc Tct v ++=2cos2ππ(D 为常数)代入初始条件:0=t 时,0=v ,故c TD π2-=即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos2T t T t c v ππ 又因为dtds v =所以=ds dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos2ππ 对等式两边同时积分,可得:⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=t T t T T t c s 2sin 22212πππ1.6 解 由题可知质点的位矢速度r λ=//v ①沿垂直于位矢速度μθ=⊥v又因为 r r λ== //v , 即r rλ=μθθ==⊥r v 即rμθθ= ()()j i v a θ r dtd r dt d dt d +==(取位矢方向i ,垂直位矢方向j ) 所以()j i i i θ r rdtd r i dt r d r dt d +=+=()dtd r dt d r dt dr r dt d j j j j θθθθ ++=i j j 2r r r θθθ -+= 故()()j i a θθθ r r r r22++-= 即 沿位矢方向加速度()2θ r ra -= 垂直位矢方向加速度()θθr r a 2+=⊥ 对③求导r rr 2λλ== 对④求导θμμθθr rr +-=2⎪⎭⎫⎝⎛+=λμμθr 把③④⑦⑧代入⑤⑥式中可得rr a 222//θμλ-= ⎪⎭⎫ ⎝⎛+=⊥r a μλμθ1.7 解 由题可知⎩⎨⎧==θθsin cos r y r x ①②对①求导θθθ sin cos r r x-= ③ 对③求导2 ④对②求导θθθcos sin r r y+=⑤ 对⑤求导θθθθθθθsin cos cos 2sin 2 r r r ry -++=⑥ 对于加速度a ,我们有如下关系见题1.7.1图题1.7.1图即⎩⎨⎧+=+=θθθθθθcos sin sin cos a a y a a x r r⑦--⑧ 对⑦⑧俩式分别作如下处理:⑦θcos ⨯,⑧θsin ⨯ 即得⎩⎨⎧+=-=θθθθθθθθθθcos sin sin sin cos sin cos cos a a y a a x r r⑨--⑩ ⑨+⑩得θθsin cos yx a r += ⑾ 把④⑥代入 ⑾得2θr r a r -= 同理可得θθθ r r a 2+= 1.8解 以焦点F 为坐标原点,运动如题1.8.1图所示]题1.8.1图则M 点坐标⎩⎨⎧==θθsin cos r y r x 对y x ,两式分别求导⎪⎩⎪⎨⎧+=-=θθθθθθcos sin sin cos r r yr r x 故()()22222cos sin sin cos θθθθθθ r r r r y xv ++-=+=222ωr r+= 如图所示的椭圆的极坐标表示法为()θcos 112e e a r +-=对r 求导可得(利用ωθ= )又因为()()221cos 111e a e e a r -+-=θ即()rer e a --=21cos θ 所以()()2222222221211cos 1sin e r e ar r e a --+--=-=θθ故有()2222224222sin 1ωθωr e a r e v +-=()2224221ea r e -=ω()()]1211[2222222e r e ar r ea --+--22ωr +()()⎥⎦⎤⎢⎣⎡--+-⋅-=2222222221121e e ar r r e e a r ω()r r a b r -=2222ω 即()r a r br v -=2ω(其中()b a e b ,1222-=为椭圆的半短轴)1.9证 质点作平面运动,设速度表达式为j i v y x v v +=令为位矢与轴正向的夹角,所以dt d v dt dv dt d v dt dv dt d y y x x j j i i v a +++==j i ⎪⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=θθ x y y x v dt dv v dt dv 所以[]j i a ⎪⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛-=θθ x yy x v dt dv v dt dv ()j i y x v v +⋅ θθ y x y y y x x x v v dt dv v v v dt dv v ++-=dtdv v dt dv v y yxx += 又因为速率保持为常数,即C C v v y x ,22=+为常数对等式两边求导022=+dtdv v dt dv v y y xx所以0=⋅v a即速度矢量与加速度矢量正交.1.10解 由题可知运动轨迹如题1.10.1图所示,题1.10.1图则质点切向加速度dtdv a t =法向加速度ρ2n v a =,而且有关系式ρ2v 2k dt dv -= ①又因为()232y 1y 1'+''=ρ②2px y 2=所以yp y =' ③ 32yp y -='' ④ 联立①②③④2322322y p 1y p 2kv dtdv⎪⎪⎭⎫ ⎝⎛+-= ⑤又dydv ydt dy dy dv dt dv =⋅=把2px y 2=两边对时间求导得pyy x= 又因为222y xv += 所以22221py v y+= ⑥ 把⑥代入⑤23223222122121⎪⎪⎭⎫ ⎝⎛+⋅-=⋅⎪⎪⎭⎫ ⎝⎛+y p y p kv dydvp y v既可化为222py dykp v dv +-= 对等式两边积分222py dykp v dv p p vu+-=⎰⎰- 所以πk ue v -=1.11解 由题可知速度和加速度有关系如图1.11.1所示题1.11.1图⎪⎪⎩⎪⎪⎨⎧====ααcos sin 2a dt dv a a r v a t n 两式相比得dtdvr v ⋅=ααcos 1sin 2 即2cot 1vdv dt r =α 对等式两边分别积分200cot 1v dv dt rv v t⎰⎰=α 即αcot 11rtv v -=此即质点的速度随时间而变化的规律.1.12证 由题1.11可知质点运动有关系式⎪⎪⎩⎪⎪⎨⎧==ααcos sin 2a dtdv a r v ①② 所以 ωθθθd dv dt d d dv dt dv =⋅=,联立①②,有ααωθcos sin 2r v d dv = 又因为r v ω=所以 θαd vdv cot =,对等式两边分别积分,利用初始条件0=t 时,0θθ=()αθθcot 00-=e v v1.13 证(a )当00=v ,即空气相对地面上静止的,有牵相绝v v v +=.式中绝v 质点相对静止参考系的绝对速度, 相v 指向点运动参考系的速度, 牵v 指运动参考系相对静止参考系的速度.可知飞机相对地面参考系速度:绝v =v ',即飞机在舰作匀速直线运动.所以飞机来回飞行的总时间v l t '=20. (b )假定空气速度向东,则当飞机向东飞行时速度01v v v +'=飞行时间1v v lt +'=当飞机向西飞行时速度0v v v v v -'=+=牵相飞行时间2v v lt -'=故来回飞行时间021v v l t t t +'=+=0v v l -'+222v v lv -''= 即2200220112v v t v v v lt '-='-'= 同理可证,当空气速度向西时,来回飞行时间2201v v t t '-=(c )假定空气速度向北.由速度矢量关系如题1.13.1图v 题1.13.1图v v v '+=0绝202v v v -'= 所以来回飞行的总时间222vv l t -'=2200220112v vt v v v l '-='-'=同理可证空气速度向南时,来回飞行总时间仍为2201v v t t '-=1.14解 正方形如题1.14.1图。
理论力学解答(清华版)

第一章 静力学基本概念1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2FB.2F - 1FC.1F +2F图1-18 图1-191-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体;B. 变形体;C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.-F/31-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21第二章力系的简化2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A指向B的力F,在z轴上投影为,对z轴的矩的大小为。
答:F/2;62F/5。
2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b,c,则力F在轴z和y上的投影:Fz= ;Fy= ;F对轴x的矩M x(F)= 。
答:Fz=F·sinφ;Fy=-F·cosφ·cosφ;Mx(F)=F(b·sinφ+c·cosφ·cosθ)图2-40 图2-412-3.力通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力在x轴上的投影为,对x轴的矩为。
理论力学课后习题及答案[高等教育]
![理论力学课后习题及答案[高等教育]](https://img.taocdn.com/s3/m/19db2b230a4c2e3f5727a5e9856a561252d3218b.png)
应按下列要求进行设计(D )A.地震作用和抗震措施均按8度考虑B.地震作用和抗震措施均按7度考虑C.地震作用按8度确定,抗震措施按7度采用答题(共38分)1、什么是震级什么是地震烈度如何评定震级和烈度的大小(6分)震级是表示地震本身大小的等级,它以地震释放的能量为尺度,根据地震仪记录到的地震波来确定(2分)地震烈度是指某地区地面和各类建筑物遭受一次地震影响的强弱程度,它是按地震造成的后果分类的。
(2分)震级的大小一般用里氏震级表达(1分)地震烈度是根据地震烈度表,即地震时人的感觉、器物的反应、建筑物破坏和地表现象划分的。
(1分)D.地震作用按7度确定,抗震措施按8度采用4.关于地基土的液化,下列哪句话是错误的(A)A.饱和的砂土比饱和的粉土更不容易液化B.地震持续时间长,即使烈度低,也可能出现液化C.土的相对密度越大,越不容易液化D.地下水位越深,越不容易液化5.考虑内力塑性重分布,可对框架结构的梁端负弯矩进行调幅( B )A.梁端塑性调幅应对水平地震作用产生的负弯矩进行B.梁端塑性调幅应对竖向荷载作用产生的负弯矩进行C.梁端塑性调幅应对内力组合后的负弯矩进行D.梁端塑性调幅应只对竖向恒荷载作用产生的负弯矩进行6.钢筋混凝土丙类建筑房屋的抗震等级应根据那些因素查表确定( B )A.抗震设防烈度、结构类型和房屋层数B.抗震设防烈度、结构类型和房屋高度C.抗震设防烈度、场地类型和房屋层数D.抗震设防烈度、场地类型和房屋高度7.地震系数k与下列何种因素有关( A )A.地震基本烈度B.场地卓越周期一、 C.场地土类1.震源到震中的垂直距离称为震源距(×)2.建筑场地类别主要是根据场地土的等效剪切波速和覆盖厚度来确定的(√)3.地震基本烈度是指一般场地条件下可能遭遇的超越概率为10%的地震烈度值(×)4.结构的刚心就是地震惯性力合力作用点的位置(×)5.设防烈度为8度和9度的高层建筑应考虑竖向地震作用(×)6.受压构件的位移延性将随轴压比的增加而减小C.地震作用按8度确定,抗震措施按7度采用答题(共38分)1、什么是震级什么是地震烈度如何评定震级和烈度的大小(6分)震级是表示地震本身大小的等级,它以地震释放的能量为尺度,根据地震仪记录到的地震波来确定(2分)地震烈度是指某地区地面和各类建筑物遭受一次地震影响的强弱程度,它是按地震造成的后果分类的。
理论力学习题册答案精品

【关键字】活动、情况、方法、条件、动力、空间、质量、地方、问题、系统、密切、主动、整体、平衡、保持、提升、合力、规律、位置、支撑、作用、结构、水平、速度、关系、分析、简化、倾斜、满足、带动、支持、方向、推动、推进、中心第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
a(球A )b(杆AB)d(杆AB、CD、整体)c(杆AB、CD、整体)f(杆AC、CD、整体)e(杆AC、CB、整体)四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
a(球A、球B、整体)b(杆BC、杆AC、整体)第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体 )c (杆AB 、CD 、整体)d (杆BC 带铰、杆AC 、整体 )e (杆CE 、AH 、整体)f (杆AD 、杆DB 、整体 )g (杆AB 带轮及较A 、整体)h (杆AB 、AC 、AD 、整体 第二章 平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F = - F ’,所以力偶的合力等于零。
( )2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
理论力学课后习题答案_清华大学出版社_2004年版_范钦珊,刘燕,王琪 编著
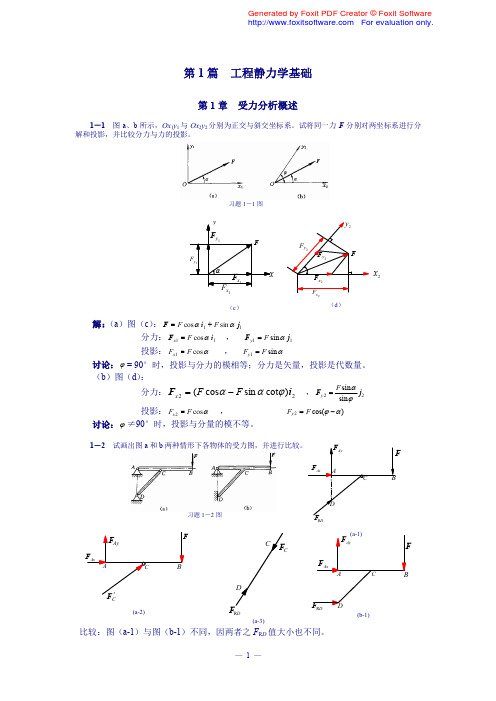
习题 1-1 图
y
y2
F
F y1
F y1
F y2 F y2
F
Fx1 Fx1
(c)
x
F x2
Fx 2
x2
(d)
解: (a)图(c) : F F cos i1 F sin j1 分力: F x1 F cos i1 投影: Fx1 F cos , ,
F y1 F sin j1 Fy1 F sin
讨论: = 90°时,投影与分力的模相等;分力是矢量,投影是代数量。 (b)图(d) : 分力: F x 2 ( F cos F sin cot ) i 2 投影: Fx 2 F cos , 讨论: ≠90°时,投影与分量的模不等。
1-2 试画出图 a 和 b 两种情形下各物体的受力图,并进行比较。
F Ax
, Fy 2
F sin j2 sin
Fy 2 F cos( )
FAy
A
C
F
B
D
习题 1-2 图
FRD
FAy
F Ax
A
C
F
C
FC
F Ax
FAy
(a-1)
F
C
B
A
B
D
' FC
(a-2)
FRD
(a-3)
FRD
D
(b-1)
比较:图(a-1)与图(b-1)不同,因两者之 FRD 值大小也不同。
解: 图(a) : 2F3 cos 45 F 0
F3 2 F (拉) 2
F1 = F3(拉)
F2 2 F3 cos 45 0
F2 = F(受压) 图(b) : F3 F3 0 F1 = 0 F2 = F(受拉)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ww w.
4
2 v=6 2m s 2
kh da
题 4-11 图 题 4-12 图 题 4-13 图
v2 = 36 2 m s ρ
4-12 已知图示机构的尺寸如下: O1 A = O2 B = AM = r = 0.2m ; O1O2 = AB 。如轮 O1 按 ϕ = 15π t ( ϕ 单位为 rad)的规律转动,求当 t = 0.5 s 时,杆 AB 上的点 M 的速度和加速度。 解: 点 M 与点 A 有相同的速度和加速度, 即
̇= v=x
hω , cos 2ωt
̇= a=̇ x
2
w.
2hω 2sinωt . cos3ωt
速度和加速度。 解:由右图所示
co
4-5
若将题 4-4 中的顶杆换成平底的物块 M, 其余条件不变。 试求物块上 B 点的运动方程、
m
4-7
图示滑道连杆机构。已知 BO = 0.1 m; OA = 0.1 m,滑道连杆 BC 绕轴 B 按 ϕ = 10t
课 后
上无滑动运动的速度和加速度, 并求在滚子上与钢板
答
v = vM ' = vM =
钢板加速度
案
2πnd = 0.524m / s 2 × 60
网
dv a= =0 dt
2v2 m = 2.742 m / s 2 d
滚子上 M 点的加速度
n aτ M = 0 , aM =
w.
co
题 4-14 图
题 4-15 图
OC 杆转角 ϕ 满足 tan ϕ = 4-14 纸盘由厚度为 a 的纸条卷成,令纸盘的中心不动,而以等速 v 拉纸条。求纸盘的角加 速度(以半径 r 的函数表示) 。 解: 设纸盘在 t=0 时刻的初始半径为 R,则在 t 时 刻纸盘减 少的面积为
πR 2 − πr 2 = avt
v = rω
将以上两式分别对时间求导,得
2 2 v = vρ + vϕ = 20 OA2 = 2 m s .
题 4-7 图
A 点的加速度为
aρ =
2 2 a = aρ + aϕ = 40 m s .
也可以用直角坐标法求解,并求出 A 点地切向和法向加速度。 4-8 如图所示,一直杆以 ϕ = ω 0 t 绕其固定端 O 转动,其中 ω 0 为常量。沿此杆有一滑块
e cos 2ωt R 2 − e 2 sin 2 ω
+
2
e 2 sin 2 ωt
4( R − e sin ωt )
2 2 3 2
).
题 4-4 图
vB =
dy B = −eω sin ωt , dt dv B = eω 2 cos ωt . dt
aB =
4-6
ww w.
b)
题 4-6 图
kh da
解:经分析图 a)、b) 、c) 中 M 点速度和加速度相同。以 O 为原点,水平方向为 x 轴,竖直方 向为 y 轴。对图在 a)、 b) 、c) 中 M 点都有
课 后
a)
答
3)杆 OA 绕 O 轴转动时,通过套在杆上的套筒 M 带动杆 MN 沿水平轨道运动,求 MN 上
案
网
x = h ⋅ tgϕ = h ⋅ tgω t ,
题 4-5 图 c)
y B = R + e cos ωt ,
图示 a 、b、c 三种机构,已知机构尺寸 h 和杆 OA 与铅直线的夹角 ϕ = ωt ,其中 ω 为
常量,分析并比较它们的运动: 1)穿过小环 M 的杆 OA 绕 O 轴转动,同时拨动小环沿水平导杆滑动,求小环的速度和加 2)绕 O 轴转动的杆 OA,推动物块 M 沿水平面滑动,求物块 M 上一点的速度和加速度。 一点的速度和加速度。 速度。
有 ρ = 2 2 , θ = arctan y = 45 , a n =
'
o
∴ 当 y = 1m 时点的速度和加速度在坐标轴上的投影为:
vx = v y = ax = −
CB = r 。求摇杆转动方程。
课 后
r sin ϕ = (h − r cos ϕ ) tan θ
由此解出杆的转动方程为
答
解:由题图所示:
m
4-16 图示机构中,杆 AC 以匀速 v 0 沿水平导槽向右运动,通过滑块 A 使杆 OB 绕 O 轴转 动。已知 O 轴与导槽相距 h。试求杆 OB 的角速度 和角加速度。 解: OA 杆转角 ϕ 满足 tan ϕ = 导得
v0 t , 对时间 t 求 h
̇= ϕ
其中
v0 v ̇̇ = − 0 sin 2ϕ ϕ ̇ cos 2 ϕ , ϕ h h
解: 采用直角坐标法,取图示直角坐标系 Oxy, 则 A 点 位置坐标为 x = s + l sin ϕ , y = −l cos ϕ ,即
4-4 如图所示,半径为 R 的圆形凸轮可绕 O 轴转动,带动顶杆 BC 作铅垂直线运动。设 凸轮圆心在 A 点,偏心距 OA = e , ϕ = ωt ,其中 ω 为常量。试求顶杆上 B 点的运动方程、 速度和加速度。 解:以 O 点为原点建立坐标系,由余弦定理可得
v A = v M = ωr = 15π ⋅ 0.2 = 9.42 m s a A = a M = ω 2 r = (15π ) 2 ⋅ 0.2 = 444.15 m s 2
4-13 机构如图所示,假设 AB 杆以匀速 u 运动, 开始时 ϕ = 0 。试求当 ϕ =
π 时,摇杆 OC 的角速度 4
第四章
4-1
点的运动和刚体基本运动
习题解答
图示曲线规尺的杆长 OA = AB = 200 mm, CD = DE = AC = AE = 50 mm。杆 OA
绕 O 轴转动的规律为 ϕ =
π t rad,并且当运动开始时,角 5
ϕ = 0 ,求尺上 D 点的运动方程和轨迹。 解: 已知 ϕ = 0.2π t ,故点 D 的运动方程为 xD = 200 cos 0.2π t mm yD = 100 sin 0.2π t mm
w.
dy d2 y (1 + y′2 ) 2 ̇= ̇= 式中 ρ = , y = ex , ̇ y = ex 2 ′ ′ y dx dx ̇ = 1, ̇ ̇ 当 y = 1 时, x = 0 , y y =1
co
3
m
v2 dv , ; at = an = =0 dt ρ
和角加速度。 解:
vt , 对时间 t 求导得 l v v ̇ = cos 2 ϕ , ϕ ̇̇ = − sin 2ϕϕ ̇ ϕ l l π 将 ϕ = 代入得 4 v v2 ω= , α =− 2 . 2l 2l 负号表示 α 与 ϕ 方向相反。
以匀速 v 0 滑动。 设运动开始时, 杆在水平位置, 滑块在 O 点, 试求滑块的轨迹 (以极坐标表示) 。 解: 以 O 为极点,水平方向为极轴,点 M 的运动方程为
ρ = v0 t , ϕ = ω 0 t
消去时间 t,得到滑块以极坐标表示的轨迹方程为
答
课 后
ρ=
案
v0 ϕ. ω0 π t 3 π t 3
案
2 2 a n = −36 m s 2 , a y = a n = 36 m s 2 2 2 ω 4-11 如图所示,曲柄 CB 以等角速度 0 绕 C 轴转动,其 转动方程为 ϕ = ω 0 t 。 通过滑块 B 带动摇杆 OA 转动。 设 OC = h ,
网
θ = arctan
r sin ω 0 t h − r cos ω 0 t
网
ww w.
3
kh da
题 4-8 图
aϕ =
1 d 2 dϕ (ρ ) = −4 ⋅ OA ⋅ sin (10t ) . ρ dt dt
4-9 点在平面上运动,其轨迹的参数方程为
x = 2sin
(m )
y = 4 + 4sin
设 t = 0 时, s = 0 ;坐标 s 的起点和 t = 0 时点的位置一致,s 的正方向相当于 x 增大的方向。 试求轨迹的直角坐标方程 y = f ( x) 、点沿轨迹运动的方程 s = g (t ) 、点的速度和切向加速度 与时间的函数关系。 解:由运动方程消去 t,得轨迹方程: (−2 < x < 2) y = 2x + 4 ,
w.
(m ) ,
d2ρ dϕ − ρ ( ) 2 = −400 ⋅ OA ⋅ cos(10t ) , 2 dt dt
co
m
t = 0 时,由 ds = dx 2 + dy 2 = s = 4.472 sin π t; 3
π πt ⋅ 20 ⋅ cos dt ,积分得点的运动方程 3 3
点的速度和加速度在轨迹切线上的投影为:
题 4-16 图 ,
带动穿过小环的摆杆 OB 绕 O 轴转动。 4-17 小环 A 沿半径为 R 的固定圆环以匀速 v0 运动, 试求 OB 的角速度和角加速度。若 OB = l ,试求 B 点的速度 和加速度。 解: 设角 ADC 为 θ ,由题义知
的角速度为
̇= ω =ϕ
课 后
角加速度 α = 0 以 O 为原点取直角坐标系,B 坐标为
的规律转动( ϕ 以 rad 计) 。试求滑块 A 的速度和加速度。 解: 如右图所示。以 B 为极点和 BO 为极轴建立极坐标系,则 A 点的运动方程为
ρ = 2 ⋅ OA ⋅ cos(10t ) , ϕ = 10t .
A 点的速度为
vρ =
dρ dϕ = −20 ⋅ OA ⋅ sin (10t ) , vϕ = ρ = 20 ⋅ OA ⋅ cos(10t ) , dt dt
kh da ww w.
