大学物理静电场的高斯定理
大学物理常用公式(电场磁场 热力学)

第四章 电 场一、常见带电体的场强、电势分布2)均匀带电球面(球面半径 )的电场:3)无限长均匀带电直线(电荷线密度为): E = ,方向:垂直于带电直线。
2r( rR ) 4)无限长均匀带电圆柱面(电荷线密度为):E =2r (rR )5)无限大均匀带电平面(电荷面密度为)的电场: E =/20 ,方向:垂直于平面。
二、静电场定理 1、高斯定理:e = ÑE v dS v = q 静电场是有源场。
Sq 指高斯面内所包含电量的代数和;E 指高斯面上各处的电场强度,由高斯面内外的全 部电荷产生; Ñ E vdS v 指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理: Ñ E v dl v =0 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统: E v = E v i ;连续电荷系统: E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统:U =U i ;连续电荷系统: U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力: F = qE电势差: U ab =U a -U b = b EdraE =1 qU =q4r 24r1)点电荷:E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能:W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -(W b -W a )六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为 0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E v ⊥表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
大学物理 高斯定理
第8章 静电场和稳恒电场
17
8-2 电通量 高斯定理
例8.6 均匀带电球面的电场强度 一半径为 R , 均匀带电 q 的球 求球面内外任意点的电场强度. 面 . 求球面内外任意点的电场强度
r
+ + 1+ + + +
S
O
v v ∫ E ⋅ dS = 0
S1
解(1) 0 < r < R )
r
R
+ + +
1 q d Φ e = E cos 0d S = dS 2 4π ε 0 r
qd S Φe = dΦe = ∫S ∫ S 4πε 0 r 2
=
=
r
+
v dS
q
4 πε 0r q
2
∫
S
dS
ε0
Φ e 与r无关
第8章 静电场和稳恒电场
12
8-2 电通量 高斯定理
点电荷在任意闭合曲面内 点电荷在任意闭合曲面内
+ q 发出的 q / ε 0
条电力线不会中断, 条电力线不会中断,仍全 部穿出封闭曲面 S ,即:
+
Φe =
q
ε0
点电荷位于球面中心
Φe =
q
ε0
第8章 静电场和稳恒电场
13
8-2 电通量 高斯定理
点电荷在闭合曲面之外 点电荷在闭合曲面之外
r v d Φ1 = E 1 ⋅ d S 1 > 0 v v d Φ2 = E 2 ⋅ d S 2 < 0
6
8-2 电通量 高斯定理
带电平行板电容器的电力线 + + + + + + + + + + + +
大学物理高斯定理
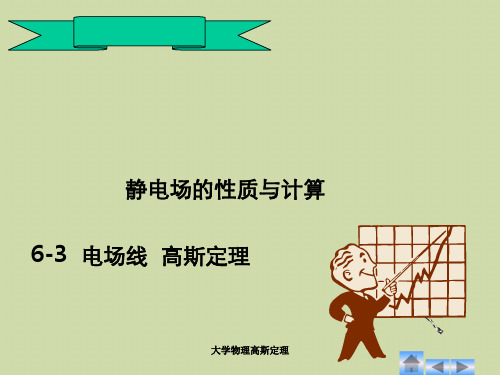
球对称分布:包括 均匀带电的球面, 球体和多层同心球 壳等
轴对称分布:包 括无限长均匀带 电的直线,圆柱 面大,学物圆理高柱斯壳定理等;
无限大平面电荷: 包括无限大的均 匀带电平面,平 板等。
步骤:
1.进行对称性分析,即由电荷分布的对称性,分 析场强分布的对称性,判断能否用高斯定理来求 电场强度的分布(常见的对称性有球对称性、轴 对称性、面对称性等); 2.根据场强分布的特点,作适当的高斯面,要求:
静电场的性质与计算 6-3 电场线 高斯定理
大学物理高斯定理
6-3 电场线 高斯定理
一、电场线
1、定义
在电场中画一组带箭头的曲线,
这些曲线与电场强度 E 之间具有
E
以下关系:
①电场线上任一点的切线方向给出了该点电场 强度的方向;
②某点处电场线密度与该点电场强度的大小相 等。
大学物理高斯定理
电场线密度:经过电场中任一点, 作一面积元dS,并使它与该点的 场强垂直,若通过dS面的电场线 条数为dN,则电场线密度
大学物理高斯定理
高斯定理的应用
例1. 求球面半径为R,带电为q的均匀带电球面的电场的
空间分布。
解: 电场分布也应有球对称性,方向沿径向。
作同心且半径为r的高斯面.
S E dS
E 4r2
q
0
q
E 40 r 2
+ +
+ +
+
R
+
r
+q + +
+
rR时,高斯面无电荷,
E=0
+
+
+++ +
大学物理电磁学知识点总结

大学物理电磁学知识点总结篇一:大学物理电磁学知识点总结大学物理电磁学总结一、三大定律库仑定律:在真空中,两个静止的点电荷q1和q2之间的静电相互作用力与这两个点电荷所带电荷量的乘积成正比,与它们之间距离的平方成反比,作用力的方向沿着两个点电荷的连线,同号电荷相斥,异号电荷相吸。
uuurqqurF21=k122errurur高斯定理:a)静电场:Φe=EdS=∫s∑qiiε0(真空中)b)稳恒磁场:Φm=uurrBdS=0∫s环路定理:a)静电场的环路定理:b)安培环路定理:二、对比总结电与磁∫LurrLEdl=0∫urrBdl=0∑Ii(真空中)L电磁学静电场稳恒磁场稳恒磁场电场强度:E磁感应强度:B定义:B=ururF定义:E=(N/C)q0基本计算方法:1、点电荷电场强度:E=urrurdF(dF=Idl×B)(T)Idlsinθ方向:沿该点处静止小磁针的N极指向。
基本计算方法:urqurer4πε0r21ruruIdl×er0r1、毕奥-萨伐尔定律:dB=24πr2、连续分布的电流元的磁场强度:2、电场强度叠加原理:urnur1E=∑Ei=4πε0i=1rqiuueri∑r2i=1inrururur0Idl×erB=∫dB=∫4πr23、安培环路定理(后面介绍)4、通过磁通量解得(后面介绍) 3、连续分布电荷的电场强度:urρdVurE=∫ev4πεr2r0urdSururλdlurE=∫er,E=∫es4πεr2l4πεr2r004、高斯定理(后面介绍)5、通过电势解得(后面介绍)几种常见的带电体的电场强度公式:几种常见的磁感应强度公式:1、无限长直载流导线外:B=2、圆电流圆心处:电流轴线上:B=ur1、点电荷:E=qurer4πε0r210I2R0I2πr2、均匀带电圆环轴线上一点:urE=B=3、圆rqxi22324πε0(R+x)R2IN2(x2+R2)3210α23、均匀带电无限大平面:E=2ε0(N为线圈匝数)4、无限大均匀载流平面:B=4、均匀带电球壳:E=0(r<R)(α是流过单位宽度的电流)urE=qurer(r>R)4πε0r25、无限长密绕直螺线管内部:B=0nI(n是单位长度上的线圈匝数)6、一段载流圆弧线在圆心处:B=(是弧度角,以弧度为单位)7、圆盘圆心处:B=rurqr(rR)20I4πR0ωR2(是圆盘电荷面密度,ω圆盘转动的角速度)6、无限长直导线:E=λ2πε0xλ0(r>R)2πε0r7、无限长直圆柱体:E=E=λr(r<R)4πε0R2电场强度通量:N·m2·c-1)(磁通量:wb)(sΦe=∫dΦe=∫EcosθdS=∫ssururEdS通量uurrΦm=∫dΦm=∫BdS=∫BcosθdSsss若为闭合曲面:Φe=∫sururEdS若为闭合曲面:uurrΦm=BdS=BcosθdS∫∫ss均匀电场通过闭合曲面的通量为零。
大学物理常用公式(电场磁场-热力学)
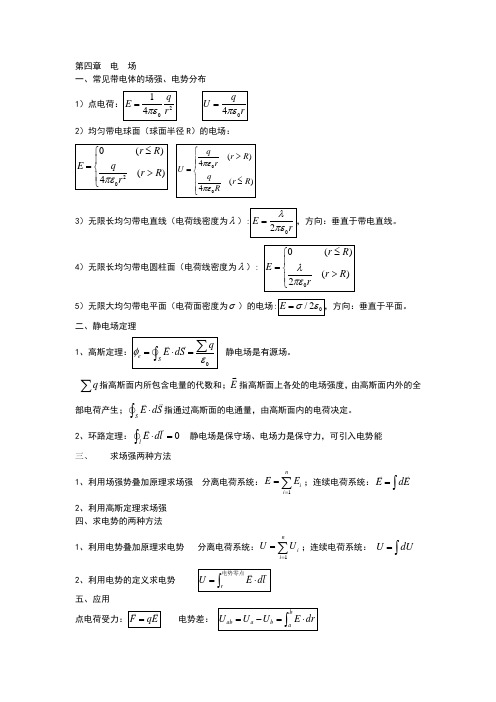
第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04q U rπε=2)均匀带电球面(球面半径R )的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。
4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。
二、静电场定理 1、高斯定理:0e Sq E dS φε=⋅=∑⎰静电场是有源场。
q ∑指高斯面内所包含电量的代数和;E指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;SE dS ⋅⎰指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理:0lE dl⋅=⎰ 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1ni i E E ==∑;连续电荷系统:E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力:F qE = 电势差: bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E ⊥表表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
2)导体腔内无电荷: 电荷都分布在导体外表面,空腔内表面无电荷。
3)导体腔内有电荷+q ,导体电量为Q :静电平衡时,腔内表面有感应电荷-q ,外表面有电荷Q +q 。
大学物理 静电场总结

5. 电势定义:
a
Wpa q0
ur r E dl
a
静电场力作的功与电势差、电势能之间的关系:
b ur r
Aab qE dl q(a b ) (Wpb Wpa ) a
6. 电势分布的典型结论
1) 点电荷: q 4 0r
2) 均匀带电圆环轴线上:
4 0
q R2 x2
3) 均匀带电球面的电势分布:
1)平行板电容器 C 0S
d
2) 电容器的串并联:
串联 1 1 1 1
C C1 C2
Cn
并联 C C1 C2 Cn
4. 电场能量
电容器的静电能: W Q2
2C
电场能量密度:
w
1 2
0E2
各向同性的电介质:
电介质 电位移
D ε0E P
D ε0εr E εE
Gauss定理
2. 静电平衡时导体上的电荷分布 1) 实心导体: 电荷只分布在表面,导体内部没有净电荷.
2) 空腔导体: • 腔内无电荷 电荷分布在外表面,内表面无电荷. •:腔内有电荷: 腔体内表面所带的电量和腔内带电体所带 的电量等量异号。 • 接地空腔导体 外表面不带电, 静电屏蔽 :
3. 电容 C Q
q
4
q
0R
L L rR L L rR
40r
4) 无限长均匀带电直线: ln rB 20 r
(B 0)
7. 电势的计算 叠加法 定义法
第6章 静电场中的导体与电介质
1. 导体的静电平衡条件:
电场描述: ⑴ 导体内部任意一点的场强为零。 ⑵ 导体表面处的场强方向与该处表面垂直.
电势描述: 导体是一等势体,表面是一等势面.
大学物理常用公式

第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04qU rπε=2)均匀带电球面(球面半径R)的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。
4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。
二、静电场定理 1、高斯定理:0e SqE dS φε=⋅=∑⎰v v Ñ 静电场就是有源场。
q ∑指高斯面内所包含电量的代数与;E ϖ指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;S E dS ⋅⎰v v Ñ指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理:0lE dl ⋅=⎰vv Ñ 静电场就是保守场、电场力就是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1n i i E E ==∑v v ;连续电荷系统:E dE =⎰v v2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰v v 电势零点五、应用点电荷受力:F qE =v v 电势差: bab a b aU U U E dr =-=⋅⎰a 点电势能由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体就是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E ⊥v表表面。
导体表面就是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
2.大学物理-高斯定理

曲面上各点处电场强度: 曲面上各点处电场强度:
E = E1 + E2 + + En
S
所有电荷的贡献. 包括 S 内,S 外,所有电荷的贡献. 穿过 S 的电通量: 的电通量:
φe = ∫ E dS = ∫ E1 dS + ∫ E2 dS + + ∫ En dS
s
= φe1 + φe 2 + + φen =
r
ρ 均匀 r′ R oρ ρ 非均匀
S
dV = 4πr dr
2
r ≥ R: r ≤ R:
∑ q内 = ∫ ρ( r ) dV = q
0
R
∑ q内 = ∫ ρ( r ) dV = qr
0
r
ρ 均匀 ≠ ρ V ρ 非均匀 = ρ V ρ 均匀
= ρ V
≠ ρ Vr ρ 非均匀
r
[例二] 例二]
n = en
(各面元一致) 各面元一致)
开放面:双向,任指定一向为正. 开放面:双向,任指定一向为正. 封闭面:单向,已规定向外为正. 封闭面:单向,已规定向外为正. 向外为正
2.概念 流量为例 2.概念 以流量为例 面元的流量 (1)通过面元的流量: )通过面元的流量:
vdt
hθ
dS⊥ dS vn
λr E= 2πε0 R2
R
λL 2
讨论: 讨论:
1. 无限长均匀带电柱面的电场分布 对称性分析: 对称性分析:视 为无限长均匀带 电直线的集合; 电直线的集合; 选高斯面; 选高斯面;同轴 圆柱面
R
λ
o o
r
r
P
dE
由高斯定理计算
大学物理静电场的高斯定理
§4.2 静电场的高斯定理
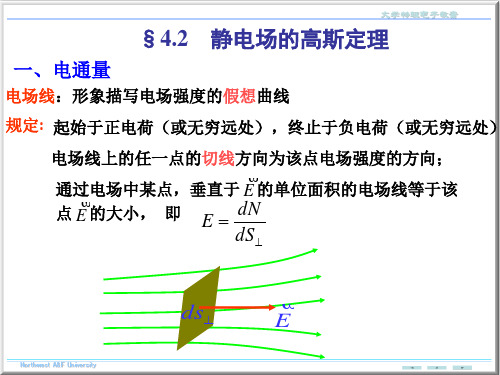
一、电通量
电场线:形象描写电场强度的假想曲线
规定: 起始于正电荷(或无穷远处),终止于负电荷(或无穷远处) 电场线上的任一点的切线方向为该点电场强度的方向; 通过电场中某点,垂直于 E 的单位面积的电场线等于该 点 E 的大小, 即 E dN
E dS
右底
E dS
0 ES ES 2ES
2 ES S 根据高斯定理有 1
0
E 2 0
E
n
n
E n
思考:两块带电等量异号电荷的“ 无限大 ”平
行平面的电场强度如何计算?
例 均匀带电球面,总电量为Q,半径为R
求 电场强度分布 +R +
E r 3 0
E r 3 0
+ +
r'
+ + R
dS
ds
E
电场线 电场线的特点: • 起始于正电荷,终止于负电荷(或
从正电荷起伸向无穷远处,或来自 无穷远到负电荷止)
• 反映电场强度的分布
场强方向沿电场线切线方向,
场强大小取决于电场线的疏密
dN E dS
dN
dSE
• 静电场的电场线不会形成闭合曲线 • 任何两条电场线不会在没有电荷的地方相交
0
ds
R
2.由于电力线在空间不能中断,当以 任意一闭合曲面包含点电荷,则通过 q 此闭合曲面的电通量仍为
大学物理Ⅱ 高斯定理
P
l
e
E dS S
E dS
侧 E dS 上底 E dS 下底 E dS
侧 EdS E 侧 dS E 2r l
根据高斯定理得 E 2r l 1 l 0
E 2 0 r
用高斯定理求场强小结:
1 . 对称性分析
电荷分布对称性→场强分布对称性
点电荷 球对称性 均匀带电球面
均匀带电球壳
球体
轴对称性 柱对称
无限带电直线
无限带电圆柱 无限圆柱面 无限同轴圆柱面
无限大平面 面对称性 无限大平板
若干无限大平面
2. 高斯面的选择
①高斯面必须通过所求的场强的点。
②高斯面上各点场强大小处处相等,方向处处与该 面元线平行;或者使一部分高斯面的法线与场强方 向垂直;或者使一部分场强为零。
+ q+ +
+
0
R
r
高斯定理的应用
例2 均匀带电球体的电场。球半径为R,带电为q。
解:电场分布也应有球对称性,方向沿径向。
作同心且半径为r的高斯面
1)r R时 ,
E ds E ds
E 4r2
s
s
r
q
0
4 r3
3
0
q
4 R3
4 r3330E qr4 0R3
R
高斯面
高斯定理的应用
Φe前 Φe后 Φe下
s
E
dS
0
y
P
N
en
o
zM
en
E
en
Q
Rx
Φe左
s左
E
dS
ES左
cosπ
ES左
Φe右 s右E dS ES右 cos ES左
大学物理之高斯定理

的代数和除以 0,而与闭合曲面(高斯面)外的
电荷无关。
•
其数学表达式为 e
s
E dS
1
0
qi
• 注意: E是高斯面上任一点的电场强度,该E与所 有产生电场的场源有关。
2、高斯定理的验证---以点电荷为例
• 已知 E q ------q为场源点电荷的带电量
S
S/
E
e E S
e ES cos
• 非匀强电场中(曲面)的电通量求法
E
de E dS
S
e
E dS
S
• 电场中的任意闭合曲面S、非均匀电场强度E的通量:
e E cosdS
SE dS
2、有关电通量的注意点
场源电荷为点电荷系或电荷连续分布的带电体qjs?dsie?e??niiee1??????jjiieee???s内s外???ssdee??sdeesjjii????????????????????sjjsiisesedd??????????????ijsjsisese????dd00??iiq0?内q结论?在真空静电场中穿过任一闭合曲面的电场强度通量等于该曲面所包围的所有电荷的代数和除以而与闭合曲面高斯面外的电荷无关
• 2、(静电场中)电场线不是闭合曲线,在静电场中,电场线起 始于正电荷(或无穷远处),终止于负电荷(或无穷远处),不 形成闭合曲线。
• 3、电场线的每一点的切线方向都跟该点的场强方向一致。 • 4、电场线的疏密与电场强弱的关系:电场线的疏密程度与场强
大小有关,电场线密处电场强,电场线疏处电场弱。 • 5、电场线在空间不相交、不相切、不闭合。
《大学物理》高斯定理知识点

(2)库仑定律只适用于静电场,高斯定理不 但适用于静电场, 对变化电场也是适用的。
第六章 静电场
6 - 2 高斯定理
四 高斯定理应用举例
面内例部1和外设部有任一意半点径的为电R场, 均强匀度带E 电。为Q
分析:
的球面。求球
E
解: r R q 0
R S1 Q
E d S E 4 r2 0 S E 0 (r R)
第六章 静电场
6 - 2 高斯定理
高斯定理的应用
能用高斯定理求解的静电场必须具有一定的对称性。 其步骤为
对称性分析:轴对称、面对称、球对称。
根据对称性选择合适的高斯面:
·高斯面上所有点的场强都相等;
·高斯面上的部分面上各点的场强都相等,另一 些面上场强与该面的法线相垂直;
应用高斯定理计算:
一般高斯面会分为几部分,要分别计算出各面上 的电通量;求出高斯面内包围的净电荷量;计算待求 电场强度。
拓展:若为一半径为R的均匀带电球体,所带电荷量为Q。 则其球内外的电场如何分布?
第六章 静电场
6 - 2 高斯定理
例2 设有一无限大的均匀带电平面,单位面积上所
带的电荷即电荷面密度为 。求距离该平面为 r 处某点
的电场强度。
分析:
E
E E
E
S
解:根据高斯定理
2ES S 0
第六章 静电场
E
e E cos dS E cos dS E cos dS
S
底面1
底面2
E cos dS 0 0 E 2 rl 2 Rl
侧面
0
l
所以场强:E R
令圆柱面每单位长度的电0r量为λ,则有λ =σ2πR・1。
则: 2R
大学物理作业2.高斯定理

《大学物理》作业 No .2 静电场中的高斯定理班级 ___________ 学号 ___________ 姓名 ___________ 成绩 ________ 说明:字母为黑体者表示矢量内容提要1.电通量⎰⋅=Φs d S E 电场强度穿过任意曲面的电通量在数值上等于穿过该面的电场线条数;对于封闭曲面,电场线穿出规定电通量为正。
2.真空中高斯定理∑⎰=⋅内q d s 01εS E(1).高斯定理表明穿过封闭曲面的电通量仅与面内电荷有关,面外电荷分布对该通量无贡献;(2).空间任意一点(包括高斯面上各点)的电场由高斯面内外所有场源电荷共同决定;(3).高斯定理是静电学的一条重要基本定理,反映了静电场的有源性,同时该定理又是从库仑定律导出的,反映了库仑平方反比律的正确性;(4).运用高斯定理可以方便地求解具有某些对称性分布的电场,根据电场的对称性分布特点,选取恰当的高斯面,从而简化积分,求出电场。
基本要求1.理解电通量概念,掌握电通量计算2.理解并掌握真空中高斯定理3.会用高斯定理计算几种典型对称电荷分布的电场一、 选择题1. 将一个点电荷(忽略重力)无初速地放入静电场中,关于电荷的运动情况,正确的是:[ ] (A )电荷一定顺着电场线加速运动;(B )电荷一定逆着电场线加速运动;(C )到底是顺着还是逆着电场线运动,由电荷的正负决定;(D )以上说法均不正确。
2.关于电场线,以下说法正确的是[ ] (A) 电场线上各点的电场强度大小相等;(B) 电场线是一条曲线,曲线上的每一点的切线方向都与该点的电场强度方向平行;(C) 电场线是电场空间实际存在的系列曲线;(D) 在无电荷的电场空间,电场线可以相交.3.如图2.1,一半球面的底面圆所在的平面与均强电场E 的夹角为30° ,球面的半径为R ,球面的法线向外,则通过此半球面的电通量为 [ ] (A) π R 2E/2 . (B) -π R 2E/2.(C) π R 2E .(D) -π R 2E .4.关于高斯定理的理解有下面几种说法,其中正确的是[ ] (A) 如高斯面上E 处处为零,则该面内必无电荷;(B) 如高斯面内无电荷,则高斯面上E 处处为零;(C) 如高斯面上E 处处不为零,则高斯面内必有电荷;(D) 如高斯面内有净电荷,则通过高斯面的电通量必不为零;(E) 高斯定理仅适用于具有高度对称的电场5. 两个同心均匀带电球面,半径分别为a R 和b R (b a R R <) , 所带电量分别为a Q 和b Q ,设某点与球心相距r , 当b a R r R <<时, 该点的电场强度的大小为:[ ] (A) 2b a 041r Q Q +⋅πε (B) 2b a 041r Q Q -⋅πε (C))(412bb 2a 0R Q r Q +⋅πε (D) 2a 041r Q ⋅πε 6. 如图2.2所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电,轴线方向单位长度上的带电量分别为1λ 和2λ, 则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小 [ ] (A) r0212πελλ+ (B) 20210122R R πελπελ+ (C) 1014R πελ (D) 0 二、 填空题1.将一电量为q 的点电荷置于一正方体盒子的中心,则穿过盒子六个面的电通量是多少 ,如果将点电荷置于盒子的一个顶点处,穿过盒子各个面的电通量又是多少 .2.如图2.3所示,真空中两个正点电荷,带电量都为Q ,相距2R ,若以其中一点电荷所在处O 点为中心,以R 为半径作高斯球面S ,则通过该球面的电场强度通量Φ= ;若以r 0表示高斯面外法线方向的单位矢量,则高斯面上a 、b 两点的电场强度的矢量式分别为 , .三、计算题 1. 一半径为R 的带电球体,其电荷体密度分布为⎩⎨⎧><=)(0)(R r R r Ar ρ , 其中A 为一常数,试求球体内、外的场强分布。
大学物理静电场的高斯定理

高斯定理的数学表达形式简洁明了,是解决静电场问题的重要
03
工具。
高斯定理在物理中的重要性
高斯定理在物理学中具有广泛 的应用,不仅限于静电场。
它可用于分析恒定磁场、时 变电磁场以及相对论性电磁
场中的问题。
高斯定理是电磁学理论体系中 的重要基石,对于深入理解电 磁场的本质和规律具有不可替
代的作用。
THANKS FOR WATCHING
高斯定理的重要性
总结词
高斯定理是静电场理论中的基本定理之一,它揭示了电场与电荷之间的内在联 系。
详细描述
高斯定理的重要性在于它提供了一种计算电场分布的方法,特别是对于电荷分 布未知的情况。同时,它也揭示了电场线总是从正电荷出发,终止于负电荷, 或者穿过不带电的区域。
高斯定理的历史背景
总结词
高斯定理的发现和证明经历了漫长而曲折的历史过程。
VS
按空间位置分类
静电场可分为点电荷产生的电场、线电荷 产生的电场、面电荷产生的电场等类型。 这些不同类型的电场具有不同的分布规律 和性质。
05
高斯定理的推导过程
利用高斯定理推导电场强度与电通量的关系
总结词
通过高斯定理,我们可以推导出电场强度与 电通量之间的关系,即电场线穿过任意闭合 曲面的电通量等于该闭合曲面所包围的电荷 量与真空电容率的乘积。
静电场的电场强度与电势具有相对独立性
电场强度与电势之间没有直接关系,改变电场中某点的电势,不会影响该点的电场强度。
静电场的分类
按产生方式分类
静电场可分为感应起电和接触起电两种 方式。感应起电是由于带电体在接近导 体时,导体内部电荷重新分布而产生电 场;接触起电是两个不同物体相互接触 时,由于电子的转移而产生电场。
大学物理-高斯定理
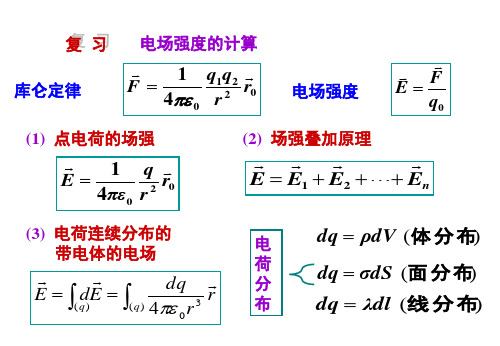
电场强度的计算
F
1
4 0
q1q2 r2
r0
电场强度
E
F
q0
(1) 点电荷的场强
E
1 4πε0
q r2
r0
(2) 场强叠加原理
E E1 E2 En
(3) 电荷连续分布的 带电体的电场
电 荷
E dE
dq
r
(q)
(q) 4 0r 3
分 布
dq ρdV (体 分 布) dq σdS (面 分 布) dq λdl (线 分 布)
q2 A P*
s
q2 B
q1
在点电荷 和q 的q静电场中,做如下的三个闭合面
求通过各闭合S面1 ,的S电2 ,通S量3。,
Φe1
E dS
q
S1
0
Φe2 0
Φe3
q
0
q
q
S1
S2
S3
例:一点电荷位于边长为 a 的立方体的顶角上, 求:通过该立方体表面总的电通量。
解: 顶角所在的三个面上的通量为零。 其余三个面上直接计算困难
(3) 天文学和大地测量学中:如小行星轨道的计算,地球大 小和形状的理论研究等。统计 理论和误差理论,发明了最小二乘法,引入高斯误差曲线。
(5) 高斯还创立了电磁量的绝对单位制。
一、电通量 1、电场线 ( Electric Field Line ) (电场的几何描述)
E
n
dS
E
S E cos dS
Φe
E dS
S
为通过 S 面的电通量。
dS 有两个法线方向,dφ 可正可负。
S为封闭曲面
规定:闭合面上各面元的外法
6.2静电场的高斯定理

三、高斯定理
在真空中, 在真空中,通过任一闭合曲面的电通量等于 该曲面所包围的所有电荷的代数和的1/ 该曲面所包围的所有电荷的代数和的1/εo倍。
φe = ∫ E⋅ dS = S
1
ε0
∑q
i
i
验证高斯定理: 验证高斯定理:
1、点电荷在球形高斯面的圆心处 球面上场强: 球面上场强: E =
E
dS
+ +
q 4 0R πε
2
dΦe = E⋅ dS = EdS =
Φe = ∫ q 4 0R πε
2
q 4 0R πε
q
2
dS
q
0
S
dS =
4 0R πε
2 S
∫dS = ε
2、点电荷在任意形状的高斯面内
Φe = ∫ E⋅ dS = ∫ E⋅ dS =
S S'
q
ε0
S
S’
+
3、点电荷在闭合曲面以外
Φ = ∫ E⋅ dS =0 e
R
dE
x
P
解:利用细圆环解得结果
dE=
4 0 x +r πε
2
(
xdq
2 3/ 2
)
dr r
R
dq =σ2 rdr π
dE = 4 0 ( x +r πε
2
R 0
dE
x
P
x⋅σ 2 rdr π
2 32
)
E =∫ dE = ∫
σ x = 1 − 2 32 2 2 2 0 (x + R2)1 2 ε 4 0 ( x +r ) πε
S
+ +
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
过P点作高斯面
eSE dS
P
侧 E d S 上 E 底 d S 下 E 底 d S
侧 E d S E 侧 d S E 2 r l
根据高斯定理得
r
l n E n
E2rl 1l 0
E 2 0 r
例题2 已知“无限大”均匀带电平面上电荷面密度为
求 电场强度分布
解 电场强度分布具有面对称性
§4.2 静电场的高斯定理
一、电通量
电场线:形象描写电场强度的假想曲线
规定: 起始于正电荷(或无穷远处),终止于负电荷(或无穷远处)
电场线上的任一点的切线方向为该点电场强度的方向;
通点过E电的场大中小某,点即,垂E直于dEN的单位面积的电场线等于该 dS
ds
E
电场线
电场线的特点:
• 起始于正电荷,终止于负电荷(或
(3) 通过闭合曲面的电通量
e de S E d S
穿出、穿入闭合面电力线条数之差
dS2 E
二、静电场的高斯定理
高斯定理的推导
1.点电荷q处在任一球面的球心,则通过此球面的电通量为
eE ds 4 q 0R 2d sq 0
q
则穿过球面的电力线条数为 0
ds
2.由于电力线在空间不能中断,当以
q1 q2 q3
高斯定理
e SE dS10q内
(不连续分布的源电荷)
Φe SE dSV10dV
(连续分布的源电荷)
E
是高斯面内外所有电荷产生的;
e
只与内部电荷有关。
真空中的任何静电场中,穿过任一闭合曲面的电通量,
等于该曲面所包围的电荷电量的代数和乘以
1 0
讨论 静电场的高斯定理适用于一切对称分布的静电场;反映电场 是有源场;
从正电荷起伸向无穷远处,或来自
无穷远到负电荷止)
• 反映电场强度的分布
场强方向沿电场线切线方向,
场强大小取决于电场线的疏密
E dN
•
dS
静电场的电场线不会形成闭合曲线
• 任何两条电场线不会在没有电荷的地方相交
dN
d
S
E
电通量 穿过任意曲面的电场线
条数称为电通量。 Φ e
1.均匀场中dS 面元的电通量
求 电场强度分布
解 对球面外一点P:
取过场点P的同心球面为高斯面
EdS
EdS E dS E4r2
s
s
s
根据高斯定理
qi
E4r2 i
0
rR qi Q
i
qi
E
i
4 0r 2
Q
E 4 0r 2
P
+
+ R r+
++
Q+
对球面内一点:
rR qi 0
i
EdS E4r2 0 s
E0
例 已知球体半径为R,带电量为q
(电荷体密度为)
求 均匀带电球体的电场强度分布
解 球外 rR
E
1
40
q r2
r0
3 0
R3 r2
r0
球内 rR
SEdSE4r210
4r31q'
3
0
E r 3 0
E
r
3 0
r
++ R
++
r'
++ R
++
任意一闭合曲面包含点电荷,则通过
此闭合曲面的电通量仍为 q 0
q
R•
3. q在闭合曲面外,由于穿入和穿出的电力线条数相等,
则
e 0
4. 任意闭合曲面内外有多个点电荷
任 意e闭合E 面d 电S通量为
( E 1 E 2 . .E . 5 )d S
q5
q1 q2 q3
0 0 0
q4
EdS10 q内
dedN EdS
E c o d S s
矢量面元 d S d Sn
deE dS
2.非均匀场中曲面的电通量
ed e SE d S
nEBiblioteka dSdSS
dS E
3. 闭合曲面电通量
e de S E d S
说明
(1) n方向的规定:
(2) 电通量是代数量
dS1
π π
2
0 π
2
d Φ e 1 E d S 1 0穿入为负 d Φ e 2 E d S 2 0穿出为正
选取一个圆柱形高斯面
eSE dS
侧 E d S 左 E d 底 S 右 E d 底 S
0 E E S 2 E S S
n
根据2E高S斯 定1理S有 0
E 2 0
E n
思考:两块带电等量异号电荷的“ 无限大 ”平
行平面的电场强度如何计算?
E n
例 均匀带电球面,总电量为Q,半径为R
E 与电荷量,电荷的分布有关;
E dS 与闭合面内的电量有关,与电荷的分布无关;
S
利用高斯定理求解特殊电荷分布电场的思路:
分析电荷对称性(线.面.体对称);
根据对称性取高斯面;
根据高斯定理求电场强度。
例题1 已知“无限长”均匀带电直线的电荷线密度为
求 直线+r 处一点P 的电场强度
解 电场分布具有轴对称性
