有序聚类算法实现
聚类方法(Clustering)

因此衍生出一系列度量 K 相似性的算法
Q
J
大配对和小配对 Major and minor suits
聚类分析原理介绍
相似性Similar的度量(统计学角度) 距离Q型聚类(主要讨论)
主要用于对样本分类 常用的距离有(只适用于具有间隔尺度变量的聚类):
明考夫斯基距离(包括:绝对距离、欧式距离、切比雪夫距离) 兰氏距离 马氏距离 斜交空间距离 此不详述,有兴趣可参考《应用多元分析》(第二版)王学民
首先要明确聚类的目的,就是要使各个类之间的距离 尽可能远,类中的距离尽可能近,聚类算法可以根据 研究目的确定类的数目,但分类的结果要有令人信服 的解释。
在实际操作中,更多的是凭经验来确定类的数目,测 试不同类数的聚类效果,直到选择较理想的分类。
不稳定的聚类方法
算法的选择没有绝对
当聚类结果被用作描述或探查工具时,可以 对同样的数据尝试多种算法,以发现数据可 能揭示的结果。
该法利用了所有样本的信息,被认为是较好的 系统聚类法
广泛采用的类间距离:
重心法(centroid hierarchical method)
类的重心之间的距离 对异常值不敏感,结果更稳定
广泛采用的类间距离
离差平方和法(ward method)
D2=WM-WK-WL
即
研究目的:挖掘不同人群拨打电话的特征 下面用SAS/Enterprise Miner演示
Q&A
推荐参考书目
《应用多元分析》(第二版)王学民 上海财经大学出版社
《应用多元统计分析》即《Appied Mulhnson, Dean W. Wichern中国统计出版社
数学建模里的聚类分析

聚类分析聚类,或称分集,即所谓“物以类聚”,它是按某种相似规则对给定样本集、指标簇进行某种性质的划分,使之成为不同的类.将数据抽象化为样本矩阵()ij n m X X ⨯=,ij X 表示第i 个样本的第j 个变量的值.聚类目的,就是从数据出发,将样本或变量分成类.其方法大致有如下几个.(1) 聚类法.即谱系聚类法.将n 个样本看成n 类,将性质最接近的两类并为一新类,得1-n 类;再从1-n 类中找出最接近的两类加以合并,得2-n 类;继之,最后所有样本都成一类,得一聚类谱系,从谱系中可确定划分多少类,每类含有哪些样本.(2) 分解法.它是系统聚类的逆过程,将所有样本视为一类,按某种最优准则将它分成两类,继之,每一类都分到只含一个样本为止.(3) 动态聚类.即快速聚类法.将n 个样本粗糙地分成若干类,然后用某种最优准则进行调整,直至不能调整为止.(4) 有序样本聚类.按时间顺序,聚在一类的样本必须是次序相邻的样本.(5) 模糊聚类.它是将模糊数学用于样本聚类.(6) 运筹学聚类.它是将聚类问题化为线性规划、动态规划、整数规划模型的聚类.(7) 神经网络聚类.它是将样本按自组织特征映射的方法进行,也是我们要加以叙述的一个重点.(8) 预测中聚类.它是聚类在预测中的应用,以弥补非稳定信号回归的预测与分析.这里主要介绍谱系聚类法和快速聚类法. 一、距离定义样本矩阵()ij n m X x ⨯=,是m 维空间中n 个点,以距离度量样本之间的贴近度,就是距离聚类方法.最常用的第i 个与第j个样本的Minkowski 距离为p mk p jk ik ijx x d /11)||(∑=-=式中p 为一正整数.当2=p , ij d 就是欧几里德距离;当1=p ,ij d 就是绝对距离,或称“布洛克(cityblock )”距离.而切比雪夫距离为||max 1jk ik mk ij x x d -=≤≤设m m C ⨯是变量的协方差矩阵,i x ,j x 为第i 行与第j 行m 个变量构成的向量,则马哈兰罗比斯距离定义为1()()T ij i j i j d x x C x x -=-- 根据距离的定义,就获得距离矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n d d d d d d d d d d 212222111211 由距离性质可知,d 为实对称矩阵,ij d 越小,两样本就越相似,其中01211====nn d d d ,根据)(j i d ij ≠的n 个点分类,依聚类准则分为不同的类.对d 常用的系统聚类准则有: 1、类间距离定义(1) 最短距离;,min p qpq ij i Gj GD d ∈∈= (2) 最长距离;,maxpqpq ij i G j GD d ∈∈=(3) 质心距离;(,)pq p q D d x x = (4) 平均距离;1p qpq iji G j G p qD d n n ∈∈=∑∑(5) 平方距离:2()()p q T pqp q p q p qn n D x x x x n n =--+2.类间距离的递推公式(1)最短距离:min{,}rk pk qk D D D = (2)最长距离:max{,}rk pk qk D D D = (3)类平均距离:p q rk pk qk rrn n D D D n n =+(4)重心距离:2222pqp q rkpkqkpq r r r rn n n n D D D D n n n n =+-⋅(5)离差平方和距离:2222p k q k krkpk qk pq r kr kr kn n n n n D D D D n n n n n n ++=+-+++二、谱系聚类法例: 假如抽取5个样本,每个样本只测一个指标,即数据为x =[1,0;2,0;4.5,0;6,0;8,0] 试以最短距离准则进行距离聚类说明.解 这时,样本间的绝对距离、欧几里德距离或切比雪夫距离均一致,见表3.1.以最短距离准则聚类.根据定义,当令p Ω与q Ω中分别有pn 与q n 个样本,则最短距离为:},|min{),(q p ij nearj i d q p Ω∈Ω∈=δ于是,对于某步,假定具有样本为p n 的第p 集合与样本为q n 的第q 集合,聚成为具有样本为q p s n n n +=的第s 集合,则第k 集合与第s 集合的最短距离,可写为)},(),,(min{),(q k p k s k near near nearδδδ=(1)表1 绝对距离数据表中数据1、2、4.5、6、8视为二叉树叶子,编号为1、2、3、4、5.当每一个样本看成一类时,则式子(1)变为ij neard j i =),(δ,最小距离为1,即1与2合聚于6号,得表2.表中5.2)5.2,5.3min()}2,3(),1,3(min{)6,3(===δδδnear near near表2 一次合聚表2中最小距离为1.5,即4.5与6合聚于7,得表3.表中(6,7)min{(6,4.5),(6,6)}min(2.5,4) 2.5near nearnearδδδ===.表3 二次合聚表3中最小距离为2,即{4.5,6}元素(为7号)与8(为5号)合聚于8号,得表4.表中5.2)6,4,5.2min()}8,6(),6,6(),5.4,6(min{)8,6(===δδδδnear near near near表4 三次合聚最后集合{1,2}与{4.5,6,8}聚成一集丛.此例的Matlab 程序如下:x =[1,0;2,0;4.5,0;6,0;8,0])();'sin ',();'',(z dendrogram gle y linkage z CityBlock x pdist y ==绘得最短距离聚类谱系如图1所示,由图看出分两类比较合适.1号、2号数据合聚于6号,最小聚距为1;3号、4号数据合聚于7号,最小聚距为1.5;7号于5号数据合聚于8号,最小聚距为2;最后6号和8号合聚,最小聚距为2.5。
kmeans聚类算法的算法流程

K-means聚类算法是一种经典的基于距离的聚类算法,它被广泛应用于数据挖掘、模式识别、图像分割等领域。
K-means算法通过不断迭代更新簇中心来实现数据点的聚类,其算法流程如下:1. 初始化:首先需要确定要将数据分成的簇的个数K,然后随机初始化K个簇中心,可以从数据集中随机选择K个样本作为初始簇中心。
2. 分配数据:对于每个数据点,计算它与各个簇中心的距离,将该数据点分配给距离最近的簇,并更新该数据点所属簇的信息。
3. 更新簇中心:计算每个簇中所有数据点的均值,将该均值作为新的簇中心,更新所有簇中心的位置。
4. 重复迭代:重复步骤2和步骤3,直到簇中心不再发生变化或者达到预定的迭代次数。
5. 输出结果:最终得到K个簇,每个簇包含一组数据点,形成了聚类结果。
K-means算法的优点在于简单易实现,时间复杂度低,适用于大规模数据;但也存在一些缺点,如对初始聚类中心敏感,对噪声和离裙点敏感,需要事先确定聚类个数K等。
K-means聚类算法是一种常用的聚类方法,通过迭代更新簇中心的方式逐步将数据点划分为不同的簇,实现数据的聚类分析。
通过对算法流程的详细了解,可以更好地应用K-means算法解决实际问题。
K-means算法是一种非常经典的聚类算法,它在数据挖掘和机器学习领域有着广泛的应用。
在实际问题中,K-means算法可以帮助我们对数据进行分组和分类,从而更好地理解数据的内在规律,为我们提供更准确的数据分析和预测。
接下来,我们将对K-means聚类算法的一些关键要点进行探讨,包括算法的优化、应用场景、以及与其他聚类算法的比较等方面。
1. 算法的优化:在实际应用中,K-means算法可能会受到初始簇中心的选择和迭代次数的影响,容易收敛到局部最优解。
有一些改进的方法可以用来优化K-means算法,例如K-means++算法通过改进初始簇中心的选择方式,来减少算法收敛到局部最优解的可能性;另外,Batch K-means算法通过批量更新簇中心的方式来加快算法的收敛速度;而Distributed K-means算法则是针对大规模数据集,通过并行计算的方式来提高算法的效率。
有序聚类过程
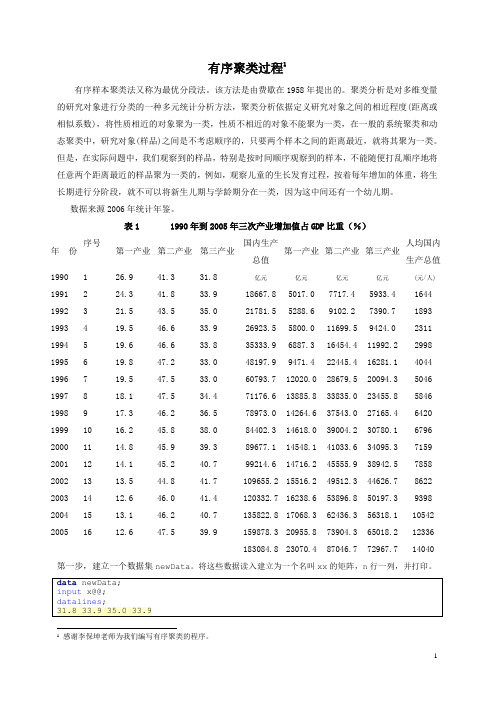
有序聚类过程1有序样本聚类法又称为最优分段法。
该方法是由费歇在1958年提出的。
聚类分析是对多维变量的研究对象进行分类的一种多元统计分析方法,聚类分析依据定义研究对象之间的相近程度(距离或相似系数),将性质相近的对象聚为一类,性质不相近的对象不能聚为一类,在一般的系统聚类和动态聚类中,研究对象(样品)之间是不考虑顺序的,只要两个样本之间的距离最近,就将其聚为一类。
但是,在实际问题中,我们观察到的样品,特别是按时间顺序观察到的样本,不能随便打乱顺序地将任意两个距离最近的样品聚为一类的,例如,观察儿童的生长发育过程,按着每年增加的体重,将生长期进行分阶段,就不可以将新生儿期与学龄期分在一类,因为这中间还有一个幼儿期。
数据来源2006年统计年鉴。
表1 1990年到2005年三次产业增加值占GDP比重(%)年份序号第一产业第二产业第三产业国内生产总值第一产业第二产业第三产业人均国内生产总值1990 1 26.9 41.3 31.8 亿元亿元亿元亿元 (元/人) 1991 2 24.3 41.8 33.9 18667.8 5017.0 7717.4 5933.4 1644 1992 3 21.5 43.5 35.0 21781.5 5288.6 9102.2 7390.7 1893 1993 4 19.5 46.6 33.9 26923.5 5800.0 11699.5 9424.0 2311 1994 5 19.6 46.6 33.8 35333.9 6887.3 16454.4 11992.2 2998 1995 6 19.8 47.2 33.0 48197.9 9471.4 22445.4 16281.1 4044 1996 7 19.5 47.5 33.0 60793.7 12020.0 28679.5 20094.3 5046 1997 8 18.1 47.5 34.4 71176.6 13885.8 33835.0 23455.8 5846 1998 9 17.3 46.2 36.5 78973.0 14264.6 37543.0 27165.4 6420 1999 10 16.2 45.8 38.0 84402.3 14618.0 39004.2 30780.1 6796 2000 11 14.8 45.9 39.3 89677.1 14548.1 41033.6 34095.3 7159 2001 12 14.1 45.2 40.7 99214.6 14716.2 45555.9 38942.5 7858 2002 13 13.5 44.8 41.7 109655.2 15516.2 49512.3 44626.7 8622 2003 14 12.6 46.0 41.4 120332.7 16238.6 53896.8 50197.3 9398 2004 15 13.1 46.2 40.7 135822.8 17068.3 62436.3 56318.1 10542 2005 16 12.6 47.5 39.9 159878.3 20955.8 73904.3 65018.2 12336183084.8 23070.4 87046.7 72967.7 14040 第一步,建立一个数据集newData。
agnes聚类算法 算法实例

agnes聚类算法算法实例
AGNES(Advanced Grouping and Ordering by Evaluation of Scarcity) 聚类算法是一种基于资源分配的聚类算法,常用于图像分割、计算机视觉和信号处理等领域。
下面是 AGNES 聚类算法的算法实例:
1. 数据预处理:对于输入的数据集,需要进行预处理以提高聚类效果。
例如,对于图像数据,可以进行预处理以提高对比度和清晰度,而对于音频数据,可以进行预处理以提高语音清晰度和减少噪声。
2. 定义距离度量:距离度量是聚类算法的核心,AGNES 聚类算法使用欧几里得距离和曼哈顿距离度量数据之间的距离。
3. 初始化聚类中心:对于每个数据点,计算其到所有其他数据点的距离,选择距离最小的数据点作为该聚类的中心点。
4. 生成簇:计算每个数据点到当前簇的中心点的距离,并将每个数据点分配到距离最近的簇中。
重复此步骤,直到所有数据点都被分配到聚类中。
5. 调整簇中心:对于每个簇,计算其中心点,并将其作为新的簇中心。
6. 重复步骤 4 和步骤 5,直到聚类保持不变或无法继续调整为止。
7. 输出聚类结果:输出聚类结果,通常是每个簇的中心点及其包含的数据点数量。
有序样品聚类法

������ ������ − ������������ ′ |(1.2)
������ ������ =1 ������ (������������
, ������������ +1 − 1)(1.3)
当 n,k 固定时,L[b(n , k)]越小表示各类的离差平方和越小,分类是合理的。因此要寻找 一种分法b(n , k),使分类损失函数 L 达最小。记 P(n , k)是使 L 达到极小的分类法。 3. ������[������(������ , ������)]的递推公式 Fisher 算法最核心的部分是利用以下两个递推公式: L[P n , 2 = min2≤������ ≤������ {������ 1, ������ − 1 + ������(������, ������)} (1.4) L[P n , k = min������≤������ ≤������ {������[������ (������ − 1, ������ − 1)] + ������(������, ������)} 以上两个公式由定义即可证明。 第二个公式表明,若要找将 n 个样品分为 k 类的最优分割,应建立在将 j-1 个样品分为 k-1 类的最优分割基础上(这里 j=2,3,· · · ,n) 4. 最优解的求法 若分类数 k(1<k<n)已知,求分类法 P(n , k),使它在损失函数意义下达最小.其求法如下: 首先找分点 jk,使(1.4)达极小,即 L[P(n ,k)= L[P(jk-1 , k-1)] + D(jk, n). 于是得第 k 类 Gk = {jk, jk+1 ,· · · , n}. 然后找 jk-1,使它满足 L[P(jk-1 ,k-1)= L[P(jk-1-1 , k-2)] + D(jk-1, jk-1),得到第 k-1 类 Gk-1 = {jk-1, jk-1+1 ,· · · , jk-1},类似的方法依次可得到所有类 G1,G2,· · · Gk,这就是我们欲 求的最优解,即 P(n , k)={G1,G2,· · · Gk}。 总之,为了求最优解,主要是计算{D(i ,j);1≤i<j≤n}和{L[P(i ,j)];1≤i≤n,i≤j≤n}. 三.应用举例 下面通过一个例子来说明最优解的具体求法。 【例】为了了解儿童的生长发育规律,今统计了男孩从出生到十一岁每年平均增长的重 量如下: 年龄 1 2 3 4 5 6 7 8 9 10 2.3 11 2.1 增加重量 9.3 (kg) 1.8 1.9 1.7 1.5 1.3 1.4 2.0 1.9
基于有序样品聚类最优二分割算法的滑坡演化阶段划分

基于有序样品聚类最优二分割算法的滑坡演化阶段划分黄丽;樊孝菊;罗文强【摘要】利用有序样品聚类的最优二分割算法,对新滩滑坡检测累计位移数据进行有序聚类划分,再结合加速度变化特征对滑坡演化阶段进行划分。
结果显示新滩滑坡初始变形阶段和中等变形阶段划分点为1979年8月,中等变形阶段和加速变形阶段划分点为1982年9月,而加速变形阶段中初等加速与中等加速的分界点为1983年7月,中等加速与临滑阶段的分界点为1984年10月,与实际监测基本吻合。
表明根据有序样品聚类最优二分割算法和滑坡变形加速度变化特征可以对滑坡演化阶段进行准确划分,并为滑坡预警预报提供依据。
%The deformation of landslide from the beginning to the end is divided into three stages, the initial deformation, constant speed deformation and accelerated deformation. The displacement and acceleration of landslide at different stages have different characteristics. The optimal segmentation algorithm of orderly sample cluster is used to divide the stages of Xintan landslide in this paper, August, 1979 is the split point between initial deformation and constant speed deformation, September, 1982 is the split point between constant speed deformation and accelerated deformation, July, 1983 is the split point between initial accelerated deformation and constant accelerated deformation, October 1984 is the split point between constant accelerated deformation and critical sliding stage. The results show that this method can correctly divide the stages of landslide accurately and provide powerful criterion for landslide warning and forecast.【期刊名称】《湖北文理学院学报》【年(卷),期】2015(000)002【总页数】4页(P13-16)【关键词】有序样品聚类;最优二分割算法;滑坡演化阶段划分;新滩滑坡【作者】黄丽;樊孝菊;罗文强【作者单位】湖北文理学院数学与计算机科学学院,湖北襄阳 441053; 中国地质大学武汉数学与物理学院,湖北武汉 430074;湖北文理学院数学与计算机科学学院,湖北襄阳 441053;中国地质大学武汉数学与物理学院,湖北武汉 430074【正文语种】中文【中图分类】P642.22;O212.4目前,滑坡预报的判断方法种类很多,如许强、曾欲平发现加速度的变化表现出与累计位移和变形速率完全不同的特点,依托大量监测数据,对滑坡从开始变形到失稳破坏的全过程进行系统的分析和研究[1];金海元设计出适合锦屏一级水电站边坡的综合预测预报模型,初步给定边坡4项预警临界值(位移速率、位移切线角、地震峰值加速度、降雨量) [2];王尚庆,徐进军,罗勉把滑坡宏观前兆信息与关键部位监测点的变形速率及相关影响因素有机结合和集成的滑坡险情预警综合预报方法[3]等,为滑坡预报提供了可靠地依据,但位移变化是滑坡变形最直接的变化特征,因此滑坡演化阶段划分考虑位移变化是非常有必要的.由于滑坡处于不同阶段对滑坡累积位移有相应的变化,本文以1978年1月到1985年6月新滩滑坡监测数据为例,利用有序聚类最优二分割算法就直接将滑坡累积位移序列进行有序分类,并结合加速度变化特征对滑坡演化阶段进行划分.有序样品聚类分析[4]是对有序的样品进行分段的统计方法,对n个有序样品进行分割,就可能有2n-1种分割方法,这每一种分法成为一种分割,在所有的这些分割中,有一种分割使得各段内部之间差异性最小,各段之间差异性最大,这种对n 个样品分段使组内离差平方和最小的分割方法,称为最优分隔.1.1 一个变量或指标分割的段内差异设有n个样品对某一个变量(或指标)进行测试,记作. 现需对X作分割,记()是分割后的某一个样品段,其段内样品之间的差异用段内极差表示为1.2 有序样品聚类最优二分割算法模型设有n个有序样品数据,将有序样品数据x正则化得到. 其中现对进行二分割,则共有n-1种分法,分别表示为;;…….若用记号Sn(2, j)表示n个样品被分割成2段后段内的总离差和,j表示分割点且j=1,2,…,n-1. 那么上述分割所对应的段内总离差和分别为;;……;……;,其中有d1,1=dn,n=0.若j=a对应的Sn(2,a)在所有分割对应的段内总离差和Sn(2, j)中最小,即则Sn(2,a)为最小损失函数,对应分割为有序样品最优二分割.新滩滑坡位于长江西陵峡上段兵书宝剑峡出口的北岸,隶属湖北省秭归县,下距宜昌市约72km. 滑坡长近2 000m,上、中、下部分别宽250m,400m、500~800m,面积约为0.75×106 m2,总体方量3×107 m3;滑坡后壁至河床相对高度差800m左右,向长江倾斜,放纵平均坡度为23°,局部陡缓不一. 新滩滑坡监测数据来源于文献[11],本文选取其1978年1月到1985年6月共90个月的累计位移监测数据x(mm),根据滑坡变形加速度变化特征利用有序聚类算法进行分类,作新滩滑坡加速度a和滑新滩坡累积位移x的数据如表1、2,观测曲线如图1、2所示.2.1 滑坡初始变形阶段研究资料表明,加速度在不同演化阶段表现出完全不同的变化特点,在初始变形阶段加速度有一个由0增大到一定值后很快降为0甚至为负值的过程,反映出此阶段滑坡变形突然启动后又迅速减弱的特点[10].由图2可以看出新滩滑坡的初始变形与加速变形的分界点大致在1979年7月至10月. 选取1978年1月到1979年12月滑坡累计位移数据正则化得X=[0, 0.0049, 0.0156, 0.0249, 0.0346, 0.0478, 0.0677, 0.0782, 0.0855, 0.0882, 0.0909, 0.1023, 0.1048, 0.1157, 0.1172, 0.1196, 0.1272, 0.1432, 0.1518,0.1817, 0.6923, 0.9371, 0.9976, 1.0000]对1978年1月到1979年12月滑坡累积位移做二分割,得出最优分割点为X20,最小损失函数值与X20对应时间点为1979年8月,根据加速度特点将此时间点定为新滩滑坡初等变形与中等变形的分界点.2.2 滑坡中等变形阶段在滑坡中等变形阶段,加速度在等速变形阶段主要以0为中心作上下震荡,其均值基本为0. 依据此特征,从图2可以看出滑坡等速变形阶段和加速变形阶段的划分点大致在1982年6月至9月. 选取1980年1月到1982年12月36个滑坡累计位移数据正则化得X =[0, 0.0046, 0.0078, 0.0096, 0.0136, 0.0176, 0.0512, 0.0717, 0.0964, 0.1050, 0.1089, 0.1166, 0.1261, 0.1290, 0.1316, 0.1360, 0.1387, 0.1407, 0.1421,0.1464, 0.1500, 0.1548, 0.1576, 0.1584, 0.1618, 0.1649, 0.1678, 0.1815,0.2092, 0.2433, 0.2659, 0.4087, 0.5874, 0.8055, 0.9854, 1.0000]对1980年1月到1982年12月滑坡累积位移做二分割,得出最优分割点为X33,最小损失函数值与X33相应时间点为1982年9月,因此将此时间点定为新滩滑坡中等变形与加速变形阶段的分界点.2.3 滑坡加速变形阶段在加速变形阶段中,滑坡累积位移又可被划分为初等加速变形阶段、中等加速变形阶段及临滑阶段. 分别选取数据段1983年1月到1983年12月,1984年1月到1985年5月,分别对应的最小损失函数值为由此可推出初等加速与中等加速的分界点1983年7月,中等加速与临滑阶段的分界点为1984年10月.综上所述,利用有序样品聚类的最优二分割算法,结合新滩滑坡加速度特征能对滑坡演化阶段进行完整划分(见图3、4). 可以看到,当滑坡从初等变形进入中等变形时,滑坡加速度有一个由0增大到一定值后很快降为0甚至为负值的过程,在相应时间点的滑坡累积位移也有一个较快增长,而随着加速度很快降到零,累积位移增长速度也趋于平缓;当滑坡从中等变形进入加速变形时,滑坡加速度结束以0为中心作上下震荡,呈现一个明显增大过程,在相应时间点的滑坡累积位移也有一个明显增长. 对于滑坡处于初等加速阶段、中等加速阶段、临滑阶段时,其加加速度与滑坡处于初等变形、中等变形、加速变形时的加速度变化特征是类似的. 从图中可以看出有序样品聚类最优分割算法对滑坡演化阶段划分较为准确.滑坡累计位移为有序序列,利用有序样品聚类算法对滑坡累计位移序列进行阶段划分. 根据加速度变化特征,滑坡变形处于某一个变形阶段时,变形加速度处于一个相对稳定的状态,滑坡累计位移也相对稳定;当滑坡从一个阶段进入另一个阶段时,加速度会有一个明显的变化,相应的滑坡累计位移值也会有明显的变化. 因此将使得滑坡累计位移序列段内离差平方和最小(总的离差和一定,段间的平方和最大)的点定为最优分割点具有一定合理性.有序聚类最优分割算法为滑坡预警预报具有一定参考价值. 但滑坡变形时,滑坡速度、加速度都会有相应变化;而降雨、库水位对滑坡变形也有一定影响,联合多判据划分滑坡演化阶段有待研究.[1] 许强, 曾裕平. 具有蠕变特点滑坡的加速度变化特征及临滑预警指标研究[J]. 岩石力学与工程学报, 2009, 28(6): 1099-1106.[2] 金海元, 徐卫亚, 孟永东, 等. 锦屏一级水电站左岸边坡稳定综合预研究[J]. 岩石力学及工程学报, 2008, 27(10): 2058-2063.[3] 王尚庆, 徐进军, 罗勉. 三峡库区白水河滑坡险情预警方法研究[J]. 武汉大学学报: 信息科学版, 2009, 34(10): 1218-1221.[4] 向东进, 李宏伟, 刘小雅. 实用多元统计分析[M]. 武汉: 中国地质大学出版社, 2005.[5] 许强, 黄润秋, 李秀珍. 滑坡时间预测预报研究进展[J]. 地球科学进展, 2004, 19(3): 478-483.[6] 刘小珊, 罗文强, 李飞翱, 等. 基于SVR的滑坡位移研究[J]. 长江大学学报: 自科版, 2013, 10(4): 76-78.[7] 杜鹃, 殷坤龙, 柴波. 基于诱发因素响应分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报, 2009, 28(9): 1783-1789.[8] 刘小珊, 罗文强, 李飞翱, 等. 基于关联规则的滑坡演化阶段判识指标[J]. 地质科技情报, 2014, 33(2): 160-164.[9] 李聪, 姜清辉, 周创兵, 等. 基于实例推理系统的滑坡预警判据研究[J]. 岩土力学, 2011, 32(4): 1069-1076.[10] 李远耀. 三峡库区渐进式库岸滑坡的预测预报研究[D]. 武汉: 中国地质大学, 2010.[11] 周斌. 新滩滑坡预测预报分析[J]. 路基工程, 2012, 163 (4): 182-185.。
应用多元统计分析课后答案

-4454.39
-62.75
9
3.41
0.04
0.2
67.86
98.51
1.25
-11.25
-11.43
10
1.16
0.01
0.54
43.7
100
1.03
-87.18
-7.41
11
30.22
0.16
0.4
87.36
94.88
0.53
729.41
-9.97
12
8.19
0.22
0.38
30.31
应用多元统计分析课后答案
第五章聚类分析
5.1判别分析和聚类分析有何区别?
答:即根据一定的判别准则,判定一个样本归属于哪一类。具体而言,设有n个样本,对每个样本测得p项指标(变量)的数据,已知每个样本属于k个类别(或总体)中的某一类,通过找出一个最优的划分,使得不同类别的样本尽可能地区别开,并判别该样本属于哪个总体。聚类分析是分析如何对样品(或变量)进行量化分类的问题。在聚类之前,我们并不知道总体,而是通过一次次的聚类,使相近的样品(或变量)聚合形成总体。通俗来讲,判别分析是在已知有多少类及是什么类的情况下进行分类,而聚类分析是在不知道类的情况下进行分类。
有序聚类就是解决样品的次序不能变动时的聚类分析问题。如果用 表示 个有序的样品,则每一类必须是这样的形式,即 ,其中 且 ,简记为 。在同一类中的样品是次序相邻的。一般的步骤是(1)计算直径{D(i,j)}。(2)计算最小分类损失函数{L[p(l,k)]}。(3)确定分类个数k。(4)最优分类。
5.7检测某类产品的重量,抽了六个样品,每个样品只测了一个指标,分别为1,2,3,6,9,11.试用最短距离法,重心法进行聚类分析。
聚类算法

返回
LOGO
划分法 划分法从一个初始的划分开始,不断的在 不同的群集之间重定位实体。这种方法通 常要求群集的数量被用户事先设定好。为 了达到全局最优,基于划分的聚类要求穷 举所有可能的划分。基于划分的方法 (Partitioning Method),其代表算法有KMEANS、K-MEDOIDS等。
LOGO
聚类与分类
聚类 分类
聚类是一种 无监督的学 习方法,目 的是描述
分类是一种 有监督的学 习方法,目 的是预测
返回
LOGO
相似性判断
聚类方法的核心问 题是对相似的对象 进行分组,因此需 要一些方法来判断 两个对象是否相似 。主要有两种方法 ,距离方法和相似 性方法。
距离度量
相似性度量
LOGO
距离度量 距离度量 用d(xi,xj) 表示两个对象间的距离,该 距离应满足下列条件: d(xi,xj) ≥0 当且仅当i=j,d(xi,xj)=0 反身性 d(xi,xj)= d(xj,xi) 对称性 d(xi,xk)≦d(xi,xj)+ d(xj,xk) 三角不等关系
LOGO
距离度量
数值
二进制
返回
LOGO
基于密度的算法
基于密度的方法假设属于一个聚类的所有的点来自一个特 定的概率分布。数据的全部分布被认为是各种分布的组合。 这种方法的目标是识别出聚类以及它们的参数分布。这种 方法被设计用于发现任意形状的聚类。 该算法以一个对参数向量的初始评估开始,经过两阶段的 选择:“E阶段”,该阶段关于被观察数据的完全数据可能 的条件期望和当前参数的估值被计算。在“M阶段”, “E阶段”的期望可能最大的参数被决定。这个算法可以 收敛为一个对被观察数据的可能性的局部最大值。
通过排序点确定聚类结构的聚类方法

通过排序点确定聚类结构的聚类方法
聚类是一种常见的数据分析方法,它可以将数据集中的相似对象分组成为一个簇。
聚类方法可以帮助我们发现数据集中的内在结构,从而更好地理解数据。
而通过排序点确定聚类结构的聚类方法是一种常见的聚类方法。
通过排序点确定聚类结构的聚类方法是一种基于距离的聚类方法。
它的基本思想是将数据集中的每个对象看作是一个点,然后通过计算这些点之间的距离来确定它们之间的相似度。
在这个过程中,我们需要选择一个排序点,它可以是数据集中的任何一个点。
然后,我们将数据集中的所有点按照与排序点的距离进行排序,距离越近的点排在越前面。
最后,我们可以将数据集中的点分成两个簇,其中一个簇包含距离排序点更近的点,另一个簇包含距离排序点更远的点。
通过排序点确定聚类结构的聚类方法可以重复执行,每次选择不同的排序点。
这样,我们可以得到不同的聚类结果,从而更好地理解数据集中的结构。
此外,通过排序点确定聚类结构的聚类方法还可以用于处理大规模数据集,因为它只需要计算每个点与排序点之间的距离,而不需要计算所有点之间的距离。
通过排序点确定聚类结构的聚类方法有一些缺点。
首先,它对排序点
的选择非常敏感。
如果选择的排序点不合适,可能会导致聚类结果不
准确。
其次,它只能将数据集分成两个簇,而无法处理多个簇的情况。
最后,它对噪声数据比较敏感,可能会将噪声数据误判为一个簇。
总之,通过排序点确定聚类结构的聚类方法是一种常见的聚类方法,
它可以帮助我们发现数据集中的内在结构。
但是,它也有一些缺点,
需要根据具体情况选择合适的聚类方法。
10种Python聚类算法完整操作示例(建议收藏)

10种Python聚类算法完整操作示例(建议收藏)聚类或聚类分析是无监督学习问题。
它通常被用作数据分析技术,用于发现数据中的有趣模式,例如基于其行为的客户群。
有许多聚类算法可供选择,对于所有情况,没有单一的最佳聚类算法。
相反,最好探索一系列聚类算法以及每种算法的不同配置。
在本教程中,你将发现如何在 python 中安装和使用顶级聚类算法。
完成本教程后,你将知道:•聚类是在输入数据的特征空间中查找自然组的无监督问题。
•对于所有数据集,有许多不同的聚类算法和单一的最佳方法。
•在 scikit-learn 机器学习库的 Python 中如何实现、适配和使用顶级聚类算法。
让我们开始吧。
教程概述本教程分为三部分:1.聚类2.聚类算法3.聚类算法示例•库安装•聚类数据集•亲和力传播•聚合聚类•BIRCH•DBSCAN•K-均值•Mini-Batch K-均值•Mean Shift•OPTICS•光谱聚类•高斯混合模型一.聚类聚类分析,即聚类,是一项无监督的机器学习任务。
它包括自动发现数据中的自然分组。
与监督学习(类似预测建模)不同,聚类算法只解释输入数据,并在特征空间中找到自然组或群集。
聚类技术适用于没有要预测的类,而是将实例划分为自然组的情况。
—源自:《数据挖掘页:实用机器学习工具和技术》2016年。
群集通常是特征空间中的密度区域,其中来自域的示例(观测或数据行)比其他群集更接近群集。
群集可以具有作为样本或点特征空间的中心(质心),并且可以具有边界或范围。
这些群集可能反映出在从中绘制实例的域中工作的某种机制,这种机制使某些实例彼此具有比它们与其余实例更强的相似性。
—源自:《数据挖掘页:实用机器学习工具和技术》2016年。
聚类可以作为数据分析活动提供帮助,以便了解更多关于问题域的信息,即所谓的模式发现或知识发现。
例如:•该进化树可以被认为是人工聚类分析的结果;•将正常数据与异常值或异常分开可能会被认为是聚类问题;•根据自然行为将集群分开是一个集群问题,称为市场细分。
构建聚类算法模型过程结果

构建聚类算法模型过程结果
聚类算法模型是一种机器学习模型,通过对数据样本进行分组
(或聚类)来发现数据之间的内在结构和相似性。
在构建聚类算法模
型时,需要以下步骤:
1. 数据清洗和预处理
首先,需要对数据进行清洗和预处理,包括去除异常值、处理缺失值、归一化等操作,以提高聚类结果的准确性和稳定性。
2. 特征选择和提取
接着,需要对数据样本进行特征选择和提取,即从样本中选择最具代
表性和区分性的特征,或通过特征变换等方式提取出新的特征。
3. 簇数确定
在建立聚类模型前,需要确定簇的数量。
一般可以采用肘部法、轮廓
系数等方法来选择最优的聚类数。
4. 选择聚类算法
根据研究需求和数据特点,选择最合适的聚类算法,如层次聚类、K-means聚类、DBSCAN聚类等。
5. 建立聚类模型
利用选定的聚类算法,结合样本数据进行训练,生成聚类模型。
6. 模型评估与优化
通过各种指标来评估聚类模型的优良程度,并对模型进行优化和改进,以提升聚类效果。
最终,在聚类算法模型的帮助下,我们可以将数据样本划分为具
有相似特征和类别的若干个聚类,得到更为清晰和具体的数据分析结果,并为决策提供参考依据。
聚类算法原理

聚类算法原理
聚类算法是一种无监督学习的方法,用于将具有相似特征的数据样本归为一类。
其基本原理是通过计算样本之间的相似度或距离,将相似度较高的样本归为同一类别。
一种常用的聚类算法是K均值算法。
该算法的核心思想是:
首先随机选择K个样本作为初始的聚类中心,然后计算所有
样本到这K个聚类中心的距离,并将每个样本分配到距离最
近的聚类中心所属的类别。
接着,根据每个类别中的样本,重新计算聚类中心的位置。
重复以上两个步骤,直到聚类中心的位置不再改变或达到预定的迭代次数。
K均值算法的收敛性证明依赖于所使用的距离度量和聚类中心的初始化方法。
在算法的应用中,常常采用欧氏距离或余弦相似度作为距离度量,而聚类中心的初始化则通过随机选择或其他启发式方法进行。
另一种常见的聚类算法是层次聚类算法。
该算法从单个样本作为一个初始聚类开始,然后将距离最近的样本逐渐合并为更大的聚类,直到所有样本都被聚为一个类别或达到预定的聚类数。
层次聚类算法的核心思想是通过计算样本之间的距离或相似度,将距离最近的样本合并为一类。
不同的合并策略会导致不同的层次聚类结果,常见的合并策略有单链接、完全链接和均值链接等。
聚类算法对于数据样本的分布情况和样本之间的关系并无要求,
因此适用于各种类型的数据。
在实际应用中,聚类算法通常用于数据分析、图像处理、推荐系统和生物信息学等领域,为数据挖掘和模式识别提供了有力的工具。
通过排序点确定聚类结构的聚类方法

通过排序点确定聚类结构的聚类方法介绍在数据分析和机器学习领域,聚类是一种常用的无监督学习方法,用于将相似的数据点归类到一起。
聚类分析的目标是将数据集分成多个组(称为聚类),使得组内的数据点相似度最高,组间的相似度最低。
通过聚类分析,我们可以发现数据集中的内在结构,并将相似的数据点放在一起,有助于后续的数据分析和决策制定。
聚类算法有很多种,其中一种常用的方法是通过排序点确定聚类结构。
这种方法通过对数据点进行排序,然后根据排序结果确定聚类的边界和结构。
在本文中,我们将详细讨论通过排序点确定聚类结构的聚类方法。
一级标题一:排序点聚类方法的基本原理排序点聚类方法是一种基于排序的聚类算法,其基本原理是通过将数据点按照某种特定的排序规则进行排列,然后根据排序结果确定聚类的边界和结构。
这种方法能够有效地发现数据集中的聚类,因为相似的数据点通常会被排在一起。
排序点聚类方法的基本步骤如下: 1. 将数据集中的每个数据点视为一个排序点;2. 根据某种相似度度量方法,计算每对数据点之间的相似度;3. 将相似度作为排序的依据,对数据点进行排序;4. 根据排序结果,确定聚类的边界和结构。
一级标题二:常用的排序点聚类方法排序点聚类方法有很多种,下面介绍几种常用的方法。
二级标题一:K-means算法K-means算法是一种经典的聚类算法,其基本思想是将数据集划分成K个类别,并将数据点分配到不同的类别中。
K-means算法通过迭代优化来确定聚类结果,具体步骤如下:1.随机选择K个初始聚类中心;2.将每个数据点分配到与其最近的聚类中心所对应的类别;3.更新聚类中心为每个类别中所有数据点的平均值;4.重复步骤2和3,直到聚类结果收敛。
K-means算法适用于处理数值型数据,但对于非数值型数据需要进行适当的处理。
二级标题二:DBSCAN算法DBSCAN算法是一种基于密度的聚类算法,其基本思想是将数据集中的稠密区域视为聚类,将稀疏区域视为噪声。
有序事物聚类分析

有序事物聚类分析分类是人类认识世界的客观需要,人类就是依靠分类认识世界的。
有一些有顺序的事物不能简单的依靠它们的属性去分类,分类的时候不能破坏它们之间的顺序。
这时候就需要运用有序事物的聚类分析的方法。
關键词:聚类分析分类有序事物分类是人类认识客观世界的基本方法之一,人们把所研究的对象分成若干类,然后分门别类的进行仔细的研究,从而加深对事物的认识。
将每个事物都看作数学空间中的一点,在这个数学空间中规定两点的距离,以距离来表示事物的差别。
分类时,常把距离靠近的点归为一类,这种方法叫做聚类分析法。
聚类分析是我们实际生活和工作中常用的分类工具之一,它按照研究的目的,找出物与物之间的相同点和类与类之间的差异,使我们在解决不同类问题时具有很强的针对性,能做到“具体问题具体分析”[1]。
聚类的一般步骤是先确定一个方式用来确定事物之间的距离,用以表示事物之间的差别,同时规定出类与类之间的距离,表示类的差别。
开始分类的时候,假设有100个事物,此时可以视为100个类,此时类和类之间的距离就是事物间的距离,将距离较小的类合并,重新计算新类和剩余类的距离,再将距离最近的类合并,这样每次都减少类的数目,最终减少到满足聚类的要求为止,是一种逐步合并的聚类方法。
许多实际问题都是按照一定的顺序排列的,如儿童的年龄、朝代的顺序、地质勘探的按地层的深浅排序等。
对于这种有顺序的事物的分类,不能够打乱它们本身的顺序[2]。
有序事物分类显著体现在婴幼儿的奶粉上,现在的父母对孩子倾注了很大的心血和很多的疼爱。
尤其对于婴幼儿时期的哺育,奶粉生产商们生产了0-6个月、7-12个月、1-3岁、3岁以上几个阶段。
这样分段就是为了使奶粉的营养成分比例适合各阶段的宝宝们的身体需要和消化能力。
下面我们以儿童的成长体重的增长表示1-11岁儿童的成长。
从表格中可以获得一些简单的信息,比如明显发现1岁的儿童成长速度极快,6岁儿童的体重增长最慢。
但是如果要给儿童发育分段,应该如何分段呢?好的分类方法,需要使同一类事物之间的差别尽可能小,而不同类之间的差别尽可能大。
