热力学习题课
合集下载
热力学习题课超经典 共24页PPT资料
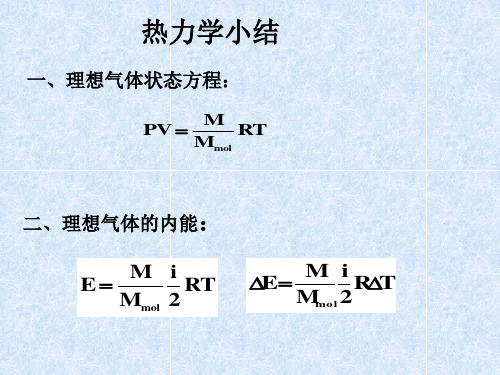
1、求Ta、Tb、Tc。 2、求气体在ab和bc 过程中吸收的热量， 气体内能的变化各如 何？ 3、气体在abc过程中 最高温度如何？
P(105Pa)
1.5 b
1a
0.5
c
0 1 2 3 V(10-3m3)
P(105Pa)
1.5 b
1、由 PV M RT 1 a
Mmol
0.5
求出求Ta、Tb、Tc。 0 1
T
Skn （玻氏熵公式）
热力学第二定律的实质：一切与热现象有 关的实际宏观过程都是不可逆的。
无摩擦的准静态过程才是可逆的
熵增加原理：孤立系统内部所发生的过程 总是向着状态几率增大的方向进行
= 可逆过程
孤立系统 dS0 > 不可逆过程
例：0.1mol的单原子理想气体，经历一准 静态过程abc，ab、bc均为直线。
(A) (1)过程中吸热，(2) 过程中放热．
√(B) (1)过程中放热，(2) 过程p中吸热．
(C) 两种过程中都吸热． (D) 两种过程中都放热．
a
(2)
分析： 作一循环a(1)ba, 这是逆循环.
(1)
b
W<0, △E=0, Q<0,
O
V
(1)过程中放热;
同理可得(2) 过程中吸热。
练习13 第四题 容积为10L的盒子以速度 v=200m/s匀速运动，容器中充有质量为50g 温度为18C的氢气，设盒子突然停止，气体 的全部定向运动动能都变为气体分子热运动 动能，容器与外界没有热交换，则达到热平 衡后，氢气的温度将增加——K;氢气的压强将 增加 —— Pa
c
2 3 V(10-3m3)
2、a
b，
M QabMmoC lV(TbTa) E
习题课—热力学第一定律及其应用
W = −∆U = 3420.0 J
'
[P26 例1-4]
1-29 求25℃、Pθ下反应 ℃
4 NH 3 ( g ) + 5O2 ( g ) = 4 NO ( g ) + 6 H 2O ( g )
的△rHmθ（298.15k）。已知下列数据 △ 298.15k）。 ）。已知下列数据
(1)2 NH 3 ( g ) = N 2 ( g ) + 3H 2 ( g ) (2)2 H 2 ( g ) + O2 ( g ) = 2 H 2O ( l ) (3) H 2O ( l ) = H 2O ( g ) (4) N 2 ( g ) + O2 ( g ) = 2 NO ( g )
∆ H ( 298.15k ) = −5154.19 KJ ⋅ mol c m
θ
−1
, CO ( g ) 、H O ( l ) 的标准摩尔 2 2
分别为-393.51KJ﹒mol-1、 生成焓 ∆ f H m ( 298.15k ) 分别为 试求C (s)的标准摩尔生成焓 -285.84KJ﹒mol-1,试求C10H8(s)的标准摩尔生成焓 θ ∆ H ( 298.15k ) 。 f m
解：原式可由(1)×2+ (2)× 3+ (3)× 6+ (4)× 2所得 原式可由 × × × × 所得
θ θ θ θ θ ∴∆ r H m = 2∆ r H m (1) + 3∆ r H m ( 2 ) + 6∆ r H m ( 3) + 2∆ r H m ( 4 )
= 2 × 92.38 + 3 × ( −571.69 ) + 6 × 44.02 + 2 ×180.72 = −904.69kJ ⋅ mol
4习题课热学
6
例2 若气体分子的速率分布曲线如图，图中A、B两 部分面积相等，则图中V0的物理意义为何？ 1.最可几速率；2.平均速率；3.方均根速率； 4.大于和小于速率v0的分子各占一半。 解：由f(v)-v曲线下面积物理意义可知， A、B两部分面 积相等意味着大于和小于速率v0的分子各占一半。 注：最可几速率的物理 意义是曲线的最大值所 对应的速率值。 应选（4）
P dp 得斜率 = − v dv T 由 热线 pvγ = C 绝
P P1 O A
P dp 得 率 = −γ 斜 v dv Q
B
v1
v2
13
v
P dp − dv 由题意 T v = 1 = 0.714 = P γ dp −γ dv Q v 1 得 γ= =1.4 0.714 γ γ 再由绝热方程 p1v1 = p2v2
T2 卡诺循环 η卡 =1− T 1 T2 ω卡 = T −T2 1
2
过程 特征
参量关系
Q
A
∆E
等容 V 常量 （P/T）=常量 ） 常量
νcV ∆T
0
p∆V ∆
νcV ∆T νcV ∆T
V1
） 常量 等压 P 常量 （V/T）=常量 ν c p ∆ T
νR∆T ∆
V1
νRT ln V2
T 常量
PV = 常量
V2 νRT ln
等温
νRT ln
p1
p2
νRT ln
p1
0
p2
绝热
PV = 常量 dQ γ −1 V T = 常量 =0 γ −1 − γ = P T 常量
γ
− νcV ∆T
0
p2V2 − p1V1 ν cV ∆T 3 1− γ
热力学与统计物理 - 习题课一 2024-11-18
第一章 习题10.(a)等温条件下,气体对外作功为22ln 2V VVVdVW pdV RT RT V===⎰⎰ln 2Q W RT =-=- ()0U ∆=(b)等压条件下,由PV RT =,得RTP V =所以 o o o o o o RT V P V V P W ==-=)2( 当体积为2V 时 22P VPV T T R R=== 1252TP P T Q C dT C T RT ===⎰11.(1) ()521 2.110P Q C n T T cal =-=⨯⎪⎭⎫⎝⎛==25041000n (2) 51.510VU nC T cal ∆=∆=⨯ (3)4610W Q U cal =-∆=⨯ (4) 因为0W =,所以51.510Q U cal =∆=⨯12.由热力学第肯定律Q d W d dU += (1)对于准静态过程有PdV W d -=对志向气体V dU C dT =气体在过程中汲取的热量为dTC Q d n =由此()n V C C dT PdV -= (2)由志向气体物态方程RT n PV += (3) 且 P VC C n R +-= 所以 ()()n V P V dT dVC C C C T V-=- (4) 对志向气体物态方程(3)求全微分有dV dP dT V P T+= (5)(4)与(5)联立,消去dTT ,有()()0n V n P dP dVC C C C P V-+-= (6)令n Pn V C C n C C -=-,可将(6)表示为0dV dPn V P += (7)若,,n V P C C C 均为常量,将(7)式积分即得nPV C = (8)式(8)表明,过程是多方过程.14. (a) 以T,P 为电阻器的状态参量,设想过程是在大气压下进行的,假如电阻器的温度也保持为27C 不变,则电阻器的熵作为状态函数也保持不变.(b) 若电阻器被绝热壳包装起来,电流产生的焦耳热Q 将全部被电阻器汲取而使其温度由i T 升为f T ,所以有2()P f imC T T i Rt -= 2600f i Pi RtT T K mC =+= （1卡 = 4.1868焦耳）139.1ln-•===∆⎰K cal T T mC TdT mC S ifT T p p fi15．依据热力学第肯定律得输血表达式Q d W d dU += （1）在绝热过程中，有0=Q d ，并考虑到对于志向气体dT C dU v = （2）外界对气体所作的功为：pdV w d -=，则有0=+pdV dT C v （3）由物态方程nRT pV =,全微分可得nRdT Vdp pdV =+ （4）考虑到对于志向气体有)1(-=-=γv v p C C C nR ，则上式变为dTC Vdp pdV v )1(-=+γ （5）把（5）和（3）式，有0=+pdV Vdp γ （6）所以有 V p V p sγ-=⎪⎭⎫⎝⎛∂∂ （7）若m 是空气的摩尔质量,m +是空气的质量，则有V m +=ρ和m m n +=ss s VV p p ⎪⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ρρ ssV p m V p ⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂+2ρ （8）将式（7）代入（8）式，有+=⎪⎪⎭⎫ ⎝⎛∂∂m pV p sγρ （9） 由此可得+=⎪⎪⎭⎫ ⎝⎛∂∂=m pV p v sγρ有物态方程RT m m nRT pV +==，代入上式，得m RTmpVv γγ==+17.(1) 0C 的水与温度为100C 的恒温热源接触后水温升为100C ,这一过程是不行逆过程.为求水、热源和整个系统的熵变，可以设想一个可逆过程，通过设想的可逆过程来求不行逆过程前后的熵变。
大学物理热学习题课
dN m 32 4 ( ) e Ndv 2kT
v2
对于刚性分子自由度 单原子 双原子 多原子
i tr
(1)最概然速率
2kT 2 RT RT vp 1.41 m
(2)平均速率
i=t=3 i = t+r = 3+2 = 5 i = t+r = 3+3 =6
6、能均分定理
8kT 8 RT RT v 1.60 m
M V RT ln 2 M mol V1
QA
绝热过程
PV 常量
M E CV T M mol
(2)由两条等温线和两条绝热线 组成的循环叫做 卡诺循环。 •卡诺热机的效率
Q0
Q2 T2 卡诺 1 1 Q1 T1
M P1V1 P2V2 A CV T M mol 1
E 0
•热机效率
A Q1 Q2
M E CV T M mol M Q C P T M mol
A Q1 Q2 Q2 1 Q1 Q1 Q1
A=P(V2-V1) 等温过程
A
E 0
Q1 Q2 •致冷系数 e W Q1 Q2
热机效率总是小于1的， 而致冷系数e可以大于1。
定压摩尔热容
比热容比
CP ( dQ )P dT i2 i
8、平均碰撞次数 平均自由程
z
2d v n
2
CV •对于理想气体：
Cp
v z
1.热力学第一定律
1 2 2d n
二、热 力 学 基 础
Q ( E2 E1 ) A dQ dE dA
准静态过程的情况下
4. 摩尔数相同的两种理想气体 一种是氦气，一种是氢气，都从 相同的初态开始经等压膨胀为原 来体积的2倍，则两种气体( A ) (A) 对外做功相同，吸收的热量 不同. (B) 对外做功不同，吸收的热量 相同. (C) 对外做功和吸收的热量都不 同. (D) 对外做功和吸收的热量都相 同. A=P(V2-V1)
第5章热力学第二定律习题课
a 1000 1.5 1.7 0.65
0.73
解： 取容器内全部气体为系统。 按题给，对所定义的系统应有 Q = 0, W = 0, U = UA + UB = 0 据此， 若UA 反之， 若UA UB UB
s 部 组 u 分 别 kJ/kg kJ/(kgK ) A a 1000 1.5
例 5-7 右图所示为 3 个可逆的热机 循环 A 、 B 、 C ，试分析比较它们 的热效率大小关系。 解：所给三个循环的平均吸热温度 和平均放热温度分别为：
TA1 T1； TA2 T2； 1 TB1 （T1 T2）； 2 TB2 T2；
T T1 A B C
T2
s
TC1 T1 TC 2 1 (T1 T2 ) 2
]
例 5.10 已知室内温度为 20℃ ，电冰箱内恒定地保持为 15℃，如果为此每分钟需从冰箱内排除热量221 kJ的热 量，问该电冰箱的压缩机功率至少需有多少kW？ 解：当电冰箱按逆卡诺循环工作时耗功最少 卡诺电冰箱的制冷系数应为 T2 258 c 7.3417 T1 T2 293 258 电冰箱每分钟的功耗 q2 221 w 29.98 kJ/min c 7.3714 电冰箱压缩机所需的功率至少为 N = w / 60 = 29.98 / 60 = 0.5 kW
2
q
T
1
0
因此，题给t2＝180℃是不可能的。
b.按题给，当t2=250℃时，过程的熵产量为
T2 s g s cP ln R ln T1 523 1.004 ln 0.287 ln 298 0..10283kJ /( kg K )
因此，过程造成的可用能损失
P2 P 1 0.5 0.1
0.73
解： 取容器内全部气体为系统。 按题给，对所定义的系统应有 Q = 0, W = 0, U = UA + UB = 0 据此， 若UA 反之， 若UA UB UB
s 部 组 u 分 别 kJ/kg kJ/(kgK ) A a 1000 1.5
例 5-7 右图所示为 3 个可逆的热机 循环 A 、 B 、 C ，试分析比较它们 的热效率大小关系。 解：所给三个循环的平均吸热温度 和平均放热温度分别为：
TA1 T1； TA2 T2； 1 TB1 （T1 T2）； 2 TB2 T2；
T T1 A B C
T2
s
TC1 T1 TC 2 1 (T1 T2 ) 2
]
例 5.10 已知室内温度为 20℃ ，电冰箱内恒定地保持为 15℃，如果为此每分钟需从冰箱内排除热量221 kJ的热 量，问该电冰箱的压缩机功率至少需有多少kW？ 解：当电冰箱按逆卡诺循环工作时耗功最少 卡诺电冰箱的制冷系数应为 T2 258 c 7.3417 T1 T2 293 258 电冰箱每分钟的功耗 q2 221 w 29.98 kJ/min c 7.3714 电冰箱压缩机所需的功率至少为 N = w / 60 = 29.98 / 60 = 0.5 kW
2
q
T
1
0
因此，题给t2＝180℃是不可能的。
b.按题给，当t2=250℃时，过程的熵产量为
T2 s g s cP ln R ln T1 523 1.004 ln 0.287 ln 298 0..10283kJ /( kg K )
因此，过程造成的可用能损失
P2 P 1 0.5 0.1
大学物理第五版 热力学习题课
3 2 R 定压摩尔热容 ，定压摩尔热容C
3 ，定
p,m=
5
2
R 。
9、一定量的理想气体，从相同状态开始分别经过等压、 、一定量的理想气体，从相同状态开始分别经过等压、
等体及等温过程， 等体及等温过程，若气体在上述各过程中吸收的热量 等温 相同，则气体对外界作功最多的过程为____________ 相同，则气体对外界作功最多的过程为____________。
热 力 学
习 题 课
第12章 提要
掌握两方面内容： 掌握两方面内容： 理想气体状态方程； 理想气体的压强、 一、理想气体状态方程；二、理想气体的压强、能量计算 1、气态方程； 、气态方程；
m′ pV = RT M R ( K=N A
)
N n= V
1 2 2 p = nmv = nεk 3 3
2、气体的压强 、
5 5 ∆E2 = R(T3 −T2 ) = ( pV3 − p2V2 ) 3 2 2 5 2 2 = ×(1.01×32×10 − 4.04×2×10 ) J 2 3 = 6.06×10 J
过程II气体吸热 过程II气体吸热 II
Ι
( p1 , V1 )
ΙΙ
p3 = p1
O
V
Q2 = W2 +∆E2 = 4.85×103 J+ 6.06×103 J =1.09×104 J
;
P = P =100Pa ; B c
VA =Vc =1m3
VB = 3m
3
（1）C—A为等容过程： A为等容过程：
PA TA PTA = ∴Tc = c =100K P Tc c P
A
C—B为等压过程： B为等压过程：
VB TB = Vc Tc
3 ，定
p,m=
5
2
R 。
9、一定量的理想气体，从相同状态开始分别经过等压、 、一定量的理想气体，从相同状态开始分别经过等压、
等体及等温过程， 等体及等温过程，若气体在上述各过程中吸收的热量 等温 相同，则气体对外界作功最多的过程为____________ 相同，则气体对外界作功最多的过程为____________。
热 力 学
习 题 课
第12章 提要
掌握两方面内容： 掌握两方面内容： 理想气体状态方程； 理想气体的压强、 一、理想气体状态方程；二、理想气体的压强、能量计算 1、气态方程； 、气态方程；
m′ pV = RT M R ( K=N A
)
N n= V
1 2 2 p = nmv = nεk 3 3
2、气体的压强 、
5 5 ∆E2 = R(T3 −T2 ) = ( pV3 − p2V2 ) 3 2 2 5 2 2 = ×(1.01×32×10 − 4.04×2×10 ) J 2 3 = 6.06×10 J
过程II气体吸热 过程II气体吸热 II
Ι
( p1 , V1 )
ΙΙ
p3 = p1
O
V
Q2 = W2 +∆E2 = 4.85×103 J+ 6.06×103 J =1.09×104 J
;
P = P =100Pa ; B c
VA =Vc =1m3
VB = 3m
3
（1）C—A为等容过程： A为等容过程：
PA TA PTA = ∴Tc = c =100K P Tc c P
A
C—B为等压过程： B为等压过程：
VB TB = Vc Tc
热学习题课
绝热
Qo
dQ o
CV ,m T
1 p1V 1 p2V2 1
0
p 1T c3
pV c1 TV 1 c2
dp p dV V
5、循环过程
A Q1
T2 1 T1
Q2 A Q1 Q2 1 Q1 Q1 Q1
解：
TV1 1
1
T2V2
1
T1 V2 T2 V1
1
v
8RT
v2 T2 V1 v1 T1 V2
1
2
2
1
2
5. 图为一理想气体几种状态变化过程的 p-V 图，其中 MT 为等温线，MQ 为绝热线，在 AM, BM, CM 三种准静态过程中： （1） 温度升高的是 BM, CM CM （2） 气体吸热的是 过程； 过程。
最概然速率 三种速率
vp 2kT m
3/ 2
ve
2 RT RT 1.41 M M
平均速率
方均根速率
v
vrms
8kT m
3kT m
8RT RT 1.59 M M
3RT RT 1.73 M M
7、玻耳兹曼分布律 在温度为T 的平衡态，系统的微观粒子按状态的分布与粒子的 能量 E 有关，且与成
S k ln
dQ dS T S S B S A
B A
dQ T
对孤立系统的自然过程，总有
S 0
绝 V 1T 常量 热 pV 常量 方 1 程 p T 常量
熵 的计算
dQ S 2 S1 (1) T R
( 2)
热力学基础习题课PPT学习教案
热量Q= 280 J 。
解：Q E W E 350130 220J Q 40 220 260J Q 60 220 280J
第11页/共20页
5.设在某一过程P中，系统由状态A变为状态B，如果 沿相反方 向进行，可以经过与原来一样的那些中间过程，而重新回到初 态，外界未发生任何变化，则过程P称为可逆过程；如果沿相 反方向进行，不能重复与原来一样的那些中间过程回到初态， 或回到初态而外界不能完全恢复，则过程P称为不可逆过程。 6. 一卡诺制冷机，低温热源的温度为300K，高温热源的温度 为450K，每一循环过程从低温热源吸热400J，则每一循环过
Wab
P(Vb
Va )
1.25105 5
(20) 103
2.5103
J
Qab CP (Tb Ta ) 2 8.31 (300) 6232.5 J
b c 等体过程
3 Wbc 0 Qbc CV (Tc Tb ) 2 8.31 300 3739.5 J
c a 等温过程
Wca
WQcWa aRbTlWnbVVacc
程外界必须做功为200 J 。
解： Q2 T2 W T1 T2
第12页/共20页
三、计算题
1. 一定质量的单原子分子理想气体，开始时处于状态a，体积 为1升，压强为3atm，先作等压膨胀至b态，体积为2升，再作 等温膨胀至c态，体积为3升，最后等体降压到1atm的压强， 求：（1）气体在全过程中内能的改变；（2）气体在全过程 中所作的功和吸收的热量。
J
Wadb Qadb 4.54103 J E 0
第16页/共20页
4.如图示，为1摩尔理想气体（其 ）。ln 2 0.69
C p 5 ）的循环过程（
解：Q E W E 350130 220J Q 40 220 260J Q 60 220 280J
第11页/共20页
5.设在某一过程P中，系统由状态A变为状态B，如果 沿相反方 向进行，可以经过与原来一样的那些中间过程，而重新回到初 态，外界未发生任何变化，则过程P称为可逆过程；如果沿相 反方向进行，不能重复与原来一样的那些中间过程回到初态， 或回到初态而外界不能完全恢复，则过程P称为不可逆过程。 6. 一卡诺制冷机，低温热源的温度为300K，高温热源的温度 为450K，每一循环过程从低温热源吸热400J，则每一循环过
Wab
P(Vb
Va )
1.25105 5
(20) 103
2.5103
J
Qab CP (Tb Ta ) 2 8.31 (300) 6232.5 J
b c 等体过程
3 Wbc 0 Qbc CV (Tc Tb ) 2 8.31 300 3739.5 J
c a 等温过程
Wca
WQcWa aRbTlWnbVVacc
程外界必须做功为200 J 。
解： Q2 T2 W T1 T2
第12页/共20页
三、计算题
1. 一定质量的单原子分子理想气体，开始时处于状态a，体积 为1升，压强为3atm，先作等压膨胀至b态，体积为2升，再作 等温膨胀至c态，体积为3升，最后等体降压到1atm的压强， 求：（1）气体在全过程中内能的改变；（2）气体在全过程 中所作的功和吸收的热量。
J
Wadb Qadb 4.54103 J E 0
第16页/共20页
4.如图示，为1摩尔理想气体（其 ）。ln 2 0.69
C p 5 ）的循环过程（
习题课1-热力学第一定律
理想气体或实际体系
H Qp T2CpdT T1
理想气体
T2
U T1 CV dT
（4）相变过程
可逆相变（等温等压过程），如1mol水在373K, pθ 下蒸发为1mol、373K、pθ的水蒸气
H Qp
V2
W
V1
pdV
p(V2 V 1)
pV2 （忽略液体体积Vi）
p1
A
C
2B 图1-4
3
V
解析 （1）A为等容过程，则
p1 T1 p2 T2
， T2=273K
ΔAU=nCV,m(T2-T1) =1mol× 3 R(273K-546K)J=-3.40kJ
2
WA=0, QA=ΔAU= -3.40kJ
ΔAH=nCp,m(T2-T1) =1mol× 5 R(273K-546K)J=-5.67kJ
ΔΗ。假设液态水的体积可以忽略不计，水蒸 气为理想气体，水的汽化热为2259 J·g-1。
解析：解决热力学问题首先要明确体系、状 态及过程。本题如不分清在过程中相态变化及水 蒸气量的变化，而直接用理想气体等温可逆方程 W= nRTln(10/100)就错了。整个过程可分解为下 列两个过程（1）和（2），如图1-3所示：
H2O(g) 0.5p V1 T1
(1)
H2O(g)
p V2 T1
图1-3
(2)
H2O(g)+H2O(l)
p V3 T1
其 中 p1=0.5pθ ， V1=100dm3 ， T1=373K ； p2=pθ ， T2=373K，V2=？；p3=pθ，V3=10dm3，T3=373K。
过程（1）为恒温可逆压缩过程，可直接用理想气 体求W的公式，另外，由P1V1=P2V2，得V2=50dm3。
热学习题课
Ω2 熵增加原理： 熵增加原理：在一个孤 ∆S = k ln ≥0 立系统（或绝热系统）可 立系统（或绝热系统） Ω1 能发生的过程是熵增加或保持不变的过程。 能发生的过程是熵增加或保持不变的过程。
孤立系统内进行的过程总是由微观状态数 小的状态向微观状态数大的宏观状态进行。 小的状态向微观状态数大的宏观状态进行。
B
i E = vRT ∝ V , pV = vRT 2 ⇒ p = constant
E V
8/8
例2：对于氢气(刚性双原子分子气体)和氦气， 对于氢气(刚性双原子分子气体)和氦气， 压强、体积和温度都相等时， 1．压强、体积和温度都相等时，它们的质量比 M(He)=______，内能比E(H ______； M(H2)⁄ M(He)=______，内能比E(H2)⁄ E(He)= ______； 压强和温度相同，(a)各为单位体积时的内能之 2．压强和温度相同，(a)各为单位体积时的内能之 =______，(b)各为单位质量时的内能之比 比 =______，(b)各为单位质量时的内能之比 = ______。 ______。
适用范围：可逆过程， 适用范围：可逆过程，只存在体积功
7/8
例1：一定质量的理想气体的内能E 随体积V 的变化 关系为一直线， 关系为一直线，则此直线表示的过程为 ［ ］ (A)等温过程 等温过程。 等压过程。(C)等容过程 (D)绝 等容过程。 (A)等温过程。(B)等压过程。(C)等容过程。(D)绝 热过程。 热过程。
解：（1） ：（ ）
1
dS = δ Q / T
T
Hale Waihona Puke T = const.Q = const.
3 2
1
dT = 0
2
清华大学工程热力学习题课
For personal use only in study and research; not for commercial use工程热力学课程习题第一章1-1 试将1物理大气压表示为下列液体的液柱高(mm)，(1) 水，(2) 酒精，(3) 液态钠。
它们的密度分别为1000kg/m3，789kg/m3和860kg/m3。
1-4 人们假定大气环境的空气压力和密度之间的关系是p=cρ1.4，c为常数。
在海平面上空气的压力和密度分别为1.013×105Pa和1.177kg/m3，如果在某山顶上测得大气压为5×104Pa。
试求山的高度为多少。
重力加速度为常量，即g=9.81m/s2。
1-7如图1-15 所示的一圆筒容器，表A的读数为360kPa，表B读数为170kPa，表示室Ⅰ压力高于室Ⅱ的压力。
大气压力为760mmHg。
试求(1) 真空室以及Ⅰ室和Ⅱ室的绝对压力；(2) 表C的读数；(3) 圆筒顶面所受的作用力。
图1-151-8 若某温标的冰点为20°，沸点为75°，试导出这种温标与摄氏度温标的关系(一般为线性关系)。
1-10 若用摄氏温度计和华氏温度计测量同一个物体的温度。
有人认为这两种温度计的读数不可能出现数值相同的情况，对吗？若可能，读数相同的温度应是多少？1-14一系统发生状态变化，压力随容积的变化关系为pV1.3=常数。
若系统初态压力为600kPa，容积为0.3m3，试问系统容积膨胀至0.5m3时，对外作了多少膨胀功。
1-15气球直径为0.3m，球内充满压力为150kPa的空气。
由于加热，气球直径可逆地增大到0.4m，并且空气压力正比于气球直径而变化。
试求该过程空气对外作功量。
1-16 1kg气体经历如图1-16所示的循环，A到B为直线变化过程，B到C为定容过程，C到A为定压过程。
试求循环的净功量。
如果循环为A-C-B-A则净功量有何变化？图1-16第二章2-2 水在760mmHg下定压汽化，温度为100℃，比容从0.001m3/kg增加到1.1763m3/kg，汽化潜热为2250kJ/kg。
热力学基础第5讲——热力学习题课
b
V1 V
1 Q1 CV (T A T 0) ( P A P0)(V A V 0) 0 , 2 1 Q 2 CV (T 1 T A) ( P A P1)(V 1 V A) 0 , 2 Q2 1 52.34 % Q1
作
业
题： 习题9.13 、9.18、9.21
8： 1 mol 单原子理想气体从初态压强 P0 32 Pa ,
P1 V0
b
V1 V
P V , 255 31 3 ( Pa ). ( Pa / m ) , 则： 7 56
在直线上一个微小过程中，
dA PdV , dE CV dT , dP dV , P V PdV VdP RdT PV RT dQ PdV CV dT
p a (2) b V
(1) O
4、下图为一理想气体几种状态变化过程的 P－V图， 其中MT为等温线，MQ为绝热线，在AM、BM、CM三种 准静态过程中： (1) 温度降低的是__________过程； AM (2) 气体放热的是__________过程． AM、BM
p M A T B Q O
C
V
预习内容：
6.1 — 6.3
复习内容：
第 9 章
由于 AB、CA 均为绝热线，系统与外界没有热量 交换， 系统在此循环中只在等温过程 BC 与外界存在热 量交换。 系统是从单一热源吸热。
另一方面，曲线 ABCA 所围 面积不为零，即系统在此循环过 程中对外做正功。 因此，该循环的总效果是： 系统从单一热源吸热，使之完全 变为功而不产生其它影响。
Q Ⅱ
Ⅰ
P P2 P0 (V0 / V1 ) 2.64atm 1 T1 1081K
热力学习题课
4.一定量的理想气体经历acb过程时吸热500 J．则经历 acbda过程时，吸热为(指的是总热量） (A) –1200 J． (B) –700 J． (C) –400 J． (D) 700 J． ［B］
解法（一） 整个循环： E 0,
Q W
Wacb ?
Wda ? Wbd ?
C p TAB CV TAB WAB
0 CV TAD WAD
TAB
i3
7/28
| TAD |
W AD 2 R i
3.氦气、氮气、水蒸汽(均视为刚性分子理想气体)，它们的摩 尔 数相同，初始状态相同，若使它们在体积不变情况下吸收相等 的热量，则 (A) 它们的温度升高相同，压强增加相同．
热力学基础 小结及习题课
1/28
一、热力学第一定律
系 E 统
W
Q E W
注意正负号的规定
Q吸
2/28
二、热力学第一定律的应用
Q E W
热一律
QV E
过程 过程特点 过程方程
等体
内能增量
dV 0
P C T V C T
PV C
E CV T
等压 dP 0
S1 S 2
p a 1 2 O S1 b S2 V
S1 则它对外做功W＝_______________
13/28
10.某理想气体等温压缩到给定体积时外界对气体作 功| W1 | ，又经绝热膨胀返回原来体积时气体对外作功 | W2 | 则整个过程中气体 放热 | W1 | (1) 从外界吸收的热量Q = ________ | W2 | (2) 内能增加了 E _________
p
工程热力学习题(1)
δQ = dECV
c22 c 21 f f + h2 + + gz 2 δmout − h1 + + gz1 δmin + δWi 2 2
因为绝热，所以δQ=0。B中气体不作功， 中气体不作功， 因为绝热，所以 。 中气体不作功 所以δWi=0。B中只有流体流入，没有流 所以 。 中只有流体流入， 中只有流体流入 体流出，所以δ 体流出，所以 mout=0。忽略宏观动能和 。 势能后上式可变为： 势能后上式可变为：
答：门窗紧闭的房间视为与外界没有热 量交换，可看作是绝热闭口系。 量交换，可看作是绝热闭口系。当系统 内部电冰箱运转时，有电功输入系统， 内部电冰箱运转时，有电功输入系统， 为负值。 即W为负值。因此按照闭口系能量方程 为负值 有：
0 = ∆U + W
因此， 为正值， 因此，△U为正值，即温度升高，不能 为正值 即温度升高， 达到降温的目的。 达到降温的目的。
答：由热力学第一定律：Q=△U+w,因为 由热力学第一定律： △ 因为 刚性容器绝热，所以Q=0，空气自由膨 刚性容器绝热，所以 ， 胀不作功， 胀不作功，即w=0，因此，△U=0，即空 ，因此， ， 气的热力学能保持不变。 气的热力学能保持不变。 若隔板上开有一个小孔， 若隔板上开有一个小孔，取B为热力系 为热力系 进行分析。 进行分析。
w = q − ∆u = ( −50) − 146.5 = −196.5kJ
(2)生产压缩空气， (2)生产压缩空气，进、排气阀要周期性 生产压缩空气 地打开和关闭，气体进出汽缸， 地打开和关闭，气体进出汽缸，此时气 体与外界交换的功为轴功w 体与外界交换的功为轴功 s，忽略气体 动能和势能时，轴功即为技术功w 动能和势能时，轴功即为技术功 t.选汽 缸进出口、 缸进出口、汽缸内壁及活塞左端所围空 间为热力系，此为开口系， 间为热力系，此为开口系，由开口系能 量方程得
热力学基础习题课
解：两种气体经历等容过程,升高相同温度 Q2 CV2 ,m 5 对于氦气 对于氢气 3 Q C 1 V , m 1 Q2 CV2 ,m 2 RT Q1 CV1 ,m 1 RT， 由于两种气体初始状态 pV RT 具有完全相同的p,V,T
1 2
4. 如图，一定质量的理想气体，其状态在p-T图上沿着 一条直线从平衡态a变到平衡态b，下列说法正确的是：
p
b
80 C
20 C
a
V1
c
d
2V1 V
解：初态：1mol氢气, p=1atm,20C
对abc过程：
p
5 E CV ,m T R(80 20) 150R 2 2V W RT1 ln 1 (273 80)R ln 2 353R ln 2 V1
b
80 C
20 C
a
V1
c
d
Q E W 150R 353R ln2
2V1 V
对adc过程：
E CV ,m T 5 R(80 20) 150R 2
2V1 W RT2 ln (273 20)R ln 2 293R ln 2 V1
Q E W 150 R 293R ln 2
(2)等压过程
(4)绝热过程
2
E
解：理想气体的内能 E i RT 理想气体状体方程 pV RT
i E pV 2
O
V
因此，在E~V中p表示直线的 斜率，即在该过程p保持恒量
6. 处于平衡态A的一定量的理想气体，若经准静态等 体过程变到平衡态B，将从外界吸收热量416J，若经 准静态等压过程变到与平衡态B有相同温度的平衡态 C，将从外界吸收热量582J，所以，从平衡态A变到 平衡态C的准静态等压过程中气体对外界所作的功为 166 J 解：题设包括两个的过程T相同E相同 AB，等容过程 AC，等压过程
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A B 30 30 C 35 20
ΔfHm(kJ· -1) mol
Cp,m(J· -1· -1) K mol
-15 10
解:(1)
1/2A(g) 298K ＋ 1/2B(g) 398K Qp= ΔH C(g) 498K
ΔH1
1/2A(g) 298K ＋
1/2B(g) 298K
ΔH3 ΔH2
C(g) 298K
1 298 K H 1 C p ,m B dT 1.5 103 J 2 398 K
ΔH2 =∑νBΔfHm(B)=27.5×103J
H 3
498 K 298 K
C p ,m C dT 4 103 J
Q=ΔH=ΔH1+ΔH2+ΔH3=30kJ
W=－pΔV=-p(V产－V反) =－R(nCTC－nATA－nBTB)=1.247kJ ΔU=Q+W=28.75kJ (2) Q p H 400K H 298K
一选择题 1. 1mol 单原子分子理想气体，经过一个循环过程W为 －100J，则Q为： ∵ΔU=0 ∴Q=-W b a. 0; b. 100J; c. -100J; d.求不出(因不知过程可逆与否) 2.理想气体在可逆绝热膨胀过程中 ∵dS=δQr/T b a. U 增加； b. S 不变； c. S 增大； d. T 不变。 3.1mol 纯液体在其正常沸点时完全气化,该过程增大的量 是： c a.蒸气压； b.气化热； c.熵； d.吉布斯函数。 4.液态水在100℃及101kPa下气化，则该过程 d a. ΔH=0； b. ΔS=0; c. ΔA=0; d. ΔG=0. c 5. 1mol 理想气体经一等温可逆压缩过程，则 a. ΔG> ΔA; b. ΔG< ΔA; c. ΔG= ΔA; d.二者无法比较。 ΔA=ΔU-TΔS= -TΔS ΔG=ΔH-TΔS= -TΔS
m m
B
2.封闭系统 ΔA、 ΔG何者必为零。 ΔU a.绝热密闭刚性容器中进行的化学反应过程＿＿＿＿＿ ΔG b.某物质的恒温、恒压可逆相变过程＿＿＿＿＿＿＿ c.系统所经历的任一不可逆循环过程＿＿＿＿＿＿＿ 全部 三.计算题 1. 1mol 理想气体(CV,,m=2.5R)在300K,101kPa下恒熵压缩 到4×101kPa，再恒容升温到500K，最后恒压降温至 400K,求整个过程的W、ΔS、ΔA及 ΔG。 已知Sm(300K)=20J· -1mol-1 K
400 K
H 298K 0 27.5kJ
298 K
C p ,m dT
W=－pΔV=－Δ(nRT)= ΔnRT= 0 ΔU=Q+W=Q=ΔH
例2.10mol水与1mol水蒸气在100 ℃ 、101325Pa的 压力下处于气、液两相平衡态,若将该平衡系统 绝热可逆膨胀到80 ℃的末态,试求80 ℃时水的饱 和蒸气压及上述过程的体积功W。已知100 ℃时 水的摩尔蒸发热ΔvapHm为40.668 kJ· -1;H2O(l) mol 与H2O(g)在80～100 ℃之间的平均定压摩尔热容 分别为75.75 J· -1· -1及34.16 J· -1· -1.计算时 mol K mol K 可忽略外压对水的气化热的影响
1mol H2O(g) 10mol H2O(l) T1=373.75K p1=101325Pa 通过ΔS=0可算出 水的蒸发量Δn
S S 1 S 2 T1
(1+Δn)mol H2O(g) 绝热可逆 (10-Δn)mol H2O(l) T2=353.75K p2 2
1 (1+Δn)mol H2O(g) (10-Δn)mol H2O(l) T1 p1
RT 积分可得
d ln p
vap H
2
dT
56187.3J mol
RT
1
C p ,m T
2
dT
p2 561873 J mol 1 T2 T1 C p ,m T2 . ln ln 101325/ Pa RT2T1 R T1 p 2 47.857kPa
6. 工作在100℃和25 ℃两个热源之间的卡诺热机的热机效 T1 T2 75 率是 a 20% 373 a. 20% ; b. 25%; T1 c. 75%; d.100% 7. 在-20 ℃和101kPa下，过冷水结成冰，则系统、环境及 总熵变为 d 过冷水结冰是自发 a. ΔS(系统)<0, ΔS(环境)<0, ΔS(总)<0；过程则:ΔS(总)>0; b. ΔS(系统)>0, ΔS(环境)>0, ΔS(总)>0；有序性增加则: c. ΔS(系统)<0, ΔS(环境)>0, ΔS(总)<0；ΔS(系统)<0; 则:ΔS(环境)>0; d. ΔS(系统)<0, ΔS(环境)>0, ΔS(总)>0； 二.填空 H m U m B RT B 6 7.5 1.5 1.25 ℃时有恒温反应C6H6(l)+7.5O2(g) →3H2O(l)+6CO2(g) -3718J 则该反应的ΔHm与ΔUm之差为_______若液体苯在置于 密闭容器中完全燃烧，同时释放出热量3264kJ，则其恒 压 燃烧热H U RT 3264 3.7kJ 3268 _______________________________________ kJ
解: 由克－克方程计算80℃时水的饱和蒸气压 -1 -1
ΔCp,m=Cp,m(g)－Cp,m(l)=－41.59J· · K mol ΔvapHm= ΔvapHm(T1)+ΔCp,m(T－T1) =40.668×103 J· -1+ΔCp,m(T－373.15K) mol =56187.3J· -1+ΔCp,mT mol
n vap H m T1
T2 10mol n C p ,m l ln T1
T2 p1 1mol n C p ,m g ln R ln 0 T1 p2
n 0.3180 mol
ΔH=ΔH1+ΔH2 =ΔnΔvapHm(T1)+(1mol+Δn)Cp,m(g)(T2-T1) +(10mol-Δn)Cp,m(l)(T2-T1)=-2636.3J Δ(pV)=Δ(nRT)=1.318molRT2-1molRT1=767.4J (忽略液体体积) W=ΔU=ΔH- Δ(pV)=-3403.7J
A U TS nCV ,m T4 T1 356J 1723 J G H TS nC p ,m T4 T1 356J 2554 J
T4 p1 S nC p ,m ln nRln 4.11J K 1 T1 p4 S4 S1 S 20 4.11J K 1 15.89J K 1 TS T4 S 4 T1 S1 356J
ΔS=0 T ΔV=0 T =500K Δp=0 T1=300K 2 3 P1=101.3kPa P2=405.3kPa P3
T4=400K P4= P3
解:
p2 T2 T1 p 1
W W1 W 2 W 3 nCV ,m T2 T1 0 p4 V4 V1 nCV ,m T2 T1 nRT4 T3 3862J
-
1.41 1.4 300 4 K 445.8 K T3 500 p4 p3 p2 405.3 Pa 454.6kPa T2 445.8
1
例：理想气体恒压下进行下列反应 A(g) + B(g) → 2C(g) 298K 398K 498K 试计算:(1).在上述条件下生成1molC时过程的Q、 W、 Δ U 和Δ H (2).上述反应在400K恒温恒压下进行,生成1molC 时过程的Q、W、 Δ U 和Δ H 已知各物质在298K时Δ fHm(298K)及Cp,m分别为
ΔfHm(kJ· -1) mol
Cp,m(J· -1· -1) K mol
-15 10
解:(1)
1/2A(g) 298K ＋ 1/2B(g) 398K Qp= ΔH C(g) 498K
ΔH1
1/2A(g) 298K ＋
1/2B(g) 298K
ΔH3 ΔH2
C(g) 298K
1 298 K H 1 C p ,m B dT 1.5 103 J 2 398 K
ΔH2 =∑νBΔfHm(B)=27.5×103J
H 3
498 K 298 K
C p ,m C dT 4 103 J
Q=ΔH=ΔH1+ΔH2+ΔH3=30kJ
W=－pΔV=-p(V产－V反) =－R(nCTC－nATA－nBTB)=1.247kJ ΔU=Q+W=28.75kJ (2) Q p H 400K H 298K
一选择题 1. 1mol 单原子分子理想气体，经过一个循环过程W为 －100J，则Q为： ∵ΔU=0 ∴Q=-W b a. 0; b. 100J; c. -100J; d.求不出(因不知过程可逆与否) 2.理想气体在可逆绝热膨胀过程中 ∵dS=δQr/T b a. U 增加； b. S 不变； c. S 增大； d. T 不变。 3.1mol 纯液体在其正常沸点时完全气化,该过程增大的量 是： c a.蒸气压； b.气化热； c.熵； d.吉布斯函数。 4.液态水在100℃及101kPa下气化，则该过程 d a. ΔH=0； b. ΔS=0; c. ΔA=0; d. ΔG=0. c 5. 1mol 理想气体经一等温可逆压缩过程，则 a. ΔG> ΔA; b. ΔG< ΔA; c. ΔG= ΔA; d.二者无法比较。 ΔA=ΔU-TΔS= -TΔS ΔG=ΔH-TΔS= -TΔS
m m
B
2.封闭系统 ΔA、 ΔG何者必为零。 ΔU a.绝热密闭刚性容器中进行的化学反应过程＿＿＿＿＿ ΔG b.某物质的恒温、恒压可逆相变过程＿＿＿＿＿＿＿ c.系统所经历的任一不可逆循环过程＿＿＿＿＿＿＿ 全部 三.计算题 1. 1mol 理想气体(CV,,m=2.5R)在300K,101kPa下恒熵压缩 到4×101kPa，再恒容升温到500K，最后恒压降温至 400K,求整个过程的W、ΔS、ΔA及 ΔG。 已知Sm(300K)=20J· -1mol-1 K
400 K
H 298K 0 27.5kJ
298 K
C p ,m dT
W=－pΔV=－Δ(nRT)= ΔnRT= 0 ΔU=Q+W=Q=ΔH
例2.10mol水与1mol水蒸气在100 ℃ 、101325Pa的 压力下处于气、液两相平衡态,若将该平衡系统 绝热可逆膨胀到80 ℃的末态,试求80 ℃时水的饱 和蒸气压及上述过程的体积功W。已知100 ℃时 水的摩尔蒸发热ΔvapHm为40.668 kJ· -1;H2O(l) mol 与H2O(g)在80～100 ℃之间的平均定压摩尔热容 分别为75.75 J· -1· -1及34.16 J· -1· -1.计算时 mol K mol K 可忽略外压对水的气化热的影响
1mol H2O(g) 10mol H2O(l) T1=373.75K p1=101325Pa 通过ΔS=0可算出 水的蒸发量Δn
S S 1 S 2 T1
(1+Δn)mol H2O(g) 绝热可逆 (10-Δn)mol H2O(l) T2=353.75K p2 2
1 (1+Δn)mol H2O(g) (10-Δn)mol H2O(l) T1 p1
RT 积分可得
d ln p
vap H
2
dT
56187.3J mol
RT
1
C p ,m T
2
dT
p2 561873 J mol 1 T2 T1 C p ,m T2 . ln ln 101325/ Pa RT2T1 R T1 p 2 47.857kPa
6. 工作在100℃和25 ℃两个热源之间的卡诺热机的热机效 T1 T2 75 率是 a 20% 373 a. 20% ; b. 25%; T1 c. 75%; d.100% 7. 在-20 ℃和101kPa下，过冷水结成冰，则系统、环境及 总熵变为 d 过冷水结冰是自发 a. ΔS(系统)<0, ΔS(环境)<0, ΔS(总)<0；过程则:ΔS(总)>0; b. ΔS(系统)>0, ΔS(环境)>0, ΔS(总)>0；有序性增加则: c. ΔS(系统)<0, ΔS(环境)>0, ΔS(总)<0；ΔS(系统)<0; 则:ΔS(环境)>0; d. ΔS(系统)<0, ΔS(环境)>0, ΔS(总)>0； 二.填空 H m U m B RT B 6 7.5 1.5 1.25 ℃时有恒温反应C6H6(l)+7.5O2(g) →3H2O(l)+6CO2(g) -3718J 则该反应的ΔHm与ΔUm之差为_______若液体苯在置于 密闭容器中完全燃烧，同时释放出热量3264kJ，则其恒 压 燃烧热H U RT 3264 3.7kJ 3268 _______________________________________ kJ
解: 由克－克方程计算80℃时水的饱和蒸气压 -1 -1
ΔCp,m=Cp,m(g)－Cp,m(l)=－41.59J· · K mol ΔvapHm= ΔvapHm(T1)+ΔCp,m(T－T1) =40.668×103 J· -1+ΔCp,m(T－373.15K) mol =56187.3J· -1+ΔCp,mT mol
n vap H m T1
T2 10mol n C p ,m l ln T1
T2 p1 1mol n C p ,m g ln R ln 0 T1 p2
n 0.3180 mol
ΔH=ΔH1+ΔH2 =ΔnΔvapHm(T1)+(1mol+Δn)Cp,m(g)(T2-T1) +(10mol-Δn)Cp,m(l)(T2-T1)=-2636.3J Δ(pV)=Δ(nRT)=1.318molRT2-1molRT1=767.4J (忽略液体体积) W=ΔU=ΔH- Δ(pV)=-3403.7J
A U TS nCV ,m T4 T1 356J 1723 J G H TS nC p ,m T4 T1 356J 2554 J
T4 p1 S nC p ,m ln nRln 4.11J K 1 T1 p4 S4 S1 S 20 4.11J K 1 15.89J K 1 TS T4 S 4 T1 S1 356J
ΔS=0 T ΔV=0 T =500K Δp=0 T1=300K 2 3 P1=101.3kPa P2=405.3kPa P3
T4=400K P4= P3
解:
p2 T2 T1 p 1
W W1 W 2 W 3 nCV ,m T2 T1 0 p4 V4 V1 nCV ,m T2 T1 nRT4 T3 3862J
-
1.41 1.4 300 4 K 445.8 K T3 500 p4 p3 p2 405.3 Pa 454.6kPa T2 445.8
1
例：理想气体恒压下进行下列反应 A(g) + B(g) → 2C(g) 298K 398K 498K 试计算:(1).在上述条件下生成1molC时过程的Q、 W、 Δ U 和Δ H (2).上述反应在400K恒温恒压下进行,生成1molC 时过程的Q、W、 Δ U 和Δ H 已知各物质在298K时Δ fHm(298K)及Cp,m分别为