有限元上机实验报告
ABAQUS有限元上机报告 南理工

有限元上机实验报告[——以Abaqus软件进行的有限元分析]汪健强1008320139实验1——平面问题应力集中分析目的要求:掌握平面问题的有限元分析方法和对称性问题建模的方法。
通过简单力学分析,可以知道本实验问题属于平面应力问题,基于结构和载荷的对称性,可以只取模型的1/4进行分析。
用8节点四边形单元分析X=0截面σx的分布规律和最大值,计算圆孔边的应力集中系数,并与理论解对比。
一、实验过程概述:1、启动ABAQUS/CAE2、创建部件3、创建材料和截面属性4、定义装配件5、设置分析步6、定义边界条件和载荷7、划分网格8、提交分析作业9、后处理10、退出ABAQUS/CAE二、实验结果:(1)边界受力图(1)X方向应力分量σx应力云图:(2)左边界直线与圆弧边交点的σx值为: 2.96714 MPa;(2)左右对称面上的σx曲线:三、实验内容分析:a)模型全局σx应力分布:σx应力集中分布于中心圆孔与x、y轴相交的地方,且与x轴相交处应力为负,与y轴相交处应力为正;沿圆周向周围,σx迅速减小;沿y 方向的σx应力大于沿x方向的σx应力。
b)应力集中系数为 2.92975,小于理论值3.0。
误差来源:有限元分析方法是将结构离散化,网格划分得越稀疏,计算出的结果就越偏离理论值。
分的越密集,结果越接近与理论值。
四、实验小结与体会:通过本次实验,对理论课所学有限元基本方法有了一个更加直观、深入的理解。
通过对Abaqus软件三个步骤:前处理、分析计算、后处理的操作,了解了这款软件的基本应用和它对有限元的一些很好的应用。
试验中,遇到诸多问题,仔细思考,加之请教老师,逐一解决,确实很有收获。
更增加了对有限元的认识,和对其功能之强大有了更深的理解。
实验二平面问题有限元解的收敛性一、实验目的和要求:(1)在ABAQUS软件中用有限元法探索整个梁上σx和σy的分布规律。
(2)计算梁底边中点正应力σx的最大值;对单元网格逐步加密,把σx的计算值与理论解对比,考察有限元解的收敛性。
有限元法基础及应用实验上机报告实例

一,实验描述:1、本作业属于哪类问题在本作业中,根据板的结构特点和受力情况,确定该问题属于平面对称应力问题,定义分析类型为静力学分析。
2、本文采用如何的单位制本题中,长度单位为m,故为方便起见,采用力的单位为N,压强的单位为pa,时间的单位为s,质量的单位为kg。
3、单元类型:对单元描述;材料;实常数单元类型为选取shell Elastic 4node63单元材料:弹性模量为2.1e11pa,泊松比为0.33。
由题意确定时常数,即厚度为0.1m4、划分网格。
网格划分设置。
单元数,节点数。
网格化分设置:设置单元边长值为0.1m,指定单元形状为Areas。
5、加载描述(1)对整体模型,首先对四周固定端加载位移约束,设定其位移值为0;然后,对面施加面载荷,设置面载荷为20000N;接着将施加在实物体上的载荷转换到有限元模型上,并显示施加在有限元模型上的载荷。
加载完后,对该有限元模型进行求解。
(2)对四分之一模型,首先对两边固定端加载位移约束,设定其位移值为0;然后,对两坐标轴所在的边施加对称载荷,最后对面施加面载荷,设置面载荷为20000N;接着将施加在实物体上的载荷转换到有限元模型上,并显示施加在有限元模型上的载荷。
加载完后,对该有限元模型进行求解。
6、后处理:最大MISIS应力和最大位移的位置和大小。
绘制结构的应力和变形图。
二,实验步骤(一)绘制整体实体模型1,在ANSYS中构造实体模型,如下图所示2,根据结构特点及所受载荷地情况,选取shell Elastic 4node63单元,设置材料常数:弹性模量E=2.1e11,u=0.33,单元边值为0.1m对其进行网格剖分,网格划分图如下:3,正确施加载荷和边界条件,结果如下:边界条件施加载荷20000N/m求解以后4,绘制平板的应力和变形图,并给出最大应力和变形的位置及大小:应力图应变图从图中可以看出其中实体边界中点位置的应力最大为0.583e+07pa,最大变形在中间圆弧的位置,0.144e-3m(二)绘制四分之一的实体模型1,在ANSYS中构造实体模型,如下图所示2,根据结构特点及所受载荷地情况,选取shell Elastic 4node63单元,设置材料常数:弹性模量E=2.1e11,u=0.33,单元边值为0.1m对其进行网格剖分,网格划分图如下:3,正确施加载荷和边界条件,注意此处有一个对称载荷的加载,结果如下:4,绘制平板的应力和变形图,并给出最大应力和变形的位置及大小:应力图应变图三,实验小结这次ANSYS上机实验课是使用shell中的Elastic 4node63单元,这使我对ANSYS软件中的单元有了更深的认识,同时对平面问题的静力分析的基本思路和操作步骤更加熟悉。
有限元上机实验报告

有限元ANSYS实验报告
学校:华北水利水电大学
学院:机械学院
专业:机械设计制造及其自动化
姓名:
学号:2010
指导老师:纪占玲
(一)带孔板壳模型静力分析一、新建文件
二、预处理,选择材料模型类型等。
三、建模
四、划分单元
五、施加约束、载荷
六、求解
七、查看结果
(二)内六角扳手静力分析
问题:
一个截面宽度为10mm的内六角扳手,在手柄的顶部施加扭矩为100N,然后在相同的部位施加垂直向下的力20N,分析在两种荷载作用下扳手的应力分布。
尺寸如下:截面宽度10mm、形状为正六边形、手柄长20cm、杆长7.5cm,倒角半径1cm、弹性模量2.1×10¹¹Pa,泊松比0.3 。
一、新建文建,预处理和上面一样,把不同的模型类型选择如下:
二、建模
三、划分单元网格,并生成实体模型
四、施加约束、载荷
五、查看结果
(三)其它练习实例。
有限元上机报告

有限元上机报告模板一、实验目的题目:图示折板上端固定,右侧受力F=1000N,该力均匀分布在边缘各节点上;板厚t=2mm,材料选用低碳钢,弹性模量E=210GPa,u=0.33。
此题属于平面应力问题,采用的单元类型为:Solid Quad-8node单位制:力(N)、弹性模量(MPa)、长度(mm)。
二、实体建模的方法1.定义矩形:Main Menu>Preprocessor>Modeling>Create>Areas>Rectangle>By Dimensions。
输入:X1=0,X2=30,Y1=0,Y2=60。
点击对话框上的Apply按钮创建第一个矩形。
输入X1=30,X2=60,Y1=0,Y2=30。
点击对话框上的OK按钮创建第二个矩形。
2. 面图元的加运算:Main Menu>Preprocessor>Modeling>Operate>Booleans>Add>Areas。
点击对话框上的Pick All按钮,所有的面被加在一起。
点击SAVE_DB保存数据。
三、单元类型1. 此题属于平面应力问题,采用Solid单元的Plane82。
2. 材料属性:弹性模量为21e4MPa,泊松比为0.33。
3. 实常数:板厚2mm。
四、划分网格以边长为2mm的正方形划分单元,总共有675个单元,736个节点。
具体操作如下:1. Main Menu >Preprocessor>Meshing>Mesh Tool.2. 在Mesh Tool面板上点击Size Controls模块内的Global Set 按钮,在弹出的对话框中输入Element edge length为2,按ok完成。
3. 在Mesh下拉框中选Areas。
4. 点击Mesh按钮网格划分,点击Pick All按钮,点击Close关闭Mesh Tool 面板。
南京理工大学2016年有限元上机实验报告(ABAQUS)

点线性等参元(完全积分 Quad,Linear;减缩积分 Quad,linear,Reduced integration;非协调模式 Quad,Linear,Incompatible modes)和 8 节点二次等参 元(Quad,Quadratic) 。
7 创建并提交分析。 ○ 8 查看结果并分析。 ○
4 计算结果分析讨论与结论
4.1 粗网格下梁中部应力分量和上下边法向应力对比
1 理论解: ○
X 方向正应力由下式计算:
已知 q=1N/mm2 ,h=160mm,L=1000mm, ymax
h 代入上式得: 2
3
x max
6 106 1 1 1 3 0 0.08 106 4 29.497MPa 3 0.16 4 2 4 5
分别应用 3 节点三角形单元、4 节点线性等参元(完全积分、减缩积分、 非协调模式) 、8 节点二次等参元完全积分进行下列各项数值实验:1)用粗网 格求解梁中部应力分量 x 最大值和上下边法向应力分量,并通过精确解对采用 不同单元的 x 计算精度进行对比分析;2)对粗网格下梁中部铅直(y 向)位移 进行对比分析;3)通过多次网格加密,对比试验 3 节点三角形单元和 8 节点二 次等参元的收敛速度。总结出研究结论,撰写实验报告。
2 3 节点三角形单元计算结果: ○
x 的应力云图
梁中部应力分量 x 变化曲线
上边法向应力分量
4
下边法向应力分量
梁中部应力分量 x 最大值为 17.03Mpa。 梁上边法向应力分量最大值为-1.3428Mpa 梁下边法向应力分量最大值为 0.3428Mpa
3 4 节点线性等参单元完全积分: ○
-0.130665
有限元上机实验报告
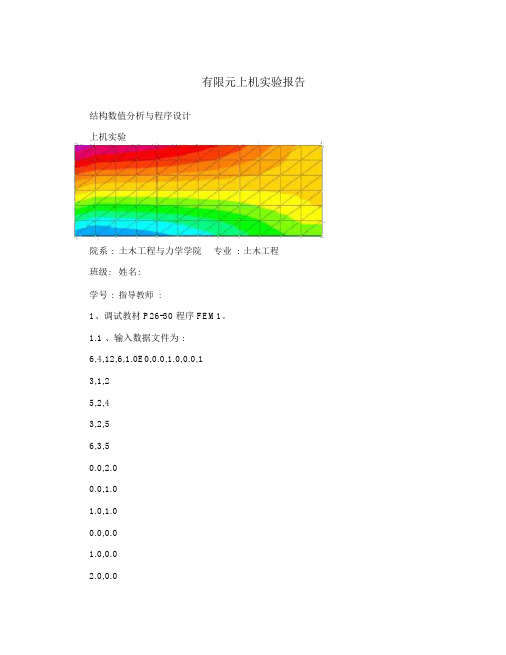
有限元上机实验报告结构数值分析与程序设计上机实验院系 :土木工程与力学学院专业:土木工程班级:姓名:学号 :指导教师:1、调试教材 P26-30 程序 FEM1。
1.1 、输入数据文件为 :6,4,12,6,1.0E0,0.0,1.0,0.0,13,1,25,2,43,2,56,3,50.0,2.00.0,1.01.0,1.00.0,0.01.0,0.02.0,0.01,3,7,8,10,121.2 、输出数据文件为 :NN NE ND NFIX E ANU T GM NTYPE6 4 12 60.1000E+01 0.000 1.0000.0000E+00 1 NODE X-LOAD Y-LOAD1 0.000000E+00 -0.100000E+012 0.000000E+00 0.000000E+003 0.000000E+00 0.000000E+004 0.000000E+00 0.000000E+005 0.000000E+00 0.000000E+006 0.000000E+00 0.000000E+00NODE X-DISP Y-DISP1 -0.879121E-15 -0.325275E+012 0.879121E-16 -0.125275E+013 -0.879121E-01 -0.373626E+004 0.117216E-15 -0.835165E-155 0.175824E+00 -0.293040E-156 0.175824E+00 0.263736E-15ELEMENT X-STR Y-STR XY-STR1 -0.879121E-01 -0.200000E+01 0.439560E+002 0.175824E+00 -0.125275E+01 0.256410E-153 -0.879121E-01 -0.373626E+00 0.307692E+004 0.000000E+00 -0.373626E+00 -0.131868E+00 2、修改 FEM1,计算 P31例 2-2 。
上机报告--有限元分析

有限元分析上机报告上海电机学院机械学院目录Project1 桁架结构静力有限元分析 (1)Project2 梁结构静力有限元分析 (3)Project3 平面结构静力有限元分析 (5)Project4 实体结构静力有限元分析 (6)有限元分析上机报告Project1 桁架结构静力有限元分析上机地点上机日期指导教师班级学号姓名一、上机目的二、主要仪器设备三、上机结果1、根据任务要求提交图片或者数据;2、提交.log文件;3、验证有限元分析结果。
四、体会与建议有限元分析上机报告Project2 梁结构静力有限元分析上机地点上机日期指导教师班级学号姓名一、上机目的二、主要仪器设备三、上机结果1、根据任务要求提交图片或者数据;2、提交.log文件;3、验证有限元分析结果。
四、体会与建议有限元分析上机报告Project3 平面结构静力有限元分析上机地点上机日期指导教师班级学号姓名一、上机目的二、主要仪器设备三、上机结果1、根据任务要求提交图片或者数据;2、提交.log文件。
四、体会与建议有限元分析上机报告Project4 实体结构静力有限元分析上机地点上机日期指导教师班级学号姓名一、上机目的二、主要仪器设备三、上机结果1、根据任务要求提交图片或者数据;2、提交.log文件。
四、体会与建议出师表两汉:诸葛亮先帝创业未半而中道崩殂,今天下三分,益州疲弊,此诚危急存亡之秋也。
然侍卫之臣不懈于内,忠志之士忘身于外者,盖追先帝之殊遇,欲报之于陛下也。
诚宜开张圣听,以光先帝遗德,恢弘志士之气,不宜妄自菲薄,引喻失义,以塞忠谏之路也。
宫中府中,俱为一体;陟罚臧否,不宜异同。
若有作奸犯科及为忠善者,宜付有司论其刑赏,以昭陛下平明之理;不宜偏私,使内外异法也。
侍中、侍郎郭攸之、费祎、董允等,此皆良实,志虑忠纯,是以先帝简拔以遗陛下:愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。
将军向宠,性行淑均,晓畅军事,试用于昔日,先帝称之曰“能”,是以众议举宠为督:愚以为营中之事,悉以咨之,必能使行阵和睦,优劣得所。
有限元上机实验报告(董妍)

有限元实验报告
董妍-学号 5070309005
1000000,同时时间步长的控制采取根据温度自适应的方式控制步长。 将 Max # increments 设为 1000000,Initial Time Step 设为 0.01,Finish when exceed 设为 900, Max Temperature Change Allowed 设为 10。 前两个参数是在定义为自适应步长控制 时需要给出的希望完成给定时间长度内分析所需的最大时间增量步数和建议初始时间 步长。第三个是指定当所有节点的温度都高于这一指定的基准温度时,程序结束运行。 而最后一个参数是指最大允许的温度改变值——改变这个值可以控制计算结果的精度。
2 / 13
Hale Waihona Puke 有限元实验报告董妍-学号 5070309005
elements 为 0 则说明操作成功。 如果为 200, 则点击 Flip Elements 下的 All Selected 翻转 所有单元后再次检查。 在 SWEEP 命令下点击 ALL,Unused PTS 和 NODES,扫除一些重叠的损坏的点。 再次进入 CHECK 下点击 Cross Elements 察看,如果重叠元素为 0 则操作成功。 进入 RENUMBER 命令下查看目前的节点数和单元数,然后点击 Renumber All 为所有 的节点和单元重新编号以便后续操作。这样,一个有限元模型就建立好了(如图) 。
2 2 3
为了比较不同参数下对内部温度场分布的影响情况, 我计划在实验过程中将内部换热系数、材料导热系数、材 料比热以及模具尺寸作一些变化,考察这几个参数的变化 对温度场分布的影响。参数的选择会在“参数设计”部份 详细说明。
电机CAD有限元及CAD制图上机实验报告

现代电机CAD技术仿真报告题目有限元及CAD制图上机实验报告任课教师作者专业学号上课时间作业完成时间________浙江大学电气学院有限元及CAD制图上机实验报告课程现代电机CAD技术实验名称有限元及CAD上机实验系别____电气工程及其自动化______ 实验日期 2016年月日专业班级_____组别_____________ 实验报告日期 2016年月日姓名___学号__ 报告退发 ( 订正、重做 )实验名称有限元及CAD上机实验一.题目1、绘制给定的电机二维截面图。
2、完成该电机的电磁场有限元分析。
3、基本假设●假设为单位电机(轴向长度1m,每相绕组匝数1匝)。
●6/4极、8/6极电机,相对两极正向串联,构成一相,形成两极磁场;12/8极电机,相互垂直四极串联,构成一相,形成四极磁场。
励磁安匝只对一相绕组施加。
●冲片材料DR510-50●尺寸单位:mm。
●SRM x-x-0、-7、-145、-18、-225、-30表示定子极中心线与转子槽中心线的夹角,分别为0度、7度、14.5度、18度、22.5度、30度。
●绕组未给尺寸,可以近似绘制二.环境Windows 7_64bitAnsoft Maxwell V15、AutoCAD2014Office 2016三.实验数据、结果分析1.建AutoCAD图我的电机型号为SRM9-2-18,下图为使用AutoCAD绘制的电机二位截面图。
图1 AutoCAD绘制的电机截面图做好图后,首先对这一电机进行初步分析,如图所视,该电机为开关磁阻电机,定、转子的凸极均由普通硅钢片叠压而成(本实验中选用了DR510-50电工硅钢薄板)。
转子既无绕组也无永磁体,定子极上绕有集中绕组,径向对称的两个绕组联接起来,称为“一相”,本电机为四相8/6极,是现在应用较多的相数结构。
开关磁阻电机的控制系统由功率变换器、控制器与转子位置检测器四部分组成,其中控制器内包含功率变换器和控制电路。
有限元分析实验报告

现代机械设计理论及方法——有限元分析上机实验报告书学院:机械工程学院年级:2009级专业班级:机械设计制造及其自动化4班学生:於军红学号:20092572指导教师:张大可报告日期:2012.12.19重庆大学机械工程学院机械设计制造及其自动化系二零一二年十一月制《现代设计方法》有限元部分上机作业题1题目概况1.1基本数据:板长300mm,宽100mm,厚5mm,25/=,E?102mmN泊松比0.27;a c边固定,ab边受垂直于边的向下均布载荷p=20N/mm.1.2分析任务:分析在板上开不同形状的槽时板的变形以及应力应变的异同,讨论槽的形状对板强度以及应力集中的影响。
2.模型建立2.1利用前处理器的moldling功能建立板的几何模型。
1)用create画出基本几何要素。
2)用moldling模块的布尔运算得出开方槽的板的几何模型。
2.2定义材料性质,实常数,单元类型,最后单元划分。
1)开方槽时的单元划分情况。
DEC 19 201222:45:082)开半圆形槽的单元划分情况。
DEC 19 201223:34:222.3定义载荷,将cd边位移设置为0(即将cd边固定),在ab边上施加均匀分布载荷p=20N/mm.DEC 19 201223:08:193.计算分析。
3.1位移分析1)开方槽时的变形情况DEC 19 201222:59:132)开圆形槽时的变形情况DEC 19 201223:38:413)分析:由上面ansys软件分析结果我们可以清楚地看到不管是方槽还是圆形槽,离固定边越远的地方位移越大,此外,开圆形槽时最大位移为1.678mm,而开方形槽时最大位移为1.731mm。
3.2 应力应变分布1)开方槽时的应力和应变:DEC 19 2012DEC 19 20122)开圆形槽时的应力和应变:DEC 19 2012温馨推荐您可前往百度文库小程序享受更优阅读体验不去了立即体验DEC 19 20123)应力应变分析:由以上分析运算结果我们可以清楚地看到在ab边上施加均布载荷时在离固定边较近的上下槽底部应力最大,应变也最大,即靠近约束的两个槽底部为危险截面,a,c点应力也比较大,在远离固定边的部位应力应变都很小几乎可以忽略。
有限元上机实验报告分析

有限元法基础及应用上机报告南京理工大学2015年12月上机实验一1 实验题目设计一个采用减缩积分线性四边形等参元的有限元模型,通过数值试验来研究网格密度、位移约束条件与总刚度矩阵奇异性、沙漏扩展、求解精度的关系,并验证采用减缩积分时保证总刚度矩阵非奇异的必要条件。
总结出你的研究结论,撰写实验报告。
2 实验目的通过实验来研究减缩积分方案中网格密度和位移约束条件对总体刚度矩阵奇异性和求解精度的影响,以此加深对有限元减缩积分的理解,和对减缩积分中保证总体刚度矩阵非奇异性的认识。
3建模概述先保持位移约束条件不变,研究网格密度对总体刚度矩阵奇异性和求解精度的影响,并验证采用减缩积分时保证总刚度矩阵非奇异的必要条件。
如下图1所示,建立一个简支和链杆的约束条件,然后不断增加网格密度,通过ABAQUS 来计算位移和应力的变化规律。
简支(两个约束)链杆(一个约束)积分点(3个独立关系式)节点(两个自由度)4 计算结果分析讨论与结论 1)1*1单元四边形减缩积分实验载荷 布种/单元应力云图2)2*1单元四边形减缩积分实验载荷 单元应力云图3)4*4单元四边形减缩积分实验载荷布种单元应力云图结果分析5 实验体会与小结单元刚度矩阵的特征:(1)对称性(2)奇异性(3)主元恒正K相同(4)平面图形相似、弹性矩阵D、厚度t相同的单元,eK的分块子矩阵按结点号排列,每一子矩阵代表一个结点,占两行两(5)e列,其位置与结点位置对应。
整体刚度矩阵的特征:(1)对称性(2)奇异性(3)主元恒正(4)稀疏性(5)非零元素呈带状分布。
[K]的物理意义是任意给定结构的结点位移所得到的结构结点力总体上满足力和力矩的平衡。
为消除[K]的奇异性,需要引入边界条件,至少需给出能限制刚体位移的约束条件。
对于一个给定形式的单元,如果采用精确积分,则插值函数中所有项次在|J|=常数的条件下能被精确积分,并能保证刚度矩阵的非奇异性。
如果采用减缩积分,因为插值函数中只有完全多项式的项次能被精确积分,因此需要进行刚度矩阵非奇异必要条件的检查。
有限元上机报告一

有限元作业一上机报告20120430231 余凯峰T1243-2一、题目图示折板上端固定,右侧受力F=1000N,该力均匀分布在边缘各节点上;板厚t=2mm,材料选用低碳钢,弹性模量E=210Gpa,μ=0.33.二、有限元分析的目的1、利用ANSYS构造实体模型;2、根据结构的特点及所受载荷的情况,确定所用单元类型;正确剖分网格并施加外界条件;3、绘制结构的应力和变形图,给出最大应力和变形的位置及大小;并确定折板角点A处的应力和位移;4、研究网格密度对A处角点应力的影响;5、若在A处可用过渡圆角,研究A处圆角半径对A处角点应力的影响三、有限元模型的特点1、作业类型:平面应力2、单位制:N mm MPa3、单元类型:在Preferences选Structural,Preprocessor>ElemmentType>Add/Edit/Delete中定义单元类型为Plane-82,K3设置为Plane strs w/thk材料: EX=2.10E5MPa, PRXY=0.33 实常数:THK=2mm4、划分网格:Preprocessor—Meshing—Mesh Tool—Size Controls下的Global 点击Set—在第一行输入你要定义的网格长度—OK—点击Clear旁边的Mesh—Pick All这一步划分网格5、加载描述:Preprocessor—Loads—Define Loads—Apply—Structural—Displacement—On Lines—拾取模型被固定的上边—ok—All DOF—okPreprocessor—Loads—Define Loads—Apply—Structural—Pressure—On Lines—拾取右边线—Load pres valu输入-1000/60—ok6、后处理:网格密度设置为“3”时应力和位移图如下:网格密度设置为“4”时应力和位移图如下网格密度设置为“5”时应力和位移图如下移也减小但变化不大。
弹塑性力学有限元上机报告(abaqus版)

有限元上机作业系所:同济大学土木工程学院专业:建筑与土木工程 .学号: ####### .姓名: ## .指导教师: ### .二零一五年一月二十八日目录第1题 (3)1 问题描述 (3)1.1运用弹性力学方法求解 (3)1.2 Abaqus有限元分析 (4)1.2.1 材料只考虑弹性时 (5)1)创建部件 (5)2)划分网格 (5)3)创建材料和截面属性 (6)4)装配部件 (6)5)设置分析步 (6)6)定义边界条件和荷载 (7)7)提交作业 (8)8)后处理 (8)9)误差分析 (8)10)误差验证 (8)1.2.2材料考虑弹塑性时 (9)1.2.3 对比分析 (11)第2题 (12)2.1 问题描述 (13)2.2 Abaqus建立模型 (13)1)创建部件 (13)2)划分网格 (14)3)创建材料和截面属性 (14)4)装配部件 (14)5)设置分析步 (15)6)定义边界条件和荷载 (15)7)提交作业 (16)2.3结果分析 (16)第3题 (19)3.1 问题描述 (19)3.2 Abaqus建立模型 (20)3.2.1对12边同时施加x和y方向的位移约束 (20)1)创建部件 (20)2)划分网格 (20)3)创建材料和截面属性 (21)4)装配部件 (21)5)设置分析步 (21)6)定义荷载和边界条件 (21)7)提交作业 (22)8)结果分析 (22)3.2.2对12边施加x方向的位移约束,对12边的中间一点施加y方向的位移约束 (22)3.2.3结果对比分析 (23)1)Mises应力分析 (23)2)S11应力分析 (24)3)S22应力分析 (24)4)S12应力分析 (25)5)Max principle应力分析 (25)6)Mid principle应力分析 (26)7)Min principle应力分析 (26)8)结论: (27)第1题(原题号5) 通过Abaqus 有限元软件模拟具有小圆孔的平板均匀拉伸产生的应力集中问题,验证弹性力学中的结论以及对比材料只考虑弹性和考虑弹塑性的区别。
有限元上机报告2

有限元上机报告(二)题目:图示正方形平板,板厚t=0.1m,材料常数为:弹性模量E=210GPa,u=0.33,承受垂直于板平面的均布载荷p=20kN/m2,平板外缘各边采用固定的约束方式.1、属于那类力学问题;属于薄板弯曲问题2、单位制:N,m, pa单元类型:shell63,每个单元有四个节点,每个节点4个自由度。
实常数:t=0.1m材料常数:E=210GPa=2.1e11pa u=0.33Main Menu > Preferences>structuralMain Menu > Preprocessor> Element Type>Add/Edit/Delete>Add> structural shell>4 nodes 63>OKMain Menu > Preprocessor>Real Constants>Add>只在no I框中输入0.1Main Menu>Preprocessor>Material Props>Material Models>Structural>Linear>Elastic>IsotropicEX=2.1E11,PRXY=0.333、通过如下操作生成实体模型;Main Menu > Preprocessor>Modeling >Create>Areas>Rectangle>By DimensionsX1=0,X2=4 Y1=0,Y2=4Main Menu > Preprocessor>Modeling >Create>Lines>Lines Fillet选择直线L1,L2 Apply,形成一个圆角,同样方式形成4个圆角Plot>linesMain Menu > Preprocessor>Modeling >Create>Areas>Arbitrary>By line 将四个圆角与直角间的部分形成面Main Menu > Preprocessor>Modeling >Create>Areas>Circle>Solid CircleWP X=2,WP Y=2 R=1 形成圆Main Menu > Preprocessor>Modeling>Opreate>Blooeans>Subtract>Areas通过布尔减运算形成实体如图:4、执行网格划分:直接划分网格,采用NDIV=10Main Menu > Preprocessor> Meshing>Mesh Tool(Size Controls) Global: Set →input NDIV:10 →OK >Mesh>Pick All>OK 如图:5、施加载荷及边界条件;直接将约束加在每一平板外缘,载荷面上施加。
有限元上机报告

在以常应变三角形单元计算弹性力学平面问题原理的基础上,编写可计算平面应力问题,亦可计算平面应变问题的通用程序。
给出程序设计的流程图,程序源代码和程序应用的工程算例及其结果分析。
一、程序流程图此程序采用本人比较熟悉C语言编写。
C语言相比于FORTRAN语言拥有更强大的实用编程环境,同时由于提供了指针变量、动态内存分配函数和结构体变量等,使其编写的软件在维护性、可读性和内存利用效率方面具有明显的优势。
1.程序总框图开始结束图1程序总框图整个程序由一个主调主程序(主函数main())和七个子程序组成,其中数据子程序DATA()用来接受输入的参数和变量。
单刚子程序ELEST()为含有参数的函数,功能控制参数iask可取1、2、3,分别计算相应单元的面积、应力矩阵和单元刚度矩阵,主程序不直接调用它,而通过总刚子程序、载荷子程序和求应力子程序间接调用。
总刚子程序TOTSTI()用来合成总刚矩阵,载荷子程序LOAD()用来计算合成载荷,支承子程序SUPPOR()用来引入约束,解方程子程序SOLVEQ()用来求解并输出各个结点的位移,求应力子程序STRESS()用来计算和输出应力、主应力及主平面角。
2.主函数及各子程序流程图输入6个基本参数 结点个数nj 单元个数ne 支杆个数nz 半带宽ndd 结点载荷个数npj 问题类型码ind计算位移分量个数nj2=nj*2确定输入节点载荷数组的行数npj1=npj+1图 2 void main()和 void DATA()图 3 void ELEST(int meo,int iask)输入单元结点码数组 ((JM[i][j],j=1~3),i=1~ne) 结点坐标数组 ((CJZ[i]jj=1〜2),i=1〜nj) 支承数组(NZC[i],i=1~nz) 结点载荷数组 ((PJ[i]jj=1〜2),i=1〜npj+1)J打印结点坐标数组——((CJZ[i]jj=1〜2),i=1〜nj)——输入弹性模量eo泊松比un 密度gama 厚度 te开始单元行码 lii =2*(i-1)+ii半带行码 ldh=2*(jm 〔meo-1][i-1]-1)+iiF eke[6][6忡子块列码j 由1到3循环L图 4 void TOTSTI()■■,mz<ndd?-_J是 ___________j0=mz j0=nddtkz[mz-1][j-1]=0p[mz-1]=0I 初始化整体刚,度矩阵tkz[nj2][ndd]={0}初始化载荷向量p[nj2]={0}■■■■单元码meo 由1到ne 循环调用单元刚度矩阵子程序ELEST(meo,3) . 否npj>0? -否 J 是 eke[6][6忡子块行码i 由1到3循环L i 由1到npj 循环 该子块中的元素码ii 由1到2循环/j=(int)(pj[i][1]) p[j-1]=pj[j][0]该子块中的元素列码jj 由1到2循环 二单元列码l =2*(j-1)+jj整体列码 lz=2*(jm[meo-1][j-1]-1)+jj ----- 半带列码ld<=0厂* 调用了程序ELEST (meo , 1)up0=-game*ae*te/3imeo 由 1 到ne 循环.■■■■■'------------------- ^否 ---------------- tkz[ldh-1][ld-1]=tkz[ldh-1][ld-1]+eke[lii-1][l-1] je=jm[meo-1][1]me=jm[meo-1][2] p[2*ie-1]=p[2*ie-1]+p0 p[2*je-1]=p[2*je-1]+p0 p[2*me-1]=p[2*me-1]+p0gama>0? -否l 是图 5 void LOAD()p[nj2-1]=p[nj2:]/tkz[nj2-1][0] *行码ii 由1到nj2-1循环* 行码i 由1到im 循环l=i-k+1c=tkz[k-1][j1]/tkz[k-1][0] *列码j 由1到ndd-l+1循环m=j+i-ktkz[i-1][j-1]=tkz[i-1i[j-1]-c*tkz[k-1][m-1]p[i-1]=p[i-1]-c*p[k-1] ■--ndd<=nj2-i+1?.---: -----I 丁是 I | _______________jo=ndd jo=nj2-i+1_____ T _____— 列码j 由2到jo 循环lh=j+i-1p[i-1]=p[i-1]-tkZ[i-1][j-1]*p[lh-1]玉p[i-1]=p[i-1]/tkz[i-1][0]/打印结点位移p[nj2]图 8 void STRESS()二、程序源代码/*有限元计算程序*/ #include <stdio.h> #include <math.h> int nj,ne,nz,ndd,ind,nj2; int jm[100][3],nzc[200],npj1,npj; float eo,un,gama,te,ae; float cjz[100]⑵,pj[100][2];float b[3][6],d[3][3],s[3][6],eke[6][6],tkz[200][20],p[200];i=nj2-ii否图 7 void SOLVEQ()* 消元码k 由1到nj2-1循环nj2>=k+ndd-1 ?void DATA() /*数据输入函数*/{ int i,j;printf("Qing shu ru 6 ge can shu\n");scanf("%d,%d,%d,%d,%d,%d”,&nj,&ne,&nz,&ndd,&npj,&ind);nj2=nj*2;npj1=npj+1;getchar();printf("Qing shu ru 4 ge ji suan can shu\n");scanf("%f,%f,%f,%f”,&eo,&un,&gama,&te);getchar();printf("nj=%d ne=%d nz=%d ndd=%d npj=%d ind=%d\n”,nj,ne,nz,ndd,npj,ind);printf("eo=%f un=%f gama=%f te=%f\n”,eo,un,gama,te);getchar();printf("Qing shu ru JM ju zheng\n");for(i=0;i<ne;i++){ for(j=0;j<3;j++)scanf("%d”,&jm[i][j]);getchar();}printf("Qing shu ru CJZ ju zheng\n");for(i=0;i<nj;i++){ for(j=0;j<2;j++)scanf("%f”,&cjz[i][j]);getchar();}printf("Qing shu ru NZC ju zheng\n");for(i=0;i<nz;i++)scanf("%d”,&nzc[i]);getchar();printf("Qing shu ru PJ ju zheng\n");for(i=0;i<npj1;i++){ for(j=0;j<2;j++)scanf("%f”,&pj[i][j]);getchar();}getchar();printf("CJZ ju zheng ru xia\n");for(i=0;i<nj;i++){ for(j=0;j<2;j++){printf("%f ",cjz[i][j]);if(j%2==1)printf("\n");}}getchar();}void ELEST(int meo,int iask)/* 单元刚度矩阵*/ ( int ie,je,me,i,j,k;float cm,bm,cj,bj;ie=jm[meo-1][0];je=jm[meo-1][1];me=jm[meo-1][2];cm=cjz[je-1][0]-cjz[ie-1][0];bm=cjz[ie-1][1]-cjz[je-1][1];cj=cjz[ie-1][0]-cjz[me-1][0];bj=cjz[me-1][1]-cjz[ie-1][1];ae=(bj*cm-bm*cj)/2;if(iask>1){ for(i=0;i<3;i++){ for(j=0;j<6;j++)b[i][j]=0;}b[0][0]=-bj-bm;b[0 H2] =bj;b[0][4]=bm;b[1][1]=-cj-cm;b[1][3]=cj;b[1][5]=cm;b[2][0]=-cj-cm;M2] [1]=-bj-bm;b⑵⑵=cj;M2] [3]=bj;b⑵[4]=cm;M2] [5]=bm;for(i=0;i<3;i++){for(j=0;j<6;j++)b[i][j]=b[i][j]/(2*ae);}d[0][0]=eo/(1-un*un);d[0][1]=eo*un/(1-un*un);d[0]⑵=0;d[1][0]=eo*un/(1-un*un);d[1][1]=eo/(1-un*un);d[1]⑵=0;d⑵[0]=0;d[2][1]=0;d⑵[2 ]=eo/(2*(1+un));for(i=0;i<3;i++){for(j=0;j<6;j++){s[i][j]=0;for(k=0;k<3;k++)s[i][j]=s[i][j]+d[i][k]*b[k][j];}}if(iask>2){for(i=0;i<6;i++){for(j=0;j<6;j++){eke[i][j]=0;for(k=0;k<3;k++)eke[i][j]=eke[i][j]+s[k][i]*b[k][j]*ae*te;}}}}}void TOTSTI(void) /* 总的刚度矩阵*/{int i,j,ii,jj,meo,lii,l,lz,ldh,ld;for(i=0;i<nj2;i++){for(j=0;j<ndd;j++)tkz[i][j]=0;}for(meo=1;meo<=ne;meo++){ELEST(meo,3);for(i=1;i<4;i++){for(ii=1;ii<3;ii++){lii=2*(i-1)+ii;ldh=2*(jm[meo-1][i-1]-1)+ii;for(j=1;j<4;j++){for(jj=1;jj<3;jj++){l=2*(j-1)+jj;lz=2*(jm[meo-1][j-1]-1)+jj;ld=lz-ldh+1;if(ld>0)tkz[ldh-1][ld-1]=tkz[ldh-1][ld-1]+eke[lii-1][l-1];}}}}}}void LOAD() /* 添加载荷*/ (int i,j,meo,ie,je,me;float p0;for(i=0;i<nj2;i++)p[i]=0;if(npj>0)(for(i=1;i<npj;i++)(j=(int)(pj[i][1]);p[j-1]=pj[i][0];}}if(gama>0)(for(meo=1;meo<=ne;meo++)(ELEST(meo,1);p0=-gama*ae*te/3;ie=jm[meo-1][0];je=jm[meo-1][1];me=jm[meo-1][2];p[2*ie-1]=p[2*ie-1]+p0;p[2*je-1]=p[2*je-1]+p0;p[2*me-1]=p[2*me-1]+p0;}}}void SUPPOR() /* 添加约束*/ (int i,j,mz,j0;for(i=1;i<=nz;i++)(mz=nzc[i-1];tkz[mz-1][0]=1;for(j=1;j<ndd;j++)tkz[mz-1][j]=0;if(mz<ndd)j0=mz;elsej0=ndd;for(j=2;j<=j0;j++)tkz[mz-j][j-1]=0;p[mz-1]=0;}}void SOLVEQ() /*求解过程*/ (int k,i,j,im,l,m,ii,jo,lh;float c;for(k=1;k<=nj2-1;k++)(if(nj2>=k+ndd-1)im=nj2;elseim=k+ndd-1;for(i=k+1;i<=im;i++)(l=i-k+1;c=tkz[k-1][l-1]/tkz[k-1][0];for(j=1;j<=ndd-l+1;j++)(m=j+i-k;tkz[i-1][j-1]=tkz[i-1][j-1]-c*tkz[k-1][m-1];}p[i-1]=p[i-1]-c*p[k-1];}}p[nj2-1]=p[nj2-1]/tkz[nj2-1][0];for(ii=1;ii<=nj2-1;ii++)(i=nj2-ii;if(ndd<=nj2-i+1)jo=ndd;elsejo=nj2-i+1;for(j=2;j<=jo;j++)(lh=j+i-1;p[i-1]=p[i-1]-tkz[i-1][j-1]*p[lh-1];}p[i-1]=p[i-1]/tkz[i-1][0];}printf("\n");printf("Shu chu jie dian wei yi\n");printf(" u v\n");for(i=0;i<nj2;i++)(printf(" %16f”,p[i]);if(i%2==1)printf(”\n”);}printf("\n");}void STRESS() /* 应力计算*/( double ceta,ceta1,sigx,sigy,toxy,py1,ry1,sig1,sig2;int meo,i,j,lh,ldh;float wy[6],yl[3];printf("Shu chu yingli zhuyingli zhupingmianjiao\n");for(meo=1;meo<=ne;meo++){ELEST(meo,2);for(i=1;i<=3;i++){for(j=1;j<=2;j++){lh=2*(i-1)+j;ldh=2*(jm[meo-1][i-1])+j;wy[lh-1]=p[ldh-1];}}for(i=1;i<=3;i++){yl[i-1]=0;for(j=1;j<=6;j++)yl[i-1]=yl[i-1]+s[i-1][j-1]*wy[j-1];}sigx=yl[0];sigy=yl[1];toxy=yl[2];py1=(sigx+sigy)/2;ry1=sqrt((sigx-sigy)*(sigx-sigy)/4+toxy*toxy);sig1=py1+ry1;sig2=py1-ry1;if(sigy==sig2)ceta=0;else{ceta1=toxy/(sigy-sig2);ceta=90-57.29578*atan(ceta1);}printf("Danyuan%d \n”,meo);printf("sigx=%12f sigy=%12f toxy=%12f sig1=%12f sig2=%12f ceta=%12f\n”,sigx,sigy,toxy,sig1,sig2,ceta);}}void main() /* 主程序*/{printf("*****Ping mian you xian yuan ji suan cheng xu*****\n"); printf("\n"); DATA(); if(ind!=0){ eo=eo/(1-un*un);un=un/(1-un); } TOTSTI(); LOAD(); SUPPOR(); SOLVEQ(); STRESS(); getchar(); printf("\n");printf(" R-jixie-063 0618030303 Zhang chunqing \n"); printf(" 2010/11/20 \n");getchar();}三、工程算例如图所示有一刚性基础的钢件,受垂直和水平向左的压力作用,以平面问题计算 取〃=1/6,将结构分成24个单元,按图中所示的网格划分,用程序计算结点位移及 各单元中的应力,设弹性模量E=1.0。
ABAQUS有限元上机报告南理工

ABAQUS有限元上机报告南理工标题:ABAQUS有限元上机报告引言:ABAQUS是一种常用的有限元分析软件,具有强大的模拟功能和广泛的应用范围,在工程领域有着重要的地位。
本次上机实验通过使用ABAQUS软件进行有限元分析,对一个简单的结构进行建模和分析,探讨了有限元分析方法的基本原理和应用。
一、实验目的本次实验的目的主要有以下几点:1.了解有限元分析的基本原理和步骤;2.熟悉ABAQUS软件的基本界面和操作方法;3.学习建立有限元模型和进行分析的基本步骤;4.掌握ABAQUS软件中常用的载荷和约束设置方法。
二、实验内容本次实验选择了一个简单的梁模型进行分析,主要包括以下几个步骤:1.模型的建立:首先根据实际需要建立合适的几何模型,包括梁的尺寸、材料等参数。
2.材料属性的定义:根据实际材料性质,定义材料的弹性模量、泊松比等参数。
3.网格划分:将模型进行网格划分,将连续体分割为小单元。
4.载荷和约束的设置:根据实际情况设置梁的边界条件,包括外力载荷和约束条件。
5.边界条件的施加:对模型进行力的施加和约束的设置。
6.分析类型的选择:根据分析的目标选择合适的分析类型。
7.求解和后处理:进行模型的求解和结果的后处理。
8.结果分析和讨论:对模型的结果进行分析和讨论。
三、实验结果在进行了上述步骤后,我们成功建立了一个简单的梁模型,并进行了有限元分析。
通过ABAQUS软件提供的分析结果功能,我们得到了梁的应力、应变等结果,并进行了相应的分析和讨论。
四、实验总结通过本次实验,我们深入了解了ABAQUS有限元分析软件的基本原理和操作方法,熟悉了有限元分析的基本步骤。
同时,我们也学习到了如何进行模型的建立、加载和后处理等操作,并掌握了如何进行结果的分析和讨论。
这对于今后进行更加复杂的结构分析和优化设计具有重要的意义。
在今后的学习和研究中,我们将进一步深入学习ABAQUS软件的使用,提高对于有限元分析方法的理解和掌握,以更好地应用于实际工程问题的解决中。
有限元分析及理论上机报告

有限元分析及理论上机报告报告(一)Demo7 stress一、问题描述一个承受拉力的平板,在其中心位置有一个小圆孔,其结构尺寸如下图所示,要求分析其结构圆孔处的Mises应力分布。
材料特性:弹性模量E = 210000 MPa,泊松比 =0.3拉伸载荷:P=100MPa平板厚度:d=1mm二、方法概述,建模思路和分析策略1由于薄板只在边缘上受到了平行于板面的并沿厚度均匀分布的力,所以平板处于平面应力状态。
在创建部件(Part)时,薄板的模型所在空间(Space)设置为(2D Planer),绘制图形。
2由于该平板受力模型的结构和载荷是对称的,所以,可以取用模型的1/4进行分析。
其图形如下所示。
3材料为线弹性材料,其材料属性设置为Elasticity中的Elastic,设置其弹性模量(E=210000MPa)和泊松比( =0.3)。
薄板属于实体,其截面属性种类为实体(Solid),然后赋予其截面属性。
4由薄板的受力情况和分析要求可知,薄板的应力分析为线性/非线性的静力学分析,所以其分析步的类型为Static、General,不用考虑几何非线性(NLgeom>off)。
5模型所受的载荷为均布压力,使用载荷类型为(pressure)。
由于模型的对称,所以对模型的左侧和底部的边界线设置边界条件,固定边界。
由受力分析结果可得:左侧边界为XSYMM,底部边界为YSYMM。
6中心圆孔处为应力集中区域,且为分析结果要求重点,应局部网格加密。
划分网格,然后提交分析。
三、分析过程中遇到的问题及解决方法分析过程中没有遇到什么问题,但是需要注意几个方面。
1、在定义截面属性时,应注意的是平面应力分析问题的截面属性不是shell,而应该是solide(实体)。
其次注意平面的厚度。
一会吧其次,边界条件应该在分析步的第一步(initial)里添加,否则会导致有限元分析的失败。
载荷的添加应该是在第二步,注意载荷的方向为由里向外—100 三,由于取用的是板子的1/4作为分析的模型,所以将边界条件固定来模仿相应的应力情况,即固定相应边的XY方向上的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元法基础及应用上机报告南京理工大学2015年12月上机实验一1 实验题目设计一个采用减缩积分线性四边形等参元的有限元模型,通过数值试验来研究网格密度、位移约束条件与总刚度矩阵奇异性、沙漏扩展、求解精度的关系,并验证采用减缩积分时保证总刚度矩阵非奇异的必要条件。
总结出你的研究结论,撰写实验报告。
2 实验目的通过实验来研究减缩积分方案中网格密度和位移约束条件对总体刚度矩阵奇异性和求解精度的影响,以此加深对有限元减缩积分的理解,和对减缩积分中保证总体刚度矩阵非奇异性的认识。
3建模概述先保持位移约束条件不变,研究网格密度对总体刚度矩阵奇异性和求解精度的影响,并验证采用减缩积分时保证总刚度矩阵非奇异的必要条件。
如下图1所示,建立一个简支和链杆的约束条件,然后不断增加网格密度,通过ABAQUS 来计算位移和应力的变化规律。
简支(两个约束)链杆(一个约束)积分点(3个独立关系式)节点(两个自由度)4 计算结果分析讨论与结论 1)1*1单元四边形减缩积分实验载荷 布种/单元应力云图2)2*1单元四边形减缩积分实验载荷 单元应力云图3)4*4单元四边形减缩积分实验载荷布种单元应力云图结果分析5 实验体会与小结单元刚度矩阵的特征:(1)对称性(2)奇异性(3)主元恒正K相同(4)平面图形相似、弹性矩阵D、厚度t相同的单元,eK的分块子矩阵按结点号排列,每一子矩阵代表一个结点,占两行两(5)e列,其位置与结点位置对应。
整体刚度矩阵的特征:(1)对称性(2)奇异性(3)主元恒正(4)稀疏性(5)非零元素呈带状分布。
[K]的物理意义是任意给定结构的结点位移所得到的结构结点力总体上满足力和力矩的平衡。
为消除[K]的奇异性,需要引入边界条件,至少需给出能限制刚体位移的约束条件。
对于一个给定形式的单元,如果采用精确积分,则插值函数中所有项次在|J|=常数的条件下能被精确积分,并能保证刚度矩阵的非奇异性。
如果采用减缩积分,因为插值函数中只有完全多项式的项次能被精确积分,因此需要进行刚度矩阵非奇异必要条件的检查。
上机实验二1 实验题目图示一个简支梁平面应力模型。
梁截面为矩形,高度h=160mm ,长度L=1000mm ,厚度t=10mm 。
上边承受均布压力q =1N/mm 2,材料E=206GPa ,μ=0.29。
X 方向正应力弹性力学理论解为:)534()4(622223-+-=h y h y q y x L h q x σ分别应用3节点三角形单元、4节点线性等参元(完全积分、减缩积分、非协调模式)、8节点二次等参元完全积分进行下列数值实验:1)用较粗单元网格求解梁中部应力分量σx 的最大值和上下边法向应力分量,并对各单元计算精度进行比较分析;2)对粗网格下梁中部最大位移进行对比和分析;3)通过网格加密对比试验3节点三角形单元和8节点二次等参元的收敛速度。
总结出研究结论,撰写实验报告。
2 实验目的(1)通过ABAQUS 软件,用有限元法分析整个梁上的σ_x 的分布规律,讨论σ_y 的有限元解与材料力学解的区别;(2)用有限元法求梁顶边和底边中点正应力σx 的最大值;(3)比较3节点三角形单元、4节点线性等参元(完全积分、减缩积分、非协调模式)、8节点二次等参元完全积分求得的参数与理论解的接近程度; (4)逐步加密单元网格,把有限元法求得的σx 值与理论值进行对比,考察解的收敛性;(5)针对以上力学模型,对比分析3节点三角形平面单元和8节点四边形平面单元的求解精度和收敛性;(6)绘制σx 的误差——计算次数曲线,并进行分析说明。
3 建模概述(1)启用ABAQUS/CAE 程序;(2)创建部件(Module :Part ),选择2D Planar ,Approximate size=2000,绘制长度为1000,高度为200的矩形;(3)创建材料和截面属性(Module:Property),弹性模量为E=210000 MPa,泊松比为0.3;(4)定义装配件(Module:Assembly),选择Independent;(5)设置分析步(Module:Step);(6)定义边界条件和载荷(Module:Load),将左右两边界在中点分成两段,在梁的上侧面施加1Mpa的载荷,选取左边界中点设置U1=0和U2=0,选取右边界中点设置U2=0;(7)划分网格(Module:Mesh),全局尺寸设为50,采用3节点线性平面应力三角形单元CPS3划分网格;(8)提交分析作业(Module:Job);(9)后处理(Module:Visualization):①显示的应力云图;②查询底边中点的最大值,与理论最大应力值比较考察其精度;③绘制底边上各点的应力的曲线;(10)细化网格验证收敛性,重设单元尺寸为20和10,给出和的应力云图,考察收敛于理论解的程度;(11)高阶单元分析,将单元类型改为CPS8,单元尺寸分别取为100、50、20:①绘制和的云图;②查询底边中点的最大值,对比(10)和(11)中的结果,体会高精度有限元网格的精度和收敛性;③查询模型中从上至下的值。
4 计算结果分析讨论与结论(1)尺寸大小为50的3节点三角形单元计算云图如下:1)x方向应力云图梁中部x方向应力分量最大值为:19.57512)y 方向应力云图上边界xσ方向应力分布曲线:上边界法向最大应力:-1.54372下边界xσ方向应力分布曲线:下边界法向最大应力:0.5437243)y方向位移云图梁中部y方向最大位移:-0.157743(2)尺寸大小为50的四节点完全积分计算云图如下:1)x方向应力云图梁中部x方向应力分量最大值为:28.6935 2)y方向应力云图上边界x σ方向应力分布曲线:上边界法向最大应力:-3.1434下边界xσ方向应力分布曲线:下边界法向最大应力:2.14343)位移云图梁中部y 方向最大位移:-0.188218(3)尺寸大小为50的四节点减缩积分1)x 方向应力云图梁中部x 方向应力分量最大值为:23.33512)y 方向应力云图上边界x方向应力分布曲线:上边界法向最大应力:-1.04348下边界x 方向应力分布曲线:下边界法向最大应力:0.04348213)位移云图梁中部y 方向最大位移:-0.240197(4)尺寸大小为50的四节点非协调模式积分1)x 方向应力云图梁中部x 方向应力分量最大值为:29.27662)y 方向应力云图上边界xσ方向应力分布曲线:上边界法向最大应力:-0.900612下边界xσ方向应力分布曲线:下边界法向最大应力:-0.09938853)位移云图梁中部y方向最大位移:-0.196154(5)尺寸大小为50的八节点二次等参元完全积分1)x方向应力云图梁中部x方向应力分量最大值为:29.5572 2)y方向应力云图上边界x σ方向应力分布曲线:上边界法向最大应力:-1.04859下边界xσ方向应力分布曲线:下边界法向最大应力:0.04859323)位移云图梁中部y 方向最大位移:-0.198043(6)尺寸大小为20的3节点三角形单元1)x 方向应力云图梁中部x 方向应力分量最大值为:25.68172)y 方向应力云图上边界x方向应力分布曲线:上边界法向最大应力:-1.35765下边界x 方向应力分布曲线:下边界法向最大应力:0.3576523)位移云图梁中部y 方向最大位移:-0.187793(7)尺寸大小为10的3节点三角形单元1)x 方向应力云图梁中部x 方向应力分量最大值为:27.90662)y 方向应力云图上边界xσ方向应力分布曲线:上边界法向最大应力:-1.19271下边界xσ方向应力分布曲线:下边界法向最大应力:0.1927053)位移云图梁中部y方向最大位移:-0.195956(8)尺寸大小为20的8节点二次等参元1)x方向应力云图梁中部x方向应力分量最大值为:29.5085 2)y方向应力云图上边界x σ方向应力分布曲线:上边界法向最大应力:-1.01358下边界xσ方向应力分布曲线:下边界法向最大应力:0.01358293)位移云图梁中部y 方向最大位移:-0.199315(9)尺寸大小为10的8节点四边形等参单元1)x 方向应力云图梁中部x 方向应力分量最大值为:27.59812)y 方向应力云图上边界x方向应力分布曲线:上边界法向最大应力:-1.00365下边界x 方向应力分布曲线:下边界法向最大应力:0.003645013)位移云图梁中部y 方向最大位移:-0.200394单元尺寸为50的不同类型单元有限元分析结果:相同类型单元不同网格密度下的有限元分析对比:在同等网格密度下计算水平方向应力分量时,二次单元的计算精度要优于线性单元。
在单元阶数相同的情况下,三角形单元计算精度次于四节点单元。
此外,减缩积分的线性四节点单元因为存在沙漏模式,其应力的计算精度要比同为线性四节点单元的完全积分单元和非协调模式的单元低。
在同等网格密度下计算法向应力分量时,减缩积分的线性四节点单元的计算精度最高,其次依次是八节点二次单元、非协调模式的线性四节点单元、三角形单元、完全积分的线性四节点单元。
用八节点二次单元和线性四节点非协调单元计算应力是比较合适的方案。
在同等网格密度下计算位移,八节点二次单元的精度最高,非协调模式的线性四节点单元的精度次之,这两种单元的误差都在5%以内,而其他单元的计算精度都偏大。
5 实验体会与小结通过本次实验,我基本掌握了使用ABAQUS软件建模求解平面应力问题,学会了查询应力以及位移分布情况的方法。
了解了单元尺寸变化和单元类型不同对结果精度的影响。
单元尺寸越小,精度越高,收敛性越好。
高精度单元收敛速度快,运算精度高。
但要根据实际情况选择合理的单元,提高计算效率。
上机实验三1 实验题目一个矩形平板,长1000mm,宽100mm ,厚度5mm 。
材料的E=200GPa ,0.3=μ, 3-6/107.82mm Kg ⨯=ρ。
板的一对短边简支。
进行下列计算分析并撰写实验报告。
1)在相同的粗网格(厚度方向1层单元)下,分别用8节点线性六面体全积分等参元、8节点六面体非协调元、20节点二次六面体等参元计算其前六阶自由振动频率(Hz ),对计算结果用表格作汇总对比和分析(不要附图)。
2)采用适当网格密度的8节点六面体非协调元,用隐式直接积分法对该平板进行瞬态响应研究。
板的上表面受对称三角形脉冲均布压力,最大值0.05MPa 。
要求:(1)通过计算获得平板下表面中心位置沿长边方向的正应力分量响应最大值随载荷脉宽(0.2毫秒、1.0毫秒、6毫秒、100毫秒、1秒、静载)变化的曲线;(2)板的厚度改50mm ,研究上述规律的变化,并进行归纳和对比分析讨论。
