用计算机模拟掷硬币的试验
Buffon掷针实验的计算机模拟实验的设计与实现

Buffon 掷针实验的计算机模拟实验的设计与实现收稿日期:2018-12-05基金项目:长沙理工大学大学生研究性学习与创新性实验项目(1203058);长沙理工大学教研教改项目(CNJG201808)作者简介:周浙泉,王志宇,张棣妍(女),隆超怡(女),长沙理工大学信息与计算科学专业2014级学生;万勇(1963-),硕士研究生,教授,研究方向:几何分析与偏微分方程。
一、研究背景18世纪,蒲丰(Buffon )提出Buffon 投针问题:(1)取一张白纸,在上面画上许多条间距为a 的平行线。
(2)取一根长度为l (l ≤a/2)的针,随机地向画有平行直线的纸上掷n 次,观察针与直线相交的次数,记为m 。
(3)计算针与直线相交的概率。
蒲丰证明了这个概率是:p=2l πa。
因为它与π有关,人们想到利用投针实验来估计圆周率的值。
历史上,有不少人做过蒲丰掷针实验:这个问题十分有趣,只是人工实验往往耗时、耗力,而用计算机模拟实验,却能迅速获得结果。
自从20世纪90年代美国率先开始数学实验以来,数学实验改变了人们传统的数学思维方式,人们发现数学是可以借助计算机去探索和发现的。
近十年来,国内外已有不少的数学实验教材和一些好的数学实验范例,但是这需要一定的计算机编程能力,如math-ematica 编程、matlab 编程等,才能实现人机对话,因此数学实验只能在具有一定数学知识和较高计算机编程能力的特定人群中使用,不能“飞入寻常百姓家”。
二、系统的设计本系统研发工具为Java 语言。
Java 是一门面向对象编程语言,不仅吸收了C++语言的各种优点,还作为静态面向对象编程语言的代表,极好地实现了面向对象理论,允许程序员以优雅的思维方式进行复杂的编程。
Java 看起来设计得很像C++,但是能够自动处理对象的引用和间接引用,实现自动的无用单元收集,使用户不必为存储管理问题烦恼,能将更多的时间和精力花在研发上。
Java 是一个面向对象的语言。
概率论实验报告_2

概率论试验报告试验一:随机掷硬币1、模拟掷一枚硬币的随机试验(可用0——1随机数来模拟试验结果),取n=100,模拟掷n次硬币的随机试验。
记录试验结果,观察样本空间的确定性及每次试验结果的偶然性,统计正面出现的次数,并计算正面的出现的频率;试验结果如下:测试中出现零代表正面,出现一代表反面,其中共计50次正面50次反面。
2、取试验次数n=1000,将过程(1)重复三次,比较三次试验结果试验结果如下3、三次结果分别是0.501,0.503,0.521 。
这充分说明模拟情况接近真实情况,频率接近概率0.5。
试验二:高尔顿钉板试验1、自高尔顿钉板上端放一个小球, 任其自由下落. 在其下落过程中,当小球碰到钉子时从左边落下的概率为p , 从右边落下的概率为,1p -碰到下一排钉子又是如此, 最后落到底板中的某一格子. 因此任意放入一球, 则此球落入哪个格子事先难以确定. 设横排共有20=m 排钉子, 下面进行模拟实验:(1) 取,5.0=p 自板上端放入一个小球, 观察小球落下的位置; 将该实验重复作5次, 观察5次实验结果的共性及每次实验结果的偶然性;(2) 分别取,85.0,5.0,15.0=p 自板上端放入n 个小球, 取,5000=n 观察n 个小球落下后呈现的曲线我们分析可知,这是一个经典的古典概型试验问题2、具体程序:3、我们分析实验结果可知,若小球碰钉子后从两边落下的概率发生变化, 则高尔顿钉板实验中小球落入各个格子的频数发生变化, 从而频率也相应地发生变化. 而且, 当,5.0p曲线峰值的格子位置向右偏; 当><p曲线峰值的格子位置向左偏。
,5.0试验三:抽签试验1、我们做模拟实验,用1-10的随机整数来模拟实验结果。
在1-10十个随机数中,假设10代表抽到大王,将这十个数进行全排,10出现在哪个位置,就代表该位置上的人摸到大王。
每次随机排列1-10共10个数,10所在的位置随机变化,分别输出模拟实验10次, 100次,1000次的结果, 将实验结果进行统计分析, 给出分析结果。
概率论与数理统计实验2:抛硬币实验的随机模拟实验报告

10000000
5000153
4999847
0.5000153
2.数据处理
实验编号
频率
3.数据分析
(1)对于每次实验,实验之前,实验的结果是不确定的;
(2)对于每次实验,正面向上的频率有时大于0.5,有时小于0.5,正面向上的频率并不是确定值;
(3)随着实验次数的增加,正面出现的频率逐渐趋近于0.5
scanf("%d,&m"); //无用输入函数,只是为了让此程序直接可以在win7系统上以dos窗口运行
}
三、实验结果及分析
1.实验数据
投硬币实验
实验编号
实验次数
正面向上的次数
反面向上的次数
正面向上的频率
1
10
3
7
0.3
2
30
15
15
0.5
3
50
28
22
0.56
4
100
48
52
0.48
5
1000
507
30000
15088
14912
0.502933333
14
50000
24124
25876
0.48248
15
100000
50145
49855
0.50145
16
200000
1002Байду номын сангаас8
99792
0.50104
17
500000
249955
250045
0.49991
18
1000000
500198
499802
0.500198
初中信息技术 Python编程 《计算机来抛硬币》教案教学设计

初中信息技术Python编程《计算机来抛硬币》教案教学设计一、教学目标1. 知识与技能:(1)了解Python编程的基本概念;(2)掌握Python中的随机数方法;(3)能够编写简单的Python程序模拟抛硬币实验。
2. 过程与方法:(1)通过案例分析,培养学生分析问题、解决问题的能力;(2)通过动手实践,提高学生编写Python程序的能力;(3)培养学生团队合作、交流分享的良好学习习惯。
3. 情感态度与价值观:(1)培养学生对编程感兴趣,激发学生学习编程的热情;(2)培养学生勇于尝试、积极进取的精神风貌;二、教学内容1. 导入:介绍Python编程的基本概念,引导学生进入本节课的学习。
2. 抛硬币实验:讲解抛硬币实验的基本原理,让学生明白抛硬币的结果是随机的。
3. Python随机数:讲解Python中随机数的方法,如使用random 库中的randint、random等函数。
4. 编写抛硬币程序:引导学生动手编写Python程序,模拟抛硬币实验,并分析程序运行结果。
5. 拓展与应用:引导学生思考如何使用Python编程解决实际问题,如模拟掷骰子、抽奖等。
三、教学过程1. 课堂导入:(1)介绍Python编程的基本概念;(2)引导学生关注编程在现实生活中的应用。
2. 抛硬币实验:(1)讲解抛硬币实验的基本原理;(2)让学生亲自动手进行抛硬币实验,感受随机性。
3. Python随机数:(1)讲解Python中随机数的方法;(2)让学生动手实践,随机数并观察结果。
4. 编写抛硬币程序:(1)引导学生分析抛硬币实验的程序逻辑;(2)让学生动手编写Python程序,模拟抛硬币实验;(3)组织学生分享程序运行结果,讨论程序的优缺点。
5. 拓展与应用:(1)引导学生思考如何使用Python编程解决实际问题;(2)让学生尝试编写其他随机数程序,如掷骰子、抽奖等。
四、教学评价1. 学生对Python编程的基本概念的理解程度;2. 学生掌握Python随机数方法的情况;3. 学生能够独立编写抛硬币程序的能力;4. 学生对编程解决实际问题的兴趣和意识。
计算机模拟抛硬币实验教学设计
教学过程教师活动学生活动教学意图一、引入1、随机事件当你把硬币抛上去的时候,你能知道它落下来是正面朝上还是反面朝上吗?这种可能发生也可能不发生的事件,我们称为随机事件。
2、等可能事件在抛硬币试验中,只可能出现两个不同的结果,而且这两种结果出现的可能性是相等的,这一类的随机事件,我们称之为等可能事件。
3、研究问题:多次抛一枚硬币,其正面朝上和反面朝上出现的次数一样吗?4、设计实验,验证你的猜想任何结论的得出都要有依据,不能凭感觉直觉,要能有真实的数据来支撑你的结论。
实验是获取数据的更一般的方法。
“抛硬币”实验设计抛硬币的次数正面朝上反面朝上二、模拟“抛硬币”实验分析任务:1.界面设计根据你刚刚的抛硬币实验设计,填写下表。
现实中抛硬币实验计算机模拟实验所需实物所需角色所需数据所需变量2.逻辑设计现实生活中抛硬币过程:学生根据自己的生活经验回答问题学生设计探索抛硬币随机事件概率的实验学生根据现实中的抛硬币实验,对比分析计算机模拟实验的界面设计和逻辑设计从学生的生活经验出发,容易引起学生的兴趣和思考培养学生设计实验验证猜想,探索未知的能力引导学生学会从现实生活中抽象出问题模型探索随机函数的作用,填写下表命令语句输出结果四、运行程序,搜集数据运行程序,并记录数据。
实验次数正面向上反面向上10050010001500五、分析数据,并得出实验结论事实上,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示一定的稳定性。
六、科学探究过程一般要经历的步骤1.提出问题2.猜想与假设3.设计实验4.进行实验与搜集数据5.分析数据6.得出结论七、课堂小结1.随机函数2.分支结构、循环结构八、升华通过编程模拟完成生活中的大量重复实验,加强对循环结构的理解运行程序并进一步搜集数据,对数据进行分析学生回顾整个实验设培养学生用信息技术处理数据的意识让学生了解科学探究的。
浙江省金华市东阳市东阳中学2025届数学九上期末统考模拟试题含解析

浙江省金华市东阳市东阳中学2025届数学九上期末统考模拟试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)1.如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果下面有三个推断:①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.1.其中合理的是( )A .①B .②C .①②D .①③2.正五边形的每个外角度数为( )A .36︒B .72︒C .108︒D .120︒3.已知关于x 的一元二次方程2240x ax -+=的一个根是2,则a 的值为( )A .-1B .1C .-2D .24.若圆锥的底面半径为2,母线长为5,则圆锥的侧面积为( )A .5πB .10πC .20πD .40π5.下列图形中,不是中心对称图形的是( )A .B .C .D .6.已知二次函数y =kx 2-7x-7的图象与x 轴没有交点,则k 的取值范围为( )A .k >74-B .k≥74-且k≠0C .k <74-D .k >74-且k≠0 7.已知三点()11,x y 、()22,x y 、()33,x y 均在双曲线上4y x =,且1230x x x <<<,则下列各式正确的是( ) A .123y y y <<B .213y y y <<C .312y y y <<D .321y y y << 8.若O 的半径为3,且点P 到O 的圆O 的距离是5,则点P 在( ) A .O 内 B .O 上 C .O 外 D .都有可能9.如图,一只箱子沿着斜面向上运动,箱高AB =1.3cm ,当BC =2.6m 时,点B 离地面的距离BE =1m ,则此时点A 离地面的距离是( )A .2.2mB .2mC .1.8mD .1.6m10.对于反比例函数2y x=,下列说法不正确的是( ) A .点(﹣2,﹣1)在它的图象上 B .它的图象在第一、三象限C .当x >0时,y 随x 的增大而增大D .当x <0时,y 随x 的增大而减小 二、填空题(每小题3分,共24分)11.已知抛物线2y x bx c =++经过点()0,5A 、()4,5B ,那么此抛物线的对称轴是___________.12.如图是二次函数y =ax 2﹣bx +c 的图象,由图象可知,不等式ax 2﹣bx +c <0的解集是_______.13.已知二次函数222(1)22y x m x m m =--+--(m 为常数),若对于一切实数m 和均有y ≥k ,则k 的最大值为____________.142a +与52a --a =________.15.如图,在ABC 中,3AB =,6BC =,点P 是AB 边的中点,点Q 是BC 边上一个动点,当BQ =__________时,BPQ BCA △∽△相似.16.将直角边长为5cm 的等腰直角△ABC 绕点A 逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是_____cm 1.17.若一元二次方程230x x m -+=的一个根是2x =,则m =__________.18.如图,直线m ∥n ,以直线m 上的点A 为圆心,适当长为半径画弧,分别交直线m ,n 于点B 、C ,连接AC 、BC ,若∠1=30°,则∠2=_____.三、解答题(共66分)19.(10分)关于x 的一元二次方程x 2+(m +4)x ﹣2m ﹣12=0,求证:(1)方程总有两个实数根;(2)如果方程的两根相等,求此时方程的根.20.(6分)如图,直线y =﹣x +2与反比例函数y =k x的图象在第二象限内交于点A ,过点A 作AB ⊥x 轴于点B ,OB =1.(1)求该反比例函数的表达式;(2)若点P 是该反比例函数图象上一点,且△PAB 的面积为3,求点P 的坐标.21.(6分)已知关于x 的一元二次方程 2220x x m m -+-=有两个相等的实数根,求m 的值.22.(8分)(1)计算()213sin 6013605--+︒--+⨯ (2)解不等式组:()56231531123x x x x ⎧+>-⎪⎨-+-≥-⎪⎩23.(8分)定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形ABCD 中,若,A C B D ∠=∠∠≠∠,则称四边形ABCD 为准平行四边形.(1)如图①,,,,A P B C 是O 上的四个点,60APC CPB ∠=∠=︒,延长BP 到Q ,使AQ AP =.求证:四边形AQBC 是准平行四边形;(2)如图②,准平行四边形ABCD 内接于O ,,AB AD BC DC +=,若O 的半径为5,6AB =,求AC 的长;(3)如图③,在Rt ABC 中,90,30,2C A BC ∠=︒∠=︒=,若四边形ABCD 是准平行四边形,且BCD BAD ∠≠∠,请直接写出BD 长的最大值.24.(8分)如图,转盘A 的三个扇形面积相等,分别标有数字1,2,3,转盘B 的四个扇形面积相等,分别有数字1,2,3,1.转动A 、B 转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).(1)用树状图或列表法列出所有可能出现的结果;(2)求两个数字的积为奇数的概率.25.(10分)如图,二次函数的图象交x 轴于点()()1,0,4,0A B -,交y 轴于点()0,4,C P -是直线BC 下方抛物线上一动点.(1)求这个二次函数的表达式;(2)连接,PB PC ,是否存在点P ,使PBC ∆面积最大,若存在,求出点P 的坐标;若不存在,请说明理由.26.(10分)如图,已知抛物线y =﹣214x +bx +4与x 轴相交于A 、B 两点,与y 轴相交于点C ,若已知A 点的坐标为A (﹣2,0). (1)求抛物线的解析式及它的对称轴方程;(2)求点C 的坐标,连接AC 、BC 并求线段BC 所在直线的解析式;(3)在抛物线的对称轴上是否存在点Q ,使△ACQ 为等腰三角形?若存在,求出符合条件的Q 点坐标;若不存在,请说明理由.参考答案一、选择题(每小题3分,共30分)1、B【分析】随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5,据此进行判断即可.【详解】解:①当抛掷次数是100时,计算机记录“正面向上”的次数是47,“正面向上”的概率不一定是0.47,故错误;②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5,故正确;③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率不一定是0.1,故错误.故选:B .【点睛】本题考查了利用频率估计概率,明确概率的定义是解题的关键.2、B【解析】利用多边形的外角性质计算即可求出值.【详解】360°÷5=72°,故选:B .【点睛】此题考查了多边形的内角与外角,熟练掌握多边形的外角性质是解本题的关键.3、D【分析】把2x =代入原方程得到关于a 的一元一次方程,解方程即可.【详解】解:把2x =代入原方程得:4440,a -+=48,a ∴=2,a ∴=故选D .【点睛】本题考查的是一元二次方程的解的含义,掌握方程解的含义是解题的关键.4、B【分析】利用圆锥面积=Rr 计算.【详解】Rr =2510,故选:B.【点睛】此题考查圆锥的侧面积公式,共有三个公式计算圆锥的面积,做题时依据所给的条件恰当选择即可解答.5、B【分析】将一个图形绕某一点旋转180°后能与自身完全重合的图形是中心对称图形,根据定义依次判断即可得到答案.【详解】解:A 、是中心对称图形,故本选项错误;B 、不是中心对称图形,故本选项正确;C 、是中心对称图形,故本选项错误;D 、是中心对称图形,故本选项错误;故选:B .【点睛】此题考查中心对称图形的定义,熟记定义并掌握各图形的特点是解题的关键.6、C【分析】根据二次函数图像与x 轴没有交点说明240b ac -< ,建立一个关于k 的不等式,解不等式即可.【详解】∵二次函数277y kx x =--的图象与x 轴无交点,∴2040k b ac ≠⎧⎨-<⎩即049280k k ≠⎧⎨+<⎩解得74k <- 故选C .【点睛】本题主要考查一元二次方程根的判别式和二次函数图像与x 轴交点个数的关系,掌握根的判别式是解题的关键. 7、B【分析】根据反比例函数的增减性解答即可.【详解】解:∵ k=4>0,∴函数图象在一、三象限,∵1230x x x <<<∴横坐标为x 1,x 2的在第三象限,横坐标为x 3的在第一象限;∵第三象限内点的纵坐标小于0,第一象限内点的纵坐标大于0,∴y 3最大,∵在第三象限内,y 随x 的增大而减小,∴213y y y <<故答案为B .【点睛】本题考查了反比例函数的增减性,对点所在不同象限分类讨论是解答本题的关键.8、C【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系,设点与圆心的距离d ,则d >r 时,点在圆外;当d=r 时,点在圆上;当d <r 时,点在圆内.【详解】解:∵点到圆心的距离5,大于圆的半径3,∴点在圆外.故选C .【点睛】判断点与圆的位置关系,也就是比较点与圆心的距离和半径的大小关系.9、A【分析】先根据勾股定理求出CE,再利用相似三角形的判定与性质进而求出DF、AF的长即可得出AD的长.【详解】解:由题意可得:AD∥EB,则∠CFD=∠AFB=∠CBE,△CDF∽△CEB,∵∠ABF=∠CEB=90°,∠AFB=∠CBE,∴△CBE∽△AFB,∴BEFB=BCAF=ECAB,∵BC=2.6m,BE=1m,∴EC=2.4(m),即1FB=2.6AF=2.41.3,解得:FB=1324,AF=169120,∵△CDF∽△CEB,∴DFEB=CFCB,即132.624 1 2.6 DF-=解得:DF=19 24,故AD=AF+DF=1924+169120=2.2(m),答:此时点A离地面的距离为2.2m.故选:A.【点睛】本题考查了勾股定理、相似三角形的判定和性质,利用勾股定理,正确利用相似三角形的性质得出FD的长是解题的关键.10、C【详解】由题意分析可知,一个点在函数图像上则代入该点必定满足该函数解析式,点(-2,-1)代入可得,x=-2时,y=-1,所以该点在函数图象上,A正确;因为2大于0所以该函数图象在第一,三象限,所以B正确;C中,因为2大于0,所以该函数在x >0时,y 随x 的增大而减小,所以C 错误;D 中,当x <0时,y 随x 的增大而减小,正确, 故选C.考点:反比例函数【点睛】本题属于对反比例函数的基本性质以及反比例函数的在各个象限单调性的变化二、填空题(每小题3分,共24分)11、直线2x =【分析】根据点A 、B 的纵坐标相等判断出A 、B 关于对称轴对称,然后列式计算即可得解.【详解】解:∵点()0,5A 、()4,5B 的纵坐标都是5相同, ∴抛物线的对称轴为直线0422x +==. 故答案为:直线2x =.【点睛】此题考查二次函数的性质,观察出A 、B 是对称点是解题的关键.12、x <-1或x >1【分析】根据二次函数的对称性求出与x 轴的另一个交点坐标,然后根据函数图象写出x 轴上方部分的x 的取值范围即可.【详解】解:由对称性得:抛物线与x 轴的另一个交点为(-1,0),∴不等式ax 2﹣bx +c <0的解集是:x <-1或x >1,故答案为:x <-1或x >1.【点睛】本题考查了二次函数与不等式组,二次函数的性质,此类题目,利用数形结合的思想求解是解题的关键.13、134- 【分析】因为二次函数系数大于0,先用含有m 的代数式表示出函数y 的最小值,得出min y 23m m =+-,再求出于m 的函数23M m m =+-的最小值即可得出结果.【详解】解: 222(1)22y x m x m m =--+--,22min 41(22)4(1)41m m m y ⨯⨯----=⨯23m m =+-, 关于m 的函数为23M m m =+-,2min 41(3)113=414M ⨯⨯--=-⨯, ∴134k -≥, ∴k 的最大值为134-. 【点睛】 本题考查二次函数的最值问题,先将函数化为顶点式,即可得出最值.14、1【分析】根据同类二次根式的定义可得a+2=5a-2,即可求出a 值.与∴a+2=5a-2,解得:a=1.故答案为:1【点睛】本题考查了同类二次根式:把各二次根式化为最简二次根式后若被开方数相同,那么这样的二次根式叫同类二次根式;熟记定义是解题关键.15、34【分析】直接利用BPQ BCA △∽△,找到对应边的关系,即可得出答案.【详解】解:当BPQ BCA △∽△时, 则BP BQ BC AB=, ∵3AB =,点P 是AB 边的中点, ∴1133222BP AB ==⨯= ∵6BC =, ∴3263BQ =则34BQ = 综上所述:当BQ=34时,BPQ BCA △∽△. 故答案为:34.【点睛】此题主要考查了相似三角形的性质,得到对应边成比例是解答此题的关键.16 【解析】∵等腰直角△ABC 绕点A 逆时针旋转15°后得到△AB′C′,∵∠CAC′=15°,∴∠C′AB=∠CAB ﹣∠CAC′=45°﹣15°=30°,AC′=AC=5,∴阴影部分的面积=12×5×tan30°×. 17、1【分析】将x=1代入一元二次方程230x x m -+=,即可求得m 的值,本题得以解决.【详解】解:∵一元二次方程230x x m -+=有一个根为x=1,∴11-6+m=0,解得,m=1,故答案为1.【点睛】本题考查一元二次方程的解,解答本题的关键是明确题意,求出m 的值.18、75°【解析】试题解析:∵直线l 1∥l 2,∴130.A ∠=∠= ,AB AC =75.ACB B ∴∠=∠=2180175.ACB ∴∠=-∠-∠=故答案为75.三、解答题(共66分)19、(1)见解析;(1)x 1=x 1=1.【分析】(1)由△=(m +4)1−4(−1m−11)=(m +8)1≥0知方程有两个实数根;(1)如果方程的两根相等,则△=(m +8)1=0,据此求出m 的值,代入方程求解可得.【详解】(1)∵△=(m+4)1﹣4(﹣1m ﹣11)=m 1+16m+64=(m+8)1≥0,∴方程总有两个实数根;(1)如果方程的两根相等,则△=(m+8)1=0,解得m =﹣8,此时方程为x 1﹣4x+4=0,即(x ﹣1)1=0,解得x 1=x 1=1.【点睛】本题考查了一元二次方程ax 1+bx +c =0(a≠0)的根的判别式△=b 1−4ac :当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.20、(1)3y x=-;(2)(﹣3,1)或(1,﹣3). 【分析】(1)先利用一次解析式确定A 点坐标为(﹣1,3),然后把A 点坐标代入y =k x 中求出k 得到反比例函数解析式;(2)设P (t ,﹣3t ),利用三角形面积公式得到12×3×|﹣3t+1|=3,然后解方程求出t ,从而得到P 点坐标. 【详解】(1)∵AB ⊥x 轴于点B ,OB =1.∴A 点的横坐标为﹣1,当x =﹣1时,y =﹣x +2=3,则A (﹣1,3),把A (﹣1,3)代入y =k x得k =﹣1×3=﹣3, ∴反比例函数解析式为3y x=-; (2)设P (t ,﹣3t ), ∵△PAB 的面积为3, ∴12×3×|﹣3t+1|=3, 解得t =﹣3或t =1,∴P 点坐标为(﹣3,1)或(1,﹣3).【点睛】此题考查待定系数法求函数解析式,一次函数与反比例函数的图象结合求几何图形的面积.21、m 1=12,m 2=12. 【解析】根据一元二次方程有两个相等实数根得△=0,再表示出含m 的一元二次方程,解方程即可.【详解】解:∵原方程有两个相等的实数根,即△=0,△=4-4(2m m -)=0,整理得:210m m --=,求根公式法解得:, ∴m 1,m 2. 【点睛】本题考查了含参一元二次方程的求解,属于简单题,熟悉求根公式和根的判别式是解题关键.22、(1)109+ (2)143x -<≤ 【分析】(1)先算乘方、特殊三角函数值、绝对值,再算乘法,最后算加减法即可.(2)分别解各个一元一次不等式,即可解得不等式组的解集.【详解】(1)()23sin 601--+︒--119=+1092=-+1092=+. (2)()56231531123x x x x ⎧+>-⎪⎨-+-≥-⎪⎩()5623x x +>-5626x x +>-312x >-解得4x >-1531123x x -+-≥- 315626x x ---≥-721x ≥解得13x ≤ 故解集为 143x -<≤. 【点睛】本题考查了实数的混合运算和解不等式组的问题,掌握实数的混合运算法则、特殊三角函数值、绝对值的性质、解不等式组的方法是解题的关键.23、(1)见解析;(2)(3)2【分析】(1)先根据同弧所对的圆周角相等证明三角形ABC 为等边三角形,得到∠ACB=60°,再求出∠APB=60°,根据AQ=AP 判定△APQ 为等边三角形,∠AQP=∠QAP=60°,故∠ACB=∠AQP ,可判断∠QAC >120°,∠QBC <120°,故∠QAC≠∠QBC ,可证四边形AQBC 是准平行四边形;(2)根据已知条件可判断∠ABC≠∠ADC ,则可得∠BAD=∠BCD=90°,连接BD ,则BD 为直径为10,根据BC=CD 得△BCD 为等腰直角三角形,则∠BAC=∠BDC=45°,在直角三角形BCD 中利用勾股定理或三角函数求出BC 的长,过B 点作BE ⊥AC ,分别在直角三角形ABE 和△BEC 中,利用三角函数和勾股定理求出AE 、CE 的长,即可求出AC 的长.(3)根据已知条件可得:∠ADC=∠ABC=60°,延长BC 到E 点,使BE=BA ,可得三角形ABE 为等边三角形,∠E=60°,过A 、E 、C 三点作圆o ,则AE 为直径,点D 在点C 另一侧的弧AE 上(点A 、点E 除外),连接BO 交弧AE 于D 点,则此时BD 的长度最大,根据已知条件求出BO 、OD 的长度,即可求解.【详解】(1)∵60APC CPB ∠=∠=︒∴∠ABC=∠BAC=60°∴△ABC 为等边三角形,∠ACB=60°∵∠APQ=180°-∠APC-∠CPB=60° 又AP=AQ∴△APQ 为等边三角形∴∠AQP=∠QAP=60°∴∠ACB=∠AQP∵∠QAC=∠QAP+∠PAB+∠BAC=120°+∠PAB >120° 故∠QBC=360°-∠AQP-∠ACB-∠QAC <120° ∴∠QAC≠∠QBC∴四边形AQBC 是准平行四边形(2)连接BD ,过B 点作BE ⊥AC 于E 点∵准平行四边形ABCD 内接于O ,,≠=AB AD BC DC∴∠ABC≠∠ADC ,∠BAD=∠BCD∵∠BAD+∠BCD=180°∴∠BAD=∠BCD=90°∴BD 为O 的直径 ∵O 的半径为5∴BD=10∵BC=CD,∠BCD=90°∴∠CBD=∠BDC=45°∴BC=BD ⨯ sin ∠BDC=102=52⨯,∠BAC=∠BDC=45° ∵BE ⊥AC∴∠BEA=∠BEC=90°∴AE=AB ⨯sin ∠BAC=6⨯2=322 ∵∠ABE=∠BAE=45°∴BE=AE=32在直角三角形BEC 中,222BC BE -=∴AC=AE+EC=72(3)在Rt ABC 中,90,30∠=︒∠=︒C A∴∠ABC=60°∵四边形ABCD是准平行四边形,且BCD BAD∠≠∠∴∠ADC=∠ABC=60°延长BC 到E点,使BE=BA,可得三角形ABE为等边三角形,∠E=60°,过A、E、C三点作圆o,因为∠ACE=90°,则AE为直径,点D在点C另一侧的弧AE上(点A、点E除外),此时,∠ADC=∠AEC=60°,连接BO交弧AE于D点,则此时BD的长度最大.在等边三角形ABE中,∠ACB=90°,BC=2∴AE=BE=2BC=4∴OE=OA=OD=2∴BO⊥AE∴BO=BE⨯sin∠E=43=232⨯∴BD=BO+0D=2+23即BD长的最大值为2+23【点睛】本题考查的是新概念及圆的相关知识,理解新概念的含义、掌握圆的性质是解答的关键,本题的难点在第(3)小问,考查的是与圆相关的最大值及最小值问题,把握其中的不变量作出圆是关键.24、(1)结果见解析;(2).【解析】解:(1)画树状图得:则共有12种等可能的结果;(2)∵两个数字的积为奇数的1种情况, ∴两个数字的积为奇数的概率为: .试题分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;(2)由两个数字的积为奇数的情况,再利用概率公式即可求得答案.25、(1)234y x x =--;(2)存在点P ,使PBC ∆面积最大,点P 的坐标为()2, 6-. 【分析】(1)由A 、B 、C 三点的坐标,利用待定系数法可求得抛物线解析式;(2)过P 作PE ⊥x 轴,交x 轴于点E ,交直线BC 于点F ,用P 点坐标可表示出PF 的长,则可表示出△PBC 的面积,利用二次函数的性质可求得△PBC 面积的最大值及P 点的坐标.【详解】(1)∵二次函数的图象交y 轴于点()0,4C -,∴设二次函数表达式为24y ax bx =+-, 把A 、B 二点坐标代入可得4016440a b a b --=⎧⎨+-=⎩, 解这个方程组,得13a b =⎧⎨=-⎩, ∴抛物线解析式为:234y x x =--;(2))∵点P 在抛物线上,∴设点P 的坐标为()2,34t t t --过P 作PE x ⊥轴于E ,交直线BC 于F设直线BC 的函数表达式y mx n =+,将B (4,0),C (0,-4)代入得404m n n +=⎧⎨=-⎩,解这个方程组,得14m n =⎧⎨=-⎩, ∴直线BC 解析式为4y x =-,∴点F 的坐标为(),4t t -,()()224344PF t t t t t ∴=----=-+, ()2114422PBC S PF OB t t ∆∴==-+⨯ ()2228t =--+,∵20a =->,∴当2t =时,PBC S ∆最大,此时223423246y t t =--=-⨯-=-,所以存在点P ,使PBC ∆面积最大,点P 的坐标为()2, 6-.【点睛】本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、三角形的面积、方程思想等知识.在(1)中注意待定系数法的应用,在(2)中用P 点坐标表示出△PBC 的面积是解题的关键.26、(1)y=-14x 2+32x+2,x=1;(2)C (0,2);y=−12x+2;(1)Q 1(1,0),Q 2(1,),Q 1(1,). 【分析】(1)利用待定系数法求出抛物线解析式,利用配方法或利用公式x=−2b a 求出对称轴方程; (2)在抛物线解析式中,令x=0,可求出点C 坐标;令y=0,可求出点B 坐标.再利用待定系数法求出直线BD 的解析式;(1)本问为存在型问题.若△ACQ 为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解. 【详解】解:(1)∵抛物线y=-14x 2+bx+2的图象经过点A (-2,0), ∴-14×(-2)2+b×(-2)+2=0, 解得:b=32, ∴抛物线解析式为 y=-14x 2+32x+2, 又∵y=-14x 2+32x+2=-14(x-1)2+254, ∴对称轴方程为:x=1.(2)在y=-14x 2+32x+2中,令x=0,得y=2, ∴C (0,2); 令y=0,即-14x 2+32x+2=0,整理得x2-6x-16=0,解得:x=8或x=-2, ∴A (-2,0),B (8,0).设直线BC 的解析式为y=kx+b ,把B (8,0),C (0,2)的坐标分别代入解析式,得: 804k b b +=⎧⎨=⎩, 解得124k b ⎧=-⎪⎨⎪=⎩,∴直线BC 的解析式为:y=−12x+2. ∵抛物线的对称轴方程为:x=1,可设点Q (1,t ),则可求得:===.i )当AQ=CQ, 25+t 2=t 2-8t+16+9,解得t=0,∴Q 1(1,0);ii )当AC=AQ时,有=t 2=-5,此方程无实数根,∴此时△ACQ 不能构成等腰三角形;iii )当AC=CQ=, 整理得:t 2-8t+5=0,解得:,∴点Q 坐标为:Q 2(1,),Q 1(1,).综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(1,0),Q2(1,),Q1(1,).【点睛】本题考查二次函数综合题,综合性较强,有一定难度,注意分类讨论是本题的解题关键.。
概率的实验报告之硬币实验

实验一频率的稳定性
——模拟投币试验及其推广
实验序号:1日期:2013年3月31日
实验目的和内容:
实验目的:让实验者学习在计算机上模拟投币试验和抛掷骰子试验的方法,通过本实验熟悉在Excle中产生常见随机数的步骤,并从实验结果中观察体会频率的稳定性。
内容:利用Excle中的随机数发生器分别产生:伯努利随机数(即0-1随机数)、(0,1)区间上均匀分布随机数来模拟投币试验并对试验结果进行分析以及产生离散均匀分布随机数来模拟投掷骰子试验并对试验结果进行分析。
然而,在实践过程中也遇到了许多问题,例如,EXCEL的工具,菜单很多,不易记住,所以要多练习才能熟练掌握。而且,EXCEL中涉及的数学函数很多也很容易混淆,它们都是我们在掌握和使用EXCEL的一大问题,当然,通过不断的学习和总结是可以克服这些问题的。
在使用EXCEL这个工具时是还需要注意很多细节问题,比如在实验时要多想一想同一个问题可以用不同的数学函数来解决,故在选择时就要注意每种方法的优与劣,争取使用最简捷和便易的方式来服务我们的工作和学习。
实验所用软件及版本:Excle和Excle2010
实验过程:
1.1利用Excle自带的随机数发生器产生10000个伯努利随机数(即0-1随机数)来模拟10000次投币试验的结果,统计其中随机数1(表示出现正面)和(表示出现反面)出现的次数,并对试验结果进行分析。
1.2利用随机数发生器产生10000个均匀分布U(0,1)随机数,分别记录其中小于0.5(表示出现正面)和小于0.5(表示出现反面)的随机数个数,并对试验结果进行分析。
案例9古典概型

3. 求古典概型概率的基本步骤 1) 算出所有基本事件的个数 n; 2) 求出事件 A 包含的所有基本事件数 m; 3)代入公式 P(A)=m/n,求出 P(A)。 4. 概率分布 事件的概率表示了一次试验某一个结果发生的可能性大小。 若要全面了解试 验, 则必须知道试验的全部可能结果及各种可能结果发生的概率,即必须知道随 机试验的概率分布。
币、掷骰子)。即从装有 m 个白球 n 个黑球的袋子中有放回摸球,求在摸到 a 次黑球前摸到 b 次白球的概率。 由此又可以转化为大量的应用问题, 而二项分布、 几何分布、 负பைடு நூலகம்项分布等常见离散型分布均可由点数问题引申出来,所以点数问 题的圆满解决被认为是概率论诞生的标志之一。 实验 2 赌徒梅勒的第二个问题: 当时赌徒梅勒问帕斯卡的另一个问题是:
9.2 点数问题
实验 1 点数问题: 通常认为概率论起于骰子的应用,源于点数问题(又
称分赌本问题)。所谓点数问题是:A,B 两人赌博,其技巧相当,约定谁先胜 s 局则获全部赌金。若进行到 A 胜 s1 局而 B 胜 s2 局(s1<s,s2<s)时,因故停止, 赌金该如何分配才公平?点数问题最早见于意大利数学家帕乔利(L.Pacioli, 1445-1517)的《算术、几何及比例性质摘要》中。该书记载:A,B 两人进行 一场公平赌博,约定先赢得 s=6 局者获胜。而在 A 胜 s1=5 局且 B 胜 s2=2 局时中 断。帕乔利认为该赌博最多需要进行 2(s-1)+1=11 局,因而赌金分配方案为 s1/(2s-1)与 s2/(2s-1)之比,即 s1/ s2=5/2。帕乔利的方案实际上是按已胜局数 比例分配(这也是一般人的看法), 这种分法合理吗?我们不妨通过如下实验结果 来探讨这个问题。 问题分析:在 A 已经五胜两负的基础上,用计算机模拟两人以后的博弈,计 算他们应得的赌金。 由于两位技巧相当,不妨假定他们在以后的每局比赛中胜负 机会相等。连续模拟 n 次(为了使结果更有说服力,取 n 较大,如 n>1000), 每次模拟到 A,B 双方有一方先胜 6 局为止,胜者获得全额赌金,n 次模拟结束 后,计算双方所获赌金的比例,以该比例作为赌金分配方案。 实验过程:Matlab 实验程序如下(stake.m 文件): function [Awin,Bwin,p]=stake(s1,s2,s,n) %定义函数 stake, 输入参数 s1,s2
随机模拟实验

计算结果N是n个数的一维数组,分别表示data中各个小区间的数据量。 这种方式只计算而不绘图。
数学实验
例: 统计10000个均匀随机数在五个小区间的分布。
即观察10000 个随机数在[0,0.2],[0.2,0.4], [0.4,0.6],[0.6,0.8],[0.8,1]的分布情况。 data=rand(10000,1); figure(1),hist(data,5) N5=hist(data,5) figure(2),bar(N5,'r')
(1)甲比乙先到码头:x
数学实验
function F=shipmeet(N) if nargin==0, N=2000; end P=24*rand(2,N); X=P(1,:);Y=P(2,:); I=find(X<=Y&Y<=X+2); J=find(Y<=X&X<=Y+1); F=(length(I)+length(J))/N plot(X,Y,’b.’) ,hold on axis([0 24 0 24]) h1=plot([0 24],[0,24],’k’) h2=plot([1 24],[0,23],’r’) h3=plot([0 22],[2,24],’b’) set([h1,h2,h3],’linewidth’,2)
0, 0 r 0.5 f(r ) 0.5 r 1 1,
如果 0.5<r<1,认为出现数字面X=1,否则出现图案面
数学实验
算法设计: 输入:抛硬币次数n
输出:抛硬币出现数字面的概率估计值 p
1. 2. 3. 4. 5. 6.
初始化count=0 对于i=1,2,…,n,执行第3~4步 产生[0,1]上的随机数r 如果0.5<r<1,则count=count+1 计算p=count/n 输出p
基于计算工具模拟抛硬币实验
3 基于Vs a C+ 模 拟抛硬 币实验 i l + u
31编程 环境及 思路 . 本程序基于M c o o t V s a c+ 60 ir s f iu l 十 .编写, 利用tm 函 ie
数和s a d r n 函数构成 sa d(i e(U L ) 使随机数种子随时 rn tm N L ) ,
o re a ng f l ti ma he t mat c e peri i a1 x men i hi to . ts n s ry
K y w r s c i o sn ;M TA ;L n a o g u ni lG nr t r (C ) a d m e o d :on t s ig A L B ie r C n r e ta e e ao L G:r n o
正面 背面 总计
代代数学家不懈探索 , 进行 了大量 实验并为我们 留下 了宝贵 的实验 数据 。 随着 科学技 术 的发展 , 学计算 器 、 A L B 科 M T A 和
V s a C + 台卓越的计算能力为我们在不耗 费大 量时间的 iu l +平
情况下进 行大 量抛硬币模拟和结论的验证提供了可能。 过科 通 学计 算器上 自带的线性同余数 生成器, 以及在M T A 和V sa A L B iu l c + 过优化 的随机 数生 成函数得到相应数 量的数据 , 比于 +经 相
数学建模-计算机仿真分析

我缉私雷达发现前方(南)c km处有一艘走私船正 以速度a沿直线向东匀速行驶,缉私艇立即以最大速度b 追赶,若用雷达进行跟踪,缉私艇的瞬时速度方向始终 指向走私船,是求缉私艇追逐路线和追赶上的时间。
分析 此问题可以建立微分方程模型,这里我们建立差分方 程模型,用仿真的方法求解。
取时间步长为h,在第i 步时的时间即t=hi,走私船的位
(1)从发出订货到收到货物需隔三天; (2)每辆自行车保管费为0.75元/天,每辆自行车的缺货损
失为1.8元/天,每次的订货费为75元; (3)每天自行车的需求量服从0到99之间的均匀分布; (4)原始库存为115辆,并假设第一天没有发出订货。 若现在已有如下表所示的五种库存策略,请选择一种总费用
求解方法: 1、高数中的方法
f(x0,
x0
y0)
n
i1
Qi(xi x0)
0
((xi x0)2 (yi y0)2
f(x0,
y0
y0)
n
i1
Qi(yi x0)
0
((xi x0)2 (yi y0)2
2、数值计算方法
3、计算机仿真: 离散化,遍历!
16
计算机仿真案例2
例2 (赶火车过程仿真)一列火车从A站经过B站开 往C站,某人每天赶往B站乘这趟火车。已知火车从 A站到B站的运行时间是均值为30min、标准差为 2min的正态随机变量。火车大约在下午1点离开A 站。火车离开时刻的频率分布和这个人到达B站时
产生一个均值为 ,方差为 的正态分布的随机数: normrnd ( , )
•当研究对象视为大量相互独立的随机变量之和,且其中每 一种变量对总和的影响都很小时,可以认为该对象服从正态 分布.
•机械加工得到的零件尺寸的偏差、射击命中点与目标的偏差、 各种测量误差、人的身高、体重等,都可近似看成服从正态 分布.
计算机模拟抛硬币实验

Scratch编程模拟抛硬币实验
任务一:模拟随机事件
Scratch编程模拟抛硬币实验
任务二:根据随机数的结果,让硬币切换造型,并记录正面 向上和反面向上的次数
分支结构
Scratch编程模拟抛硬币实验
循任环结务构 三:多次重复实验
Scratch编程模拟抛硬币实验
任务:设计程序,模拟抛硬币实验
现实中的抛硬币游戏过程
Scratch趣味编程
THANK YOU
人大附中朝阳分校
王慧敏
Scratch编程模拟抛硬币实验
scratch中的随机函数
Scratch编程模拟抛硬币实验
活动:探索随机函数的作用
设计一个简单的程序,分别使用下面的命令语句,观察程序的输出结果
0,1 0.00,0.01,0.23,0.78,…1.00 0,1,3,4,5,… 10 -2,-1,0,1,2
Scratch编程模拟抛硬币实验
计算机模拟抛硬币实验
Scratch趣味编程
从抛硬币说起
从抛硬币说起
随机事件
当你把硬币抛上去的时候,你能知道它落下来是正面向上 还是反面向上吗?
这种可能发生也可能不发生的事件,我们称为随机事件。
从抛硬币说起
等可能事件
在抛硬币试验中,只可能出现两个不同的结果,而且这两种结果 出现的可能性是相等的,这一类的随机事件,我们称之为等可能 事件。
计算机模拟抛硬币游戏过程
分支结构
解决问题的关键 用计算机模拟能够产生两种结果的随机事件。
Scratch编程模拟抛硬币实验
现实中的抛硬币游戏过程
抛硬币
重
产生两种结果之一 复
多
次
正
反
实 验
随机事件的模拟-----模拟掷均匀硬币的随机试验报告

教师评语与成绩:
实验所用软件及版本:Microsoft office Excel 2010
主要内容(要点):
利用Excel中的随机数发生器分别产生伯努利随机数,(0-1)区间上均匀分布随机数来模拟投币实验并对实验结果进行分析以及产生离散均匀分布随机数来模拟投掷骰子实验并对实验结果进行分析。
实验过程:(含解决方法和基本步骤,主要程序清单及异常情况记录等)
二、统计随机数的个数
(1)打开“插入函数”,在弹出的对话框中,在“或选择类别”处选择“统计”,在“选择函数”处选择“COUNTIF”后单击“确定”;
(2)在弹出的另一个对话框中,在“range”处填上要统计的这n个数在表格中的位置,,单击“确定”后就会在表格中的指定位置处出现“0”或“1”的个数。三、分析数据
实验目的:
(1)学习和掌握Excel的有关命令
(2)了解均匀分布随机数的产生
(3)理解掌握随机模拟的方法.
(4)体会频率的稳定性.
实验原理与数学模型:
本实验的关键在于如何产生随机数,即如何模拟抛硬币。分析硬币可能出现的现象为正反面,则他们的概率各位0.5。用Excel随机产生n个数(0或1),其原理同随机抛一枚均匀硬币出现正反面的结果,其中“1”代表“出现正面”,“0”代表出现“出现反面”。从而通过统计0和1的个数就可以知道出现正反面的次数,也就可以直达出现正反面的概率。
班级
姓名
学号
实验
名称
随机事件的模拟-----模拟掷均匀硬币的随机试验
问题的背景:
抛硬币实是一个古老而现实的问题,我们可以从中得出许多结论.但要做这个简单而重复的试验,很多人没有多余的时间或耐心来完成它,现在有了计算机的帮助,人人都可很短的时间内完成它.
模拟投硬币试验

通过数据分析得出结论:当n的值很大时,出现1和0的概率更稳定。
(2)、掷骰子的实验数据如下图:
通过数据分析:当投掷次数越大时。各点数才越接近1/6,且概率差不多。
实验结果与实验总结(体会):
实验结果:通过数据分析,得出的结论是:“出现1”和“出现0”的概率均趋于0.5,就是出现正面和出现反面的概率均趋于0.5,而且随着n值的增大,概率越稳定。
实验过程:(含解决方法和基本步骤,主要程序清单及异常情况记录等)
一、产生随机数
(1)用Excel表格完成模拟实验,打开Excel,在“工具栏”中选择“数据分析”,在弹出的对话框中选择“随机发生器”,单击“确定”后弹出“随机发生器”;
(2)在“变量”处填上“1”,在“随机数个数”处填上“n”,在“分布”处填上“伯努利”,在“p(A)”处填上“0.5”,在“输出区域”处填上要输出的第一个数据的位置,单击“确定”后就产生了n个随机数。
数学模型:
本实验利用Excel数据分析工具中的随机数发生器,分别产生伯努利随机数和均匀分布随机数来模拟投币试验出现的正面和反面的实验结果,再产生离散均匀分布随机数来模拟掷骰子试验的结果,从而在计算机上快速模拟这些试验的整个过程并对试验结果将进行分析总结。
实验所用软件及版本:Microsoftoffice Excel 2007
实验总结:概率论与数理统计的研究对象都是随机事件,所以产生的数必须是随机数数,而且需要通过大量的实验数据才能统计出实验结果,所以随机数应尽量大一些,实实验数组也该多一些才能得到相对正确的答案。
进一步讨论或展望:
通过本次实验,我们以后也可以用Excel模拟随机事件,从而确定出现的现象的概率。
教师评语与成绩:
概率论抛硬币和抛筛子实验报告

学 号:1250901235
2013-2014学年第_2_ _学期
数学与统计学院制
实验地点
三教A510
课程类
别
①公共课口②
专业课"
实验日期
14324
实验编
组
第1
组
实验所
用时间
2
小时
实验名称
掷均匀硬币和骰子实验模拟结果及有关数据统计表
实 验 目 的
(1)理解频率具有客观稳疋性;
(2)理解概率是频率的稳定值;
0.1717
0.1582
0.2088
0.1380
147
0.1497
0.1361
0.2177
0.1905
0.1088
0.1973
123
0.2114
0.2033
0.1789
0.1951
0.1138
0.0976
1245
0.1719
0.1663
0.1679
0.1695
0.1823
0.1422
23456
模拟次数为289次的统计图
function Tybsy(N)
X=bi nornd(1,0.5,1,N)
n1=0;
n2=0;
for i=1:N
if X(i)==0
n1=n1+1;
else
n2=n2+1;
end
end
n1
n2
pn仁n1/N
pn2=n2/N
n=[ n1,n 2];
bar( n);
编程如下:
function pszsy (N)
实验内容
实验一:抛硬币实验
92模拟随机抛硬币实验

9.2模拟随机抛硬币实验(一)参数变量的系统初始值和重新赋值对于测量得到的第一个结果,系统会自动用变量m000表示。
这样做的好处是便于后面利用这个测量结果参加更复杂的运算。
就像我们习惯用△表示b2-4ac,只要将ax2+bx+c=0的根表示为:然后第二个、第三个、第四个...测量结果分别用m001、m002、m003 ...表示。
实际上对于每一个参数变量,例如m000、m001、...,系统内部都有一个初始值,只不过我们在进行测量操作的过程中,将这些测量结果依次赋值给了变量m000、m001、...。
这就像前面在程序工作区中对一个参数变量赋值的操作一样:例如在程序工作区中输入“a=1;b=2;”,然后执行命令。
为了验证这一点,你可以一个新建文档中,没有进行任何测量操作之前,通过【插入】菜单中的【变量对象...】插入参数变量m000的变量控制对象,如下图所示,可以观察它当前的系统初始值。
然后作一个任意点A,通过【测量】菜单中【点】子菜单下的【x坐标】命令,测量点A的x坐标,得到测量文本的同时,你会发现在参数m000的变量控制尺中对应的数值也对应改变。
这个过程就类似于在程序工作区中对一个参数变量重新赋值。
(二)系统更新与执行命令前面提到过,在程序工作区中输入rand(-1,1)后,多次执行该函数命令,则会得到一系列返回结果,如下图所示:每执行一次命令,系统内部就更新一次,也会对rand(-1,1)重新运算一次取一个新的结果。
在作图区中,执行一个动作,例如拖动一下坐标原点O,系统内部也会自动更新,从而在屏幕上重新画出坐标系的图像。
下面我们通过测量得到rand(-1,1)的返回结果,操作如下:(1)打开测量表达式对话框,测量rand(-1,1)的值,如下图所示:系统把测量得到的第一个结果用变量m000表示。
然后第二、第三...个测量结果分别用m001、m002、...表示。
在程序工作区中我们可以通过执行一次语句命令“a=a+1;”,让a的值增加1。
10.3.1频率的稳定性10.3.2 随机模拟

三、例题精讲
例1.从你所在班级任意选出6名同学,调查他们出生月份,假设出生在一月, 二月,··· ···十二月是等可能的.设事件A=“至少有两人出生月份相同”, 设计一种试验方法,模拟20次,估计事件A发生的概率.
方法1:
方法2:随机模拟
例2.在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设 每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验, 估计甲获得冠军的概率.
随机模拟
四、课堂变式
盒子中仅有4个白球和5个黑球, 从中任意取出一个球.
(1)“取出的球是黄球”是什么事件?它的概率是多少? (2)“取出的球是白球”是什么事件?它的概率是多少? (3)“取出的球是白球或黑球”是什么事件?它的概率 是多少?
(4)设计计算机模拟上面的取球试验,并模拟100次,估计“取出的 球是白球”的概率.
10.3.2随 机 模 拟 制作:申占宝
一、引入新课 用频率估计概率,需要做大量的重复试验,有没有其他办法可以代替试验呢? 抛掷硬币,出现正面向上为事件A,求概率
二、探究新知
一个袋中装有2个红球和3个白球,这些球除颜色不同外没有其他差别,估计从
袋中摸出一个球为红球的概率.
n 下表是用电子表格软件模拟上述摸球试验的结果,其中
10.3.1 频率的稳定性 制作:申占宝
一、探究
重复做同时抛掷两枚质地均匀的硬币的试验,设事件A=“一个正面朝上, 一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较.你发
现了什么规律?
1、利用计算机模拟掷两枚硬币的试验,在重复试验次数为 20,100,500 时各做 5 组试验,得到事件 A=“一个正面 朝上,一个反面朝上”发生的频数 nA 和频率 fn ( A) 如下表:
用 MATLAB 模拟掷硬币过程
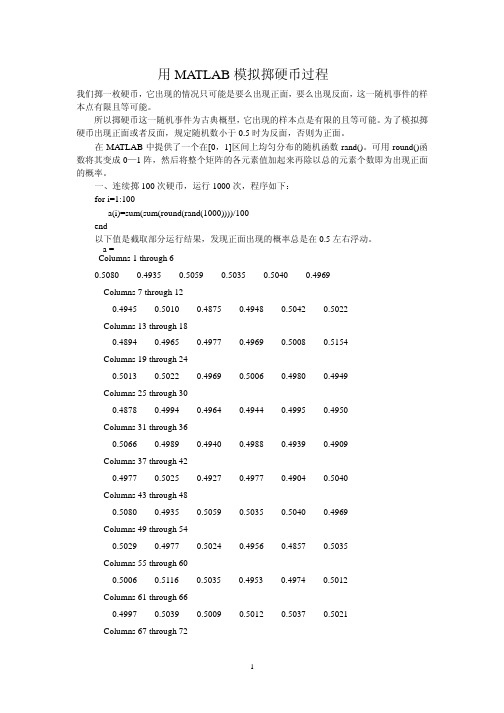
用MATLAB模拟掷硬币过程我们掷一枚硬币,它出现的情况只可能是要么出现正面,要么出现反面,这一随机事件的样本点有限且等可能。
所以掷硬币这一随机事件为古典概型,它出现的样本点是有限的且等可能。
为了模拟掷硬币出现正面或者反面,规定随机数小于0.5时为反面,否则为正面。
在MATLAB中提供了一个在[0,1]区间上均匀分布的随机函数rand()。
可用round()函数将其变成0—1阵,然后将整个矩阵的各元素值加起来再除以总的元素个数即为出现正面的概率。
一、连续掷100次硬币,运行1000次,程序如下:for i=1:100a(i)=sum(sum(round(rand(1000))))/100end以下值是截取部分运行结果,发现正面出现的概率总是在0.5左右浮动。
a =Columns 1 through 60.5080 0.4935 0.5059 0.5035 0.5040 0.4969Columns 7 through 120.4945 0.5010 0.4875 0.4948 0.5042 0.5022Columns 13 through 180.4894 0.4965 0.4977 0.4969 0.5008 0.5154Columns 19 through 240.5013 0.5022 0.4969 0.5006 0.4980 0.4949Columns 25 through 300.4878 0.4994 0.4964 0.4944 0.4995 0.4950Columns 31 through 360.5066 0.4989 0.4940 0.4988 0.4939 0.4909Columns 37 through 420.4977 0.5025 0.4927 0.4977 0.4904 0.5040Columns 43 through 480.5080 0.4935 0.5059 0.5035 0.5040 0.4969Columns 49 through 540.5029 0.4977 0.5024 0.4956 0.4857 0.5035Columns 55 through 600.5006 0.5116 0.5035 0.4953 0.4974 0.5012Columns 61 through 660.4997 0.5039 0.5009 0.5012 0.5037 0.5021Columns 67 through 720.4952 0.4959 0.5035 0.4921 0.5061 0.4969 Columns 73 through 780.4998 0.4978 0.5084 0.5059 0.5069 0.4978 Columns 79 through 840.5105 0.4888 0.5007 0.4994 0.5024 0.4951 Columns 85 through 900.5012 0.4989 0.5017 0.4980 0.4893 0.5078 Columns 91 through 960.5013 0.5022 0.4969 0.5006 0.4980 0.4949 Columns 97 through 1000.4926 0.5038 0.4885 0.5069=二、连续掷200次硬币,运行1000次,程序如下:for i=1:100a(i)=sum(sum(round(rand(1000))))/200end以下是截取部分结果,发现正面出现的概率依然在0.5附近浮动。
