汉诺塔运行过程
启发式规则_分治法汉诺塔4

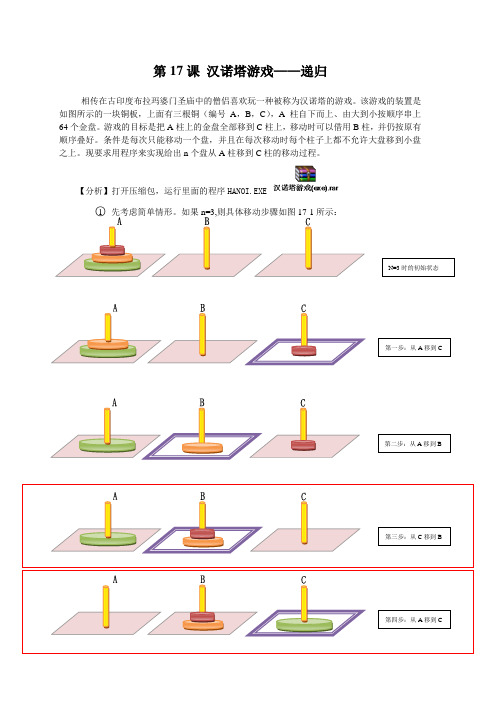
汉诺塔问题可以通过以下三个步骤实现: (1)将塔A上的n-1个碟子借助塔C先移到塔B上。 (2)把塔A上剩下的一个碟子移到塔C上。 (3)将n-1个碟子从塔B借助塔A移到塔C上。 显然,这是一个递归求解的过程
Hanoi塔问题, 算法分析如下,设A上有n个盘子。 如果n=1,则将圆盘从A直接移动到C。 如果n=2,则: (1)将A上的n-1(等于1)个圆盘移到B上; (2)再将A上的一个圆盘移到C上; (3)最后将B上的n-1(等于1)个圆盘移到C上。 如果n=3,则: A)将A上的n-1(等于2,令其为n`)个圆盘移到B(借助于C),步 骤如下: (1)将A上的n`-1(等于1)个圆盘移到C上。 (2)将A上的一个圆盘移到B。 (3)将C上的n`-1(等于1)个圆盘移到B。 B)将A上的一个圆盘移到C。 C)将B上的n-1(等于2,令其为n`)个圆盘移到C(借助A),步骤 如下: (1)将B上的n`-1(等于1)个圆盘移到A。 (2)将B上的一个盘子移到C。 (3)将A上的n`-1(等于1)个圆盘移到C。到此,完成了三个圆盘的 移动过程。
5, 3, A, B, C ⑴
5, 2, A, C, B 5, 3, A, B, C
⑹ 7, 1, A, B, C 7, 2, B, A, C 5, 3, A, B, C ⑾
5, 3, A, B, C ⑺
7, 2, B, A, C 5, 3, A, B, C
⑻
7, 2, B, A, C 5, 3, A, B, C ⑽
4.2 递 归
4.2.1 递归的定义
4.2.2 递归函数的运行轨迹
4.2.3 递归函数的内部执行过程
4.2.1 递归的定义
递归(Recursion)就是子程序(或函数)直 接调用自己或通过一系列调用语句间接调用自己, 是一种描述问题和解决问题的基本方法。 递归有两个基本要素: ⑴ 边界条件:确定递归到何时终止; ⑵ 递归模式:大问题是如何分解为小问题的。
汉诺塔简介

汉诺塔简介汉诺塔(又称河内塔)问题是印度的一个古老的传说。
开天辟地的神勃拉玛在一个庙里留下了三根金刚石的棒,第一根上面套着64个圆的金片,最大的一个在底下,其余一个比一个小,依次叠上去,庙里的众僧不倦地把它们一个个地从这根棒搬到另一根棒上,规定可利用中间的一根棒作为帮助,但每次只能搬一个,而且大的不能放在小的上面。
解答结果请自己运行计算,程序见尾部。
面对庞大的数字(移动圆片的次数)15,看来,众僧们耗尽毕生精力也不可能完成金片的移动。
后来,这个传说就演变为汉诺塔游戏:1.有三根杆子A,B,C。
A杆上有若干碟子2.每次移动一块碟子,小的只能叠在大的上面3.把所有碟子从A杆全部移到C杆上经过研究发现,汉诺塔的破解很简单,就是按照移动规则向一个方向移动金片: 如3阶汉诺塔的移动:A?C,A?B,C?B,A?C,B?A,B?C,A?C此外,汉诺塔问题也是程序设计中的经典递归问题。
算法思路:1.如果只有一个金片,则把该金片从源移动到目标棒,结束。
2.如果有n个金片,则把前n-1个金片移动到辅助的棒,然后把自己移动到目标棒,最后再把前n-1个移动到目标棒using System;using System.Text.RegularExpressions;class tower{private static void Move(int count, char A, char B, char C){if (count == 1){Console.WriteLine("Move disc {0}----->{1}", A, C);return;}Move(count-1, A, C, B);Console.WriteLine("Move disc {0}----->{1}", A, C);Move(count-1, B, A, C);}public static void Main(string[] args){Regex r = new Regex("^[0-9]*[1-9][0-9]*$");Match m = r.Match(args[0]);if (!m.Success){Console.WriteLine("输入有误,请输入正整数~");return;}int count = int.Parse(args[0]);Console.WriteLine("Task: Move {0} discs from A pass B to C", count); Move(count, 'A', 'B', 'C');}}当前位置: 首页 >> 程序设计 >> 数据结构和算法 >> 汉诺塔非递归算法汉诺塔非递归算法作者: 来源:zz 发表时间:2008-01-08 浏览次数: 6160 字号:大中小/*《数学营养菜》(谈祥柏著)提供的一种方法,编了一个程序来实现。
【精品】汉诺塔游戏攻略

文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持. 【关键字】精品3层:第1步: x -移到-> y第2步: x -移到-> z第3步: y -移到-> z第4步: x -移到-> y第5步: z -移到-> x第6步: z -移到-> y第7步: x -移到-> y4层:第1步: x -移到-> z第2步: x -移到-> y第3步: z -移到-> y第4步: x -移到-> z第5步: y -移到-> x第6步: y -移到-> z第7步: x -移到-> z第8步: x -移到-> y第9步: z -移到-> y第10步: z -移到-> x第11步: y -移到-> x第12步: z -移到-> y第13步: x -移到-> z第14步: x -移到-> y第15步: z -移到-> y文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持. 5层:第1步: x -移到-> y第2步: x -移到-> z第3步: y -移到-> z第4步: x -移到-> y第5步: z -移到-> x第6步: z -移到-> y第7步: x -移到-> y第8步: x -移到-> z第9步: y -移到-> z第10步: y -移到-> x第11步: z -移到-> x第12步: y -移到-> z第13步: x -移到-> y第14步: x -移到-> z第15步: y -移到-> z第16步: x -移到-> y第17步: z -移到-> x第18步: z -移到-> y第19步: x -移到-> y第20步: z -移到-> x第21步: y -移到-> z第22步: y -移到-> x第23步: z -移到-> x第24步: z -移到-> y第26步: x -移到-> z 第27步: y -移到-> z 第28步: x -移到-> y 第29步: z -移到-> x 第30步: z -移到-> y 第31步: x -移到-> y 6层:第1步: x -移到-> z 第2步: x -移到-> y 第3步: z -移到-> y 第4步: x -移到-> z 第5步: y -移到-> x 第6步: y -移到-> z 第7步: x -移到-> z 第8步: x -移到-> y 第9步: z -移到-> y 第10步: z -移到-> x 第11步: y -移到-> x 第12步: z -移到-> y 第13步: x -移到-> z 第14步: x -移到-> y 第15步: z -移到-> y 第16步: x -移到-> z 第17步: y -移到-> x第19步: x -移到-> z 第20步: y -移到-> x 第21步: z -移到-> y 第22步: z -移到-> x 第23步: y -移到-> x 第24步: y -移到-> z 第25步: x -移到-> z 第26步: x -移到-> y 第27步: z -移到-> y 第28步: x -移到-> z 第29步: y -移到-> x 第30步: y -移到-> z 第31步: x -移到-> z 第32步: x -移到-> y 第33步: z -移到-> y 第34步: z -移到-> x 第35步: y -移到-> x 第36步: z -移到-> y 第37步: x -移到-> z 第38步: x -移到-> y 第39步: z -移到-> y 第40步: z -移到-> x 第41步: y -移到-> x 第42步: y -移到-> z第44步: y -移到-> x第45步: z -移到-> y第46步: z -移到-> x第47步: y -移到-> x第48步: z -移到-> y第49步: x -移到-> z第50步: x -移到-> y第51步: z -移到-> y第52步: x -移到-> z第53步: y -移到-> x第54步: y -移到-> z第55步: x -移到-> z第56步: x -移到-> y第57步: z -移到-> y第58步: z -移到-> x第59步: y -移到-> x第60步: z -移到-> y第61步: x -移到-> z第62步: x -移到-> y第63步: z -移到-> y7层:第1步: x -移到-> y 第2步: x -移到-> z第3步: y -移到-> z第4步: x -移到-> y第6步: z -移到-> y 第7步: x -移到-> y 第8步: x -移到-> z 第9步: y -移到-> z 第10步: y -移到-> x 第11步: z -移到-> x 第12步: y -移到-> z 第13步: x -移到-> y 第14步: x -移到-> z 第15步: y -移到-> z 第16步: x -移到-> y 第17步: z -移到-> x 第18步: z -移到-> y 第19步: x -移到-> y 第20步: z -移到-> x 第21步: y -移到-> z 第22步: y -移到-> x 第23步: z -移到-> x 第24步: z -移到-> y 第25步: x -移到-> y 第26步: x -移到-> z 第27步: y -移到-> z 第28步: x -移到-> y 第29步: z -移到-> x第31步: x -移到-> y 第32步: x -移到-> z 第33步: y -移到-> z 第34步: y -移到-> x 第35步: z -移到-> x 第36步: y -移到-> z 第37步: x -移到-> y 第38步: x -移到-> z 第39步: y -移到-> z 第40步: y -移到-> x 第41步: z -移到-> x 第42步: z -移到-> y 第43步: x -移到-> y 第44步: z -移到-> x 第45步: y -移到-> z 第46步: y -移到-> x 第47步: z -移到-> x 第48步: y -移到-> z 第49步: x -移到-> y 第50步: x -移到-> z 第51步: y -移到-> z 第52步: x -移到-> y 第53步: z -移到-> x 第54步: z -移到-> y第56步: x -移到-> z 第57步: y -移到-> z 第58步: y -移到-> x 第59步: z -移到-> x 第60步: y -移到-> z 第61步: x -移到-> y 第62步: x -移到-> z 第63步: y -移到-> z 第64步: x -移到-> y 第65步: z -移到-> x 第66步: z -移到-> y 第67步: x -移到-> y 第68步: z -移到-> x 第69步: y -移到-> z 第70步: y -移到-> x 第71步: z -移到-> x 第72步: z -移到-> y 第73步: x -移到-> y 第74步: x -移到-> z 第75步: y -移到-> z 第76步: x -移到-> y 第77步: z -移到-> x 第78步: z -移到-> y 第79步: x -移到-> y第81步: y -移到-> z 第82步: y -移到-> x 第83步: z -移到-> x 第84步: y -移到-> z 第85步: x -移到-> y 第86步: x -移到-> z 第87步: y -移到-> z 第88步: y -移到-> x 第89步: z -移到-> x 第90步: z -移到-> y 第91步: x -移到-> y 第92步: z -移到-> x 第93步: y -移到-> z 第94步: y -移到-> x 第95步: z -移到-> x 第96步: z -移到-> y 第97步: x -移到-> y 第98步: x -移到-> z 第99步: y -移到-> z 第100步: x -移到-> y 第101步: z -移到-> x 第102步: z -移到-> y 第103步: x -移到-> y 第104步: x -移到-> z第106步: y -移到-> x第107步: z -移到-> x第108步: y -移到-> z第109步: x -移到-> y第110步: x -移到-> z第111步: y -移到-> z第112步: x -移到-> y第113步: z -移到-> x第114步: z -移到-> y第115步: x -移到-> y第116步: z -移到-> x第117步: y -移到-> z第118步: y -移到-> x第119步: z -移到-> x第120步: z -移到-> y第121步: x -移到-> y第122步: x -移到-> z第123步: y -移到-> z第124步: x -移到-> y第125步: z -移到-> x第126步: z -移到-> y第127步: x -移到-> y此文档是由网络收集并进行重新排版整理.word可编辑版本!。
汉诺塔移动超详细步骤分解4到6层

汉诺塔移动超详细步骤分解4到6层汉诺塔(Tower of Hanoi)是一个经典的数学谜题和递归问题。
它由三根柱子和一些大小不同的圆盘组成,初始时,所有圆盘按照从大到小的顺序堆叠在一根柱子上,目标是将这些圆盘全部移动到另一根柱子上,并且在移动过程中,大盘不能放在小盘上面。
接下来,我们将详细分解 4 到 6 层汉诺塔的移动步骤。
一、4 层汉诺塔的移动步骤首先,让我们来看看 4 层汉诺塔的情况。
我们有 4 个圆盘,分别标记为 1(最小)、2、3、4(最大)。
1、把 1、2 号圆盘从 A 柱移动到 B 柱。
先把 1 号圆盘从 A 柱移动到 C 柱。
再把 2 号圆盘从 A 柱移动到 B 柱。
最后把 1 号圆盘从 C 柱移动到 B 柱。
2、把 3 号圆盘从 A 柱移动到 C 柱。
3、把 1、2 号圆盘从 B 柱移动到 C 柱。
先把 1 号圆盘从 B 柱移动到 A 柱。
再把 2 号圆盘从 B 柱移动到 C 柱。
最后把 1 号圆盘从 A 柱移动到 C 柱。
5、把 1、2 号圆盘从 C 柱移动到 A 柱。
先把 1 号圆盘从 C 柱移动到 B 柱。
再把 2 号圆盘从 C 柱移动到 A 柱。
最后把 1 号圆盘从 B 柱移动到 A 柱。
6、把 3 号圆盘从 C 柱移动到 B 柱。
7、把 1、2 号圆盘从 A 柱移动到 B 柱。
先把 1 号圆盘从 A 柱移动到 C 柱。
再把 2 号圆盘从 A 柱移动到 B 柱。
最后把 1 号圆盘从 C 柱移动到 B 柱。
经过以上 15 步,4 层汉诺塔就从 A 柱成功移动到了 B 柱。
二、5 层汉诺塔的移动步骤对于 5 层汉诺塔,我们有 5 个圆盘,分别标记为 1(最小)、2、3、4、5(最大)。
1、把 1、2、3 号圆盘从 A 柱移动到 B 柱。
先把 1、2 号圆盘从 A 柱移动到 C 柱。
再把 3 号圆盘从 A 柱移动到 B 柱。
然后把 1、2 号圆盘从 C 柱移动到 B 柱。
3、把 1、2、3 号圆盘从 B 柱移动到 C 柱。
汉诺塔游戏设计过程

兰州交通大学数理与软件工程学院课程设计报告2011 ~2012学年第二学期2012年6月一、实验目的:通过此次C++实训,一方面加深了对C++语言的了解,而不只是单单的在课本中学到的那些理论。
通过学生动手亲自编写,平时乏味的课程,变的生动有趣。
平时在课堂上学到的东西可以自己动手编写,将其转化成一些实用的技能。
另一方面,通过学生小组完成任务,提高团队意识,增加凝聚力,让同学们意识到团结就是力量,每个人都是重要的一份子。
二、题目:汉诺塔游戏程序<1> 问题描述:在平面上有三个位置A、B、C,在A位置上有n个大小不等的圆盘、小盘压在大盘上形成圆盘堆。
要求将A位置的N个圆盘通过B位置移动到C位置上,并按同样的顺序叠放。
移动圆盘时必须遵循以下规则:1.每一次只能移动一个圆盘2.圆盘可以放在A、B、C任何一个塔座上3.任何时刻都不能将大圆盘压在小圆盘上<2> 基本要求:圆盘的个数从键盘输入(如3-64等);用动画的形式在屏幕上显示盘的移动。
三、问题分析和任务定义1、已知有三个塔(1、2、3)和n个从大到小的金碟子,初始状态时n个碟子按从大到小的次序从塔1的底部堆放至顶部。
2、要求把碟子都移动到塔2(按从大到小的次序从塔2的底部堆放至顶部)。
3、每次移动一个碟子。
4、任何时候、任何一个塔上都不能把大碟子放到小碟子的上面。
5、可以借助塔3。
先考虑a杆下面的盘子而非杆上最上面的盘子,于是任务变成了:1、将上面的N个盘子移到b杆上;2、将a杆上剩下的盘子移到c杆上;3、将b杆上的全部盘子移到c杆上。
将这个过程继续下去,就是要先完成移动n个盘子、n-1个盘子、n-2个盘子....1个盘的工作。
四、课题介绍:4.1 汉诺塔问题初始模型:4.2 实现步骤:为满足题目中盘子的移动问题,必须遵循的条件是:一次仅能移动一个盘,且不允许大盘放在小盘的上面。
设要解决的汉诺塔共有N个圆盘,对A杆上的全部N个圆盘从小到大顺序编号,最小的圆盘为1号,次之为2号,依次类推,则最下面的圆盘的编号为N。
汉诺塔问题的详解课件

04
数据结构与排序
汉诺塔问题也可以用来解释和演示不同的 数据结构和排序算法。
05
06
通过汉诺塔问题,人们可以更好地理解如 堆、栈等数据结构的应用和优劣。
在物理学中的应用
复杂系统与自组织
汉诺塔问题在物理学中常被用来研究复杂系统和自组织现 象。
通过对汉诺塔问题的深入研究,人们可以发现其在物理学 中的一些应用,如量子计算、自旋玻璃等。
人工智能与机器学习
在人工智能和机器学习中,汉诺塔问题可以被用来演示 如何使用不同的算法来解决问题。
06
总结与展望
对汉诺塔问题的总结
汉诺塔问题是一个经典的递归问题,其核心在于将一个复杂的问题分解为若干个简单的子问题来解决 。
通过解决汉诺塔问题,我们可以了解到递归算法在解决复杂问题中的重要性,以及将大问题分解为小问 题的方法。
此外,汉诺塔问题还被广泛应用于数学教育和计算机 科学教育中,成为许多课程和教材中的经典案例之一
。
02
汉诺塔问题的数学模型
建立数学模型
定义问题的基本参数
盘子的数量、柱子的数量和塔的直径 。
建立数学方程
根据问题的特点,我们可以建立如下 的数学方程。
递归算法原理
递归的基本思想
将一个复杂的问题分解成更小的子问题来解决。
通过深入研究汉诺塔问题的本质和解决方法,我们可以 为解决其他领域的问题提供有益的启示和方法。
THANKS
感谢观看
其他移动规则
除了传统的规则(盘子只能放在更大的盘子下面)之外,还 可以有其他移动规则,这会改变问题的性质和解决方案。
05
汉诺塔问题的应用场景
在计算机科学中的应用
算法设计与优化
01
汉诺塔移动次数的规律

汉诺塔移动次数的规律嘿,朋友们!今天咱来聊聊汉诺塔移动次数的规律,这可有意思啦!你看啊,汉诺塔就好像是我们生活中的一个小挑战,那几个盘子在柱子之间挪来挪去,别看它简单,里面的门道可深着呢!咱们先从最少的盘子开始,一个盘子的时候,那多简单呀,一下子就挪过去了,移动次数就是 1。
那两个盘子呢?嘿,这可得动点小脑筋了。
先把小盘子挪到中间柱子,这就 1 次,再把大盘子挪到目标柱子,又 1 次,最后把小盘子挪到目标柱子,又是 1 次,总共 3 次。
等盘子越来越多的时候,你就会发现这移动次数涨得可快啦!就好像是小树苗长成大树一样,不知不觉就变得很庞大了。
三个盘子的时候,哇塞,那次数就变成 7 次啦!这是怎么来的呢?其实就是前面两个盘子移动次数的2 倍加 1 呀!这不就跟我们学习一样嘛,一开始学一点东西觉得挺轻松,可知识越积累越多,难度也跟着上去啦。
但咱可不能怕呀,就像面对汉诺塔一样,慢慢研究,总能找到规律。
再想想,这汉诺塔的规律是不是也像我们的人生呀!有时候我们要跨越一些困难,可能一开始觉得挺容易,可随着目标越来越远大,遇到的挑战也越来越多。
但只要我们像研究汉诺塔一样,一步一个脚印,总能找到解决问题的办法。
你说这汉诺塔神奇不神奇?每多一个盘子,那移动次数就好像坐上了火箭一样往上窜。
四个盘子就得 15 次,五个盘子就更不得了啦!咱可别小瞧了这小小的汉诺塔游戏,它里面蕴含的智慧可大着呢!它告诉我们,面对复杂的问题不要慌,先从简单的情况入手,慢慢摸索出规律。
而且呀,要有耐心,别想着一下子就把所有问题都解决了。
那我们在生活中遇到困难的时候,是不是也可以想想汉诺塔呢?别着急,慢慢来,一步一步地去解决。
就像汉诺塔的盘子一样,总会一个一个地到达它们该去的地方。
汉诺塔移动次数的规律,不只是数学上的一个有趣现象,更是我们生活中的一个启示呀!它让我们知道,只要我们用心去发现,去探索,就能在看似普通的事物中找到意想不到的智慧和乐趣。
汉诺塔最少步数公式

汉诺塔最少步数公式汉诺塔是一种经典的数学游戏,它的目标是将三个柱子上按照大小顺序排列的盘子,从起始柱子移动到目标柱子上。
为了达成这个目标,我们可以使用递归的方式来解决。
最少步数公式当我们需要将 n 个盘子从柱子 A 移动到柱子 C 时,最少需要多少步呢?经过数学推导可知,我们可以使用一个简单的公式来计算出最少步数:F(n) = 2F(n-1) + 1其中,n 表示盘子的数量,F(n) 表示将 n 个盘子从柱子 A 移动到柱子C 所需的最少步数。
公式意义为:将 n 个盘子从柱子 A 移动到柱子 C所需的最少步数等于先将 n-1 个盘子从柱子 A 移动到柱子 B,再将剩余的 1 个盘子从柱子 A 移动到柱子 C,最后将 n-1 个盘子从柱子 B 移动到柱子 C 所需的步数再加上 1。
举个例子,当盘子数量为 3 时,根据公式可知:F(3) = 2F(2) + 1 = 2(2F(1) + 1) + 1 = 2(2*1+1) + 1 = 7即将 3 个盘子从柱子 A 移动到柱子 C 最少需要 7 步。
递归算法通过递归算法,我们可以将盘子的移动过程拆分成多个小的子问题,每次处理一个子问题,直到最终解决所有问题。
具体的过程如下:1. 将前 n-1 个盘子从柱子 A 移动到柱子 B2. 将第 n 个盘子从柱子 A 移动到柱子 C3. 将前 n-1 个盘子从柱子 B 移动到柱子 C在每一次递归中,我们需要将当前问题拆分成三个子问题,并逐步解决这些子问题。
当盘子数量越来越少时,递归的规模也逐渐缩小,最终问题得到解决。
时间复杂度汉诺塔问题的时间复杂度为 O(2^n),其中 n 表示盘子数量。
这是由于在每一次递归中,我们需要处理两个子问题,因此总共需要递归 2^n-1 次。
虽然时间复杂度比较高,但在实际运用中,汉诺塔算法的问题规模往往比较小,因此并不会产生太大的性能问题。
总结汉诺塔问题是一种经典的递归算法,它的解法可以简单地用一个公式表示,并通过分治的方式实现。
汉诺塔移动超详细步骤分解4到6层

汉诺塔移动超详细步骤分解4到6层关键信息项:1、汉诺塔层数:4 层、5 层、6 层2、移动规则3、具体步骤分解4、注意事项11 汉诺塔介绍汉诺塔(Tower of Hanoi)是源于印度一个古老传说的益智玩具。
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
111 规则说明在移动汉诺塔圆盘时,需遵循以下规则:1、每次只能移动一个圆盘。
2、较大的圆盘不能放在较小的圆盘之上。
112 4 层汉诺塔移动步骤分解首先,我们来分析 4 层汉诺塔的移动步骤。
第 1 步:将最上面的 3 个圆盘(即第 1 到第 3 个)从起始柱移动到辅助柱。
第 2 步:把第 4 个圆盘从起始柱移动到目标柱。
第 3 步:再把之前放在辅助柱上的 3 个圆盘移动到目标柱。
具体移动过程如下:假设起始柱为 A 柱,辅助柱为 B 柱,目标柱为 C 柱。
初始状态:圆盘 1、2、3、4 依次在 A 柱。
第一步,将圆盘 1 从 A 柱移动到 B 柱。
第二步,将圆盘 2 从 A 柱移动到 C 柱。
第三步,将圆盘 1 从 B 柱移动到 C 柱。
第四步,将圆盘 3 从 A 柱移动到 B 柱。
第五步,将圆盘 1 从 C 柱移动到 A 柱。
第六步,将圆盘 2 从 C 柱移动到 B 柱。
第七步,将圆盘 1 从 A 柱移动到 B 柱。
第八步,将圆盘 4 从 A 柱移动到 C 柱。
第九步,将圆盘 1 从 B 柱移动到 C 柱。
第十步,将圆盘 2 从 B 柱移动到 A 柱。
第十二步,将圆盘 3 从 B 柱移动到 C 柱。
第十三步,将圆盘 1 从 A 柱移动到 B 柱。
第十四步,将圆盘 2 从 A 柱移动到 C 柱。
第十五步,将圆盘 1 从 B 柱移动到 C 柱。
12 5 层汉诺塔移动步骤分解对于 5 层汉诺塔,步骤会更加复杂。
玩汉诺塔规律

玩汉诺塔规律
单左双右,先小后大,一步两步,循环往复。
设3个柱子分别是甲,乙,丙,把3根柱子看成一个循环,也就是说,甲的右边是乙,乙的右边是丙,而丙的右边则回到甲,同理,甲的左边就是丙。
简单点,记住丙的右边是甲,和甲的左边是丙就行了。
盘子分别是盘1,盘2,盘3,盘4……盘1最小。
按照“单左双右”的规律,先移动小的,也就是先移动盘1,再移动盘2,盘3,按顺序,把能移动的都移动一次,每次移动一步,如果不符合游戏规则,就移动两步,还是不符合的话,就找到盘1,重新按照“单左双右”的规则走,直到完成游戏。
例:3个盘子,单数,向左走。
1,盘1向左移动一步,到丙柱。
2,盘2向左移动一步,不符合游戏规则,移动两步,到乙柱。
3,盘3向左移动一步,不符合游戏规则,移动两步,不符合游戏规则。
找到最小的盘1,向左移动一步,移动到乙柱。
4,盘2被盘1压住,无法移动。
盘3向左移动一步,到丙柱。
5,找到最小的盘1,向左移动一步,到甲柱。
6,盘2向左移动一步,不符合游戏规则,移动两步,到丙柱。
7,盘3被盘2压住,无法移动。
找到最小的盘1,向左移动一步,到丙柱。
游戏完成。
1. 把最小的圆盘向右移动到下一个位置,如果已经到最右边,就回到左边第一个位置
2. 把除最小圆盘所在位置的另外两个位置上的圆盘中较小的一个移动到大的上面(只可能有一种移法)
3. 重复1/2,直到所有盘子从一个柱子移到另一个柱子
【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注,我们将会做得更好】。
汉诺塔动画演示课件

汉诺塔的规则和玩法
01
02
03
04
05
规则:汉诺塔的规则是 要求将所有的圆盘从起 始柱子移到目标柱子上, 移动过程中必须遵循以 下三个原 则
1. 每次只能移动一个圆 盘;
2. 圆盘只能放在比它大 3. 圆盘只能放在空柱子
的圆盘上;
上。
玩法:汉诺塔的玩法是 从起始柱子开始,按照 规则将圆盘逐个移到目 标柱子上。在移动过程 中,需要不断地将圆盘 进行分解和组合,以找 到最优的移动方案。
03
人工智能与机器学习
汉诺塔问题可以作为人工智能和机器学习领域的基准测试案例,用于评
估和优化算法和模型的性能。
在物理学中的应用
力学与运动学
汉诺塔问题涉及到物体的运动和相互作用,可以用来解释和演示力学和运动学的基本原理,如牛顿运 动定律、动量守恒定律等。
光学与视觉
汉诺塔问题中的不同颜色和形状的盘子可以用来模拟光线和颜色的传播和反射,可以用来解释和演示 光学和视觉的基本原理。
效地降低时间复杂度,提高求解效率。
优化二:使用遗传算法求解
总结词
遗传算法是一种基于生物进化原理的优化算法,可以用于求解组合优化问题。
详细描述
遗传算法是一种基于生物进化原理的优化算法,它通过模拟生物进化过程中的基因选择、交叉和变异等过程来寻 找最优解。在汉诺塔问题中,我们可以使用遗传算法来求解。首先,我们定义一个表示汉诺塔问题的染色体,然 后通过模拟选择、交叉和变异等过程来不断优化染色体的适应度,最终得到最优解。
02
汉诺塔动画演示
演示一:移动三个盘子
总结词:通过演示,展示汉诺塔问题最简单的情形,即只 有三个盘子需要移动。
详细描述
1. 起始状态:三个盘子叠在一起,放在第一个柱子上。
河内塔实验报告原理

一、引言河内塔实验,又称为汉诺塔问题,起源于印度一个古老的传说。
该问题是一个经典的递归问题,也是认知心理学中研究问题解决策略的典型实验。
河内塔实验通过模拟将圆盘从一根柱子移动到另一根柱子的过程,来探讨人类问题解决过程中的思维策略和决策能力。
二、实验原理1. 实验背景河内塔问题由三根柱子和若干个大小不同的圆盘组成。
在实验开始时,所有圆盘按照从小到大的顺序依次放在第一根柱子上,构成一个金字塔状。
实验的目标是将所有圆盘按照原来的顺序移动到第三根柱子上,且在移动过程中,每次只能移动最上面的一个圆盘,且大圆盘不能放在小圆盘上面。
2. 实验目的(1)了解被试在解决河内塔问题时所用的思维策略。
(2)研究口头报告对思维的影响。
(3)探讨人类在问题解决过程中的认知过程。
3. 实验方法(1)被试:选取一定数量的被试,要求其完成河内塔实验。
(2)实验材料:河内塔实验装置,包括三根柱子和若干个大小不同的圆盘。
(3)实验步骤:①将圆盘按照从小到大的顺序依次放在第一根柱子上,构成金字塔状。
②要求被试将所有圆盘按照原来的顺序移动到第三根柱子上。
③在实验过程中,记录被试的移动次数、用时和策略。
④在实验结束后,对被试进行口头报告,了解其思维过程。
4. 实验结果与分析(1)被试在解决河内塔问题时,通常会采用以下策略:①递归法:将问题分解为更小的子问题,逐步解决。
②记忆法:通过记忆已解决的子问题,来推测如何解决当前问题。
②试错法:通过不断尝试和错误,寻找解决问题的方法。
(2)口头报告显示,被试在解决问题过程中,会经历以下认知过程:①发现问题:意识到需要将所有圆盘移动到第三根柱子上。
②分析问题:分析问题结构,找出问题的约束条件。
③制定解决方案:根据问题结构,制定解决问题的步骤。
④实施解决方案:按照制定的步骤,将所有圆盘移动到第三根柱子上。
⑤评价结果:评估解决问题的效果,分析存在的问题。
5. 结论河内塔实验是一种有效的研究问题解决策略和认知过程的实验。
汉诺塔问题的程序实现(hanoi塔)

汉诺塔问题的程序实现(hanoi塔)问题重述:有三根柱A、B、C,在柱A上有N块盘⽚,所有盘⽚都是⼤的在下⾯,⼩⽚能放在⼤⽚上⾯。
现要将A上的N块盘⽚移到C柱上,每次只能移动⼀⽚,⽽且在同⼀根柱⼦上必须保持上⾯的盘⽚⽐下⾯的盘⽚⼩,输⼊任意的N,输出移动⽅法。
(注意:这是⼀个古⽼的传说,传说是如果把64个盘⼦由A柱移到了C柱的话,那么世界末⽇就到了,事实上如果要把64个盘⼦从A柱移到C柱的话,即使⽤计算机运算,也要计算数亿年,所以这个预⾔未必不是真实。
)【分析】我们可以这样考虑,当n=1时,我们只要直接将A柱的盘⼦移到C柱,当n>1时,我们可以先把n-1个盘⼦由A柱通过C柱移到B 柱,此时就可以把A柱剩下的最后⼀个盘⼦直接移到C柱,这样接下来只要把n-1个盘⼦通过A柱移到C 柱即可,如果就构成了递归的思路,我们可以定义个移动过程mov(n,a,b,c)表⽰将n个盘⼦从a通过b移到c1.只要求输出搬运的次数#includeusing namespace std;int m=0;void move(){m++;}void I(int n){if(n==1)move();else{I(n-1);move();I(n-1);}}int main(){I(3);cout<cout<<"输出完毕!"<return 0;}更加简单的⽅法!#includeusing namespace std;int fact(int n){if(n==1)return(1);elsereturn((2*fact(n-1)+1));}int main(){cout<}2.不仅要求输出搬运的次数,⽽且要输出每个步骤的详细搬运#includeusing namespace std;int m=0;void Move(int n,char x,char y){cout<<"把"<m++;}void Hannoi(int n,char a,char b,char c){if(n==1)Move(1,a,c);else{Hannoi(n-1,a,c,b);Move(n,a,c);Hannoi(n-1,b,a,c);}}int main(){int i;cout<<"请输⼊圆盘数"<cin>>i;Hannoi(3,'a','b','c');cout<<"总的搬运次数"<cout<<"输出完毕!"<return 0;}}另外⼀种不利⽤递归的解法(很抱歉,我⾃⼰也没调出来,实在太复杂了)#includeusing namespace std;//圆盘的个数最多为64const int MAX = 1;//⽤来表⽰每根柱⼦的信息struct st{int s[MAX]; //柱⼦上的圆盘存储情况int top; //栈顶,⽤来最上⾯的圆盘char name; //柱⼦的名字,可以是A,B,C 中的⼀个int Top()//取栈顶元素{return s[top];}int Pop()//出栈{return s[top--];}void Push(int x)//⼊栈{s[++top] = x;}} ;long Pow(int x, int y); //计算x^yvoid Creat(st ta[], int n); //给结构数组设置初值void Hannuota(st ta[], long max); //移动汉诺塔的主要函数int main(void){int n;cin >> n; //输⼊圆盘的个数st ta[3]; //三根柱⼦的信息⽤结构数组存储Creat(ta, n); //给结构数组设置初值long max = Pow(2, n) - 1;//动的次数应等于2^n - 1 Hannuota(ta, max);//移动汉诺塔的主要函数system("pause");return 0;}void Creat(st ta[], int n){ta[0].name = 'A';ta[0].top = n-1;//把所有的圆盘按从⼤到⼩的顺序放在柱⼦A 上for (int i=0; ita[0].s[i] = n - i;//柱⼦B,C 上开始没有没有圆盘ta[1].top = ta[2].top = 0;for (int j=0; jta[1].s[j] = ta[2].s[j] = 0;//若n 为偶数,按顺时针⽅向依次摆放A B Cif (n%2 == 0){ta[1].name = 'B';ta[2].name = 'C';}else //若n 为奇数,按顺时针⽅向依次摆放A C B {ta[1].name = 'C';ta[2].name = 'B';}}long Pow(int x, int y){long sum = 1;for (int i=0; isum *= x;return sum;}void Hannuota(st ta[], long max){int k = 0; //累计移动的次数int i = 0;int ch;while (k < max){//按顺时针⽅向把圆盘1 从现在的柱⼦移动到下⼀根柱⼦ch = ta[i%3].Pop();ta[(i+1)%3].Push(ch);cout << ++k << ": " <<"Move disk " << ch << " from " << ta[i%3].name <<" to " << ta[(i+1)%3].name << endl;i++;//把另外两根柱⼦上可以移动的圆盘移动到新的柱⼦上if (k < max){ //把⾮空柱⼦上的圆盘移动到空柱⼦上,当两根柱⼦都为空时,移动较⼩的圆if (ta[(i+1)%3].Top() == 0 ||ta[(i-1)%3].Top() > 0 &&ta[(i+1)%3].Top() > ta[(i-1)%3].Top()){ch = ta[(i-1)%3].Pop();ta[(i+1)%3].Push(ch);cout << ++k << ": " << "Move disk "<< ch << " from " << ta[(i-1)%3].name<< " to " << ta[(i+1)%3].name << endl;}else{ch = ta[(i+1)%3].Pop();ta[(i-1)%3].Push(ch);cout << ++k << ": " << "Move disk " << ch << " from " << ta[(i+1)%3].name << " to " << ta[(i-1)%3].name << endl; }}}}补充知识:【典型例题1】求阶乘n!#includeusing namespace std;int fact(int n){if(n==0)return(1);elsereturn(n*fact(n-1)); }int main(){cout<。
汉诺塔游戏递归
qiu(n); {调用子程序}
writeln(s:2:0)
end.
展示实力
万炽洋的程序:
1、某人写了n封信和n个信封,结果所有信都装错信封。求所有的信都装错信封共有多少种不同的情况。
2、楼梯有n阶台阶,上楼可以一步上一阶,也可以一步上二阶。请用递归方法编程计算共有多少种不同的走法。
3、用递归方法方法完成:有52张牌,使它们全部正面朝上,第一轮是从第2张开始,凡是2的倍数位置上的牌翻成正面朝下;第二轮从第三张牌开始,凡是3的倍数位置上的牌以,正面朝上的翻成正面朝下,正面朝下的翻成正面朝上;第三轮从第4张牌开始,凡是4的倍数位置上的牌按上面相同规则翻转,从此类推,直到第一张要翻的牌超过52为止。统计最后有几张牌正面朝上,以及它们的位置号。
〖分析〗读入一个字符,判断是否为"#"号,如果不是就继续读入,即可以调用程序本身。如果是“#”,则输出字符
〖参考程序〗
program P17_4;
procedure rever;
var c:char;
begin
read(c);
if c<>'#' then rever; {递归调用的地方,下一次调用会分配新单元c}
C语言汉诺塔问题,用C语言实现汉诺塔

C语言汉诺塔问题,用C语言实现汉诺塔汉诺塔问题是指:一块板上有三根针A、B、C。
A 针上套有64 个大小不等的圆盘,按照大的在下、小的在上的顺序排列,要把这64 个圆盘从A 针移动到C 针上,每次只能移动一个圆盘,移动过程可以借助B 针。
但在任何时候,任何针上的圆盘都必须保持大盘在下,小盘在上。
从键盘输入需移动的圆盘个数,给出移动的过程。
算法思想对于汉诺塔问题,当只移动一个圆盘时,直接将圆盘从A 针移动到C 针。
若移动的圆盘为n(n>1),则分成几步走:把(n-1) 个圆盘从A 针移动到B 针(借助C 针);A 针上的最后一个圆盘移动到C 针;B 针上的(n-1) 个圆盘移动到C 针(借助A 针)。
每做一遍,移动的圆盘少一个,逐次递减,最后当n 为1 时,完成整个移动过程。
因此,解决汉诺塔问题可设计一个递归函数,利用递归实现圆盘的整个移动过程,问题的解决过程是对实际操作的模拟。
程序代码1.#include<stdio.h>2.int main()3.{4.int hanoi(int,char,char,char);5.int n,counter;6.printf("Input the number of diskes:");7.scanf("%d",&n);8.printf("\n");9. counter=hanoi(n,'A','B','C');10.return0;11.}12.13.int hanoi(int n,char x,char y,char z)14.{15.int move(char,int,char);16.if(n==1)17.move(x,1,z);18.else19.{20.hanoi(n-1,x,z,y);21.move(x,n,z);22.hanoi(n-1,y,x,z);23.}24.return0;25.}26.27.int move(char getone,int n,char putone)28.{29.static int k=1;30.printf("%2d:%3d # %c---%c\n",k,n,getone,putone);31.if(k++%3==0)32.printf("\n");33.return0;34.}调试运行结果当移动圆盘个数为3 时,具体移动步骤如下所示:。
汉诺塔的移动 递归函数

汉诺塔的移动递归函数汉诺塔是一种经典的递归问题,需要用递归函数来解决。
汉诺塔由三根柱子和若干个圆盘组成,每个圆盘大小不同,大的在下面,小的在上面。
初始状态下,所有圆盘都在第一根柱子上,按大小顺序从下到上依次摆放。
目标状态是所有圆盘都移到第三根柱子上,同样按大小顺序从下到上依次摆放。
移动圆盘的规则是:每次只能移动一个圆盘,大圆盘不能放在小圆盘上面。
为了解决汉诺塔问题,需要定义一个递归函数,输入参数为圆盘的个数和起始柱子、目标柱子、辅助柱子。
函数的实现思路如下:1. 如果圆盘只有一个,直接将其从起始柱子移动到目标柱子。
2. 如果圆盘不止一个,将其分为两部分:最下面的大圆盘和上面的所有圆盘,将上面的所有圆盘从起始柱子移到辅助柱子,然后将最下面的大圆盘从起始柱子移到目标柱子,最后将辅助柱子上的所有圆盘移动到目标柱子上。
递归函数的代码如下:def hanoi(n, start, end, assist):if n == 1:print('{} -> {}'.format(start, end))else:hanoi(n-1, start, assist, end)print('{} -> {}'.format(start, end))hanoi(n-1, assist, end, start)其中,n为圆盘的个数,start为起始柱子,end为目标柱子,assist为辅助柱子。
调用函数的代码如下:hanoi(3, 'A', 'C', 'B')运行结果如下:A -> CA -> BC -> BA -> CB -> AB -> CA -> C这就是汉诺塔问题的解决方法。
虽然看起来有些复杂,但实际上只需要理解递归的思想,就能轻松解决这个问题。
汉诺塔的时间复杂度递推公式

汉诺塔的时间复杂度递推公式
汉诺塔问题是经典的递归问题,其时间复杂度可以用递推公式表示。
设移动n个盘子的汉诺塔问题需要T(n)次移动。
显然,移动n个盘子可以分为三个步骤:
1. 将n-1个盘子从起始柱移动到辅助柱上,共需要T(n-1)次移动。
2. 将第n个盘子从起始柱移动到目标柱上,共需要1次移动。
3. 将n-1个盘子从辅助柱移动到目标柱上,共需要T(n-1)次移动。
因此,移动n个盘子的汉诺塔问题可以表示为:
T(n) = 2T(n-1) + 1
其中,2T(n-1)表示将n-1个盘子从起始柱移动到辅助柱和从辅助柱移动到目标柱所需的次数之和,加上1表示将第n个盘子从起始柱移动到目标柱所需的1次移动。
根据递推公式,可以得到移动1个盘子、2个盘子、3个盘子……n个盘子所需的次数,从而求出时间复杂度。
具体计算方法可以使用递归或迭代的方式实现。
- 1 -。
