MATLAB二分法和牛顿迭代法实验报告

（1）计算f(x)在有解区间[a, b]端点处的值。
（2）计算在区间中点处的值。
（3）判断若 ,则即是根，否则检验：
①若与异号，则知道解位于区间，
②若与同号，则知道解位于区间，，
反复执行步骤2、3，便可得到一系列有根区间：
（4）当，则即为根的近似值。
Newton迭代法原理：设已知方程的近似根 ,则在附近可用一阶泰勒多项式近似代替.因此,方程可近似地表示为 .用表示的根,它与的根差异不大.
3.在MATLAB命令行窗口求解方程f(x)
4.得出计算结果
设 ,由于满足解得
重复这一过程,得到迭代格式
实验所用软件及版本：MATLAB R2014a
主要内容（要点）：
实验过程记录（含：基本步骤、主要程序清单及异常情况记录等）：
二分法:
1.在MATLAB编辑器中建立一个实现二分法的M文件bisect.m
2.在MATLAB命令行窗口求解方程f(x)
3.得出计算结果
数学应用软件大型实验实验报告
实验序号：日期：年月日
班级
姓名
学号
实验
名称
二分法和Newton迭代法
问题背景描述：
分别编写一个用二分法和用Newton-Raphson法求连续函数的零点通用程。
实验目的：
用以求方程x^2-3*x+exp(X)=2的正根（要求精度ε=10^-6）。
实验原理与数学模型：
二分法原理：如果函数y=f(x)在闭区间[a,b]上连续，且已知函数在两端点的函数f（a）与f（b）取异号，即两端点函数值的乘积f(a)*f(b)<0,则函数y=f(x)在区间（a,b）内至少有一个零点，即至少存在一点c，使得f(x)=0的解。

MAAB计算方法迭代法牛顿法二分法实验报告

MAAB计算方法迭代法牛顿法二分法实验报告实验目的：比较MAAB计算方法中迭代法、牛顿法和二分法的优缺点，探究它们在求解方程中的应用效果。

实验原理：1、迭代法：将方程转化为x=f(x)的形式，通过不断迭代逼近方程的根。

2、牛顿法：利用函数在特定点的切线逼近根的位置，通过不断迭代找到方程的根。

3、二分法：利用函数值在区间两端的异号性质，通过不断二分缩小区间，最终逼近方程的根。

实验步骤：1、选择一元方程进行求解，并根据方程选择不同的计算方法。

2、在迭代法中，根据给定的初始值和迭代公式，进行迭代计算，直到满足预设的迭代精度要求。

3、在牛顿法中，选择初始点，并根据切线方程进行迭代计算，直到满足预设的迭代精度要求。

4、在二分法中，选择区间，并根据函数值的异号性质进行二分，直到满足预设的迭代精度要求。

5、根据计算结果，比较三种方法的求解效果，包括迭代次数、计算时间、求解精度等指标。

实验结果与分析：通过对多个方程进行测试，得到了以下实验结果：1、迭代法的优点是简单易懂，适用范围广，但当迭代公式不收敛时会导致计算结果不准确。

2、牛顿法的优点是收敛速度较快，但需要计算函数的一阶导数和二阶导数，对于复杂函数较难求解。

3、二分法的优点是收敛性较好，不需要导数信息，但收敛速度较慢。

4、对于线性方程和非线性方程的求解，牛顿法和迭代法通常比二分法更快速收敛。

5、对于多重根的方程，二分法没有明显优势，而牛顿法和迭代法能更好地逼近根的位置。

6、在不同的方程和初值选择下，三种方法的迭代次数和求解精度略有差异。

7、在时间效率方面，二分法在收敛速度较慢的同时，迭代次数较少，牛顿法在收敛速度较快的同时，迭代次数较多，而迭代法对于不同方程有较好的平衡。

结论：1、对于不同类型的方程求解，可以根据具体情况选择合适的计算方法。

2、迭代法、牛顿法和二分法各有优缺点，没有绝对的最优方法，需要权衡各种因素选择最适合的方法。

3、在实际应用中，可以根据方程的特点和精度要求综合考虑不同方法的优劣势，以获得较好的求解效果。

用Matlab编写二分法和Newton迭代法求解非线性函数

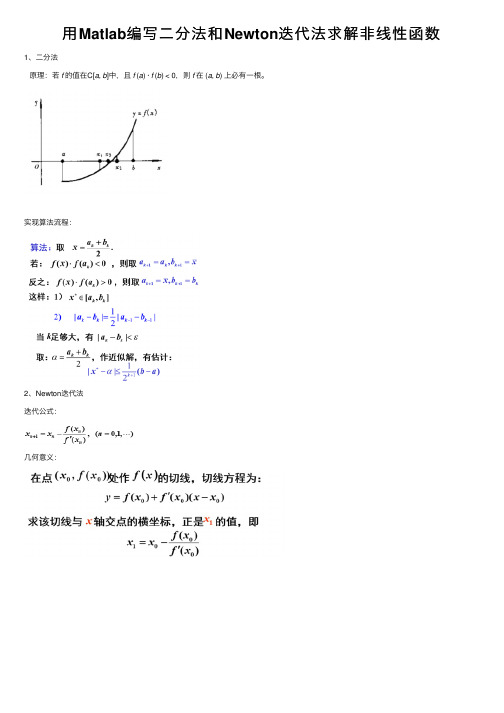
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理：若f的值在C[a, b]中，且f (a) · f (b) < 0，则f在 (a, b) 上必有⼀根。

实现算法流程：2、Newton迭代法迭代公式：⼏何意义：3、求解问题⽤Newton法和⼆分法求的解。

4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值：12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间：[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥，请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值：p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数：48 %⽅程近似解：p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。

MATLAB计算方法迭代法牛顿法二分法实验报告

MATLAB计算方法迭代法牛顿法二分法实验报告实验报告一、引言计算方法是数学的一门重要应用学科，它研究如何用计算机来解决数学问题。

其中，迭代法、牛顿法和二分法是计算方法中常用的数值计算方法。

本实验通过使用MATLAB软件，对这三种方法进行实验研究，比较它们的收敛速度、计算精度等指标，以及它们在不同类型的问题中的适用性。

二、实验方法1.迭代法迭代法是通过不断逼近解的过程来求得方程的根。

在本实验中，我们选择一个一元方程f(x)=0来测试迭代法的效果。

首先，我们对给定的初始近似解x0进行计算，得到新的近似解x1，然后再以x1为初始近似解进行计算，得到新的近似解x2，以此类推。

直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。

本实验将通过对复杂方程的迭代计算来评估迭代法的性能。

2.牛顿法牛顿法通过使用函数的一阶导数来逼近方程的根。

具体而言，对于给定的初始近似解x0，通过将f(x)在x0处展开成泰勒级数，并保留其中一阶导数的项，得到一个近似线性方程。

然后，通过求解这个近似线性方程的解x1，再以x1为初始近似解进行计算，得到新的近似解x2，以此类推，直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。

本实验将通过对不同类型的方程进行牛顿法的求解，评估它的性能。

3.二分法二分法是通过将给定区间不断二分并判断根是否在区间内来求方程的根。

具体而言，对于给定的初始区间[a,b]，首先计算区间[a,b]的中点c，并判断f(c)与0的大小关系。

如果f(c)大于0，说明解在区间[a,c]内，将新的区间定义为[a,c]，再进行下一轮的计算。

如果f(c)小于0，说明解在区间[c,b]内，将新的区间定义为[c,b]，再进行下一轮的计算。

直到新的区间的长度小于规定的误差阈值为止。

本实验将通过对复杂方程的二分计算来评估二分法的性能。

三、实验结果通过对一系列测试函数的计算，我们得到了迭代法、牛顿法和二分法的计算结果，并进行了比较。

二分法,牛顿迭代法,matlab

二分法、牛頓迭代法求方程近似解在一些科學計算中常需要較為精確的數值解，本實驗基於matlab 給出常用的兩種解法。

本實驗是以解決一個方程解的問題說明兩種方法的精髓的。

具體之求解方程e^(-x)+x^2-2*x=0，精度e<10^-5;;程序文本文檔如下%%%%%%二分法求近似解cleardisp('二分法求方程的近似解')format longsyms xf=inline('exp(-x)+x^2-2*x');%原函數%通過[x,y]=fminbnd(f,x1,x2)求出極小值點和極小值，進而確定%區間端點，從而確定解區間矩陣CX=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點，C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數，即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e1=b-a;%解一的精度e0=10^-5;%精度ya=f(a);while e1>=e0x0=1/2*(a+b);y0=f(x0);if y0*ya<=0b=x0;elsea=x0;ya=y0;ende1=b-a;endA=[a,b,e1];%解的區間和精度X=[X;A];%解與精度構成的矩陣endX%%%%%%%牛頓迭代法disp('牛頓迭代法解方程的近似解')clear %清空先前變量syms x %定義變量y=exp(-x)+x^2-2*x;%原函數f=inline(y);f1=diff(y); %一階導函數g=inline(f1);format long %由於數值的默認精度為小數點后四位，故需要定義長形X=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點，C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數，即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e0=10^-5; %要求精度i=1; %迭代次數x0=(a+b)/2;A=[i,x0]; %迭代次數，根值的初始方程t=x0-f(x0)/g(x0); %%%%迭代函數while abs(t-x0)>=e0 %%迭代循環i=i+1;x0=t;A=[A;i,x0];t=x0-f(x0)/g(x0);endA ;B=A(i,:);%迭代次數及根值矩陣X=[X;B];endX運行結果如下如若使用matal內置函數fzero,得到如下結果由兩者求得的結果知，使用函數fzero求得的結果精度不夠。

数值分析上机实践报告

数值分析上机实践报告一、实验目的本次实验主要目的是通过上机操作，加深对数值分析算法的理解，并熟悉使用Matlab进行数值计算的基本方法。

在具体实验中，我们将实现三种常见的数值分析算法：二分法、牛顿法和追赶法，分别应用于解决非线性方程、方程组和线性方程组的求解问题。

二、实验原理与方法1.二分法二分法是一种常见的求解非线性方程的数值方法。

根据函数在给定区间端点处的函数值的符号，不断缩小区间的长度，直到满足精度要求。

2.牛顿法牛顿法是求解方程的一种迭代方法，通过构造方程的泰勒展开式进行近似求解。

根据泰勒展式可以得到迭代公式，利用迭代公式不断逼近方程的解。

3.追赶法追赶法是用于求解三对角线性方程组的一种直接求解方法。

通过构造追赶矩阵，采用较为简便的向前追赶和向后追赶的方法进行计算。

本次实验中，我们选择了一组非线性方程、方程组和线性方程组进行求解。

具体的实验步骤如下：1.调用二分法函数，通过输入给定区间的上下界、截止误差和最大迭代次数，得到非线性方程的数值解。

2.调用牛顿法函数，通过输入初始迭代点、截止误差和最大迭代次数，得到方程组的数值解。

3.调用追赶法函数，通过输入追赶矩阵的三个向量与结果向量，得到线性方程组的数值解。

三、实验结果与分析在进行实验过程中，我们分别给定了不同的参数，通过调用相应的函数得到了实验结果。

下面是实验结果的汇总及分析。

1.非线性方程的数值解我们通过使用二分法对非线性方程进行求解，给定了区间的上下界、截止误差和最大迭代次数。

实验结果显示，根据给定的输入，我们得到了方程的数值解。

通过与解析解进行比较，可以发现二分法得到的数值解与解析解的误差在可接受范围内，说明二分法是有效的。

2.方程组的数值解我们通过使用牛顿法对方程组进行求解，给定了初始迭代点、截止误差和最大迭代次数。

实验结果显示，根据给定的输入，我们得到了方程组的数值解。

与解析解进行比较，同样可以发现牛顿法得到的数值解与解析解的误差在可接受范围内，说明牛顿法是有效的。

数值分析实验报告(包括高斯消去、二分法、牛顿迭代法)

N=input('please enter the largest number of iterations:N=');
for k=1:N
x=(a+b)/2;
fx=feval(f,x);fa=feval(f,a);
if abs((b-a)/2)<e || abs(fx)<e
disp('the number of iterations is');k
f=input('please enter a function:f(x)=');
x0=input('please enter the initial value:x0=');
e=input('please enter error:e=');
N=input('please enter the largest number of iterations:N=');
disp('the approximate solution is');x
disp('f(x) is');fx
disp('the number of iterations is');k
return
else
x0=x;
end
end
end
disp('The maximum number of iterations is reached, stop calculation');
开课学院、实验室：实验时间：2014年1月1日
课程
名称
数值分析基础性实验
实验项目
名称
数值计算算法及实现

数值分析实验五(二分法,牛顿迭代法)

实验五一、实验目的与要求：1、通过对二分法和牛顿迭代法作编程练习和上机运算，进一步体会它们在方程求根中的不同特点；2、比较二者的计算速度和计算精度。

二、实验内容：通过对二分法和牛顿迭代法作编程练习和上机运算，进一步体会它们在方程求根中的不同特点。

二分法算法：给定区间[a,b]，并设与符号相反，取为根的容许误差，为的容许误差。

（1）令c=(a+b)/2（2）如果(c-a)<或，则输出，结束；否则执行（3）（3）如果，则令；否则则令，重复（1），（2），（3）。

牛顿迭代法算法：给定初值，为根的容许误差，为的容许误差，N 为迭代次数的容许值。

（1）如果 =0或迭代次数大于N ，则算法失败，结束；否则执行（2）。

（2）计算 = - （3）若 < 或 < ，则输出，程序结束；否则执行（4）。

x 0εη)(x f )('x f x 1x 0)()('0x x o f f x x 01-ε)(1x f ηx 1x0x1（4）令= ，转向（1）。

三、实验题目：1、用二分法求方程f(x)=x^3+4*x*x-10在区间[1，1.5]上的根，要求求出具有3位有效数的近似根。

2、用牛顿法求方程x^3-3x-1=0在x=2附近的根。

四、程序：一、二分法#include<stdio.h>float f(float x){return x*x*x+4*x*x-10;}void main(){float a,b,c;a=1.0;b=1.5;for(;b-a>=0.01;){c=(a+b)/2;if(f(a)*f(c)==0)break;else if(f(a)*f(c)<0)b=c;elsea=c;}printf("方程的近似根为%f\n",c);printf("保留三位有效数字为%0.2f\n",c); }二、牛顿迭代法#include<stdio.h>#include<math.h>float f(float x){return x*x*x-3*x-1;}float g(float x){return 3*x*x-3;}void main(){float x0,x1,a,b,N;int i;i=0;printf("请输入初值X0,根的容许误差,|f(x)|的容许误差,迭代次数的容许值N。

MATL新编计算方法迭代法牛顿法二分法实验报告

M A T L新编计算方法迭代法牛顿法二分法实验报告 Prepared on 22 November 2020姓名实验报告成绩评语：指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存。

实验一方程求根一、实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ，b]上，或某一点附近的实根。

并比较方法的优劣。

二、实验原理(1)、二分法对方程0)(=x f 在[a ，b]内求根。

将所给区间二分，在分点2a b x -=判断是否0)(=x f ；若是，则有根2ab x -=。

否则，继续判断是否0)()(<•x f a f ,若是，则令x b =,否则令x a =。

否则令x a =。

重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。

（2）、迭代法将方程0)(=x f 等价变换为x =ψ（x ）形式，并建立相应的迭代公式=+1k x ψ（x ）。

（3）、牛顿法若已知方程的一个近似根0x ，则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似，因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。

取x 作为原方程新的近似根1x ，然后将1x 作为0x 代入上式。

迭代公式为：=+1k x -0x )(')(k k x f x f 。

三、实验设备：MATLAB 软件四、结果预测（1）11x = （2）5x = （3）2x =0,09052五、实验内容（1）、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根，要求误差不超过3105.0-⨯。

（2）、取初值00=x ，用迭代公式=+1k x -0x )(')(k k x f x f ，求方程0210=-+x e x 的近似根。

MATLAB数值分析实验四(雅各比、高斯赛德尔迭代,以及二分法和牛顿迭代解非线性方程)

佛山科学技术学院实验报告课程名称数值分析实验项目迭代法专业班级机械工程姓名余红杰学号 2111505010指导教师陈剑成绩日期月日一. 实验目的1、在计算机上用Jacobi 迭代法和Gauss-Seidel 迭代法求线性方程组。

2、在计算机上用二分法和Newton 迭代法求非线性方程的根。

二. 实验要求1、按照题目要求完成实验内容；2、写出相应的Matlab 程序；3、给出实验结果(可以用表格展示实验结果)；4、分析和讨论实验结果并提出可能的优化实验。

5、写出实验报告。

三. 实验步骤1、用Matlab 编写Jacobi 迭代法和Gauss-Seidel 迭代法求线性方程组Ax b =的程序。

2、用Matlab 编写二分法和Newton 法求非线性方程()0f x =的根程序。

3、设⎪⎪⎪⎭⎫ ⎝⎛--=212120203A ,T b )1,3,1(=,对于线性方程组b Ax =，考虑如下问题：（1）分别写出Jacobi 迭代矩阵和Gauss-Seidel 迭代矩阵（2）用Jacobi 迭代法和Gauss-Seidel 迭代法解该方程时，是否收敛？谁收敛的更快？（3）用实验步骤1编好的两种迭代法程序进行实验，通过数值结果验证（2）的结论。

4、用调试好的二分法和Newton 迭代法程序解决如下问题求020sin 35=-+-x x e x 的根，其中控制精度810-=eps ，最大迭代次数50=M 。

四. 实验结果1.%Jacob.mfunction [x,B] = Jacob(A,b,n)%Jacobi迭代求解方程组Ax=b，系数矩阵A，迭代次数n%求解的准备工作，构建各迭代系数阵等：m = length(A);D = diag(diag(A));L = -tril(A,-1);U = -triu(A, 1);J = D^(-1)*(L+U);B = J;f = D^(-1)*b;%初始化x即启动值：x = zeros(m,1);%根据x(k+1)=Jx(k)+f进行矩阵运算：for i=1:nx = J*x + f;end%GauSeid.mfunction [x,G] = GauSeid(A,b,n)%Gauss-Seidel迭代求解方程组Ax=b，系数矩阵A，迭代次数n %求解的准备工作，构建各迭代系数阵等：m = length(A);D = diag(diag(A));L = -tril(A,-1);U = -triu(A, 1);G = inv(D-L)*U;f = inv(D-L)*b;%初始化矩阵：%根据x(k+1)=Gx(k)+f进行矩阵运算：x = zeros(m,1);for i = 1:nx = G*x + f;end2.%Dichotomy.mfunction x=Dichotomy(x1,x2,p,n)%利用二分法求根，区间[x1,x2]%p为精度a = x1;b = x2;%进行n次二分：%第一个条件判断根在a,b区间内%第二个条件判断是否中间点就是根，是则迭代终止；%第三个条件判断二分后根在中点左侧还是右侧；%第四个条件判断精度是否达标，用区间长度代替for i=1:nif f(a)*f(b)<0x0 = (a+b)/2;p0 = (b-a)/(2^i);if f(x0)==0x = x0;elseif f(a)*f(x0)<0b = x0;else a= x0;endendendif p0>pcontinue;elsex = x0;break;endend%NewIterat.mfunction x=NewIterat(x0,p,n)%利用牛顿迭代法求根；%x0为启动点，估计的靠近根的值，p为精度，n为迭代次数；syms x1;%设置一个自变量x1，方便后面的求导:f1 = diff(f(x1));%进行n次迭代，精度达标会提前终止；%第一个判断是根据控制条件来确定真实误差是选绝对还是相对误差；%第二个判断是确定精度是否满足要求for i=1:nx1 = x0;x = x0-f(x0)/eval(f1);if x<1RealDiv = abs(x-x0);else RealDiv = abs(x-x0)/abs(x); endif RealDiv>px0 = x;else break;endend3.run43.mclc,clear;A = [3 0 -2;0 2 1;-2 1 2];b = [1;3;1];n1 = 50;n2 =100;%输入A,b矩阵，设置迭代次数为50次；%调用迭代函数，返回迭代矩阵；[x,B] = Jacob(A,b,n1);xj50 = x;f1 = max(abs(eig(B)))%显示谱半径，确定收敛性；[x,B] = GauSeid(A,b,n1);xg50 = x;f2 = max(abs(eig(B)))%谱半径；xj100 = Jacob(A,b,n2);xg100 = GauSeid(A,b,n2); Jacobi= [xj50,xj100]%对比迭代50次和100次的结果GauSei= [xg50,xg100]%很容易看出准确解为[1；1；1]4.f.mfunction y = f(x)%所有f(x)=0中f(x)函数；y = exp(5*x)-sin(x)+x^3-20; 下页是具体解时的程序：%run44.mclc,clear;%很容易看出在[0,1]间有解；x = Dichotomy(0,1,10^(-8),50)x = NewIterat(0,10^(-8),50)五. 讨论分析4.3实验中的迭代矩阵在上个部分，分别为J 和G ；对于收敛性，看下图中的f1,f2，也就是迭代矩阵的谱半径，都是小于1的，但是可以看出后者的谱半径更小，就是说它的收敛速度更快；最终求x 的值，每种迭代方法分别迭代50次（第一列）和100次（第二列）；实际值为[1；1；1]可以看出用高斯赛德尔迭代更精确，速度更快。

数值分析实验二分法

x =
0.73908513321516
三本次实验总结
通过做此实验，我对MATLAB有更进一步的了解，了解了MATLAB强大的功能以及如何用MATLAB来解决实际问题，激发了我学习MATLAB的兴趣，更加使我认识到MATLAB在我们的工作生活中都有广泛的应用。对于此次编程实验，我也意识到自己对MATLAB还不够了解，今后需要花更多时间在这门课上，以求更好的掌握MATLAB，同时这次试验也让我对用二分法和牛顿法解决数学问题有了更深一步的了解。
源代码
clc
close all
format long;
f=input('f(x)=');
qujian=input('输入区间=') ;
err=input('误差范围;');
a=qujian(1);
b=qujian(2);
yc=1;
while((b-a)>err)&(yc~=0);
c=(a+b)/2; %设定中点
x =
1.73205566406250
2牛顿法实验f(x)=x-cosx的正根（精度精确到0.000001）
算法实现
1：构造区间[-1,1],代入方程f(x),如果f(-1)*f(1)<0说明根的区间在[-1,1];
2：利用fzero（’x-cos(x)’），取得临界点0.5;
3：取f(x)的一介导数，构造牛顿方法;
四教师评语
牛顿法和弦截法：与牛顿法相比，弦截法的收敛速度也是比较快的。可以证明，弦截法具有超线性收敛速度。
相同之处：都是线性化方法。
不同之处：牛顿法在计算xk+1时只用到前一步的值xk，故这种方法称为单点迭代法。

用MATLAB计算椭圆周长及牛顿迭代的MATLAB实现

一、实验方案:用二分法和牛顿迭代法（包括弦截法）编程求方程02sin 2=-x x 的实根，要求误差不超过410-。

输出迭代次数，初始值和根的近似值；构造不同的迭代函数，用迭代法求解，并进行比较。

编写M 文件绘制该函数图形，源程序如下：function y=EX0111x=-1:0.1:2;y=sin(x)-(x.^2)/2;plot(x,y,'r')hold onplot(x,zeros(size(x)))hold offgrid运行后可以看出，函数的根在区间[1，1.5]。

所以，分析题意，编写二分法源程序如下：function y=EX0110syms x y ;y=sin(x)-(x.^2)/2;a=1;b=1.5;delta=0.0001;ya=subs(y,a);yb=subs(y,b);N=1+round((log(b-a)-log(delta))/log(2));for k=1:Ndx=yb*(b-a)/(yb-ya+eps);c=b-dx;ab=b-a;yc=subs(y,c);if yc==0,break ;elseif ya*yc<0b=c;yb=yc;elsea=c;ya=yc;enddd=min(abs(ab),abs(yc));if dd<delta,break ,endendddkc=b-dx运用牛顿迭代法编程，源程序如下：function y=fun(x)y=sin(x)-(x.^2)/2;和该函数导数：function y=dfun(x)y=cos(x)-x;以及牛顿迭代法：function [xk,k]=newtoneq(x0,n,derta)k=1;xk(1)=x0;t=x0-fun(x0)./dfun(x0);while abs(t-x0)>=dertax0=t;k=k+1;xk(k)=t;t=x0-fun(x0)./dfun(x0);if (k-1)>n error('n is full'),endend构造新的迭代函数为k k x x sin 21⨯=+，编辑源程序如下：function y=iter()syms x y ;y=sqrt(2*sin(x));x0=1;max=20;derta=0.0001;t=[x0];x=subs(y,x0);k=0;while abs(x-x0)>=dertat=[t,x];x0=x;x=subs(y,x0);k=k+1;if k>maxdisp('迭代次数超过最大次数。

二分法和牛顿迭代法求解方程的比较

二分法和牛顿迭代法求解方程的比较200822401018 徐小良一、问题叙述求解12 -3x +2COS X =0的解；通过编写 matlab程序分别用分析二分法和牛顿迭代法求解方程，通过两种方法的比较，分析二者求解方程的快慢程度。

二、问题分析由matlab画图命令，容易得到此方程解的范围为（2，4）;两种迭代方法，在使用相同的误差（0.00001 ）的情况下，得出 matlab迭代次数，通过次数的比较得出二者求解速度快慢比较。

三、实验程序及注释（1）、二分法程序：clear;f=inlin e('12-3*x+2*cos(x)'); format long%清除所有内存数据;%数据显示格式设为长型;a=2;b=4;er=b-a;ya=f(a);k=0;er0=0.00001; while er>er0x0=.5*(a+b); y0=f(x0);if ya*y0<0b=x0;elsea=x0;ya=y0;enddis p([a,b]);er=b-a;k=k+1%求解区间；%误差分析;%二分法求解程序;%显示各个区间值和求解次数;enddis %显示最后一个区间值;(2)、牛顿迭代法程序：clear;f=inlin e('12-3*x+2*cos(x)'); %清除所有内存数据;%数据显示格式设为长型;b=3;a=4;k=0;y0=f(b);y=f(a);while abs(b-a)>0.00001 t=a-y*(a-b)/(y-y0); b=a;y0=y;%求解区间;、%牛顿迭代法求解程序;四、实验数据结果及分析五、实验结论通过表1可知，在二分法下，程序迭代了 17次后和第18次的结果一致，即程序迭代了 17次达到要求的试验误差；通过表 2可知，在牛顿迭代法下，程序迭代了 4次后和第5次的结果一致，即程序迭代了 4次达到要求的试验误差；二者比较明显可以看出牛顿迭代法的求解效率要远远优于二分法。

数值分析上机实验报告

一、实验目的通过本次上机实验，掌握数值分析中常用的算法，如二分法、牛顿法、不动点迭代法、弦截法等，并能够运用这些算法解决实际问题。

同时，提高编程能力，加深对数值分析理论知识的理解。

二、实验环境1. 操作系统：Windows 102. 编程语言：MATLAB3. 实验工具：MATLAB数值分析工具箱三、实验内容1. 二分法求方程根二分法是一种常用的求方程根的方法，适用于连续函数。

其基本思想是：从区间[a, b]中选取中点c，判断f(c)的符号，若f(c)与f(a)同号，则新的区间为[a, c]，否则为[c, b]。

重复此过程，直至满足精度要求。

2. 牛顿法求方程根牛顿法是一种迭代法，适用于可导函数。

其基本思想是：利用函数在某点的导数值，求出函数在该点的切线方程，切线与x轴的交点即为方程的近似根。

3. 不动点迭代法求方程根不动点迭代法是一种迭代法，适用于具有不动点的函数。

其基本思想是：从初始值x0开始，不断迭代函数g(x)的值，直至满足精度要求。

4. 弦截法求方程根弦截法是一种线性近似方法，适用于可导函数。

其基本思想是：利用两点间的直线近似代替曲线，求出直线与x轴的交点作为方程的近似根。

四、实验步骤1. 二分法求方程根（1）编写二分法函数：function [root, error] = bisection(a, b, tol)（2）输入初始区间[a, b]和精度要求tol（3）调用函数计算根：[root, error] = bisection(a, b, tol)2. 牛顿法求方程根（1）编写牛顿法函数：function [root, error] = newton(f, df, x0, tol)（2）输入函数f、导数df、初始值x0和精度要求tol（3）调用函数计算根：[root, error] = newton(f, df, x0, tol)3. 不动点迭代法求方程根（1）编写不动点迭代法函数：function [root, error] = fixed_point(g, x0, tol)（2）输入函数g、初始值x0和精度要求tol（3）调用函数计算根：[root, error] = fixed_point(g, x0, tol)4. 弦截法求方程根（1）编写弦截法函数：function [root, error] = secant(f, x0, x1, tol)（2）输入函数f、初始值x0和x1，以及精度要求tol（3）调用函数计算根：[root, error] = secant(f, x0, x1, tol)五、实验结果与分析1. 二分法求方程根以方程f(x) = x^2 - 2 = 0为例，输入初始区间[a, b]为[1, 3]，精度要求tol 为1e-6。

MATLAB计算方法迭代法牛顿法二分法实验报告

MATLAB计算方法迭代法牛顿法二分法实验报告实验目的：本实验旨在通过MATLAB编程实现迭代法、牛顿法和二分法，并通过实例验证其准确性和收敛速度。

实验原理：迭代法是一种通过不断迭代逼近根的方法，其基本原理是选择一个初始值，然后通过迭代公式不断逼近根的值，直到满足给定的精度要求。

牛顿法是一种通过不断迭代求函数的零点的方法，其基本原理是通过当前点的切线与x轴的交点来逼近根的值，直到满足给定的精度要求。

二分法是一种通过不断将区间一分为二来逼近根的方法，其基本原理是通过判断根是否落在区间的两个端点之间，然后将区间一分为二，直到满足给定的精度要求。

实验步骤：1.编写迭代法的MATLAB代码，实现对给定函数的根的逼近。

2.编写牛顿法的MATLAB代码，实现对给定函数的根的逼近。

3.编写二分法的MATLAB代码，实现对给定函数的根的逼近。

4.针对不同的函数，分别使用迭代法、牛顿法和二分法进行根的逼近，并记录每种方法的迭代次数和逼近结果。

5.对比三种方法的迭代次数和逼近结果，分析其准确性和收敛速度。

实验结果：以求解方程x^3-2x-5=0为例，使用迭代法、牛顿法和二分法进行根的逼近。

迭代法：迭代公式：x(n+1)=(2x(n)+5)^(1/3)初始值：x(0)=2迭代次数：6逼近结果：2.0946牛顿法：初始值：x(0)=2迭代次数：4逼近结果：2.0946二分法：初始区间：[1,3]迭代次数：11逼近结果：2.0946实验结论：通过对比三种方法的迭代次数和逼近结果可以发现，迭代法和牛顿法的收敛速度都要快于二分法，并且迭代法和牛顿法的逼近结果也更为接近真实根。

这是因为迭代法和牛顿法都是通过不断逼近根的值来求解，而二分法则是通过将区间一分为二来逼近根的值，所以迭代法和牛顿法的收敛速度更快。

总结：本实验通过MATLAB编程实现了迭代法、牛顿法和二分法，并通过实例验证了它们的准确性和收敛速度。

实验结果表明，迭代法和牛顿法在求解根的过程中具有更快的收敛速度和更接近真实根的逼近结果，而二分法的收敛速度较慢。

MATLAB计算方法迭代法牛顿法二分法实验报告

完美WORD格式姓名实验报告成绩评语：指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存。

实验一方程求根一、实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ，b]上，或某一点附近的实根。

并比较方法的优劣。

二、实验原理 (1)、二分法对方程0)(=x f 在[a ，b]内求根。

将所给区间二分，在分点2a b x -=判断是否0)(=x f ；若是，则有根2a b x -=。

否则，继续判断是否0)()(<∙x f a f ,若是，则令x b =,否则令x a =。

否则令x a =。

重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。

（2）、迭代法将方程0)(=x f 等价变换为x =ψ（x ）形式，并建立相应的迭代公式=+1k x ψ（x ）。

（3）、牛顿法若已知方程的一个近似根0x ，则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似，因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。

取x 作为原方程新的近似根1x ，然后将1x 作为0x 代入上式。

迭代公式为：=+1k x -0x )(')(k k x f x f 。

三、实验设备：MATLAB 7.0软件四、结果预测（1）11x =0.09033 （2）5x =0.09052 （3）2x =0,09052 五、实验内容（1）、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根，要求误差不超过3105.0-⨯。

（2）、取初值00=x ，用迭代公式=+1k x -0x )(')(k k x f x f ，求方程0210=-+x e x的近似根。

要求误差不超过3105.0-⨯。

MAAB计算方法迭代法牛顿法二分法实验报告

姓名实验报告成绩评语：指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存。

实验一方程求根一、实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ，b]上，或某一点附近的实根。

并比较方法的优劣。

二、实验原理(1)、二分法对方程0)(=x f 在[a ，b]内求根。

将所给区间二分，在分点2a b x -=判断是否0)(=x f ；若是，则有根2ab x -=。

否则，继续判断是否0)()(<•x f a f ,若是，则令x b =,否则令x a =。

否则令x a =。

重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。

（2）、迭代法将方程0)(=x f 等价变换为x =ψ（x ）形式，并建立相应的迭代公式=+1k x ψ（x ）。

（3）、牛顿法若已知方程的一个近似根0x ，则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似，因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。

取x 作为原方程新的近似根1x ，然后将1x 作为0x 代入上式。

迭代公式为：=+1k x -0x )(')(k k x f x f 。

三、实验设备：MATLAB 7.0软件四、结果预测（1）11x =0.09033 （2）5x =0.09052 （3）2x =0,09052五、实验内容（1）、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根，要求误差不超过3105.0-⨯。

（2）、取初值00=x ，用迭代公式=+1k x -0x )(')(k k x f x f ，求方程0210=-+x e x 的近似根。

要求误差不超过3105.0-⨯。

牛顿迭代法与二分法1

用二分法和牛顿迭代法编程一. 实验课题用二分法和牛顿迭代法编程求方程sinx-x²/2=0的实根，要求误差不超过0.00001。

输出迭代次数，初始值和根的近似值；再构造不同的迭代函数，用迭代法求解，并进行比较。

二. 实验步骤(一) 用matlab作函数y=sinx-x²/2的图，步骤如下：先作一个名为fun1.m的 M文件function y1=fun1(x)y1=sinx-x²/2；接着使用下列命令在区间[-0.5，2]上作该函数的图象，并估计y1=0时x的根的大致区间。

x=-0.5:0.01:2;plot (x,fun1(x),‘b’)hold onplot(x,zeros(size(x)))hold offgrid由图象的结果观察可知：上述方程在（1，1.5）上有一实根。

（二）用二分法求方程的近似根由|b-a|/(2^(n+1))≤ε可以得到n≥13，故预定最大计算次数为15次。

作一个名为fun2.m的M文件，步骤如下：function X=fun2(a,b)n=15; ε=0.01; k=1; X=(a+b)/12;while fabs(a-b)≥εif fun1(X)==0;breakendif fun1(a)*fun1(X)<0; b=X;else a=X;endk=k+1;if k>n,k, error(‘fail’)else X=(a+b)/2;endend[‘Iterative times=’,int2str(k)]在命令窗口输入命令：r=fun2(1,1.5)运行后得到结果为：ans=Iterative times=13 r=1.4408（三）用牛顿迭代法求方程的近似根具体步骤如下：1. 选择迭代函数φ(x)=x-f(x)/f’(x)。

2.选定初始值x0与x1，并算出相应的f(x0)与f(x1),并保证迭代算出的x1比x0更接近所求的根。

二分法、牛顿法、割线法、Steffencen法求非线性方程MATLAB实现

x0=a; else
x0=b; end m=min(abs(df(a)),abs(df(b))); k=0; while abs(f(x0))>m*dlt
k=k+1; x1=x0-f(x0)/df(x0); x0=x1; fprintf('k=%d x=%.5f\n',k,x0); end
三、实验结果
%加速公式 gen=x1-(y-x1)^2/(z-2*y+x1); wucha=abs(gen-x1); time=time+1; %迭代加一次的记录 end end; %计算结果
四、结果分析
由实验结果分析可知，Steffensen 迭代算法的收敛速度在一定条件下可以达到二次收敛，相对割线法和二分法收敛速度较快，且其在一定程度上避免了两个值很近时造成的误差，也对牛顿法要求函数导数值这一缺点进行了克服，整体上比较来说是一个计算量较小且有较高精度的迭代算法。
二、算法描述
MATLAB 程序代码如下： function [gen,time]=Steff(fun,x0,tol) %如果缺省误差参数，默认为 10 的-5 次方 if(nargin==2) tol=1.0e-5; end %设置误差初值 time=0; %记迭代次数 wucha=0.1; %设置前后两次迭代的误差 gen=x0; while(wucha>tol) x1=gen; y=subs(fun,x1)+x1; z=subs(fun,y)+y;
(b1
−
a1 )
；对[a2 ,b2 ] 重复上述做法得：
1
[a1, b1] ⊃ [a2 , b2 ] ⊃ ...... ⊃ [an , bn ] ⊃ ...... 且 bn − an