第2章 材料的晶体结构
第2章 晶体结构讲解

第2章晶体结构为了便于对材料进行研究,常常将材料进行分类。
如果按材料的状态进行分类,可以将材料分成晶态材料,非晶材料及准晶材料。
因所有的晶态材料有其共同的规律,近代晶体学知识就是为研究这些共同规律而必备的基础。
同时为了研究非晶材料与准晶材料及准晶材料也必须以晶体学理论做为基础。
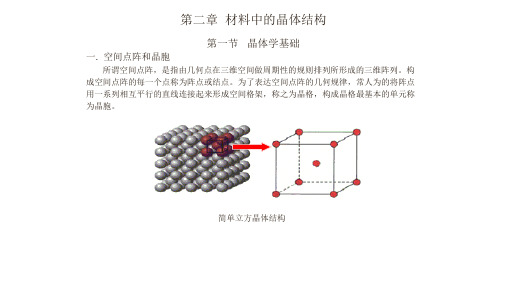
在一般的教材中对晶体学的基础知识已经有了不同深度的阐述,作为辅导教材,对教科书上已经有较多阐述的内容,本章中就简要的进行说明,而重点在于用动画形式,将在教材中难以用文字表达清楚的内容进行较多的阐述,加深对教材内容的理解记忆2.1晶体学基础2.1.1 空间点阵和晶胞具有代表性的基本单元(最小平行六面体)作为点阵的组成单元,称为晶胞。
将晶胞作三维的重复堆砌就构成了空间点阵。
为了便于分析研究晶体中质点的排列规律性,可先将实际晶体结构看成完整无缺的理想晶体并简化,将其中每个质点抽象为规则排列于空间的几何点,称之为阵点。
这些阵点在空间呈周期性规则排列并具有完全相同的周围环境,这种由它们在三维空间规则排列的阵列称为空间点阵,简称点阵。
同一空间点阵可因选取方式不同而得到不相同的晶胞<晶胞、晶轴和点阵矢量>根据6个点阵参数间的相互关系,可将全部空间点阵归属于7种类型,即7个晶系。
按照"每个阵点的周围环境相同"的要求,布拉菲(Bravais A.)用数学方法推导出能够反映空间点阵全部特征的单位平面六面体只有14种,这14种空间点阵也称布拉菲点阵。
空间点阵是晶体中质点排列的几何学抽象。
1 空间点阵最初人们认为凡是具有规则外形的天然矿物均为晶体。
但现在人们认识到晶体的规则的几何外形是内部结构规律的外在反映. 近代的科学研究表明了下面的两个基本事实:1)如果说某一种材料是晶体,其基本的特征是:组成该材料的内部的微观粒子(原子,分子,离子等)在三微的空间做有规则的周期性的排列。
2)这种排列的规律决定了材料的性能。
根据这样的事实我们可以抽象出个的重要概念即空间点阵。
材料化学第2章完美晶体的结构

3.有固定的熔点
晶体熔化过程是晶体长程序解体的过程。破坏长程序所需的能 量就是熔化热。所以晶体具有特定的熔点。反之,也说明晶体内部 结构的规则性是长程有序的。
温度/ ℃
液体 tm/ ℃ tg/ ℃ 晶体 玻璃
时间
过冷液体
液体
晶体物质熔化是 有熔点Tm,玻璃 态没有熔点,存 在一个玻璃化温 度Tg!
可以采用晶面法 线的取向表征晶 面的方位,而共 顶点的晶面法线 的夹角表示晶面 之间的夹角。
水溶液中 结晶立方 NaCl
α
含尿素水 溶液中结 晶削角立 方NaCl
对于一定类型的晶体来说,不论其外形如何,总存在一组特定
的夹角,如石英晶体的m与m两面夹角为60°0′,m与r面之间的夹角 为 38°13′ , m 与 z 面的夹角为 38°13′ 。对于其它品种晶体,晶面间 则有另一组特征夹角。这一普遍规律称为晶面角守恒定律,即同一 种晶体在相同的温度和压力下,其对应晶面之间的夹角恒定不变。
中,空间的一个点或原子的位置可以用3个数(x,y,z)来规定。
P 相应的原子的位置可以表示为向 量 op ,即 op=xa+yb+cz 。其中, x , y , z 为标量。由于该坐标系以向量 a 、 b 、 c为坐标轴长度,所以x,y,z≤1,故 将坐标( x , y , z )称作原子的分数 坐标。
图中4种粒 都可以在三 维方向平移, 严格遵守周 期性。
晶体中的原子、分子或离子沿空间三个不同方向,各按一定
的距离周期性地平移而构成,基元每一平移距离称为周期。在一 定方向有着一定周期,不同方向上周期一 般不相同。
周期
b
周期
a
⑵结构单元:我们把这种具有一定组成的原子、分子或其集团 及其在空间按一定方式排列的结构,即周期性重复的单元,称作晶 体的结构单元。 例如:干冰晶体结构单元为CO2;食盐晶体结构单元为一个Na+ 离子和一个 Cl - 离子;萤石晶体结构单元为一个Ca2+ 离子和二个 F - 离子。
无机材料科学基础___第二章晶体结构

第 2 章结晶结构一、名词解释1.晶体:晶体是内部质点在三维空间内周期性重复排列,具有格子构造的固体2.空间点阵与晶胞:空间点阵是几何点在三维空间内周期性的重复排列晶胞:反应晶体周期性和对称性的最小单元3.配位数与配位多面体:化合物中中心原子周围的配位原子个数成配位关系的原子或离子连线所构成的几何多面体4.离子极化:在离子化合物中,正、负离子的电子云分布在对方离子的电场作用下,发生变形的现象5.同质多晶与类质同晶:同一物质在不同的热力学条件下具有不同的晶体结构化学成分相类似物质的在相同的热力学条件下具有相同的晶体结构6.正尖晶石与反尖晶石:正尖晶石是指2价阳离子全部填充于四面体空隙中,3价阳离子全部填充于八面体空隙中。
反尖晶石是指2价阳离子全部填充于八面体空隙中,3价阳离子一半填充于八面体空隙中,一半填充于四面体空隙。
二、填空与选择1.晶体的基本性质有五种:对称性,异相性,均一性,自限性和稳定性(最小内能性)。
2.空间点阵是由 C 在空间作有规律的重复排列。
( A 原子 B离子 C几何点 D分子)3.在等大球体的最紧密堆积中有面心立方密堆积和六方密堆积二种排列方式,前者的堆积方式是以(111)面进行堆积,后者的堆积方式是以(001)面进行堆积。
4.如晶体按立方紧密堆积,单位晶胞中原子的个数为 4 ,八面体空隙数为 4 ,四面体空隙数为 8 ;如按六方紧密堆积,单位晶胞中原子的个数为 6 ,八面体空隙数为6 ,四面体空隙数为 12 ;如按体心立方近似密堆积,单位晶胞中原子的个数为 2 ,八面体空隙数为 12 ,四面体空隙数为 6 。
5.等径球体最紧密堆积的空隙有两种:四面体空隙和八面体空隙。
一个球的周围有 8个四面体空隙、 6 个八面体空隙;n个等径球体做最紧密堆积时可形成 2n 个四面体空隙、 n 个八面体空隙。
不等径球体进行堆积时,大球做最紧密堆积或近似密堆积,小球填充于空隙中。
6.在离子晶体中,配置于正离子周围的负离子数(即负离子配位数),决定于正、负离子半径比(r +/r -)。
第二章 晶体结构

第二章晶体结构【例2-1】计算MgO和GaAs晶体中离子键成分的多少。
【解】查元素电负性数据得,,,,则MgO离子键%=GaAs离子键%=由此可见,MgO晶体的化学键以离子键为主,而GaAs则是典型的共价键晶体。
【提示】除了以离子键、共价键结合为主的混合键晶体外,还有以共价键、分子间键结合为主的混合键晶体。
且两种类型的键独立地存在。
如,大多数气体分子以共价键结合,在低温下形成的晶体则依靠分子间键结合在一起。
石墨的层状单元内共价结合,层间则类似于分子间键。
正是由于结合键的性质不同,才形成了材料结构和性质等方面的差异。
从而也满足了工程方面的不同需要。
【例2-2】NaCl和MgO晶体同属于NaCl型结构,但MgO的熔点为2800℃, NaC1仅为80l℃,请通过晶格能计算说明这种差别的原因。
【解】根据:晶格能(1)NaCl晶体:N0=6.023×1023 个/mol,A=1.7476,z1=z2=1,e=1.6×10-19 库仑,,r0===0.110+0.172=0.282nm=2.82×10-10 m,m/F,计算,得:E L=752.48 kJ/mol(2)MgO晶体:N0=6.023×1023个/mol,A=1.7476,z1=z2=2,e=1.6×10-19库仑,r0==0.080+0.132=0.212 nm=2.12×10-10 m,m/F,计算,得:E L=3922.06 kJ/mol则:MgO晶体的晶格能远大于NaC1晶体的晶格能,即相应MgO的熔点也远高于NaC1的熔点。
【例2-3】根据最紧密堆积原理,空间利用率越高,结构越稳定,但是金刚石的空间利用率很低,只有34.01%,为什么它也很稳定?【解】最紧密堆积的原理只适用于离子晶体,而金刚石为原子晶体,由于C-C共价键很强,且晶体是在高温和极大的静压力下结晶形成,因而熔点高,硬度达,很稳定。
第二章 晶体结构

晶胞
• 有实在的具体质点所 组成
平行六面体
• 由不具有任何物理、化学 特性的几何点构成。
是指能够充分反映整个晶体结构特征的最小结构单位, 其形状大小与对应的单位平行六面体完全一致,并可用 晶胞参数来表征,其数值等同于对应的单位平行六面体 参数。
晶胞棱边长度a、b、c,其单位为nm ,棱间夹角α、β、 γ。这六个参数叫做点阵常数或晶格常数。
面网密度:面网上单位面积内结点的数目; 面网间距:任意两个相邻面网的垂直距离。
相互平行的面网的面网密度
和面网间距相等; 面网密度大的面网其面网间 距越大。
空间格子―――连接分布在三维空间的结点构成空 间格子。由三个不共面的行列就决定一个空间格子。
空间格子由一系列 平行叠放的平行六 面体构成
2-1 结晶学基础
一、空间点阵
1.晶体的基本概念 人们对晶体的认识,是从石英开始的。 人们把外形上具有规则的几何多面体形态的 固体称为晶体。 1912年劳厄(德国的物理学家)第一次成功 获得晶体对X射线的衍射线的图案,才使研究 深入到晶体的内部结构,才从本质上认识了 晶体,证实了晶体内部质点空间是按一定方 式有规律地周期性排列的。
第二章 晶体结构
第二章 晶体结构
1
结晶学基础 晶体化学基本原理 非金属单质晶体结构
2
3 4 5
无机化合物晶体结构
硅酸盐晶体结构
重点:重点为结晶学指数,晶体中质点的堆 积,氯化钠型结构,闪锌矿型结构,萤石型 (反萤石型)结构,钙钛矿型结构,鲍林规 则,硅酸盐晶体结构分类方法。 难点:晶体中质点的堆积,典型的晶体结构 分析。
• 结点分布在平行六面
体的顶角; •平行六面体的三组棱长 就是相应三组行列的结 点间距。
材料科学基础第2章材料中的晶体结构

材料科学基础第2章材料中的晶体结构晶体是由原子、离子或分子按照一定的规则排列而成的固体。
晶体结构是指晶体中原子,离子或分子的排列方式。
晶体结构的特点是重复性和周期性。
晶体结构可以通过晶体的晶胞来描述,晶胞是晶体中最小重复单元,是由若干个原子,离子或分子组成的。
晶体结构的分类可以根据晶体的对称性进行。
常见的晶体结构类型有立方晶系、四方晶系、正交晶系、单斜晶系、三斜晶系、六角晶系和三角晶系。
立方晶系是最常见的晶体结构类型,它具有最高的对称性。
立方晶系包括体心立方晶体、面心立方晶体和简单立方晶体。
体心立方晶体每个晶胞中有一个原子位于立方体的中心,面心立方晶体每个晶胞中有一个原子位于每个立方体的面心,简单立方晶体每个晶胞中只有一个原子。
四方晶系的晶体中,晶胞的底面为矩形,其中一个边与底面垂直。
正交晶系的晶胞基本上和四方晶系相似,但它的底面为正方形。
单斜晶系的晶胞有一个倾斜的边,它是在不同轴上分别有两面成直角。
三斜晶系的晶体是最复杂的结构类型,它的晶胞没有任何对称性。
六角晶系的晶体结构可以看作是体心立方晶体和单斜晶体的组合,晶胞为底面呈六角形的棱柱。
三角晶系的晶体结构最特殊,晶胞为三角形。
晶体结构的研究对于材料科学非常重要。
通过了解晶体结构,我们可以预测和解释材料的物理性质,如硬度、热膨胀系数和电导率等。
晶体结构还对材料的合成和制备起到了指导作用。
例如,通过改变晶体结构,可以改变材料的性质,如增加或减少导电性。
总之,材料中的晶体结构是材料科学基础中的重要内容。
了解晶体结构有助于我们理解材料的性质和行为,并为材料设计和合成提供基础。
晶体结构的研究对于材料科学的发展非常重要,并在材料的合成和制备中起到了指导作用。
材料科学基础第二章

y
[111]
x
[111]
例:画出晶向
[112 ]
2.立方晶系晶面指数
晶面指数的确定方法
(a)建立坐标系,结点为原点, 三棱为方向,点阵常数为单位 (原点在标定面以外,可以采 用平移法); (b)晶面在三个坐标上的截距a1 a2 a3 ; (c)计算其倒数 b1 b2 b3 ; (d)化成最小、整数比h:k:l ; 放在圆方括号(hkl),不加逗号, 负号记在上方 。
3.六方晶系晶面和晶向指数
三指数表示六方晶系晶面和晶向的缺点:晶体学上等价的 晶面和晶向不具有类似的指数。 例:
晶面指数
(11 0)
(100)
[010] [100]
从晶面指数上不能明确表示等同晶面,为了克服这一缺点, 采用a1、a2、a3及c四个晶轴, a1、a2、a3之间的夹角均 为120º ,晶面指数以(hkil)表示。 根据立体几何,在三维空间中独立的坐标轴不会超过三 个可证明 : i= - (h+k) 或 h+k+i=0
六方晶系
d hkl
h k l a b c
2 2 2
d hkl
a h2 k 2 l 2
1 l c
2
4 h 2 hk k 2 3 a2
注:以上公式是针对简单晶胞而言的,如为复杂晶胞, 例如体心、面心,在计算时应考虑晶面层数增加的影 响,如体心立方、面心立方、上下底(001)之间还有 一层同类型晶面,实际
[1 00 ]
[0 1 0]
[010]
[1 00]
y
[100]
x
[00 1]
机械工程材料 第二章 金属的晶体结构与结晶

均匀长大
树枝状长大
2-2
晶粒度
实际金属结晶后形成多晶体,晶粒的大小对力学性能影响很大。 晶粒细小金属强度、塑性、韧性好,且晶粒愈细小,性能愈好。
标准晶粒度共分八级, 一级最粗,八级最细。 通过100倍显微镜下的 晶粒大小与标准图对 照来评级。
2-2
• 影响晶粒度的因素
• (1)结晶过程中的形核速度N(形核率) • (2)长大速度G(长大率)
面心立方晶 格
912 °C α - Fe
体心立方晶 格
1600
温 度
1500 1400
1300
1200
1100
1000
900
800
700 600 500
1534℃ 1394℃
体心立方晶格
δ - Fe
γ - Fe
γ - Fe
912℃
纯铁的冷却曲线
α – Fe
体心立方晶 格
时间
由于纯铁具有同素异构转变的特性,因此,生产中才有可能通过 不同的热处理工艺来改变钢铁的组织和性能。
2-3
• 铁碳合金—碳钢+铸铁,是工业应用最广的合金。 含碳量为0.0218% ~2.11%的称钢 含碳量为 2.11%~ 6.69%的称铸铁。 Fe、C为组元,称为黑色金属。 Fe-C合金除Fe和C外,还含有少量Mn 、Si 、P 、 S 、 N 、O等元素,这些元素称为杂质。
2-3
• 铁和碳可形成一系列稳定化合物: Fe3C、 Fe2C、 FeC。 • 含碳量大于Fe3C成分(6.69%)时,合金太脆,已无实用价值。 • 实际所讨论的铁碳合金相图是Fe- Fe3C相图。
2-2
物质从液态到固态的转变过程称为凝固。 材料的凝固分为两种类型:
材料科学基础,第2章,材料中的晶体结构

晶面间距与晶面指数的关系: 晶面间距是现代测试中一个重要的
参数。在简单点阵中,通过晶面指数 (hkl)可以方便地计算出相互平行的一 组晶面之间的距离d。
晶系 晶面间距
立方
1 h2 k 2 l2
d2
a2
正方
1
h2 k2
l2
d2
a2
c2
六方
( ) 1
4 h2 hk k 2
l2
d2
3
a2
c2
1.晶面、晶向及其表征
1)晶面 (1)定义:晶体点阵在任何方向上可分
解为相互平行的结点平面,称为晶面。 (2)特征: 晶面上的结点在空间构成一个二维点阵。 同一取向上的晶面,不仅相互平行、间
距相等,而且结点的分布也相同。 不同取向的结点平面其特征各异。
(3)晶面指数:
结晶学中经常用(hkl)来表示一组平 行晶面,称为晶面指数。
不同方向的直线组,其质点分布不尽相同。
(3)晶向指数: 用[uvw]来表示。 其 中 u 、 v 、 w 三 个 数 字 是 晶 向 矢 量
在参考坐标系X、Y、Z轴上的矢量 分量经等比例化简而得出。
晶向指数求法:
①确定坐标系; ②过坐标原点,作直线与待求晶向
平行; ③在该直线上任取一点,并确定该
{110}晶面族
Z
(011)
(110) (011) (101)
(101)
Y (110)
X
2)晶向:
(1)定义:
点阵可在任何方向上分解为相互平行的直线组, 结点等距离地分布在直线上。位于一条直线上 的结点构成一个晶向。
(2)特征:
同一直线组中的各直线,其结点分布完全相同, 故其中任何一直线,可作为直线组的代表。
第2章 材料中的晶体结构

b. 已知两不平行晶向[u1v1w1]和[u2v2w2 ],由其决定的 晶面指数(hkl)为:
h v1 w 2 v 2 w 1 , k w 1u 2 w 2 u 1, l u 1 v 2 u 2 v1
补充
cos
2
(对于立方晶系)
两个晶面(h1k1l1)与(h2k2l2)之间的夹角φ
h h
1 2
k k
1 2
2
2
ll
1
2 2 2
(h1
k
2 1
l1 )
(h 2
k
l
2 2
)
两个晶向[u1v1w1]与[u2v2w2]之间的夹角θ
cos
2
u u
1
2
vv
1 2
2
w w
1 2
2
(u 1
v
2 1
w1)
(u 2
v
2 2
w
2 2
)
晶面(hkl)与晶向[uvw]之间的夹角ψ
晶向指数用[uvtw] 来表示。其中 t =-(u+v)
120° 120°
晶面指数的标定
1.求晶面与四个轴的截距
2.取倒数
3.再化成简单整数
4.用圆括号括起来(h k i l)
六方系六个侧面的指数分别为:
(1 1 00),(01 1 0),(10 1 0),(1 100),(0 1 10),(1 010)
(210)
(012)
(362)
注意
选坐标原点时,应使其位于待定晶面以外,防止 出现零截距。 已知截距求晶面指数,则指数是唯一的;而已知 晶面指数,画晶面时,这个晶面就不是唯一的。
机械工程材料:第二章 金属的晶体结构与结晶

亚晶界:实际金属晶体内部,晶粒内原子排列也不完全理想 的规则排列,也存在很小位向差的小晶块,即亚晶 粒,亚晶粒的交界即亚晶界。
在实际晶体中,这三种缺陷随加工条件变化而变化,可产 生、发展,也可消失,对材料性能有很大影响。
常见的利用增加材料的缺陷,提高强度的方法
第二章 金属的晶体结构与结晶
金属特性与金属键 金属的晶体结构 实际金属结构 金属的结晶 金属铸锭组织
一、金属特性与金属键
原子的构造
①金属原子的最外层轨道电子少。 ②金属原子易失去电子而成为正离子。 ③金属键
金属正离子与自由电子间的静电作用, 使金属原子结合起来形成金属整体。
金属特性
关系
①优良的导电性和导热性。 ①导电:在电势作用下,自由
②不透明和具有金属光泽。
电子定向移动;
③较高的强度和较好的塑性。②正的电阻温度系数:
④正的电阻温度系Βιβλιοθήκη 。T↗,离子振动↗,电子运动阻力↗ ③塑性:金属中离子与电子间能保
持一定的相对关系。
二、金属的晶体结构
1. 晶体的基本知识
晶体与非晶体 晶体:内部原子在空间呈一定的有规则排列,具有固定熔 点和各向异性。(金刚石、盐) 非晶体:内部原子是无规则堆积在一起的。没有固定的熔 点,具有各向同性。(玻璃、石蜡)
晶格(点阵) 表示晶体中的原子(正离子)排列方式的空间几何体。 假设:A.金属中的原子(正离子)都是刚性小球; B.金属中的原子都缩小为一个点,线将点连 接起来,线与线的交点为节点。
晶胞:表示晶格几何特征的最小几何单元。 (1)晶格常数: 棱边长度 (a,b,c),单位A0(10-10m) ; 轴间夹角 (α、β、γ ) (2)晶面、晶向 : 晶面:在晶体中通过原子中心的平面,用晶面指数表示。
第二章材料中的晶体结构
TiO2
体心四方
1个正离子 2个负离子
6
3
八面体 VO2, NbO2, MnO2, SnO2, PbO2, …
7. MgAl2O4(尖晶石)晶型
8.Al2O3(刚玉)晶型
第四节 共价晶体的结构
一、共价晶体的主要特点 1. 共价键结合,键合力通常强于离子键 2. 键的饱和性和方向性,配位数低于金属和离 子晶体 3. 高熔点、高硬度、高脆性、绝缘性
(2) 求投影.以晶格常数为单位,求待定 晶向上任一阵点的投影值。
(3) 化整数.将投影值化为一组最小整数。
(4) 加括号.[uvw]。
2.晶面指数及其确定方法
1) 晶面指数 — 晶体点阵中阵点面的 方向指数。 2) 确定已知晶面ห้องสมุดไป่ตู้指数。
(1) 建坐标.右手坐标,坐标轴为晶胞 的棱边,坐标原点不能位于待定晶面内。
cph
a=b≠c
a 2r
5. 致密度 — 晶胞中原子体积占总体积的分数
bcc
fcc
cph
3 0.68
8
2 0.74
6
2 0.74
6
6. 间隙 — 若将晶体中的原子视为球形,则相 互接触的最近邻原子间的空隙称为间隙。
间隙内能容纳的最大刚性球的半径称为
间隙半径 rB。 间隙大小常用间隙半径与原子半径 rA之
比 rB / rA 表示。
1) 面心立方结构晶体中的间隙 正八面体间隙:位于晶胞各棱边中点及体心位置.
一个晶胞中共有4个.
rB / rA 0.414
正四面体间隙:位于晶胞体对角线的四分之一处. 一个晶胞中共有8个.
rB / rA 0.225
2) 体心立方结构晶体中的间隙 扁八面体间隙:位于晶胞各棱边中点及面心处. 一个晶胞中共有6个. rB / rA 0.155
大学材料科学基础第二章材料中的晶体结构

4.晶面间距(Interplanar crystal spacing)
两相邻近平行晶面间的垂直距离—晶面间 距,用dhkl表示,面间距计算公式见(1-6)。 通常,低指数的面间 距较大,而高指数的 晶面间距则较小 晶面间距愈大,该晶 面上的原子排列愈密 集;晶面间距愈小, 该晶面上的原子排列 愈稀疏。
晶体结构 = 空间点阵 + 结构单元
如:Cu, NaCl, CaF2有不同的晶体结构, 但都属于面心立方点阵。 思考题:空间点阵与布拉菲点阵。
三、 晶向指数与晶面指数
(Miller Indices of Crystallographic Directions and Planes) 在晶体中,由一系列原子所组成的平面称 为晶面,原子在空间排列的方向称为晶向。 晶体的许多性能都与晶体中的特定晶面和晶 向有密切关系。为区分不同的晶面和晶向, 采用晶面和晶向指数来标定。
5.晶带 (Crystal zone) 所有平行或相交于同一直线的晶面构 成一个晶带,此直线称为晶带轴。
晶带轴[u v w]与该晶带的晶面(h k l) 之间存在以下关系: hu + kv + lw = 0 凡满足此关系的晶面都属于以[u v w]为 晶带轴的晶带,律应用举例
1 晶胞中原子数 (Number of Atoms in Unit Cell)
一个晶胞内所包含的原子数目。 体心立方晶胞:2个。 面心立方晶胞:4个。 密排六方晶胞:6个。
2 原子半径 r 与点阵常数 a 的关系
严格的说,原子半径并不是一个常数,它 随外界条件(温度)、原子结合键、配位数而 变,在理论上还不能精确地计算原子半径。 定义为晶胞中原子密排方向上相邻两原子 之间平衡距离的一半,用点阵常数表示。
机械工程材料-2章 晶体结构、结晶

晶胞原子数与原子半径
致密度与配位数
2.1.4 晶向指数与晶面指数
1 晶向指数
我们把任何两个或多个原子所在直线所指 的方向,称为晶向。 〖例1〗计算图(a)中的AB的晶向指数。 解:①选晶胞的三条棱边建立X、Y、Z坐标 轴,以晶格常数a b c 为坐标轴的度量单位。从坐 标轴的原点O引一条有向直线OC,平行于待定晶 向AB; ②在所引的有向直线上任取一点C(为方便 起见,通常取距原点最近的阵点),求出该点C 在三坐标轴的坐标值,C(1/2,1/2, 1)。 ③将三个坐标值按比例化简为最小简单整数, 并加上方括号,表示为[u v w]=[1 1 2],即为 所求的晶向指数。整数之间不用标点分开。如果 u、v、w中有某一数为负,则将负号用上划线的 形式标注于该数之上。 AB的晶向指数为[1 1 2]。
例如:石墨是靠分子键结合, 硬度很低。塑料也是靠分子键结 合,强度较低。
由于范德瓦尔斯引力很弱, 所以分子晶体的结合力很小,熔 点很低,硬度也很低。
5 结合力与结合能
当大量原子结合成固体时,为 使晶体具有最低的能量,以保持其 稳定状态,原子之间也必须保持一 定的平衡距离,这就是固态金属中 的原子趋于规则排列的原因。 当原子间以离子键或共价键结 合时,原子达不到紧密排列状态, 这是由于这些结合方式对周围的原 子数有一定的限制之故。
体心立方
面心立方
密排六方
2.1.6 实际金属的晶体结构
若整个晶体完全是晶胞规则重 复排列的,这种晶体为理想晶体。 实际晶体中,由于各因素的影 响,总会存在一些不完整、原子排 列偏离理想状态的区域,这些区域 称为晶体缺陷。 按缺陷在空间的几何形状和尺 寸不同,缺陷分为:
点缺陷
晶体缺陷
线缺陷
材料科学基础-第2章

a b c,
90o
13
14种Bravais点阵
3. 正交Orthorhombic: 简单正交 (4) 底心正交 (5) 体心正交 (6) 面心正交 (7)
a b c,
90
o
14
14种Bravais点阵
4. 六方Hexagonal:
简单六方(8)
a x
O
b
y
点阵矢量
ruvw ua vb wc
11
7种晶系,14种布拉菲Bravais点阵
晶系 Crystal systems 点阵参数 Lattice parameters 布拉维点阵类型 Types of Bravais lattice 简单三斜(1) 简单单斜(2) 底心单斜(3) 简单正交(4) 底心正交(5) 体心正交(6) 面心正交(7) 简单六方(8) 实例 Instances K2CrO7 -S CaSO4•H2O Fe3C Ga -S Mg, Zn Cd, Ni, As As, Sb, Bi -Sn, TiO2 Fe, Cr, Cu, Ag, Ni,V
abc
90
abc
90%以上 的金属具 有立方晶 系和六方 晶系
12
90
14种Bravais点阵
1. 三斜Triclinic :简单三斜(1)
a b c,
90
o
2. 单斜Monoclinic : 简单单斜(2) 底心单斜(3)
(321)取倒数为 0.333,0.5 ,1
Z
(321)
Y
X
(200)、(333)等是否存在? 具有公因子的晶面不存在
第2章材料的晶体结构

cos2
对直角坐标系的简单点阵(简单正交,简单正 方,简单立方)点阵,有
cos2+cos2+ cos2 =1
所以 dhkl
1
h
2
k
2
l
2
a b c
对简单立方可简化为
dhkl
a h2 k2 l2
对六方晶系
dhkl
1
4
h2
hk
(一箭双雕)
证实了X射线是电磁波, 也证明了晶体排列的规律性
Si(110)晶面的高分辨率电镜(High Resolution Electron Microscopy, HREM)照片
金(200)晶面的透射电 镜(Transmission
Electron Microscopy , TEM)晶格像
? 三维的原子(分子)排列如何描述?
液态(非晶体):在2r0(原子半径)以上间距 都有原子;在2r0左右处有峰值——距离不大时, 与有序结构相似;距离远处的原子密度趋于平 均值——长程无序。
2.1.5 准晶体(Quasicrystal)
1984年在急冷Al-Mn合金中首次发现。 准晶体的特征
c-ZrO2单晶的电子衍射
单晶: 规则排列的斑点
原子(分子)在三维空间的两种紧密堆积
晶胞(cell, crystal cell)
为说明点阵排列 的规律和特点, 在点阵中取出一 个具有代表性的 基本单元(通常 取最小的平行六 面体)作为点阵 的组成单元,称 为晶胞。
二维晶胞的不同取法
初级晶胞(简单晶胞)
一般选取每个角上有一个阵点的平行六面体作 为晶胞,称为初级晶胞或简单晶胞。
固体物理课件第二章_晶体的结构

Na+构成面心立方格子 Cl-也构成面心立方格子
(6) CsCl: 由两个简单立方子晶格彼此沿 立方体空间对角线位移1/2 的长度套构而成
(7) 闪锌矿结构
化合物半导体 —— 锑化铟、砷化镓、磷化铟 面心立方的嵌套
(8) 钙钛矿结构
钛酸钙(CaTiO3) 钛酸钡(BaTiO3) 锆酸铅(PbZrO3) 铌酸锂(LiNbO3) 钽酸锂(LiTaO3)等
面心立方格子:原点和12个近邻格点连线的垂 直平分面围成的正十二面体
体心立方格子:原点和8个近邻格点连线的垂直 平分面围成的正八面体,沿立方轴的6个次近 邻格点连线的垂直平分面割去八面体的六个角, 形成的14面体 —— 八个面是正六边形,六个面是正四边形
§1.2 晶列和晶面
思考: 金刚石为什么有固定的面? 这些面和晶格结构有什么关系?
根据周期性:
f e
k k
ikx
fk e
k
ik ( x na )
f k eikx f k eik( x na)
k k
e
ik na
1
m 0,1,2,
k na k Rn 2m
2 k h Gh a
k=b的波传过一个晶格长度,相位改变2π
晶面:所有结点可以看成分布在一系列相互平 行等距的平面族上,每个平面族称为一个晶面 晶面用法向或晶面指数标志
例:同一个格子,两组不同的晶面族
晶面的性质: –晶格中一族的晶面不仅平行,并且等距 –一族晶面必包含了所有格点 –三个基矢末端的格点必分别落在该族的不 同晶面上(有理指数定理)
晶面(米勒)指数:晶面把基矢 a1 , a2 , a3 分别
02第二章 金属的晶体结构与结晶

放大100∼2000倍的组织称高倍组织或显微组织。 在电子显微镜下放大几千∼几十万倍的组织称精细组织或电镜组
织。
显微组织实质上是指在显微镜下观察到的金属中各相或各晶粒的
形态、数量、大小和分布的组合。
二、合金的相结构
1、固溶体 合金组元通过溶解形成一种成分和性能均匀的,且结构与组元之
理工艺的重要依据。
根据组元数, 分为二元相图、三元相图和多元相图。
Fe-C二元相图
三元相图
1. 二元相图的建立
几乎所有的相图都是通过实验得到的,最常用
的是热分析法。
二元相图的建立步骤为:[以Cu-Ni合金(白铜)为例] 1、配制不同成分的合金,测出各合金的冷却曲线,找出曲线 上的相变点(停歇点或转折点)。 2、在温度-成分坐标中做成分垂线,将相变点标在成分垂线上 3、将这些相变点连接起来,即得到Cu-Ni相图。
因而细晶粒无益。但晶粒太粗易产生应力集中。因而
高温下晶粒过大、过小都不好。
2.细化晶粒的方法
晶粒的大小取决于晶核的形成速度和长大速度。
单位时间、单位体积内形成的晶核数目叫形核率(N)。
单位时间内晶核生长的长度
叫长大速度(G)。
N/G比值越大,晶粒越细小。 因此,凡是促进形核、抑制长 大的因素,都能细化晶粒。
第二章 金属的晶体结构 与结晶
不同的金属具有不同的
力学性能,主要是由于材 料内部具有不同的成分、
组织和结构。
第一节 金属的晶体结构
一、晶体与非晶体
晶体是指原子呈规则排列的固体。常态下金属
主要以晶体形式存在。晶体具有各向异性。 非晶体是指原子呈无序排列的固体。在一定条 件下晶体和非晶体可互相转化。
T= T0 –T1
2 《材料科学基础》第二章 晶体结构(下)

思考题
Ca2+:000,½ ½ 0,½ 0 ½ ,0 ½ ½ F
-
:¼ ¼ ¼, ¾ ¾ ¼, ¾ ¼ ¾, ¼ ¾ ¾, ¾ ¾ ¾, ¼ ¼ ¾, ¼ ¾ ¼, ¾ ¼ ¼
思考题:
据晶体结构简要解释:
•为什么CaF2比NaCl容易形成弗仑克尔缺陷?
•为什么萤石结构中一般存在着负离子扩散机制?
了解
Al3+的分布原则符合鲍林规则:在同一层
和层与层之间, Al3+之间的距离应保持
最远。
空隙
α-Al2O3中的氧与铝的排列次序可写成: OAAlDOBAlEOAAlFOBAlDOAAlEOBAlFOAAlD……6层一个周期
Al3+的CN=6, Z=
O2-的CN= 4
2
属于刚玉型结构的晶体:
• 硅酸盐结构的特点:
2/3八面体间隙(A、B) 1/2八面体间隙(A) l/8四面体间隙(B) 全部立方体中心 1/2立方体中心
尖晶石
反尖晶石 纤锌矿 砷化镍 刚 玉 钛铁矿 橄榄石 氯化铯 萤 石 硅石型
二、硅酸盐晶体结构
1. 岛状结构
2. 组群状结构
3. 链状结构 4. 层状结构 5. 架状结构
•硅酸盐晶体的组成表征:
4:6:4AB2O4
4:6:4B(AB)O4 4:4MO 6:6MO 6:4M2O3 6:6:4ABO3 6:4:4A2BO4 8:8MO 8:4MO2 4:2MO2
1/8四面体间隙(A) 1/2八面体间隙(B) 1/8四面体间隙(B) 1/2八面体间隙(A、B) 1/2四面体间隙 全部八面体间隙 2/3八面体间隙
8
性质:硬度最高、极好的导热性、具半导体性能 与其结构相同的有硅、锗、灰锡、合成立方氮化硼等
材料科学基础-2

[ 1 11]
[1 1 1]
[1 1 1]
[11 1 ]
[1 1 1]
[1 1 1]
[1 1 1]
例:在一个面心立方晶胞中画出[012]、[123] 晶向。
晶面:通过空间点阵中任一组阵点的平面代表晶 体中的原子平面,称为晶面 晶面指数:表示晶体中点阵平面的指数,由晶面 与三个坐标轴的截距值所决定。 晶面指数的标定步骤: 建坐标:所定晶面不应通过原点; 求截距:求出待定晶面在三个坐标轴上的截距, 如果该晶面与某坐标轴平行,则其截距为∞; 取倒数:取三个截距值的倒数; 化整并加圆括号:将三个截距的倒数化为最小 整数h、k、l,并加圆括号,即(hkl),如果截距 为负值,则在负号标注在相应指数的上方。
正交
三、晶向指数与晶面指数(Miller指数)
晶向:空间点阵中各阵点列的方向代表晶体中原子排列的 方向,称为晶向,即空间点阵中任意两阵点的连接矢量。 晶向指数:表示晶体中点阵方向的指数。 晶向指数的确定步骤:
z
[ 1 11]
[112] • 建立坐标系; • 确定坐标值:在待定晶向上确定 [1 1 1] [1 1 0] 距原点最近的一个阵点的三个坐标值; • 化整并加方括号:将三个坐标值化为最小 [001] [111] 整数u、v、w,并加方括号。如有负值,在 [010] o 该数值上方标负号。 [100] [110]
• 在立方晶系中,具有相同指数的晶面和晶向 必定相互垂直。不适合其它晶系。 如: [121] (121) 即:晶向 [121] 为晶面 (121)的法向量。 ★ 因此,晶面指数可作为向量进行运算。
例:在一个面心立方晶胞中画出(102)、 (223) 晶面。
六方晶系的晶向指数和晶面指数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
2.1.2晶格常数与晶系
晶胞的大小和形状表征 晶格常数:晶胞的棱边长度a、b、c 棱边夹角:、、 方向确定:前、右、上
X Z c
表示
β a a γ
α
b
Y
6
2.1.2晶格常数与晶系
按晶胞中三个棱边的长度及夹角是否相等,还有夹角是否为直角等原 则,分为7种类型
晶系 晶胞 简单立方 体心立方 面心立方 晶胞棱边 棱边夹角
把晶体看成有原子按一定几何规律作周期性排列而成,即晶体
内部的晶格位向是完全一致的,这种晶体称为单晶体 半导体、磁性材料、高温合金材料
各向异性
34
2.2.1单晶体与多晶体的概念
晶粒、晶界
晶粒与晶粒之间的界面称为晶界。显然晶界处的原子排列为适 应两晶粒间不同晶格位向的过渡,总是不规则的。这种实际上由
25
2.1.4立方晶系中的晶向与晶面
2. 晶面指数
(1)以晶胞的三条相互垂直的棱边为参考坐标
轴X、Y、Z,坐标原点O应位于待定晶面之 外,以免出现零截距。
(2)以棱边长度(即晶格常数)为度量单位,求
出待定晶面在各轴上的截距。 (3)取各截距的倒数,并化为最小简单整数,
放在圆括号内,即为所求的晶面指数。
2.2.2晶体中的缺陷
1.点缺陷
异类原子 钢中的氢、氮、碳、硼 比空位畸形严重
(b) 间隙原子
38
2.2.2晶体中的缺陷
1.点缺陷
换原子的半径与金属原子的半径相接近或较大
(c) 置换式异类原子
39
影响
造成晶格畸变,这将对金属的性能产生影响,如使屈服强
度升高、硬度升高、电阻增大、体积膨胀等。
第2章 材料的晶体结构
§2.1晶体结构及其表达
§2.2金属晶体结构的特点
1
2.1晶体结构及其表达
2.1.1晶格结构与晶胞 2.1.2晶格常数与晶系 2.1.3金属的晶体结构
2.1.4立方晶系中的晶向与晶面
2
2.1.1晶格结构与晶胞
自然界中的固态物质千奇百怪,由
原子(离子、分子)堆积
晶体结构是指晶体中原子在三维空
该晶面在X、Y、Z坐标轴上的截距分别 为1、1/2、1/2,取其倒数为1、2、2, 故其晶面指数为(122)。
26
2.1.4立方晶系中的晶向与晶面
2. 晶面指数
说出下面晶面指数?
27
2.1.4立方晶系中的晶向与晶面
2. 晶面指数
晶面族,用大括号{hkl}表示
{100}包括(100)、(010)、(001)
49
50
51
在晶体结构中,由一系列原子所组成的平面称为晶面,任意两 个原子连线所指的方向称为晶向。
通常以[uvw]表示晶向指数的普遍形式,若晶向指向坐标为
负方向时,则坐标值中出现负值,这时在晶向指数的这一数字 之上冠以负号。
23
2.1.4立方晶系中的晶向与晶面
1. 晶向指数
(1)以晶格中某原子为原点,并以晶胞三个棱边
10
2.1.3金属的晶体结构
1 体心立方结构(BBC)
(2)晶胞原子数: 体心立方晶胞每个角上原子为相邻的8个晶胞所共有。晶胞中心原子 完全属于这个晶胞。所以体心立方晶胞中的原子数为1/8×8 + 1=2个
11
2.1.3金属的晶体结构
1 体心立方结构(BBC)
(3)原子半径: r= 体对角线长度等于4个原子半径, 所以体心立方晶胞的原子半径
3 4
a
12
2.1.3金属的晶体结构
1 体心立方结构(BBC)
(4)配位数: 指晶体结构中与任一个原子最邻近、等距离的原子数目。 8
配位数越大,晶体中的原子排列便越紧密。
13
2.1.3金属的晶体结构
1 体心立方结构(BBC)
(4) 致密度或密集系数:
若把原子看做刚性圆球,那么原子之间必然有空隙存在,原子排列
分开。
24
2.1.4立方晶系中的晶向与晶面
1. 晶向指数
在晶体中,尤其在立方晶系中,由于原子
排列具有高度的对称性,存在许多原子排
列完全相同但彼此不平行的晶向,在晶体 学上,这些晶向是等同的,统称为晶向族
,用尖括号表示〈uvw〉
晶向族〈100〉包括[100]、[010],[001]、 [1(-)00]、[01(-)0]、[001(-)]等六个晶向。
28
2.1.4立方晶系中的晶向与晶面
2. 晶面指数
{110}包括(110)、(101)、(011)、(1(-)10)、(1(-)01)、(01(-)1)
图2-12立方晶系的{110}晶面族
29
2.1.4立方晶系中的晶向与晶面
2. 晶面指数
(111)
(1(-)11)
(11 (-) 1)
(111 (-))
21
2.1.3金属的晶体结构
3密排六方晶格(HCP)
对于典型的密排六方金属,其原子半径为a/2,致密度:
4 3 6 r 3 3 3 2 8 a a 2 3
4 6 3
nV K=
V
1
=
=
a 2
3
3
3 2a
2 0.74 = 6
22
2.1.4立方晶系中的晶向与晶面
1. 晶面指数和晶向指数
间有规律的周期性的具体排列方式
把原子(离子、分子)看成是固定的
等径刚球质点
晶体就是由这些刚球堆垛而成,即 原子堆垛模型
为原子堆垛模型。
3
2.1.1晶格结构与晶胞
阵点:为了清楚的表明原子在空间排
列的规律性,常将构成晶体的原子忽 略,而将其抽象为几何点,所有阵点
的外部环境都相同。
空间点阵:由这些阵点有规则地周期
总结
晶体缺陷并不是静止不变的,而是随着温度及加
工过程等各种条件的改变而不断变动。它们可以
产生运动和交互作用,而且能合并和消失。
结构的不完整性会对晶体的性能产生重大的影响
,特别是对金属的塑性变形、固态相变以及扩散
等过程都起着重要的作用。
47
作业:
p33,2-1、2-2、2-9、
48
谢 谢!
多晶粒组成的晶体结构称为多晶体
各向同性
35
2.2.2晶体中的缺陷
晶体中原子完全为规则排列时,称为理想晶体。
实际金属的晶体结构总不可避免地存在一些原子偏离规
则排列的不完整区域,这就是晶体缺陷
晶体缺陷分为点缺陷、线缺陷和面缺陷三大类
36
2.2.2晶体中的缺陷
1.点缺陷
热振动
(a) 空位
37
构
最典型、最常见的金属晶体结构有3种类型:体心立方结构、面 心立方结构和密排六方结构。 前两种属于立方晶系,后一种属于六方晶系。
9
2.1.3金属的晶体结构
1 体心立方结构(BBC)
(1)晶格常数:晶胞的三个棱边长度相等,三个轴间夹角均为90 o (即a=b=c,α=β=γ=90o),其晶格常数只用1个a即可表示。
式中:L—位错线总长度;V—体积,单位是cm/cm3(或cm-2)。
42
2.2.2晶体中的缺陷
2.线缺陷
位错对金属材料的性能影响?
图2-18 位错密度与屈服强度的关系
图2-19 透射电子显微镜观察到的晶体中位错 43
位错影响
位错的存在使晶体强度降低,但当大量位错产生后,
强度反而提高,生产中可通过增加位错的办法对金属
3
3
0.68
15
2.1.3金属的晶体结构
1 体心立方结构(BBC)
具有体心立方结构的金属有Na、K、α-Fe、Cr、V、Nb、Mo、W等 约30种
16
2.1.3金属的晶体结构
2面心立方结构(FCC)
在晶胞的八个角上各有一个原子,构成立方体,在立方体六
个面的中心各有一个原子。
原子半径 ?
单斜系
三斜系
a≠b≠c
a≠b≠c
α=γ=90o≠β
α≠β≠γ≠90o
7
2.1.2晶格常数与晶系
(a)简单立方; (h)体心正交; (b)面心立方; (i)底心正交; (c)体心立方 (j)面心正交;
(d)简单正方; (k)菱方;
(e)体心正方; (l)简单单斜;
(f)六方;
(m)底心单斜;
(g)简单正交; (n)简单三斜
立方系 正方(四方)系
六方系 正交(斜方)系 菱方(三角)系
a=b=c a=b≠c
a=b≠c a≠b≠c a=b=c
α=β=γ=90o α=β=γ=90o
α=β=90o,γ=120o α=β=γ=90o α=β=γ≠90o
简单正方 体心正方
简单正方 简单正交 底心正交 体心正交 面心正交 简单菱方 简单单斜 底心单斜 简单三斜
图2-13立方晶系的{111}晶面族
30
31
2.1.4立方晶系中的晶向与晶面
1、实际晶体结构是什么样的? 2、晶体缺陷对晶体有什么样的影响?(性能) 为什么要研究它? 3、有哪些晶体缺陷?
32
§2.2金属晶体结构的特点
2.2.1单晶体与多晶体的概念 2.2.2晶体中的缺陷
33
2.2.1单晶体与多晶体的概念
将加速金属中的扩散过程,因而凡与扩散有关的相变、化 学热处理、高温下的塑性变形和断裂等都与点缺陷的存在 和运动有着密切的关系。
40
2.2.2晶体中的缺陷
2.线缺陷
(a)刃型位错立体图
(b)正刃型位错和负刃型位错
41
2.2.2晶体中的缺陷
2.线缺陷
位错密度以单位体积内所包含的位错线的总长度来表示,符号为ρ, ρ=L/V
