高中数学必修4_三角函数上经典提升培优题组
高中数学必修4_三角函数上经典提升培优题组.docx

数学 4 必修)第一章三角函数(上)[ 基础训练 A 组]一、选择题1.设角属于第二象限,且cos cos,则角属于()222A.第一象限 B .第二象限 C .第三象限 D .第四象限2.给出下列各函数值:①sin( 1000 0 ) ;② cos( 22000 ) ;sin 7cos③ tan( 10) ;④10. 其中符号为负的有()17tan9A.①B.② C .③ D .④3.sin 2 1200等于()A.333D1 2B .C ..2224.已知sin 4是第二象限的角,那么,并且tan5的值等于()A.4B.3C.34 344D.5.若3是第四象限的角,则是()A. 第一象限的角B.第二象限的角C. 第三象限的角D. 第四象限的角6.sin 2 cos3tan 4的值()A. 小于0B. 大于0C.等于 0D.不存在二、填空题1.设分别是第二、三、四象限角,则点P(sin ,cos) 分别在第___、___、___象限.2.设MP和OM分别是角17的正弦线和余弦线,则给出的以下不等式:18①MP OM0;② OM0 MP;③OM MP 0;④ MP 0OM ,其中正确的是 _____________________________ 。
3.若角与角的终边关于 y 轴对称,则与的关系是 ___________ 。
4.设扇形的周长为8cm,面积为4cm2,则扇形的圆心角的弧度数是。
5.与2002 0终边相同的最小正角是 _______________ 。
三、解答题1.已知tan,1是关于 x 的方程 x2kx k 2 3 0 的两个实根,tan且 37,求 cos sin 的值.22.已知tanx 2,求cos xsin x 的值。
cos x sin x3.化简: sin(5400x)1x)cos(3600x)tan(9000x) tan(4500x) tan(8100sin( x)4.已知sin x cos x m, ( m2, 且m1) ,求( 1)sin3x cos3 x ;(2) sin 4 x cos4x 的值。
高一数学必修四三角函数综合训练(培优提高)(2021年整理)

高一数学必修四三角函数综合训练(培优提高)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高一数学必修四三角函数综合训练(培优提高)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高一数学必修四三角函数综合训练(培优提高)(word版可编辑修改)的全部内容。
高一数学必修四--—--——-三角函数综合练习(培优提高卷)1。
【2012高考安徽文7】要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象 (A ) 向左平移1个单位 (B ) 向右平移1个单位(C ) 向左平移 12个单位 (D ) 向右平移12个单位【答案】C 【解析】 cos 2cos(21)y x y x =→=+左+1,平移12。
2。
【2012高考新课标文9】已知ω〉0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=(A)错误! (B )错误! (C )错误! (D )错误! 【答案】A 【解析】因为4π=x 和45π=x 是函数图象中相邻的对称轴,所以2445T=-ππ,即ππ2,2==T T 。
又πωπ22==T ,所以1=ω,所以)sin()(ϕ+=x x f ,因为4π=x 是函数的对称轴所以ππϕπk +=+24,所以ππϕk +=4,因为πϕ<<0,所以4πϕ=,检验知此时45π=x 也为对称轴,所以选A.3。
【2012高考山东文8】函数2sin (09)63x y x ππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为(A)2 (B )0 (C)-1 (D )1-【答案】A 【解析】因为90≤≤x ,所以6960ππ≤≤x ,369363πππππ-≤-≤-x ,即67363ππππ≤-≤-x ,所以当336πππ-=-x 时,最小值为3)3sin(2-=-π,当236πππ=-x 时,最大值为22sin2=π,所以最大值与最小值之和为32-,选A 。
高中数学必修4三角函数公式大全附带练习题

高中数学必修4三角函数公式大全附带练习题三角函数诱导公式sin〔-α〕=-sinα,cos〔-α〕=cosα,tan〔-α〕=-tanαcot〔-α〕=-cotαsin〔π/2-α〕=cosα,cos〔π/2-α〕=sinα,tan〔π/2-α〕=cotα,cot〔π/2-α〕=tanα,sin〔π/2+α〕=cosα,cos〔π/2+α〕=-sinα,tan〔π/2+α〕=-cotα,cot〔π/2+α〕=-tanα,sin〔π-α〕=sinαcos〔π-α〕=-cosα,tan〔π-α〕=-tanα,cot〔π-α〕=-cotαsin〔π+α〕=-sinα,cos〔π+α〕=-cosα,tan〔π+α〕=tanαcot〔π+α〕=cotα,sin〔3π/2-α〕=-cosα,cos〔3π/2-α〕=-sinαtan〔3π/2-α〕=cotα,cot〔3π/2-α〕=tanα,sin〔3π/2+α〕=-cosαcos〔3π/2+α〕=sinα,tan〔3π/2+α〕=-cotα,cot〔3π/2+α〕=-tanαsin〔2π-α〕=-sinα,cos〔2π-α〕=cosα,tan〔2π-α〕=-tanαcot〔2π-α〕=-cotα,sin〔2kπ+α〕=sinα,cos〔2kπ+α〕=cosαtan〔2kπ+α〕=tanα,cot〔2kπ+α〕=cotα(其中k∈Z)习题精选一、选择题1.假设,那么的值为〔〕.A.B.C.D.2.的值等于〔〕.A.B.C.D.3.在△ 中,以下各表达式为常数的是〔〕.A. B.C.D.4.如果,且,那么可以是〔〕.A. B. C. D.5.是方程的根,那么的值等于〔〕.A.B.C.D.二、填空题6.计算.7.,,那么,.8.假设,那么.9.设,那么.10..三、解答题11.求值:12.角终边上一点的坐标为,〔1〕化简以下式子并求其值:;〔2〕求角的集合.13.,求证:.14.假设,求的值.15.、、为△ 的内角,求证:〔1〕;〔2〕.16.为锐角,并且,,求的值.参考答案:一、选择题1.B 2.D 3.C 4.D 5.A二、填空题6.2 7.,8.9.10.三、解答题11..12.〔1〕;〔2〕.13.提示:.14.18.提示:先化简,再将代入化简式即可.15.提示:注意及其变式.16..提示:化简条件,再消去得.。
高中数学必修4_三角函数上经典提升培优题组.docx

高中数学必修4_三角函数上经典提升培优题组.docx数学 4 必修)第一章三角函数(上)[ 基础训练 A 组]一、选择题1.设角属于第二象限,且cos cos,则角属于()222A.第一象限 B .第二象限 C .第三象限 D .第四象限2.给出下列各函数值:①sin( 1000 0 ) ;② cos( 22000 ) ;sin 7cos③ tan( 10) ;④10. 其中符号为负的有()17tan9A.①B.② C .③ D .④3.sin 2 1200等于()A.333D1 2B .C ..2224.已知sin 4是第二象限的角,那么,并且tan5的值等于()A.4B.3C.34 344D.5.若3是第四象限的角,则是()A. 第一象限的角B.第二象限的角C. 第三象限的角D. 第四象限的角6.sin 2 cos3tan 4的值()A. 小于0B. 大于0C.等于 0D.不存在二、填空题1.设分别是第二、三、四象限角,则点P(sin ,cos) 分别在第___、___、___象限.2.设MP和OM分别是角17的正弦线和余弦线,则给出的以下不等式:18①MP OM0;② OM0 MP;③OM MP 0;④ MP 0OM ,其中正确的是 _____________________________ 。
3.若角与角的终边关于 y 轴对称,则与的关系是 ___________ 。
4.设扇形的周长为8cm,面积为4cm2,则扇形的圆心角的弧度数是。
5.与2002 0终边相同的最小正角是 _______________ 。
三、解答题1.已知tan,1是关于 x 的方程 x2kx k 2 3 0 的两个实根,tan,求 cos sin 的值.22.已知tanx 2,求cos xsin x 的值。
cos x sin x3.化简: sin(5400x)1x)cos(3600x)tan(9000x) tan(4500x) tan(8100sin( x)4.已知sin x cos x m, ( m2, 且m1) ,求( 1)sin3x cos3 x ;(2) sin 4 x cos4x 的值。
人教A版高中数学必修四课时提升作业(四) 1.2.1 任意角的三角函数(二)1 Word版含解析

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(四)任意角的三角函数(二)(15分钟30分)一、选择题(每小题5分,共10分)1.sin 1°,sin 1,sinπ°的大小顺序是( )A.sin 1°<sin 1<sinπ°B.sin 1°<sinπ°<sin 1C.sinπ°<sin 1°<sin 1D.sin 1<sin 1°<sinπ°【解析】选B.因为1弧度≈57.3°,1°<π°<1,观察三角函数线知在内,正弦线方向始终向上,且角越大正弦线越长,所以sin 1°<sinπ°<sin 1.2.(2015·葫芦岛高一检测)已知函数f(x)=sinx(-<x<),则满足f(x)<的x的取值范围是( )A. B.C. D.【解析】选C.作角的正弦线MP,如图所示,为使x满足-<x<且f(x)<,x的终边所在区域如图阴影所示,故x∈.【补偿训练】函数y=的定义域为( )A.B.C.{x|x≠2kπ,k∈Z}D.【解析】选A.因为1+sinx≠0,所以sinx≠-1.所以x≠+2kπ,k∈Z.二、填空题(每小题5分,共10分)3.下列结论:①α一定时,单位圆中的正弦线一定;②单位圆中,有相同正弦线的角相等;③α和α+π有相同的正切线;④具有相同正切线的两个角终边在同一条直线上.其中正确结论的序号是________.【解析】单位圆中,与有相同的正弦线,但≠,②错;α=时,α+π=,与都不存在正切线,③错,①与④正确.答案:①④4.若θ∈,则sinθ的取值范围是________.【解题指南】观察θ在区间上变化时,角θ的正弦线的变化情况.【解析】sin=1,sin=-,观察角的正弦线的变化可知:sinθ的取值范围是.答案:三、解答题5.(10分)求下列函数的定义域.(1)y=lg.(2)y=.【解析】(1)为使y=lg有意义,则-sinx>0,所以sinx<,所以角x 终边所在区域如图所示,所以2kπ-<x<2kπ+,k∈Z.所以原函数的定义域是{x|2kπ-<x<2kπ+,k∈Z}.(2)为使y=有意义,则3tanx-≥0,所以tanx≥,所以角x终边所在区域如图所示,所以kπ+≤x<kπ+,k∈Z,所以原函数的定义域是{x|kπ+≤x<kπ+,k∈Z}.【拓展延伸】三角函数线的作用(1)三角函数线是利用数形结合思想解决有关问题的工具,要注意利用其来解决问题.(2)三角函数线的主要作用是解三角不等式、比较大小及求函数的定义域,在求三角函数定义域时,一般转化为不等式(组),因此必须牢固掌握三角函数线的画法及意义.(15分钟30分)一、选择题(每小题5分,共10分)1.(2015·大连高一检测)已知MP,OM,AT分别为θ的正弦线、余弦线、正切线,则一定有( )A.MP<OM<ATB.OM<MP<ATC.AT<OM<MPD.OM<AT<MP【解析】选B.作出角θ的正弦线、余弦线、正切线(如图所示),由于<θ<,所以OM<MP,由图可以看出MP<AT,故可得OM<MP<AT.2.已知sinα>sinβ,那么下列结论成立的是( )A.若α,β是第一象限角,则cosα>cosβB.若α,β是第二象限角,则tanα>tanβC.若α,β是第三象限角,则cosα>cosβD.若α,β是第四象限角,则tanα>tanβ【解析】选D.如图(1),α,β的终边分别为OP,OQ,sinα=MP>NQ=sinβ,此时OM<ON,所以cosα<cosβ,故A错;如图(2),OP,OQ分别为角α,β的终边,MP>NQ,即sinα>sinβ,所以AC<AB,即tanα<tanβ,故B错;如图(3),角α,β的终边分别为OP,OQ,MP>NQ,即sinα>sinβ,所以OM<ON,即cosα<cosβ,故C错,所以选D.二、填空题(每小题5分,共10分)3.(2015·南昌高一检测)sin1,cos1,tan1的大小关系是________.【解析】作出1弧度角的正弦线、余弦线和正切线如图所示:观察图可知:cos1<sin1<tan1.答案:cos1<sin1<tan1【延伸探究】将本题中的“1”改为“-1”,结果又如何?【解析】作出-1弧度角的正弦线、余弦线和正切线如图所示:观察图可知:tan<sin<cos.4.设0≤α<2π,若sinα>cosα,则α的取值范围是________.【解题指南】可分以下三种情况讨论:(1)cosα=0.(2)cosα>0.(3)cosα<0.【解析】(1)当cosα=0时,sinα=±1,为使sinα>cosα,须有sinα=1,又0≤α<2π,所以α=.(2)当cosα>0时,原不等式可化为tanα>,解得<α<.(3)当cosα<0时,原不等式可化为tanα<,解得<α<.综上可知,α的取值范围是.答案:三、解答题5.(10分)(2014·吉林高一检测)利用三角函数线证明:+≥1.【解题指南】分角α的终边在坐标轴上和角α的终边在四个象限上两类情况讨论.【解析】(1)当角α的终边在坐标轴上时,显然有+=1.(2)当角α的终边在四个象限上时,设角α的终边与单位圆交于点P(x,y),过P 作PM⊥x轴于点M(如图),则=,=,利用三角形两边之和大于第三边有:+=+>1.综上有+≥1.【补偿训练】如图所示,已知单位圆O与y轴交于A,B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y 轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?【解析】设单位圆与x轴正半轴交于D,过D作DT垂直x轴交CO的延长线于T,过C作CE⊥x轴交x轴于E,如图.由图可得△OCE∽△OTD,所以=,又CE=OA=OD=1.所以=OE=AC.根据任意角的三角函数的定义可得tanθ=DT.所以AC=.关闭Word文档返回原板块。
人教A版高中数学必修四课时提升作业(七) 1.3 三角函数的诱导公式(二)2 Word版含解析

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(七)三角函数的诱导公式(二)一、选择题(每小题3分,共18分)1.(2014·铜陵高一检测)已知sin=,α∈,则tanα等于( ) A.-2 B.2 C.- D.【解析】选A.因为sin=cosα=,且α∈,所以sinα=-=-,所以tanα==-2.2.若cos+sin(π+θ)=-m,则cos+2sin(6π-θ)的值是( ) A. B.- C.- D.【解题指南】先化简cos+sin(π+θ)=-m,得出sinθ的值,再化简cos+2sin(6π-θ)得到其与sinθ的关系,从而求解.【解析】选B.cos+sin(π+θ)=-sinθ-sinθ=-m,即sinθ=,所以cos+2sin(6π-θ)=-sinθ-2sinθ=-3sinθ=-.3.已知sin10°=k,则cos620°的值等于( )A.kB.-kC.±kD.不能确定【解析】选B.cos620°=cos260°=cos(180°+80°)=-cos80°=-sin10°=-k.4.已知f(sinx)=cos3x,则f(cos10°)的值为( )A.-B.C.-D.【解析】选A.f(cos10°)=f(sin80°)=cos240°=cos(180°+60°)=-cos60°=-. 【变式训练】(2014·朔州高一检测)若f(cosx)=cos2x,则f(sin15°)等于.【解析】f(sin15°)=f(cos(90°-15°))=f(cos75°)=cos150°=-.答案:-5.已知tanθ=2,则等于( )A.2B.-2C.0D.-1【解析】选B.原式====-2.6.已知sin(π-α)-cos(π+α)=,则sin+cos= ( )A.-B.C.±D.-【解析】选A.由已知得sinα+cosα=,两边平方得1+2sinαcosα=,所以2sinαcosα=-,而sin+cos=cosα-sinα,(cosα-sinα)2=1-2sinαcosα=1-=,又<α<π,得sinα>0,cosα<0,所以cosα-sinα=-.二、填空题(每小题4分,共12分)7.(2014·天水高一检测)已知角α的终边经过点P0(-3,-4),则cos的值为.【解析】由题意知,cos=sinα==-.答案:-8.(2014·成都高一检测)已知tan(α-π)=,且α∈,则sin=. 【解析】tan(α-π)=⇒tanα=.又因为α∈,所以α为第三象限角,sin=cosα=-.答案:-9.(2014·天津高一检测)在△ABC中,sin=3sin(π-A),且cosA=-cos(π-B),则C=.【解题指南】将已知条件利用诱导公式化简后可得角A,角B,进而得角C. 【解析】由已知化简得cosA=3sinA.①cosA=cosB.②由①得tanA=,又因为0<A<π,所以A=,由②得cosB=·cos=,又因为0<B<π,所以B=,所以C=π-A-B=.答案:三、解答题(每小题10分,共20分)10.已知cosα=,且-<α<0,求的值.【解析】原式==tanα,因为cosα=,-<α<0,所以sinα=-=-,所以tanα==-2.11.已知角α的终边经过点P.(1)求sinα的值.(2)求的值.【解析】(1)P,所以sinα=-.(2)==,由三角函数定义知cosα=,故所求式子的值为. 【变式训练】化简:-.【解析】原式=-=sinα-(-sinα)=2sinα.一、选择题(每小题4分,共16分)1.已知=2,则sin(θ-5π)·sinπ-θ等于( )A. B.± C. D.-【解析】选C.由=2,得tanθ=3,sin(θ-5π)·sin=sinθcosθ===.2.(2014·焦作高一检测)已知sin(π+α)=-,则cos等于( )A.-B.C.-D.【解题指南】利用诱导公式分别化简sin(π+α)与cos,然后再求值. 【解析】选A.sin(π+α)=-sinα=-,所以sinα=,cos=cos=-cos=-sinα=-.【举一反三】本题条件不变,求cos的值.【解析】cos=cos=-cos=sinα=.3.若sinα是5x2-7x-6=0的根,则= ( )A. B. C. D.【解析】选B.方程5x2-7x-6=0的两根为x1=-,x2=2,则sinα=-.原式==-=.4.已知锐角α终边上一点P的坐标是(2sin2,-2cos2),则α等于( )A.2B.-2C.2-D.-2【解析】选C.由条件可知点P到原点的距离为2,所以P(2cosα,2sinα),所以根据诱导公式及α为锐角可知,所以α=2-.二、填空题(每小题5分,共10分)5.(2014·邯郸高一检测)若cosα=,且α是第四象限角,则cos=. 【解析】因为cosα=,且α是第四象限角,所以sinα=-=-=-.所以cos=-sinα=.答案:6.(2014·广州高一检测)已知cos=,且-π<α<-,则cos=.【解析】cos=cos=sin,又-π<α<-,所以-π<+α<-,所以sin=-,所以cos=-.答案:-三、解答题(每小题12分,共24分)7.已知cos=,求sin+cos2-α的值.【解析】因为cos=,所以sin+cos2=sin+cos2=-cos+=-+=.8.已知sin(α+β)=1,求证:tan(2α+β)+tanβ=0.【证明】因为sin(α+β)=1,所以α+β=2kπ+,k∈Z,所以α=2kπ+-β,k∈Z,所以tan(2α+β)+tanβ=tan+tanβ=tan(4kπ+π-2β+β)+tanβ=tan(π-β)+tanβ=-tanβ+tanβ=0.即tan(2α+β)+tanβ=0.关闭Word文档返回原板块。
2020-2021学年北师大版高中数学必修四《三角函数的简单应用》课时提升题及答案

(新课标)最新北师大版高中数学必修四课时提升作业 三角函数的简单应用一、选择题(每小题4分,共16分)1.电流I(A)随时间t(s)变化的关系是I=2sin100πt,t ∈(0,+∞),则电流I 变化的周期是( ) A.1100B.100C.150 D.50【解析】选C.由题意知,T=2πω=2π100π=150.2.(2014·亳州高一检测)某人的血压满足函数关系式f(t)=24sin(160πt)+110,其中f(t)为血压,t 为时间,则此人每分钟心跳的次数为( ) A.60B.70C.80D.90【解题指南】本题的实质是求函数的频率. 【解析】选C.T=2π160π=180,所以频率f=80.3.如图为一半径r 为3米的水轮,水轮圆心O 距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P 到水面的距离y(米)与时间x(秒)满足函数关系y= Asin(ωx+φ)+2,则有( )A.ω=152π,A=3B.ω=2π15,A=3 C.ω=2π15,A=5D.ω=152π,A=5【解析】选B.水轮每分钟旋转4圈,即每秒钟旋转215πrad,所以ω=215π. 又水轮上最高点离水面的距离为r+2=5(米),即y max =A+2=5,所以A=3.【变式训练】(2013·杭州高一检测)如图,一个大风车的半径是8米,每12分钟旋转一周,最低点离地面2米,若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点P 离地面的距离h(米)与时间t(分钟)之间的函数解析式是 ( )A.h=8cos π6t+10B.h=-8cos π3t+10C.h=-8sin π6t+10D.h=-8cos π6t+10【解析】选D.首先考虑建立直角坐标系,以最低点的切线作为x 轴,最低点作为坐标原点,建立如图所示的直角坐标系.那么,风车上翼片端点所在位置P 可由函数x(t),y(t)来刻画,而且h(t)=y(t)+2. 所以,只需要考虑y(t)的解析式.又设P 的初始位置在最低点,即y(0)=0. 在Rt △O 1PQ 中,由cos θ=8−y(t)8,得y(t)=-8cos θ+8.又2π12=θt ,所以θ=π6t,y(t )=-8cos π6t+8, h(t)=-8cos π6t+10.4.(2014·西安高一检测)稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价进行了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x 季度之间近似满足:y=500sin(ωx+φ)+9500(φ>0),已知第一、二季度平均单价如下表所示:则此楼群在第三季度的平均单价大约是 ( ) A.10000元 B.9500元 C.9000元D.8500元【解析】选C.由表格数据可知,10000=500sin(ω+φ)+9500, 9500=500sin(2ω+φ)+9500, 所以sin(ω+φ)=1,sin(2ω+φ)=0; ω+φ=2k 1π+π2(k 1∈Z),① 2ω+φ=2k 2π+π(k 2∈Z),② ②×2-①得3ω+φ=4k 2π-2k 1π+3π2=2k 3π+3π2(k 3∈Z),所以x=3时,y=500sin (3ω+φ)+9500=9000(元).故选C. 二、填空题(每小题5分,共10分) 5.有一种波,其波形为函数y=sin πx 2的图像,若在区间[0,t](t>0)上至少有2个波峰(图像的最高点),则正整数t 的最小值是 . 【解析】因为函数y=sin πx 2的周期T=4,y=sinπx 2的图像在[0,t]上至少有2个波峰,所以t ≥54T=5,故正整数t 的最小值是5. 答案:56.(2014·潍坊高一检测)某同学利用描点法画函数y=Asin(ωx+φ)(其中A >0,0<ω<2,−π2<φ<π2)的图像,列出的一组数据如下表:经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+φ)的解析式应是 .【解析】因为(0,1)和(2,1)关于直线x=1对称, 故x=1与函数图像的交点应是最高点或最低点, 故数据(1,0)错误,从而由(4,-2)在图像上知A=2, 由过(0,1)点知2sin φ=1,因为-π2<φ<π2,所以φ=π6,所以y=2sin (ωx +π6),再将点(2,1)代入得,2sin (2ω+π6)=1,所以2ω+π6=π6+2k π或2ω+π6=5π6+2k π,k ∈Z,因为0<ω<2,所以ω=π3,所以函数解析式为y=2sin (π3x +π6). 答案:y=2sin (π3x +π6)三、解答题(每小题12分,共24分)7.以一年为一个周期调查某商品出厂价格及该商品在商店的销售价格时发现:该商品的出厂价格是在6元基础上按月份随正弦曲线波动的,已知3月份出厂价格最高为8元,7月份出厂价格最低为4元,而该商品在商店的销售价格是在8元基础上按月随正弦曲线波动的,并已知5月份销售价最高为10元,9月份销售价最低为6元,假设某商店每月购进这种商品m 件,且当月售完,请估计哪个月盈利最大?并说明理由. 【解析】由条件可得:出厂价格函数为y 1=2sin (π4x −π4)+6, 销售价格函数为y 2=2sin (π4x −3π4)+8,则利润函数为: y=m(y 2-y 1)=m 2sin (π4x −3π4)+8-2sin (π4x −π4)-6=m(2-2√2sin π4x),所以,当x=6时,y=(2+2√2)m,即6月份盈利最大.8.如图表示电流I 与时间t 的函数解析式:I=Asin(ωt+φ)(A >0,|φ|<π2)在同一周期内的图像.(1)根据图像写出I=Asin(ωt+φ)的解析式.(2)为了使I=Asin(ωt+φ)中t 在任意-段1100秒的时间内电流I 能同时取得最大值和最小值,那么正整数ω的最小值是多少?【解题指南】先由图中的数据观察出函数的最值、周期,从而确定A,ω,再代入图像中的一个点的坐标求φ;根据(1)求出的解析式,列出不等式求ω的范围后确定最小值. 【解析】(1)由图知A=300,t 1=-1300,t 3=1150,因为T=2(t 3-t 1)=2(1150+1300)=150, 所以ω=2πT=100π.由ωt 1+φ=0得φ=-ωt 1=π3, 所以I=300sin (100πt +π3). (2)问题等价于T2≤1100,即πω≤1100,所以ω≥100π,所以正整数ω的最小值为314.一、选择题(每小题4分,共12分)1.(2013·烟台高一检测)车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分,上班高峰期某十字路口的车流量由函数F (t)=50+4sin t2(0≤t ≤20)给出,F(t)的单位是辆/分,t 的单位是分,则下列哪个时间段内车流量是增加的( ) A.[0,5]B.[5,10]C.[10,15]D.[15,20]【解析】选C.由2k π-π2≤t2≤2k π+π2得4k π-π≤t ≤4k π+π(k ∈Z),由于0≤t ≤20,所以0≤t ≤π或3π≤t ≤5π,从而车流量在时间段[10,15]内是增加的.2.(2014·合肥高一检测)绳子绕在半径为50cm 的轮圈上,绳子的下端B 处悬挂着物体W,如果轮子按逆时针方向每分钟匀速旋转4圈,那么把物体W 的位置向上提升100cm 需要 ( ) A.15πsB.10πsC.5πsD.1πs【解析】选A.设需x 秒上升100cm. 则x60×4×2π×50=100, 所以x=15π.3.(2014·青岛高一检测)海水受日月的引力作用,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是港口在某季节每天的时间与水深关系的表格:选用函数y=Asin(ωx+φ)+b(A>0,ω>0)来模拟港口的水深与时间的关系.如果一条货船的吃水深度是4米,安全条例规定至少有2.25米的安全间隙(船底与洋底的距离),则该船一天之内在港口内呆的时间总和为小时. ( )A.10B.8C.6D.4【解析】选B.由题意可得y=2.5sinπ6x+5(0≤x≤24),则2.5sinπ6x+5≥6.25,sinπ6x≥12,2kπ+π6≤π6x≤5π6+2kπ,k∈Z,即12k+1≤x≤5+12k,该船可以1点进港,5点离港,或13点进港,17点离港,在港口内呆的时间总和为4+4=8小时.二、填空题(每小题4分,共8分)4.如图,点P是半径为r的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω(rad/s)做圆周运动,则点P的纵坐标y关于时间t的函数关系式为.【解析】当质点P从P0转到点P位置时,点P转过的角度为ωt,则∠POx=ωt+φ,由任意角的三角函数定义知P点的纵坐标y=rsin(ωt+φ).答案:y=rsin(ωt+φ)5.(2014·北京高一检测)一观览车的主架示意图如图所示,其中O为轮轴的中心,距地面32m(即OM长),巨轮的半径为30m,AM=BP=2m,巨轮逆时针旋转且每12min转动一圈.若点M为吊舱P的初始位置,经过tmin,该吊舱P距离地面的高度为hm,则h= .【解析】过点O作地面的平行线ON,过点B作ON的垂线BM交ON于M点.点A在☉O上逆时针运动的角速度是2π12=π6,所以tmin转过的弧度数为π6t,设θ=π6t,当θ>π2时,∠BOM=θ-π2,h=OA+BM=30+30sinθ-π2,当0<θ≤π2时,上述关系式也适合.故h=30+30sin(θ−π2)=30sin(π6t−π2)+30.答案:30sin(π6t−π2)+30三、解答题(每小题10分,共20分)6.如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.(1)求这一天6~14时的最大温差.(2)写出这段曲线的函数解析式.【解析】(1)由图可知:这段时间的最大温差是20℃.(2)从图可以看出:从6~14是y=Asin(ωx+φ)+b的半个周期的图像,所以T2=14-6=8,所以T=16,因为T=2πω,所以ω=π8,又因为{A =30−102=10,b =30+102=20,所以{A =10,b =20,所以y=10sin (π8x +φ)+20, 将点(6,10)代入得:sin (3π4+φ)=-1,所以3π4+φ=2k π+3π2,k ∈Z,所以φ=2k π+3π4,k ∈Z,可取φ=3π4,所以y=10sin (π8x +3π4)+20(6≤x ≤14).【拓展延伸】三角函数的建模问题关键点(1)解决实际问题时的关键是观察出周期性,搜集数据,作出相应的散点图. (2)求解的关键是能抽象出三角函数模型,解决的步骤是:审题,建模,求解,还原.7.(2014·虹口区高一检测)某种型号汽车的四个轮胎半径相同,均为R=40cm,该车的底盘与轮胎中心在同一水平面上.该车的涉水安全要求是:水面不能超过它的底盘高度.如图所示:某处有一“坑形”地面,其中坑ABC 形成顶角为120°的等腰三角形,且AB=BC=60cm,如果地面上有h(cm)(h<40)高的积水(此时坑内全是水,其他因素忽略不计).(1)当轮胎与AB,BC 同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为d=10+80√33-h. (2)假定该汽车能顺利通过这个坑(指汽车在过此坑时,符合涉水安全要求),求h 的最大值.(精确到1cm)【解析】(1)当轮胎与AB,BC 同时接触时, 设轮胎与AB 边的切点为T, 轮胎中心为O,则|OT|=40,由∠ABC=120°,知∠OBT=60°,故|OB|=√3.所以,从B点到轮胎最上部的距离为√3+40,此轮胎露在水面外的高度为d=√3+40-(60·cos60°+h)=√3+10-h=10+80√33-h,得证.(2)只要d≥40,即3+10-h≥40,解得h≤16cm,所以h的最大值为16cm.【变式训练】单摆从某点开始来回摆动,离开平衡位置的距离s(厘米)和时间t(s)的关系式为s=6sin(2πt+π6).(1)作出它的图像.(2)单摆开始摆动(t=0)时,离开平衡位置多少厘米?(3)单摆摆到最右边时,离开平衡位置多少厘米?【解析】(1)列表如下:描点作图.(2)t=0时,s=3厘米,此时离开平衡位置3厘米.(3)离开平衡位置6厘米.。
三角函数培优题

必修四第一章三角函数高考题一、角的概念和同角关系: 1、已知α是第三象限角,则2α所在的象限为( )A 第一,二象限B 第二,三象限C 第一,三象限D 第二,四象限 2、已知cos θtan θ<0,那么角θ是( )A 第一,二象限B 第二,三象限C 第三,四象限D 第一,四象限3、如果111A B C ∆的三个内角的余弦值分别等于222A B C ∆的三个内角的正弦值,则( ) A .111A B C ∆和222A B C ∆都是锐角三角形 B .111A B C ∆和222A B C ∆都是钝角三角形C .111A B C ∆是钝角三角形,222A B C ∆是锐角三角形D .111A B C ∆是锐角三角形,222A B C ∆是钝角三角形4、若cos θ>0且sin2θ<0,则角的终边所在象限是( ) A 第一象限 B 第二象限 C 第三象限 D 第四象限5、α是第四象限角,cos α=1312,则sin α=( ) A 135 B -135 C 125 D -1256、已知sin α=552,2π<α<π,则tan α=( ) 7、α是第四象限角,tan α=-125则sin α=( ) A 51 B -51 C 135 D -1358、已知sin α=55则sin 4α- cos 4α的值是( ) A -53 B -51 C 51 D 53 9、已知α是第二象限的角,tan α=1/2,则cos α=__________二、三角函数图像与性质:1、函数y=1+cosx 的图象( )A 关于x 轴对称B 关于y 轴对称C 关于原点对称D 关于直线x=2π对称 2、已知a ∈R ,函数y= sinx-∣a ∣(x ∈R )为奇函数,则a=( ) A 0 B 1 C -1 D 1±3、函数y=cos2x 在下列哪个区间上是减函数( ) A [-4π,4π] B [4π,43π] C [0,2π] D [2π,π]4、已知函数y=sin (πx-2π)-1,则下列命题正确的是( ) A f (x )是周期为1的奇函数 B f (x )是周期为2的偶函数C f (x )是周期为1的非奇非偶函数D f (x )是周期为2的非奇非偶函数5、已知)(x f 的定义在(0,3)上的函数,)(x f 的图象如图所示,那么不等式0cos )(<x x f 的解集是( )A .(0,1)∪(2,3)B .)3,2()2,1(ππC .)3,2()1,0(πD .)3,1()1,0( 6、已知)(x f 是定义在)3,3(-上的奇函数,当30<<x 时,)(x f 的图象如图所示,那么不等式0cos )(<x x f 的解集是( )(A ))3,2()1,0()2,3(ππ-- (B ) )3,2()1,0()1,2(ππ --(C ))3,1()1,0()1,3( -- (D ) )3,1()1,0()2,3( π--7、下列函数中周期2π为的是( ) A y=sin2x B y=sin2x C y=cos 4xD y=cos4x 8、设f (x )=sin3x+∣sin3x ∣,则f (x )为( )A 周期函数,最小正周期为3πB 周期函数,最小正周期为32πC 周期函数,最小正周期为 2πD 非周期函数9、函数y=5tan (2x+1)的最小正周期为( )A4π B 2πC πD 2π 10、(6)下列函数中,周期为π,且在[,]42ππ上为减函数的是(A )sin(2)2y x π=+ (B )cos(2)2y x π=+(C )sin()2y x π=+ (D )cos()2y x π=+11、函数y=∣sinx ∣的一个单调增区间是( ) A (-4π, 4π ) B (4π,43π) C (π,23π) D (23π,2π)12、已知函数y=∣sin (x+3π)∣(x ∈R ),则f (x )( ) A 在区间[32π,67π]上 是增函数 B 在区间[-π,-2π]上 减函数C 在区间[4π,3π]上 增函数D 在区间[3π,65π]上减函数13、定义在R 上的偶函数满足f (x )= f (x+2),当x ∈[3,4] 时,f (x )=x-2则( ) A f (sin21) <f (cos 21) B f (sin 3π)>f (cos 3π)O xyππ-π-πO xy ππ-π-πO xy ππ-π-πO xy ππ-π-πABC D C f (sin1)< f (cos1) D f (sin 23)>f (cos 23) 14、已知函数y=tan (x+4π),则( ) A f (0)> f (-1)>f (1) B f (0)>f (1)>f (-1) C f (1)>f (0)>f (-1) D f (-1)>f (0)>f (1)15、若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则MN 的最大值为( )A .1B .2C .3D .216、10、定义在区间⎪⎭⎫⎝⎛20π,上的函数y=6cosx 的图像与y=5tanx 的图像的交点为P ,过点P 作PP 1⊥x 轴于点P 1,直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为________________________。
人教A版高中数学必修四课时提升作业三 1-2-1 任意角的三角函数一2 含解析 精品

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(三)任意角的三角函数(一)一、选择题(每小题3分,共18分)1.α是第四象限角,则下列数值中一定是正值的是( )A.sinαB.cosαC.tanαD.cosα或tanα【解析】选B.α是第四象限角,则cosα为正.2.若角α的终边落在y=-x上,则tanα的值为( )A.1B.-1C.-1或1D.0【解析】选B.由角α的终边落在y=-x上,故tanα=-1.3.已知tanα>0,且sinα+cosα>0,那么角α是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角【解析】选A.由tanα>0,得α为第一、三象限角.而α为第三象限角时,sinα+cosα>0不成立,故α为第一象限角.4.(2014·龙岩高一检测)有下列说法:①终边相同的角的同名三角函数的值相等;②终边不同的角的同名三角函数的值不等;③若sinα>0,则α是第一、二象限的角;④若α是第二象限的角,且P(x,y)是其终边上一点,则cosα=-错误!未找到引用源。
.其中正确的个数为( )A.0B.1C.2D.3【解析】选B.①正确;②不正确,举例如sin错误!未找到引用源。
=sin错误!未找到引用源。
;③不正确,如α=错误!未找到引用源。
时,sinα>0,但是α不是第一、二象限的角;④不正确,α是第二象限的角,cosα=错误!未找到引用源。
.5.如果α的终边过点P(2sin30°,-2cos30°),则sinα的值等于( )A.错误!未找到引用源。
B.-错误!未找到引用源。
C.-错误!未找到引用源。
D.-错误!未找到引用源。
【解析】选C.因为P(1,-错误!未找到引用源。
),所以r=错误!未找到引用源。
=2,所以sinα=-错误!未找到引用源。
北师大版数学高一必修4优化练习3.3二倍角的三角函数
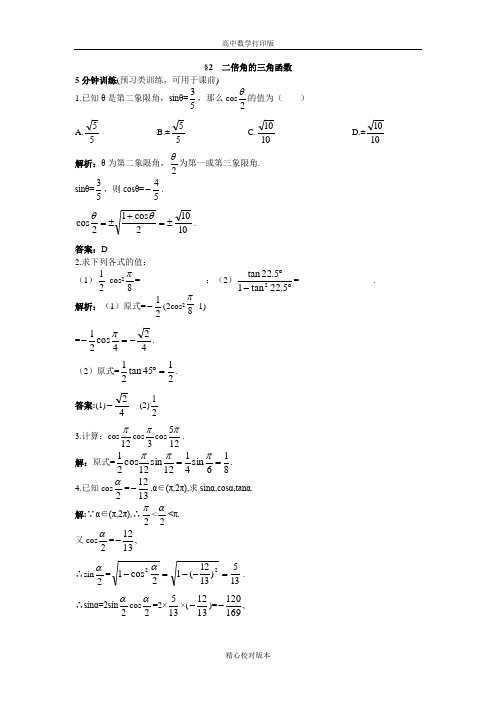
§2 二倍角的三角函数5分钟训练(预习类训练,可用于课前) 1.已知θ是第二象限角,sinθ=53,那么cos 2θ的值为( ) A.55 B.±55 C.1010 D.±1010解析:θ为第二象限角,2θ为第一或第三象限角. sinθ=53,则cosθ=54-. 10102cos 12cos±=+±=θθ. 答案:D2.求下列各式的值:(1)21-cos 28π=_______________;(2)︒-︒5.22tan 15.22tan 2=_________________. 解析:(1)原式=21-(2cos 28π-1)=424cos 21-=-π. (2)原式=2145tan 21=︒. 答案:(1)42-(2)21 3.计算:cos 12πcos 3πcos 125π. 解:原式=.816sin 4112sin 12cos 21==πππ4.已知cos 2α=1312-,α∈(π,2π),求sinα,cosα,tanα.解:∵α∈(π,2π),∴2π<2α<π.又cos 2α=1312-,∴sin2α=135)1312(12cos 122=--=-α.∴sinα=2sin2αcos 2α=2×135×(1312-)=169120-,cosα=2cos 22α-1=2(1312-)2-1=169119.∴tanα=119120cos sin -=a α. 10分钟训练(强化类训练,可用于课中) 1.已知2sinθ=1+cosθ,则tan 2θ的值是( ) A.21 B.2 C.21或不存在 D.不存在 解析:2sinθ=1+cosθ,当2sinθ≠0,1+cosθ≠0,得出2tan 21cos 1sin θθθ==+,当sinθ=0时,cosθ=-1,θ=2kπ+π,2tan θ不存在.答案:C 2.已知cos(α+4π)=53,2π≤α<23π,则cos(2α+4π)的值为____________________.解析:cos(2α+4π)=cos2αcos 4π-sin2αsin 4π=22(cos2α-sin2α). ∵2π≤α<23π,∴43π≤α+474ππ<.又∵cos(α+4π)>0,∴23π<α+474ππ<.∴sin(α+4π)=54)4(cos 12-=+--πα.∴cos2α=sin(2α+2π)=2sin(α+4π). cos(α+4π)=2524-,sin2α=-cos(2π+2α)=1-2cos 2(α+4π)=257.∴原式=22×(2572524--)=50231-. 答案:50231-3.当x ∈[2π-,2π]时,求f(x)=sin 2x+2sinxcosx+3cos 2x 的周期、最大值及此时x 的值. 解:f(x)=1+cos2x+1+sin2x=2sin(2x+4π)+2,周期T=π.当x ∈[2,2ππ-]时,2x+4π∈[45,43ππ-],sin(2x+4π)∈[-1,1]. ∴f(x)∈[22,22+-].∴f(x)max =22+.由2x+224πππ+=k ,得x=8ππ+k .又∵x ∈[2,2ππ-],∴x=8π, 即当x=8π时,f(x)的最大值为22+.4.求值:cos 275°+cos 215°+cos75°cos15°.解:原式=230cos 12150cos 1︒++︒++sin15°·cos15° =21(1-cos30°)+21(1+cos30°)+21sin30°=21+21+41=45. 5.设sin(4π-x)=135,0<x <4π,求)4cos(2cos x x +π的值.解法一:∵0<x<4π,∴0<4π-x<4π.∴cos(4π-x)=)4(sin 12x --π.=1312)135(12=-. 又cos(4π+x)=sin(4π-x)=135,∴原式=)4sin()4cos()4sin(2)4sin()]4(2sin[x x x x x ---=--πππππ =2cos(4π-x)=1324.解法二:cos2x=cos 2x-sin 2x=(cosx+sinx)(cosx-sinx)=2sin(x+4π)·2cos(x+4π) =2sin(x+4π)cos(x+4π),∴原式=)4cos()4cos()4sin(2πππ++•+x x x =2sin(x+4π)=2cos(4π-x).后面同解法一. 30分钟训练(巩固类训练,可用于课后) 1.已知450°<α<540°,则α2cos 21212121++等于( ) A.-sin2α B.cos 2α C.sin 2α D.-cos 2α 解析:利用公式αααα22sin 22cos 1,cos 22cos 1=-=+,原式=α2cos 2121+,∵450°<α<540°, ∴cosα<0. ∴原式=2sin cos 21212αα=-. ∵450°<α<540°,∴225°<2α<270°. ∴sin2α<0. ∴原式=2sin 2α=-sin2α. 答案:A2.已知θ为第三象限角,sin 4θ+cos 4θ=95,那么sin2θ等于( ) A.322-B.322C.32D.32- 解析:sin 4θ+cos 4θ=(sin 2θ+cos 2θ)2-2sin 2θ·cos 2θ=95, ∴2sin 2θ·cos 2θ=94,sin 22θ=98.θ为第三象限角,sinθ<0,cosθ<0,sin2θ>0, ∴sin2θ=322. 答案:B3.设5π<θ<6π,cos2θ=a,则sin 4θ的值等于( )A.21a +-B.21a- C.21a + D.21a -- 解析:∵5π<θ<6π, ∴25π<2θ<3π,45π<4θ<23π. ∴2122cos 14sina --=--=θθ.故D 正确.答案:D4.tan5°+cot5°-︒80cos 2=_____________.解析:原式=︒-︒︒+︒︒10sin 25sin 5cos 5cos 5sin =010sin 210sin 21110sin 25cos 5sin 5cos 5sin 22=︒-︒=︒-︒︒︒+︒. 答案:05.已知ta n2θ=22-,2π<2θ<π,求)4sin(21sin 2cos 22θπθθ+--的值.解:tan2θ=22-,22tan 1tan 22-=-θθ, ∵2tanθ=22-(1-tan 2θ), 则2tan 2θ-tanθ-2=0, ∴(tanθ-2)(2tanθ+1)=0.∴tanθ=2或tanθ=22-(舍). (∵2π<2θ<π,∴4π<θ<2π) 原式=223tan 1tan 1sin cos sin cos )4sin(2sin 12cos 22+-=+-=+-=+--θθθθθθθπθθ.6.在△ABC 中,tanA+tanB+33=tanAtanB 且sinAcosA=43,试判断三角形的形状.解:由sinAcosA=43,得 21sin2A=43,即sin2A=23,∴2A=60°或120°.∴A=30°或60°.又由tanA+tanB=3-(1-tanAtanB),得tan(A+B)=3tan tan 1)tan tan 1(3-=---BA B A .∴A+B=120°. 当A=30°时,B=90°,tanB 无意义, ∴A=60°,B=60°,即三角形为等边三角形.7.(2005高考天津卷,文17)已知sin(α-4π)=1027,cos2α=257,求sinα及tan(α+3π).解:由sin(α4π-)=1027,得22 (sinα-cosα)=1027,即sinα-cosα=57. ① 又由cos2α=257得cos 2α-sin 2α=257,即(cosα+sinα)(cosα-sinα)=257.∴cosα+sinα=51-. ②由①②得sinα=53,cosα=54-.∴tanα=43-.tan(α+3π)=ta nα+11325483343344331433tan 313tan -=+-=+-=-+αα. 8.已知f(x)=2sin(x+2θ)cos(x+2θ)+32cos 2(x+2θ)-3. (1)化简f(x)的解析式;(2)若0≤θ≤π,求使函数f(x)为奇函数的θ值;(3)在(2)的条件下,求满足f(x)=1,x ∈[-π,π]的x 的取值集合. 解:(1)f(x)=sin(2x+θ)+3[1+cos(2x+θ)]-3 =sin(2x+θ)+3cos(2x+θ) =2sin(2x+θ+3π). (2)若f(x)为奇函数,则当x=0时,f(x)=0,即θ+3π=kπ(k ∈Z ).∴θ=3ππ-k .又∵0≤θ≤π,∴θ=32π.(3)此时f(x)=2sin(2x+π)=-2sin2x , 由f(x)=1得sin2x=21-. 当x ∈[-π,π]时,2x ∈[-2π,2π],∴2x=611,67,65,6ππππ--. ∴x 的取值集合为{1211,127,125,12ππππ--}. 9.有一块半径为R 、中心角为45°的扇形铁皮材料,为了截取面积最大的矩形铁皮,工人师傅常将矩形的一边放在扇形的半径上,然后作其最大的内接矩形.你能帮工人师傅设计一方案,选出矩形的四点吗?解:如图,设∠POA=θ,则PN=Rsinθ.OM=QM=PN=Rsinθ,ON=Rcosθ. MN=ON-OM=Rcosθ-Rsinθ. 则S 矩形PQMN =MN·PN =R(cosθ-sinθ)·Rsinθ =R 2(sinθcosθ-sin 2θ) =221R (sin2θ-1+cos2θ) =222R [sin(2θ+4π)22-].当2θ+24ππ=,即θ=8π时,S 矩形PQMN 最大且最大值为2212R -. 因此可以这样选点,以扇形一半径OA 为一边在扇形上作∠AOP=8π,P 为边OP 与扇形的交点,自P作PN⊥OA于N,PQ∥OA交OB于Q,若作QM⊥OA于M,则矩形MNPQ为所求的面积最大的矩形.。
人教A版高中数学必修四学能力提升训练+随堂检测+章末综合检测任意角的三角函数能力提升含答案解析

1.设α角属于第二象限,且|cos α2|=-cos α2,则α2角属于( ) A .第一象限 B .第二象限C .第三象限D .第四象限解析:选C.2k π+π2<α<2k π+π (k ∈Z ), k π+π4<α2<k π+π2(k ∈Z ). 当k =2n (n ∈Z )时,α2终边在第一象限; 当k =2n +1(n ∈Z )时,α2终边在第三象限. 而|cos α2|=-cos α2⇒cos α2≤0,∴α2终边在第三象限. 2.已知角α的终边过点(-3cos θ,4cos θ),其中θ∈(π2,π),则cos α=________. 解析:∵θ∈(π2,π),∴cos θ<0,r =5|cos θ|=-5cos θ, ∴cos α=-3cos θ-5cos θ=35. 答案:353.(1)求函数y =2cos x -1的定义域;(2)求满足tan x =-1的角x 的集合.解:(1)如图,∵2cos x -1≥0,∴cos x ≥12. ∴函数定义域为[2k π-π3,2k π+π3](k ∈Z ).(2)在单位圆过点A (1,0)的切线上取AT =-1,连结OT ,OT 所在直线与单位圆交于P 1、P 2,则OP 1或OP 2是角α的终边,则α的取值集合是{α|α=3π4+2k π或α=7π4+2k π,k ∈Z }.如图.4.已知1|sin α|=-1sin α,且lg(cos α)有意义. (1)试判断角α所在的象限;(2)若角α的终边与单位圆相交于点M (35,m ),求m 的值及sin α的值. 解:(1)由1|sin α|=-1sin α可知sin α<0, ∴α是第三或第四象限角或y 轴的负半轴上的角.由lg(cos α)有意义可知cos α>0,∴α是第一或第四象限角或x 轴的正半轴上的角. 综上可知角α是第四象限的角.(2)∵点M (35,m )在单位圆上, ∴(35)2+m 2=1,解得m =±45. 又α是第四象限角,故m <0,从而m =-45. 由正弦函数的定义可知sin α=-45.。
数学人教A版必修4同步优化训练:1.3三角函数的诱导公

1.3 三角函数的诱导公式5分钟训练(预习类训练,可用于课前)1.(高考湖南卷,文2)tan600°的值是( ) A.33- B.33 C.3- D.3 解析:tan600°=tan(360°+240°)=tan240°=tan(180°+60°)=tan60°=3.答案:D2.下列各式中成立的是( )A.sin(-20°)+sin200°=0B.sin370°-sin(-190°)=0C.cos(3π+4π)=cos(-4π) D.cos 625π=cos(619π-) 解析:sin(-20°)+sin200°=-sin20°+sin(180°+20°)=-2sin20°;sin370°-sin(-190°)=sin10°+sin(180°+10°)=sin10°-sin10°=0; cos(3π+4π)=cos(π+4π)=-cos 4π≠cos(-4π)=cos 4π; cos 625π=cos(4π+6π)=cos 6π≠cos(619π-)=cos(4π-65π)=cos(π-6π)=-cos 6π. 答案:B3.已知f(x)=xx +-11,若α∈(2π,π),则f(cosα)+f(-cosα)可化为_________________. 解析:f(cosα)+f(-cosα) =αααααααααsin 2sin )cos 1(sin )cos 1(cos 1cos 1cos 1cos 12222=++-=-+++-. 答案:αsin 2 4.求下列三角函数值: (1)sin 37π;(2)cos 417π;(3)tan(623π-);(4)sin(-765°). 解:(1)sin37π=sin(2π+3π)=sin 3π=23. (2)cos 417π=cos(4π+4π)=cos 4π=22. (3)tan(623π-)=tan(-4π+6π)=tan 6π=33.(4)sin(-765°)=sin [360°×(-2)-45°]=sin(-45°)=-sin45°=22-. 10分钟训练(强化类训练,可用于课中)1.tan300°+sin450°的值是( ) A.31+ B.31- C.31-- D.31+-解析:tan300°+sin450°=)60360cos()60360sin(︒-︒︒-︒+sin(360°+90°)=-tan60°+sin90°=31-. 答案:B 2.)3cos()3sin(21+-+ππ化简的结果是( )A.sin3-cos3B.cos3-sin3C.±(sin3-cos3)D.以上都不对 解析:)3cos()3sin(21+-+ππ =2)3sin 3(cos 3cos 3sin 21)3cos (3sin 21-=-=-+=|cos3-sin3|.2π<3<π,∴sin3>0>cos3. ∴原式=sin3-cos3.答案:A3.如果α+β=180°,那么下列等式中成立的是( )A.cosα=cosβB.cosα=-cosβC.sinα=-sinβD.以上都不对解析:cosα=cos(180°-β)=-cosβ.答案:B4.已知cos(-100°)=a ,求tan80°.解:cos(-100°)=cos100°=cos(180°-80°)=-cos80°=a.∴cos80°=-a,sin80°=21a --.∴tan80°=aa 2180cos 80sin -=︒︒. 5.设f(θ)=)cos()(cos 23)2sin()2(sin cos 2223θθπθπθπθ-+++-++-+,求f(3π)的值. 解:f(θ)=θθθθθθθθθθcos cos 223cos cos 1cos 2cos cos 223cos sin cos 2223223++-+-+=++-++ =θθθθθθθθθθcos cos 22)1(cos cos )1(cos 2cos cos 22)cos (cos 2cos 223223++---=++---=θθθθθθθθθθθθcos cos 22)2cos cos 2)(1(cos cos cos 22)1(cos cos )1cos )(cos 1(cos 22222++++-=++--++- =cosθ-1.∴f(3π)=cos 3π-1=21-1=21-. 30分钟训练(巩固类训练,可用于课后)1.如果|cosx|=cos(x+π),则x 的取值集合是( ) A.-2π+2kπ≤x≤2π+2kπ B.-2π+2kπ≤x≤23π+2kπ C.2π+2kπ≤x≤23π+2kπ D.(2k+1)π≤x≤2(k+1)π(以上k ∈Z )解析:由|cosx |=-cosx ,可知cosx≤0,所以2π+2kπ≤x≤23π+2kπ,k ∈Z . 答案:C 2.sin(619π-)的值是( ) A.21 B.21- C.23 D.23- 解析:sin(619π-)=sin(-2×2π+65π)=sin 65π=sin(π-6π)=sin 6π=21. 答案:A 3.下列三角函数,其中函数值与sin3π的值相同的是( ) ①sin(nπ+34π) ②cos(2nπ+6π) ③sin(2nπ+3π) ④cos [(2n+1)π-6π] ⑤sin [(2n+1)π-3π](以上n ∈Z )A.①②B.①③④C.②③⑤D.①③⑤解析:②cos(2nπ+6π)=cos 6π=23=sin 3π. ③sin(2nπ+3π)=sin 3π. ⑤sin [(2n+1)π-3π]=sin [2nπ+(π-3π)]=sin(π-3π)=sin 3π. 答案:C4.若cos(π+α)=510-,且α∈(-2π,0),则tan(23π+α)的值为( )A.36-B.36 C.26- D.26 解析:cos(π+α)=-cosα=510-,∴cosα=510. 又α∈(-2π,0),∴sinα=515cos 12-=--α. ∴tan(23π+α)=-cotα=-ααsin cos =36. 答案:B5.设A 、B 、C 是三角形的三个内角,下列关系恒等成立的是( )A.cos(A+B)=cosCB.sin(A+B)=sinCC.tan(A+B)=tanCD.sin 2B A +=sin 2C 解析:根据三角形的内角和及诱导公式判断.答案:B6.已知f(cosx)=2cos2x ,则f(sin15°)等于( )A.1B.23- C.3- D.21 解析:f(sin15°)=f [sin(90°-75°)]=f(cos75°)=2cos(2×75°)=2cos150° =2cos(180°-30°)=-2cos30°=3-.答案:C7.sin 2(3π-x)+sin 2(6π+x)=_______________. 解析:观察出(3π-x)+(6π+x)=2π,再利用诱导公式化为sin 2α+cos 2α=1的形式求解. 答案:18.sin 21°+sin 22°+sin 23°+…+sin 289°=_______________.解析:把给定式子利用诱导公式化为sin 2α+cos 2α=1的形式,再求和. 答案:289 9.化简:)4sin()8cos()3sin()2cos()3cos()5sin(πθθππθθπθππθ---∙--∙--+sin(-θ). 解:)4sin()8cos()3sin()2cos()3cos()5sin(πθθππθθπθππθ---∙--∙--+sin(-θ)=)4sin(cos )3sin(sin )cos()5sin(θπθθπθθπθπ+-∙--∙---+sin(-θ) =θθθππθθθππsin cos )](2sin[sin cos )](4sin[-∙--∙--+--sinθ =θθθπθθθπsin cos )sin(sin cos )sin(-∙--∙----sinθ =θθθθθθsin cos sin sin cos sin --∙-∙---sinθ =1-sinθ.10.已知cos(75°+α)=31,其中α为第三象限角,求cos(105°-α)+sin(α-105°)的值. 解:cos(105°-α)=cos [180°-(75°+α)]=-cos(75°+α)= 31-. sin(α-105°)=-sin(105°-α)=-sin [180°-(75°+α)]=-sin(75°+α).∵cos(75°+α)=31>0,又α为第三象限角,可知角75°+α为第四象限角, 则有sin(75°+α)=322)31(1)75(cos 122-=--=+︒--α. 故cos(105°-α)+sin(α-105°)=322132231+-=--. 快乐时光 生 气老师问:“文中说蜜蜂给花园增加了生气,是什么意思啊?” 一个学生回答:“蜜蜂偷了花蜜,花儿就生气了啊!”大家听了笑个不停.那学生又说:“笑什么?要是鲜花不生气,哪来鲜花怒放呢?”。
高中数学必修4三角函数上拔高训练

(数学4必修)第一章三角函数(上)[提高训练C 组]一、选择题1.化简0sin 600的值是()A .0.5B .0.5−C .2D .2−2.若10<<a ,ππ<<x 2,则11cos cos )(2−−+−−−x x a a x x a x x a 的值是()A .1B .1−C .3D .3−3.若⎟⎠⎞⎜⎝⎛∈3,0πα,则αsin log 33等于()A .αsin B .αsin 1C .αsin −D .αcos 1−4.如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为()A .5.0sin 1B .sin 0.5C .2sin 0.5D .tan 0.55.已知sin sin αβ>,那么下列命题成立的是()A .若,αβ是第一象限角,则cos cos αβ>B .若,αβ是第二象限角,则tan tan αβ>C .若,αβ是第三象限角,则cos cos αβ>D .若,αβ是第四象限角,则tan tan αβ>6.若θ为锐角且2cos cos 1−=−−θθ,则θθ1cos cos −+的值为()A .22B .6C .6D .4二、填空题1.已知角α的终边与函数)0(,0125≤=+x y x 决定的函数图象重αααsin 1tan 1cos −+的值为_____________.2.若α是第三象限的角,β是第二象限的角,则2βα−是第象限的角.3.在半径为30m 的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为0120,若要光源恰好照亮整个广场,则其高应为_______m (精确到0.1m )4.如果,0sin tan <αα且,1cos sin 0<+<αα那么α的终边在第象限。
5.若集合|,3A x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭,{}|22B x x =−≤≤,则B A ∩=_______。
高中数学 第一章 三角函数 1.7 正切函数优化训练 北师大版必修4(2021年整理)

高中数学第一章三角函数1.7 正切函数优化训练北师大版必修4 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章三角函数1.7 正切函数优化训练北师大版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章三角函数1.7 正切函数优化训练北师大版必修4的全部内容。
1.6 正切函数5分钟训练(预习类训练,可用于课前) 1。
函数y=tan (4π—x )的定义域是( )A.{x|x≠4π,x∈R } B 。
{x |x≠4π-,x∈R }C.{x|x≠kπ+4π,k∈Z ,x∈R } D 。
{x|x≠kπ+43π,k∈Z ,x∈R }解析:要使函数有意义,需满足4π—x≠2π+kπ(k∈Z ),所以x≠4π-+kπ(k∈Z ),也可写成x≠43π+kπ(k∈Z ).答案:D2.作出函数y=|tanx |的图像,并根据图像求其单调区间。
解:y=|tanx |⎪⎪⎩⎪⎪⎨⎧-∈-+∈=),2(,tan ),2,[,tan ππππππk k x x k k x x (k∈Z ),所以其图像如图所示,单调增区间为[kπ,kπ+2π)(k∈Z );单调减区间为(kπ-2π,kπ](k∈Z )。
3.x 取什么值时,xxx tan cos sin +有意义?解:由题意得tanx≠0,∴x≠kπ(k∈Z ).又x≠kπ+2π(k∈Z ),∴x≠21kπ(k∈Z ).故当x∈{x|x≠21kπ,k∈Z }时,xxx tan cos sin +有意义。
10分钟训练(强化类训练,可用于课中)1.函数y=tanx (4π-≤x≤4π且x≠0)的值域是( ) A 。
人教A版数学必修四1.6三角函数模型的简单应用能力提升(含答案解析).docx

高中数学学习材料马鸣风萧萧*整理制作1.有一冲击波,其波形为函数y =-sin(π2x )的图象,若其区间[0,t ]上至少有2个波峰(图象的最高点),则正整数t 的最小值是( )A .5B .6C .7D .8解析:选C.由y =-sin(π2x )的图象知,要想在区间[0,t ]上至少有2个波峰,必须使区间[0,t ]的长度不小于2T -T 4=7T 4,即t ≥74·2πω=74·2ππ2=7,故选C. 2.据市场调查,某种商品每件的售价按月呈f (x )=A sin(ωx +φ)+B ⎝⎛⎭⎫A >0,ω>0,|φ|<π2的模型波动(x 为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,则f (x )=________.解析:由题意得⎩⎪⎨⎪⎧A +B =8,-A +B =4,解得A =2,B =6. 周期T =2(7-3)=8,∴ω=2πT =π4. ∴f (x )=2sin ⎝⎛⎭⎫π4x +φ+6. 又当x =3时,y =8,∴8=2sin ⎝⎛⎭⎫3π4+φ+6. ∴sin ⎝⎛⎭⎫3π4+φ=1,取φ=-π4. ∴f (x )=2sin ⎝⎛⎭⎫π4x -π4+6.答案:2sin ⎝⎛⎭⎫π4x -π4+63.已知方程sin(x +π3)=m 2在[0,π]上有两个解,求实数m 的取值范围. 解:函数y =sin(x +π3),x ∈[0,π]的图象如图所示,方程sin(x +π3)=m 2在[0,π]上有两个解等价于函数y 1=sin(x +π3),y 2=m 2在同一平面直角坐标系中的图象在[0,π]上有两个不同的交点, ∴32≤m 2<1,即实数的取值范围为3≤m <2. 4.已知某海滨浴场的海浪高度y (米)是时间t (0≤t ≤24,单位:小时)的函数,记作:y =f (t ).下表是某日各时的浪高数据:t (时)0 3 6 9 12 15 18 21 24 y (米) 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5 经长期观测,y =f (t )的曲线可近似看成是函数y =A cos ωt +b .(1)根据以上数据,求出函数y =A cos ωt +b 的最小正周期T ,振幅A 及函数表达式;(2)根据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8∶00时至晚上20∶00时之间,有多少时间可供冲浪者进行活动?解:(1)由表中数据,知周期T =12,∴ω=2πT =π6. 由t =0,y =1.5,得A +b =1.5.又由t =3,y =1.0,得b =1.0,∴A =0.5,b =1.0,即振幅为12. ∴y =12cos π6t +1. (2)由题意知,当y >1时才对冲浪者开放,∴12cos π6t +1>1,∴cos π6t >0, ∴2k π-π2<π6t <2k π+π2,即12k -3<t <12k +3. ∵0≤t ≤24,∴令k 分别为0,1,2,得0≤t <3或9<t <15或21<t ≤24,∴在规定时间上午8∶00时至晚上20∶00时之间有6个小时可供冲浪者进行活动,即上午9∶00至下午15∶00.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学4必修)第一章 三角函数(上)[基础训练A 组]一、选择题1.设α角属于第二象限,且2cos2cosαα-=,则2α角属于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 2.给出下列各函数值:①)1000sin(0-;②)2200cos(0-;③)10tan(-;④917tancos 107sinπππ.其中符号为负的有( ) A .① B .② C .③ D .④ 3.02120sin 等于( )A .23±B .23C .23-D .21 4.已知4sin 5α=,并且α是第二象限的角,那么 tan α的值等于( ) A.43- B.34- C.43 D.345.若α是第四象限的角,则πα-是( )A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角 6.4tan 3cos 2sin 的值( )A.小于0B.大于0C.等于0D.不存在二、填空题1.设θ分别是第二、三、四象限角,则点)cos ,(sin θθP 分别在第___、___、___象限. 2.设MP 和OM 分别是角1817π的正弦线和余弦线,则给出的以下不等式: ①0<<OM MP ;②0OM MP <<; ③0<<MP OM ;④OM MP <<0, 其中正确的是_____________________________。
3.若角α与角β的终边关于y 轴对称,则α与β的关系是___________。
4.设扇形的周长为8cm ,面积为24cm ,则扇形的圆心角的弧度数是 。
5.与02002-终边相同的最小正角是_______________。
三、解答题1.已知1tan tan αα,是关于x 的方程2230x kx k -+-=的两个实根, 且παπ273<<,求ααsin cos +的值.2.已知2tan =x ,求xx xx sin cos sin cos -+的值。
3.化简:)sin()360cos()810tan()450tan(1)900tan()540sin(00000x x x x x x --⋅--⋅--4.已知)1,2(,cos sin ≠≤=+m m m x x 且,求(1)x x 33cos sin +;(2)x x 44cos sin +的值。
(数学4必修)第一章 三角函数(上)[综合训练B 组]一、选择题1.若角0600的终边上有一点()a ,4-,则a 的值是( )A .34B .34-C .34±D .32.函数xxx x x x y tan tan cos cos sin sin ++=的值域是( ) A .{}3,1,0,1- B .{}3,0,1- C .{}3,1- D .{}1,1- 3.若α为第二象限角,那么α2sin ,2cosα,α2cos 1,2cos1α中,其值必为正的有( )A .0个B .1个C .2个D .3个4.已知)1(,sin <=m m α,παπ<<2,那么=αtan ( ).A .21mm - B .21m m -- C .21m m-± D . m m 21-±5.若角α的终边落在直线0=+y x 上,则ααααcos cos 1sin 1sin 22-+-的值等于( ). A .2 B .2- C .2-或2 D .06.已知3tan =α,23παπ<<,那么ααsin cos -的值是( ). A .231+-B .231+-C .231-D . 231+ 二、填空题1.若23cos -=α,且α的终边过点)2,(x P ,则α是第_____象限角,x =_____。
2.若角α与角β的终边互为反向延长线,则α与β的关系是___________。
3.设99.9,412.721-==αα,则21,αα分别是第 象限的角。
4.与02002-终边相同的最大负角是_______________。
5.化简:0360sin 270cos 180sin 90cos 0tan r q p x m ---+=____________。
三、解答题1.已知,9090,90900000<<-<<-βα求2βα-的范围。
2.已知⎩⎨⎧>--<=,1,1)1(1,cos )(x x f x x x f π求)34()31(f f +的值。
3.已知2tan =x ,(1)求x x 22cos 41sin 32+的值。
(2)求x x x x 22cos cos sin sin 2+-的值。
4.求证:22(1sin )(1cos )(1sin cos )αααα-+=-+(数学4必修)第一章 三角函数(上)[提高训练C 组] 一、选择题1.化简0sin 600的值是( )A .0.5B .0.5-C .2.若10<<a ,ππ<<x 2,则11cos cos )(2--+---x xa ax x a x x a的值是( )A .1B .1-C .3D .3- 3.若⎪⎭⎫ ⎝⎛∈3,0πα,则αsin log 33等于( ) A .αsin B .αsin 1 C .αsin - D .αcos 1- 4.如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )A .5.0sin 1B .sin0.5C .2sin0.5D .tan0.55.已知sin sin αβ>,那么下列命题成立的是( )A.若,αβ是第一象限角,则cos cos αβ>B.若,αβ是第二象限角,则tan tan αβ>C.若,αβ是第三象限角,则cos cos αβ>D.若,αβ是第四象限角,则tan tan αβ>6.若θ为锐角且2coscos 1-=--θθ,则θθ1coscos -+的值为( )A .22B .6C .6D .4二、填空题1.已知角α的终边与函数)0(,0125≤=+x y x 决定的函数图象重合,αααsin 1tan 1cos -+的值为_____________.2.若α是第三象限的角,β是第二象限的角,则2βα-是第 象限的角.3.在半径为30m 的圆形广场中央上空,设置一个照明光源, 射向地面的光呈圆锥形,且其轴截面顶角为0120,若要光源 恰好照亮整个广场,则其高应为_______m (精确到0.1m )4.如果,0sin tan <αα且,1cos sin 0<+<αα那么α的终边在第 象限。
5.若集合|,3A x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭,{}|22B x x =-≤≤, 则B A I =_______________________________________。
三、解答题1.角α的终边上的点P 与),(b a A 关于x 轴对称)0,0(≠≠b a ,角β的终边上的点Q 与A 关于直线x y =对称,求βαβαβαsin cos 1tan tan cos sin ++之值.2.一个扇形OAB 的周长为20,求扇形的半径,圆心角各取何值时, 此扇形的面积最大?3.求66441sin cos 1sin cos αααα----的值。
4.已知,tan tan ,sin sin ϕθϕθb a ==其中θ为锐角,求证:11cos 22--=b a θ数学4(必修)第一章 三角函数(上) [基础训练A 组]一、选择题 22,(),,(),2422k k k Z k k k Z ππαππαππππ+<<+∈+<<+∈当2,()k n n Z =∈时,2α在第一象限;当21,()k n n Z =+∈时,2α在第三象限; 而coscoscos0222ααα=-⇒≤,2α∴在第三象限;sin(1000)sin 800-=>;0cos(2200)cos(40)cos 400-=-=>tan(10)tan(310)0π-=-<;77sincos sin 7171010,sin 0,tan 01717109tan tan 99πππππππ-=><sin120==43sin 4sin ,cos ,tan 55cos 3ααααα==-==- πααπ-=-+,若α是第四象限的角,则α-是第一象限的角,再逆时针旋转018032,sin 20;3,cos30;4,tan 40;sin 2cos3tan 40222ππππππ<<><<<<<>< 二、填空题1.四、三、二 当θ是第二象限角时,sin 0,cos 0θθ><;当θ是第三象限角时,sin 0,cos 0θθ<<;当θ是第四象限角时,sin 0,cos 0θθ<>;2.② 1717sin0,cos 01818MP OM ππ=>=< 3.2k αβππ+=+ α与βπ+关于x 轴对称 4.2 21(82)4,440,2,4,22lS r r r r r l rα=-=-+===== 5.0158 020022160158,(21603606)-=-+=⨯三、解答题 1. 解:21tan 31,2tan k k αα⋅=-=∴=±Q ,而παπ273<<,则1tan 2,tan k αα+==得tan 1α=,则sin cos 2αα==-,cos sin αα∴+= 2.解:cos sin 1tan 123cos sin 1tan 12x x x x x x +++===----3.解:原式=000sin(180)1cos tan()tan(90)tan(90)sin()x x x x x x -⋅⋅---- sin 1tan tan ()sin tan tan x x x x x x=⋅⋅-=-4.解:由sin cos ,x x m +=得212sin cos ,x x m +=即21sin cos ,2m x x -= (1)233313sin cos (sin cos )(1sin cos )(1)22m m m x x x x x x m --+=+-=-=(2)24244222121sin cos 12sin cos 12()22m m m x x x x --+++=-=-= 数学4(必修)第一章 三角函数(上) [综合训练B 组]一、选择题00tan 600,4tan 6004tan 604aa ==-=-=-- 当x 是第一象限角时,3y =;当x 是第二象限角时,1y =-; 当x 是第三象限角时,1y =-;当x 是第四象限角时,1y =-22,(),4242,(),2k k k Z k k k Z ππαππππαππ+<<+∈+<<+∈,(),422k k k Z παπππ+<<+∈2α在第三、或四象限,sin 20α<, cos2α可正可负;2α在第一、或三象限,cos 2α可正可负sin cos tan cos αααα===sin sin cos cos cos ααααα+=+, 当α是第二象限角时,sin sin tan tan 0cos cos αααααα+=-+=;当α是第四象限角时,sin sin tan tan 0cos cos αααααα+=-=41,cos sin 32πααα=-=-=二、填空题1.二,-cos 0α=<,则α是第二、或三象限角,而20y P => 得α是第二象限角,则12sin ,tan 2x x αα====-2.(21)k βαπ=++3.一、二 07.4122,2ππ<-<得1α是第一象限角;9.994,2πππ<-+<得2α是第二象限角4.0202- 020025360(202)-=-⨯+-5.0 00000tan 00,cos900,sin1800,cos 2700,sin 3600===== 三、解答题 1.解:0000009090,4545,9090,2ββα-<-<-<-<-<<()22ββαα-=+-Q ,001351352βα-<-<2.解:11411()cos,()()1332332f f f π===-=-Q 14()()033f f ∴+= 3.解:(1)222222222121sin cos tan 2173434sin cos 34sin cos tan 112x x x x x x x x +++===++ (2)2222222sin sin cos cos 2sin sin cos cos sin cos x x x x x x x x x x -+-+=+ 22tan tan 17tan 15x x x -+==+4.证明:右边2(1sin cos )22sin 2cos 2sin cos αααααα=-+=-+-2(1sin cos sin cos )2(1sin )(1cos )αααααα=-+-=-+22(1sin )(1cos )(1sin cos )αααα∴-+=-+数学4(必修)第一章 三角函数(上) [提高训练C 组]一、选择题sin 600sin 240sin(18060)sin 60==+=-=1cos cos 0,10,1(1)(1)1cos 1xxx ax x a x a x a -<->->-+=--+-=- 3331log log sin log sin sin 31log sin 0,333sin ααααα-<===作出图形得111sin 0.5,,sin 0.5sin 0.5r l r r α===⋅=画出单位圆中的三角函数线12121(cos cos )(cos cos )48,cos cos θθθθθθ---+=-+=+=二、填空题1.7713-在角α的终边上取点1255(12,5),13,cos ,tan ,sin 131213P r ααα-==-=-= 2.一、或三 111222322,(),222,(),22k k k Z k k k Z ππππαππαππ+<<+∈+<<+∈1212()()422k k k k παβπππ--+<<-+3.17.30tan 30,30hh ==4.二 2sin tan sin 0,cos 0,sin 0cos αααααα=<<> 5.[2,0][,2]3π-U 2|,...[,0][,]...333A x k x k k Z πππππππ⎧⎫=+≤≤+∈=-⎨⎬⎩⎭U U U 三、解答题1.解:(,),sin tan bP a b aααα-===-(,),sin tan a Q b a bβββ===22222sin tan 110cos tan cos sin b a b a aααββαβ+∴++=--+=。
