初中数学竞赛——-等腰三角形

合集下载

八年级等腰三角形数学教案【优秀6篇】

八年级等腰三角形数学教案【优秀6篇】作为一名专为他人授业解惑的人民教师，总归要编写教案，编写教案有利于我们科学、合理地支配课堂时间。

来参考自己需要的教案吧！小编为您精心收集了6篇《八年级等腰三角形数学教案》，如果能帮助到您，小编将不胜荣幸。

等腰三角形篇一9.3章等腰三角形教案（一）、温故知新，激发情趣：1、轴对称图形的有关概念，什么样的三角形叫做等腰三角形？2、指出等腰三角形的腰、底边、顶角、底角。

(首先教师提问了解前置知识掌握情况，学生动脑思考、口答。

)(二) 、构设悬念，创设情境：3、一般三角形有哪些特征？（三条边、三个内角、高、中线、角平分线）4、等腰三角形除具有一般三角形的特征外，还有那些特殊特征？(把问题3作为教学的出发点，激发学生的学习兴趣。

问题4给学生留下悬念。

)（三）、目标导向，自然引入：本节课我们一起研究——9.3 等腰三角形(板书课题) 9.3 等腰三角形(了解本节课的学习内容)(四)、设问质疑，探究尝试：结合问题4请同学们拿出准备好的不同规格的等腰三角形，与教师一起演示（模型）等腰三角形是轴对称图形的实验，引导学生观察实验现象。

[问题]通过观察，你发现了什么结论？（让学生由实验或演示指出各自的发现，并加以引导，用规范的数学语言进行逐条归纳，最后得出等腰三角形的特征）[结论]等腰三角形的两个底角相等。

（板书学生发现的结论）等腰三角形特征1：等腰三角形的两个底角相等在△ ABC中，△AB=AC（）△△B=△C（）[方法]可由学生从多种途径思考，纵横联想所学知识方法，为命题的证明打下基础。

例1：已知：在△ABC中，AB=AC,△B＝80°，求△C和△A的度数。

〔学生思考，教师分析，板书〕练习思考：课本P84 练习2（等腰三角形的底角可以是直角或钝角吗？为什么？）〔继续观察实验纸片图形〕（以下内容学生可能在前面实验中就会提出）[问题]纸片中的等腰三角形的对称轴可能是我们以前学习过的什么线？（通过设问、质疑、小组讨论，归纳总结，培养学生概括数学问题的能力）[引导学生观察]折痕AD是等腰三角形的对称轴，AD可能还是等腰三角形的什么线？[学生发现]AD是等腰三角形的顶角平分线、底边中线、底边上的高。

初中数学等腰三角形内角关系的应用

等腰三角形内角关系的应用根据等腰三角形的两个底角相等及三角形的内角和等于180°的结论，我们可以推出等腰三角形的顶角和底角的如下两个关系：1.＝180°－2；2.＝90°－. 灵活应用它们，能帮我们巧妙而迅捷地解答一些与等腰三角形内角有关的求值问题. 例1（希望杯初一数学竞赛试题）如图，D 是△ABC 内一点，DA ＝DB ＝DC ，且∠DAB ＝30°, ∠DBC ＝50°，则∠DAC 的值是（）（A ）10° （B ）20°（C ）30° （D ）40°．析解：在△ADC 中，由DA ＝DC ，得∠DAC ＝90°－∠ADC ．那么要求∠DAC 的度数，应先确定∠ADC 的度数．因为△ADB 和△BDC 中，DA ＝DB ， DB ＝DC ，所以∠ADB ＝180°－2∠DAB ＝120°，∠BDC ＝180°－2∠DBC ＝80°．所以∠ADC ＝360°－∠ADB －∠BDC ＝160°．αβαββ12αB C 12从而∠DAC ＝90°－∠ADC ＝10°，应选A ．例2（全国初二数学公开赛试题）如图，在△ABC 中，D 、E 是斜边AB 上的点，且BD ＝BC ，AE ＝AC ，则∠DCE 的度数是______．析解：在△DCE 中，∠DCE ＝180°－（∠CED ＋∠CDE ）．那么要求∠DCE 的度数，应先确定∠CED ＋∠CDE 的度数．因为△ACE 和△BCD 中，AE ＝AC ，BD ＝BC ，所以∠CED ＝90°－∠A ，∠CDE ＝90°－∠B ．所以∠CED ＋∠CDE ＝180°－（∠A ＋∠B ）．因为△ABC 是直角三角形，AB 是斜边，所以∠C ＝90°，∠A ＋∠B ＝90°．所以∠CED ＋∠CDE ＝135°．从而∠DCE ＝180°－（∠CED ＋∠CDE ）＝45°．12Rt A C B121212。

新人教版初中数学——等腰三角形与直角三角形-知识点归纳及典型题解析

新人教版初中数学——等腰三角形与直角三角形知识点归纳与典型题解析一、等腰三角形1．等腰三角形的性质定理：等腰三角形的两个底角相等（简称：等边对等角）．推论1：等腰三角形顶角平分线平分底边并且垂直于底边，即等腰三角形的顶角平分线、底边上的中线、底边上的高重合．推论2：等边三角形的各个角都相等，并且每个角都等于60°．2．等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．推论1：三个角都相等的三角形是等边三角形．推论2：有一个角是60°的等腰三角形是等边三角形．推论3：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．二、等边三角形1．定义：三条边都相等的三角形是等边三角形．2．性质：等边三角形的各角都相等，并且每一个角都等于60°．3．判定：三个角都相等的三角形是等边三角形；有一个角等于60°的等腰三角形是等边三角形．三、直角三角形与勾股定理1．直角三角形定义：有一个角是直角的三角形叫做直角三角形．性质：（1）直角三角形两锐角互余；（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；（3）在直角三角形中，斜边上的中线等于斜边的一半．判定：（1）两个内角互余的三角形是直角三角形；（2）三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形．2．勾股定理及逆定理（1）勾股定理：直角三角形的两条直角边a 、b 的平方和等于斜边c 的平方，即：a 2+b 2=c 2．（2）勾股定理的逆定理：如果三角形的三条边a 、b 、c 有关系：a 2+b 2=c 2，那么这个三角形是直角三角形．考向一等腰三角形的性质1．等腰三角形是轴对称图形，它有1条或3条对称轴． 2．等腰直角三角形的两个底角相等且等于45°．3．等腰三角形的底角只能为锐角，不能为钝角（或直角），但顶角可为钝角（或直角）． 4．等腰三角形的三边关系：设腰长为a ，底边长为b ，则2b<a ． 5．等腰三角形的三角关系：设顶角为顶角为∠A ，底角为∠B 、∠C ，则∠A =180°-2∠B ，∠B =∠C =2180A∠-︒．典例1 等腰三角形的一个内角为40°，则其余两个内角的度数分别为（） A ．40°，100° B ．70°，70°C ．60°，80°D ．40°，100°或70°，70°【答案】D【解析】①若等腰三角形的顶角为40°时，另外两个内角=（180°–40°）÷2=70°； ②若等腰三角形的底角为40°时，它的另外一个底角为40°，顶角为180°–40°–40°=100°．所以另外两个内角的度数分别为：40°、100°或70°、70°．故选D ．【名师点睛】考查了等腰三角形的性质和三角形的内角和为180o ，解题关键是分情况进行讨论①已知角为顶角时；②已知角为底角时．典例2 如图，在ABC ∆中，AB =AC ，D 是BC 的中点，下列结论不正确的是（）A．AD BC B．∠B=∠CC．AB=2BD D．AD平分∠BAC【答案】C【解析】因为△ABC中，AB=AC，D是BC中点，根据等腰三角形的三线合一性质可得，A．AD⊥BC，故A选项正确；B．∠B=∠C，故B选项正确；C．无法得到AB=2BD，故C选项错误；D．AD平分∠BAC，故D选项正确．故选C．【名师点睛】此题主要考查了等腰三角形的性质，本题关键熟练运用等腰三角形的三线合一性质.1．等腰三角形的周长为13cm，其中一边长为4cm，则该等腰三角形的底边为__________cm.考向二等腰三角形的判定1．等腰三角形的判定定理是证明两条线段相等的重要依据，是把三角形中的角的相等关系转化为边的相等关系的重要依据．2．底角为顶角的2倍的等腰三角形非常特殊，其底角平分线将原等腰三角形分成两个等腰三角形．典例3 如图，在△ABC中，AB=AC，AD⊥BC于D，E是AB上的一点，EF∥AD交CA的延长线于F．求证：△AEF是等腰三角形．【解析】∵AB=AC，AD⊥BC，∴∠BAD=∠CAD．又∵AD∥EF，∴∠F=∠CAD，∠FEA=∠BAD，∴∠FEA=∠F，∴△AEF是等腰三角形．2．已知在△ABC中，AB=5，BC=2，且AC的长为奇数．（1）求△ABC的周长；（2）判断△ABC的形状．考向三等边三角形的性质1．等边三角形具有等腰三角形的一切性质．2．等边三角形是轴对称图形，它有三条对称轴．3．等边三角形的内心、外心、重心和垂心重合．典例4 如图，在△ABC中，∠B=∠C=60°，点D为AB边的中点，DE⊥BC于E，若BE=1，则AC 的长为__________．【答案】4【解析】∵DE ⊥BC ，∠B =∠C =60°， ∴∠BDE =30°，∴BD =2BE =2，∵点D 为AB 边的中点，∴AB =2BD =4， ∵∠B =∠C =60°，∴△ABC 为等边三角形， ∴AC =AB =4，故答案为：4．【名师点睛】本题主要考查直角三角形的性质、等边三角形的判定和性质，利用直角三角形的性质求得AB =2BD 是解题的关键.3．如图，ABC ∆是等边三角形，点D 在AC 上，以BD 为一边作等边BDE ∆，连接CE ．（1）说明ABD CBE ∆≅∆的理由；（2）若080BEC ∠=，求DBC ∠的度数．考向四等边三角形的判定在等腰三角形中，只要有一个角是60°，无论这个角是顶角还是底角，这个三角形就是等边三角形．典例5 下列推理中，错误的是A ．∵∠A =∠B =∠C ，∴△ABC 是等边三角形 B ．∵AB =AC ，且∠B =∠C ，∴△ABC 是等边三角形 C ．∵∠A =60°，∠B =60°，∴△ABC 是等边三角形D ．∵AB =AC ，∠B =60°，∴△ABC 是等边三角形【答案】B【解析】A，∵∠A=∠B=∠C，∴△ABC是等边三角形，故正确；B，条件重复且条件不足，故不正确；C，∵∠A=60°，∠B=60°，∴∠C=60°，∴△ABC是等边三角形60°，故正确；D，根据有一个角是60°的等腰三角形是等边三角形可以得到，故正确．故选B．4．如图，已知OA=5，P是射线ON上的一个动点，∠AON=60°．当OP=__________时，△AOP为等边三角形．考向五直角三角形在直角三角形中，30°的角所对的直角边等于斜边的一半，这个性质常常用于计算三角形的边长，也是证明一边（30°角所对的直角边）等于另一边（斜边）的一半的重要依据．当题目中已知的条件或结论倾向于该性质时，我们可运用转化思想，将线段或角转化，构造直角三角形，从而将陌生的问题转化为熟悉的问题．典例6 如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若∠B=30°，BD=6，则CD 的长为__________．【答案】3【解析】∵在Rt△ABC中，∠C=90°，∠B=30°，∴∠BAC=60°．又AD平分∠BAC，∴∠BAD=∠CAD=30°，∴∠BAD=∠B=30°，∴AD=BD=6，∴CD=12AD=3，故答案为：3．5．已知直角三角形的两条边分别是5和12，则斜边上的中线的长度为__________．考向六勾股定理1．应用勾股定理时，要分清直角边和斜边，尤其在记忆a 2+b 2=c 2时，斜边只能是c ．若b 为斜边，则关系式是a 2+c 2=b 2；若a 为斜边，则关系式是b 2+c 2=a 2．2．如果已知的两边没有明确边的类型，那么它们可能都是直角边，也可能是一条直角边、一条斜边，求解时必须进行分类讨论，以免漏解．典例7 cm cm ，则这个直角三角形的周长为__________.【答案】【解析】∵直角边长为cm cm ，∴斜边（cm ），∴周长cm ）.故答案为:【名师点睛】本题考查了二次根式与三角形边长，面积的综合运用.熟练掌握勾股定理的计算解出斜边是关键6．如图所示，在ABC ∆中，90B ∠=︒，3AB =，5AC =，D 为BC 边上的中点.（1）求BD 、AD 的长度；（2）将ABC ∆折叠，使A 与D 重合，得折痕EF ；求AE 、BE 的长度.1．直角三角形两直角边长分别为6和8，则此直角三角形斜边上的中线长是 A ．3B ．4C ．7D ．52．如图，ABC △是等边三角形，0,20BC BD BAD =∠=，则BCD ∠的度数为A ．50°B ．55°C ．60°D ．65°3．如图是“人字形”钢架，其中斜梁AB =AC ，顶角∠BAC =120°，跨度BC =10m ，AD 为支柱（即底边BC 的中线），两根支撑架DE ⊥AB ，DF ⊥AC ，则DE +DF 等于A ．10mB ．5mC ．2.5mD ．9.5m4．如图，ABC ∆是边长为1的等边三角形，BDC ∆为顶角120BDC ∠=︒的等腰三角形，点M 、N 分别在AB 、AC 上，且60MDN ∠=︒，则AMN ∆的周长为A．2 B．3 C．1.5 D．2.55．如图，△ABC中，D、E两点分别在AC、BC上，AB=AC，CD=DE．若∠A=40°，∠ABD：∠DBC=3：4，则∠BDE=A．24°B．25°C．30°D．35°6．已知等腰三角形的一边长等于4，一边长等于9，则它的周长为A．22 B．17C．17或22 D．267．如图，△ABC中，AB=AC=5，BC=6，点D在BC上，且AD平分∠BAC，则AD的长为A．6 B．5C．4 D．38．如图，A、B两点在正方形网格的格点上，每个方格都是边长为1的正方形，点C也在格点上，且△ABC是等腰三角形，则符合条件是点C共有A ．8个B ．9个C ．10个D ．11个9．如图，Rt △ABC 中，∠B =90〬，AB =9，BC =6，，将△ABC 折叠，使A 点与BC 的中点D 重合，折痕为MN ，则线段AN 的长等于A ．5B ．6C ．4D ．310．将一个有45°角的三角尺的直角顶点C 放在一张宽为3 cm 的纸带边沿上，另一个顶点A 在纸带的另一边沿上，测得三角尺的一边AC 与纸带的一边所在的直线成30°角，如图，则三角尺的最长边的长为A ．6B ．C ．D ．11．三角形的三边a ，b ，c （b ﹣c ）2=0；则三角形是_____三角形. 12．如图，等腰△ABC 中，AB =AC =13cm ，BC =10cm ，△ABC 的面积=________．13．已知等腰三角形一腰上的高与另一腰的夹角为35°，则这个等腰三角形顶角的度数为__________. 14．若一个等腰三角形的周长为26，一边长为6，则它的腰长为__________．15．如图，在ABC △中，AB AC =，D 、E 分别是BC 、AC 上一点，且AD AE =，12EDC ∠=︒，则BAD ∠=__________．16．如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG=CD，DF=DE，则∠EFD=__________°．17．如图，在矩形ABCD中，AB=5，BC=7，点E是AD上的一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A1恰好落在∠BCD的平分线上时，CA1的长为__________．18．如图，在Rt△ABC中，点E在AB上，把△ABC沿CE折叠后，点B恰好与斜边AC的中点D 重合.（1）求证：△ACE为等腰三角形；（2）若AB=6，求AE的长.19．如图，一架2.5 m 长的梯子斜立在竖直的墙上，此时梯足B 距底端O 为0.7 m ．（1）求OA 的长度；（2）如果梯子顶端下滑0.4米，则梯子将滑出多少米？20．ABC ∆与DCE ∆有公共顶点C （顶点均按逆时针排列），AB AC =，DC DE =，180BAC CDE ∠+∠=︒，//DE BC ，点G 是BE 的中点，连接DG 并延长交直线BC 于点F ，连接,AF AD .（1）如图，当90BAC ∠=︒时，求证：①BF CD =； ②AFD ∆是等腰直角三角形.（2）当60BAC ∠=︒时，画出相应的图形（画一个即可），并直接指出AFD ∆是何种特殊三角形.21．已知：如图，有人在岸上点C 的地方，用绳子拉船靠岸，开始时，绳长CB =10米，CA ⊥AB ，且CA =6米，拉动绳子将船从点B 沿BA 方向行驶到点D 后，绳长CD （1）试判定△ACD 的形状，并说明理由；（2）求船体移动距离BD 的长度．1．如图，在OAB △和OCD △中，,,,40OA OB OC OD OA OC AOB COD ==>∠=∠=︒，连接,AC BD 交于点M ，连接OM ．下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠．其中正确的个数为A ．4B ．3C ．2D ．12．在△ABC 中，AB =AC ，∠A =40°，则∠B =__________．3．如图，在△ABC 中，AB =AC ，点D ，E 都在边BC 上，∠BAD =∠CAE ，若BD =9，则CE 的长为__________．4．如图，在四边形ABCD 中，AB CD ∥，连接AC ，BD ．若90ACB ∠=︒，AC BC =，AB BD =，则ADC ∠=__________︒．5．腰长为5，高为4的等腰三角形的底边长为__________．6．若等腰三角形的一个底角为72︒，则这个等腰三角形的顶角为__________．7．如图，△ABC 中，AB =BC ，∠ABC =90°，F 为AB 延长线上一点，点E 在BC 上，且AE =CF ，若∠BAE =25°，则∠ACF =__________度．8．如图，ABC △中，点E 在BC 边上，AE AB =，将线段AC 绕点A 旋转到AF 的位置，使得CAF BAE ∠=∠，连接EF ，EF 与AC 交于点G ．（1）求证：EF BC =；（2）若65ABC ∠=︒，28ACB ∠=︒，求FGC ∠的度数．9．如图，在△ABC 中，AB =AC ，AD ⊥BC 于点D ．（1）若∠C =42°，求∠BAD 的度数；（2）若点E 在边AB 上，EF ∥AC 交AD 的延长线于点F ．求证：AE =FE ．10．如图，在△ABC 中，AB =AC ，点D 、E 分别在AB 、AC 上，BD =CE ，BE 、CD 相交于点O ．求证：（1）DBC ECB △≌△；（2）OB OC =．11．如图，在△ABC 中，AB =AC ，D 是BC 边上的中点，连结AD ，BE 平分∠ABC 交AC 于点E ，过点E 作EF ∥BC 交AB 于点F ．（1）若∠C =36°，求∠BAD 的度数．（2）若点E 在边AB 上，EF ∥AC 叫AD 的延长线于点F ．求证：FB =FE ．12．在ABC △中，90BAC ∠=︒，AB AC =，AD BC ⊥于点D ．（1）如图1，点M ，N 分别在AD ，AB 上，且90BMN ∠=︒，当30AMN =︒∠，2AB =时，求线段AM 的长；（2）如图2，点E ，F 分别在AB ，AC 上，且90EDF ∠=︒，求证：BE AF =；（3）如图3，点M 在AD 的延长线上，点N 在AC 上，且90BMN ∠=︒，求证：AB AN +=．1．【答案】4cm 或5cm【解析】当长是4cm 的边是底边时，腰长是12（13–4）=4.5，三边长为4cm ，4.5cm ，4.5cm ，等腰三角形成立；当长是4cm 的边是腰时，底边长是：13–4–4=5cm ，等腰三角形成立．故底边长是：4cm 或5cm ．故答案是：4cm 或5cm【名师点睛】本题考查的是等腰三角形的性质，在解答此题时要注意进行分类讨论，不要漏解． 2．【解析】（1）由题意得：5−2<AB <5+2，即：3<AB <7，∵AB 为奇数，∴AB =5， ∴△ABC 的周长为5+5+2=12．（2）∵AB =AC =5， ∴△ABC 是等腰三角形． 3．【答案】（1）见解析；（2）20°.【解析】（1）由060ABC DBE ∠=∠=，得ABD CBE ∠=∠，由,AB BC BD BE ==，得ABD CBE ∆≅∆（SAS ）；（2）由ABD CBE ∆≅∆，得060BCE A ∠=∠=，所以00000180180806040CBE BEC BCE ∠=-∠-∠=--=，所以000060604020DBC CBE ∠=-∠=-=.【名师点睛】本题主要考查全等三角形的判定和性质以及三角形内角和定理，先证明三角形全等是解决本题的突破口． 4．【答案】5【解析】已知∠AON =60°，当OP =OA =5时，根据有一个角为60°的等腰三角形为等边三角形，可得△AOP 为等边三角形．故答案为：5． 5．【答案】6或6.5【解析】分两种情况：①5和12是两条直角边，根据勾股定理求得斜边为13，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6.5；②5是直角边，12为斜边，利用直角三角形斜边的中线等于斜边的一半即可得斜边上的中线的长度为6，故答案为：6或6.5．6．【答案】（1）BD =2，AD =2）136AE =，56BE = 【解析】（1）∵在ABC ∆中，90B ∠=︒，3AB =，5AC =， ∴在Rt ABC ∆中，222225316BC AC AB =-=-=， ∴4BC =，又∵D 为BC 边上的中点， ∴122BD DC BC ===， ∴在Rt ABD ∆中，222222133AD AB BD =+=+=，∴AD =（2）ABC ∆折叠后如图所示，EF 为折痕，连接DE ，设AE x =，则DE x =，3BE x =-，在Rt BDE ∆中，222BE BD DE +=，即()22232x x -+=，解得：136x =， ∴136AE =， ∴135366BE =-=．【名师点睛】本题主要考查了勾股定理的应用，也考查了折叠的性质.是常见中考题型.1．【答案】D【解析】∵两直角边分别为6和8，∴斜边10=， ∴斜边上的中线=12×10=5，故选D ．【名师点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质以及勾股定理的应用，熟记性质是解题的关键． 2．【答案】A 【解析】ABC △是等边三角形，AC AB BC ∴==，又BC BD =，AB BD ∴=，∴20BAD BDA ∠=∠=︒0180CBD BAD BDA ABC ∴∠=-∠-∠-∠0000018020206080=---=，BC BD =，∴11(180)(18080)5022BCD CBD ∠=⨯︒-∠=⨯︒-︒=︒，故选A ．【名师点睛】本题考查了等边三角形、等腰三角形的性质、等边对等角以及三角形内角和定理，熟练掌握性质和定理是正确解答本题的关键. 3．【答案】B【解析】∵AB =AC ，∠BAC =120°，∴∠B =∠C =30°， ∵DE ⊥AB ，DF ⊥AC ，垂足为E ，F ，∴DE =12BD ，DF =12DC ， ∴DE +DF =12BD +12DC =12（BD +DC ）=12B C ．∴DE +DF =12BC =12×10=5m ．故选B ．【名师点睛】本题考查等腰三角形和直角三角形的性质，熟练掌握相关知识点是解题关键. 4．【答案】A【解析】如图所示，延长AC 到E ，使CE =BM ，连接DE ，∵BD =DC ，∠BDC =120°，∴∠CBD =∠BCD =30°， ∵∠ABC =∠ACB =60°，∴∠ABD =∠ACD =∠DCE =90°，在△BMD 和△CED 中，90BD CDDBM DCE BM CE =⎧⎪∠=∠=︒⎨⎪=⎩，∴△BMD ≌△CED （SAS ），∴∠BDM =∠CDE ，DM =DE ，又∵∠MDN =60°，∴∠BDM +∠NDC =60°， ∴∠EDC +∠NDC =∠NDE =60°=∠NDM ，在△MDN 和△EDN 中，DM DEMDN NDE DN DN =⎧⎪∠=∠⎨⎪=⎩，∴△MDN ≌△EDN （SAS ）， ∴MN =NE =NC +CE =NC +BM ，所以△AMN 周长=AM +AN +MN =AM +AN +NC +BM =AB +AC =2. 故选A.【名师点睛】本题考查全等三角形的判定和性质，做辅助线构造全等三角形，利用等边三角形的性质得到全等条件是解决本题的关键.5．【答案】C【解析】∵AB=AC，CD=DE，∴∠C=∠DEC=∠ABC，∴AB∥DE，∵∠A=40°，∴∠C=∠DEC=∠ABC=18040702，∵∠ABD：∠DBC=3：4，∴设∠ABD为3x，∠DBC为4x，∴3x+4x=70°，∴x=10°，∴∠ABD=30°，∵AB∥DE，∴∠BDE=∠ABD=30°，故答案为C．【名师点睛】本题主要考查了等腰三角形的性质：等边对等角和三角形内角和定理求解，难度适中．6．【答案】A【解析】分两种情况：①当腰为4时，4+4<9，所以不能构成三角形；②当腰为9时，9+9>4，9-9<4，所以能构成三角形，周长是：9+9+4=22．故选A．7．【答案】C【解析】∵AB=AC=5，AD平分∠BAC，BC=6，∴BD=CD=3，∠ADB=90°，∴AD=4．故选C．8．【答案】B【解析】如图，①点C以点A为标准，AB为底边，符合点C的有5个；②点C以点B为标准，AB为等腰三角形的一条边，符合点C的有4个．所以符合条件的点C共有9个．故选B．9．【答案】A【解析】设AN=x，由翻折的性质可知DN=AN=x，则BN=9-x．∵D是BC的中点，∴BD=1632⨯=．在Rt△BDN中，由勾股定理得:ND2=NB2+BD2，即x2=（9-x）2+32，解得x=5，AN=5，故选A．10．【答案】D【解析】如图，作AH⊥CH，在Rt △ACH 中，∵AH =3，∠AHC =90°，∠ACH =30°，∴AC =2AH =6，在Rt △ABC 中，AB ==D ．11．【答案】等边【解析】三角形的三边a ，b ，c 2()0b c -=，20,()0b c =-=，0,0a b b c ∴-=-=，解得：,a b b c ==，即a b c ==，则该三角形是等边三角形.故答案为：等边.【名师点睛】本题是一道比较好的综合题，考查了算术平方根的非负性、平方数的非负性、等边三角形的定义. 12．【答案】60cm 2．【解析】过点A 作AD ⊥BC 交BC 于点D ， ∵AB =AC =13cm ，BC =10cm ， ∴BD =CD =5cm ，AD ⊥BC ，由勾股定理得：AD （cm ）， ∴△ABC 的面积=12×BC ×AD =12×10×12=60（cm 2）．【名师点睛】本题考查的是等腰三角形的性质及勾股定理，能根据等腰三角形的“三线合一”正确的添加辅助线是关键. 13．【答案】55°或125°【解析】如图，分两种情况进行讨论：如图1，当高在三角形内部时，则∠ABD =35°，∴∠BAD =90°–35°=55°；如图2，当高在三角形外部时，则∠ABD =35°，∴∠BAD =90°–35°=55°； ∴∠CAB =180°–55°=125°，故答案为55°或125°．【名师点睛】本题主要考查等腰三角形的性质，熟记三角形的高相对于三角形的三种位置关系是解题的关键. 14．【答案】10【解析】①当6为腰长时，则腰长为6，底边=26-6-6=14，因为14>6+6，所以不能构成三角形； ②当6为底边时，则腰长=（26-6）÷2=10，因为6-6<10<6+6，所以能构成三角形，故腰长为10．故答案为：10． 15．【答案】24︒【解析】∵ADC ∠是三角形ABD 的外角，AED ∠是三角形DEC 的一个外角，CDE x ∠=︒， ∴ADC BAD B ADE EDC ∠=∠+∠=∠+∠，AED EDC C ∠=∠+∠，B BAD ADE x ∠+∠=∠+︒，AEDC x ∠=∠+︒，∵AB AC =，D 、E 分别在BC 、AC 上，AD AE =，CDE x ∠=︒，∴B C ∠=∠，20ADE AED C ∠=∠=∠+︒，∴C BAD C x x ∠+∠=∠︒++︒，∵12EDC ∠=︒，∴24BAD ∠=︒，故答案为：24︒．16．【答案】15【解析】∵△ABC 是等边三角形，∴∠ACB =60°，∠ACD =120°， ∵CG =CD ，∴∠CDG =30°，∠FDE =150°， ∵DF =DE ，∴∠E =15°．故答案为：15．17．【答案】【解析】如图，过点A 1作A 1M ⊥BC 于点M ．∵点A 的对应点A 1恰落在∠BCD 的平分线上，∠BCD =90°，∴∠A 1CM =45°，即△AMC 是等腰直角三角形，∴设CM =A 1M =x ，则BM =7-x ．又由折叠的性质知AB =A 1B =5，∴在直角△A 1MB 中，由勾股定理得A 1M 2=A 1B 2-BM 2=25-（7-x ）2，∴25-（7-x ）2=x 2，解得x 1=3，x 2=4，∵在等腰Rt △A 1CM 中，CA 1A 1M ，∴CA 1．故答案为：18．【答案】（1）见解析；（2）4.【解析】（1）∵把△ABC 沿CE 折叠后，点B 恰好与斜边AC 的中点D 重合， ∴CD =CB ，∠CDE =∠B =90°，AD =CD ，在△ADE 和△CDE 中，90AD CDADE CDE ED ED =⎧⎪∠=∠=⎨⎪=⎩，∴△ADE ≌△CDE （SAS ）， ∴EA=EC ，∴△ACE 为等腰三角形；（2）由折叠的性质知：∠BEC =∠DEC ， ∵△ADE ≌△CDE ，∴∠AED =∠DEC ， ∴∠AED =∠DEC =∠BEC =60°，∴∠BCE =30°，∴12BE CE =，又∵EA=EC ，∴11223BE AE AB ===，∴AE=4.【名师点睛】本题考查了折叠的性质、全等三角形的判定和性质、等腰三角形的定义和30°角的直角三角形的性质，属于常考题型，熟练掌握上述图形的性质是解题关键. 19．【解析】在直角△ABO 中，已知AB =2.5 m ，BO =0.7 m ，则AO ， ∵AO =AA ′+OA ′，∴OA ′=2 m ，∵在直角△A ′B ′O 中，AB =A ′B ′，且A ′B ′为斜边， ∴OB ′=1.5 m ，∴BB ′=OB ′-OB =1.5 m -0.7 m=0.8 m ．答：梯足向外移动了0.8 m ．20．【答案】（1）①详见解析；②详见解析；（2）详见解析；【解析】（1）证明：①∵//DE BC ，∴GBF GED ∠=∠. 又,BG EG FGB DGE =∠=∠， ∴(ASA)GBF GED ∆∆≌，∴BF ED =. 又CD ED =，∴BF CD =；②当90BAC ∠=︒时，45ABC ACB ∠=∠=︒， ∵180BAC CDE ︒∠+∠=，∴90CDE ︒∠=.∵//DE BC ，∴90,45BCD CDE ACD ︒︒∠=∠=∠=，∴ABF ACD ∠=∠；又,AB AC BF CD ==，∴()ABF ACD SAS ∆∆≌， ∴,AF AD BAF CAD =∠=∠， ∴BAF FAC CAD FAC ∠+∠=∠+∠ 即90BAC FAD ∠=∠=︒，∴AFD ∆是等腰直角三角形.（2）所画图形如图1或图②，此时AFD ∆是等边三角形.图1 图2 与（1）同理，可证ABF ACD ∆∆≌， ∴AF =AD ，60BAC FAD ∠=∠=︒， ∴△AFD 是等边三角形.【名师点睛】本题考查了等边三角形的判定，等腰三角形的判定和性质，以及全等三角形的判定和性质，平行线的性质，解题的关键是正确找到证明三角形全等的条件，利用全等三角形的性质得到边的关系，角的关系.21．【解析】（1）由题意可得：AC =6 m ，DCm ，∠CAD =90°，可得AD（m ），故△ACD 是等腰直角三角形．（2）∵AC =6 m ，BC =10 m ，∠CAD =90°， ∴AB（m ），则BD =AB -AD =8-6=2（m ）．答：船体移动距离BD 的长度为2 m ．1．【答案】B【解析】∵40AOB COD ∠=∠=︒，∴AOB AOD COD AOD ∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC △和BOD △中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴AOC BOD △≌△，∴OCA ODB AC BD ∠=∠=，，①正确；∴OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠， ∴40AMB AOB ∠=∠=°，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=°，在OCG △和ODH △中，OCA ODBOGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴OCG ODH △≌△，∴OG OH =，∴MO平分BMC ∠，④正确，正确的个数有3个，故选B ． 2．【答案】70°【解析】∵AB =AC ，∴∠B =∠C ， ∵∠A +∠B +∠C =180°，∴∠B =12（180°-40°）=70°．故答案为：70°． 3．【答案】9【解析】∵AB =AC ，∴∠B =∠C ，在△BAD 和△CAE 中，BAD CAE AB ACB C ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BAD ≌△CAE ， ∴BD =CE =9，故答案为：9． 4．【答案】105【解析】作DE AB ⊥于E ，CF AB ⊥于F ，如图所示，则DE CF =，∵CF AB ⊥，90ACB ∠=︒，AC BC =，∴12CF AF BF AB ===， ∵AB BD =，∴1122DE CF AB BD ===，BAD BDA ∠=∠， ∴30ABD ∠=︒，∴75BAD BDA ∠=∠=︒，∵AB CD ∥，∴180ADC BAD ∠+∠=︒，∴105ADC ∠=︒，故答案为：105．5．【答案】6或【解析】①如图1，当5AB AC ==，4AD =，则3BD CD ==，∴底边长为6； ②如图2，当5AB AC ==，4CD =时，则3AD =，∴2BD =，∴BC == ③如图3，当5AB AC ==，4CD =时，则3AD ==，∴8BD =，∴BC =∴此时底边长为6或【名师点睛】本题考查了勾股定理，等腰三角形的性质，解题的关键是分三种情况分类讨论． 6．【答案】36°【解析】∵等腰三角形的一个底角为72︒，∴等腰三角形的顶角180727236=︒-︒-︒=︒，故答案为：36︒．【名师点睛】本题考查了等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键． 7．【答案】70【解析】∵∠ABC =90°，AB =AC ，∴∠CBF =180°–∠ABC =90°，∠ACB =45°，在Rt △ABE 和Rt △CBF 中，AB CBAE CF=⎧⎨=⎩，∴Rt △ABE ≌Rt △CBF ，∴∠BCF =∠BAE =25°，∴∠ACF =∠ACB +∠BCF =45°+25°=70°，故答案为：70．【名师点睛】本题考查了等腰直角三角形的性质，全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键． 8．【解析】（1）∵CAF BAE ∠=∠，∴BAC EAF ∠=∠，∵AE AB AC AF ==，， ∴BAC EAF △≌△， ∴EF BC =．（2）∵65AB AE ABC =∠=︒，， ∴18065250BAE ∠=︒-︒⨯=︒， ∴50FAG ∠=︒， ∵BAC EAF △≌△， ∴28F C ∠=∠=︒， ∴502878FGC ∠=︒+︒=︒．【名师点睛】本题主要考查全等三角形证明与性质，等腰三角形性质，旋转性质等知识点，比较简单，基础知识扎实是解题关键． 9．【解析】（1）∵AB =AC ，AD ⊥BC 于点D ，∴∠BAD =∠CAD ，∠ADC =90°，又∠C =42°，∴∠BAD =∠CAD =90°-42°=48°．（2）∵AB =AC ，AD ⊥BC 于点D ， ∴∠BAD =∠CAD ， ∵EF ∥AC ， ∴∠F =∠CAD ， ∴∠BAD =∠F ，∴AE =FE ．10．【解析】（1）∵AB =AC ，∴∠ECB =∠DBC ，在DBC △与ECB △中，BD CE DBC ECB BC CB =⎧⎪∠=∠⎨⎪=⎩，∴DBC △≌ECB △．（2）由（1）DBC △≌ECB △， ∴∠DCB =∠EBC ， ∴OB =OC ．11．【解析】（1）∵AB AC =，∴C ABC ∠=∠，∵36C ∠=︒， ∴36ABC ∠=︒，∵D 为BC 的中点，∴AD BC ⊥，∴90903654BAD ABC ∠=-∠=-︒=︒︒︒．（2）∵BE 平分ABC ∠，∴ABE EBC ∠=∠，又∵EF BC ∥，∴EBC BEF ∠=∠， ∴EBF FEB ∠=∠， ∴BF EF =．【名师点睛】本题考查等腰三角形的性质，平行线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．12．【解析】（1）∵90BAC ∠=︒，AB AC =，AD BC ⊥，∴AD BD DC ==，45ABC ACB ∠=∠=︒，45BAD CAD ∠=∠=︒， ∵2AB =，∴AD BD DC ===，∵30AMN ∠=︒，∴180903060BMD ∠=︒-︒-︒=︒， ∴30BMD ∠=︒，∴2BM DM =，由勾股定理得，222BM DM BD -=，即222(2)DM DM -=，解得DM =∴AM AD DM =-=（2）∵AD BC ⊥，90EDF ∠=︒，∴BDE ADF ∠=∠，在BDE △和ADF △中，B DAF DB DA BDE ADF ∠=∠=∠=∠⎧⎪⎨⎪⎩，∴BDE ADF △≌△， ∴BE AF =．（3）如图，过点M 作//ME BC 交AB 的延长线于E ，∴90AME ∠=︒，则AE =，45E ∠=︒，∴ME MA =，∵90AME ∠=︒，90BMN ∠=︒， ∴BME AMN ∠=∠，在BME △和AMN △中，E MAN ME MA BME AMN ∠=∠=∠=∠⎧⎪⎨⎪⎩，∴BME AMN △≌△，∴BE AN =，∴AB AN AB BE AE +=+==．【名师点睛】本题考查的是等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的性质，掌握全等三角形的判定定理和性质定理是解题的关键．。

初中数学精品试题：等腰三角形

2.2等腰三角形A 组1.等腰三角形的对称轴是 ( )A ．过顶点的直线B ．底边上的高C ．顶角平分线所在的直线D ．腰上的高2.如图，在正方形ABCD 中，AC ，BD 交于点O ，则图中共有几个等腰三角形( )A ．5个B ．6个C ．7个D ．8个3.周长为l3，边长为整数的等腰三角形共有( )A ．2个B ．3个C ．4个D ．5个4.如果等腰三角形有一边长是6，另一边长是8，那么它的周长是；如果等腰三角形的两边长分别是4、8，那么它的周长是 .5.已知：等腰三角形的腰长为8cm ，则底边a 的取值范围是________________.已知a ,b ,c 分别是△ABC 的三边，且满足022=-c b c a ，则这个三角形的形状是 .有一个等腰三角形，三边长分别为4x-1,5x-3,4-2x ，求这个等腰三角形的周长.8. 在如图的网格中，请找出格点，使每一个格点与A ，B 两点构成等腰三角形．B 组9.用长为10m 的钢筋制作一个等腰三角形的铁架，使铁架的底边长比腰多lm ，则这个等腰三角形的腰长是________m ．10.如图，在△ABC 中，AB ＝AC ，DE 是AB 的中垂线，△BCE 的周长为14，BC =6，则AB 的长为（）A.6B.7C.8D.9l B A 如图所示，在直线l 上找一点P ，使△PAB 为等腰三角形，请问这样的P 点有几个?在图上标出来．等腰三角形一腰上的中线把这个三角形的周长分为20cm 和36cm 两个部分，求这个三角形各边的长．已知等边三角形ABC 和点P ，设点P 到△ABC 三边AB ,AC ,BC 的距离分别是1h ，2h ，3h ，△ABC 的高为h ，请你探索以下问题（1）若点P 在一边BC 上（如图（1）），此时3h =0，问1h ，2h 与h 之间有怎样的关系？请说明理由：（2）若点P 在△ABC 内部（如图（2）），此时1h ，2h ，3h 与h 之间有怎样的关系？请说明理由：（3）若点P 在△ABC 外部（如图（3）），此是1h ，2h ，3h 与h 之间有怎样的关系？__ __ _（直接写出你的猜想，不需要说明理由）。

初中数学中的等边三角形与等腰三角形的特性研究及其在实际问题中的应用

多做练习题，通过不断的练习提高自己的解题能力和技巧。
练习经典题目
练习等边三角形与等腰三角形的性质和判定定理的题目
练习等边三角形与等腰三角形在实际问题中的应用题目
总结解题方法和思路
熟悉等边三角形与等腰三角形的性质和特点，这是解决问题的关键。
掌握等边三角形与等腰三角形的判定定理，以便准确判断图形。
学会运用等边三角形与等腰三角形的性质进行证明和计算，提高解题效率。
运动器材：在运动器材设计中，等边三角形和等腰三角形用于支撑和保持平衡，提高运动的安全性和稳定性。
建筑设计：利用等边三角形和等腰三角形的特性，优化建筑设计，提高结构强度。
航海学中的应用
等边三角形用于计算船只的速度和航程
等边三角形与等腰三角形用于确定方向和距离
航海图上的三角形标记用于定位和导航
等腰三角形用于确定船只的航向和航速
吊装施工：利用等边三角形的角度特性，可以更加精确地控制吊装施工的精度
建筑测量：等边三角形在建筑测量中也有广泛的应用，例如测量建筑物的角度、高度等
物理学中的应用
桥梁稳定性：等边三角形和等腰三角形用于支撑结构，保持桥梁的稳定。
机械零件：在机械零件设计中，等边三角形和等腰三角形用于固定和传递力量，确保机械的正常运转。
等边三角形与等腰三角形的特性
01
边长特性
等边三角形的三边相等
等腰三角形的两边相等
等边三角形的角平分线、中线、垂线合一
等腰三角形的角平分线、中线不合一
角度特性
等边三角形是轴对称图形，对称轴是三条边的垂直平分线
等腰三角形也是轴对称图形，对称轴是顶角平分线所在的直线
等边三角形每个角都是60度
等腰三角形至少有两个角相等，顶角与底角互补

初中数学课件等腰三角形的性质(几何)ppt课件

接求出等腰三角形的面积。
利用三角函数
通过已知角度和边长，利用三角函数求出高或底，再代入公式计算面积。
利用向量
在平面直角坐标系中，可以利用向量表示三角形的顶点，通过向量的运算求出三角形的面积。
案例分析：不同类型题目解法
01
02
03
04
已知等腰三角形的底和高，直接代入公式求解。
已知等腰三角形三边长度，利用海伦公式求解。
勾股定理在等腰三角形中的推广
对于非直角的等腰三角形，可以通过作高将其分为两个直角三角形，再利用勾股定理求解相关问题。
相似三角形与等腰三角形关系探讨
相似三角形定义
两个三角形如果它们的对应角相等，则称这两个三角形相似。
等腰三角形的相似性质
对于两个等腰三角形，如果它们的顶角相等，则这两个三角形相似。此外，如果两个等腰三角形的底边和腰成比例，则这两个三角形也相似。
实际应用：测量、作图等问题
01
测量
在实际生活中，等腰三角形的性质可以应用于测量问题。例如，在无法
直接测量某一边长时，可以通过测量等腰三角形的底角和腰长来间接计
算。
02
作图
在几何作图中，等腰三角形的性质也有广泛应用。例如，可以通过作等
腰三角形的高来平分底边，或者通过作等腰三角形的角平分线来得到对
称的图形。
初中数学课件等腰三角形的性质(几何)ppt课件
目录
• 等腰三角形基本概念与性质 • 等腰三角形判定方法 • 等腰三角形面积计算 • 等腰三角形在生活中的应用 • 等腰三角形相关定理和推论 • 练习题与课堂互动环节
01
等腰三角形基本概念与性质
等腰三角形定义及特点
定义
有两边相等的三角形叫做等腰三角形。

2023初中数学培优竞赛例题+练习专题36 全国初中数学竞赛分类汇编卷(七)三角形(提优)

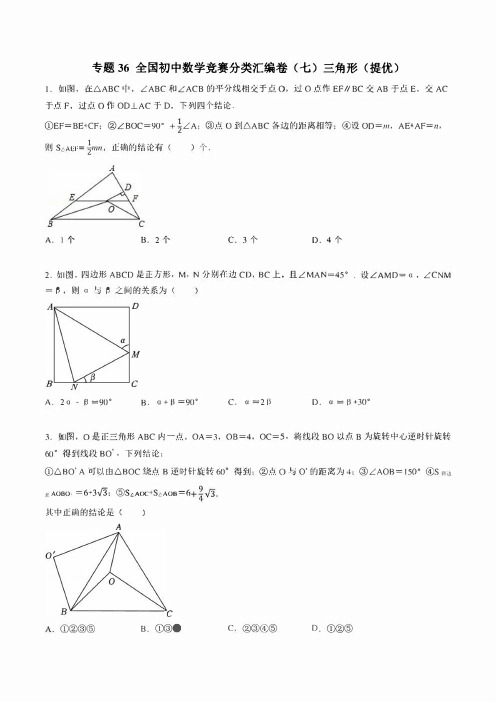
专题36全国初中数学竞赛分类汇编卷〈七〉三角形〈提优〉I.如｜蜀，在.6.ABC中，LABC和ζACB的平分线相交子点。

，过0点作EF//BC交AB子点E，交AC 于点F，过点。

你OD_l_AC于D，下列四个结论．1①EF=BE+CF：②LBOC=90。

＋2LA；＠点O itl.6.ABC各边的距离相等；④设OD=m,AE+AF=n, 则S c,A EF=�mn，正确的结论有（）个AB cA.l个B.2个 c.3个。

.4个2.如图，四边形ABCD是正方形，M,N分别在边CD,BC上，且LMAN=45。

．设LAMD＝口，ζCNM ＝白，则。

与自之间的关系为（〉DcNA.2 a －白＝90。

B.a+fJ=90。

C.a =2日。

.a＝自＋30。

3.如图，0是正三角形ABC内一点，OA=3,08=4, OC=S，将线段BO以点B为旋转中心逆时针旋转60。

得到线段BO’，下列结论：①.6.BO' A司以由.6.BOC绕点B逆时针旋转60。

得到；②点。

与O’的距离为4；③LAOB=l50。

④s P.!I地11;AOBO ＝削σ；⑤S叫＋S c,A O时1士；中正E角的结论是〈）A℃B.①③④C②＠④⑤ D.①＠⑤4.AD与BE是6ABC的角平分线，D,E分别在BC,AC上，若AD=AB,BE=BC，贝�L'.C=()Bc AA.69。

ωTRU900c.（τ3)° D.不能确定5.在四边形ABCD中，AD=DC=2，ζDAB＝ζDCB=90。

，BC,A D的延长线交于P，求AB•S i:.PAB的最小值pDBA6.着，1个等腰三角形的顶角a1、a2、…、an两两不等，它们的共同特点是：被一条直线分得的两个较小三角形也是等腰三角形，则a1+ a 2＋…＋an＝·fα－ 2b = m-7 7设。

、b分别是等腰三角形的两条边的长，m是这个三角形的周长，当。

、b、川满足方程t R Ja+b＝号＋2时，m的值是8.己知ID.ABC中，AB=AC,L'.BAC=90。

等腰三角形性质习题库

总结词
等腰三角形是轴对称图形，其对称轴为底边的垂直平分线；等腰三角形的两个底角相等，顶角平分底边所对的角；等腰三角形的三线合一，即底边上的高、中线和顶角的角平分线三线合一。
详细述
可以通过两边相等或两角相等来判定一个三角形为等腰三角形。
如果一个三角形的两边长度相等，则这个三角形是等腰三角形；如果一个三角形的两个角相等，则这个三角形是等腰三角形。
总结词：根据等腰三角形的判定定理，可以判断一个三角形是否为等腰三角形，从而解决一些几何问题。
总结词
详细描述
示例
分析
利用等腰三角形的面积公式，可以解决一些与面积有关的几何问题。
在解题过程中，利用等腰三角形的面积公式，可以计算出三角形的面积，从而进一步解决问题。
在等腰三角形ABC中，AB=AC，D为BC上一点，且CD=BD=2AD，求△ABC的面积与△ABD的面积之比。
等腰三角形在实际生活中有着广泛的应用，如建筑、工程、艺术等领域。等腰三角形的稳定性和美观性使得它在许多实际场景中成为优选的几何形状。
总结词
在建筑领域，等腰三角形可以用于设计美观的屋顶、塔尖等建筑元素，同时其稳定性也使得它在桥梁、高层建筑等工程结构中得到广泛应用。此外，在艺术领域，等腰三角形也常被用于设计图案、雕塑等艺术作品。
详细描述
总结词
等腰三角形是数学竞赛中常见的考点之一，常与其他几何图形结合，考察学生的综合解题能力和数学思维能力。
详细描述
在数学竞赛中，等腰三角形往往与勾股定理、全等三角形等知识点结合，形成难度较大的题目。解题时需要灵活运用等腰三角形的性质和相关定理，通过推理、计算和证明来找到解题思路。
等腰三角形的解题技巧
CATALOGUE
03
总结词

初中数学：等腰三角形测试题(含答案)

初中数学：等腰三角形测试题（含答案）时间40分钟总分100分一、选择题(每题5分)1、若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为（）A、75°或15°B、30°或60°C、75°D、30°【答案】A【解析】试题分析：分等腰三角形的顶角是锐角和钝角两种情况求解.解：当等腰三角形的顶角是锐角时,如图所示,∵BD=12 AB,∴∠A=30°,∴∠ABC=∠C=75°；当等腰三角形的顶角是钝角时,如图所示,∵BD=12 AB,∴∠BAD=30°,∴∠BAC=150°,∴∠ABC=∠C=15°.故应选A.考点：等腰三角形的性质.2、等腰三角形的底边为7cm,一边上的中线把其周长分为两部分的差为3cm,则腰长为（）Ａ．20cm Ｂ．10cm Ｃ．10cm或4cm Ｄ．4cm 【答案】C【解析】试题分析：解：等腰三角形底边上的中线把等腰三角形分成的两部分的长度相等,∴把等腰三角形的周长分成差为3cm的两部分的中线是腰上的中线,设等腰三角形的腰长是2xcm,则被分成的两部分的长度分别是3xcm和(7+x)cm,当3x-(7+x)=3时,解得：x=5,则2x=10,∴等腰三角形的腰长为5cm；当(7+x)-3x=3时,解得：x=2,则2x=4,∴等腰三角形的腰长是4cm或10cm.故应选C考点：等腰三角形的性质.3、如图,坐标平面内一点A（2,﹣1）,O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为（）A． 2 B． 3 C． 4 D． 5【答案】C【解析】试题分析：根据等腰三角形的定义分情况讨论.解：如下图所示,当OA为等腰三角形的底边时,点P是线段OA的垂直平分线与x轴的交点；当AP为等腰三角形的底边时,符合条件的点P有2个；当OP为等腰三角形的底边时,符合条件的点P有1个.符合条件的点共有4个.故应选C考点：等腰三角形的定义.4、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件：①OB=OC；②∠EBO=∠DCO；③∠BEO=∠CDO；④BE=CD．上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有（）A．2种B．3种C．4种D．6种【答案】C【解析】试题分析：利用等腰三角形的定义和判定定理进行判断.解：可以证明△ABC是等腰三角形的方法有：①②①③②④③④,所以共有4种,故应选C.考点：等腰三角形的判定5、下列说法中：（1）顶角相等,并且有一腰相等的两个等腰三角形全等；（2）底边相等,且周长相等的两个等腰三角形全等；（3）腰长相等,且有一角是50°的两个等腰三角形全等；（4）两条直角边对应相等的两个直角三角形全等；错误的有（）A．1个B． 2个C．3个D．4个【答案】A【解析】试题分析：根据等腰三角形的性质和全等三角形的判定定理进行判断.解：(1)顶角相等,并且有一腰相等的两个等腰三角形,根据SAS可证全等,故(1)正确；(2) 底边相等,且周长相等的两个等腰三角形,根据SSS可证全等,故(2)正确；(3)腰长相等,且有一角是50°的两个等腰三角形,50°角可能是等腰三角形的顶角也可能是等腰三角形的底角,所以这两个等腰三角形不一定全等,故(3)错误；(4) 两条直角边对应相等的两个直角三角形,根据SAS可证全等,故(4)正确.所以错误的有1个.故应选A.考点：1.等腰三角形的性质；2.全等三角形的判定6、已知：如图,下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是（）A．①③④B．①②③④C．①②④D．①③【答案】A【解析】试题分析：根据三角形各内角的度数进行划分.解：如下图所示,所以①③④都可以.故应选A.考点：等腰三角形的判定二、填空题(每题6分)7、若一个等腰三角形的周长是20cm,一边长是5cm,则另两边的长是__________。

初中数学等腰三角形和垂直平分线

等腰三角形和垂直平分线模块一等腰三角形1．等腰三角形等腰三角形解释定义有两条边相等的三角形叫做等腰三角形，其中相等的边的叫做腰，另外一条边叫做底边．性质（1）两腰相等、两底角相等．（2）“三线合一”，即顶角平分线、底边上的中线、底边上的高重合．（3）是轴对称图形，底边的垂直平分线是它的对称轴．判定（1）有两条边相等的三角形是等腰三角形．（2）有两个角相等的三角形是等腰三角形．2．等边三角形和等腰直角三角形等边三角形等腰直角三角形1．定义：三条边都相等的三角形叫做等边三角形，也叫正三角形．2．性质：三边都相等，三角都是60︒．3．判定：（1）三条边都相等的三角形是等边三角形．（2）三个角都相等的三角形是等边三角形．（3）有一个角是60︒的等腰三角形是等边三角形．1．定义：有两条边相等，并且中间的夹角是90︒的三角形叫做等腰直角三角形．2．性质：两个底角为45︒．3．判定：有一个角是90︒的等腰三角形是等腰直角三角形．模块二垂直平分线垂直平分线解释示例定义经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也称之为中垂线．如图，若AC BC=，AB CD⊥，则直线DE就是线段AB的垂直平分线．性质线段垂直平分线上的点到这条线段两个端点的距离相等．如图，已知直线DE是线段AB的垂直平分线，则DA DB=．A BDCEADCEB判定到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．如图，若DA DB=，则点D在线段AB的垂直平分线上．（1）（2015—2016年七育周练）等腰三角形的一边长为10，另一边长为4，则这个等腰三角形的周长是__________．（2）等腰三角形的一边长为6cm，且周长为16cm，则这个三角形的底边为_________．（3）等腰三角形两内角的度数之比为1:4，则该三角形底角的度数为__________．（4）等腰三角形一个角为30︒，则这个三角形腰上的高与底边所夹角的度数为_____．（5）等腰三角形一腰上的中线将三角形的的周长分为两部分，分别是12与15，则腰长为__________．【解析】（1）24；（2）4cm或6cm；（3）30︒或80︒；（4）30︒或15︒；（5）①12315a ba+=⎧⎨=⎩；=57ab⎧⎨=⎩，腰长为10；②31215aa b=⎧⎨+=⎩；=411ab⎧⎨=⎩，腰长为8．【教师备课提示】这道题主要考查等腰三角形的定义，腰或底角不确定．（1）等腰三角形一腰上的高与另一腰的夹角为45︒，则这个等腰三角形的顶角为______．（2）已知BD是等腰ABC△一腰上的高，且50ABD∠=︒，则ABC△的底角为_______．【解析】（1）45︒或135︒（提示：等腰三角形可能是锐角三角形或钝角三角形）；（2）20︒或40︒或70︒；EDC BA2abaaaab2a模块一等腰三角形例题1例题2若ABC △为钝角三角形时，A ∠为顶角时，三内角大小为140︒，20︒，20︒；若ABC △为钝角三角形时，A ∠为底角时，三内角大小为100︒，40︒，40︒；若ABC △为锐角三角形时，A ∠为顶角，三内角大小为40︒，70︒，70︒．【教师备课提示】这道题主要考查分类讨论，锐角等腰和钝角等腰．（1）如图3-1，在第1个1ABA △中，20B ∠=︒，1AB A B =，在1A B 上取一点C ，延长1AA 到2A ，使得在第2个12A CA △中，121A A AC =；在2A C 上取一点D ，延长12A A 到3A ，使得在第3个23A DA △中，232A A A D =；……，按此做法进行下去，第n 个三角形中以n A 为顶点的内角的度数为_____________．（2）如图3-2的钢架中，焊上13根钢条来加固钢架．若1223131414AP PP P P P P P A =====，则C 的度数是___________．图3-1 图3-2【解析】（1）1602n︒；（2）12︒．【教师备课提示】这道题主要考查等腰三角形的性质结合外角倒角找规律．（1）如图4-1，ABC △中，AB AC =，点D 、E 、F 分别在BC 、AB 、AC 上，且BD CF =，BE CD =，G 是EF 的中点，求证：DG EF ⊥.（2）（14—15年嘉祥期末）如图4-2，在ABC △中，AB AC =，90BAC ∠=︒，点M 、N 分别在边AB 、AC 上，BM AN =，点D 是BC 的中点，连接AD ． ①求证：AD BD =；②求证：DM DN =，且DM DN ⊥．图4-1 图4-2A n A 4A 3A 2A 1EDCB AP 14P 13P 12P 11P 10P 9P 8P 7P 6P 5P 4P 3P 2P 1A例题3例题4A MBCNA B E GFD C【解析】（1）连接ED、DF，AB AC=，B C∴∠=∠，在EDB△和DFC△中BD CFB CBE CD=⎧⎪∠=∠⎨⎪=⎩(SAS)EDB DFC∴△△≌，DE DF∴=，G是EF的中点，∴DG EF⊥．（2）①AB AC=，90BAC∠=︒，45B C∴∠=∠=︒点D是BC的中点，1452BAD BAC∴∠=∠=︒，AD BD∴=，②由①知45DAN∠=︒在ADN△和BDM△中AN BMDAN DBMAD BD=⎧⎪∠=∠⎨⎪=⎩(SAS)ADN BDM∴△△≌，DM DN∴=，MDB NDA∠=∠，90ADB∠=︒，DM DN∴⊥．【教师备课提示】这两道小题主要考查等腰三角形三线合一的性质结合全等．（1）如图，ABC△中，AD是BC边上的中线，又是BC边上的高，求证：ABC△是等腰三角形．（2）如图，ABC△中，AD是BAC∠的角平分线，AD是BC边上的高，求证：ABC△是等腰三角形．（3）如图，ABC△中，AD是BAC∠的角平分线，AD是BC边上的中线，求证：ABC△是等腰三角形．【解析】（1）AD为BC中垂线，所以AB AC=，所以ABC△是等腰三角形（2）ABD△和ACD△中，D CBAFEDCBA 例题5ABEG FD C∴ABD ACD △≌△，∴AB AC =， ∴ABC △是等腰三角形（3）过点D 作DF AC ⊥于点F ，作DE AB ⊥于点E ，∵AD 是BAC ∠的角平分线，DF AC ⊥，DE AB ⊥，∴DE DF =， ∵AD 为中线，∴ADB ADC S S =△△，∵，，∴，∴ABC △是等腰三角形．【教师备课提示】这道题主要考查三线合一的性质倒过来推等腰三角形．（1）如图6-1，P 为等腰三角形ABC 的底边AB 上的任意一点，PE AC ⊥于点E ，PF ⊥BC 于点F ，AD BC ⊥于点D ，求证：PE PF AD +=．（2）如图6-2，如果P 为等腰三角形ABC 的底边BA 延长线上的任意一点，其余条件保持不变，（1）中的结论还成立吗？若成立，请说明理由；不成立，请求出PE ，PF 和AD 三边满足的关系．（3）如果P 为等腰三角形ABC 的底边AB 延长线上的任意一点，请直接写出PE ，PF 和AD 三边满足的关系．（4）如图6-3，如果ABC △是等边三角形，点P 为三角形ABC 内任意一点，PE AC ⊥于点E ，PF BC ⊥于点F ，PG AB ⊥于点G ，AD ⊥BC 于点D ．PE 、PF 、PG 、AD 之间存在怎样的数量关系，并说明理由．图6-1 图6-2 图6-3【解析】（1）连接CP ．∵APC BPC ABC S S S ∆∆∆+=，即111222AC EP BC PF BC AD ⋅+⋅=⋅，而AC BC =，∴PE PF AD +=；（2）连接CP ，由CPB CPA CAB S S S ∆∆∆-=，=90BAD CAD AD ADADB ADC ∠=∠⎧⎪=⎨⎪∠=∠︒⎩12ADB S AB DE =⋅⋅△12ADC S AC DF =⋅⋅△AB AC =AB CE D PF ABCEDP F AB CDEG PF 例题6得：111222BC PF AC PE BC AD⋅-⋅=⋅又∵AC BC=，∴PF PE AD-=；（3）PE PF AD-=；（4）连接CP、AP、BP，∴APC PBC APB ABCS S S S∆∆∆∆++=，∴11112222AC EP BC PF AB PG BC AD⋅+⋅+⋅=⋅，而AC BC AB==，∴EP FP GP AD++=．【教师备课提示】这道题主要考查等腰三角形的一个常见题型，面积法．（1）如图7-1，AB AC=，54A∠=︒，DE垂直平分AB交AC于E，垂足为D，ABC△周长为28cm，8cmBC=，则BCE△的周长为__________，EBC∠=__________．（2）如图7-2，ABC△的两边AB和AC的垂直平分线分别交BC于点D、E，若150BAC DAE∠+∠=︒，则BAC∠的度数为___________．图7-1 图7-2【解析】（1）18cm，9︒；（2）110︒．【教师备课提示】这道题主要考查垂直平分线的性质．A BCEDPFA BCEDPFA BCDEGPFCBEDAHFEDCBA模块二垂直平分线例题7（1）如图8-1，已知：在ABC △中，22.5B ∠=︒，边AB 的垂直平分线交BC 于D ，DF AC ⊥于F ，交BC 边上的高于G ．求证：EG EC =．（2）如图8-2，ABC △中，AB AC =，54BAC ∠=︒，BAC ∠的平分线与AB 的垂直平分线交于点O ，将C ∠沿EFCE 在BC 上，F 在AC 上折叠，点C 与点O 恰好重合，则OEC∠为____________．【解析】（1）连接AD ，∵D 为AB 的垂直平分线上一点，∴DA DB =，22.5B ∠=︒，∴22.5BAD B ∠=∠=︒， ∴45ADE ∠=︒，AE BC ⊥，∴45DAE ADE ∠=∠=︒， ∴AE DE =，DF AC ⊥，90FDC C ∴∠+∠=︒，又∵90EAC C ∠+∠=︒，∴EAC EDG ∠=∠，在EDG △和EAC △中 EAC EDG ED EAAEC DEG ∠=∠⎧⎪=⎨⎪∠=∠⎩(ASA)EDG EAC ∴△≌△，∴EG EC =．（2）如图，连接OB 、OC ， ∵54BAC ∠=︒，AO 为BAC ∠的平分线，∴11542722BAO BAC ∠=∠=⨯︒=︒，又∵AB AC =，∴11(180)(18054)6322ABC BAC ∠=︒-∠=︒-︒=︒,∵DO 是AB 的垂直平分线，∴OA OB =，∴27ABO BAO ∠=∠=︒， ∴632736OBC ABC ABO ∠=∠-∠=︒-︒=︒，∵DO 是AB 的垂直平分线，AO 为BAC ∠的平分线，∴点O 是ABC △的外心，∴OB OC =，∴36OCB OBC ∠=∠=︒，∵将C ∠沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，∴OE CE =，∴36COE OCB ∠=∠=︒，在OCE △中，1801803636108OEC COE OCB ∠=︒-∠-∠=︒-︒-︒=︒．GF EDCBA例题8 ABCDEF G BA OF CEB A O FC E证明：三角形三边的垂直平分线交于一点．【解析】如图，在ABC△中，设AB、AC的垂直平分线相交于点O，连接OA、OB、OC，由垂直平分线的性质可知：OA OB=，OA OC=，∴OB OC=，∴点O在BC的垂直平分线上，∴三角形三边的垂直平分线交于一点．（1）已知一个等腰三角形的两条边分别为3cm和4cm，则这个三角形的周长为______．（2）等腰三角形的一个外角为100︒，则顶角为__________．（3）等腰三角形一腰上的中线将它们的周长分为6和12两部分，则腰长为________．（4）等腰三角形一腰上的高与另一腰的夹角为40︒，则这个等腰三角形的底角为______．【解析】（1）10cm或11cm；（2）20︒或80︒；（3）8；（4）65︒或25︒．（1）（武侯区期末）如图，在下列三角形中，若AB AC=，则能被一条直线分成两个小等腰三角形的有（）A．1个B．2个C．3个D．4个AB C①AB C②③④364590108AB CAB C例题9复习巩固模块一等腰三角形演练1演练2OCBA（2）如图，AOB ∠是一个钢架，且10AOB ∠=︒，为了使钢架更加牢固，需要在内部添加一些钢管EF 、FG 、GH 、HI ，且有OE EF FG GH HI ====，则IHB ∠=__________．（3）如图，AD 是等边三角形ABC 的中线，AE AD =，则EDC ∠=（）度． A ．30 B ．20 C ．25 D ．15【解析】（1）C ；（2）50︒；（3）D ．【解析】【解析】如图，在ABC △中，AB AC =，点D 、E 、F 分别在AB 、BC 、AC 边上，且BE CF =，BD CE =．（1）求证：DEF △是等腰三角形；（2）当40A ∠=︒时，求DEF ∠的度数．【解析】（1）AB AC =，B C ∴∠=∠，在EDB △和FEC △中： BE CF B C BD CE =⎧⎪∠=∠⎨⎪=⎩ (SAS)EDB FEC ∴△△≌，DE EF ∴=，DEF ∴△是等腰三角形．（2）40A ∠=︒，70B C ∴∠=∠=︒，110EFC FEC ∴∠+∠=︒，由（1）知EFC DEB ∠=∠，110DEB FEC ∴∠+∠=︒，70DEF ∴∠=︒．（1）如图4-1：已知等边ABC △中，D 是AC 的中点，E 是BC 延长线上的一点，且CE CD =，DM BC ⊥，垂足为M ，求证：M 是BE 的中点．（2）如图4-2，等边三角形ABC 中，E ，D 分别在AC ，BC 上，且AE DC =，求AD 与BE 所夹锐角的度数．图4-1 图4-2【解析】（1）连接BD ，演练3演练4PDA B C EO EF H B AGIA BCD EA BCEFDB A M E D∵ABC△为等边三角形，D为AC中点，∴1302DBC ABC∠=∠=︒，∵CD CE=，∴CDE E∠=∠，又∵等边ABC△中60ACB∠=︒，∴160302E∠=⨯︒=︒,∴CBD E∠=∠，∴BD ED=，又∵DM BE⊥，∴M为BE中点．（2）60︒．（1）（15年育才期末）如图5-1，在ABC△中，AB边上的中垂线DE分别交AB、BC于点E、D，连接AD，若ADC△的周长为7cm，2cmAC=，则BC的长为（）．A．4cm B．5cm C．3cm D．以上答案都不对（2）（15年嘉祥半期）如图5-2，50ABC∠=︒，AD垂直平分线段BC于点D，ABC∠的平分线BE交AD于点E，连接EC，则AEC∠的度数是______________．图5-1 图5-2【解析】（1）B；（2）115︒．如图，在ABC△中，D为BC中点，DE BC⊥交BAC∠的平分线于点E，EF AB⊥于F，EG AC⊥的延长线于G．求证：BF CG=．模块二垂直平分线演练5演练6BAM C EDAEB D CAB CDEABFD CGEABFD CGE笔记区【解析】连接BE 、CE ．DE 垂直平分BC ，BE CE ∴=， AE 平分BAC ∠，EF AB ⊥，EG AC ⊥， EF EG ∴=，又90BFE CGE ∠=∠=︒， Rt Rt (HL)BEF CEG ∴△≌△， BF CG ∴=．。

八年级数学竞赛等腰三角形的判定

等腰三角形的判定阅读与思考在学习了等腰三角形性质与判定后，我们可以对等腰三角形的判定、证明线段相等的方法作出归纳总结．1．等腰三角形的判定：⑴从定义入手，证明一个三角形的两条边相等； ⑵从角入手，证明一个三角形的两个角相等． 2．证明线段相等的方法：⑴当所证的两条线段位于两个三角形，通过全等三角形证明； ⑵当所证的两条线段位于同一个三角形，通过等角对等边证明； ⑶寻找某条线段，证明所证的两条线段都与它相等．善于发现、构造等腰三角形，进而利用等腰三角形的性质为解题服务，是解几何题的一个常用技巧．常见的构造方法有：平分线+平行线、平分线+垂线、中线+垂线．如图所示：例题与求解【例1】如图，在△ABC 中，AB =7，AC =11，点M 是BC 的中点，AD 是∠BAC 的平分线，MF ∥AD ，则CF 的长为____________．（全国初中数学竞赛试题）解题思路：角平分线+平行线易构造等腰三角形，解题的关键是利用条件“中点M ”．【例2】如图，在△ABC 中，∠B =2∠C ，则AC 与2AB 之间的关系是（） A ．AC ＞2AB B ．AC ＝2AB C ．AC ≤2AB D ．AC ＜2AB(山东省竞赛试题)解题思路：如何条件∠B =2∠C ，如何得到2AB ，这是解本题的关键．ABCABDM FC【例3】两个全等的含300，600角的三角板ADE 和三角板ABC ，如图所示放置，E 、A 、C 三点在一条直线上，连结BD ，取BD 中点M ，连结ME ，MC ，试判断△EMC 的形状，并说明理由．（山东省中考试题）解题思路：从△ADE ≌△BAC 出发，先确定△ADB 的形状，为判断△EMC 的形状奠定基础．【例4】如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE =AC ，延长BE 交AC 于F ，求证：AF =EF ．（天津市竞赛试题）解题思路：只需证明∠F AE =∠AEF ，利用中线倍长，构造全等三角形、等腰三角形．【例5】如图，在等腰△ABC 中，AB =AC ，∠A =200，在边AB 上取点D ，使AD =BC ，求∠BDC 度数．（“祖冲之杯”竞赛试题）解题思路：由条件知底角为300，这些角并不是特殊角，但它们的差却为600，600使我们联想到等边三角形，由此找到切入口．如图1，以BC 为边在△ABC 内作等边△BCO ；如图②，以AC 为边作等边△ACE ．BCA D图2B CA D图1O ABCMD EEA BDCFBCAD能力训练A 级1．已知△ABC 为等腰三角形，由顶点A 所引BC 边的高线恰等于BC 边长的一半，则 ∠BAC =__________．2．如图，在Rt △ABC 中，∠C =900，∠ABC =660，△ABC 以点C 为中点旋转到△A ′B ′C 的位置，顶点B 在斜边A ′B ′上，A ′C 与AB 相交于D ，则∠BDC =_________．3．如图，△ABC 是边长为6的等边三角形，DE ⊥BC 于E ，EF ⊥AC 于F ，FD ⊥AB 于D ，则AD =_______．（天津市竞赛试题）4．如图，一个六边形的六个内角都是1200，其连续四边的长依次是1cm ，9cm ，9cm ，5cm ，那么这个六边形的周长是____________cm ．（“祖冲之杯”邀请赛试题）5．如图，△ABC 中，AB =AC ，∠B =360，D 、E 是BC 上两点，使∠ADE =∠AED =2∠BAD ，则图中等腰三角形共有（）A ．3个B ．4个C ．5个D ．6个6．若△ABC 的三边长是a ，b ，c ，且满足44422a b c b c =+-，44422b ac a c =+-，44422c a b a b =+-，则△ABC （）A ．钝角三角形B ．直角三角形C ．等腰直角三角形D ．等边三角形（“希望杯”邀请赛试题）7．等腰三角形一腰上的高等于该三角形某一条边的长度的一半，则其顶角等于（）A ．300B ．300或1500C ．1200或1500D ．300或1200或1500（“希望杯”邀请赛试题）8．如图，已知Rt △ABC 中，∠C =900，∠A =300，在直线BC 或AC 上取一点P ，使得△P AB 是等腰三角形，则符合条件的P 点有（）A ．2个B ．4个C ．6个D ．8个（江苏省竞赛试题）ADBB ′A ′(第2题)AB CDEF (第3题)(第4题)9915第5题图第8题图第9题图9．如图在等腰Rt △ABC 中，∠ACB =900，D 为BC 中点，DE ⊥AB ，垂足为E ，过点B 作BF ∥AC 交DE 的延长线于点F ，连接CF 交AD 于G ．⑴ 求证：AD ⊥CF ；⑵ 连结AF ，度判断△ACF 的形状，并说明理由．10．如图，△ABC 中，AD ⊥BC 于D ，∠B =2∠C ，求证：AB +BD =CD ．（天津市竞赛试题）11．如图，已知△ABC 是等边三角形，E 是AC 延长线上一点，选择一点D ，使得△CDE 是等边三角形，如果M 是线段AD 的中点，N 是线段BE 的中点，求证：△CMN 是等边三角形．（江苏省竞赛试题）12．如图1，Rt △ABC 中，∠ACB =900，CD ⊥AB ，垂足为D ，AF 平分∠CAB ，交CD 于点E ，交CB 于点F ．B ACDBACD EBCABCADFG EENMBD⑴ 求证：CE =CF ；⑵ 将图1中的△ADE 沿AB 向右平移到△A ′D ′E 的位置，使点E ′落在BC 边上，其他条件不变，如图2所示，试猜想：BE ′与CF 有怎样的数量关系？请证明你的结论．（山西省中考试题）B 级1．如图，△ABC 中，AD 平分∠BAC ，AB +BD =AC ，则∠B ：∠C 的值=__________．2．如图，△ABC 的两边AB 、AC 的垂直平分线分别交BC 于D 、E ，若∠BAC +∠DAE =1500，则∠BAC 的度数是____________．3．在等边△ABC 所在平面内求一点P ，使△P AB 、△PBC 、△P AC 都是等腰三角形，具有这样性质的点P 有_________个．4．如图，在△ABC 中，∠ABC =600，∠ACB =450，AD 、CF 都是高，相交于P ，角平分线BE 分别交AD 、CF 于Q 、S ，则图中的等腰三角形的个数是（）A ．2B ．3C ．4D ．55．如图，在五边形ABCDE 中，∠A =∠B =1200，EA =AB =BC =12DC =12DE ，则∠D =（） A ．300B ．450C ．600D ．67.50（“希望杯”竞赛试题）6．如图，∠MAN =160，A 1点在AM 上，在AN 上取一点A 2，使A 2A 1=AA 1，再在AM 上取一点A 3，A BDFE C图1A B D FEC图2A ′E ′D ′ABC(第1题)(第2题)ABD E CA BD CEF PQS (第4题)A B CED第5题AA 1NMA 2A 3(第6题)使A3A2=A2A1，如此一直作下去，到不能再作为止，那么作出的最后一点是（）A．A5B．A6C．A7D．A87．若P为△ABC所在平面内一点，且∠APB=∠BPC=∠CP A=1200，则点P叫作△ABC的费尔马点，如图1．⑴若点P为锐角△ABC的费尔马点，且∠ABC=600，P A=3，PC=4，则PB的值为_____．⑵如图2，在锐角△ABC外侧作等边△ACB′，连结BB′．求证：BB′过△ABC的费尔马点P，且BB′=P A+PB+PC．（湖州市中考试题）8．如图，△ABC中，∠BAC=600，∠ACB=400，P、Q分别在BC、AC上，并且AP、BQ分别是∠BAC、∠ABC的角平分线，求证：BQ+AQ=AB+BP．（全国初中数学联赛试题）9．如图，在△ABC中，AD是∠BAC的平分线，M是BC的中点，过M作ME∥AD交BA延长线于E，交AC于F，求证：BE=CF=12(AB+AC)．（重庆市竞赛试题）ABQCAB PACBB′图1 图210．在等边△ABC 的边BC 上任取一点D ，作∠DAE =600，DE 交∠C 的外角平分线于E ，那么△ADE 是什么三角形？证明你的结论．（《学习报》公开赛试题）11．如图，在平面直角坐标系中，O 为坐标原点，直线l ：12y x m =-+与x 轴、y 轴的正半轴分别相交于点A 、B ，过点C (－4，－4)作平行于y 轴的直线交AB 于点D ，CD =10．⑴求直线l 的解析式；⑵求证：△ABC 是等腰直角三角形；⑶将直线l 沿y 轴负方向平移，当平移恰当的距离时，直线与x ，y 轴分别相交于点A ′、B ′，在直线CD 上存在点P ，使得△A ′B ′P 是等腰直角三角形，请直接写出所有符合条件的点P 的坐标．（宁波市江东区模拟题）12．如图1，在平面直角坐标系中，△AOB 为等腰直角三角形，A (4，4)．ABD MCFE⑴求B点坐标；⑵如图2，若C为x轴正半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=900，连接OD，求∠AOD度数；⑶如图3，过点A作y轴于E，F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH，过A作x轴垂线交EH于点M，连接FM，等式AM FMOF=1是否成立？若成立，请证明；若不成立，说明理由．图1 图2 图3。

八年级数学竞赛专题训练16 等腰三角形的性质(附答案)

八年级数学竞赛专题训练16 等腰三角形的性质阅读与思考等腰三角形是一类特殊三角形，具有特殊的性质，这些性质为角度的计算、线段相等、直线位置关系的证明等问题提供了新的理论依据．因此，在解与等腰三角形相关的问题时，除了要运用全等三角形知识方法外，又不能囿于全等三角形，应善于利用等腰三角形的性质探求新的解题途径，应熟悉以下基本图形、基本结论．⑴ 图1中，01802A B ∠=-∠，01802AB C -==∠∠∠，22DAC B C ==∠∠∠．⑵ 图2中，只要下述四个条件：①AB AC =；②12=∠∠；③CD DB =；④AD BC ⊥中任意两个成立，就可以推出其余两个成立．例题与求解【例1】如图，在△ABC 中，D 在AC 上，E 在AB 上，且AB =AC ，BC =BD ，AD =DE =BE ，则∠A =___________．（五城市联赛试题）解题思路：图中有很多相关的角，用∠A 的代数式表示这些角，建立关于∠A 的等式．【例2】如图，在△ABC 中，已知∠BAC =900，AB =AC ，D 为AC 中点，AE ⊥BD 于E ，延长AE 交BC 于F ，求证：∠ADB =∠CDF ．（安徽省竞赛试题）解题思路：∠ADB 与∠CDF 对应的三角形不全等，因此，需构造全等三角形，而在等腰三角形中，作顶角的平分线或底边上的高(中线)是一条常用的辅助线．BC AD 图1A BC1 2图2A BCD E A BCD EF【例3】如图，在△ABC 中，AC =BC ，∠ACB =900，D 是AC 上一点，且AE 垂直BD 的延长线于E ，又AE =12BD ，求证：BD 是∠ABC 的角平分线．（北京市竞赛试题）解题思路：∠ABC 的角平分线与AE 边上的高重合，故应作辅助线补全图形，构造全等三角形、等腰三角形．【例4】如图，在△ABC 中，∠BAC =∠BCA =440，M 为△ABC 内一点，使∠MCA =300，∠MAC =160，求∠BMC 度数．（北京市竞赛试题）解题思路：作等腰△ABC 的对称轴(如图1)，通过计算，证明全等三角形，又440+160=600；可以AB 为一边，向点C 所在的一侧作等边△ABN ，连结CN ，MN (如图2)；或以AC 为一边，向点B 所在的一侧作等边△ACN ，连结BN (如图3)．BCMAA EBCDB C M A 图 1 DO BC M A 图 2NBC MA 图 3 N【例5】如图，△ABC 是边长为1的等边三角形，△BDC 是顶角∠BDC =1200的等腰三角形，以D 为顶点作一个600角，角的两边分别交AB 于M ，交AC 于N ，连结MN ，形成一个三角形．求证：△AMN 的周长等于2．（天津市竞赛试题）解题思路：欲证△AMN 的周长等于2，只需证明MN =BM +CN ，考虑用补短法证明．【例6】如图，△ABC 中，∠ABC =460，D 是BC 边上一点，DC =AB ，∠DAB =210，试确定∠CAD 的度数．（北京市竞赛试题）解题思路：解本题的关键是利用DC =AB 这一条件．能力训练A 级1．如果等腰三角形一腰上的高另一腰的夹角为450，那么这个等腰三角形的底角为_____________． 2．如图，已知∠A =150，AB =BC =CD =DE =EF ，则∠FEM =_____________．3．如图，在等边△ABC 的AC ，BC 边上各取一点P 、Q ，使AP =CQ ，AQ ，BP 相交于点O ，则 ∠BOQ =____________.4．如图，在△ABC 中，∠BCA =900，∠BAC =600，BC =4，在CA 的延长线取点D ，使AD =AB ，则D ，B 两点之间的距离是____________．BD ABACDN M (第2题)ACEM NABC QPO(第3题)ABC D(第4题)5．如图，在△ABC 中，AB =AC ，D 为BC 上一点，BF =CD ，CE =BD ，那么∠EDF 等于（） A ．900-12∠A B ．900-∠AC ．1800-∠AD ．450-12∠A 6．如图，在△ABC 中，∠ACB =900，AC =AE ，BC =BF ，则∠ECF =（）A ．600B ．450C ．300D ．不确定（安徽省竞赛试题）B第5题图第6题图7．△ABC 的一个内角的大小是400，且∠A =∠B ，那么∠C 的外角的大小是（）A ．1400B ．800或1000C ．1000或1400D ．800或1400(“希望杯”邀请赛试题) 8．三角形三边长a ，b ，c 满足1111a b c a b c -+=-+，则三角形一定是（） A ．等边三角形 B ．以a 为底边的等腰三角形C ．以c 为底边的等腰三角形D ．等腰三角形（北京市竞赛试题）9．如图，在△ABC 中，AB =AC ，D ，E 分别是腰AB ，AC 延长线上的点，且BD =CE ，连结DE 交BC 于G ，求证：DG =EG ．（湖北省竞赛试题）ABC D GE ABEF10．如图，在△ABC 中，∠BAC =900，AB =AC ，BE 平分∠ABC ，CE ⊥BE ，求证：CE =12BD ．（江苏省竞赛试题）11．已知Rt △ABC 中，AC =BC ，∠C =900，D 为AB 边中点，∠EDF =900，将∠EDF 绕D 点旋转，它的两边分别交AC ，BC (或它们的延长线)于E 、F ，当∠EDF 绕D 点旋转到DE ⊥AC 于E 时(如图1)，易证：S △DEF +S △CEF =12S △ABC ，当∠EDF 绕D 点旋转到DE 和AC 不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，S △DEF ，S △CEF ，S △ABC 又有怎样的数量关系？请写出你的猜想，不需证明．（牡丹江市中考试题）12．如图，在△ABC 中，AB =AC ，∠BAC =800，O 为△ABC 内一点，且∠OBC =100，∠OCA =200，求∠BAO 的度数．（天津市竞赛试题）BA B CAB CAB CE D FE DF DF图1图2图3A B C D EB 级1．如图，在△ABC 中，∠ABC =1000，AM =AN ，CN =CP ，则∠MNP =_________．2．如图，在△ABC 中，AB =AC ，∠BAC =900，直角∠EPF 的顶点P 是BC 的中点，两边PE ，PF 分别交AB ，AC 于点E ，F ，给出以下4个结论：①AE =CF ；②△EPF 是等腰直角三角形；③S 四边形AEPF =12S △ABC；④EF =AP ．当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A ，B 重合)．上述结论正确的是____________．（苏州市中考试题）3．如图，在△ABC 中，AB =BC ，M ，N 为BC 边上两点，并且∠BAM =∠CAN ，MN =AN ，则∠MAC 的度数是____________．4．如图，在△ABC 中，AB =AC ，∠BAC 与∠ACB 的平分线相交于D ，∠ADC =1300，那么∠CAB 的大小是（）A ．800B ．500C ．400D ．2005．如图，在△ABC 中，∠BAC =1200，AD ⊥BC 于D ，且AB +BD =DC ，则∠C 的大小是（）A ．200B ．250C ．300D ．450 6．如图，在△ABC 中，AC =BC ，∠ACB =900，AE 平分∠BAC 交BC 于E ，BD ⊥AE 于D ，DM ⊥AC 交AC 的延长线于M ，连CD ，下列四个结论：①∠ADC =450；②BD =12AE ；③AC +CE =AB ；④AB -BC =2MC ．其中正确结论的个数为（）A ．1个B ．2个C ．3个D ．4个7．如图，已知△ABC 为等边三角形，延长BC 至D ，延长BA 至E ，并且使AE =BD ，连结CE 、DE ，求证：CE =DE ．ABCNP (第1题)ABC PEF(第2题)AB CN M(第3题)A(第4题)BCD(第5题)ABCD ABD ECM(第6题)A BCDE8．如图，△ABC 中，已知∠C =600，AC ＞BC ，又△ABC ′、△A ′BC 、△AB ′C 都是△ABC 外的等边三角形，而点D 在AC 上，且BC =DC ．⑴ 证明：△C ′BD ≌△B ′DC ； ⑵ 证明：△AC ′D ≌△DB ′A ；⑶ 对△ABC 、△ABC ′、△A ′BC 、△AB ′C ，从面积大小关系上，你能得出什么结论？（江苏省竞赛试题）9．在△ABC 中，已知AB =AC ，且过△ABC 某一顶点的直线可将△ABC 分成两个等腰三角形，试求△ABC 各内角的度数．（江苏省扬州中学测试题）10．如图，在△ABC 中，∠C =900，∠CAD =300，AC =BC =AD ，求证：CD =BD ．11．已知△ABC 中，∠B 为锐角，从顶点A 向边BC 或BC 的延长线引垂线交BC 于H 点，又从顶点C 向边AB 或AB 的延长线引垂线交AB 于K ，试问：当2BH BC ，2BKAB是整数时，△ABC 是怎样的三角形？并证明你的结论．（“智能杯”通讯赛试题）ABCDA ′B ′C ′AC D专题16 等腰三角形的性质例1 45°例2 提示：过点A作∠A的平分线BD交于G，先证明△ABG≌△ACF，再证明△AGD≌△CFFD例3 提示：延长BC，AE交于一点.、例4 提示：如图，作BD⊥AC于D，则∠OCD=∠OAD=30°，∴∠BA0=44°－30°=14°，∠MAO=∠OAC－∠MAC=14°，∴∠BAO=∠MAO，又∵∠AOD=∠COD=90°－30°=60°，∴∠AOB=∠AOM=120°，∴OB=OM.又∵AO=AO，∴△AOB≌△AOM又∵∠BOM=120°，∴∠OMB=30°，故∠BMC=180°－∠OMB=150°.例5 如图，在AC延长线上截取CM1=BM，由Rt△BDM≌Rt△CDM1，得MD=M1D，∠MDB= ∠M1DC.∴∠MDM1=120°－∠MDB+∠M1DC=120°，又∠MDN=60°，∴∠NDM1=60°，∵MD=MD1，∠MDN=∠NDM1=60°，DN=DN，∴△MDN≌△M1DN，得MN=NM1，故△AMN周长：AM+MN+AN=AM+AN+NM1=AM+AM1=AB+AC=2.例6 解法1 如图a，作△ABD关于AD的轴对称图形△ADC，则∠EAD=21°，AE=AB，∴DE=BD，又∠ADC=21°+46°=67°，故∠ADE=∠ADB=180°－67°=113°，∠CDE=113°－67°=56°，连CE，可证△CDE≌△ABD≌△AED，∠ODE=∠OED=46°，得OD=OE，又DC=AE，则AO=CO，∠OCA=∠OAC，∠COE=2∠ACO，∠COE=2×46°=92°=2∠ACO.从而∠ACO=46°=∠OAC，∴∠DAE+∠EAC=67°.解法2 如图b，过A点作AE∥BC.过D作DE∥AB，连接EC.∵∠EDC=∠ABC=46°，DE=AB=CD，∴∠DCE=∠CED=12×（180°－46°）=67° ∵∠ADC=∠ABC+∠BAD=46°+21°=67° ∴∠ADC=∠DCE ，，∴AD=EC. ∴梯形ADCE 为等腰梯形∴AC=DE （等腰梯形对角线相等），∴AB=AC=CD ，∴∠DAC=∠ADC=67°.A 级1. 67.5°或22.5° 2.75°3.60°4.85.A6.B7.B8.D 提示：由已知得(b －c)(a －b)(a+c)=0，故b=c 或a=b.9. 提示：过D 作DF ∥AC 交BC 于F ，证明△DFG ≌△ECG .10. 提示：延长CE 交BA 的延长线于F ，证明△BEC ≌△BEF ，再证明△AFC ≌△ADB. 11. 提示：图2成立，联系图1，可证明△ECD ≌△FBD ，12DEF CEF ECD CDF FBD CDF CDB ACB S S S S S S S S ∆∆∆∆∆∆∆∆+=+=+==图3不成立，此时12DEF CEF ABC S S S ∆∆∆-=12.作∠BAC 的角平分线与CO 的延长线交于D ，连BD ，则△ABD ≌△ACD ，则∠ABD=∠ACD=30°， ∠OBD=∠ABC －∠OBC －∠ABD=20°=∠ABD ， ∠DOB=∠OBC+∠OCB=40°=∠DAB ，从而△ABD ≌△OBD ，AB=OB ，即△ABO 为等腰三角形，得∠BAO=12（180°－40°）=70° B 级1.40°2.①②③ 提示：连AP.3. 60°提示：设∠CAN =∠BAM =α，∠MAN =β，则∠C =∠BAC =2α+β，∠AMN =β4. D5.A6.D7. 提示：延长BD 到F ，使DF =BC ，则△BEF 为等边三角形，再证明△BCE ≌△FDE8.⑴证明略；⑵由①得C ´D =AC =AB ´，由②得DB ´=BA =C ´A ，又AD =AD ，∴△AC ´D ≌△DB ´A ；⑶S △AB ´C ＞S △ABC ´＞S △ABC ＞S △A ´BC ，S △ABC + S △ABC ´= S △AC ´B + S △A ´BC 9.满足题意的图形有以下四种情形：10.提示：在△ACD 内以CD 为边作等边△ECD ，连AE ，则△ACE ≌△ADE .∴∠CAE =12∠CAD =15°，又∵∠DCB =90°-∠ACD =90°-75°=15°，∴∠CAE =∠BCD =∠ECA . 又∵AC =BC ，CE =CD ，∴△ACE ≌△BCD ，∴∠DBC =∠EAC =15°. ∴∠DCB =∠DBC ，∴DC =DB .ABE C图bABC F图c图dABC GABD C图a11.设2BHm BC =，2BK n AB =，因BH ＜BA ，BK ＜BC ，故mn ＜4，得11m n =⎧⎨=⎩；12m n =⎧⎨=⎩；13m n =⎧⎨=⎩；21m n =⎧⎨=⎩；31m n =⎧⎨=⎩ ①当m =n =1时，BH =12BC ，BK =12AB ，△ABC 是等边三角形.②当m =1，n =2时，BH =12BC ，BK =AB ，△ABC 是∠A 为直角的等腰直角三角形. ③当m =1，n =3时，BH =12BC ，BK =32AB ，△ABC 是∠A 为120°的等腰三角形. ④当m =2，n =1时，△ABC 是以∠C 为直角的等腰直角三角形. ⑤当m =3，n =1时，△ABC 是以∠C 为120°的等腰三角形.A CB ED。

初中数学竞赛几何中常用的24个必备定理

初中数学竞赛几何中常用的24个必备定理在初中数学竞赛中，几何部分是一个重要的考察内容。

在几何题中，经常会涉及到一些常用的定理，掌握这些定理不仅能够帮助我们解题，还能够提高我们的解题速度和准确性。

下面列举了初中数学竞赛中常用的24个必备定理，希望能够帮助大家在竞赛中取得更好的成绩。

1. 垂径定理：直径是直角，半径垂直于弦。

2. 圆心角定理：圆心角是弦对圆心的角，两倍弦对圆心的角等于弧度。

3. 等腰三角形底角定理：等腰三角形的底角相等。

4. 等腰三角形等腰定理：等腰三角形的底边相等。

5. 等边三角形定理：等边三角形的三边相等。

6. 同位角定理：同位角相等。

7. 同旁内角定理：同旁内角相等。

8. 同旁外角定理：同旁外角相等。

9. 余角定理：余角相等。

10. 三角形内角和定理：三角形的内角和等于180度。

11. 三角形外角和定理：三角形的外角和等于360度。

12. 三角形角平分定理：角平分线把角分成两个相等的角。

13. 同角的角平分定理：同角的角平分线相等。

14. 三角形角平分线定理：角平分线相等。

15. 等角三角形角平分线定理：等角三角形角平分线相等。

16. 三角形中线定理：三角形的中线平行于底边，且等于底边的一半。

17. 三角形角平分线定理：角平分线交角的角度相等。

18. 三角形角平分线定理：角平分线角度相等。

19. 三角形角平分线定理：角平分线角度相等。

20. 三角形角平分线定理：角平分线角度相等。

21. 三角形角平分线定理：角平分线角度相等。

22. 三角形角平分线定理：角平分线角度相等。

23. 三角形角平分线定理：角平分线角度相等。

24. 三角形角平分线定理：角平分线角度相等。

这些定理是初中数学竞赛中常用的定理，掌握这些定理可以帮助我们更好地理解和解题。

希望大家在备战初中数学竞赛的过程中，能够充分掌握这些定理，提高自己的数学水平，取得理想的成绩。

祝大家都能在数学竞赛中取得好成绩！。

初中数学：等腰三角形练习(含答案)

初中数学：等腰三角形练习（含答案）一、选择题1、等腰三角形一底角为50°,则顶角的度数为（）A、65B、70C、80D、40【答案】C【解析】试题分析：根据三角形的内角和定理求解.解：等腰三角形的顶角度数=180°-50°-50°=80°.故应选C考点：等腰三角形的性质2、如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC,∠ACB的角平分线,则图中等腰三角形共有（）A． 5个B． 6个C．7个D．8个【答案】D【解析】试题分析：根据等腰三角形两底角相等和∠A=36°,求出∠ABC和∠ACB的度数,再根据角平分线的定义求出∠ABD、∠CBD、∠ACE、∠BCE的度数,利用三角形外角定理求出∠BOE、∠COD的度数,根据等角对等边进行判断.解：如下图所示,∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°,∵BD平分∠ABC,CE平分∠ACB,∴∠ABD=∠C BD=∠ACE=∠BCE=∠A=36°,∴△ABD、△BCD、△ACE、△BCE、△OBC是等腰三角形；∴∠BEC=∠A+∠ACE=72°,∠BOE=∠BCE+∠CBD=72°,∴∠BEC=∠BOE,同理可得：∠CDO=∠COD,∴△BOE、△COD是等腰三角形；又△ABC是等腰三角形,∴共有8个等腰三角形.故应选D.考点：1.等腰三角形的性质；2.等腰三角形的判定3、下列条件中不能确定是等腰三角形的是（）A．三条边都相等的三角形B．一条中线把面积分成相等的两部分的三角形C．有一个锐角是45°的直角三角形D．一个外角的平分线平行于三角形一边的三角形【答案】D【解析】试题分析：根据等腰三角形的定义和等腰三角形的判定定理进行判断.解：A选项、三条边都相等的三角形是特殊的等腰三角形,故A选项正确；B选项、三角形任何一条边上的中线都能把三角形分成面积相等的两个三角形,故B选项错误；C选项、有一个锐角是45°的直角三角形的另一个锐角也是45°,根据等角对等边可得这是一个等腰三角形,故C选项正确；D选项、如果一个外角的平分线平行于三角形一边,利用平行线的性质可证三角形的两个角相等,根据等角对等边可证这是一个等腰三角形,故D选项正确.故应选B考点：等腰三角形的判定4、下列能断定△ABC为等腰三角形的是（）A．∠A=30°,∠B=60°B．∠A=50°,∠B=80°C． AB=AC=2,BC=4 D．AB=3,BC=7,周长为13【答案】B【解析】试题分析：根据等腰三角形的判定定理进行判断.解：A选项、若∠A=30°,∠B=60°,则∠C=90°,不能判定△ABC为等腰三角形；B选项、若∠A=50°,∠B=80°,则∠C=50°,根据等角对等边能判定△ABC为等腰三角形；C选项、若AB=AC=2,BC=4,因为2+2=4,所以不能构成三角形；D选项、若AB=3,BC=7,周长为13,则AC=3,因为3+3<7,所以不能构成三角形.故应选B.考点：等腰三角形的判定5、已知下列各组数据,可以构成等腰三角形的是（）A． 1,2,1 B．2,2,1 C． 1,3,1 D．2,2,5【答案】B【解析】试题分析：根据三角形三边的关系进行判断.解：A选项、因为1+1=2,所以不能构成三角形；B选项、因为2+1>2,能构成三角形,所以可以构成等腰三角形；C选项、因为1+1<3,所以不能构成三角形；D选项、因为2+2<5,所以不能构成三角形.故应选B.考点：三角形三边关系6、小明将两个全等且有一个角为60°的直角三角形拼成如图所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是（）Ａ．4 Ｂ．3 Ｃ．2 Ｄ．1【答案】B【解析】试题分析：根据直角三角形的性质求出各角的度数,根据等角对等边进行判断. 解：∵∠B=∠E=60°,∴∠A=∠D=30°,∴△MAD是等腰三角形；∵∠EMG-∠A+∠D=60°,∴△EGM是等腰三角形；同理可证△BHM是等腰三角形.∴共有三个等腰三角形.故应选B考点：1.直角三角形的性质；2.等腰三角形的判定二、填空题7、一个等腰三角形的两边分别为3cm和4cm,则它的周长为_________；【答案】10cm或11cm【解析】试题分析：根据三角形的周长公式分情况进行计算.解：当三角形三边分别是3cm、3cm、4cm时,三角形的周长是3+3+4=10cm；当三角形三边分别是3cm、4cm、4cm时,三角形的周长是3+4+4=11cm.故答案是10cm或11cm.考点：等腰三角形的性质8、在方格纸上有一个△ABC,它的顶点位置如图所示,则这个三角形是三角形.【答案】等腰【解析】试题分析：根据点A在BC的垂直平分线上,可证AB=AC,所以这个三角形是等腰三角形.解：∵点A在BC的垂直平分线上,∴AB=AC,∴△ABC是等腰三角形.故答案是等腰.考点：1.线段垂直平分线的性质；2.等腰三角形的定义9、如果一个三角形有两个角分别为80°,50°,则这个三角形是_________三角形．【答案】等腰【解析】试题分析：根据三角形内角和求出三角形的另一个内角,根据等角对等边进行判断.解：∵第三个角=180°-50°-80°=50°.∴这个三角形是等腰三角形.故答案是等腰.考点：等腰三角形的判定10、用若干根火柴（不折断）紧接着摆成一个等腰三角形,一边用了10根火柴,则至少还要用_________根火柴．【答案】11【解析】试题分析：根据用10根火柴组成的边是等腰三角形的底边和腰,分两种情况进行讨论.解：当用10根火柴组成的边是等腰三角形的底边时,则每个腰上至少用6根火柴棍,∴共需要12根火柴棍；当用10根火柴组成的边是等腰三角形的腰时,则另一个腰上需要用10根火柴棍,底边至少用1根火柴,∴共需要11根火柴棍.∴至少还要用11根火柴.故答案是11.考点：1.等腰三角形的定义；2.三角形三边关系11、如图,△ABC是等腰三角形,且AB=AC,BM,CM分别平分∠ABC,∠ACB,DE 经过点M,且DE∥BC,则图中有_________个等腰三角形．【答案】5【解析】试题分析：根据等腰三角形的性质可得∠ABC=∠ACB,根据平行线的性质可证∠ADE=∠AED,根据角平分线的性质可证∠DBM=∠MBC=∠DMB=∠EMC=∠ECM=∠BCM,根据等角对等边进行证明.解：∵△ABC是等腰三角形,∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠AED,∴△ADE是等腰三角形；∵BM平分∠ABC,∴∠DBM=∠CBM,∵BC∥DE,∴∠DMB=∠CBM,∴∠DBM=∠DMB,∴△DBM是等腰三角形,同理可得△EMC是等腰三角形；又∵∠ABC=∠ACB,∴∠MBC=∠MCB,∴△MBC是等腰三角形.∵△ABC是等腰三角形.∴共有5个等腰三角形.故答案是5.考点：1.等腰三角形的性质；2.等腰三角形的判定三、解答题12、已知：如图,OA平分∠BAC,∠1=∠2．求证：△ABC是等腰三角形．【答案】证明见解析【解析】试题分析：首先过点O作OE⊥AB于E,OF⊥AC于F,根据角平分线的性质可证OE=OF,根据HL可证Rt△OBE≌Rt△OCF,利用全等三角形的性质可证∠5=∠6,所以可证∠ABC=∠ACB,根据等角对等边可证结论成立.证明：如下图所示,过点O作OE⊥AB于E,OF⊥AC于F,∵AO平分∠BAC,∴OE=OF（角平分线上的点到角两边的距离相等）．∵∠1=∠2,∴OB=OC．∴Rt△OBE≌Rt△OCF（HL）．∴∠5=∠6．∴∠1+∠5=∠2+∠6．即∠ABC=∠ACB．∴AB=AC．∴△ABC是等腰三角形．考点：1.角平分线的性质；2.等腰三角形的判定定理；3.全等三角形的判定和性质13、如图,△ABC中,∠A=36°,AB=AC,CD平分∠ACB,试说明△BCD是等腰三角形．【答案】证明见解析【解析】试题分析：根据等腰三角形的性质求出∠B=∠ACB=72°,根据角平分线的定义可以求出∠ACD=∠A=36°,根据三角形外角的性质可以求出∠ADB=72°,再根据等角对等边可证结论成立.证明：∵∠A=36°,AB=AC,∴∠B=∠ACB=72°,∵CD平分∠ACB,∴∠ACD=∠A=36°,∴∠BDC=∠A+∠ACD,∴∠BDC=∠B=72°,∴△BCD是等腰三角形．考点：1.等腰三角形的性质；2.等腰三角形的判定14、如图,ABC△中,∠ABC、∠ACB的平分线交于点F,过点F作DE∥BC分别交AB、AC于D、E,已知△ADE的周长为20cm,且BC=12cm,求△ABC的周长【答案】32cm.【解析】试题分析：首先根据角平分线的性质可证∠DBF=∠FBC,根据平行线的性质可证∠DFB=∠DBF,所以可证BD=DF,同理可证EC=EF,所以可证AD+AE+DF+EF=20cm,再根据BC的长度求出△ABC的周长.解：∵∠ABC、∠ACB的平分线交于点F,∴∠DBF=∠FBC,又∵DE∥BC,∴∠DFB=∠FBC,∴∠DFB=∠DBF,∴BD=DF,同理EC=EF,∵△ADE的周长为20cm,∴AD+AE+DF+EF=20cm,∴AD+AE+BD+EC=AB+AC=20cm又∵BC=12cm,∴AB+AC+BC=32cm即△ABC的周长为32cm.考点：1.等腰三角形的判定；2.等腰三角形的性质。

八年级数学竞赛题：等腰三角形的判定

八年级数学竞赛题：等腰三角形的判定等腰三角形判定的基本方法有：从定义出发，证明一个三角形的两条边相等；从角入手，证明一个三角形的两个角相等．善于发现、构造等腰三角形，进而利用等腰三角形的性质为解题服务，是解几何题的一个常用技巧．常见的构造方法有：平分线+平行线、平分线+垂线、中线+垂线．如图所示：例1 如图，四边形ABDC中，△EDC是由△ABC绕顶点C旋转40°所得，顶点A恰好转到AB上一点E的位置，则∠l+∠2=______________度．例2 在平面直角坐标系中，O是坐标原点，已知A点的坐标为（1，1）．请你在坐标轴上找出点B，使△AOB为等腰三角形，则符合条件的点B共有（）．A．6个B．7个C．8个D．9个例3 如图，△ABC中，AD⊥BC于D，∠B=2∠C，求证：AB+BD=CD．例4 如图，△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC 于F，求证：AF=EF．例5 两个全等的含30°、60°角的三角板ADE和三角板ABC，如图所示放置，E、A、C 三点在一条直线上，连结BD，取BD的中点M，连结ME、MC，试判断△EMC的形状，并说明理由．1．如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是_____________cm．2．如图，在△ABC中，AD平分∠BAC，AB+BD=AC，∠B：∠C的值为_____________．3．在△ABC中，AB=AC，AB的垂直平分线与AC所在的直线相交所得的锐角为50°，则∠B等于_____________．4．如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别为∠ABC、∠ACB的角平分线，且相交于点F，则图中的等腰三角形有（）．A．6个B．7个C．8个D．9个5．如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，则∠ABC=（）．A．40°B．45°C．50°D．60°6．如图，在△ABC中，∠ACB=90°，∠A=20°，将△ABC绕点C按逆时针方向旋转到△A’B’C 的位置，B在A’ B’上，CA’交AB于D．则∠BDC的度数为（）．A．40°B．45°C．50°D．60°7．如图所示，在△ABC中，D、E分别是AC和AB上的一点，BD与CE交于点O，给出下列四个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD；④OB=OC．（1）上述四个条件中，哪两个条件可以判定△ABC是等腰三角形（用序号写出所有情形）；（2）选择（1）中的一种情形，证明△ABC是等腰三角形．8．如图，在四边形ABCD中，AB⊥BC，DC⊥BC,BC=AB+DC，取AD的中点P，连结PB，PC．判断△PBC的形状．9．如图，在凸五边形ABCDE中，∠B=∠E，∠C=∠D，BC=DE，M为CD的中点，求证：AM⊥CD．10．如图，在△ABC中，AB=7，AC=11，点M是BC的中点，AD是∠BAC的平分线，MF ∥AD，则FC的长为____________．11．如图，△ABC的两边AB、AC的垂直平分线分别交BC于D、E，若∠BAC+∠DAE=150°，则∠BAC的度数是_____________．12．一个等腰三角形的一条高等于腰长的一半，则这个等腰三角形的底角的度数是_________．13．如图，已知D为△ABC边BC的中点，DE⊥DF，则BE+CF（）．A．大于EF B．小于EF C．等于EF D．于EF的大小关系无法确定14．如图，已知Rt△ABC中，∠C=90°，∠A=30°，在直线BC或AC上取一点P，使得△P AB是等腰三角形，则符合条件的P点有（）．A．2个B．4个C．6个D．8个15．如图，在△ABC中，∠ABC=60°，∠ACB=45°，AD、CF都是高，相交于P，角平分线BE分别交AD、CF于Q、S，则图中的等腰三角形的个数是（）．A．2 B．3 C．4 D．516．如图，在△ABC中，AD为∠BAC的平分线，BP⊥AD于P，已知AB=5，BP=2，AC=9，试说明∠ABC=3∠ACB．17．如图，△ABC中，∠BAC=60°，∠ACB=40°，P、Q分别在BC、AC上，并且AP、BQ分别是∠BAC、∠ABC的角平分线，求证：BQ+AQ=AB+BP．18．如图，△ABC中，AD是∠BAC的平分线，M是BC的中点，过M作ME∥AD交BA延长线于E，交AC于F．求证：BE=CF=12（AB+AC）．19．如图是一个小巷的截面，把长度为a 米的梯子，下端放在C 点，向左靠在墙上的D 点，梯子倾斜角为45°，向右靠在离地面b 米的E 点，倾斜角为75°．（1）连结DE ，想一想，请回答△CDE 是什么三角形．（2）猜一猜，请选择小巷宽度AB 的正确答案是（）． ‘A ．2a b +米B ．2a b -米 C ．a 米 D ．b 米并用“全等三角形”等知识说明你选择的理由。

初中数学等腰三角形的性质教案优秀9篇

初中数学等腰三角形的性质教案优秀9篇初中数学等腰三角形的性质教案篇一教学重点：认识等腰三角形和等边三角形以及它们的特征教学目标：1、让学生在实际操作中认识等腰三角形和等边三角形，知道等腰三角形边和角的名称，知道等腰三角形两个底角相等，等边三角形3个内角相等。

2、让学生在探索图形特征以及相关结论的活动中，进一步发展空间观念，锻炼思维能力。

3、让学生在学习活动中，进一步产生对数学的好奇心，增强动手能力和创新意识。

教学准备：长方形、正方形纸，剪刀、尺等教学过程：一、复习：关于三角形，你有那些知识？1、按角分成三种角2、三个内角和是180度算第三个角的度数，如果是一般三角形，那就用180去减；如果是直角三角形，那就是90去减二、认识等腰三角形1、比较老师手边的两块三角板，他们有什么相同？（都是直角三角形）有什么不同？（其中有一块三角板的两条边相等，两个角相等；而另一块三角板的角和边都不相同。

）指出：像这种两条边相等的三角形，我们叫它等腰三角形2、折一折、剪一剪取一张长方形纸，对折；画出它的对角线，沿对角线剪开；展开观察：这样剪出来的三角形就是我们今天要认识的等腰三角形。

想一想：为什么要对折后再剪呢？（这样剪出来的两条边肯定是相等的。

）除了两条边是相等的，还有什么也是相等的？你是怎么知道的？初中数学等腰三角形的性质教案篇二教学目标1、掌握证明的基本步骤和书写格式。

2、经历“探索－发现－猜想－证明”的过程。

能够用综合法证明直角三角形的有关性质定理和等边三角形的判定定理。

教学重点等边三角形的。

判定定理和直角三角形的性质定理。

教学难点能够用综合法证明等边三角形的判定定理和直角三角形的性质定理。

教学方法教学后记教学内容及过程一、定理：一个角等于60°的等腰三角形是等边三角形1．引导学生回忆上节课的内容，让学生思考：等腰三角形满足什么条件时便成为等边三角形？让学生对普遍联系和相互转化有一个感性的认识。

2．肯定学生的回答，并让学生进一步思考：有一个角是60°的等腰三家形是等边三角形吗？组织学生交流自己的想法。

八年级数学竞赛专题训练17 等腰三角形的判定(附答案)

八年级数学竞赛专题训练17 等腰三角形的判定阅读与思考在学习了等腰三角形性质与判定后，我们可以对等腰三角形的判定、证明线段相等的方法作出归纳总结．1．等腰三角形的判定：⑴从定义入手，证明一个三角形的两条边相等； ⑵从角入手，证明一个三角形的两个角相等． 2．证明线段相等的方法：⑴当所证的两条线段位于两个三角形，通过全等三角形证明； ⑵当所证的两条线段位于同一个三角形，通过等角对等边证明； ⑶寻找某条线段，证明所证的两条线段都与它相等．善于发现、构造等腰三角形，进而利用等腰三角形的性质为解题服务，是解几何题的一个常用技巧．常见的构造方法有：平分线+平行线、平分线+垂线、中线+垂线．如图所示：例题与求解【例1】如图，在△ABC 中，AB =7，AC =11，点M 是BC 的中点，AD 是∠BAC 的平分线，MF ∥AD ，则CF 的长为____________．（全国初中数学竞赛试题）解题思路：角平分线+平行线易构造等腰三角形，解题的关键是利用条件“中点M ”．【例2】如图，在△ABC 中，∠B =2∠C ，则AC 与2AB 之间的关系是（） A ．AC ＞2AB B ．AC ＝2AB C ．AC ≤2AB D ．AC ＜2AB(山东省竞赛试题)解题思路：如何条件∠B =2∠C ，如何得到2AB ，这是解本题的关键．ABCABDM FC【例3】两个全等的含300，600角的三角板ADE 和三角板ABC ，如图所示放置，E 、A 、C 三点在一条直线上，连结BD ，取BD 中点M ，连结ME ，MC ，试判断△EMC 的形状，并说明理由．（山东省中考试题）解题思路：从△ADE ≌△BAC 出发，先确定△ADB 的形状，为判断△EMC 的形状奠定基础．【例4】如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE =AC ，延长BE 交AC 于F ，求证：AF =EF ．（天津市竞赛试题）解题思路：只需证明∠FAE =∠AEF ，利用中线倍长，构造全等三角形、等腰三角形．【例5】如图，在等腰△ABC 中，AB =AC ，∠A =200，在边AB 上取点D ，使AD =BC ，求∠BDC 度数．（“祖冲之杯”竞赛试题）解题思路：由条件知底角为300，这些角并不是特殊角，但它们的差却为600，600使我们联想到等边三角形，由此找到切入口．如图1，以BC 为边在△ABC 内作等边△BCO ；如图②，以AC 为边作等边△ACE ．BCA D图2B CA D图1O BCMD EEABDCF BCAD能力训练A 级1．已知△ABC 为等腰三角形，由顶点A 所引BC 边的高线恰等于BC 边长的一半，则 ∠BAC =__________．2．如图，在Rt △ABC 中，∠C =900，∠ABC =660，△ABC 以点C 为中点旋转到△A ′B ′C 的位置，顶点B 在斜边A ′B ′上，A ′C 与AB 相交于D ，则∠BDC =_________．3．如图，△ABC 是边长为6的等边三角形，DE ⊥BC 于E ，EF ⊥AC 于F ，FD ⊥AB 于D ，则AD =_______．（天津市竞赛试题）4．如图，一个六边形的六个内角都是1200，其连续四边的长依次是1cm ，9cm ，9cm ，5cm ，那么这个六边形的周长是____________cm ．（“祖冲之杯”邀请赛试题）5．如图，△ABC 中，AB =AC ，∠B =360，D 、E 是BC 上两点，使∠ADE =∠AED =2∠BAD ，则图中等腰三角形共有（）A ．3个B ．4个C ．5个D ．6个6．若△ABC 的三边长是a ，b ，c ，且满足44422a b c b c =+-，44422b ac a c =+-，44422c a b a b =+-，则△ABC （）A ．钝角三角形B ．直角三角形C ．等腰直角三角形D ．等边三角形（“希望杯”邀请赛试题）7．等腰三角形一腰上的高等于该三角形某一条边的长度的一半，则其顶角等于（） A ．300 B ．300或1500 C ．1200或1500 D ．300或1200或1500（“希望杯”邀请赛试题）8．如图，已知Rt △ABC 中，∠C =900，∠A =300，在直线BC 或AC 上取一点P ，使得△PAB 是等腰三角形，则符合条件的P 点有（）A ．2个B ．4个C ．6个D ．8个（江苏省竞赛试题）第5题图第8题图第9题图ACDB B ′A ′(第2题)AB CDEF (第3题)(第4题)9915BACBCABC ADFG E9．如图在等腰Rt △ABC 中，∠ACB =900，D 为BC 中点，DE ⊥AB ，垂足为E ，过点B 作BF ∥AC 交DE 的延长线于点F ，连接CF 交AD 于G ．⑴ 求证：AD ⊥CF ；⑵ 连结AF ，度判断△ACF 的形状，并说明理由．10．如图，△ABC 中，AD ⊥BC 于D ，∠B =2∠C ，求证：AB +BD =CD ．（天津市竞赛试题）11．如图，已知△ABC 是等边三角形，E 是AC 延长线上一点，选择一点D ，使得△CDE 是等边三角形，如果M 是线段AD 的中点，N 是线段BE 的中点，求证：△CMN 是等边三角形．（江苏省竞赛试题）12．如图1，Rt △ABC 中，∠ACB =900，CD ⊥AB ，垂足为D ，AF 平分∠CAB ，交CD 于点E ，交CB 于点F ．⑴ 求证：CE =CF ；⑵ 将图1中的△ADE 沿AB 向右平移到△A ′D ′E 的位置，使点E ′落在BC 边上，其他条件不变，如图2所示，试猜想：BE ′与CF 有怎样的数量关系？请证明你的结论．（山西省中考试题）B ACDA BDFE C图1A B DFE C图2A ′ E ′D ′ AENMBDB 级1．如图，△ABC 中，AD 平分∠BAC ，AB +BD =AC ，则∠B ：∠C 的值=__________．2．如图，△ABC 的两边AB 、AC 的垂直平分线分别交BC 于D 、E ，若∠BAC +∠DAE =1500，则∠BAC 的度数是____________．3．在等边△ABC 所在平面内求一点P ，使△PAB 、△PBC 、△PAC 都是等腰三角形，具有这样性质的点P 有_________个．4．如图，在△ABC 中，∠ABC =600，∠ACB =450，AD 、CF 都是高，相交于P ，角平分线BE 分别交AD 、CF 于Q 、S ，则图中的等腰三角形的个数是（）A ．2B ．3C ．4D ．55．如图，在五边形ABCDE 中，∠A =∠B =1200，EA =AB =BC =12DC =12DE ，则∠D =（）A ．300B ．450C ．600D ．67.50（“希望杯”竞赛试题）6．如图，∠MAN =160，A 1点在AM 上，在AN 上取一点A 2，使A 2A 1=AA 1，再在AM 上取一点A 3，使A 3A 2=A 2A 1，如此一直作下去，到不能再作为止，那么作出的最后一点是（）A ．A 5B ．A 6C ．A 7D ．A 87．若P 为△ABC 所在平面内一点，且∠APB =∠BPC =∠CPA =1200，则点P 叫作△ABC 的费尔马点，如图1．⑴若点P 为锐角△ABC 的费尔马点，且∠ABC =600，PA =3，PC =4，则PB 的值为_____．⑵如图2，在锐角△ABC 外侧作等边△ACB ′，连结BB ′．求证：BB ′过△ABC 的费尔马点P ，且BB ′=PA +PB +PC ．（湖州市中考试题）ABC D(第1题)(第2题)ABD E CABPACBB ′图1图2A BD CEF PQS (第4题)A B CED第5题AA 1NMA 2A 3(第6题)8．如图，△ABC 中，∠BAC =600，∠ACB =400，P 、Q 分别在BC 、AC 上，并且AP 、BQ 分别是∠BAC 、∠ABC 的角平分线，求证：BQ +AQ =AB +BP ．（全国初中数学联赛试题）9．如图，在△ABC 中，AD 是∠BAC 的平分线，M 是BC 的中点，过M 作ME ∥AD 交BA 延长线于E ，交AC 于F ，求证：BE =CF =12(AB +AC )．（重庆市竞赛试题）10．在等边△ABC 的边BC 上任取一点D ，作∠DAE =600，DE 交∠C 的外角平分线于E ，那么△ADE 是什么三角形？证明你的结论．（《学习报》公开赛试题）ABPQCABD MCFE11．如图，在平面直角坐标系中，O为坐标原点，直线l：12y x m=-+与x轴、y轴的正半轴分别相交于点A、B，过点C(－4，－4)作平行于y轴的直线交AB于点D，CD=10．⑴求直线l的解析式；⑵求证：△ABC是等腰直角三角形；⑶将直线l沿y轴负方向平移，当平移恰当的距离时，直线与x，y轴分别相交于点A′、B′，在直线CD上存在点P，使得△A′B′P是等腰直角三角形，请直接写出所有符合条件的点P的坐标．（宁波市江东区模拟题）12．如图1，在平面直角坐标系中，△AOB为等腰直角三角形，A(4，4)．⑴求B点坐标；⑵如图2，若C为x轴正半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=900，连接OD，求∠AOD度数；⑶如图3，过点A作y轴于E，F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH，过A作x轴垂线交EH于点M，连接FM，等式AM FMOF-=1是否成立？若成立，请证明；若不成立，说明理由．图1 图2 图3专题17 等腰三角形的判定例1 延长MF ，BA 交于E ，延长FM 至点P ，使MP =MF ，连BP ，则△BMP ≌△CMF ，∴BP =CF . ∵AD 平分∠BAC ，AD ∥FM ，∠BAD =∠DAC =∠MFC =∠AFE =∠E =∠P ，∴AE =AF ，BE =BP ，即AB +AE =AB +AF =AB +AC -CF =CF ，∴CF =12(AB +AC )= 12(7+11)=9.例2 D例3 提示：△EMC 为等腰直角三角形，连AM ，易证：△ADE ≌△BAC .∴AD =AB ，又∠DAB =90°.又∵M 为BD 中点，∴AM ⊥DB 且DM =BM =AM . 又∵∠MDE =∠MAC =105°，∴△EDM ≌△CAM . ∴EM =MC ，∠DME =∠AMC ， ∴∠DME +∠EMA =∠AMC +∠EMA =90°. ∴△EMC 为等腰直角三角形.例4延长AD 至G ，使DG =AD ，连接BG . 由△ADC ≌△GDB ，得AC =BG ，AC ∥BG . ∵BE =AC ，∴BE =BG ，得∠BED =∠BGD ， ∴∠F AE =∠BGD =∠BED =∠AEF ，故AF =EF .例5 提示：结合图1，给出解答过程.由图形的轴对称性知：△ABO ≌△ACO ，∴∠BAO =∠CAO =10°，∴∠ABO =∠ACO =20°，∴∠AOB =∠AOC =150°.又∵BO =BC =CO = AD ，∴△ACD ≌△CAO ，∴∠AOC =∠CDA =150°，故∠BDC =30°.A 级1.90°或75°或15°2.72°3.24.375.D6.D 提示：将三式相加7.D8.C9.⑴先证△ACD ≌△CBF ，∴∠CAD =∠BCF .又∵∠CAD +∠CDG =∠BCF +∠CDG =90°， ∴∠CGD =90°，∴AD ⊥CF . ⑵△ACF 为等腰三角形.10.提示：延长DB 至E ，使BE =AB ，连结AE ，证明∠E =∠C ，AC =AE . 11. 提示：证明△DCA ≌△ECB 、△DCM ≌△ECN ，∠NCM =60°. 12. ⑴提示：先证明∠CEF =∠CFE .⑵作EG ⊥AC 于G ，证明△CEG ≌△BE ´D ´，可得CE = BE ´，又CF =CE ，BE ´=CF .B 级1.2:12.110°3.104.D5.C 提示：在五边形内作等边三角形ABF ，则E 、F 、C 在一条直线上.6.B7. 提示：⑴ ⑵ 在BB ´上取点P ，使∠BPC =120°，再在PB ´上取点E 使PE =PC ，连结CE . 则由△PCE 为等边三角形，可得：PC =CE ，∠PCE =60°，∠CEB ´=120°∵△ACB ´为正三角形，∴可证：△ACP ≌△B ´CE . ∴∠APC =∠B ´EC =120°，P A =EB ´.ACGDEF∴∠APC =∠BPC =∠CP A =120°，∴P 为△ABC 的费马点. ∴BB ´过△ABC 的P ，且BB ´=EB ´+PB +PE =P A +PB +PC .8. 提示：延长AB 至M ，使BM =BP ，连结PM ，则AB +BP =AM ，可证明BQ =QC . ∴AQ +QB =AQ +QC =AC ，又由△AMP ≌△ACP 得AM =AC ，故AB +BP =AQ +BQ .9. 提示：延长FM 至P ，使PM =FM ，连结BP ，则△BMP ≌△CMF ，AE =AF ，BE =BP .10. 提示：当D 为BC 的端点，显见△AED 是等边三角形；当D 为BC 边的中点，取AC 的中点F ，连接DF ，易证△CDF 为等边三角形，又△ADF ≌△EDC ，故△ADE 为等边三角形．猜测：当D 为BC 上任意点时，△ADE 也为等边三角形． 11．（1）142y x =-+；（2）过点C 作CH ⊥y 轴于H ，证明△AOB ≌△BHC 即可；（3）符合条件的P 点共有5个，分别为()()()()84,12,4,,4,8,4,4,4,43⎛⎫-------- ⎪⎝⎭．12．提示：（1）B (8，0)；（2）如图a ，过A 作AS ⊥OB 于S ，过D 作DT ⊥x 轴于T ． ∵△OAB 为等腰直角三角形，∴OS =AS =BS ，再由△ASC ≌△CTD ，可得：AS =CT ，SC =TD ． ∴CT =AS =OS ，∴OT =CS =TD ． ∴∠TOD =45°，则∠AOD =90°；（3）等式成立，理由如下：如图b ，在AM 上截取AS =OF ，连ES ，可证△EAS ≌△EOF ，可得：ES =EF ，∠AES =∠OEF ∴∠SEF =∠AEO =90°，∴∠FEM =∠SEM =45°．又∵EM =EM ，∴△EFM ≌△ESM ，∴FM =SM ， ∴AM =AS +SM =OF +FM ，∴1AM FMOF-=．x图a图b。

全国初中数学优秀课一等奖教师说课稿：等腰三角形--说课稿

全国初中数学优秀课一等奖教师说课稿：等腰三角形–说课稿一. 教材分析等腰三角形是初中数学中的重要内容，是学生认识三角形的基础。

通过学习等腰三角形，学生可以掌握三角形的性质，培养观察、思考、归纳的能力。

人教版初中数学八年级上册第五章《三角形》的第二节《等腰三角形》是本节课的主要内容。

教材从生活实例引入等腰三角形的概念，接着引导学生通过观察、思考、归纳等腰三角形的性质，最后通过练习巩固所学知识。

二. 学情分析八年级的学生已经学习了三角形的基础知识，对图形的观察、思考、归纳能力有一定的提高。

但部分学生对抽象的数学概念理解仍有一定难度，需要通过具体的生活实例和动手操作来加深理解。

此外，学生的学习兴趣和积极性对课堂效果有很大影响，因此在教学过程中需要注重激发学生的兴趣。

三. 说教学目标根据新课程标准，本节课的教学目标为：1.知识与技能：理解等腰三角形的概念，掌握等腰三角形的性质，能够运用等腰三角形的性质解决实际问题。

2.过程与方法：通过观察、思考、归纳等腰三角形的性质，培养学生的观察能力、思考能力和归纳能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养学生的团队合作精神，使学生感受到数学与生活的紧密联系。

四. 说教学重难点1.教学重点：等腰三角形的性质及其应用。

2.教学难点：等腰三角形性质的推导和理解。

五. 说教学方法与手段本节课采用以下教学方法与手段：1.情境教学法：通过生活实例引入等腰三角形的概念，激发学生的学习兴趣。

2.启发式教学法：引导学生观察、思考、归纳等腰三角形的性质，培养学生的自主学习能力。

3.小组合作学习：分组讨论，共同完成等腰三角形性质的探究，培养学生的团队合作精神。

4.信息技术辅助教学：利用多媒体课件展示等腰三角形的性质，使抽象的知识具体化、形象化。

六. 说教学过程1.导入：以生活实例引入等腰三角形，让学生感受到等腰三角形在生活中的应用。

2.探究等腰三角形的性质：引导学生观察、思考、归纳等腰三角形的性质，分组讨论，共同完成探究。