初中数学九年级二次函数基础练习题
人教版(2024)数学九年级上册第二十二章 二次函数 单元测试(含答案)

第二十二章二次函数一、选择题1. 关于二次函数y=x2与y=−x2的图象,下列说法错误的是( )A.对称轴都是y轴B.顶点都是坐标原点C.与x轴都有且只有一个交点D.它们的开口方向相同2. 如图,关于抛物线y=(x−1)2−2,下列说法错误的是( )A.顶点坐标为(1,−2)B.对称轴是直线x=1C.开口方向向上D.当x>1时,y随x的增大而减小3. 将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )A.y=3(x+2)2+3B.y=3(x−2)2+3C.y=3(x+2)2−3D.y=3(x−2)2−34. 如图是二次函数y=−x2+2x+4的图象,使y≤4成立的x的取值范围是( )A . 0≤x ≤2B . x ≤0C . x ≥2D . x ≤0 或 x ≥25. 一抛物线的形状、开口方向与 y =12x 2−2x +3 相同,顶点为 (−2,1),则此抛物线的解析式为 A . y =12(x−2)2+1 B . y =12(x +2)2−1 C . y =12(x +2)2+1D . y =12(x +2)2−16. 心理学家发现:学生对概念的接受能力 y 与提出概念的时间 x (min) 之间是二次函数关系,当提出概念 13 min 时,学生对概念的接受能力最大,为 59.9;当提出概念 30 min 时,学生对概念的接受能力就剩下 31,则 y 与 x 满足的二次函数表达式为 ( )A .y =−(x−13)2+59.9B .y =−0.1x 2+2.6x +31C .y =0.1x 2−2.6x +76.8D .y =−0.1x 2+2.6x +437. 已知点 (−1,y 1),(−312,y 2),(12,y 3) 在函数 y =3x 2+6x +12 的图象上,则 y 1,y 2,y 3 的大小关系为 ( ) A . y 1>y 2>y 3B . y 2>y 1>y 3C . y 2>y 3>y 1D . y 3>y 1>y 28. 在某建筑物上从 10 m 高的窗口 A 用水管向外喷水,喷出的水流呈抛物线状,如图所示,如果抛物线的最高点 M 离墙 1 m ,离地面403 m ,则水流落在点 B 与墙的距离 OB 是 ( )A . 2 mB . 3 mC . 4 mD . 5 m9. 二次函数 y =ax 2+bx +c (a ≠0) 的大致图象如图所示,顶点坐标为 (−2,−9a ),下列结论:① 4a +2b +c >0;② 5a−b +c =0;③若方程a(x+5)(x−1)=−1有两个根x1和x2,且x1<x2,则−5<x1<x2<1;④若方程∣ax2+bx+c∣=1有四个根,则这四个根的和为−4.其中正确的结论有( )A.1个B.2个C.3个D.4个二、填空题10. 如果y=(m2−1)x m2−m是二次函数,则m=.11. 若x=1是方程2ax2+bx=3的根,当x=2时,函数y=ax2+bx的函数值为.12. 若抛物线y=x2−2x+m(m为常数)与x轴没有公共点,则实数m的取值范围为.13. 如图,抛物线y=ax2+bx与直线y=mx+n相交于点A(−3,−6),点B(1,−2),则关于x的不等式ax2+bx<mx+n的解集为.14. 如图,二次函数y=ax2+bx+3的图象经过点A(−1,0),B(3,0),那么一元二次方程ax2+bx=0的根是.15. 已知抛物线:y=ax2+bx+c(a<0)经过A(2,4),B(−1,1)两点,顶点坐标为(ℎ,k),则下列正确结论的序号是.①b>1;②c>2;③ℎ>1;④k≤1.216. 物体自由下落的高度 ℎ(单位:m )与下落时间 t (单位:s )之间的关系是 ℎ=4.9t 2,有一个物体从 44.1m 高的建筑物上自由下落,到达地面需要s .17. 如图,在平面直角坐标系中,抛物线 y =13x 2 经过平移得到抛物线 y =13x 2−2x ,其对称轴与两段抛物线所围成的阴影部分的面积为.三、解答题18. 已知二次函数 y =a (x−1)2+4 的图象经过点 (−1,0).(1) 求这个二次函数的解析式;(2) 判断这个二次函数的开口方向,对称轴和顶点坐标.19. 已知二次函数 y =x 2+4x +3.(1) 用配方法将二次函数的表达式化为 y =a (x−ℎ)2+k 的形式;(2) 在平面直角坐标系 xOy 中,画出这个二次函数的图象;(3) 根据(2)中的图象,写出一条该二次函数的性质.20. 如图,在平面直角坐标系xOy中,抛物线顶点为C(1,2),且与直线y=x交于点B(32,32);点P为抛物线上O,B两点之间一个动点(不与O,B两点重合),过P作PQ∥y轴交线段OB于点Q.(1) 求抛物线的解析式;(2) 当PQ的长度为最大值时,求点Q的坐标;(3) 点M为抛物线上O,B两点之间一个动点(不与O,B两点重合),点N为线段OB上一个动点;当四边形PQNM为平行四边形,且PN⊥OB时,请直接写出Q点坐标.21. 在平面直角坐标系xOy中,抛物线y=ax2−4ax+3a−2(a≠0)与x轴交于A,B两点(点A在点B左侧).(1) 当抛物线过原点时,求实数a的值;(2) ①求抛物线的对称轴;②求抛物线的顶点的纵坐标(用含a的代数式表示);(3) 当AB≤4时,求实数a的取值范围.22. 如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A,B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米.(1) 请建立适当的直角坐标系,求抛物线的函数解析式;(2) 为了安全美观,现需在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA,PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P?(无需证明)(3) 为了施工方便,现需计算出点O,P之间的距离,那么两根支柱用料最省时点O,P之间的距离是多少?(请写出求解过程)23. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1) 求y与x之间的函数表达式.(2) 当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少元?(3) 若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?24. 如图所示抛物线y=ax2+bx+c过点A(−1,0),点C(0,3),且OB=OC.(1) 求抛物线的解析式及其对称轴.(2) 点D,E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长最小值.(3) 点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.答案一、选择题1. D2. D3. A4. D5. C6. D7. C8. B9. B二、填空题10. 211. 612. m>113. x<−3或x>114. x1=−1,x2=315. ①②③16. 317. 9三、解答题18.(1) 把(−1,0)代入二次函数解析式得:4a+4=0,即a=−1,则函数解析式为y=−(x−1)2+4.(2) ∵a=−1<0,∴抛物线开口向下,顶点坐标为(1,4),对称轴为直线x=1.19.(1) y=x2+4x+3=x2+4x+22−22+3 =(x+2)2−1.(2) 略(3) 当x<−2时,y随x的增大而减小,当x>−2时,y随x的增大而增大.(答案不唯一)20.(1) ∵抛物线顶点为C(1,2),∴设抛物线的解析式为y=a(x−1)2+2(a≠0).∵点B(32,32)在抛物线上,∴32=a(32−1)2+2,∴a=−2,∴抛物线的解析式为y=−2(x−1)2+2,即y=−2x2+4x.(2) 设点P的坐标为(x,−2x2+4x)(0<x<32),则点Q的坐标为(x,x),∴PQ=−2x2+4x−x=−2x2+3x=−2(x−34)2+98,∵−2<0,∴当x=34时,PQ的长度取最大值,∴当PQ的长度为最大值时,点Q的坐标为(34,34).(3) (12,12)21.(1) ∵点O(0,0)在抛物线上,∴3a−2=0,a=23.(2) ①对称轴为直线x=2;②顶点的纵坐标为−a−2.(3) (i)当a>0时,依题意,{−a−2<0,3a−2≥0.解得a≥23.(ii)当a<0时,依题意,{−a−2>0,3a−2≤0,解得a<−2.综上,a<−2或a≥23.22.(1) 以点O为原点、射线OC为y轴的正半轴建立直角坐标系,设抛物线的函数解析式为y=ax2,由题意知点A的坐标为(4,8).∵点A在抛物线上,∴8=a×42,解得a=12,∴所求抛物线的函数解析式为:y=12x2.(2) 找法:延长AC,交建筑物造型所在抛物线于点D,则点A,D关于OC对称.连接BD交OC于点P,则点P即为所求.(3) 由题意知点B的横坐标为2,∵点B在抛物线上,∴点B的坐标为(2,2),又∵点A的坐标为(4,8),∴点D的坐标为(−4,8),设直线BD的函数解析式为y=kx+b,∴{2k+b=2,−4k+b=8,解得:k=−1,b=4.∴直线BD的函数解析式为y=−x+4,把x=0代入y=−x+4,得点P的坐标为(0,4),两根支柱用料最省时,点O,P之间的距离是4米.23.(1) y=300+30(60−x)=−30x+2100.(2) 设每星期的销售利润为W元,则W=(x−40)(−30x+2100)=−30(x−55)2+6750.所以当x=55时,W取最大值,为6750.所以每件售价定为55元时,每星期的销售利润最大,最大利润是6750元.(3) 由题意得(x−40)(−30x+2100)≥6480,解得52≤x≤58.当x=52时,销售量为300+30×8=540(件);当x=58时,销售量为300+30×2=360(件).所以若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装360件.24.(1) ∵OB=OC,∴点B(3,0),则抛物线的表达式为:y=a(x+1)(x−3)=a(x2−2x−3)=ax2−2ax−3a,故−3a=3,解得a=−1,故抛物线的表达式为:y=−x2+2x+3 ⋯⋯①,对称轴为:直线x=1.(2) ACDE的周长=AC+DE+CD+AE,其中AC=10,DE=1是常数,故CD+AE最小时,周长最小,取点C关于函数对称点Cʹ(2,3),则CD=CʹD,取点Aʹ(−1,1),则AʹD=AE,故:CD+AE=AʹD+DCʹ,则当Aʹ,D,Cʹ三点共线时,CD+AE=AʹD+DCʹ最小,周长也最小,四边形ACDE的周长的最小值=AC+DE+CD+AE=10+1+AʹD+DCʹ=10+1+AʹCʹ=10+1+13.(3) 如图,设直线CP交x轴于点E,直线CP把四边形CBPA的面积分为3:5两部分,又∵S△PCB:S△PCA=12EB×(y C−y P):12AE×(y C−y P)=BE:AE,则BE:AE=3:5或5:3,则AE=52或32,即:点E的坐标为(32,0)或(12,0),将点E,C的坐标代入一次函数表达式:y=kx+3,解得:k=−6或−2,故直线CP的表达式为:y=−2x+3或y=−6x+3 ⋯⋯②,联立①②并解得:x=4或8(不合题意已舍去),故点P的坐标为(4,−5)或(8,−45).。
(完整版)初三中考复习二次函数专题练习题含答案

二次函数专题练习题一、选择题1 抛物线y=x2+2x+3的对称轴是( )A.直线x=1 B.直线x=-1 C.直线x=-2 D.直线x=22.在平面直角坐标系中,将抛物线y=x2-x-6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则|m|的最小值为( )A.1 B.2 C.3 D.63.如图,在平面直角坐标系中,抛物线y=12x2经过平移得到抛物线y=12x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为( )A.2 B.4 C.8 D.164. 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )A.b2>4acB.ax2+bx+c≥-6C.若点(-2,m),(-5,n)在抛物线上,则m>nD.关于x的一元二次方程ax2+bx+c=-4的两根为-5和-15. 如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0;②2a+b>0;③b2-4ac>0;④ac>0.其中正确的是( )A.①② B.①④ C.②③ D.③④6. 如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )7. 如图,在正方形ABCD中,AB=8 cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以 1 cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )二、填空题8.若y=(2-m)xm2-3是二次函数,且开口向上,则m的值为.9.已知点A(x1,y1),B(x2,y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1____y2.(填或“=”)“>”“<”10.已知二次函数y=-2x2-4x+1,当-3≤x≤0时,它的最大值是____,最小值是____.11.一个足球被从地面向上踢出,它距地面的高度h(m)与足球被踢出后经过的时间t(s)之间具有函数关系h=at2+19.6t,已知足球被踢出后经过 4 s落地,则足球距地面的最大高度是____m.12. 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为.三、解答题13.如果抛物线y=ax2+bx+c过定点M(1,1),则称此抛物线为定点抛物线.(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式.小敏写出了一个答案:y=2x2+3x-4,请你写出一个不同于小敏的答案;(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c+1,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.14.用铝合金材料做一个形状如图①所示的矩形窗框,设窗框的一边为x m,窗户的透光面积为y m2,y与x的函数图象如图②所示.(1)观察图象,当x为何值时,窗户的透光面积最大?最大透光面积是多少?(2)要使窗户的透光面积不小于 1 m2,则窗框的一边长x应该在什么范围内取值?15. 某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数关系如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间的函数关系如图②所示.(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是____元,小张应得的工资总额是____元;此时,小李种植水果____亩,小李应得的报酬是____元;(2)当10<n≤30时,求z与n之间的函数关系式;(3)设农庄支付给小张和小李的总费用为W(元),当10<m≤30时,求W与m之间的函数关系式.16. 如图,抛物线y=-12x2+bx+c与x轴分别交于点A(-2,0),B(4,0),与y轴交于点C,顶点为点P.(1)求抛物线的解析式;(2)动点M,N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB,OC上向点B,C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H,当四边形OMHN为矩形时,求点H的坐标.答案:一、1. B2. B3. B4. C5. C6. A7. B二、8. -59. >10. 3 -511. 19.612. (1+2,2)或(1-2,2)三、13. 解:(1)答案不唯一,如y=x2-2x+2(2)∵定点抛物线的顶点坐标为(b,b2+c+1),且-1+2b+c+1=1,∴c=1-2b,∵顶点纵坐标c+b2+1=2-2b+b2=(b-1)2+1,∴当b=1时,c+b2+1最小,抛物线顶点纵坐标的值最小,此时c=-1,∴抛物线的解析式为y=-x2+2x14. 解:(1)由图象可知当x=1时,窗户的透光面积最大,最大透光面积是 1.5 m2(2)由题意可设二次函数解析式为y=a(x-1)2+1.5,将(0,0)代入可求a=-1.5,∴解析式为y=-1.5(x-1)2+1.5,令y=1,则-1.5(x-1)2+1.5=1,解得x1=1-33,x2=1+33,由图象可知,当1-33≤x≤1+33时,透光面积不小于 1 m215. (1) 140 2800 10 1500(2) z=120n+300(10<n≤30)(3)当10<m≤30时,y=-2m+180,∵m+n=30,又∵当0≤n<10时,z=150n;当10≤n<20时,z=120n+300,∴当10<m≤20时,10≤n<20,∴W=m(-2m+180)+120n+300=m(-2m+180)+120(30-m)+300=-2m2+60m+3900;当20<m≤30时,0≤n<10,∴W=m(-2m+180)+150n=m(-2m+180)+150(30-m)=-2m2+30m+4500,∴W=-2m2+60m+3900(10<m≤20)-2m2+30m+4500(20<m≤30)16. 解:(1)y=-12x2+x+4(2)根据题意可设ON=OM=t,则MH=-12t2+t+4,∵ON∥MH,∴当ON=MH时,四边形OMHN为矩形,即t=-12t2+t+4,解得t=22或t=-22(不合题意,舍去),把t=22代入y=-12t2+t+4得y=22,∴H(22,22)。
初三数学二次函数的练习题

初三数学二次函数的练习题1. 求解方程:2x² - 5x + 3 = 0解:首先,我们可以使用求根公式来求解二次方程:x = (-b ± √(b² - 4ac)) / (2a)根据给定方程,我们可以将其对应的a、b和c的值代入计算:a = 2b = -5c = 3将这些值代入求根公式:x = (-(-5) ± √((-5)² - 4(2)(3))) / (2(2))x = (5 ± √(25 - 24)) / 4x = (5 ± √1) / 4x₁ = (5 + 1) / 4 = 6 / 4 = 1.5x₂ = (5 - 1) / 4 = 4 / 4 = 1所以,方程2x² - 5x + 3 = 0的解为 x₁ = 1.5 和 x₂ = 1。
2. 求解方程:3x² + 7x - 2 = 0解:同样地,我们使用求根公式求解二次方程:a = 3b = 7c = -2将这些值代入求根公式:x = (-7 ± √(7² - 4(3)(-2))) / (2(3))x = (-7 ± √(49 + 24)) / 6x = (-7 ± √73) / 6这里的根数是无理数,所以我们保留根的精确形式:x₁ = (-7 + √73) / 6x₂ = (-7 - √73) / 6所以,方程3x² + 7x - 2 = 0的解为 x₁ = (-7 + √73) / 6 和 x₂ = (-7 -√73) / 6。
3. 求二次函数y = x² - 4x + 3的顶点坐标和对称轴方程。
解:二次函数的顶点坐标可以通过求x轴对称的线(x = -b / 2a)来找到,对称轴方程为x = -b / 2a。
对于给定的二次函数 y = x² - 4x + 3,我们可以计算出a、b和c的值:a = 1b = -4c = 3顶点坐标为(x, y),其中x = -b / 2a = -(-4) / (2*1) = 4 / 2 = 2。
九年级数学二次函数练习题

九年级数学二次函数练习题一、选择题1. 已知二次函数y = ax² + bx + c 的图象在 x 轴上有两个不同的零点,那么判断条件为:A. a > 0B. b > 0C. c > 0D. δ > 02. 已知二次函数y = 2x² + kx + 3 在 x 轴上只有一个零点,那么 k 的取值范围是:A. k ≤ 0B. k < 3C. 0 < k < 3D. k > 33. 根据二次函数y = ax² + bx + c 的图像,当 a > 0 且 b > 0 时,函数图像的开口方向和最小值分别是:A. 上,最小值存在B. 上,最小值不存在C. 下,最小值存在D. 下,最小值不存在4. 对于二次函数y = ax² + bx + c,当 a < 0 时,它的图像是关于x 轴的对称图形。
那么当 a > 0 时,它的图像是关于:A. y 轴的对称图形B. 原点的对称图形C. x 轴的对称图形D. 零点的对称图形5. 已知二次函数y = ax² - bx + c 的两个零点的和为 4,积为 -3,那么 a, b, c 的值分别为:A. 1, 7, 12B. 1, -3, 12C. 1, 3, 12D. 1, -7, 12二、填空题1. 已知二次函数y = ax² + bx + c 的图象在点(1, 2)上,且 a + b +c = 6,求函数的表达式。
2. 已知二次函数y = 2x² - 5x + 3,求函数的最小值。
3. 当二次函数y = ax² + bx + c 的图象过点(1, 3)时,若 a = 2, b= 1,求 c 的值。
4. 如果抛物线y = ax² + bx + c 的图象关于 y 轴对称,且 (1, 3) 在图象上,求 a, b, c 的值。
九年级二次函数基础分类练习题

1、 下列函数:① y =;②()21y x x x =-+;③()224y x x x =+-;④21y x x =+;⑤()1y x x =-,其中是二次函数的是 ,其中a = ,b = ,c =2、当m 时,函数()2235y m x x =-+-(m 为常数)是关于x 的二次函数3、当____m =时,函数()2221m m y m m x --=+是关于x 的二次函数4、当____m =时,函数()2564m m y m x-+=-+3x 是关于x 的二次函数5、若点 A ( 2, m ) 在函数 12-=x y 的图像上,则 A 点的坐标是____.6、在圆的面积公式 S =πr 2 中,s 与 r 的关系是( )A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系 7、如图,矩形的长是 4cm ,宽是 3cm ,如果将长和宽都增加 x cm ,那么面积增加 ycm 2,① 求 y 与 x 之间的函数关系式.② 求当边长增加多少时,面积增加 8cm 2.8、已知二次函数),0(2≠+=a c ax y 当x=1时,y= -1;当x=2时,y=2,求该函数解析式. 9、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料,建造猪舍三间,如图,它们的平面图是一排大小相等的长方形.(1) 如果设猪舍的宽AB 为x 米,则猪舍的总面积S 与x 有怎样的函数关系? (2) 请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如何安排猪舍的长BC和宽AB 的长度?旧墙的长度是否会对猪舍的长度有影响?怎样影响?函数2ax y =的图象与性质1、填空:(1)抛物线221x y =的对称轴是 (或 ),顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ; (2)抛物线221x y -=的对称轴是 (或 ),顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ;2、对于函数22x y =下列说法:①当x 取任何实数时,y 的值总是正的;②x 的值增大,y 的值也增大;③y 随x 的增大而减小;④图象关于y 轴对称.其中正确的是 .3、抛物线 y =-x 2 不具有的性质是( )A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点 4、苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足 S =12gt 2(g =9.8),则 s 与t 的函数图像大致是( )A B C D5、函数2ax y =与b ax y +-=的图象可能是( )A .B .C .D .6、已知函数24m m y mx --=的图象是开口向下的抛物线,求m 的值.7、二次函数12-=m mx y 在其图象对称轴的左侧,y 随x 的增大而增大,求m 的值.ttt8、二次函数223x y -=,当x 1>x 2>0时,求y 1与y 2的大小关系.9、已知函数()422-++=m mx m y 是关于x 的二次函数,求:(1) 满足条件的m 的值;(2) m 为何值时,抛物线有最低点?求出这个最低点,这时x 为何值时,y 随x 的增大而增大;(3) m 为何值时,抛物线有最大值?最大值是多少?当x 为何值时,y 随x 的增大而减小?10、如果抛物线2y ax =与直线1y x =-交于点(),2b ,求这条抛物线所对应的二次函数的关系式.二次函数基础分类练习题(练习三)函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小. 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标 、 .3、任给一些不同的实数k ,得到不同的抛物线k x y +=2,当k 取0,1±时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其中判断正确的是 .4、将抛物线122-=x y 向上平移4个单位后,所得的抛物线是 ,当x= 时,该抛物线有最 (填大或小)值,是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称,则m =________;6、二次函数c ax y +=2()0≠a 中,若当x 取x 1、x 2(x 1≠x 2)时,函数值相等,则当x 取x 1+x 2时,函数值等于 .二次函数基础分类练习题(练习四)函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ,顶点坐标是 ,当x 时,y 随x 的增大而减小, 函数有最 值 .2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标. (1)右移2个单位;(2)左移32个单位;(3)先左移1个单位,再右移4个单位. 3、请你写出函数()21+=x y 和12+=x y 具有的共同性质(至少2个).4、二次函数()2h x a y -=的图象如图:已知21=a ,OA=OC , 试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ,与y 轴交点为B ,求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ,当自变量x 由0增加到2时,函数值增加6.(1)求出此函数关系式.(2)说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上,求k 的值.。
九年级数学二次函数专题训练含答案解析-精选5份

九年级数学上册《二次函数》专题测试题(附答案)一.选择题(共8小题,满分32分)1.若y=(a+1)x|a+3|﹣x+3是关于x的二次函数,则a的值是()A.1B.﹣5C.﹣1D.﹣5或﹣12.下列关于二次函数y=﹣(x﹣m)2+m2+1(m为常数)的结论错误的是()A.当x>0时,y随x的增大而减小B.该函数的图象一定经过点(0,1)C.该函数图象的顶点在函数y=x2+1的图象上D.该函数图象与函数y=﹣x2的图象形状相同3.已知:抛物线的解析式为y=﹣3(x﹣2)2+1,则抛物线的对称轴是直线()A.x=﹣1B.x=1C.x=2D.x=﹣24.将二次函数y=2x2向左平移5个单位,再向上平移3个单位,所得新抛物线表达式为()A.y=2(x+5)2﹣3B.y=2(x+5)2+3C.y=2(x﹣5)2﹣3D.y=2(x﹣5)2+35.二次函数y=ax2+bx+c的图象如图所示,下列结论:(1)4ac<b2;(2)abc<0;(3)2a+b<0;(4)(a+c)2<b2其中正确的个数是()A.1B.2C.3D.46.已知抛物线y=ax2+4ax﹣8与直线y=n相交于A,B两点(点A在点B左侧),AB=4,且抛物线与x轴只有一个交点,则n的值为()A.﹣8B.﹣4C.4D.87.已知二次函数y=ax2+bx+c的图象经过(﹣3,0)与(1,0)两点,关于x的方程ax2+bx+c+m =0(m>0)有两个整数根,其中一个根是3,则另一个根是()A.﹣5B.﹣3C.﹣1D.38.物理课上我们学习了竖直上抛运动,若从地面竖直向上抛一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示,下列结论:①小球在空中经过的路程是40m②小球抛出3s后,速度越来越快③小球抛出3s时速度为0④小球的高度h=30m时,t=1.5s其中正确的是()A.①②③B.①②C.②③④D.②③二.填空题(共8小题,满分32分)9.已知抛物线y=x2+bx+c关于直线x=2对称,设x=1,2,4时对应的函数值依次为y1,y2,y4,那么y1,y2,y4的大小关系是.(用“<”连接)10.已知抛物线y=ax2﹣2ax﹣1(a<0)(I)抛物线的对称轴为;(2)若当﹣2≤x≤2时,y的最大值是1,求当﹣2≤x≤2时,y的最小值是.11.已知二次函数y=ax2﹣2ax+c(a≠0)的图象与x轴的一个交点为(﹣1,0),则关于x 的一元二次方程ax2﹣2ax+c=0的两根之积是.12.已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是.13.将抛物线y=﹣(x﹣3)2﹣1向右平移5个单位,再向上平移2个单位,所得的抛物线的解析式为.14.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣3,9),B(1,1),则方程ax2﹣bx﹣c=0的解是.15.抛物线y=ax2+bx+tc(a<0)交x轴于点A、B,交y轴于点C(0,3),其中点B坐标为(1,0),同时抛物线还经过点(2,﹣5).(1)抛物线的解析式为;(2)设抛物线的对称轴与抛物线交于点E,与x轴交于点H,连接EC、EO,将抛物线向下平移n(n>0)个单位,当EO平分∠CEH时,则n的值为.16.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y (个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额﹣总成本).三.解答题(共6小题,满分56分)17.已知二次函数y=x2+mx+m2﹣3(m为常数,m>0)的图象经过点P(2,4).(1)求m的值;(2)判断二次函数y=x2+mx+m2﹣3的图象与x轴交点的个数,并说明理由.18.对于向上抛的物体,如果空气阻力忽略不计,有下面的关系式:h=v0t﹣gt2(h是物体离起点的高度,v0是初速度,g是重力系数,取10m/s2,t是抛出后经过的时间).杂技演员抛球表演时,以10m/s的初速度把球向上抛出.(1)球抛出后经多少秒回到起点?(2)几秒后球离起点的高度达到1.8m?(3)球离起点的高度能达到6m吗?请说明理由.19.在平面直角坐标系中,已知二次函数y=ax2+(a﹣1)x﹣1.(1)若该函数的图象经过点(1,2),求该二次函数图象的顶点坐标.(2)若(x1,y1),(x1,y2)为此函数图象上两个不同点,当x1+x2=﹣2时,恒有y1=y2,试求此函数的最值.(3)当a<0且a≠﹣1时,判断该二次函数图象的顶点所在象限,并说明理由.20.某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.(1)求y与x的函数关系式(不要求写出自变量x的取值范围);(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?(3)设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?21.如图,抛物线y=﹣x2+bx+c过点A(4,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点D、N.(1)求直线AB的表达式和抛物线的表达式;(2)若DN=3DM,求此时点N的坐标;(3)若点P为直线AB上方的抛物线上一个动点,当∠ABP=2∠BAC时,求点P的坐标.22.如图,已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(3,﹣2),点C(0,﹣5),顶点为点M,过点A作AB∥x轴,交y轴于点D,交二次函数y=x2+bx+c的图象于点B,连接BC.(1)求该二次函数的表达式及点M的坐标;(2)若将该二次函数图象向上平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)若E为线段AB上一点,且BE:EA=3:1,P为直线AC上一点,在抛物线上是否存在一点Q,使以B、P、E、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的横坐标;若不存在,请说明理由.参考答案一.选择题(共8小题,满分32分)1.解:∵函数y=(a+1)x|a+3|﹣x+3是关于x的二次函数,∴|a+3|=2且a+1≠0,解得a=﹣5,故选:B.2.解:A.∵y=﹣(x﹣m)2+m2+1(m为常数),∴抛物线开口向下,对称轴为直线x=m,∴x>m时,y随x增大而减小,故A错误,符合题意;∵当x=0时,y=1,∴该函数的图象一定经过点(0,1),故B正确,不合题意;∵y=﹣(x﹣m)2+m2+1,∴抛物线顶点坐标为(m,m2+1),∴抛物线顶点在抛物线y=x2+1上,故C正确,不合题意;∵y=﹣(x﹣m)2+m2+1与y=﹣x2的二次项系数都为﹣1,∴两函数图象形状相同,故D正确,不合题意.故选:A.3.解:∵y=﹣3(x﹣2)2+1,∴抛物线对称轴为直线x=2.故选:C.4.解:将二次函数y=2x2向左平移5个单位,再向上平移3个单位,所得新抛物线表达式为y=2(x+5)2+3,故选:B.5.解:根据图象知道抛物线与x轴有两个交点,∴b2﹣4ac>0,即4ac<b2,故(1)正确.∵抛物线开口朝下,∴a<0,∵对称轴在y轴右侧,∴b>0,∵抛物线与y轴的交点在x轴的上方,∴c>0,∴abc<0,故(2)正确;∵对称轴x=﹣>1,∴2a+b>0,故(3)错误;根据图象知道当x=1时,y=a+b+c>0,根据图象知道当x=﹣1时,y=a﹣b+c<0,∴(a+c)2﹣b2=(a+c+b)(a+c﹣b)<0,故(4)正确;故选:C.6.解:∵抛物线与x轴只有一个交点,∴a≠0且Δ=16a2﹣4a×(﹣8)=0,∴a=﹣2,∴抛物线解析式为y=﹣2x2﹣8x﹣8,∵抛物线的对称轴为直线x=﹣=﹣2,而AB平行x轴,AB=4,∴A点的横坐标为﹣4,B点的横坐标为0,当x=0时,y=﹣8,∴n的值为﹣8.故选:A.7.解:∵二次函数y=ax2+bx+c的图象经过(﹣3,0)与(1,0)两点,∴函数y=ax2+bx+c的对称轴是直线x=﹣1,又∵关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是3.∴二次函数y=ax2+bx+c的图象与直线y=﹣m的一个交点的横坐标为3,∵对称轴是直线x=﹣1,∴二次函数y=ax2+bx+c的图象与直线y=﹣m的另一个交点的横坐标为﹣5,∴关于x的方程ax2+bx+c+m=0(m>0)的另一个根是﹣5,故选:A.8.解:①由图象知小球在空中达到的最大高度是40m;故①错误;②小球抛出3秒后,速度越来越快;故②正确;③小球抛出3秒时达到最高点即速度为0;故③正确;④设函数解析式为:h=a(t﹣3)2+40,把O(0,0)代入得0=a(0﹣3)2+40,解得,∴函数解析式为,把h=30代入解析式得,,解得:t=4.5或t=1.5,∴小球的高度h=30m时,t=1.5s或4.5s,故④错误;故选D.二.填空题(共8小题,满分32分)9.解:∵抛物线y=x2+bx+c的开口向上,对称轴是直线x=2,∴当x=2时取最小值,又|1﹣2|<|4﹣2|,∴y1<y4,故答案为:y2<y1<y4.10.解:(1)抛物线的对称轴为:直线x=﹣=1,故答案为:直线x=1;(2)∵抛物线y=ax2﹣2ax﹣1=a(x﹣1)2﹣a﹣1(a<0),∴该函数图象的开口向下,对称轴是直线x=1,当x=1时,取得最大值﹣a﹣1,∵当﹣2≤x≤2时,y的最大值是1,∴x=1时,y=﹣a﹣1=1,得a=﹣2,∴y=﹣2(x﹣1)2+1,∵﹣2≤x≤2,∴x=﹣2时,取得最小值,此时y=﹣2(﹣2﹣1)2+1=﹣17,故答案为:﹣17.11.解:∵二次函数y=ax2﹣2ax+c(a≠0)的图象与x轴的一个交点为(﹣1,0),∴该函数的对称轴是直线x=﹣=1,∴该函数图象与x轴的另一个交点坐标为(3,0),∴关于x的一元二次方程ax2﹣2ax+c=0的两实数根是x1=﹣1,x2=3,∴两根之积为﹣3,故答案为:﹣3.12.解:如图,当y=0时,﹣x2+4x+5=0,解得x1=﹣1,x2=5,则A(﹣1,0),B(5,0),将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+1)(x﹣5),即y=x2﹣4x﹣5(﹣1≤x≤5),当直线y=﹣x+b经过点A(﹣1,0)时,1+b=0,解得b=﹣1;当直线y=﹣x+b与抛物线y=x2﹣4x﹣5(﹣1≤x≤5)有唯一公共点时,方程x2﹣4x﹣5=﹣x+b有相等的实数解,解得b=﹣,所以当直线y=﹣x+b与新图象有4个交点时,b的取值范围为﹣<b<﹣1.故答案为:﹣<b<﹣1.13.解:将抛物线y=﹣(x﹣3)2﹣1向右平移5个单位,再向上平移2个单位,所得的抛物线的解析式为y=﹣(x﹣3﹣5)2﹣1+2,即y=﹣(x﹣8)2+1,故答案为:y=﹣(x﹣8)2+1.14.解:∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣3,9),B(1,1),∴方程ax2=bx+c的解为x1=﹣3,x2=1,∴ax2﹣bx﹣c=0的解是x1=﹣3,x2=1,故答案为:x1=﹣3,x2=1.15.解:(1)将点C(0,3)、B(1,0)、(2,﹣5)代入抛物线y=ax2+bx+tc中,得:a+b+c=0,c=3,4a+2b+c=﹣5;解得:a=﹣1,b=﹣2,c=3,∴抛物线的解析式为y=﹣x2﹣2x+3.(2)抛物线向下平移n个单位后,E为(﹣1,4﹣n),C为(0,3﹣n),∴EC=,∵CO∥EH,∴当CO=CE=时,∠CEO=∠COE=∠OCH,∴3﹣n=或n﹣3=,即n=3﹣或3+.16.解:当10≤x≤20时,设y=kx+b,把(10,20),(20,10)代入可得:,解得,∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为y=﹣x+30,设该食品零售店每天销售这款冷饮产品的利润为w元,w=(x﹣8)y=(x﹣8)(﹣x+30)=﹣x2+38x﹣240=﹣(x﹣19)2+121,∵﹣1<0,∴当x=19时,w有最大值为121,故答案为:121.三.解答题(共6小题,满分56分)17.解:(1)将(2,4)代入y=x2+mx+m2﹣3得4=4+2m+m2﹣3,解得m1=1,m2=﹣3,又∵m>0,∴m=1.(2)∵m=1,∴y=x2+x﹣2,∵Δ=b2﹣4ac=12+8=9>0,∴二次函数图象与x轴有2个交点.18.解:∵初速度为10m/s,g取10m/s2,∴h=10t﹣×10t2=10t﹣5t2,(1)当h=0时,10t﹣5t2=0,解得t=0或t=2,∴球抛出后经2秒回到起点;(2)当h=1.8时,10t﹣5t2=1.8,解得t=0.2或t=1.8,∴0.2秒或1.8秒后球离起点的高度达到1.8m;(3)球离起点的高度不能达到6m,理由如下:若h=6,则10t﹣5t2=6,整理得5t2﹣10t+6=0,Δ=(﹣10)2﹣4×5×6=﹣20<0,∴原方程无实数解,∴球离起点的高度不能达到6m.19.解:(1)∵函数图象过点(1,2),∴将点代入y=ax2+(a﹣1)x﹣1,解得a=2,∴二次函数的解析式为y=2x2+x﹣1,∴x=﹣=﹣,∴y=2×﹣﹣1=﹣,∴该二次函数的顶点坐标为(﹣,﹣);(2)函数y=ax2+(a﹣1)x﹣1的对称轴是直线x=﹣,∵(x1,y1),(x2,y2)为此二次函数图象上的两个不同点,且x1+x2=﹣2,则y1=y2,∴﹣===﹣1,∴a=﹣1,∴y=﹣x2﹣2x﹣1=﹣(x+1)2≤0,∴当x=﹣1时,函数有最大值0;(3)∵y=ax2+(a﹣1)x﹣1,∴由顶点公式得:x=﹣=﹣+,y==﹣,∵a<0且a≠﹣1,∴x<0,y>0,∴该二次函数图象的顶点在第二象限.20.解:(1)设一次函数的关系式为y=kx+b,由题图可知,函数图象过点(25,50)和点(35,30).把这两点的坐标代入一次函数y=kx+b,得,解得,∴一次函数的关系式为y=﹣2x+100;(2)根据题意,设当天玩具的销售单价是x元,由题意得,(x﹣10)×(﹣2x+100)=600,解得:x1=40,x2=20,∴当天玩具的销售单价是40元或20元;(3)根据题意,则w=(x﹣10)×(﹣2x+100),整理得:w=﹣2(x﹣30)2+800;∵﹣2<0,∴当x=30时,w有最大值,最大值为800;∴当玩具的销售单价定为30元时,日销售利润最大;最大利润是800元.21.解:(1)设直线AB的解析式为y=px+q,把A(4,0),B(0,2)代入得,,解得,∴直线AB的解析式为y=﹣x+2;把A(4,0),B(0,2)代入y=﹣x2+bx+c得,,解得;∴抛物线解析式为y=﹣x2+x+2;(2)∵MN⊥x轴,M(m,0),点D在直线AB上,点N在抛物线上,∴N(m,﹣m2+m+2),D(m,﹣m+2),∴DN=﹣m2+2m,DM=﹣m+2,∵DN=3DM,∴﹣m2+2m=3(﹣m+2),解得m=3或m=4(舍),∴N(3,2).(3)如图,作点B关于x轴的对称点B′,∴OB=OB′,B′(0,﹣2),∵∠AOB=∠AOB′=90°,OA=OA,∴△AOB≌△AOB′,∴∠OAB′=∠OAB,∴∠BAB′=2∠BAC,∵A(4,0),B′(0,﹣2),∴直线AB′的解析式为:y=x﹣2,过点B作BP∥AB′交抛物线于点P,则∠ABP=∠BAB′=2∠BAC,即点P即为所求,∴直线BP的解析式为:y=x+2,令x+2=﹣x2+x+2,解得x=2或x=0(舍),∴P(2,3).22.解:(1)将点A(3,﹣2),点C(0,﹣5)代入y=x2+bx+c,∴,解得,∴y=x2﹣2x﹣5,∴M(1,﹣6);(2)平移后的函数解析式为y=(x﹣1)2﹣6+m,∴平移后的顶点坐标为(1,m﹣6),∴抛物线的顶点在x=1的直线上,设直线CA的解析式为y=kx+b,∴,∴,∴y=x﹣5,当x=1时,y=﹣4,∴﹣4<m﹣6<﹣2,解得2<m<4;(3)存在一点Q,使以B、P、E、Q为顶点的四边形是平行四边形,理由如下:当y=﹣2时,x2﹣2x﹣5=﹣2,解得x=﹣1或x=3,∴B(﹣1,﹣2),∴AB=4,∵BE:EA=3:1,∴AE=1,∴E(2,﹣2),设P(t,t﹣5),Q(x,x2﹣2x﹣5),①当BE为平行四边形的对角线时,,解得或,∴Q(,)或(,);②当BP为平行四边形的对角线时,,解得或,∴Q(,)或(,);③当BQ为平行四边形的对角线时,,此时无解;综上所述:Q点坐标为(,)或(,)或(,)或(,).九年级数学上册二次函数的图象与性质练习题(附答案)一.选择题1.如果在二次函数的表达式y=ax2+bx+c中,a>0,b<0,c<0,那么这个二次函数的图象可能是()A.B.C.D.2.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为()A.﹣2B.2C.±2D.03.已知A(,y1),B(2,y2),C(﹣,y3)是二次函数y=3(x﹣1)2+k图象上三点,则y1、y2、y3的大小关系为()A.y1>y2>y3B.y2>y1>y3C.y3>y2>y1D.y2>y3>y1 4.二次函数的部分图象如图所示,对称轴是直线x=﹣1,则这个二次函数的表达式为()A.y=﹣x2+2x+3B.y=x2+2x+3C.y=﹣x2+2x﹣3D.y=﹣x2﹣2x+35.在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为()A.B.C.D.6.关于抛物线y=﹣x2+2x﹣3的判断,下列说法正确的是()A.抛物线的开口方向向上B.抛物线的对称轴是直线x=﹣1C.抛物线对称轴左侧部分是下降的D.抛物线顶点到x轴的距离是27.已知二次函数y=x2﹣4x+5(0≤x≤3),则它的最大值是()A.1B.2C.3D.58.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<﹣1或x>3.其中,正确的说法有()A.①②④B.①②⑤C.①③⑤D.②④⑤9.已知函数y=2(x+1)2+1,则()A.当x<1 时,y随x的增大而增大B.当x<1 时,y随x的增大而减小C.当x<﹣1 时,y随x的增大而增大D.当x<﹣1 时,y随x的增大而减小10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的有()个.①abc>0;②2a+b=0;③9a+3b+c<0;④4ac﹣b2<0;⑤a+b≥m(am+b)(m为任意实数).A.3B.2C.1D.0二.填空题11.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是.(请用“>”连接排序)12.抛物线y=3x2+6x+11的顶点坐标为.13.二次函数y=3(x﹣1)2+5的最小值为.14.已知二次函数y=2x2+bx+4顶点在x轴上,则b=.15.二次函数y=x2﹣2x+1在2≤x≤5范围内的最小值为.16.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是(填写序号).三.解答题17.已知二次函数的顶点坐标为A(1,﹣4),且经过点B(3,0).(1)求该二次函数的解析式;(2)判断点C(2,﹣3)是否在该函数图象上,并说明理由.18.如图,已知直线l过点A(4,0),B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP=4,试求二次函数的表达式.19.如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B (1,1).(1)求m的值;(2)过动点P(n,0)且垂直于x轴的直线与L1,L2的交点分别为C,D,当点C 位于点D上方时,请直接写出n的取值范围.20.已知二次函数y=a(x+a)(x+a﹣1).(1)当a=2时,求该二次函数图象的对称轴.(2)当a<0时,判断该二次函数图象的顶点所在的象限,并说明理由.(3)当0<x<3时,y随着x增大而增大,求a的取值范围.21.已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),求△OAB的面积.22.抛物线y=﹣x2+bx+c经过点A(3,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.(1)求抛物线的解析式;(2)连接AB、AC、BC,求△ABC的面积.23.如图,在平面直角坐标系中,直线AB与抛物线y=﹣x2+bx+c交于A(﹣1,0)和B(2,3)两点,抛物线与y轴交于点C.(1)求一次函数和二次函数的解析式;(2)求△ABC的面积.参考答案一.选择题1.解:∵a>0,b<0,c<0,∴﹣>0,∴抛物线的图象开口向上,对称轴在y轴的右边,交y轴于负半轴,故选:C.2.解:∵y=(m+2)x|m|+2是y关于x的二次函数,∴|m|=2且m+2≠0.解得m=2.故选:B.3.解:∵二次函数y=3(x﹣1)2+k图象的对称轴为直线x=1,而A(,y1)到直线x=1的距离最近,C(﹣,y3)到直线x=1的距离最远,∴y3>y2>y1.故选:C.4.解:由图象知抛物线的对称轴为直线x=﹣1,设抛物线解析式为y=a(x+1)2+k,将(﹣3,0)、(0,3)代入,得:,解得:,则抛物线解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3,故选:D.5.解:A、由抛物线可知,a<0,x=﹣<0,得b<0,由直线可知,a<0,b<0,故本选项正确;B、由抛物线可知,a>0,由直线可知,a<0,故本选项错误;C、由抛物线可知,a>0,x=﹣>0,得b<0,由直线可知,a>0,b>0,故本选项错误;D、由抛物线可知,a>0,由直线可知,a<0,故本选项错误.故选:A.6.解:∵y=﹣x2+2x﹣3=﹣(x﹣1)2﹣2,∴抛物线开口向下,对称轴为x=1,顶点坐标为(1,﹣2),在对称轴左侧,y随x的增大而增大,∴A、B、C不正确;∵抛物线顶点到x轴的距离是|﹣2|=2,∴D正确,故选:D.7.解:y=x2﹣4x+5=(x﹣2)2+1,由于0≤x≤3,所以当x=2时,y有最小值1,当x=0时,y有最大值5.故选:D.8.解:根据图象可知:①对称轴﹣>0,故ab<0,正确;②方程ax2+bx+c=0的根为x1=﹣1,x2=3,正确;③x=1时,y=a+b+c<0,错误;④当x<1时,y随x值的增大而减小,错误;⑤当y>0时,x<﹣1或x>3,正确.正确的有①②⑤.故选:B.9.解:∵y=2(x+1)2+1,∴当x>﹣1时,y随x的增大而增大,故选项A错误,当x<﹣1时,y随x的增大而减小,故选项B错误、选项C错误、选项D正确;故选:D.10.解:∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a>0,∵抛物线与y轴的交点坐标在x轴上方,∴c>0,∴abc<0,所以①错误;∵b=﹣2a,∴2a+b=0,所以②正确;∵x=3时,y<0,∴9a+3b+c<0,所以③正确.∵抛物线与x轴有2个交点,∴Δ=b2﹣4ac>0,即4ac﹣b2<0,所以④正确;∵抛物线的对称轴为直线x=1,∴函数的最大值为a+b+c,∴a+b+c≥am2+bm+c(m为任意实数),即a+b≥m(am+b),所以⑤正确.故选:C.二.填空题11.解:如图所示:①y=a1x2的开口小于②y=a2x2的开口,则a1>a2>0,③y=a3x2的开口大于④y=a4x2的开口,开口向下,则a4<a3<0,故a1>a2>a3>a4.故答案为:a1>a2>a3>a412.解:∵y=3x2+6x+11=3(x+1)2+8,∴抛物线y=3x2+6x+11的顶点坐标为(﹣1,8),故答案为(﹣1,8).13.解:由于二次函数y=3(x﹣1)2+5中,a=3>0,所以当x=1时,函数取得最小值为5,故答案为5.14.解:∵二次函数y=2x2+bx+4顶点在x轴上,∴=0,解得b=,故答案为:±4.15.解:∵二次函数y=x2﹣2x+1=(x﹣1)2,∴当x>1时,y随x的增大而增大,∴在2≤x≤5范围内,当x=2时,y取得最小值,此时y=(2﹣1)2=1,故答案为:1.16.解:∵抛物线的对称轴为直线x=﹣=1,∴2a+b=0,所以①正确;∵x=﹣1时,y<0,∴a﹣b+c<0,即a+c<b,所以②错误;∵抛物线与x轴的一个交点为(﹣2,0)而抛物线的对称轴为直线x=1,∴抛物线与x轴的另一个交点为(4,0),所以③错误;∵抛物线开口向上,∴a>0,∴b=﹣2a<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以④正确.故答案为①④.三.解答题17.解:(1)设二次函数的解析式是y=a(x﹣h)2+k,∵二次函数的顶点坐标为A(1,﹣4),∴y=a(x﹣1)2﹣4,∵经过点B(3,0),∴代入得:0=a(3﹣1)2﹣4,解得:a=1,∴y=(x﹣1)2﹣4,即二次函数的解析式为y=x2﹣2x﹣3;(2)点C(2,﹣3)在该函数图象上,理由是:把C(2,﹣3)代入y=x2﹣2x﹣3得:左边=﹣3,右边=4﹣4﹣3=﹣3,即左边=右边,所以点C在该函数的图象上.18.解:设直线l的解析式为y=kx+b,把A(4,0),B(0,4)分别代入得,解得,∴直线l的关系式为y=﹣x+4,设P(t,﹣t+4),∵S△AOP=4,∴×4×(﹣t+4)=4,解得t=2,∴P(2,2),把P(2,2)代入y=ax2得4a=2,解得a=,∴二次函数的表达式为y=x2.19.解:(1)把B(1,1)代入y=ax2得:a=1,∴抛物线解析式为y=x2.把A(m,4)代入y=x2得:4=m2,∴m=±2.∵点A在二象限,∴m=﹣2.(2)观察函数图象可知:当﹣2<x<1时,直线在抛物线的上方,∴n的取值范围为:﹣2<n<1.20.解:(1)当a=2时,y=2(x+2)(x+1),∴二次函数的对称轴为x=.(2)由题知二次函数与x轴的交点坐标为(﹣a,0),(1﹣a,0);∵a<0,∴二次函数的开口方向向下;又﹣a>0,1﹣a>0,所以对称轴所在直线为x==>0,当x=时,y=﹣>0,所以顶点坐标(,﹣)在第一象限.(3)由(2)知,二次函数的对称轴为直线x=,∵当0<x<3时,y随着x增大而增大,∴当a>0时,≤0,解得a≥;当a<0,≥3,解得a≤﹣.∴a的取值范围为a≥或a≤﹣.21.解:∵一次函数y=kx﹣2的图象相过点A(﹣1,﹣1),∴﹣1=﹣k﹣2,解得k=﹣1,∴一次函数表达式为y=﹣x﹣2,∴令x=0,得y=﹣2,∴G(0,﹣2),∵y=ax2过点A(﹣1,﹣1),∴﹣1=a×1,解得a=﹣1,∴二次函数表达式为y=﹣x2,由一次函数与二次函数联立可得,解得,,∴S△OAB=OG•|A的横坐标|+OG•点B的横坐标=×2×1+×2×2=1+2=3.22.解:(1)∵抛物线经过A、B(0,3)∴由上两式解得∴抛物线的解析式为:;(2)由(1)抛物线对称轴为直线x=把x=代入,得y=4则点C坐标为(,4)设线段AB所在直线为:y=kx+b,则有,解得∴AB解析式为:∵线段AB所在直线经过点A、B(0,3)抛物线的对称轴l于直线AB交于点D∴设点D的坐标为D将点D代入,解得m=2∴点D坐标为,∴CD=CE﹣DE=2过点B 作BF ⊥l 于点F ∴BF =OE =∵BF +AE =OE +AE =OA =∴S △ABC =S △BCD +S △ACD =CD •BF +CD •AE ∴S △ABC =CD (BF +AE )=×2×=23.解:(1)∵抛物线y =﹣x 2+bx +c 交于A (﹣1,0)和B (2,3)两点 ∴,解得:, ∴抛物线解析式为y =﹣x 2+2x +3,设直线AB 的解析式为y =mx +n (m ≠0),则,解得,∴直线AB 的解析式为y =x +1; (2)令x =0,则y =﹣x 2+2x +3=3, ∴C (0,3),则OC =3,BC =2,BC ∥x 轴, ∴S △ABC =×BC ×OC ==3.九年级数学二次函数专题精练含答案一、单选题1.关于二次函数22(4)6y x =-+的最大值或最小值,下列说法正确的是( ) A .有最大值4B .有最小值4C .有最大值6D .有最小值62.已知抛物线24y x x c =-++经过点(4,3),那么下列各点中,该抛物线必经过的点是( ) A .(0,2)B .(0,3)C .(0,4)D .(0,5)3.在平面直角坐标系中,已知抛物线245y x x =-+,将该抛物线沿y 轴翻折所得的抛物线的表达式为( ) A .245y x x =--+B .245y x x =++C .245y x x =-+-D .245y x x =---4.正方形的边长为4,若边长增加x ,那么面积增加y ,则y 关于x 的函数表达式为( ) A .216y x =+B .2(4)y x =+C .28y x x =+D .2164y x =-5.把抛物线22y x =向右平移2个单位,然后向下平移1个单位,则平移后得到的抛物线解析式是( ) A .22(2)1y x =-+- B .22(2)1y x =--+ C .22(2)1y x =++D .22(2)1y x =--6.如图,二次函数2y ax bx c =++的图象关于直线1x =对称,与x 轴交于1(,0)A x ,2(,0)B x 两点,若121x -<<-,则下列四个结论:①234x <<,②320a b +>,③24b a c ac >++,④a c b >>.正确结论的个数为( ) A .1个B .2个C .3个D .4个7.对于抛物线23(1)2y x =-+-,下列说法正确的是( ) A .抛物线开口向上B .当1x >-时,y 随x 增大而减小C .函数最小值为﹣2D .顶点坐标为(1,﹣2)8.关于二次函数()215y x =-+,下列说法正确的是( )A .函数图象的开口向下B .函数图象的顶点坐标是()1,5-C .该函数有最大值,是大值是5D .当1x >时,y 随x 的增大而增大9.已知A (−3,−2) ,B (1,−2),抛物线y =ax 2+bx +c (a >0)顶点在线段AB 上运动,形状保持不变,与x 轴交于C ,D 两点(C 在D 的右侧),下列结论: ①c ≥−2 ;②当x >0时,一定有y 随x 的增大而增大;③若点D 横坐标的最小值为−5,点C 横坐标的最大值为3; ④当四边形ABCD 为平行四边形时,a =12.其中正确的是( ) A .①③B .②③C .①④D .①③④10.已知二次函数2243y mx m x =--(m 为常数,0m ≠),点(),p p P x y 是该函数图象上一点,当04p x ≤≤时,3p y ≤-,则m 的取值范围是( ) A .m 1≥或0m < B .m 1≥ C .1m ≤-或0m >D .1m ≤-11.已知函数()211y ax a x =-++,则下列说法不正确的个数是( )①若该函数图像与x 轴只有一个交点,则1a =②方程()2110ax a x -++=至少有一个整数根③若11x a<<,则()211y ax a x =-++的函数值都是负数 ④不存在实数a ,使得()2110ax a x -++≤对任意实数x 都成立A .0B .1C .2D .312.如图,在正方形ABCD 中,4AB =,点P 从点A 出发沿路径A B C →→向终点C 运动,连接DP ,作DP 的垂直平分线MN 与正方形ABCD 的边交于M ,N 两点,设点P 的运动路程为x ,PMN 的面积为y ,则下列图象能大致反映y 与x 函数关系的是( )A .B .C .D .二、填空题13.已知点(3,a )在抛物线y =-2x 2+2x 上,则=a ______.14.如图是二次函数21y ax bx c =++ 和一次函数y 2=kx +t 的图象,当y 1≥y 2时,x 的取值范围是_____.15.小亮同学在探究一元二次方程2ax bx c 0++=的近似解时,填好了下面的表格:根据以上信息请你确定方程2ax bx c 0++=的一个解的范围是________. 16.已知二次函数223y x x =--+,当12a x 时,函数值y 的最小值为1,则a 的值为_______. 17.已知抛物线2122y x bx =+-与x 轴交于A ,B 两点,与y 轴交于C 点. (1)若(1,0)A -,则b =______. (2)若(1,0)M -,(1,0)N ,抛物线2122y x bx =+-与线段MN 没有交点,则b 的取值范围为______. 三、解答题18.已知抛物线经过点()1,0A -,()5,0B ,()0,5C ,求该抛物线的函数关系式19.如图,抛物线212y x bx c =++与直线132y x =+分别相交于A 、B 两点,其中点A 在y 轴上,且此抛物线与x 轴的一个交点为()3,0C -.(1)求抛物线的解析式(2)在抛物线对称轴l 上找一点M ,使MBC ∆的周长最小,请求出这个周长的最小值.20.如图,一次函数y =A 、B ,二次函数2y bx c ++图象过A 、B 两点.(1)求二次函数解析式;(2)点B 关于抛物线对称轴的对称点为点C ,点P 是对称轴上一动点,在抛物线上是否存在点Q ,使得以B 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出Q 点坐标;若不存在,请说明理由.21.如图,二次函数y =ax 2+bx +c 的图象与x 轴交于点A (﹣2,0)和点B (8,0),与y 轴交于点C (0,﹣8),连接AC ,D 是抛物线对称轴上一动点,连接AD ,CD ,得到△ACD .(1)求该抛物线的函数解析式.(2)△ACD 周长能否取得最小值,如果能,请求出D 点的坐标;如果不能,请说明理由.(3)在(2)的条件下,在抛物线上是否存在点E ,使得△ACE 与△ACD 面积相等,如果存在,请求出点的坐标;如果不存在,请说明理由.参考答案1--10DBCCD BBDDA 11--12CA13.-1214.﹣1≤x ≤215.3.24x 3.25<<16.1-17. 32- 3322b -<< 18.解:△抛物线经过点()1,0A -,()5,0B ,()0,5C ,△设抛物线的表达式为()()15y a x x =+-,将点()0,5C 代入得:55a =-,解得:1a =-,△()()21545y x x x x =-+-=-++.△该抛物线的函数关系式为245y x x =-++.19..解:(1)抛物线212y x bx c =++与直线132y x =+交于y 轴上一点A , 令0,x = 则3,y =∴ 点()0,3A把()0,3A ,()3,0C -代入212y x bx c =++得: 39302c b c =⎧⎪⎨-+=⎪⎩, 解得:523b c ⎧=⎪⎨⎪=⎩, ∴抛物线的解析式是215322y x x =++; (2)将直线132y x =+与二次函数215322y x x =++联立得方程组: 213215322y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ 215133,222x x x ∴++=+ 240,x x ∴-=解得:0x =或4x =-,04,,31x x y y ==-⎧⎧∴⎨⎨==⎩⎩()0,3A ,()4,1B ∴-BC ∴==如图,要使MBC △的周长最小,则MB MC +最小,设二次函数215322y x x=++与x 轴的另一交点为D , 抛物线的对称轴为:552,1222x =-=-⨯ ()3,0C -∴ 点()2,0D -,连接,BD 交对称轴于,MMD MC ∴=,此时,MB MC MB MD BD +=+=最小,此时:BD =MBC ∴20.解:(1)对于y =x =0时,y =当y =0时,03x -=,妥得,x =3 △A (3,0),B (0,把A (3,0),B (0,2y bx c++得:+=0b c c ⎧⎪⎨=⎪⎩解得,b c ⎧=⎪⎨⎪=⎩△抛物线的解析式为:2y =(2)抛物线的对称轴为直线12b x a =-== 故设P (1,p ),Q (m ,n )①当BC 为菱形对角线时,如图,△B ,C 关于对称没对称,且对称轴与x 轴垂直,△△BC 与对称轴垂直,且BC //x 轴△在菱形BQCP 中,BC △PQ△PQ △x 轴△点P 在x =1上,△点Q 也在x =1上,当x =1时,211y△Q (1,); ②当BC 为菱形一边时,若点Q 在点P 右侧时,如图,△BC //PQ ,且BC =PQ△BC //x 轴,△令y =2y 解得,120,2x x ==△(2,C△PQ=BC=22=△PB=BC=2△迠P在x轴上,△P(1,0)△Q(3,0);若点Q在点P的左侧,如图,同理可得,Q(-1,0)综上所述,Q点坐标为(1,)或(3,0)或(-1,0)21.解:(1)由题意可得:0=4206488a b ca b cc-+⎧⎪=++⎨⎪=-⎩,解得:1238abc⎧=⎪⎪=-⎨⎪=-⎪⎩,△抛物线的解析式为:y=12x2﹣3x﹣8;(2)△ACD周长能取得最小值,△点A(﹣2,0),点B(8,0),△对称轴为直线x=3,△△ACD周长=AD+AC+CD,AC是定值,△当AD+CD取最小值时,△ACD周长能取得最小值,△点A,点B关于对称轴直线x=3对称,△连接BC交对称轴直线x=3于点D,此时AD+CD有最小值,设直线BC 解析式为:y =kx ﹣8,△0=8k ﹣8,△k =1,△直线BC 解析式为:y =x ﹣8,当x =3,y =﹣5,△点D (3,﹣5);(3)存在,△点A (﹣2,0),点C (0,﹣8),△直线AC 解析式为y =﹣4x ﹣8,如图,△△ACE 与△ACD 面积相等,△DE △AC ,△设DE 解析式为:y =﹣4x +n ,△﹣5=﹣4×3+n ,△n =7,△DE 解析式为:y =﹣4x +7, 联立方程组可得:2471382y x y x x =-+⎧⎪⎨=--⎪⎩,解得:12111x y ⎧=⎪⎨=-⎪⎩,22111x y ⎧=⎪⎨=⎪⎩, △点E1,﹣1,).九年级上册数学二次函数同步练习一、单选题1.下列函数中,是二次函数的是( )A .y =(2x ﹣1)2B .y =(x +1)2﹣x 2C .y =ax 2D .y =2x +3 2.若抛物线258(3)23mm y m x x -+=-+-是关于x 的二次函数,那么m 的值是( ) A .3 B .2-C .2D .2或3 3.若抛物线y =x 2-x -2经过点A (3,a ),则a 的值是( )A .2B .4C .6D .84.已知二次函数2135y x x =-+,则其二次项系数a ,一次项系数b ,常数项c 分别是( )A .1,3,5a b c ==-=B .1,3,5a b c ===C .5,3,1a b c ===D .5,3,1a b c ==-= 5.如果函数2(2)25y a x x =-+-是二次函数,则a 的取值范围是( )A .2a ≠B .a≥0C .a=2D .a>0 6.下列函数中①31y x ;②243y x x =-;③1y x =;④225=-+y x ,是二次函数的有()A .①②B .②④C .②③D .①④ 7.若抛物线2y x bx c =-++经过点()2,3-,则247c b --的值是( )A .6B .7C .8D .208.函数y=ax2+bx+c(a ,b ,c 是常数)是二次函数的条件是( )A .a≠0,b≠0,c≠0B .a<0,b≠0,c≠0C .a>0,b≠0,c≠0D .a≠0 二、填空题9.若()2321mm y m x --=+是二次函数,则m 的值为______. 10.若22a y x -=是二次函数,则=a ________.11.在二次函数21y x =-+中,二次项系数、一次项系数、常数项的和为_____. 12.下列函数一定是二次函数的是__________.①2y ax bx c =++;②3y x=-;③2431y x x =-+;④2(1)y m x bx c =-++;⑤y =(x -3)2-x 213.当常数m ≠______时,函数y =(m 2﹣2m ﹣8)x 2+(m +2)x +2是二次函数;当常数m =___时,这个函数是一次函数.14.已知函数2135m y x -=-① 当m = _________时,y 是关于x 的一次函数;② 当m =_________时,y 是关于x 的二次函数 .15.二次函数()22339y m x x m =+++-的图象经过原点,则m =__________.16.已知二次函数2y x bx 3=-++,当x 2=时,y 3=.则这个二次函数的表达式是________.三、解答题17.下列函数中(x ,t 是自变量),哪些是二次函数?22322113,25,22,1522y x y x x y x s t t =-+=-+=+=++.18.已知函数y =(m 2-2)x 2+(m )x +8.(1)若这个函数是一次函数,求m 的值;(2)若这个函数是二次函数,求m 的取值范围.19.若函数y=(a -1)x b+1+x 2+1是二次函数,试讨论a 、b 的取值范围.20.篱笆墙长30m ,靠墙围成一个矩形花坛,写出花坛面积y(m 2)与长x 之间的函数关系式,并指出自变量的取值范围.参考答案:1.A2.C3.B4.D5.A6.B7.B8.D9.410.2±11.012.③13. 4,-2 414. 13215.316.2y x 2x 3=-++17.2132y x =-+和215s t t =++是二次函数 18.(1)m =(2)m ≠m ≠19.①a≠0;②b=0或-1,a 取全体实数③当a=1,b 为全体实数时,y=x 2+1是二次函数 20.y= 21152x x -+, x 的取值范围为0<x<30.九年级数学上册二次函数单元综合测试卷一.选择题(共10小题)1.下列各式中,是y 关于x 的二次函数的是( )A .y =4xB .y =3x ﹣5C .y =D .y =2x 2+12.已知:a >b >c ,且a +b +c =0,则二次函数y =ax 2+bx +c 的图象可能是下列图象中的( )A.B.C.D.3.二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是()A.(2,6)B.(4,6)C.(3,﹣5)D.(3,5)4.将二次函数y=x2+2x﹣1转化为y=a(x﹣h)2+k的形式,结果为()A.y=(x﹣1)2B.y=(x+1)2C.y=(x+1)2﹣1D.y=(x+1)2﹣2 5.已知0≤x≤,则函数y=﹣2x2+8x﹣6的最大值是()A.﹣10.5B.2C.﹣2.5D.﹣66.顶点坐标为(3,1),形状与函数y=的图象相同且开口方向相反的抛物线的解析式为()A.y=+1B.y=+1C.y=﹣+1D.y=﹣+17.已知点A(﹣1,y1),B(1,y2),C(2,y3)都在二次函数y=(x﹣1)2的图象上,则y1,y2,y3的大小关系正确的是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y3<y2<y1 8.抛物线y=ax2+bx+c纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…则下列说法中正确的个数是()①方程ax2+bx+c=0,有两根为x1=﹣2,x2=3;②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=1;④抛物线开口向上.A.1B.2C.3D.49.如图,在正方形ABCD中,AB=4,AC与BD交于点O,E,F分别为边BC,CD上的点(点E,F不与线段BC,CD的端点重合),BE=CF,连接OE,OF,EF.关于以下三个结论,下列判断正确的是()结论Ⅰ:∠BOF始终是90°;结论Ⅱ:△OEF面积的最小值是2;结论Ⅲ:四边形OECF的面积始终是8.A.结论Ⅰ和Ⅱ都对,结论Ⅲ错B.结论Ⅰ和Ⅱ都对,结论Ⅱ错C.结论Ⅱ和Ⅲ都对,结论Ⅰ错D.三个结论都对10.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为()A.37.5°B.40°C.42.5°D.45°二.填空题(共6小题)11.函数是二次函数,则m的值为.12.已知抛物线y=x2﹣4x+c.与直线y=m相交于A,B两点,若点A的横坐标;x A=﹣1,。
九年级数学二次函数专项训练含答案-精选5篇

九年级数学二次函数专题精练含答案一、单选题1.关于二次函数22(4)6y x =-+的最大值或最小值,下列说法正确的是( ) A .有最大值4 B .有最小值4 C .有最大值6 D .有最小值6 2.已知抛物线24y x x c =-++经过点(4,3),那么下列各点中,该抛物线必经过的点是( )A .(0,2)B .(0,3)C .(0,4)D .(0,5) 3.在平面直角坐标系中,已知抛物线245y x x =-+,将该抛物线沿y 轴翻折所得的抛物线的表达式为( )A .245y x x =--+B .245y x x =++C .245y x x =-+-D .245y x x =--- 4.正方形的边长为4,若边长增加x ,那么面积增加y ,则y 关于x 的函数表达式为( ) A .216y x =+ B .2(4)y x =+ C .28y x x =+ D .2164y x =- 5.把抛物线22y x =向右平移2个单位,然后向下平移1个单位,则平移后得到的抛物线解析式是( )A .22(2)1y x =-+-B .22(2)1y x =--+C .22(2)1y x =++D .22(2)1y x =--6.如图,二次函数2y ax bx c =++的图象关于直线1x =对称,与x 轴交于1(,0)A x ,2(,0)B x 两点,若121x -<<-,则下列四个结论:①234x <<,①320a b +>,①24b a c ac >++,①a c b >>.正确结论的个数为( )A .1个B .2个C .3个D .4个7.对于抛物线23(1)2y x =-+-,下列说法正确的是( )A .抛物线开口向上B .当1x >-时,y 随x 增大而减小C .函数最小值为﹣2D .顶点坐标为(1,﹣2)8.关于二次函数()215y x =-+,下列说法正确的是( )A .函数图象的开口向下B .函数图象的顶点坐标是()1,5-C .该函数有最大值,是大值是5D .当1x >时,y 随x 的增大而增大 9.已知A (−3,−2) ,B (1,−2),抛物线y =ax 2+bx +c (a >0)顶点在线段AB 上运动,形状保持不变,与x 轴交于C ,D 两点(C 在D 的右侧),下列结论:①c ≥−2 ;①当x >0时,一定有y 随x 的增大而增大;①若点D 横坐标的最小值为−5,点C 横坐标的最大值为3;①当四边形ABCD 为平行四边形时,a =12. 其中正确的是( )A .①①B .①①C .①①D .①①① 10.已知二次函数2243y mx m x =--(m 为常数,0m ≠),点(),p p P x y 是该函数图象上一点,当04p x ≤≤时,3p y ≤-,则m 的取值范围是( )A .m 1≥或0m <B .m 1≥C .1m ≤-或0m >D .1m ≤-11.已知函数()211y ax a x =-++,则下列说法不正确的个数是( )①若该函数图像与x 轴只有一个交点,则1a =①方程()2110ax a x -++=至少有一个整数根①若11x a<<,则()211y ax a x =-++的函数值都是负数 ①不存在实数a ,使得()2110ax a x -++≤对任意实数x 都成立A .0B .1C .2D .312.如图,在正方形ABCD 中,4AB =,点P 从点A 出发沿路径A B C →→向终点C 运动,连接DP ,作DP 的垂直平分线MN 与正方形ABCD 的边交于M ,N 两点,设点P 的运动路程为x ,PMN 的面积为y ,则下列图象能大致反映y 与x 函数关系的是( )A .B .C .D .二、填空题13.已知点(3,a )在抛物线y =-2x 2+2x 上,则=a ______.14.如图是二次函数21y ax bx c =++ 和一次函数y 2=kx +t 的图象,当y 1≥y 2时,x 的取值范围是_____.15.小亮同学在探究一元二次方程2ax bx c 0++=的近似解时,填好了下面的表格:根据以上信息请你确定方程2ax bx c 0++=的一个解的范围是________.16.已知二次函数223y x x =--+,当12a x时,函数值y 的最小值为1,则a 的值为_______.17.已知抛物线2122y x bx =+-与x 轴交于A ,B 两点,与y 轴交于C 点.(1)若(1,0)A -,则b =______.(2)若(1,0)M -,(1,0)N ,抛物线2122y x bx =+-与线段MN 没有交点,则b 的取值范围为______.三、解答题18.已知抛物线经过点()1,0A -,()5,0B ,()0,5C ,求该抛物线的函数关系式 19.如图,抛物线212y x bx c =++与直线132y x =+分别相交于A 、B 两点,其中点A 在y 轴上,且此抛物线与x 轴的一个交点为()3,0C -.(1)求抛物线的解析式(2)在抛物线对称轴l 上找一点M ,使MBC ∆的周长最小,请求出这个周长的最小值.20.如图,一次函数y A 、B ,二次函数2y bx c ++图象过A 、B 两点.(1)求二次函数解析式;(2)点B 关于抛物线对称轴的对称点为点C ,点P 是对称轴上一动点,在抛物线上是否存在点Q ,使得以B 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出Q 点坐标;若不存在,请说明理由.21.如图,二次函数y =ax 2+bx +c 的图象与x 轴交于点A (﹣2,0)和点B (8,0),与y 轴交于点C (0,﹣8),连接AC ,D 是抛物线对称轴上一动点,连接AD ,CD ,得到①ACD .(1)求该抛物线的函数解析式.(2)①ACD 周长能否取得最小值,如果能,请求出D 点的坐标;如果不能,请说明理由.(3)在(2)的条件下,在抛物线上是否存在点E ,使得①ACE 与①ACD 面积相等,如果存在,请求出点的坐标;如果不存在,请说明理由.参考答案1--10DBCCD BBDDA 11--12CA13.-1214.﹣1≤x ≤215.3.24x 3.25<<16.1-17. 32- 3322b -<< 18.解:①抛物线经过点()1,0A -,()5,0B ,()0,5C ,①设抛物线的表达式为()()15y a x x =+-,将点()0,5C 代入得:55a =-,解得:1a =-,①()()21545y x x x x =-+-=-++.①该抛物线的函数关系式为245y x x =-++.19..解:(1)抛物线212y x bx c =++与直线132y x =+交于y 轴上一点A , 令0,x = 则3,y = ∴ 点()0,3A把()0,3A ,()3,0C -代入212y x bx c =++得: 39302c b c =⎧⎪⎨-+=⎪⎩, 解得:523b c ⎧=⎪⎨⎪=⎩, ∴抛物线的解析式是215322y x x =++; (2)将直线132y x =+与二次函数215322y x x =++联立得方程组: 213215322y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ 215133,222x x x ∴++=+ 240,x x ∴-=解得:0x =或4x =-,04,,31x x y y ==-⎧⎧∴⎨⎨==⎩⎩()0,3A ,()4,1B ∴-BC ∴==如图,要使MBC △的周长最小,则MB MC +最小,设二次函数215322y x x =++与x 轴的另一交点为D ,抛物线的对称轴为:552,1222x=-=-⨯()3,0C-∴点()2,0D-,连接,BD交对称轴于,MMD MC∴=,此时,MB MC MB MD BD+=+=最小,此时:BD=MBC∴20.解:(1)对于y x=x=0时,y=当y=0时,03x-=,妥得,x=3①A(3,0),B(0,把A(3,0),B(0,2y bx c++得:+=0b cc⎧⎪⎨=⎪⎩解得,bc⎧=⎪⎨⎪=⎩①抛物线的解析式为:2y x x=-(2)抛物线的对称轴为直线12bxa=-==故设P(1,p),Q(m,n)①当BC为菱形对角线时,如图,①B ,C 关于对称没对称,且对称轴与x 轴垂直,①①BC 与对称轴垂直,且BC //x 轴①在菱形BQCP 中,BC ①PQ①PQ ①x 轴①点P 在x =1上,①点Q 也在x =1上,当x =1时,211y①Q (1,); ①当BC 为菱形一边时,若点Q 在点P 右侧时,如图,①BC //PQ ,且BC =PQ①BC //x 轴,①令y =2y 解得,120,2x x ==①(2,C①PQ=BC=22①PB=BC=2①迠P在x轴上,①P(1,0)①Q(3,0);若点Q在点P的左侧,如图,同理可得,Q(-1,0)综上所述,Q点坐标为(1,)或(3,0)或(-1,0)21.解:(1)由题意可得:0=4206488a b ca b cc-+⎧⎪=++⎨⎪=-⎩,解得:1238abc⎧=⎪⎪=-⎨⎪=-⎪⎩,①抛物线的解析式为:y=12x2﹣3x﹣8;(2)△ACD周长能取得最小值,①点A(﹣2,0),点B(8,0),①对称轴为直线x=3,①①ACD周长=AD+AC+CD,AC是定值,①当AD+CD取最小值时,△ACD周长能取得最小值,①点A,点B关于对称轴直线x=3对称,①连接BC交对称轴直线x=3于点D,此时AD+CD有最小值,设直线BC 解析式为:y =kx ﹣8,①0=8k ﹣8,①k =1,①直线BC 解析式为:y =x ﹣8,当x =3,y =﹣5,①点D (3,﹣5);(3)存在,①点A (﹣2,0),点C (0,﹣8),①直线AC 解析式为y =﹣4x ﹣8,如图,①①ACE 与①ACD 面积相等,①DE ①AC ,①设DE 解析式为:y =﹣4x +n ,①﹣5=﹣4×3+n ,①n =7,①DE 解析式为:y =﹣4x +7, 联立方程组可得:2471382y x y x x =-+⎧⎪⎨=--⎪⎩,解得:12111x y ⎧=⎪⎨=-⎪⎩,22111x y ⎧=⎪⎨=⎪⎩, ①点E1,﹣1,).九年级上册数学二次函数同步练习一、单选题1.下列函数中,是二次函数的是( ) A .y =(2x ﹣1)2 B .y =(x +1)2﹣x 2 C .y =ax 2D .y =2x +32.若抛物线258(3)23m m y m x x -+=-+-是关于x 的二次函数,那么m 的值是( )A .3B .2-C .2D .2或33.若抛物线y =x 2-x -2经过点A (3,a ),则a 的值是( ) A .2B .4C .6D .84.已知二次函数2135y x x =-+,则其二次项系数a ,一次项系数b ,常数项c 分别是( ) A .1,3,5a b c ==-= B .1,3,5a b c ===C .5,3,1a b c ===D .5,3,1a b c ==-=5.如果函数2(2)25y a x x =-+-是二次函数,则a 的取值范围是( ) A .2a ≠ B .a≥0C .a=2D .a>06.下列函数中①31y x ;①243y x x =-;①1y x=;①225=-+y x ,是二次函数的有() A .①①B .①①C .①①D .①①7.若抛物线2y x bx c =-++经过点()2,3-,则247c b --的值是( ) A .6B .7C .8D .208.函数y=ax2+bx+c(a ,b ,c 是常数)是二次函数的条件是( ) A .a≠0,b≠0,c≠0 B .a<0,b≠0,c≠0 C .a>0,b≠0,c≠0 D .a≠0二、填空题 9.若()2321m m y m x --=+是二次函数,则m 的值为______.10.若22ay x -=是二次函数,则=a ________.11.在二次函数21y x =-+中,二次项系数、一次项系数、常数项的和为_____. 12.下列函数一定是二次函数的是__________.①2y ax bx c =++;①3y x =-;①2431y x x =-+;①2(1)y m x bx c =-++;①y =(x -3)2-x 213.当常数m ≠______时,函数y =(m 2﹣2m ﹣8)x 2+(m +2)x +2是二次函数;当常数m =___时,这个函数是一次函数. 14.已知函数2135m y x -=-① 当m = _________时,y 是关于x 的一次函数; ① 当m =_________时,y 是关于x 的二次函数 .15.二次函数()22339y m x x m =+++-的图象经过原点,则m =__________.16.已知二次函数2y x bx 3=-++,当x 2=时,y 3=.则这个二次函数的表达式是________. 三、解答题17.下列函数中(x ,t 是自变量),哪些是二次函数? 22322113,25,22,1522y x y x x y x s t t =-+=-+=+=++.18.已知函数y =(m 2-2)x 2+(m x +8. (1)若这个函数是一次函数,求m 的值; (2)若这个函数是二次函数,求m 的取值范围.19.若函数y=(a -1)x b+1+x 2+1是二次函数,试讨论a 、b 的取值范围.20.篱笆墙长30m ,靠墙围成一个矩形花坛,写出花坛面积y(m 2)与长x 之间的函数关系式,并指出自变量的取值范围.参考答案:1.A 2.C 3.B 4.D 5.A 6.B 7.B 8.D 9.4 10.2± 11.0 12.①13. 4,-2 4 14. 1 3215.316.2y x 2x 3=-++17.2132y x =-+和215s t t =++是二次函数18.(1)m (2)m ≠m ≠19.①a≠0;①b=0或-1,a 取全体实数①当a=1,b 为全体实数时,y=x 2+1是二次函数 20.y= 21152x x -+, x 的取值范围为0<x<30.九年级数学上册二次函数的图象与性质练习题(附答案)一.选择题1.如果在二次函数的表达式y =ax 2+bx +c 中,a >0,b <0,c <0,那么这个二次函数的图象可能是( )A.B.C.D.2.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为()A.﹣2B.2C.±2D.03.已知A(,y1),B(2,y2),C(﹣,y3)是二次函数y=3(x﹣1)2+k图象上三点,则y1、y2、y3的大小关系为()A.y1>y2>y3B.y2>y1>y3C.y3>y2>y1D.y2>y3>y14.二次函数的部分图象如图所示,对称轴是直线x=﹣1,则这个二次函数的表达式为()A.y=﹣x2+2x+3B.y=x2+2x+3C.y=﹣x2+2x﹣3D.y=﹣x2﹣2x+3 5.在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为()A.B.C.D.6.关于抛物线y=﹣x2+2x﹣3的判断,下列说法正确的是()A.抛物线的开口方向向上B.抛物线的对称轴是直线x=﹣1C.抛物线对称轴左侧部分是下降的D.抛物线顶点到x轴的距离是27.已知二次函数y=x2﹣4x+5(0≤x≤3),则它的最大值是()A.1B.2C.3D.58.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<﹣1或x>3.其中,正确的说法有()A.①②④B.①②⑤C.①③⑤D.②④⑤9.已知函数y=2(x+1)2+1,则()A.当x<1 时,y随x的增大而增大B.当x<1 时,y随x的增大而减小C.当x<﹣1 时,y随x的增大而增大D.当x<﹣1 时,y随x的增大而减小10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的有()个.①abc>0;②2a+b=0;③9a+3b+c<0;④4ac﹣b2<0;⑤a+b≥m(am+b)(m为任意实数).A.3B.2C.1D.0二.填空题11.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是.(请用“>”连接排序)12.抛物线y=3x2+6x+11的顶点坐标为.13.二次函数y=3(x﹣1)2+5的最小值为.14.已知二次函数y=2x2+bx+4顶点在x轴上,则b=.15.二次函数y=x2﹣2x+1在2≤x≤5范围内的最小值为.16.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是(填写序号).三.解答题17.已知二次函数的顶点坐标为A(1,﹣4),且经过点B(3,0).(1)求该二次函数的解析式;(2)判断点C(2,﹣3)是否在该函数图象上,并说明理由.18.如图,已知直线l过点A(4,0),B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP=4,试求二次函数的表达式.19.如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).(1)求m的值;(2)过动点P(n,0)且垂直于x轴的直线与L1,L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.20.已知二次函数y=a(x+a)(x+a﹣1).(1)当a=2时,求该二次函数图象的对称轴.(2)当a<0时,判断该二次函数图象的顶点所在的象限,并说明理由.(3)当0<x<3时,y随着x增大而增大,求a的取值范围.21.已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),求△OAB的面积.22.抛物线y=﹣x2+bx+c经过点A(3,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.(1)求抛物线的解析式;(2)连接AB、AC、BC,求△ABC的面积.23.如图,在平面直角坐标系中,直线AB与抛物线y=﹣x2+bx+c交于A(﹣1,0)和B(2,3)两点,抛物线与y轴交于点C.(1)求一次函数和二次函数的解析式;(2)求△ABC的面积.参考答案一.选择题1.解:∵a>0,b<0,c<0,∴﹣>0,∴抛物线的图象开口向上,对称轴在y轴的右边,交y轴于负半轴,故选:C.2.解:∵y=(m+2)x|m|+2是y关于x的二次函数,∴|m|=2且m+2≠0.解得m=2.故选:B.3.解:∵二次函数y=3(x﹣1)2+k图象的对称轴为直线x=1,而A(,y1)到直线x=1的距离最近,C(﹣,y3)到直线x=1的距离最远,∴y3>y2>y1.故选:C.4.解:由图象知抛物线的对称轴为直线x=﹣1,设抛物线解析式为y=a(x+1)2+k,将(﹣3,0)、(0,3)代入,得:,解得:,则抛物线解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3,故选:D.5.解:A、由抛物线可知,a<0,x=﹣<0,得b<0,由直线可知,a<0,b<0,故本选项正确;B、由抛物线可知,a>0,由直线可知,a<0,故本选项错误;C、由抛物线可知,a>0,x=﹣>0,得b<0,由直线可知,a>0,b>0,故本选项错误;D、由抛物线可知,a>0,由直线可知,a<0,故本选项错误.故选:A.6.解:∵y=﹣x2+2x﹣3=﹣(x﹣1)2﹣2,∴抛物线开口向下,对称轴为x=1,顶点坐标为(1,﹣2),在对称轴左侧,y随x的增大而增大,∴A、B、C不正确;∵抛物线顶点到x轴的距离是|﹣2|=2,∴D正确,故选:D.7.解:y=x2﹣4x+5=(x﹣2)2+1,由于0≤x≤3,所以当x=2时,y有最小值1,当x=0时,y有最大值5.故选:D.8.解:根据图象可知:①对称轴﹣>0,故ab<0,正确;②方程ax2+bx+c=0的根为x1=﹣1,x2=3,正确;③x=1时,y=a+b+c<0,错误;④当x<1时,y随x值的增大而减小,错误;⑤当y>0时,x<﹣1或x>3,正确.正确的有①②⑤.故选:B.9.解:∵y=2(x+1)2+1,∴当x>﹣1时,y随x的增大而增大,故选项A错误,当x<﹣1时,y随x的增大而减小,故选项B错误、选项C错误、选项D正确;故选:D.10.解:∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a>0,∵抛物线与y轴的交点坐标在x轴上方,∴c>0,∴abc<0,所以①错误;∵b=﹣2a,∴2a+b=0,所以②正确;∵x=3时,y<0,∴9a+3b+c<0,所以③正确.∵抛物线与x轴有2个交点,∴Δ=b2﹣4ac>0,即4ac﹣b2<0,所以④正确;∵抛物线的对称轴为直线x=1,∴函数的最大值为a+b+c,∴a+b+c≥am2+bm+c(m为任意实数),即a+b≥m(am+b),所以⑤正确.故选:C.二.填空题11.解:如图所示:①y=a1x2的开口小于②y=a2x2的开口,则a1>a2>0,③y=a3x2的开口大于④y=a4x2的开口,开口向下,则a4<a3<0,故a1>a2>a3>a4.故答案为:a1>a2>a3>a412.解:∵y=3x2+6x+11=3(x+1)2+8,∴抛物线y=3x2+6x+11的顶点坐标为(﹣1,8),故答案为(﹣1,8).13.解:由于二次函数y=3(x﹣1)2+5中,a=3>0,所以当x=1时,函数取得最小值为5,故答案为5.14.解:∵二次函数y=2x2+bx+4顶点在x轴上,∴=0,解得b=,故答案为:±4.15.解:∵二次函数y=x2﹣2x+1=(x﹣1)2,∴当x>1时,y随x的增大而增大,∴在2≤x≤5范围内,当x=2时,y取得最小值,此时y=(2﹣1)2=1,故答案为:1.16.解:∵抛物线的对称轴为直线x=﹣=1,∴2a+b=0,所以①正确;∵x=﹣1时,y<0,∴a﹣b+c<0,即a+c<b,所以②错误;∵抛物线与x轴的一个交点为(﹣2,0)而抛物线的对称轴为直线x=1,∴抛物线与x轴的另一个交点为(4,0),所以③错误;∵抛物线开口向上,∴a>0,∴b=﹣2a<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以④正确.故答案为①④.三.解答题17.解:(1)设二次函数的解析式是y=a(x﹣h)2+k,∵二次函数的顶点坐标为A(1,﹣4),∴y=a(x﹣1)2﹣4,∵经过点B(3,0),∴代入得:0=a(3﹣1)2﹣4,解得:a=1,∴y=(x﹣1)2﹣4,即二次函数的解析式为y=x2﹣2x﹣3;(2)点C(2,﹣3)在该函数图象上,理由是:把C(2,﹣3)代入y=x2﹣2x﹣3得:左边=﹣3,右边=4﹣4﹣3=﹣3,即左边=右边,所以点C在该函数的图象上.18.解:设直线l的解析式为y=kx+b,把A(4,0),B(0,4)分别代入得,解得,∴直线l的关系式为y=﹣x+4,设P(t,﹣t+4),∵S△AOP=4,∴×4×(﹣t+4)=4,解得t=2,∴P(2,2),把P(2,2)代入y=ax2得4a=2,解得a=,∴二次函数的表达式为y=x2.19.解:(1)把B(1,1)代入y=ax2得:a=1,∴抛物线解析式为y=x2.把A(m,4)代入y=x2得:4=m2,∴m=±2.∵点A在二象限,∴m=﹣2.(2)观察函数图象可知:当﹣2<x<1时,直线在抛物线的上方,∴n的取值范围为:﹣2<n<1.20.解:(1)当a=2时,y=2(x+2)(x+1),∴二次函数的对称轴为x=.(2)由题知二次函数与x轴的交点坐标为(﹣a,0),(1﹣a,0);∵a<0,∴二次函数的开口方向向下;又﹣a>0,1﹣a>0,所以对称轴所在直线为x==>0,当x=时,y=﹣>0,所以顶点坐标(,﹣)在第一象限.(3)由(2)知,二次函数的对称轴为直线x=,∵当0<x<3时,y随着x增大而增大,∴当a>0时,≤0,解得a≥;当a<0,≥3,解得a≤﹣.∴a的取值范围为a≥或a≤﹣.21.解:∵一次函数y=kx﹣2的图象相过点A(﹣1,﹣1),∴﹣1=﹣k﹣2,解得k=﹣1,∴一次函数表达式为y=﹣x﹣2,∴令x=0,得y=﹣2,∴G(0,﹣2),∵y=ax2过点A(﹣1,﹣1),∴﹣1=a×1,解得a=﹣1,∴二次函数表达式为y=﹣x2,由一次函数与二次函数联立可得,解得,,∴S△OAB=OG•|A的横坐标|+OG•点B的横坐标=×2×1+×2×2=1+2=3.22.解:(1)∵抛物线经过A、B(0,3)∴由上两式解得∴抛物线的解析式为:;(2)由(1)抛物线对称轴为直线x=把x=代入,得y=4则点C坐标为(,4)设线段AB所在直线为:y=kx+b,则有,解得∴AB解析式为:∵线段AB所在直线经过点A、B(0,3)抛物线的对称轴l于直线AB交于点D∴设点D的坐标为D将点D代入,解得m=2∴点D坐标为,∴CD=CE﹣DE=2过点B作BF⊥l于点F∴BF=OE=∵BF+AE=OE+AE=OA=∴S△ABC=S△BCD+S△ACD=CD•BF+CD•AE∴S△ABC=CD(BF+AE)=×2×=23.解:(1)∵抛物线y=﹣x2+bx+c交于A(﹣1,0)和B(2,3)两点∴,解得:,∴抛物线解析式为y=﹣x2+2x+3,设直线AB的解析式为y=mx+n(m≠0),则,解得,∴直线AB的解析式为y=x+1;(2)令x=0,则y=﹣x2+2x+3=3,∴C(0,3),则OC=3,BC=2,BC∥x轴,∴S△ABC=×BC×OC==3.九年级数学上册二次函数单元综合测试卷一.选择题(共10小题)1.下列各式中,是y关于x的二次函数的是()A.y=4x B.y=3x﹣5C.y=D.y=2x2+12.已知:a>b>c,且a+b+c=0,则二次函数y=ax2+bx+c的图象可能是下列图象中的()A.B.C.D.3.二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是()A.(2,6)B.(4,6)C.(3,﹣5)D.(3,5)4.将二次函数y=x2+2x﹣1转化为y=a(x﹣h)2+k的形式,结果为()A.y=(x﹣1)2B.y=(x+1)2C.y=(x+1)2﹣1D.y=(x+1)2﹣2 5.已知0≤x≤,则函数y=﹣2x2+8x﹣6的最大值是()A.﹣10.5B.2C.﹣2.5D.﹣66.顶点坐标为(3,1),形状与函数y=的图象相同且开口方向相反的抛物线的解析式为()A.y=+1B.y=+1C.y=﹣+1D.y=﹣+17.已知点A(﹣1,y1),B(1,y2),C(2,y3)都在二次函数y=(x﹣1)2的图象上,则y1,y2,y3的大小关系正确的是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y3<y2<y1 8.抛物线y=ax2+bx+c纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…则下列说法中正确的个数是()①方程ax2+bx+c=0,有两根为x1=﹣2,x2=3;②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=1;④抛物线开口向上.A.1B.2C.3D.49.如图,在正方形ABCD中,AB=4,AC与BD交于点O,E,F分别为边BC,CD上的点(点E,F不与线段BC,CD的端点重合),BE=CF,连接OE,OF,EF.关于以下三个结论,下列判断正确的是()结论Ⅰ:∠BOF始终是90°;结论Ⅱ:△OEF面积的最小值是2;结论Ⅲ:四边形OECF的面积始终是8.A.结论Ⅰ和Ⅱ都对,结论Ⅲ错B.结论Ⅰ和Ⅱ都对,结论Ⅱ错C.结论Ⅱ和Ⅲ都对,结论Ⅰ错D.三个结论都对10.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为()A.37.5°B.40°C.42.5°D.45°二.填空题(共6小题)11.函数是二次函数,则m的值为.12.已知抛物线y=x2﹣4x+c.与直线y=m相交于A,B两点,若点A的横坐标;x A=﹣1,则点B的横坐标.x B的值为.13.已知二次函数y=ax2开口向上,且|2﹣a|=3,则a=.14.已知抛物线y=x2﹣3x+1的图象上有一点A(m,n),则m﹣n的最大值是.15.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,交抛物线于另一点D,若AB+CD=3,则c的值为.16.如图,在矩形ABCD中,AB=12,BC=16,点E、F分别是边AB、BC上的动点,且EF=10,点G是EF的中点,AG、CG,则四边形AGCD面积的最小值为.三.解答题(共7小题)17.看图回答.(1)当y=0时,求x的值;(2)当y>5时,求x的范围;(3)y随x的增大而增大时,求x的范围.18.已知二次函数y=x2﹣6x+8.(1)将解析式化成顶点式;(2)写出它的开口方向、对称轴和顶点坐标;(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.19.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.20.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在云南省广泛种植.长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售,平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)若降价2元,则每天的销售利润是多少元(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)(3)将商品的销售单价定为多少元时,商场每天销售该商品获得的利润w最大?最大利润是多少元?21.如图,抛物线与x轴交于A(﹣1,0)、B(4,0),与y轴交于C.(1)求抛物线的解析式;(2)如图1,已知线段DE与线段BC关于平面内某点成中心对称,其中DE的两端点刚好一个落在抛物线上,一个落在对称轴上,求落在对称轴上的点的坐标;(3)如图2,点M为第二象限抛物线上,作MN∥BC交抛物线于点N,直线NB、MC 交于点P,求P点的横坐标.22.在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y'),给出如下定义:若y'=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)点(﹣5,﹣2)的“可控变点”坐标为;(2)若点P在函数y=﹣x2+16的图象上,其“可控变点”Q的纵坐标y′是7,求“可控变点”Q的横坐标;(3)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,求实数a的取值范围.23.在平面直角坐标系中,抛物线y=x2+bx+c经过A(﹣4,0),点M为抛物线的顶点,点B在y轴上,直线AB与抛物线在第一象限交于点C(2,6),如图①.(1)求抛物线解析式;(2)直线AB的函数解析式为,点M的坐标为.(3)在y轴上找一点Q,使得△AMQ的周长最小,具体作法如图②,作点A关于y轴的对称点A',连接MA′交y轴于点Q,连接AM,AQ,此时△AMQ的周长最小,请求出点Q的坐标;(4)在坐标平面内是否存在点N,使以点A,O,C,N为顶点的四边形是平行四边形?若存在请直接写出点N的坐标;若不存在,请说明理由.参考答案一.选择题(共10小题)1.下列各式中,是y关于x的二次函数的是()A.y=4x B.y=3x﹣5C.y=D.y=2x2+1解:A.根据二次函数的定义,y=4x是一次函数,不是二次函数,故A不符合题意.B.根据二次函数的定义,y=3x﹣5不是二次函数,是一次函数,故B不符合题意.C.根据二次函数的定义,y=是反比例函数,不是二次函数,故C不符合题意.D.根据二次函数的定义,y=2x2+1是二次函数,故D符合题意.故选:D.2.已知:a>b>c,且a+b+c=0,则二次函数y=ax2+bx+c的图象可能是下列图象中的()A.B.C.D.解:A、由图知a>0,﹣=1,c>0,即b<0,∵已知a>b>c,故本选项错误;B、由图知a<0,而已知a>b>c,且a+b+c=0,必须a>0,故本选项错误;C、图C中条件满足a>b>c,且a+b+c=0,故本选项正确;D、∵a+b+c=0,即当x=1时a+b+c=0,与图中与x轴的交点不符,故本选项错误.故选:C.3.二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是()A.(2,6)B.(4,6)C.(3,﹣5)D.(3,5)解:∵二次函数可化为y=(x﹣3)2+5,∴二次函数y=(x﹣2)(x﹣4)+6的顶点坐标是(3,5),故选:D.4.将二次函数y=x2+2x﹣1转化为y=a(x﹣h)2+k的形式,结果为()A.y=(x﹣1)2B.y=(x+1)2C.y=(x+1)2﹣1D.y=(x+1)2﹣2解:y=x2+2x﹣1=(x2+2x+1)﹣2=(x+1)2﹣2,即y=(x+1)2﹣2.故选:D.5.已知0≤x≤,则函数y=﹣2x2+8x﹣6的最大值是()A.﹣10.5B.2C.﹣2.5D.﹣6解:y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2,∴当x<2时,y随着x增大而增大,∴当x=时有最大值y=﹣2(﹣2)2+2=﹣2.5,故选:C.6.顶点坐标为(3,1),形状与函数y=的图象相同且开口方向相反的抛物线的解析式为()A.y=+1B.y=+1C.y=﹣+1D.y=﹣+1解:设所求的抛物线解析式为y=a(x﹣3)2+1,∵所求抛物线与函数y=的图象相同且开口方向相反,∴a=﹣,∴所求的抛物线解析式为y=﹣(x﹣3)2+1.故选:D.7.已知点A(﹣1,y1),B(1,y2),C(2,y3)都在二次函数y=(x﹣1)2的图象上,则y1,y2,y3的大小关系正确的是()A.y1<y2<y3B.y2<y1<y3C.y2<y3<y1D.y3<y2<y1解:当x=﹣1时,y1=(x﹣1)2=(﹣1﹣1)2=4;当x=1时,y2=(x﹣1)2=(1﹣1)2=0;当x=2时,y3=(x﹣1)2=(2﹣1)2=1,所以y2<y3<y1.故选:C.8.抛物线y=ax2+bx+c纵坐标y的对应值如下表:x…﹣2﹣1012…y…04664…则下列说法中正确的个数是()①方程ax2+bx+c=0,有两根为x1=﹣2,x2=3;②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=1;④抛物线开口向上.A.1B.2C.3D.4解:根据表格数据可知:抛物线的对称轴是直线x==,∴③错误;∵抛物线与x轴的一个交点为(﹣2,0),∴抛物线与x轴的另一个交点为(3,0),∴方程ax2+bx+c=0有两根为x1=﹣2,x2=3;故①正确;从表格可知当x=0时,y=6,∴抛物线与y轴的交点为(0,6);∴②正确;从表格可知:当x<时,y随x的增大而增大,当x>时,y随x的增大而减小,∴抛物线开口向下,故④错误.故选:B.9.如图,在正方形ABCD中,AB=4,AC与BD交于点O,E,F分别为边BC,CD上的点(点E,F不与线段BC,CD的端点重合),BE=CF,连接OE,OF,EF.关于以下三个结论,下列判断正确的是()结论Ⅰ:∠BOF始终是90°;结论Ⅱ:△OEF面积的最小值是2;结论Ⅲ:四边形OECF的面积始终是8.A.结论Ⅰ和Ⅱ都对,结论Ⅲ错B.结论Ⅰ和Ⅱ都对,结论Ⅱ错C.结论Ⅱ和Ⅲ都对,结论Ⅰ错D.三个结论都对解:∵四边形ABCD是正方形,∴OB=OC,∠BOC=90°,∴∠OBE=∠OCF=45°,∵BE=CF,∴△BOE≌△COF,∴OE=OF,∠BOE=∠COF,∴∠BOE+∠COE=∠COF+∠COE,即∠EOF=∠BOC=90°,且S△COE+S△COF=S△COE+S△BOE,即S四边形OECF=S△BOC=S正方形ABCD=×4×4=4,由垂线段最短可得,当OE⊥BC时,OE=BC=×4=2,△OEF面积取最小值为×2×2=2,∴结论Ⅰ和Ⅱ都对,结论Ⅲ错,故选:A.10.使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0<x≤90)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为()A.37.5°B.40°C.42.5°D.45°解:把(25,0.725),(50,0.06),(60,0.09)代入y=ax2+bx+c得:,解得,∴y=0.0001x2﹣0.008x+0.21=0.0001(x﹣40)2+0.05,∵0.0001>0,∴x=40时,y最小为0.05,∴燃气灶烧开一壶水最节省燃气的旋钮角度约为40°,故选:B.二.填空题(共6小题)11.函数是二次函数,则m的值为3.解:∵函数是二次函数,∴m2﹣7=2且m+3≠0,解得:m=3.则m的值为3.故答案为:3.12.已知抛物线y=x2﹣4x+c.与直线y=m相交于A,B两点,若点A的横坐标;x A=﹣1,则点B的横坐标.x B的值为5.解:∵y=x2﹣4x+c,∴抛物线开口向上,对称轴为直线x=﹣=2,∴点A,B关于直线x=2对称,∵点A横坐标为﹣1,∴点B横坐标为5,故答案为:5.13.已知二次函数y=ax2开口向上,且|2﹣a|=3,则a=5.解:∵|2﹣a|=3,∴2﹣a=±3,解得:a=﹣1或5,又二次函数y=ax2开口向上,则a>0,故a=5.故答案为:5.14.已知抛物线y=x2﹣3x+1的图象上有一点A(m,n),则m﹣n的最大值是3.解:∵点A(m,n)在抛物线y=x2﹣3x+1上,∴n=m2﹣3m+1,∴m﹣n=﹣m2+4m﹣1=﹣(m﹣2)2+3,∴当m=2时,m﹣n有最大值为3,故答案为:3.15.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,交抛物线于另一点D,若AB+CD=3,则c的值为﹣.解:设A(x1,0),B(x2,0),令y=0,则y=﹣x2+2x+c=0,由根与系数的关系得:x1+x2=2,x1•x2=﹣c,则AB=|x1﹣x2|===2,令x=0,则y=c,∴C(0,c),∵CD∥x轴,∴点D纵坐标为c,当y=c时,则﹣x2+2x+c=c,解得:x=2,或x=0,∴D(2,c),∴CD=2,∵AB+CD=3,∴2+2=3,解得:c=﹣,故答案为:﹣.16.如图,在矩形ABCD中,AB=12,BC=16,点E、F分别是边AB、BC上的动点,且EF=10,点G是EF的中点,AG、CG,则四边形AGCD面积的最小值为142.解:连接AC,过B作BH⊥AC于H,以B为圆心,BG为半径作圆,交BH于G',如图:∵四边形ABCD是矩形,∴∠EBF=90°,∵EF=10,点G是EF的中点,∴BG=EF=10=5,∴G在以B为圆心,5为半径的弧上,当G运动到G'时,S△ACG最小,此时四边形AGCD 面积的最小值,最小值即为四边形AG'CD的面积,∵AB=12=CD,BC=16=AD,∴AC=20,S△ACD=×12×16=96,∴BH==,∴G'H=BH﹣5=﹣5=,∴S△ACG'=AC•G'H=×20×=46,∴S四边形AG'CD=S△ACD+S△ACG'=46+96=142,即四边形AGCD面积的最小值是142.故答案为:142.三.解答题(共7小题)17.看图回答.(1)当y=0时,求x的值;(2)当y>5时,求x的范围;(3)y随x的增大而增大时,求x的范围.解:(1)由图象可知,抛物线经过点(﹣1,0),对称轴为直线x=1,∴抛物线与x轴的另一个交点为(3,0),∴当y=0时,x的值为﹣1和3;(2)∵抛物线经过点(﹣1,0),(3,0),(0,﹣3),∴设抛物线的解析式为y=a(x+1)(x﹣3),代入(0,﹣3)得,﹣3=﹣3a,解得a=1,∴抛物线的解析式为y=(x+1)(x﹣3),令y=5得5=(x+1)(x﹣3),解得x1=4,x2=﹣2,∴当y>5时,求x的范围是x>4或x<﹣2;(3)∵y=(x+1)(x﹣3)=(x﹣1)2+4,∴抛物线开口向上,顶点为(1,4),对称轴为直线x=1,∴y随x的增大而增大时,x的范围是x>1.18.已知二次函数y=x2﹣6x+8.(1)将解析式化成顶点式;(2)写出它的开口方向、对称轴和顶点坐标;(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.解:(1)y=x2﹣6x+8=x2﹣6x+9﹣1=(x﹣3)2﹣1;(2)开口向上,对称轴是直线x=3,顶点坐标是(3,﹣1);(3)x>3时,y随x的增大而增大;x<3时,y随x增大而减小.19.如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=﹣5r2+20t,求小球飞行高度达到最高时的飞行时间.解:∵h=﹣5t2+20t=﹣5(t﹣2)2+20,且﹣5<0,∴当t=2时,h取最大值20,答:小球飞行高度达到最高时的飞行时间为2s.20.“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种,在云南省广泛种植.长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动,经过调查往年的统计数据发现,云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售,平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元,那么平均每天的销售量会增加10斤,为了尽快减少库存,该水果商决定降价销售.(1)若降价2元,则每天的销售利润是多少元(2)若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元,那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元?(其它成本忽略不计)(3)将商品的销售单价定为多少元时,商场每天销售该商品获得的利润w最大?最大利润是多少元?解:(1)根据题意,降价2元则销售量为60+2×10=80(斤),销售利润为:(30﹣15﹣2)×80=1040(元),。
九年级数学二次函数测试题含答案(精选5套)

九年级数学二次函数测试题含答案(精选5套)九年级数学二次函数测试题含答案(精选5套)第一套:1. 将函数 $y = 2x^2 - 3x - 2$ 化简为标准形式,并求出它的顶点坐标。
答案:将函数化简为标准形式得到 $y = 2(x-\frac{3}{4})^2 -\frac{33}{8}$,顶点坐标为 $(\frac{3}{4}, -\frac{33}{8})$。
2. 求函数 $y = -x^2 + 4x + 1$ 的零点。
答案:将函数化简为标准形式得到 $y = -(x-2)^2 + 5$,令 $y = 0$,解得 $x = 2 \pm \sqrt{5}$,即零点为 $x_1 = 2 + \sqrt{5}$ 和 $x_2 = 2 -\sqrt{5}$。
3. 给定函数 $y = x^2 - 6x + 5$,求其对称轴的方程式。
答案:对称轴的方程式为 $x = \frac{-b}{2a}$,代入 $a = 1$ 和 $b = -6$ 得到 $x = \frac{6}{2} = 3$。
4. 若函数 $y = ax^2 + bx - 9$ 与 $y = -x^2 + 7x$ 有相同的图像,求$a$ 和 $b$ 的值。
答案:由于两个函数有相同的图像,所以它们的系数相等。
比较两个函数的对应系数得到 $a = -1$ 和 $b = 7$。
5. 已知函数 $y = x^2 - 4x + 5$ 的图像上存在一点 $(h, k)$,使得 $x= h - 3$ 时,$y = 2k + 12$,求点 $(h, k)$ 的坐标。
答案:将 $x = h - 3$ 代入函数得到 $y = (h-3)^2 - 4(h-3) + 5$。
代入$y = 2k + 12$ 得到 $(h-3)^2 - 4(h-3) + 5 = 2k + 12$。
整理得到 $(h-3)^2 -4(h-3) - 2k - 7 = 0$。
由于该方程为二次方程,必然存在实数解。
完整版)初三数学二次函数专题训练(含标准答案)-

完整版)初三数学二次函数专题训练(含标准答案)-二次函数专题训练(含答案)一、填空题1.把抛物线y=-1/2x向左平移2个单位得抛物线,接着再向下平移3个单位,得抛物线.2.函数y=-2x+x^2图象的对称轴是x=1,最大值是1.3.正方形边长为3,如果边长增加x面积就增加y=x^2+6x+9.4.二次函数y=-2x+8x-6,通过配方化为y=a(x-2)^2-2的形为.5.二次函数y=ax+c(c不为零),当x取x1,x2(x1≠x2)时,函数值相等,则x1与x2的关系是x1+x2=-2a/c.6.抛物线y=ax^2+bx+c当b=0时,对称轴是x=0,当a,b同号时,对称轴在y轴侧,当a,b异号时,对称轴在x=-b/2a 处.7.抛物线y=-2(x+1)^2-3开口向下,对称轴是x=-1,顶点坐标是(-1,-3).如果y随x的增大而减小,那么x的取值范围是x<-1.8.若a5/2a时,函数值随x的增大而减小.9.二次函数y=ax^2+bx+c(a≠0)当a>0时,图象的开口向上;当a<0时,图象的开口向下,顶点坐标是(-b/2a,c-b^2/4a).10.抛物线y=-2(x-2)^2+2,开口向下,顶点坐标是(2,2),对称轴是x=2.11.二次函数y=-3(x-1)^2+2的图象的顶点坐标是(1,2).12.已知y=(x+1)^2-2,当x≥1时,函数值随x的增大而减小.13.已知直线y=2x-1与抛物线y=5x+k交点的横坐标为2,则k=9,交点坐标为(2,13).14.用配方法将二次函数y=x^2+x-2化成y=a(x-(-1/2))^2-9/4的形式是y=(x+1/2)^2-9/4.15.如果二次函数y=x^2-6x+m的最小值是1,那么m的值是10.二、选择题:16.在抛物线y=2x^2-3x+1上的点是(D)(3,4)17.直线y=5x/2-2与抛物线y=x^2-x的交点个数是(C)2个18.关于抛物线y=ax^2+bx+c(a≠0),下面几点结论中,正确的有(A、B、C)①当a>0时,对称轴左边y随x的增大而减小,对称轴右边y随x的增大而增大,当a<0时,情况相反。
二次函数基础测试题

九年级数学《二次函数》基础测试题一、选择题(每题3分,共27分)1、下列关系式中,属于二次函数的是(x 为自变量)( )A 218y x =B y 21y x= D 22y a x =2、当m 不为何值时,函数2(2)45y m x x =-+-(m 是常数)是二次函数( ) A -2 B 2 C 3 D -33、抛物线y=x 2-1的顶点坐标是( ).A (0,1)B (0,一1)C (1,0)D (一1,0) 4、22y x =+的对称轴是直线( )A x=2B x=0C y=0D y=2 5、二次函数247y x x =-+的最小值为( )A 2B -2C 3D -3 6、经过原点的抛物线是( )A y=2x 2+xB 221)y x =+(C y=2x 2-1D y=2x 2+1 7、已知二次函数232)1y x =-+(,当x=3时,y 的值为( ) A 4 B -4 C 3 D -38、下列函数中,当x<0时,y 随x 的增大而减小的函数是( )A y=-3xB y=4xC 2y x =- D y=-x 29、已知二次函数2210y x x =+-,小明利用计算器列出了下表: ( )那么方程22100x x +-=的一个近似根是: A.-4.1 B.-4.2 C.-4.3 D.-4.4二、填空题(每空3分,共18分)10、将抛物线3)3(22+-=x y 向右平移1个单位后,在向下平移6个单位后所得抛物线的解析式为11、将函数y=x 2+6x+7化为2)y a x h k =-+(形式为 12、写出一个开口向上,顶点是原点的二次函数的解析式:xyO13、若42)2(--=mx m y 是二次函数,则m=14、已知二次函数22-=ax y 的图象经过点(1,-1),则这个二次函数的关系式为 15、已知二次函数2y ax bx c =++的图象如图所示, 则a 0,b 0,c 0。
初三数学二次函数练习题及答案

初三数学二次函数练习题及答案一、基础练习1.把抛物线y=2x向上平移1个单位,得到抛物线_______,把抛物线y=-2x?向下平移个单位,得到抛物线________..抛物线y=3x-1的对称轴是_____,顶点坐标为________,它是由抛物线y=3x?向_______平移______个单位得到的..把抛物线向左平移1个单位,得到抛物线_________,把抛物线 ?向右平移3个单位,得到抛物线________.24.抛物线y=x-1)的开口向________,对称轴是______,顶点坐标是_________,222222?它是由抛物线x2向______平移______个单位得到的..把抛物线y=-13132向_____平移______个单位,就得到抛物线y=-13x2.6.把抛物线y=42向______平移_______个单位,就得到函数y=42的图象..函数y=-的最大值为________,函数y=-x-22213的最大值为________.8.若抛物线y=a的对称轴为x=-3,且它与抛物线y=-2x2的形状相同,?开口方向相同,则点关于原点的对称点为________..已知抛物线y=a2过点,则该函数y=a2当x=________?的时候,?有最____值______.10.若二次函数y=ax2+b,当x取x1,x2时,函数值相等,则x取x1+x2时,函数的值为________.11.一台机器原价50万元.如果每年的折旧率是x,两年后这台机器的价格为y?万元,则y与x的函数关系式为A.y=50B.y=50C.y=50-x2D.y=5012.下列命题中,错误的是 A.抛物线221212x2-1不与x轴相交;B.抛物线x2-1与121222形状相同,位置不同;12C.抛物线y= D.抛物线y=2的顶点坐标为;12)的对称轴是直线x=13.顶点为且开口方向、形状与函数y=- A.y=-13 1313x的图象相同的抛物线是 D.y=1222B.y=-13x2-5C.y=-13214.已知a x-2的图象上,则A.y1 2在同一坐标系中的图象大致为二、整合练习 1.已知反比例函数y=kx的图象经过点A,若二次函数y=12x2-x?的图象平移后经过该反比例函数图象上的点B,C,求平移后的二次函数图象的顶点坐标.2.如图,在正方形ABCD中,AB=2,E是AD边上一点.BE?的垂直平分线交AB于M,交DC于N.设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;当AE为何值时,四边形ADNM的面积最大?最大值是多少?3.将二次函数y=-2x2+8x-5的图象开口反向,并向上、下平移得一新抛物线,新抛物线与直线y=kx+1有一个交点为.求:这条新抛物线的函数解析式;这条新抛物线和直线y=kx+1的另一个交点.答案: 一、1.y=2x2+1 y=-2x2-2.y轴下 1.x+1)2x-3)2.上直线x=1 右 1.右,6.左.0138..大 0 10.11.A 12.D 13.C 14.C15.B+k过原点,所以0=1+k,k=-1,双曲线y=-1x )二、1.由反比例函数y=kx的图象过点A,所以1k2=4,k=2,?所以反比例函数的解析式为y=2x.又因为点B,C在y=2x的图象上,所以m=2,n=1222=1,设二次函数y=12x-x的图象平移后的解析式为y=2+k,它过点B,C,所以平移后的二次函数图象的顶点为.2.连接ME,设MN交BE交于P,根据题意得MB=ME,MN⊥BE.过N作NG⊥AB于F,在Rt△MBP和Rt△MNE中,∠MBP+∠BMN=90°,∠FNM+∠BMN=90°,∠MBP=∠MNF,又AB=FN,Rt△EBA≌Rt△MNE,MF=AE=x.在Rt△AME中,由勾股定理得 ME2=AE2+AM2,所以MB2=x2+AM2,即2=x2+AM2,解得AM=1- 所以四边形ADNM的面积S=AM?DN2?AD?12AM?AF214x2.×2=AM+AM+MF=2AM+AE=2+x=-12x2+x+2.即所求关系式为S=-S=-12x2+x+2.52x2+x+2=-12+=-122+52.52当AE=x=1时,四边形ADNM的面积S的值最大,此时最大值是.3.y=-2x2+8x-5=-22+3,将抛物线开口反向,且向上、?下平移后得新抛物线方程为y=22+m.因为它过点,所以4=22+m,m=2,这条新抛物线方程为y=22+2,即y=2x2-8x+10.直线y=kx+1过点,4=3k+1,k=1,求得直线方程为y=x+1.另一个交点坐标为。
新人教版九年级上册数学:《二次函数》基础练习及答案(5套)
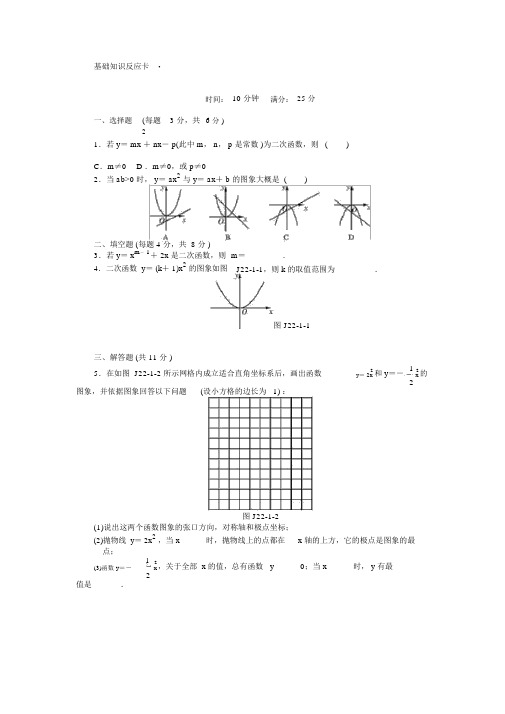
基础知识反应卡·时间:10 分钟满分: 25 分一、选择题(每题3 分,共6 分 )21.若 y = mx + nx - p(此中 m , n , p 是常数 )为二次函数,则 ( )C .m ≠0D .m ≠0,或 p ≠02.当 ab>0 时, y = ax 2 与 y = ax + b 的图象大概是 ()二、填空题 (每题 4 分,共 8 分 )3.若 y = x m -1+ 2x 是二次函数,则 m = ________.4.二次函数 y = (k + 1)x 2 的图象如图 J22-1-1,则 k 的取值范围为 ________.图 J22-1-1三、解答题 (共 11 分 )5.在如图 J22-1-2 所示网格内成立适合直角坐标系后,画出函数2和 y =-1 2 的 y = 2x x(设小方格的边长为 1) :2图象,并依据图象回答以下问题图 J22-1-2(1)说出这两个函数图象的张口方向,对称轴和极点坐标;(2)抛物线 y = 2x 2 ,当 x______时,抛物线上的点都在 x 轴的上方,它的极点是图象的最______点;1 2,关于全部 x 的值,总有函数 y______0;当 x______时, y 有最 ______(3)函数 y =- x 2值是 ______.基础知识反应卡 ·时间: 10 分钟满分: 25 分一、选择题 (每题 3 分,共 6 分 )1.以下抛物线的极点坐标为 (0,1)的是 ( )A . y = x 2+ 1B . y = x 2- 1C .y = (x + 1)22D .y = (x - 1)2.二次函数 y =- x 2 +2x 的图象可能是 ()二、填空题 (每题 4 分,共 8 分 ) 3.抛物线 y = x 2+1的张口向 ________,对称轴是 ________.44.将二次函数 y = 2x 2+ 6x + 3 化为 y = a(x - h)2+ k 的形式是 ________. 三、解答题 (共 11 分 ) 5.已知二次函数 y =- 1x 2+ x + 4.2(1)确立抛物线的张口方向、极点坐标和对称轴; (2)当 x 取何值时, y 随 x 的增大而增大?当x 取何值时, y 随 x 的增大而减小?*基础知识反应卡·时间:10 分钟满分:25 分一、选择题 (每题 3 分,共 6 分 )1.已知二次函数的图象过(1,0), (2,0)和 (0,2) 三点,则该函数的分析式是()A . y= 2x2+ x+ 2B . y= x2+ 3x+ 2C.y= x2- 2x+ 3 D . y= x2- 3x+ 22.若二次函数的图象的极点坐标为(2,- 1),且抛物线过(0,3),则二次函数的分析式是()A . y=- (x- 2)2- 1B. y=-1(x- 2)2-1 2C.y= (x- 2)2- 1 D. y=1(x- 2)2- 1 2二、填空题 (每题 4分,共8 分 )3.如图 J22-1-3,函数 y=- (x- h)2+ k 的图象,则其分析式为____________.图 J22-1-34.已知抛物线y= x2+(m- 1)x-14的极点的横坐标是2,则m 的值是________.三、解答题(共 11 分)5.已知当x= 1 时,二次函数有最大值5,且图象过点(0,- 3),求此函数关系式.基础知识反应卡 ·22.2时间: 10 分钟 满分: 25 分一、选择题 (每题 3 分,共6 分 )1.下表是二次函数 y = ax 2+ bx +c 的自变量 x 的值与函数 y 的对应值,判断方程 ax 2+bx + c = 0(a ≠ 0, a , b , c 为常数 )的一个解的范围是 ( )x 6.17 6.18 6.19 6.20 y = ax 2+ bx + c- 0.03- 0.010.020.04A.6< x<6.17 B . 6.17<x<6.18C .6.18< x<6.19D . 6.19< x<6.202.二次函数 y =2x2+3x - 9 的图象与 x 轴交点的横坐标是 ()33 A. 2和 3 B.2和- 3 C .-3和 2 D .-3和- 22 2二、填空题 (每题 4 分,共 8 分 )3.已知抛物线y =x 2- x -1 与 x 轴的交点为 (m,0),则代数式m 2-m + 2 011 的值为__________.4.如图 J22-2-1 是抛物线 y = ax 2+bx + c 的图象,则由图象可知,不等式ax 2 +bx + c<0的解集是 ________.图 J22-2-1三、解答题 (共 11 分 )5.如图 J22-2-2,直线 y = x + m 和抛物线 y = x 2+ bx + c 都经过点 A(1,0), B(3,2). (1)求 m 的值和抛物线的关系式;(2)求不等式 x 2+bx + c>x + m 的解集 (直接写出答案 ).图 J22-2-2基础知识反应卡·22.3时间: 10 分钟满分: 25 分一、选择题 (每题 3分,共 6分 )2,1.在半径为 4 cm 的圆中,挖去一个半径为x cm 的圆,剩下一个圆环的面积为y cm 则 y 与 x 的函数关系为 ()22A . y=πx - 4 B. y=π(2-x)C.y=- (x2+ 4) D. y=-πx2+ 16πt(s)的关系式是 h=-52.已知某种礼炮的升空高度h(m)与飞翔时间t2+ 20t+ 1.若此礼2炮在升空到最高处时引爆,则引爆需要的时间为()A . 3 s B. 4 s C. 5 s D. 6 s二、填空题 (每题 4分,共 8分 )3.销售某种手工艺品,若每个赢利x 元,一天可售出 (8 - x) 个,则当 x= ________元,一天销售该种手工艺品的总收益y 最大.4.如图 J22-3-1,某省大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8 m,双侧距地面 4 m 的高处各有一个挂校名横匾用的铁环,两铁环的水平距离为 6 m,则校门的高度为 (精准到 0.1 m,水泥建筑物厚度忽视不计)________ .图 J22-3-1三、解答题 (共 11 分 )5.杂技团进行杂技表演,演员从跷跷板右端 A 处弹跳到人梯顶端椅子 B 处,其身体(看成一个点)的路线是抛物线y=- 3x2+ 3x+ 1 的一部分,如图5J22-3-2.(1)求演员弹跳离地面的最大高度;(2)已知人梯高BC= 3.4 米,在一次表演中,人梯到起跳点 A 的水平距离是 4 米,问这次表演能否成功?说明原因.图 J22-3-2基础知识反应卡 ·1. C 2.D 3.3 4.k>- 1 5. 解: 图略.(1)函数 y = 2x 2 的图象张口向上,对称轴为 y 轴,极点坐标为 (0,0). 函数 y =- 1x 2 的图象张口向下,对称轴为y 轴,极点坐标为 (0,0).2(2)≠ 0 低 (3)≤ = 0 大 0 基础知识反应卡 ·1. A 2.Bx + 3 2- 33.上 y 轴 4.y = 22 21 21 2 9 5. 解: (1) 将二次函数 y =- x+ x + 4 配方,得 y =- (x - 1)+ .2 229因此抛物线的张口向下,极点坐标为1, 2 ,对称轴为 x = 1.(2)当 x>1 时, y 随 x 的增大而减小;当x<1 时, y 随 x 的增大而增大.*基础知识反应卡 ·1.D2.C3.y =- (x + 1)2+ 54.- 35.解: 由题意可设函数关系式为 y = a(x - 1)2+ 5,∵图象过点 (0,- 3),∴ a(0- 1)2+ 5=- 3,解得 a =- 8.∴ y =- 8(x - 1)2+ 5,即 y =- 8x 2+ 16x - 3.基础知识反应卡 ·22.21. C 2.B 3.2 012 4.- 2<x<3 5. 解: (1) ∵直线 y = x +m 经过点 A(1,0) ,∴ 0= 1+m.∴m =- 1. 即 m 的值为- 1. ∵抛物线 y = x 2+ bx + c 经过点 A(1,0), B(3,2),0= 1+ b + c ,b =- 3,∴解得2= 9+ 3b +c , c = 2.∴二次函数的关系式为 y =x 2- 3x + 2.(2){ x|x<1 或 x>3} . 基础知识反应卡 ·22.31. D2.B3.44.9.1 m3 25. 解: (1)y =- x + 3x + 15=- 35 2 19 5 x - 2 + 4 .故函数的最大值是 19,419米.∴演员弹跳离地面的最大高度是(2)当 x = 4 时, y =- 3×424+3× 4+ 1= 3.4= BC.5∴此次表演成功.基础知识反应卡 ·23.11. D 2.A3.∠ D ∠E DE DC 4. C 顺时针 905. 解: (1) 旋转中心是点 B. (2)旋转了 90 度.(3)AC 与 EF 垂直且相等.。
初三数学二次函数专题训练(含答案)-

二次函数专题训练(含答案)一、 填空题1.把抛物线221x y -=向左平移2个单位得抛物线,接着再向下平移3个 单位,得抛物线.2.函数x x y +-=22图象的对称轴是,最大值是.3.正方形边长为3,如果边长增加x 面积就增加y ,那么y 与x 之间的函数关系是.6.抛物线异号时,7.抛物线x 的取值8.若a . 9...15.如果二次函数m x x y +-=62的最小值是1,那么m 的值是.二、选择题:16.在抛物线1322+-=x x y 上的点是()A.(0,-1)B.⎪⎭⎫ ⎝⎛0,21 C.(-1,5)D.(3,4) 17.直线225-=x y 与抛物线x x y 212-=的交点个数是()A.0个B.1个C.2个D.互相重合的两个18.关于抛物线c bx ax y ++=2(a ≠0),下面几点结论中,正确的有()① 当a ?0时,对称轴左边y 随x 的增大而减小,对称轴右边y 随x 的增大而增大,当a ?0时,情况相反.② 抛物线的最高点或最低点都是指抛物线的顶点.③ 只要解析式的二次项系数的绝对值相同,两条抛物线的形状就相同.④ 一元二次方程02=++c bx ax (a ≠0)的根,就是抛物线c bx ax y ++=2与x 轴交点的横坐标.A.①②③④B.①②③C.①②D.①19.二次函数y=(x+1)(x-3),则图象的对称轴是()20.如果一次函数b ax y +=的图象如图代bx -3图代21.若抛物线c bx ax y ++=2 A.2B.2122.若函数xa y =的图象经过点(1,-2)轴左侧,图象与负半y 轴相交轴右侧,图象与负半y 轴相交b+c=0,则那时图象经过的点是(),-1)D.(-1,1)与y 轴交于A 点,与x 轴正半轴交于B ,△ABC =6,则b 的值是()A.b=5B.b=-5C.b=±5D.b=4图代13-3-1426.二次函数2ax y =(a ?0),若要使函数值永远小于零,则自变量x 的取值范围是()A .X 取任何实数B.x ?0C.x ?0D.x ?0或x ?027.抛物线4)3(22+-=x y 向左平移1个单位,向下平移两个单位后的解析式为()A.6)4(22+-=x yB.2)4(22+-=x yC.2)2(22+-=x yD.2)3(32+-=x y28.二次函数229k ykx x y ++=(k ?0)图象的顶点在()A.y 轴的负半轴上B.y 轴的正半轴上C.x 轴的负半轴上D.x 轴的正半轴上29.四个函数:xy x y x y 1,1,-=+=-=(x ?0),2x y -=(x ?0),其中图象经过原 点的函数有()A.1个B.2个30.不论x 为值何,函数c bx ax y ++=2A.a ?0,Δ?C .a ?0,Δ?31.已知二次函数1222+-+=b ax x y 和轴上两上不同的点32.已知二次函数c bx ax y ++=2y 轴上.33.A ,B 两点,该ABC=90°,求:(1)直线AB 的解析式;(2)抛 图代13-3-16c 交x 轴正方向于A ,B 两点,交y 轴正方向于C .(1)求a ,c 满足的关系;(2)设∠ACB=PA 与⊙O 的位置关系并证明.35.y 轴,桥拱的DGD '部分为一段抛物线,顶点C 的高度为8米,AD 和A 'D '是两侧高为5.5米的支柱,OA 和OA '为两个方向的汽车通行区,宽都为15米,线段CD 和C 'D '为两段对称的上桥斜坡,其坡度为1∶4.求(1)桥拱DGD '所在抛物线的解析式及CC '的长;(2)BE 和B 'E '为支撑斜坡的立柱,其高都为4米,相应的AB 和A 'B '为两个方向的行人及非机动车通行区,试求AB 和A 'B '的宽;(3)按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于0.4米,车载大型设备的顶部与地面的距离均为7米,它能否从OA (或OA ')区域安全通过?请说明理由.图代13-3-1736.已知:抛物线2)4(2+++-=m x m x y 与x 轴交于两点)0,(),0,(b B a A (a ?b ).O为坐标原点,分别以OA ,OB 为直径作⊙O 1和⊙O 2在y 轴的哪一侧?简要说明理由,并指出两圆的位置关系.37.如果抛物线1)1(22++-+-=m x m x y 与x 轴都交于A ,B 两点,且A 点在x 轴的正半轴上,B 点在x 同的负半轴上,OA 的长是a ,OB 的长是b.(1) 求m 的取值范围;(2) 若a ∶b=3∶1,求m 的值,并写出此时抛物线的解析式;(3) 设(2)中的抛物线与y 轴交于点C ,抛物线的顶点是M ,问:抛物线上是否存在点P ,使△PAB 的面积等于△BCM 面积的8倍?若存在,求出P 点的坐标;若不存在,请说明理由.38.已知:如图代13-3-18,EB 是⊙O 的直径,且EB=6,在BE 的延长线上取点P ,使EP=EB.A 是EP 上一点,过A 作⊙O 的切线AD ,切点为D ,过D 作DF ⊥AB 于F ,过B 作AD 的垂线BH ,交AD 的延长线于H ,连结ED 和FH.图代(1) 若AE=2,求AD 的长.(2) 当点A 在EP 上移动(点A 不与点E 论;②设ED=x ,BH=y ,求y 与x 39.已知二次函数(2)254(222--+--=m x m m x y A ,B (点A 在点B 右边),与y 轴的交点为(1) 若△ABC 为Rt △,求m 的值;(2) 在△ABC 中,若AC=BC ,求∠ACB (3)40.满足(1)(2)y 轴于F ,求直线EF 的解析式.(3)C 点,顶点在⊙C 上,与y 轴交点为B ,求41.q px x ++2图象的顶点为M. (1) m 取何实数值, 二次函数q px x y ++=2的图象与直线m x y +-=总有两个不同的交点.(2) 在(1)的条件下,若直线m x y +-=过点D (0,-3),求二次函数q px x y ++=2的表达式,并作出其大致图象.图代13-3-20(3) 在(2)的条件下,若二次函数q px x y ++=2的图象与y 轴交于点C ,与x 同 的左交点为A ,试在直线x y 21=上求异于M 点P ,使P 在△CMA 的外接圆上.42.如图代13-3-20,已知抛物线b ax x y ++-=2与x 轴从左至右交于A ,B 两点,与y 轴交于点C ,且∠BAC=α,∠ABC=β,tg α-tg β=2,∠ACB=90°.(1) 求点C 的坐标;(2) 求抛物线的解析式;(3) 若抛物线的顶点为P ,求四边形ABPC 的面积.参考答案动脑动手1. 设每件提高x 元(0≤x ≤10),即每件可获利润(2+x )元,则每天可销售(100-10x ) 件,设每天所获利润为y 元,依题意,得∴当x=4时(0≤x ≤10)所获利润最大,即售出价为14元,每天所赚得最大利润360元.当32-=m 时,432322++-=x x y . (3) 当AB=BC 时,22344343⎪⎭⎫ ⎝⎛+=-m m , ∴78-=m . ∴42144782++-=x x y .可求抛物线解析式为:43232,461161,494222+--=+-=+-=x x y x x y x y 或42144782++-=x x y . 3.(1)∵)62(4)]5([222+---=∆m m图代13-3-21∴不论m 取何值,抛物线与x 轴必有两个交点.令y=0,得062)5(222=+++-m x m x0)3)(2(2=---m x x ,∴3,221+==m x x .(2)由(132-+=m d ∵m 2+10?0(3)①当∴A (2,0)142+-=xx y 该抛物线的对称轴是直线x=7225=b .①25)2-.②0,121=-=b b .不存在,b=0,舍去.∴b=-1. .-25≤b ?-1;b ?-1,且b ≠0.同步题库一、 填空题1.3)2(21,)2(2122-+-=+-=x y x y ;2.81,41=x ;3.9)3(2-+=x y ;4. 2)2(22+--=x y ;5.互为相反数;6.y 轴,左,右;7.下,x=-1,(-1,-3),x ?-1;8.四,增大;9.向上,向下,a b x a b ac a b 2,44,22-=⎪⎪⎭⎫ ⎝⎛--;10.向下,(h,0),x=h ;11.-1,-2;12.x ?-1;13.-17,(2,3);14.91312-⎪⎭⎫ ⎝⎛+=x y ;15.10. 二、选择题16.B17.C18.A19.A20.C21.D22.B23.B24.D25.B26.D27.C28.C29.A30.D三、解答题31.解法一:依题意,设M (x 1,0),N (x 2,0),且x 1≠x 2,则x 1,x 2为方程x 2+2ax-2b+1=0的两个实数根,∴a x x 221-=+,1x ·122+-=b x .∵x 1,x 2又是方程3(2-+-a x ∴x 1+x 2=a-3∴⎩⎨⎧+--22b a 解得⎩⎨⎧==1b a 当a=1,b=0∴a=1,12+-b 的图象对称轴为a x -=,1的图象的对称轴为23-=a x , x 轴上两个不同的点M ,N ,. 23-a . 1=.12+-b x 和1222-+--=b x x y .依题意,令y=0,得01222=+-+b x x ,01222=-+--b x x .①+②得022=-b b .解得2,021==b b .∴⎩⎨⎧==;0,1b a 或⎩⎨⎧==.2,1b a 当a=1,b=0时,二次函数的图象与x 轴只有一个交点,∴a=1,b=0舍去.当a=1,b=2时,二次函数为322-+=x x y 和322+--=x x y 符合题意.∴a=1,b=2.32.解:∵c bx ax y ++=2的图象与x 轴交于点B (x 1,0),C (x 2,0), ∴c x x b x x =⋅-=+21,.又∵132221=+x x 即(x ∴(2--a b 又由y 的图象过点A (2,2-a b与y 设y (1)6,3,==OD OC . 0,4)或(0,-4).P ,B 两点直线的解析式为或3,6,2,====OC OD OB OCOP OD OB . ∴OP=1,这时P 点坐标为(0,1)或(0,-1).当P 点坐标为(0,1)时,可设过P ,B 两点直线的解析式为y=kx+1.有0=-2k+1.得21=k . ∴121+-=x y .当P 点坐标为(0,-1)时,可设过P ,B 两点直线的解析式为y=kx-1,有0=-2k-1, 得21-=k . ∴121--=x y . (2) 当B (3,0),C (-2,0),D (0,6)时,同理可得y=-3x+9,或y=3x-9, 或11+-=x y ,(解法二:设抛物线的解析式为:c bx ax y ++=2,又设点A (4,0)关于x=-1的对称是D.∵CA=1+4=5,∴CD=5.∴OD=6.∴D 点坐标为(-6,0).将点A (4,0),B (0,2),D (-6,0)代入抛物线方程,得解得2,61,121=-=-=c b a .∴抛物线的解析式为:2611212+--=x x y . 34.解:(1)A ,B 的横坐标是方程032=+-c x ax 的两根,设为x 1,x 2(x 2?x 1),C 的纵坐标是C.又∵y 轴与⊙O 相切,∴OA ·OB=OC 2.∴x 1·x 2=c 2.又由方程032=+-c x ax 知 c x x =⋅,∴在Rt △PAE 中,a PE 4=. ∴25==AE PE tg β. ∴tg β=tg α.∴β=α.∴∠PAE=∠ADE.∵∠ADE+∠DAE=90°∴PA 和⊙D 相切.35.解:(1)设DGD '所在的抛物线的解析式为c ax y +=2,由题意得G (0,8),D (15,5.5).∴⎩⎨⎧+==.255.5,8c a c 解得⎪⎩⎪⎨⎧=-=.8,901c a∴DGD '所在的抛物线的解析式为89012+-=x y . ∵41=AC AD 且AD=5.5, ∴AC=5.5×4=22(米). ∴2215(2)(22+⨯=+⨯=='AC OA OC c c )=74答:cc (2)∵BC EB ∴∴答:AB 和A 'B (3) 在901-=x y 1(OA ')区域安全通过.O 2外切于原点O ,a ?0,b ?0.02=的两个根a ,b 异号.,∴m ?-2.PO 1O 2Q 是直角梯形.2212b Q O =(或221a 或1). PO 1O 2Q 是矩形.根据题意,计算得22121b S Q O PO =四边形(或221a 或1). (3)∵4)2()2(4)4(22++=+-+=∆m m m ?0∴方程02)4(2=+++-m x m x 有两个不相等的实数根.∵m ?-2,∴⎩⎨⎧+=+=+.02,04 m ab m b a∴a ?0,b ?0.∴⊙O 1与⊙O 2都在y 轴右侧,并且两圆内切.37.解:(1)设A ,B 两点的坐标分别是(x 1,0)、(x 2,0),∵A ,B 两点在原点的两侧,∴x 1x 2?0,即-(m+1)?0,解得m ?-1.∵)1()1(4)]1(2[2+⨯-⨯--=∆m m当m ?-1时,Δ?0,∴m 的取值范围是m ?-1.(2)∵a ∶b=3∶1,设a=3k ,b=k (k ?0),则x 1=3k ,x 2=-k ,∴⎩⎨⎧-⋅-(33k k k k 解得1=m ∵31=m 时,21=+x x ∴2+-⋅+⋅.)1(,1q q ==.2,2q py=2x+2.N 点坐标是(0,2),MNC BCN S ∆∆+设P 点坐标是(x,y ),∵BCM ABP S S ∆∆=8,∴1821⨯=⨯⨯y AB . 即8421=⨯⨯y . ∴4=y .∴4±=y .当y=4时,P 点与M 点重合,即P (1,4),当y=-4时,-4=-x 2+2x+3, 解得221±=x .∴满足条件的P 点存在.P 点坐标是(1,4),)4,221(),4,221(---+.38.(1)解:∵AD 切⊙O 于D ,AE=2,EB=6,∴AD 2=AE ·AB=2×(2+6)=16.∴AD=4.图代13-2-23(2)①无论点A 在EP 上怎么移动(点A 不与点E 重合),总有ED AD =.证法一:连结∵AH 是⊙∴∠又∵BH ⊥AH ∴∠有∠=90°=∠在△DFB DF ⊥AB ,∠DFB=∠DHB=90FHED AH AD =. DB ,的切线,∠DEF.,BH ⊥DH ,∠DBH.F ,H 两点,EDF=∠DFH.FH. ∴FHED AH AD =. ②∵ED=x ,BH=,BH=y ,BE=6,BF=BH ,∴EF=6y.又∵DF 是Rt △BDE 斜边上的高,∴△DFE ∽△BDE , ∴EBED ED EF =,即EB EF ED ⋅=2. ∴)6(62y x -=,即6612+-=x y . ∵点A 不与点E 重合,∴ED=x ?0.A 从E 向左移动,ED 逐渐增大,当A 和P 重合时,ED 最大,这时连结OD ,则OD ⊥PH.∴OD ∥BH.又12,936==+=+=PB EO PE PO ,4,=⋅==POPB OD BH PB PO BH OD , ∴246,4=-=-===BF EB EF BH BF ,由ED 2=EF ·EB 得12622=⨯=x ,2⎭⎝2过A 作AD ⊥BC ,垂足为D ,∴AB ·OC=BC ·AD.∴58=AD .∴545258sin ===∠AC AD ACB .图代13-3-25(3)CO AB S ABC ⋅=∆21 ∵212942≥+-=m m u , ∴当21=u ,即2=m 时,S 有最小值,最小值为45. 40.解:(1)∵OA ⊥OB ,OA ∶OB=4∶3,⊙D 的半径为2,∴⊙C 过原点,OC=4,AB=8. A 点坐标为⎪⎭⎫ ⎝⎛0,532,B 点坐标为⎪⎫ ⎛24,0.∴⊙C 的圆心C (2)由EF 是⊙D ∵∴∠COA=∠CAO ∴Rt △AOB ∽Rt ∴OA OC AB OE =32034+-=x y . ⎪⎭⎫ ⎝⎛+4512,516,可得 5242++x . ⎪⎭⎫ ⎝⎛-4512,516,得 ∴5244852+--=x x y . 综合上述,抛物线解析式为5243252++-=x x y 或5244852+-=x x y . 41.(1)证明:由有m x x +-=21, ∴m y m x m x 31,32,23===.∴交点)31,32(m m M . 此时二次函数为m m x y 31322+⎪⎭⎫ ⎝⎛-= m m mx x 31943422++-=. 由②③联立,消去y ,有0329413422=-+⎪⎭⎫ ⎝⎛--m m x m x .∴无论m 为何实数值,二次函数x y +=2图代(2)解:∵直线∴∴∴M (-21)2(22-=-+=x x y 为△CMA 外接圆的直径,P 在这个圆上, ∠.过M 作MS ⊥y 轴于S ,MS 的延长线与PR 的Q.222121)2(⎪⎭⎫ ⎝⎛+++=n n MP . 22222213n n NP NC CP +⎪⎭⎫ ⎝⎛-=+=. 202=CM. 而222CM CP MP =+,∴20213121)2(2222=+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+++n n n n ,即062252=-+n n , ∴012452=-+n n ,0)2)(65(=+-n n . ∴2,5621-==n n . 而n 2=-2即是M 点的横坐标,与题意不合,应舍去. ∴56=n ,42.0,当0122=++-x x 时,21±=x .∴)0,21(),0,21(+-B A .延长PC 交x 轴于点D ,过C ,P 的直线为y=x+1,∴点D 坐标为(-1,0).∴DCA DPB ABPC S S S ∆∆-=四边形。
九年级数学二次函数测试题含答案(精选5套)

1、抛物线y =x 2-2x +1的对称轴是( )(A )直线x =1 (B )直线x =-1(C )直线x =2 (D )直线x =-22、对于2)3(22+-=x y 的图象下列叙述正确的是 ( )A 、顶点坐标为(-3,2) B 、对称轴为y=3C 、当3≥x 时y 随x 增大而增大D 、当3≥x 时y 随x 增大而减小3、函数y =ax 2(a ≠0)的图象经过点(a ,8),则a 的值为 ( )A.±2 B.-2 C.2 D.3 4、自由落体公式h =21gt 2(g 为常量),h 与t 之间的关系是 ( ) A.正比例函数 B.一次函数C.二次函数 D.以上答案都不对 5、对于任意实数m ,下列函数一定是二次函数的是 ( )A .22)1(x m y -=B .22)1(x m y +=C .22)1(x m y +=D .22)1(x m y -= 6、二次函数y=x 2图象向右平移3个单位,得到新图象的函数表达式是 ( ) A.y=x 2+3 B.y=x 2-3C.y=(x+3)2D.y=(x-3)27、某工厂第一年的利润是20万元,第三年的利润是y 万元,与平均年增长率x 之间的函数关系式是_____。
8、某学校去年对实验器材投资为2万元,预计今明两年的投资总额为y 万元,年平均增长率为x 。
则y 与x 的函数解析式_____。
9、m 取___时,函数)1()(22+++-=m mx x m m y 是以x 为自变量的二次函数. 10、已知二次函数y=-41x 2+x+2指出 (1)函数图像的对称轴和顶点坐标;(2)把这个函数的图像向左、向下平移2个单位,得到哪一个函数的图像?1、抛物线y=x2-2x+1的对称轴是( )(A)直线x=1 (B)直线x=-1(C)直线x=2 (D)直线x=-22、对于2)3(22+-=x y 的图象下列叙述正确的是 ( )A 、顶点坐标为(-3,2) B 、对称轴为y=3C 、当3≥x 时y 随x 增大而增大D 、当3≥x 时y 随x 增大而减小3、函数y =ax 2(a ≠0)的图象经过点(a ,8),则a 的值为 ( )A.±2 B.-2 C.2 D.3 4、自由落体公式h =21gt 2(g 为常量),h 与t 之间的关系是 ( ) A.正比例函数 B.一次函数C.二次函数 D.以上答案都不对 5、对于任意实数m ,下列函数一定是二次函数的是 ( )A .22)1(x m y -=B .22)1(x m y +=C .22)1(x m y +=D .22)1(x m y -= 6、二次函数y=x 2图象向右平移3个单位,得到新图象的函数表达式是 ( ) A.y=x 2+3 B.y=x 2-3C.y=(x+3)2D.y=(x-3)27、某工厂第一年的利润是20万元,第三年的利润是y 万元,与平均年增长率x 之间的函数关系式是_____。
初三数学二次函数必刷题

初三数学二次函数必刷题以下是一些初三数学二次函数的必刷题,涵盖了二次函数的基本概念、性质以及应用等方面:一、选择题1.下列函数中,哪些是二次函数?A. y = 3x + 5B. y = x^2 - 2xC. y = 1/xD. y = x3答案:B2.二次函数y = ax^2 + bx + c的对称轴是直线()。
A. x = -b/aB. x = b/aC. x = -b/2aD. x = b/2a答案:C3.已知二次函数y = 2x^2 + 9x + 34,当x取何值时,y有最小值?A. x = -9/4B. x = -3/4C. x = 9/4D. x = 3/4答案:A(通过公式x=-b/2a求得)二、填空题4.二次函数y = -3x^2 + 6x的顶点坐标为______。
答案:(1,3)(通过公式-b/2a求得x坐标,再代入求得y坐标)5.已知二次函数y = ax^2经过点(2,4),则a的值为______。
答案:2(代入点(2,4)到y=ax^2中求解)三、解答题6.已知二次函数y = x^2 - 4x + 3。
(1)求该二次函数的顶点坐标和对称轴;答案:顶点坐标为(2,-1),对称轴为直线x=2(通过公式-b/2a求得对称轴,再代入求得顶点坐标)(2)求该二次函数与x轴的交点坐标;答案:交点坐标为(1,0)和(3,0)(令y=0,求解x的值)(3)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?答案:当x>2时,y随x的增大而增大;当x<2时,y随x的增大而减小(根据二次函数的开口方向和对称轴判断)7.某商店销售一种商品,每件的成本为40元。
若按每件50元销售,一个月能售出500件。
销售单价每涨1元,月销售量就减少10件。
设销售单价为x元,月销售利润为y元。
(1)求y与x的函数关系式;答案:y=-10x^2+1400x-40000(根据题意,利润=销售量×(销售单价-成本),销售量=500-10(销售单价-50))(2)当销售单价定为多少元时,该商店一个月销售这种商品所获得的利润最大?最大利润是多少元?答案:当销售单价定为70元时,利润最大,最大利润为9000元(将y=-10x^2+1400x-40000转化为顶点式求解)8.抛物线y = -x^2 + 3x + 4与x轴负半轴相交于点A,正半轴相交于点B,与y轴相交于点C。
初三数学二次函数基础练习题

初三数学二次函数基础练习题一、基础概念回顾二次函数是指形式为f(x) = ax^2 + bx + c的函数,其中a、b、c为实数且a ≠ 0。
在解题前,我们首先需要回顾一些基础概念。
1. 顶点坐标:二次函数的顶点坐标可通过公式(-b/2a, f(-b/2a))求得。
其中,b和a代表二次项和一次项的系数。
2. 对称轴:二次函数的对称轴是垂直于x轴通过顶点的直线。
3. 开口方向:当a > 0时,二次函数开口朝上;当a < 0时,二次函数开口朝下。
4. 判别式:二次函数的判别式D = b^2 - 4ac。
判别式的正负决定了二次函数的图像与x轴的交点情况。
二、基础练习题1. 以下哪个为二次函数的解析式?A) y = -3x + 2B) y = x^3 - 4x^2 + x + 6C) y = 2x^2 + 5x - 3D) y = |x|答案:C2. 求二次函数f(x) = 3x^2 + 4x - 7的顶点坐标。
解答:由公式可知,顶点坐标为(-b/2a, f(-b/2a))。
代入a = 3和b = 4,得到顶点坐标为(-2/3, f(-2/3))。
我们还需要计算f(-2/3)的值。
将x = -2/3代入二次函数,得到f(-2/3) = 3(-2/3)^2 + 4(-2/3) - 7 = -12/3 - 8/3 - 7 = -27/3 = -9。
因此,二次函数f(x) = 3x^2 + 4x - 7的顶点坐标为(-2/3, -9)。
3. 判断二次函数g(x) = -2x^2 + 3x + 1的开口方向。
解答:由于a = -2 < 0,所以二次函数g(x)的开口方向朝下。
4. 求解二次方程x^2 - x - 2 = 0的解。
解答:对于二次方程ax^2 + bx + c = 0,可以使用求根公式x = (-b ±√(b^2 - 4ac)) / 2a求解。
将a = 1,b = -1,c = -2代入公式,得到x = (-(-1) ± √((-1)^2 - 4·1·(-2))) / 2·1= (1 ± √(1 + 8)) / 2= (1 ± √9) / 2= (1 ± 3) / 2因此,二次方程x^2 - x - 2 = 0的解为x = (1 + 3) / 2 = 2和x = (1 - 3) / 2 = -1。
初中数学九年级二次函数基础练习题

二次函数(一)基础练习题1.抛物线)0(2≠++=a c bx ax y 过第二、三、四象限,则a 0,b 0,c 0. 2. 抛物线)0(2≠++=a c bx ax y 过第一、二、四象限,则a 0,b 0,c 0. 3.已知抛物线c x ax y ++=22与x 轴的交点都在原点的右侧,则点M (c a ,)在第象限. 4.二次函数c bx ax y ++=2的图象如图所示,则a 0,b 0,c 0, b 2-4ac 0,a +b +c 0,a -b +c 0;5. 二次函数y ax bx c =++2的图象如图所示,则a 0,b 0,c 06.二次函数c bx ax y ++=2的图象如图所示,那么下列四个结论: ①a <0 ;②c >0 ;③ac b 42->0 ;④a b<0中, 正确的结论有( )个7. 已知:抛物线 (a <0)经过点(-1,0),且满足4a +2b +c >0.以下结论: ①a +b >0;②a +c >0;③-a +b +c >0;④ > 0 .其中正确的个数有( )个8.已知二次函数c bx ax y ++=2中0,0,0<><c b a ,则此函数的图象不经过第 象限 9.已知二次函数c bx ax y ++=2中0,0,0><>c b a ,则此函数的图象不经过第 象限 10.已知二次函数c bx ax y ++=2中0,0,0<<<c b a ,则此函数的图象只经过第 象限11.如图,函数c bx ax y ++=2的图象中函数值0>y 时,对应x 的取值范围是 函数值0<y 时,对应x 的取值范围是12.如图,函数c bx ax y ++=2的图象中函数值0<y 时, 对应x 的取值范围是13.二次函数c bx x y ++=2的图象如图所示,则函数值0<y 时,对应x 的取值范围是 。
初三下二次函数练习题及答案

初三下二次函数练习题及答案一、选择题1.下面哪一个函数是二次函数?A. y = 3x + 1B. y = x² + 2x + 1C. y = 4^xD. y = √x2.二次函数y = ax² + bx + c图象是抛物线,开口向上的条件是:A. a > 0B. a < 0C. b > 0D. b < 03.已知二次函数y = x² - 4x + 3的顶点为(2,-1),则a、b、c的值分别为:A. a = 1,b = -4,c = -1B. a = 1,b = 4,c = -3C. a = 1,b = -4,c = 3D. a = 1,b = -2,c = -3二、计算题1.已知二次函数y = x² - 3x + 2,求该函数的顶点坐标和对称轴的方程式。
解答:顶点的横坐标为x = -b/2a,所以 x = -(-3)/(2*1) = 3/2。
将x = 3/2代入原函数可得y = (3/2)² - 3*(3/2) + 2 = -1/4。
所以,该二次函数的顶点坐标为(3/2, -1/4)。
对称轴的方程式为x = 3/2。
2.已知二次函数y = 2x² - 4x + 1,求该函数的零点。
解答:函数的零点即为使得y = 0的x的值。
将y = 0代入原函数可得2x² - 4x + 1 = 0。
使用求根公式可解得x = (4 ± √(16 - 4*2*1))/(2*2) = (4 ± √8)/4 = (1 ± √2)/2。
所以,该二次函数的零点为x = (1 + √2)/2和x = (1 - √2)/2。
三、应用题1.小明将一长方形花坛围起来,其中一边贴着墙,另外三边用栅栏围起来。
已知墙的一段长为4米,花坛的面积为12平方米。
若栅栏的费用为每米15元,求栅栏的总费用。
解答:设花坛的另外两条边长分别为x和y,则有xy = 12。
人教版初中数学九年级二次函数(经典例题含答案)

二次函数经典例题答案班级小组姓名成绩(满分120)一、二次函数(一)二次函数的定义(共4小题,每题3分,共计12分)例 1.下列函数:①225y xz =++;②258y x x =-+-;③2y ax bx c =++;④()()2324312y x x x =+--;⑤2y mx x =+;⑥21y bx =+(b 为常数,0b ≠);⑦220y x kx =++,其中y 是x 的二次函数的有②⑥.例1.变式1.函数24233y x x =--中,a =3-,b =34,c =2-.例1.变式2.若()232my m x -=-是二次函数,且2m >,则m 等于(B)A.C. D.5例1.变式3.已知函数()22346mm y m m x -+=+-是二次函数,求m 的值.2122342:1,2602,31m m m m m m m m m -+===+-≠∴≠≠-∴ 解:由题意得:解得的值为(二)列二次函数的表达式(共4小题,每题3分,共计12分)例2.一台机器原价60万元,每次降价的百分率均为x ,那么连续两次降价后的价格y (万元)为(C )A.()601y x =-B.()601y x =+ C.()2601y x =- D.()2601y x =+例2.变式1.一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s (米)与时间t (秒)的数据如下表:写出用t 表示s 的函数关系式:22t s =.例2.变式2.矩形的长为x cm,宽比长少2cm,请你写出矩形的面积y (2cm )与x (cm)之间的关系式xx y 22-=.时间t (秒)1234…距离s (米)281832…例2.变式3.某商场将进价为每套40元的某种服装按每套50元出售时,每天可以售出300套.据市场调查发现,这种服装销售单价每提高1元,销量就减少5套.如果商场将销售单价定为x 元,请你写出每天销售利润y (元)与销售单价x (元)之间的函数表达式.[]2200075055)50(300)40(2-+-=⨯---=x x y x x y 即解:由题意得:二、二次函数的图象和性质(一)形如2y ax =和2y ax c =+的二次函数的图象和性质(共4小题,每题3分,共计12分)例3.对于二次函数2y x =-的图象,在y 轴的右边,y 随x 的增大而减小.例3.变式1.二次函数2y ax =的图象大致如下,请将图中抛物线字母的序号填入括号内.(1)22y x =如图(D );(2)212y x =如图(C );(3)2y x =-如图(A);(4)213y x =-如图(B);(5)219y x =如图(F);(6)219y x =-如图(E).例3.变式2.与抛物线222y x =-+开口方向相同,只是位置不同的是(D)A.22y x =B.2211y x =- C.221y x =+ D.221y x =--例3.变式3.坐标平面上有一函数22448y x =-的图象,其顶点坐标为(C )A.()0,2- B.()1,24- C.()0,48- D.()2,48(二)二次函数()2y a x h =-与()2y a x h k =-+的图像和性质(共4小题,每题3分,共计12分)例4.将抛物线2y x =-向左平移2个单位长度后,得到的抛物线的表达式是(A )A.()22y x =-+ B.22y x =-+ C.()22y x =-- D.22y x =--例4.变式1.二次函数()221y x =-,当x 1<时,y 随着x 的增大而减小,当x 1>时,y 随着x 的增大而增大.例4.变式2.已知二次函数()2231y x =-+.有下列说法:①其图象的开口向下;②其图象的对称轴为直线3x =-;③其图象顶点坐标为(3,-1);④当3x <时,y 随着x 的增大而减小.则其中说法正确的有(A )A.1个B.2个C.3个D.4个例4.变式3.将抛物线21y x =+先向左平移2个单位长度,再向下平移3个单位长度,那么所得抛物线的表达式是(B )A.()222y x =++ B.()222y x =+- C.()222y x =-+ D.()222y x =--(三)二次函数()20y ax bx c a =++≠的图象和性质(共4小题,每题3分,共计12分)例5.二次函数225y x x =+-有(D)A.最大值为-5B.最小值-5C.最大值-6D.最小值-6例5.变式1.如图是二次函数224y x x =-++的图象,使1y ≤成立的x 的取值范围是(D )A.13x -≤≤B.1x ≤-C.1x ≥ D.13x x ≤-≥或例5.变式2.抛物线2y x bx c =++向右平移2个单位长度再向下平移3个单位长度,所得图象的表达式为223y x x =--,求b ,c 的值.,2234)21(:32324)1(3222222==∴+=+-+-=--=--=--=c b x x x y x x y x x x y 得个单位个单位,再向上平移向左平移将抛物线解:例5.变式3.如图,已知二次函数()20y ax bx c a =++≠的图象如图所示,下列4个结论:①0abc <;②b a c <+;③420a b c ++>;④240b ac ->,其中正确结论的有(B)A.①②③B.①②④C.①③④D.②③④三、确定二次函数的表达式(共4小题,每题3分,共计12分)例6.已知二次函数的图象的顶点坐标是(-2,-3),且经过点(0,5),求这个函数表达式.5823)2(22:53)20()5,0(3)2()3,2(),0()(22222++=-+=∴==-+∴-+=∴--≠++=x x x y a a x a y a k h x a y 解得此二次函数图象经过点又坐标为此二次函数图象的顶点达式为解:设此二次函数的表 例6.变式1.已知抛物线与y 轴交点的纵坐标为52-,且还经过(1,-6)和(-1,0)两点,求抛物线的表达式.22(0)5(0,),(1,6),(1,0)251226305215322y ax bx c a c a a b c b a b c c y x x =++≠---⎧⎧=-=-⎪⎪⎪⎪++=-=-⎨⎨⎪⎪-+=⎪⎪=-⎩⎩∴=---解:设抛物线表达式为将代入得:解得:抛物线表达式为:例6.变式2.已知,一抛物线与x 轴的交点是A(-2,0),B(1,0),且经过点C(2,8).(1)求该抛物线的函数表达式;4224228240024)8,2(),0,1(),0,2()0(22-+=∴⎪⎩⎪⎨⎧-===⎪⎩⎪⎨⎧=++=++=+--≠++=x x y c b a c b a c b a c b a C a c bx ax y 抛物线表达式为:解得:代入得:将解:设抛物线表达式为(2)求该抛物线的顶点坐标.)29,21(2921(242222---+=-+=顶点坐标为:x x x y 例6.变式3.已知抛物线()20y ax bx c a =++≠经过A(-1,0),B(3,0),C (0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数表达式;321)3,0()1)(3(2++-=∴-=+-=x x y a C x x a y 抛物线表达式为:代入,解得:将点线表达式为:解:由题意得:设抛物(2)设点P 是直线l 上的一个动点,当△PAC 的周长最小时,求点P 的坐标.:,(2,3,,(1,0),(2,30123111,2(1,2)l C C C AC l P PAC AC y kx m A C k m k k m m AC y x x y P ''∴'∆''=+--+==⎧⎧⎨⎨+==⎩⎩'∴=+==解过直线作点的对称点)连接交直线于点此时的周长最小设直线表达式为将)代入得:解得:直线表达式为:令则点的坐标为:四、二次函数的应用(一)利用二次函数解决“面积最大问题”(共4小题,每题3分,共计12分)例7.小敏用一根长为8cm 的细铁丝围成一个矩形,则矩形的最大面积是(A)A.24cm B.28cm C.216cm D.232cm 例7.变式1.在Rt ABC ∆中,∠A=90°,AB=4,AC=3,D 在BC 上运动(不与B,C 重合),过点D 分别向AB,AC 作垂线,垂足分别为E,F,则矩形AEDF 的面积最大值为3.例7.变式2.如图,正方形ABCD 的边长为2cm,E,F,G,H 分别从A,B,C,D 向B,C,D,A 同时以0.5cm/s的速度移动,设运动时间为t(s).(1)求证:△HAE≌△EBF;)90,,:SAS EBF HAE B A EB HA BF AE (由题意得:解∆≅∆∴=∠=∠==(2)设四边形EFGH 的面积为S(2cm ),求S 与t 的函数关系式,并写出自变量t 的取值范围;)40(4221)5.02()5.0(901,5.02,5.0222222222≤≤+-=-+=+==∴∴=∠+∠∆≅∆+=∆-===t t t t t AE AH HE S HEFG AHE DHG EBF HAE AE AH HE AEH Rt t AH t AE DH 是正方形四边形可得)又由(中则解:由题意得 (3)t 为何值时,S 最小?最小是多少?222)2(21422122最小,最小为时,当S t t t t S =∴+-=+-=例7.变式3.在青岛市开展的创建活动中,某小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长度为40m 的栅栏围成(如图所示).若设花园BC 边的长为x m ,花园的面积为y 2m .(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围;)(解:由题意得:15020212402≤<+-=-⋅=x x x x x y (2)满足条件的花园面积能达到2002m 吗?若能,求出此时的x 的值;若不能,请说明理由;.20015020,2002m x x x y 到此时花园的面积不能达的取值范围是而,时当∴≤<==(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当x 取何值时,花园的面积最大?最大面积为多少?.5.18715150,20202122m y x x y x x x x y 有最大值,最大值为时,当的增大而增大随范围内,在对称轴为直线线图象是开口向下的抛物=∴≤<=+-=(二)二次函数的综合运用(共4小题,每题3分,共计12分)例8.一件工艺品进价为100元,标价135元出售,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为(A)A.5元B.10元C.0元D.3600元例8.变式1.小明在某次投篮中,球的运动路线是抛物线213.55y x =-+的一部分(如图),若命中篮圈中心,则他与篮底的距离l 是(B )A.3.5mB.4mC.4.5mD.4.6m例8.变式2.某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是多少元?元租金高,每张床收费则为使租出的床位少且时,时,为整数,则又因为有最大值时,当则有元元,每天收入为个解:设每张床位提高1602031001120031120025.22100001000200)10100)(20100(202=⨯+======-=++-=-+=y x y x x y abx x x x x y y x 例8.变式3.某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)假设每台冰箱降价x 元,商场每天销售这种冰箱的利润是y 元,请写出y 与x 之间的函数表达式;(不要求写自变量的取值范围)3200242525048)(20002400(2++-=+--=x x x x y 由题意得:(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?元即每台冰箱应降价降价越多越好要使百姓得到实惠,则解得:得:代入将200200200,1004800320024252,30002425248002122=∴===++-++-==x x x x x x x y y (3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?元。
九年级数学二次函数全章例题+练习(基础、培优)

二次函数概念1.一般地,形如y =ax 2+bx +c(a ,b ,c 是常数,a≠0)的函数,叫做二次函数.其中二次项系数、一次项系数和常数项分别为a ,b ,c .(1)下列函数中,不是二次函数的是( )A .y =1-2x 2B .y =(x -1)2-1C .y =12(x +1)(x -1) D .y =(x -2)2-x 2(2)二次函数y =x 2+4x 中,二次项系数是 ,一次项系数是 ,常数项是 . 【点拨】 判断二次函数要紧扣定义.2.现在我们已学过的函数有一次函数、二次函数,它们的表达式分别是y =ax +b(a ,b 是常数,a≠0)、y =ax 2+bx +c(a ,b ,c 是常数,a≠0).二次函数y =ax 2的图象和性质1.一般地,当a>0时,抛物线y =ax 2的开口向上,对称轴是y 轴,顶点是原点,顶点是抛物线的最低点,a 越大,抛物线的开口越小.2.一般地,当a<0时,抛物线y =ax 2的开口向下,对称轴是y 轴,顶点是原点,顶点是抛物线的最高点,a 越小,抛物线的开口越小.3.从二次函数y =ax 2的图象可以看出:如果a>0,当x<0时,y 随x 的增大而减小,当x>0时,y 随x 的增大而增大;如果a<0,当x<0时,y 随x 的增大而增大,当x>0时,y 随x 的增大而减小.4.(1)抛物线y =2x 2的开口向上,对称轴是y 轴,顶点是原点,顶点是抛物线的最低点; (2)抛物线y =-3x 2的开口向下,对称轴是y 轴,顶点是原点,顶点是抛物线的最高点;(3)在抛物线y =2x 2对称轴的左侧,y 随x 的增大而减小,在对称轴的右侧,y 随x 的增大而增大; (4)在抛物线y =-3x 2对称轴的左侧,y 随x 的增大而增大,在对称轴的右侧,y 随x 的增大而减小.二次函数y=ax2+k的图象和性质二次函数y=ax2+k的图象和性质二次函数y=a(x-h)2+k的图象和性质二次函数y=ax2+bx+c的图象和性质例1、求二次函数y=2x2+4x-1的对称轴,顶点坐标,并画出其函数图象.例2、将下列二次函数写成顶点式y=a(x-h)2+k的形式,并写出其开口方向,顶点坐标,对称轴.(1)y=x2-4x+5;(2)y=-2x2-12x-22.用待定系数法确定二次函数的解析式例1如果一个二次函数的图象经过(-1,10),(1,4),(2,7)三个点,能求出这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.【跟踪训练1】已知二次函数y =ax 2+bx +c ,当x =0时,y =1;当x =-1时,y =6;当x =1时,y =0.求这个二次函数的解析式.例2已知抛物线的顶点坐标为(-1,-3),与y 轴的交点为(0,-5),求此抛物线的解析式.【点拨】 特别地,当抛物线的顶点为原点时,h =0,k =0,可设函数的解析式为y =ax 2; 当抛物线的对称轴为y 轴时,h =0,可设函数的解析式为y =ax 2+k ; 当抛物线的顶点在x 轴上时,k =0,可设函数的解析式为y =a (x -h )2.【跟踪训练2】 已知抛物线的顶点坐标是(3,-1),与y 轴的交点是(0,-4),则这个二次函数的解析式是 .例3已知抛物线与x 轴交于点A (-1,0),B (1,0)并经过点M (0,1),求此抛物线的解析式.【点拨】 交点式y =a (x -x 1)(x -x 2)中,x 1和x 2分别是抛物线与x 轴的两个交点的横坐标,这两个交点关于抛物线的对称轴对称,则直线x =x 1+x 22就是抛物线的对称轴.【跟踪训练3】 已知一个二次函数的图象与x 轴的两个交点的坐标分别为(-1,0)和(2,0),与y 轴的交点坐标为(0,-2),则该二次函数的解析式为 .巩固训练1.已知抛物线y =ax 2+bx +c 过(1,0),(2,0),(3,4)三点,则该抛物线的解析式为( )A .y =x 2-3x +2B .y =2x 2-6x +4C .y =2x 2-6x -4D .y =x 2-3x -22.如果抛物线的顶点坐标是(3,-1),与y 轴的交点是(0,-4),则它的解析式为( )A .y =-13x 2+2x -4B .y =-13x 2-2x -4C .y =-13(x +3)2-1 D .y =-x 2+6x -123.如图,抛物线的解析式为( )A .y =-x 2-x +2B .y =x 2+x +2C .y =-2x 2+x +2D .y =-x 2+x +24.若y =ax 2+bx +c ,则由表格中信息可知y 与x 之间的函数关系式为( )x -1 0 1 ax 21 ax 2+bx +c83A .y =x 2-3x +3B .y =x 2-3x +4C .y =x 2-4x +3D .y =x 2-4x +85、已知二次函数y =ax 2+bx+c 中,自变量x 与函数y 之间的部分对应值如表: x … 0 1 2 3 … y …﹣1232…在该函数的图象上有A(x 1,y 1)和B(x 2,y 2)两点,且﹣1<x 1<0,3<x 2<4,y 1与y 2的大小关系正确的是( ) A. y 1≥y 2 B. y 1>y 2 C. y 1≤y 2 D. y 1<y 26.函数y =ax +1与y =ax 2+bx +1(a ≠0)的图象可能是( )B .C .D .1111xoyyoxyoxxoy7.已知0≠a ,在同一直角坐标系中,函数ax y =与2ax y =的图象有可能是( ▲ )8.在同一直角坐标系中,函数y mx m =+和函数222y mx x =-++(m 是常数,且0m ≠)的图象可能..是Oy x1-1A . xyO 1-1B . xy O1-1xyO1-1图像性质提高1.作出二次函数y=x2-2x-3的图象,当y=0时,自变量x= ;当y<0时,自变量x的取值范围是;当y>0时,自变量x的取值范围是.2、抛物线y=ax2+bx+c的对称轴是直线x=-1,且过点(1,0).顶点位于第二象限,其部分图象如图所示,给出以下判断:①ab>0且c<0;②4a-2b+c>0;③8a+c>0;④c=3a-3b;⑤直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1,x2,则x1+x2+x1x2=5.其中正确的结论是(只填序号)3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是()A.c>0 B.2a+b=0 C.b2﹣4ac>0 D.a﹣b+c>04.如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2),下列结论:①abc>0;②a+b+c>0;③2a+b <0;④b<﹣1;⑤b2﹣4ac<8a,正确的结论是(只填序号)5、小明在某次投篮中,球的运动路线是抛物线y=-51x 2+3.5的一部分,如图所示,若球命中篮圈中心,则他与篮底的距离L 是 m6、如图所示,二次函数y=ax 2+bx+c (a ≠0)的图象经过点(-1,2),且与x 轴交点的横坐标分别为x 1、x 2,其中-2<x 1<-1,0<x 2<1,下列结论:①4a-2b+c <0;②2a-b >0;③a <-1;④b 2+8a >4ac.其中正确的有: (填写番号).7、已知二次函数y=ax 2+bx+c 的图象如图所示,下列结论:①9a-3b+c=0;②4a-2b+c >0;③方程ax 2+bx+c-4=0有两个相等的实数根;④方程a (x-1)2+b (x-1)+c=0的两根是x 1=-2,x 2=2.其中正确的有: (填写番号).8.如图,二次函数y =ax 2+bx +c (a ≠0)的图象过点(﹣1,2),下列结论:①abc >0;②a +b +c >0;③2a +b <0;④b <﹣1;⑤b 2﹣4ac <8a ,正确的结论是 (只填序号)9.二次函数y =ax 2+bx +c (a ≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x =2,下列结论:①4a +b =0;②9a +c >3b ;③8a +7b +2c >0;④若方程a (x +1)(x ﹣5)=﹣3的两根为x 1和x 2,且x 1<x 2,则x 1<﹣1<5<x 2;⑤若点A (﹣3,y 1)、点B (﹣,y 2)、点C (,y 3)在该函数图象上,则y 1<y 3<y 2.其中正确的结论是 .二次函数的应用1.如图,某小区决定要在一块一边靠墙(墙长10米)的空地上用栅栏围成一个矩形绿化带ABCD,绿化带的一边靠墙,中间用栅栏隔成两个小矩形,所用栅栏总长为36米,设AB的长为x米,矩形绿化带的面积为S平方米.(1)求S与x之间的函数关系式,并直接写出x的取值范围;(2)求围成矩形绿化带ABCD面积S的最大值.2.如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1,在AB上的一点P,使矩形PNDM有最大面积,则矩形PNDM的面积最大值是 .3.天府新区某商场开业后要经营一种新上市的文具进价为10元/件.试营销阶段发现:当销售单价是13元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件,设该商场销售这种文具每天的销售量为y件,销售单价为x元/件(x≥13).(1)写出y与x之间的函数关系式;(2)设商场每天的销售利润为w(元),若每天销售量不少于150件,求商场每天的最大利润.4.每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲.节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况,得到了如下数据,同时发现每天的销售量y(件)是销售单价x(元/件)的一次函数.销售单价x(元/件)…30 40 50 60 …每天销售量y(件)…350 300 250 200 …(1)求出y与x的函数关系;(2)物价局要求,销售该鲜花礼盒获得的利润不得高于100%:①当销售单价x取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价﹣成本价);②试确定销售单价x取何值时,花店销该鲜花礼盒每天获得的利润W(元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.5.某商场以每件20元的价格购进一种商品,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间满足一次函数关系,其图象如图所示.设该商场销售这种商品每天获利w (元).(1)求y与x之间的函数关系式.(2)求w与x之间的函数关系式.(3)该商场规定这种商品每件售价不低于进价,又不高于36元,当每件商品的售价定为多少元时,每天销售利润最大?最大利润是多少?6.某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚,到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.(1)求y与x的函数关系式,并写出x的取值范围;(2)当该品种的蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.7.2020年,新型冠状病毒肆虐,给人们的生活带来许多不便,网络销售成为这个时期最重要的一种销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中2<x≤10).(1)求y与x之间的函数关系式;(2)销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?8.某企业销售某商品,以“线上”与“线下”相结合的方式一共销售了100件.设该商品线下的销售量为x(10≤x≤90)件,线下销售的每件利润为y1元,线上销售的每件利润为y2元.如图中折线ABC、线段DE分别表示y1、y2与x之间的函数关系.(1)求y1与x之间的函数表达式;(2)若70≤x≤90,问线下的销售量为多少时,售完这100件商品所获得的总利润最大?最大利润是多少?{)5840(1402)7158(82≤≤+-≤<+-=x x x x y(3)①求他的销售利润w (元)与销售单价x (元/双)之间的函数关系式.(4)②小王每月需向银行还贷2075元,另童鞋店每月需缴纳水电费、营业税等固定费用3000元,通过计算判断,小王每月(按30天计算)能否有盈余?如果有,最多盈余多少元?(盈余=销售利润-固定费用-银行贷款)二次函数的综合如图,二次函数y=(x-2)2+m 的图象与y 轴交于点C ,点B 是点C 关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b 的图象经过该二次函数图象上点A (1,0)及点B . (1)求一次函数与二次函数的解析式;(2)根据图象,写出满足kx+b ≥(x-2)2+m 的x 的取值范围.练习1:如图所示,二次函数的图象与x 轴相交于A 、B 两点,与y 轴相交于点C ,点C 、D 是二次函数图象上的一对对称点,一次函数的图象过点B 、D .(1)求D 点的坐标和一次函数、二次函数的解析式;(2)根据图象写出使一次函数值大于二次函数值的x 的取值范围.练习2:在同一直角坐标系,开口向上的抛物线与坐标轴分别交于A (-1,0),B (3,0),C (0,-3),一次函数图象与二次函数图象交于B 、C 两点. (1)求一次函数和二次函数的解析式.(2)当自变量x 为何值时,两函数的函数值都随x 的增大而增大? (3)当自变量x 为何值时,一次函数值大于二次函数值. (4)当自变量x 为何值时,两函数的函数值的积小于0.ABC Oxy一次函数和二次函数的交点有关的面积类问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学九年级二次函数基础练习题
-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
-2 2
二次函数基础练习题
1.抛物线)0(2≠++=
a c bx ax y 过第二、三、四象限,则a 0,
b 0,
c 0. 2. 抛物线)0(2≠++=a c bx ax y 过第一、二、四象限,则a 0,b 0,c 0.
3.已知抛物线c x ax y ++=22与x 轴的交点都在原点的右侧,则点M (c a ,)在第 象限.
4.二次函数c bx ax y ++=2
的图象如图所示,则a 0, b 0, c 0, b 2
-4ac 0,a +b +c 0,a -b +c 0;
5. 二次函数y ax bx c =++2的图象如图所示,则a 0, b 0, c 0
6.二次函数c bx ax y ++=2的图象如图所示,那么下列四个结论: ①a <0 ;②c >0 ; ③ac b 42->0 ;④a
b
<0中, 正确的结论有( )个
7. 已知:抛物线
(a <0)经过点(-1,0),且满足4a +2b +c >0.以下结论:
①a +b >0;②a +c >0;③-a +b +c >0;④ > 0 .其中正确的个数有( )个 8.已知二次函数c bx ax y ++=2中0,0,0<><c b a ,则此函数的图象不经过第 象限
9.已知二次函数c bx ax y ++=2
中0,0,0><>c b a ,则此函数的图象不经过第 象限
10.已知二次函数c bx ax y ++=2中0,0,0<<<c b a ,则此函数的图象只经过第 象限
11.如图,函数c bx ax y ++=2
的图象中函数值0>y 时,对应x 的取值范围是 函数值0<y 时,对应x 的取值范围是
12.如图,函数c bx ax y ++=2的图象中函数值0<y 时, 对应x 的取值范围是
-5 1
c bx ax y ++=2
ac
b 22-
13. 二次函数c
bx x y ++=2
的图象如图所示,则函数值0<y 时,对应x 的取值范围是 。
14. 已知抛物线 经过三点A (2,6),B (-1,2),C (0,1),那么它的解析
式是 ,
15. 已知二次函数图象经过(-1,10)(2,7)和(1,4)三点,这个函数的解析式是 16. 若抛物线与x
轴交于点(-1,0)和(3,0),且过点(0, ),那么抛物线的解析式
是
17. 已知抛物线经过三个点A (2,6),B (-1,0),C (3,0),那么二次函数的解析式是 ,它的顶点坐标是
18. 抛物线与x 轴的两个交点的横坐标是-3和1,且过点(0, ),此抛物线的解析式是 19. 已知抛物线的顶点是A(-1,2),且经过点(2,3),其表达式是 。
21. 顶点为(-2,-5)且过点(1,-14)的抛物线的表达式为 .
22. 抛物线 的顶点是(2,4),则b = ,c
= ;
23. 二次函数y=ax 2+bx+c 的对称轴为x =3,最小值为-2,且过(0,1),此函数的解析式是 24. 对称轴是y 轴且过点A (1,3)、点B (-2,-6)的抛物线的解析式为 . 25. 对称轴是直线x =1且过点A (2,3)、点B (-1,6)的抛物线的解析式为 .
26. 已知二次函数的图象顶点坐标(2,1),且与x 轴相交两点的距离为2,则其表达式为 27. 抛物线的顶点为(-1,-8),它与x 轴的两个交点间的距离为4,此抛物线的解析式 28.函数2y ax =的图象若是一条不经过一、二象限的抛物线。
则a 0 29.函数2mx y -=开口向上,则 m ;
30.二次函数c bx ax y ++=2的值永远为负值的条件是a 0,ac b 42- 0.
31.对于)0(2≠=a ax y 的图象下列叙述正确的是 ( ) A .a 的值越大,开口越大 B .a 的值越小,开口越小 C.a 的绝对值越小,开口越大 D.a 的绝对值越小,开口越小
32.在同一直角坐标系中,函数b ax y +=2与)0(≠+=ab b ax y 的图象大致如图 ( )
c bx ax y ++=22
3
c bx x y ++=223
33.直线)0(≠+=ab b ax y 不经过第三象限,那么bx ax y +=2的图象大致为 ( )
A B C D
34.二次函数c bx ax y ++=2的图象如图所示,则abc ,ac b 42-,b a +2,
c b a ++这四个式子中,值为正数的有( ) A .4个
B .3个
C .2个
D .1个
35.如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A (-1,0)、 点B (3,0)和点C (0,-3),一次函数的图象与抛物线交于B 、C 两点。
⑴二次函数的解析式为 .
⑵当自变量x 时,两函数的函数值都随x 增大而增大. ⑶当自变量 时,一次函数值大于二次函数值. ⑷当自变量x 时,两函数的函数值的积小于0.
36. 二次函数y=ax 2+bx+c 的对称轴为x=3,最小值为-2,,且过(0,1),求此函数的解析式。
37.二次函数c bx ax y ++=2的图像与x 轴交于B 、C 两点,与y 轴交于A 点.
1)根据图像确定a 、b 、c 的符号,并说明理由;
2)如果点A 的坐标为(0,-3),∠ABC =45°,∠ACB =60°,求这个二次函数的解析式.
38.已知点A (1,2)和B (–2,5).试写出两个二次函数,使它们的图象都经过A 、B 两点。
O x
y
-1
1 1 -
-
3
x
y O A B
C
扬州
39.试写出一个开口方向向上,对称轴为直线x = 2,且与y 轴的交点坐标为(0,3)的抛物线的解析_________;
40.若二次函数c ax y +=2,当x 取1x 、2x (1x ≠2x )时,函数值相等,则当x 取1x +2x 时,函数值为( )(A ) a +c (B ) a -c (C )-c (D )c
41.已知 a <- 1,点(a -1,1y )、(a ,2y )(a +1,3y )都在函数2x y =的图象上,则( ) (A )1y <2y <3y (B )1y <3y <2y (C )3y <2y <1y (D )2y <1y <3y
42.已知抛物线C 1的解析式是5422+-=x x y 抛物线C 2与抛物线C 1关于x 轴对称,求抛物线C 2的解析式.
43.如图,抛物线的对称轴是直线1x =,它与x 轴交于A 、B 两点,
与y 轴交于C 点.点A 、C 的坐标分别是(1,0)-、(0,)3 2
. (1) 求此抛物线对应的函数解析式;
(2) 若点P 是抛物线上位于x 轴上方的一个动点,求△ABP 面积的最大值.
44.已知抛物线c bx ax y ++=2开口向下,并且经过A (0,1)和M (2,-3)两点。
(1)若抛物线的对称轴为直线x =-1,求此抛物线的解析式; (2)如果抛物线的对称轴在y 轴的左侧,试求a 的取值范围;
(3)如果抛物线与x 轴交于B 、C 两点,且∠BAC =90°,求此时a 的值。
