4-6卷积积分及零状态响应的卷积计算法
卷积积分及零状态响应的卷积计算法.
t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积,实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义,函数在0到t区间内的定积分值,决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
§4-6 卷积积分及零状态响 应的卷积计算法
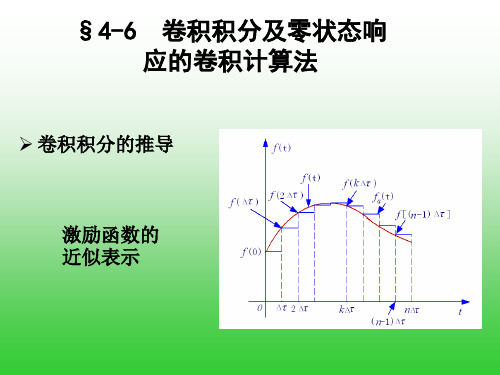
➢ 卷积积分的推导
激励函数的 近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解: [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解: 用卷积积分公式求uC(t),应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限
信号与系统题库(完整版)

信号与系统题目部分,(卷面共有200题,0.0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中,若h '(0)=1,且该系统为稳定的因果系统,则该系统的冲激响应()h t 为。
A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x[n]如下图所示,则x[n]的偶分量[]e x n 是。
[3]波形如图示,通过一截止角频率为50rad sπ,通带内传输值为1,相移为零的理想低通滤波器,则输出的频率分量为() A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ,其中2TπΩ=;又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭;则()f t 的傅里叶变换为________。
A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+,则该系统是________系统。
A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为(23kk --+)u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。
2.求零状态响应

d v(t ) 1 t C v(t ) v ( )d i S ( t ) dt R L 2
二、微分方程的求解
1. 微分方程的一般形式
d r (t ) d r (t ) dr ( t ) C0 C C C r ( t ) 1 n 1 n n n 1 dt dt dt m m 1 d e( t ) d e( t ) de( t ) E0 E1 m 1 E m 1 E m e( t ) m dt dt dt
2. 特解的形式由激励信号决定,特解的系数 Bi 由系统本身特性和激励信号共同决定。 特解也称系统的强迫响应分量。
§2.3 起始点的跳变 —— 从0-到0+状态转变
一、运用电路定律 二、运用冲激函数匹配法
§2.3 起始点的跳变 —— 从0-到0+状态转变
完全解中的齐次解的系数Ai 是由初始条件 确定的。而初始条件应如何求得是本节要 讨论的问题。
Be a t B1 cos( t ) B2 sin( t )
( B1 t p B p t B p 1 )e a t cos( t ) ( D1 t p D p t D p 1 )e a t sin( t )
例 2-4 给定系统方程如下
d r (t ) dr ( t ) de( t ) 2 3r ( t ) e( t ) 2 dt dt dt
4. 完全解:
uC 2 ( t ) rh ( t ) rp ( t ) 3 21 t 6 t A1e A2e sin 2t cos 2t 50 50
uC 1 (0) 0, uC 2 (0) 0
因为电容两端初始电压为零,
又由
uC 1
电路原理课件-卷积积分

7) t≥7时,
y(t ) 0
注意:积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示,uS=15e-0.25t(t)V。采用卷积计算uC。
解:以uC为响应,求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1
k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图,R=10,L=1H,激励uS的波形如图 所示,求零状态响应i(t)。
解:以电流i 为响应,求单位阶跃响应为:
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为:
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为:
g(t ) 0.5(1 e t ) (t )
第八章·电路系统对任意激励的零状态响应-卷积积分

2.分配律:
f1(t) [ f2 (t) f3 (t)] f1(t) f2 (t) f1(t) f3 (t)
3.结合律:
[ f1(t) f2 (t)] f3 (t) f1(t) [ f2 (t) f3 (t)]
证明:
[ f1(t) f2 (t)] f3(t)
观察这个输入作用引起响应的瞬间。因为 时刻作用的信号,
到t时刻才观察到输出,这之间时间差值即为
可以t 理解电路对输入作用的记忆时间。
t 。即0
因为 t 不能为负,所以积分上限只能取到t,而不能到∞。
其实电路上的这种卷积积分只不过是数学上卷积的特例,并
赋予物理意义。
2. 利用卷积积分求电路系统零状态响应的方法: 方法步骤: (1)求出系统的冲击响应h(t) (2)代公式进行卷积积分,或利用卷积性质,求得yzs(t)
k
n
当 ( 0)时, d, k d , 求和 积分
任意信号: f (t) f ( ) (t )d
任意信号产生的零状态响应:
yzs (t)
f ( )h(t )d
因为对于一切物理可实现系统(因果系统),t<0时,
(b)
f (t) h(t)
t
1 2
1
1 2
(t
)d
t2 4
t 1 4 16
(c)
f (t) h(t)
1
11 2
1 (t 2
)d
3t 4
3 16
(d)
f (t) h(t) 1 1 1 (t )d t 2 t 3
卷积的几种计算方法以及程序实现FFT算法

e ( t 1) )u(t 2)
Made by 霏烟似雨
数字信号处理
ht 1
e
t 2
u (t ) u (t 2)
e t 1
e t u (t )
O
t
波形
O
2
t
2. 今有一输油管道,长 12 米,请用数字信号处理的方法探测管道内部的损伤,管道的损伤可能为焊 缝,腐蚀。叙述你的探测原理,方法与结果。 (不是很清楚) 探测原理:因为输油管道不是很长,可以考虑设计滤波器器通过信号测量来测试管道的损伤,当有 焊缝时,所接受的信号会有所损失,当管道式腐蚀时,由于管壁变得不再是平滑的时候,信号的频率 就会有所改变。
rk r ( k N / 2)
,则后半段的 DFT 值表达式:
X 1[
N N / 2 1 N / 2 1 r ( k ) N N rk k ] x1[r ]WN / 22 x1[r ]WN , k ] X 2 [k ] ( k=0,1, … ,N/2-1 ) / 2 X 1[ k ] ,同样, X 2 [ 2 2 r 0 r 0
d it L Ri t et dt
t
t 2
u(t ) u(
i(t )
L 1H
2) 冲激响应为 h(t ) e u(t ) 3)
i(t ) e( ) h(t ) d
程序: function test x = rand(1 , 2 .^ 13) ; tic X1 = fft(x) ; toc tic X2 = dit2(x) ; toc tic X3 = dif2(x) ; toc tic X4 = real_fft(x) ; toc max(abs(X1 - X2)) max(abs(X1 - X3)) max(abs(X1 - X4)) return ; function X = dit2(x) N = length(x) ; if N == 1 X=x; else X1 = dit2(x(1:2:(N-1))) ; X2 = dit2(x(2:2:N)) ; W = exp(-1i * 2 * pi / N * (0:(N/2-1))) ; X = [X1 + W .* X2 , X1 - W .* X2] ; end return ;
离散时间系统的零状态响应

离散时间系统的零状态响应
重点:零输入响应;卷积和; 因果和稳定性
1)经典法:分通解和特解两部分分别求解。 2)时域卷积和法:类似与连续时间系统中的卷积积 分方法。 3)变换域法:Z.T. ,类似于L.T.
充分条件
n
h(k )
例4:h(k ) 14 (k ) (2k 1 12 5k 1 ) (k 1)
此系统为不稳定系统
七 离散系统的全响应 例4:已知一离散因果系统
y(k 2) 0.7 y(k 1) 0.1 y(k ) 7e(k 2) 2e(k 1)
r(0) =0
r(1) =A
r(1)= r(0)+ A(0)
r(k+1) - r(k)= 0 k>=1
r(k+1) = r(k)
k>=1
1 若H ( S ) ( S )2
h(k ) (k 1) k 2 (k 1)
bm S bm1S bm2 S ... b1S b0 H (S ) n n 1 n2 S an1S an2 S ... a1S a0
离散系统的描述与模拟
S y(k ) y(k 1)
e (t)
1/S
x ( n)
D
x(n 1)
∑ -a
e (k)
y(t) y'(t)+ay(t)=e(t)
∑ -a
D
y(k)
y(k+1)+ay(k)=e(k)
一、离散信号的时域分解
(k )
讨论课卷积、系统响应

t <0 f2(t-) 左移
t 从 到 , 对应f 2 t 从左向右移动
t
浮动坐标:
下限 t- 2
上限 t
f 2 t
f1
0
1
t 0
f 2 t
f1
第 8 页
a
t
O
t2
1
t0
两波形没有公共处,二者乘积为0,即积分为0
第一部分、卷积计算
第 3 页
e( t )
h( t )
r (t )
如何求解系统零状态响应信号 r ( t ) ?
第
例1
已知:
4 页
f 1 t a, 0 t 1
求:
f1 t 1 t
b f 2 t t , 0 t 2 2
f2 t
f 1 t f 2 t f 3 t
g(t ) f1 ( ) f 2 ( t ) d
0 t
1 t 2
f 2 t
a f1
第 10 页
t2
O
1 t
t 2 0 t 1
即1 t 2
1
g(t ) f1 ( ) f 2 ( t ) d
0
2t3
第 16 页
[ f1 f 2 t u( )u( t ) f1 f 2 t u( )u( t 2)
f1 f 2 t u( 1)u( t ) f1 f 2 t u( 1)u( t 2)]d
[ f1 f 2 t u( )u( t ) f1 f 2 t u( )u( t 2)
信号第二章3卷积

若将此信号作用到冲激信号为h(t)的线性时不 变系统,则系统的响应为
r (t ) H [e(t )] H [ e( ) (t )d ]
e( ) H [ (t )]d
e( )h(t )d
零状态响应:rzs (t ) e( )h(t )d h(t ) e(t )
def
2.算子符号基本规则
(1)算子多项式可以进行因式分解 ( p 2)( p 3) p 2 5 p 6 例如: (2)等式两端的算子符合因式不能相消 ( p 2) r (t ) ( p 1) e(t ) ( p 2)( p 3) r (t ) ( p 2 4 p 3) e(t ) 不能简化为: (3)算子的乘除顺序不能随意颠倒
(3)结合律: f1(t) f2 (t) f3 (t) f1(t) f2 (t) f3 (t)
e(t)
h1(t)
h2(t)
r(t)
串联系统 r (t ) e(t ) h1 (t ) h2 (t )
2.卷积的微分与积分
d f1 (t ) f 2 (t ) df 2 (t ) (4)微分性: f1 (t ) dt dt df1 (t ) (适于高阶微分) f 2 (t ) dt
r (t ) e( )h(t )d
1 (a) t 2
e(t ) * h(t ) 0
h(t )
e( )
1
1 2
t 2
(b)
0
1 t 1 2
相乘
t
1
1 t 1 2 t 1 e(t ) * h(t ) 1 1 (t )d 2 2 t2 t 1 4 4 16 (b)
离散系统的零状态响应

k
对比 : g (t ) h( )d
t
2. 已知g (k )求h(k ) :
(k ) (k ) (k 1) h(k ) g (k ) g (k 1)
X
例题(书P127例5-9)(自学,不要求)
求离散系统 y k 4 y k 1 3 y k 2 2 k y 1 1, y( 2) 1 的单位响应 (其中k 0)
(k ) (k j ) (k ) (k 1) (k j )
第 7 页
由于 (k ) h(k )根据LTI性质
g ( k ) h( k j )
j 0 i
j 0
i
(i)
k
h(i)
单位序列响应的初值h1 (0),1h1 (1), h(2)可由下式递推得到
h1 (k ) (k ) a1h1 (k 1) an 1h1 (k n 1) anh1 (k n)
h(k ) b0 h1 (k ) b1h1 (k-1) bm 1h (k m 1) bmh1 (k m)
ik 6 4
k i 0
i
k-6
k 0
y (k ) 0
k i a
3.k 4
k-6 k
k 6 0
k
4.k 6 0 k 6 4
4
i0
k-6
5.k 6 4即 : k 10
k-6
k
y(k) 0
X
1.k 0, y (k ) 0
2.0 k 4 y (k ) a
设系统激励仅在是δ(k) →h1(k),此时系统差分方程变为:
信号与系统连续时间LTI系统的几种响应求解方法及例题

利用信号分解和线性时不变系统的特性求解。
卷积法求解系统零状态响应yf (t)的思路
1) 将任意信号分解为单位冲激信号的线性组合 2) 求出单位冲激信号作用在系统上的响应
—— 冲激响应 3) 利用线性时不变系统的特性,即可求出任意
信号f(t)激励下系统的零状态响应yf (t) 。
解:y f (t) f (t) h(t) f ( ) h(t )d = 3u( ) 2e3(t )u(t )d
= 0t 3 2e 3(t )d
0 2(1 e3t ) = 0 = 2(1 e3t )u(t)
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et u(t),求 系统的完全响应y(t)。
解:
(3) 求方程的全解
y(t)
yh (t)
yp (t)
Ae 2t
Be 4t
1 et 3
y(0) A B 1 1
y' (0)
2A
3 4B
1
2
解得 A=5/2,B= 11/6
解得 K1= 6,K2= 5
yx (t) 6e2t 5e3t , t 0
[例2] 已知某线性时不变系统的动态方程式为:
y" (t)+4y ' (t) +4y (t) = 2f ' (t )+3f(t), t>0 系统的初始状态为y(0) = 2,y'(0) = 1, 求系统的零输入响应yx(t)。
系统的初始状态为y(0) = 1,y' (0) = 3, 求系统的零输入响应yx(t)。
卷积积分介绍

h(t)
(1) 1
O
(1) t
g(t)
1
O12 1
g(t)f(1)(t)h(1)(t)
t 3 2t
t 3
0t 1 1t 2 2t 3
3 t
注意
28
注意
当f1(t)
t df1(t)dt时, dt
f 1 ( t) f 2 ( t) f 1 ( t) f 2 ( 1 )( t)
例 sg t: n t
系统并联运算
3.结合律
f ( t ) f 1 ( t ) f 2 ( t ) f ( t ) [ f 1 ( t ) f 2 ( t )]
系统级联运算
22
系统并联
f 1 ( t ) [ f 2 ( t ) f 3 ( t ) f ] 1 ( t ) f 2 ( t ) f 1 ( t ) f 3 ( t ) 系统并联,框图表示:
一般数学表示: g(t) f1()f2(t)d 信号无起因时: g(t) f()h(t)d
(4)卷积是数学方法,也可运用于其他学科 。
(5)积分限由 f1(t),f2(t)存在的区间决定,即由
f1()f2(t)0的范围决定。
20
总结
求解响应的方法: 时域经典法: 完全解=齐次解 + 特解 双零法:
: 信号作用的时刻,积分变量
从因果关系看,必定有 t
(2)分析信号是手段,卷积中没有冲激形式,但有其内容;
f() 是h(t-)的加权,求和
即d f() 是h(t-)的加权,积分
(t-)的响应
19
(3)卷积是系统分析中的重要方法,通过冲激响应h(t)建 立了响应r(t)与激励e(t)之间的关系。
零输入响应:解齐次方程,用初(起)始条件求系数;
如何用卷积定理求零状态响应__解释说明

如何用卷积定理求零状态响应解释说明1. 引言1.1 概述本文旨在介绍如何使用卷积定理来求解零状态响应。
卷积定理是信号处理领域中一项重要的数学工具,它可以将卷积运算转化为频域乘法运算,从而简化计算过程。
通过了解卷积定理的定义和原理,我们可以更加方便地求解系统的零状态响应。
1.2 文章结构本文将分为五个主要部分进行阐述。
首先,在第二部分中,我们将对卷积定理进行简要介绍,包括其定义和原理以及在不同领域中的应用。
然后,在第三部分中,我们将详细讲解如何使用卷积定理来求解零状态响应,并按照步骤进行说明。
接下来,在第四部分中,我们将提供一个具体的示例分析,以便读者更好地理解和应用所学知识。
最后,在第五部分中,我们将对全文进行总结,并展望相关领域未来的研究价值和发展方向。
1.3 目的本文的目标是帮助读者了解并掌握如何利用卷积定理来求取系统的零状态响应。
深入理解卷积定理的定义和原理,掌握求解零状态响应的具体步骤,并通过实例分析加深对相关概念的理解。
通过本文的阅读,读者将能够在实践中运用卷积定理来解决信号处理中的问题,并对其应用领域有一定了解。
2. 卷积定理简介2.1 定义和原理卷积定理是信号处理中一种重要的数学工具,它表明在频率域中进行乘法运算等效于在时域中进行卷积运算。
具体而言,对于两个函数的卷积,在频率域中等于这两个函数的傅里叶变换的乘积。
设两个函数为f(t) 和g(t),它们在时域上的卷积为h(t),则在频率域上有如下关系:H(f) = F(f) * G(f)其中,H(f) 是h(t) 的傅里叶变换,F(f) 和G(f) 分别是f(t) 和g(t) 的傅里叶变换。
2.2 卷积定理的应用领域卷积定理广泛应用于信号处理、图像处理、通信系统等领域。
它可以帮助我们分析和处理复杂系统、信号或图像之间的关系。
在信号处理中,卷积定理常用来分析滤波器对输入信号的影响。
通过将输入信号和滤波器的频谱相乘得到输出信号的频谱,然后再进行反傅里叶变换,可以得到系统对输入信号的零状态响应。
4-6卷积积分及零状态响应的卷积计算法
f (k ) (t k )
k 0
n 1
(t ) NzS h(t )
(t K ) NzS h(t k )
f (k ) (t k ) NzS f (k )h(t k )
f (k ) (t k )
e
0
t
( t )
d e ( t ) d
t
e
0 t
t
( t )
d e
e d e
0 t
t
t
(e 1) (1 e ) (t )
t t t ( t 1)
e d e (e e) (1 e ) (t 1) t ( t 1) rzS (t ) (1 e ) (t ) (1 e ) (t 1)
3 1 2 n t
1
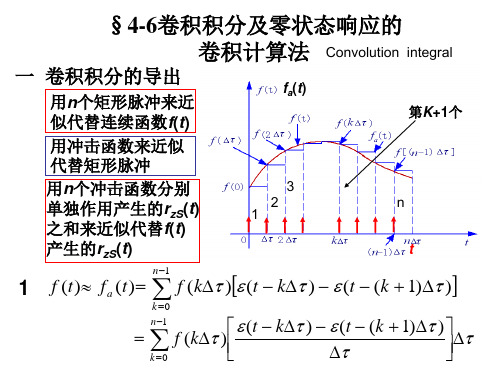
f (t ) f a (t ) f (k ) (t k ) (t (k 1) )
(t k ) (t (k 1) ) f (k ) k 0
k 0 n 1
§4-6卷积积分及零状态响应的 卷积计算法 Convolution integral
一 卷积积分的导出
用n个矩形脉冲来近 似代替连续函数f(t) 用冲击函数来近似 代替矩形脉冲 用n个冲击函数分别 单独作用产生的rzS(t) 之和来近似代替f(t) 产生的rzS(t)
n 1
f a( t ) 第K+1个
k 0
n 1
NzS f (k ) h(t k )
k 0
n 1
f (t )
n 1 k 0 n 1
rzS (t )
f (t ) f (k ) (t k )
卷积图解法

rs
0
.d
.d
ls
ls
t rl
.d
0 t
定义域和卷积结果
例: 1.求出关于 的不定积分
2
f(t)
h(t)
1
4 5 1 3
f s ( )hl (t )d 2 1d 2
2.将两函数的时限值两两相加,得出定义域 1+4=5; 1+5=6; 3+4=7; 3+5=8 3.确定积分限
u ( 1)u (t 2)d u ( 1)u (t 3)d
t 2
d d (t 2 1) (t 3 1) 1
1
t 2
t 3
1
du (t 2 1) du (t 3 1)
0.25ab
0 1 2 3
结语:若f1(t)与f2(t)为有限宽度的脉冲,f1*f2的面积为f1和 f2面 积之积, f1*f2的宽度为f1和 f2宽度之和. Gtk [(t t j ) t i ] 方法二.利用门函数直接计算卷积分
Gtk [(t t j ) t i ] u ( t i )u (t t j )
4...if ...2 t 3
b f1 f 2 a (t )d t 2 2 ab ab 2 1 (t ) 1t 2 (3 2t t 2 ) 4 4
1
ab (2t 1) 4
t-2
0
1 t
0 t-2 1
t
5...if ...3 t .......... f1 f 2 0
卷积积分上下限的确定与计算方法1

卷积积分上下限的确定与计算方法卷积积分上下限的确定与计算方法 第 l5 卷第 4 期 2006 年 12 月 河南教育学院(自然科学版) J(1uma1ofHenanInstituteofEducation(NaturalScience) VoI.I5NIJ.4 1)ec.2o(】6 卷积积分上下限的确定与计算方法 黄裕建 (广东轻工职业技术学院电子通信工程系.广东广州 510300) 摘要:本文结合连续 时间 LTI 采统零状态响应的实倒分析给出确定卷积积分上下限的一般原则,讨论利用图 解法和解析法计b5E2RGbCAP算卷积积分的基本方法应该注意的若干问题. 美键词:零状态响应;卷积积分;极限;方法 中圈分类号:O172;TN91 文献标识码:A 文章编号:1007—0834(2006)04—0014—03p1EanqFDPw0 引言 卷积积分在信号与系统理论中占有相当重要的地位,根 据信号与系统理论,连续的 堋系统的数学模型是常系数微 分方程,其全响应可以分解为零输入响应和零状态响应 之 和.卷积积分是计算连续的 LTI 系统的零状态响应的十分重 要的手段.DXDiTa9E3d1 / 12计算卷积的方法可以采用如下四种方法:?用图解法计 算卷积;?用解析式计算卷 积;?数值解法,利用性质计算卷 积;?MATLB 仿真.利用?,?的方法计算卷积是利用计算 机 求解.有关文献对利用?,?的方法计算卷积积分,积分上下 限的确定问题讨论得都不 够全面,本文结合系统零状态响应 的实例分析给出确定卷积积分上下限的一般方法并 给出利 RTCrpUDGiT 用图解法和解析法计算卷积积分的基本方法应该注意的若 干问题. 1 卷积积分的定义 定义: * f(t)=(t)?,2(t)=厂 2(t)?()=I(r)A(t 一一? ? r)dr=If2(r)(t—r)dr(1)J 一* 称为信号(t),(t)的卷积. 卷积积分的定义来源于信号的分解.为了求解在任意激 励下通过 LTI 系统的零状 态响应,可以把输入的激励信号分 解为一系列具有不同强度(幅度)和不同时延的基本 信号,然 后再让这些基本信号一一通过系统,根据线性时不变的特性 进行响应的合成, 就可以得到系统的零状态响应. 如图 1 所示.5PCzVD7HxAJr(t),(O)[E(t)一 E(t—at)]+,(?r)[E(t—at)一 ,(t 一 2At)]+f(2ar)[E(t 一 2Ar)一 E(t 一 3At)]+…+ f【(n 一 1)Ar][E(t 一(,l 一 1)At]一 e(t—nat)] =?f(kAr)[E(t—kAr)一 e(t 一(k+1)Ar)] = c)[一 =?厂(kAr)A(t—kAr)2 / 12jLBHrnAILg幽1 设对于(t)通过 LTI 系统的冲激响应为 h(t),则: (t)一 h(t) f(O)Arr~(t)---~f(0)Arh(t) : Jr(kAr)Ar~(t 一?r)一,(kAr)Arh(t—kAr) lim?Jr(kAr)Ar~()一 lim?f(kAh)?(t—kAr) ?r-Ok0 故:零状态响应的近似解和准确解分别为: Y(t)一?f(kAr)Arh(t—kAr),' =U 收稿日期:2006—06—20 作者简介:黄裕建(1969 一),女,广东和平人,广东轻工职业技术学院电子通信工程 系讲师 ? l4? ,,(t)=1.厂()h(t—r)df=f(t)?h(t).Jo 推 J'到一般情况,即是对于连续信号 (t),(t)的卷积 积分为式(1).而对于电路系统而言,对任意激励的零状态响 应的物理 意义就是:LTI 在任意时刻 t 对任意激励的零状态 响应等于从激励函数开始作用的时刻 t 到指定时刻 t 区间 内,无穷多个幅度不同,连续出现的冲激响应的总和.电路上 的这 类卷积积分只不过是数学上卷积的特例. 2 卷积积分上下限的确定 2.1 采用图解法计算卷积xHAQX74J0X3 / 12卷积图解法将使数学的抽象关系变得形象直观,物理意 义清晰.根据卷积的定义式 (1),通过波形的反褶,平移,相 乘,积分四个步骤,最后得到一个仅与平移时间 t 有关的 函 数波形.做卷积积分时必须注意分清 t 和 r 的含义:r 是积分 变量;t 是积分中的参变 量,也是平移时间._1?J 最后卷积的 结果是参变量 t 的函数.与 r 无关.积分上,下限应 取两个被 卷积函数波形乘积不为零的区段.两函数波形若不相交,即 乘积为零,则卷积 积分为零.当 t 改变时,将引起两函数波形 LDAYtRyKfE 乘积不为零的区段的改变,从而引起积分上,下限的改变,所 以在积分时,要按 t 平 移在 r 轴的不同区段来确定积分的 上,下限.下面通过例题来说明图解法执行卷积的过 程. 例 1 已知 f(t);,(t),h(t)=Ae,,(t)波形,试作图 计算两信号的卷积 ',(t)=f(t)?h(t). 解法 1 利用图解法实现两个信号的卷积可以按照如下 四个步骤:Zzz6ZB2Ltk(1)将信号,(t)=,(t),h(t)=Ae—fE(t)的自变量用 r 代替;将 h(r)=Ae,(r)以纵坐 标为轴线反转,就得到了 h(一 r),如图 2 例 1 示图(a),(b)所示.dvzfvkwMI1(2)将折叠信号 h(一 r)沿 r 轴平移 t,t 为参变量,从而 得到平移信号 h(t—r),其 中,t<0 时 h(I—r)信号向右平移, t>0 时 h(t—r)信号向左平移,如图 2 例 1 示图(d)所 示. (3)将厂()=,(),h(t—r)相乘,从而得到相乘信号 厂(r)h(t—r),如图 2 例 1 示图(e) 所示.rqyn14ZNXI(4)将在区间(一,)上积分得到如图 2 例 1 示图(f) 所示. 础 佐 (d) 0tf 图 2 例 1 示图4 / 12从例 1 示图(c),(d)上可以看出:h(t—r)=一'? s(t—r)非零值的下限是 一,f(r)=,(r)的非零值的下限 是 0,故积分的下限是 0;当积分中的参变量 t<0 时,两个 图 像无重叠,h(t—r)非零值的卜限是 O,,(f)的非零值的上限 足..,故积分的上限足 0.EmxvxOtOco. 即 t<0,沿横轴向右移动 t,两个图像无重叠,卷积结果: rO ,,(,)=,(,)?h(,)=I,(r)?h(,一 f)dr=0 t>0,沿横轴向右移动 t 如图 2 例 1 示图(e) 所示.两个 图像有重叠,h(t—r)=e,(1',(t—r)非零值的下限仍足 一SixE2yXPq5,f(r)=e(r)的非零值的下限是 0,故积分的限仍足 O;h(t—r)非零值的上限是 t,f(r)的非零值的上限是,故 积分的.限是 t. 即 t>0 的卷积结果: r' ,,(')=f(')?h(t)=I,(f)?h(,一 r)dr =IAe 一(1 一 rdf J0 :(1 一 e 一),(,) 结论:若两个函数的左边界分别为[tt],右边界分别 为[t 刖,t 艘],积分的下限为 max[ttL2];积分的上限为 rain[tt2]. 2.2 卷积积分上下限的讨论 卷积积分的严格定义应如式 1 所示,其积分的上下限应 为区间(一*,*).但在具体 计算时,积分的上下限可视函数 (t)与(t)的特性而做些简化.y6v3ALoS89 kavU42VRUs 6ewMyirQFL(1)若(t)和(t)均为因果信号,则积分的上下限可 写为(0 一,t),即 rf5 / 12,,(,);(,)?,2(,)=I(r)?(t—r)dr (2)若(t)为因果信号,(t)为无时限信号,则积分的 上下限可写为(0 一,*),即 ? ,,(t)=(t)?(t)=I(r)?(,一 r)drJ0 一 (3)若(t)为无时限信号,(t)为因果信号,则积分的 上下限可写为(一,t),即 rl ,,(')=(t)?(t)=I(r)?(,一 r)dr (4)若(t)和(t)均为无时限信号,则积分的上下限 可写为(一,),即 ? ,,(,)=(,)?(t)=I(f)?(t—r)dr 2.3 利用解析法计算卷积积分 利用解析法计算卷积积分的方法一般可以概括如下:直 接卷积积分利用定义计算; 利用卷积积分的性质计算; 利用算符计算_4J.M2ub6vSTnP解法 2 直接卷积积分利用定义求例题 1: r* ,,(t)=f(t)?h(t)=I,(r)?h(,一 r)dr : I,(r)?Ae(),(,一 f)drJ 一* = l,(r)?Ae,"),(,一 r)dr+l,(f)?J 一?J0 Ae 一(一)E(,一 r)dr+I,(f)?Ae-~(一 r1,(, 一 J,0YujCfmUCwf)df6 / 12? l5? ; ,(,一 r)dr+r1.^一 n(—r). r0.Aea(t-r) E(,一 r)dr+10-Ae 一'',(#一 r)drJ :r1.Ae-O(—r),(,一 r)'Ir:(1 一 e),(,)J0 口 利用卷积积分的性质汁算例题 1 时, 要利用其微积分特 性,尤其要重视应用奇异信号的特性.卷积积分的微积分和 (t)卷积 特性如 F: r? ,(,)=(t)-,2(,)=,2(,)?I,l()dx = I()dx?(,),f(,)?(,)=,(t) 解法 3 利用卷积积分的微积分特性分析例题 l 可得: r ),(t)=,(t)-h(t)=,(t)?IAe…,()dx r^e—()d r,^e—()dJ0 (1 一 e)e(#) a : a(1 一 e)e(,) 应该注意的是:卷积积分的微积分特性是一个等效特 性,它的成立存在有限制条件. 要求信号必须满足: lira,(t)=0 或者 I,(,)dt=07 / 12sQsAEJkW5T eUts8ZQVRd解法 4 利用算符计算. 定义:1,i2f(,)=(,),,(*)d=-f(t),则称 p, — 分别为微分算符和积分算符.根据奇异信号的特性容易 P 得出: (1)上 p (f)=,(t),1 P (#):据(f),… P (,):'1. E(t) (2))f,(1),)e(f),… )=E(1) 所以: y(t)=(t)?,2(t),(t)-AeE(t) : ^l_l(,).——L(,) = ^I_)=a『上 p 一赤 :8 / 12【P(I)一 P-I-)]口 L 口 J' : 【1 一 e]E(,) 3 结论 实现信号卷积积分的方法虽然有别,但就一般而言,各 有应用的场合,对于时域有 限信号和分段信号,一般采用图 解法;但要注意其积分的上下限,否则不易得到正确的 结论. 对于时域无限信号图解法往往不易解决,一般采用解析法 Lt 较有效;但要注意 公式,性质应用的范围和条件.在实际信号 与系统的零状态响应分析中,应该根据信号 的特点灵活选用 不同的方法. 参考文献 [1]郑君咀,杨为理,心珩.信系统(第 2 版)[M].北京:高等 教育出版 杜.2000:66—68. [2]吴大正.信号与线性系统分析(第 3 版)[M].北京:高等教白 I 出 版社.1998:60—72. [3]OppenheimAV.Signals&Systems[M].NewJersey:Prentice—Hall InternationalIne.1997:94—98. [4]禹思敏.关于因果信号卷积积分的解析法浅析[J].电气电子教 学,2001(2):102—103. FixonUpandDownLimitandComputationalMethods ofConvolutionIntegral HUANGYu-jianTIrRGchYzg GMsIasNXkA9 / 12(DepartmentofElectronicsandCommunicationEngineering,GuangdongIndustryTechni calCollege,Guangzhou510300,China)7EqZcWLZNXAbstract:Inthispaper,weanalyzethequestionhowtodeterminethelimitoftheconvolu tionintegralonthezero—state responseoflinear—time—lzq7IGf02Einvariantsystem(LTI),thendiscusssomequestionsoftheimprovementofgraphicmetho d andformulamethodinroughaboutcomputationalmethodsofconvolutionintegra1. Keywords:zem—stateresponse;convolutionintegral;limit;method ? l6?zvpgeqJ1hk本文档来源于第一 文库网:https ://www.wenku /news/C AC92398F154E 92A.htmlNrpoJac3v110 / 12。
卷积与零状态响应

课 时
第 4 周 第 1 - 2 课时
课题:卷积与零状态响应
一、教学目的:
1、 熟悉卷积与零状态响应 2、 掌握卷积的图解法 3、 了解任意信号的分解
二、教学重点:
卷积的图解法
三、教学难点:
−∞
∞
2.7.2 卷积与零状态响应
x(t ) =
k = −∞
∑ [x(k∆τ )∆τ ]δ (t − k∆τ ) ∑ [x(k∆τ )∆τ ]h (t − k∆τ )
∞
∞
若把它作用于冲激响应为 h(t)的 LTIS,则响应为
y zs (t ) =
简记为:
= ∫ x(τ )h (t − τ )dτ
−∞
利用图解法求卷积
四、教学方法:
讲授法
五、教学用具:
电脑多媒体和黑板
六、教学过程:
2.7.1 任意信号的分解 任意信号 x ( t ) 可表示为冲激序列之和
∞
x(t ) = lim x∆ (t ) = lim
∆t →0
∆t → 0
k = −∞
∑ x(k∆τ )∆τδ (t − k∆τ )
= ∫ x(τ )δ (t − τ )dτ
∞
k = −∞
y ( t ) x( t ) h( t ) = * zs
这就是系统的零状态响应。 2.7.3 卷积的图解法 卷积图解法是借助于图形计算卷积积分的一种基本计算方法。 图解法具体步骤为:
七、课程小结:
卷积的图解法
八、课后作业
(书面作业)
系统零状态响应

21 页
1 2, 2 5
ih t A1e 2 t A2e 5 t
t 0
特解 由于t 0 时 et 4V 方程右端自由项为 4 4,因此令特解 ip t B, 代入式(1) 16 8 10B 4 4 B 10 5 要求系统的完全响应为 8 2t 5t t 0 i t A1e A2e X 5
代入上面元件伏安关系,并化简有 d iS t d 2 v t 1 d v t 1 C v t 2 dt R dt L dt 这是一个代表RCL并联电路系统的二阶微分方程。
X
第
例2-2-2机械位移系统,质量为m的刚体一端由弹簧
k
14 页
m
f
Fs
牵引,弹簧的另一端固定在壁上。刚体与地面间的摩 擦力为 f,外加牵引力为 FS t ,其外加牵引力FS t 与 刚体运动速度 v t 间的关系可以推导出为 d FS t d 2 v t d v t m f kv t 2 dt dt dt 这是一个代表机械位移系统的二阶微分方程。 两个不同性质的系统具有相同的数学模型,都是线 性常系数微分方程,只是系数不同。对于复杂系统,则 可以用高阶微分方程表示。
激励函数e(t) 响应函数r(t)的特解
第
12 页
E (常数)
B(常数)
B1t p B2 t p1 B p t B p1
tp e t
cos t sin t
t pe t t pe t sin t
Be t
B1 cos t B2 sin t
X
第
例2-2-3
d3 d2 d 求微分方程 3 r t 7 2 r t 16 r t 12r t et dt dt dt 的齐次解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 ∴iC (0) = δ (t ) A 2
1 + u C (0 + ) = ∫ 0 0.5δ (t )dtV = 10 V 0.05 1 τ = RC = 20 × 0.05S = 1S u(0+ ) = uC (0+ ) = 5 V
2 h (t ) = uδ (t ) = [5δ (t ) + 5e t ε (t ) ]V
t
t
t
当 0<t <1S 时
rzS (t) = ∫ e ε (τ )dτ = ∫ e dτ = 1 e
0 0
t
τ
t
τ
t
当 t >1S 时
面积 = rzS (t )
rzS (t) = ∫ e ε(τ )dτ = ∫ eτ dτ = e(t1) et
t1 t1
t
τ
t
分时间段表示 当 0<t <1S 时 当 t >1S 时
dτ
t
= e
1
α
ατ 0+
=
1
α
(1 e
αt
)ε ( t )
设图示RC串联电路中电压源的电压 例2 设图示 串联电路中电压源的电压
u (t ) = u 0
t e T ε (t )
零状态响应电压u . 求 零状态响应电压 C(t). 用卷积积分公式求u 解 用卷积积分公式求 CzS(t),应先求冲激响应 ,
∑ f ( kτ ) τ h (t kτ )
k =0 t
n 1
用 ∞ 多个强度不同 , 依次 连续出现的冲击函数分 别单独作用产生的 rzS 之 和来代替 f ( t )产生的 rzS
rzS ( t ) =
∫
0
f (τ )h ( t τ ) d τ
五,卷积积分几何解释 的卷积, 求f(t)与h(t)的卷积,实质上是求一个新函数 与 的卷积 的区间内的定积分. f(τ)h(tτ)在τ 由0到t的区间内的定积分.根据 在 到 的区间内的定积分 定积分的几何意义,函数在0到 区间内的定 定积分的几何意义,函数在 到t区间内的定 积分值,决定于被积函数f( 积分值,决定于被积函数 τ)h(tτ)的曲线在 的曲线在 轴之间所限定的面积. 该区间内与τ 轴之间所限定的面积. 设
f (t) = ε (t)
f(t)
h(t ) = e ε (t )
rzS (t ) = f (t ) h(t ) = ∫ f (τ )h(t τ ) dτ
0 t
t
t h(t)
rzS (t) = h(t) f (t) = ∫ h(τ ) f (t τ ) dτ
0
t
t
rzS (t) = f (t) h(t) = ∫ f (τ )h(t τ ) dτ
注意 卷积计算法只用于求r 卷积计算法只用于求 zS(t) 首先要求h(t) 首先要求
求零状态响应u(t) 例4 iS(t)的波形如图 所示 求零状态响应 的波形如图 所示,求零状态响应
δ (t) A iS (t )
iC (t) + uC(t) -
∵uC (0 ) = 0 解 先求冲激响应 1 u ( 0 ) = δ ( t ) × 10 = 5δ ( t )V 2 0
1 uC ( 0 + ) = C 1 1 δ (t )dt = R RC
∫
0+ 0
1 h (t ) = e RC
t RC ε (t )
零状态响应电压为
u C (t ) =
∫ = ∫u e
0 t
0 0
t
u (τ ) h ( t τ ) d τ
τ
T
1 ε (τ ) e RC
t τ RC
ε (t τ ) dτ
n 1
fa(t) 第K+1个 个
3 1 2 n t
1
f (t ) ≈ f a (t ) = ∑ f ( kτ )[ε (t kτ ) ε (t ( k + 1) τ )] ε (t kτ ) ε (t (k + 1)τ ) = ∑ f (kτ ) τ τ k =0
k =0 n 1
解2 按rzS (t ) = h(t ) f (t ) = ∫ h(τ ) f (t τ ) dτ 计算
f (τ )
0
t
h (τ )
f (τ )
1
τ
τ
-1
0
τ
当 0<t <1S 时
面积 = rzS (t )
rzS (t) = ∫ e ε (τ )dτ = ∫ e dτ = 1 e
τ τ 0 0
§4-6卷积积分及零状态响应的 卷积积分及零状态响应的 卷积计算法 Convolution integral
一 卷积积分的导出
用n个矩形脉冲来近 个矩形脉冲来近 似代替连续函数f(t) 似代替连续函数 用冲击函数来近似 代替矩形脉冲 用n个冲击函数分别 个冲击函数分别 单独作用产生的r 单独作用产生的 zS(t) 之和来近似代替f(t) 之和来近似代替 产生的r 产生的 zS(t)
用∞多个强度不同 , 依次 连续出现的冲击函数之 和来代替连续函数 f (t )
用 n 个强度不同 , 断续出 现的冲击函数分别单独 作用产生的 rzS 之和来近 似代替 f ( t ) 产生的 rzS
∑
n 1
→
∫
t 0
dt
f (t ) = ∫ f (τ )δ (t τ )dτ
0
t
≈→=
rzS ( t ) ≈
t t t ( t 1)
∫ e dτ = e (e e) = (1 e )ε (t 1) t (t1) ∴rzS (t) = (1 e )ε (t) (1 e )ε (t 1) ∫e
1 t t 1
( t τ )
dτ = e
τ
积分上下限应由被积函数存在的时域范围的上下限确定. 积分上下限应由被积函数存在的时域范围的上下限确定. 用作图的方法可方便地确定出积分上下限. 用作图的方法可方便地确定出积分上下限.
u C (t ) =
∫
t
0
u (τ ) h ( t τ ) d τ
0
=
∫u
0teτ源自T1 ε (τ ) e RC
t RC
t τ RC
ε (t τ ) dτ
u0 = e RC
u0 e = RC
∫e
0+
t
T RC τ RCT
dτ
t
t RC
1 T RC RCT
e
T RC τ RCT
0+
t t u 0T T = e e RC T RC
k =0 =0
n 1
NzS →
∑
n 1
f (kτ )τ h (t kτ )
k =0
≈ f (t )
n 1 k =0 n 1
≈ rzS (t )
f (t ) ≈ ∑ f ( kτ ) τδ (t kτ )
3
rzS ( t ) ≈
∑
f (k τ ) τ h (t k τ )
k =0
f (t ) ≈ ∑ f ( kτ ) τδ (t kτ )
≈ ∑ f ( kτ ) τδ (t kτ )
k =0
n 1
δ (t ) → NzS → h(t)
δ (t Kτ ) → NzS → h(t kτ )
f ( kτ ) τδ ( t kτ ) → NzS → f ( k τ ) τh ( t k τ )
∑ f (kτ )τδ (t kτ ) →
∵δ (t ) f (t ) = ∫ δ (τ ) f (t τ )dτ = f (t )∫ δ (τ )dτ = f (t )
t t
δ (t ) f (t ) = f (t ) δ (t ) = f (t )
δ (t t0 ) f (t ) = ∫ δ (τ t 0 ) f (t τ ) dτ
0
t
rzS (t) = ∫ [ε (τ ) ε (τ 1)]e(tτ )ε (t τ )dτ
t 0 t
= ∫ ε (τ )e
0 t
(t τ )
ε (t τ )dτ ∫ ε (τ 1)e
0 t 1
t
(t τ )
ε (t τ )dτ
=∫ e
0
(t τ )
dτ ∫ e(tτ )dτ
rzS (t) = ∫ [ε (τ ) ε (τ 1)]e(tτ )ε (t τ )dτ
0
t
f(t)
h(t)
t
t
将h (τ )取纵轴 的镜象对称
把h( τ )向右 平移到t
t 0
作f (τ )h(t τ )曲线
求面积
褶迭
Convolution
面积 = ∫ f (τ )h(t τ ) dτ = rzS (t )
如按式 rzS ( t ) = h ( t ) f ( t ) =
∫ h (τ ) f ( t τ ) d τ计算
t 0 t 0
0
0
= f (t t0 )∫ δ (τ t 0 )dτ = f (t t0 )
三 卷积积分的计算举例 例1 求卷积 [e 解
α t
α t
ε (t )] ε (t )
t ατ 0
[e ε (t)] ε (t) = ∫ e ε (τ )ε (t τ )dτ
=∫ e
0+ t ατ
∫ (t ) = ∫
f (τ )δ ( t τ ) d τ
f (τ )h ( t τ ) d τ
= f (t) δ (t)
=
f (t ) h (t )
记为
