八数码难题Matlab
matlab知识题及答案解析

2. 用MATLAB 语句输入矩阵A 和B3.假设已知矩阵A ,试给出相应的MATLAB 命令,将其全部偶数行提取出来,赋给B 矩阵,用magic(8)A =命令生成A 矩阵,用上述命令检验一下结果是不是正确。
4.用数值方法可以求出∑=++++++==6363622284212i i S ,试不采用循环的形式求出和式的数值解。
由于数值方法是采用double 形式进行计算的,难以保证有效位数字,所以结果不一定精确。
试采用运算的方法求该和式的精确值。
5.选择合适的步距绘制出下面的图形。
(1))/1sin(t ,其中)1,1(-∈t ; (2))tan(sin )sin(tan t t -,其中),(ππ-∈t6. 试绘制出二元函数2222)1(1)1(1),(yx yx y x f z ++++-==的三维图和三视图7. 试求出如下极限。
(1)xxxx 1)93(lim +∞→; (2)11lim0-+→→xy xy y x ; (3)22)()cos(1lim222200y x y x ey x y x +→→++-8. 已知参数方程⎩⎨⎧-==tt t y t x sin cos cos ln ,试求出x y d d 和3/22d d π=t x y9. 假设⎰-=xyt t e y x f 0d ),(2,试求222222y fy x f x f y x ∂∂+∂∂∂-∂∂ 10. 试求出下面的极限。
(1)⎥⎦⎤⎢⎣⎡-++-+-+-∞→1)2(1161141121lim 2222n n ; (2))131211(lim 2222ππππn n n n n n n ++++++++∞→ 11. 试求出以下的曲线积分。
(1)⎰+ls y x d )(22,l 为曲线)sin (cos t t t a x +=,)cos (sin t t t a y -=,)20(π≤≤t 。
(2)⎰-+++ly y y xe x e yx )dy 2(xy d )(33,其中l 为22222c y b x a =+正向上半椭圆。
大学matlab考试题及答案

大学matlab考试题及答案大学MATLAB考试题及答案一、选择题1. MATLAB的全称是什么?A. Matrix LaboratoryB. Microprocessor Application Tool SetC. Microsoft Advanced Tool SetD. Microprocessor Application Test System答案:A2. 在MATLAB中,以下哪个命令用于绘制三维图形?A. plotB. scatterC. surfD. bar答案:C3. MATLAB中用于求解线性方程组的函数是?A. solveB. linsolveC. linprogD. fsolve答案:A二、简答题1. 简述MATLAB的基本数据类型有哪些,并给出至少两个每种类型的示例。
答案:MATLAB的基本数据类型包括数值数组、字符数组和单元数组。
数值数组可以是向量、矩阵或多维数组。
例如,向量 `v = [1 2 3]`,矩阵 `M = [1 2; 3 4]`。
字符数组是由单引号或双引号括起来的字符序列,如 `C = 'Hello'`。
单元数组可以包含不同类型的数据,如`{1, 'text', [1; 2; 3]}`。
2. 描述如何在MATLAB中实现矩阵的转置和翻转。
答案:矩阵的转置可以通过 `'T'` 来实现,例如 `A'` 表示矩阵A 的转置。
矩阵的翻转可以通过 `flip` 函数实现,例如 `flip(A)` 可以翻转矩阵A的所有行和列,`flipud(A)` 仅翻转矩阵A的行,而`fliplr(A)` 仅翻转矩阵A的列。
三、编程题1. 编写一个MATLAB函数,该函数接受一个向量作为输入,并返回向量中所有元素的和以及平均值。
```matlabfunction [sumVal, avgVal] = calculateSumAndAverage(V)sumVal = sum(V);avgVal = mean(V);end```2. 设计一个MATLAB脚本来解决以下问题:给定一个3x3的矩阵,找出其中最大的元素,并显示其位置。
人工智能8位数码难题的问题求解

#define DOWN 1
#define LEFT 2
#define RIGHT 3
#define Bit char
typedef struct maps
{
Bit detail[9];
int myindex; //记录自己节点在hash表中的位置
Bit position; //记录空格(0)在序列中的位置
实验软硬件要求:网络计算机,c++编程环境
实验内容、方法和步骤(可附页)
我们将八数码难题分布在3×3方格棋盘上,分别放置了标有数字1,2,3,4,5,6,7,8的八张牌,初始状态S0,目标状态如图所示,可以使用的操作有:空格上移,空格左移,空格右移,空格下移。我们将是用广度优先搜索算法来解决这一问题。
int newindex = Parent.myindex ;
Bit *p = Parent.detail;
switch(direct)
{
case UP :
{
newindex -= 3*40320 ;
newindex += ( p[ i - 2 ] > p[ i - 3 ]) ? ( Factorial[ p[ i - 3 ] ] ) : ( - Factorial[ p[ i - 2 ] ] );
}p,*PMap;
Map org; //初始状态
int EndIndex; //目标,上移,下移,左移,右移
int const derection[4] ={ -3 , 3 , -1 , 1 } ;
//可移动的四个方向
int const Factorial[9] = {40320 , 5040 , 720 , 120 , 24 , 6 , 2 , 1 , 1 };
人工智能实验总结

总结
宽度优先搜索法
在有解的情形总能保证搜索到最短路经,也 就是移动最少步数的路径。但宽度优先搜索法的 最大问题在于搜索的结点数量太多,因为在宽度 优先搜索法中,每一个可能扩展出的结点都是搜 索的对象。随着结点在搜索树上的深度增大,搜 索的结点数会很快增长,并以指数形式扩张,从 而所需的存储空间和搜索花费的时间也会成倍增 长。
1 2
0 1 0 1
0 0 1 1
0 1 1 0
神经网络设计
用两层神经网络来实现,其中隐层为随机 感知器层(net1),神经网络元数目设计为 3,其权值和阈值是随机的,它的输出作为 输出层(分类层)的输入;输出层为感知 器层(net2),其神经元数为1,这里仅对 该层进行训练。
程序运行结果
随机感知器层的权值向量 iw1 = 0.4267 -0.6556 -0.5439 0.9376 -0.1007 -0.2886 随机感知器层的阈值向量 b1 = 0.4074 0.0441 0.8658
运行结果分析
上面实验结果可以看出,城市数目为30的 时候,当迭代次数为100,算法收敛慢,在 迭代次数内最优解没有达到稳定,没有搜 索到最好的解。 迭代次数为200和250的时候,算法基本达 到收敛,最优解在100代以后趋于稳定,表 明搜索到问题的最优解。
运行结果
当城市数目改变的时候: CityNum=50;最大代数gnmax=100;
程序运行结果
第二层感知器层的权值向量和阈值向量 iw2 = -3 -2 2 b2 = 2
八数码难题--Matlab

b1=zhao(a1); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [a1,b1]=zuo(a)[x,y]=find(a==0);a1=a;a1(x,y)=a(x,y-1);a1(x,y-1)=0;b1=zhao(a1); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [a1,b1]=you(a)[x,y]=find(a==0);a1=a;a1(x,y)=a(x,y+1);a1(x,y+1)=0;b1=zhao(a1); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function z=panduan(a)global E;global I;I=2;[x,y]=size(E);z=1;for i=1:yb=E{i};v=(b-a).^2;if sum(sum(v))==0z=0;break;endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function y=zhao(a)wan=[1 2 3;8 0 4;7 6 5];y=0;b=a-wan;for i=1:3for j=1:3if b(i,j)~=0y=y+1;endendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% global Eglobal Ia=[2 8 3;1 0 4;7 6 5];b=[1 2 3;8 0 4;7 6 5];I=1;E(1)={a};for i=2:20q=b-E{i};if sum(sum(q.^2))E(i)={kaka(E{i-1})};celldisp(E(i))elsebreak;endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [a1]=kaka(a)global I;global E;c=[2 8 3;1 0 4;7 6 5];E(1)={c};[x,y]=find(a==0);z=9;if x==1if y==1[x1,y1]=xia(a);if y1<zif panduan(x1)b=x1;z=y1;endend[x2,y2]=you(a);if y2<zif panduan(x2)b=x2;z=y2;endenda1=b;endif y==2[x1,y1]=xia(a);if y1<zif panduan(x1)z=y1;endend[x2,y2]=zuo(a);if y2<zif panduan(x2) b=x2;z=y2;endend[x3,y3]=you(a);if y3<zif panduan(x3) b=x3;z=y3;endenda1=b;endif y==3[x1,y1]=xia(a);if y1<zif panduan(x1) b=x1;z=y1;endend[x2,y2]=zuo(a);if y2<zif panduan(x2) b=x2;z=y2;endenda1=b;endendif x==2if y==1[x1,y1]=shang(a);if y1<zif panduan(x1) b=x1;endend[x2,y2]=xia(a);if y2<zif panduan(x2) b=x2;z=y2;endend[x3,y3]=you(a);if y3<zif panduan(x3) b=x3;z=y3;endenda1=b;endif y==2[x1,y1]=shang(a);if y1<zif panduan(x1); b=x1;z=y1;endend[x2,y2]=xia(a);if y2<zif panduan(x2); b=x2;z=y2;endend[x3,y3]=zuo(a);if y3<zif panduan(x3); b=x3;z=y3;endend[x4,y4]=you(a);if y4<z;if panduan(x4)z=y4;endenda1=b;endif y==3[x1,y1]=shang(a);if y1<zif panduan(x1) b=x1;z=y1;endend[x2,y2]=xia(a);if y2<zif panduan(x2) b=x2;z=y2;endend[x3,y3]=zuo(a);if y3<zif panduan(x3) b=x3;z=y3;endenda1=b;endendif x==3if y==1[x1,y1]=shang(a);if y1<zif panduan(x1) b=x1;z=y1;endend[x4,y4]=you(a);if y4<z;if panduan(x4) b=x4;endenda1=b;endif y==2[x1,y1]=shang(a);if y1<zif panduan(x1) b=x1;z=y1;endend[x3,y3]=zuo(a);if y3<zif panduan(x3) b=x3;z=y3;endend[x4,y4]=you(a);if y4<z;if panduan(x4) b=x4;z=y4;endenda1=b;endif y==3[x1,y1]=shang(a);if y1<zif panduan(x1) b=x1;z=y1;endend[x3,y3]=zuo(a);if y3<zif panduan(x3) b=x3;z=y3;endenda1=b;endendE(I)={a1};五、实验结论1、启发式搜索算法A*流程图和算法框图。
人工智能A星算法解决八数码难题程序代码

#include "Stdio.h"#include "Conio.h"#include "stdlib.h"#include "math.h"void Copy_node(struct node *p1,struct node *p2);void Calculate_f(int deepth,struct node *p);void Add_to_open(struct node *p);void Add_to_closed(struct node *p);void Remove_p(struct node *name,struct node *p);int Test_A_B(struct node *p1,struct node *p2);struct node * Search_A(struct node *name,struct node *temp); void Print_result(struct node *p);struct node // 定义8数码的节点状态{int s[3][3]; //当前8数码的状态int i_0; //当前空格所在行号int j_0; //当前空格所在列号int f; //当前代价值int d; //当前节点深度int h; //启发信息,采用数码"不在位"距离和struct node *father; //指向解路径上该节点的父节点struct node *next; //指向所在open或closed表中的下一个元素} ;struct node s_0={{2,8,3,1,6,4,7,0,5},2,1,0,0,0,NULL,NULL}; //定义初始状态struct node s_g={{1,2,3,8,0,4,7,6,5},1,1,0,0,0,NULL,NULL}; //定义目标状态struct node *open=NULL; //建立open表指针struct node *closed=NULL; //建立closed表指针int sum_node=0; //用于记录扩展节点总数//***********************************************************//********************** **********************//********************** 主函数开始**********************//********************** **********************//***********************************************************void main(){int bingo=0; //定义查找成功标志,bingo=1,成功struct node s; //定义头结点sstruct node *target,*n,*ls,*temp,*same; //定义结构体指针Copy_node(&s_0,&s); //复制初始状s_0态给头结点s Calculate_f(0,&s); //计算头结点的代价值Add_to_open(&s); //将头结点s放入open表while(open!=NULL) //只要open表不为空,进行以下循环{n=open; //n指向open表中当前要扩展的元素ls=open->next;Add_to_closed(n);open=ls; //将n指向的节点放入closed表中if(Test_A_B(n,&s_g)) //当前n指向节点为目标时,跳出程序结束;否则,继续下面的步骤{bingo=1;break;}elseif(n->j_0>=1) //空格所在列号不小于1,可左移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0&&temp->j_0-1==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同,或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝n指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0-1]; //空格左移temp->s[temp->i_0][temp->j_0-1]=0;temp->j_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小,加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小,加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点,加入open表{Add_to_open(temp);sum_node++;}}}//end左移if(n->j_0<=1) //空格所在列号不大于1,可右移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0&&temp->j_0+1==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同,或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0+1]; //空格右移temp->s[temp->i_0][temp->j_0+1]=0;temp->j_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小,加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小,加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点,加入open表{Add_to_open(temp);sum_node++;}}}//end右移if(n->i_0>=1) //空格所在列号不小于1,上移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0-1&&temp->j_0==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同,或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0-1][temp->j_0];//空格上移temp->s[temp->i_0-1][temp->j_0]=0;temp->i_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小,加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小,加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点,加入open表{Add_to_open(temp);sum_node++;}}}//end上移if(n->i_0<=1) //空格所在列号不大于1,下移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0+1&&temp->j_0==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同,或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0+1][temp->j_0]; //空格下移temp->s[temp->i_0+1][temp->j_0]=0;temp->i_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小,加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小,加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点,加入open表{Add_to_open(temp);sum_node++;}}}//end下移}if(bingo=1) Print_result(n); //输出解路径else printf("问题求解失败!");}//主函数结束//************************************************************************* //********************** ********************** //********************** 计算某个节点状态的代价值********************** //********************** ********************** //*************************************************************************void Calculate_f(int deepth,struct node *p){int i,j,temp;temp=0;for(i=0;i<=2;i++) //计算所有"不在位"数码的距离和{for(j=0;j<=2;j++){if((p->s[i][j])!=(s_g.s[i][j]))temp++;}}p->h=temp;p->f=deepth+p->h;}//*************************************************************************//********************** **********************//********************** 添加p指向的节点到open表中********************** //********************** **********************//*************************************************************************void Add_to_open(struct node *p){struct node *p1,*p2;p1=open; //初始时p1指向open表首部p2=NULL;if(open==NULL) //open表为空时,待插入节点即为open表第一个元素,open 指向该元素{p->next=NULL;open=p;}else //open表不为空时,添加待插入节点,并保证open表代价递增的排序{while(p1!=NULL&&p->f>p1->f){p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}if(p2==NULL) //待插入节点为当前open表最小{p->next=open;open=p;}else if(p1==NULL) //待插入节点为当前open表最大{p->next=NULL;p2->next=p;}else //待插入节点介于p2、p1之间{p2->next=p;p->next=p1;}}}//***************************************************************************//********************** **********************//********************** 添加p指向的节点到closed表中**********************//********************** **********************//***************************************************************************void Add_to_closed(struct node *p){if(closed==NULL) //closed表为空时,p指向节点为closed表第一个元素,closed{p->next=NULL;closed=p;}else //closed表不为空时,直接放到closed表首部{p->next=closed;closed=p;}}//************************************************************************************* *************//********************************************//********************** 在open表或closed表中搜索和temp指向的节点相同的节点**********************//********************************************//*************************************************************************************struct node * Search_A(struct node *name,struct node *temp){struct node *p1;p1=name; //p1指向open表或closed表while(p1!=NULL){if(Test_A_B(p1,temp)) //找到相同的节点,返回该节点地址return p1;elsep1=p1->next;}return NULL;}//************************************************************************************* **********//********************************************//********************** 判断两个节点状态是否相同,相同则返回1,否则返回0 **********************//********************************************//************************************************************************************* **********int Test_A_B(struct node *p1,struct node *p2){int i,j,flag;flag=1;for(i=0;i<=2;i++)for(j=0;j<=2;j++){if((p2->s[i][j])!=(p1->s[i][j])) { flag=0; return flag; }else ;}return flag;}//******************************************************************************//********************** **********************//********************** 从open表或closed表删除指定节点********************** //********************** **********************//******************************************************************************void Remove_p(struct node *name,struct node *p){struct node *p1,*p2;p1=NULL;p2=NULL;if(name==NULL) //如果name指向的链表为空,则不需要进行删除return;else if(Test_A_B(name,p)&&name->f==p->f) //指定节点为name指向的链表的第一个元素{open=name->next;name->next=NULL;return;}else{p2=name;p1=p2->next;while(p1){if(Test_A_B(p1,p)&&p1->f==p->f) //找到指定节点{p2->next=p1->next;return;}else{p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}}return;}}//************************************************************************************* *//********************************************//********************** 将p1指向的节点状态拷贝到p2指向的节点中**********************//********************************************//************************************************************************************* *void Copy_node(struct node *p1,struct node *p2){int i,j;for(i=0;i<=2;i++){for(j=0;j<=2;j++){ p2->s[i][j]=p1->s[i][j]; }}p2->i_0=p1->i_0;p2->j_0=p1->j_0;p2->f=p1->f;p2->d=p1->d;p2->h=p1->h;p2->next=p1->next;p2->father=p1->father;}//*********************************************************** //********************** ********************** //********************** 输出结果********************** //********************** ********************** //***********************************************************void Print_result(struct node *p){struct node *path[100];struct node *temp,*temp_father;int i,j,k;for(i=0;i<=99;i++) //初始化路径指针数组path[i]=0;temp=p;printf("总共扩展%d 个节点\n",sum_node);printf("总共扩展%d 层\n",temp->d);printf("解路径如下:\n");for(i=p->d;i>=0;i--) //存储解路径上各节点的地址{path[i]=temp;temp=temp->father;}for(k=0;k<=p->d;k++) //输出解路径{temp=path[k]; //建立节点指点指针printf("第%d步",temp->d);if(k-1>=0) //输出移动策略{temp_father=path[k-1];if(temp->i_0<temp_father->i_0) printf("->上移\n");if(temp->i_0>temp_father->i_0) printf("->下移\n");if(temp->j_0<temp_father->j_0) printf("->左移\n");if(temp->j_0>temp_father->j_0) printf("->右移\n");}elseprintf("\n");printf("当前节点状态为:\n");for(i=0;i<=2;i++){for(j=0;j<=2;j++){printf("%d ",temp->s[i][j]);}printf("\n");}printf("\n");}}THANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
Matlab 考题题整理 带答案

MATLAB 考试试题(1)产生一个1x10的随机矩阵,大小位于(-5 5),并且按照从大到小的顺序排列好!(注:要程序和运行结果的截屏)答案:a=10*rand(1,10)-5;b=sort(a,'descend')1.请产生一个100*5的矩阵,矩阵的每一行都是[1 2 3 4 5]2. 已知变量:A=’ilovematlab’;B=’matlab’, 请找出:(A)B在A中的位置。
(B)把B放在A后面,形成C=‘ilovematlabmatlab’3. 请修改下面的程序,让他们没有for循环语句!A=[1 2 3; 4 5 6; 7 8 9];[r c]=size(A);for i=1:1:rfor j=1:1:cif (A(i,j)>8 | A(i,j)<2)A(i,j)=0;endendend4. 请把变量A=[1 2 3; 4 5 6; 7 8 9]写到文件里(output.xls),写完后文件看起来是这样的1 2 3 4 5 6 7 8 95.试从Yahoo网站上获得微软公司股票的2008年9月的每日收盘价。
6.编写M文件,从Yahoo网站批量读取60000.SH至600005.SH在2008年9月份的每日收盘价(提示:使用字符串函数)。
7. 将金牛股份(000937)2005年12月14日至2006年1月10日的交易记录保存到Excel中,编写程序将数据读入MATLAB中,进一步将数据读入Access数据库文件。
8.已知资产每日回报率为0.0025,标准差为0.0208,资产现在价值为0.8亿,求5%水平下资产的10天在险价值(Var)。
9.a=[1 2 3 4 5],b=a(1)*a(5)+a(2)*a(4)+a(3)*a(3)+a(4)*a(2)+a(5)*a(1).试用MATLAB中最简单的方法计算b,注意最简单哦。
1、求下列联立方程的解3x+4y-7z-12w=45x-7y+4z+ 2w=-3x +8z- 5w=9-6x+5y-2z+10w=-8求系数矩阵的秩;求出方程组的解。
智能控制(研究生)习题集
习题集第一章概论1.试从学科和能力两个方面说明什么是人工智能。
2.哪些思想、思潮、时间和人物在人工智能发展过程中起了重要作用?3.近年来人工智能研究取得哪些重要进展?4.为什么能够用计算机模拟人类智能?5.目前人工智能学界有哪些学派?它们的认知观为何?6.自动控制存在什么机遇与挑战?为什么要提出智能控制?7.简述智能控制的发展过程,并说明人工智能对自动控制的影响。
8.傅京孙对智能控制有哪些贡献?9.什么是智能控制?它具有哪些特点?10.智能控制器的一般结构和各部分的作用为何?它与传统控制器有何异同?11.智能控制学科有哪几种结构理论?这些理论的内容是什么?12.为什么要把信息论引入智能控制学科结构?13.人工智能不同学派的思想在智能控制上有何反映?第二章知识表示方法1.状态空间法、问题归约法、谓词逻辑法和语义网络法的要点是什么?它们有何本质上的联系及异同点?2.设有3个传教士和3个野人来到河边,打算乘一只船从右岸渡到左岸去。
该船的负载能力为两人。
在任何时候,如果野人人数超过传教士人数,那么野人就会把传教士吃掉。
他们怎样才能用这条船安全地把所有人都渡过河去?3.利用下图,用状态空间法规划一个最短的旅行路程:此旅程从城市A开始,访问其他城市不多于一次,并返回A。
选择一个状态表示,表示出所求得的状态空间的节点及弧线,标出适当的代价,并指明图中从起始节点到目标节点的最佳路径。
4.试说明怎样把一棵与或解树用来表达下图所示的电网络阻抗的计算。
单独的R、L或C可分别用R、jωL或1/jωC来计算,这个事实用作本原问题。
后继算符应以复合并联和串联阻抗的规则为基础。
5.试用四元数列结构表示四圆盘梵塔问题,并画出求解该问题的与或图。
6.用谓词演算公式表示下列英文句子(多用而不是省用不同谓词和项。
例如不要用单一的谓词字母来表示每个句子)。
A computer system is intelligent if it can perform a task which,if performed by a human, requires intelligence.7.把下列语句表示成语义网络描述:(1)All man are mortal.(2)Every cloud has a silver lining.(3)All branch managers of DEC participate in a profit-sharing plan.8.作为一个电影观众,请你编写一个去电影院看电影的剧本。
八叉树算法 matlab代码

八叉树算法简介在计算机图形学和计算机视觉领域,八叉树算法是一种常用的数据结构,用于对三维空间进行分割和索引。
八叉树是一种树形结构,每个节点可以有最多8个子节点,因此得名为八叉树。
它的主要思想是将三维空间递归地划分为八个子立方体,从而实现对三维数据的快速检索和查询。
八叉树的构造八叉树的构造过程是通过递归实现的。
下面是八叉树的构造算法:1.初始化根节点,将整个空间作为根节点的区域。
2.对于每个节点,判断其区域中是否存在点或物体。
3.如果节点的区域中只有一个点或物体,则将该节点标记为叶子节点,并保存相应的点或物体信息。
4.如果节点的区域中有多个点或物体,则将该节点划分为八个子节点,每个子节点负责其父节点区域的1/8子区域。
5.对于每个子节点,重复步骤2-4,直到满足终止条件。
6.构造完整的八叉树后,可以根据需要进行查询和检索。
八叉树的应用八叉树算法在计算机图形学和计算机视觉领域有广泛的应用,以下是几个常见的应用场景:三维场景管理八叉树可以用于对三维场景进行管理和索引。
它可以将复杂的三维场景分割为多个子立方体,每个子立方体都有自己的节点,从而实现对场景中物体的高效检索和渲染。
点云数据处理八叉树也常用于处理点云数据。
点云是由大量点组成的三维数据集,通过八叉树可以对点云进行高效的存储和处理。
八叉树可以将点云数据划分为多个子区域,从而减少不必要的计算和存储开销。
基于体素的渲染八叉树在体素渲染中也有应用。
体素渲染是一种基于体素(三维像素)的渲染方法,八叉树可以对体素数据进行分割和索引,加速体素渲染的计算速度。
碰撞检测八叉树还可以用于碰撞检测。
在计算机游戏中,需要检测物体之间是否发生碰撞,八叉树可以将物体进行精确的划分,通过判断物体所在的子节点是否重叠,可以有效地进行碰撞检测。
八叉树的优缺点八叉树作为一种常用的数据结构,具有以下优点和缺点:优点•高效的数据检索和查询能力,可以减少不必要的计算和存储开销。
•可以对大规模的三维数据进行高效的管理和处理,提高计算效率。
《人工智能及其应用》实验指导书

《人工智能及其应用》实验指导书浙江工业大学计算机科学与技术学院—人工智能课程组2011年9月前言本实验是为了配合《人工智能及其应用》课程的理论学习而专门设置的。
本实验的目的是巩固和加强人工智能的基本原理和方法,并为今后进一步学习更高级课程和信息智能化技术的研究与系统开发奠定良好的基础。
全书共分为八个实验:1.产生式系统实验;2.模糊推理系统实验;3.A*算法求解8数码问题实验;4.A*算法求解迷宫问题实验;5.遗传算法求解函数最值问题实验;6.遗传算法求解TSP问题实验;7.基于神经网络的模式识别实验;8.基于神经网络的优化计算实验。
每个实验包括有:实验目的、实验内容、实验条件、实验要求、实验步骤和实验报告等六个项目。
本实验指导书包括两个部分。
第一个部分是介绍实验的教学大纲;第二部分是介绍八个实验的内容。
由于编者水平有限,本实验指导书的错误和不足在所难免,欢迎批评指正。
人工智能课程组2011年9月目录实验教学大纲 (1)实验一产生式系统实验 (3)实验二模糊推理系统实验 (5)实验三A*算法实验I (9)实验四A*算法实验II (12)实验五遗传算法实验I (14)实验六遗传算法实验II (18)实验七基于神经网络的模式识别实验 (20)实验八基于神经网络的优化计算实验 (24)实验教学大纲一、学时:16学时,一般安排在第9周至第16周。
二、主要仪器设备及运行环境:PC机、Visual C++ 6.0、Matlab 7.0。
三、实验项目及教学安排序号实验名称实验平台实验内容学时类型教学要求1 产生式系统应用VC++ 设计知识库,实现系统识别或分类等。
2 设计课内2 模糊推理系统应用Matlab 1)设计洗衣机的模糊控制器;2)设计两车追赶的模糊控制器。
2 验证课内3 A*算法应用I VC++ 设计与实现求解N数码问题的A*算法。
2 综合课内4 A*算法应用II VC++ 设计与实现求解迷宫问题的A*算法。
matlab上机考试题及答案

matlab上机考试题及答案1. 题目:编写一个MATLAB函数,计算并返回一个向量中所有元素的平方和。
答案:函数定义如下:```matlabfunction sumOfSquares = calculateSumOfSquares(vector)sumOfSquares = sum(vector.^2);end```2. 题目:使用MATLAB的内置函数,找出一个矩阵中的最大元素及其位置。
答案:可以使用`max`函数来找出矩阵中的最大元素,同时使用`find`函数来获取其位置。
示例代码如下:```matlabA = [1, 2, 3; 4, 5, 6; 7, 8, 9];[maxValue, linearIndex] = max(A(:));[row, col] = ind2sub(size(A), linearIndex);```3. 题目:给定一个向量,使用MATLAB编写代码,实现向量元素的逆序排列。
答案:可以使用`flip`函数来实现向量的逆序排列。
示例代码如下:```matlabvector = [1, 2, 3, 4, 5];reversedVector = flip(vector);```4. 题目:编写一个MATLAB脚本,计算并绘制一个正弦波的图像。
答案:可以使用`sin`函数生成正弦波数据,并使用`plot`函数绘制图像。
示例代码如下:```matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);xlabel('x');ylabel('sin(x)');title('Sine Wave');```5. 题目:给定一个3x3的矩阵,使用MATLAB编写代码,计算其行列式。
答案:可以使用`det`函数来计算矩阵的行列式。
示例代码如下:```matlabmatrix = [1, 2, 3; 4, 5, 6; 7, 8, 9];determinant = det(matrix);```结束语:以上是MATLAB上机考试的题目及答案,希望能够帮助大家更好地掌握MATLAB的编程技巧和函数使用。
人工智能大作业八数码问题

基于A星算法的八数码问题求解学号:姓名:摘要:在人工智能领域中, 八数码问题一直都是一个游戏难题。
介绍了八数码问题, 然后在启发式搜索算法上对A * 算法定义进行了解释, 并在其旨在提高搜索效率的方面作了比较详尽的介绍, 详细描述了基于图搜索算法的解决此类问题的一种启发式搜索算法:A* 算法。
再依据这种算法用可视化编程语言VC+ + 6. 0 来实现八数码问题的求解过程, 取得了预期的搜索解, 提高了搜索效率。
关键词:八数码问题; 启发式搜索; A* 算法本组成员:本人分工:主要负责进行问题分析,提出解决方案,进行系统设计,算法上具体负责主函数的编写。
1 引言八数码问题是人工智能的一个经典的问题。
文中通过设计一个基于A* 算法的状态空间搜索程序, 对于给定的初始状态, 采用h ( n ) = p ( n ) 表示以每一个将牌与目标位置之间距离的总和作为启发函数的度量, 并用可视化编程语言VC+ + 来实现该问题。
2 算法原理与系统设计1)A*算法思想A*算法是对A算法的估价函数f(n)=g(n)+h(n)加上某些限制后得到的一种启发式搜索算法。
A*算法对A算法中的g(n)和h(n)分别提出如下限制:第一,g(n)是对最小代价g*(n)的估计,且g(n)>0;第二,h(n)是最小代价h*(n)的下界,即对任意节点n 均有h(n)≤h*(n)。
即满足上述两条限制的A算法称为A*算法。
2)估价函数用来估算节点希望程度的量度,叫估价函数f(x),f(x)=g(x)+h(x)。
g(x)为从初始节点到当前节点已经付出的代价,h(x)为从当前节点到目标节点的最优路径的估计代价。
本算法中令g(x)为当前节点的深度depth,h(x)为当前节点每个数字位与目标节点数字位间距离和dist,进一步考虑当前结点与目标结点的距离信息,令启发函数h ( n )为当前8个数字位与目标结点对应数字位距离和(不考虑中间路径),满足h ( n ) <= h * ( n ),且对于目标节点有h ( t ) = 0,对于结点m和n (n 是m的子结点)有h ( m ) – h ( n ) <= 1满足单调限制条件。
八数码问题求解--实验报告讲解

实验报告一、实验问题八数码问题求解二、实验软件VC6.0 编程语言或其它编程语言三、实验目的1. 熟悉人工智能系统中的问题求解过程;2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用;3. 熟悉对八数码问题的建模、求解及编程语言的应用。
四、实验数据及步骤(一、)实验内容八数码问题:在3 ×3 的方格棋盘上,摆放着1 到8 这八个数码,有1 个方格是空的,其初始状态如图1 所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。
2 83 1 2 31 4 8 47 6 5 7 6 5(a) 初始状态(b) 目标状态图1 八数码问题示意图(二、)基本数据结构分析和实现1. 结点状态我采用了struct Node 数据类型typedef struct _Node{int digit[ROW][COL];int dist; // distance between one state and the destination 个表和目的表的距离int dep; // the depth of node 深度// So the comment function = dist + dep. 估价函数值int index; // point to the location of parent 父节点的位置} Node; 2. 发生器函数定义的发生器函数由以下的四种操作组成:(1) 将当前状态的空格上移Node node_up;Assign(node_up, index);// 向上扩展的节点int dist_up = MAXDISTANCE;(2) 将当前状态的空格下移Node node_down;Assign(node_down, index);// 向下扩展的节点int dist_down = MAXDISTANCE;(3) 将当前状态的空格左移Node node_left;Assign(node_left, index);// 向左扩展的节点int dist_left = MAXDISTANCE;(4) 将当前状态的空格右移Node node_right;Assign(node_right, index);// 向右扩展的节点int dist_right = MAXDISTANCE;通过定义结点状态和发生器函数,就解决了8 数码问题的隐式图的生成问题。
基于A算法求解八数码问题-哈尔滨工程大学

基于A算法求解八数码问题-哈尔滨工程大学基于A* 算法求解八数码问题班级:20110616 学号:2011061618 姓名:唐宗林摘要:利用人工智能中的经典启发式搜索算法求解八数码问题,在启发式搜索算法上对A* 算法的定义进行了解释,详细的描述了启发式A* 搜索算法,并将之运用至解决八数码问题,对八数码问题求解过程进行了详细解释,取得了预期的搜索解,达到了本实验课程的预期目的。
关键词:人工智能;启发式搜索算法;A* 算法;八数码问题本组成员:唐宗林,陶涛,汤芦山本人分工:主要承担A* 算法中启发函数的设计、八数码问题解存在问题判断等工作。
1 引言在信息社会中,人们越来越依赖于搜索技术来获取有用的信息,搜索是人工智能中的一个基本问题,是推理不可分割的一部分,它直接关系到智能系统的性能及运行效率。
通常搜索策略的主要任务是确定如何选取规则的方式。
一般有两种方式:一种是不考虑所给问题所具有的的特定知识系统根据事先确定好的某种固定排序,一次调用规则或随机调用规则,这实际上是盲目搜索的策略;另一种是考虑问题领域可应用的知识,动态的确定规则的排序,优先调用较合适的规则排序,这就是通常所称为的启发式搜索策略。
启发式搜索是利用问题所拥有的启发式信息来引导搜索,以达到减少搜索范围,降低问题复杂度的目的。
在本课程实验中我们以八数码问题为背景,运用启发式搜索算法来达到求解目的。
通过解决八数码问题来加深对A* 算法的理解及运用,以更好地将课堂所学知识运用到实际问题的解决之中。
在实验中我的任务主要是A* 算法中启发函数的设计、八数码问题解存在问题判断等工作,所以接下来的叙述也将围绕这几项工作来展开。
2 算法原理与系统设计2.1 八数码问题八数码游戏(八数码问题)描述为:在3X3组成的九宫格棋盘上,摆有八个将牌,每一个将牌都刻有1-8 八个数码中的某一个数码。
棋盘中留有一个空格,允许其周围的某一个将牌向空格移动,这样通过移动将牌就可以不断改变将牌的布局。
人工智能实验一_八数码问题

用A*算法解决八数码问题1 问题描述1.1 待解决问题的解释八数码游戏(八数码问题)描述为:在3×3组成的九宫格棋盘上,摆有八个将牌,每一个将牌都刻有1-8八个数码中的某一个数码。
棋盘中留有一个空格,允许其周围的某一个将牌向空格移动,这样通过移动将牌就可以不断改变将牌的布局。
这种游戏求解的问题是:给定一种初始的将牌布局或结构(称初始状态)和一个目标的布局(称目标状态),问如何移动将牌,实现从初始状态到目标状态的转变。
1.2 问题的搜索形式描述(4要素)初始状态:8个数字将牌和空格在九宫格棋盘上的所有格局组成了问题的状态空间。
其中,状态空间中的任一种状态都可以作为初始状态。
后继函数:通过移动空格(上、下、左、右)和周围的任一棋子一次,到达新的合法状态。
目标测试:比较当前状态和目标状态的格局是否一致。
路径消耗:每一步的耗散值为1,因此整个路径的耗散值是从起始状态到目标状态的棋子移动的总步数。
1.3 解决方案介绍(原理)对于八数码问题的解决,首先要考虑是否有答案。
每一个状态可认为是一个1×9的矩阵,问题即通过矩阵的变换,是否可以变换为目标状态对应的矩阵?由数学知识可知,可计算这两个有序数列的逆序值,如果两者都是偶数或奇数,则可通过变换到达,否则,这两个状态不可达。
这样,就可以在具体解决问题之前判断出问题是否可解,从而可以避免不必要的搜索。
如果初始状态可以到达目标状态,那么采取什么样的方法呢?常用的状态空间搜索有深度优先和广度优先。
广度优先是从初始状态一层一层向下找,直到找到目标为止。
深度优先是按照一定的顺序前查找完一个分支,再查找另一个分支,以至找到目标为止。
广度和深度优先搜索有一个很大的缺陷就是他们都是在一个给定的状态空间中穷举。
这在状态空间不大的情况下是很合适的算法,可是当状态空间十分大,且不预测的情况下就不可取了。
他的效率实在太低,甚至不可完成。
由于八数码问题状态空间共有9!个状态,对于八数码问题如果选定了初始状态和目标状态,有9!/2个状态要搜索,考虑到时间和空间的限制,在这里采用A*算法作为搜索策略。
八数码问题求解与界面设计

基于启发式搜索的九宫图问题求解及其界面设计一、九宫图问题简介九宫图问题又称八数码问题,在3×3的九宫格棋盘上,每一个将牌都刻有1—8中的某一个数码。
棋盘中留有一个空格,允许其周围的某一个将牌向空格移动,这样通过移动将牌就可以不断改变将牌的布局。
给定一种初始的将牌布局(称初始状态)和一个目标布局(称目标状态),如何移动将牌,实现从初始状态到目标状态的转变。
问题的解答也就是给出一个合法的走步序列。
二、求解算法简介1.解的存在性分析九宫图问题的状态空间共有9!个状态,对于给定的初始状态和目标状态,有9!/2个状态要搜索,九宫图问题不一定能进行求解,因此对于给定的初始状态和目标状态需首先进行解存在性判断。
引入线性代数中逆序数的概念:在一个排列中,如果一对数的前后位置和大小顺序相反,即前面的数大于后面的数,那么它们就成为一个逆序,排列中逆序的总数就称为这个排列的逆序数。
只有当初始状态的排列逆序数与目标状态的排列逆序数奇偶性相同时,初始状态才能通过移动到达目标状态。
2.A*算法简介本文选用A*算法进行九宫图问题求解。
A*算法是一种静态路网中求解最短路径最有效的直接搜索方法。
A*算法结合了深度优先算法和广度优先,是一种启发式搜索算法。
评估函数为:f(n)=g(n)+h(n),f(n)表示从初始状态经由状态n 到目标状态的估计,g(n)是在状态空间中从初始状态到状态n 的实际代价,h(n)是从状态n 到目标状态的最佳路径的估计代价,本文算法中g(n)为从初始状态到当前状态的深度,h (n )为节点n 的每一数码与其目标位置之间的曼哈顿距离之和,可表示为:81()(||||)ni ti ni ti i h n x x y y ==-+-∑其中ni x 为n 状态下数字i 所在的行,ti x 为目标状态数字i 所在行,ni y 表示n 状态下数字i 所在列,ti y 表示目标状态数字i 所在列。
3.搜索动作空间简介空格移动空间为{上、下、左、右},但并非所有位置均能进行全空间搜索,判断空格所在位置,根据其所在位置对其搜索动作进行限制,其动作空间如表1所示。
洛谷P1379八数码难题(BFS)

洛⾕P1379⼋数码难题(BFS)题意:有⼀个3x3的的棋盘,有⼋个1~8的棋⼦,每次可以将⼀枚棋⼦移动到四周的空位,问最少移动多少次,使得最后的状态为123804765.题解:直接BFS,⽤map来Hash存步数,这⼉有个⽐较难想的点,就是把⼀维的坐标转化为⼆维的坐标(代码中有注释),然后我们找到0的位置,将四周可能的情况⼊队,不断下⼀层去找即可.代码:#include <iostream>#include <cstdio>#include <cstring>#include <cmath>#include <algorithm>#include <stack>#include <queue>#include <vector>#include <map>#include <set>#include <unordered_set>#include <unordered_map>#define ll long long#define fi first#define se second#define pb push_back#define me memsetconst int N = 1e6 + 10;const int mod = 1e9 + 7;const int INF = 0x3f3f3f3f;using namespace std;typedef pair<int,int> PII;typedef pair<ll,ll> PLL;const int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};string s;int bfs(string s){string end="123804765";queue<string> q;unordered_map<string,int> dis;q.push(s);dis[s]=0;while(!q.empty()){auto tmp=q.front();q.pop();int d=dis[tmp];if(tmp==end) return d;int pos=tmp.find('0');int x=pos/3; // dim 2int y=pos%3;int y=pos%3;for(int i=0;i<4;++i){int a=x+dx[i];int b=y+dy[i];if(a>=0 && a<3 && b>=0 && b<3){swap(tmp[pos],tmp[a*3+b]); //dim 1 if(!dis.count(tmp)){dis[tmp]=d+1;q.push(tmp);}swap(tmp[pos],tmp[a*3+b]);}}}return -1;}int main() {ios::sync_with_stdio(false);cin.tie(0);cin>>s;cout<<bfs(s)<<endl;return 0;}。
八数码难题代码与基本思路 Eight puzzles
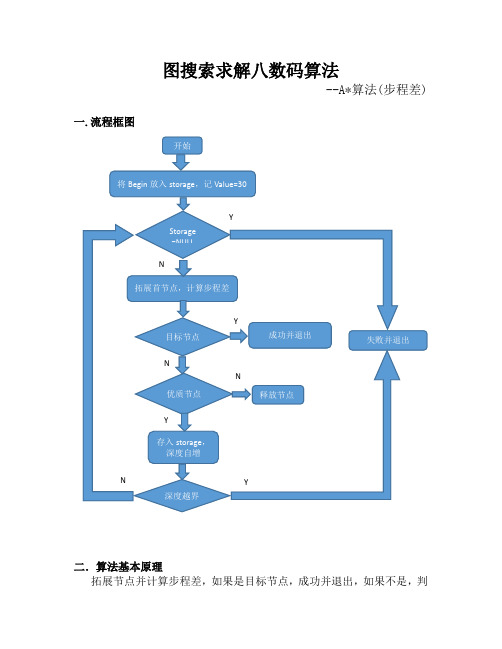
图搜索求解八数码算法--A*算法(步程差) 一.流程框图二.算法基本原理拓展节点并计算步程差,如果是目标节点,成功并退出,如果不是,判断是否为优质节点,是则拓展为子节点,否则舍弃;判断深度是否越界,是则失败,未越界则继续拓展节点,若拓展表为空,则失败退出。
八数码结构体由矩阵Array,步程差Value,屏蔽方向Undirect和父节点指针*parent四部分组成,Array存放矩阵数字状态,Value存放估值函数值,Undirect记录上一步移动方向避免逆推,*parent记录父子关系用于寻径。
三.模块分析Getgraph 键盘输入获得初始数码组并返回Graph结构体指针。
Printgraph 输入八数码结构体地址,打印矩阵数字状态与当前步程差。
Evaluate 输入目标矩阵与当前矩阵,计算步程差并返回值。
Move 输入当前矩阵与移动方向Direct,移动并返回新结构体地址。
Search 输入起始结构体与目标结构体,尝试寻径并记录路径并返回终点地址(若成功)或返回空指针(若失败)。
Main 主函数,定义目标矩阵并调用函数。
四.源代码// Eight-figure puzzle// A*#include"stdafx.h"#include<stdio.h>#include<stdlib.h>#define N 3 //数码组长度#define MAX 50 //最大搜索深度typedefstruct node//八数码结构体{int array[N][N];//数码组int Value;//评估值int Undirect;//所屏蔽方向,防止往回推到上已状态,1上2下3左4右struct node *parent;//父节点}Graph;Graph *Storage[MAX]; //拓展节点存储队列Graph *path[MAX]; //路径堆栈Graph *GetGraph(Graph *New_graph) ////////自定义初始数码组{int x;for (x = 0; x <N; x++){scanf("%d %d %d", &New_graph->array[x][0], &New_graph->array[x][1],&New_graph->array[x][2]);}New_graph->Value = 30;New_graph->Undirect = 0;New_graph->parent = NULL;return New_graph;}void PrintGraph(Graph *point_graph) /////////打印数码组{int i, j;if (point_graph == NULL)printf("NULL\n");else{printf(" ---------------\n");for (i = 0; i<N; i++){printf("| ");for (j = 0; j<N; j++){printf("%d ", point_graph->array[i][j]);}printf("|");if (i==N-1)printf(" Value %d ", point_graph->Value);//评估函数值printf("\n");}printf(" ---------------\n");}}int Evaluate(Graph *point_graph, Graph *End_graph) /////////评价函数{int value = 0;//评估值int i, j,m ,n ;for (i = 0; i<N; i++){for (j = 0; j<N; j++){for (m = 0; m <N; m++){for (n = 0; n <N; n++){if (point_graph->array[i][j] == End_graph->array[m][n])value = value + abs(i - m) + abs(j - n); //数字当前位置与目标位置步程差之和}}}}point_graph->Value = value;return value;}Graph *Move(Graph *point_graph, int Direct) /////////移动数码组{Graph *New_graph;int BlankLocate = 0;//定位空格指示int Movable = 1;//移动有效int i, j, x0, y0, x, y;for (i = 0; i<N; i++)//空格坐标i,j{for (j = 0; j<N; j++){if (point_graph->array[i][j] == 0){BlankLocate = 1;break;}}if (BlankLocate == 1)break;}x0 = i;y0 = j;switch (Direct){case 1://上x0--;if (x0<0)Movable = 0;break;case 2://下x0++;if (x0 >= N)Movable = 0;break;case 3://左y0--;if (y0<0)Movable = 0;break;case 4://右y0++;if (y0 >= N)Movable = 0;break;}if (Movable == 0)//不能移动则返回原节点return point_graph;New_graph = (Graph *)malloc(sizeof(Graph));//生成节点for (x = 0; x<N; x++){for (y = 0; y<N; y++){New_graph->array[x][y] = point_graph->array[x][y];//复制数码组}}New_graph->array[i][j] = New_graph->array[x0][y0];New_graph->array[x0][y0] = 0;return New_graph;}Graph *Search(Graph *Begin, Graph *End) /////////搜索函数{Graph *St1, *St2, *ta;int Step = 0;//深度int Direct = 0;//方向int i;int front, rear;front = rear = -1;//队列初始化ta = NULL;rear++;//入队Storage[rear] = Begin;while (rear != front)//队列不空{front++;//出队St1 = Storage[front];for (i = 1; i <= 4; i++)//分别从四个方向推导出新子节点{Direct = i;if (Direct == St1->Undirect)//跳过屏蔽方向continue;St2 = Move(St1, Direct);//移动数码组if (St2 != St1)//数码组是否可以移动{Evaluate(St2, End);//评价新的节点sif (St2->Value == 0)//为0则搜索完成{St2->parent = St1;rear++;Storage[rear] = St2;//存储节点到待处理队列ta = St2;break;}if (St2->Value <= St1->Value + 1){St2->parent = St1;//st2->Undirect=Direct>2?(Direct==3)+3:(Direct==1)+1;/屏蔽方向switch (Direct)//设置屏蔽方向,防止往回推{case 1://上St2->Undirect = 2;break;case 2://下St2->Undirect = 1;break;case 3://左St2->Undirect = 4;break;case 4://右St2->Undirect = 3;break;}rear++;Storage[rear] = St2;//存储节点到待处理队列}else{free(St2);//抛弃劣质节点St2 = NULL;}}}if (ta != NULL)//为0则搜索完成break;Step++;//统计深度if (Step>=MAX){break;}}return ta;}int main(int argc, constchar * argv[]){// 8 1 3 7 4 5 6 2 0// 4 1 3 2 7 5 8 0 6// 4 5 1 2 7 3 0 8 6 //16 steps in fact but failed//目标数码组Graph End_graph = {{{ 1, 2, 3 },{ 8, 0, 4 },{ 7, 6, 5 }}, 0, 0, NULL};//初始数码组Graph New_graph;Graph *Begin_graph;printf("Enter initial matrix line by line\n For example:\t1 3 4 ENTER\n\t\t8 2 5 ENTER\n\t\t7 6 0 ENTER\n\n");Begin_graph = GetGraph(&New_graph);Evaluate(Begin_graph, &End_graph);printf("Initial matrix:\n");PrintGraph(Begin_graph);printf("Target matrix:\n");PrintGraph(&End_graph);Graph *W, *P;int top = -1;//图搜索W = Search(Begin_graph, &End_graph);if (W){P = W; //压栈while (P != NULL){top++;path[top] = P;P = P->parent;}printf("<<<<<< The Path >>>>>>\n");//弹栈打印while (top>-1){P = path[top];top--;PrintGraph(P);}printf("<<<<< Mission Complete >>>>>\n");system("pause");}else{printf("Path not found ,Search depth is %d\n", MAX);system("pause");}return 0;}五.运行结果将初始数码组改写为 2 5 4 3 7 1 8 6 ,定义某个数前面比他小的数个数为Xi,所有数字的Xi相加为Y,因为四向移动只可能改变Y的大小,不改变其奇偶性。
matlab考试题B卷及答案

matlab考试题B卷及答案1. MATLAB基础操作题:请在MATLAB中创建一个名为`myVector`的向量,包含元素1, 2, 3, 4, 5,并计算其元素之和。
答案:首先,创建向量`myVector`可以使用以下代码:```matlabmyVector = [1 2 3 4 5];```然后,计算元素之和可以使用`sum`函数:```matlabsumOfElements = sum(myVector);```最终,`sumOfElements`的值将为15。
2. MATLAB矩阵运算题:给定一个3x3的矩阵A,其元素为A=[1 2 3;4 5 6; 7 8 9],请计算矩阵A的转置。
答案:计算矩阵A的转置可以使用`transpose`函数或者简单的`.'`操作符。
以下是使用`transpose`函数的代码:```matlabA = [1 2 3; 4 5 6; 7 8 9];A_transpose = transpose(A);```或者使用`.'`操作符:```matlabA_transpose = A.';```得到的转置矩阵`A_transpose`将是:```1 4 72 5 83 6 9```3. MATLAB编程题:编写一个MATLAB函数,该函数接受一个整数n作为输入,并返回一个n阶的魔方矩阵。
答案:魔方矩阵是一个方阵,其中每一行、每一列以及两条对角线上的元素之和都相等。
以下是一个生成n阶魔方矩阵的MATLAB函数:```matlabfunction magicMatrix = createMagicSquare(n)if mod(n, 2) == 0error('n must be an odd number.');endmagicMatrix = zeros(n);num = 1;for i = 1:nfor j = 1:nif i == 1j = j;elsej = (j + 2 * (i - 1) - n) % n + 1;endmagicMatrix(i, j) = num;num = num + 1;endendend```调用此函数并传入一个奇数n,例如`createMagicSquare(3)`,将返回一个3阶魔方矩阵。
人工智能导论实验一 基于图搜索技术的八数码问题求解

广州大学学生实验报告开课学院及实验室:计算机科学与工程实验室 2020年10月14日(***报告只能为文字和图片,老师评语将添加到此处,学生请勿作答***)一、实验内容1. 分别用广度优先搜索策略、深度优先搜索策略和启发式搜索算法(至少两种)求解八数码问题;分析估价函数对启发式搜索算法的影响;探究讨论各个搜索算法的特点。
二、实验设备1. 实验设备:计算机;2. 平台:Windows操作系统,Visual C++ 6.0 / Python Anaconda三、实验步骤1. 随机生成一个八数码问题分布,设计一个可解的目标状态(要求棋盘9个位置都不同)2. 分别用广度优先搜索策略、深度优先搜索策略和至少两种启发式搜索算法求解八数码问题3. 分析估价函数对启发式搜索算法的影响4. 探究讨论各个搜索算法的特点四、分析说明(包括核心代码及解释)广度优先搜索:首先创建一个结构体node,来记录节点移动方向和扩展的节点。
struct node{int ab[3][3];//节点int direction;//方向};struct node sh[102], end;int count = 1;然后创建一个init函数来初始化棋盘起始状态和目标状态,使用for语句填写棋盘数字用loction函数确定0节点的位置,通过for语句和if语句判断sh[num].ab[i / 3][i % 3] == 0,即可得到0节点的位置Sign函数用来获取棋盘状态,将当前棋盘数字顺序生成一个数,即可得知棋盘状态。
Mobile函数用来移动0节点,先用loction函数获取0节点的位置,再通过if语句来判断0节点位置和所能移动方向,然后进行移动。
Display函数使用for语句来打印当前棋盘。
Search函数使用display函数来打印从初始状态移动到目标状态的中间状态棋盘,在while(1)语句下利用mobile函数移动0节点,直到目标状态找到或者超过寻找次数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验目的1、熟悉和掌握启发式搜索的定义、估价函数和算法过程。
2、利用A*算法求解N数码难题,理解求解流程和搜索顺序。
二、实验内容以八数码为例实现A或A*算法。
1、分析算法中的OPEN表CLOSE表的生成过程。
1)建立一个队列,计算初始结点的估价函数f,并将初始结点入队,设置队列头和尾指针。
2)取出队列头(队列头指针所指)的结点,如果该结点是目标结点,则输出路径,程序结束。
否则对结点进行扩展。
3)检查扩展出的新结点是否与队列中的结点重复,若与不能再扩展的结点重复(位于队列头指针之前),则将它抛弃;若新结点与待扩展的结点重复(位于队列头指针之后),则比较两个结点的估价函数中g的大小,保留较小g值的结点。
跳至第五步。
4)如果扩展出的新结点与队列中的结点不重复,则按照它的估价函数f大小将它插入队列中的头结点后待扩展结点的适当位置,使它们按从小到大的顺序排列,最后更新队列尾指针。
5)如果队列头的结点还可以扩展,直接返回第二步。
否则将队列头指针指向下一结点,再返回第二步。
2、分析估价函数对搜索算法的影响。
3、分析启发式搜索算法的特点。
广度优先搜索和双向广度优先搜索都属于盲目搜索,这在状态空间不大的情况下是很合适的算法,可是当状态空间十分庞大时,它们的效率实在太低,往往都是在搜索了大量无关的状态结点后才碰到解答,甚至更本不能碰到解答。
搜索是一种试探性的查寻过程,为了减少搜索的盲目性引,增加试探的准确性,就要采用启发式搜索了。
所谓启发式搜索就是在搜索中要对每一个搜索的位置进行评估,从中选择最好、可能容易到达目标的位置,再从这个位置向前进行搜索,这样就可以在搜索中省略大量无关的结点,提高了效率。
启发式函数选取为:f*(n)=g*(n)+ h*(n)其中:g*(n)是搜索树中节点n的深度h*(n)用来计算对应于节点n的数据中错放的棋子个数。
三、实验结果四、程序function [a1,b1]=shang(a)[x,y]=find(a==0);a1=a;a1(x,y)=a(x-1,y);a1(x-1,y)=0;b1=zhao(a1);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function [a1,b1]=xia(a)[x,y]=find(a==0);a1=a;a1(x,y)=a(x+1,y);a1(x+1,y)=0;b1=zhao(a1);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function [a1,b1]=zuo(a)[x,y]=find(a==0);a1=a;a1(x,y)=a(x,y-1);a1(x,y-1)=0;b1=zhao(a1); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [a1,b1]=you(a)[x,y]=find(a==0);a1=a;a1(x,y)=a(x,y+1);a1(x,y+1)=0;b1=zhao(a1); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function z=panduan(a)global E;global I;I=2;[x,y]=size(E);z=1;for i=1:yb=E{i};v=(b-a).^2;if sum(sum(v))==0z=0;break;endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function y=zhao(a)wan=[1 2 3;8 0 4;7 6 5];y=0;b=a-wan;for i=1:3for j=1:3if b(i,j)~=0y=y+1;endendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% global Eglobal Ia=[2 8 3;1 0 4;7 6 5];b=[1 2 3;8 0 4;7 6 5];I=1;E(1)={a};for i=2:20q=b-E{i};if sum(sum(q.^2))E(i)={kaka(E{i-1})};celldisp(E(i))elsebreak;endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [a1]=kaka(a)global I;global E;c=[2 8 3;1 0 4;7 6 5];E(1)={c};[x,y]=find(a==0);z=9;if x==1if y==1[x1,y1]=xia(a);if y1<zif panduan(x1)b=x1;z=y1;endend[x2,y2]=you(a);if y2<zif panduan(x2)b=x2;z=y2;endenda1=b;endif y==2[x1,y1]=xia(a);if y1<zif panduan(x1)b=x1;z=y1;endend[x2,y2]=zuo(a);if y2<zif panduan(x2)b=x2;z=y2;endend[x3,y3]=you(a);if y3<zif panduan(x3)b=x3;z=y3;endenda1=b;endif y==3[x1,y1]=xia(a);if y1<zif panduan(x1)b=x1;z=y1;endend[x2,y2]=zuo(a);if y2<zif panduan(x2)b=x2;z=y2;endenda1=b;endendif x==2if y==1[x1,y1]=shang(a); if y1<zif panduan(x1)b=x1;z=y1;endend[x2,y2]=xia(a);if y2<zif panduan(x2)b=x2;z=y2;endend[x3,y3]=you(a);if y3<zif panduan(x3)b=x3;z=y3;endenda1=b;endif y==2[x1,y1]=shang(a); if y1<zif panduan(x1);b=x1;z=y1;endend[x2,y2]=xia(a);if y2<zif panduan(x2);b=x2;z=y2;endend[x3,y3]=zuo(a);if y3<zif panduan(x3);b=x3;z=y3;endend[x4,y4]=you(a);if y4<z;if panduan(x4)b=x4;z=y4;endenda1=b;endif y==3[x1,y1]=shang(a); if y1<zif panduan(x1)b=x1;z=y1;endend[x2,y2]=xia(a);if y2<zif panduan(x2)b=x2;z=y2;endend[x3,y3]=zuo(a);if y3<zif panduan(x3)b=x3;z=y3;endenda1=b;endendif x==3if y==1[x1,y1]=shang(a); if y1<zif panduan(x1)b=x1;z=y1;endend[x4,y4]=you(a);if y4<z;if panduan(x4)b=x4;z=y4;endenda1=b;endif y==2[x1,y1]=shang(a);if y1<zif panduan(x1)b=x1;z=y1;endend[x3,y3]=zuo(a);if y3<zif panduan(x3)b=x3;z=y3;endend[x4,y4]=you(a);if y4<z;if panduan(x4)b=x4;z=y4;endenda1=b;endif y==3[x1,y1]=shang(a);if y1<zif panduan(x1)b=x1;z=y1;endend[x3,y3]=zuo(a);if y3<zif panduan(x3)b=x3;z=y3;endenda1=b;endendE(I)={a1};五、实验结论1、启发式搜索算法A*流程图和算法框图。
算法框图:算法方法:利用MATLAB软件,因为MATLAB是基于矩阵运算的,八数码可以看做是一个3*3的矩阵,将八数码中的空位可看成矩阵的为0代替,已进行矩阵之间的运算,首先建立了4个函数,这4个函数应有在矩阵的上,下,左,右的变换,然后经过变换,输出两个值,一个为变换后的矩阵,一个为变化后的放错位置的数值,然后利用kaka函数,分别分9中情况来条用这4个函数,来输出下一层的矩阵并判断最小放错位置的数值,然后将其矩阵放入全局变量E中的元胞数组中,记录下其实的矩阵,然后再每次生成下一层矩阵时,利用panduan函数来判断生成的矩阵是否和E元胞数组中的矩阵相同,防止出现矩阵变化中的内部死循环。
然后利用celldisp函数输出E元胞数组中的矩阵,即为起始棋局到目标棋局的路径。
2、分析估价函数的值对搜索算法速度的影响。
考虑到八数码问题的特点,在本实验中使用A*算法求解。
A*搜索是一种效的搜索算法,它把到达节点的耗散g(n)和从该节点到目标节点的消耗h(n)结合起来对节点进行评价:f(n)=g(n)+h(n)。
当h(n)是可采纳时,使用Tree-Search的A*算法将是最优的。
3、根据A*算法分析启发式搜索的特点。
启发式搜索是一种试探性的查寻过程,为了减少搜索的盲目性引,增加试探的准确性,就要采用启发式搜索了。
所谓启发式搜索就是在搜索中要对每一个搜索的位置进行评估,从中选择最好、可能容易到达目标的位置,再从这个位置向前进行搜索,这样就可以在搜索中省略大量无关的结点,提高了效率。
11 / 11。
