利用线段图解应用题
用图解法解应用题

用图解法解应用题(一)例1乐乐比丫丫大5岁,洋洋比乐乐小2岁,那么丫丫和洋洋相差多少岁?【分析】根据题意,我们可以画一个线段图:很明显,丫丫和洋洋相差5-2=3岁。
例2朝阳学校三年级四班开展集邮活动,阿呆有92张邮票,笨笨有54张邮票。
问阿呆给笨笨多少张邮票,才能使两人的邮票数相等?【分析】从下面的线段图可以清楚地看到:阿呆给笨笨的邮票数,是阿呆与笨笨邮票的相差数的一半,因此要求本题的解,只要将他们邮票的相差数平均分成两份,每一份就是阿呆给笨笨的邮票数。
(92-54)÷2=19(张)即阿呆要给笨笨19张邮票,才能使两人的邮票数相等。
通过例2的分析,可以看出画线段图既能充分一线出题中的已知条件,又能形象地把数量关系展示出来,帮助我们很快地找到解题的捷径。
例3把两块一样长的木板像右图这样钉在一起,成了一块木板。
如果这块钉在一起的木板长120厘米,中间重叠部分是16厘米。
这两块木板各长多少厘米?【分析】把长度相等的两木板的一端钉起来,钉在一起的长度部分就是重叠部分,重叠的部分是16厘米,所以这两块木板的总长度是120+16=136(厘米),每块木板的长度就是136厘米的一半。
【解】(120+16)÷2=68(厘米)答:这两块木板各长68厘米。
【诀窍】类似这样的问题,是要把重复的部分再加一次,求出原来没有重复大的总长度。
当你觉得这样的问题不知如何思考的时候,可以先画出图,借助图形进行思考是一种很好的办法。
例4兄弟俩的年龄和是35岁,哥哥比弟弟大5岁,问哥哥和弟弟各多少岁?【分析】还是用线段图来帮助我们分析:从图中观察出,如果从35岁中去掉5岁,就可以得到两个弟弟的年龄,而列式得:(35-5)÷2=15(岁)(弟弟的岁数)15+5=20(岁)(哥哥的岁数)验算:15+20=35(岁)20-15=5(岁)所以哥哥的年龄是20岁,弟弟的年龄是15岁。
还可以这样分析,如果35岁加上5岁,就可以得到两个哥哥的年龄,则:(35+5)÷2=20(岁)(哥哥的岁数)20-5=15(岁)(弟弟的岁数)例5陈红喜爱集邮,她的中国邮票枚数是外国邮票的3倍,中国邮票比外国邮票多86枚。
二年级思维训练—线段图解

线段图解
图解法 让数学变得更有趣
更生动的方法!
美国著名数学家斯蒂恩说:“如果一个特定的 问题可以转化为一个图像,那么就整体地把握 了问题,并且能创造性地思索问题的解法。”
因此,将问题转化为图形,把问题中的 条件和结论直观地、整体地表露出来, 是一种十分重要的解题方法。
[ 例1 ]看图列算式
看图判断:求总数 用加法:4+4+4=12(米)
4米
[ 例4 ]根据线段图编应用题并解答。
39朵花
牡丹花 有19朵
兰花有 20 朵
注意用上关键词:“共有”“其中”等
编题: _______________ _______________ _______________ _______________ _______________
多少名学生?
倒推法
9+9=18(名) 18+18=36(名)
答:这个班原来有36名学生。
3Hale Waihona Puke 224+=
56
基本数量关系是: 部分数+部分数=总数 总数-部分数=部分数
-+ = -= -=
[ 例2 ] 看线段图猜数
(1)明明有 31 张邮票。
看图判断:求较小数 用减法:35-4=31(张)
35张邮票
丁丁
4
------
明明
---------
[ 例3 ] 一根绳子如下面右图所示分成相等的 三段,这根绳子有 12 米。
39-19=20(朵) 答:兰花有20朵。
一桶油连桶共重9千克,用去一半后,连桶共重5千
克,那么原来油重多少千克? 9千克
9-5=4(千克) 4+4=8(千克) 答:油重8千克。
利用画线段图,巧解小学数学难题,运算能力提高一倍,值得收藏

利用画线段图,巧解小学数学难题,运算能力提高一倍,值得收藏在小学数学中,有不少的难题,学生抓耳挠腮,百思不得其解。
这是因为小学生理解能力较差,不会审题,对于题目给出的条件,没有全面、综合去考虑。
结果,得不出正确的解法。
有没有一种巧妙的方法,能让小学生直观地去解题呢?有!那就是利用画线段图来解。
因为线段图非常简洁非常直观明了,通过观察,小学生能够容易地判断出解法,并能通过这种方式,提高自己的分析能力。
举例子来说明吧:两个小同学折纸鹤,小红折的数量比小丽的3倍还多5个,她俩一共折了53个,问题,两个人分别折了多少个?这道题,初看之下,条件有三个,小学生很容易被3倍还多5个这句话给绕住,那么,就可以动手画个线段图,来帮助理解。
看这个线段图,一目了然,学生会马上明白,这道题应该用53-5,得出的结果再平均分成四份,其中的一份就是小丽折的个数,那么小红的也能很容易计算出来了。
再比如这道题:小明买3支笔用了27元,那么,买同样的8支笔,需要多少元?我们继续用线段图来解,如下图:学生一看,就明白了,27元买了三个,先算出一个的价格,再去算8个的价格。
再来看一道复杂一些的分数应用题:某工程队修一条路,前5月修了20千米,正好修了全长的四分之一,照这样计算,剩下的路,需要修多长时间?怎么解呢?依旧用画线段图的方法。
来看看线段图,算法是不是呼之欲出呢!总结一下,如何使用画线段图这种数学方法?使用画线段图需要注意些什么呢?画线段图是一种有效的解决数学问题的方法,可以把复杂的数量关系变的简单易懂,尤其是对于理解能力较弱的同学,使用这一方法更有效。
在使用当中,首先要搞清所有的条件和数量关系,其次,在画图时,还应注意以下几点:第一个,线段的长短得适中,不用太长,只要能等量地表示出数量关系即可。
最好用尺子按照刻度去画,不要画的太随意了。
第二个,画出图以后,得标明数量和条件,像上面的三幅图中,都逐一标明了每一个数量关系,甚至问题也用问号来表示。
用画线段图解决实际问题

(2)补充一个条件,使它成为一
道两步计算的问题。
小华
小力
我第二次比第 一次多跳8下
我第二次比第 一次少跳13下
小华
小力
我第二次比第 一次多跳8下
我第二次比第 一次少跳13下今天这节课你有什么收获?上衣的价钱是裤子的3倍
你能画出表示上衣价钱 的线段吗?
?元
上衣的价钱是裤子的3倍
返回
养兔场有黑兔24只,白兔的只数是 黑兔的3倍。
(1)黑兔和白兔一共有多少只?
(2)白兔比黑兔多多少只?
湖中黑天鹅有12只,
,
白天鹅和黑天鹅共有多少只?
(1)补充一个条件,使它成为一
道一步计算的问题;
本编为大家提供各种类型的PPT课件,如数学课件、语文课件、 英语课件、地理课件、历史课件、政治课件、化学课件、物理课 件等等,想了解不同课件格式和写法,敬请下载! Moreover, our store provides various types of classic sample essays, such as contract agreements, documentary evidence, planning plans, summary reports, party and youth organization materials, reading notes, post reading reflections, essay encyclopedias, lesson plan materials, other sample essays, etc. If you want to learn about different formats and writing methods of sample essays, please stay tuned!
四年级线段图练习题

四年级线段图练习题线段图是图示统计数据的一种方式,通过线段的长短来表示不同数量或比例的数据。
在四年级数学中,线段图常用来解决一些实际问题,帮助我们更好地理解数据的分布。
接下来,我们将通过一些练习题来巩固和提升我们对线段图的理解和应用。
练习题1:下图是小明一周每天上学所花时间的线段图,请根据图中信息回答以下问题:1. 小明一周上学所花的总时间是多少?2. 周三上学的时间和周五上学的时间之间相差多少分钟?3. 哪天上学时间最长,上学时间是多少分钟?4. 周二上学的时间和周四上学的时间加起来是多少分钟?练习题2:下图是小华一周每天学习不同科目所花时间的线段图,请根据图中信息回答以下问题:1. 小华一周学习的总时间是多少分钟?2. 哪一天学习英语的时间最短,学习时间是多少分钟?3. 周三学习的总时间和周五学习的总时间之间相差多少分钟?4. 数学和科学两门学科的总学习时间是多少分钟?练习题3:下图是小杰一周每天跑步的距离线段图,请根据图中信息回答以下问题:1. 小杰一周跑步的总距离是多少米?2. 周三和周五跑步的距离之差是多少米?3. 哪一天跑步距离最多,跑了多少米?4. 周二和周四跑步的距离加起来是多少米?练习题4:小明、小华和小杰一周每天阅读的时间线段图如下图所示,请根据图中信息回答以下问题:1. 三人一周阅读的总时间是多少分钟?2. 哪个孩子一周阅读的总时间最长,阅读的时间是多少分钟?3. 哪一天三人阅读的总时间最短,总时间是多少分钟?4. 哪一天小明和小杰阅读的总时间比小华多,差多少分钟?通过以上练习题,我们可以加深对线段图表示数据的理解和分析能力。
希望通过不断的练习和探索,大家能够更加熟练地运用线段图解决实际问题,并且在数学学习中取得更好的成绩!。
《数形结合》之“用画线段图解题”的图解及练习
学会画线段图解题--练习
“数形结合”这一解题方式是数学学习最有效的解题方式 无论是小学、初中、高中、乃至大学,都是最简单实用的方法 画线段图,无疑是“数形结合”中的典范,也是最常用的方式
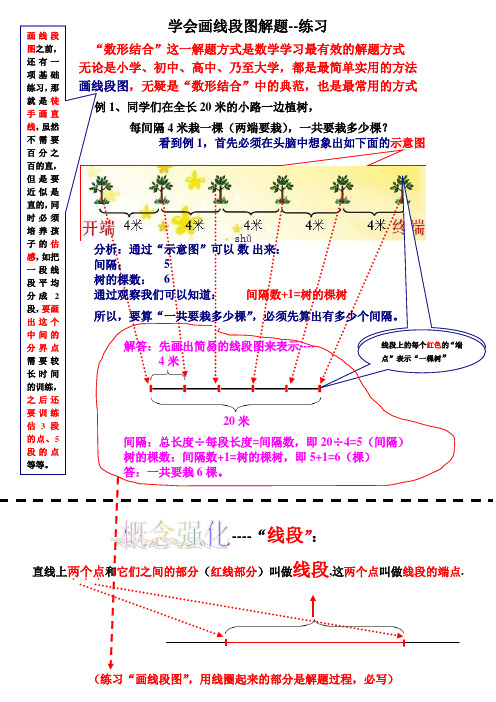
例 1、同学们在全长 20 米的小路一边植树, 每间隔 4 米栽一棵(两端要栽) ,一共要栽多少棵? 看到例 1,首先必须在头脑中想象出如下面的示意图
画线段 图之前, 还有一 项基础 练习, 那 就是徒 手画直 线, 虽然 不需要 百分之 百的直, 但是要 近似是 直的, 同 时必须 培养孩 子的估 感, 如把 一段线 段平均 分成 2 段, 要画 出这个 中间的 分界点 需要较 长时间 的训练, 之后还 要训练 估 3 段 的点、5 段的点 等等。
----“线段” :
直线上两个点和它们之间的部分(红线部分)叫做线段,这两个点叫做线段的端点. ...
Байду номын сангаас
(练习“画线段图” ,用线圈起来的部分是解题过程,必写)
二、动手试一试 1、同学们在全长 40 米的小路一边植树, 每间隔 8 米栽一棵(两端要栽) ,一共要栽多少棵? 解答:先画出简易的线段图来表示----
2、同学们在全长 42 米的小路一边植树, 每间隔 6 米栽一棵(两端要栽) ,一共要栽多少棵? 解答:先画出简易的线段图来表示----
3、同学们在全长 32 米的小路一边植树, 每间隔 4 米栽一棵(两端要栽) ,一共要栽多少棵? 解答:先画出简易的线段图来表示----
shǔ 分析:通过“示意图”可以 数 出来: 间隔: 5 树的棵数: 6 通过观察我们可以知道: 间隔数+1=树的棵树 所以,要算“一共要栽多少棵” ,必须先算出有多少个间隔。 解答:先画出简易的线段图来表示---4米
画线段图解应用题_四年级数学_数学_小学教育_教育专区

画线段图解应用题1、果园里有256棵苹果树,梨树比苹果树多39棵,梨树有多少棵?2、果园里有256棵苹果树,梨树比苹果树少39棵,梨树有多少棵?3、果园里有256棵苹果树,比梨树少39棵,梨树有多少棵?4、果园里有256棵苹果树,比梨树多39棵,梨树有多少棵?5、修一条公路,第一天修了395米,比第二天多修29米,第二天修了多少米?6、修一条公路,第一天修了395米,比第二天少修29米,第二天修了多少米?7、修一条公路,第一天修了395米,第二天比第一天多修29米,第二天修了多少米?8、修一条公路,第一天修了395米,第二天比第一天少修29米,第二天修了多少米?9、学校有一堆煤,第一天烧了75吨,比第二天少用5 4 吨,两天一共用了多少吨?10、学校有一堆煤,第一天烧了75吨,比第二天多用5 1 吨,两天一共用了多少吨?11、水果店运进苹果和香蕉共56.9千克,已知香蕉比苹果多23.1千克,苹果和香蕉各多少千克?12、水果店运进苹果和香蕉共56.9千克,已知香蕉比苹果少23.1千克,求苹果和香蕉各多少千克?13、水果店运进苹果29.8千克,运进的香蕉是苹果的3倍,运进香蕉多少千克?14、水果店运进苹果29.8千克,是运进香蕉的4倍,运进香蕉多少千克?15、水果店运进苹果29.8千克,运进的香蕉是苹果的4倍,运进香蕉多少千克?多少千克?17、水果店运进苹果29.8千克,运进的香蕉比苹果的5倍少12.7千克,运进香蕉多少千克?18、水果店运进苹果29.8千克,比运进的香蕉的3倍多0.4千克,运进香蕉多少千克?少千克?20、水果店运进苹果和香蕉共56.4千克,已知苹果是香蕉的2倍,求苹果和香蕉各多少千克?21、水果店运进苹果和香蕉共92.56千克,已知苹果是香蕉的4 1 ,求苹果和香蕉各多少千克?22、水果店运进苹果和香蕉共74.6千克,已知苹果比香蕉的3倍还多5.6千克,求苹果和香蕉各多少千克?23、水果店运进苹果和香蕉共98.5千克,已知苹果比香蕉的4倍少2.6千克,求苹果和香蕉各多少千克?。
画线段图解决问题.pptx

大米:
思考: 1、谁是标 准量?
2、先画什 么?怎么画?
3、再画什 么?怎么画? 为什么?
4、大米的质量比面粉少
1 4
面粉:
1 少4
大米:
思考: 1、谁是标准量?
2、先画什么? 怎么画?
3、再画什么? 怎么画?为什么?
画线段图分析问题
1、大米有100千克,比面粉少 25%,面粉有多 少千克?
面粉: 大米:
x千克
少25%
100千克
画线段图分析问题
2、饲养场有白兔200只,比黑兔只数的3倍 少40只,饲养场养黑兔多少只?
x只
黑兔:
3x
白兔:
200只 40只
1、根据数学信息和问题确定是画单条线段, 还是双条线段并列图分析比较合适。
2、正确的画出线段图表示数学信息和问题 的关系。
3、用字母代替解决问题中的未知量,从不 同的角度观察,发现相等的数量关系,列出 方程并解方程。
同学们本节课你学会了什么?
2
一套衣服共550元,其中裤子的价钱是上衣价钱
的 。裤子和上一各多少元钱?
3
一、说一说
பைடு நூலகம்
1、大米的质量是面粉的4倍 面粉: 大米:
思考: 1、谁是标准量?
2、先画什么?怎 么画?
3、再画什么?怎 么画?为什么?
1 2、大米的质量是面粉的 4
面粉:
大米: 1 4
思考: 1、谁是标准 量?
2、先画什么? 怎么画?
3、再画什么? 怎么画?为 什么?
3、大米的质量比面粉多
1 4
面粉: 1
学会用线段图解答应用题

我们 先选 择 一条 线段 来表 示 小明 3 前 的岁 数 ,再 在 年
下面画出 5倍多一点的线段来表示 “ 爸爸的年龄比小明的
年 龄 的 5 还大 3 ” 倍 岁 。借助 直观 图 , 生不 难看 出 : 学 从 父子 年龄 之差 的 2 7岁中 去掉 3 , 与父 子年 龄 差 岁 就
。一 口=2 …… 0
o去 掉 2 个 和 口同样 多 0
4角 5角 +一 船笔 —— 一 一盒蜡笔的栈 ——+
②把算式转化为推理
因为 △比 口 多 1 ,而 。 比口 多 2 ,所 以原 来 的 O 比 2 0 △多 , :0—1 多 2 2=8( ) 个 。
先画 出两 条线 段 , 的表 示 5角 , 的 表示 4角 ; 着 , 长 短 接
例 3 △比 口多 l , : 2 o去掉 2 0个和 口同样 多 , △和 原 来
随后借助等式, 引导学生分析 : 因为同样的铅笔价格相
同, பைடு நூலகம்比之下 , 如果付出的钱越多 , 那么 , 男买的东西就越
贵 , 以 , 盒 蜡 笔 的 钱 比 一 个 卷 笔 刀 贵 , l (— 所 一 贵 角 5 4=
1嘲曙嘲
. / /
教学经纬 ・ 姜术
痕祈个幢化款嗲在小学美术教学申 庄用
浙江新昌县新 民小学( 15 0 石剑青 320 )
“ 术 课 程 具 有 人 文性 质 ,是 学 美 校 进 行 美 育 的主 要 途 径 , 实施 素 质 在 教 育 的 过 程 中 具 有 不 可 替 代 的 作 物。 是表 达和 抒 发情 感 的方 式 。 “ 美术 课 程 具 有 人 文 性 质 ,是 学 校进 行 美 育 的主 要 途 径 , 在实 施 素 质 教 育 的 过 程 中 具 有 不 可 替 代 的 作 用 。” 正如 新课 标 中所提 到 的 , 小学 美 为主 , 我 国小学 美 术教学 的开 端 。 是 17 年 6 , 99 月 教育 部 颁发 了第 二
【三年级】线段图巧解应用题

【三年级】线段图巧解应用题
线段图是一种常用的统计图表,它用线段的长度或高度来表示数量的大小。
在解决实际问题时,线段图能帮助我们更直观地理解数据之间的关系,并找出其中的规律。
小明家有3只宠物猫,小红家有5只宠物猫,小明和小红家的猫的数量可以用线段图表示如下:
小明家的猫:XXX
(表示小明家有3只猫)
通过线段图我们可以一目了然地发现,小红家的猫比小明家的猫多了两只。
下面,我将通过一些线段图的应用题,来帮助大家更好地理解线段图的使用。
1. 小明和小红家各自在一天内售出的冰淇淋数量用线段图表示如下:
小明家的冰淇淋:XXXXX
小红家的冰淇淋:XXXXXXX
由于小红家售出的冰淇淋多,所以小红家比小明家售出的冰淇淋数量更多。
2. 在一个班级里,小明的语文成绩是80分,小红的语文成绩是90分,小亮的语文成绩是70分。
将这些成绩用线段图表示如下:
小明的语文成绩:XXXXXXXXXXXX
小红的语文成绩:XXXXXXXXXXXXXXXXX
小亮的语文成绩:XXXXXXXXXX
由图可知,小红的语文成绩最高,小亮的语文成绩最低,小明的语文成绩居中。
3. 小明和小红两个人一起搬砖,小明搬了2堆砖,小红搬了3堆砖。
他们每堆都有10块砖。
将他们搬的砖用线段图表示如下:
小明搬的砖:XX
小红搬的砖:XXX
由图可知,小红搬的砖比小明搬的砖多。
通过以上的例子,我们可以发现线段图的应用在于比较数量的大小,找出最大值和最小值,以及比较两个或多个数据的差异。
通过线段图,我们可以通过直观的方式来比较和分析数据,更好地理解问题背后的关系。
六年级数学用线段图解复杂应用题

3 8
3 8
借出
购进360本
这时存书
7、有一批货物,上午运走30%,下午运走的比余下 多5吨, 最后还剩下15 吨没有运完,这些货物共有多少吨?
2 7
上午运30%
余下的
2 7
下午运的
5吨
还剩下15吨
8、一堆煤,第一次用去了 ,第二次用去余下的 ,这时 还剩300千克,这堆煤原有多少千克?
1 5
1 4
(5+15)÷(1- )=28(吨) 28 ÷(1-30%)=40(吨)
2 7
8、一堆煤,第一次用去了 ,第二次用去余下的 ,这时 还剩300千克,这堆煤原有多少千克?
1 5
1 4
第一次
1 5
余下的
1 4
还剩下300千克
300÷(1- )÷(1- )=500(千克) 答:这堆煤原有500千克。
1 5
1 5
第二天看的
7页
还剩56页
(56+7)÷ (1- - )=105(页)
1 5
1 5
3、食堂有若干袋面粉,用去 后,又运进了25 袋,这时的面粉正好是原来袋数的一半,食堂 原有面粉多少袋?
3 5
4、有一堆煤运走54吨以后,余下的重量比原有重量的 少6吨,这堆煤原有多少吨?
2 3
2 3
2 3
2 3
2 3
2 3
30×
2 3
30 ×(1+ )
2 3
2 3
2 3
2 3
2 3
30 ×(1- )
30÷
30 ÷(1+ )
30 ÷(1- )
看图列式:
“1”
?米
小学数学5种画图法解应用题,孩子轻松理解题意

小学数学5种画图法解应用题,孩子轻松理解题意如果一个学生学会了画应用题,可以有把握地说,他一定学会了解应用题。
“画图法“可以说是帮助学生理解题意,解决应用题最有效的工具!下面一一举例:一、线段图法例:两个小同学折纸鹤,小红折的数量比小丽的3倍还多5个,她俩一共折了53个,问两个人分别折了多少个?根据题意作图:解析:看这个线段图,很容易发现53-5,得出的结果再平均分成4份,其中的1份就是小丽折的纸鹤个数。
列式计算:小丽折的个数:(53-5)÷4=12(个),小红折的个数:12 ×3+5=41(个)。
二、平面图法例:有两个自然数A和B,如果把A增加12,B不变,积就增加72;如果A不变,B增加12,积就增加120,求原来两数的积。
解析:这道题可以画长方形图来具象化,长表示A,宽表示B,那么两数的积就是长方形的面积。
A、B原来两数用长方形图a表示,当A增加12即长增加12,宽不变,即B不变,如图b;当B增加12即宽增加12,长不变,也就是A不变,如图c。
所以:长方形的宽也就是B=72÷12=6,长方形的长也就是A=120÷12=10,那么,A、B的积为6×10=60。
三、立体图法例:把一个正方体切成两个长方体,表面积就增加了8平方米。
原来正方体的表面积是多少平方米?根据题意作图:解析:由图可知,增加的8平方米,就是正方体的2个面,每个面的面积是8÷2=4(平方米),则正方体的表面积是:4×6=24(平方米)。
四、列表图法例:有一个5分币,4个2分币,8个1分币。
要拿9分钱,有几种拿法?根据题意作图:由列表图,可以清楚看到共有7种拿法。
五、树状图法例:小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清就随便穿了两只。
小明正好穿的是同一双袜子的可能性是多少?解析:假设2双袜子为A袜、B袜,那么4只袜子分别是A1、A2、B1、B2,根据题意作图:由树状图可知,2双袜子任意搭配有12种情况,其中同一双的情况有4种,所以小明穿同一双袜子的的可能性是4/12,也就是1/3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在教科书中,关于线段的定义是:直线上两点间的部分叫做线段。
特点:有两个端点。
有限长。
关于线段图没有定义,词典中也没有解释。
可以这样理解:线段图是有几条线段组合在一起,用来表示应用题中的数量关系,帮助人们分析题意,解答问题的一种平面图形。
特点:从抽象的文字到直观的再创造、再演示的过程。
应用线段图解答应用题有什么作用。
借助于线段图解题,可以化抽象的语言到具体、形象、直观图形。
小学生年龄小,理解能力有限,而且社会经历又少,给理解题意带来很大的困难。
教师引导学生用线段图的形式表示题目中的数量关系,更直观,形象,具体。
借助线段图,可以化难为易,判断准确。
有的应用题,数量关系比较复杂,学生难以理清,借助线段图可以准确的找出数量间的对应关系,很容易解出要求的问题。
借助线段图,可以化繁为简,发展学生思维。
有些应用题数量较多,数量关系学生感觉比较乱,学生容易混。
借助线段图,可以化知识为能力。
线段图不但使学生解答应用题不再困难,而且借助线段图,可以对学生进行多种能力的培养。
如一题多解能力的培养、根据线段图来编应用题,进行说话能力的培养、还可以直接根据线段图进行列式计算。
线段图画的美观大方,结构合理,还可以对学生进行审美观念,艺术能力的训练。
开阔学生思维,帮助学生一题多解线段图的正确运用能开拓学生思维,加大了能力培养的力度,使学生的思维方式由浅性思维向非浅性思维的多元化方向发展,学会创造性地开展学习,对于同一个问题,从不同的角度,用不同的方法进行全方位思考,让学生轻松地进行一题多解。
如:人教版六年级上册第 90 页“例 2”,通过线段图:原计划: 12 公顷实际: 14 公顷学生可以理解到同一个问题可以用两种不同的方法:①(14-12)÷12=2÷12≈0.167=16.7% ②14÷12≈1.167=116.7% 116.7%-100%=16.7% 比原计划增加的。
学会画线段图,提高解决问题的能力学会画线段图,提高解决问题的能力。
教孩子看线段图培养识图能力新课程中有大量的情景图和实物图,特别是低年级的教材中更是充分考虑到孩子的年龄特点以图为主。
以北师大版教材与老教材相比,从时间上看线段图出现比老教材晚,到了四年级上册教学路程问题时才在练习中出现实物图与线段相结合的图形,四年级下方程问题的教学中才正式出现常规线段图。
从数量上讲新教材比老教材出现线段图的频率少的多。
所以虽说我的课题面对五年级学生,但学生接触线段图的机会还是很少,许多学生存在不会看线段图问题。
在教学中有意识用线段图教学,提高线段图在孩子面前出现的频率,让线段图深入孩子的脑海。
线段图可以提高学生判断的准确性。
“比()多()”、“比()少()”的应用题教学是个难点,难在学生一看“比()多()”不加分析就判断用加法计算,反之则用减法计算。
而线段的正确使用能避免学生出现这种错误判断。
例:黄花有9朵,比红花少5朵,红花有几朵?引导学生作图分析:先画出黄花的朵数,再由“比红花少”可知哪种花多?怎样画红花的朵数?
教师的指导、示范、点拨是培养学生画图能力的关键。
学生刚学习画线段图,不知道从那下手,如何去画。
教师的指导、示范就尤为重要。
(1)教师可以指导学生跟教师一步一步来画,找数量关系。
也可以教师示范画出以后,让学生仿照重画一遍,即使是把老师画的图照抄一边,也是有收获的。
(2)学生可边画边讲,或互相讲解。
教师对有困难的学生一定要给以耐心的指导。
(3)学生掌握了一定的技能后,教师可以放手让学生自己去画,教师给以适时的点拨,要注意让学生讲清这样画图的道理,可自己讲,也可分组合作讲。
教师一定要让学生体会用图解题的直观,形象,体会简洁、方便、易理解的特点,提高应用的自觉性、主动性。
知识的拓展和迁移,是线段图应用的难点。
不少的学生遇到应用题想到用线段图来辅助
解题,而其他类型的题目就想不到应用。
实际上,不但应用题可以应用线段图帮助分析题意,而且还可以迁移到其他类型的题。
掌握一个解题方法,比做一百道题更重要。
实践证明,线段图具有直观性、形象性、实用性,如果学生从小掌握了用线段图辅助解题的方法,分析问题和解决问题的能力将会有大大的提高,对今后的学习生活将有很大的帮助。
