单重态三重态
单重态三重态自由能能量差计算

单重态和三重态是指在分子体系中,由同一组电子构成的两种不同的激发态。
这两种激发态的自由能能量差计算在理论化学中是非常重要的,因为它可以用来解释和预测分子体系的性质和行为。
在本文中,我们将探讨单重态和三重态的自由能能量差的计算方法,并讨论其在化学研究中的应用。
1. 单重态和三重态的定义单重态和三重态是分子体系中激发态的两种基本类型。
在单重态中,分子中的所有电子都处于自旋相反的态,总自旋为零。
而在三重态中,分子中至少有一个电子处于与其余电子自旋相反的态,总自旋不为零。
这两种激发态的自由能能量差可以通过一系列计算方法来确定。
2. 自由能能量差的计算方法自由能能量差的计算通常可以利用量子化学计算软件来进行,其中最常用的方法包括密度泛函理论(DFT)、含时密度泛函理论(TDDFT)、多体微扰理论(MBPT)等。
这些方法可以通过求解分子的薛定谔方程或是利用近似方法来计算分子在不同激发态下的能量。
3. 应用领域单重态和三重态的自由能能量差的计算在许多化学研究领域都有重要的应用。
在有机光电子材料的设计中,通过计算单重态和三重态的能量差可以预测材料的光学性质和稳定性;在催化剂设计中,自由能能量差可以用来解释反应中间体的稳定性和反应性能等。
4. 研究进展近年来,随着计算机技术和量子化学方法的不断进步,对于单重态和三重态自由能能量差的计算方法也在不断地得到改进和完善。
开发了一些新的密度泛准理论方法,如双杂化密度泛准理论(DH-DFT)和自洽场双杂化密度泛准理论(SC-DH-DFT),在计算复杂体系的单重态和三重态能量差时取得了一定的成功。
5. 结论在化学研究中,单重态和三重态的自由能能量差计算对于理解和预测分子体系的性质具有重要意义。
通过合理选择计算方法和不断创新,我们可以更准确地计算出这两种激发态的能量差,为材料设计、催化剂设计等领域的研究提供有力的支持。
希望未来能够有更多的研究取得突破,为该领域的发展做出贡献。
在现代理论化学研究中,单重态和三重态的自由能能量差的计算在许多领域都有着广泛的应用。
从碳烯的单重态和三重态谈起

從碳烯的單重態和三重態談起我在談碳烯時提到單重態(singlet state)和三重態(triplet state),基本上與兩個電子的spin state組合有關,如果是配對的 (paired) 一定是單重態;如果是未配對的而且是spin parallel,則會是三重態。
在同一軌域的兩個電子spin一定要配對的,但是分在兩個軌域的兩個電子(每一個軌域各一)就可能有單重態或三重態兩種狀態,那將以三重態的能量較低。
但是由於一個系統的spin必須守恆(conserved),所以通常從單重態得到的產物一開始一定是單重態,例如下圖(稱為Perrin-Jablonski diagram) 所示,在基態的物質受到光的激發,某一軌域中的配對電子其中之一提升至高能階軌域,進入某激發態,但因spin守恆之故,一定是個單重激發態,但若是透過系間交換(intersystem crossing)或直接透過熱的釋放才會轉成三重態。
此處所謂的“系"指單重態系統或三重態系統,系統相同者之轉換稱為系內,系統不同者之轉換稱為系間,系間轉換因spin不守恆,是不易發生的,常需要透過自旋與軌域之間的作用 (spin-orbital interaction) 來發生,因此一旦產生了單重激發態最容易發生的就是很快速的透過放光,稱為螢光 (fluorescence),回至基態,或是透過分子的振動釋放能量回到基態。
若透過某些方式從單重激發態進入了三重激發態,此時要以放光的方式回到單重基態變得很慢,分子在三重激發態的存留時間長(long half-life),這種放光稱為磷光。
Perrin-Jablonski diagrama: 吸收光子b: 螢光(fluorescence)c: 系內轉換(internal conversion; IC)d: 系間交換(intersystem crossing; ISC)e: 磷光(phosphorescence)→: 有光放射或吸收的能階轉換~~>:無光放射的能階轉換S1:能階最低的單重激發態S2:能階第二低的單重激發態T1:能階最低的三重激發態T2:能階最低的三重激發態具有放光性質的分子不但在材料科學中受到重視,在生命科學的領域中也有很重要的運用,透過發光基團(常稱發色團;chromophor)上取代基的修飾,改變能階,化學家有能力調控吸光與放光的波長。
发光学与发光材料复习总结终极版-参考资料

第一章发光学与发光材料1、发光:当某种物质受到激发(射线、高能粒子、电子束、外电场等)后,物质将处于激发态,激发态的能量会通过光或热的形式释放出来。
如果这部分的能量是位于可见、紫外或是近红外的电磁辐射,此过程称之为发光过程。
2、单重态:一个分子中所有电子自旋都配对的电子状态三重态:有两个电子的自旋不配对而平行的状态3.振动弛豫:由于分子间的碰撞,激发态分子由同一电子能级中的较高振动能级转至较低振动能级的过程,其效率较高。
4.内转换:相同多重态的两个电子能级间,电子由高能级回到低能级的分子内过程。
5.系间窜越:激发态分子的电子自旋发生倒转而使分子的多重态发生变化的过程。
6.外转换:激发态分子与溶剂或其他溶质相互作用和能量转换而使荧光(或磷光)减弱甚至消失的过程。
7.荧光:受光激发的分子经振动驰豫、内转换、振动驰豫到达第一电子激发单重态的最低振动能级,以辐射的形式回到基态,发出荧光。
8.磷光:若第一激发单重态的分子通过系间窜跃到达第一激发三重态,再通过振动驰豫转至该激发的最低振动能级,然后以辐射的形式回到基态,发出的光线称为磷光。
9.光致发光:用光激发产生的发光叫做光致发光。
10.电致发光:用电场或电流激发产生的发光。
11.阴极射线发光:发光物质在电子束的激发下产生的发光。
荧光灯:是一种充有氩气的低气压汞蒸气的气体放电灯,在低压汞蒸气放电过程中会产生大量的波长为253.7mm的紫外线,以及少量波长为185nm的紫外线和可见光。
在灯管表面涂有荧光粉,可以将波长为253.7nm的紫外线转化为可见光。
11.激光器的基本结构包括三部分,即工作物质、激励能源和光学谐振腔。
12.等离子体:是指正负电荷共存,处于电中性的放电气体的状态。
14.晶体:有许多质点包括原子、离子、分子或原子群,在三维空间作有规则排列而成的固体物质。
单晶:整个晶格是连续的。
多晶:有大量小单晶颗粒组成的集体。
非晶:组成物质的原子或离子的排列不具有周期性。
分子的三重态

分子的三重态在化学领域中,分子的三重态是指分子处于一个具有三个不同能级的电子激发态。
这些能级是由分子的电子构型和分子中的电子相互作用所决定的。
分子的三重态具有独特的性质和行为,对于理解分子的结构、反应和性质至关重要。
在三重态中,分子的电子处于高能级,激发态的状态。
这种状态与分子的基态不同,因为它具有不同的电子分布和电子自旋状况。
由于电子自旋的相互作用,分子的三重态可能具有两种不同的自旋状态,分别称为自旋三重态和自旋单态。
自旋三重态和自旋单态的能级之间存在能量差异,这使得分子在不同的电子激发态之间进行跃迁成为可能。
这些跃迁可以通过吸收或发射光的形式进行,从而产生各种各样的光谱现象。
这些光谱现象可以用于分析分子的结构和动力学行为。
分子的三重态还可以通过化学反应进行转化。
在一些反应中,分子的基态可以被激发为三重态,然后再回到基态。
这种转化可以通过光激发或化学反应来实现。
分子的三重态在这些反应中起到了重要的作用,它们可以作为反应中间体或过渡态,参与到反应的进行中。
除了在化学反应中的作用,分子的三重态还对分子的氧化还原性质和磁性质有重要影响。
分子的三重态可以影响其与其他分子或离子的相互作用,从而改变其化学性质。
此外,分子的三重态也可以影响分子的磁性,从而影响分子在外磁场中的行为。
分子的三重态是分子电子激发态的一种形式,具有重要的化学和物理性质。
通过研究分子的三重态,我们可以更好地理解分子的结构、反应和性质。
同时,分子的三重态也为开发新的材料和化学反应提供了潜在的机会。
因此,对于分子的三重态的研究具有重要的科学意义和应用价值。
ADF教程:如何计算单重态到三重态的激发(相对论、许可跃迁)
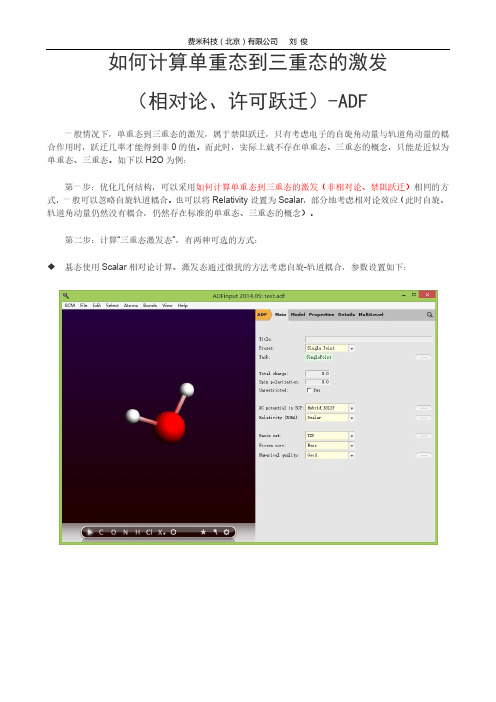
如何计算单重态到三重态的激发
(相对论、许可跃迁)-ADF
一般情况下,单重态到三重态的激发,属于禁阻跃迁,只有考虑电子的自旋角动量与轨道角动量的耦合作用时,跃迁几率才能得到非0的值。
而此时,实际上就不存在单重态、三重态的概念,只能是近似为单重态、三重态。
如下以H2O为例:
第一步:优化几何结构,可以采用如何计算单重态到三重态的激发(非相对论、禁阻跃迁)相同的方式,一般可以忽略自旋轨道耦合。
也可以将Relativity设置为Scalar,部分地考虑相对论效应(此时自旋、轨道角动量仍然没有耦合,仍然存在标准的单重态、三重态的概念)。
第二步:计算“三重态激发态”,有两种可选的方式:
基态使用Scalar相对论计算、激发态通过微扰的方法考虑自旋-轨道耦合,参数设置如下:
基态计算考虑自旋-轨道耦合、激发态精确地考虑自旋-轨道耦合,参数设置如下:
这两种方式,后者精确度更高,但前者可以计算自旋轨道耦合矩阵元。
后者计算得到的跃迁几率非常小(例如0.0000001以下)的激发态,并且三个激发态能量很接近,这就是对应的T1态劈裂开的3个激发态,具体可以参考三重态的劈裂。
前者得到的三个态能量完全一样,不能处理三重态的劈裂问题。
第21讲6电子自旋单三重态3

ˆ ˆ2 J,J 2 2 =0 ˆ ˆ2 ˆ ˆ ˆ2 ˆ2 ˆ2 ˆ ˆ ˆ2 J,J ,J1 = J1 +J2 +2J1 J2 ,J1 =0 1 = J1 +J 2 ˆ2 ˆ2 ˆ J J J ˆ ,J ˆ ,J ˆ ,J =0 =0 =0 z 1 z 2 z 2
2
1
3 2 ˆ1x 1 s1z s ˆ2 x 1 s 2z 2[s 2 2 2 ˆ1y 1 s1z s ˆ2 y 1 s 2 z s ˆ1z 1 s1z s ˆ2 z 1 s 2 z ] s
2 (1) 2 2 S 2 2 2
• §6.1 • §6.2 • §6.3
提纲
电子自旋 电子的自旋算符和自旋函数 自旋单态和自旋三重态
第21讲 第六章 自旋和角动量
§6.3 自旋单态和自旋三重态 作业:6.8
结束
§6.3 自旋单态和自旋三重态
• 引言 • 研究体系 • 两自旋角动量的耦合—单态和三重态的概 念 • 耦合表象中自旋平方和分量的本征值 返回
jmin = j1 -j2
j=j1 +j2 ,j1 +j2 -1,..., j1 -j2
返回
研究体系
两粒子体系,自旋都是1/2的粒子 哈密顿算符不含自旋 总自旋波函数特点:
s1z ,s2 z s1z s2 z
1 2
等于每一个粒子的自旋波函数的乘积。
返回
两自旋角动量的耦合—单态和三重态的概念
耦合表象中自旋平方和分量的本征值
结论之二:三个对称波函数的区别(三重态) 共性:两个粒子的自旋都平行P265 ˆ 作用在对称波函数上时本征值分别是 S 、 - 、 0 z 1 S 自旋都平行于z轴,方向都朝上; 2 S 自旋都反平行于z轴,方向都朝下; 3 S 自旋虽平行,但与z轴不平行,合成后 的总自旋角动量与z轴垂直,z轴分量为零。
自旋相关自由基对单重态氧或三重态氧的选择结合规律

自旋相关自由基对单重态氧或三重态氧的选择结合规律自旋相关自由基对单重态氧或三重态氧的选择结合规律1. 引言自旋相关自由基作为有机合成化学领域中的重要研究对象,其对于选择性合成和反应机理的理解具有重要意义。
其中,自旋相关自由基与单重态氧(singlet oxygen)或三重态氧(triplet oxygen)的选择结合规律是一个备受关注的研究领域。
2. 自旋相关自由基的概念与性质自旋相关自由基是指在分子结构中,两个自由基中的未成对电子自旋方向呈现关联的现象。
两个自由基的自旋方向可以同时垂直向上或垂直向下,这被称为α-α自旋关联;或者自旋方向可以一个向上一个向下,这被称为α-β自旋关联。
自旋相关自由基可以通过不同反应途径生成,并且其存在可以对化学反应产率、立体选择性等方面产生重要影响。
深入研究自旋相关自由基对单重态氧或三重态氧的选择结合规律,对于探索反应机理、合成方法的优化具有重要意义。
3. 单重态氧与自旋相关自由基的选择结合规律在研究中发现,自旋相关自由基与单重态氧的选择结合规律与自由基的自旋状态密切相关。
一般来说,α-α自旋相关自由基更倾向于选择性地与单重态氧反应,而α-β自旋相关自由基则更倾向于与三重态氧反应。
此选择性反应可以通过能级匹配原理进行解释。
单重态氧和自旋相关的α-α自由基具有相似的自旋多重度,从而可以形成较为稳定的中间态,从而促进反应的进行。
而与α-β自旋相关的自由基相比,反应物之间的能量差异较大,从而导致其反应不够稳定。
4. 三重态氧与自旋相关自由基的选择结合规律对于α-β自旋相关自由基与三重态氧的选择结合规律,理论研究发现其关系较为复杂。
在一些情况下,α-β自旋相关自由基可以与三重态氧有选择性地反应,但通常其反应速率较慢。
这可以解释为,三重态氧与自旋相关自由基反应的选择性与反应物之间的距离以及能级差异有关。
在有些情况下,由于反应物之间的空间隔离或能级差异较大,使得反应难以发生或速率较慢。
自旋单态和自旋三重态

类似有
$ 2 χ (2) = 2h 2 χ (2) S S S S χ (2) = h χ (2)
z S S
$ 2 χ (3) = 2h 2 χ (3) S S S S χ (3) = 0
z S
$ 2χ = 0 S A S χ =0
z A
6.7 自旋单态和自选三重态
$ 2作用在对称波函数 综合(6.7.15)至(6.7.22)式得出, S (1) (2) (3) $ 2 的本征值表示 2 χ , χ , χ 上时,其本征值为 2h ,若将 S
(1) χ S ,两个粒子的自旋都平行于 z轴; ① 态
1 1 + 2 2
6.7 自旋单态和自选三重态
(2) ② 态 χ S 两个粒子的自旋都反平行于 z 轴; (3) χ S 两个粒子的自旋虽然平行,但合成后的总 ③ 态 自旋角动量与z 轴垂直; ④ 态 χ A 两个粒子的自旋反平行。
S S S
为 s( s + 1)h 2,即得总自旋角动量量子数 s = 1 ,这正是
$ 2作用在反对称波函数 χ A 上,其本 耦合的结果。同理,将 S 1 1 征值为零,相应的 s = 0 ,这时 耦合的结果。 2 2 (1) (2) (3) $2 χ S , χ S , χ S 各不同的。 表现在作用在这些波 说明:态 S 函数上,分别得出 h , -h , 0 三个不同的值。
2 2 2 2 (1) =2h 2 χ S
(6.7.15)
6.7 自旋单态和自选三重态
(1) (1) S z χ S = ( s1z + s2 z ) χ 1 ( s1z ) χ 1 ( s2 z ) = h χ S 2 2
(6.7.16) (6.7.17) (6.7.18) (6.7.19) (6.7.20) (6.7.21) (6.7.22)
分子发光分析法

第7章分子发光分析法【7-1】解释下列名词。
(1)单重态;(2)三重态;(3)荧光;(4)磷光;(5)化学发光;(6)量子产率;(7)荧光猝灭;(8)振动弛豫;(9)系间跨越;(10)内转换;(11)重原子效应。
答:(1)单重态:在给定轨道中的两个电子,必定以相反方向自旋,自旋量子数分别为1/2和-1/2,其总自旋量子数s=0。
电子能级的多重性用M=2s+1=1,即自旋方向相反的电子能级多重性为1。
此时分子所处的电子能态称为单重态或单线态,用S表示。
(2)三重态:当两个电子自旋方向相同时,自旋量子数都为1/2,其总自旋量子数s=1。
电子能级的多重性用M=2s+1=3,即自旋方向相同的电子能级多重性为3,此时分子所处的电子能态称为三重态或三线态,用T表示。
(3)荧光:分子受到激发后,无论处于哪一个激发单重态,都可通过振动弛豫及内转换,回到第一激发单重态的最低振动能级,然后以辐射形式回到基态的各个振动能级发射的光。
(4)磷光:分子受到激发后,无论处于哪一个激发单重态,都可通过内转换、振动弛豫和体系间跨越,回到第一激发三重态的最低振动能级,然后以辐射形式回到基态的各个振动能级发射的光(5)化学发光:化学反应物或反应产物受反应释放的化学能激发而产生的光辐射。
表示。
(6)量子产率:激发态分子发射荧光的光子数与基态分子吸收激发光的光子数之比,常用f(7)荧光猝灭:指荧光物质分子与溶剂分子之间发生猝灭,荧光猝灭分为静态猝灭和动态猝灭。
(8)振动弛豫:处于激发态最高振动能级的外层电子回到同一电子激发态的最低振动能级以非辐射的形式将能量释放的过程。
(9)系间跨越:处于激发态分子的电子发生自旋反转而使分子的多重性发生变化的过程。
即分子由激发单重态以无辐射形式跨越到激发三重态的过程。
(10)内转换:相同多重态的两个电子态之间的非辐射跃迁。
(11)重原子效应:使用含有重原子的溶剂(如碘乙烷、溴乙烷)或在磷光物质中引入重原子取代基,都可以提高磷光物质的磷光强度,这种效应称为重原子效应。
4 自旋单态与三重态 - 西安交通大学教师个人主页 - 首页

2
2
= s1z c 1 (s1z )c 1 (s2z ) + c 1 (s1z )s2z c 1 (s2z )
2
2
2
2
=
1 2
hc 1 (s1z )c 1 (s2z ) +
2
2
1 2
hc 1 (s1z )c 1 (s2z
2
2
)
= hc 1 (s1z )c 1 (s2z )
2
2
计算表明,
c
I s
是
S2
2 个Bose 子体系,其对称化波函数是:
F( S q1 , q2 ) =
1 2
[F(q1
,
q2
)
+
F(q2
,
q1
)]
1,2 粒子在 i,j 态中的一种排列
=
1 2
[f(i q1
)f
j
(q2
)
+
f(i q2
)f
j
(q1
)]
N 个 粒子在 i,j … k 态
N 个Bose 子体系,其对称化波函数可类推是:
I。n1=n2=n3=1
F
1 ( 1 1
S
q1
,
q2
,
q3
)
=
1 3
[f(1 q1
)f2 (q2
)f 3
(q3
)
+
f(1 q2
)f2 (q3
)f 3
(q1
)
+ f(1 q3 )f2 (q1 )f3 (q2 ) + f(1 q3 )f2 (q2 )f3 (q1 )
+ f(1 q2 )f2 (q1 )f3 (q3 ) + f(1 q1 )f2 (q3 )f3 (q2 )]
武汉大学《分析化学》(第5版)(下册)课后习题(分子发光分析法) 【圣才出品】

第8章 分子发光分析法8-1 解释下列名词:(1)单重态;(2)三重态;(3)系间窜越;(4)振动弛豫;(5)荧光猝灭;(6)荧光量子产率;(7)重原子效应。
答:(1)单重态是指分子中的全部电子都自旋配对的分子能态,用符号S 表示,单重态分子具有抗磁性。
(2)三重态是指分子中存在两个自旋不配对的电子的分子能态,用符号T 表示,三重态分子具有顺磁性。
(3)系间窜越是指不同多重态的两个电子态间的非辐射跃迁的过程。
(4)振动弛豫是指分子将多余的振动能量传递给介质而衰变到同一电子能级的最低振动能级的过程。
(5)荧光猝灭是指荧光物质与溶剂分子间发生导致荧光强度下降的化学或物理过程。
(6)荧光量子产率是指荧光物质吸光后发射的荧光光子数与吸收的激发光光子数的比值。
(7)重原子效应是指磷光测定体系中存在原子序数较大的原子时,重原子的高核电荷引起或增强了溶质分子自旋轨道的耦合作用,从而增大了,体系间的窜11S T →01S T →跃概率,有利于磷光的产生的现象。
8-2 说明磷光与荧光在发射特性上的差别及其原因。
答:磷光与荧光在发射特性上的差别及其原因如下:(1)磷光是来自最低激发三重态的辐射跃迁过程所伴随的发光现象,发光过程速率常数小,激发态的寿命相对较长。
第一激发单重态的最低振动能级,通过系间窜越至第一激发三重态,再经振动弛豫,转至最低振动能级进而发射磷光,系间窜跃是自旋禁阻的,因此过程速率常数小。
(2)荧光是来自最低激发单重态的辐射跃迁过程所伴随的发光现象,发光过程速率常数大,激发态的寿命短。
8-3 简要说明荧光发射光谱的形状通常与激发波长无关的原因。
答:荧光发射光谱的形状通常与激发波长无关的原因为:荧光的产生是由第一电子激发态的最低振动能级开始,而与荧光分子被激发至哪一能级无关。
8-4 与分光光度法比较,荧光分析法有哪些优点?原因何在?答:(1)荧光分析法的优点相对分光光度法,荧光分析法具有更高的灵敏度。
(2)原因①荧光强度与激发光强度成正比,提高激发光强度可以使荧光强度增大,而分光光度法检测的是吸光度,增大入射光强度,透过光信号与入射光信号同比例增大,吸光度值不会发生变化,因此不能提高灵敏度;②荧光的测量是在与激发光垂直的方向上进行的,消除了杂散光和透射光对荧光测量的影响。
[训练]激发三重态
![[训练]激发三重态](https://img.taocdn.com/s3/m/87ed2a1c3186bceb19e8bbf6.png)
[训练]激发三重态激发三重态在一般温度下,大多数分子处在基态的最低振动能级。
处于基态的分子吸收能量(电能、热能、化学能或光能等)后被激发为激发态。
激发态是很不稳定的,它将很快地释放出能量又重新跃迁回基态。
若分子返回基态时以发射电磁辐射(即光)的形式释放能量,就称为“发光”。
如果物质的分子吸收了光能而被激发,跃迁回基态所发射的电磁辐射,称为荧光和磷光。
现从分子结构理论来讨论荧光和磷光的产生机理。
每个分子中都具有一系列严格分立相隔的能级,称为电子能极,而每个电子能级中又包含有一系列的振动能级和转动能级。
分子中电子的运动状态除了电子所处的能级外,还包含有电子的多重态,用M=2S+1表示,S为各电子自旋量子数的代数和,其数值为0或1 。
根据Pauli不相容原理,分子中同一轨道所占据的两个电子必须具有相反的自旋方向,即自旋配对。
若分子中所有电子都是自旋配对的,则S=0,M=1,该分子便处于单重态(或叫单重线),用符号S表示。
大多数有机化合物分子的基态都处于单重态。
基态分子吸收能量后,若电子在跃迁过程中,不发生自旋方向的变化,这时仍然是M=1,分子处于激发的单重态;如果电子在跃迁过程中伴随着自旋方向的变化,这时分子中便具有两个自旋不配对的电子,即S=1,M=3,分子处于激发的三重态,用符号T表示。
图14.1为电子重态示意图。
图14.1 单重态系三重态激发示意图处于分立轨道上的非成对电子,自旋平行要比自旋配对更稳定些(洪特规则),因此在同一激发态中,三重态能级总是比单重态能级略低。
图14.2为能级及跃迁示意图,其中S0、S1和S2分别表示分子的基态、第一和第二电子激发的单重态;T1和T2则分别表示分子的第一和第二电子激发的三重态。
V=0、1、2、3、…表示基态和激发态的振动能级。
图14.2 荧光和磷光体系能级图处于激发态的分子是很不稳定的,它可能通过辐射跃迁和非辐射跃迁的形式去活化(去激发)释放出多余的能量而返回基态。
单线态氧和三重态

单线态氧和三重态一、氧的“变脸”氧,是我们每天都离不开的东西,对吧?每一口气都得靠它。
我们生活中的氧,基本上就是那种你在空气中自由游走的“普通氧分子”,大家都叫它三重态氧。
别小看它,尽管它貌似很普通,但它可比我们见过的好多明星都要神秘得多,尤其是在化学反应中。
这不,氧一不小心就能“变脸”,从平时的三重态氧变成了那种“暴躁的”单线态氧。
你以为单线态氧就是个不怎么重要的小角色?大错特错!它可是个相当高能的家伙。
单线态氧的出现,就像是一个不太听话的孩子,时不时就要掀个桌子。
它的能量比三重态氧高得多,而且性格也比较“暴躁”,会和周围的分子疯狂反应,产生一些很激烈的化学变化。
所以它总是给很多实验带来不可预见的结果。
你别看它现在只是个气体,别看它可能只在微小的空间里活动,它在化学反应中的作用可大得很呢。
二、三重态氧的“低调”生活三重态氧到底是啥?说白了,三重态氧其实就是我们平常在大气中吸进肺里的氧气。
它有着比较稳定的能量状态,也就是说,它在平时不会随便去“闹事”。
想象一下,这个家伙就像一个中规中矩的“上班族”,做事慢条斯理,一切都很理性,不打扰别人。
它的存在是为了维持宇宙的平衡,不会突然来个“反转”,把你给吓一跳。
说白了,它就是那种你可以靠得住、不至于爆炸的“好氧”。
但,三重态氧可不是软柿子,也不是简单的“好人”。
它也能做出些奇怪的事,比如在紫外线的照射下,它会变成不太稳定的单线态氧。
你说,怎么一个氧分子,能有那么多“面孔”?它就是那种能把自己演绎得淋漓尽致的“戏精”。
你总能看到它在不同环境中,变得越来越不一样。
三、单线态氧的“火爆脾气”单线态氧简直可以说是个化学界的“暴脾气”,一旦它出现在某个环境中,立刻就会乱得不可收拾。
它的能量那么高,没事就喜欢四处碰撞。
它不仅会和别的氧分子较劲,还会去捣乱其他分子,尤其是那些比较不小心的有机物。
它就像是一个能量满满的“火爆脾气的小孩”,总是挑起麻烦,制造反应。
单线态氧的这种“反应欲”可不是一般的强,它甚至能破坏一些细胞,伤害生物体内的分子。
三重态

自旋单态的两个电子可以处于相同的空间态,而三重态不可以。
如果无外磁场,并且先不考虑电子间库伦作用,则两个电子都处于空间波函数的基态时具有最低能级,即只有自旋单态可以达到最稳定状态。
如果具有强外磁场,自旋三重态在空间态能级上将劈裂为三个能级,并且能级差随磁场增加而增加,其中有一个能级可以比空间波函数基态能级更低,在这种能级上三重态更稳定。
至于电子之间的库伦相互作用,同处于基态时的相互作用和三态时的相互作用之差似乎总是小于空间波函数激发态和基态之差(我不确定有没有哪个定理明确指出过,位力定理可能对此支持),因此考虑库伦相互作用不改变单态比三重态稳定的结果。
严格的分析涉及到多体相互作用,电子数的增加会改变空间态的能级和本征态,不过在原子这种例子中,原子核对电子的吸引总是强于电子相互作用因而能级结构改变不大,以上的简明图象是适用的。
单重态三重态

单重态S0 为基态,可以激发为单重激发态或者三重激发态。
分子吸收辐射使电子能级从基态跃迁到激发态能级,同时伴随着振动能级和转动能级的跃迁。
在分子能级跃迁的过程中,电子的自旋状态也可能发生改变。
应用于分析化学中的荧光和磷光物质几乎都含有π→π* 跃迁的吸收过程,它们不含有偶数电子。
根据泡里不相容原理,在同一轨道上的两个电子的自旋方向要彼此相反,即基态分子的电子是自旋成对的,净自旋为零,这种电子都配对的分子电子能态称为单重态(singlet state ),具有抗磁性。
分子处于激发的三重态,即分子中含有两个自旋不配对的电子。
电子激发态的多重度用M=2s+1 表示,s 为电子自旋量子数的代数和,其数值为0 或1.根据pauli 不相容原理,分子中同一轨道所占据的两个电子必须具有相反的自旋方向,即自旋配对。
假如分子中全部轨道里的电子都是自旋配对的,即s=0,分子的多重度M=1 ,该分子体系便处于单重态,用符号S 表示。
大多数有机物分子的基态是处于单重态的。
电子的跃迁过程中如果还同时伴随了自旋方向的改变,这时分子便具有了两个自旋不配对的电子,即s=1, 分子的多重度M=3 ,分子处于激发的三重态,用符号T 表示。
处于分立轨道上的非成对电子,平行自旋要比成对自旋更稳定些(Hund 定则),因此三重态能级总是比相应的单重态略低。
Proposed luminescence mechanism; short-wavelength PF(emission at around 525 nm), long-wavelength PFand TADF(emission at 610 - 650 nm), and IC (internal conversion).Welcome To Download !!!欢迎您的下载,资料仅供参考!。
基态氧和激发态氧

基态氧和激发态氧
基态氧指的是氧分子处于最稳定的状态下,即两个氧原子之间共享两个电子,形成一个双键。
基态氧的化学符号为O2。
激发态氧则指的是氧分子在受到能量的激发后,其中一个电子跃迁到了更高的能级。
这种情况下,氧分子呈现出三个不同的态:单重态氧(O2(a1Δg))、双重态氧(O2(b1Σg+))、三重态氧(O2(c1Πg))。
这些不同的态受到的能量和化学行为也不同。
在大气化学中,激发态氧在自然界中的化学反应中起着重要的作用。
例如,在大气层中,太阳辐射会激发氧分子形成激发态氧,在这种状态下,氧分子与其他大气分子发生反应,从而引发一系列的化学反应,其中包括臭氧的形成和消耗等。
总之,基态氧和激发态氧是两种不同形态的氧分子,它们在化学和大气化学反应中具有不同的作用。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单重态S0为基态,可以激发为单重激发态或者三重激发态。
分子吸收辐射使电子能级从基态跃迁到激发态能级,同时伴随着振动能级和转动能级的跃迁。
在分子能级跃迁的过程中,电子的自旋状态也可能发生改变。
应用于分析化学中的荧光和磷光物质几乎都含有π→π*跃迁的吸收过程,它们不含有偶数电子。
根据泡里不相容原理,在同一轨道上的两个电子的自旋方向要彼此相反,即基态分子的电子是自旋成对的,净自旋为零,这种电子都配对的分子电子能态称为单重态(singlet state),具有抗磁性。
分子处于激发的三重态,即分子中含有两个自旋不配对的电子。
电子激发态的多重度用M=2s+1表示,s为电子自旋量子数的代数和,其数值为0或1.根据pauli不相容原理,分子中同一轨道所占据的两个电子必须具有相反的自旋方向,即自旋配对。
假如分子中全部轨道里的电子都是自旋配对的,即s=0,分子的多重度M=1,该分子体系便处于单重态,用符号S表示。
大多数有机物分子的基态是处于单重态的。
电子的跃迁过程中如果还同时伴随了自旋方向的改变,这时分子便具有了两个自旋不配对的电子,即s=1,分子的多重度M=3,分子处于激发的三重态,用符号T表示。
处于分立轨
道上的非成对电子,平行自旋要比成对自旋更稳定些(Hund定则),因此三重态能级总是比相应的单重态略低。
Proposed luminescence mechanism; short-wavelength PF(emission at around 525 nm), long-wavelength PF and TADF(emission at 610−650 nm), and IC (internal conversion).
(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
