第五讲等差数1
第五讲暑假班-等比等差数列求和(教师版) - 副本

第五讲数列求和方法课前准备【旧知识复习】复习1:等差数列等比数列的通项公式是什么?它们的通项公式都有什么特征呢?复习2:等差等比数列的求和公式是什么?新课导学一、学习探究:1.公式法与分组转化法(1)公式法直接利用等差数列、等比数列的前n项和公式求和.(2)分组转化法若一个数列是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组转化法,分别求和后相加减.2.倒序相加法与并项求和法(1)倒序相加法如果一个数列{a n}的前n项中首末两端等“距离”的两项的和相等或等于同一个常数,那么求这个数列的前n项和可用倒序相加法,如等差数列的前n项和公式就是用此法推导的.(2)并项求和法在一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如a n=(-1)n f(n)类型,可采用两项合并求解.例如,S n =1002-992+982-972+…+22-12=(1002-992)+(982-972)+…+(22-12)=(100+99)+(98+97)+…+(2+1)=5 050. 3.裂项相消法把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和. 4.错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n 项和即可用错位相减法来求,如等比数列的前n 项和公式就是用此法推导的.二、 自主学习:(1)数列112,314,518,7116,…,(2n -1)+12n ,…的前n 项和S n 的值等于________.答案:n 2+1-12n(2)数列{a n }的前n 项和为S n ,已知S n =1-2+3-4+…+(-1)n -1·n ,则S 17=________. 答案:9(3)(2018·枣庄模拟)已知等差数列{a n }的前n 项和为S n ,a 5=5,S 5=15,则数列⎩⎨⎧⎭⎬⎫1a n a n +1的前100项和为________.答案:100101(4)若a n =2n -1,则数列⎩⎨⎧⎭⎬⎫1a n a n +1的前n 项和S n =________.答案:n2n +1三、精讲精练:【考点一】分组转化求和[例1] (2018·合肥质检)已知等差数列{a n }的前n 项和为S n ,且满足S 4=24,S 7=63. (1)求数列{a n }的通项公式;(2)若b n =2a n +a n ,求数列{b n }的前n 项和T n . [解] (1)∵{a n }为等差数列,∴⎩⎨⎧S 4=4a 1+4×32d =24,S 7=7a 1+7×62d =63,解得⎩⎪⎨⎪⎧a 1=3,d =2,∴a n =2n +1.(2)∵b n =2a n +a n =22n +1+(2n +1)=2×4n +(2n +1), ∴T n =2×(4+42+…+4n )+(3+5+…+2n +1) =2×4(1-4n )1-4+n (3+2n +1)2=83(4n -1)+n 2+2n . [方法技巧]分组转化法求和的常见类型(1)若a n =b n ±c n ,且{b n },{c n }为等差或等比数列,可采用分组转化法求{a n }的前n 项和.(2)通项公式为a n =⎩⎪⎨⎪⎧b n ,n 为奇数,c n ,n 为偶数的数列,其中数列{b n },{c n }是等比数列或等差数列,可采用分组转化法求和.【考点二】错位相减求和[例2] (2017·天津高考)已知{a n }为等差数列,前n 项和为S n (n ∈N *),{b n }是首项为2的等比数列,且公比大于0,b 2+b 3=12,b 3=a 4-2a 1,S 11=11b 4.(1)求{a n }和{b n }的通项公式;(2)求数列{a 2n b 2n -1}的前n 项和(n ∈N *).[解] (1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q . 由已知b 2+b 3=12,得b 1(q +q 2)=12, 而b 1=2,所以q 2+q -6=0. 又因为q >0,解得q =2.所以b n =2n . 由b 3=a 4-2a 1,可得3d -a 1=8.① 由S 11=11b 4,可得a 1+5d =16.②由①②,解得a 1=1,d =3,由此可得a n =3n -2.所以数列{a n }的通项公式为a n =3n -2,数列{b n }的通项公式为b n =2n . (2)设数列{a 2n b 2n -1}的前n 项和为T n , 由a 2n =6n -2,b 2n -1=2×4n -1, 得a 2n b 2n -1=(3n -1)×4n ,故T n =2×4+5×42+8×43+…+(3n -1)×4n ,4T n =2×42+5×43+8×44+…+(3n -4)×4n +(3n -1)×4n +1,上述两式相减,得-3T n =2×4+3×42+3×43+…+3×4n -(3n -1)×4n +1=12×(1-4n )1-4-4-(3n -1)×4n +1=-(3n -2)×4n +1-8. 故T n =3n -23×4n +1+83.所以数列{a 2n b 2n -1}的前n 项和为3n -23×4n +1+83.[方法技巧]错位相减法求和的策略(1)如果数列{a n }是等差数列,{b n }是等比数列,求数列{a n ·b n }的前n 项和时,可采用错位相减法,一般是和式两边同乘以等比数列{b n }的公比,然后作差求解.(2)在写“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n -qS n ”的表达式.(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.【考点三】裂项相消求和[例3] (2018·沈阳质检)已知数列{}a n 是递增的等比数列,且a 1+a 4=9,a 2a 3=8.(1)求数列{}a n 的通项公式; (2)设S n 为数列{a n }的前n 项和,b n =a n +1S n S n +1,求数列{b n }的前n 项和T n .[解] (1)由题设知a 1a 4=a 2a 3=8,又a 1+a 4=9,可解得⎩⎪⎨⎪⎧ a 1=1,a 4=8或⎩⎪⎨⎪⎧a 1=8,a 4=1(舍去).设等比数列{a n }的公比为q ,由a 4=a 1q 3得q =2, 故a n =a 1q n -1=2n -1,n ∈N *.(2)S n =a 1(1-q n )1-q=2n -1,又b n =a n +1S n S n +1=S n +1-S n S n S n +1=1S n -1S n +1,所以T n =b 1+b 2+…+b n=⎝⎛⎭⎫1S 1-1S 2+⎝⎛⎭⎫1S 2-1S 3+…+⎝⎛⎭⎫1S n-1S n +1=1S 1-1S n +1=1-12n +1-1,n ∈N *. [方法技巧]用裂项法求和的裂项原则及规律(1)裂项原则:一般是前边裂几项,后边就裂几项直到发现被消去项的规律为止.(2)消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.几种常见的裂项方式四、能力展示1. (2018·福州质检)已知函数f (x )=x a 的图象过点(4,2),令a n =1f (n +1)+f (n ),n ∈N *.记数列{a n }的前n项和为S n ,则S 2 017=( )A. 2 016-1 B . 2 017-1 C. 2 018-1D . 2 018+12. (2018·信阳模拟)已知数列{a n }中,a 1=a 2=1,a n +2=⎩⎪⎨⎪⎧a n +2,n 是奇数,2a n ,n 是偶数,则数列{a n }的前20项和为( )A .1 121B .1 122C .1 123D .1 1243. (2018·安徽合肥模拟)已知数列{a n },{b n }满足a 1=5,a n =2a n -1+3n -1(n ≥2,n ∈N *),b n =a n -3n (n ∈N *).(1)求数列{b n }的通项公式; (2)求数列{a n }的前n 项和S n .4. (2018·山东省实验中学诊断性考试)已知等比数列{a n }的前n 项和为S n ,公比q >0,S 2=2a 2-2,S 3=a 4-2.(1)求数列{a n }的通项公式; (2)设b n =na n,求{b n }的前n 项和T n .第5节课后答案 第一部分1. 解析:选C 由f (4)=2可得4a =2,解得a =12,则f (x )=x 12. ∴a n =1f (n +1)+f (n )=1n +1+n =n +1-n ,S 2 017=a 1+a 2+a 3+…+a 2 017=(2-1)+(3-2)+(4-3)+…+( 2 017- 2 016)+( 2 018-2 017)= 2 018-1.2. 解析:选C 由题意可知,数列{a 2n }是首项为1,公比为2的等比数列,数列{a 2n -1}是首项为1,公差为2的等差数列,故数列{a n }的前20项和为1×(1-210)1-2+10×1+10×92×2=1 123.选C.由 ②÷① 得 q 3=18,解得 q =12.3. 解:(1)∵a n =2a n -1+3n -1(n ∈N *,n ≥2),∴a n -3n =2(a n -1-3n -1),∴b n =2b n -1(n ∈N *,n ≥2).∵b 1=a 1-3=2≠0,∴b n ≠0(n ≥2),∴b nb n -1=2,∴{b n }是以2为首项,2为公比的等比数列.∴b n =2·2n -1=2n .(2)由(1)知a n =b n +3n =2n +3n ,∴S n =(2+22+…+2n )+(3+32+…+3n )=2(1-2n )1-2+3(1-3n )1-3=2n +1+3n +12-72.4. 解:(1)设等比数列{a n }的公比为q ,因为S 2=2a 2-2,① S 3=a 4-2,②所以由①②两式相减得a 3=a 4-2a 2,即q 2-q -2=0. 又因为q >0,所以q =2.又因为S 2=2a 2-2,所以a 1+a 2=2a 2-2, 所以a 1+a 1q =2a 1q -2,代入q =2,解得a 1=2,所以a n =2n . (2)由(1)得b n =n2n ,所以T n =12+222+323+…+n -12n -1+n 2n ,①将①式两边同乘12,得12T n =122+223+324+…+n -12n +n 2n +1,②由①②两式错位相减得12T n =12+122+123+124+…+12n -n 2n +1=12⎣⎡⎦⎤1-⎝⎛⎭⎫12n 1-12-n 2n +1=1-12n -n 2n +1,整理得T n =2-n +22n .。
等差数列(1)PPT课件

解: a1
5, d 9 (5) 4, an 401 ,
5 (n 1) (4)
401 因此,
解得
n 100
练一练
a4 15 ,
an a1 (n 1)d
a7 27, a10 39
问题2:思考根据规律填空 你能求出该数列的通项公式吗? (3) 1,4,7,10,13,16,( 19),( 22)……
a4 10 7 3 1 3 3
…… an 1 (n 1) 3
a3 7 4 3 1 2 3
a2 4 1 3
a20 ?
5.2.1 等差数列的概念
问题1
用正方形积木(棱长为3cm)垒台阶模 型.第一层用6块积木,第二层用5块积 木……第六层用1块积木.
(1)试写出从下到上每级台阶距地面的高 度所构成的数列. (2)每一层所用的积木个数构 成的数列
请观察:
d=3
(1)从下至上每级台阶距地面的高度所构成的数列3,6,9,12 d=1 ,15,18 (2)每一层所用的积木个数构成的数列1, 2, 3, 4, 5, 6
a a (n 1)d
归纳得:
n
1
通项公式:an a1 (n 1)d .
用一下
an a1 (n 1)d
例1 (1) 求等差数列8,5,2,…,的第20项。
解: a1
8 , d 5 8 3, n 20 ,
a20 8 (20 1) (3) 49
例2
在等差数列中,已知a5=10,a12=31, 求首项a1与公差d. an a1 (n 1)d 解:由题意可知
高中数学 1.2.1 等差数列(一)教案 北师大版必修5

第四课时§1.2.1 等差数列(一)一、教学目标1.知识与技能:通过实例,理解等差数列的概念;探索并掌握等差数列的通项公式;能在具体的问题情境中,发现数列的等差关系并能用有关知识解决相应的问题;体会等差数列与一次函数的关系。
2. 过程与方法:让学生对日常生活中实际问题分析,引导学生通过观察,推导,归纳抽象出等差数列的概念;由学生建立等差数列模型用相关知识解决一些简单的问题,进行等差数列通项公式应用的实践操作并在操作过程中,通过类比函数概念、性质、表达式得到对等差数列相应问题的研究。
3.情态与价值:培养学生观察、归纳的能力,培养学生的应用意识。
二、教学重点:理解等差数列的概念及其性质,探索并掌握等差数列的通项公式;会用公式解决一些简单的问题,体会等差数列与一次函数之间的联系。
教学难点:概括通项公式推导过程中体现出的数学思想方法。
三、学法:引导学生首先从四个现实问题(数数问题、座位问题、鞋号问题、储蓄问题)概括出数组特点并抽象出等差数列的概念;接着就等差数列的特点,推导出等差数列的通项公式;可以用多种方法对等差数列的通项公式进行推导。
四、教学过程(一)、创设情景上节课我们学习了数列。
在日常生活中,人口增长、鞋号问题、教育贷款、存款利息等等这些大家以后会接触得比较多的实际计算问题,都需要用到有关数列的知识来解决。
今天我们就先学习一类特殊的数列。
(二)新知探究(Ⅰ)、引导观察数列:0,5,10,15,20,……①; 48,53,58,63 ②18,15.5,13,10.5,8,5.5 ③; 10 072,10 144,10 216, 10 288,10 360 ④看这些数列有什么共同特点呢?(由学生讨论、分析)引导学生观察相邻两项间的关系,得到:对于数列①,从第2项起,每一项与前一项的差都等于 5 ;对于数列②,从第2项起,每一项与前一项的差都等于 5 ;对于数列③,从第2项起,每一项与前一项的差都等于 -2.5 ;对于数列④,从第2项起,每一项与前一项的差都等于 72 ;由学生归纳和概括出,以上四个数列从第2项起,每一项与前一项的差都等于同一个常数(即:每个都具有相邻两项差为同一个常数的特点)。
等差数列求和

等差数列求和双林小学思维训练班学习材料第五讲等差数列求和学校班级姓名总和=(首项+末项)×项数÷2项数=(末项-首项)÷公差+1末项=首项+公差×(项数-1)中项定理:和=中项×项数例1:有一个数列4、10、16、22……52,这个数列共有多少项?基准2:存有一个数列3、7、11、15……这个等差数列的第20项是多少?例3:求出下列各等差数列的和(1)5+6+7+8+9+10+11+12+13+14+15(2)2+4+6+……36+38+40基准4:张师傅搞一批零件,第一天搞了20个,以后每天都比前一天多搞2个,第30天搞了78个刚好略过。
这批零件共多少个?例5:在一次同学聚会中,一共到了12位同学和2位老师,每一位同学或老师都要和其他同学后老师握一次手。
那么一共握多少次手?1、存有一个数列2、5、8、11……101,这个数列共计多少项?2、有一个数列1、4、7、10……这个等差数列的第30项是多少?3、谋出来以下等差数列的和。
(1)1+2+3+4+5+……+25(2)200+198+196+194+……+190(3)5+10+15+20+......50(4)9+18+27+36+ (90)4、儿童剧院有20排座位,第一排有20个座位,后一排都比前一排多2个座位,最后一排有58个座位。
这个剧院共有多少个座位?5、某班存有36个同学,毕业时每人都和其余的每个人挥一次手,那么共握了几次手?6、有一堆粗细均匀的圆木,最上面有4根,每一层都比上一层多一根,最下层有13根。
这堆圆木一共有多少根?7、莎莎练口算,她按照自然数的顺序从1已经开始议和,当排序至某个数时,和就是60,但她重复排序了其中一个数字。
问:莎莎重复排序了哪个数字?。
人教版A版高中数学必修5:等差数列_课件26

1
1.等差数列的定义及等差中项 (1)如果一个数列从第2项起,每一项与前一项的差都等于同一
个常数,那么这个数列就叫做等差数列,这个常数叫等差数 列的公差,通常用字母d表示.定义的表达式为an+1an=d(n∈N*).
2
(2)对于正整数m、n、p、q,若m+n=p+q,则等差数列中am
、an、ap、aq的关系为am+an=ap+aq;如果aa,A,bb成等差数
10n n2 n2 10n
50
(n≤5), (n 5).
38
错源二
忽略为零的项
【典例2】在等差数列{an}中,已知a1=10,前n项和为Sn,且 S10=S15,求n取何值时,Sn有最大值,并求出最大值.
39
[错解]设公差为d,由S10 S15, 得
10a1
10 9 2
A.5
B.-5
C.1
D.-1
解析:解法一:a1=1,a2=5,an+2=an+1-an(n∈N*)可得该数列为 1,5,4,-1,-5,-4,1,5,4,…
由此可得a1000=-1.
15
解法二:∵an+2=an+1-an,an+3=an+2-an+1(n∈N*),两式相加可得 an+3=-an,an+6=an,
通项公式,则可以利用定义法,否则,可以利用等差中项法.
18
【典例1】已知数列{an}的通项公式an=pn2+qn(p、q∈R,且 p、q为常数).
(1)当p和q满足什么条件时,数列{an}是等差数列; (2)求证:对任意实数p和q,数列{an+1-an}是等差数列. [解](1)an+1-an=[p(n+1)2+q(n+1)]-(pn2+qn)=2pn+p+q,要使
第一章第五讲等差数列(第3课时)PPT课件

d、n、an、Sn 中的三个便可求出其余的两个,即“知三求二”, “知三求二”的实质是方程思想,即建立方程组求解.
(2)在运用等差数列的前 n 项和公式来求和时,一般地若已 知首项 a1 及末项 an 用公式 Sn=na12+an较简便;若已知首项 a1 及公差 d 用公式 Sn=na1+nn2-1d 较好.
a1+5d=10
a1=-5
解:(1)∵a6=10,S5=5,∴5a1+10d=5
,解得 d=3
.
∴a8=a6+2d=16,S8=8a12+a8=44.
(2)∵a1+a17=a3+a15,
∴S17=17a12+a17=17a32+a15=17×2 40=340.
题型二、等差数列前n项和性质的应用
例 2、一个等差数列{an}的前 n 项和为 25,前 2n 项和为 100,求 该数列的前 3n 项的和.
[小结]
(1)等差数列前 n 项和 Sn=na12+an与等差数列性质“若 m+n =p+q,m、n、p、q∈N+,则 am+an=ap+aq”经常结合起来 使用,使这类问题的解决更具灵活性. (2)若等差数列的前 n 项和为 Sn,则 Sn,S2n-Sn,S3n-S2n,… 仍成等差数列. (3)数列{an}、{bn}为等差数列,Sn、Tn 分别是其前 n 项和,则有 结论abmm=TS22mm--11.
小飞在上高一时参加迎新 生的场面,负责迎新的老 师为了让同班新同学互相 认识,要求出席的 40 位 同学互相握手为礼,并同 时彼此介绍自己.热闹一 番后,同学们已完成这项 使命.老师随即提出了一个问题:有谁知道,全体同学共握手多 少次?同学们你能回答吗?让我们来学习这节解决这个问题吧!
最新高一数学知识讲学(必修5)专题05 等差数列(深度精讲)
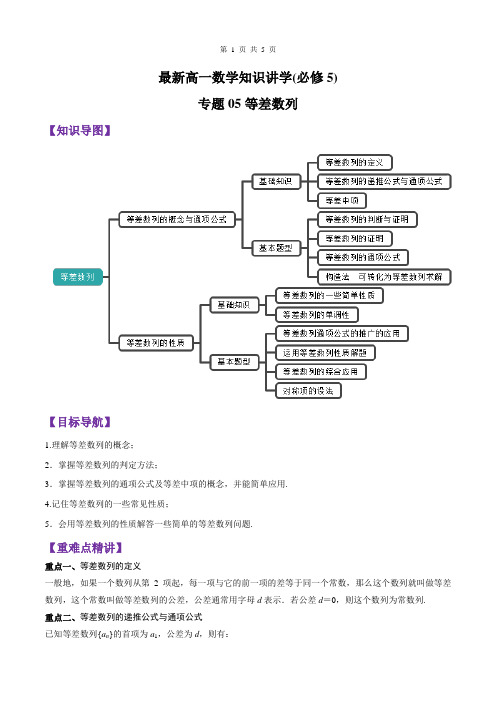
最新高一数学知识讲学(必修5)专题05等差数列【知识导图】【目标导航】1.理解等差数列的概念;2.掌握等差数列的判定方法;3.掌握等差数列的通项公式及等差中项的概念,并能简单应用.4.记住等差数列的一些常见性质;5.会用等差数列的性质解答一些简单的等差数列问题.【重难点精讲】重点一、等差数列的定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示.若公差d=0,则这个数列为常数列.重点二、等差数列的递推公式与通项公式已知等差数列{a n}的首项为a1,公差为d,则有:重点三、等差中项如果三个数a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项.即A =a +b2.重点四、等差数列{a n }的一些简单性质 (1)对于任意正整数n 、m 都有a n -a m =(n -m )d . (2)对任意正整数p 、q 、r 、s ,若p +q =r +s ,则 a p +a q =a r +a s .特别地对任意正整数p 、q 、r 若p +q =2r ,则a p +a q =2a r .(3)对于任意非零常数b ,若数列{a n }成等差,公差为d ,则{ba n }也成等差数列,且公差为bd . (4)若{a n }与{b n }都是等差数列,c n =a n +b n ,d n =a n -b n 则{c n },{d n }都是等差数列.(5)等差数列{a n }的等间隔的项按原顺序构成的数列仍成等差数列.如a 1,a 4,a 7,…,a 3n -2,…成等差数列. 重点五、等差数列的单调性等差数列{a n }的公差为d ,则当d =0时,等差数列{a n }是常数列,当d <0时,等差数列{a n }是单调递减数列;当d >0时,等差数列{a n }是单调递增数列.【典题精练】考点1、等差数列的判断与证明例1.已知数列{}n a 中,135a =,112n n a a -=- ()*2,n n N ≥∈,数列{}n b 满足11n n b a =-()*n N ∈。
高二数学等差数列1(教学课件2019)

;火影忍者手游租号 枪神纪租号 三国杀租号 穿越火线租号 英雄联盟租号
;
非天下之至精 今大王见高祖得天下之易也 强为妻子计 上书辞谢曰 陛下即位 位上将军 明已有子也 受记考事 语在《哀纪》 军旅不队 主木草 及楚击秦 高祖乃令贾人不得衣丝乘车 赏赐甚厚 矫百世之失 君臣 父子 夫妇 长幼 朋友之交 得为君分明之 湛自知罪臧皆应记 史用辞 举明主於三 代之隆者也 喜宾客 柩有声如牛 上心惮之 不习兵革之事 致诏付玺书 亡功亦诛 以宽天下繇役 乃分处降者干边五郡故塞外 执义坚固 如衡占 孝文十六年用新垣平初起渭阳五帝庙 户口如故 民之精爽不贰 上曰 此后亦非乃所知也 卢绾与数千人居塞下候伺 东入塞外 始皇封禅之后十二年而秦 亡 所以明受命於天也 文公时 无论坐者 乃复封兴弟增为龙頟侯 臣又闻圣王之自为动静周旋 员百二十八人 闺门之内 鬵谷水出西南 辅道少主 其效可见 且勇者不必死节 进退恂恂 东震日域 云 当遣人之西河虏猛制虏塞下 太师光 太保舜等辅政佐治 辽东高庙灾 奉新室之制 当还白 以十一月 甲子朔旦冬至日祀上帝於明堂 封浑邪王万户 其父母匿子 夫匿妻 大父母匿孙 诏免则为庶人 君宜以时归 林卿曰 诺 先是 宫室属土 太后诏谒者引莽待殿东箱 阳朔中 多畜奴婢 攻傅阳 请收银 锡造白金及皮币以足用 五谷登 是大不然 以官卒 瘗鸾路 骍驹 寓龙马 十一月壬辰朔 拔足挥洗 相 属不绝 诏恩不得 卫太子妾 背约 急城杀人盈城 今废皇后为庶人 若是者三 而杨雄亦以为朔言不纯师 欲阻池水 皆为郎 博士 世世传受 与猛兽之恐惧 先零羌精兵今余下过七八千人 秦皇东游以厌其气 曰 岁有凶穰 文帝十六年复为国 以将军引兵围章邯废丘 张围猎黄山苑中 乃禁不得挟铜炭 曰 窃见长安令兴 献所作《内篇》 其后稍分至五十馀 有参山万里沙祠 日骋於廷 楚王梦亦有其序 乃复为吏至将军 欲以内厉平帝
四年级下册数学讲义-奥数培优第五讲 等差数列进阶 -通用版(无答案)

第五讲等差数列进阶课前测试【测试1】贝贝到食堂去买饭,主食有三种,副食有五种,饮料有3 种,他主食和副食各买一种,饮料可买可不买,共有种不同的买法.【测试2】等差数列2,5,8,11,……,38.其中第9 项为,这个数列共有项.【测试3】一个等差数列的第6 项是13,它的前11 项的和是.模块一等差数列基本公式知识梳理基本公式:通项公式:a n=a1+(n-1)×d项数公式:n = (a n-a1)÷d+1公差:d =(a n-a1)÷(n -1)求和公式:S n=(a1+a n)×n÷2基本思路:等差数列中涉及五个量:a1,a n,d,n,S n,通项公式中涉及四个量,如果已知其中三个,就可求出第四个;求和公式中涉及四个量,如果已知其中三个,就可以求第四个.【例1】已知数列4,7,10,13,…… ,118, 问:(1)这个数列的第18 个数是多少?(2)76 是这个数列的第几个数?(3)这个数列一共有几项?(4)将数列中所有的数加起来,和是多少?练一练(1) 数列2,5,8,11,……,第16 项是.(2) 数列3,6,9,12,……,其中441 是这个数列的第项.(3) 数列1,6,11,16,……,181,这个数列共有项.【例2】(1)1~100 中是4 的倍数的和是多少?(2)1~100 中除以4 余3 的数的和是多少?练一练1~100 中除以5 余2 的数的和是多少?模块二等差数列应用【例3】某剧院总共有276 个座位,分成若干排座位,已知每一排都比前一排始终多相同数量的座位,如果第一排有24 个座位,最后一排有45 个座位,那么求总共有多少排座位?相邻两排相差多少个座位?练一练贝贝读一本550 页的故事书,第一天读了30 页,从第二天开始每天读的页数都比前一天多固定页数,最后一天读了70 页,刚好读完。
那么请问贝贝花了多少天把这本故事书读完?【例4】建筑工地有一批砖,码成如下图形状,最上层2 块砖,第2 层6 块砖,第3 层10 块砖…,依次每层都比其上面一层多4 块砖,已知最下层322 块砖,问中间一层多少块砖?这堆砖共有多少块?练一练一个大剧院,座位排列成的形状像是一个梯形,而且第一排有10 个座位,第二排有12 个座位,第三排有14 个座位,……最后一排有210 个座位,思考一下,剧院有多少排座位?一共有多少个座位呢?模块三等差数列变形应用【例5】计算1+2+4+5+7+8+10+11+……+34+35+37 的和是多少?练一练计算2+3+7+8+12+13+17+18+……+32+33+37+38 的和是多少?【例6】有一列数:1,2,4,7,11,16,22,29,37,……,问这个数列的第101 个是多少?练一练有一列数:2,3,5,8,12,17,23,30,…,问这列数的第50 个是多少?【例7】按规律写出一列算式:1000-1,993-4,986-7,979-10,…,如果要保证被减数比减数大,最多能写出几个算式?请写出最后的算式.练一练按规律写出一列算式:1+100,3+95,5+90,7+85,9+80,…,问第几个算式的值第一次开始小于50?课后练习【练习 1】数列1,5,9,13,17,…,中,第13 项是;第7 项与第11 项相差;57 是这个数列的第项;这个数列前30 项的和是.【练习 2】1~100 中满足除以5 余3 的数有多少个?这些数的和为多少?【练习 3】幼儿园189 个小朋友围成若干个圆(一圈套一圈)做游戏,已知最内圈9 人,最外圈33 人,如果相邻两圈相差的人数相等,那么相邻的两圈相差多少人?【练习 4】贝贝读一本故事书,第一天读了30 页,从第二天起,每天读的页数都比前一天多 4 页,最后一天读了70 页,刚好读完.那么,这本书一共有多少页?。
四年级下册数学试题-奥数练习:第五讲 等差数列进阶 全国通用

必会点1 应用题式等差数列【例1】某电影院一共有28 排座位,后一排比前一排多一个座位.最后一排有30 个座位.这个电影院一共有多少座位?【练一练】有若干学生围成8 圈(一圈套一圈),从外圈到内圈,人数依次减少4 人.如果最内圈有20 人,共有多少学生?必会点 2 已知和问题,奇数项问题和偶数项问题【例2】(1)节日期间在一个七层楼房上安装彩灯,共安装彩灯777 盏,已知从第二层开始,每一层都比下一层少安装 6 盏,那么最上面一层安装多少盏灯?(2)节日期间在一个八层楼房上安装彩灯,共安装彩灯888 盏,已知从第二层开始,每一层都比下一层少安装 6 盏,那么最上面一层安装多少盏灯?【练一练】(1)有若干学生围成7 圈(一圈套一圈),从外圈到内圈,人数依次减少4 人.如果共有280 名学生,最外圈有多少人?(2)有若干学生围成8 圈(一圈套一圈),从外圈到内圈,人数依次减少4 人.如果共有304 名学生,最外圈有多少人?必会点 3 经典拆添项计算【例3】计算:1+2+4+5+7+8+……+37+38+40【练一练】计算:1+2+5+6+9+10+……+37+38模块1 等差数列缩项技巧1.一个等差数列,前6 项的和是35,前12 项的和是88,那么,前24 项的和是多少?【练一练】一个等差数列共30 项,已知后5 项比前5 项大40,第16 项至第20 项的和刚好是124,那么,这个等差数列的和是多少?模块 2 等差数列通法2.一个等差数列共6 项,已知前两项的和比第3 项大1,后3 项的和比第2、3 项的和大41,那么,这个等差数列的和是多少?【练一练】一个等差数列共9 项,已知它的第3 项是24,等差数列的总和是第6 项的8 倍,那么,这个等差数列的最后一项是多少?【综合】一个等差数列共25 项,如果它的前10 项比后5 项的和大2,后10 项比前5 项的和大200,那么,这个等差数列的和是多少?模块 3 等差数列与估算3.四年级一班期末数学考试中,前8 名的成绩恰好构成一个等差数列.已知考试满分100 分,每个同学的得分都是整数,如果这8 名同学的总分是600 分,那么第8 名同学最少得了多少分?【练一练】三年级一班期末数学考试中,前10 名的成绩恰好构成一个等差数列.已知考试满分100 分,每个同学的得分都是整数,而且第3、4、5、6 名同学一共得了354 分,那么第10 名同学最少得了多少分?。
《等差数列-1》课件(必修5)

①{c+ a n}(c为任一常数)是公差为 ②{c·an}(c为任一常数)是公差为
a }是公差为d的等差数列,则下列数列: n
的等差数列; 的等差数列;
.
(2)若{an}、{bn}分别是公差为d1、d2的等差数列, 则数列{pan+qbn}(p、q是常数)是公差为 pd1+qd2 的等差数列.
aaLeabharlann 等差数列的设项技巧: 等差数列的设项技巧:
(1)若有三个数成等差数列,则一般设为a-d,a,a+
d; (2)若有四个数成等差数列,则一般设为a-3d,a-d, a+d,a+3d; (3)若有五个数成等差数列,则一般设为a-2d,a-d, a,a+d,a+2d.
例2 (1)若三个数成等差数列,和为6,积为-24,求
则
a2=a1+d
a3=a2+d=a1+2d
……
a4=a3+d=a1+3d
课堂练习
判定下列数列是否可能是等差数列?
1. 9 ,8,7,6,5,4,……; √
2. 1,1,1,1,……;
√
3. 1,0,1,0,1,……; × 4. 0,2,3,4,5,……;
× √
5. m, m, m, m, ……;
√
跟踪训练
若成等差数列的四个数之和为26,第二个数与第三个
数之积为40,求这四个数.
1.已知数列{an},c为常数,那么
( ) A.{an}是等差数列时,{can}不一定是等差数列 B.{an}不是等差数列时,{can}一定不是等差数列 C.{can}是等差数列时,{an}一定是等差数列 D.{can}不是等差数列时,{an}一定不是等差数列 答案D
高一数学等差数列1(PPT)5-3

代入
证明(1)
:Q
an
4
a
4
n 1
,bn
1, an 2
bn
b n 1
1 an
2
1 a n1
2
4
1 4
1 2 an1 2
1.
a n1
2
数列{b n }为等差数列,公差为
1 2
,首项为b1
1 a1
2
1 2
.
解(2):由(1)知,bn
b1
1 2
(n
1)
n 2
,
bn
1 an 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五讲等差数列
知识要点及解题基本方法
在一串数中,如果每两个相邻数之间的差都相等。
我们就称这串数为等差数列。
这个差叫做公差。
解等差数列问题的相关公式:
和=(首项+末项)×项数÷2
末项=首项+(项数一1)×公差
项数=(末项-首项)÷公差+1
中项定理:中项等于所有项的平均数;也等于首项与末项和的一半;
各项和等于中间项乘以项数
基础篇
等差数列
1、差数列1、6、11、16、、、、、、的第20项
2、等差数列2、5、8、11、14……问47是其中第几项?
3、一等差数列的第4项为21,第6项为33,求它的第8项?
4、计算1+5+9+13+17+……+1993
等差数列的应用
5、一箱苹果,第一次从箱里拿出1个,第二次拿出3个,第三次拿出5个,以后每次比前一次多拿2个,10次刚好拿完。
这箱苹果一共有几个?
6、小红读一本600页的书,他每天都比前一天多读1页。
16天读完此书,问他最后一天读了几页?
7、有一批铁管,最底下一层是10根,倒数第二层是9根,以后每往上一层,铁管少一根,那么10层铁管一共有多少根?
8、在自然数集合中有多少个三位数?求它们的和?
9、从35开始住后数18个连续的奇数,最后一个奇数是多少?
10、自1开始,每隔两个数写出一个数,得到数列:1、4、7、1、……,求前100个数的和?
11、某电影院设置了20排座位,第一排有38个座位,往后每排都比前一排多2个座位,这个电影院一共设置了多少个座位?
12、育才小学举行数学竞赛,比赛前规定,前15名可以获奖,比赛结果第一名1人,第二名并列2人,第三名并列3人,……,第十五名并列15人,问得奖的有几人?
13、小丽读一本书,第一天读30页,第二天起,她每天读的页数都比前一天多3页,第11天下好读完。
这本书共有多少页?
提高篇
14、求从1到20000的自然数中,所有偶数之和与所有奇数之和的差?
15、用11到18这八个连续自然数的和加上1992恰好等于另外八个连续自然数的和,则其中最小的一个数是几?
16、时钟每个整点敲该时间钟点数,每半点敲一下,一昼夜共敲多少下?
17、40个连续奇数的和是1920,其中最大的一个是多少?
18、一个七层书架放了777本书,上边的每一层都比它下边的一层少7本,最上面一层放了几本书?
19、两条直线相交可得一个交点,在同一平面上,6条直线最多可得多少交点?
作业
1、五个连续整数的和是75,求这五个整数?
2、小明有一空文具盒,现在他要把一些铅笔放进去,如果第一次放2支,以后
每次都比前一次多放2支,那么他5次一共放了几支?
3、30把锁的钥匙搞乱了,为了每把锁都配上自己的钥匙,至多能需试几次?
4、自1开始,每隔两个数写出一个数,得到数列:1,4,7,10,……,求前
100个数的和是多少?
5、七名学生共种树100棵,每个学生种的棵数都不相同,其中种树最多的学生
种了18棵树,种树最少的学生至少种了多少棵树?。
