上海历年中考数学压轴题复习
上海历年中考数学压轴题复习(试题附答案)

上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即yxx +=-252,得225212-+-=x x y ,1<x <4.②AP=2或AP=3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7 探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =22.5°,∠APB =90°-22.5°=67.5°, ∠ABP =180°-(45°+67.5°)=67.5°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD中,AB=1,弧AC是点B为圆心,AB长为半径的圆的一段弧。
上海历年中考数学压轴题复习试题附答案

上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程). 27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即y xx +=-252,得225212-+-=x x y ,1<x <4.②AP =2或AP =3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q .图567探究:设A 、P 两点间的距离为x .(1)当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系?试证明你观察得到结论; (2)当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域;(3)当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置,并求出相应的x 的值;如果不可能,试说明理由. (图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用) 五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分) 27.图1 图2 图3??(1)解:PQ =PB……………………(1分)证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1). ∴NP =NC =MB . ……………………(1分)∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.?而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴PQ =PB .(2)解法一由(1)△QNP ≌△PMB .得NQ =MP .∵AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分)S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分)S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1.即y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形. ∴PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN(2分)????=CN 2=(1-x 22)2=21x 2-x 2+1 ∴y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, ?此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分)解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分)解法二 此时∠CPQ =21∠PCN =22.5°,∠APB =90°-22.5°=67.5°, ∠ABP =180°-(45°+67.5°)=67.5°,得∠APB =∠ABP , ∴AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD 中,AB =1,弧AC 是点B 为圆心,AB 长为半径的圆的一段弧。
上海市中考数学压轴题总复习(附答案解析)

2021年上海市中考数学压轴题总复习
中考数学压轴题是想获得高分甚至满分必须攻破的考题,得分率低,需要引起重视。
从近10年中考压轴题分析可得中考压轴题主要考查知识点为二次函数,圆,多边形,相似,锐角三角形等。
预计2021年中考数学压轴题依然主要考查这些知识点。
1.如图1,在平而直角坐标系中,直线/:y =勃+m与x轴、y轴分别交于点.4和点
(2)点。
在抛物线上,且点。
的横坐标为f(0Vf<4). 轴交直线/于点£点产在直线/上,且四边形。
FEG为矩形(如图2).若矩形。
尸EG的周长为p,求°与,的函数关系式以及R的最大值:
(3)M是平面内一点,将A4O8绕点M沿逆时针方向旋转90°后,得到△川。
山1,点
A.。
、B的对应点分别是点由、。
1、51.若入41。
1历的两个顶点恰好落在抛物线上,请直
接写出点出的横坐标.
2.已知,抛物线y=aF+Gr+6 (。
#0)与直线y=2rb〃有一个公共点Af (1, 0),且a〈b.
(1)求6与。
的关系式和抛物线的顶点。
坐标(用。
的代数式表示):
(2)直线与抛物线的另外一个交点记为N,求AOMV的面积与。
的关系式:
(3)々=-1时,直线y=-2x与抛物线在第二象限交于点G,点G、H关于原点对称,
现将线段GH沿y轴向上平移,个单位(r>0),若线段GH与抛物线有两个不同的公共点,试求,的取值范围.。
上海历年中考数学压轴题复习(试题附答案)

上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即yxx +=-252,得225212-+-=x x y ,1<x <4.②AP=2或AP=3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7 探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =22.5°,∠APB =90°-22.5°=67.5°, ∠ABP =180°-(45°+67.5°)=67.5°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD中,AB=1,弧AC是点B为圆心,AB长为半径的圆的一段弧。
上海历年中考数学压轴题复习(试题附答案)

上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即yxx +=-252,得225212-+-=x x y ,1<x <4.②AP=2或AP=3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7 探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =22.5°,∠APB =90°-22.5°=67.5°, ∠ABP =180°-(45°+67.5°)=67.5°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD中,AB=1,弧AC是点B为圆心,AB长为半径的圆的一段弧。
上海中考数学压轴题汇总—25题(2012-2021)-真题

2012-2021年上海中考数学真题解答题第25题201225.(本题满分14分,第(1)小题满分3分,第(2)小题满分5分,第(3)小题满分6分)如图,在半径为2的扇形AOB 中,∠=90AOB,点C 是弧AB 上的一个动点(不与点A 、B 重合)OD ⊥BC ,OE ⊥AC ,垂足分别为D 、E .(1)当=1BC 时,求线段OD 的长;(2)在△DOE 中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;(3)设=BD x ,△DOE 的面积为y ,求y 关于x 的函数关系式,并写出它的定义域.公众号:奥孚升学孚升学公众号:奥孚:奥孚升学众号公众号:奥孚升公众号:奥孚升学孚升学公众号:奥孚升学众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:201325.在矩形ABCD 中,点P 是边AD 上的动点,联结BP ,线段BP 的垂直平分线交边BC 于点Q ,垂足为点M ,联结QP (如图10).已知13AD =,5AB =,设AP x BQ y ==,.(1)求y 关于x 的函数解析式,并写出x 的取值范围;(2)当以AP 长为半径的⊙P 和以QC 长为半径的⊙Q 外切时,求x 的值;(3)点E 在边CD 上,过点E 作直线QP 的垂线,垂足为F ,如果4EF EC ==,求x的值.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升孚升学公众号:奥孚升公众公众号:奥孚升学号:奥孚升学公众号:奥孚公众号:奥孚升公众号:奥孚升学图10备用图公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升公众号:奥孚升学公众号公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升公众号:奥孚升学公众号201425.如图,已知在平行四边形ABCD 中,AB=5,BC=8,cosB=45,点P 是边BC 上的动点,以CP 为半径的圆C 与边AD 交于点EF(点F 在点E 的右侧),射线CE 与射线BA 交于点G.(1)当圆C 经过点A 时,求CP 的长;(2)联结AP ,当AP//CG 时,求弦EF 的长;(3)当AGE 是等腰三角形时,求圆C 的半径长.201525.已知,如图,AB 是半圆O 的直径,弦//CD AB ,动点,P Q 分别在线段,OC CD 上,且,DQ OP AP =的延长线与射线OQ 相交于点E ,与弦CD 相交于点F (点F 与点C ,D不重合),420,cos 5AB AOC =∠=设OP x =,CPF 的面积为y .(1)求证:AP OQ =;(2)求y 关于x 的函数关系式,并写出它的定义域;(3)当OPE 是直角三角形时,求线段OP的长.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚公众号201625.如图所示,梯形ABCD 中,AB ∥DC ,90B ∠=︒,15AD =,16AB =,12BC =,点E 是边AB 上的动点,点F 是射线CD 上一点,射线ED 和射线AF 交于点G ,且AGE DAB ∠=∠;(1)求线段CD 的长;(2)如果AEG ∆是以EG 为腰的等腰三角形,求线段AE 的长;(3)如果点F 在边CD 上(不与点C 、D 重合),设AE x =,DF y =,求y 关于x 的函数解析式,并写出x 的取值范围;公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公公众学公众公众号:奥孚升学公众号:奥孚升学学奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号孚公众号201725.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图9,已知O e 的半径长为1,AB 、AC 是O e 的两条弦,且AB AC ,BO 的延长线交AC 于点D ,联结OA 、OC.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升学公众号公众公众号:奥孚升学公众号:奥孚升学升学公众号公众号:(1)求证:OAD ABD V :V ;(2)当OCD V 是直角三角形时,求B 、C 两点的距离;(3)记AOB V 、AOD V 、COD V 的面积分别为1S 、2S 、3S ,如果2S 是1S 和3S 的比例中项,求OD 的长.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:孚升学孚升学奥孚升学公众号:奥孚升学孚公众号:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升学公众号孚升学公众:奥孚升学公众号公众号:奥孚升201825.(14分)已知⊙O 的直径AB=2,弦AC 与弦BD 交于点E .且OD ⊥AC ,垂足为点F .(1)如图1,如果AC=BD ,求弦AC 的长;(2)如图2,如果E 为弦BD 的中点,求∠ABD 的余切值;(3)联结BC 、CD 、DA ,如果BC 是⊙O 的内接正n 边形的一边,CD 是⊙O 的内接正(n +4)边形的一边,求△ACD的面积.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升公众号:奥孚升学公众号公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升公众号:奥孚升学公众号201925.(14分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分6分)如图10,AD 、BD 分别是A4BC 的内角∠BAC 、∠4BC 的平分线,过点A 作AE 上AD ,交BD 的延长线于点E.(1)求证:∠E =21∠C ;(2)如图11,如果AE =AB ,且BD :DE =2:3,求cos ∠ABC 的值;(3)如果∠ABC 是锐角,且△ABC 与△ADE 相似,求∠ABC 的度数,并直接写出ABCADES S △△的值.孚升学公众号:奥孚升公众号:奥孚升学孚升学众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:202025.如图,△ABC 中,AB =AC ,⊙O 是△ABC 的外接圆,BO 的延长交边AC 于点D .(1)求证:∠BAC =2∠ABD ;(2)当△BCD 是等腰三角形时,求∠BCD 的大小;(3)当AD =2,CD =3时,求边BC的长.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号公众号:公众公众号:奥孚升学公众号:奥孚升学公:奥孚升学公众号:奥孚升公众号:孚升学孚升学公众公众公众号:奥孚升学号:奥孚升公众号:奥孚升学202125.如图,在梯形ABCD 中,//,90,,AD BC ABC AD CD O ∠=︒=是对角线AC 的中点,联结BO 并延长交边CD 或边AD 于E .(1)当点E 在边CD 上时,①求证:DAC OBC ∽;②若BE CD ⊥,求ADBC的值;(2)若2,3DE OE ==,求CD 的长.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:学孚升号:奥孚升学公众号:奥孚升学:公众号:奥孚升学公众号:公众号:奥孚孚升学公公众号公众奥孚升学学号:奥孚升孚升学公众号公众号:。
上海中考数学压轴题汇总—24题(2012-2021)-真题

2012-2021年上海中考数学真题解答题第24题201224.(本题满分12分,第(1)小题满分3分,第(2)小题满分5分,第(3)小题满分4分)如图,在平面直角坐标系中,二次函数26y ax x c =++的图像经过点()4,0A 、()1,0B -,与y 轴交于点C ,点D 在线段OC 上,=OD t ,点E 在第二象限,∠=90ADE,1=2tan DAE ∠,EF OD ⊥,垂足为F .(1)求这个二次函数的解析式;(2)求线段EF 、OF 的长(用含t 的代数式表示);(3)当∠ECA =∠OAC 时,求t的值.公众号:奥孚升学公众号:奥孚:奥孚升学公众号:奥孚升学孚升学众号:奥孚升学众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:201324.如图9,在平面直角坐标系xoy 中,顶点为M 的抛物线2(0y ax bx a =+>)经过点A和x 轴正半轴上的点B ,AO OB ==2,0120AOB ∠=.(1)求这条抛物线的表达式;(2)联结OM ,求AOM ∠的大小;公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:孚升学公众号:奥奥孚升学公众公众奥孚升学公众号:奥孚公众号:奥孚升升学公众号公众号:(3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标.图9公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:201424.在平面直角坐标系中(如图),已知抛物线223y x bx c =++与x 轴交于点A (-1,0)和点B ,与y 轴相较于点C (0,-2).(1)求该抛物线的表达式,并写出其对称轴;(2)点E 为该抛物线的对称轴与x 轴的交点,点F 在对称轴上,四边形ACEF 为梯形,求点F 的坐标;(3)点D 为该抛物线的顶点,设点(),0P t ,且3t >,如果BDP 和CDP 的面积相等,求t 的值.公众号:奥孚升学孚升学公众号:奥公众号:奥孚升:奥孚升学公众号学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:201524.已知在平面直角坐标系xOy 中(如图),抛物线24y ax =-与x 轴的负半轴(XRS )相交于点A ,与y 轴相交于点B ,AB=P 在抛物线上,线段AP 与y 轴的正半轴交于点C ,线段BP 与x 轴相交于点D ,设点P 的横坐标为m .(1)求这条抛物线的解析式;(2)用含m 的代数式表示线段CO 的长;(3)当3tan 2ODC ∠=时,求PAD ∠的正弦值.201624.如图,抛物线25y ax bx =+-(0a ≠)经过点(4,5)A -,与x 轴的负半轴交于点B ,与y 轴交于点C ,且5OC OB =,抛物线的顶点为D ;(1)求这条抛物线的表达式;(2)联结AB 、BC 、CD 、DA ,求四边形ABCD 的面积;(3)如果点E 在y 轴的正半轴上,且BEO ABC ∠=∠,求点E的坐标;公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号孚升学公众号:奥孚升学公众号:奥孚升学号:奥孚升学奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:201724.(本题满分12分,每小题满分各4分)已知在平面直角坐标系xOy 中(如图8),已知抛物线2y x bx c =-++经过点()2,2A ,对称轴是直线1x =,顶点为B .(1)求这条抛物线的表达式和点B的坐标;公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号公众号:奥孚升学公众号:奥孚升学公公众号公众:奥孚升学公众号:奥孚升升学公众号公众号:(2)点M 在对称轴上,且位于顶点上方,设它的纵坐标为m ,联结AM ,用含m 的代数式表示AMB ∠的余切值;(3)将该抛物线向上或向下平移,使得新抛物线的顶点C 在x 轴上.原抛物线上一点P 平移后的对应点为点Q ,如果OP OQ =,求点Q 的坐标.行计算、画(作)图行计算、画(作)图计合理、有效的运算途径程,合理解释推理演绎的正确性算、画(作)图公众号升学公众号:奥孚升学:奥孚升学公众号:奥孚升学孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:201824.(12分)在平面直角坐标系xOy 中(如图).已知抛物线y=﹣x 2+bx +c 经过点A (﹣1,0)和点B (0,),顶点为C ,点D 在其对称轴上且位于点C 下方,将线段DC 绕点D 按顺时针方向旋转90°,点C 落在抛物线上的点P 处.(1)求这条抛物线的表达式;(2)求线段CD 的长;(3)将抛物线平移,使其顶点C 移到原点O 的位置,这时点P 落在点E 的位置,公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号奥孚升学公众号:奥孚升学公众号:奥孚升学公公众号:奥孚升学公众号:奥孚升学公众公众孚升学学:奥孚升孚升学公众号众号:如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求点M 的坐标.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:201924.(12分,第(1)小题满分4分,第(2)①小题满分3分,第(2)②小题满分5分)在平面直角坐标系xOy 中(如图9),已知抛物线y =x 2-2x ,其顶点为A.(1)写出这条抛物线的开口方向、顶点A 的坐标,并说明它的变化情况;(2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”①试求抛物线y =x 2-2x 的“不动点”的坐标;②平移抛物线y =x 2-2x ,使所得新抛物线的顶点B 是该抛物线的“不动点”,其对称轴与x 轴交于点C ,且四边形QABC 是梯形,求新抛物线的表达式.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:202024.在平面直角坐标系xOy 中,直线y =﹣12x +5与x 轴、y 轴分别交于点A 、B (如图).抛物线y =ax 2+bx (a ≠0)经过点A .(1)求线段AB 的长;(2)如果抛物线y =ax 2+bx 经过线段AB 上的另一点C ,且BC(3)如果抛物线y =ax 2+bx 的顶点D 位于△AOB 内,求a的取值范围.公众号:奥孚升学公众号:奥孚升:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚升学公众号:奥孚升学公众号公众号:202124.已知抛物线2(0)y ax c a =+≠过点(3,0),(1,4)P Q.公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公公众号:孚升学公众号:奥孚公众公众众号:奥孚升学公众号:奥孚升升学(1)求抛物线的解析式;(2)点A 在直线PQ 上且在第一象限内,过A 作AB x 轴于B ,以AB 为斜边在其左侧作等腰直角ABC .①若A 与Q 重合,求C 到抛物线对称轴的距离;②若C 落在抛物线上,求C的坐标.学公众号:奥孚升学公众号:奥孚升学孚升学升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升公众号:奥孚升学公众号公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥公众号:奥孚升公众号:奥孚升学公众号公众号:奥孚升学孚升学公众号:奥孚升学公众号:奥孚升学:奥孚升学公众号:奥孚升学公众号:奥孚升学公众号:奥孚升公众号:奥孚孚升学公众号:奥孚升学公众号:公众号公众公众号:奥孚升学:奥孚升学公众号:奥孚升公众号:奥孚升学。
上海中考数学压轴题集锦

压轴题集锦2013年2月---2013年6月一.圆背景下的综合题:1.(10金山)如图1,在Rt△ABC中,∠C=90°,AC=BC,D是AB边上一点,E是在AC 边上的一个动点(与点A、C不重合),DF⊥DE,DF与射线BC相交于点F。
(1)如图2,如果点D是边AB的中点,求证:DE=DF;(2)如果AD∶DB=m,求DE∶DF的值;(3)如果AC=BC=6,AD∶DB=1∶2,设AE=x,BF=y,①求y关于x的函数关系式,并写出定义域;②以CE为直径的圆与直线AB是否可相切,若可能,求出此时x的值,若不可能,请说明理由。
图1 图2备用图2 备用图12. (10浦东)如图,已知在矩形ABCD 中,AB =3,BC =4,P 是边BC 延长线上的一点,联接AP 交边CD 于点E ,把射线AP 沿直线AD 翻折,交射线CD 于点Q ,设CP =x ,DQ =y . (1)求y 关于x 的函数解析式,并写出定义域.(2)当点P 运动时,△APQ 的面积是否会发生变化?如果发生变化,请求出△APQ 的面积S 关于x 的函数解析式,并写出定义域;如果不发生变化,请说明理由.(3)当以4为半径的⊙Q 与直线AP 相切, 且⊙A 与⊙Q 也相切时,求⊙A 的半径.A B C Q D P E3. (10青浦)如图,已知△ABC 中,AB=AC=5,BC=4,点O 在BC 边上运动,以O 为圆心,OA 为半径的圆与边AB 交于点D (点A 除外),设OB x =,AD y = . (1)求ABC ∠sin 的值;(2)求y 关于x 的函数解析式,并写出函数的定义域;(3)当点O 在BC 边上运动时,⊙O 是否可能与以C 为圆心,41BC 长为半径的⊙C 相切?如果可能,请求出两圆相切时x 的值;如果不可能,请说明理由.COD BA4. (11松江)如图,在Rt △ABC 中,∠C =90°,AC =4,BC =5,D 是BC 边上一点,CD =3,点P 在边AC 上(点P 与A 、C 不重合),过点P 作PE // BC ,交AD 于点E . (1)设AP =x ,DE =y ,求y 关于x 的函数解析式,并写出x 的取值范围; (2)当以PE 为半径的⊙E 与DB 为半径的⊙D 外切时,求DPE 的正切值;(3)将△ABD 沿直线AD 翻折,得到△AB /D ,联结B /C .如果∠ACE =∠BCB /,求AP 的值.备用图DCBAE P DCBA5. (11浦东)如图,已知在△ABC中,AB=4,BC=2,以点B为圆心,线段BC长为半径的弧交边AC于点D,且∠DBC=∠BAC,P是边BC延长线上一点,过点P作PQ⊥BP,交线段BD的延长线于点Q.设CP=x,DQ=y.(1)求CD的长;(2)求y关于x的函数解析式,并写出它的定义域;(3)当∠DAQ=2∠BAC时,求CP的值.6. (11徐汇)在ABC Rt ∆中,︒=∠90C ,6=AC ,53sin =B ,⊙B 的半径长为1,⊙B 交边CB 于点P ,点O 是边AB 上的动点.(1)如图,将⊙B 绕点P 旋转︒180得到⊙M ,请判断⊙M 与直线AB 的位置关系; (2)如图,在(1)的条件下,当OMP ∆是等腰三角形时,求OA 的长;(3)如图,点N 是边BC 上的动点,如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切,设y NB =,x OA =,求y 关于x 的函数关系式及定义域.BOACPBOACPONBAC7. (12静安)如图,⊙O的半径为6,线段AB与⊙O相交于点C、D,AC=4,∠BOD=∠A,OB与⊙O相交于点E,设OA=x,CD=y.(1)求BD长;O(2)求y关于x的函数解析式,并写出定义域;E (3)当CE⊥OD时,求AO的长.A C D B8. (12黄浦)如图,已知ABC ∆中,90C ∠=︒,AC BC =,6AB =,O 是BC 边上的中点,N 是AB 边上的点(不与端点重合),M 是OB 边上的点,且MN ∥AO ,延长CA 与直线MN 相交于点D ,G 点是AB 延长线上的点,且BG AN =,联结MG ,设AN x =,BM y =.(1)求y 关于x 的函数关系式及其定义域;(2)联结CN ,当以DN 为半径的D 和以MG 为半径的M 外切时,求ACN ∠的正切值; (3)当ADN ∆与MBG ∆相似时,求AN 的长.A B C O NMDG 备用图a A B C O 备用图b ABCO9.(10崇明)已知:如图,直角梯形ABCD 中,AD ∥BC ,︒=∠90B ,8=AB ,12=AD ,34tan =C ,AM ∥DC ,E 、F 分别是线段AD 、AM 上的动点(点E 与A 、D 不重合)且AMB FEM ∠=∠,设x DE =,y MF =. (1)求证:DM AM =;(2)求y 与x 的函数关系式并写出定义域;(3)若点E 在边AD 上移动时, EFM ∆为等腰三角形,求x 的值; (4)若以BM 为半径的⊙M 和以ED 为半径的⊙E 相切,求EMD ∆的面积.AEFDBMC10. (10奉贤)已知,在边长为6的正方形ABCD 的两侧如图作正方形BEFG 、正方形DMNK ,恰好使得N 、A 、F 三点在一直线上,联结MF 交线段AD 于点P ,联结NP ,设正方形BEFG 的边长为x ,正方形DMNK 的边长为y ,(1)求y 关于x 的函数关系式及自变量x 的取值范围; (2)当△NPF 的面积为32时,求x 的值; (3)以P 为圆心,AP 为半径的圆能否与以G 为圆心,GF 为半径的圆相切,若能请求x 的值,若不能,请说明理由。
上海十年中考数学压轴题及复习资料解析

上海十年中考数学压轴题解析2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 及点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴∠ABP =∠DPC .∵在梯形ABCD 中,AD ∥BC ,AB =CD ,∴∠A =∠D .∴△ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPDAP AB =,即252x x -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴DQAPPDAB =.即y xx +=-252,得225212-+-=x x y ,1<x <4.②AP =2或AP =3-5.(题27是一道涉及动量及变量的考题,其中(1)可看作(2)的特例,故(2)的推断及证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边及射线DC 相交于点Q .图1 图2 图3探究:设A 、P 两点间的距离为x .(1)当点Q 在边CD 上时,线段PQ 及线段PB 之间有怎样的大小关系?试证明你观察得到结论;(2)当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 及x 之间的函数解析式,并写出函数的定义域;(3)当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置,并求出相应的x 的值;如果不可能,试说明理由.五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分) 27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2.得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2 (1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1.即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形. ∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN . S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN…(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 及点A 重合,点Q 及点D 重合,这时PQ =QC ,△PCQ 是等腰三角形,此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3)……………………(1分) 解法一 此时,QN =PM =x22,CP =2-x ,CN =22CP =1-x 22.∴CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分)解法二此时∠CPQ=21∠PCN=22.5°,∠APB=90°-22.5°=67.5°,∠ABP=180°-(45°+67.5°)=67.5°,得∠APB=∠ABP,∴AP=AB=1,∴x=1.……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD中,AB=1,弧AC是点B为圆心,AB长为半径的圆的一段弧。
上海十年中考数学压轴题及答案解析

上海十年中考数学压轴题解析2001年上海市数学中考27.已知在梯形 ABCD 中,AD// BC ADc BC ,且 AD= 5, AB= DC= 2.① 求证;△ DPC② 求AP 的长.(2)如果点P 在AD 边上移动(点 P 与点A D 不重合),且满足/ BPE =Z A , PE 交直线BC 于点E,同时交直线 DC 于点Q 那么① 当点Q 在线段DC 的延长线上时,设 AP= x , CQ y ,求y 关于x 的函数解析式,并写出函数的定义域; ② 当CE= 1时,写出AP 的长(不必写出解题过程).27. (1)①证明:是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化, 事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的 途径.)(1)如图8, P 为AD 上的一点,满足/BPC=Z A.•••/ ABP= 180°—/ A -Z APB中,AD// BC AB= CD •••/ A=Z D.②解:设 AP= x ,则 DP= 5 — x , 或4./ DPC= 180。
一/ BPC-Z APB ABP^A DPC由厶 ABP^ DPC 得 AB 空AP DC 'AB(2)①解:类似(1)①,易得△ ABP^A DPQ .——PD② AP = 2 或 AP = 3— <5 .(题27是一道涉及动量与变量的考题,其中(1)可看作 / BPC=Z A,A Z ABP=Z DPC V 在梯形 ABCD5 x 解得X 1= 1 , X 2= 4,则AP 的长为12-x 2- x 2 , 1v x v 4.2 2(2)的特例,故 (2)的推断与证明均可借鉴 (1)的思路.这这是中学生学数学应具备的一种基本素质,世上的万 BC图8上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为 1的正方形ABCD 上,并使它的直角顶点 P 在对角线AC 上滑动,直角的一边始终经过点B,另一边与射线DC 相交于点Q探究:设A 、P 两点间的距离为x .(1) 当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系?试证明你观察得到结论;(2) 当点Q 在边CD 上时,设四边形 PBCQ 勺面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域; (3)当点P 在线段AC 上滑动时,△ PCC 是否可能成为等腰三角形?如果可能,指出所有能使厶 PCC 成为等腰三角形 的点Q 的位置,并求出相应的 x 的值;如果不可能,试说明理由. 五、(本大题只有1题,满分12分,(1)、(2)、( 3)题均为4分)27.(1)解:PQ= PB证明如下:过点 P 作M2 BC 分别交AB 于点M 交CD 于点N,那么四边形 AMN 和四边形BCNh 都是矩形,△ AMP 和厶CNP 都是等腰直角三角形(如图 1).••• NP= NC= MB...................... ( 1 分)/ BPQ 90°,「./ QPN ■/ BPM= 90°.而/ BPM ■/PBM= 90°,「. / QPI 4Z PBM ...................... ( 1 分)又••• / QNP=Z PMB= 90°,二 △ QN B^ PMB ............................... ( 1 分)(1 分)图1图2 图3PQ= PB① 当点P 与点A 重合,点Q 与点D 重合,这时PQ= QC △ PCQ!等腰三角形, 此时x = 0........................... ( 1分)② 当点Q 在边DC 的延长线上,且 CP= CQ 时,△ PCC !等腰三角形(如图3)(1 分)(2)解法一由(〔)△ QN B^ PMB 得 NQ=MP[2 AP= x ,••• AM= MP= NQ= DN= x , 2 [2BM= PN= CN= 1- x ,2 CQ= CD- DQ= 1 - 2・-^x = 1- 2x .2得 S,PB = 1BC- BM= 1 x 1x (1-_^x )2 2 21分)S四边形 -CQ PN= - x ( 1 - 2x ) (1-」x )2 2 21 - 3Zx + 1x2 2 4 2(1 分)PBCh S ^PBC ^ S , PCQ-x -' 2 x + 1 '即 y = —x — . 2x + 1 (0w x v —).2 2分,1分)解法二作PT 丄BC, T 为垂足(如图2),那么四边形PTCh 为正方形. • PT = CB- PN又/ PN (=Z PTB-90°, PB- PQPBT^, PQNS四边形PBC=S△四边形PBT + S四边形PTC= S 四边形PTC + S \ PQNS正方形PTCN(2 分)2=C N =(1」2= 1x 2- 2x + 12y = 1 x 2- 2x + 1 (0 w x v丄).22(1分)(3)△ PCQ 可能成为等腰三角当.2 — x = 2x — 1 时,得 x = 1.1解法二 此时/ CPQ=—/ PCN= 22.5 ° / APB= 90°— 22.5 °= 67.5 °2/ ABP= 180°—( 45°+ 67.5 ° = 67.5 ° 得/ APB=Z ABP••• AP= AB= 1,二 x = 1................ ( 1 分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形 ABCD 中, AB= 1 ,弧AC 是点B 为圆心,AB 长为半径的圆的一段弧。
上海中考数学最难压轴题

选择题:在平面直角坐标系中,点A的坐标为(3,4),若点A关于直线x=2的对称点为B,则点B的坐标为:A. (1,4) (正确答案)B. (2,-4)C. (-3,4)D. (3,-4)已知二次函数y=ax2+bx+c的图像经过点(1,0),(2,0)和(3,4),则a的值为:A. -4/3B. 4/3 (正确答案)C. -2D. 2在直角三角形ABC中,∠C=90°,AC=3,BC=4,则AB的长度为:A. 5 (正确答案)B. 6C. 7D. 8已知等差数列{an}的首项a1=1,公差d=2,则a5的值为:A. 7B. 8C. 9 (正确答案)D. 10在平面直角坐标系中,直线y=2x+1与y轴的交点坐标为:A. (0,1) (正确答案)B. (1,0)C. (0,-1)D. (-1,0)已知圆的方程为x2+y2=9,则圆心到直线x+y-2=0的距离为:A. √2/2 (正确答案)B. √2C. 2√2D. 3√2在平行四边形ABCD中,AB=3,BC=4,且∠ABC=60°,则平行四边形ABCD的面积为:A. 6√3 (正确答案)B. 12√3C. 6D. 12已知二次函数y=ax2+bx+c的顶点坐标为(1,2),且经过点(0,1),则a的值为:A. -1B. 1C. -2D. 2 (正确答案)在∠ABC中,∠A=60°,∠B=45°,AB=2,则AC的长度为:A. √2B. √3C. √6 (正确答案)D. 2√2。
上海十年中考数学压轴题24,25题
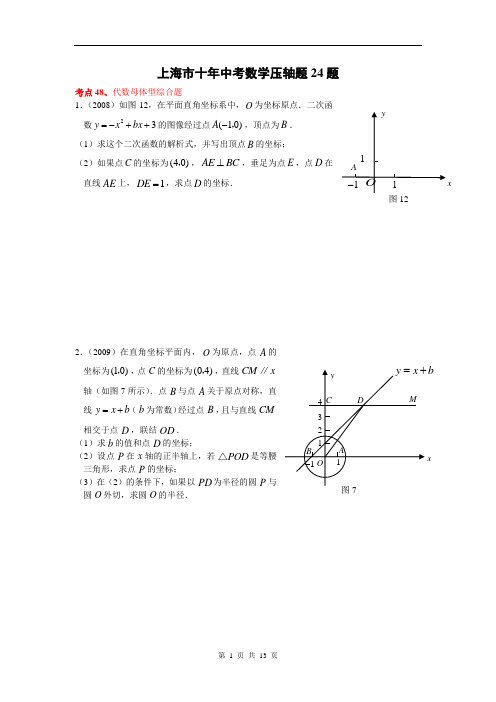
x图12上海市十年中考数学压轴题24题考点48、代数母体型综合题 1.(2008)如图12,在平面直角坐标系中,O 为坐标原点.二次函数23y x bx =-++的图像经过点(10)A -,,顶点为B . (1)求这个二次函数的解析式,并写出顶点B 的坐标;(2)如果点C 的坐标为(40),,AE BC ⊥,垂足为点E ,点D 在直线AE 上,1DE =,求点D 的坐标.2.(2009)在直角坐标平面内,为原点,点的坐标为,点的坐标为,直线轴(如图7所示).点与点关于原点对称,直线(为常数)经过点,且与直线相交于点,联结. (1)求的值和点的坐标;(2)设点在轴的正半轴上,若是等腰三角形,求点的坐标;(3)在(2)的条件下,如果以为半径的圆与圆外切,求圆的半径.O A (10),C (04),CM x ∥B A y x b =+b B CM D OD b D P x POD △P PD P O Oxb3.(2010)如图,已知平面直角坐标系x O y ,抛物线y =-x 2+bx +c 过点A (4,0)、B (1,3) .(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l ,设抛物线上的点P(m ,n )在第四象限,点P 关于直线l 的对称点为E ,点E 关于y 轴的对称点为F ,若四边形OAPF 的面积为20,求m 、n 的值.4.(2011)已知平面直角坐标系xOy (如图1),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M . (1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.5.(2012)如图7,在平面直角坐标系中,二次函数26y ax x c =++的图像经过()()4,0,1,0A B -与y 轴交于C ,点D 在线段OC 上,OD t =,点E 在第二象限内,90ADE ∠=︒,1tan ,2DAE EF OD ∠=⊥,垂足为F .(1)求这个二次函数的解析式;(2)求线段,EF OF 的长(用含t 的代数式表示); (3)当ECA CAO ∠=∠时,求t 的值.6.(2013)如图9,在平面直角坐标系中,顶点为的抛物线经过点和轴正半轴上的点,= 2,.(1)求这条抛物线的表达式;(2)联结,求的大小;(3)如果点在轴上,且△与△相似,求点的坐标.xoy M 2(0y ax bx a =+>)A x B AO OB =0120AOB ∠=OM AOM ∠C x ABC AOM C MAB Oxy图97.(2014)在平面直角坐标系中(如图9),已知抛物线223y x bx c =++与x 轴交于点A (-1,0)和点B ,与y 轴交于点C (0,-2). (1)求该抛物线的表达式,并写出其对称轴;(2)点E 为该抛物线的对称轴与x 轴的交点,点F 在对称轴上,四边形ACEF 为梯形,求点F 的坐标;(3)点D 为该抛物线的顶点,设点P (t ,0),且t ﹥3,如果△BDP 和△CDP 的面积相等,求t 的值.8.(2015)已知在平面直角坐标系xOy 中(如图),抛物线y =ax 2-4与x 轴的负半轴相交于点A ,与y 轴相交于点B ,AB =25.点P 在抛物线上,线段AP 与y 轴的正半轴交于点C ,线段BP 与x 轴相交于点D .设点P 的横坐标为m . (1)求这条抛物线的解析式;(2)用含m 的代数式表示线段CO 的长;(3)当tan ∠ODC =23时,求∠P AD 的正弦值.图99.(2016)如图,抛物线25y ax bx =+-(0a ≠)经过点(4,5)A -,与x 轴的负半轴交于点B ,与y 轴交于点C ,且5OC OB =,抛物线的顶点为D ; (1)求这条抛物线的表达式;(2)联结AB 、BC 、CD 、DA ,求四边形ABCD 的面积; (3)如果点E 在y 轴的正半轴上,且BEO ABC ∠=∠, 求点E 的坐标.10.(2017)在平面直角坐标系xOy 中(如图8),已知抛物线y =-x 2+bx +c 经过点A (2, 2),对称轴是直线x =1,顶点为B .(1)求这条抛物线的表达式和点B 的坐标;(2)点M 在对称轴上,且位于顶点上方,设它的纵坐标为m ,联结AM ,用含m 的代数式表示∠AMB 的余切值;(3)将该抛物线向上或向下平移,使得新抛物线的顶点C原抛物线上一点P 平移后的对应点为点Q ,如果OP =OQ图 811.(2018)在平面直角坐标系xOy 中(如图10),已知抛物线c bx x y ++-=221经过 A (–1,0)和点B (0,25),顶点为C .点D 在其对称轴上且位于点C 下方,将线段DC 绕点D 按顺时针方向转90°,点C 落在抛物线上的点P 处. (1)求这条抛物线的表达式; (2)求线段CD 的长;(3)将抛物线平移,使其顶点C 移到原点O 的位置.这时点P 落在点E 的位置,如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求M 的坐标.12.(2019)在平面直角坐标系xOy 中(如图9),已知抛物线22=-y x x ,其顶点为A . (1)写出这条拋物线的开口方向、顶点A 的坐标,并说明它的变化情况; (2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”. ①试求抛物线22=-y x x 的“不动点”的坐标;②平移抛物线22=-y x x ,使所得新拋物线的顶点B 是该抛物线的“不动点”其对称轴与x 轴交于点C ,且四边形OABC上海市十年中考数学压轴题25题考点49、几何母体型综合题1.(2008)已知24AB AD ==,,90DAB ∠=,AD BC ∥(如图13).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1)设BE x =,ABM △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (2)如果以线段AB 为直径的圆与以线段DE 为直径的圆外切,求线段BE 的长;(3)联结BD ,交线段AM 于点N ,如果以A N D ,,为顶点的三角形与BME △相似,求线段BE 的长.2.(2009)已知为线段上的动点,点在射线上,且满足(如图8所示). (1)当,且点与点重合时(如图9所示),求线段的长; (2)在图8中,联结.当,且点在线段上时,设点之间的距离为,,其中表示的面积,表示的面积,求关于的函数解析式,并写出函数定义域;(3)当,且点在线段的延长线上时(如图10所示),求的大小.9023ABC AB BC AD BC P ∠===°,,,∥,BD Q AB PQ ADPC AB=2AD =Q B PC AP 32AD =Q AB B Q 、x APQ PBCS y S =△△APQ S △APQ △PBC S △PBC △yx AD AB <Q AB QPC ∠B A D M E C图13B A DC 备用图 AD P Q D A PA D P3.(2010)如图,在Rt △ABC 中,∠ACB =90°.半径为1的圆A 与边AB 相交于点D ,与边AC 相交于点E ,连结DE 并延长,与线段BC 的延长线交于点P . (1)当∠B =30°时,连结AP ,若△AEP 与△BDP 相似,求CE 的长; (2)若CE=2,BD=BC ,求∠BPD 的正切值; (3)若,设CE=x ,△ABC 的周长为y ,求y 关于x 的函数关系式.(备用) (备用) 4.(2011)在Rt △ABC 中,∠ACB =90°,BC =30,AB =50.点P 是AB 边上任意一点,直线PE ⊥AB ,与边AC 或BC 相交于E .点M 在线段AP 上,点N 在线段BP 上,EM =EN ,12sin 13EMP ∠=.(1)如图1,当点E 与点C 重合时,求CM 的长;(2)如图2,当点E 在边AC 上时,点E 不与点A 、C 重合,设AP =x ,BN =y ,求y 关于x 的函数关系式,并写出函数的定义域;(3)若△AME ∽△ENB (△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应),求AP 的长.图1 图2 备用图1tan 3BPD ∠=5.(2012)如图8,在半径为2的扇形AOB 中,90AOB ∠=︒,点C 是AB 上的一个动点(不与点A 、B 重合),,OD BC OE AC ⊥⊥,垂足分别为D E 、. (1)当=1BC 时,求线段OD 的长;(2)在DOE ∆中是否存在长度不变的边?若存在,请指出并求其长度;如果不存在,请说明理由; (3)设=BD x ,DOE ∆的面积为y ,求y 关于x 的函数关系式,并指出它的定义域.6.(2013)在矩形ABCD 中,点P 是边AD 上的动点,联结BP ,线段BP 的垂直平分线交边BC 于点Q ,垂足为点M ,联结QP (如图10).已知AD =13,AB =5,设AP =x ,BQ =y . (1)求关于的函数解析式,并写出的取值范围;(2)当以AP 长为半径的⊙P 和以QC 长为半径的⊙Q 外切时,求x 的值;(3)点E 在边CD 上,过点E 作直线QP 的垂线,垂足为F ,如果EF =EC =4,求x 的值.y x x OABCDE图8图10备用图7.(2014)如图10,已知在平行四边形ABCD 中,AB =5,BC =8,cos B =45,点P 是边BC 上的动点,以CP 为半径的圆C 与边AD 交于点E 、F (点F 在点E 的右侧),射线CE 与射线BA 交于点G .(1)当圆C 经过点A 时,求CP 的长; (2)联结AP ,当AP ∥CG 时,求弦EF 的长; (3)当△AGE 是等腰三角形时,求圆C 的半径长.8.(2015)已知:如图,AB 是半圆O 的直径,弦CD ∥AB ,动点P 、Q 分别在线段OC 、CD 上,且DQ =OP ,AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F (点F 与点C 、D 不重合),AB =20,cos ∠AOC =54.设OP =x ,△CPF 的面积为y . (1)求证:AP =OQ ;(2)求y 关于x 的函数关系式,并写出它的定义域; (3)当△OPE 是直角三角形时,求线段OP 的长.GB EFDCP图10 ABDC备用图 AOPQ F EDCBA备用图O DCBA第 11 页 共 13 页9.(2016)如图所示,梯形ABCD 中,AB ∥DC ,90B ∠=︒,15AD =,16AB =,12BC =,点E 是边AB 上的动点,点F 是射线CD 上一点,射线ED 和射线AF 交于点G ,且AGE DAB ∠=∠;(1)求线段CD 的长;(2)如果AEG ∆是以EG 为腰的等腰三角形,求线段AE 的长;(3)如果点F 在边CD 上(不与点C 、D 重合),设AE x =,DF y =,求y 关于x 的函 数解析式,并写出x 的取值范围.10.(2017)如图9,已知⊙O 的半径长为1,AB 、AC 是⊙O 的两条弦,且AB =AC ,BO 的延长线交AC 于点D ,联结OA 、OC .(1)求证:△OAD ∽△ABD ;(2)当△OCD 是直角三角形时,求B 、C 两点的距离;(3)记△AOB 、△AOD 、△COD 的面积分别是S 1、S 2、S 3,如果S 2是S 1和S 3的比例中项,求OD 的长.备用图图9第 12 页 共 13 页11.(2018)已知⊙O 的直径AB =2,弦AC 与弦BD 交于点E ,且OD ⊥AC ,垂足为点F .(1)如图11,如果AC =BD ,求弦AC 的长;(2)如图12,如果E 为弦BD 的中点,求∠ABD 的余切值;(3)联结BC 、CD 、DA ,如果BC 是⊙O 的内接正n 边形的一边,CD 是⊙O 的内接正(n +4)边形的一边,求△ACD 的面积.12.(2019)如图10,AD 、BD 分别是△ABC 的内角∠BAC 、∠ABC 的平分线,过点A 作AE ⊥AD ,交BD 的延长线于点E . (1)求证: 12∠=∠E C ; (2)如图11,如果AE =AB ,且BD :DE =2:3,求cos ∠ABC 的值;(3)如果∠ABC 是锐角,且△ABC 与△ADE 相似,求∠ABC 的度数,并直接写出S △ADE ∶S △ABC 的值.图10图11 A BC D E E D CB A A BCD FE O 图11 O B A C D EF 图12 A B O 备用图第13 页共13 页。
上海十年中考数学压轴题24,25题

x图12上海市十年中考数学压轴题24题考点48、代数母体型综合题 1.(2008)如图12,在平面直角坐标系中,O 为坐标原点.二次函数23y x bx =-++的图像经过点(10)A -,,顶点为B . (1)求这个二次函数的解析式,并写出顶点B 的坐标;(2)如果点C 的坐标为(40),,AE BC ⊥,垂足为点E ,点D 在直线AE 上,1DE =,求点D 的坐标.2.(2009)在直角坐标平面内,为原点,点的坐标为,点的坐标为,直线轴(如图7所示).点与点关于原点对称,直线(为常数)经过点,且与直线相交于点,联结. (1)求的值和点的坐标;(2)设点在轴的正半轴上,若是等腰三角形,求点的坐标;(3)在(2)的条件下,如果以为半径的圆与圆外切,求圆的半径.O A (10),C (04),CM x ∥B A y x b =+b B CM D OD b D P x POD △P PD P O Oxb3.(2010)如图,已知平面直角坐标系x O y ,抛物线y =-x 2+bx +c 过点A (4,0)、B (1,3) .(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l ,设抛物线上的点P(m ,n )在第四象限,点P 关于直线l 的对称点为E ,点E 关于y 轴的对称点为F ,若四边形OAPF 的面积为20,求m 、n 的值.4.(2011)已知平面直角坐标系xOy (如图1),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M . (1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.5.(2012)如图7,在平面直角坐标系中,二次函数26y ax x c =++的图像经过()()4,0,1,0A B -与y 轴交于C ,点D 在线段OC 上,OD t =,点E 在第二象限内,90ADE ∠=︒,1tan ,2DAE EF OD ∠=⊥,垂足为F .(1)求这个二次函数的解析式;(2)求线段,EF OF 的长(用含t 的代数式表示); (3)当ECA CAO ∠=∠时,求t 的值.6.(2013)如图9,在平面直角坐标系中,顶点为的抛物线经过点和轴正半轴上的点,= 2,.(1)求这条抛物线的表达式;(2)联结,求的大小;(3)如果点在轴上,且△与△相似,求点的坐标.xoy M 2(0y ax bx a =+>)A x B AO OB =0120AOB ∠=OM AOM ∠C x ABC AOM C MAB Oxy图97.(2014)在平面直角坐标系中(如图9),已知抛物线223y x bx c =++与x 轴交于点A (-1,0)和点B ,与y 轴交于点C (0,-2). (1)求该抛物线的表达式,并写出其对称轴;(2)点E 为该抛物线的对称轴与x 轴的交点,点F 在对称轴上,四边形ACEF 为梯形,求点F 的坐标;(3)点D 为该抛物线的顶点,设点P (t ,0),且t ﹥3,如果△BDP 和△CDP 的面积相等,求t 的值.8.(2015)已知在平面直角坐标系xOy 中(如图),抛物线y =ax 2-4与x 轴的负半轴相交于点A ,与y 轴相交于点B ,AB =25.点P 在抛物线上,线段AP 与y 轴的正半轴交于点C ,线段BP 与x 轴相交于点D .设点P 的横坐标为m . (1)求这条抛物线的解析式;(2)用含m 的代数式表示线段CO 的长;(3)当tan ∠ODC =23时,求∠P AD 的正弦值.图99.(2016)如图,抛物线25y ax bx =+-(0a ≠)经过点(4,5)A -,与x 轴的负半轴交于点B ,与y 轴交于点C ,且5OC OB =,抛物线的顶点为D ; (1)求这条抛物线的表达式;(2)联结AB 、BC 、CD 、DA ,求四边形ABCD 的面积; (3)如果点E 在y 轴的正半轴上,且BEO ABC ∠=∠, 求点E 的坐标.10.(2017)在平面直角坐标系xOy 中(如图8),已知抛物线y =-x 2+bx +c 经过点A (2, 2),对称轴是直线x =1,顶点为B .(1)求这条抛物线的表达式和点B 的坐标;(2)点M 在对称轴上,且位于顶点上方,设它的纵坐标为m ,联结AM ,用含m 的代数式表示∠AMB 的余切值;(3)将该抛物线向上或向下平移,使得新抛物线的顶点C原抛物线上一点P 平移后的对应点为点Q ,如果OP =OQ图 811.(2018)在平面直角坐标系xOy 中(如图10),已知抛物线c bx x y ++-=221经过 A (–1,0)和点B (0,25),顶点为C .点D 在其对称轴上且位于点C 下方,将线段DC 绕点D 按顺时针方向转90°,点C 落在抛物线上的点P 处. (1)求这条抛物线的表达式; (2)求线段CD 的长;(3)将抛物线平移,使其顶点C 移到原点O 的位置.这时点P 落在点E 的位置,如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求M 的坐标.12.(2019)在平面直角坐标系xOy 中(如图9),已知抛物线22=-y x x ,其顶点为A . (1)写出这条拋物线的开口方向、顶点A 的坐标,并说明它的变化情况; (2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”. ①试求抛物线22=-y x x 的“不动点”的坐标;②平移抛物线22=-y x x ,使所得新拋物线的顶点B 是该抛物线的“不动点”其对称轴与x 轴交于点C ,且四边形OABC上海市十年中考数学压轴题25题考点49、几何母体型综合题1.(2008)已知24AB AD ==,,90DAB ∠=,AD BC ∥(如图13).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1)设BE x =,ABM △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (2)如果以线段AB 为直径的圆与以线段DE 为直径的圆外切,求线段BE 的长;(3)联结BD ,交线段AM 于点N ,如果以A N D ,,为顶点的三角形与BME △相似,求线段BE 的长.2.(2009)已知为线段上的动点,点在射线上,且满足(如图8所示). (1)当,且点与点重合时(如图9所示),求线段的长; (2)在图8中,联结.当,且点在线段上时,设点之间的距离为,,其中表示的面积,表示的面积,求关于的函数解析式,并写出函数定义域;(3)当,且点在线段的延长线上时(如图10所示),求的大小.9023ABC AB BC AD BC P ∠===°,,,∥,BD Q AB PQ ADPC AB=2AD =Q B PC AP 32AD =Q AB B Q 、x APQ PBCS y S =△△APQ S △APQ △PBC S △PBC △yx AD AB <Q AB QPC ∠B A D M E C图13B A DC 备用图 AD P Q D A PA D P3.(2010)如图,在Rt △ABC 中,∠ACB =90°.半径为1的圆A 与边AB 相交于点D ,与边AC 相交于点E ,连结DE 并延长,与线段BC 的延长线交于点P . (1)当∠B =30°时,连结AP ,若△AEP 与△BDP 相似,求CE 的长; (2)若CE=2,BD=BC ,求∠BPD 的正切值; (3)若,设CE=x ,△ABC 的周长为y ,求y 关于x 的函数关系式.(备用) (备用) 4.(2011)在Rt △ABC 中,∠ACB =90°,BC =30,AB =50.点P 是AB 边上任意一点,直线PE ⊥AB ,与边AC 或BC 相交于E .点M 在线段AP 上,点N 在线段BP 上,EM =EN ,12sin 13EMP ∠=.(1)如图1,当点E 与点C 重合时,求CM 的长;(2)如图2,当点E 在边AC 上时,点E 不与点A 、C 重合,设AP =x ,BN =y ,求y 关于x 的函数关系式,并写出函数的定义域;(3)若△AME ∽△ENB (△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应),求AP 的长.图1 图2 备用图1tan 3BPD ∠=5.(2012)如图8,在半径为2的扇形AOB 中,90AOB ∠=︒,点C 是AB 上的一个动点(不与点A 、B 重合),,OD BC OE AC ⊥⊥,垂足分别为D E 、. (1)当=1BC 时,求线段OD 的长;(2)在DOE ∆中是否存在长度不变的边?若存在,请指出并求其长度;如果不存在,请说明理由; (3)设=BD x ,DOE ∆的面积为y ,求y 关于x 的函数关系式,并指出它的定义域.6.(2013)在矩形ABCD 中,点P 是边AD 上的动点,联结BP ,线段BP 的垂直平分线交边BC 于点Q ,垂足为点M ,联结QP (如图10).已知AD =13,AB =5,设AP =x ,BQ =y . (1)求关于的函数解析式,并写出的取值范围;(2)当以AP 长为半径的⊙P 和以QC 长为半径的⊙Q 外切时,求x 的值;(3)点E 在边CD 上,过点E 作直线QP 的垂线,垂足为F ,如果EF =EC =4,求x 的值.y x x OABCDE图8图10备用图7.(2014)如图10,已知在平行四边形ABCD 中,AB =5,BC =8,cos B =45,点P 是边BC 上的动点,以CP 为半径的圆C 与边AD 交于点E 、F (点F 在点E 的右侧),射线CE 与射线BA 交于点G .(1)当圆C 经过点A 时,求CP 的长; (2)联结AP ,当AP ∥CG 时,求弦EF 的长; (3)当△AGE 是等腰三角形时,求圆C 的半径长.8.(2015)已知:如图,AB 是半圆O 的直径,弦CD ∥AB ,动点P 、Q 分别在线段OC 、CD 上,且DQ =OP ,AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F (点F 与点C 、D 不重合),AB =20,cos ∠AOC =54.设OP =x ,△CPF 的面积为y . (1)求证:AP =OQ ;(2)求y 关于x 的函数关系式,并写出它的定义域; (3)当△OPE 是直角三角形时,求线段OP 的长.GB EFDCP图10 ABDC备用图 AOPQ F EDCBA备用图O DCBA第 11 页 共 13 页9.(2016)如图所示,梯形ABCD 中,AB ∥DC ,90B ∠=︒,15AD =,16AB =,12BC =,点E 是边AB 上的动点,点F 是射线CD 上一点,射线ED 和射线AF 交于点G ,且AGE DAB ∠=∠;(1)求线段CD 的长;(2)如果AEG ∆是以EG 为腰的等腰三角形,求线段AE 的长;(3)如果点F 在边CD 上(不与点C 、D 重合),设AE x =,DF y =,求y 关于x 的函 数解析式,并写出x 的取值范围.10.(2017)如图9,已知⊙O 的半径长为1,AB 、AC 是⊙O 的两条弦,且AB =AC ,BO 的延长线交AC 于点D ,联结OA 、OC .(1)求证:△OAD ∽△ABD ;(2)当△OCD 是直角三角形时,求B 、C 两点的距离;(3)记△AOB 、△AOD 、△COD 的面积分别是S 1、S 2、S 3,如果S 2是S 1和S 3的比例中项,求OD 的长.备用图图9第 12 页 共 13 页11.(2018)已知⊙O 的直径AB =2,弦AC 与弦BD 交于点E ,且OD ⊥AC ,垂足为点F .(1)如图11,如果AC =BD ,求弦AC 的长;(2)如图12,如果E 为弦BD 的中点,求∠ABD 的余切值;(3)联结BC 、CD 、DA ,如果BC 是⊙O 的内接正n 边形的一边,CD 是⊙O 的内接正(n +4)边形的一边,求△ACD 的面积.12.(2019)如图10,AD 、BD 分别是△ABC 的内角∠BAC 、∠ABC 的平分线,过点A 作AE ⊥AD ,交BD 的延长线于点E . (1)求证: 12∠=∠E C ; (2)如图11,如果AE =AB ,且BD :DE =2:3,求cos ∠ABC 的值;(3)如果∠ABC 是锐角,且△ABC 与△ADE 相似,求∠ABC 的度数,并直接写出S △ADE ∶S △ABC 的值.图10图11 A BC D E E D CB A A BCD FE O 图11 O B A C D EF 图12 A B O 备用图第13 页共13 页。
上海历年中考数学压轴题复习

上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2.(1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC . ②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252x x -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即y x x +=-252,得225212-+-=x x y ,1<x <4. ②AP =2或AP =3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB .(2)解法一由(1)△QNP ≌△PMB .得NQ =MP .∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2 (1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分) 解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN…(2分)=CN 2=(1-x 22)2=21x 2-x 2+1∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形,此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3)……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =°,∠APB =90°-°=°, ∠ABP =180°-(45°+°)=°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD 中,AB =1,弧AC 是点B 为圆心,AB 长为半径的圆的一段弧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2.(1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC . ②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252x x -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即y x x +=-252,得225212-+-=x x y ,1<x <4. ②AP =2或AP =3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB .(2)解法一由(1)△QNP ≌△PMB .得NQ =MP .∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2 (1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分) 解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN…(2分)=CN 2=(1-x 22)2=21x 2-x 2+1∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形,此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3)……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =°,∠APB =90°-°=°, ∠ABP =180°-(45°+°)=°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD 中,AB =1,弧AC 是点B 为圆心,AB 长为半径的圆的一段弧。
点E 是边AD 上的任意一点(点E 与点A 、D 不重合),过E 作弧AC 所在圆的切线,交边DC 于点F ,G 为切点:(1)当∠DEF =45º时,求证:点G 为线段EF 的中点;(2)设AE =x ,FC =y ,求y 关于x 的函数解析式,并写出函数的定义域;(3)将△DEF沿直线EF翻折后得△D1EF,如图,当EF=65时,讨论△AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由。
2004年上海市中考数学试卷27、(2004•上海)数学课上,老师提出:如图,在平面直角坐标系中,O为坐标原点,A点的坐标为(1,0),点B在x轴上,且在点A的右侧,AB=OA,过点A和B作x轴的垂线,分别交二次函数y=x2的图象于点C和D,直线OC交BD于点M,直线CD交y轴于点H,记点C、D的的横坐标分别为x C、x D,点H的纵坐标为y H.同学发现两个结论:①S△CMD:S梯形ABMC=2:3 ②数值相等关系:x C•x D=﹣y H(1)请你验证结论①和结论②成立;(2)请你研究:如果上述框中的条件“A的坐标(1,0)”改为“A的坐标(t,0)(t>0)”,其他条件不变,结论①是否仍成立(请说明理由);(3)进一步研究:如果上述框中的条件“A的坐标(1,0)”改为“A的坐标(t,0)(t >0)”,又将条件“y=x2”改为“y=ax2(a>0)”,其他条件不变,那么x C、x D与y H有怎样的数值关系(写出结果并说明理由)考点:二次函数综合题。
专题:压轴题。
分析:(1)可先根据AB=OA得出B点的坐标,然后根据抛物线的解析式和A,B的坐标得出C,D两点的坐标,再依据C点的坐标求出直线OC的解析式.进而可求出M点的坐标,然后根据C、D两点的坐标求出直线CD的解析式进而求出D点的坐标,然后可根据这些点的坐标进行求解即可;(2)(3)的解法同(1)完全一样.解答:解:(1)由已知可得点B的坐标为(2,0),点C坐标为(1,1),点D的坐标为(2,4),由点C坐标为(1,1)易得直线OC的函数解析式为y=x,故点M的坐标为(2,2),所以S△CMD=1,S梯形ABMC=所以S△CMD:S梯形ABMC=2:3,即结论①成立.设直线CD的函数解析式为y=kx+b,则,解得所以直线CD的函数解析式为y=3x﹣2.由上述可得,点H的坐标为(0,﹣2),y H=﹣2因为x C•x D=2,所以x C•x D=﹣y H,即结论②成立;(2)(1)的结论仍然成立.理由:当A的坐标(t,0)(t>0)时,点B的坐标为(2t,0),点C坐标为(t,t2),点D的坐标为(2t,4t2),由点C坐标为(t,t2)易得直线OC的函数解析式为y=tx,故点M的坐标为(2t,2t2),所以S△CMD=t3,S梯形ABMC=t3.所以S△CMD:S梯形ABMC=2:3,即结论①成立.设直线CD的函数解析式为y=kx+b,则,解得所以直线CD的函数解析式为y=3tx﹣2t2;由上述可得,点H的坐标为(0,﹣2t2),y H=﹣2t2因为x C•x D=2t2,所以x C•x D=﹣y H,即结论②成立;(3)由题意,当二次函数的解析式为y=ax2(a>0),且点A坐标为(t,0)(t>0)时,点C坐标为(t,at2),点D坐标为(2t,4at2),设直线CD的解析式为y=kx+b,则:,解得所以直线CD的函数解析式为y=3atx﹣2at2,则点H的坐标为(0,﹣2at2),y H=﹣2at2.因为x C•x D=2t2,所以x C •x D =﹣y H .点评:本题主要考查了二次函数的应用、一次函数解析式的确定、图形面积的求法、函数图象的交点等知识点.2005年上海市初中毕业生统一学业考试数学试卷1、 (本题满分12分,每小题满分各为4分)在△ABC 中,∠ABC =90°,AB =4,BC =3,O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D ,交线段OC 于点E ,作EP ⊥ED ,交射线AB 于点P ,交射线CB 于点F 。
(1) 如图8,求证:△ADE ∽△AEP ;(2) 设OA =x ,AP =y ,求y 关于x 的函数解析式,并写出它的定义域;(3) 当BF =1时,求线段AP 的长.25.1909090AP D ODA PED OD OE ODE OED ODE OEDEDA PEA A AADE AEP∴∠=∠=︒=∴∠=∠∴︒+∠=︒+∠∴∠=∠∠=∠∴∆∆Q Q Q :()证明:连结OD切半圆于,又,,又22334,555846416584525555(0)OD CB OA ACOD OD x OE AD x x ADE AEPx AP AE y xy x y x AE AD x x x ==⇒===∆∆∴=⇒=⇒=⇒=>Q :()同理可得:(3)5(46,90512661255E C x AP AB DO BE HDHE DJEHD x PBE PDH PFB PHDPBPB AP x x>>∆≅∆∴=∠=∠=︒∴∆∆∴=⇒=⇒=Q :由题意可知存在三种情况但当在点左侧时BF显然大于4所以不合舍去当时如图)延长,交于易证54,1261255422x P B DO PE HDHE EJDPBF PDH BPBP x xAP <∆≅∆∆∆∴=⇒=∴=-=:当时点在点的右侧延长交于点同理可得2006 年上海市初中毕业生统一学业考试数学试卷25(本题满分14分,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分3分)已知点P 在线段AB 上,点O 在线段AB 的延长线上。
