模式识别基础实验报告

合集下载

《模式识别》实验报告-贝叶斯分类

《模式识别》实验报告---最小错误率贝叶斯决策分类一、实验原理对于具有多个特征参数的样本（如本实验的iris 数据样本有4d =个参数），其正态分布的概率密度函数可定义为112211()exp ()()2(2)T d p π-⎧⎫=--∑-⎨⎬⎩⎭∑x x μx μ 式中，12,,,d x x x ⎡⎤⎣⎦=x 是d 维行向量，12,,,d μμμ⎡⎤⎣⎦=μ是d 维行向量，∑是d d ⨯维协方差矩阵，1-∑是∑的逆矩阵，∑是∑的行列式。

本实验我们采用最小错误率的贝叶斯决策，使用如下的函数作为判别函数()(|)(),1,2,3i i i g p P i ωω==x x （3个类别）其中()i P ω为类别i ω发生的先验概率，(|)i p ωx 为类别i ω的类条件概率密度函数。

由其判决规则，如果使()()i j g g >x x 对一切j i ≠成立，则将x 归为i ω类。

我们根据假设：类别i ω，i=1,2,……,N 的类条件概率密度函数(|)i p ωx ，i=1,2,……,N 服从正态分布，即有(|)i p ωx ~(,)i i N ∑μ，那么上式就可以写为1122()1()exp ()(),1,2,32(2)T i i dP g i ωπ-⎧⎫=-∑=⎨⎬⎩⎭∑x x -μx -μ对上式右端取对数，可得111()()()ln ()ln ln(2)222T i i i i dg P ωπ-=-∑+-∑-i i x x -μx -μ上式中的第二项与样本所属类别无关，将其从判别函数中消去，不会改变分类结果。

则判别函数()i g x 可简化为以下形式111()()()ln ()ln 22T i i i i g P ω-=-∑+-∑i i x x -μx -μ二、实验步骤（1）从Iris.txt 文件中读取估计参数用的样本，每一类样本抽出前40个，分别求其均值，公式如下11,2,3ii iii N ωωω∈==∑x μxclear% 原始数据导入iris = load('C:\MATLAB7\work\模式识别\iris.txt'); N=40;%每组取N=40个样本%求第一类样本均值 for i = 1:N for j = 1:4w1(i,j) = iris(i,j+1); end endsumx1 = sum(w1,1); for i=1:4meanx1(1,i)=sumx1(1,i)/N; end%求第二类样本均值 for i = 1:N for j = 1:4 w2(i,j) = iris(i+50,j+1);end endsumx2 = sum(w2,1); for i=1:4meanx2(1,i)=sumx2(1,i)/N; end%求第三类样本均值 for i = 1:N for j = 1:4w3(i,j) = iris(i+100,j+1); end endsumx3 = sum(w3,1); for i=1:4meanx3(1,i)=sumx3(1,i)/N; end（2）求每一类样本的协方差矩阵、逆矩阵1i -∑以及协方差矩阵的行列式i ∑，协方差矩阵计算公式如下11()(),1,2,3,41i ii N i jklj j lk k l i x x j k N ωωσμμ==--=-∑其中lj x 代表i ω类的第l 个样本，第j 个特征值；ij ωμ代表i ω类的i N 个样品第j 个特征的平均值lk x 代表i ω类的第l 个样品，第k 个特征值；iw k μ代表i ω类的i N 个样品第k 个特征的平均值。

模式识别专业实践报告(2篇)

第1篇一、实践背景与目的随着信息技术的飞速发展，模式识别技术在各个领域得到了广泛应用。

作为人工智能领域的一个重要分支，模式识别技术对于图像处理、语音识别、生物识别等领域的发展具有重要意义。

为了更好地理解和掌握模式识别技术，提高实际应用能力，我们组织了一次为期一个月的模式识别专业实践。

本次实践旨在通过实际操作，加深对模式识别理论知识的理解，提高解决实际问题的能力。

二、实践内容与过程1. 实践内容本次实践主要包括以下几个方面：（1）图像识别：利用深度学习算法进行图像分类、目标检测等。

（2）语音识别：实现语音信号处理、特征提取和识别。

（3）生物识别：研究指纹识别、人脸识别等生物特征识别技术。

（4）模式分类：运用机器学习算法进行数据分类和聚类。

2. 实践过程（1）理论学习：在实践开始前，我们首先对模式识别的基本理论进行了系统学习，包括图像处理、信号处理、机器学习等相关知识。

（2）项目准备：根据实践内容，我们选取了具有代表性的项目进行实践，如基于深度学习的图像识别、基于HMM的语音识别等。

（3）实验设计与实施：在导师的指导下，我们设计了实验方案，包括数据预处理、模型选择、参数调整等。

随后，我们使用Python、C++等编程语言进行实验编程，并对实验结果进行分析。

（4）问题分析与解决：在实验过程中，我们遇到了许多问题，如数据不足、模型效果不佳等。

通过查阅文献、请教导师和团队成员，我们逐步解决了这些问题。

三、实践成果与分析1. 图像识别我们使用卷积神经网络（CNN）对CIFAR-10数据集进行了图像分类实验。

实验结果表明，经过多次迭代优化，模型在测试集上的准确率达到89.5%，优于传统机器学习方法。

2. 语音识别我们采用HMM（隐马尔可夫模型）对TIMIT语音数据集进行了语音识别实验。

实验结果表明，经过特征提取和模型训练，模型在测试集上的词错误率（WER）为16.3%，达到了较好的识别效果。

3. 生物识别我们研究了指纹识别和人脸识别技术。

模式识别实习报告

一、实习背景随着科技的飞速发展，人工智能、机器学习等技术在各个领域得到了广泛应用。

模式识别作为人工智能的一个重要分支，具有广泛的应用前景。

为了更好地了解模式识别技术，提高自己的实践能力，我在2023年暑假期间参加了某科技有限公司的模式识别实习。

二、实习单位简介某科技有限公司是一家专注于人工智能、大数据、云计算等领域的科技创新型企业。

公司致力于为客户提供智能化的解决方案，业务涵盖智能识别、智能监控、智能分析等多个领域。

此次实习，我将在该公司模式识别部门进行实践学习。

三、实习内容1. 实习前期（1）了解模式识别的基本概念、原理和应用领域；（2）熟悉模式识别的相关算法，如神经网络、支持向量机、决策树等；（3）掌握Python编程语言，学会使用TensorFlow、Keras等深度学习框架。

2. 实习中期（1）参与实际项目，负责模式识别算法的设计与实现；（2）与团队成员协作，完成项目需求分析、算法优化和系统测试；（3）撰写项目报告，总结实习过程中的收获与不足。

3. 实习后期（1）总结实习期间的学习成果，撰写实习报告；（2）针对实习过程中遇到的问题，查找资料、请教同事，提高自己的解决问题的能力；（3）为后续实习工作做好充分准备。

四、实习收获与体会1. 理论与实践相结合通过实习，我深刻体会到理论与实践相结合的重要性。

在实习过程中，我将所学的模式识别理论知识运用到实际项目中，提高了自己的动手能力。

同时，通过解决实际问题，我更加深入地理解了模式识别算法的原理和应用。

2. 团队协作能力实习期间，我学会了与团队成员有效沟通、协作。

在项目中，我们共同面对挑战，分工合作，共同完成项目任务。

这使我认识到团队协作的重要性，为今后的工作打下了基础。

3. 解决问题的能力在实习过程中，我遇到了许多问题。

通过查阅资料、请教同事、独立思考等方式，我逐渐学会了如何分析问题、解决问题。

这种能力对我今后的学习和工作具有重要意义。

4. 深度学习框架的使用实习期间，我学会了使用TensorFlow、Keras等深度学习框架。

模式识别实习报告

实习报告一、实习背景及目的随着科技的飞速发展，模式识别技术在众多领域发挥着越来越重要的作用。

模式识别是指对数据进行分类、识别和解释的过程，其应用范围广泛，包括图像处理、语音识别、机器学习等。

为了更好地了解模式识别技术的原理及其在实际应用中的重要性，我参加了本次模式识别实习。

本次实习的主要目的是：1. 学习模式识别的基本原理和方法；2. 掌握模式识别技术在实际应用中的技巧；3. 提高自己的动手实践能力和团队协作能力。

二、实习内容及过程实习期间，我们团队共完成了四个模式识别项目，分别为：手写数字识别、图像分类、语音识别和机器学习。

下面我将分别介绍这四个项目的具体内容和过程。

1. 手写数字识别：手写数字识别是模式识别领域的一个经典项目。

我们使用了MNIST数据集，这是一个包含大量手写数字图片的数据集。

首先，我们对数据集进行预处理，包括归一化、数据清洗等。

然后，我们采用卷积神经网络（CNN）作为模型进行训练，并使用交叉验证法对模型进行评估。

最终，我们得到了一个识别准确率较高的模型。

2. 图像分类：图像分类是模式识别领域的另一个重要应用。

我们选择了CIFAR-10数据集，这是一个包含大量彩色图像的数据集。

与手写数字识别项目类似，我们先对数据集进行预处理，然后采用CNN进行训练。

在模型训练过程中，我们尝试了不同的优化算法和网络结构，以提高模型的性能。

最终，我们得到了一个识别准确率较高的模型。

3. 语音识别：语音识别是模式识别领域的又一项挑战。

我们使用了TIMIT数据集，这是一个包含大量语音样本的数据集。

首先，我们对语音样本进行预处理，包括特征提取、去噪等。

然后，我们采用循环神经网络（RNN）作为模型进行训练。

在模型训练过程中，我们尝试了不同的优化算法和网络结构。

最后，我们通过对模型进行评估，得到了一个较为可靠的语音识别系统。

4. 机器学习：机器学习是模式识别领域的基础。

我们使用了UCI数据集，这是一个包含多个数据集的数据集。

北科大模式识别基础实验报告

学院：自动化学院班级：姓名：学号：2014年11月实验一 Bayes 分类器的设计一、实验目的：1. 对模式识别有一个初步的理解，能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识；2. 理解二类分类器的设计原理。

二、实验条件：1. PC 微机一台和MATLAB 软件。

四、实验内容：假定某个局部区域细胞识别中正常（1ω）和非正常（2ω）两类先验概率分别为：正常状态：)(1ωP =0.9；异常状态：)(2ωP =0.1。

现有一系列待观察的细胞，其观察值为x ：-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531-2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752-3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682-1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532)|(1ωx P )|(2ωx P 类条件概率分布正态分布分别为（-2，0.25）（2,4）。

《模式识别》实验报告-贝叶斯分类

《模式识别》实验报告-贝叶斯分类一、实验目的通过使用贝叶斯分类算法，实现对数据集中的样本进行分类的准确率评估，熟悉并掌握贝叶斯分类算法的实现过程，以及对结果的解释。

二、实验原理1.先验概率先验概率指在不考虑其他变量的情况下，某个事件的概率分布。

在贝叶斯分类中，需要先知道每个类别的先验概率，例如：A类占总样本的40%，B类占总样本的60%。

2.条件概率后验概率指在已知先验概率和条件概率下，某个事件发生的概率分布。

在贝叶斯分类中，需要计算每个样本在各特征值下的后验概率，即属于某个类别的概率。

4.贝叶斯公式贝叶斯公式就是计算后验概率的公式，它是由条件概率和先验概率推导而来的。

5.贝叶斯分类器贝叶斯分类器是一种基于贝叶斯定理实现的分类器，可以用于在多个类别的情况下分类，是一种常用的分类方法。

具体实现过程为：首先，使用训练数据计算各个类别的先验概率和各特征值下的条件概率。

然后，将测试数据的各特征值代入条件概率公式中，计算出各个类别的后验概率。

最后，取后验概率最大的类别作为测试数据的分类结果。

三、实验步骤1.数据集准备本次实验使用的是Iris数据集，数据包含150个Iris鸢尾花的样本，分为三个类别：Setosa、Versicolour和Virginica，每个样本有四个特征值：花萼长度、花萼宽度、花瓣长度、花瓣宽度。

2.数据集划分将数据集按7:3的比例分为训练集和测试集，其中训练集共105个样本，测试集共45个样本。

计算三个类别的先验概率，即Setosa、Versicolour和Virginica类别在训练集中出现的频率。

对于每个特征值，根据训练集中每个类别所占的样本数量，计算每个类别在该特征值下出现的频率，作为条件概率。

5.测试数据分类将测试集中的每个样本的四个特征值代入条件概率公式中，计算出各个类别的后验概率，最后将后验概率最大的类别作为该测试样本的分类结果。

6.分类结果评估将测试集分类结果与实际类别进行比较，计算分类准确率和混淆矩阵。

哈工大模式识别实验报告

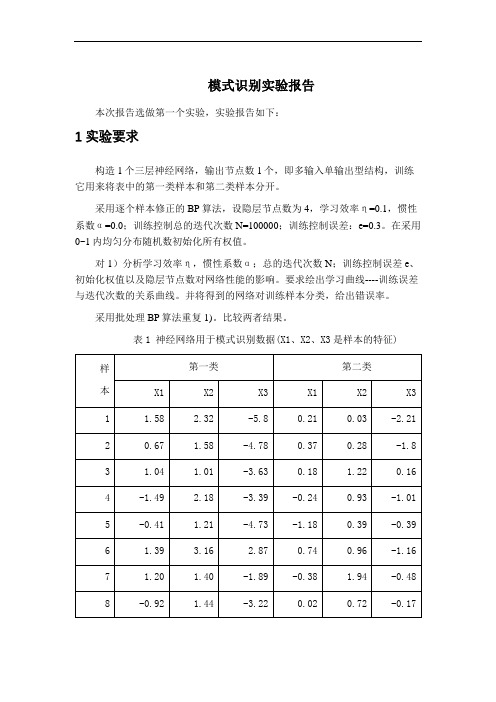
模式识别实验报告本次报告选做第一个实验，实验报告如下：1 实验要求构造1个三层神经网络，输出节点数1个，即多输入单输出型结构，训练它用来将表中的第一类样本和第二类样本分开。

采用逐个样本修正的BP算法，设隐层节点数为4，学习效率η=0.1，惯性系数α=0.0；训练控制总的迭代次数N=100000；训练控制误差：e=0.3。

在采用0~1内均匀分布随机数初始化所有权值。

对1）分析学习效率η，惯性系数α；总的迭代次数N；训练控制误差e、初始化权值以及隐层节点数对网络性能的影响。

要求绘出学习曲线----训练误差与迭代次数的关系曲线。

并将得到的网络对训练样本分类，给出错误率。

采用批处理BP算法重复1)。

比较两者结果。

表1 神经网络用于模式识别数据(X1、X2、X3是样本的特征)2 BP 网络的构建三层前馈神经网络示意图，见图1.图1三层前馈神经网络①网络初始化，用一组随机数对网络赋初始权值，设置学习步长η、允许误差ε、网络结构（即网络层数L 和每层节点数n l ）；②为网络提供一组学习样本； ③对每个学习样本p 循环a ．逐层正向计算网络各节点的输入和输出；b ．计算第p 个样本的输出的误差Ep 和网络的总误差E ；c ．当E 小于允许误差ε或者达到指定的迭代次数时，学习过程结束，否则，进行误差反向传播。

d ．反向逐层计算网络各节点误差)(l jp δ如果l f 取为S 型函数，即xl e x f -+=11)(，则对于输出层))(1()()()()(l jp jdp l jp l jp l jp O y O O --=δ 对于隐含层∑+-=)1()()()()()1(l kj l jp l jp l jp l jp w O O δδe ．修正网络连接权值)1()()()1(-+=+l ip l jp ij ij O k W k W ηδ式中，k 为学习次数，η为学习因子。

η取值越大，每次权值的改变越剧烈，可能导致学习过程振荡，因此，为了使学习因子的取值足够大，又不至产生振荡，通常在权值修正公式中加入一个附加动量法。

模式识别实验报告1_简单线性分类实验_实验报告(例)

3.随机给出一个样本并判别类别。
二、实验环境、内容和方法
环境：windows XP，matlab R2007a
内容：有两类样本（如鲈鱼和鲑鱼），每个样本有两个特征（如长度和亮度），每类有若干个（比如20个）样本点，假设每类样本点服从二维正态分布，自己随机给出具体数据，计算每类数据的均值点，并且把两个均值点连成一线段，用垂直平分该线段的直线作为分类边界。再根据该分类边界对一随机给出的样本判别类别。并画出相应的图形。
方法：线性分类器
三、实验过程描述
1.首先用正态分布normrnd产生两类样本，每类样本两个特征。用不同的均值(ax,ay)=(18,8),(bx,by)=(12,20)。并画出两类样本点。
2.然后，求判别分界线y=k*x+b中的k,b的值。分界线垂直于两类样本的均值点的连线。K,b的值分别为：
k=-(bx-ax)/(by-ay)
y2(:,1) = normrnd(by,6,1,20);
%分解线为y=k*x+b
k=-(bx-ax)/(by-ay);%计算类样本均值连线垂直平分线的斜率k
b=(ay+by)/2+(bx^2-ax^2)/(2*by-2*ay);%计算b的值
figure;%画点
plot(x1,y1,'om',...
实验报告（例子）
课程名称：模式识别实验名称：简单线性分类
提交时间：
专业：计算机应用技术年级：2009级姓名：
一、实验目的和要求
目的：设计简单的线性分类器，了解模式识别的基本方法。
要求：
1.产生两类样本，每类样本两个特征。
2.计算每类数据的均值点，并且把两个均值点连成一线段，用垂直平分该线段的直线作为分类边界。

模式识别实验报告

模式识别实验报告关键信息项：1、实验目的2、实验方法3、实验数据4、实验结果5、结果分析6、误差分析7、改进措施8、结论1、实验目的11 阐述进行模式识别实验的总体目标和期望达成的结果。

111 明确实验旨在解决的具体问题或挑战。

112 说明实验对于相关领域研究或实际应用的意义。

2、实验方法21 描述所采用的模式识别算法和技术。

211 解释选择这些方法的原因和依据。

212 详细说明实验的设计和流程，包括数据采集、预处理、特征提取、模型训练和测试等环节。

3、实验数据31 介绍实验所使用的数据来源和类型。

311 说明数据的规模和特征。

312 阐述对数据进行的预处理操作，如清洗、归一化等。

4、实验结果41 呈现实验得到的主要结果，包括准确率、召回率、F1 值等性能指标。

411 展示模型在不同数据集或测试条件下的表现。

412 提供可视化的结果，如图表、图像等，以便更直观地理解实验效果。

5、结果分析51 对实验结果进行深入分析和讨论。

511 比较不同实验条件下的结果差异，并解释其原因。

512 分析模型的优点和局限性，探讨可能的改进方向。

6、误差分析61 研究实验中出现的误差和错误分类情况。

611 分析误差产生的原因，如数据噪声、特征不充分、模型复杂度不足等。

612 提出减少误差的方法和建议。

7、改进措施71 根据实验结果和分析，提出针对模型和实验方法的改进措施。

711 描述如何优化特征提取、调整模型参数、增加训练数据等。

712 预测改进后的可能效果和潜在影响。

8、结论81 总结实验的主要发现和成果。

811 强调实验对于模式识别领域的贡献和价值。

812 对未来的研究方向和进一步工作提出展望。

在整个实验报告协议中，应确保各项内容的准确性、完整性和逻辑性，以便为模式识别研究提供有价值的参考和借鉴。

模式识别实验【范本模板】

《模式识别》实验报告班级：电子信息科学与技术13级02 班姓名：学号：指导老师:成绩：通信与信息工程学院二〇一六年实验一最大最小距离算法一、实验内容1. 熟悉最大最小距离算法,并能够用程序写出。

2. 利用最大最小距离算法寻找到聚类中心,并将模式样本划分到各聚类中心对应的类别中.二、实验原理N 个待分类的模式样本{}N X X X ， 21,，分别分类到聚类中心{}N Z Z Z ， 21,对应的类别之中.最大最小距离算法描述：（1）任选一个模式样本作为第一聚类中心1Z 。

（2）选择离1Z 距离最远的模式样本作为第二聚类中心2Z 。

（3）逐个计算每个模式样本与已确定的所有聚类中心之间的距离，并选出其中的最小距离.（4）在所有最小距离中选出一个最大的距离，如果该最大值达到了21Z Z -的一定分数比值以上，则将产生最大距离的那个模式样本定义为新增的聚类中心，并返回上一步.否则，聚类中心的计算步骤结束。

这里的21Z Z -的一定分数比值就是阈值T ，即有：1021<<-=θθZ Z T（5）重复步骤（3）和步骤（4），直到没有新的聚类中心出现为止。

在这个过程中，当有k 个聚类中心{}N Z Z Z ， 21,时,分别计算每个模式样本与所有聚类中心距离中的最小距离值,寻找到N 个最小距离中的最大距离并进行判别,结果大于阈值T 是，1+k Z 存在，并取为产生最大值的相应模式向量；否则,停止寻找聚类中心。

（6)寻找聚类中心的运算结束后，将模式样本{}N i X i ,2,1, =按最近距离划分到相应的聚类中心所代表的类别之中。

三、实验结果及分析该实验的问题是书上课后习题2。

1，以下利用的matlab 中的元胞存储10个二维模式样本X ｛1}=［0;0］；X{2}=［1；1];X ｛3｝=[2;2]；X{4｝=[3；7]；X{5｝=[3;6］; X{6}=［4；6］；X{7}=［5；7];X{8}=[6；3］;X{9｝=［7;3］;X{10}=［7;4]；利用最大最小距离算法，matlab 运行可以求得从matlab 运行结果可以看出，聚类中心为971,,X X X ，以1X 为聚类中心的点有321,,X X X ,以7X 为聚类中心的点有7654,,,X X X X ，以9X 为聚类中心的有1098,,X X X 。

模式识别的报告(1)

模式识别实验报告（2）姓名：某某某班号：075113学号：2011100xxxx指导老师：马丽基于kNN算法的遥感图像分类一、目标：1. 掌握KNN算法原理2. 用MATLAB实现kNN算法，并进行结果分析二、算法分析：所谓K最近邻，就是k个最近的邻居的意思，说的是每个样本都可以用她最接近的k个邻居来代表。

kNN算法的核心思想是如果一个样本在特征空间中的k 个最相似的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。

该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

kNN方法在类别决策时，只与极少量的相邻样本有关。

由于kNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。

三、实验内容：1.利用所有带标记的数据作为train数据，调用KNN分类函数KNN_Cla（）对整个图像进行分类，得到整个图像的分类结果图。

2.随机在所有带标记的数据中选择train和test数据（50%train数据，50%test 数据）然后进行kNN分类。

随机选择10次，计算总体分类精度OA，然后求平均结果，作为最终对算法的评价。

K值依次选择1,3,5,7,9,11，分别用这6种K的取值进行kNN算法，得到每种K值下的总体分类精度OA，然后进行比较。

分类结果：四、数据介绍：zy3sample1：资源三号卫星遥感图，Img为读入遥感图生成的400*400*4矩阵。

xy3roi：ROI数据，GT为读入ROI生成的400*400矩阵。

INP_200：INP高光谱数据145*145*200。

92A V3GT_cls：ROI数据45*145。

五、实验程序：function [result,OA]=knn_classifier(X_train,Y_train,X_test,Y_test,options)%% 实现KNN分类% 输入参数% X_train : N*D% Y_train : 1*N% X_test : N*D% 输出参数% result ：N*1% OA ：精确度for k=1:len%一次处理1个点len=length(X_test);d=Euclidian_distance(X_train,X_test(k,:);%计算所有待分类点到所有训练点的距离[D,n]=sort(d);ind=n(1:option.K);%找到所有距离中最小的K个距离for k=1:len%一次处理1个点C(k)=length(find(Y_train(ind)==k);endindc=find(max(C));result(k)=indc(1);end;error=length(find(result'~=Y_test));%求出差错率OA=1-error/len;六、实验结果：zy3sample数据KNN分类结果（K=1）：不同k值下的OA变化曲线图：七、心得体会：这次的程序主要是弄懂KNN 算法的思想就可以画出流程图其实最主要的就是搞清楚中间迭代部分的写法。

模式识别实验报告

的分类。
二、实验步骤前提条件：只考虑第三种情况：如果 di(x) >dj(x) 任意 j≠ i ，则判 x∈ωi 。
○1 、赋初值，分别给 c 个权矢量 wi(1)（i=1,2,…c）赋任意的初
值，选择正常数ρ ，置步数 k=1；
○2 、输入符号未规范化的增广训练模式 xk, xk∈{x1, x2… xN} ,
二、实验步骤
○1 、给出 n 个混合样本，令 I=1，表示迭代运算次数，选取 c
个初始聚合中心，j=1,2,…,c;
○2 、计算每个样本与聚合中心的距离
，
。
若
，，则
。
○3 、计算 c 个新的聚合中心：
，
。
○4 、判断：若
，
，则 I=I+1，返回
第二步 b 处，否则结束。三、程序设计
聚类没有影响。但当 C=2 时，该类别属于正确分类。而类别数目大于 2 时，初始聚合中心对聚类的影响非常大，仿真
结果多样化，不能作为分类标准。 2、考虑类别数目对聚类的影响：当类别数目变化时，结果也随之出现变化。 3、总结综上可知，只有预先分析过样本，确定合适的类别数目，才能对
样本进行正确分类，而初始聚合中心对其没有影响。
8
7
6
5
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
初始聚合中心为（0,0），（2,2）,（5,5），（7,7），（9,9）
K-均值聚类算法：类别数目 c=5 9
8
7
6
5
4

模式识别实验报告

模式识别实验报告班级：电信08-1班姓名：黄**学号：********课程名称：模式识别导论实验一安装并使用模式识别工具箱一、实验目的：1．掌握安装模式识别工具箱的技巧，能熟练使用工具箱中的各项功能；2．熟练使用最小错误率贝叶斯决策器对样本分类；3．熟练使用感知准则对样本分类；4．熟练使用最小平方误差准则对样本分类；5．了解近邻法的分类过程，了解参数K值对分类性能的影响（选做）；6．了解不同的特征提取方法对分类性能的影响（选做）。

二、实验内容与原理：1．安装模式识别工具箱；2．用最小错误率贝叶斯决策器对呈正态分布的两类样本分类；3．用感知准则对两类可分样本进行分类，并观测迭代次数对分类性能的影响；4．用最小平方误差准则对云状样本分类，并与贝叶斯决策器的分类结果比较；5．用近邻法对双螺旋样本分类，并观测不同的K值对分类性能的影响（选做）；6．观测不同的特征提取方法对分类性能的影响（选做）。

三、实验器材（设备、元器件、软件工具、平台）：1．PC机－系统最低配置512M 内存、P4 CPU；2．Matlab 仿真软件－7.0 / 7.1 / 2006a等版本的Matlab 软件。

四、实验步骤：1．安装模式识别工具箱。

并调出Classifier主界面。

2．调用XOR.mat文件，用最小错误率贝叶斯决策器对呈正态分布的两类样本分类。

3.调用Seperable.mat文件，用感知准则对两类可分样本进行分类。

4.调用Clouds.mat文件，用最小平方误差准则对两类样本进行分类。

5.调用Spiral.mat文件，用近邻法对双螺旋样本进行分类。

6.调用XOR.mat文件，用特征提取方法对分类效果的影响。

五、实验数据及结果分析：（1）Classifier主界面如下（2）最小错误率贝叶斯决策器对呈正态分布的两类样本进行分类结果如下：（3）感知准则对两类可分样本进行分类当Num of iteration=300时的情况：当Num of iteration=1000时的分类如下：（4）最小平方误差准则对两类样本进行分类结果如下：（5）近邻法对双螺旋样本进行分类，结果如下当Num of nearest neighbor=3时的情况为：当Num of nearest neighbor=12时的分类如下：（6）特征提取方法对分类结果如下当New data dimension=2时，其结果如下当New data dimension=1时，其结果如下六、实验结论：本次实验使我掌握安装模式识别工具箱的技巧，能熟练使用工具箱中的各项功能；对模式识别有了初步的了解。

模式识别技术实验报告

模式识别技术实验报告本实验旨在探讨模式识别技术在计算机视觉领域的应用与效果。

模式识别技术是一种人工智能技术，通过对数据进行分析、学习和推理，识别其中的模式并进行分类、识别或预测。

在本实验中，我们将利用机器学习算法和图像处理技术，对图像数据进行模式识别实验，以验证该技术的准确度和可靠性。

实验一：图像分类首先，我们将使用卷积神经网络（CNN）模型对手写数字数据集进行分类实验。

该数据集包含大量手写数字图片，我们将训练CNN模型来识别并分类这些数字。

通过调整模型的参数和训练次数，我们可以得到不同准确度的模型，并通过混淆矩阵等评估指标来评估模型的性能和效果。

实验二：人脸识别其次，我们将利用人脸数据集进行人脸识别实验。

通过特征提取和比对算法，我们可以识别不同人脸之间的相似性和差异性。

在实验过程中，我们将测试不同算法在人脸识别任务上的表现，比较它们的准确度和速度，探讨模式识别技术在人脸识别领域的应用潜力。

实验三：异常检测最后，我们将进行异常检测实验，使用模式识别技术来识别图像数据中的异常点或异常模式。

通过训练异常检测模型，我们可以发现数据中的异常情况，从而做出相应的处理和调整。

本实验将验证模式识别技术在异常检测领域的有效性和实用性。

结论通过以上实验，我们对模式识别技术在计算机视觉领域的应用进行了初步探索和验证。

模式识别技术在图像分类、人脸识别和异常检测等任务中展现出了良好的性能和准确度，具有广泛的应用前景和发展空间。

未来，我们将进一步深入研究和实践，探索模式识别技术在更多领域的应用，推动人工智能技术的发展和创新。

【字数：414】。

模式识别实验报告哈工程

一、实验背景随着计算机科学和信息技术的飞速发展，模式识别技术在各个领域得到了广泛应用。

模式识别是指通过对数据的分析、处理和分类，从大量数据中提取有用信息，从而实现对未知模式的识别。

本实验旨在通过实践操作，加深对模式识别基本概念、算法和方法的理解，并掌握其应用。

二、实验目的1. 理解模式识别的基本概念、算法和方法；2. 掌握常用的模式识别算法，如K-均值聚类、决策树、支持向量机等；3. 熟悉模式识别在实际问题中的应用，提高解决实际问题的能力。

三、实验内容本次实验共分为三个部分：K-均值聚类算法、决策树和神经网络。

1. K-均值聚类算法（1）实验目的通过实验加深对K-均值聚类算法的理解，掌握其基本原理和实现方法。

（2）实验步骤① 准备实验数据：选取一组二维数据，包括100个样本，每个样本包含两个特征值；② 初始化聚类中心：随机选择K个样本作为初始聚类中心；③ 计算每个样本到聚类中心的距离，并将其分配到最近的聚类中心；④ 更新聚类中心：计算每个聚类中所有样本的均值，作为新的聚类中心；⑤ 重复步骤③和④，直到聚类中心不再变化。

（3）实验结果通过实验，可以得到K个聚类中心，每个样本被分配到最近的聚类中心。

通过可视化聚类结果，可以直观地看到数据被分成了K个类别。

2. 决策树（1）实验目的通过实验加深对决策树的理解，掌握其基本原理和实现方法。

（2）实验步骤① 准备实验数据：选取一组具有分类标签的二维数据，包括100个样本，每个样本包含两个特征值；② 选择最优分割特征：根据信息增益或基尼指数等指标，选择最优分割特征；③ 划分数据集：根据最优分割特征，将数据集划分为两个子集；④ 递归地执行步骤②和③，直到满足停止条件（如达到最大深度、叶节点中样本数小于阈值等）；⑤ 构建决策树：根据递归分割的结果，构建决策树。

（3）实验结果通过实验，可以得到一棵决策树，可以用于对新样本进行分类。

3. 神经网络（1）实验目的通过实验加深对神经网络的理解，掌握其基本原理和实现方法。

模式识别实验报告

模式识别实验报告实验一、线性分类器的设计与实现1. 实验目的：掌握模式识别的基本概念，理解线性分类器的算法原理。

2. 实验要求：（1）学习和掌握线性分类器的算法原理；（2）在MATLAB 环境下编程实现三种线性分类器并能对提供的数据进行分类；（3）对实现的线性分类器性能进行简单的评估（例如算法适用条件，算法效率及复杂度等）。

注：三种线性分类器为，单样本感知器算法、批处理感知器算法、最小均方差算法批处理感知器算法算法原理：感知器准则函数为J p a=(−a t y)y∈Y，这里的Y(a)是被a错分的样本集，如果没有样本被分错，Y就是空的，这时我们定义J p a为0.因为当a t y≤0时，J p a是非负的，只有当a是解向量时才为0，也即a在判决边界上。

从几何上可知，J p a是与错分样本到判决边界距离之和成正比的。

由于J p梯度上的第j个分量为∂J p/ða j,也即∇J p=(−y)y∈Y。

梯度下降的迭代公式为a k+1=a k+η(k)yy∈Y k，这里Y k为被a k错分的样本集。

算法伪代码如下：begin initialize a，η(∙)，准则θ，k=0do k=k+1a=a+η(k)yy∈Y k|<θuntil | ηk yy∈Y kreturn aend因此寻找解向量的批处理感知器算法可以简单地叙述为：下一个权向量等于被前一个权向量错分的样本的和乘以一个系数。

每次修正权值向量时都需要计算成批的样本。

算法源代码：unction [solution iter] = BatchPerceptron(Y,tau)%% solution = BatchPerceptron(Y,tau) 固定增量批处理感知器算法实现%% 输入：规范化样本矩阵Y,裕量tau% 输出：解向量solution，迭代次数iter[y_k d] = size(Y);a = zeros(1,d);k_max = 10000; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% k=0;y_temp=zeros(d,1);while k<k_maxc=0;for i=1:1:y_kif Y(i,:)*a'<=tauy_temp=y_temp+Y(i,:)';c=c+1;endendif c==0break;enda=a+y_temp';k=k+1;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %k = k_max;solution = a;iter = k-1;运行结果及分析：数据1的分类结果如下由以上运行结果可以知道，迭代17次之后，算法得到收敛，解出的权向量序列将样本很好的划分。

模式识别实验报告_3

模式识别实验报告_3第⼀次实验实验⽬的：1.学习使⽤ENVI2.会⽤MATLAB读⼊遥感数据并进⾏处理实验内容：⼀学习使⽤ENVI1.使⽤ENVI打开遥感图像（任选3个波段合成假彩⾊图像，保存写⼊报告）2.会查看图像的头⽂件（保存或者copy⾄报告）3.会看地物的光谱曲线（保存或者copy⾄报告）4.进⾏数据信息统计（保存或者copy⾄报告）5.设置ROI，对每类地物⾃⼰添加标记数据，并保存为ROI⽂件和图像⽂件（CMap贴到报告中）。

6.使⽤⾃⼰设置的ROI进⾏图像分类（ENVI中的两种有监督分类算法）（分类算法名称和分类结果写⼊报告）⼆MATLAB处理遥感数据（提交代码和结果）7.⽤MATLAB读⼊遥感数据（zy3和DC两个数据）8.⽤MATLAB读⼊遥感图像中ROI中的数据（包括数据和标签）9.把图像数据m*n*L（其中m表⽰⾏数，n表⽰列数，L表⽰波段数），重新排列为N*L的⼆维矩阵（其中N=m*n），其中N表⽰所有的数据点数量m*n。

（提⽰，⽤reshape函数，可以help查看这个函数的⽤法）10.计算每⼀类数据的均值（平均光谱），并把所有类别的平均光谱画出来(plot)（类似下⾯的效果）。

11.画出zy3数据中“农作物类别”的数据点（⾃⼰ROI标记的这个类别的点）在每个波段的直⽅图（matlab函数：nbins=50;hist(Xi,nbins)，其中Xi表⽰这类数据在第i波段的数值）。

计算出这个类别数据的协⽅差矩阵，并画出（figure,imagesc(C),colorbar）。

1.打开遥感图像如下：2.查看图像头⽂件过程如下：3.地物的光谱曲线如下：4.数据信息统计如下：（注：由于保存的txt⽂件中的数据信息过长，所以采⽤截图的⽅式只显⽰了出⼀部分数据信息）5.设置ROI，对每类地物⾃⼰添加标记数据，CMap如下:6.使⽤⾃⼰设置的ROI进⾏图像分类(使⽤⽀持向量机算法和最⼩距离算法），⽀持向量机算法分类结果如下：最⼩距离算法分类结果如下：对⽐两种算法的分类结果可以看出⽀持分量机算法分类结果⽐最⼩距离算法分类结果好⼀些。