等腰三角形典型试题解析
(完整版)等腰三角形典型例题

等腰三角形1.如图,已知点C为线段AB上一点,和都是等边三角形,AN、BM相交于点O,AN、CM交于点P,BM、CN交于点Q.(1)求证:.(2)求的度数.(3)求证:.【分析】(1)欲证,只需证明它所在的两个三角形全等.(2)的度数可用的外角来求,但要注意全等所得到这一条件的使用.(3)要,则,应该为一个等边三角形,可证明≌,从而得到.(1)证明:和都是等边三角形,,,,,即.在和中,≌,.(2)由(1)知,≌,.,即.(3)在和中,≌,,.又,,即,.【点拨】(1)要证明线段相等(或角相等),找它们所在的三角形全等.(2)本题的图形规律:共一个顶点的两个等边三角形构成的图形中,存在一对或多对绕公共点旋转变换的三角形全等.2.如图,在中,,,的平分线AM的长15,求BC的长.【分析】由AM平分,,可得,,则,所以.在中,,可得,由,可求出BC的长.解:在中,,,.AM平分,,,.在中,,.【点拨】含30度的直角三角形的性质常与直角三角形的两个锐角互余一起运用,此性质是求线段长度和证明线段倍分问题的重要方法.3.如图,,,,.求证:.【分析】根据已知“,”联想到等腰三角形“三线合一”,通过辅助线将证明转化为证明.证明:延长CE、BA交于点F.,.在和中,≌,,即.,.在和中,≌,,.【点拨】(1)利用等腰三角形“三线合一”不仅能得到线段相等、角相等,而且能得到线段的倍半关系.(2)联系等腰三角形“三线合一”作顶角平分线或底边的中线或底边的高线是常用的辅助线.4.如图,△ABC中,AB=AC,在AB边上取点D,在AC延长线上取点E,使BD=CE,连结DE交BC于G.求证:DG=GE.【分析】由于△ABC是等腰三角形,D为AB上一点,E为AC延长线上一点,故可考虑过D或E作腰AC或AB的平行线,通过构造等腰三角形,可获得结论.证法1:过D作DF∥AC,交BC于F(如图).∴∠DFB=∠ACB.又∵AB=AC,∴∠B=∠ACB.∴∠B=∠DFB.∴DB=DF.∵CE=BD(已知),∴DF=CE.又∠DGF=∠CGE,∠GDF=∠E,∴△DFG≌△ECG(AAS).∴DG=GE.证法2:过E作EM∥AB交BC延长线于M.∴∠B=∠M.又∵AB=AC,∴∠B=∠ACB.又∠ACB=∠ECM,∴∠M=∠ECM.∴EC=EM.∵CE=BD(已知),∴EM=BD.在△BDG与△MEG中,∴△BDG≌△MEG(AAS).∴DG=GE.【点拨】(1)本题的证明方法很多,其思路是通过利用等腰三角形ABC的底角相等并借助BD=CE条件,构造新的等腰三角形来寻求结论.(2)本题在推证含DG、GE为对应边的两个三角形全等时,寻找等边是一个难点,也是本题最易出错的地方,主要表现为把BD=CE这一条件直接作为三角形全等时的对应边.5.已知:如图,△ABC中,AB=AC,∠A=36°,仿照图(1),请你再设计两种不同的方法,将△ABC分割成3个三角形,使得每个三角形都是等腰三角形(如图(1)).(2)图(2)(3)供画图用,作图工具不限,不要求写画法,不要求证明;要求标出所分得的每个等腰三角形三个内角的度数).【分析】由于所给三角形是一个含36°的等腰三角形,因而将它分成三个等腰三角形时仍只需考虑以36°,72°,108°等为内角的等腰三角形即可.解:本题显然应有多种结果,现提供3种,以供同学们参考,如图中(2)、(3)、(4);【点拨】像本例这种图形的分割问题的求解,一方面应把握原图形的特征,借助经验予以解决,另一方面还应大胆尝试,在操作中获得结果.6.如图,在一个宽度为的小巷内,一个梯子的长度为b,梯子的脚位于P点.将梯子的顶端放于一堵墙上Q点时,Q点离地面的高度为c,此时梯子与地面的夹角为.将梯子顶端放于对面一堵墙上R点,离开地面的高度为d,此时梯子与地面的夹角为.可知,为什么?【分析】由,,可知,又,可知为等边三角形,则,可推得.证明:连接RQ、RB.,,.又,为等边三角形,.在中,,,,,在线段PQ的垂直平分线上,.在中,,.在中,,,,即。
等腰等边三角形典型题

等腰等边三角形典型题一、等腰三角形典型题1. 题目:在等腰△ABC中,AB = AC,∠A = 50°,求∠B和∠C的度数。
- 解析:因为AB = AC,所以△ABC是等腰三角形,等腰三角形两底角相等。
三角形内角和为180°,已知∠A=50°,设∠B = ∠C = x,则可列方程x + x+50° = 180°,2x=180° - 50°,2x = 130°,解得x = 65°,所以∠B = ∠C = 65°。
2. 题目:等腰三角形的一个角是70°,求这个等腰三角形的顶角的度数。
- 解析:分两种情况讨论。
- 当这个70°的角是底角时,因为等腰三角形两底角相等,所以另一个底角也是70°,根据三角形内角和为180°,则顶角为180°-70°×2 = 180° - 140°=40°。
- 当这个70°的角是顶角时,顶角就是70°。
3. 题目:已知等腰三角形的腰长为5cm,底边长为6cm,求这个等腰三角形的面积。
- 解析:先作等腰三角形底边上的高。
因为等腰三角形三线合一(底边上的高、中线、顶角平分线三线合一),所以底边上的高将底边平分。
底边长为6cm,则底边的一半是3cm。
根据勾股定理,高h=√(5^2)-3^{2}=√(25 - 9)=√(16) = 4cm。
三角形面积S=(1)/(2)×底×高=(1)/(2)×6×4 = 12cm^2。
二、等边三角形典型题1. 题目:等边三角形ABC的边长为6,求它的高和面积。
- 解析:- 求高:因为等边三角形三线合一,设等边三角形的高为h,边长为a = 6,根据勾股定理h=√(a^2)-<=ft((a)/(2))^{2}=√(6^2)-3^{2}=√(36 - 9)=√(27)=3√(3)。
等腰三角形的性质与判定(6类热点题型讲练)(解析版) 八年级数学下册
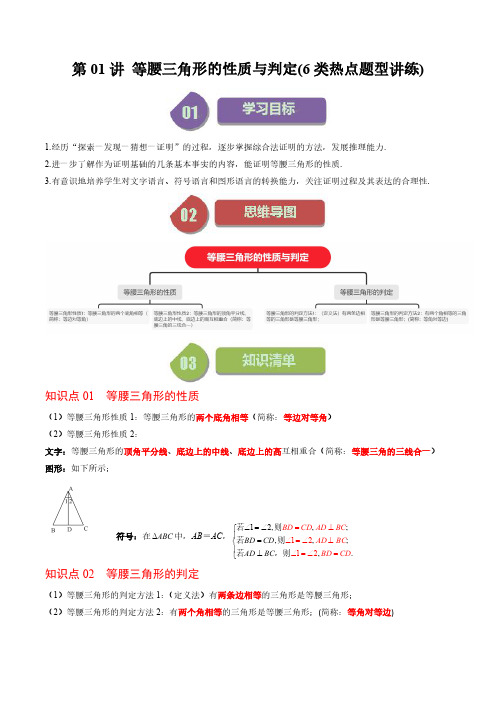
第01讲等腰三角形的性质与判定(6类热点题型讲练)1.经历“探索一发现一猜想一证明”的过程,逐步掌握综合法证明的方法,发展推理能力.2.进一步了解作为证明基础的几条基本事实的内容,能证明等腰三角形的性质.3.有意识地培养学生对文字语言、符号语言和图形语言的转换能力,关注证明过程及其表达的合理性.知识点01等腰三角形的性质(1)等腰三角形性质1:等腰三角形的两个底角相等(简称:等边对等角)(2)等腰三角形性质2:文字:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称:等腰三角的三线合一)图形:如下所示;符号:在ABC ∆中,AB =AC ,1212,,;,,;,12.BD CD AD BC AD B BD CD AD BC C BD CD ∠=∠⎧⎪=⊥∠=∠⊥∠=∠⎨⎪⊥⎩==若则若则若,则知识点02等腰三角形的判定(1)等腰三角形的判定方法1:(定义法)有两条边相等的三角形是等腰三角形;(2)等腰三角形的判定方法2:有两个角相等的三角形是等腰三角形;(简称:等角对等边)题型01根据等腰三角形腰相等求第三边或周长【例题】(2023上·河南商丘·八年级商丘市实验中学校考阶段练习)一个等腰三角形的两条边长分别为8cm 和4cm ,则第三边的长为cm .【答案】8【分析】本题考查等腰三角形的性质及三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,是解题的关键.【详解】解:①若一腰长为8cm ,则底边为4cm ,则第三边的长为8cm ,488+>,故能组成三角形;②若一腰长为4cm ,则底边为8cm ,则第三边的长为4cm ,448+=,故不能组成三角形.故答案为:8.【变式训练】1.(2023上·甘肃陇南·八年级校考阶段练习)一个等腰三角形有两边分别为3cm 和8cm ,则周长是cm .【答案】19【分析】本题考查了等腰三角形的性质和三角形的三边关系.等腰三角形两边的长为3cm 和8cm ,具体哪条是底边,哪条是腰没有明确说明,因此要分两种情况讨论.【详解】解:①当腰是3cm ,底边是8cm 时:338+<,不满足三角形的三边关系,因此舍去.②当底边是3cm ,腰长是8cm 时,388+>,能构成三角形,则其周长()38819cm =++=.故答案为:19.2.(2023上·山东潍坊·八年级校考阶段练习)若()2450a b -+-=,则以a ,b 为边长的等腰三角形的周长为.【答案】13或14【分析】本题考查了等腰三角形的概念,非负数的性质,以及三角形的三边关系,注意利用分类讨论思想解题.根据非负数的和为零,可得每个非负数同时为零,可得a ,b 的值,根据等腰三角形的概念进行分类讨论,可得答案.【详解】解:∵()2450a b -+-=,且()240a -≥,50b -≥,∴40a -=,50b -=,解得:4a =,5b =,当4为等腰三角形的腰长,5为等腰三角形的底边时,则等腰三角形的周长为44513++=,当5为等腰三角形的腰长,4为等腰三角形的底边时,则等腰三角形的周长为55414++=,故答案为:13或14.题型02根据等腰三角形等边对等角求角的度数题型03根据等腰三角形三线合一进行求解【答案】25【详解】解:如图,作BE ∵AB BC =,∴AE CE =,∵AC CD ⊥,90BAD ∠=︒∴EBA BAE BAE ∠+∠=∠+EBA CAD BAE ∠=∠∠=,【答案】10【详解】解:AB 5BD CD ∴==,210BC BD ∴==,故答案为:10.2.两个同样大小的含(1)求AF 的长.(2)求CD 的长.【详解】(1)解:连接AF ,如下图,根据题意,90BAC ∠=︒,AB ∴222(2)BC AB AC =+=∴190452B ACB ∠=∠=⨯︒=︒,∵F 为BC 中点,题型04根据等腰三角形三线合一进行证明(1)若106BAC DAE ∠∠=︒,(2)求证:BD EC =.【详解】(1)解:∵AB AC =(1180ADE AED ∠=∠=︒∵,AB AC AD AE ==,∴,BF CF DF EF ==,∴BD CE =.【变式训练】1.(2023上·山东威海·七年级校联考期中)如图,已知AB AE ABC AED BC ED =∠=∠=,,,点F 是CD 的中点,连接AF ,请判断AF 与CD 的位置关系.【答案】垂直【分析】此题考查全等三角形的判定和性质,等腰三角形三线合一的性质:连接AC AD ,,证明ABC AED ≌△△,得到AC AD =,根据等腰三角形三线合一的性质得到AF CD ⊥,熟练掌握全等三角形的判定定理及等腰三角形的性质是解题的关键.【详解】答:AF CD⊥连接AC AD,∵AB AE ABC AED BC ED=∠=∠=,,∴ABC AED≌△△∴AC AD=又∵点F 是CD 的中点∴AF CD ⊥.2.如图,在ABC 中,AB AC =,40BAC ∠︒=,AD 是BC 边上的高.线段AC 的垂直平分线交AD 于点E ,交AC 于点F ,连接BE .(1)试问:线段AE 与BE 的长相等吗?请说明理由;(2)求EBD ∠的度数.【详解】(1)解:线段AE 与BE 的长相等,理由如下:连接CE ,如图所示:=,AD∵AB AC=,∴BD CD∴AD为BC的垂直平分线,∵点E在AD上,=,∴BE CE又∵线段AC的垂直平分线交题型05根据等角对等边证明等腰三角形∠,【例题】(2023上·广西玉林·八年级统考期中)如图,点E在BA的延长线上,已知AD平分CAE ∥.求证:ABCAD BC是等腰三角形.【答案】证明见解析【分析】本题主要考查了等角对等边,平行线的性质与角平分线的定义,先根据平行线的性质得到EAD B CAD C ∠=∠∠=∠,,再由角平分线的定义和等量代换得到B C ∠=∠,即可证明ABC 是等腰三角形.【详解】证明:∵AD BC ∥,∴EAD B CAD C ∠=∠∠=∠,,∵AD 平分CAE ∠,∴EAD CAD ∠=∠,∴B C ∠=∠,∴ABC 是等腰三角形.【变式训练】【答案】ABC 是等腰三角形,理由见解析【分析】本题主要考查了等腰三角形的判定,三角形外角的性质,角平分线的定义,设4ACD x ∠=,3ECD x =∠,由角平分线的定义得到13BEC x ABC =-∠∠,A =∠【答案】证明见解析【分析】本题考查了平行线的性质,等腰三角形的性质和判定,证明根据角平分线的定义可得,以及直线平行的性质证明题型06等腰三角形的性质和判定综合应用【例题】如图,在ABC 中,AB AC =,D 是BC 边的中点,连接AD ,BE 平分ABC ∠交AC 于点E .(1)若40C ∠=︒,求BAD ∠的度数;(2)过点E 作EF BC ∥交AB 于点F ,求证:BEF △是等腰三角形.(3)若BE 平分ABC 的周长,AEF △的周长为15,求ABC 的周长.【详解】(1)解:AB AC = ,C ABC ∴∠=∠,∵40C ∠=︒,∴40ABC ∠=︒,AB AC = ,D 为BC 的中点,AD BC ∴⊥,90BDA ∴∠=︒,∴90904050BAD ABC ︒︒︒︒∠=-∠=-=;(2)证明:BE 平分ABC ∠,ABE EBC ∴∠=∠,又∵EF BC ∥,∴EBC BEF ∠=∠,∴EBF FEB ∠=∠,BF EF ∴=,BEF ∴ 是等腰三角形;(3)解:AEF 的周长为15,15AE AF EF ∴++=,BF EF = ,15AE AF BF ∴++=,即15AE AB +=,BE 平分ABC 的周长,=15AE AB BC CE ∴++=,ABC ∴ 的周长+1515=30AE AB BC CE ++=+.【变式训练】1.如图,在ABC 中,AB AC =,D 为CA 延长线上一点,DE BC ⊥于点E ,交AB 于点F .(1)求证:ADF △是等腰三角形(2)若6,3,4AD BE EF ===,求线段AB 的长.(1)试判断折叠后重叠部分△的面积.(2)求重叠部分AFC△【详解】(1)解:AFC∵四边形ABCD是长方形,∥,∴AD BC一、单选题1.(2023上·河南许昌·八年级统考期中)等腰三角形的一个底角为80︒,则这个等腰三角形的顶角为().A .20︒B .80︒C .100︒D .20︒或100︒【答案】A【分析】本题主要查了等腰三角形的性质.根据“等腰三角形两底角相等”,即可求解.【详解】解:∵等腰三角形的一个底角为80︒,∴等腰三角形的顶角为180808020︒-︒-︒=︒.故选:A2.(2024下·全国·七年级假期作业)如图,在ABC 中,,AB AC AD =为BC 边上的中线,30B ∠=︒,则CAD ∠的度数为()A .50︒B .60︒C .70︒D .80︒【答案】B【解析】略3.(2023上·广东珠海·八年级校考阶段练习)下列条件中,可以判定ABC 是等腰三角形的是()A .40B ∠=︒,80C ∠=︒B .123A BC ∠∠∠=::::C .2A B C∠=∠+∠D .三个角的度数之比是2:2:1【答案】D 【分析】本题考查了等腰三角形的判定,三角形内角和定理,熟练掌握等腰三角形的判定是解题的关键.利用三角形内角和定理,等腰三角形的判定,进行计算并逐一判断即可解答.【详解】解:A .∵40B ∠=︒,80C ∠=︒,A .16【答案】A 【分析】此题考查的是全等三角形的判定与性质、等腰三角形的性质,解题关键是掌握并会运用全等三角形的判定与性质、等腰三角形性质定理.先得出ABD ACF ∠=∠,进而得到AF 长,求出AB 出即可.【详解】CE BD ⊥ ,90BEF ∴∠=︒,90BAC ∠=︒ ,90CAF ∴∠=︒,90FAC BAD ∴∠=∠=︒ABD ACF ∴∠=∠.在ABD △和ACF △中【答案】10︒,80︒,140︒或20︒【详解】本题考查了等腰三角形的性质,先利用三角形内角和定理可得:AP AB =时;当AP AB =时;当BA BP =解:∵130ABC ∠=︒,30ACB ∠=︒,+∵BAC ∠是ABP 的一个外角,∴20BAC APB ABP ∠=∠+∠=︒,∵AB AP =,∵AB AP=,20BAP∠=︒,∴180802BAPABP APB︒-∠∠=∠==︒;当BA BP=时,如图:∵BA BP=,∴20BAP BPA∠=∠=︒,∴180140ABP BAP BPA∠=︒-∠-∠=︒;当PA PB=时,如图:∵PA PB=,∴20BAP ABP∠=∠=︒;综上所述:当ABP是等腰三角形时,故答案为:10︒,80︒,140︒或20︒.11.(2023上·广东汕尾·八年级校联考阶段练习)用一条长为21cm的细绳围成一个等腰三角形.(1)如果腰长是底边长的3倍,那么各边的长是多少?(2)能围成有一边的长为5cm的等腰三角形吗?如果能,请求出另两边长.【答案】(1)三角形的三边分别为3cm9cm9cm、、(2)能围成一个底边是5cm,腰长是8cm的等腰三角形【分析】本题考查了等腰三角形的性质,三角形的周长,难点在于要分情况讨论并利用三角形的三边关系进行判断.(1)设底边长为x cm,表示出腰长,然后根据周长列出方程求解即可;(1)求BD的长.(2)求BE的长.【答案】(1)4 (2)5,AE CD ⊥Q ,AD AC =,AE ∴平分CAD ∠,CAE DAE ∴∠=∠,在CAE V 和DAE 中,AC AD CAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩,()SAS CAE DAE ∴ ≌,CE DE ∴=,90ADE ACE ∠=∠=︒,设BE x =,则8CE DE x ==-,由勾股定理可得:222DE BD BE +=,()22284x x ∴-+=,解得:5x =,5BE ∴=.14.(2023上·浙江宁波·八年级统考期末)如图,在ABC 中,AB AC =,ED AB ∥,分别交BC 、AC 于点D 、E ,点F 在BC 的延长线上,且CF DE =,(1)求证:CEF △是等腰三角形;(2)连接AD ,当AD BC ⊥,8BC =,CEF △的周长为16时,求DEF 的周长.【答案】(1)证明见解析(2)20【分析】本题考查了等腰三角形的判定与性质,掌握等腰三角形的性质,等腰三角形的三线合一,是解答本题的关键.(1)利用等腰三角形的性质得到B ACB ∠=∠,然后推出EDC ECD ∠=∠,DE EC =,结合已知条件,得到结论.当AD BC ⊥时,AB AC =,∴142BD CD BC ===, DEF 的周长DE DF EF =++,∴DEF 的周长CE EF CD =+++15.(2023上·湖北武汉·八年级校联考阶段练习)的平分线,DF AB 交AE 的延长线于(1)若120BAC ∠=︒,求BAD ∠(2)求证:ADF △是等腰三角形.【答案】(1)60度(2)见解析(1)求证:BD CE =;(2)若BD AD =,B DAE ∠=∠,求【答案】(1)见解析(2)108BAC ∠=︒【答案】(1)等腰;(2)3;(3)12;(4)30;(5)5cm【分析】本题考查平行线的性质,角平分线的定义,对角对等边.(1)平行线的性质结合角平分线平分角,得到B C ∠=∠,即可得出结果;(2)平行线的性质结合角平分线平分角,得到A ABC CB =∠∠,进而得到AB AC =即可;(3)同法(2)可得:BD DE =,利用AB AD BD =+,求解即可;(5)同法(2)得到,PD BD PE CE ==,推出PDE △的周长等于BC 的长即可.掌握平行线加角平分线往往存在等腰三角形,是解题的关键.【详解】解:(1)∵AE BC ∥,∴,DAE B CAE C ∠=∠∠=∠,∵AE 平分DAC ∠,∴DAE CAE ∠=∠,∴B C ∠=∠,∴ABC 是等腰三角形;故答案为:等腰;(2)∵BC 平分ABD ∠,AC BD ∥,∴,ABC DBC ACB DBC ∠=∠∠=∠,∴A ABC CB =∠∠,∴3AB AC ==;故答案为:3;(3)同法(2)可得:7BD DE ==,∴5712AB AD BD =+=+=;故答案为:12;(4)同法(2)可得:,FD BD CE EF ==,∴ADE V 的周长30AD AE DE AD AE DF EF AD AE BD CE AB AC =++=+++=+++=+=;故答案为:30;(5)同法(2)可得:,PD BD PE CE ==,∴PDE △的周长5cm PD PE DE BD CE DE BC =++=++==;故答案为:5cm .18.(2023上·福建龙岩·八年级校考期中)概念学习规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.(3)当ACD 是等腰三角形,DA DC =时,如图,则50ACD A ∠=∠=︒,50BCD A ∠=∠=︒∴100ACB ACD BCD ∠=∠+=︒∠;当ACD 是等腰三角形,DA AC =时,如图,则65ACD ADC ∠=∠=︒,50BCD A ∠=∠=︒,∴5065115ACB ∠=︒+︒=︒;当ACD 是等腰三角形,CD AC =的情况不存在;当BCD △是等腰三角形,DC BD =时,如图,则1803ACD BCD B ︒-∠=∠=∠=∴2603ACB ACD BCD ∠=+=∠∠当BCD △是等腰三角形,DB =则BDC BCD ∠=∠,设BDC BCD x ∠=∠=,则B ∠=则1802ACD B x ∠=∠=︒-,由题意得,180250x x ︒-+︒=,解得,2303x ︒=,∴8018023ACD x ︒∠=︒-=,∴3103ACB ︒∠=,综上所述:ACB ∠的度数为100。
人教版八年级数学上册单元测试题:等腰三角形(含答案解析)

人教版八年级数学上册单元测试题:等腰三角形(含答案解析)第一题已知等腰三角形ABC中,AB = AC,角BAC = 70°。
求角ABC和角ACB的度数。
解析由于AB = AC,所以角ABC = 角ACB,设角ABC和角ACB 的度数都为 x。
根据角度和定理,得到方程:x + x + 70° = 180°解方程得到:2x + 70° = 180°移项得:2x = 110°解得:x = 55°所以,角ABC和角ACB的度数分别为 55°。
第二题在等腰三角形PQR中,PR = PQ,角PQR = 130°。
求角RPQ 的度数。
解析由于PR = PQ,所以角RPQ = 角RQP,设角RPQ和角RQP的度数都为 y。
根据角度和定理,得到方程:y + y + 130° = 180°解方程得到:2y + 130° = 180°移项得:2y = 50°解得:y = 25°所以,角RPQ的度数为 25°。
第三题在等腰三角形XYZ中,XY = YZ,角YXZ = 45°。
求角XYZ 和角YZX的度数。
解析由于XY = YZ,所以角XYZ = 角YZX,设角XYZ和角YZX 的度数都为 z。
根据角度和定理,得到方程:z + z + 45° = 180°解方程得到:2z + 45° = 180°移项得:2z = 135°解得:z = 67.5°所以,角XYZ和角YZX的度数分别为 67.5°。
初二数学等腰三角形试题答案及解析

初二数学等腰三角形试题答案及解析1.如图,已知在△ABC中,AB=AC=10cm,BC=12cm,点E、F都在中线AD上,连接EB、EC、FB、FC,则图中阴影部分的面积为.【答案】24cm2【解析】根据等腰三角形的性质求得△ABC底边上的高线AD的长度,然后求图中阴影部分,即三个等高三角形的面积和.解:∵在△ABC中,AB=AC=10cm,BC=12cm,AD是中线,∴AD⊥BC,BD=CD=BC=6cm,∴AD=8cm(勾股定理),∴S阴影=S△ABE+S△EFC+S△BDE=BD•(AE+EF+FD)=BD•AD=×6cm×8cm=24cm2.故答案是:24cm2.点评:本题考查了等腰三角形的性质、三角形的面积.解答此题时,可以发现图中阴影部分的面积实际上是由三个等高不等底的三角形的和,而这三个三角形的底边的和恰好是等腰△ABC的高线AD的长度.2.如图,在△ABC中,B是AC上一点,AD=BD=BC,若∠C=25°,则∠ADB= .【答案】80°【解析】首先利用等腰三角形的性质得到∠C=∠BDC,利用三角形的外角的性质得到∠A和∠ABD的度数,从而确定∠ADB的度数.解:∵BD=BC,∠C=25°,∴∠C=∠BDC=50°,∴∠ABD=∠C+∠BDC=50°,∵AD=BD,∴∠A=∠DBA=50°,∴∠ADB=180°﹣∠A﹣∠DBA=80°,答案为:80°.点评:本题考查了等腰三角形的性质,解答过程中两次运用“等边对等角”,难度不大.3.已知实数x,y满足|x﹣4|+(y﹣8)2=0,则以x,y的值为两边长的等腰三角形的周长是.【答案】20【解析】先根据非负数的性质列式求出x、y的值,再分4是腰长与底边两种情况讨论求解.解:根据题意得,x﹣4=0,y﹣8=0,解得x=4,y=8,①4是腰长时,三角形的三边分别为4、4、8,∵4+4=8,∴不能组成三角形,②4是底边时,三角形的三边分别为4、8、8,能组成三角形,周长=4+8+8=20,所以,三角形的周长为20.故答案为:20;点评:本题考查了等腰三角形的性质,绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0求出x、y的值是解题的关键,难点在于要分情况讨论并且利用三角形的三边关系进行判断.4.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D、E为垂足,BD与CE交于点O,则图中全等三角形共有对.【答案】3【解析】根据等腰三角形性质推出∠ABC=∠ACB,根据垂线定义证∠ADB=∠AEC,∠BEO=∠CDO,根据AAS证△BEC≌△BDC,根据AAS证△ADB≌△AEC,根据AAS证△BEO≌△CDO即可解:有3对:理由是∵AB=AC,∴∠ABC=∠ACB,∵BD⊥AC,CE⊥AB,∴∠BDC=∠BEC=90°,∵BC=BC,∴△BEC≌△BDC,∵∠ADB=∠AEC,∠A=∠A,AB=AC,∴△ADB≌△AEC,∴AD=AE,∴BE=DC,∵∠EOB=∠DOC,∠BEC=∠BDC,∴△BEO≌△CDO,故答案为:3.点评:本题主要考查对全等三角形的性质和判定,等腰三角形性质,垂线定义等知识点的理解和掌握,能推出证三角形全等的三个条件是解此题的关键.5.等腰三角形的两边长分别是3和5,则这个等腰三角形的周长为.【答案】11或13【解析】分3是腰长与底边两种情况讨论求解.解:①3是腰长时,三角形的三边分别为3、3、5,能组成三角形,周长=3+3+5=11,②3是底边长时,三角形的三边分别为3、5、5,能组成三角形,周长=3+5+5=13,综上所述,这个等腰三角形的周长是11或13.故答案为:11或13.点评:本题考查了等腰三角形的性质,难点在于分情况讨论并利用三角形的三边关系判断是否能组成三角形.6.已知等腰三角形的两条边长分别为3和7,那么它的周长等于.【答案】17【解析】分两种情况讨论:当3是腰时或当7是腰时.根据三角形的三边关系,知3,3,7不能组成三角形,应舍去.解:当3是腰时,则3+3<7,不能组成三角形,应舍去;当7是腰时,则三角形的周长是3+7×2=17.故答案为:17.点评:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.此类题不要漏掉一种情况,同时注意看是否符合三角形的三边关系.7.已知等腰三角形一腰上的中线将它周长分成18cm和12cm两部分,则这个等腰三角形的底边长是.【答案】6cm或8cm【解析】设等腰三角形的腰长、底边长分别为xcm,ycm,根据题意列二元一次方程组,注意没有指明具休是哪部分的长为18,故应该列两个方程组求解.解:∵等腰三角形的周长是18cm+12cm=30cm,设等腰三角形的腰长、底边长分别为xcm,ycm,由题意得或,解得或∴等腰三角形的底边长为6cm或8cm.(1分)故答案为:6cm或8cm.点评:此题主要考查等腰三角形的性质,解二元一次方程组和三角形三边关系的综合运用,此题的关键是分两种情况分析,求得解之后注意用三角形三边关系进行检验.8.等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是 cm.【答案】20【解析】本题可先根据三角形三边关系,确定等腰三角形的腰和底的长,然后再计算三角形的周长.解:当腰长为4时,则三角形的三边长为:2、2、9;∵2+2<9,∴不能构成三角形;因此这个等腰三角形的腰长为9,则其周长=9+9+2=20.故答案为:20.点评:本题考查了等腰三角形的性质和三角形的三边关系;对于已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.9.如图,直角三角形ABC中,∠BAC=90°AD⊥BC,AE是BC边上的中线,①若∠C=40°,则∠DAE= °;②若∠DAE=20°,则∠C= °.【答案】10°,35°【解析】利用∠C=40°,可先求∠BAC,再利用AE是∠BAC的角平分线,可求∠EAC,在Rt△ADC中,可求∠DAC,从而可求∠DAE.解:①∵直角三角形ABC中,∠BAC=90°AD⊥BC,AE是BC边上的中线∠C=40°,∴BE=AE=CE,∴∠EAC=∠C=40°,∠DAC=50°,∴∠DAE=∠DAC﹣∠EAC=50°﹣40°=10°,②∵∠DAE=20°,∴∠AEC=70°∴∠C=∠EAC=35°,故答案为10°,35°.点评:本题利用了三角形内角和定理、角平分线定理.三角形的内角和等于180°.10.如图,在△ABC中,AB=AC,∠BAD=15°,且AE=AD,则∠CDE= °.【答案】7.5°【解析】根据等腰三角形性质推出∠1=∠2,∠B=∠C,根据三角形的外角性质得到∠1+∠3=∠B+15°,∠2=∠C+∠3,推出2∠3=15°即可.解:∵AD=AE,AC=AB,∴∠1=∠2,∠B=∠C,∵∠1+∠3=∠B+∠BAD=∠B+15°,∠2=∠1=∠C+∠3,∴∠C+∠3+∠3=∠B+15°,2∠3=15°,∴∠3=7.5°,即∠CDE=7.5°,故答案为:7.5°.点评:本题主要考查对等腰三角形的性质,三角形的外角性质等知识点的理解和掌握,熟练地运用性质进行推理是解此题的关键.11.如图,在△ABC中,已知BA=BC,∠B=120°,AB的垂直平分线DE交AC于点D.(1)求∠A的度数;(2)若AC=6cm,求AD的长度.【答案】(1)30°(2)2cm【解析】(1)根据等腰三角形的两个底角相等、三角形内角和定理来求∠A的度数;(2)连接BD.根据线段垂直平分线的性质知△ABD是等腰三角形;然后利用(1)中的∠A=∠C=30°和已知条件∠B=120°可以推知△CDB是直角三角形,利用30度角所对的直角边是斜边的一半即可求得BD与CD间的数量关系;最后利用等腰三角形ABD的两腰相等(AD=BD)通过等量代换即可求得AC=3AD,从而求得线段AD的长度.解:(1)∵在△ABC中,已知BA=BC,∴∠A=∠C(等边对等角);又∵∠B=120°,∴∠A=(180°﹣120°)=30°(三角形内角和定理);(2)连接BD.∵AB的垂直平分线DE交AC于点D,∴AD=BD,∠A=∠ABD=30°,∴∠CBD=90°;由(1)知∠A=∠C=30°,∴BD=CD(30°所对的直角边是斜边的一半),∴CD=2AD=2BD,∴AC=AD+CD=AD+2AD=3AD;又∵AC=6cm,∴AD=2cm.点评:本题综合考查了等腰三角形的性质、含30度角的直角三角形以及三角形内角和定理.解答(2)题时,要充分利用等腰三角形的“三线合一”的性质.12.如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数.【答案】21°【解析】求出∠ABC,根据三角形内角和定理求出∠A,根据线段垂直平分线得出AD=BD,求出∠ABD,即可求出答案.解:∵AB=AC,∠C=67°,∴∠ABC=∠C=67°,∴∠A=180°﹣67°﹣67°=46°,∵EF是AB的垂直平分线,∴AD=BD,∴∠A=∠ABD=46°,∴∠DBC=67°﹣46°=21°.点评:本题考查了线段垂直平分线,三角形的能或定理,等腰三角形的性质和判定等知识点,关键是求出∠ABC和∠ABD的度数,题目比较好.13.如图,△ABC中,AB=AC,BD平分∠ABC交AC于点D,若∠A=52°,则∠BDC等于()A.84°B.64°C.52°D.32°【答案】A【解析】根据角平分线的性质,依据∠A=52°,AB=AC,可求得△ABC中三个内角的度数,然后根据三角形的外角性质可求出∠BDC=∠A+∠ABD.解:∵△ABC中,AB=AC,∠A=52°,∴∠ABC=∠C=(180﹣∠A)÷2=64°;又∵BD平分∠ABC交AC于点D,∴∠ABD=32°,∴∠BDC=∠A+∠ABD=32°+52°=84°.故选A.点评:主要考查了等腰三角形的性质.解题时,需要熟知三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.14.下列性质中,等腰三角形具有而直角三角形不一定具有的是()A.任意两边之和大于第三边B.内角和等于180°C.有两个锐角的和等于90°D.有一个角的平分线垂直于这个角的对边【答案】D【解析】根据等腰三角形与直角三角形的性质作答.解:A、对于任意一个三角形都有两边之和大于第三边,不符合题意;B、对于任意一个三角形都有内角和等于180°,不符合题意;C、只有直角三角形才有两个锐角的和等于90°,不符合题意;D、等腰三角形顶角的平分线垂直于顶角的对边,而直角三角形(等腰直角三角形除外)没有任何一个角的平分线垂直于这个角的对边,符合题意.故选D.点评:本题主要考查了三角形的性质,等腰三角形与直角三角形的性质的区别.15.如图,在四边形ABCD中,△ABC与△ADC关于对角线AC对称,则以下结论正确的是()①AC平分∠BAD②CA平分∠BCD③BD⊥AC④BE=DE.A.①②③④B.①②③C.①②D.④【答案】A【解析】根据轴对称的性质推出△ABC≌△ADC,推出∠BAC=∠DAC,∠BCA=∠DCA,AD=AB,根据等腰三角形性质求出BE=DE,AE⊥BD,根据以上结论判断即可.解:∵△ABC与△ADC关于对角线AC对称,∴△ABC≌△ADC,∴∠BAC=∠DAC,∠BCA=∠DCA,∴①正确;②正确;AB=AD,∴BE=DE,AE⊥BD,∴④正确;即BD⊥AC,∴③正确.故选A.点评:本题主要考查对轴对称的性质,全等三角形的性质和判定,等腰三角形的性质等知识点的理解和掌握,能推出△ABC≌△ADC是解此题的关键.16.如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,AD=8cm,BC=6cm,点E、F是AD上的两点,则图中阴影部分的面积是()A.48B.24C.12D.6【答案】C【解析】根据等腰三角形性质求出BD=DC ,AD ⊥BC ,推出△CEF 和△BEF 关于直线AD 对称,得出S △BEF =S △CEF ,根据图中阴影部分的面积是S △ABC 求出即可.解:∵AB=AC ,AD 是∠BAC 的平分线,∴BD=DC=8,AD ⊥BC , ∴△ABC 关于直线AD 对称, ∴B 、C 关于直线AD 对称, ∴△CEF 和△BEF 关于直线AD 对称, ∴S △BEF =S △CEF ,∵△ABC 的面积是×BC×AD=×8×6=24,∴图中阴影部分的面积是 S △ABC =12.故选C .点评:本题主要考查对等腰三角形性质,三角形的面积,轴对称性质等知识点的理解和掌握,能求出图中阴影部分的面积是S △ABC 是解此题的关键.17. 已知等腰三角形的一个外角等于140°,则这个三角形的三个内角的度数分别是( )A .20°、20°、140°B .40°、40°、100°C .70°、70°、40°D .40°、40°、100°或70°、70°、40°【答案】D【解析】由于140°的外角不明确等腰三角形顶角和底角的外角,故应分两种情况讨论.解:(1)当40°角是顶角时,另两个底角度数为70°,70°;(2)当40°角是底角时,另两个底角度数为40°,100°.故选D .点评:本题考查了等腰三角形的性质及三角形内角和定理;等腰三角形的角度计算,要注意区别顶角,底角的不同情况,不要漏解.18. 如图,△ABC 中,D 为AB 上一点,E 为BC 上一点,且AC=CD=BD=BE ,∠A=50°,则∠CDE 的度数为( )A .50°B .51°C .51.5°D .52.5°【答案】D【解析】根据等腰三角形的性质推出∠A=∠CDA=50°,∠B=∠DCB ,∠BDE=∠BED ,根据三角形的外角性质求出∠B=25°,由三角形的内角和定理求出∠BDE ,根据平角的定义即可求出选项. 解:∵AC=CD=BD=BE ,∠A=50°,∴∠A=∠CDA=50°,∠B=∠DCB ,∠BDE=∠BED ,∵∠B+∠DCB=∠CDA=50°, ∴∠B=25°, ∵∠B+∠EDB+∠DEB=180°,∴∠BDE=∠BED=(180°﹣25°)=77.5°,∴∠CDE=180°﹣∠CDA ﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故选D .点评:本题主要考查对等腰三角形的性质,三角形的内角和定理,三角形的外角性质,邻补角的定义等知识点的理解和掌握,熟练地运用这些性质进行计算是解此题的关键.19.如图,在△ABC中,AB=AC,AB的垂直平分线交BC于D,M是BC的中点,若∠BAD=30°,则图中等于30°的角的个数是()A.1个B.2个C.3个D.4个【答案】D【解析】本题先运用线段垂直平分线的性质得出∠BAD=∠ABD=∠C,又因为△ABC为等腰三角形可得AM⊥BC,然后证得△ADM∽△ACM,然后可求解.解:已知AB的垂直平分线交BC于D可得∠BAD=∠B=30°又因为△ABC为等腰三角形,所以∠BAD=∠ABD=∠CM为等腰三角形△ABC的中线,故AM⊥BC∴△ADM∽△ACM,∴∠DAM=∠C=30°.故选D.点评:本题先看清图中三角形的关系,再根据线段垂直平分线的性质以及等腰三角形中线的性质求解,难度一般.20.如图,AD=BC=BA,那么∠1与∠2之间的关系是()A.∠1=2∠2B.2∠1+∠2=180°C.∠1+3∠2=180°D.3∠1﹣∠2=180°【答案】B【解析】由已知条件可得到∠2=∠B,∠1=∠BCA,在△ABC中,由∠1+∠ACB+∠B=180°,可推出结论.解:∵AB=BC,∴∠1=∠BCA,∵AB=AD,∴∠B=∠2,∵∠1+∠B+∠ACB=180°,∴2∠1+∠2=180°.故选B.点评:本题考查了对等边对等角和三角形内角和定理的应用.。
初二数学等腰三角形的性质试题答案及解析

初二数学等腰三角形的性质试题答案及解析1.如图,△ABC中,∠B,∠C的平分线相交于O点,作MN∥BC,EF∥AB,GH∥AC,BC=a,AC=b,AB=c,则△GMO的周长+△ENO的周长-△FHO的周长= .【答案】b+c-a【解析】由角平分线及平行线可得等腰三角形,进而得边长相等,再通过转化,即可得出结论.∵OB、OC分别平分∠ABC、∠ACB,MN∥BC,EF∥AB,GH∥AC,∴OM=BM,ON=NC,OG=AE,OE=AG,∴△GMO周长+△ENO的周长-△FHO的周长=OG+OM+GM+OE+ON+EN-OH-OF-FH=AE+EN+NC+BM+GM+AG-HC-FH-BF=b+c-a,故应填b+c-a.【考点】本题主要考查角平分线的性质,平行线的性质点评:解答本题的关键是掌握由角平分线及平行线可得等腰三角形,再通过转化求解。
2.△ABC中,AB=AC,∠A=∠C,则∠B=_______.【答案】60°【解析】由AB=AC根据等边对等角可得∠B=∠C,即可得到∠A=∠B=∠C,再根据三角形的内角和180°即可求得结果。
∵AB=AC,∴∠B=∠C,∵∠A=∠C,∴∠A=∠B=∠C,∵∠A+∠B+∠C=180°,∴∠A=∠B=∠C=60°,故答案为60°.【考点】本题考查的是等腰三角形的性质,三角形的内角和定理点评:解答本题的关键是根据等边对等角得到∠A=∠B=∠C.3.如图,Rt△ACB中,∠ACB=90°,点D、E在AB上,AC=AD,BE=BC,则∠DCE等于()A、45°B、60°C、50°D、65°【答案】A【解析】根据等腰三角形的性质可得到几组相等的角,再根据三角形内角和定理可分别表示出∠ACD,∠BCE,再根据角之间的关系,不难求得∠DCE的度数.∵AC=AD,BC=BE∴∠ACD=∠ADC,∠BCE=∠BEC∴∠ACD=(180°-∠A),∠BCE=(180°-∠B)∴∠DCE=∠ACD+∠BCE-∠ACB=90°-(∠A+∠B)∵∠A+∠B=90°∴∠DCE=45°故选A.【考点】此题主要考查等腰三角形的性质及三角形内角和定理的综合运用点评:解答本题的关键是熟练掌握等腰三角形的性质及三角形内角和定理的综合运用。
等腰三角形典型题解析

B
E
∴△ABC≌△AED(SAD) ∴AC=AD(全等三角形的对应边相等)
C FD
又∵△ACD 中 AF 是 CD 边的中线(已知)
燕园教育辅导中心
∴AF⊥CD(等腰三角形底边上的高和底边上的中线互相重合)
三、练习
(一)、选择题
1.等腰三角形的对称轴是( )
A.顶角的平分线
B.底边上的高
C.底柱 BD、DE 要多长?
B D
以发现在 Rt△AED 与 Rt△ACB 中,由于∠A=30°, A E C
1
1
AB,又由 D 是 AB 的中点,所以 DE= AB.
2
4
[例]等腰三角形的底角为 15°,腰长为 2a,求腰上的高.
分析:观察图形可
1
所 以 DE= AD, BC=
燕园教育辅导中心
A D
E
B
C
答案: 10.60°或 120° 11.∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°, ∴在 Rt△ADC 中 CD=2AD, ∵∠BAC=120°,∴∠BAD=120°-90°=30°, ∴∠B=∠BAD,∴AD=BD,∴BC=3AD 12.①∵∠ACB=∠DCE=60°,
⊥CD.
分析:要证明 AF⊥CD,而点 F 是 CD 的中点,联想到这是等腰三角形特有的性质,于是连接 AC、
AD,证明 AC=AD,利用等腰三角形“三线合一”的性质得到结论.
在△ABC 和△AED 中
证 明 : 连 接 AC、 AD A
AB AE(三 三 ) ABC AED(三 三 ) BC ED(三 三 )
等边三角形
一、复习知识要点
1.三条边都相等的三角形叫做等边三角形,也叫做正三角形.
初二数学-等腰三角形10道典型题剖析

思路分析:由BD平分∠ABC,
A
易知∠1=∠2, 则设∠1=∠2
=x,由AB=AC可得
1
∠C=∠1+∠2=2x,在△DBC中
2
由三角形内角和定理可列出x B
D C
的方程,求出x.
解:设1 x,
BD平分ABC,
A
1 2 x, AB AC,
1 2
B
D C
C ABC 1 2 2x.
在DBC中,
提示: 本题为文字命题,解题时应分为以下 三个步骤: (1)根据题意作图; (2)写出已知, (3)进行求证.
已知:在ABC中,AB AC, D为底边BC
的中点,DE AB于点E, DF AC于点F.
求证:DE DF.
A
思路分析:由等腰三角形的性质易得
E
F
B C,又BD DC,DE AB, DF AC,
∴∠FBC+∠C+∠FBC=3∠C,
∴∠FBC=∠C, ∴BF=FC, ∴AC-AB=2BE.
例8.如图,△ABD、 △AEC都是等边三角 形,求证: △AFG是等边三角形.
思路分析:利用等边三角 形的性质可推出,边、角 的等量关系,从而易证三 角形全等,进而说明
△AFG是等边三角形.
证明:∵△ABD 和△AED是正三角形, ∴AB=AD,AC=AE,∠BAD=∠CAE=60°, ∴ ∠CAD=∠BAD+∠CAB=60°+∠CAB, ∠BAE=∠CAE+∠CAB=60°+∠CAB, ∴ ∠CAD=∠BAE, △ADC≌△BAE, ∴ ∠ADF=∠GBA.
70°、40°或55°、55°
引申: 已知等腰三角形的一个角是110°, 求其余两角.
初二数学等腰三角形的判定试题答案及解析

初二数学等腰三角形的判定试题答案及解析1.有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,则灯塔与船之间的最近距离是海里.【答案】10【解析】过P作PD⊥AB于D,则PD的长就是灯塔与船之间的最近距离,求出∠APB=∠PAB,推出PA=PB=20,根据含30度角的直角三角形性质求出PD=PB,代入求出即可.解:如图:过P作PD⊥AB于D,则PD的长就是灯塔与船之间的最近距离,∴∠PDB=90°,∵∠PBD=30°,∠PAB=15°,∴∠APB=∠PBD﹣∠PAB=15°=∠PAB,∴PB=AB=20,在Rt△PBD中,PB=20,∠PBD=30°,∴PD=PB=10,故答案为:10.点评:本题考查了含30度角的直角三角形,等腰三角形的性质和判定,三角形的外角性质等知识点的应用,关键是求出PB的长和得出PD=PB,题目比较典型,是一道比较好的题目,主要考查学生的理解能力和计算能力.2.如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,有下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD;⑤BE=CH.其中你认为正确的有.(填序号就可以)【答案】①②③【解析】①由CD是斜边AB上的高,∠ACB=90°,得到∠ACD+∠BCD=90°,∠BCD+∠B=90°,即可得到答案;②由角平分线的性质得到CE=EF,根据三角形的外角性质能求出∠CHE=∠CEA,推出CH=CE即可得到答案;③根据直角三角形全等的判定定理HL即可;④⑤根据边得关系即可判断.解:①∵CD是斜边AB上的高,∠ACB=90°,∴∠CDB=90°,∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,∴∠ACD=∠B,∴①正确;②∵AE平分∠CAB,∴∠CAE=∠BAE,∵∠C=90°,EF⊥AB,∴CE=FE,∵∠CHE=∠CAE+ACD,∠CEA=∠BAE+∠B,∠ACD=∠B,∴∠CHE=∠CEA,∴CH=CE,即:CH=CE=EF,∴②正确;③∵在Rt△ACE和Rt△AFE中AE=AE,CE=EF,∴Rt△ACE≌Rt△AFE,∴AC=AF,∴③正确;④∵CH=EF,∴CH≠HD,∴④错误;⑤∵在Rt△BFE中,BE>EF,而EF=CH,∴⑤错误;故答案为:①②③.点评:本题主要考查了角平分线的性质,等腰三角形的性质和判定,全等三角形的性质和判定,三角形的外角性质等知识点,解此题的关键是综合运用性质进行证明.此题题型较好,综合性强.3.下列说法:①如图1,△ABC中,AB=AC,∠A=45°,则△ABC能被一条直线分成两个小等腰三角形.②如图2,△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC,∠ACB的角平分线,且相交于点F,则图中等腰三角形有6个.③如图3,△ABC是等边三角形,CD⊥AD,且AD∥BC,则AD=AB.④如图4,△ABC中,点E是AC上一点,且AE=AB,连接BE并延长至点D,使AD=AC,∠DAC=∠CAB,则∠DBC=∠DAB其中,正确的有(请写序号,错选少选均不得分)【答案】③④.【解析】不管过A(或过B或过C)作直线,都不能把三角形ABC分成两个等腰三角形,即可判断①;求出∠A=∠ABD=∠DBC=∠ACE=∠BCE=36°,根据三角形的内角和定理求出三角形其余角的度数,根据等腰三角形的判定定理推出边相等,即可判断②;求出∠ACD=30°,根据含30度角的直角三角形性质求出AD=AC,即可判断③;过C作CF∥BD交AB的延长线于F,连接DC,EF,求出EF=BC,证三角形全等推出DE=EF,DC=CF,推出CD=BC,推出∠CDB=∠CBD,根据三角形的内角和定理求出∠CDB=∠CAB即可.解:若△ABC中,AB=AC,∠A=45°,不论过A作直线(或过B作直线或过C作直线)都不能把三角形ABC化成两个等腰三角形,∴①错误;图②中,有等腰三角形7个:△ABD,△CBD,△ACE,△CDE,△BEF,△CDF,△FBC,∴②错误;∵等边△ABC,∴AB=AC,∠ACB=60°,∵AD∥BC,CD⊥AD,∴∠DCB=∠D=90°,∴∠ACD=30°,∴AD=AC=AB,∴③正确;过C作CF∥BD交AB的延长线于F,连接DC,EF,∴=,∵AE=AB,AD=AC,∴AF=AC=AD,∴CE=BF,即BE∥CF,CE=BF,∴四边形BECF是等腰梯形,∴EF=BC,在△DAC和△FAC中,∴△DAC≌△FAC,∴CD=CF,同理DE=EF,∵AD=AC,AE=AB,∴∠ADC=∠ACD,∠AEB=∠ABE,∵∠DAC=∠BAC,∠DAC+∠ACD+∠ADC=180°,∠CAB+∠AEB+∠ABE=180°,∴∠ACD=∠AEB,∵∠AEB=∠DEC,∴∠ACD=∠DEC,∴DE=CD,∴DC=CF=EF=ED,∵EF=CB,∴DC=BC,∴∠CBD=∠CDE,∵∠DCA=∠DEC=∠AEB=∠ABE,由三角形的内角和定理得:∠CDE=∠CAB=∠DAB,∴∠DBC=∠DAB,∴④正确.故答案为:③④.点评:本题考查了等边三角形性质,含30度角的直角三角形性质,等腰三角形的性质和判断,角平分线定义,全等三角形的性质和判定,三角形的内角和定理等知识点的综合运用,第④小题证明过程偏难,对学生提出较高的要求,熟练地运用性质进行推理是解此题的关键.4.如图,线段OP的一个端点O在直线a上,以OP为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能有个.【答案】4个【解析】当O为等腰三角形的两条腰的交点时,以O为圆心,OP为半径画弧,交直线a于两点;当P为等腰三角形的两条腰的交点时,以P为圆心,OP为半径画弧,交直线a于一点;当所求的第三点为等腰三角形的两条腰的交点时,可作OP的垂直平分线,与直线a交于一点,那么可作出等腰三角形共4个.解:△AOP,△BOP,△COP,△DOP就是所求的三角形.点评:本题考查了等腰三角形的性质;等腰三角形有2条边相等,注意可选不同的顶点为等腰三角形的两条腰的交点.5.如图所示,在△ABC中,已知AB=AC,∠A=36°,BC=2,BD是△ABC的角平分线,则AD= .【答案】2【解析】根据等腰三角形的性质,先证∠B=∠C=72°,再由角平分线的定义可证∠ABD=∠CBD=36°,即可求∠BDC=72°,即证BD=BC=AD=2.解:∵AB=AC,∠A=36°,∴∠B=∠C=72°,∵BD是△ABC的角平分线,∴∠ABD=∠CBD=36°,∴∠BDC=180°﹣36°﹣72°=72°=∠C,∴BD=BC=AD=2.故填2.点评:本题考查了等腰三角形的判定与性质;由已知条件结合性质得到BD=BC=AD是正确解答本题的关键.6.如图,在△ABC中,∠ABC=2∠ACB,BD平分∠ABC,AD∥BC,则图中的等腰三角形有个,分别为.【答案】4;△BOC,△AOD,△ABD,△ACD【解析】根据已知条件可以推知∠OBC=∠OCB,∠OAD=∠DOA,∠ABD=∠ADB,∠DAC=∠DCA,然后由等角对等边可以找出图中的等腰三角形.解:∵在△ABC中,∠ABC=2∠ACB,BD平分∠ABC,∴∠ABD=∠CBD=∠ACB,即∠CBD=∠ACB,∴OB=OC(等角对等边),∴△BOC是等腰三角形;又∵AD∥BC,∴∠DAC=∠ACB,∠ADB=∠CBD(两直线平行,内错角相等),∴∠OAD=∠DOA,∠ABD=∠ADB,∠DAC=∠DCA,∴OA=OD,AB=AD,AD=DC,∴△AOD,△ABD,△ACD是等腰三角形;故答案是:4;△BOC,△AOD,△ABD,△ACD.点评:本题考查了等腰三角形的判定.角的等量代换的运用是正确解答本题的关键.7.已知:如图,在△ABC中,∠C=90°,AC=BC=4,点M是边AC上一动点(与点A、C不重合),点N在边CB的延长线上,且AM=BN,连接MN交边AB于点P.(1)求证:MP=NP;(2)若设AM=x,BP=y,求y与x之间的函数关系式,并写出它的定义域;(3)当△BPN是等腰三角形时,求AM的长.【答案】(1)见解析(2)y与x之间的函数关系式为,它的定义域是0<x<4(3)【解析】(1)过点M作MD∥BC交AB于点D,求出DM=BN,证△MDP≌△NBP即可;(2)求出AB,根据△MDP≌△NBP推出DP=BP,推出方程即可;(3)求出BP=BN,所得方程的解即可.(1)证明:过点M作MD∥BC交AB于点D,∵MD∥BC,∴∠MDP=∠NBP,∵AC=BC,∠C=90°,∴∠A=∠ABC=45°,∵MD∥BC,∴∠ADM=∠ABC=45°,∴∠ADM=∠A,∴AM=DM.∵AM=BN,∴BN=DM,在△MDP和△NBP中,∴△MDP≌△NBP,∴MP=NP.(2)解:在Rt△ABC中,∵∠C=90°,AC=BC=4,∴.∵MD∥BC,∴∠AMD=∠C=90°.在Rt△ADM中,AM=DM=x,∴.∵△MDP≌△NBP,∴DP=BP=y,∵AD+DP+PB=AB,∴,∴所求的函数解析式为,定义域为0<x<4.答:y与x之间的函数关系式为,它的定义域是0<x<4.(3)解:∵△MDP≌△NBP,∴BN=MD=x.∵∠ABC+∠PBN=180°,∠ABC=45°,∴∠PBN=135°.∴当△BPN是等腰三角形时,只有BP=BN,即x=y.∴,解得,∴当△BPN是等腰三角形时,AM的长为.答:AM的长为.点评:本题主要考查对等腰三角形的性质和判定,全等三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.8.如图,在△ABC中,AB=AC,∠A=20゜,在AB、AC上分别取点E、D,使∠CBD=60°,∠BCE=50°,求∠AED的度数.【答案】50°【解析】作DF∥BC,与AB相交于F,连接CF,设CF与BD相交于G,连接EG,证DF=DG,BC=BG,求出∠BEC,推出BE=BG,求出△EFG是等腰三角形,推出EF=EG,证△DFE≌△DGE,求出△EDB,根据三角形外角性质求出即可.解:∵AB=AC,∠A=20°,∴∠ABC=∠ACB=80°,∴∠ABD=20°,作DF∥BC,与AB相交于F,连接CF,设CF与BD相交于G,连接EG.∴四边形DFBC为等腰梯形.∵∠DBC=∠FCB=60°,∴△BGC,△DGF都是正三角形,即BG=CG,∵∠BCE=50°,∠EBC=80°,∴∠BEC=50°,即BE=BC,知△BGE是等腰三角形.得:∠BGE=80°,∠FGE=40°.又因∠EFG=∠BDC=40°,∴△EFG是等腰三角形,EF=GE.∵DF=DG,∴△DFE≌△DGE.∴DE平分∠FDG,∴∠EDB=30°,∴∠AED=∠EDB+∠EBD=50°.答:∠AED的度数是50°.点评:本题主要考查对等腰三角形的性质和判定,等腰梯形的性质,全等三角形的性质和判定,三角形的外角性质,三角形的内角和定理等知识点的连接和掌握,能综合运用这些性质进行推理是解此题的关键.9.已知:如图,在△ABC中,CD⊥AB垂足为D,BE⊥AC垂足为E,连接DE,点G、F分别是BC、DE的中点.求证:GF⊥DE.【答案】见解析【解析】作辅助线(连接DG、EG)构建Rt△BCD和Rt△BCE斜边上的中线,然后根据斜边上的中线等于斜边的一半求得DG=EG=BC,从而判定△DEG是等腰三角形;最后根据等腰三角形的“三线合一”的性质推知GF⊥DE.证明:连接DG、EG.∵CD⊥AB,点G是BC的中点,∴在Rt△BCD中,DG=BC(直角三角形的斜边上的中线是斜边的一半).(2分)同理,EG=BC.(2分)∴DG=EG(等量代换).(1分)∵F是DE的中点,∴GF⊥DE.(2分)点评:本题考查了直角三角形斜边上的中线、等腰三角形的判定与性质.熟练运用等腰直角三角形“三线合一”的性质、直角三角形斜边上的中线等于斜边的一半,是解题的关键.10.在△ABC中,已知∠A=∠B,且该三角形的一个内角等于100°.现有下面四个结论:①∠A=100°;②∠C=100°;③AC=BC;④AB=BC.其中正确结论的个数为()A.1个B.2个C.3个D.4个【答案】B【解析】假如∠A=100°,求出∠B=100°,不符合三角形的内角和定理,即可判断①;假如∠C=100°,能够求出∠A、∠B的度数;关键等腰三角形的判定推出AC=BC,即可判断③④.解:∠A=∠B=100°时,∠A+∠B+∠C>180°,不符合三角形的内角和定理,∴①错误;∠C=100°时,∠A=∠b=(180°﹣∠c)=40°,∴②正确;∵∠A=∠B,∴AC=BC,③正确;④错误;正确的有②③,2个,故选B.点评:本题考查了等腰三角形的判定和三角形的内角和定理等知识点的应用,能根据定理进行说理是解此题的关键,分类讨论思想的运用.11.如图所示.△ABC中,∠B=∠C,D在BC上,∠BAD=50°,AE=AD,则∠EDC的度数为()A.15°B.25°C.30°D.50°【答案】B【解析】根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,代入数据计算即可求出∠BAD的度数.解:如图,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,∵AD=AE,∴∠AED=∠ADE,∵∠B=∠C,∴∠B+∠BAD=∠EDC+∠C+∠EDC,即∠BAD=2∠EDC,∵∠BAD=50°,∴∠EDC=25°.故选B.点评:本题主要考查利用三角形的一个外角等于和它不相邻的两个内角的和的性质,熟练掌握性质是解题的关键.12.如图,已知直线PQ⊥MN于点O,点A,B分别在MN,PQ上,OA=1,OB=2,在直线MN或直线PQ上找一点C,使△ABC是等腰三角形,则这样的C点有()A.3个B.4个C.7个D.8个【答案】D【解析】根据等腰三角形的判定分类别分别找寻,分AB可能为底,可能是腰进行分析.解:使△ABC是等腰三角形,当AB当底时,则作AB的垂直平分线,交PQ,MN的有两点,即有两个三角形.当让AB当腰时,则以点A为圆心,AB为半径画圆交PQ,MN有三点,所以有三个.当以点B为圆心,AB为半径画圆,交PQ,MN有三点,所以有三个.所以共8个.故选D.点评:本题考查了等腰三角形的判定;解题的关键是要分情况而定,所以学生一定要思维严密,不可遗漏.13.下列三角形中,是正三角形的为()①有一个角是60°的等腰三角形;②有两个角是60°的三角形;③底边与腰相等的等腰三角形;④三边相等的三角形.A.①④B.②③C.③④D.①②③④【答案】D【解析】等边三角形的判定定理有①三个都相等的三角形是等边三角形,②有一个角是60°的等腰三角形是等边三角形,③三边都相等的三角形是等边三角形,根据以上定理判断即可.解:∵AB=AC,∠A=60°,∴△ACB是等边三角形,∴①正确;∵∠A=∠B=60°,∴AC=BC,∴△ACB是等边三角形,∴②正确;∵AB=AC,AB=BC,∴AB=AC=BC∴△ACB是等边三角形,∴③正确;∵AB=AC=BC,∴△ACB是等边三角形,∴④正确.故选D.点评:本题考查了等腰三角形的判定和等边三角形的判定等的应用,主要检查学生是否掌握等边三角形的判定定理,题型较好,但是一道容易出错的题目.14.在等边△ABC所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形.这样的点一共有()A.1个B.4个C.7个D.10个【答案】D【解析】本题利用了等边三角形是轴对称图形,三条高所在的直线也是对称轴,也是边的中垂线.解:在等边△ABC中,三条边上的高交于点O,由于等边三角形是轴对称图形,三条高所在的直线也是对称轴,也是边的中垂线,点O到三个顶点的距离相等,△ADB,△BOC,△AOC是等腰三角形,则点O是满足题中要求的点,高与顶角的两条边成的锐角为30°,以点A为圆心,AB为半径,做圆,延长AO交圆于点E,由于点E在对称轴AE上,有EC=EB,AE=AC=AB,△ECB,△AEC,△ABE都是等腰三角形,点E也是满足题中要求的点,作AD⊥AE交圆于点D,则有AC=AD,AD=AB,即△DAB,△ADC是等腰三角形,点D也是满足题中要求的点,同理,作AF⊥AE交圆于点F,则点F也是满足题中要求的点;同理,以点B为圆心,AB为半径,做圆,以点C为圆心,AB为半径,做圆,都可以分别得到同样性质的三个点满足题中要求,于是共有10个点能使点与三角形中的任意两个顶点所组成的三角形都是等腰三角形.故选D.点评:本题容易找出三条边上的高交于点O,是满足题中要求的点,其它点容易漏掉,这样的点不一定是等腰三角形的顶角所在的点,也可以是底角所在的点,明白这点后,就要做圆来找到所要求的点.15.如图,已知△ABC中,AC+BC=24,AO,BO分别是角平分线,且MN∥BA,分别交AC于N,BC于M,则△CMN的周长为()A.12B.24C.36D.不确定【答案】B【解析】由AO,BO分别是角平分线求得∠1=∠2,∠3=∠4,利用平行线性质求得,∠1=∠6,∠3=∠5,利用等量代换求得∠2=∠6,∠4=∠5,即可解题.解:由AO,BO分别是角平分线得∠1=∠2,∠3=∠4,又∵MN∥BA,∴∠1=∠6,∠3=∠5,∴∠2=∠6,∠4=∠5,∴AN=NO,BM=OM.∵AC+BC=24,∴AC+BC=AN+NC+BM+MC=24,即MN+MC+NC=24,也就是△CMN的周长是24.故选B.点评:此题考查学生对等腰三角形的判定与性质和平行线行至的理解和掌握,此题主要求得△ANO△BMO是等腰三角形,这是解答此题的关键.16.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点AB之间的距离是()A.13B.9C.18D.10【答案】C【解析】运用勾股定理可将三角形的直角边求出,将两个直角边进行相加即为两个固定点之间的距离.解:∵电线杆高为12m,铁丝长15m,∴固定点与电线杆的距离==9m,∵两个直角三角形全等,∴两个固定点之间的距离=9×2=18m.故选C.点评:本题考查正确运用勾股定理,关键是从实际问题中找到直角三角形,并利用勾股定理进行有关的运算.17.如图,在△ABC中,BD=DE=EC,△ADE为等边三角形,则图中等腰三角形的个数是()A.2B.3C.4D.5【答案】C【解析】根据已知的BD=DE=EC和△ADE为等边三角形,利用等腰三角形的判定进行判断即可.解:∵△ADE为等边三角形,∴AD=DE=AE,∵BD=DE=EC,∴AD=DE=AE=BD=EC,∴等腰三角形有△ABD、△ACE、△ADE、△ABC共四个.故选C.点评:本题考查了等腰三角形的判定及等边三角形的性质,属于基础题,应该重点掌握.18.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为()A.5B.6C.7D.8【答案】A【解析】根据OB和OC分别平分∠ABC和∠ACB,和DE∥BC,利用两直线平行,内错角相等和等量代换,求证出DB=DO,OE=EC.然后即可得出答案.解:∵在△ABC中,OB和OC分别平分∠ABC和∠ACB,∴∠DBO=∠OBC,∠ECO=∠OCB,∵DE∥BC,∴∠DOB=∠OBC=∠DBO,∠EOC=∠OCB=∠ECO,∴DB=DO,OE=EC,∵DE=DO+OE,∴DE=BD+CE=5.故选A.点评:此题主要考查学生对等腰三角形的判定与性质平行线段性质的理解和掌握,此题关键是求证DB=DO,OE=EC,难度不大,是一道基础题.19.推理:如图,∵∠A=∠ACD,∠B=∠BCD,(已知)∴AD=CD,CD=DB(等腰三角形的性质)∴AD=DB,依据是()A.旋转不改变图形的大小B.连接两点的所有线中线段最短C.等量代换D.整体大于部分【答案】C【解析】由∠A=∠ACD,得AD=CD,再由∠B=∠BCD得CD=DB,利用等量代换即可解题.解:∵∠A=∠ACD,∴AD=CD,∵∠B=∠BCD∴CD=DB,因AD和DB都等于同一个量CD,所以AD=DB,依据是等量代换.故选C.点评:此题考查学生对等腰三角形的判定与性质的理解和掌握,此题主要利用了等量代换求得两边相等.20.如图,在下列三角形中,若AB=AC,则不能被一条直线分成两个小等腰三角形的是()A.B.C.D.【答案】B【解析】A、D是黄金三角形,C、过A点作BC的垂线即可;只有B选项不能被一条直线分成两个小等腰三角形.解:A、中作∠B的角平分线即可;C、过A点作BC的垂线即可;D、中以A为顶点AB为一边在三角形内部作一个72度的角即可;只有B选项不能被一条直线分成两个小等腰三角形.故选B.点评:此题主要考查学生对等腰三角形的判定与性质的理解和掌握,此题的4个选项中只有D选项有点难度,所以此题属于中档题.。
等腰三角形经典练习试题及详细含答案
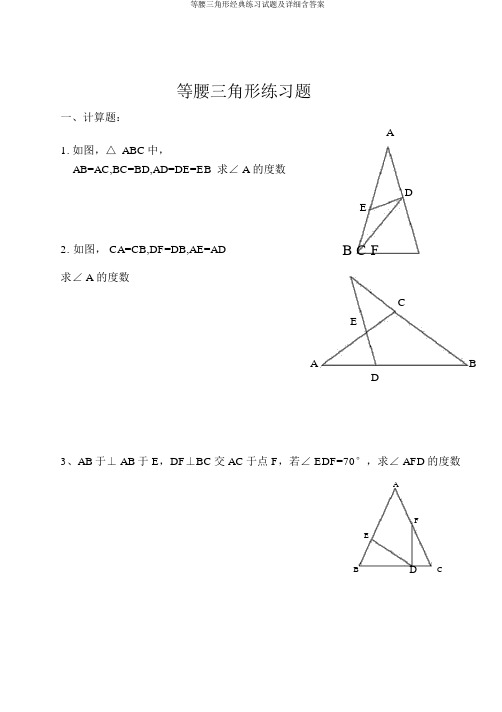
等腰三角形练习题一、计算题:A1.如图,△ ABC中,AB=AC,BC=BD,AD=DE=EB求∠ A 的度数DE2. 如图, CA=CB,DF=DB,AE=AD B C F求∠ A 的度数CEA BD3、AB于⊥ AB于 E,DF⊥BC交 AC于点 F,若∠ EDF=70°,求∠ AFD的度数AFEB D C4. 如图,△ ABC 中, AB=AC,BC=BD=ED=EAA求∠ A 的度数EDBC5. 如图,△ ABC 中, AB=AC ,D 在 BC 上,A∠ B AD=30°, 在 AC 上取点 E ,使 AE=AD,求∠ EDC 的度数30°EBDC6. 如图,△ ABC 中,∠ C=90°, D 为 AB 上一点,作 DE ⊥BC 于 E ,若1BE=AC,BD=2,DE+BC=1,求∠ ABC 的度数ADCB7.如图,△ ABC中,AD均分∠ BAC,若AC=AB+BD求∠ B:∠ C的值AB D C二、证明题:8.如图,△ DEF中,∠ EDF=2∠E,FA⊥DE于点A,问:DF、AD、AE间有什么样的大小关系DAE F9.如图,△ ABC中,∠ B=60°,角均分线 AD、CE交于点 O求证: AE+CD=AC BE DA C12. 如图 , △ABC 中,AB=AC,D 为△ ABC 外一点,且∠ ABD=∠ACD =60°A求证: CD=AB-BDBDC13. 已知:如图, AB=AC=BE ,CD 为△ ABC 中 AB 边上的中线1A求证: CD=2CEDBCE14. 如图,△ ABC 中,∠ 1=∠2,∠ EDC=∠BACA求证: BD=ED1 2EBCD15. 如图,△ ABC中, AB=AC,BE=CF,EF交 BC于点 GA求证: EG=FGECBG F16. 如图,△ABC中,∠ABC=2∠C,AD是 BC边上的高, B 到点 E,使 BE=BD 求证: AF=FCAFBDCE17. 如图,△ ABC中, AB=AC,AD和 BE两条高,交于点 H,且 AE=BE求证: AH=2BD AEHB D C18. 如图,△ ABC中, AB=AC, ∠BAC=90°,BD=AB, ∠ABD=30°求证: AD=DCADB C19.如图,等边△ ABC中,分别延伸 BA至点 E,延伸 BC至点 D,使 AE=BD 求证: EC=ED EABC D20.如图,四边形 ABCD中,∠ BAD+∠BCD=180°,AD、BC的延伸线交于点F,DC、 AB的延伸线交于点E,∠ E、∠ F 的均分线交于点H求证: EH⊥FHFDCHABE一、计算题:1. 如图,△ ABC中,AB=AC,BC=BD,AD=DE=EB求∠ A 的度数A设∠ ABD为 x, 则∠ A 为 2x2x由 8x=180°D 得∠ A=2x=45°E 2xx3xx2. 如图, CA=CB,DF=DB,AE=ADB 2x3xC 求∠ A 的度数F设∠ A 为 x, XC由 5x=180°E得∠ A=36°2xxA x2x BD3.如图,△ ABC中,AB=AC,D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠ EDF=70°,求∠ AFD的度数∠A FD=160°AFEB D C4. 如图,△ ABC 中, AB=AC,BC=BD=ED=EAA求∠ A 的度数x设∠ A 为 x180E∠A=72xx2xD3x x3x BC5. 如图,△ ABC 中, AB=AC ,D 在 BC 上,∠ B AD=30°, 在 AC 上取点 E ,使 AE=AD,求∠ EDC 的度数设∠ ADE 为 xA∠EDC=∠AED -∠ C=15°180°-2x30°x -15°x Ex BDCx -15°6. 如图,△ ABC 中,∠ C=90°, D 为 AB 上一点,作 DE ⊥BC 于 E ,若1BE=AC,BD=2,DE+BC=1,求∠ ABC 的度数延伸 DE 到点 F, 使 EF=BC可证得 : △ABC ≌△ BFE所以∠ 1=∠F由∠ 2+∠F=90°,得∠ 1+∠F=90°1ADC E12B在 Rt △DBF 中, BD= 2,DF=1F所以∠ F = ∠1=30°7. 如图,△ ABC 中, AD 均分∠ BAC ,若 AC=AB+BD求∠ B :∠ C 的值在 AC 上取一点 E, 使 AE=AB A可证△ ABD ≌△ ADE所以∠ B=∠AEDEB D C由AC=AB+BD,得 DE=EC,所以∠ AED=2∠C 故∠ B:∠ C=2:1二、证明题:8.如图,△ ABC中,∠ ABC,∠CAB的均分线交于点P,过点 P 作 DE∥AB,分别交 BC、AC于点 D、E求证: DE=BD+AEC证明△ PBD和△ PEA是等腰三角形 D P EB A9.如图,△ DEF中,∠ EDF=2∠E,FA⊥DE于点A,问:DF、AD、AE间有什么样的大小关系DDF+AD=AE A在 AE上取点 B, 使 AB=ADBE F10.如图,△ ABC中,∠ B=60°,角均分线 AD、CE交于点 O求证: AE+CD=AC B在 AC上取点 F, 使 AF=AE易证明△ AOE≌△ AOF, E DO得∠ AOE=∠AOF由∠ B=60°,角均分线 AD、CE,A F C得∠ AOC=120°所以∠ AOE=∠AOF=∠COF=∠COD=60°故△ COD≌△ COF,得 CF=CD所以 AE+CD=AC11. 如图,△ ABC中, AB=AC, ∠A=100°, BD均分∠ ABC,求证: BC=BD+AD延伸 BD到点 E, 使 BE=BC,连接 CE A在 BC上取点 F, 使 BF=BA D E 易证△ ABD≌△ FBD,得 AD=DF再证△ CDE≌△ CDF,得 DE=DF BF CA故 BE=BC=BD+ADD也可 : 在 BC上取点 E, 使 BF=BD,连接 DF在 BF 上取点 E, 使 BF=BA,连接 DEB先证 DE=DC,再由△ ABD≌△ EBD,得 AD=DE,最后证明 DE=DF即可 E FC 12. 如图 , △ABC中,AB=AC,D为△ ABC外一点,且∠ ABD=∠ACD =60°求证: CD=AB-BD AE在 AB上取点 E,使 BE=BD,在 AC上取点 F,使 CF=CDF得△ BDE与△ CDF均为等边三角形,DB只要证△ ADF≌△ AEDC13. 已知:如图, AB=AC=BE ,CD 为△ ABC 中 AB 边上的中线1A求证: CD=2CEE延伸 CD 到点 E, 使 DE=CD 连.结 AED证明△ ACE ≌△ BCEBC14. 如图,△ ABC 中,∠ 1=∠2,∠ EDC=∠BAC E求证: BD=EDA 1 2在 CE 上取点 F, 使 AB=AFEF易证△ ABD ≌△ ADF,得 BD=DF,∠B=∠AFDBCD由∠ B+∠BAC+∠C=∠DEC+∠EDC+∠C=180°所以∠ B=∠DEC所以∠ DEC=∠AFD所以 DE=DF,故 BD=ED15. 如图,△ ABC 中, AB=AC,BE=CF,EF 交 BC 于点 GA求证: EG=FGECBGF16. 如图,△ABC中,∠ABC=2∠C,AD是 BC边上的高, B 到点 E,使 BE=BD 求证: AF=FC AFB17.如图,△ ABC中, AB=AC,AD和 BE两条高,交E于点求证: AH=2BD由△ AHE≌△ BCE,得 BC=AH18. 如图,△ ABC中, AB=AC, ∠BAC=90°,BD=AB,∠ABD=30°求证: AD=DC作AF⊥BD于 F,DE⊥AC于 E可证得∠ DAF=DAE=15°,所以△ ADE≌△ ADF B得AF=AE,由AB=2AF=2AE=AC,DH,且 AE=BEAHB DAEFDCCEC所以 AE=EC,所以 DE是 AC的中垂线 , 所以 AD=DC19. 如图,等边△ ABC 中,分别延伸 BA 至点 E ,延伸 BC 至点 D ,使 AE=BD求证: EC=EDE延伸 BD 到点 F, 使 DF=BC,A可得等边△ BEF,BCD F只要证明△ BCE ≌△ FDE 即可20. 如图,四边形 ABCD 中,∠ BAD+∠BCD=180°,AD 、BC 的延伸线交于点F ,DC 、 AB 的延伸线交于点 E ,∠ E 、∠ F 的均分线交于点 H求证: EH ⊥FHF延伸 EH 交 AF 于点 G由∠ BAD+∠BCD=180° ,∠DCF+∠BCD=180° D得∠ BAD=∠DCF,CG1由外角定理 , 得∠ ∠2 MH1= 2,故△ FGM 是等腰三角形ABE由三线合一 , 得 EH ⊥。
等腰三角形经典试题综合训练(含解析)

等腰三角形经典试题综合训练(含解析)一.选择题(共18小题)1.若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为()A.2cm B.4cm C.6cm D.8cm2.等腰三角形腰长为5,则其底边长a的取值范围为()A.0<a≤5 B.5≤a≤10 C.0<a<10 D.0<a<53.等腰三角形的一个角是80°,则它的底角是()A.50°B.80°C.50°或80°D.20°或80°4.等腰三角形一腰上的高于另一腰的夹角为50°,那么这个三角形的顶角为()A.40°B.100°C.140°D.40°或140°5.下列说法中,正确的有()①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.A.1个B.2个C.3个D.4个6.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为()A.40°B.36°C.30°D.25°7.如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()A.AE=EC B.AE=BE C.∠EBC=∠BAC D.∠EBC=∠ABE8.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC 于M、N,则△AMN的周长为()A.12 B.4 C.8 D.不确定9.如图,在△ABC中,AB=AC,AD平分∠BAC,交BC于点D,DE⊥AB于点E,DF⊥AC于点F,对于下列结论:①AD⊥BC;②AE=AF;③AD上任意一点到AB,AC的距离相等;④AD上任意一点到点B,点C 的距离相等.其中正确结论的个数是()A.1 B.2 C.3 D.410.如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点,则∠DGE 的度数是()A.45°B.60°C.90°D.120°11.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有()A.1个B.2个C.3个D.4个12.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有()A.2个B.3个C.4个D.无数个13.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为()A.44°B.66°C.88°D.92°14.如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是()A.24 B.18 C.16 D.1215.如图,△ABC中,∠ABC=63°,点D,E分别是△ABC的边BC,AC上的点,且AB=AD=DE=EC,则∠C 的度数是()A.21°B.19°C.18°D.17°16.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠A n﹣1A n B n﹣1(n>2)的度数为()A.B.C.D.17.如图钢架中,∠A=10°,焊上等长的钢条来加固钢架,若P1A=P1P2,则这样的钢条至多需要()A.5根B.6根C.7根D.8根18.如图,已知△ABC是等腰三角形,AC=BC=5,AB=8,D为底边AB上的一个动点(不与A、B重合),DE⊥AC,DF⊥BC,垂足分别为E、F,则DE+DF的值为()A.3 B.4 C.D.二.填空题(共8小题)19.如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A=度.20.如图,AB=AC,FD⊥BC于D,DE⊥AB于E,若∠AFD=145°,则∠EDF=度.21.如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b 的代数式表示△ABC的周长为.22.如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,则∠C=度.23.如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=°.24.如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是.25.如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm 每秒的速度运动,设运动时间为t秒,当t为时,△ACP是等腰三角形.26.如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点,若使点P,M,N 构成等腰三角形的点P恰好有三个,则x的值是.三.解答题(共9小题)27.如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=42°,求∠BED的度数.28.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.求证:OE=OF.29.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.(1)求证:∠CBE=∠BAD;(2)当△ABC满足什么条件时,AE=CE.直接写出条件.30.文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:文文:“过点A作BC的中垂线AD,垂足为D”;彬彬:“作△ABC的角平分线AD”.数学老师看了两位同学的辅助线作法后,说:“彬彬的作法是正确的,而文文的作法需要订正.”(1)请你简要说明文文的辅助线作法错在哪里;(2)根据彬彬的辅助线作法,完成证明过程.31.如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:DF=EF.32.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠BAD=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.33.如图1,△ABC中,AB=AC,∠A=36°,我们发现这个三角形有一种特性,即经过它某一顶点的一条射线可把它分成两个小等腰三角形.为此,请你解答问题;如图2,△ABC中,AB=AC,∠A=108°,请你在图中画一条射线(不必写画法),把它分成两个小等腰三角形,并写出底角的大小.34.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PE∥AB 交BC于点D,交AC于点F.(1)若点P在BC上(如图一),此时PD=0,可得结论:PD+PE+PF AB(填“>”“<”或“=”)(2)当点P在△ABC内(如图二)时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请直接写出你的猜想,不需要证明.35.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.(1)当D点在BC的什么位置时,DE=DF?并证明.(2)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明:(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?等腰三角形综合训练参考答案与试题解析一.选择题(共18小题)1.若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为()A.2cm B.4cm C.6cm D.8cm【分析】分为两种情况:2cm是等腰三角形的腰或2cm是等腰三角形的底边,然后进一步根据三角形的三边关系进行分析能否构成三角形.【解答】解:若2cm为等腰三角形的腰长,则底边长为10﹣2﹣2=6(cm),2+2<6,不符合三角形的三边关系;若2cm为等腰三角形的底边,则腰长为(10﹣2)÷2=4(cm),此时三角形的三边长分别为2cm,4cm,4cm,符合三角形的三边关系;故选A.2.等腰三角形腰长为5,则其底边长a的取值范围为()A.0<a≤5 B.5≤a≤10 C.0<a<10 D.0<a<5【分析】由已知条件腰长是5,底边长为a,根据三角形三边关系列出不等式,通过解不等式即可得到答案.【解答】解:根据三边关系可知:5﹣5<a<5+5,即0<a<10.故选C.3.等腰三角形的一个角是80°,则它的底角是()A.50°B.80°C.50°或80°D.20°或80°【分析】因为题中没有指明该角是顶角还是底角,则应该分两种情况进行分析.【解答】解:①当顶角是80°时,它的底角=(180°﹣80°)=50°;②底角是80°.所以底角是50°或80°.故选C.4.等腰三角形一腰上的高于另一腰的夹角为50°,那么这个三角形的顶角为()A.40°B.100°C.140°D.40°或140°【分析】分三角形是锐角三角形时,利用直角三角形两锐角互余求解;三角形是钝角三角形时,利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:如图1,三角形是锐角三角时,∵∠ACD=50°,∴顶角∠A=90°﹣50°=40°;如图2,三角形是钝角时,∵∠ACD=50°,∴顶角∠BAC=50°+90°=140°,综上所述,顶角等于40°或140°.故答案为:40°或140°.5.下列说法中,正确的有()①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.A.1个B.2个C.3个D.4个【分析】认真阅读每一问题给出的已知条件,根据等腰三角形的概念、性质判断正误.【解答】解:①等腰三角形的两腰相等,正确;②等腰三角形的两底角相等,正确;③等腰三角形底边上的中线与底边上的高相等,正确;④等腰三角形是轴对称图形,对称轴就是底边上的高所在的直线,正确.故选D.6.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为()A.40°B.36°C.30°D.25°【分析】根据AB=AC可得∠B=∠C,CD=DA可得∠ADB=2∠C=2∠B,BA=BD,可得∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.【解答】解:∵AB=AC,∴∠B=∠C,∵CD=DA,∴∠C=∠DAC,∵BA=BD,∴∠BDA=∠BAD=2∠C=2∠B,又∵∠B+∠BAD+∠BDA=180°,∴5∠B=180°,∴∠B=36°,故选B.7.如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()A.AE=EC B.AE=BE C.∠EBC=∠BAC D.∠EBC=∠ABE【分析】利用等腰三角形的性质分别判断后即可确定正确的选项.【解答】解:∵AB=AC,∴∠ABC=∠ACB,∵以点B为圆心,BC长为半径画弧,交腰AC于点E,∴BE=BC,∴∠ACB=∠BEC,∴∠BEC=∠ABC=∠ACB,∴∠A=∠EBC,故选C.8.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC 于M、N,则△AMN的周长为()A.12 B.4 C.8 D.不确定【分析】根据角平分线的定义可得∠ABE=∠CBE,∠ACE=∠BCE,再根据两直线平行,内错角相等可得∠CBE=∠BEM,∠BCE=∠CEN,然后求出∠ABE=∠BEM,∠ACE=∠CEN,根据等角对等边可得BM=ME,CN=NE,然后求出△AMN的周长=AB+AC.【解答】解:∵∠ABC和∠ACB的平分线交于点E,∴∠ABE=∠CBE,∠ACE=∠BCE,∵MN∥BC,∴∠CBE=∠BEM,∠BCE=∠CEN,∴∠ABE=∠BEM,∠ACE=∠CEN,∴BM=ME,CN=NE,∴△AMN的周长=AM+ME+AN+NE=AB+AC,∵AB=AC=4,∴△AMN的周长=4+4=8.故选C.9.如图,在△ABC中,AB=AC,AD平分∠BAC,交BC于点D,DE⊥AB于点E,DF⊥AC于点F,对于下列结论:①AD⊥BC;②AE=AF;③AD上任意一点到AB,AC的距离相等;④AD上任意一点到点B,点C 的距离相等.其中正确结论的个数是()A.1 B.2 C.3 D.4【分析】首先根据角平分线的性质可得AD上任意一点到AB,AC的距离相等,根据等腰三角形的性质得到AD⊥BC,根据全等三角形的性质得到AE=AF,根据线段垂直平分线的性质得到AD上任意一点到点B,点C的距离相等.【解答】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,AD上任意一点到AB,AC的距离相等,故①③正确;∵DE⊥AB于点E,DF⊥AC于点F,∴DE=DF,在Rt△ADE与Rt△AFD中,∴Rt△ADE≌Rt△AFD,∴AE=AF;故②正确;∵AB=AC,AD平分∠BAC,∴AD垂直平分BD,∴AD上任意一点到点B,点C的距离相等,故④正确;故选D.10.如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点,则∠DGE 的度数是()A.45°B.60°C.90°D.120°【分析】首先连接DE,DF,由AB=AC,可得∠B=∠C,又由BE=CD,BD=CF,利用SAS可判定△BDE≌△CFD,即可得DE=DF,然后由三线合一的性质,证得DG⊥EF,继而求得答案.【解答】解:连接DE,DF,∵AB=AC,∴∠B=∠C,在△BDE和△CFD中,,∴△BDE≌△CFD(SAS),∴DE=DF,∵G为EF的中点,∴DG⊥EF,即∠DGE=90°.故选C.11.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有()A.1个B.2个C.3个D.4个【分析】根据△OAB为等腰三角形,分三种情况讨论:①当OB=AB时,②当OA=AB时,③当OA=OB时,分别求得符合的点B,即可得解.【解答】解:要使△OAB为等腰三角形分三种情况讨论:①当OB=AB时,作线段OA的垂直平分线,与直线b的交点为B,此时有1个;②当OA=AB时,以点A为圆心,OA为半径作圆,与直线b的交点,此时有1个;③当OA=OB时,以点O为圆心,OA为半径作圆,与直线b的交点,此时有2个,1+1+2=4,故选:D.12.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有()A.2个B.3个C.4个D.无数个【分析】如图在OA、OB上截取OE=OF=OP,作∠MPN=60°,只要证明△PEM≌△PON即可推出△PMN是等边三角形,由此即可对称结论.【解答】解:如图在OA、OB上截取OE=OF=OP,作∠MPN=60°.∵OP平分∠AOB,∴∠EOP=∠POF=60°,∵OP=OE=OF,∴△OPE,△OPF是等边三角形,∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,∴∠EPM=∠OPN,在△PEM和△PON中,,∴△PEM≌△PON.∴PM=PN,∵∠MPN=60°,∴△PNM是等边三角形,∴只要∠MPN=60°,△PMN就是等边三角形,故这样的三角形有无数个,故选D13.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为()A.44°B.66°C.88°D.92°【分析】根据等腰三角形的性质得到∠A=∠B,证明△AMK≌△BKN,得到∠AMK=∠BKN,根据三角形的外角的性质求出∠A=∠MKN=44°,根据三角形内角和定理计算即可.【解答】解:∵PA=PB,∴∠A=∠B,在△AMK和△BKN中,,∴△AMK≌△BKN,∴∠AMK=∠BKN,∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,∴∠A=∠MKN=44°,∴∠P=180°﹣∠A﹣∠B=92°,故选:D.14.如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是()A.24 B.18 C.16 D.12【分析】因为AB=AC,所以△ABC为等腰三角形,由DE∥AB,可证△CDE为等腰三角形,同理△BDF也为等腰三角形,根据腰长相等,将线段长转化,求周长.【解答】解:∵AB=AC=15,∴∠B=∠C,由DF∥AC,得∠FDB=∠C=∠B,∴FD=FB,同理,得DE=EC.∴四边形AFDE的周长=AF+AE+FD+DE=AF+FB+AE+EC=AB+AC=8+8=16.故四边形AFDE的周长是16.故选C.15.如图,△ABC中,∠ABC=63°,点D,E分别是△ABC的边BC,AC上的点,且AB=AD=DE=EC,则∠C 的度数是()A.21°B.19°C.18°D.17°【分析】设∠C=x.由DE=EC,根据等边对等角得出∠C=∠EDC=x,根据三角形外角的性质得出∠AED=∠C+∠EDC=2x.同理表示出∠ADB=∠ABC=3x,则3x=63°,求出x即可.【解答】解:设∠C=x.∵DE=EC,∴∠C=∠EDC=x,∴∠AED=∠C+∠EDC=2x.∵AD=DE,∴∠AED=∠DAE=2x,∴∠ADB=∠DAE+∠C=3x.∵AB=AD,∴∠ADB=∠ABC=3x,∴3x=63°,∴x=21°.故选A.16.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠A n﹣1A n B n﹣1(n>2)的度数为()A.B.C.D.【分析】根据三角形外角的性质及等腰三角形的性质分别求出∠B1A2A1,∠B2A3A2及∠B3A4A3的度数,找出规律即可得出∠A n﹣1A n B n﹣1的度数.【解答】解:∵在△ABA1中,∠A=70°,AB=A1B,∴∠BA1A=70°,∵A1A2=A1B1,∠BA1A是△A1A2B1的外角,∴∠B1A2A1==35°;同理可得,∠B2A3A2=17.5°,∠B3A4A3=×17.5°=,∴∠A n﹣1A n B n﹣1=.故选:C.17.如图钢架中,∠A=10°,焊上等长的钢条来加固钢架,若P1A=P1P2,则这样的钢条至多需要()A.5根B.6根C.7根D.8根【分析】由于焊上的钢条长度相等,并且AP1=P1P2,所以∠A=∠P1P2A,则可算出∠P2P1P3的度数,并且和∠P1P3P2度数相等,根据平角的度数为180度和三角形内角和为180度,结合等腰三角形底角度数不大于90度即可求出最多能焊上的钢条数.【解答】解:如图:∵∠A=∠P1P2A=10°,∴∠P2P1P3=20°,∠P1P3P2=20°,∴∠P1P2P3=140°,∴∠P3P2P4=30°∴∠P3P4P2=30°∴∠P2P3P4=120°∴∠P4P3P5=40°∴∠P3P5P4=40°∴∠P3P4P5=100°∴∠P5P4P6=50°∴∠P4P6P5=50°∴∠P4P5P6=80°∴∠P6P5P7=60°,∴∠P6P7P5=60°,∴∠P5P6P7=60°,∴∠P8P6P7=70°,∴∠P6P8P7=70°,∴∠P6P7P8=40°,∴∠P8P7P9=80°,∴∠P7P9P8=80°,∴∠P9P8P7=20°,∴∠P9P8C=90°,此时就不能在往上焊接了,综上所述总共可焊上8条.故选D.18.如图,已知△ABC是等腰三角形,AC=BC=5,AB=8,D为底边AB上的一个动点(不与A、B重合),DE⊥AC,DF⊥BC,垂足分别为E、F,则DE+DF的值为()A.3 B.4 C.D.【分析】连接AD,过点C作CE⊥AB于点E,根据勾股定理求出CE的长,再由三角形的面积公式即可得出结论.【解答】解:连接AD,过点C作CE⊥AB于点E,∵AC=BC=5,AB=8,∴AE=4,∴CE==3,∴S△ABC=AB•CE=×8×3=12.∵DE⊥AC,DF⊥BC,∴S△ABC=S△ACD+S△BDC=AC•DE+BC•DF=×5×(DE+DF)=12,∴DE+DF=.二.填空题(共8小题)19.如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A=75度.【分析】根据等腰三角形的性质和三角形的内角和即可得到结论.【解答】解:∵OA=OB,∠AOB=30°,∴∠A=(180°﹣30°)=75°,故答案为:75.20.如图,AB=AC,FD⊥BC于D,DE⊥AB于E,若∠AFD=145°,则∠EDF=55度.【分析】首先求出∠C的度数,再根据等腰三角形的性质求出∠A,从而利用四边形内角和定理求出∠EDF.【解答】解:∵∠AFD=145°,∴∠CFD=35°又∵FD⊥BC于D,DE⊥AB于E ∴∠C=180°﹣(∠CFD+∠FDC)=55°∵AB=AC ∴∠B=∠C=55°,∴∠A=70°根据四边形内角和为360°可得:∠EDF=360°﹣(∠AED+∠AFD+∠A)=55°∴∠EDF为55°.故填55.21.如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b 的代数式表示△ABC的周长为2a+3b.【分析】由题意可知:AC=AB=a+b,由于DE是线段AC的垂直平分线,∠BAC=36°,所以易证AE=CE=BC=b,从可知△ABC的周长;【解答】解:∵AB=AC,BE=a,AE=b,∴AC=AB=a+b,∵DE是线段AC的垂直平分线,∴AE=CE=b,∴∠ECA=∠BAC=36°,∵∠BAC=36°,∴∠ABC=∠ACB=72°,∴∠BCE=∠ACB﹣∠ECA=36°,∴∠BEC=180°﹣∠ABC﹣∠ECB=72°,∴CE=BC=b,∴△ABC的周长为:AB+AC+BC=2a+3b 故答案为:2a+3b.22.如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,则∠C=36度.【分析】根据已知题目中所给的等量关系,用一个角分别表示出其他的角,利用三角形内角和等于180°,便可得出∠C的度数.【解答】解:由题意知,在△ABC中,AB=AC,所以∠B=∠C,又AB=BD,AD=DC,所以∠C=∠DAC,∠BAD=∠BDA=2∠C,由三角形内角和为180°可得,∠C+∠C+3∠C=180°,得∠C=36°.故填36.23.如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=80°.【分析】先利用SSS证明△ABD≌△EBD,再根据全等三角形对应角相等即可求出∠BED.【解答】解:在△ABD与△EBD中,,∴△ABD≌△EBD,∴∠BED=∠A=80°.故答案为80.24.如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是cm2.【分析】过点P作PE⊥BP,垂足为P,交BC于点E,由角平分线的定义可知∠ABP=∠EBP,结合BP=BP 以及∠APB=∠EPB=90°即可证出△ABP≌△EBP(ASA),进而可得出AP=EP,根据三角形的面积即可得出S=S EPC,再根据S△PBC=S△BPE+S EPC=S△ABC即可得出结论.△APC【解答】解:过点P作PE⊥BP,垂足为P,交BC于点E,如图所示.∵AP垂直∠B的平分线BP于点P,∴∠ABP=∠EBP.在△ABP和△EBP中,,∴△ABP≌△EBP(ASA),∴AP=EP.∵△APC和△EPC等底同高,∴S△APC=S EPC,∴S△PBC=S△BPE+S EPC=S△ABC=cm2.故答案为:cm2.25.如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm 每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.【分析】由于没有说明哪一条边是腰,故需要分情况讨论.【解答】解:∵AC=6,BC=8,∴由勾股定理可知:AB=10,当点P在CB上运动时,由于∠ACP=90°,∴只能有AC=CP,如图1,∴CP=6,∴t==3,当点P在AB上运动时,①AC=AP时,如图2,∴AP=6,PB=AB﹣CP=10﹣6=4,∴t==6,②当AP=CP时,如图3,此时点P在线段AC的垂直平分线上,过点P作PD⊥AC于点D,∴CD=AC=3,PD是△ACB的中位线,∴PD=BC=4,∴由勾股定理可知:AP=5,∴PB=5,∴t==6.5;③AC=PC时,如图4,过点C作CF⊥AB于点F,∴cos∠A==,∴AF=3.6,∴AP=2AF=7.2,∴PB=10﹣7.2=2.8,∴t==5.4;综上所述,当t为3或6或6.5或5.4时,△ACP是等腰三角形.故答案为:3或6或6.5或5.4.26.如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点,若使点P,M,N 构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4﹣4或4<x<4.【分析】分三种情况讨论:先确定特殊位置时成立的x值,①如图1,当M与O重合时,即x=0时,点P恰好有三个;②如图2,构建腰长为4的等腰直角△OMC,和半径为4的⊙M,发现M在点D的位置时,满足条件;③如图3,根据等腰三角形三种情况的画法:分别以M、N为圆心,以MN为半径画弧,与OB的交点就是满足条件的点P,再以MN为底边的等腰三角形,通过画图发现,无论x取何值,以MN为底边的等腰三角形都存在一个,所以只要满足以MN为腰的三角形有两个即可.【解答】解:分三种情况:①如图1,当M与O重合时,即x=0时,点P恰好有三个;②如图2,以M为圆心,以4为半径画圆,当⊙M与OB相切时,设切点为C,⊙M与OA交于D,∴MC⊥OB,∵∠AOB=45°,∴△MCO是等腰直角三角形,∴MC=OC=4,∴OM=4,当M与D重合时,即x=OM﹣DM=4﹣4时,同理可知:点P恰好有三个;③如图3,取OM=4,以M为圆心,以OM为半径画圆,则⊙M与OB除了O外只有一个交点,此时x=4,即以∠PMN为顶角,MN为腰,符合条件的点P有一个,以N圆心,以MN为半径画圆,与直线OB相离,说明此时以∠PNM为顶角,以MN为腰,符合条件的点P不存在,还有一个是以NM为底边的符合条件的点P;点M沿OA运动,到M1时,发现⊙M1与直线OB有一个交点;∴当4<x<4时,圆M在移动过程中,则会与OB除了O外有两个交点,满足点P恰好有三个;综上所述,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是:x=0或x=4﹣4或4.故答案为:x=0或x=4﹣4或4.三.解答题(共9小题)27.如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=42°,求∠BED的度数.【分析】已知AE平分∠BAC,ED∥AC,根据两直线平行同旁内角互补,可求得∠DEA的度数,再由三角形外角和为360°求得∠BED度数.【解答】解:∵BE⊥AE∴∠AEB=90°∵AE平分∠BAC∴∠CAE=∠BAE=42°又∵ED∥AC∴∠AED=180°﹣∠CAE=180°﹣42°=138°∴∠BED=360°﹣∠AEB﹣∠AED=132°28.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.求证:OE=OF.【分析】根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案.【解答】证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠2=∠5,∠4=∠6,∵MN∥BC,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,∴EO=CO,FO=CO,∴OE=OF.29.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.(1)求证:∠CBE=∠BAD;(2)当△ABC满足什么条件时,AE=CE.直接写出条件.【分析】(1)根据三角形三线合一的性质可得∠CAD=∠BAD,根据同角的余角相等可得:∠CBE=∠CAD,再根据等量关系得到∠CBE=∠BAD.(2)根据等边三角形的性质即可求解.【解答】(1)证明:∵AB=AC,AD是BC边上的中线,BE⊥AC,∴∠CBE+∠C=∠CAD+∠C=90°,∠CAD=∠BAD,∴∠CBE=∠BAD.(2)当△ABC满足是等边三角形的条件时,AE=CE.30.文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:文文:“过点A作BC的中垂线AD,垂足为D”;彬彬:“作△ABC的角平分线AD”.数学老师看了两位同学的辅助线作法后,说:“彬彬的作法是正确的,而文文的作法需要订正.”(1)请你简要说明文文的辅助线作法错在哪里;(2)根据彬彬的辅助线作法,完成证明过程.【分析】(1)线段BC的中垂线可以直接作出的,不需要附带“过点A作”;(2)根据已知条件利用AAS可证△ABD≌△ACD,得出AB=AC.【解答】(1)解:作辅助线不能同时满足两个条件;(2)证明:作△ABC的角平分线AD.∴∠BAD=∠CAD,在△ABD与△ACD中,∵,∴△ABD≌△ACD(AAS).∴AB=AC.31.如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:DF=EF.【分析】首先过点D作DM∥AC交BC于M,易证得△DMF≌△ECF,继而证得DF=EF.【解答】证明:过点D作DM∥AC交BC于M,∴∠DMB=∠ACB,∠FDM=∠E,∵AB=AC,∴∠B=∠ACB,∴∠B=∠DMB,∴BD=MD,∵BD=CE,∴MD=CE,在△DMF和△ECF中,,∴△DMF≌△ECF(AAS),∴DF=EF.32.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠BAD=25°;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.【分析】(1)根据三角形内角和定理,将已知数值代入即可求出∠BAD,根据点D的运动方向可判定∠BDA的变化情况.(2)假设△ABD≌△DCE,利用全等三角形的对应边相等得出AB=DC=2,即可求得答案.(3)假设△ADE是等腰三角形,分为三种情况:①当AD=AE时,∠ADE=∠AED=40°,根据∠AED>∠C,得出此时不符合;②当DA=DE时,求出∠DAE=∠DEA=70°,求出∠BAC,根据三角形的内角和定理求出∠BAD,根据三角形的内角和定理求出∠BDA即可;③当EA=ED时,求出∠DAC,求出∠BAD,根据三角形的内角和定理求出∠ADB.【解答】解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;故答案为:25°;小.(2)当△ABD≌△DCE时.DC=AB,∵AB=2,∴DC=2,∴当DC等于2时,△ABD≌△DCE;(3)∵AB=AC,∴∠B=∠C=40°,①当AD=AE时,∠ADE=∠AED=40°,∵∠AED>∠C,∴此时不符合;②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,∵∠BAC=180°﹣40°﹣40°=100°,∴∠BAD=100°﹣70°=30°;∴∠BDA=180°﹣30°﹣40°=110°;③当EA=ED时,∠ADE=∠DAE=40°,∴∠BAD=100°﹣40°=60°,∴∠BDA=180°﹣60°﹣40°=80°;∴当∠ADB=110°或80°时,△ADE是等腰三角形.33.如图1,△ABC中,AB=AC,∠A=36°,我们发现这个三角形有一种特性,即经过它某一顶点的一条射线可把它分成两个小等腰三角形.为此,请你解答问题;如图2,△ABC中,AB=AC,∠A=108°,请你在图中画一条射线(不必写画法),把它分成两个小等腰三角形,并写出底角的大小.【分析】先根据AB=AC,∠A=108°,求得∠C=36°,再过点A作∠DAC=36°,则△ACD和△ABD均为等腰三角形.【解答】解:如图2所示,由AB=AC,∠A=108°,可知∠C=36°,过点A在∠BAC内部作射线AD,使得∠DAC=36°,则△ABD中,∠BAD=72°,∠ADB=72°,△ACD中,∠DAC=∠C=36°,故△ACD和△ABD均为等腰三角形,故射线AD即为所求.34.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PE∥AB 交BC于点D,交AC于点F.(1)若点P在BC上(如图一),此时PD=0,可得结论:PD+PE+PF=AB(填“>”“<”或“=”)(2)当点P在△ABC内(如图二)时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请直接写出你的猜想,不需要证明.【分析】(1)先求出四边形PFAE是平行四边形,根据平行四边形对边相等可得PF=AE,再根据两直线平行,同位角相等可得∠BPE=∠C,然后求出∠B=∠BPE,利用等角对等边求出PE=BE,然后求解即可;(2)根据平行四边形的判定得出四边形AEPF为平行四边形,根据平行四边形的性质,平行线的性质即可得证.【解答】解:(1)答:PD+PE+PF=AB.证明如下:∵点P在BC上,∴PD=0,∵PE∥AC,PF∥AB,∴四边形PFAE是平行四边形,∴PF=AE,∵PE∥AC,∴∠BPE=∠C,∴∠B=∠BPE,∴PE=BE,∴PE+PF=BE+AE=AB,∵PD=0,∴PD+PE+PF=AB;(2)当点P在△ABC内时,结论PD+PE+PF=AB仍然成立.证明:∵PE∥AC,PF∥AB,∴四边形AEPF为平行四边形,∴PE∥AF ∵PF∥AB,∴∠FDC=∠B,又∵AB=AC,∴∠B=∠C,∴∠FDC=∠C,∴DF=CF,∴DF+PE=CF+AF,即DF+PE=AC,又∵DF=PD+PF,AC=AB,∴PD+PF+PE=AB,即上述结论成立.35.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.(1)当D点在BC的什么位置时,DE=DF?并证明.(2)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明:(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?【分析】(1)当点D在BC的中点时,DE=DF,根据AAS证△BED≌△CFD,根据全等三角形的性质推出即可;(2)连接AD,根据三角形ABC的面积=三角形ABD的面积+三角形ACD的面积,进行分析证明;(3)类似(2)的思路,仍然用计算面积的方法来确定线段之间的关系.即三角形ABC的面积=三角形ABD的面积﹣三角形ACD的面积.【解答】解:(1)当点D在BC的中点时,DE=DF,理由如下:∵D为BC中点,∴BD=CD,∵AB=AC,∴∠B=∠C,∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,在△BED和△CFD中,∴△BED≌△CFD(AAS),∴DE=DF.(2)DE+DF=CG.证明:连接AD,则S△ABC=S△ABD+S△ACD,即AB•CG=AB•DE+AC•DF,∵AB=AC,∴CG=DE+DF.(3)当点D在BC延长线上时,(1)中的结论不成立,但有DE﹣DF=CG.理由:连接AD,则S△ABD=S△ABC+S△ACD,即AB•DE=AB•CG+AC•DF∵AB=AC,∴DE=CG+DF,即DE﹣DF=CG.同理当D点在CB的延长线上时,则有DE﹣DF=CG,说明方法同上.。
第18讲 等腰三角形(解析版)

中考数学一轮复习资料五合一《核心考点+重点题型+高分秘籍+题组特训+过关检测》(全国通用版)第18讲等腰三角形题组特训详解一、选择题1.如图,在ABC V 中,AB AC =,AB 的垂直平分线交边AB 于D 点,交边AC 于E 点,若ABC V 与EBC V 的周长分别是20,12,则AB 为( )A .4B .6C .8D .10【答案】C 【分析】首先根据DE 是AB 的垂直平分线,可得AE BE =;然后根据ABC V 的周长AB AC BC =++,EBC V 的周长BE EC BC AE EC BC AC BC =++=++=+,可得ABC V 的周长EBC -V 的周长AB =,据此求出AB 的长度是多少即可.【详解】解:∵DE 是AB 的垂直平分线,∴AE BE =,∵ABC V 的周长AB AC BC =++,EBC V 的周长BE EC BC AE EC BC AC BC =++=++=+,∴ABC V 的周长EBC -V 的周长AB =,∴20128AB =-=.故选:C .【点睛】此题主要考查了垂直平分线的性质,要熟练掌握,解答此题的关键是要明确:垂直平分线上任意一点,到线段两端点的距离相等.此题还考查了等腰三角形的性质,以及三角形的周长的求法,要熟练掌握.2.已知边长为4的等边ABC、、的中点,P为线段DE上一动点,则V,D、E、F分别为边AB BC AC+的最小值为( )PF PCA.B.3C.4D.段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.3.如图,等腰ABC V 内接于O e ,点D 是圆中优孤上一点,连接DB DC 、,已知,70AB AC ABC =Ð=°,则BDC Ð的度数为( )A .10°B .20°C .30°D .40°【答案】D 【分析】先根据等边对等角和三角形内角和定理求出40A Ð=°,再由同弧所对的圆周角相等即可得解答.【详解】解:∵AB AC =,70ABC Ð=°,∴70ABC ACB Ð=Ð=°,∴18040A ABC ACB Ð=°-Ð-Ð=°,∴40BDC A Ð==°∠.故选D .【点睛】本题主要考查了同弧所对的圆周角相等、等腰三角形的性质、三角形内角和定理等知识点,掌握同弧所对的圆周角相等是解题的关键.4.如图,若50MON Ð=°,MON Ð内有一个定点P ,点A ,B 分别在射线OM ON ,上移动,当PAB V 周长最小时,则APB Ð的度数为( )A .60°B .80°C .100°D .120°【答案】B 【分析】作点P 关于OM 的对称点P ¢,点P 关于ON 的对称点P ¢¢,连接OP ¢,OP ¢¢,P P ¢¢¢,其中P P ¢¢¢交OM 于A ,交ON 于B ,此时PAB V 的周长最小值等于P P ¢¢¢的长,由轴对称性质可知:OP OP ¢=,OP OP ¢¢=,AOP AOP ¢Ð=Ð,BOP BOP ¢¢Ð=Ð,且2250100P OP AOB ¢¢¢Ð=Ð=´°=°,从而得出180100240P P ¢¢¢Ð=Ð=°-°¸=°(),即可得出答案.【详解】解:如图,作点P 关于OM 的对称点P ¢,点P 关于ON 的对称点P ¢¢,连接OP ¢,OP ¢¢,P P ¢¢¢,其中P P ¢¢¢交OM 于A ,交ON 于B ,此时PAB V 的周长最小值等于P P ¢¢¢的长,由轴对称性质可知:OP OP ¢=,OP OP ¢¢=,AOP AOP ¢Ð=Ð,BOP BOP ¢¢Ð=Ð,∴2250100P OP AOB ¢¢¢Ð=Ð=´°=°,∴180100240P P ¢¢¢Ð=Ð=°-°¸=°(),∴80APB P P ¢¢¢Ð=Ð+Ð=°,故选:B .【点睛】本题主要考查了轴对称的性质,等腰三角形的性质,三角形内角和定理等知识,将PAB V 的周长最小值转化为P P ¢¢¢的长是解题的关键.5.如图,等腰ABC V 中,AB AC =,70BAC Ð=°,D 是BC 边的中点,DE AB ^于点E ,延长DE 至点F ,使EF DE =,则F Ð的度数为( )A .45°B .50°C .55°D .60°∵DE AB ^,∴90BED Ð=°,∴903555ADE Ð=°-°=°,∵EF DE =,DE AB ^,∴AF AD =,∴55F ADE Ð=Ð=°,故答案为:C .【点睛】本题考查的知识点主要是等腰三角形的性质与线段垂直平分线的性质,理解性质并熟练的应用是解题的关键.6.如图,在ABC V 中,AB AC =,边BC 在x 轴上,且点()10B -,,点()24A ,,则AOC V 的面积为( )A .10B .12C .20D .26【答案】A 【分析】作AD x ^轴于点D,求得4=AD ,2OD =,利用等腰三角形的性质求得3BD CD ==,根据三角形的性质即可求解.【详解】解:作AD x ^轴于点D,∵()24A ,,∴()20D ,,4=AD ,2OD =,7.如图,在正方形ABCD中,4V沿AE折叠,使点B落在正方形内点AB=,E为BC的中点,将ABEF处,连接CF,则CF的长为()A.B C D.2.25∵四边形ABCD为正方形,8.如图,已知长方形ABCD 沿着直线BD 折叠,使点C 落在点C ¢处,BC ¢交AD 于点E ,168AD AB ==,,则DE 的长为( )A .9B .10C .11D .12【答案】B 【分析】由四边形ABCD 为长方形可知AD BC ∥,8CD AB ==,从而得出ADB CBD Ð=Ð,结合折叠的性质得出ADB C BD ¢Ð=Ð,进而得出BE DE =.设BE DE x ==,则16AE x =-,在Rt ABE △中,根据勾股定理可列出关于x 的等式,解出x 的值,即得出答案.【详解】∵四边形ABCD 为长方形,∴AD BC ∥,8CD AB ==∴ADB CBD Ð=Ð.由折叠的性质可知C BD CBD ¢Ð=Ð,8C D CD AB ¢===,∴ADB C BD ¢Ð=Ð,∴BE DE =.设BE DE x ==,则16AE AD DE x =-=-,在Rt ABE △中,222AE AB BE +=,∴()222168x x -+=,解得:10x =,∴10DE =.故选B .【点睛】本题主要考查折叠的性质,勾股定理等知识.利用数形结合的思想是解题关键.9.如图,在一个直角三角形中,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形,其作法不一定正确的是( )A .B .C .D .【答案】B【分析】对尺规作图进行分析,再利用等腰三角形的判定条件逐一进行判断即可得到答案.【详解】解:A 、如图1,由作法可知,BD BC =,即BCD △是等腰三角形,不符合题意,选项错误;B 、如图2,由作法可知,所做线段为AC 的垂直平分线,但不能证明线段相等,无法推出等腰三角形,符合题意,选项正确;C 、如图3,由作法可知,所做线段为AB 的垂直平分线,AD BD =,即ABD △是等腰三角形,不符合题意,选项错误;D 、如图4,由作法可知,所做线段为AC 的垂直平分线,AD CD =,即ACD V 是等腰三角形,不符合题意,选项错误,故选B .【点睛】本题考查了尺规作图,垂直平分线的性质,等腰三角形的判定,熟练掌握尺规作图的基本图形做法是解题关键.10.如图,将长方形ABCD 沿EF 折叠,B ,C 分别落在点H ,G 的位置,CD 与HE 交于点M .下列说法中,不正确的是( ).A .ME HG=B .ME MF =C .HM FM EB+=D .GFM MEAÐ=Ð【答案】A 【分析】由折叠的性质知BEF MEF Ð=Ð,BC HG =,AD AB ^,结合平行线的性质可证M MEF FE =ÐÐ,可证选项B 正确;由点到直线的距离可得ME HG ¹,故选项A 不正确;由折叠的性质知HE BE =,再由HE HM ME HM MF =+=+,可得选项C 正确,利用平行线的性质可得MEA HMD Ð=Ð,GFM HMD Ð=Ð,可证选项D 正确.【详解】解:如图,过点M 作MK AB ^,由折叠的性质知BEF MEF Ð=Ð,BC HG =,AD AB ^,由题意知CD AB ∥,AD BC HG ==,∴BEF MFE Ð=Ð,AD MK HG ==,∴M MEF FE =ÐÐ,∴ME MF =,故选项B 正确,不合题意;∵ME MK >,∴ME HG ¹,故选项A 不正确,符合题意;由折叠的性质得:HE BE =,∵HE HM ME HM MF =+=+,∴HM FM EB +=,故选项C 正确,不合题意;∵CD AB ∥,∴MEA HMD Ð=Ð,由题意知HE GF ∥,∴GFM HMD Ð=Ð,∴GFM MEA Ð=Ð,故选项D 正确,不合题意;故选A .【点睛】本题考查折叠的性质,平行线的性质等知识点,解题的关键是牢记折叠前后对应边相等、对应角相等.11.如图,在矩形ABCD 中,1AB =,2AD =,点M 在边BC 上,若MA 平分DMB Ð,则CM 的长是( )A .B .1C .D 【答案】D 【分析】由矩形的性质得出1CD AB ==,AD BC ∥,2BC AD ==,90C Ð=°,由平行线的性质得出DAM AMB Ð=Ð,再由角平分线证出AMB AMD Ð=Ð,又勾股定理求出CM 即可.【详解】∵四边形ABCD 是矩形,∴1CD AB ==,AD CB ∥,2BC AD ==,90C Ð=°,∴DAM AMB Ð=Ð,∵MA 平分DMB Ð,∴AMB AMD Ð=Ð,∴DAM AMD Ð=Ð,∴2DM AD ==,12.如图,ABC V 中,AB AC =,BD 平分ABC Ð交AC 于G ,DM ∥BC 交ABC Ð的外角平分线于M ,交AB 、AC 于F 、E ,下列结论正确的是( )A .EF ED=B .FD BC =C .EC MF =D .EC AG=【答案】C 【分析】通过证明BF EC =,BF FM =即可解决问题;【详解】解:∵AB AC =,∴ABC C Ð=Ð,∵DM ∥BC ,∴,AFE ABC AEF C Ð=ÐÐ=Ð,∴AFE AEF Ð=Ð,∴AF AE =,∴BF EC =,∵D DBC FBD Ð=Ð=Ð,∴DF BF =,同理可证:BF FM =,∴EC FM =,故选:C .【点睛】本题主要考查了等腰三角形的判定及其性质,平行线的性质,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.13.如图,等边三角形ABC 中,D 、E 分别为AB BC 、边上的两个动点,且总使AD BE =,AE 与CD 交于点F ,AG CD ^于点G ,则:FG AF 等于( )A .1B .2C .13D .1214.如图,在平面直角坐标系xOy 中,直线MN 分别与x 轴,y 轴交于点M ,N ,且6OM =,30OMN Ð=°,等边AOB V 的顶点A ,B 分别在线段MN OM ,上,则OB 的长为( )A .1B .2C .3D .415.如图,在ABC V 中,以各边为边分别作三个等边三角形BCF ,ABD ,ACE ,若3AB =,4AC =,5BC =,则下列结论:①AB AC ^;②四边形ADFE 是平行四边形;③150DFE Ð=°;④5ADFE S =四边形,其中正确的有( )A .4个B .3个C .2个D .1个【答案】B 【分析】由222AB AC BC +=,得出90BAC Ð=°,则①正确;由等边三角形的性质得60DAB EAC Ð=Ð=°,则150DAE Ð=°,由SAS 证得ABC DBF V V ≌,得4AC DF AE ===,同理()SAS ABC EFC V V ≌,得3AB EF AD ===,得出四边形AEFD 是平行四边形,则②正确;由平行四边形\12AEFD S DF AM DF AD =×=×Y 故④不正确;\正确的个数是3个,故选:B .二、解答题16.如图,ABC V 是等腰三角形,AB AC =,060BAC °<Ð<°,分别在AB 的右侧,AC 的左侧作等边三角形ABD 和等边三角形ACE ,BD 与CE 相交于点F .(1)求证:BF CF =;(2)作射线AF 交BC 于点G ,交射线DC 于点H .①补全图形,当40BAC Ð=°时,求AHD Ð的度数;②当BAC Ð的度数在给定范围内发生变化时,AHD Ð的度数是否也发生变化?若不变,请直接写出AHD Ð的度数;若变化,请给出AHD Ð的度数的范围.17.如图,在ABCÐ的平V中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交DAC分线于E,交BC于G,且AE BC∥.(1)求证:ABC V 是等腰三角形;(2)若8AE =,2GC BG =,求BC 长.【答案】(1)答案见解析(2)12【分析】(1)先根据平行线的性质证明B DAEC CAE ÐÐÐÐ=,=,然后根据角平分线的定义得出B C Ð=Ð,则可证明ABC V 为等腰三角形;(2)证明AFE CFG △≌△,从而得到CG 的长,则可求得BC 的长.【详解】(1)解:AE BC Q ∥,B D A E ,C C A E \Ð=ÐÐ=Ð,AE Q 平分DAC Ð,DAE CAE \Ð=Ð,B C \Ð=Ð,AB AC \=,ABC \V 是等腰三角形;(2)F Q 是AC 的中点,AF CF \=,在AFE △和CFG △中,C FAE CF AFGFC EFA Ð=Ðìï=íïÐ=ÐîA FE C FG \V V ≌,8G C A E \==,2GC BG =Q ,4BG \=,12B C B G G C \=+=.【点睛】本题考查了等腰三角形的性质和三角形全等的判定,解题的关键是熟练运用等腰三角形的性质和三角形全等的判定定理.18.在ABCV中,AB BC=,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE OF,.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当90Ð=°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由;ABC(3)若2,POFCF AE EF-==V为等腰三角形时,请直接写出线段OP的长.19.如图,在Rt ABC △中,90ACB Ð=°,30BAC Ð=°,E 为AB 边的中点,以BE 为边作等边BDE V ,连接AD ,CD .(1)求证:ACD V 为等边三角形;(2)若3BC =,在AC 边上找一点H ,使得BH EH +最小,并求出这个最小值.由作图可知:最小值为∴60EAE¢Ð=°,∴EAE¢△为等边三角形,∴12EE EA AB¢==,∴90AE BТ=°,20.在ABC V 中,AB AC =,120BAC Ð=°,AD BC ^,垂足为G ,且AD AB =.60EDF Ð=°,其两边分别交边AB ,AC 于点E ,F .(1)求证:ABD △是等边三角形;(2)求证:AE CF =.60DBE DAF BD ADBDE ADF Ð=Ð=°ìï=íïÐ=Ðî,∴()ASA BDE ADF △△≌.∴BE AF =.又∵AB AC =,∴AB BE AC AF -=-,∴AE CF =.【点睛】本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.过关检测详细解析一.选择题1.如图,在ABC V 中,AC BC =,边AC 的垂直平分线分别交,AC BC 于点D 、E .若45BAE Ð=°,3DE =,则AE 的长为( )A .2B .4C .6D .82.已知等腰三角形一边长为4,另一边长为6,则这个等腰三角形的面积等于()A.B.C.D.3.如图,四边形ABCD 是O e 的内接四边形,连接AC .若AC AD =,40CAD Ð=°,则B Ð的大小为( )A .70°B .100°C .110°D .120°【答案】C 【分析】根据AC AD =,40CAD Ð=°,得到70ACD D Ð=Ð=°,根据+180B D ÐÐ=°计算选择即可.【详解】∵AC AD =,40CAD Ð=°,∴70ACD D Ð=Ð=°,∵+180B D ÐÐ=°,∴110B Ð=°,故选C .【点睛】本题考查了等腰三角形的性质,圆内接四边形的性质,熟练掌握两个性质是解题的关键.4.如图,在正方形ABCD 中,4AB =,E 为BC 的中点,将ABE V 沿AE 折叠,使点B 落在正方形内点F 处,连接CF ,则CF 的长为( )A .BCD .2.25∵四边形ABCD 为正方形,∴4AB BC ==,∵E 为BC 的中点,∴122BE CE BC ===,在Rt ABE △中,根据勾股定理可得:5.如图1为一张正三角形纸片ABC ,其中D 点在AB 上,E 点在BC 上.以DE 为折痕将B 点往右折如图2所示,BD BE 、分别与AC 相交于F 点、G 点.若10AD =,16AF =,14DF =,8BF =,则CG 长度为( )A .7B .8C .9D .106.如图,已知ABC V 是等边三角形,2BDC BAC Ð=Ð,BD CD =,点M ,N 分别是B ,AC 边上的点,且60MDN Ð=°.连接MN ,若AMN V 的周长是6,则ABC V 的边长是( )A .2B .3C .3.5D .4【答案】B 【分析】延长AB 至F ,使BF CN =,连接DF ,由“SAS ”可证BDF CDN V V ≌,V V ≌DMN DMF ,可得Ð=ÐBDF CDN ,DF DN =,MN MF =,即可求解.【详解】解:延长AB 至F ,使BF CN =,连接DF ,∵ABC V 是等边三角形,∴60Ð=Ð=Ð=°ABC BAC BCA ,∵BD CD =,2BDC BAC Ð=Ð,∴BDC V 是等腰三角形,120BDC Ð=°,∴30Ð=Ð=°BCD DBC ,∴90Ð=Ð=°DBA DCA ,在DBF V 和CND △中,BF CN DBF DCN DB DC =ìïÐ=Ðíï=î,∴()SAS BDF CDN V V ≌,∴Ð=ÐBDF CDN ,DF DN =,∵60MDN Ð=°,∴60Ð+Ð=°BDM CDN ,∴60BDM BDF FDM MDN Ð+Ð=°=Ð=Ð,在DMN V 和V DMF 中,DN DF MDN MDF DM MD =ìïÐ=Ðíï=î,∴()SAS DMN DMF V V ≌,∴MN MF =,∴MF BF BM BM CN MN =+=+=,∴AMN V 的周长2AM AN MN AM MB BF AN AB AN CN AB AC AB ++=+++=++=+=.∵AMN V 的周长是6∴3AB =故选:B .【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质,等腰三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.7.如图,已知点D E 、分别是等边ABC V 边BC AB 、的中点,6AD =,点F 是线段AD 上一动点,则BF EF +的最小值为( )A .3B .6C .9D .12【答案】B 【分析】连接CE 交AD 于点F ,连接BF ,此时BF EF +的值最小,最小值为CE .【详解】解:连接CE 交AD 于点F ,连接BF ,如下图:∵ABC V 是等边三角形,D 是BC 的中点,∴BF CF =,∴BF EF CF EF CE +=+=,此时BF EF +的值最小,最小值为CE ∵D E 、分别是等边ABC V 边BC AB 、的中点,∴AD CE =,∵6AD =,∴6CE =,∴BF EF +的值最小值为6.故选:B .【点睛】此题主要考查了轴对称求最短距离,解题关键是掌握轴对称求最短距离的方法,等边三角形的性质.8.如图,在等边ABC V 中,4BC cm =,动点D 从点B 出发,以1cm/s 的速度沿BA 方向运动.同时动点E 从点B 出发以相同的速度沿BC 方向运动,当点D 运动到点A 时,点E 也随之停止运动.连接DE ,将BDE V 沿DE 折叠,点B 的对称点为点F ,设点D 的运动时间为t 秒,DEF V 与ABC V 重叠部分的面积为y ,则下列图象能大致反映y 与t 之间函数关系的是( )A .B .C .D .【答案】A【分析】根据等边三角形的性质和折叠的性质,利用分类讨论的思想方法求得y 与t 的函数关系式,再结合自变量的取值范围判定出函数的大致图象.【详解】解:由折叠的性质可得:BDE DEF S S =△△,①当02t ££时,DEF V 与ABC V 重叠部分的面积为BDE y S =V ,由题意得:cm BD BE t ==,过点D 作DH BE ^于点H ,如图,∵ABC V 是等边三角形,由题意得:cm==,则BD BE t∵60,,B BD BEÐ=°=∴BDEV是等边三角形,4综上,y 与t 之间函数关系式为由二次函数图象的性质可知,第一个函数的图象是开口向上的抛物线的一部分,第二个函数的图象是开9.点D 是等边三角形ABC 的边AB 上的一点,且12AD BD ==,,现将ABC V 折叠,使点C 与点D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,若54BF =,则CE 的长为( )A .53B .75C .125D .3510.如图,在等边三角形ABC 中,10cm AB AC ==,4cm DC =.如果点M ,N 都以1cm/s 的速度运动,点M 在线段CB 上由点C 向点B 运动,点N 在线段BA 上由点B 向点A 运动.它们同时出发,当两点运动时间为t 秒时,BMN V 是一个直角三角形,则t 的值为( )A .103B .209C .103或203D .53或103【答案】C【分析】根据题意,用含t 的式子表示出,,10CM t BN t BM t -===,分两种情况讨论,当90BMN Ð=°时,2BN BM =,求出t 的值;当90BNM Ð=°时,2BM BN =,求出t 的值.【详解】解:∵ABC V 是等边三角形,10AB AC ==cm ,∴10BC =cm ,∵点M 、N 都以1cm/s 的速度运动,设CM t =,BN t =,线PQ,切点为Q,则PQ的最小值为()A.5B C.D.6【答案】A【分析】连接CQ、CP,过点C作CH AB^,根据勾股定理求出^于H,根据切线的性质得到CQ PQPQ,根据等边三角形的性质求出CH,根据垂线段最短解答即可.【详解】解:连接CQ、CP,过点C作CH AB^于H,∵PQ 是C e 的切线,∴CQ PQ ^,∴22PQ CP CQ =-=当CP AB ^时,CP 最小,12.如图,O 为ABC V 的外心,OCP △为正三角形,OP 与AC 相交于D 点,连接OA .若70BAC Ð=°,AB AC =,则ADP Ð为( )A .110°B .90°C .85°D .80°【答案】C 【分析】由三角形的外心可知OA OC =,结合AB AC =,70BAC Ð=°先求出ACO Ð,再利用OCP △是正三角形以及外角的性质即可求解ADP Ð的度数.【详解】解:O Q 是ABC V 的外心,AB AC=OA OC BAO CAO ACO\=Ð=Ð=Ð,=70BAC аQ =35CAO ACO \Ð=аOCP Q △是正三角形60PCO P \Ð=Ð=°25PCD PCO ACO \Ð=Ð-Ð=°256085ADP PCD P \Ð=Ð+Ð=°+°=°故选C .【点睛】本题主要考查外心的性质,等边三角形的性质及三角形外角性质,熟练掌握外心的性质及外角的性质是解决本题的关键.13.如图,点B 是线段AC 上任意一点(点B 与点A ,C 不重合),分别以AB 、BC 为边在直线AC 的同侧作等边三角形ABD 和等边三角形BCE ,AE 与BD 相交于点G ,CD 与BE 相交于点F ,AE 与CD 相交于点H ,则下列结论:①AE CD =;②120AHC Ð=°;③ABG DBF ≌△△;④连接GF ,则GBF V 是等边三角形,以上结论正确的有( )A .4个B .3个C .2个D .1个【答案】A 【分析】利用等边三角形,ABD BCE V V 的性质,证明 ,ABE DBC V V ≌ 从而可判断①,由,ABE DBC V V ≌可得,EAB CDB Ð=Ð 再利用三角形的内角和定理可判断②,得出60ABG DBF Ð=Ð=°,进而证明ABG DBF ≌△△,判断③,得出BG BF =,即可判断④【详解】解:,ABD BCE QV V 为等边三角形,,60,60BA BD ABD BC BE CE CBE \=Ð=°==Ð=°,,,ABD DBE CBE DBE \Ð+Ð=Ð+Ð 即,ABE DBC Ð=Ð()SAS ,ABE DBC \V V ≌,AE DC \= 故①正确;Q ,ABE DBC V V ≌,EAB CDB \Ð=Ð,DGH AGB Ð=ÐQ180,180,DHG CDB DGH ABD EAB AGB Ð=°-Ð-ÐÐ=°-Ð-ÐQ60DHG ABD \Ð=Ð=°,120AHC \Ð=°,故②正确;60ABD EBC Ð=Ð=°Q ,60DBF \Ð=°,,EAB CDB Ð=ÐQ 则GAB FDBÐ=Ð在,ABG DBF V V 中GAB FDB AB DBABG DBF Ð=Ðìï=íïÐ=Ðî()ASA ABG DBF \V V ≌,故③正确;BF BG\=又60DBF Ð=°Q ,\GBF V 是等边三角形,故④正确故选:A .【点睛】本题考查的是三角形的内角和定理的应用,全等三角形的判定与性质,等边三角形的判定与性质,掌握以上知识是解题的关键.14.如图,P 为O e 外一点,PA PB 、分别切O e 于点A 、B ,AC 是O e 的直径,若10AC =,30BAC Ð=°,则PAB V 的周长为( )A.8B.C.20D.【点睛】本题主要考查了切线的性质,切线长定理,等边三角形的性质与判定,勾股定理,直径所对的圆周角是直角,含30度角的直角三角形的性质等等,正确作出辅助线构造直角三角形是解题的关键.15.如图,在Rt ABC △中,90ACB Ð=°,60A Ð=°,10AC =,将ABC V 绕点C 按逆时针方向旋转得到A B C ¢¢△,此时点A ¢恰好在AB 边上,则点B ¢与点B 之间的距离为( )A .10B .20C .D .【答案】D 【分析】连接BB ¢,证明ACA ¢V 是等边三角形,得出60ACA ¢Ð=°,从而得出60BCB ¢Ð=°,证明BCB ¢V 是等边三角形,得出BB BC ¢=,根据勾股定理,结合含30°角的直角三角形性质,求出BC 即可.【详解】解:如图,连接BB ¢,∵将ABC V 绕点C 按逆时针方向旋转得到A B C ¢¢△,∴BCB ACA ¢¢Ð=Ð,CB CB ¢=,CA CA ¢=,∵60A Ð=°,∴ACA ¢V 是等边三角形,∴60ACA ¢Ð=°,∴60BCB ¢Ð=°,二、解答题16.在AOB V 中,已知90AOB Ð=°,OA OB =,点P 、D 分别在AB OB 、上.(1)如图1,若45PO PD OPD =Ð=°,,则POB Ð=______°(直接写答案)(2)如图1,在(1)的条件下,求证:BOP △是等腰三角形.(3)如图2中,若12AB =,点P 在AB 上移动,且满足PO PD =,DE AB ^于点E ,试问:此时PE 的长度是否变化?若变化,说明理由:若不变,请予以证明.【答案】(1)67.5°(2)见解析(3)PE 的值不变,6PE =,理由见解析【分析】(1)根据等腰三角形的性质和三角形内角和定理求解即可;(2)首先根据等腰直角三角形的性质得到45B A Ð=Ð=°,然后利用三角形内角和定理和067.5BOP P D Ð=Ð=°得到BOP BPO Ð=Ð,进而求解即可;(3)解:PE的值不变,如图,过点O作OM∵90Ð=°,AOB AO∴BOMV是等腰直角三角形,1∴()AAS POM DPE ≌V V ,∴6OM PE ==,∴PE 的值不变,PE 的值为6.【点睛】此题考查了全等三角形的性质和判定,等腰直角三角形的性质,三角形内角和定理等知识,解题的关键是熟练掌握以上知识点.17.如图,ABC V 中, 15AB AC ==,AB 的垂直平分线DE 交AB 、AC 于E 、D .(1)若BCD △的周长为21,求BC 的长;(2)若42A Ð=°,求DBC Ð的度数.【答案】(1)6(2)27DBC Ð=°【分析】(1)通过垂直平分线的性质判断边等,将三角形周长换成边的和,据此求解即可.(2)等腰三角形推出角等,通过角度的数量关系求解即可.【详解】(1)Q AB 的垂直平分线DE 交AB 、AC 于E 、D .\BD AD =,Q BCD △的周长是21,15AB AC ==,\BCD △的周长21BD CD BC AD CD BC AC BC =++=++=+=,\6BC =;(2)Q AB 的垂直平分线DE 交AB 、AC 于E 、D .\AD BD =,ABD A Ð=Ð,Q ABC V 中,AB AC =,\ABC C Ð=Ð,Q 42A Ð=°,\69ABC C Ð=Ð=°,\27DBC Ð=°.【点睛】此题考查垂直平分线的性质,解题关键是找到等角和等边的数量关系求解.18.已知,点P 为等边三角形ABC 所在平面内一点,且120BPC Ð=°.(1)如图(1),90ABP Ð=°,求证:BP CP =;(2)如图(2),点P 在ABC V 内部,且90APB Ð=°,求证:2BP CP =;(3)如图(3),点P 在ABC V 内部,M 为BC 上一点,连接PM ,若180BPM APC Ð+Ð=°,求证:BM CM =.【答案】(1)见解析(2)见解析(3)见解析【分析】(1)证明BPC BCP Ð=Ð即可;(2)将ABP V 绕A 逆时针旋60°转,得到ACE △,点P 的对应点为E ,连接PE ,首先证明EAP V 是等边三角形,从而得出3090CEP CPE Ð=°Ð=°,,再利用含30°角的直角三角形的性质,可得答案;(3)将ABP V 绕A 逆时针旋60°转,得到ACE △,点P 的对应点为E ,连接PE ,同理得EAP V 是等边三角形,过点C 作CN 平行于BP ,交PM 的延长线于点N ,再利用ASA 证明CPE CPN @V V ,得CE CN =,再证明()AAS CMN BPM @V V ,从而解决问题.【详解】(1)ABC QV 是等边三角形,60ABC ACB A \Ð=Ð=Ð=°,90,ABP Ð=°Q 90906030,PBC ABP ABC °\Ð=-Ð-Ð=°-°=°30BPC °Ð=Q ,180PBC BPC BCP Ð+Ð+Ð=°,1801801203030PCB BPC PBC \Ð=°-Ð-Ð=°-°-°=°,,PBC BPC \Ð=Ð,BP CP \=;(2)AP BP ^Q ,90APB \Ð=°,将ABP V 绕A 逆时针旋转60°,得到ACE △,点P 的对应点为E ,连接PE ,则90AE AP CE BP CAE BAP AEC APB ==Ð=ÐÐ=Ð=°,,,,∴EAP CAE CAP Ð=Ð+Ð60BAP CAP BAC =Ð+Ð=Ð=°,∴EAP V 是等边三角形,∴60APE AEP Ð=Ð=°,∴906030CEP AEC AEP Ð=Ð-Ð=°-°=°,∵360360906012090CPE APB APE BPC Ð=°-Ð-Ð-Ð=°-°-°-°=°,∴2CE CP =,∴2BP CP =;(3)将ABP V 绕A 逆时针旋60°转,得到ACE △,点P 的对应点为E ,连接PE ,同理可知,EAP V 是等边三角形,∴60APE AEP Ð=Ð=°,180,APC BPM Ð+Ð=°Q 180APE EPC BPM \Ð+Ð+Ð=°,120EPC BPM \Ð+Ð=°,又120,BPC CPM BPM Ð=Ð+Ð=°.FPC CPD \Ð=Ð,过点C 作,CN BP ∥交PM 的延长线于点N ,则,PBC NCB Ð=Ð120,BPC Ð=°Q 18012060,PBC PCB \Ð+Ð=°-°=°又60,60ACP PCB ABP PBC Ð+Ð=°Ð+Ð=°,,ACP PBC \Ð=Ð由旋转得,,ACE ABP BP CEÐ=Ð=∴60ACE ACP PBC ABP Ð+Ð=Ð+Ð=°又60NCB BCP PBC BCP Ð+Ð=Ð+Ð=°,∴PCE PCN Ð=Ð,在PCE V 和PCN △中,EPC NPC PC PCPCE PCN Ð=Ðìï=íïÐ=Ðî,∴PCE PCN @V V ,∴CE CN =,∴BP CN =,在BPM △和CNM V 中,PBM NCM PMB CMN BP CN Ð=ÐìïÐ=Ðíï=î,∴BM CM=【点睛】本题主要考查了等边三角形的判定与性质,旋转的性质,全等三角形的判定与性质,含30°角的直角三角形的性质等知识,利用旋转将分散条件集中到一个三角形中是解题的关键.19.在ABC V 中,90B Ð=°,1AB =,D 为BC 延长线上一点,点E 为线段AC ,CD 的垂直平分线的交点,连接EA ,EC ,ED .(1)如图1,当50BAC Ð=°时,则AED Ð的大小;(2)当60BAC Ð=°时,①如图2,连接AD ,AED △的形状是 三角形;②如图3,直线CF 与ED 交于点F ,满足CFD CAE Ð=Ð.P 为直线CF 上一动点.说明P 点在什么位置时,PE PD -有最大值;请直接写出这个最大值.(提示:作点D 关于直线CF 的对称点)【答案】(1)80AED Ð=°(2)①等边②点P 在ED ¢的延长线上时,PE PD -的值最大,最大值为2,理由见解析【分析】(1)利用线段的垂直平分线的性质以及三角形内角和定理,四边形内角和定理解决问题即可;(2)①ADE V 是等边三角形,证明EA ED =,60AED Ð=°即可;②结论:2PE PD AB -=.如图3中,作点D 关于直线CF 的对称点D ¢,连接CD ¢,DD ¢,ED ¢.当点P 在ED ¢的延长线上时,PE PD -的值最大,此时PE PD ED -=¢,利用全等三角形的性质证明ED AC ¢=,可得结论.【详解】(1)解:如图1中,Q 点E 是线段AC ,CD 的垂直平分线的交点,EA EC ED \==,EAC ECA \Ð=Ð,ECD EDC Ð=Ð,90ABC Ð=°Q ,50BAC Ð=°,905040ACB \Ð=°-°=°,18040140ACD \Ð=°-°=°,280EAC ACD EDC \Ð+Ð+Ð=°,36028080AED \Ð=°-°=°.(2)解:①如图2中,Q 点E 是线段AC ,CD 的垂直平分线的交点,EA EC ED \==,EAC ECA \Ð=Ð,ECD EDC Ð=Ð,90ABC Ð=°Q ,60BAC Ð=°,906030°°\Ð=-°=ACB ,18030150ACD \Ð=°-°=°,300EAC ACD EDC \Ð+Ð+Ð=°,36030060AED \Ð=°-°=°,ADE \V 是等边三角形;②如图3中,作点D 关于直线CF 的对称点D ¢,连接CD ¢,DD ¢,ED ¢.当点P 在ED ¢的延长线上时,PE PD -的值最大,此时PE PD ED -=¢,180CFD CFE Ð+Ð=°Q ,CFD CAE Ð=Ð,。
初中数学特殊三角形(等腰三角形、等边三角形、30°直角三角形)常考题及答案解析

特殊三角形(等腰三角形、等边三角形、30°直角三角形)常考题及答案解析1.(2020秋•喀什地区期末)下列说法错误的是()A.等腰三角形的两个底角相等B.等腰三角形的高、中线、角平分线互相重合C.三角形两边的垂直平分线的交点到三个顶点距离相等D.等腰三角形顶角的外角是其底角的2倍2.(2020秋•顺城区期末)已知等腰三角形的周长为17cm,一边长为4cm,则它的腰长为()A.4cm B.6.5cm C.6.5cm或9cm D.4cm或6.5cm 3.(2017•海南)已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画()条.A.3B.4C.5D.6 4.(2019•白银)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k=.5.(2013•凉山州)已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是.6.(2020秋•五常市期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.(1)求证:AB=AC;(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.7.(2019秋•龙岩期末)如图,AB=AC,AE=EC=CD,∠A=60°,若EF=2,则DF=()A.3B.4C.5D.6 8.(2006•烟台)如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于()A.25°B.30°C.45°D.60°9.(2020秋•慈溪市期中)已知:如图,AB=BC,∠A=∠C.求证:AD=CD.10.(2014秋•青山区期中)已知:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.求证:△DEF是等边三角形.11.(2018秋•六合区期中)如图,△ABC为等边三角形,BD平分∠ABC交AC于点D,DE ∥BC交AB于点E.(1)求证:△ADE是等边三角形.(2)求证:AE=AB.12.(2017•裕华区校级模拟)已知,如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AD=BE=CF.请你说明△DEF是正三角形.13.(2012秋•姜堰市校级期中)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC =α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)△COD是什么三角形?说明理由;(2)若AO=n2+1,AD=n2﹣1,OD=2n(n为大于1的整数),求α的度数;(3)当α为多少度时,△AOD是等腰三角形?14.(2000•内蒙古)如图,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连接CE,DE.求证:EC=ED.15.(2020秋•连山区期末)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=()A.2B.4C.6D.816.(2020秋•肇州县期末)如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AE=6cm,则AC=()A.6cm B.5cm C.4cm D.3cm 17.(2020秋•朝阳县期末)如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC 的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为()A.4.5B.5C.5.5D.618.(2020秋•抚顺县期末)右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,则DE长为.19.(2020秋•宽城区期中)如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AD等于()A.10B.8C.6D.420.(2020秋•无棣县期中)如图,在△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是()A.4B.4.5C.5D.721.(2020秋•云县期中)如图,点D是AB的中点,DE⊥AC,AB=7.2,∠A=30°,则DE=()A.1.8B.2.4C.3.6D.4.822.(2020秋•北碚区校级期中)如图,已知∠AOB=60°,P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=5,则ON的长度是()A.9B.6.5C.6D.5.523.(2020秋•天宁区校级期中)如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P 在斜边AB所在的直线m上运动,连结PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有()A.6个B.5个C.4个D.3个24.(2020秋•连江县期中)如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE ⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是()A.2﹣x B.3﹣x C.1D.2+x 25.(2020秋•赣榆区期中)如图,在△ABC中,AB=AC=6,∠BAC=120°,AD是△ABC 的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长是()A.5B.2C.4D.326.(2019秋•勃利县期末)如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D 作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有()①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.A.①②③B.①②④C.②③④D.①②③④27.(2019春•秦淮区期末)如图,△ABC是等边三角形,P是三角形内任意一点,D、E、F分别是AC、AB、BC边上的三点,且PF∥AB,PD∥BC,PE∥AC.若PF+PD+PE=a,则△ABC的边长为()A.a B.a C.a D.a28.下列说法中,正确的个数是()①三条边都相等的三角形是等边三角形;②有一个角为60°的等腰三角形是等边三角形;③有两个角为60°的三角形是等边三角形;④底角的角平分线所在的直线是这等腰三角形的对称轴,则这个三角形是等边三角形A.1个B.2个C.3个D.4个29.(2020•和平区三模)如图,在边长为2的等边三角形ABC中,D为边BC上一点,且BD=CD.点E,F分别在边AB,AC上,且∠EDF=90°,M为边EF的中点,连接CM交DF于点N.若DF∥AB,则CM的长为()A.B.C.D.30.(2020秋•天心区期中)下列说法错误的是()A.有一个角是60°的等腰三角形是等边三角形B.如果一个三角形有两个角相等,那么这两个角所对的边相等C.等腰三角形的角平分线,中线,高相互重合D.三个角都相等的三角形是等边三角形.31.(2019春•杏花岭区校级期中)关于等边三角形,下列说法中错误的是()A.等边三角形中,各边都相等B.等腰三角形是特殊的等边三角形C.两个角都等于60°的三角形是等边三角形D.有一个角为60°的等腰三角形是等边三角形32.(2019•城步县模拟)一个六边形的六个内角都是120°(如图),连续四条边的长依次为1,3,3,2,则这个六边形的周长是()A.13B.14C.15D.16 33.(2018•柳州一模)如图,在四边形ABCD中,∠A=∠B=60°,∠D=90°,AB=2,则CD长的取值范围是()A.<CD<B.CD>2C.1<CD<2D.0<CD<34.(2018秋•罗庄区期中)如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=()A.30°B.45°C.60°D.90°参考答案与试题解析1.【考点】线段垂直平分线的性质;等腰三角形的性质.【专题】线段、角、相交线与平行线;三角形;推理能力.【分析】根据等腰三角形的性质即可判断A;根据三角形的高、角平分线、中线的定义和等腰三角形的性质即可判断B;根据角平分线的性质即可判断C;根据三角形的外角性质和等腰三角形的性质即可判断D.【解答】解:A.等腰三角形的两底角相等,故本选项不符合题意;B.等腰三角形的两个底角的高、角平分线和中线不一定互相重合,故本选项符合题意;C.过O作OM⊥AB于M,OQ⊥AC于Q,ON⊥BC于N,∵O是∠ABC和∠ACB的角平分线的交点,∴OM=ON,ON=OQ,∴OM=ON=OQ,即三角形的两边的垂直平分线的交点到三个顶点的距离相等,故本选项不符合题意;D.∵AB=AC,∴∠B=∠C,∵∠EAC=∠B+∠C,∴∠EAC=2∠B,即等腰三角形顶角的外角是其底角的2倍,故本选项不符合题意;故选:B.【点评】本题考查了角平分线的性质,等腰三角形的性质,三角形的外角性质等知识点,能灵活运用知识点进行推理是解此题的关键.2.【考点】三角形三边关系;等腰三角形的性质.【专题】等腰三角形与直角三角形.【分析】分两种情况讨论:当4cm为腰长时,当4cm为底边时,分别判断是否符合三角形三边关系即可.【解答】解:①若4cm是腰长,则底边长为:20﹣4﹣4=12(cm),∵4+4<12,不能组成三角形,舍去;②若4cm是底边长,则腰长为:=6.5(cm).则腰长为6.5cm.故选:B.【点评】此题考查等腰三角形的性质与三角形的三边关系.此题难度不大,注意掌握分类讨论思想的应用是解此题的关键.3.【考点】等腰三角形的判定.【专题】三角形.【分析】根据等腰三角形的性质,利用4作为腰或底边长,得出符合题意的图形即可.【解答】解:如图所示:当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形(AD,AE,AF,AG分别为分割线).故选:B.【点评】此题主要考查了等腰三角形的判定以及应用设计与作图等知识,正确利用图形分类讨论得出是解题关键.4.【考点】等腰三角形的性质.【专题】等腰三角形与直角三角形.【分析】可知等腰三角形的两底角相等,则可求得底角的度数.从而可求解.【解答】解:①当∠A为顶角时,等腰三角形两底角的度数为:=50°∴特征值k==②当∠A为底角时,顶角的度数为:180°﹣80°﹣80°=20°∴特征值k==综上所述,特征值k为或故答案为或【点评】本题主要考查等腰三角形的性质,熟记等腰三角形的性质是解题的关键,要注意到本题中,已知∠A的度数,要分∠A是顶角和底角两种情况,以免造成答案的遗漏.5.【考点】非负数的性质:绝对值;非负数的性质:算术平方根;三角形三边关系;等腰三角形的性质.【专题】压轴题;分类讨论.【分析】先根据非负数的性质列式求出x、y的值,再分4是腰长与底边两种情况讨论求解.【解答】解:根据题意得,x﹣4=0,y﹣8=0,解得x=4,y=8,①4是腰长时,三角形的三边分别为4、4、8,∵4+4=8,∴不能组成三角形,②4是底边时,三角形的三边分别为4、8、8,能组成三角形,周长=4+8+8=20,所以,三角形的周长为20.故答案为:20.【点评】本题考查了等腰三角形的性质,绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0求出x、y的值是解题的关键,难点在于要分情况讨论并且利用三角形的三边关系进行判断.6.【考点】等腰三角形的判定.【专题】几何图形.【分析】(1)首先过点A作AF⊥BC于点F,由AD=AE,根据三线合一的性质,可得DF=EF,又由BD=CE,可得BF=CF,然后由线段垂直平分线的性质,可证得AB=AC.(2)根据等腰三角形的判定解答即可.【解答】证明:(1)过点A作AF⊥BC于点F,∵AD=AE,∴DF=EF,∵BD=CE,∴BF=CF,∴AB=AC.(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,【点评】此题考查了等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.7.【考点】等边三角形的判定与性质.【专题】数形结合;三角形;等腰三角形与直角三角形;运算能力;推理能力.【分析】过点E作EG⊥BC,交BC于点G,先证明△ABC是等边三角形,再证明∠AFE =90°,然后利用等腰三角形的“三线合一”性质及角平分线的性质定理求得EG的长,随后利用含30度角的直角三角形的性质求得DE的长,最后将EF与DE相加即可.【解答】解:如图,过点E作EG⊥BC,交BC于点G∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵EC=CD,∴∠CED=∠CDE=∠ACB=30°,∴∠AEF=30°,∴∠AFE=90°,即EF⊥AB,∵△ABC是等边三角形,AE=CE,∴BE平分∠ABC,∴EG=EF=2,在Rt△DEG中,DE=2EG=4,∴DF=EF+DE=2+4=6;方法二、∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵EC=CD,∴∠CED=∠CDE=∠ACB=30°,∵△ABC是等边三角形,AE=CE,∴BE平分∠ABC,∴∠ABE=∠CBE=30°=∠CDE,∴BE=DE,∠BFD=90°,∴BE=2EF=4=DE,∴DF=DE+EF=6;故选:D.【点评】本题考查了等边三角形的判定与性质、等腰三角形的“三线合一”性质及含30度角的直角三角形的性质,熟练掌握相关性质及定理是解题的关键.8.【考点】等边三角形的判定与性质.【分析】先根据图形折叠的性质得出BC=CE,再由直角三角形斜边的中线等于斜边的一半即可得出CE=AE=BE,进而可判断出△BEC是等边三角形,由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论.【解答】解:△ABC沿CD折叠B与E重合,则BC=CE,∵E为AB中点,△ABC是直角三角形,∴CE=BE=AE,∴△BEC是等边三角形.∴∠B=60°,∴∠A=30°,故选:B.【点评】考查直角三角形的性质,等边三角形的判定及图形折叠等知识的综合应用能力及推理能力.9.【考点】等腰三角形的判定与性质.【专题】几何图形.【分析】连接AC,根据等边对等角得到∠BAC=∠BCA,因为∠A=∠C,则可以得到∠CAD=∠ACD,根据等角对等边可得到AD=DC.【解答】证明:连接AC,∵AB=BC,∴∠BAC=∠BCA.∵∠BAD=∠BCD,∴∠CAD=∠ACD.∴AD=CD.【点评】重点考查了等腰三角形的判定方法,即:如果一个三角形有两个角相等,那么这两个角所对的边也相等.10.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题.【分析】由△ABC是等边三角形,AD=BE=CF,易证得△ADF≌△BED,即可得DF=DE,同理可得DF=EF,即可证得:△DEF是等边三角形.【解答】证明:∵△ABC是等边三角形,∴AB=BC=AC,∵AD=BE=CF,∴AF=BD,在△ADF和△BED中,,∴△ADF≌△BED(SAS),∴DF=DE,同理DE=EF,∴DE=DF=EF.∴△DEF是等边三角形.【点评】此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.11.【考点】平行线的性质;等腰三角形的判定与性质;等边三角形的判定与性质.【专题】几何图形.【分析】(1)根据等边三角形的性质和平行线的性质证明即可.(2)根据等边三角形的性质解答即可.【解答】证明:(1)∵△ABC为等边三角形,∴∠A=∠ABC=∠C=60°.∵DE∥BC,∴∠AED=∠ABC=60°,∠ADE=∠C=60°.∴△ADE是等边三角形.(2)∵△ABC为等边三角形,∴AB=BC=AC.∵BD平分∠ABC,∴AD=AC.∵△ADE是等边三角形,∴AE=AD.∴AE=AB.【点评】此题考查等边三角形的判定和性质,关键是根据等边三角形的性质和平行线的性质解答.12.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题.【分析】根据等边△ABC中AD=BE=CF,证得△ADE≌△BEF≌△CFD即可得出△DEF 是等边三角形.【解答】解:∵△ABC为等边三角形,且AD=BE=CF,∴AE=BF=CD,又∵∠A=∠B=∠C=60°,∴△ADE≌△BEF≌△CFD(SAS),∴DE=EF=FD,∴△DEF是等边三角形.【点评】本题主要考查了等边三角形的判定与性质和全等三角形判定,根据已知得出△ADE≌△BEF≌△CFD是解答此题的关键.13.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】分类讨论.【分析】(1)根据旋转的性质可得CO=CD,∠OCD=60°,根据有一个角是60°的等腰三角形是等边三角形解答;(2)利用勾股定理逆定理判定△AOD是直角三角形,并且∠ADO=90°,从而求出∠ADC=150°,再根据旋转变换只改变图形的位置不改变图形的形状与大小可得α=∠ADC;(3)根据周角为360°用α表示出∠AOD,再根据旋转的性质表示出∠ADO,然后利用三角形的内角和定理表示出∠DAO,再分∠AOD=∠ADO,∠AOD=∠DAO,∠ADO=∠DAO三种情况讨论求解.【解答】解:(1)△COD是等边三角形.理由如下:∵△BOC绕点C按顺时针方向旋转60°得△ADC,∴CO=CD,∠OCD=60°,∴△COD是等边三角形;(2)∵AD2+OD2=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2=AO2,∴△AOD是直角三角形,且∠ADO=90°,∵△COD是等边三角形,∴∠CDO=60°,∴∠ADC=∠ADO+∠CDO=90°+60°=150°,根据旋转的性质,α=∠ADC=150;(3)∵α=∠ADC,∠CDO=60°,∴∠ADO=α﹣60°,又∵∠AOD=360°﹣110°﹣α﹣60°=190°﹣α,∴∠DAO=180°﹣(190°﹣α)﹣(α﹣60°)=180°﹣190°+α﹣α+60°=50°,∵△AOD是等腰三角形,∴①∠AOD=∠ADO时,190°﹣α=α﹣60°,解得α=125°,②∠AOD=∠DAO时,190°﹣α=50°,解得α=140°,③∠ADO=∠DAO时,α﹣60°=50°,解得α=110°,综上所述,α为125°或140°或110°时,△AOD是等腰三角形.【点评】本题考查了等边三角形的判定与性质,旋转变换只改变图形的位置不改变图形的形状与大小的性质,勾股定理逆定理,等腰三角形的性质,(3)用α表示出△AOD的各个内角是解题的关键,注意要分情况讨论.14.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题;压轴题.【分析】首先延长BD至F,使DF=BC,连接EF,得出△BEF为等边三角形,进而求出△ECB≌△EDF,从而得出EC=DE.【解答】证明:延长BD至F,使DF=BC,连接EF,∵AE=BD,△ABC为等边三角形,∴BE=BF,∠B=60°,∴△BEF为等边三角形,∴∠F=60°,在△ECB和△EDF中∴△ECB≌△EDF(SAS),∴EC=ED.【点评】此题主要考查了等边三角形的性质与判定以及全等三角形的判定等知识,作出辅助线是解决问题的关键.15.【考点】含30度角的直角三角形.【专题】计算题;等腰三角形与直角三角形;运算能力;推理能力.【分析】根据同角的余角相等求出∠BCD=∠A=60°,再根据30°角所对的直角边等于斜边的一半求出AC、AB的长,然后根据BD=AB﹣AD计算即可得解.【解答】解:∵∠ACB=90°,CD⊥AB,∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,∴∠BCD=∠A=60°,∴∠ACD=∠B=30°,∵AD=2,∴AC=2AD=4,∴AB=2AC=8,∴BD=AB﹣AD=8﹣2=6.故选:C.【点评】本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质,同角的余角相等的性质,熟记性质是解题的关键.16.【考点】线段垂直平分线的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形.【分析】根据线段垂直平分线的性质得到EB=EA,根据等腰三角形的性质得到∠EAB=∠B=15°,根据三角形的外角的性质求出∠AEC=30°,根据直角三角形的性质计算.【解答】解:∵DE垂直平分AB,∴EB=EA,∴∠EAB=∠B=15°,∴∠AEC=30°,∴AC=AE=3(cm),故选:D.【点评】本题考查的是线段垂直平分线的性质,直角三角形的性质,在直角三角形中,30°角所对的直角边等于斜边的一半.17.【考点】等腰三角形的性质;含30度角的直角三角形.【分析】根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF 的长.【解答】解:∵△ABC是等腰三角形,D为底边的中点,∴AD⊥BC,∠BAD=∠CAD,∵∠BAC=120°,∴∠BAD=60°,∠ADB=90°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=30°.∵DF∥AB,∴∠F=∠BAE=30°.∴∠DAF=∠F=30°,∴AD=DF.∵AB=11,∠B=30°,∴AD=5.5,∴DF=5.5故选:C.【点评】本题考查了含30°角的直角三角形,等腰三角形的判定与性质,平行线的性质等知识点,能求出AD=DF是解此题的关键.18.【考点】含30度角的直角三角形.【专题】推理填空题.【分析】根据直角三角形的性质求出BC,根据三角形中位线定理计算即可.【解答】解:∵∠A=30°,BC⊥AC,∴BC=AB=3.7,∵DE⊥AC,BC⊥AC,∴DE∥BC,∵点D是斜梁AB的中点,∴DE=BC=1.85m,故答案为:1.85m.【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.19.【考点】线段垂直平分线的性质;含30度角的直角三角形.【专题】计算题;等腰三角形与直角三角形;运算能力;推理能力.【分析】先由直角三角形的性质求出∠ABC的度数,由AB的垂直平分线交AC于D,交AB于E,垂足为E,可得BD=AD,由∠A=30°可知∠ABD=30°,故可得出∠DBC =30°,根据CD=2可得出BD的长,进而得出AD的长.【解答】解:连接BD,∵在△ABC中,∠C=90°,∠A=30°,∴∠ABC=60°.∵AB的垂直平分线交AC于D,交AB于E,∴AD=BD,DE⊥AB,∴∠ABD=∠A=30°,∴∠DBC=30°,∵CD=2,∴BD=2CD=4,∴AD=4.故选:D.【点评】此题考查了线段垂直平分线的性质以及含30°角的直角三角形的性质.熟练掌握直角三角形的性质是解题的关键.20.【考点】垂线段最短;含30度角的直角三角形.【专题】解直角三角形及其应用;推理能力.【分析】在Rt△ABC中,利用“在直角三角形中,30°角所对的直角边等于斜边的一半”可求出AB的长,由点P是BC边上一动点结合AC,AB的长,即可得出AP长的取值范围,再对照四个选项即可得出结论.【解答】解:在Rt△ABC中,∠C=90°,∠B=30°,AC=3,∴AB=2AC=6.∵点P是BC边上一动点,∴AC≤AP≤AB,即3≤AP≤6.故选:D.【点评】本题考查了含30度角的直角三角形以及垂线段最短,通过解含30度角的直角三角形,求出AB的长是解题的关键.21.【考点】含30度角的直角三角形.【专题】等腰三角形与直角三角形;运算能力.【分析】求出AD的长,再根据含30°角的直角三角形的性质得出DE=AD,即可求出答案.【解答】解:∵点D是AB的中点,AB=7.2,∴AD=AB=3.6,∵DE⊥AC,∴∠DEA=90°,∵∠A=30°,∴DE=AD=1.8,故选:A.【点评】本题考查了含30°角的直角三角形的性质,能根据含30°角的直角三角形的性质得出DE=AD是解此题的关键.22.【考点】等腰三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】过P作PC⊥MN于C,先由等腰三角形的性质得CM=CN=2.5,再由含30°角的直角三角形的性质求出OC的长,然后由OC+CM求出ON的长即可.【解答】解:过P作PC⊥MN于C,如图所示:∵PM=PN,MN=5,∴CM=NC=MN=2.5,在Rt△OPC中,∠AOB=60°,∴∠OPC=30°,∴OC=OP=4,则ON=OC+CM=4+2.5=6.5,故选:B.【点评】本题考查的是含30°角的直角三角形的性质、等腰三角形的性质等知识;熟练掌握含30°角的直角三角形的性质和等腰三角形的性质是解题的关键.23.【考点】三角形内角和定理;等腰三角形的判定;含30度角的直角三角形.【专题】等腰三角形与直角三角形;几何直观.【分析】根据等腰三角形的判定和含30°的直角三角形的性质解答即可.【解答】解:如图所示:以B为圆心,BC长为半径画弧,交直线m于点P4,P2,以A为圆心,AC长为半径画弧,交直线m于点P1,P3,边AC和BC的垂直平分线都交于点P3位置,因此出现等腰三角形的点P的位置有4个,故选:C.【点评】此题考查等腰三角形的判定,关键是根据等腰三角形的判定和含30°的直角三角形的性质解答.24.【考点】列代数式;等边三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】利用等边三角形的性质可得AB=BC=AC=4,∠B=∠C=60°,再利用含30度角的直角三角形的性质进行计算即可.【解答】解:∵△ABC是等边三角形,∴AB=BC=AC=4,∠B=∠C=60°,∵PD⊥BC,DE⊥AC,∴BD=PB,CE=CD,∵P A=x,∴BP=4﹣x,∴BD=PB=2﹣x,∴CD=4﹣(2﹣x)=2+x,∴CE=1+x,∴AE=4﹣(1+x)=3﹣x,故选:B.【点评】此题主要考查了等边三角形的性质和含30度角的直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.25.【考点】平行线的性质;等腰三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF 的长.【解答】解:∵△ABC是等腰三角形,D为底边的中点,∴AD⊥BC,∠BAD=∠CAD,∵∠BAC=120°,∴∠BAD=60°,∠ADB=90°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=30°,∵DF∥AB,∴∠F=∠BAE=30°,∴∠DAF=∠F=30°,∴AD=DF,∵AB=6,∠B=30°,∴AD=AB=3,∴DF=3,故选:D.【点评】本题考查了含30°角的直角三角形,等腰三角形的判定与性质,平行线的性质等知识点,能求出AD=DF是解此题的关键.26.【考点】等边三角形的判定与性质.【专题】等腰三角形与直角三角形.【分析】由在△ABC中,∠ACB=90°,DE⊥AB,易证得∠DCA=∠DAC,继而可得①∠DCB=∠B正确;由①可证得AD=BD=CD,即可得②CD=AB正确;易得③△ADC是等腰三角形,但不能证得△ADC是等边三角形;由若∠E=30°,易求得∠FDC=∠FCD=30°,则可证得DF=CF,继而证得DE=EF+CF.【解答】解:∵在△ABC中,∠ACB=90°,DE⊥AB,∴∠ADE=∠ACB=90°,∴∠A+∠B=90°,∠ACD+∠DCB=90°,∵∠DCA=∠DAC,∴AD=CD,∠DCB=∠B;故①正确;∴CD=BD,∵AD=CD,∴CD=AB;故②正确;∠DCA=∠DAC,∴AD=CD,但不能判定△ADC是等边三角形;故③错误;∵若∠E=30°,∴∠A=60°,∴△ACD是等边三角形,∴∠ADC=60°,∵∠ADE=∠ACB=90°,∴∠EDC=∠BCD=∠B=30°,∴CF=DF,∴DE=EF+DF=EF+CF.故④正确.故选:B.【点评】此题考查了等腰三角形的性质与判定以及直角三角形的性质.注意证得D是AB 的中点是解此题的关键.27.【考点】平行线的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;多边形与平行四边形.【分析】延长EP交BC于点G,延长FP交AC于点H,证出四边形AEPH、四边形PDCG 均为平行四边形,得出PE=AH,PG=CD.证出△FGP和△HPD也是等边三角形,得出PF=PG=CD,PD=DH,得出PE+PD+PF=AH+DH+CD=AC即可.【解答】解:延长EP交BC于点G,延长FP交AC于点H,如图所示:∵PF∥AB,PD∥BC,PE∥AC,∴四边形AEPH、四边形PDCG均为平行四边形,∴PE=AH,PG=CD.又∵△ABC为等边三角形,∴△FGP和△HPD也是等边三角形,∴PF=PG=CD,PD=DH,∴PE+PD+PF=AH+DH+CD=AC,∴AC=a;故选:D.【点评】本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.28.【考点】等腰三角形的判定与性质;等边三角形的判定与性质.【专题】三角形.【分析】根据等边三角形的判定、轴对称的性质即可判断;【解答】解:①三条边都相等的三角形是等边三角形;正确.②有一个角为60°的等腰三角形是等边三角形;正确.③有两个角为60°的三角形是等边三角形;正确.④底角的角平分线所在的直线是这等腰三角形的对称轴,则这个三角形是等边三角形;正确.故选:D.【点评】本题考查等边三角形的判定和性质、等腰三角形的判定和性质、轴对称等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.29.【考点】平行线的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等边三角形边长为2,在Rt△BDE中求得DE的长,再根据CM垂直平分DF,在Rt△CDN中求得CN,最后根据线段和可得CM的长.【解答】解:∵等边三角形边长为2,BD=CD,∴BD=,CD=,∵等边三角形ABC中,DF∥AB,∴∠FDC=∠B=60°,∵∠EDF=90°,∴∠BDE=30°,∴DE⊥BE,∴BE=BD=,DE=,如图,连接DM,则Rt△DEF中,DM=EF=FM,∵∠FDC=∠FCD=60°,∴△CDF是等边三角形,∴CD=CF=,∴CM垂直平分DF,∴∠DCN=30°,DN=FN,∴Rt△CDN中,DN=,CN=,∵M为EF的中点,∴MN=DE=,∴CM=CN+MN=+=,故选:C.【点评】本题主要考查了三角形的综合应用,解决问题的关键是掌握等边三角形的性质、平行线的性质、线段垂直平分线的判定等.熟练掌握这些性质是解题的关键.30.【考点】等腰三角形的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等腰三角形的性质和等边三角形的性质和判定逐个进行分析判断,即可得到答案.【解答】解:A.有一个角为60°的等腰三角形是等边三角形,故本选项不合题意;B.如果一个三角形有两个角相等,那么这两个角所对的边相等,故本选项不合题意;C.等腰三角形顶角的角平分线,底边的中线,高相互重合,说法错误,故本选项符合题意;D.三个角都相等的三角形是等边三角形,故本选项不合题意;故选:C.【点评】本题考查了等边三角形的判定和性质,等腰三角形的性质,熟练掌握等边三角形的判定和性质定理是解题的关键.31.【考点】等腰三角形的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.。
初中数学:等腰三角形练习(含答案)

初中数学:等腰三角形练习(含答案)一、选择题1、等腰三角形一底角为50°,则顶角的度数为()A、65B、70C、80D、40【答案】C【解析】试题分析:根据三角形的内角和定理求解.解:等腰三角形的顶角度数=180°-50°-50°=80°.故应选C考点:等腰三角形的性质2、如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC,∠ACB的角平分线,则图中等腰三角形共有()A. 5个B. 6个C.7个D.8个【答案】D【解析】试题分析:根据等腰三角形两底角相等和∠A=36°,求出∠ABC和∠ACB的度数,再根据角平分线的定义求出∠ABD、∠CBD、∠ACE、∠BCE的度数,利用三角形外角定理求出∠BOE、∠COD的度数,根据等角对等边进行判断.解:如下图所示,∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°,∵BD平分∠ABC,CE平分∠ACB,∴∠ABD=∠C BD=∠ACE=∠BCE=∠A=36°,∴△ABD、△BCD、△ACE、△BCE、△OBC是等腰三角形;∴∠BEC=∠A+∠ACE=72°,∠BOE=∠BCE+∠CBD=72°,∴∠BEC=∠BOE,同理可得:∠CDO=∠COD,∴△BOE、△COD是等腰三角形;又△ABC是等腰三角形,∴共有8个等腰三角形.故应选D.考点:1.等腰三角形的性质;2.等腰三角形的判定3、下列条件中不能确定是等腰三角形的是()A.三条边都相等的三角形B.一条中线把面积分成相等的两部分的三角形C.有一个锐角是45°的直角三角形D.一个外角的平分线平行于三角形一边的三角形【答案】D【解析】试题分析:根据等腰三角形的定义和等腰三角形的判定定理进行判断.解:A选项、三条边都相等的三角形是特殊的等腰三角形,故A选项正确;B选项、三角形任何一条边上的中线都能把三角形分成面积相等的两个三角形,故B选项错误;C选项、有一个锐角是45°的直角三角形的另一个锐角也是45°,根据等角对等边可得这是一个等腰三角形,故C选项正确;D选项、如果一个外角的平分线平行于三角形一边,利用平行线的性质可证三角形的两个角相等,根据等角对等边可证这是一个等腰三角形,故D选项正确.故应选B考点:等腰三角形的判定4、下列能断定△ABC为等腰三角形的是()A.∠A=30°,∠B=60°B.∠A=50°,∠B=80°C. AB=AC=2,BC=4 D.AB=3,BC=7,周长为13【答案】B【解析】试题分析:根据等腰三角形的判定定理进行判断.解:A选项、若∠A=30°,∠B=60°,则∠C=90°,不能判定△ABC为等腰三角形;B选项、若∠A=50°,∠B=80°,则∠C=50°,根据等角对等边能判定△ABC为等腰三角形;C选项、若AB=AC=2,BC=4,因为2+2=4,所以不能构成三角形;D选项、若AB=3,BC=7,周长为13,则AC=3,因为3+3<7,所以不能构成三角形.故应选B.考点:等腰三角形的判定5、已知下列各组数据,可以构成等腰三角形的是()A. 1,2,1 B.2,2,1 C. 1,3,1 D.2,2,5【答案】B【解析】试题分析:根据三角形三边的关系进行判断.解:A选项、因为1+1=2,所以不能构成三角形;B选项、因为2+1>2,能构成三角形,所以可以构成等腰三角形;C选项、因为1+1<3,所以不能构成三角形;D选项、因为2+2<5,所以不能构成三角形.故应选B.考点:三角形三边关系6、小明将两个全等且有一个角为60°的直角三角形拼成如图所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是()A.4 B.3 C.2 D.1【答案】B【解析】试题分析:根据直角三角形的性质求出各角的度数,根据等角对等边进行判断. 解:∵∠B=∠E=60°,∴∠A=∠D=30°,∴△MAD是等腰三角形;∵∠EMG-∠A+∠D=60°,∴△EGM是等腰三角形;同理可证△BHM是等腰三角形.∴共有三个等腰三角形.故应选B考点:1.直角三角形的性质;2.等腰三角形的判定二、填空题7、一个等腰三角形的两边分别为3cm和4cm,则它的周长为_________;【答案】10cm或11cm【解析】试题分析:根据三角形的周长公式分情况进行计算.解:当三角形三边分别是3cm、3cm、4cm时,三角形的周长是3+3+4=10cm;当三角形三边分别是3cm、4cm、4cm时,三角形的周长是3+4+4=11cm.故答案是10cm或11cm.考点:等腰三角形的性质8、在方格纸上有一个△ABC,它的顶点位置如图所示,则这个三角形是三角形.【答案】等腰【解析】试题分析:根据点A在BC的垂直平分线上,可证AB=AC,所以这个三角形是等腰三角形.解:∵点A在BC的垂直平分线上,∴AB=AC,∴△ABC是等腰三角形.故答案是等腰.考点:1.线段垂直平分线的性质;2.等腰三角形的定义9、如果一个三角形有两个角分别为80°,50°,则这个三角形是_________三角形.【答案】等腰【解析】试题分析:根据三角形内角和求出三角形的另一个内角,根据等角对等边进行判断.解:∵第三个角=180°-50°-80°=50°.∴这个三角形是等腰三角形.故答案是等腰.考点:等腰三角形的判定10、用若干根火柴(不折断)紧接着摆成一个等腰三角形,一边用了10根火柴,则至少还要用_________根火柴.【答案】11【解析】试题分析:根据用10根火柴组成的边是等腰三角形的底边和腰,分两种情况进行讨论.解:当用10根火柴组成的边是等腰三角形的底边时,则每个腰上至少用6根火柴棍,∴共需要12根火柴棍;当用10根火柴组成的边是等腰三角形的腰时,则另一个腰上需要用10根火柴棍,底边至少用1根火柴,∴共需要11根火柴棍.∴至少还要用11根火柴.故答案是11.考点:1.等腰三角形的定义;2.三角形三边关系11、如图,△ABC是等腰三角形,且AB=AC,BM,CM分别平分∠ABC,∠ACB,DE 经过点M,且DE∥BC,则图中有_________个等腰三角形.【答案】5【解析】试题分析:根据等腰三角形的性质可得∠ABC=∠ACB,根据平行线的性质可证∠ADE=∠AED,根据角平分线的性质可证∠DBM=∠MBC=∠DMB=∠EMC=∠ECM=∠BCM,根据等角对等边进行证明.解:∵△ABC是等腰三角形,∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠AED,∴△ADE是等腰三角形;∵BM平分∠ABC,∴∠DBM=∠CBM,∵BC∥DE,∴∠DMB=∠CBM,∴∠DBM=∠DMB,∴△DBM是等腰三角形,同理可得△EMC是等腰三角形;又∵∠ABC=∠ACB,∴∠MBC=∠MCB,∴△MBC是等腰三角形.∵△ABC是等腰三角形.∴共有5个等腰三角形.故答案是5.考点:1.等腰三角形的性质;2.等腰三角形的判定三、解答题12、已知:如图,OA平分∠BAC,∠1=∠2.求证:△ABC是等腰三角形.【答案】证明见解析【解析】试题分析:首先过点O作OE⊥AB于E,OF⊥AC于F,根据角平分线的性质可证OE=OF,根据HL可证Rt△OBE≌Rt△OCF,利用全等三角形的性质可证∠5=∠6,所以可证∠ABC=∠ACB,根据等角对等边可证结论成立.证明:如下图所示,过点O作OE⊥AB于E,OF⊥AC于F,∵AO平分∠BAC,∴OE=OF(角平分线上的点到角两边的距离相等).∵∠1=∠2,∴OB=OC.∴Rt△OBE≌Rt△OCF(HL).∴∠5=∠6.∴∠1+∠5=∠2+∠6.即∠ABC=∠ACB.∴AB=AC.∴△ABC是等腰三角形.考点:1.角平分线的性质;2.等腰三角形的判定定理;3.全等三角形的判定和性质13、如图,△ABC中,∠A=36°,AB=AC,CD平分∠ACB,试说明△BCD是等腰三角形.【答案】证明见解析【解析】试题分析:根据等腰三角形的性质求出∠B=∠ACB=72°,根据角平分线的定义可以求出∠ACD=∠A=36°,根据三角形外角的性质可以求出∠ADB=72°,再根据等角对等边可证结论成立.证明:∵∠A=36°,AB=AC,∴∠B=∠ACB=72°,∵CD平分∠ACB,∴∠ACD=∠A=36°,∴∠BDC=∠A+∠ACD,∴∠BDC=∠B=72°,∴△BCD是等腰三角形.考点:1.等腰三角形的性质;2.等腰三角形的判定14、如图,ABC△中,∠ABC、∠ACB的平分线交于点F,过点F作DE∥BC分别交AB、AC于D、E,已知△ADE的周长为20cm,且BC=12cm,求△ABC的周长【答案】32cm.【解析】试题分析:首先根据角平分线的性质可证∠DBF=∠FBC,根据平行线的性质可证∠DFB=∠DBF,所以可证BD=DF,同理可证EC=EF,所以可证AD+AE+DF+EF=20cm,再根据BC的长度求出△ABC的周长.解:∵∠ABC、∠ACB的平分线交于点F,∴∠DBF=∠FBC,又∵DE∥BC,∴∠DFB=∠FBC,∴∠DFB=∠DBF,∴BD=DF,同理EC=EF,∵△ADE的周长为20cm,∴AD+AE+DF+EF=20cm,∴AD+AE+BD+EC=AB+AC=20cm又∵BC=12cm,∴AB+AC+BC=32cm即△ABC的周长为32cm.考点:1.等腰三角形的判定;2.等腰三角形的性质。
好题共享_等腰三角形(含答案)

等腰三角形【分类解析】例1. 如图,已知在等边三角形ABC 中,D 是AC 的中点,E 为BC 延长线上一点,且CE =CD ,DM ⊥BC ,垂足为M 。
求证:M 是BE 的中点。
AD1 BM C E分析:欲证M 是BE 的中点,已知DM ⊥BC ,所以想到连结BD ,证BD =ED 。
因为△ABC 是等边三角形,∠DBE =21∠ABC ,而由CE =CD ,又可证∠E =21∠ACB ,所以∠1=∠E ,从而问题得证。
证明:因为三角形ABC 是等边三角形,D 是AC 的中点 所以∠1=21∠ABC 又因为CE =CD ,所以∠CDE =∠E 所以∠ACB =2∠E 即∠1=∠E所以BD =BE ,又DM ⊥BC ,垂足为M所以M 是BE 的中点 (等腰三角形三线合一定理)例2. 如图,已知:ABC ∆中,AC AB =,D 是BC 上一点,且CA DC DB AD ==,,求BAC ∠的度数。
ABCD分析:题中所要求的BAC ∠在ABC ∆中,但仅靠AC AB =是无法求出来的。
因此需要考虑DB AD =和CA DC =在题目中的作用。
此时图形中三个等腰三角形,构成了内外角的关系。
因此可利用等腰三角形的性质和三角形的内外角关系定理来求。
解:因为AC AB =,所以C B ∠=∠ 因为DB AD =,所以C DAB B ∠=∠=∠;因为CD CA =,所以CDA CAD ∠=∠(等边对等角) 而 DAB B ADC ∠+∠=∠ 所以B DAC B ADC ∠=∠∠=∠22, 所以B 3BAC ∠=∠又因为180=∠+∠+∠BAC C B即180B 3C B =∠+∠+∠ 所以36B =∠ 即求得108BAC =∠说明1. 等腰三角形的性质是沟通本题中角之间关系的重要桥梁。
把边的关系转化成角的关系是此等腰三角形性质的本质所在。
本条性质在解题中发挥着重要的作用,这一点在后边的解题中将进一步体现。
等腰三角形经典练习题(5套)附带详细答案

练习一一、选择题1.等腰三角形的周长为26㎝,一边长为6㎝,那么腰长为()A.6㎝B.10㎝C.6㎝或10㎝D.14㎝2.已知△ABC,AB =AC,∠B=65°,∠C度数是( )A.50°B.65°C.70°D.75°3.等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边的垂线C.顶角的平分线所在的直线D.腰上的高所在的直线二、填空题4.等腰三角形的两个_______相等(简写成“____________”).5.已知△ABC,AB =AC,∠A=80°,∠B度数是_________.6.等腰三角形的两个内角的比是1:2,则这个等腰三角形的顶角的度数是_______________.7.等腰三角形的腰长是6,则底边长5,周长为__________.三、解答题8.如图AB=AD,AD∥BC,求证:BD平分∠ABC.(写出每步证明的重要依据)9.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数一、选择题1.B2.B3.C二、填空题4.底角,等边对等角5.50°6.36°或90°7.16或17三、解答题8.如图AB=AD,AD∥BC,求证:BD平分∠ABC.证明:∵AB=AD(已知)∴∠ABD=∠ADB(等边对等角)∵AD∥BC(已知)∴∠ADB=∠CBD(两直线平行,内错角相等)∴∠ABD=∠CBD(等量代换)∴BD平分∠ABC.(角平分线定义)9.45练习2一、选择题1.△ABC是等边三角形,D、E、F为各边中点,则图中共.有正三角形( )A.2个B.3个C.4个D.5个2.△ABC中,∠A:∠B:∠C=1:2:3,则BC:AB等于( ) A.2:1 B.1:2 C.1:3 D.2 :3二、填空题3.等边三角形的周长为6㎝,则它的边长为________.4.等边三角形的两条高线相交所成钝角的度数是__________.5.在△ABC中,∠A=∠B=∠C,则△ABC是_____三角形.6.△ABC中,∠AC B=90°∠B=60°,BC=3㎝,则AB=_______.三、解答题7.△ABC是等边三角形,点D在边BC上,DE∥AC,△BDE是等边三角形吗?试说明理由.8.已知:如图,P,Q是△ABC边上BC上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.9.已知:△ABC中,∠ACB=90°,AD=BD,∠A=30°,求证:△BDC是等边三角形.一、选择题1.D2.B二、填空题3.2㎝4.120°5.等边6.6㎝三、解答题7.△ABC是等边三角形.理由是∵△ABC是等边三角形∴∠A=∠B=∠C=60°∵DE∥AC,∴∠BED=∠A=60°,∠BDE=∠C =60°AQ CPB∴∠B =∠BED =∠BDE ∴△ABC 是等边三角形 8.∠BAC=120°9.证明:∵△ABC 中,∠ACB=90°,∠A=30°(已知)∴∠A +∠B=90°(直角三角形两锐角互余) ∴∠B= 90°-∠A= 90°-30°=60°∵△ABC 中,∠ACB=90°,∠A=30°(已知) ∴BC=BD AB =21(在直角三角形中,一个锐角等于30,那么它所对的直角边等于斜边的一半)∴△BDC 是等边三角形(有一个角是60°角的等腰三角形是等边三角形)。
初一数学等腰三角形试题答案及解析

初一数学等腰三角形试题答案及解析1.如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为()A. B. C. D.【答案】A【解析】根据等边三角形的性质,利用弧长的计算方法,采用排除法求解即可.扇形CDE的圆心角是60°,半径是20•sin60°=10,则弧长是=cm,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是cm,设圆锥的底面半径是r,则得到2πr=,解得:r=故选A.2.下图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2cm时,这个六边形的周长为()cm.A.30B.40C.50D.60【答案】D【解析】因为每个三角形都是等边的,从其中一个三角形入手,比右下角的以AB为边的三角形,设它的边长为x,则等边三角形的边长依次为x,x+x+2,x+2,x+2×2,x+2×2,x+3×2.所以六边形周长是2x+2(x+2)+2(x+2×2)+(x+3×2)="7" x+18,而最大的三角形的边长AF等于AB的2倍,所以可以求出x,则可求得周长.设AB=x,∴等边三角形的边长依次为x,x+x+2,x+2,x+2×2,x+2×2,x+3×2,∴六边形周长是2x+2(x+2)+2(x+2×2)+(x+3×2)="7" x+18,∵AF=2AB,即x+6=2x,∴x=6cm,∴周长为7 x+18=60cm.故选D3.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.B.C.D.不能确定【答案】B【解析】过P作PF∥BC交AC于F,得出等边三角形APF,推出AP=PF=QC,根据等腰三角形性质求出EF=AE,证△PFD≌△QCD,推出FD=CD,推出DE=AC即可.过P作PF∥BC交AC于F.∵PF∥BC,△ABC是等边三角形,∴∠PFD=∠QCD,△APF是等边三角形,∴AP=PF=AF,∵PE⊥AC,∴AE=EF,∵AP=PF,AP=CQ,∴PF=CQ.∵在△PFD和△QCD中,,∴△PFD≌△QCD(AAS),∴FD=CD,∵AE=EF,∴EF+FD=AE+CD,∴AE+CD=DE=AC,∵AC=1,∴DE=.故选B.4.如图,点D是等边△ABC内一点,将△DBC绕点B旋转到△EBA的位置,则∠EBD的度数是()A.45°B.60°C.90°D.120°【答案】B【解析】由将△DBC绕点B旋转到△EBA的位置,即可得△DBC≌△EBA,根据全等三角形的性质可得∠ABE=∠CBD,又由△ABC是等边三角形,可得∠ABC=60°,继而由∠EBD=∠ABE+∠ABD=∠CBD+∠ABD=∠ABC,求得∠EBD的度数.解:∵将△DBC绕点B旋转到△EBA的位置,∴△DBC≌△EBA,∴∠ABE=∠CBD,∵△ABC是等边三角形,∴∠ABC=60°,∴∠EBD=∠ABE+∠ABD=∠CBD+∠ABD=∠ABC=60°.故选B.5.如图△ABC为等边三角形,⊙O的周长与等边三角形一边长相等,⊙O在△ABC的边上作无滑动滚动,从P点出发沿顺时针方向滚动,又回到P点,共滚动的圈数是()A.1B.2C.3D.4【答案】D【解析】根据直线与圆相切的性质得到圆从一边转到另一边时,圆心要绕其三角形的顶点旋转120°,则圆绕三个顶点共旋转了360°,即它转了一圈,再加上在三边作无滑动滚动时要转三圈,这样得到它回到原出发位置点P时共转了4圈.圆在AB、BC、CA三边作无滑动滚动时,∵等边三角形的边长与和圆的周长相等,∴圆转了3圈,而圆从一边转到另一边时,圆心绕三角形的一个顶点旋转了三角形的一个外角的度数,圆心要绕其三角形的顶点旋转120°,∴圆绕三个顶点共旋转了360°,即它转了一圈,∴圆回到原出发位置时,共转了4圈.故选D.6.已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,则DE= .【答案】【解析】根据等腰三角形和三角形外角性质求出BD=DE,求出BC,在Rt△BDC中,由勾股定理求出BD即可.解:∵△ABC为等边三角形,∴∠ABC=∠ACB=60°,AB=BC,∵BD为中线,∴∠DBC=∠ABC=30°,∵CD=CE,∴∠E=∠CDE,∵∠E+∠CDE=∠ACB,∴∠E=30°=∠DBC,∴BD=DE,∵BD是AC中线,CD=1,∴AD=DC=1,∵△ABC是等边三角形,∴BC=AC=1+1=2,BD⊥AC,在Rt△BDC中,由勾股定理得:BD==,即DE=BD=,故答案为:.7.已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为.【答案】()n【解析】由AB1为边长为2等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出第一个等边三角形AB1C1的面积,同理求出第二个等边三角形AB2C2的面积,依此类推,得到第n个等边三角形ABnCn的面积.解:∵等边三角形ABC的边长为2,AB1⊥BC,∴BB1=1,AB=2,根据勾股定理得:AB1=,∴第一个等边三角形AB1C1的面积为×()2=()1;∵等边三角形AB1C1的边长为,AB2⊥B1C1,∴B1B2=,AB1=,根据勾股定理得:AB2=,∴第二个等边三角形AB2C2的面积为×()2=()2;依此类推,第n个等边三角形ABn Cn的面积为()n.故答案为:()n8.如图,等边三角形ABC的边长是6cm,BD是中线,延长BC至E,使CE=CD,连接DE,则DE的长是cm.【答案】【解析】根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE.解:∵△ABC是等边三角形,BD是中线,∴∠ABC=∠ACB=60°.∠DBC=30°(等腰三角形三线合一).又∵CE=CD,∴∠CDE=∠CED.又∵∠BCD=∠CDE+∠CED,∴∠CDE=∠CED=∠BCD=30°.∴∠DBC=∠CED.∴DB=DE(等角对等边).∵等边三角形ABC的边长是6cm,∴DE=BD=.故答案为.9.下列说法错误的是()A.顶角和腰对应相等的两个等腰三角形全等B.顶角和底边对应相等的两个等腰三角形全等C.斜边对应相等的两个等腰直角三角形全等D.两个等边三角形全等【答案】D【解析】此题考查等腰三角形的性质及概念.做题时要根据已知条件结合判定方法逐个验证.解:A选项中,两边夹一角,可证明其全等; B中两角夹一边,也全等; C中斜边对应相等的两个等腰直角三角形利用两角夹一边,亦全等; D中两个等边三角形,虽然角相等,但边长不确定,所以不能确定其全等,所以D错误.故选D.10.如图,是一个5×5的正方形网格,网格中的每个小正方形的边长均为1.点A和点B在小正方形的顶点上.点C也在小正方形的顶点上.若△ABC为等腰三角形,满足条件的C点的个数为()A.6B.7C.8D.9【答案】C【解析】分为两种情况:①以AB为腰时,符合条件的有点C D E F G H;②以AB为底时,符合条件的有点I J;相加即可得出答案.①以AB为腰时,符合条件的有点C D E F G H;②以AB为底时,符合条件的有点I J;共6+2=8,故选C.11.小明用19根火柴首尾顺次相接,恰好摆成一个三角形,若要求这个三角形是等腰三角形,则不同的摆法有()A.1种B.4种C.5种D.9种【答案】C【解析】根据等腰三角形的两腰相等的性质可知两腰的和为偶数,再根据三角形的任意两边之和大于第三边可知底边的长小于19根的一半,然后列举出所有的可能情况即可得解.解:根据三角形的任意两边之和大于第三边,设底边长为x(x为整数),则x<,∴x的值可以是9,7,5,3,1,∴不同的摆法有5种.故选C.12.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是格点,若C也是格点,且△ABC为等腰三角形,则满足条件的点C的个数是()A.6 B.7 C.8 D.9【答案】C【解析】分AB是腰长时,根据网格结构,找出一个小正方形与A、B顶点相对的顶点,连接即可得到等腰三角形,AB是底边时,根据线段垂直平分线上的点到线段两端点的距离相等,AB垂直平分线上的格点都可以作为点C,然后相加即可得解.解:如图,AB是腰长时,红色的4个点可以作为点C,AB是底边时,黑色的4个点都可以作为点C,所以,满足条件的点C的个数是4+4=8.故选C.13.下列说法中:(1)顶角相等,并且有一腰相等的两个等腰三角形全等;(2)底边相等,且周长相等的两个等腰三角形全等;(3)腰长相等,且有一角是50°的两个等腰三角形全等;(4)两条直角边对应相等的两个直角三角形全等;错误的有()A.1个B.2个C.3个D.4个【答案】A【解析】认真阅读各小问题提供的已知条件,根据等腰三角形的性质,和两三角形全等是所需要的条件逐一进行验证,找出正误的具体原因,其中(3)错误.解:(1)正确,等腰三角形腰长相等,有一腰相等,另一角也相等,又因为顶角相等,两条边和它们的夹角对应相等的两个三角形全等,所以两个等腰三角形全等;(2)正确,等腰三角形中,周长为二倍的腰长+底边长,所以可以知道三边对应相等,三条边对应相等的两个三角形全等;(3)错误,腰长相等,有一角是50°,并非是顶角,如果一个是顶角,一个是底角则两个三角形是不全等的;(4)正确,两条直角边对应相等的两个直角三角形,是两条边和它们的夹角对应相等的两个三角形,所以全等.故选A.14.如图1,已知线段AB和直线m,点A在直线m上,以AB为一边画等腰△ABC,且使点C在直线m上,这样的等腰三角形最多有()A.4个B.3个C.2个D.1个【答案】A【解析】根据当AB为等腰三角形的腰时有三个;当AB为等腰三角形的底边时,有一个,那么可作出等腰三角形共4个,即可得出答案.解:如图以A为圆心,AB为半径画弧,即可得出C1、C3两点,此时:AC1=AB,AC3=AB,同理当AB为底边时,作AB的垂直平分线,AC2=BC2,以B为圆心,AB为半径画弧,即可得出C4点,∴AB=BC4,所以题中共有4个点使其为等腰三角形.故选:A.15.如图,△ABC中,BA=BC,∠C=72°,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC交AB于E,则图中的等腰三角形共有()个.A.5B.6C.7D.8【答案】C【解析】先根据等腰三角形的性质求出∠ABC及∠BAC的度数,再根据等腰三角形的判定定理即可得出结论.解:∵△ABC中,BA=BC,∴△ABC是等腰三角形;∵∠C=72°,∴∠ABC=36°,∠BAC=72°,∵AF是△ABC的角平分线,∴∠BAF=∠CAF=∠BAC=36°,∴△ABF是等腰三角形;∵∠CAF=∠BAC=36°,∠C=72°,∴∠AFC=72°,∴△AFC是等腰三角形;∵AF平分∠BAC,∴∠BAD=∠CAD,∵DE∥AC,∴∠EDA=∠CAD=∠BAD,∴AE=ED,∵∠EDB+∠ADE=90°,∴∠BDE+∠BAD=90°,∵∠EBD+∠BAD=90°,∴∠BDE=∠EBD,∴BE=ED,∴AE=BE,∴AE=BE=ED,∴△AED,△BED是等腰三角形;∵∠BAF=36°,AE=ED,∴∠ADE=36°,∴∠BED=72°,∵∠ABC=36°,∴∠BGE=∠BED=72°,∴△BEG是等腰三角形;∵∠DGF=∠BGE=72°,∠AFC=∠DFG=72°,∴△DGF是等腰三角形.综上所述,等腰三角形有:△ABC,△ABF,△AFC,△AED,△BED,△BEG,△DGF共7个.故选C.16.如图所示,共有等腰三角形()A.4个B.5个C.3个D.2个【答案】B【解析】由已知条件,根据三角形内角和定理,求出图形中未知度数的角,即可根据等角对等边求得等腰三角形的个数.解:根据三角形的内角和定理,得:∠ABO=∠DCO=36°,根据三角形的外角的性质,得∠AOB=∠COD=72°.再根据等角对等边,得等腰三角形有△AOB,△COD,△ABC,△CBD和△BOC.故选B.17.已知抛物线y=k(x+1)(x﹣)与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是.【答案】4【解析】整理抛物线解析式,确定出抛物线与x轴的一个交点A和y轴的交点C,然后求出AC 的长度,再分:①k>0时,点B在x轴正半轴时,分AC=BC、AC=AB、AB=BC三种情况求解;②k<0时,点B在x轴的负半轴时,点B只能在点A的左边,只有AC=AB一种情况列式计算即可.解:y=k(x+1)(x﹣)=(x+1)(kx﹣3),所以,抛物线经过点A(﹣1,0),C(0,﹣3),AC==,点B坐标为(,0),①k>0时,点B在x正半轴上,若AC=BC,则=,解得k=3,若AC=AB,则+1=,解得k==,若AB=BC,则+1=,解得k=;②k<0时,点B在x轴的负半轴,点B只能在点A的左侧,只有AC=AB,则﹣1﹣=,解得k==,所以,能使△ABC为等腰三角形的抛物线共有4条.故答案是:4.18.如图,∠A=20°,∠C=40°,∠ADB=80°,则图中共有等腰三角形个.【答案】2【解析】根据三角形的内角和定理,三角形的外角的性质,得∠ADB=∠ABD,∠DBC=∠C,再根据等角对等边得出图中等腰三角形的个数.解:∵∠ABD=180°﹣20°﹣80°=80°,∠DBC=∠ADB﹣∠C=40°.∴∠ADB=∠ABD=80°,∠DBC=∠C=40°,故△ABD和△BCD是等腰三角形.故填2.19.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为()A.12B.15C.12或15D.18【答案】B【解析】因为已知长度为3和6两边,没有明确是底边还是腰,所以有两种情况,需要分类讨论.解:①当3为底时,其它两边都为6,3、6、6可以构成三角形,周长为15;②当3为腰时,其它两边为3和6,∵3+3=6=6,∴不能构成三角形,故舍去,∴答案只有15.故选B.20.如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是()A.18°B.24°C.30°D.36°【答案】A【解析】根据已知可求得两底角的度数,再根据三角形内角和定理不难求得∠DBC的度数.解:∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°∵BD是AC边上的高,∴BD⊥AC,∴∠DBC=90°﹣72°=18°.故选A.21.等腰三角形的一个角是80°,则它顶角的度数是()A.80°B.80°或20°C.80°或50°D.20°【答案】B【解析】分80°角是顶角与底角两种情况讨论求解.解:①80°角是顶角时,三角形的顶角为80°,②80°角是底角时,顶角为180°﹣80°×2=20°,综上所述,该等腰三角形顶角的度数为80°或20°.故选B.22.如果等腰三角形的两边长分别为2和5,则它的周长为()A.9B.7C.12D.9或12【答案】C【解析】根据三角形三边关系推出腰长为5,底边长为2,即可推出周长为12.解:∵2+5>5,∴等腰三角形的腰长为5,底边长为2,∴周长=5+5+2=12.故选C.23.等腰三角形的顶角为80°,则它的底角是()A.20°B.50°C.60°D.80°【答案】B【解析】根据三角形内角和定理和等腰三角形的性质,可以求得其底角的度数.解:∵等腰三角形的一个顶角为80°∴底角=(180°﹣80°)÷2=50°.故选B.24.如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是()A.40°B.35°C.25°D.20°【答案】C【解析】先根据等腰三角形的性质及三角形内角和定理求出∠ADC的度数,再根据等腰三角形的性质及三角形外角与内角的关系求出∠B的度数即可.解:∵△ABC中,AC=AD,∠DAC=80°,∴∠ADC==50°,∵AD=BD,∠ADC=∠B+∠BAD=50°,∴∠B=∠BAD=()°=25°.故选C.25.如图,已知直线AB∥CD,∠DCF=110°且AE=AF,则∠A等于()A.30°B.40°C.50°D.70°【答案】B【解析】根据两直线平行,同旁内角互补得出∠BFC,根据AE=AF可得出∠E=∠EFA,根据三角形的内角和为180°可求∠A.解:∵AB∥CD,∴∠DCF+∠BFC=180°,∴∠BFC=70°,∴∠EFA=70°,又∵△AEF中,AE=AF,∴∠E=∠EFA=70°,∴∠A=180°﹣∠BFC﹣∠EFA=40°.故选B.26.如图,△ABC中,D、E两点分别在AC、BC上,则AB=AC,CD=DE.若∠A=40°,∠ABD:∠DBC=3:4,则∠BDE=()A.25° B.30° C.35° D.40°【答案】B【解析】根据已知及等腰三角形的性质可求得两底角的度数,再根据∠ABD:∠DBC=3:4,列方程求解即可求出∠BDE的度数.解:∵AB=AC,CD=DE∴∠C=∠DEC=∠ABC∴AB∥DE∵∠A=40°∴∠C=∠DEC=∠ABC==70°∵∠ABD:∠DBC=3:4∴设∠ABD为3x,∠DBC为4x∴3x+4x=70°∴x=10°∵AB∥DE∴∠BDE=∠ABD=30°故选B.27.如图,△ABC中,∠ABC=30°,∠ACB=50°,且D、E两点分别在BC,AB上.若AD为∠BAC的角平分线,AD=AE,则∠AED=()A.50° B.60° C.65° D.80°【答案】C【解析】根据三角形的内角和公式可求得∠BAC的度数,再根据角平分线的性质及等腰三角形的性质即可求得∠AED的度数.解:∵∠ABC=30°,∠ACB=50°∴BAC=100°∵AD为∠BAC的角平分线∴∠EAD=50°∵AD=AE∴∠AED=65°故选C.28.如图,在△ABC中,AB=AC,点D为BC边的中点,∠BAD=20°,则∠C=.【答案】70°【解析】由已知条件,利用等边三角形三线合一的性质进行求解.解:∵AB=CA,∴△ABC是等腰三角形,∵D是BC边上的中点,∴AD平分∠BAC,∵∠BAD=20°.∴∠C=90°﹣20°=70°.故答案为:70°.29.如图,AB∥CD,CP交AB于O,AO=PO,若∠C=50°,则∠A=度.【答案】25【解析】根据AB∥CD,CP交AB于O,可得∠POB=∠C,再利用AO=PO,可得∠A=∠P,然后即可求得∠A的度数.解:∵AB∥CD,CP交AB于O,∴∠POB=∠C,∵∠C=50°,∴∠POB=50°,∵AO=PO,∴∠A=∠P,∴∠A=25°故答案为25.30.如图,在△ABC中,AB=AC,∠A=80°,E,F,P分别是AB,AC,BC边上一点,且BE=BP,CP=CF,则∠EPF=度.【答案】50【解析】根据在△ABC中,AB=AC,∠A=80°,利用三角形内角和定理求出∠B=∠C=50°,再利用BE=BP,求出∠B,然后即可求得∠EPF,即可解题.解:∵在△ABC中,AB=AC,∠A=80°,∴∠B=∠C=50°,∵BE=BP,∴∠BEP=∠EPB=65°,同理,∠FPC=65°,∠EPF=180°﹣65°﹣65°=50°.故答案为:50.。
数学三角形试题答案及解析

数学三角形试题答案及解析1.一个等腰三角形的一条边长为5厘米,其中两条边长度之比为1:2.这个等腰三角形的周长可能是()厘米.A.10B.20C.D.25【答案】C和D【解析】由“一个等腰三角形的一条边长为5厘米,其中两条边长度之比为1:2”,可求得和它不相等的另一条边长10厘米或2.5厘米,根据三角形“两边之和大于第三边,两边之差小于第三边”,可知如果这条长为5厘米的边是此三角形的腰,那么底就是2.5厘米;如果这条长为5厘米的边是此三角形的底,那么腰就是10厘米;进而把三条边的长度合起来即为周长.解:因为一个等腰三角形的一条边长为5厘米,其中两条边长度之比为1:2,所以和它不相等的另一条边长:5×2=10(厘米),或5÷2=2.5(厘米),又因为三角形两边之和大于第三边,两边之差小于第三边,所以如果此三角形的腰为:5厘米,底是2.5厘米,则周长为:5+5+2.5=12.5=12(厘米);如果此三角形的底为:5厘米,腰是10厘米,则周长为:10+10+5=25(厘米);故选:C和D.点评:此题考查等腰三角形的特征:两腰相等;也考查了三角形三条边的关系:两边之和大于第三边,两边之差小于第三边.2.如图,三角形ABC是等腰直角三角形,斜边AB=12厘米,MN是BC的,AP是AC的,求三角形PMN的面积.【答案】9平方厘米【解析】如图所示,作三角形ABC斜边上的高CE,又因等腰直角三角形斜边上的高等于斜边的一半,则CE=AB=6厘米,于是可以求出三角形ABC的面积,又因AP=AC,则PC=AC,所以三角形PCB的面积等于三角形ABC的面积的,又因MN=BC,则三角形PMN的面积等于三角形PCD的面积的,据此即可求出阴影部分的面积.解:据分析可知:CE=AB=6厘米,则三角形ABC的面积为:=36平方厘米,又因AP=AC,则PC=AC,所以三角形PCB的面积等于三角形ABC的面积的,即三角形PCB的面积为=27平方厘米,又因MN=BC,则三角形PMN的面积等于三角形PCD的面积的,即三角形PMN的面积为27×=9平方厘米.答:三角形PMN的面积是9平方厘米.点评:解答此题的主要依据是:等腰直角三角形斜边上的高等于斜边的一半,等高不等底的三角形的面积比等于对应底边的比.3.将任意一个三角形的面积四等分,你有几种方法?【答案】【解析】将任意一条边四等分,利用等底等高的三角形面积相等可以解决;还可以利用线段的中点去做.解:如图方法1:在已知△ABC的任意一边(假设BC边)上取三个四等分点D,E,F,顺次连接AD,AE,AF,这样就将△ABC分成了面积相等的四个小三角形,如上面第一幅图.方法2:在已知△ABC的任意一边(假设BC边)上取三个四等分点D,E,F,用实线连接AD,AE(或AD,AF或AE,AF),用虚线连接AF(或AE或AD),然后在AF(或AE或AD)上取中点G,用实线连GE,GC(或GD,GF或GB,GE),这样△ABC中的实线将其分成了四个面积相等的图形,如上面第二幅图.点评:此题主要考查:①等底等高的三角形的面积相等;②等量加等量和相等.4.正方形ABCD的边长是18厘米,已知DE是EC长度的2倍,求三角形DEF的面积.【答案】54平方厘米【解析】已知正方形ABCD的边长是18厘米,已知DE是EC长度的2倍,即DE与EC的比是2:1,根据按比例分配的方法,求出DE的长度,三角形DEF的面积=三角形ADF的面积﹣三角形ADE的面积,由此列式解答.解:2+1=3(份);18×=12(厘米);18×18÷2﹣18×12÷2=162﹣108=54(平方厘米);答:三角形DEF的面积是54平方厘米.点评:此题解答关键是求出DE的长度,三角形DEF的面积=三角形ADF的面积﹣三角形ADE的面积,由此解决问题.5.一块三角形的棉田,底长是140米,高是80米,如果每株占地0.4平方米,这块棉田能种多少株棉花?【答案】14000株【解析】根据三角形的面积公式S=ah÷2,求出三角形棉田的面积再除以0.4平方米就是要求的答案.解:140×80÷2÷0.4,=11200÷2÷0.4,=5600÷0.4,=14000(株).答:这块棉田能种14000株棉花.点评:本题主要应用三角形的面积公式S=ah÷2与基本的数量关系解决问题.6.下图是用皮筋在钉板上分别围成的正方形、长方形、平行四边形和三角形.它们的面积分别是多少?【答案】4;8;6;3;【解析】分析题中所给的几个图形都是规则图形,它们的面积可以运用公式求得.而要运用公式,首先要结合点子图计算出有关的边长和高;解图(1)是正方形,边长是2,它的面积是2×2=4;图(2)是长方形,长是4,宽是2,它的面积是4×2=8;图(3)是平行四边形,从平行四边形的左边移动一个直角三角形到右边,使得平行四边形变成一个长方形,所求的面积是3×2=6;图(4)是三角形,将三角形扩展成一个长方形.三角形ABC的面积是长方形AFBC面积的一半,三角形ACD的面积是长方形ACDE面积的一半,所以三角形ABD的面积是(3×2)÷2=6÷2=3.解:根据题干分析可得:(1)正方形的面积:2×2=4;(2)长方形的面积:4×2=8;(3)平行四边形面积:3×2=6;(4)三角形的面积:(3×2)÷2=6÷2=3;答:点子图中正方形面积是4,长方形面积是8,平行四边形面积是6,三角形面积是3.点评:此题考查了这几个规则图形的面积公式的应用.7.一个三角形的底长是5m,如果底边延长1m,那么面积就增加1.5m2,请你求出原来三角形的面积是多少平方米?【答案】7.5平方米【解析】由“如果底边延长1m,那么面积就增加1.5m2”可以求出三角形的高,原三角形的底已知,进而可以求其面积.解:原三角形的高:1.5×2÷1=3(米),原三角形的面积:5×3÷2=7.5(平方米);答:原来三角形的面积是7.5平方米.点评:解答此题的关键是先求出三角形的高.8.如图中有几个三角形的面积与阴影部分的三角形面积相等?阴影部分的面积是多少?(单位:cm)【答案】3个,31平方厘米【解析】三角形的面积S=ah,只要是三角形的底和高相等,则它们的面积相等,据此即可得解.解:由图意可知:图中有3个三角形的面积与阴影部分的三角形面积相等,5×12.4÷2=31(平方厘米);答:图中有3个三角形的面积与阴影部分的三角形面积相等,阴影部分的面积是31平方厘米.点评:解答此题的主要依据是:等底等高的三角形的面积相等.9.一块三角形的小麦地面积是1620平方米,量得它的底边长36米,这块地的高是多少米?【答案】90米【解析】根据三角形的面积公式S=ah÷2,知道h=2S÷a,代入数据列式解答即可.解:1620×2÷36,=3240÷36,=90(米).答:这块地的高是90米.点评:本题主要是灵活利用三角形的面积公式S=ah÷2解决问题.10.一块梯形木板的上底长10厘米,下底比上底长7厘米,高是6厘米,这块木板的面积是多少?【答案】81平方厘米【解析】用10加7求出梯形下底的长,再根据梯形的面积公式:S=(a+b)h÷2,代入数据进行计算.解:梯形下底的长是:10+7=17(厘米),S=(a+b)h÷2,=(10+17)×6÷2,=27×6÷2,=81(平方厘米).答:这块木板的面积是81平方厘米.点评:本题的重点是求出木板的下底,再根据梯形的面积公式进行计算.11.一块三角形的玻璃,量得它的底是12.5分米,高是6.8分米,如果每平方分米玻璃的价钱是0.25元,买这块玻璃需用多少钱?(保留整数)【答案】11元【解析】先依据三角形的面积公式求出玻璃的面积,再乘每平方米的价格,问题即可得解.解:12.5×6.8÷2×0.25,=42.5×0.25,≈11(元);答:买这块玻璃需用11元钱.点评:此题主要考查三角形的面积的计算方法的灵活应用.12.一个直角三角形的面积是45平方厘米,它的一条直角边长5厘米,另一条直角边长多少厘米?【答案】18厘米【解析】依据三角形的面积S=ah,h=2S÷a,据此代入数据即可求解.解:45×2÷5,=90÷5,=18(厘米);答:另一条直角边长18厘米.点评:此题主要考查三角形的面积的计算方法的灵活应用.13.如图的直角三角形中有一个长方形,根据已知条件你能求出长方形的面积吗?(单位:厘米)【答案】35平方厘米【解析】设长方形的长为a厘米,宽为b厘米,则两个三角形的面积分别为×5a平方厘米,×7b平方厘米,长方形的面积是ab平方厘米,大三角形的面积是(a+7)×(b+5),再根据两个三角形的面积加长方形的面积等于大三角形的面积,即可求出ab的积,即长方形的面积.解:设长方形的长为a厘米,宽为b厘米,则两个三角形的面积分别为×5a平方厘米,×7b平方厘米,长方形的面积是ab平方厘米,大三角形的面积是(a+7)×(b+5),×5a+×7b+ab=(a+7)×(b+5),a+b+ab=++b+,=,ab=35,答:长方形的面积是35平方厘米.点评:关键是设出未知数,找出各个图形的面积,再根据数量关系等式列方程解答即可.14.列方程求解:等腰三角形的周长是19.6厘米.【答案】7厘米【解析】因为等腰三角形的两条腰的长度相等,据此利用三角形的周长的意义即可得解.解:设这个等腰三角形的腰为x厘米,x+x+5.6=19.6,2x=14,x=7;答:这个等腰三角形的腰是7厘米.点评:此题主要考查等腰三角形的特点以及三角形的周长的意义.15.用一根20cm长的细绳围成等腰三角形,如果底是8cm,那么腰是多少厘米?【答案】6厘米【解析】由等腰三角形的特点可知:等腰三角形的两条腰相等,则这个等腰三角形的腰=(周长﹣底长)÷2,再据“用一根20cm长的细绳围成等腰三角形,如果底是8cm”即可求解.解:(20﹣8)÷2,=12÷2,=6(厘米),答:这个等腰三角形的腰长为6厘米.点评:解答此题的主要依据是:等腰三角形的两条腰长度相等.16.一个三角形底是15厘米,高是9厘米,求面积?【答案】67.5平方厘米【解析】根据三角形的面积公式S=ah÷2,把三角形的底15厘米,高9厘米代入公式,列式解答即可.解:15×9÷2,=135÷2,=67.5(平方厘米),答:面积是67.5平方厘米.点评:本题主要是应用三角形的面积公式S=ah÷2解决问题.17.一块三角形土地,底是480米,高是240米,用这块地的种棉花.棉花地有多少公顷?【答案】1.92公顷【解析】根据三角形的面积公式:S=ah,求出这块地的面积,再乘,就是种棉花的面积.据此解答.解:×480×240×,=57600×,=19200(平方米),=1.92公顷.答:棉花地有1.92公顷.点评:本题的重点是求出这块的面积,再根据分数乘法的意义列式求出棉花地的面积,注意单位是公顷.18.用84厘米长的铁丝围成一个直角三角形,这个三角形三条边长度的比是3:4:5.这个三角形的面积是多少?【答案】294平方厘米【解析】要求直角三角形的面积,只要知道两条直角边的长度即可.先求总份数,再求两条直角边分别占总数的几分之几,求出直角边的长度,根据三角形的面积公式,列式解答即可.解:三角形的一条直角边的长度是:84×=21(厘米)三角形的另一条直角边的长度是:84×=28(厘米)三角形的面积是:21×28×=294(平分厘米)答:这个直角三角形的面积是294平方厘米.点评:此题主要考查按比例分配应用题的特点:已知两个数的比(三个数的比),两个数的和(三个数的和),求这两个数(三个数),用按比例分配解答.19.计算下列各图形的周长.【答案】10厘米,8厘米,7厘米【解析】长方形的周长=(长+宽)×2,正方形的周长=边长×4,三角形的周长计算它的三条边的长度和.由此解答即可.解:(3+2)×2,=5×2,=10(厘米);2×4=8(厘米);2+2+3=7(厘米);答:长方形的周长是10厘米,正方形的周长是8厘米,三角形的周长是7厘米.点评:此题主要考查长方形、正方形、三角形周长公式的灵活运用.20.把下面的三角形按1:3分成两个三角形.【答案】【解析】由题意得:按1:3分成两个三角形,就是分成的其中一个三角形是另一个三角形面积的3倍;所以把底边平均分成4份,其中3份为一个三角形的底,另一份是另一个三角形的底,高相等,则大三角形的面积就是小三角形的面积的3倍.解:如图所示:大三角形的面积是小三角形的面积的3倍.点评:解决本题要结合高相等时,如果一个三角形的底是另一个三角形底的3倍,那么面积就是另一个三角形面积的3倍.21.计算阴影部分的面积.【答案】90平方厘米【解析】观察图形可知:阴影部分是一个底为10厘米,高为10+8=18厘米的三角形,根据三角形的面积公式即可解答.解:10×(10+8)÷2,=10×18÷2,=90(平方厘米);答:阴影部分的面积是90平方厘米.点评:观察图形,得出三角形的底与高,再利用三角形的面积公式计算即可.22.计算周长.【答案】9厘米,20分米【解析】三角形的周长等于三条边的长度和,正方形的周长=边长×4,据此即可得解.解:(1)3+3+3=9(厘米);(2)5×4=20(分米);答:三角形的周长是9厘米,正方形的周长是20分米.点评:此题主要考查三角形和正方形的周长的计算方法.23.如图所示,BC长为5,求画阴影线的两个三角形的面积之和.【答案】15【解析】如图:利用三角形的面积公式S=ah÷2,求出三角形EBC的面积与三角形ABC的面积,用三角形EBC的面积减去三角形ABC的面积就是三角形EAB的面积,再乘2就是画阴影线的两个三角形的面积之和.解:(5×5÷2﹣5×2÷2)×2,=(12.5﹣5)×2,=7.5×2,=15,答:阴影线的两个三角形的面积之和是15.点评:关键是找出阴影部分的面积是从三角形EBC的面积减去三角形ABC的面积,再利用三角形的面积公式解决问题.24.计算下列图形的面积.【答案】24平方厘米,16.8平方厘米【解析】(1)根据三角形的面积公式S=ah÷2,把底8cm,高6cm或底9.6cm,高5cm代入公式解答即可;(2)根据平行四边形的面积公式S=ah,把底4.8cm,高3.5cm代入公式解答即可.解:(1)8×6÷2=24(平方厘米);(2)4.8×3.5=16.8(平方厘米).答:三角形的面积是24平方厘米,平行四边形的面积是16.8平方厘米.点评:本题主要考查了三角形与平行四边形的面积的计算方法.25.画一个三角形,并画出三角形的底边上的高,量出所需条件,计算出它的面积.【答案】,4平方厘米【解析】任意画出一个三角形,量得它的底边及高的长度,即可求出它的面积.解:如图所示,即为所要求画的三角形:;三角形的面积:4×2÷2=4(平方厘米);答:三角形的面积是4平方厘米.点评:此题主要考查三角形高的画法及面积计算公式.26.如图所示的梯形上底20cm,下底12cm,并且是由一个面积是180cm2的平行四边形和一个三角形拼成的.求三角形的面积.【答案】36cm2【解析】一个梯形由一个平行四边形和一个三角形拼成,只能如右图拼成;要求三角形的面积必须知道三角形的底和高,三角形的底是:20﹣12=8cm,高与左侧的平行四边形等高,平行四边形的面积是180cm2,所以高是:180÷20=9cm,那么三角形的面积是:8×9÷2=36cm2,据此解答.解:(20﹣12)×(180÷20)÷2,=8×9÷2,=36(cm2);答:三角形的面积是36cm2.点评:本题考查了平行四边形的面积S=ah和三角形的面积S=ah÷2的灵活应用.27.应用题(1)王村修一条水渠,第一天修8.5km,第二天比第一天多修3.5km,这时修完的比没修的少4km,求还有多少千米没修?(2)一列客车和一列货车同时、同地、反向而行.客车每小时比货车快24km,5h后,两车相距720km,求货车每小时行多少千米?(列方程解)(3)有一块底250m,高180m的三角形实验田,全年共产粮食4.5t,平均每公顷产粮多少吨?(4)学校食堂运来一堆煤,计划每天烧煤50kg,6.5天烧完,实际10天才烧完.实际每天比计划少烧煤多少千克?(5)客车和货车从相距852km的两地,同时相向而行,相遇时,客车行的路程比货车的2倍少189km,客车和货车各行多少千米?(用方程解)(6)读一本故事书,姐姐读完全书需要24天,妹妹读完全书需要32天.已知姐姐每天读书的页数比妹妹多4页,问妹妹每天读书多少页?(7)想一想:妈妈今年50岁,女儿今年14岁,几年前妈妈的年龄是女儿的5倍?【答案】24.5千米;60千米;2吨;17.5千克;505千米;16页;5年前【解析】(1)可用8.5千米加3.5千米计算出第二天修的长度,然后再用两天修的长度加上4千米就是没有修的路程;(2)根据题意,可设货车每小时行x千米,那么客车每小时行(x+24)千米,根据速度和×时间=路程可列方程解答即可;(3)可根据三角形的面积公式计算出三角形试验田的面积,然后再用4.5吨除以三角形试验田的面积即可;(4)根据题意,可用50减去50乘6.5再除以10的商即可,列式解答即可得到答案;(5)根据题意,可设货车行驶的路程为x千米,那么客车行驶的路程为(2x﹣189)千米,客车行驶的路程加上货车行驶的路程等于852千米,列方程解答即可得到答案;(6)根据题意,可设妹妹每天读x页,那么姐姐每天读(x+4)页,因为姐姐妹妹看的是同一本书,列方程解答即可得到答案;(7)根据题意,可设x年前妈妈的年龄是女儿的5倍,列方程解答即可得到答案.解:(1)8.5+3.5+8.5+4=24.5(千米),答:还有24.5千米没有修;(2)设:货车每小时行x千米,则客车每小时行(x+24)千米,5x+5×(x+24)=7205x+5x+120=720,10x=600,x=60,答:货车每小时行60千米;(3)三角形的面积为:250×180÷2=22500(平方米),22500平方米=2.25公顷,4.5÷2.25=2(吨),答:这块三角形试验田每公顷产粮食2吨;(4)50﹣50×6.5÷10=50﹣325÷10,=50﹣32.5,=17.5(千克),答:实际每天比计划少烧17.5千克煤;(5)设货车行驶的路程为x千米,那么客车行驶的路程为(2x﹣189)千米,x+(2x﹣189)=852x+2x﹣189=852,3x=1041,x=347,2×347﹣189=505(千米),答:货车行驶了347千米,客车行驶了505千米;(6)设妹妹每天读x页,姐姐每天读(x+4)页,32x=24×(x+4)32x=24x+96,32x﹣24x=96,8x=96,x=12,12+4=16(页),答:妹妹每天读12页,姐姐每天读16页;(7)设x年前妈妈的年龄是女儿年龄的5倍..5×(14﹣x)=50﹣x70﹣5x=50﹣x,5x﹣x=70﹣50,4x=20,x=5,答:5年前妈妈的年龄是女儿年龄的5倍.点评:解答此题的关键是找清题中的数量关系,然后再列式解答即可.28.求如图中阴影部分面积:【答案】9.63平方厘米【解析】图中的阴影部分面积为直径为6厘米的半圆面积减去两个直角边为圆的半径的三角形的面积,分别按公式计算即可.解:半圆面积:3.14×(6÷2)2÷2,=28.26÷2,=14.13(平方厘米);三角形面积:(6÷2)×(6÷2)÷2,=3×3÷2,=4.5(平方厘米);阴影部分面积:14.13﹣4.5=9.63(平方厘米).答:阴影部分面积为9.63平方厘米.点评:此题综合考查圆的面积与三角形的面积,计算半圆面积时别忘记圆的面积除以2.29.一块三角形玻璃,底是12.5dm,高是7.8dm,每平方米的价钱是68元,买这块玻璃要用多少元?【答案】33.15元【解析】先利用“三角形的面积=底×高÷2”求出这块玻璃的总面积,再据“每平方米玻璃的价钱是68元”,用乘法计算即可求出买这块玻璃需要的钱数.解:12.5×7.8÷2÷100×68,=97.5÷2÷100×68,=48.75÷100×68,=33.15(元);答:买这块玻璃需要33.15元.点评:解答此题的关键是利用三角形面积公式先求出玻璃的面积,玻璃的单价已知,从而求得这块玻璃的总价格.30.求下面各图形中涂色部分的面积【答案】1500平方厘米【解析】由图可以看出:阴影部分的面积=梯形的面积﹣三角形的面积,将数据代入公式即可求得结果.解:(60+80)×30÷2﹣60×20÷2,=2100﹣600,=1500(平方厘米);答:图形中涂色部分的面积1500平方厘米.点评:此题主要考查三角形及梯形的面积公式,将数据代入公式即可求得结果.31.想想画画并列式.(1)以BC为底边,过三角形的A点画一条与BC平行的线段,并画出底边上的高,量出高是厘米.(2)画出一个钝角三角形,使钝角三角形与三角形ABC的面积相等.(3)这两个三角形的面积列成算式是.(浙江东阳市)【答案】1,,4×1÷2【解析】(1)过A点向BC作垂线,垂足为D;(2)以底为4厘米,高为1厘米画出一个钝角三角形;(3)根据“三角形的面积=底×高÷2”进行解答即可;解:(1)高为1厘米,下图(1);(2)如图,下图(2);(3)4×1÷2;故答案为:1,4×1÷2.点评:解答此题应结合题意,根据三角形的面积计算公式进行解答.32.有一块三角形与一个长方形面积相等的草坪,已知这个三角形的底是2.4米,高是2米,而长方形长2米,则它的宽是多少米?【答案】1.2米【解析】先利用三角形的面积公式求出草坪的面积,也就等于知道了长方形的草坪的面积,进而利用长方形的面积公式即可求出长方形的宽.解:2.4×2÷2=2.4(平方米),2.4÷2=1.2(米);答:它的宽是1.2米.点评:此题主要考查三角形和长方形的面积的计算方法.33.(1)请在方格中先画一个三角形.(2)作出三角形的高(3)计算三角形的面积.【答案】;12.5平方厘米【解析】(1)根据题意,最大三角形的底为方格的一条边,然后从底边的对边(即方格的对边)一点连接底边的两个端点即可得到最大三角形;(2)从三角形的顶点向对边作垂线,顶点与垂足之间的线段叫作三角形的高;(3)根据三角形的面积公式=底×高÷2进行计算即可得到答案.解:(1)(2)根据分析作图如下:(3)5×5÷2=12.5(平方厘米),答:三角形的面积是12.5平方厘米.点评:此题主要考查的是然后做正方形内最大三角形和三角形的高的作法及三角形面积公式的灵活应用.34.(2012•宝应县模拟)如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?【答案】8秒;12秒【解析】如图所示,(1)由题意可知:当三角形ABP与长方形ABCD等底等高时,则S△ABP =S长方形ABCD,此时三角形ABP的面积应最大,所以到达D点时面积最大,再用AD的长度除以点P的速度,就可以求出到达D点的时间.(2)当点P离开点C时,面积就减小,所以保持面积最大的距离就是DC的长度,用DC的长度除以速度,就是保持面积最大需要的时间.解:(1)16÷2=8(秒);答:P点从A 点出发经过8秒时△ABP面积最大.(2)24÷2=12(秒),答:△ABP面积最大共持续12秒.点评:解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.且要明白:当三角形ABP与长方形ABCD等底等高时,三角形ABP的面积最大.35.(2012•隆昌县二模)1、将平行四边形ABCD平移后,D点的位置是(5,3),写出其他各顶点位置(不画图).A(,),B(,),C(,).2、求下图的面积:(1)补充画出解题所需线段.(2)量出解题所需数据,并标在图中相应位置(取整厘米数).(3)求出图形的面积.(不作答)【答案】4、1;7、1;8、3;5平方厘米【解析】(1)因为D点原来的位置是(2,6),将平行四边形ABCD平移后,D点的位置是(5,3),说明此点向右平移了3个单位,向下平移了3个单位,由此根据据A、B、C原来的位置分别向右平移3个单位,再向下平移3个单位即可;(2)过A做BC的垂线段AD,AD即为三角形高;用直尺测量BC的长度和AD的长度;再利用三角形的面积公式S=ah÷2,求出该图形的面积.解:(1)原来的位置A(1,4),B(4,4),C(5,6);平移后的位置:A(4,1),B(7,1)C(8,3),(2)面积为:5×2÷2=5(平方厘米),答:该图形的面积为5平方厘米;故答案为:4、1;7、1;8、3.点评:本题主要考查了数对的意义及做三角形的高及三角形面积公式的计算方法.36.如图是由两个正方形拼起来的,边长分别是7厘米和12厘米,甲三角形的面积比乙三角形面积多多少平方厘米?【答案】30平方厘米【解析】把梯形的面积设为s,如图:利用等量代换(甲的面积+s)﹣(乙的面积+s)就是甲三角形比乙三角形多的面积.解:设图中梯形的面积(大正方形当中除了三角形甲的其余部分的面积)为S,易求S+乙的面积:(12+7)×12÷2=114(平方厘米);再求S+甲的面积:12×12="144" (平方厘米);所以(S+甲)﹣(S+乙)=甲﹣乙的面积=144﹣114="30" (平方厘米);答:甲三角形的面积比乙三角形的面积大30平方厘米.点评:此题主要利用等量代换解决问题,把大正方形中的梯形面积设为S,用大正方形的面积减大三角形(s+乙)的面积,问题就得到解决.37.(2012•天津模拟)已知图中阴影部分三角形面积为5平方米,求圆的面积.【答案】15.7平方米【解析】由图形可知,三角形的高等于圆的半径(r),三角形的底等于圆的直径(2r),根据三角形的面积公式:s=ah,三角形的面积=×r×2r=r2=5;根据圆的面积公式:s=πr2,由此解答.解:三角形的面积=×r×2r=r2=5;所以圆的面积:3.14×5=15.7(平方米);答:圆的面积是15.7平方米.点评:此题解答关键是根据三角形的面积计算方法,推导出半径的平方等于5,再根据圆面积公式解答.38.奥斑马用一根长30厘米的铁丝围成一个直角三角形.这个三角形的三条边的长度之比是3:4:5,那么这个直角三角形斜边上的高是厘米.【答案】6【解析】(1)由于这个直角三角形三条边长度的比为3:4:5,周长为30厘米,所以可以得到各边长分别为7.5厘米,10厘米,12.5厘米.(2)根据三角形面积公式可得:三角形的面积为7.5×10÷2=37.5平方厘米,则斜边上的高为37.5×2÷12.5=6厘米.解:3+4+5=12,30×=7.5(厘米),30×=10(厘米),30×=12.5(厘米)7.5×10÷2=37.5(平方厘米),37.5×2÷12.5=6(厘米),答:这个直角三角形斜边上的高是6厘米.故答案为:6.点评:此题是考查了三角形的周长与面积公式的灵活应用,这里关键是根据三边长度的比和周长求出两条直角边的长度.39.如图钟面长针OA长l5厘米,短针OB长l0厘米.当三角形AOB的面积最大时,其面积是平方厘米.【答案】75【解析】在两边的长度确定的情况下,直角三角形的面积最大.钟面长针OA长l5厘米,短针。
等腰三角形典型例题练习(含答案)

等腰三角形典型例题练习一.选择题(共 2 小题)1.如图,∠ C=90°,AD 平分∠ BAC 交 BC 于 D,若 BC=5cm , BD=3cm ,则点 D 到 AB 的距离为()A .5cmB .3cm C.2cm D.不能确定2.如图,已知 C 是线段 AB 上的任意一点(端点除外),分别以 AC 、 BC 为边并且在 AB 的同一侧作等边△ ACD 和等边△ BCE,连接 AE 交 CD 于 M ,连接 BD 交 CE 于 N.给出以下三个结论:①AE=BD②CN=CM③MN ∥ AB其中正确结论的个数是()A .0B .1C.2D.3二.填空题(共 1 小题)3.如图,在正三角形ABC 中, D, E, F 分别是 BC, AC , AB 上的点, DE⊥ AC , EF⊥ AB , FD⊥ BC ,则△ DEF 的面积与△ABC 的面积之比等于_________.三.解答题(共15 小题)4.在△ ABC 中, AD 是∠ BAC 的平分线, E、 F 分别为 AB 、 AC 上的点,且∠ EDF+ ∠EAF=180 °,求证DE=DF .5.在△ ABC 中,∠ ABC 、∠ ACB 的平分线相交于点 O,过点 O 作 DE ∥ BC,分别交 AB 、AC 于点 D 、E.请说明DE=BD+EC .6.>已知:如图, D 是△ABC 的 BC 边上的中点, DE ⊥ AB ,DF ⊥ AC ,垂足分别为 E,F,且 DE=DF .请判断△ABC 是什么三角形?并说明理由.7.如图,△ ABC 是等边三角形,BD 是 AC 边上的高,延长BC 至 E,使 CE=CD .连接 DE.(1)∠ E 等于多少度?(2)△ DBE 是什么三角形?为什么?8.如图,在△ ABC 中,∠ ACB=90 °, CD 是 AB 边上的高,∠A=30 °.求证: AB=4BD .9.如图,△ ABC 中, AB=AC ,点 D 、E 分别在 AB 、 AC 的延长线上,且BD=CE , DE 与 BC 相交于点 F.求证:DF=EF .10.已知等腰直角三角形ABC , BC 是斜边.∠ B 的角平分线交AC 于 D,过 C 作 CE 与 BD 垂直且交 BD 延长线于E,求证: BD=2CE .11.(2012?牡丹江)如图①,△ ABC 中. AB=AC , P 为底边 BC 上一点, PE⊥ AB , PF⊥ AC , CH ⊥AB ,垂足分别为 E、 F、 H.易证 PE+PF=CH .证明过程如下:如图①,连接 AP.∵PE⊥AB , PF⊥ AC , CH ⊥ AB ,∴S△ABP= AB ?PE, S△ACP = AC ?PF, S△ABC= AB ?CH .又∵ S△ABP+S△ACP=S△ABC,∴AB ?PE+ AC ?PF= AB ?CH .∵AB=AC ,∴PE+PF=CH .( 1)如图②,P 为 BC 延长线上的点时,其它条件不变, PE、 PF、 CH 又有怎样的数量关系?请写出你的猜想,并加以证明:( 2)填空:若∠A=30 °,△ ABC 的面积为49,点 P 在直线 BC 上,且 P 到直线 AC 的距离为PF,当 PF=3 时,则AB 边上的高CH= _________.点P到AB边的距离PE= _________.12.数学课上,李老师出示了如下的题目:“在等边三角形ABC 中,点 E 在 AB 上,点 D 在 CB 的延长线上,且ED=EC ,如图,试确定线段AE 与 DB 的大小关系,并说明理由”.小敏与同桌小聪讨论后,进行了如下解答:( 1)特殊情况,探索结论当点 E 为 AB 的中点时,如图 1,确定线段AE 与 DB 的大小关系,请你直接写出结论: AE _________DB(填“>”,“<”或“=”).( 2)特例启发,解答题目解:题目中, AE 与 DB 的大小关系是:AE _________ DB (填“>”,“<”或“=”).理由如下:如图2,过点 E 作EF∥ BC,交 AC 于点 F.(请你完成以下解答过程)( 3)拓展结论,设计新题3在等边三角形ABC 中,点 E 在直线 AB 上,点 D 在直线 BC 上,且 ED=EC .若△ ABC 的边长为1,AE=2 ,求 CD的长(请你直接写出结果).13.已知:如图, AF 平分∠ BAC , BC ⊥ AF 于点 E,点 D 在 AF 上, ED=EA ,点 P 在 CF 上,连接 PB 交 AF 于点M .若∠ BAC=2 ∠ MPC ,请你判断∠ F 与∠ MCD 的数量关系,并说明理由.14.如图,已知△ ABC 是等边三角形,点D、 E 分别在 BC 、AC 边上,且AE=CD , AD 与 BE 相交于点F.(1)线段 AD 与 BE 有什么关系?试证明你的结论.(2)求∠ BFD 的度数.15.如图,在△ ABC 中, AB=BC ,∠ ABC=90 °, F 为 AB 延长线上一点,点 E 在 BC 上, BE=BF ,连接 AE 、EF 和CF,求证: AE=CF .16.已知:如图,在△ OAB 中,∠ AOB=90 °, OA=OB ,在△ EOF 中,∠ EOF=90 °, OE=OF,连接 AE 、 BF.问线段 AE 与 BF 之间有什么关系?请说明理由.17.( 2006?郴州)如图,在△ ABC 中, AB=AC ,D 是 BC 上任意一点,过 D 分别向 AB ,AC 引垂线,垂足分别为E,F,CG 是 AB 边上的高.(1) DE , DF, CG 的长之间存在着怎样的等量关系?并加以证明;(2)若 D 在底边的延长线上,( 1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.18.如图甲所示,在△ ABC 中, AB=AC ,在底边 BC 上有任意一点 P,则 P 点到两腰的距离之和等于定长(腰上的高),即 PD+PE=CF ,若 P 点在 BC 的延长线上,那么请你猜想 PD 、PE 和 CF 之间存在怎样的等式关系?写出你的猜想并加以证明.等腰三角形典型例题练习参考答案与试题解析一.选择题(共 2 小题)1.如图,∠ C=90°,AD 平分∠ BAC 交 BC 于 D,若 BC=5cm , BD=3cm ,则点 D 到 AB 的距离为()A .5cmB .3cm C.2cm D.不能确定考点:角平分线的性质.分析:由已知条件进行思考,结合利用角平分线的性质可得点 D 到 AB 的距离等于 D 到 AC 的距离即CD 的长,问题可解.解答:解:∵∠ C=90°, AD 平分∠ BAC 交 BC 于 D∴D 到 AB 的距离即为CD 长 CD=5 ﹣ 3=2 故选 C.2.如图,已知 C 是线段 AB 上的任意一点(端点除外),分别以 AC 、 BC 为边并且在 AB 的同一侧作等边△ ACD 和等边△ BCE,连接 AE 交 CD 于 M ,连接 BD 交 CE 于 N.给出以下三个结论:① AE=BD ② CN=CM ③ MN ∥AB 其中正确结论的个数是()B .1C.23A .D.考点:平行线分线段成比例;全等三角形的判定与性质;等边三角形的性质.分析:由△ ACD 和△ BCE 是等边三角形,根据SAS 易证得△ ACE ≌△ DCB ,即可得①正确;由△ACE ≌△ DCB ,可得∠ EAC= ∠ NDC ,又由∠ ACD= ∠ MCN=60 °,利用 ASA ,可证得△ACM ≌△ DCN ,即可得②正确;又可证得△ CMN 是等边三角形,即可证得③正确.解答:解:∵△ ACD 和△BCE 是等边三角形,∴∠ ACD= ∠ BCE=60 °, AC=DC ,EC=BC ,∴∠ ACD+ ∠ DCE= ∠ DCE+ ∠ECB ,即∠ ACE= ∠DCB ,∴△ ACE ≌△ DCB ( SAS),∴AE=BD ,故①正确;∴∠ EAC= ∠NDC ,∵∠ ACD= ∠ BCE=60 °,∴∠ DCE=60 °,∴∠ ACD= ∠ MCN=60 °,∵AC=DC ,∴△ ACM ≌△ DCN ( ASA ),∴ CM=CN ,故②正确;又∠ MCN=180 °﹣∠ MCA ﹣∠ NCB=180 °﹣ 60°﹣ 60°=60°,∴△ CMN 是等边三角形,∴∠NMC= ∠ACD=60 °,∴ MN ∥ AB ,故③正确.故选 D .二.填空题(共 1 小题)3.如图,在正三角形 ABC 中, D, E, F 分别是 BC, AC , AB 上的点, DE⊥ AC , EF⊥ AB , FD⊥ BC ,则△ DEF 的面积与△ABC 的面积之比等于1:3.考点:相似三角形的判定与性质;全等三角形的判定与性质;等边三角形的性质.分析:首先根据题意求得:∠ DFE= ∠ FED=∠ EDF=60 °,即可证得△ DEF 是正三角形,又由直角三角形中,30°所对的直角边是斜边的一半,得到边的关系,即可求得DF: AB=1 :,又由相似三角形的面积比等于相似比的平方,即可求得结果.解答:解:∵△ ABC 是正三角形,∴∠ B=∠ C=∠ A=60 °,∵DE ⊥ AC , EF⊥ AB , FD ⊥BC,∴∠ AFE= ∠ CED= ∠ BDF=90 °,∴∠ BFD= ∠ CDE= ∠AEF=30 °,∴∠ DFE= ∠ FED= ∠EDF=60 °,,∴△ DEF 是正三角形,∴ BD : DF=1 :①, BD: AB=1 : 3②,△ DEF ∽△ ABC ,①÷②, =,∴ DF : AB=1 :,∴△ DEF 的面积与△ ABC 的面积之比等于 1: 3.故答案为: 1: 3.三.解答题(共15 小题)4.在△ ABC 中, AD 是∠ BAC 的平分线, E、 F 分别为 AB 、 AC 上的点,且∠ EDF+ ∠EAF=180 °,求证DE=DF .考点:全等三角形的判定与性质;角平分线的定义.分析:过 D 作 DM ⊥AB ,于 M ,DN ⊥ AC 于 N ,根据角平分线性质求出DN=DM ,根据四边形的内角和定理和平角定义求出∠AED= ∠CFD ,根据全等三角形的判定AAS 推出△ EMD ≌△ FND 即可.解答:证明:过 D 作 DM ⊥ AB ,于 M , DN ⊥AC 于 N,即∠ EMD= ∠ FND=90 °,∵AD 平分∠ BAC ,DM ⊥AB , DN ⊥ AC ,∴ DM=DN (角平分线性质),∠ DME= ∠DNF=90 °,∵∠ EAF+ ∠ EDF=180 °,∴∠ MED+ ∠ AFD=360 °﹣ 180°=180°,∵∠ AFD+ ∠NFD=180 °,∴∠ MED= ∠ NFD ,在△ EMD 和△ FND 中,∴△ EMD ≌△ FND ,∴ DE=DF .5.在△ ABC 中,∠ ABC 、∠ ACB 的平分线相交于点 O,过点 O 作 DE ∥ BC,分别交 AB 、AC 于点 D 、E.请说明DE=BD+EC .考点:等腰三角形的判定与性质;平行线的性质.分析:根据 OB 和 OC 分别平分∠ ABC 和∠ ACB ,和 DE ∥ BC ,利用两直线平行,内错角相等和等量代换,求证出 DB=DO , OE=EC .然后即可得出答案.解答:解:∵在△ABC 中, OB 和 OC 分别平分∠ ABC 和∠ ACB ,∴∠ DBO= ∠ OBC,∠ ECO= ∠ OCB,∵DE ∥ BC ,∴∠ DOB= ∠OBC= ∠DBO ,∠ EOC= ∠OCB= ∠ECO ,∴DB=DO , OE=EC ,∵ DE=DO+OE ,∴ DE=BD+EC .6.>已知:如图, D 是△ABC 的 BC 边上的中点, DE ⊥ AB ,DF ⊥ AC ,垂足分别为 E,F,且 DE=DF .请判断△ABC 是什么三角形?并说明理由.考点:等腰三角形的判定;全等三角形的判定与性质.分析:用( HL )证明△ EBD ≌△ FCD ,从而得出∠ EBD= ∠FCD ,即可证明△ ABC 是等腰三角形.解答:△ABC 是等腰三角形.证明:连接AD ,∵ DE ⊥AB , DF⊥ AC ,∴∠ BED= ∠ CFD=90 °,且 DE=DF ,∵D 是△ABC 的 BC 边上的中点,∴BD=DC ,∴Rt△ EBD ≌ Rt△ FCD (HL ),∴∠ EBD= ∠ FCD ,∴△ ABC 是等腰三角形.7.如图,△ ABC 是等边三角形,BD 是 AC 边上的高,延长BC 至 E,使 CE=CD .连接 DE.( 1)∠ E 等于多少度?(2)△ DBE 是什么三角形?为什么?考点:等边三角形的性质;等腰三角形的判定.分析:(1)由题意可推出∠ ACB=60 °,∠ E=∠ CDE ,然后根据三角形外角的性质可知:∠ ACB= ∠E+ ∠CDE ,即可推出∠ E 的度数;(2)根据等边三角形的性质可知,BD 不但为 AC 边上的高,也是∠ABC 的角平分线,即得:∠DBC=30 °,然后再结合( 1)中求得的结论,即可推出△ DBE 是等腰三角形.解答:解:( 1)∵△ ABC 是等边三角形,∴∠ ACB=60 °,∵CD=CE ,∴∠ E=∠ CDE,∵∠ ACB= ∠ E+∠ CDE ,∴,(2)∵△ ABC 是等边三角形, BD ⊥ AC ,∴∠ ABC=60 °,∴,∵∠ E=30°,∴∠ DBC= ∠ E,∴△ DBE 是等腰三角形.8.如图,在△ ABC 中,∠ ACB=90 °, CD 是 AB 边上的高,∠A=30 °.求证: AB=4BD .考点:含30度角的直角三角形.分析:由△ ABC 中,∠ ACB=90 °,∠ A=30 °可以推出AB=2BC ,同理可得BC=2BD ,则结论即可证明.解答:解:∵∠ ACB=90 °,∠ A=30 °,∴ AB=2BC ,∠ B=60 °.又∵ CD⊥ AB ,∴∠ DCB=30 °,∴ BC=2BD .∴ AB=2BC=4BD .9.如图,△ ABC 中, AB=AC ,点 D 、E 分别在 AB 、 AC 的延长线上,且BD=CE , DE 与 BC 相交于点 F.求证:DF=EF .考点:全等三角形的判定与性质;等腰三角形的性质.分析:过 D 点作 DG ∥AE 交 BC 于 G 点,由平行线的性质得∠1=∠ 2,∠ 4=∠ 3,再根据等腰三角形的性质可得∠ B=∠ 2,则∠ B= ∠ 1,于是有 DB=DG ,根据全等三角形的判定易得△ DFG ≌△ EFC,即可得到结论.解答:证明:过 D 点作 DG∥ AE 交 BC 于 G 点,如图,∴∠ 1=∠ 2,∠ 4=∠ 3,∵AB=AC ,∴∠ B= ∠2,∴∠ B= ∠ 1,∴ DB=DG ,而 BD=CE ,∴ DG=CE ,9在△ DFG 和△ EFC 中,∴△ DFG ≌△ EFC ,∴ DF=EF .10.已知等腰直角三角形ABC , BC 是斜边.∠ B 的角平分线交AC 于 D,过 C 作 CE 与 BD 垂直且交 BD 延长线于E,求证: BD=2CE .考点:全等三角形的判定与性质.分析:延长 CE, BA 交于一点F,由已知条件可证得△ BFE全≌△ BEC,所以FE=EC,即CF=2CE,再通过证明△ ADB ≌△ FAC 可得 FC=BD ,所以 BD=2CE .解答:证明:如图,分别延长CE, BA 交于一点 F.∵BE ⊥EC,∴∠ FEB= ∠CEB=90 °,∵ BE 平分∠ ABC ,∴∠ FBE= ∠ CBE ,又∵ BE=BE ,∴△ BFE≌△ BCE (ASA ).∴ FE=CE .∴ CF=2CE .∵A B=AC ,∠ BAC=90 °,∠ ABD+ ∠ ADB=90 °,∠ ADB= ∠ EDC ,∴∠ ABD+ ∠EDC=90 °.又∵∠ DEC=90 °,∠ EDC+ ∠ ECD=90 °,∴∠ FCA= ∠ DBC= ∠ ABD .∴△ ADB ≌△ AFC .∴ FC=DB ,∴ BD=2EC .11.(2012?牡丹江)如图①,△ ABC 中. AB=AC , P 为底边 BC 上一点, PE⊥ AB , PF⊥ AC , CH ⊥AB ,垂足分别为 E、 F、 H.易证 PE+PF=CH .证明过程如下:如图①,连接 AP.∵PE⊥AB , PF⊥ AC , CH ⊥ AB ,∴ S△ABP= AB ?PE,S△ACP = AC ?PF, S△ABC= AB ?CH .又∵ S△ABP+S△ACP=S△ABC,∴AB ?PE+ AC ?PF= AB ?CH.∵ AB=AC ,∴ PE+PF=CH .( 1)如图②,P 为 BC 延长线上的点时,其它条件不变, PE、 PF、 CH 又有怎样的数量关系?请写出你的猜想,并加以证明:( 2)填空:若∠ A=30 °,△ ABC 的面积为 49,点 P 在直线 BC 上,且 P 到直线 AC 的距离为 PF,当 PF=3 时,则 AB 边上的高 CH= 7 .点 P 到 AB 边的距离 PE= 4 或 10 .考点:等腰三角形的性质;三角形的面积.分析:(1)连接 AP .先根据三角形的面积公式分别表示出S△ABP,S△ACP,S△ABC,再由S△ABP=S△ACP+S△ABC即可得出 PE=PF+PH ;(2)先根据直角三角形的性质得出AC=2CH ,再由△ ABC 的面积为 49,求出 CH=7 ,由于 CH > PF,则可分两种情况进行讨论:① P 为底边 BC 上一点,运用结论 PE+PF=CH ;② P 为 BC 延长线上的点时,运用结论 PE=PF+CH .解答:解:( 1)如图②, PE=PF+CH .证明如下:∵PE⊥AB , PF⊥ AC , CH⊥ AB ,∴ S△ABP= AB ?PE,S△ACP = AC ?PF, S△ABC= AB ?CH ,∵S△ABP=S△ACP+S△ABC,∴ AB ?PE= AC ?PF+ AB ?CH,又∵ AB=AC ,∴ PE=PF+CH ;(2)∵在△ ACH 中,∠ A=30 °,∴ AC=2CH .∵S△ABC = AB ?CH ,AB=AC ,∴×2CH ?CH=49,∴ CH=7.分两种情况:① P 为底边 BC 上一点,如图① .∵P E+PF=CH ,∴ PE=CH ﹣ PF=7﹣ 3=4;② P 为 BC 延长线上的点时,如图② .∵PE=PF+CH ,∴ PE=3+7=10 .故答案为7;4 或 10.12.数学课上,李老师出示了如下的题目:“在等边三角形 ABC 中,点 E 在 AB 上,点 D 在 CB 的延长线上,且 ED=EC ,如图,试确定线段 AE 与 DB 的大小关系,并说明理由”.小敏与同桌小聪讨论后,进行了如下解答:( 1)特殊情况,探索结论当点 E 为 AB 的中点时,如图 1,确定线段 AE 与 DB 的大小关系,请你直接写出结论: AE = DB(填“>”,“<”或“=”).( 2)特例启发,解答题目解:题目中, AE 与 DB 的大小关系是:AE = DB(填“>”,“<”或“=”).理由如下:如图2,过点 E 作EF∥ BC ,交AC 于点F.(请你完成以下解答过程)( 3)拓展结论,设计新题在等边三角形ABC 中,点 E 在直线 AB 上,点 D 在直线 BC 上,且 ED=EC .若△ ABC 的边长为1,AE=2 ,求 CD的长(请你直接写出结果).考点:等边三角形的判定与性质;三角形的外角性质;全等三角形的判定与性质;等腰三角形的性质.分析:(1)根据等边三角形性质和等腰三角形的性质求出∠D=∠ ECB=30 °,求出∠ DEB=30 °,求出 BD=BE 即可;(2)过 E 作 EF∥ BC 交 AC 于 F,求出等边三角形AEF ,证△ DEB 和△ ECF 全等,求出 BD=EF 即可;(3)当 D 在 CB 的延长线上, E 在 AB 的延长线式时,由( 2)求出 CD=3 ,当 E 在 BA 的延长线上,D 在 BC 的延长线上时,求出 CD=1 .解答:解:( 1)故答案为: =.(2)过 E 作 EF∥ BC 交 AC 于 F,∵等边三角形ABC ,∴∠ ABC= ∠ ACB= ∠ A=60 °, AB=AC=BC ,∴∠ AEF= ∠ABC=60 °,∠ AFE= ∠ ACB=60 °,即∠ AEF= ∠ AFE= ∠ A=60 °,∴△ AEF 是等边三角形,∴AE=EF=AF ,∵∠ ABC= ∠ ACB= ∠AFE=60 °,∴∠ DBE= ∠EFC=120 °,∠ D+∠ BED= ∠ FCE+∠ ECD=60 °,∵DE=EC ,∴∠ D=∠ ECD,∴∠ BED= ∠ ECF,在△ DEB 和△ ECF 中,∴△ DEB ≌△ ECF ,∴ BD=EF=AE ,即 AE=BD ,故答案为:=.(3)解: CD=1 或 3,理由是:分为两种情况:①如图 1过A 作 AM ⊥BC 于 M ,过 E 作 EN⊥ BC 于 N ,则 AM ∥EM ,∵△ ABC 是等边三角形,∴ AB=BC=AC=1 ,∵AM ⊥BC ,∴ BM=CM= BC=,∵ DE=CE,EN⊥BC,∴ CD=2CN,12∵AM ∥EN ,∴△ AMB ∽△ ENB ,∴=,∴=,∴B N= ,∴ CN=1+ = ,∴ CD=2CN=3 ;②如图 2,作 AM ⊥ BC 于 M ,过 E 作 EN⊥BC 于 N ,则 AM ∥EM ,∵△ ABC 是等边三角形,∴AB=BC=AC=1,∵AM ⊥BC ,∴ BM=CM= BC=,∵ DE=CE,EN⊥BC,∴ CD=2CN,∵AM ∥EN ,∴=,∴=,∴ MN=1,∴ CN=1﹣=,∴ CD=2CN=113.已知:如图, AF 平分∠ BAC , BC ⊥ AF 于点 E,点 D 在 AF 上, ED=EA ,点 P 在 CF 上,连接 PB 交 AF 于点M .若∠ BAC=2 ∠ MPC ,请你判断∠ F 与∠ MCD 的数量关系,并说明理由.考点:全等三角形的判定与性质;等腰三角形的性质.分析:根据全等三角形的性质和判定和线段垂直平分线性质求出AB=AC=CD ,推出∠CDA= ∠ CAD= ∠ CPM ,求出∠ MPF= ∠ CDM ,∠ PMF= ∠ BMA= ∠ CMD ,在△ DCM 和△ PMF中根据三角形的内角和定理求出即可.解答:解:∠ F=∠MCD ,理由是:∵ AF 平分∠ BAC , BC⊥ AF ,∴∠ CAE= ∠BAE ,∠ AEC= ∠AEB=90 °,在△ ACE 和△ ABE 中∵,∴△ ACE ≌△ ABE (ASA )∴ AB=AC ,∵∠ CAE= ∠CDE ∴ AM 是 BC 的垂直平分线,∴CM=BM ,CE=BE ,∴∠ CMA= ∠BMA ,∵A E=ED , CE⊥ AD ,∴ AC=CD ,∴∠ CAD= ∠ CDA ,∵∠ BAC=2 ∠ MPC ,又∵∠ BAC=2 ∠ CAD ,∴∠ MPC= ∠ CAD ,∴∠ MPC= ∠CDA ,∴∠ MPF= ∠ CDM ,∴∠ MPF= ∠CDM (等角的补角相等),∵∠ DCM+ ∠ CMD+ ∠ CDM=180 °,∠ F+∠ MPF+ ∠PMF=180 °,又∵∠ PMF= ∠ BMA= ∠ CMD ,∴∠ MCD= ∠F.14.如图,已知△ ABC 是等边三角形,点D、 E 分别在 BC 、AC 边上,且AE=CD , AD 与 BE 相交于点F.(1)线段 AD 与 BE 有什么关系?试证明你的结论.(2)求∠ BFD 的度数.考点:等边三角形的性质;全等三角形的判定与性质.分析:(1)根据等边三角形的性质可知∠BAC= ∠ C=60°,AB=CA ,结合 AE=CD ,可证明△ ABE ≌△ CAD ,从而证得结论;(2)根据∠ BFD= ∠ ABE+ ∠ BAD ,∠ ABE= ∠ CAD ,可知∠ BFD= ∠ CAD+ ∠ BAD= ∠ BAC=60 °.解答:(1)证明:∵△ABC 为等边三角形,∴∠BAC= ∠ C=60 °, AB=CA .在△ ABE 和△ CAD 中,∴△ ABE ≌△ CAD ∴ AD=BE .(2)解:∵∠ BFD= ∠ABE+ ∠BAD ,又∵△ ABE ≌△ CAD ,∴∠ ABE= ∠ CAD .∴∠ BFD= ∠CAD+ ∠ BAD= ∠ BAC=60 °.15.如图,在△ ABC 中, AB=BC ,∠ ABC=90 °, F 为 AB 延长线上一点,点 E 在 BC 上, BE=BF ,连接 AE 、EF和CF,求证: AE=CF .考点:全等三角形的判定与性质.分析:根据已知利用SAS 即可判定△ ABE ≌△ CBF,根据全等三角形的对应边相等即可得到AE=CF .解答:证明:∵∠ ABC=90 °,∴∠ ABE= ∠ CBF=90 °,又∵ AB=BC , BE=BF ,∴△ ABE ≌△ CBF ( SAS).∴ AE=CF .16.已知:如图,在△ OAB 中,∠ AOB=90 °, OA=OB ,在△ EOF 中,∠ EOF=90 °, OE=OF,连接 AE 、 BF.问线段 AE 与 BF 之间有什么关系?请说明理由.考点:全等三角形的判定与性质;等腰直角三角形.分析:可以把要证明相等的线段AE ,CF 放到△AEO ,△ BFO 中考虑全等的条件,由两个等腰直角三角形得 AO=BO ,OE=OF ,再找夹角相等,这两个夹角都是直角减去∠BOE 的结果,当然相等了,由此可以证明△AEO ≌△ BFO ;延长 BF 交 AE 于 D ,交 OA 于 C,可证明∠ BDA= ∠ AOB=90 °,则 AE ⊥ BF.解答:解: AE 与 BF 相等且垂直,理由:在△AEO 与△ BFO 中,∵R t△ OAB 与 Rt△OEF 等腰直角三角形,∴ AO=OB , OE=OF ,∠ AOE=90 °﹣∠ BOE= ∠ BOF,∴△ AEO ≌△ BFO ,∴ AE=BF .延长 BF 交 AE 于 D,交 OA 于 C,则∠ ACD= ∠BCO ,由( 1)知∠ OAE= ∠OBF ,∴∠ BDA= ∠ AOB=90 °,∴ AE ⊥ BF .17.( 2006?郴州)如图,在△ ABC 中, AB=AC ,D 是 BC 上任意一点,过 D 分别向 AB ,AC 引垂线,垂足分别为E,F,CG 是 AB 边上的高.(1) DE , DF, CG 的长之间存在着怎样的等量关系?并加以证明;(2)若 D 在底边的延长线上,( 1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.考点:等腰三角形的性质.分析:(1)连接 AD ,根据三角形ABC 的面积 =三角形 ABD 的面积 +三角形 ACD 的面积,进行分析证明;(2)类似( 1)的思路,仍然用计算面积的方法来确定线段之间的关系.即三角形ABC 的面积 =三角形 ABD 的面积﹣三角形ACD 的面积.解答:解:( 1) DE+DF=CG .证明:连接AD ,则 S△ABC =S△ABD +S△ACD,即AB ?CG= AB ?DE+AC ?DF,∵ AB=AC ,∴ CG=DE+DF .(2)当点 D 在 BC 延长线上时,( 1)中的结论不成立,但有DE ﹣ DF=CG .理由:连接AD ,则 S△ABD =S△ABC +S△ACD,即AB ?DE= AB ?CG+AC ?DF∵A B=AC ,∴ DE=CG+DF ,即 DE ﹣DF=CG .同理当 D 点在 CB 的延长线上时,则有DE ﹣ DF=CG ,说明方法同上.18.如图甲所示,在△ ABC 中, AB=AC ,在底边 BC 上有任意一点 P,则 P 点到两腰的距离之和等于定长(腰上的高),即 PD+PE=CF ,若 P 点在 BC 的延长线上,那么请你猜想 PD 、PE 和 CF 之间存在怎样的等式关系?写出你的猜想并加以证明.考点:等腰三角形的性质;三角形的面积.分析:猜想: PD、 PE、 CF 之间的关系为 PD=PE+CF .根据∵ S△PAB= AB ?PD, S△PAC=AC ?PE,S△CAB = AB ?CF, S△PAC= AC ?PE, AB ?PD= AB ?CF+ AC ?PE,即可求证.解答:解:我的猜想是: PD、PE、 CF 之间的关系为 PD=PE+CF .理由如下:连接 AP,则 S△PAC+S△CAB =S△PAB,∵S△PAB= AB ?PD, S△PAC= AC ?PE,S△CAB =AB ?CF,又∵ AB=AC ,∴ S△PAC= AB ?PE,∴AB ?PD= AB ?CF+AB ?PE,即AB (PE+CF)= AB ?PD,∴ PD=PE+CF .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在中,
说明:“一题多证”在几何证明中经常遇到,它是培养思维能力提高解 题水平的有效途径,读者在以后的几何学习中要善于从不同角度去思 考、去体会,进一步提高自身的解题能力。
【实战模拟】
1. 选择题:等腰三角形底边长为5cm,一腰上的中线把其周长分为两
部分的差为3cm,则腰பைடு நூலகம்为( )
A. 2cm
【分类解析】 例1. 如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线 上一点,且CE=CD,DM⊥BC,垂足为M。求证:M是BE的中点。 分析:欲证M是BE的中点,已知DM⊥BC,所以想到连结BD,证BD =ED。因为△ABC是等边三角形,∠DBE=∠ABC,而由CE=CD,又 可证∠E=∠ACB,所以∠1=∠E,从而问题得证。 证明:因为三角形ABC是等边三角形,D是AC的中点 所以∠1=∠ABC 又因为CE=CD,所以∠CDE=∠E 所以∠ACB=2∠E 即∠1=∠E 所以BD=BE,又DM⊥BC,垂足为M 所以M是BE的中点 (等腰三角形三线合一定理) 例2. 如图,已知:中,,D是BC上一点,且,求的度数。 分析:题中所要求的在中,但仅靠是无法求出来的。因此需要考虑和 在题目中的作用。此时图形中三个等腰三角形,构成了内外角的关系。 因此可利用等腰三角形的性质和三角形的内外角关系定理来求。 解:因为,所以 因为,所以;
求证:。 分析一:从要证明的结论出发,在BC上截取,只需证明,考虑到, 想到在BC上截取,连结DE,易得,则有,只需证明,这就要从条件出 发,通过角度计算可以得出。 证明一:在BC上截取,连结DE、DF 在和中,
又
而
即 分析二:如图,可以考虑延长BD到E,使DE=AD,这样BD+ AD=BD+DE=BE,只需证明BE=BC,由于,只需证明 易证,,故作的角平分线,则有,进而证明,从而可证出。 证明二:延长BD到E,使DE=AD,连结CE,作DF平分交BC于F。 由证明一知: 则有 DF平分 ,在和中
证明:过点A作BC边的垂线AF,垂足为F。 在中, 3 1 所以 所以(等腰三角形三线合一性质)。 所以(邻补角定义)。 所以 又因为ED垂直平分AB,所以(直角三角形两锐角互余)。 (线段垂直平分线定义)。 又因为(直角三角形中
角所对的边等于斜边的一半)。 所以 在和中, 所以 所以 即。 说明: (1)根据题意,先准确地画出图形,是解几何题的一项基本功; (2)直角三角形中角的特殊关系,沟通了边之间的数量关系,为
系的重要依据,是本节的重点。 3. 等腰三角形中常用的辅助线
等腰三角形顶角平分线、底边上的高、底边上的中线常常作为解决 有关等腰三角形问题的辅助线,由于这条线可以把顶角和底边折半,所 以常通过它来证明线段或角的倍分问题,在等腰三角形中,虽然顶角的 平分线、底边上的高、底边上的中线互相重合,添加辅助线时,有时作 哪条线都可以,有时需要作顶角的平分线,有时则需要作高或中线,这 要视具体情况来定。
得等腰三角形有8个,故选择C。
2.)已知:如图,在△ABC中,AB=AC,D是BC的中点,
DE⊥AB,DF⊥AC,E、F分别是垂足。求证:AE=AF。 证明:因为,所以 又因为 所以 又D是BC的中点,所以 所以 所以,所以 说明:证法二:连结AD,通过 证明即可
5、题形展示: 例1. 如图,中,,BD平分。
因为,所以(等边对等角) 而 所以 所以 又因为 即 所以 即求得 说明1. 等腰三角形的性质是沟通本题中角之间关系的重要桥梁。把边 的关系转化成角的关系是此等腰三角形性质的本质所在。本条性质在解 题中发挥着重要的作用,这一点在后边的解题中将进一步体现。 2. 注意“等边对等角”是对同一个三角形而言的。 3. 此题是利用方程思想解几何计算题,而边证边算又是解决这类题目 的常用方法。 例3. 已知:如图,中,于D。求证:。 分析:欲证角之间的倍半关系,结合题意,观察图形,是等腰三角形 的顶角,于是想到构造它的一半,再证与的关系。 证明:过点A作于E, 所以(等腰三角形的三线合一性质) 因为 又,所以 所以(直角三角形两锐角互余) 所以(同角的余角相等) 即 说明: 1. 作等腰三角形底边高线的目的是利用等腰三角形的三线合一性质, 构造角的倍半关系。因此添加底边的高是一条常用的辅助线; 2. 对线段之间的倍半关系,常采用“截长补短”或“倍长中线”等辅助线 的添加方法,对角间的倍半关系也同理,或构造“半”,或构造“倍”。因
此,本题还可以有其它的证法,如构造出的等角等。
4、中考题型:
1.如图,△ABC中,AB=AC,∠A=36°,BD、CE分别为 ∠ABC与∠ACB的角平分线,且相交于点F,则图中的等腰三角形有
() A. 6个 B. 7个 C. 8个 D. 9个 分析:由已知条件根据等腰三角形的性质和三角形内角和的度数可求
顺利证明打通了思路。
底边的垂直平分线上”正确地理解成“OB=OC”是关键的一点。 (2)实际上,本题也可改成开放题:“△ABC中,AB=AC,D、E
分别为AC、AB上的中点,BD、CE交于O。连结AO后,试判断AO与 BC的关系,并证明你的结论”其解决方法是和此题解法差不多的。
4. 分析:此题没有给出图形,那么依题意,应先画出图形。题目中是 求线段的倍半关系,观察图形,考虑取BC的中点。
已知:如图,在中,,D、E分别为AC、AB边中点,BD、CE交于O 点。求证:点O在BC的垂直平分线上。
分析:欲证本题结论,实际上就是证明。而OB、OC在中,于是想到 利用等腰三角形的判定角等,那么问题就转化为证含有的两个三角形全 等。
证明:因为在中, 所以(等边对等角) 又因为D、E分别为AC、AB的中点,所以(中线定义) 在和 中, 所以 所以(全等三角形对应角相等)。 所以(等角对等边)。 即点O在BC的垂直平分线上。 说明: (1)正确地理解题意,并正确地翻译成几何符号语言是非常重要 的一步。特别是把“在
B. 8cm
C. 2cm或8cm
D. 以上都不对
2. 如图,是等边三角形,,则的度数是________。
3. 求证:等腰三角形两腰中线的交点在底边的垂直平分线上.
4. 中,,AB的中垂线交AB于D,交CA延长线于E,求证:。
【试题答案】
1. B 2. 分析:结合三角形内角和定理,计算图形中角的度数是等边三角形 性质的重要应用。 解:因为是等边三角形 所以 因为,所以 所以 在中,因为 所以,所以 所以 3. 分析:首先将文字语言翻译成数学的符号语言和图形语言。
等腰三角形典型试题解析
【知识精读】 (-)等腰三角形的性质 1. 有关定理及其推论
定理:等腰三角形有两边相等; 定理:等腰三角形的两个底角相等(简写成“等边对等角”)。 推论1:等腰三角形顶角的平分线平分底边并且垂直于底边,这就是 说,等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。 推论2:等边三角形的各角都相等,并且每一个角都等于60°。等腰三 角形是以底边的垂直平分线为对称轴的轴对称图形; 2. 定理及其推论的作用 等腰三角形的性质定理揭示了三角形中边相等与角相等之间的关系, 由两边相等推出两角相等,是今后证明两角相等常用的依据之一。等腰 三角形底边上的中线、底边上的高、顶角的平分线“三线合一”的性质是 今后证明两条线段相等,两个角相等以及两条直线互相垂直的重要依 据。 (二)等腰三角形的判定 1. 有关的定理及其推论 定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等 (简写成“等角对等边”。) 推论1:三个角都相等的三角形是等边三角形。 推论2:有一个角等于60°的等腰三角形是等边三角形。 推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角 边等于斜边的一半。 2. 定理及其推论的作用。 等腰三角形的判定定理揭示了三角形中角与边的转化关系,它是证明 线段相等的重要定理,也是把三角形中角的相等关系转化为边的相等关
