高一数学函数经典练习题(含答案)

(完整版)高一函数大题训练含答案解析

(完整版)高一函数大题训练含答案解析一、解答题1．已知有穷数列{}n a 、{}n b （1,2,,n k =⋅⋅⋅），函数1122()||||||k k f x a x b a x b a x b =-+-+⋅⋅⋅+-.（1）如果{}n a 是常数列，1n a =，n b n =，3k =，在直角坐标系中在画出函数()f x 的图象，据此写出该函数的单调区间和最小值，无需证明；（2）当n n a n b ==，7k m =（m ∈*N ）时，判断函数()f x 在区间[5,51]m m +上的单调性，并说明理由；（3）当n a n =，1n b n=，100=k 时，求该函数的最小值. 2．若函数()f x 对任意的x ∈R ，均有()()()112f x f x f x -++≥，则称函数()f x 具有性质P ．（1）判断下面两个函数是否具有性质P ，并说明理由．①()1xy a a =>；②3y x =．（2）若函数()f x 具有性质P ，且()()()*002,N f f n n n >∈==，求证：对任意{}1,2,3,,1i n ∈-有()0f i ≤；（3）在（2）的条件下，是否对任意[]0,x n ∈均有()0f i ≤．若成立给出证明，若不成立给出反例．3．已知函数()y f x =，若存在实数(),0m k m ≠，使得对于定义域内的任意实数x ，均有()()()m f x f x k f x k ⋅=++-成立，则称函数()f x 为“可平衡”函数，有序数对(),m k 称为函数()f x 的“平衡”数对.（1）若1m =，判断()sin f x x =是否为“可平衡”函数，并说明理由；（2）若a R ∈，0a ≠，当a 变化时，求证：()2f x x =与()2xg x a =+的“平衡”数对相同；（3）若12,m m R ∈，且1,2m π⎛⎫ ⎪⎝⎭、2,4m π⎛⎫ ⎪⎝⎭均为函数()2cos f x x =的“平衡”数对.当04x π<≤时，求2212m m +的取值范围.4．已知定义在R 上的函数()x ϕ的图像是一条连续不断的曲线，且在任意区间上()x ϕ都不是常值函数.设011i i n a t t t t t b -=<<<<<<=，其中分点121n t t t -、、、将区间[],a b 任意划分成()*n n N ∈个小区间[]1,i i t t -，记{}()()()()()()01121,,n n M a b n t t t t t t ϕϕϕϕϕϕ-=-+-++-，称为()x ϕ关于区间[],a b 的n 阶划分“落差总和”.当{},,M a b n 取得最大值且n 取得最小值0n 时，称()x ϕ存在“最佳划分”{}0,,M a b n . (1)已知()x x ϕ=，求{}1,2,2M -的最大值0M ；(2)已知()()a b ϕϕ<，求证：()x ϕ在[],a b 上存在“最佳划分”{},,1M a b 的充要条件是()x ϕ在[],a b 上单调递增.(3)若()x ϕ是偶函数且存在“最佳划分”{}0,,M a a n -，求证：0n 是偶数，且00110i i n t t t t t -+++++=.5．已知函数2()21g x ax ax b =-++(0)a >在区间[2,3]上的最大值为4，最小值为1，记()(||)f x g x =，x ∈R ；（1）求实数a 、b 的值；（2）若不等式222()()log 2log 3f x g x k k +≥--对任意x ∈R 恒成立，求实数k 的范围；（3）对于定义在[,]p q 上的函数()m x ，设0x p =，n x q =，用任意i x (1,2,,1)i n =⋅⋅⋅-将[,]p q 划分成n 个小区间，其中11i i i x x x -+<<，若存在一个常数0M >，使得不等式01121|()()||()()||()()|n n m x m x m x m x m x m x M --+-+⋅⋅⋅+-≤恒成立，则称函数()m x 为在[,]p q 上的有界变差函数，试证明函数()f x 是在[1,3]上的有界变差函数，并求出M 的最小值；6．已知集合M 是满足下列性质的函数()f x 的全体；在定义域内存在实数t ，使得(2)()(2)f t f t f +=+．（1）判断()32f x x =+是否属于集合M ，并说明理由；（2）若2()lg2af x x =+属于集合M ，求实数a 的取值范围；（3）若2()2x f x bx =+，求证：对任意实数b ，都有()f x M ∈．7．已知函数()242 1.x xf x a =⋅--（1）当1a =时，求函数()f x 在[]3,0x ∈-的值域；（2）若()f x 存在零点，求a 的取值范围.8．已知函数()22f x x x a =+--.（1）当0a =时，求函数()f x 的零点；（2）若不等式()0f x <至少有一个负解，求实数a 的取值范围. 9．已知函数11()(,0)f x b a b R a x a x a=++∈≠-+且. （1）判断()y f x =的图象是否是中心对称图形？若是，求出对称中心；若不是，请说明理由；（2）设()(1)g x b x =+，试讨论()()y f x g x =-的零点个数情况.10．已知函数()f x ，对任意a ，b R ∈恒有()()()f a b f a f b 1+=+-，且当x 0>时，有()f x 1>．(Ⅰ)求()f 0；(Ⅱ)求证：()f x 在R 上为增函数；(Ⅲ)若关于x 的不等式(()222f[2log x)4f 4t 2log x 2⎤-+-<⎦对于任意11x ,82⎡⎤∈⎢⎥⎣⎦恒成立，求实数t 的取值范围．11．已知集合M 是满足下列性质的函数()f x 的全体：在定义域内存在0x 使得()()()0011f x f x f +=+成立．（1）函数()21f x x=+是否属于集合M ？请说明理由；（2）函数()2ln1af x x =∈+M ，求a 的取值范围；（3）设函数()23x f x x =+，证明：函数()f x ∈M ．12．已知函数()20182018,0log ,0x x f x x x ⎧≤=⎨>⎩，(1)分别求()()()()1,2018f f f f -的值: (2)讨论()()()f f x m m R =∈的解的个数:(3)若对任意给定的[)1,t ∈+∞,都存在唯一的x R ∈,满足()()222f f x a t at =-，求实数a的取值范围.13．对于函数()f x ，若在定义域内存在实数0x ，满足00()()f x f x -=-，则称()f x 为“M 类函数”.（1）已知函数()sin()3f x x π=+，试判断()f x 是否为“M 类函数”？并说明理由；（2）设()2x f x m =+是定义在[1,1]-上的“M 类函数”，求是实数m 的最小值；（3）若22log (2)()3x mx f x ⎧-=⎨-⎩,2,2x x ≥<为其定义域上的“M 类函数”，求实数m 的取值范围.14．一般地，我们把函数1110()()N --=∈n n n n h x a x a x a x a n ++++称为多项式函数，其中系数0a ，1a ，…, n a ∈R ．设()f x ，()g x 为两个多项式函数，且对所有的实数x 等式[()][()]f g x g f x =恒成立．（1）若2()3f x x =+，()(0)g x kx b k =+≠． ①求()g x 的表达式； ②解不等式()()5f x g x ->．（2）若方程()()f x g x =无实数根，证明方程[()][()]f f x g g x =也无实数解． 15．若函数()f x 满足:对于任意正数,s t ，都有()()0,0f s f t >>，且()()()f s f t f s t +<+，则称函数()f x 为“L 函数”．（1）试判断函数()21f x x =与()122f x x =是否是“L 函数”；（2）若函数()()3131x xg x a -=-+-为“L 函数”，求实数a 的取值范围；（3）若函数()f x 为“L 函数”，且()11f =，求证：对任意()()12,2N*k kx k -∈∈，都有()122x f x f x x⎛⎫->- ⎪⎝⎭．【参考答案】一、解答题1．（1）图象见解析；递减区间(],2-∞，递增区间[)2,+∞，最小值()22f =；（2）单调递增；理由见解析；（3）292071. 【解析】（1）根据条件采用零点分段的方法作出函数()f x 的图象，根据图象确定出()f x 的单调区间和最小值；（2）写出()f x 的解析式，根据[]5,51x m m ∈+分析函数()f x 的结构，从而判断出()f x 的单调性；（3）先根据条件证明出()f x 的单调性然后即可求解出()f x 的最小值. 【详解】（1）如图所示，由图象可知：单调递减区间(],2-∞，单调递增区间[)2,+∞，最小值()22f =；（2）因为()112233...77f x x x x m x m =⋅-+-+-++-且[]5,51x m m ∈+, 所以()()()()()()()()()()12233...555151...77f x x x x m x m m m x m m x =-+-+-++-+++-++-，所以()()()()()()()()()222222155517212...55152 (72)2m m m m m f x x m x m m m +⋅++⋅=-+++-++++++ ，所以()()()()()()()222222222552425152...712 (52)m m m m f x x m m m m +--=++++++-+++，所以()()()()()()()2222222+35152...712 (52)m m f x x m m m m =++++++-+++且2302m m+>，所以()f x 在[]5,51m m +上单调递增；（3）因为()12131...1001f x x x x x =-+-+-++-，显然当[)1,x ∈+∞时，()f x 单调递增，当(],0x ∈-∞时，()f x 单调递减，设存在一个值()1*t N t ∈，使得10,x t ⎛⎫∈ ⎪⎝⎭时()f x 递减，1,1x t ⎛⎫∈ ⎪⎝⎭时()f x 递增，此时最小值即为1f t ⎛⎫⎪⎝⎭，下面证明1t存在：因为若要10,x t ⎛⎫∈ ⎪⎝⎭时()f x 递减，1,1x t ⎛⎫∈ ⎪⎝⎭时()f x 递增，则有12112100......t t t t t t t t t-+++++>+++，解得：71t ≥，且()1221100 (1111111)t t t t t t t t t t -++++<+++≠------，解得：171t -<，所以7172t ≤<，所以71t =，所以存在1171t =满足条件，故假设成立，综上可知：()f x 在1,71⎛⎫-∞ ⎪⎝⎭上单调递减，在1+71⎛⎫∞ ⎪⎝⎭，上单调递增， ()()()()()()()min 1112170721731100171f x f x x x x x x ⎛⎫==-+-+⋅⋅⋅+-+-+-+⋅⋅⋅+- ⎪⎝⎭292041971x =+=【点睛】本题考查数列与函数的综合应用，其中着重考查了函数单调性方面的内容，对学生的理解与分析能力要求较高，难度较难.2．（1）①()1xy a a =>具有性质P ；②3y x =不具有性质P ，见解析；（2）见解析（3）不成立，见解析【解析】【分析】（1）①根据已知中函数的解析式，结合指数的运算性质，计算出()()()112f x f x f x -++-的表达式，进而根据基本不等式，判断其符号即可得到结论；②由3y x =，举出当1x =-时，不满足()()()112f x f x f x -++≥，即可得到结论；（2）由于本题是任意性的证明，从下面证明比较困难，故可以采用反证法进行证明，即假设()f i 为()()()1,2,,1f f f n -中第一个大于0的值，由此推理得到矛盾，进而假设不成立，原命题为真；（3）由（2）中的结论，我们可以举出反例，如()()2,,x x n x f x x x ⎧-=⎨⎩为有理数为无理数，证明对任意[]0,x n ∈均有()0f x ≤不成立．【详解】证明：（1）①函数()()1xf x a a =>具有性质P ，()()()11111222x x x x f x f x f x a a a a a a -+⎛⎫-++-=+-=+- ⎪⎝⎭，因为1a >，120x a a a ⎛⎫+-> ⎪⎝⎭，即()()()112f x f x f x -++≥，此函数为具有性质P ；②函数()3f x x =不具有性质P ，例如，当1x =-时，()()()()11208f x f x f f -++=-+=-，()22f x =-，所以，()()()201f f f -+<-，此函数不具有性质P ．（2）假设()f i 为()()()1,2,,1f f f n -中第一个大于0的值，则()()10f i f i -->，因为函数()f x 具有性质P ，所以，对于任意*n ∈N ，均有()()()()11f n f n f n f n +-≥--，所以()()()()()()11210f n f n f n f n f i f i --≥---≥≥-->，所以()()()()()()110f n f n f n f i f i f i =--+++-+>⎡⎤⎡⎤⎣⎦⎣⎦，与()0f n =矛盾，所以，对任意的{}1,2,3,,1i n ∈-有()0f i ≤．（3）不成立．例如，()()2,,x x n x f x x x ⎧-=⎨⎩为有理数为无理数证明：当x 为有理数时，1x -，1x +均为有理数，()()()112f x f x f x -++-()()()2221121122x x x n x x x =-++---++-=，当x 为无理数时，1x -，1x +均为无理数，()()()()()2221121122f x f x f x x x x -++-=-++-=所以，函数()f x 对任意的x ∈R ，均有()()()112f x f x f x -++≥，即函数()f x 具有性质P ．而当[]()0,2x n n ∈>且当x 为无理数时，()0f x >．所以，在（2）的条件下，“对任意[]0,x n ∈均有()0f x ≤”不成立．如()()()01x f x x ⎧⎪=⎨⎪⎩为有理数为无理数，()()()01x f x x ⎧⎪=⎨⎪⎩为整数为非整数， ()()()2x f x xx ⎧⎪=⎨⎪⎩为整数为非整数等．【点睛】本题考查了函数的新定义及其应用，涉及指数函数和幂函数的性质，反证法，其中在证明全称命题为假命题时，举出反例是最有效，快捷，准确的方法．3．（1）()sin f x x =是“可平衡”函数,详见解析（2）证明见解析（3）221218m m <+≤【解析】【分析】(1)利用两角和差的正弦公式求解即可.(2)根据题意可知,对于任意实数x ,()()22222=22mx x k x k x k ++-=+,再列式利用恒成立问题求解即可.(3)根据“平衡数对”的定义将12,m m 用关于x 的三角函数表达,再利用三角函数的取值范围求解即可. 【详解】（1）若1m =,则()sin m f x x ⋅=,()()()()sin sin f x k f x k x k x k ++-=++-2sin cos x k =,要使得()f x 为“可平衡”函数,需使故()12cos sin 0k x -⋅=对于任意实数x 均成立,只有1cos 2k =,此时23k n ππ=±,n Z ∈,故k 存在,所以()sin f x x =是“可平衡”函数.（2）()2f x x =及()2xg x a =+的定义域均为R ,根据题意可知,对于任意实数x ,()()22222=22mx x k x k x k ++-=+,即22222mx x k =+,即()22220m x k --=对于任意实数x 恒成立,只有2m =,0k =,故函数()2f x x =的“平衡”数对为()2,0,对于函数()2xg x a =+而言,()222x x k x k m a a a +-⋅+=+++()2222x k k a -=+⋅+, 所以()()22222x x k km a a -⋅+=+⋅+,()()22220xkkm a m -⎡⎤⋅-++⋅-=⎣⎦,()2220k k m a m -⎧=+⎪⎨⋅-=⎪⎩, 即22m m ≥⎧⎨=⎩,故2m =,只有0k =,所以函数()2xg x a =+的“平衡”数对为()2,0, 综上可得函数()2f x x =与()2xg x a =+的“平衡”数对相同.（3）2221cos cos cos 22m x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,所以221cos 2sin m x x =, 2222cos cos cos 44m x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,所以22cos 1m x =,由于04x π<≤,所以21cos 12x ≤<,故(]212tan 0,2m x =∈,(]22sec 1,2m x =∈, ()22224121tan 4tan m m x x +=++()22222145tan 2tan 15tan 55x x x ⎛⎫=++=++ ⎪⎝⎭, 由于04x π<≤,所以20tan 1x <≤时,2116tan 555x <+≤,()2212tan 238x <+-≤,所以221218m m <+≤.【点睛】本题主要考查了新定义的函数问题,需要根据题意列出参数满足的关系式,利用恒成立问题或表达出参数满足的解析式再分析求范围等.属于难题. 4．(1)3；(2)见解析；(3)见解析【解析】【分析】(1)直接利用题中给的定义求解即可；(2)利用函数的单调性和数列的信息应用求出充要条件；(3)利用函数的奇偶性和存在的最佳划分，进一步建立函数的单调区间，最后求出函数的关系式. 【详解】(1)()()()()010023M ϕϕϕϕ=--+-=； (2)若()x ϕ在[],a b 上单调递增，则{}()()()(){}11,,,,1ni i i M a b n t t b a M a b ϕϕϕϕ-==-=-=⎡⎤⎣⎦∑，故()x ϕ在[],a b 上存在“最佳划分”{},,1M a b若()x ϕ在[],a b 上存在“最佳划分”{},,1M a b ，倘若()x ϕ在[],a b 上不单调递增，则存在[]()()121212,,,,x x a b x x x x ϕϕ∈<>.由()()()()()()()()1122a b a x x x x b ϕϕϕϕϕϕϕϕ-≤-+-+-（*）等号当且仅当()()()()()()11220,0,0a x x x x b ϕϕϕϕϕϕ-≥->-≥时取得，此时()()()()()()()()()()11220a b a x x x x b a b ϕϕϕϕϕϕϕϕϕϕ-=-+-+-=-<，与题设矛盾，舍去，故（*）式中等号不成立，即：增加分点12,x x 后，“落差总和”会增加，故{},,M a b n 取最大值时n 的最小值大于1，与条件矛盾. 所以()x ϕ在[],a b 上单调递增；(3)由(2)的证明过程可知，在任间区间[],a b 上，若()x ϕ存在最佳划分{},,1a b ，则当()()a b ϕϕ=时，()x ϕ为常值函数（舍）；当()()a b ϕϕ<时，()x ϕ单调递增；当()()a b ϕϕ>时，()x ϕ单调递减，若()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ，则此时在每个小区间[]()10,1,2,,i i t t i n -=上均为最佳划分{}1,,1i i M t t -.否则，添加分点后可使()x ϕ在[],a b 上的“落差总和”增大，从而{}0,,M a b n 不是“落差总和”的最大值，与“()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ”矛盾，故()x ϕ在每个小区间[]()10,1,2,,i i t t i n -=上都是单调，若()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ，则()x ϕ在相邻的两个区间[][]11,,i i i i t t t t -+、上具有不同的单调性，否则，()()()()()()11111i i i i i t t t t t t ϕϕϕϕϕϕ-+-+-=-+-，减少分点i t ，“落差总和”的值不变，而n 的值减少1，故n 的最小值不是0n ，与“()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ”矛盾，()x ϕ存在“最佳划分”{}0,,M a a n -，故()x ϕ在每个小区间[]()10,1,2,,i i t t i n -=上都单调，而()x ϕ是偶函数，故()x ϕ在y 轴两侧的单调区间对称，共有偶数个单调区间，且当000,1,,2n i j n i ⎛⎫+== ⎪⎝⎭时，0i j t t +=，从而有00120n t t t t ++++=.【点睛】本题是信息给予题，考查了数学阅读能力，考查了函数和数列的综合应用能力，考查了数学运算能力.5．（1）0b =，1a =；（2）1[,8]2；（3）证明见解析，min 4M =；【解析】【分析】（1）由已知()g x 在区间[2,3]上的最大值为4，最小值为1，结合函数的单调性及最值，易构造关于,a b 的方程组，解得,a b 的值。

高一数学函数经典练习题(含答案)

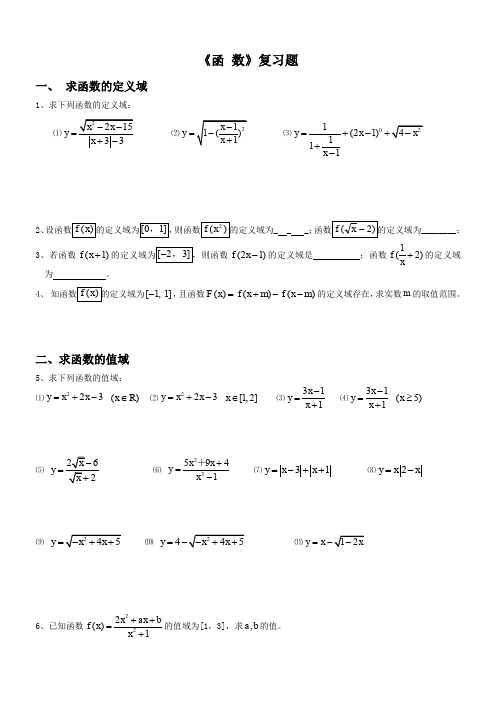
《函数》复习题一、求函数的定义域1、求下列函数的定义域：⑴33y x =+-⑵y =⑶01(21)111y x x =+-++-2、设函数f x ()的定义域为[]01，，则函数f x ()2的定义域为_ _ _；函数f x ()-2的定义域为________；3、若函数(1)f x +的定义域为[]-23，，则函数(21)f x -的定义域是；函数1(2)f x+的定义域为。

4、知函数f x ()的定义域为 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

二、求函数的值域5、求下列函数的值域：⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x -=+ (5)x ≥⑸y =⑹ 225941x x y x +=-＋ ⑺31y x x =-++ ⑻2y x x =-⑼y ⑽4y =⑾y x =-6、已知函数222()1x ax bf x x ++=+的值域为[1，3]，求,a b 的值。

三、求函数的解析式1、已知函数2(1)4f x x x -=-，求函数()f x ，(21)f x +的解析式。

2、已知()f x 是二次函数，且2(1)(1)24f x f x x x ++-=-，求()f x 的解析式。

3、已知函数()f x 满足2()()34f x f x x +-=+，则()f x = 。

4、设()f x 是R 上的奇函数，且当[0,)x ∈+∞时， ()(1f x x =+，则当(,0)x ∈-∞时()f x =____ _()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且，()f x 是偶函数，()g x 是奇函数，且1()()1f xg x x +=-，求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间：⑴ 223y x x =++ ⑵y =⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数，则2(1)f x -的单调递增区间是8、函数236xy x -=+的递减区间是；函数y =的递减区间是五、综合题9、判断下列各组中的两个函数是同一函数的为（） ⑴3)5)(3(1+-+=x x x y ， 52-=x y ； ⑵111-+=x x y ， )1)(1(2-+=x x y ；⑶x x f =)(， 2)(x x g =； ⑷x x f =)(， ()g x =； ⑸21)52()(-=x x f ， 52)(2-=x x f 。

高一数学函数与极限分析练习题及答案

高一数学函数与极限分析练习题及答案一、选择题1. 设函数$f(x)=\sqrt{1-x^2}$，其定义域为$[-1,1]$，关于该函数，下列说法正确的是：A. $f(x)$在$[-1,1]$上单调递增B. $f(x)$在$[-1,1]$上单调递减C. $f(x)$在$x=\frac{\pi}{4}$处取得最大值D. $f(x)$在$x=0$处取得最大值答案：D2. 设函数$f(x)=\frac{1}{x}$，下列说法正确的是：A. $f(x)$在$x=0$处连续B. $f(x)$在$x=0$处可导C. $f(x)$在$x=0$处极限存在D. $f(x)$在$x=0$处极限不存在答案：D3. 设函数$f(x)=e^x$，下列说法正确的是：A. $f(x)$在$x=0$处连续B. $f(x)$在$x=0$处可导C. $f(x)$在$x=0$处极限存在D. $f(x)$在$x=0$处极限不存在答案：A、B、C4. 设函数$f(x)=\sin x$，下列说法正确的是：A. $f(x)$在$x=\frac{\pi}{2}$处连续B. $f(x)$在$x=\frac{\pi}{2}$处可导C. $f(x)$在$x=\frac{\pi}{2}$处极限存在D. $f(x)$在$x=\frac{\pi}{2}$处极限不存在答案：B、C5. 设函数$f(x)=x^3$，下列说法正确的是：A. $f(x)$在$x=0$处连续B. $f(x)$在$x=0$处可导C. $f(x)$在$x=0$处极限存在D. $f(x)$在$x=0$处极限不存在答案：A、B、C二、填空题1. 函数$f(x)=\sin x$在$x=\frac{\pi}{2}$处的导数为______。

答案：12. 函数$f(x)=\frac{1}{x}$在$x=0$处的极限为______。

答案：无穷大或$+\infty$3. 函数$f(x)=e^x$在$x=0$处的连续性、可导性、极限存在性均为______。

高中数学必修一函数大题(含详细解答)

高中函数大题专练１、已知关于x 的不等式2(4)(4)0kx k x --->，其中k R ∈。

⑴试求不等式的解集A ；⑵对于不等式的解集A ，若满足A ZB =（其中Z 为整数集）。

试探究集合B 能否为有限集？若能，求出使得集合B 中元素个数最少的k 的所有取值，并用列举法表示集合B ；若不能，请说明理由。

２、对定义在[0,1]上，并且同时满足以下两个条件的函数()f x 称为G 函数。

① 对任意的[0,1]x ∈，总有()0f x ≥；② 当12120,0,1x x x x ≥≥+≤时，总有1212()()()f x x f x f x +≥+成立。

已知函数2()g x x =与()21xh x a =⋅-是定义在[0,1]上的函数。

（1）试问函数()g x 是否为G 函数？并说明理由；（2）若函数()h x 是G 函数，求实数a 的值；（3）在（2）的条件下，讨论方程(21)()xg h x m -+=()m R ∈解的个数情况。

3.已知函数||212)(x x x f -=. （1）若2)(=x f ，求x 的值；（2）若0)()2(2≥+t mf t f t对于[2,3]t ∈恒成立，求实数m 的取值范围.4.设函数)(x f 是定义在R 上的偶函数.若当0x ≥时，11,()0,f x x⎧-⎪=⎨⎪⎩0;0.x x >= （1）求)(x f 在(,0)-∞上的解析式.（2）请你作出函数)(x f 的大致图像. （3）当0a b <<时，若()()f a f b =，求ab 的取值范围. （4）若关于x 的方程0)()(2=++c x bf x f 有7个不同实数解，求,b c 满足的条件.5．已知函数()(0)||bf x a x x =-≠。

（1）若函数()f x 是(0,)+∞上的增函数，求实数b 的取值范围；（2）当2b =时，若不等式()f x x <在区间(1,)+∞上恒成立，求实数a 的取值范围；（3）对于函数()g x 若存在区间[,]()m n m n <，使[,]x m n ∈时，函数()g x 的值域也是[,]m n ，则称()g x 是[,]m n 上的闭函数。

高一数学函数经典题目及答案

1函数解析式的特殊求法例1 已知f(x)是一次函数, 且f[f(x)]=4x -1, 求f(x)的解析式例2 若x x x f 21(+=+）,求f(x)例3 已知x x x f 2)1(+=+，求)1(+x f例4已知：函数)(2x g y x x y =+=与的图象关于点)3,2(-对称，求)(x g 的解析式例5 已知f(x)满足x xf x f 3)1()(2=+，求)(x f2函数值域的特殊求法例1. 求函数]2,1[x ,5x 2x y 2-∈+-=的值域。

例2. 求函数22x 1x x 1y +++=的值域。

例3求函数y=(x+1)/(x+2)的值域例4. 求函数1e 1e y x x +-=的值域。

例1下列各组中的两个函数是否为相同的函数？ ①3)5)(3(1+-+=x x x y 52-=x y ②111-+=x x y )1)(1(2-+=x x y③21)52()(-=x x f 52)(2-=x x f2若函数)(x f 的图象经过)1,0(-，那么)4(+x f 的反函数图象经过点(A))1,4(-(B))4,1(-- (C))1,4(-- (D))4,1(-例3已知函数)(x f 对任意的a b R ∈、满足：()()()6,f a b f a f b +=+-0,()6a f a ><当时；(2)12f -=。

（1）求：(2)f 的值；（2）求证：()f x 是R 上的减函数；（3）若(2)(2)3f k f k -<-，求实数k 的取值范围。

例4已知{(,)|,,A x y x n y an b n ===+∈Z }，2{(,)|,315,B x y x m y m m ===+∈Z }，22{(,)|C x y x y =+≤14}，问是否存在实数,a b ，使得(1)A B ≠∅，(2)(,)a b C ∈同时成立.证明题1.已知二次函数2()f x ax bx c =++对于x 1、x 2∈R ，且x 1＜x 2时12()()f x f x ≠，求证：方程()f x ＝121[()()]2f x f x +有不等实根，且必有一根属于区间（x 1，x 2）.答案1解：设f(x)=kx+b 则 k(kx+b)+b=4x -1 则⎪⎩⎪⎨⎧-==⇒⎩⎨⎧-=+=3121)1(42b k b k k 或 ⎩⎨⎧=-=12b k ∴312)(-=x x f 或12)(+-=x x f 2换元法：已知复合函数[()]f g x 的表达式时，还可以用换元法求()f x 的解析式。

高一数学函数试题及答案

高一数学函数试题及答案一、选择题（每题4分，共40分）1. 函数y=f(x)=x^2-4x+3的零点个数是（）。

A. 0个B. 1个C. 2个D. 3个2. 函数y=x^3-3x的单调递增区间是（）。

A. (-∞, +∞)B. (-∞, 1)C. (1, +∞)D. (-∞, 0) ∪ (2, +∞)3. 函数y=f(x)=x^2-6x+8的值域是（）。

A. (-∞, +∞)B. [1, +∞)C. (-∞, 1]D. [1, +∞)4. 函数y=f(x)=x^3-3x的极值点是（）。

A. x=-1B. x=1C. x=-1, 1D. x=-1, 25. 函数y=f(x)=x^2-4x+3的对称轴是（）。

A. x=2B. x=-2C. x=4D. x=-46. 函数y=f(x)=x^3-3x的导数是（）。

A. f'(x)=3x^2-3B. f'(x)=x^2-3C. f'(x)=3x^2+3D. f'(x)=x^3-37. 函数y=f(x)=x^2-4x+3在x=2处的切线斜率是（）。

A. 0B. -4C. 4D. -18. 函数y=f(x)=x^3-3x的拐点是（）。

A. x=-1B. x=1C. x=-1, 1D. x=-1, 29. 函数y=f(x)=x^2-6x+8的最小值是（）。

A. 1B. 2C. 3D. 410. 函数y=f(x)=x^3-3x的二阶导数是（）。

A. f''(x)=6xB. f''(x)=6x-6C. f''(x)=3x^2D. f''(x)=3x^2-6二、填空题（每题4分，共20分）11. 函数y=f(x)=x^2-4x+3的零点是_________。

12. 函数y=f(x)=x^3-3x的单调递减区间是_________。

13. 函数y=f(x)=x^2-6x+8的对称轴是_________。

完整版)高一数学函数经典习题及答案

完整版)高一数学函数经典习题及答案函数练题一、求函数的定义域1、求下列函数的定义域：⑴y = (x-1)/(2x^2-2x-15)⑵y = 1-[(2x-1)+4-x^2]/[1/(x+1)+1/(x+3)-3]2、设函数f(x)的定义域为[0,1]，则函数f(x-2)的定义域为[-2,-1]；函数f(2x-1)的定义域为[(1/2,1)]。

3、若函数f(x+1)的定义域为[-2,3]，则函数f(2x-1)的定义域为[-3/2,2]；函数f(2)的定义域为[1,4]。

4、已知函数f(x)的定义域为[-1,1]，且函数F(x) = f(x+m)-f(x-m)的定义域存在，求实数m的取值范围。

二、求函数的值域5、求下列函数的值域：⑴y = x+2/x-3 (x∈R)⑵y = x+2/x-3 (x∈[1,2])⑶y = 2/(3x-1)-3/(x-1) (x∈R)⑷y = (x+1)/(x+1) if x≥5y = 5x^2+9x+4/2x-6 (x<5)⑸y = (x-3)/(x+2)⑹y = x-3+x+1⑺y = (x^2-x)/(2x-1)(x+2)⑼y = -x^2+4x+5⑽y = 4-1/(x^2+4x+5)⑾y = x-1-2x/(2x^2+ax+b)6、已知函数f(x) = 2x+1/(x∈R)的值域为[1,3]，求a,b的值。

三、求函数的解析式1、已知函数f(x-1) = x-4x，求函数f(x)，f(2x+1)的解析式。

2、已知f(x)是二次函数，且f(x+1)+f(x-1) = 2x-4x，求f(x)的解析式。

3、已知函数2f(x)+f(-x) = 3x+4，则f(x) = (3x+4)/5.4、设f(x)是R上的奇函数，且当x∈[0,+∞)时，f(x) =x/(1+x)，则f(x)在R上的解析式为f(x) = x/(1+x)-2/(1-x^2)。

5、设f(x)与g(x)的定义域是{x|x∈R,且x≠±1}，f(x)是偶函数，g(x)是奇函数，且f(x)+g(x) = 3x，则f(x) = x，g(x) = 3x-x^3.四、求函数的单调区间6、求下列函数的单调区间：⑴y = x+2/x+3⑵y = -x^2+2x+3⑶y = x-6/x-127、函数f(x)在[0,+∞)上是单调递减函数，则f(1-x)的单调递增区间是(0,1]。

高一数学函数经典练习题(含答案详细)

高一数学函数经典练习题(含答案详细)一、求函数的定义域1、求下列函数的定义域：⑴ $y=\frac{x^2-2x-15}{x+3-3}$答案：首先化简得到 $y=\frac{x^2+2x-15}{x}$。

然后根据分式的定义，分母不能为零，即 $x\neq0$。

同时，分子中有$x-5$ 和 $x+3$ 两个因式，因此 $x\leq-3$ 或 $x\geq5$。

综合起来得到定义域为 $\{x|x\leq-3 \text{ 或 } x\geq5 \text{ 或 }x\neq0\}$。

⑵ $y=1-\frac{x-1}{2x+2}$答案：首先化简得到 $y=\frac{x+1}{2x+2}$。

然后根据分式的定义，分母不能为零，即 $x\neq-1$。

同时，分子中有 $x-1$ 和 $x+1$ 两个因式，因此 $x\geq0$。

综合起来得到定义域为 $\{x|x\geq0 \text{ 且 } x\neq-1\}$。

2、设函数 $f(x)$ 的定义域为 $[0,1]$，则函数 $f(x^2)$ 的定义域为 _。

_。

_；函数 $x-2f(x-2)$ 的定义域为答案：对于 $f(x^2)$，$x^2\in[0,1]$，因此 $x\in[-1,1]$。

综合起来得到定义域为 $\{x|-1\leq x\leq1\}$。

对于 $x-2f(x-2)$，$x-2(x-2)\in[0,1]$，即 $2\leq x\leq3$。

因此定义域为 $\{x|2\leq x\leq3\}$。

3、若函数 $f(x+1)$ 的定义域为 $[-2,3]$，则函数 $f(2x-1)$ 的定义域是；函数 $f(\frac{x+2}{x})$ 的定义域为。

答案：对于 $f(2x-1)$，$2x-1\in[-2,3]$，因此 $-1\leqx\leq2$。

综合起来得到定义域为 $\{x|-1\leq x\leq2\}$。

对于 $f(\frac{x+2}{x})$，$x\neq0$ 且 $\frac{x+2}{x}\in[-2,3]$，即 $-2x\leq x+2\leq3x$，解得 $-3\leq x\leq-1$ 或$x\geq2$。

高一数学函数经典练习题(含答案)

《函数》复习题一、求函数的定义域1、求下列函数的定义域：⑴33y x =+-⑵y =⑶01(21)111y x x =+-++- 2、设函数的定义域为，则函数的定义域为_ _ _；函数的定义域为________；3、若函数(1)f x +的定义域为，则函数(21)f x -的定义域是；函数1(2)f x+的定义域为。

4、知函数的定义域为 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

二、求函数的值域5、求下列函数的值域：⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x -=+ (5)x ≥⑸y =⑹ 225941x x y x +=-＋ ⑺31y x x =-++ ⑻2y x x =-⑼y ⑽4y =⑾y x =-6、已知函数222()1x ax bf x x ++=+的值域为[1，3]，求,a b 的值。

三、求函数的解析式1、已知函数2(1)4f x x x -=-，求函数()f x ，(21)f x +的解析式。

2、已知()f x 是二次函数，且2(1)(1)24f x f x x x ++-=-，求()f x 的解析式。

3、已知函数()f x 满足2()()34f x f x x +-=+，则()f x = 。

4、设()f x 是R 上的奇函数，且当[0,)x ∈+∞时， ()(1f x x =+，则当(,0)x ∈-∞时()f x =____ _()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且，()f x 是偶函数，()g x 是奇函数，且1()()1f xg x x +=-，求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间：⑴ 223y x x =++ ⑵y =⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数，则2(1)f x -的单调递增区间是8、函数236xy x -=+的递减区间是；函数y =的递减区间是五、综合题9、判断下列各组中的两个函数是同一函数的为（） ⑴3)5)(3(1+-+=x x x y ， 52-=x y ； ⑵111-+=x x y ， )1)(1(2-+=x x y ；⑶x x f =)(， 2)(x x g =； ⑷x x f =)(， ()g x =； ⑸21)52()(-=x x f ， 52)(2-=x x f 。

高一数学函数经典练习题(含答案详细)

《函数》复习题一、求函数的定义域1、求下列函数的定义域：答案：x²又⑵y =答案：2111x x -⎛⎫≤ ⎪+⎝⎭, ()()22111x x -≤+, ()()2211x x -≤+,222121x x x x -+≤++,-4x ≤0, ∴x ≥0{|0}x x ≥⑶01(21)111y x x =+-+-答案：211011011210210104022x x x x x x x x x ⎧+≠⇒-≠-⇒≠⎪-⎪⎪-≠⇒≠⎨⎪-≠⇒≠⎪≥⇒-≥⇒-≤≤∴1{|220,,1}2x x x x x -≤≤≠≠≠且2、设函数f x ()的定义域为[]01，，则函数f x ()2的定义域为_ _ _2 f x ()-2的定义域为________；答案：函数f(x)的定义域为[0.1], 则0≤x ≤1于是0≤x ²≤1 解得-1≤x ≤1所以函数f x ()2的定义域为[-1,1]f∴4≤x ≤93、若函数(1)f x +的定义域为[]-23，，则函数(21)f x -的定义域是；函数1x 1(2)f x+的定义域为。

答案：y=f(x+1)的定义域是【-2,3】注：y=f(x+1)的定义域是【-2，3】指的是里面X 的定义域不是括号内整体的定义域即-2<=x<=3∴-1<=x+1<=4 ∴x+1 的范围为 [-1,4] f(x)括号内的范围相等y=f(2x-1)f(4、知函数f x ()的定义域为 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

答案解1：知函数f(x)的定义域为[-1.1],则对函数F （X ）=f(m+x)-f(x-m)来说 -1≤m+x ≤1 -1≤x-m ≤11. 由-1≤m+x 和x-m ≤1 两式相加-1+x-m ≤m+x+1 解得2m ≥-2 m ≥-12. 由m+x ≤1和-1≤x-m 两式相加 m+x-1≤x-m+12m ≤2 解得m ≤1综上：-1≤m ≤1答案解2： -1<x+m<1 →→-1-m < x<1-m-1<x-m<1 → -1+m<x<1+m定义域存在,两者的交集不为空集，（注：则只需（-m-1，1-m ）与（m-1，1-m ）有交集即可。

高一数学函数经典练习题(含答案)

《函数》复习题一、求函数的定义域1、求下列函数的定义域：⑴33y x =+-⑵y =⑶01(21)111y x x =+-++-2、_ _ _；________；3、若函数(1)f x+(21)f x -的定义域是；函数1(2)f x+的定义域为。

4、 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

二、求函数的值域5、求下列函数的值域：⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x-=+ (5)x ≥⑸ y =⑹ 225941x x y x +=-＋ ⑺31y x x =-++⑻2y x x =-⑼y ⑽4y = ⑾y x =-6、已知函数222()1x ax bf x x ++=+的值域为[1，3]，求,a b 的值。

三、求函数的解析式1、已知函数2(1)4f x x x -=-，求函数()f x ，(21)f x +的解析式。

2、已知()f x 是二次函数，且2(1)(1)24f x f x x x ++-=-，求()f x 的解析式。

3、已知函数()f x 满足2()()34f x f x x +-=+，则()f x = 。

4、设()f x 是R 上的奇函数，且当[0,)x ∈+∞时， ()(1f x x =+，则当(,0)x ∈-∞时()f x =____ _()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且，()f x 是偶函数，()g x 是奇函数，且1()()1f xg x x +=-，求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间：⑴ 223y x x =++ ⑵y =⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数，则2(1)f x -的单调递增区间是8、函数236xy x -=+的递减区间是；函数y =的递减区间是五、综合题9、判断下列各组中的两个函数是同一函数的为（） ⑴3)5)(3(1+-+=x x x y ， 52-=x y ； ⑵111-+=x x y ， )1)(1(2-+=x x y ；⑶x x f =)(， 2)(x x g =； ⑷x x f =)(， ()g x =； ⑸21)52()(-=x x f ， 52)(2-=x x f 。

高一数学函数经典练习题(含答案)

《函数》复习题一、求函数的定义域1、求下列函数的定义域：⑴33y x =+-⑵y =⑶01(21)111y x x =+-++- 2、设函数的定义域为，则函数的定义域为_ _ _；函数的定义域为________；3、若函数(1)f x +的定义域为，则函数(21)f x -的定义域是；函数1(2)f x+的定义域为。

4、知函数的定义域为 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

二、求函数的值域5、求下列函数的值域：⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x -=+ (5)x ≥⑸y =⑹ 225941x x y x +=-＋ ⑺31y x x =-++ ⑻2y x x =-⑼y ⑽4y =⑾y x =-6、已知函数222()1x ax bf x x ++=+的值域为[1，3]，求,a b 的值。

三、求函数的解析式1、已知函数2(1)4f x x x -=-，求函数()f x ，(21)f x +的解析式。

2、已知()f x 是二次函数，且2(1)(1)24f x f x x x ++-=-，求()f x 的解析式。

3、已知函数()f x 满足2()()34f x f x x +-=+，则()f x = 。

4、设()f x 是R 上的奇函数，且当[0,)x ∈+∞时， ()(1f x x =+，则当(,0)x ∈-∞时()f x =____ _()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且，()f x 是偶函数，()g x 是奇函数，且1()()1f xg x x +=-，求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间：⑴ 223y x x =++ ⑵y =⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数，则2(1)f x -的单调递增区间是8、函数236xy x -=+的递减区间是；函数y =的递减区间是五、综合题9、判断下列各组中的两个函数是同一函数的为（） ⑴3)5)(3(1+-+=x x x y ， 52-=x y ； ⑵111-+=x x y ， )1)(1(2-+=x x y ；⑶x x f =)(， 2)(x x g =； ⑷x x f =)(， ()g x =； ⑸21)52()(-=x x f ， 52)(2-=x x f 。

高一数学函数试题及答案

高一数学函数试题及答案一、选择题（每题4分，共40分）1. 函数f(x) = 2x^2 - 3x + 1在区间[-1, 2]上的最大值是：A. 1B. 7C. 9D. 112. 若函数g(x) = x^3 - 2x^2 + x - 2的零点是x0，则x0的取值范围是：A. (-∞, 1)B. (1, 2)C. (2, 3)D. (3, +∞)3. 函数h(x) = sin(x) + cos(x)的值域是：A. [-1, 0]B. [-1, 1]C. [0, 1]D. [1, 2]...20. 若函数f(x) = log_a(x)（a > 0，a ≠ 1）在区间(0, 1)上是增函数，则a的取值范围是：A. (0, 1)B. (1, +∞)C. (0, 1/e)D. (1/e, 1)二、填空题（每题3分，共15分）1. 若函数f(x) = x^2 - 4x + 4的图像关于x轴对称，则x的取值是________。

2. 函数y = 2^x的反函数是________。

3. 若函数f(x) = 1/x在点(1, 1)处的切线斜率为-1，则该切线方程是________。

...5. 若函数f(x) = x^3 - 6x^2 + 9x + 2的极小值点为x0，则x0的值为________。

三、解答题（共45分）1. 已知函数f(x) = x^3 - 3x^2 - 9x + 5，求证f(x)在(-∞, -1)上单调递增。

（10分）2. 求函数y = x^2 - 2x + 3在区间[1, 3]上的值域。

（10分）3. 已知函数f(x) = x^2 + 2x + 1，x ∈ R，求f(x)的最小值。

（10分）4. 解不等式：|x - 1| + |x - 3| ≤ 2。

（10分）5. 已知函数f(x) = log_2(x)，x ∈ (0, +∞)，求f(x)的值域。

（5分）四、附加题（10分）1. 已知函数f(x) = 2x - 1，g(x) = 3x + 2，求f(g(x))的表达式。

高一数学函数试题及答案

4．二次函数的图象经过三点 A(1 , 3), B(1,3),C(2,3) ，则这个二次函数的 24
解析式为
。
5．已知函数
f
(x)

x2
1
(x 0) ，若 f (x) 10 ,则 x
。
2x (x 0)
三、解答题
1．求函数 y x 1 2x 的值域。 2．利用判别式方法求函数 y 2x2 2x 3 的值域。
A．1 B． 0
C． 0 或1
D．1或 2
3．已知集合 A 1, 2,3, k, B 4,7, a4, a2 3a ，且 a N*, x A, y B
使 B 中元素 y 3x 1 和 A 中的元素 x 对应，则 a, k 的值分别为（）
A． 2,3 B． 3, 4 C． 3,5 D． 2,5
函数及其表示[提高训练 C 组]
一、选择题
1．若集合 S y | y 3x 2, x R，T y | y x2 1, x R ，
则 S T 是( )
A． S
B. T
C.
D.有限集
2．已知函数 y f (x) 的图象关于直线 x 1对称，且当 x (0,) 时，

x2
,
0 x
0
的图象是抛物线，
其中正确的命题个数是____________。
三、解答题
1．判断一次函数 y kx b, 反比例函数 y k ，二次函数 y ax2 bx c 的 x
单调性。
2．已知函数 f (x) 的定义域为 1,1 ，且同时满足下列条件：（1） f (x) 是奇函数；
二、填空题
1．函数 f (x) (a 2)x2 2(a 2)x 4 的定义域为 R ，值域为 ,0 ，

高一数学函数试题答案及解析

高一数学函数试题答案及解析1.函数在上的单调性为（）A．减函数B．增函数.C．先增后减.D．先减后增【答案】B【解析】主要考查函数单调性的概念及函数单调性判定方法。

由定义法或利用结论x的系数为正，一次函数是增函数，故选B。

2.函数的单调增区间为（）A．B．C．D．【答案】A【解析】主要考查函数单调性的概念及二次函数单调性判定方法。

函数图象开口向下，对称轴x=0，所以函数的单调增区间为，选A。

3.函数，当时是增函数，当时是减函数，则等于（）A．-3B．13C．7D．由m而定的常数【答案】B【解析】主要考查函数单调性的概念及二次函数单调性判定方法。

解：因为函数，当时是增函数，当时是减函数，所以函数对称轴为=－2，=－8，所以=13，故选B。

4.函数的定义域是[－2，0]，则f(x)的单调递减区间是____．【答案】[－1，1]．【解析】主要考查函数单调性的概念及二次函数单调性判定方法。

解：令t=x＋1，∵－2≤x≤0，∴－1≤t≤1，∴f(t)=(t－1)2－2(t－1)＋1=t2－4t＋4，即f(x)=x2－4x＋4=(x－2)2在区间[－1，1]上是减函数．5.如果函数在区间上是增函数，那么的取值范围是__________________.【答案】；【解析】主要考查函数单调性的概念及二次函数单调性判定方法。

解：因为函数在区间上是增函数，函数图象开口向上，所以在对称轴的右侧，即，解得，从而11。

6.函数的奇偶性是（）A．奇函数B．偶函数C．非奇非偶函数D．既是奇函数又是偶函数【答案】C【解析】主要考查函数奇偶性的概念与判定方法。

由于定义域不关于原点对称，所以函数是非奇非偶函数。

故选C。

7.已知是定义在R上的奇函数，且为周期函数，若它的最小正周期为T，则A．0B．C．D．【答案】A【解析】主要考查函数奇偶性的概念、性质及周期函数的概念。

由已知,所以，即，0.故选A。

8.定义在R上的偶函数f(x)满足f(x)=f(x+2)，当x∈[3，5]时，f(x)=2-|x-4|，则A．f(sin)<f(cos)B．f(sin1)>f(cos1)C．f(cos)<f(sin)D．f(cos2)>f(sin2)【答案】D【解析】主要考查函数奇偶性的概念、性质及函数单调性判定方法。