三年级下册数学试题-奥数专题讲练:第14讲 火柴棍游戏精英篇(解析版)全国通用
三年级下册数学试题-奥数专题讲练:第七讲 火柴棍游戏 精英篇(解析版)全国通用
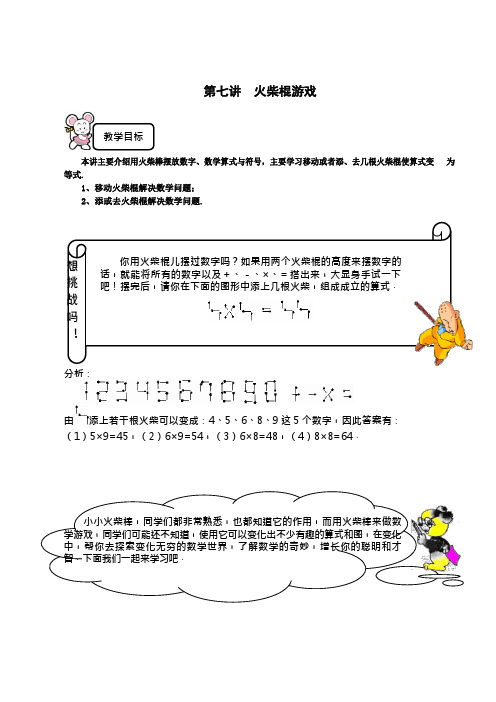
你用火柴棍儿摆过数字吗?如果用两个火柴棍的高度来摆数字的话,就能将所有的数字以及+、-、×、=搭出来,大显身手试一下吧!摆完后,请你在下面的图形中添上几根火柴,组成成立的算式.第七讲火柴棍游戏本讲主要介绍用火柴棒摆放数字、数学算式与符号,主要学习移动或者添、去几根火柴棍使算式变为等式.1、移动火柴棍解决数学问题;2、添或去火柴棍解决数学问题.分析:由添上若干根火柴可以变成:4、5、6、8、9 这 5 个数字,因此答案有:(1)5×9=45,(2)6×9=54,(3)6×8=48,(4)8×8=64.教学目标想挑战吗?小小火柴棒,同学们都非常熟悉,也都知道它的作用,而用火柴棒来做数学游戏,同学们可能还不知道,使用它可以变化出不少有趣的算式和图,在变化中,帮你去探索变化无穷的数学世界,了解数学的奇妙,增长你的聪明和才智.下面我们一起来学习吧.下列各式中的数字与符号都是由火柴棍儿搭成的,你能只移动一根火柴,就使得下面的等式成立吗?分析:①题中,观察算式两边,等号左边计算的结果是 641,右边计算的结果是141,所以基本想法是通过移动火柴棍,使左边减小而右边增加.注意到,如果把左边的减数 121 变成 21,则左边的计算结果是 741,且被拿掉一根火柴,右边 141 中,添上这根火柴,恰好变成 741,于是等式成立.想一想,试一试,每个算式中的火柴棍应该怎样移?②题中,左边的计算结果是三位数,而右边是五位数,既使将右边万位上的 1 或十位上的 1 移到左边 422 的前面,算式也不能成立.所以想到,应该把右边的五位数变成三位数与一位数的和,只能是“177+2”或“1+712”,从而使右边变为三位数.计算左边,结果是 287,所以,将 17712 变成“1+712”不行,只能考虑从左边移一根火柴到右边,使右边变成“177+2”,即 179.这需要把左边减小一些.试着把左边的“+”号变为“-”号,则左边为 422-27×7—27×2,计算得 179,满足算式.小马虎用火柴棍摆了四个算式,但是都是错误的,现在有 4 根火柴,你能每个算式只添一根火柴,把算式改成正确的等式吗?相信你可以的.(1)专题精讲用火柴棍摆成的一些数字和运算符号,可以通过动一根火柴,它的变化规律一般为:(1)添,添加一根火柴,可变为,变为,变为,还可以在数前、数后添上,另外,可以把“等.”号变为“”号,把“”变为“”号,在两个数之间增加“”号(2)去,“去”是“添”的反面,要去掉一根火柴棍,常可以变“”为“”,变“”为“”,变“”为“”,变“”为“”,变“”为“”.还可以去掉数字前面或后面的“”,以及数字之间的“”号等.(3)移,“移”是“去”和“添”的结合,移动火柴棍时,要保证火柴的根数没有变化.如“”与“”之间,“”与“”之间,“”与“”之间,“”与“”之间,“”与“”之间都可以互相转化,等等.根据以上的数字、符号变化规律,就可以解决一些火柴棍儿搭出的数学问题了.例1例2(2)(3)(4)分析:我们先来想一想:l7×2=34,34>22,要添 l 根,使(1)成立,你有什么想法呢? 类似地,看看下面的几个题如何思考?(1)算式左边计算结果是 32,比右边多 10,为了使两边相等,可以添上一根火柴棒使左边减少 10,我们考虑让被减数减少 10,即添加一根使 7 变成2,所以第(1)个式子成为正确等式12×2-2=22.另外,我们也可以把减数增加 10,就是在 2 前添1 变成12,17×2-12=22.(2)算式左边计算结果是 10,比右边少 12,为了使两边相等,可以添上一根火柴棒使左边增加 12,我们考虑把 1 变成 7,加数增加 12,所以第(2)式变为等式 4+4+7×2=22.(3)217与7和21相差太大,考虑把217拆开,变成2×7,即把“1”变成“×”,所以第(3)式变为等式2×7+7=21.(4)算式左边计算结果是 19,比右边少 8,为了使两边相等,可以添上一根火柴棒使左边增加 8,我们把“-”变成“+”后,正好增加 8,所以第(4)式变为等式 7+4+4×4=27.[巩固]圣诞老人用火柴棍摆了四个算式,它们很神奇,你只需要拿走一根,就可以把算式变成正确的等式,快来试试吧.(1)(2)(3)(4)分析:(1)把“+”变成“一”,式子变为等式:4×4-4=12. (2)把2 变成7,式子变为等式:1+4+7=12.(3)把 2 变成 7,式子变为等式:4×7-4=24. (4)把4 变成“+”,式子变为等式:4+4+4=12.添一根或去一根火柴,使等式成立,你能做到吗?到底是添一根还是去一根呢?分析:①题中,只有一个四位数 1244,且它是减数,其余的数都是三位数,所以,我们首先想到,要把 1244 千位上的 1 去掉,使它变成三位数.这时,等式左边是:772-244-417,计算的结果恰好就是 111.等式成立.①题中,由于减数是四位数 1244,我们又可以想到在被减数的前面添加一根火柴,使它变成 1772.这样,算式左边变为1772-1244-417,计算的结果也是 111,等式仍然成立.所以①题有两个答案.例3②题中,原式左边的计算结果是四位数,右边的运算结果是 109.所以,使左边减小是做这道题的想法,左边,12×7= 84,所以,应该有 4421 变成 25,注意到拿掉百位 4 上的一根火柴即可变为“4+ 21”,从而满足等式.①(1)去掉一根火柴棍:(2)添加一根火柴棍:②去掉一根火柴棍:[前铺] 添一根或去一根火柴,使等式成立(1)(2)分析: 到底是添一根还是去一根,题目中没有明确指定,我们可以先考虑其中一种,再考虑另一种. (1)添一根使 1 变为 7. 2×1+4-4=14→2×7+4-4=14 (2)把 444 中间的 4 变为“+”,即去一根.2×444+12=24→2×4+4+12=24一天,几个小动物来到数学王国的城门,看到城门上贴着一张告示,上面写着,“如果想进入我的王国,必须答对下面的问题:用火柴棍摆出所有的千位为 1 的四位数,且每个数位上的数字各不相同,计算它们的和,并用火柴棍摆出这个等式.”小动物们想了半天都没想出来,可是他们都 想进入王国,同学们你能帮助它们吗?分析:解决这个问题分两步:先用火柴摆出所有的以 1 开头的四位数,由于火柴棍可摆的数字只有 1、2、4、7,为保证不重、不漏地写出它们摆出的所有的以 1 开头的四位数,可以按从小到大(或从大到小)的顺序来写,它们是 1247、1274、1427、1472、1724、1742 共六个,计算它们的和为 8886.再用火柴棍摆出这个等式,要把它们用火柴棍摆出来,关键是把 8886 用 1、2、4、7 表示,观察发现:8886=4444×2-2用火柴棍摆出所有以 1 开头的四位数是:求它们和的等式可以表示为:例4移动一根或两根火柴,使得下列算式成为一个等式(1)(2)(3)分析:(1)把 ll44 千位上的 l 移动到 2 前,把“+”变为“-”:12 ⨯ 2 +1144 ⇒12⨯12 = 144 (2)把 444 中间的 4 变“+”,最后的 4 前的“-”变为“-”: 444 - 4 - 4 ⇒ 4 + 4 - 4 = 4 (3)把 l4 十位上的 l 移到 24 前的“-”号上,把“-”变“-”,把 24 的 2 变为 4.12 ⨯ 4 - 14 - 24 ⇒ 12 ⨯ 4 - 4 = 44移动两根火柴,使下面的算式变成等式.分析: ①题中,12×4=48,而最后一个数是 24,通过移一根火柴,可改成 44,观察算式知,可将 14 中的 1 移到 24 前面的“-”号上,变为等式.②题中,有一个四位数,一个五位数,其他是三位数,所以,可将所有数都化为不超过三位,做如 下的移动,即将 1112×2+11144 变为 112×2+1+114.这时,112×2+1+114=339,而 339—222=117, 所以只要把 117 前面的“+”变为“=”号即可.①题的答案是:l 、2、3、4、5、6、7、8、9、0 这十个数字,是我们在学数学的时候,在生活中,随时都可以看到的.我们也管它们叫“阿拉伯数字”.如果问起你为什么它要叫这个名字,你也许会毫不犹豫地说: “当然是因为它们是阿拉伯人发明的啦!”不过,你们知道吗,“阿拉伯数字”其实并不是阿拉伯人发明的,这是一个历史的误会.其实,这些数字,在公元前三世纪的时候就已经被印度人确定和应用了.阿拉伯人对数学研究作出了很多的历史贡献,而在当时,欧洲还正处在中世纪的时代,宗教思想占绝对的统治地位,科学研究得不到发展.不过欧洲的一些学者们还是通过从阿拉伯传来的书籍中得到了科学知识.通过这些书籍,欧洲人熟悉了几乎整个古代世界的数学创造,但在一开始的时候,却把它们全都当成了阿拉伯数学的成就.他们把经过阿拉伯人改进的印度数字,也当成是阿拉伯数学家的发明, 所以给它起了个名字,叫“阿拉伯数字”.后来,人们知道弄错了,但是“阿拉伯数字”这个名字已经叫开,而且成了习惯,改不过来了.所以,我们现在还是叫它“阿拉伯数字”.例5例6小聪明在玩火柴棒的游戏中过关斩将,就剩最后一关了, 但是他也只剩 6根火柴了,只有用 6 根火柴棒摆出最大的 3 位数才能顺利过关,快点帮帮他吧!分析:用火柴摆出的数字高度可以是一根火柴,也可以是两根火柴.要分别看看这两种数字每个要用多 少根火柴,再算一算哪 3 个数字结合正好用 6 根火柴,最后再比较处最大的数和最小的数.如果摆出的数字高度是 1 根火柴,那么用 6 根火柴可分别组成 1,2,7;1,4,7;7,7,7 以及 1, 1,0 四组数字,用这 4 组数字一共可组成 15 个 3 位数,其中最大的是 777,最小的是101. 如果摆出的数字高度是 2 根火柴,那么 6 根火柴只能摆出一个 111. 所以用 6 根火柴摆出的 3 位数中,最大的是 777. 摆法为:[拓展]那么 6 根火柴棒能摆出的最小的三位数是多少? 分析:通过例题的分析,可知最小的三位数是 101,即多退少补每次上体育课之前,老师总是先让学生们绕操场跑 5 圈来热身.一次刚跑到 4 圈时,学生们已经是气喘吁吁,步履艰难了.他们注意到,老师正在和别人说话,似乎没有注意到他们.于是,一个大胆的学生跑到操场边,向老师报告说:“老师,我们已经跑了 7 圈了,怎么还不让停啊?”“是吗?”老师看上去很吃惊,“全体向后转!把多跑的那两圈退回来!”刚才我们在“想挑战吗?”已经学习了数字高度是 2 根火柴的摆法,如下所示:同学们肯定想出来了,许多电子显示屏幕上的数字就是这样的.我们当然还可以搭出更高的数字, 但是没有什么意义,所以我们只考虑这两种高度的火柴棍游戏.例7例8东东用火柴棒摆出下面的算式,西西说:“我可以用 4 根火柴捧表示一些加减运算符号,然后把这 4 根火柴棒放到数字 l 至 9 中间去,使最终的运算结果等于l00.”东东觉得很不可思议,你觉得可能吗?分析:用 4 根火柴棒可以组成 2 个“+”号或 4 个“-”号,或者 l 个“+”号和 2 个“-”号.再看结果 100,它可能是和或者是差.经过分析和推理,只能用 4 根火柴棒组成 l 个“+”号和 2 个“-” 号,才能使结果等于 100. 123-45-67+89=100[拓展](2008“数学解题能力展示"读者评选活动三年级组初赛试题)用火柴棍拼成的数字和符号如下图所示,那么用火柴棍拼成一个减法等式最少要用根火柴.分析:“1”所用的火柴棍是 2 根,数目最少,所以要尽可能多用,即 1-1=0 和 2-1=1,最少共用 5+1 +2+2+2=12(根) 火柴棍.下面是由火柴棍组成的十个数字和三个运算符号:(1)移动一根火柴,使下列公元年份相等. ①②(2)添上一根火柴,使下列等式成立. ①②③分析:(1)移动一根火柴,使左右两个公元年份数相等,就是在一个数字上拿走一根火柴,放在另一 个数字上.①移动原式中等号左边“8”里的一根,使 8 变为 9;放在等号右边的“5”里,使 5 变成 9,就是 1996=1996例9也可以移动原式中等号左边“8”里的一根,使 8 变为6;放在等号右边的“5”里,使 5 变成6,就是1966=1966②移动原式中等号右边“6”里的一根,使 6 变成5;放在等号左边靠近 5 的“9”里,使 9 变为8,就是1985=1985(2)添上一根火柴,就是在原式中的某一个数字上加上一根火柴.①将原式中的“6”上加一根火柴,使 6 变成 8,就是 18+4=22②将原式中的“3”上加一根火柴,使 3 变为 9,就是 19-7=12③将原式中的“15”里的“5”上加一根火柴,使 15 变为 19,就是19×5=95下图方格里的数字,都是用火柴棒组成的,请你移动其中的一根火柴,使每一横行和竖行里的数字相加和都相等.分析:3 个横行的数字和分别是 10,16,10,3 个竖行的数字和分别是 8、l8、10,相等的和是 l0,那么,肯定要将第 2 行的前两个数字进行调整.这一讲,我们用火柴棒探索了变化无穷的数字世界,了解数字世界,希望同学们在有趣的数字世界和数学游戏中变得更聪明!在我们以后的学习中,还会学习取火柴棍的问题,让我们一起期待吧!例10专题展望1.移动 1 根火柴,使下面各题的等式成立.(1)(2)分析:(1)(2)2.在下面由火柴棍摆成的算式中,添上或去掉一根火柴棍,使算式成立.分析:3.移动两根火柴棒,使下面各等式成立.(1)(2)分析:(1)将“+”变为“-”,移一根到“-”号,变为“-”号,将“-”号中移一根到第三个“ll” 处,变为“lll”,因此,得到:(2)把第一个“22”变为“44”,得到:44-22=224.移动一根火柴,使题中不相等的公元年份变成相等的公元年份,并用火柴摆出.(1)(2)分析:(1)把1993中的3变成5(2)将1387中“8”去掉一根变成9,“3”增加一根变成9练习七5.移动一根火柴,使下面每个等式成立(1)(2)分析:(1)31+35=66(2)26×4=104推理小故事劫匪的圈套惯犯库克和比尔劫了一辆运钞车.就在两人庆幸得手的时候,身后响起了一阵警笛声,得到指示的警车追了上来.摩托车没油了,两人只得弃车逃入农田.路过一座农舍的时候,库克发现农舍的主人大概种田去了,里面空无一人,农舍外有口很深的古井,便立刻想到了一个办法.他对比尔说:“我们如果一直这样跑,终归是要被抓住的,不如躲到农舍里去.我假装是农舍的主人,一会儿警察来的时候,你就用防水袋套住钱,含上根吸管,躲到水里去.要是我不幸被抓住,钱就全部归你.”比尔有点犹豫:“这样行不行呢?警察恐怕没有那么好愚弄吧,再说井水那么深……”库克打断了他的话:“蠢货,难道你想被抓住吗?井水深怕什么,我会给你一根很长的管子的.”听到远处隐约响起来的警笛声,比尔只好同意了.库克把一根长 5 米、口径不足 2 厘米的管子交给比尔,帮他捆扎好钱放入井里,自己却没有像他说的那样装扮成农舍的主人,而是到田地里躲藏起来.半小时后,警察开始搜查这座村庄.虽然库克隐蔽得非常好,可是警犬还是凭借灵敏的嗅觉迅速找到了他.当警察把比尔打捞上来的时候,却发现他早就溺死了.警官询问了比尔躲到井下的前后经过,对库克说道:“你真是心狠手辣啊,为了独吞钱财而杀了他!现在,你除了抢劫,又添了一项故意杀人的罪名!”你知道警官为什么这么说吗?比尔好好地呆在井底,为什么说是库克杀了他呢?答案见第一讲.第六讲“图像从不闪动”答案:附近有直升机干扰,电视定会出现“雪花”.寺内既说自己在房间看电视时有直升机在公寓上空盘旋,又说电视机的图像从没有过闪动的情况.这是不可能的.即使是新电视,由于电波干扰,图像照样会紊乱的.同学们,你想到了吗?。
小学三年级奥数精品讲义1-34讲全

小学三年级奥数精品讲义目录第一讲加减法的巧算(一)第二讲加减法的巧算(二)第三讲乘法的巧算第四讲配对求和第五讲找简单的数列规律第六讲图形的排列规律第七讲数图形第八讲分类枚举第九讲填符号组算式第十讲填数游戏第十一讲算式谜(一)第十二讲算式谜(二)第十三讲火柴棒游戏(一)第十四讲火柴棒游戏(二)第十五讲从数量的变化中找规律第十六讲数阵中的规律第十七讲时间与日期第十八讲推理第十九讲循环第二十讲最大和最小第二十一讲最短路线第二十二讲图形的分与合第二十三讲格点与面积第二十四讲一笔画第二十五讲移多补少与求平均数第二十六讲上楼梯与植树第二十七讲简单的倍数问题第二十八讲年龄问题第二十九讲鸡兔同笼问题第三十讲盈亏问题第三十一讲还原问题第三十二讲周长的计算第三十三讲等量代换第三十四讲一题多解第三十五讲总复习第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小熊不禁问:“白兔弟弟,你这么快就算出了答案,有什么决窍吗?”小白兔说:“比如2号选手是93、95、98、96、88、89、87、91、93、91,去掉最高分98,去掉最低分87,剩下的都接近90为基准数,超过90的表示成90+‘零头数’,不足90的表示成90-‘零头数’。
于是(93+95+96+88+89+91+93+91)÷8=90+(3+5+6―2―1+1+3+1)÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做,果然既快又对。
小学三年级奥数精品讲义1-34讲全

小学三年级奥数精品讲义目录第一讲加减法的巧算(一)第二讲加减法的巧算(二)第三讲乘法的巧算第四讲配对求和第五讲找简单的数列规律第六讲图形的排列规律第七讲数图形第八讲分类枚举第九讲填符号组算式第十讲填数游戏第十一讲算式谜(一)第十二讲算式谜(二)第十三讲火柴棒游戏(一)第十四讲火柴棒游戏(二)第十五讲从数量的变化中找规律第十六讲数阵中的规律第十七讲时间与日期第十八讲推理第十九讲循环第二十讲最大和最小第二十一讲最短路线第二十二讲图形的分与合第二十三讲格点与面积第二十四讲一笔画第二十五讲移多补少与求平均数第二十六讲上楼梯与植树第二十七讲简单的倍数问题第二十八讲年龄问题第二十九讲鸡兔同笼问题第三十讲盈亏问题第三十一讲还原问题第三十二讲周长的计算第三十三讲等量代换第三十四讲一题多解第三十五讲总复习第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小熊不禁问:“白兔弟弟,你这么快就算出了答案,有什么决窍吗?”小白兔说:“比如2号选手是93、95、98、96、88、89、87、91、93、91,去掉最高分98,去掉最低分87,剩下的都接近90为基准数,超过90的表示成90+‘零头数’,不足90的表示成90-‘零头数’。
于是(93+95+96+88+89+91+93+91)÷8=90+(3+5+6―2―1+1+3+1)÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做,果然既快又对。
小学奥数 火柴棒游戏.解析版

火柴游戏大体分为两种:一种是摆图形和变换图形,一种是变换算式。
本讲主要学习:1.通过添加、移动火柴棒来变换图形;2.学习简单的火柴棒算式的变化,从而培养孩子的动手和观察能力.一、摆图形和变换图形方法:巧妙运用公共边。
(1) 公共边省火柴棒 (2) 独立图形费火柴棒二、火柴棒算式方法:(1) 计算等式左右两端大小 (2) 比较大小(3) 通过观察运算符号和数字之间的特点来移动火柴棒三、数字与火柴棒(1)0-9数字的摆法: 摆法一、摆法二、(2)符号(3)数字之间的转换1. 添加1根火柴,可以得到:或,,或2. 去掉1根火柴,可以得到:或或 ,3. 移动1根火柴,可以得到:或,例题精讲知识点拨8-10.火柴棒游戏模块一、摆图形和变换图形【例 1】先用14根火柴棒搭成下图的房子,再移动其中2根火柴棒,把这座房子改成面向左。
【考点】火柴棒游戏【难度】1星【题型】解答【解析】根据房子形状修改后如图【答案】【例 2】甲水池有水2600立方米,下面是一条“小鱼”,1)请你移动两根火柴棒使“小鱼”边成头朝上。
2)请你移动三根火柴棒,使“小鱼”变成头朝右。
【考点】火柴棒游戏【难度】1星【题型】解答【解析】(1)鱼头朝上需要将左端的两根移动到右上端如下图:(2)将图(1)中的虚线移动到图(2)中的实线,如下图:【答案】(1), (2)【例 3】先用火柴棒摆出下面3个三角形,然后移动3根火柴棒,使它变成5个三角形。
【考点】火柴棒游戏【难度】1星【题型】解答【解析】将底下的三角形平移到上面两个三角形的顶端得到下图这个图形有四个小三角形,但是整体也是一个三角形,共5个三角形【答案】【巩固】用16根火柴棒摆成4个正方形,移动4根火柴后,还可以摆成4个正方形,应该怎样摆法?摆成5个正方形,应该怎样摆?【考点】火柴棒游戏【难度】1星【题型】解答【解析】答案如下,答案不唯一【答案】答案不唯一【例 4】用16根火柴棒摆成4个正方形,减少4根火柴后,还可以摆成4个大小一样的正方形,应该怎样摆法?摆成5个正方形,应该怎样摆?【考点】火柴棒游戏【难度】2星【题型】解答【解析】可以摆成田子形这里面有四个大小一样的正方形和一个大的正方形,所以第一问和第二问的情况都能满足【答案】【例 5】用3根同样长的火柴棒可以摆出1个正三角形,请用6根火柴摆出8个正三角形,怎么摆呢?试一试【考点】火柴棒游戏【难度】2星【题型】解答【解析】摆放方法如下,摆两个正三角形,共有小三角形6个,加上两个大的三角形,所以一共是8个正三角形【答案】【例 6】下面是用12根火柴棒摆成的5个正方形,①拿去2根火柴棒,将原图变成两个正方形;②移动3根火柴棒,使原图变成3个相同正方形?【考点】火柴棒游戏【难度】2星【题型】解答【解析】①拿去两根使图形变成两根正方形如下图②摆成品字形【答案】①②【例 7】用8根火柴棒可以摆一个正方形,现在添2根,即用10根火柴棒能摆出与这个正方形同样大小的图形吗?【考点】火柴棒游戏【难度】2星【题型】解答【解析】8根火柴摆一个正方形,每边必须是两根,它可以分成四个小正方形如下图:因此只要用10根火柴摆出有四个同样大小的正方形即可,下面四个图形都符合题意【答案】下面四个图形都符合题意,答案不唯一【例 8】下面是用16根火柴棒摆成的5个正方形,请你移动2根火柴棒,变成4个相同的正方形.【考点】火柴棒游戏【难度】2星【题型】解答【解析】根据题意引动如下:【答案】【例 9】在右下图中移动4根火柴棒,使它变成3个三角形,并且这3个三角形的面积之和与原来的六边形面积相同。
小学三年级奥数讲义之精讲精练第14讲 数学趣味题含答案

第14讲数学趣味题一、知识要点在日常生活中,常有一些妙趣横生、带有智力测试性质的问题,如:3个小朋友同时唱一首歌要3分钟,100个小朋友同时唱这首歌要几分钟?类似这样的问题一般不需要较复杂的计算,也不能用常规方法来解决,而常常需要用小朋友的灵感、技巧和机智获得答案。
对于趣味问题,首先要读懂题意,然后要经过充分的分析和思考,运用基础知识以及自己的聪明才智巧妙地解决。
二、精讲精练【例题1】如果每人步行的速度相同,2个人一起从学校到儿童乐园要3小时,那么6个人一起从学校到儿童乐园要多少小时?练习1:1、3个人同时唱3首歌用9分钟,9个人同时唱同样的3首歌用几分钟?2、5只猫5天能捉5只老鼠,照这样计算,要在100天里捉100只老鼠要多少只猫?3、6个人从甲地到乙地用4小时,如果每人的步行速度相同,那么3个人从甲地到乙地要用几小时?【例题2】一条毛毛早由幼虫长成成虫,每天长大一倍,30天能长到20厘米。
问长到5厘米时要用多少天?练习2:1.有一个池塘中的睡莲,每天长大一倍,经过10天可以把整个池塘全部遮住。
问睡莲要遮住半个池塘需要多少天?2.一条小青虫由幼虫长成成虫,每天长大一倍,20天能长到36厘米。
问长到9厘米时要用几天?3.一条毛毛虫由幼虫长成成虫,每天长大一倍,15天能长到4厘米。
问要长到32厘米共要多少天?【例题3】小猫要把15条鱼分成数量不相等的4堆,问最多的一堆中最多可放几条鱼?练习3:1.小明要把20颗珠子分成数量不等的5堆,问最多的一堆中最多可放几颗珠子?2.老师为共有18人的舞蹈队设计队形,要求分成人数不等的5队,问最多的一队最多可排几人?3.兔妈妈拿来1盘萝卜共25个,分给4只小兔,要使每只小兔分得的个数都不同。
问分得最多的一只小兔至多分得几个?【例题4】把100只桃子分装在7个篮子里,要求每个篮子里装的桃子的只数都带有6字。
想一想,该怎样分?练习4:1.把100个鸡蛋分装在6个盒里,要求每个盒里装的鸡蛋的数目都带有6字,想想看,应该怎样分?2.有人认为8是个吉祥数字,他们得到的东西的数量都要含有数字8。
三年级奥数详解答案 第十四讲 火柴棍游戏2

第十四讲火柴棍游戏(二)这一讲将继续上一讲的内容,请看下面的例题。
例1在下面由火柴摆成的算式中,移动两根火柴使等式成立。
分析①题中,等号左边有一个四位数1112,而其他的数都是两位数,所以,基本想法是把这个四位数变成两位数,或把它变成三位数,再把其他一个数变成三位数.观察算式注意到,等号右边是42,而等号左边第一个数是41,如果能把“-1112+ 11”的计算结果凑成“+1”,就可以了,可以这样变:“+112—111”,就满足了算式。
②题中,等号左边有一个减数是1222,而其他数都是三位数.所以应考虑把1222中的1移走.观察算式,可考虑把1移到它前面的“—”号上,则算式变成:222+222+222+711=177显然,如果把711中的7变为1,而添在177上,变为777,则等式成立。
解:①题的答案是:②题的答案是:例2在下面的算式中,移动两根火柴,使算式变成等式。
①②分析①题中,12× 4=48,而最后一个数是24,通过移一根火柴,可改成44,观察算式知,可将14中的1移到24前面的“—”号上,变为等式。
②题中,有一个四位数,一个五位数,其他是三位数,所以,可将所有数都化为不超过三位,做如下的移动,即将1112×2+11144变为112×2+1+114.这时,112×2+1+114=339,而 339—222=117,所以只要把 117前面的“+”变为“=”号即可。
解:①题的答案是:②题的答案是:补充说明:在解决由添加、去掉或移动火柴,从而使算式成立的问题时,要注意以下几点:①由火柴棍摆成的数字只有1、2、4、7这四个数。
②在把火柴添、去、移时,目标经常是使等号两边各数的位数一样多,从而使等式成立。
③要有较强的运算能力和全面观察、分析问题的能力,才能顺利地解决问题。
火柴棍可以摆出许多图形,它不仅限于生活中的物品,还能摆出一些几何图形,如三角形、四边形、多边形等等,而且,通过移动几根火柴棍,使它们之间出现一些有趣的转化.例3移动四根火柴棍,把图14—1中的斧子变为三个全等的三角形。
三年级下册数学试题-奥数专题讲练:第14讲 火柴棍游戏精英篇(解析版)全国通用
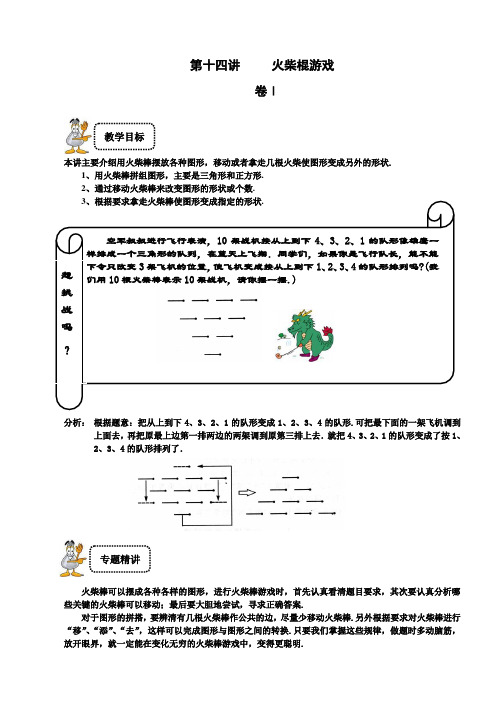
第十四讲火柴棍游戏卷Ⅰ本讲主要介绍用火柴棒摆放各种图形,移动或者拿走几根火柴使图形变成另外的形状.1、用火柴棒拼组图形,主要是三角形和正方形.2、通过移动火柴棒来改变图形的形状或个数.3、根据要求拿走火柴棒使图形变成指定的形状.空军叔叔进行飞行表演,10架战机按从上到下4、3、2、1的队形像雄鹰一样排成一个三角形的队列,在蓝天上飞翔.同学们,如果你是飞行队长,能不能下令只改变3架飞机的位置,使飞机变成按从上到下1、2、3、4的队形排列吗?(我们用10根火柴棒表示10架战机,请你摆一摆.)分析:根据题意:把从上到下4、3、2、1的队形变成1、2、3、4的队形.可把最下面的一架飞机调到上面去,再把原最上边第一排两边的两架调到原第三排上去.就把4、3、2、1的队形变成了按1、2、3、4的队形排列了.火柴棒可以摆成各种各样的图形,进行火柴棒游戏时,首先认真看清题目要求,其次要认真分析哪些关键的火柴棒可以移动;最后要大胆地尝试,寻求正确答案.对于图形的拼搭,要辨清有几根火柴棒作公共的边,尽量少移动火柴棒.另外根据要求对火柴棒进行“移”、“添”、“去”,这样可以完成图形与图形之间的转换.只要我们掌握这些规律,做题时多动脑筋,教学目标想挑战吗?专题精讲(一)摆图形游戏【例1】(★★★奥数网题库)用十六根火柴棒可以摆出四个大小相同的正方形,如下图.试问:如果用十五根、十四根、十三根、十二根火柴棒,能否摆成四个大小相同的正方形?分析:用十六根火柴棍可以摆出四个大小相同的正方形,火柴棍减少1根,如果还是摆成四个大小相同的正方形,那么就要有一根火柴棒公用.有15根火柴棒的时候有一根火柴棒公用,有14根火柴棒的时候有两根火柴棒公用,那么每减少一根就多出一根火柴棒公用,具体操作如下:[前铺] 摆一个正方形需要四根火柴棒.(1) 摆两个正方形,最少需用( 7 )根小棒.(2) 摆三个正方形,最少需用( 8 )根小棒.(3) 用6根小棒,最多能摆( 5 )个正方形.【例2】(★★★奥数网题库)用三根同样长的火柴可以摆出一个正三角形.①请用九根火柴摆出五个三角形.②请用六根火柴摆出八个正三角形.分析:(1)用九根火柴棒可摆出三个“正立”的小三角形,同时中间还出现了一个“倒立”的小三角形,最外面的六根火柴棒又形成了一个大三角形.所以这九根火柴棒共摆了五个三角形.(2)根据题意,用三根火柴可摆一个正三角形,如果用六根火柴要想摆出八个正三角形,那么其中一根火柴应是几个正三角形的边才行.先用三根同样长的火柴摆成一个正三角形,再用剩下的三根同样长的火柴把已摆好的正三角形的三条边交叉等分成3份.用六根同样长的火柴摆出八个正三角形的摆法如图:(1)(2)[拓展] 用三根同样长的火柴可以摆出一个正三角形.请用六根火柴摆出六个正三角形.卷Ⅱ(二)移动火柴,变换图形游戏【例3】(★★★奥数网题库)在下图中移动4根火柴棍,使它变成3个三角形,并且这3个三角形的面积之和与原来的六边形面积相同.分析:原图中有6个三角形,变化后剩下3个三角形,这3个三角形与原来的6个三角形的面积相同,必然有一个三角形的面积要增大.如右上图所示,移动虚线表示的4根火柴.图中下面的大三角形面积等于小三角形面积的4倍.具体操作如下图:[拓展1] 如下图用12根火柴摆成的灯,移动三根火柴,变为五个完全一样的三角形.分析:如右上图,把虚线部分移到空缺的地方,便可得到五个完全一样的三角形.[拓展2] 下图是用小棒摆成的4个小三角形和1个大三角形,请移动4根小棒,使原来大三角形的方向上下颠倒过来.分析:尽量利用原来的小棒所组成的形状,以便减少小棒移动的数量,具体操作如下:【例4】(★★★★奥数网题库)用24根火柴摆成(摆时火柴的首尾紧挨)的“回”字形方环,见下图.(1)请移动其中4根火柴,使这两个大小不等的正方形变成两个大小相等的正方形,应该怎么移?(2)求移动后所得图形的周长(已知每根火柴长4厘米).分析:由题目可见,要用24根火柴摆出两个大小相同的正方形,每个正方形可由12根火柴构成.这样,每个正方形的边长应由三根火柴棍组成,这样的两个正方形可以有下图的四种摆法.考虑到题目要求移四根火柴,若移成图中(1)(2)(4)的形状,移动的火柴都要超过四根,而图(3)则是由上图通过移动四根火柴得到的.图3符合条件:(2)移动后所得图形的周长:方法1:4×16=64(厘米)方法2:4×4×4=64(厘米)方法3:4×(3×4+4)=64(厘米)方法4:4×3×4+4×4=64(厘米)【例5】(★★★★奥数网题库)下图是用24根火柴棍摆出的两个正方形.(1)请你移动4根,把它变成三个正方形;(2)再移动8根,把(1)中所得图形变成九个完全相同的正方形;(3)在(2)中所得图形上拿走8根火柴,使它变成五个完全相同的正方形.分析:(1)具体操作如下:方法一:方法二:(2)变成一个边长是3根小火柴棒的大正方形,里面就包含了9个小正方形.(3)然后拿走四个角上的8根,就变成了5个小正方形,具体操作如下:[拓展] 如右图,用12根火柴组成6个正三角形,请按下列要求移动:(1)移动2根,变成5个正三角形.(2)再移动2根,变成4个正三角形.(3)再移动2根,变成3个正三角形.(4)再移动4根,变成2个正三角形.分析:具体操作如下:(1)移动2根: (2)再移动2根(移动4根):(3)再移动2根(移动6根): (4)再移动4根(移动10根):【例6】(★★★★奥数网题库)下图是由十一根火柴摆成的希腊式教堂,移动四根火柴,把它变为十五个正方形.分析:首先注意到题目中并没有要求这十五个正方形大小相同,而由条件,要由十一根火柴摆成十五个正方形,可以肯定这些正方形有大有小,且有很多“边”要重复使用,如果只把“房顶”的两根火柴移下来,如图1,则只能得到11个正方形(8个小的,3个大的).且只移动了两根火柴,不满足题目要求,要想增加正方形的个数,正方形应该变小,数一下图2中正方形的个数,有9个小正方形,4个由四个小正方形构成的正方形和一个大正方形,共14个正方形.那么它再加上一个正方形就满足题目要求了,而事实上,只要移为图3,恰好满足题目的要求.[拓展1]用4根火柴摆成了小酒杯,杯中有一个硬币,现在要移动2根火柴棒,使酒杯倒转过来,并且使硬币在杯外,你能做到吗?分析:具体操作如下:[拓展2] 同上题,请你移动两根火柴,变成含有11个正方形的图形.分析:移动房顶上的两根火柴棒,具体操作如下,一共有11个正方形.(三)去掉火柴,变换图形游戏【例7】(★★★★奥数网题库)用24根火柴棒组成下面的图形.根据要求拿掉火柴棒变成新的图形.(1)拿掉4根火柴,变成5个正方形;(2)拿掉8根火柴,变成5个正方形;(3)拿掉8根火柴,变成3个正方形;(4)拿掉6根火柴.使它只留下3个四边形;(5)拿掉8根火柴,使它只留下2个正方形.分析:原图用了24根火柴棒拼成了大小不同的14个正方形.要拿掉几根火柴,使正方形的个数变少,实际就要考虑“拆掉”部分正方形.(1)拿掉4根火柴,变成5个正方形; (2)拿掉8根火柴,变成5个正方形;(3)拿掉8根火柴,变成3个正方形;(4)拿掉6根火柴,剩下3个大小各异的四边形;(5)拿掉8根火柴,使它留下一大一小两个正方形.[前铺] 用12根火柴摆成下图,分别取走3根、4根、5根,使它成为3个相同的三角形,应该怎样取?分析:(1)如果取出3根,那么12根火柴还剩9根,用9根火柴摆成3个相同的三角形,9÷3=3,必须是3根火柴摆1个三角形,也就是说,它们是没有公共边的.(如图1) (2)如果取出4根,那么12根火柴还剩8根,用8根火柴摆成3个相同的三角形,8÷3=2……2,必定有1根火柴要充当2个三角形的公共边,也就是说,摆出的3个相同三角形必定有2个三角形连在一起.(如图2)(3)同理取出5根,还剩7根火柴,7--3=2……1,必定有2根火柴要充当三角形的公共边,也就是说摆出的3个相同三角形必定全部连在一起.(如图3)【例8】(★★★奥数网题库)在左下图中,去掉4根火柴棍,使它变成两个完全相同的图形组合.分析:左上图的面积等于七个边长为1根火柴棍的小正方形的面积之和.要达到规定要求,必须去掉一个小正方形.剩下的部分划分成两个面积等于三个小正方形面积的图形.去掉右上图中虚线所示的火柴棍即可.[巩固] 下图是由1 9根火柴棒组成的图形,请拿出其中的5根火柴棒,使剩下的火柴棒组成两个形状、大小完全相同的图形.分析:具体操作如右上图:【例9】(★★★★奥数网题库)下图中有30个正方形,问至少拿去几根火柴,才能使图中不存在任何正方形?分析:考虑要使原来的正方形都不能存在,拿掉的火柴应能尽量多的“破坏”正方形.而且我们还要整体进行观察,故至少要拿掉9根火柴,形成图形为下图:[前铺] 在左下图中去掉尽量少的火柴棍,使得图中不存在任何正方形.分析:拿掉的火柴应能尽量多的“破坏”正方形.如右上图拿掉虚线处的4根火柴即可.拿法不唯一. [拓展]下图中共有13个三角形,从中拿掉尽量少的火柴棍,使得图中没有三角形.分析:有多种拿法,但至少要拿掉6根火柴.具体操作如右上图:【例10】下图是用24根火柴棒摆成的,请按下面要求摆成新的图形.(1)拿走4根火柴棒,使它变成6个正方形.(2)拿走6根火柴棒,使它变成3个正方形.(3)拿走8根火柴棒,使它变成2个正方形.分析:(1)取走4根火柴棒后,图形变成图(a)形式.(2)取走6根火柴棒后,图形变成下面图(b)形式.(3)取走8根火柴棒后,图形变成下面图(c)形式.本讲我们主要学习了用火柴棒拼摆各种图形,在春季班的学习中我们将继续研究用火柴棒拼摆算式,包括加减乘除各种运算,让我们一起期待吧!练习十四.1、用10根火柴棒摆成向上飞的蝙蝠图形,如下图所示.试移动三根火柴,使它变成向下飞的蝙蝠图形Array分析:要把蝙蝠的头变成朝下的,需要把上面的头拆掉,摆出尾,还要在下面摆出头.由上面的分析,)可以移火柴摆成如图所示的样子.(注意:①、②、③所示的火柴,分别移至相应行的虚线位置Array.2. (1) 下面是用16根火柴棒摆成的5个正方形.请你移动2根火柴棒,变成4个正方形.(2) 下面是用15根火柴棒摆成的4个正方形.请你移动2根火柴棒,变成6个正方形(1)(2)3. (1) 如下面图(1)中所示.请你只移动3根火柴把3个三角形变成5个三角形.(2)下图是用18根火柴棒摆成的图形.请你拿掉4根火柴棒,变成5个三角形.分析:具体操作如下:(1)(2)4. 下图是由35根火柴组成的,请你移动4根火柴棒,使它变成3个正方形.分析:图中看似有三个比较接近的正方形,这三个正方形都差一根火柴棒就成拼成,但是一共只多出2根火柴棒,只能把外面和中间的正方形拼成,最小的正方形还差一根火柴棒,我们就要利用中间正方形的一根公共火柴棒来拼成,具体操作如右上图:5.用31根火柴棒摆成下图,共有20个正方形.请问:至少需要拿掉多少根火柴棒,才能使图中没有正方形.分析:至少取走6根火柴棒,才能使图中没有正方形.6. 下图是用24根火柴摆成的“◇”形图案.(1)请移动4根火柴,使这两个大小不等的“◇”形变成两个大小相等的“◇”形;(2)如果每根火柴的长是3厘米,那么移动后图形的周长是多少?分析:(1)把外面“◇”形上、下角的各两根火柴移动成如右上图的形状.(2)移动后图形的周长:方法--:3×16=48(厘米)方法二:3×8×2=48(厘米)方法三:3×3×4+3×4=48(厘米)好学不倦在一个漆黑的晚上,老鼠首领带领着小老鼠出外觅食,在一家人的厨房内,垃圾桶之中有很多剩余的饭菜,对于老鼠来说,就好像人类发现了宝藏.正当一大群老鼠在垃圾桶及附近范围大挖一顿之际,突然传来了一阵令它们肝胆俱裂的声音,那就是一只大花猫的叫声.它们震惊之余,便各自四处逃命,但大花猫绝不留情,不断穷追不舍,终于有两只小老鼠躲避不及,被大花猫捉到,正要向它们吞噬之际,突然传来一连串凶恶的狗吠声,令大花猫手足无措,狼狈逃命.大花猫走后,老鼠首领欣然从垃圾桶后面走出来说:"我早就对你们说,多学一种语言有利无害,这次我就因而救了你们一命."温馨提示:"多一门技艺,多一条路."不断学习实在是成功人士的终身承诺励志故事。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四讲火柴棍游戏卷Ⅰ【精品】本讲主要介绍用火柴棒摆放各种图形,移动或者拿走几根火柴使图形变成另外的形状.1、用火柴棒拼组图形,主要是三角形和正方形.2、通过移动火柴棒来改变图形的形状或个数.3、根据要求拿走火柴棒使图形变成指定的形状.空军叔叔进行飞行表演,10架战机按从上到下4、3、2、1的队形像雄鹰一样排成一个三角形的队列,在蓝天上飞翔.同学们,如果你是飞行队长,能不能下令只改变3架飞机的位置,使飞机变成按从上到下1、2、3、4的队形排列吗?(我们用10根火柴棒表示10架战机,请你摆一摆.)分析:根据题意:把从上到下4、3、2、1的队形变成1、2、3、4的队形.可把最下面的一架飞机调到上面去,再把原最上边第一排两边的两架调到原第三排上去.就把4、3、2、1的队形变成了按1、2、3、4的队形排列了.火柴棒可以摆成各种各样的图形,进行火柴棒游戏时,首先认真看清题目要求,其次要认真分析哪些关键的火柴棒可以移动;最后要大胆地尝试,寻求正确答案.对于图形的拼搭,要辨清有几根火柴棒作公共的边,尽量少移动火柴棒.另外根据要求对火柴棒进行“移”、“添”、“去”,这样可以完成图形与图形之间的转换.只要我们掌握这些规律,做题时多动脑筋,教学目标想挑战吗?专题精讲(一)摆图形游戏【例1】(★★★奥数网题库)用十六根火柴棒可以摆出四个大小相同的正方形,如下图.试问:如果用十五根、十四根、十三根、十二根火柴棒,能否摆成四个大小相同的正方形?分析:用十六根火柴棍可以摆出四个大小相同的正方形,火柴棍减少1根,如果还是摆成四个大小相同的正方形,那么就要有一根火柴棒公用.有15根火柴棒的时候有一根火柴棒公用,有14根火柴棒的时候有两根火柴棒公用,那么每减少一根就多出一根火柴棒公用,具体操作如下:[前铺] 摆一个正方形需要四根火柴棒.(1) 摆两个正方形,最少需用( 7 )根小棒.(2) 摆三个正方形,最少需用( 8 )根小棒.(3) 用6根小棒,最多能摆( 5 )个正方形.【例2】(★★★奥数网题库)用三根同样长的火柴可以摆出一个正三角形.①请用九根火柴摆出五个三角形.②请用六根火柴摆出八个正三角形.分析:(1)用九根火柴棒可摆出三个“正立”的小三角形,同时中间还出现了一个“倒立”的小三角形,最外面的六根火柴棒又形成了一个大三角形.所以这九根火柴棒共摆了五个三角形.(2)根据题意,用三根火柴可摆一个正三角形,如果用六根火柴要想摆出八个正三角形,那么其中一根火柴应是几个正三角形的边才行.先用三根同样长的火柴摆成一个正三角形,再用剩下的三根同样长的火柴把已摆好的正三角形的三条边交叉等分成3份.用六根同样长的火柴摆出八个正三角形的摆法如图:(1)(2)[拓展] 用三根同样长的火柴可以摆出一个正三角形.请用六根火柴摆出六个正三角形.卷Ⅱ(二)移动火柴,变换图形游戏【例3】(★★★奥数网题库)在下图中移动4根火柴棍,使它变成3个三角形,并且这3个三角形的面积之和与原来的六边形面积相同.分析:原图中有6个三角形,变化后剩下3个三角形,这3个三角形与原来的6个三角形的面积相同,必然有一个三角形的面积要增大.如右上图所示,移动虚线表示的4根火柴.图中下面的大三角形面积等于小三角形面积的4倍.具体操作如下图:[拓展1] 如下图用12根火柴摆成的灯,移动三根火柴,变为五个完全一样的三角形.分析:如右上图,把虚线部分移到空缺的地方,便可得到五个完全一样的三角形.[拓展2] 下图是用小棒摆成的4个小三角形和1个大三角形,请移动4根小棒,使原来大三角形的方向上下颠倒过来.分析:尽量利用原来的小棒所组成的形状,以便减少小棒移动的数量,具体操作如下:【例4】(★★★★奥数网题库)用24根火柴摆成(摆时火柴的首尾紧挨)的“回”字形方环,见下图.(1)请移动其中4根火柴,使这两个大小不等的正方形变成两个大小相等的正方形,应该怎么移?(2)求移动后所得图形的周长(已知每根火柴长4厘米).分析:由题目可见,要用24根火柴摆出两个大小相同的正方形,每个正方形可由12根火柴构成.这样,每个正方形的边长应由三根火柴棍组成,这样的两个正方形可以有下图的四种摆法.考虑到题目要求移四根火柴,若移成图中(1)(2)(4)的形状,移动的火柴都要超过四根,而图(3)则是由上图通过移动四根火柴得到的.图3符合条件:(2)移动后所得图形的周长:方法1:4×16=64(厘米)方法2:4×4×4=64(厘米)方法3:4×(3×4+4)=64(厘米)方法4:4×3×4+4×4=64(厘米)【例5】(★★★★奥数网题库)下图是用24根火柴棍摆出的两个正方形.(1)请你移动4根,把它变成三个正方形;(2)再移动8根,把(1)中所得图形变成九个完全相同的正方形;(3)在(2)中所得图形上拿走8根火柴,使它变成五个完全相同的正方形.分析:(1)具体操作如下:方法一:方法二:(2)变成一个边长是3根小火柴棒的大正方形,里面就包含了9个小正方形.(3)然后拿走四个角上的8根,就变成了5个小正方形,具体操作如下:[拓展] 如右图,用12根火柴组成6个正三角形,请按下列要求移动:(1)移动2根,变成5个正三角形.(2)再移动2根,变成4个正三角形.(3)再移动2根,变成3个正三角形.(4)再移动4根,变成2个正三角形.分析:具体操作如下:(1)移动2根: (2)再移动2根(移动4根):(3)再移动2根(移动6根): (4)再移动4根(移动10根):【例6】(★★★★奥数网题库)下图是由十一根火柴摆成的希腊式教堂,移动四根火柴,把它变为十五个正方形.分析:首先注意到题目中并没有要求这十五个正方形大小相同,而由条件,要由十一根火柴摆成十五个正方形,可以肯定这些正方形有大有小,且有很多“边”要重复使用,如果只把“房顶”的两根火柴移下来,如图1,则只能得到11个正方形(8个小的,3个大的).且只移动了两根火柴,不满足题目要求,要想增加正方形的个数,正方形应该变小,数一下图2中正方形的个数,有9个小正方形,4个由四个小正方形构成的正方形和一个大正方形,共14个正方形.那么它再加上一个正方形就满足题目要求了,而事实上,只要移为图3,恰好满足题目的要求.[拓展1]用4根火柴摆成了小酒杯,杯中有一个硬币,现在要移动2根火柴棒,使酒杯倒转过来,并且使硬币在杯外,你能做到吗?分析:具体操作如下:[拓展2] 同上题,请你移动两根火柴,变成含有11个正方形的图形.分析:移动房顶上的两根火柴棒,具体操作如下,一共有11个正方形.(三)去掉火柴,变换图形游戏【例7】(★★★★奥数网题库)用24根火柴棒组成下面的图形.根据要求拿掉火柴棒变成新的图形.(1)拿掉4根火柴,变成5个正方形;(2)拿掉8根火柴,变成5个正方形;(3)拿掉8根火柴,变成3个正方形;(4)拿掉6根火柴.使它只留下3个四边形;(5)拿掉8根火柴,使它只留下2个正方形.分析:原图用了24根火柴棒拼成了大小不同的14个正方形.要拿掉几根火柴,使正方形的个数变少,实际就要考虑“拆掉”部分正方形.(1)拿掉4根火柴,变成5个正方形; (2)拿掉8根火柴,变成5个正方形;(3)拿掉8根火柴,变成3个正方形;(4)拿掉6根火柴,剩下3个大小各异的四边形;(5)拿掉8根火柴,使它留下一大一小两个正方形.[前铺] 用12根火柴摆成下图,分别取走3根、4根、5根,使它成为3个相同的三角形,应该怎样取?分析:(1)如果取出3根,那么12根火柴还剩9根,用9根火柴摆成3个相同的三角形,9÷3=3,必须是3根火柴摆1个三角形,也就是说,它们是没有公共边的.(如图1) (2)如果取出4根,那么12根火柴还剩8根,用8根火柴摆成3个相同的三角形,8÷3=2……2,必定有1根火柴要充当2个三角形的公共边,也就是说,摆出的3个相同三角形必定有2个三角形连在一起.(如图2)(3)同理取出5根,还剩7根火柴,7--3=2……1,必定有2根火柴要充当三角形的公共边,也就是说摆出的3个相同三角形必定全部连在一起.(如图3)【例8】(★★★奥数网题库)在左下图中,去掉4根火柴棍,使它变成两个完全相同的图形组合.分析:左上图的面积等于七个边长为1根火柴棍的小正方形的面积之和.要达到规定要求,必须去掉一个小正方形.剩下的部分划分成两个面积等于三个小正方形面积的图形.去掉右上图中虚线所示的火柴棍即可.[巩固] 下图是由1 9根火柴棒组成的图形,请拿出其中的5根火柴棒,使剩下的火柴棒组成两个形状、大小完全相同的图形.分析:具体操作如右上图:【例9】(★★★★奥数网题库)下图中有30个正方形,问至少拿去几根火柴,才能使图中不存在任何正方形?分析:考虑要使原来的正方形都不能存在,拿掉的火柴应能尽量多的“破坏”正方形.而且我们还要整体进行观察,故至少要拿掉9根火柴,形成图形为下图:[前铺] 在左下图中去掉尽量少的火柴棍,使得图中不存在任何正方形.分析:拿掉的火柴应能尽量多的“破坏”正方形.如右上图拿掉虚线处的4根火柴即可.拿法不唯一. [拓展]下图中共有13个三角形,从中拿掉尽量少的火柴棍,使得图中没有三角形.分析:有多种拿法,但至少要拿掉6根火柴.具体操作如右上图:【例10】下图是用24根火柴棒摆成的,请按下面要求摆成新的图形.(1)拿走4根火柴棒,使它变成6个正方形.(2)拿走6根火柴棒,使它变成3个正方形.(3)拿走8根火柴棒,使它变成2个正方形.分析:(1)取走4根火柴棒后,图形变成图(a)形式.(2)取走6根火柴棒后,图形变成下面图(b)形式.(3)取走8根火柴棒后,图形变成下面图(c)形式.本讲我们主要学习了用火柴棒拼摆各种图形,在春季班的学习中我们将继续研究用火柴棒拼摆算式,包括加减乘除各种运算,让我们一起期待吧!练习十四.1、用10根火柴棒摆成向上飞的蝙蝠图形,如下图所示.试移动三根火柴,使它变成向下飞的蝙蝠图形Array分析:要把蝙蝠的头变成朝下的,需要把上面的头拆掉,摆出尾,还要在下面摆出头.由上面的分析,)可以移火柴摆成如图所示的样子.(注意:①、②、③所示的火柴,分别移至相应行的虚线位置Array.2. (1) 下面是用16根火柴棒摆成的5个正方形.请你移动2根火柴棒,变成4个正方形.(2) 下面是用15根火柴棒摆成的4个正方形.请你移动2根火柴棒,变成6个正方形(1)(2)3. (1) 如下面图(1)中所示.请你只移动3根火柴把3个三角形变成5个三角形.(2)下图是用18根火柴棒摆成的图形.请你拿掉4根火柴棒,变成5个三角形.分析:具体操作如下:(1)(2)4. 下图是由35根火柴组成的,请你移动4根火柴棒,使它变成3个正方形.分析:图中看似有三个比较接近的正方形,这三个正方形都差一根火柴棒就成拼成,但是一共只多出2根火柴棒,只能把外面和中间的正方形拼成,最小的正方形还差一根火柴棒,我们就要利用中间正方形的一根公共火柴棒来拼成,具体操作如右上图:5.用31根火柴棒摆成下图,共有20个正方形.请问:至少需要拿掉多少根火柴棒,才能使图中没有正方形.分析:至少取走6根火柴棒,才能使图中没有正方形.6. 下图是用24根火柴摆成的“◇”形图案.(1)请移动4根火柴,使这两个大小不等的“◇”形变成两个大小相等的“◇”形;(2)如果每根火柴的长是3厘米,那么移动后图形的周长是多少?分析:(1)把外面“◇”形上、下角的各两根火柴移动成如右上图的形状.(2)移动后图形的周长:方法--:3×16=48(厘米)方法二:3×8×2=48(厘米)方法三:3×3×4+3×4=48(厘米)好学不倦在一个漆黑的晚上,老鼠首领带领着小老鼠出外觅食,在一家人的厨房内,垃圾桶之中有很多剩余的饭菜,对于老鼠来说,就好像人类发现了宝藏.正当一大群老鼠在垃圾桶及附近范围大挖一顿之际,突然传来了一阵令它们肝胆俱裂的声音,那就是一只大花猫的叫声.它们震惊之余,便各自四处逃命,但大花猫绝不留情,不断穷追不舍,终于有两只小老鼠躲避不及,被大花猫捉到,正要向它们吞噬之际,突然传来一连串凶恶的狗吠声,令大花猫手足无措,狼狈逃命.大花猫走后,老鼠首领欣然从垃圾桶后面走出来说:"我早就对你们说,多学一种语言有利无害,这次我就因而救了你们一命."温馨提示:"多一门技艺,多一条路."不断学习实在是成功人士的终身承诺励志故事。
