用matlab编写拉格朗日插值算法的程序
matlab实现拉格朗日插值,多项式插值,邻近插值,线性插值 程序
题 7：一维函数插值算法课题内容：课题 7：一维函数插值算法课题内容：对函数||e-y x=，取[-5,5]之间步长为 1 的值*10作为粗值，以步长0.1 作为细值，编写程序实现插值算法：最邻近插值算法，线性插值算法和三次多项式函数插值算法，并对比插值效果。
课题要求：1、设计良好的人机交互 GUI 界面。
2、自己编写实现插值算法。
3、在同一个图形窗口显示对比最后的插值效果。
附录一、界面设计二、图像结果三、程序设计1、线性插值function pushbutton1_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f1=[];for x1=-5:0.1:5a=(x1-floor(x1));%请读者认真逐一带入推导if x1==floor(x1)f1=[f1,y(floor(x1)+6)];elsef1=[f1,y(floor(x1)+6)+a*(y(floor(x1)+7)-y(floor(x1)+6))]; endendm=-5:0.1:5plot(m,f1,'-r',x,y,'+')axis([-5 5 0 10])legend('liner插值','原函数');xlabel('X');ylabel('Y');title('liner插值与原函数的对比');grid2、多项式插值x0=-5:1:-3;y0=10*exp(-abs(x0));x=-5:0.1:-3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-3:1:-1;y0=10*exp(-abs(x0));x=-3:0.1:-1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-1:1:1;y0=10*exp(-abs(x0));x=-1:0.1:1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=1:1:3;y0=10*exp(-abs(x0));x=1:0.1:3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=3:1:5;y0=10*exp(-abs(x0));x=3:0.1:5;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');grid3、最邻近插值function pushbutton3_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f2=[];for x1=-5:0.1:5if abs(x1-floor(x1))<0.5f2=[f2,y(floor(x1)+6)];elsef2=[f2,y(floor(x1)+7)];endendm=[-5:0.1:5];f4=10*exp(-abs(m));plot(m,f2,'-r',x,y,'+')axis([-5 5 0 10])legend('nearest插值','原函数');xlabel('X');ylabel('Y');title('nearest插值与原函数的对比');grid。
2、拉格朗日插值的matlab实现
2、拉格朗日插值实例：根据下面的数据点求出其拉格朗日插值格式，并计算当x=1.6时y的值。
x 0 0.5 1.0 1.5 2.0 2.5 3.0y 0 0.4794 0.8145 0.9975 0.9093 0.5985 0.1411function[f,f0]=Language(x,y,x0)%求已知数据点的拉格朗日插值多项式%已知数据点的x坐标向量：x%已知数据点的y坐标向量：y%插值点的x坐标：x0%求得的拉格朗日插值多项式：f%x0处的插值：f0symst;if(length(x)==length(y))n=length(x);elsedisp('x和y的维数不相等！');return;end%检错f=0.0;for(i=1:n)l=y(i);for(j=1:i-1)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));%计算拉格朗日基函数end;f=f+l;%计算拉格朗日插值函数simplify(f);%化简endf0=subs(f,'t',x0);%计算插值点的函数值运行程序；x=0:0.5:3;y=[00.47940.84150.99750.90930.59850.1411];[f,f0]=Language(x,y,1.6)%计算输出的拉格朗日插值多项式%计算x=1.6时的插值输出值f0运行结果f=-799/3125*t*(t-1)*(t-3/2)*(t-2)*(t-5/2)*(t-3)+561/500*t*(t-1/2)*(t-3/2)*(t-2)*(t-5/2) *(t-3)-133/75*t*(t-1/2)*(t-1)*(t-2)*(t-5/2)*(t-3)+3031/2500*t*(t-1/2)*(t-1)*(t-3/2)*( t-5/2)*(t-3)-399/1250*t*(t-1/2)*(t-1)*(t-3/2)*(t-2)*(t-3)+1411/112500*t*(t-1/2)*(t-1) *(t-3/2)*(t-2)*(t-5/2)f0=仅供个人学习参考0.9996仅供个人学习参考。
例题matlab拉格朗日插值
例题matlab拉格朗日插值拉格朗日插值是一种常用的数值插值方法，它可以通过已知的数据点来估计未知点的函数值。
在MATLAB中，我们可以使用拉格朗日插值函数polyfit和polyval来实现。
假设我们有一组已知的数据点(x1, y1), (x2, y2), ..., (xn, yn)，我们想要通过这些数据点来估计一个未知点的函数值。
首先，我们需要使用polyfit函数来计算拉格朗日插值多项式的系数。
```matlabx = [x1, x2, ..., xn];y = [y1, y2, ..., yn];n = length(x) - 1; % 多项式的次数coefficients = polyfit(x, y, n);```polyfit函数返回的coefficients是一个包含多项式系数的向量，从高次到低次排列。
接下来，我们可以使用polyval函数来计算未知点的函数值。
```matlabunknown_x = ...; % 未知点的x坐标unknown_y = polyval(coefficients, unknown_x);```polyval函数接受一个多项式系数向量和一个x值作为输入，返回对应的函数值。
通过这种方式，我们可以使用拉格朗日插值来估计未知点的函数值。
下面我们来看一个具体的例子。
假设我们有一组已知的数据点(0, 1), (1, 2), (2, 3)，我们想要通过这些数据点来估计未知点(1.5, ?)的函数值。
```matlabx = [0, 1, 2];y = [1, 2, 3];n = length(x) - 1;coefficients = polyfit(x, y, n);unknown_x = 1.5;unknown_y = polyval(coefficients, unknown_x);```在这个例子中，我们得到的未知点的函数值为2.5。
这意味着在x坐标为1.5的位置，我们估计的函数值为2.5。
拉格朗日插值多项式matlab
实验报告：拉格朗日插值多项式实验目的与要求：熟练掌握拉格朗日插值的基本思想与插值公式实验内容：对于给定的一元函数)(x f y =的n+1个节点值(),0,1,,j j y f x j n ==。
试用Lagrange 公式求其插值多项式Lagrange 插值多项式。
数据如下： （1）求五次Lagrange 多项式5L ()x ，计算(0.596)f ,(0.99)f 的值。
（试构造Lagrange 多项式6L ()x ，计算的(1.8)f ,(6.15)f 值。
实验环境与器材：Matlab7.0实验过程（步骤）或程序代码： （1）fid=fopen('l3.txt','wt');fprintf(fid,'试用Lagrange 公式求其插值多项式Lagrange 插值多项式,求f(0.596),f(0.99)\n');A=[0.4,0.55,0.65,0.80,0.95,1.05];B=[0.41075,0.57815,0.69675,0.9,1,1.25382]; For p=1:2x=input('输入x=') a=1; for i=1:6a=a*(x-A(i));endl=0;for i=1:6b=1;for j=1:6if i~=jb=b*(A(i)-A(j));endendl=l+B(i)*a/((x-A(i))*b);endfprintf(fid,'x f(x)\n');fprintf(fid,'%2f %f\n',x,L);end（2）fid=fopen('l3.txt','wt');fprintf(fid,'试用Lagrange公式求其插值多项式Lagrange插值多项式,求f(1.8),f(6.15)\n');for p=1:2x=input('输入x=')A=[1,2,3,4,5,6,7];B=[0.368,0.135,0.050,0.018,0.007,0.002,0.001];a=1;for i=1:7a=a*(x-A(i));endl=0;for i=1:7b=1;for j=1:7if i~=jb=b*(A(i)-A(j));endendl=l+B(i)*a/((x-A(i))*b);endfprintf(fid,'x f(x)\n');fprintf(fid,'%2f %f\n',x,L);end实验结果与分析：（1）试用Lagrange公式求其插值多项式Lagrange插值多项式,求f(0.596),f(0.99) x f(x)0.596000 0.625732x f(x)0.990000 1.054230（2）试用Lagrange公式求其插值多项式Lagrange插值多项式,求f(1.8),f(6.15) x f(x)1.800000 0.165093x f(x)6.150000 0.001231成绩：教师签名：月日。
用matlab编写拉格朗日插值算法的程序
用matlab编写拉格朗日插值算法的程序10[ 标签：matlab,插值算法,程序 ]用matlab编写拉格朗日插值算法的程序，并以下面给出的函数表为数据基础，在整个插值区间上采用拉格朗日插值法计算f（0.6），写出程序源代码，输出计算结果x -2.15 -1.00 0.01 1.02 2.03 3.25y 17.03 7.24 1.05 2.03 17.06 23.05匿名回答:1 人气:6 解决时间:2011-05-24 19:58满意答案好评率：83%做了一个测试，希望有所帮助。
代码：% 用matlab编写拉格朗日插值算法的程序，并以下面给出的函数表为数据基础，% 在整个插值区间上采用拉格朗日插值法计算f（0.6），写出程序源代码，输出计算结果% x -2.15 -1.00 0.01 1.02 2.03 3.25% y 17.03 7.24 1.05 2.03 17.06 23.05function main()clc;x = [-2.15 -1.00 0.01 1.02 2.03 3.25]; y = [17.03 7.24 1.05 2.03 17.06 23.05 ]; x0 = 0.6;f = Language(x,y,x0)function f = Language(x,y,x0)%求已知数据点的拉格朗日插值多项式%已知数据点的x坐标向量: x%已知数据点的y坐标向量: y%插值点的x坐标: x0%求得的拉格朗日插值多项式或在x0处的插值: f syms t l;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等！');return; %检错endh=sym(0);for (i=1:n)l=sym(y(i));for(j=1:i-1)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));end;h=h+l;endsimplify(h);if(nargin == 3)f = subs (h,'t',x0); %计算插值点的函数值elsef=collect(h);f = vpa(f,6); %将插值多项式的系数化成6位精度的小数end结果：f =0.0201>>如何用MATLAB编写的拉格朗日插值算法的程序、二阶龙格-库塔方法的程序和SOR迭代法的程序，要能运行的∮初夏戀雨￠回答:2 人气:29 解决时间:2009-12-08 19:04满意答案好评率：100%拉格朗日function y=lagrange(x0,y0,x)n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endSOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/A(i,i); endif max(abs(x-x0))<=tolfid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n'); fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '%12.8f \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n'); fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数，求解失败！');fclose(fid);endMatlab中龙格-库塔(Runge-Kutta)方法原理及实现龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
Lagrange插值程序1
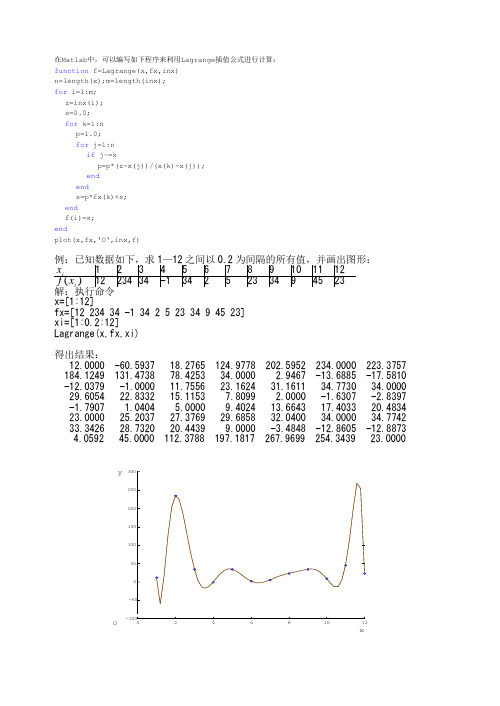
在Matlab中，可以编写如下程序来利用Lagrange插值公式进行计算：function f=Lagrange(x,fx,inx)n=length(x);m=length(inx);for i=1:m;z=inx(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x(j))/(x(k)-x(j));endends=p*fx(k)+s;endf(i)=s;endplot(x,fx,'O',inx,f)x=[1:12]fx=[12 234 34 -1 34 2 5 23 34 9 45 23]xi=[1:0.2:12]Lagrange(x,fx,xi)得出结果：12.0000 -60.5937 18.2765 124.9778 202.5952 234.0000 223.3757 184.1249 131.4738 78.4253 34.0000 2.9467 -13.6885 -17.5810 -12.0379 -1.0000 11.7556 23.1624 31.1611 34.7730 34.0000 29.6054 22.8332 15.1153 7.8099 2.0000 -1.6307 -2.8397 -1.7907 1.0404 5.0000 9.4024 13.6643 17.4033 20.4834 23.0000 25.2037 27.3769 29.6858 32.0400 34.0000 34.7742 33.3426 28.7320 20.4439 9.0000 -3.4848 -12.8605 -12.88734.0592 45.0000 112.3788 197.1817 267.9699 254.3439 23.0000拉格朗日插值法理论介绍对于给定的若n+1个点，对应于它们的次数不超过n的拉格朗日多项式只有一个。
拉格朗日插值法matlab
2．五次拉格朗日
clc
x=[-3.15-1 0.01 1.02 2.03 3.25];
y=[37.037.24 1.05 2.03 17.06 23.05];二次拉格朗日插值的误差为：R
L0=poly([x(2) x(3) x(4) x(5)
x(5)
x(5)
x(5)
x(4)
x(4) x(6)])/((x(1)-x(2))*(x(1)-x(3))*(x(1)-x(4))*(x(1)-x(5))*(x(1)-x(6)));
L1=poly([x(1) x(3) x(4) x(6)])/((x(2)-x(1))*(x(2)-x(3))*(x(2)-x(4))*(x(2)- x(5))*(x(2)-x(6))); L2=poly([x(1) x(2) x(4) x(6)])/((x(3)-x(1))*(x(3)- x(2))*(x(3)-x(4))*(x(3)-x(5))*(x(3)-x(6))); L3=poly([x(1) x(2) x(3) x(6)])/((x(4)-x(1))*(x(4)-x(2))*(x(4)-x(3))*(x(4)-x(5))*(x(4)-x(6)));
拉格朗日插值法
实验题目 拉格朗日插值法
一、实验目的及要求
利用Matlab学习拉格朗日插值法
二、研究、解答以下问题
问题：1、已知一‘⑪4；CUM辺汕，_'仏环0.爪以1字，「丄幻0. 510H26，
分别用线性插值法和二次拉格朗日插值法分别计算f(0.54)，并且说明哪个结果误差更小。
2、给出节点，「：LOU.；「到，L〔)•皿,
b = -0.6153
误差：
function [R]=wucha(M,x,X) n=length(X);
拉格朗日插值法matlab程序代码
拉格朗日插值法matlab程序代码
使用拉格朗日插值法进行数据拟合是一种常见的数值计算方法。
在matlab中，我们可以使用polyfit函数来实现拉格朗日插值法。
下面是一个简单的matlab程序代码示例：
```matlab
% 定义原始数据
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10];
% 定义插值点
xi = 2.5;
% 使用拉格朗日插值法进行拟合
p = polyfit(x, y, length(x)-1);
yi = polyval(p, xi);
% 输出结果
fprintf('插值点 %f 的函数值为 %f\n', xi, yi);
```
在这个示例中，我们首先定义了原始数据x和y，然后定义了插值点xi。
接着，我们使用polyfit函数进行拉格朗日插值法拟合，其中length(x)-1表示使用n-1次多项式进行拟合，n为原始数据的长度。
最后，我们使用polyval函数计算插值点的函数值yi，并输出结果。
需要注意的是，拉格朗日插值法虽然可以很好地拟合数据，但在插值点附近的函数值可能会出现较大误差。
因此，在实际应用中，我们需要根据具体情况选择合适的插值方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
用matlab编写拉格朗日插值算法的程序10[ 标签：matlab,插值算法,程序]用matlab编写拉格朗日插值算法的程序，并以下面给出的函数表为数据基础，在整个插值区间上采用拉格朗日插值法计算f（0.6），写出程序源代码，输出计算结果x -2.15 -1.00 0.01 1.02 2.03 3.25y 17.03 7.24 1.05 2.03 17.06 23.05 匿名回答:1 人气:6 解决时间:2011-05-24 19:58满意答案好评率：83%做了一个测试，希望有所帮助。
代码：% 用matlab编写拉格朗日插值算法的程序，并以下面给出的函数表为数据基础，% 在整个插值区间上采用拉格朗日插值法计算f（0.6），写出程序源代码，输出计算结果%x -2.15 -1.00 0.01 1.02 2.03 3.25%y 17.03 7.24 1.05 2.03 17.06 23.05 function main()clc;x =[-2.15 -1.00 0.01 1.02 2.03 3.25]; y = [17.03 7.24 1.05 2.03 17.06 23.05 ]; x0 = 0.6;f = Language(x,y,x0)function f = Language(x,y,x0)%求已知数据点的拉格朗日插值多项式%已知数据点的x坐标向量: x%已知数据点的y坐标向量: y%插值点的x坐标: x0%求得的拉格朗日插值多项式或在x0处的插值: fsyms t l;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等！');return; %检错endh=sym(0);for (i=1:n)l=sym(y(i));for(j=1:i-1)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));end;h=h+l;endsimplify(h);if(nargin == 3)f = subs (h,'t',x0); %计算插值点的函数值elsef=collect(h);f = vpa(f,6); %将插值多项式的系数化成6位精度的小数end结果：f =0.0201>>如何用MATLAB编写的拉格朗日插值算法的程序、二阶龙格-库塔方法的程序和SOR迭代法的程序，要能运行的∮初夏戀雨￠回答:2 人气:29 解决时间:2009-12-08 19:04满意答案好评率：100%拉格朗日function y=lagrange(x0,y0,x)n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endSOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/ A(i,i);endif max(abs(x-x0))<=tolfid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '%12.8f \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数，求解失败！');fclose(fid);endMatlab中龙格-库塔(Runge-Kutta)方法原理及实现龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。
该算法是构建在数学支持的基础之上的。
龙格库塔方法的理论基础来源于泰勒公式和使用斜率近似表达微分，它在积分区间多预计算出几个点的斜率，然后进行加权平均，用做下一点的依据，从而构造出了精度更高的数值积分计算方法。
如果预先求两个点的斜率就是二阶龙格库塔法，如果预先取四个点就是四阶龙格库塔法。
一阶常微分方程可以写作：y'=f(x,y),使用差分概念。
(Yn+1-Yn)/h= f(Xn,Yn)推出（近似等于，极限为Yn'）Yn+1=Yn+h*f(Xn,Yn)另外根据微分中值定理，存在0<t<1,使得Yn+1=Yn+h*f(Xn+th,Y(Xn+th))这里K＝f(Xn+th,Y(Xn+th))称为平均斜率，龙格库塔方法就是求得K的一种算法。
利用这样的原理，经过复杂的数学推导（过于繁琐省略），可以得出截断误差为O(h^5)的四阶龙格库塔公式：K1＝f(Xn,Yn);K2=f(Xn+h/2,Yn+(h/2)*K1);K3=f(Xn+h/2,Yn+(h/2)*K2);K4=f(Xn+h,Yn+h*K3);Yn+1=Yn+h*(K1+2K2+2K3+K4)*(1/6);所以，为了更好更准确地把握时间关系，应自己在理解龙格库塔原理的基础上，编写定步长的龙格库塔函数，经过学习其原理，已经完成了一维的龙格库塔函数。
仔细思考之后，发现其实如果是需要解多个微分方程组，可以想象成多个微分方程并行进行求解，时间，步长都是共同的，首先把预定的初始值给每个微分方程的第一步，然后每走一步，对多个微分方程共同求解。
想通之后发现，整个过程其实很直观，只是不停的逼近计算罢了。
编写的定步长的龙格库塔计算函数：function [x,y]=runge_kutta1(ufunc,y0,h,a,b)%参数表顺序依次是微分方程组的函数名称，初始值向量，步长，时间起点，时间终点（参数形式参考了ode45函数）n=floor((b-a)/h);%求步数x(1)=a;%时间起点y(:,1)=y0;%赋初值，可以是向量，但是要注意维数for ii=1:nx(ii+1)=x(ii)+h;k1=ufunc(x(ii),y(:,ii));k2=ufunc(x(ii)+h/2,y(:,ii)+h*k1/2);k3=ufunc(x(ii)+h/2,y(:,ii)+h*k2/2);k4=ufunc(x(ii)+h,y(:,ii)+h*k3);y(:,ii+1)=y(:,ii)+h*(k1+2*k2+2*k3+k4)/6;%按照龙格库塔方法进行数值求解end调用的子函数以及其调用语句：function dy=test_fun(x,y)dy = zeros(3,1);%初始化列向量dy(1) = y(2) * y(3);dy(2) = -y(1) + y(3);dy(3) = -0.51 * y(1) * y(2);对该微分方程组用ode45和自编的龙格库塔函数进行比较，调用如下：[T,F] = ode45(@test_fun,[0 15],[1 1 3]);subplot(121)plot(T,F)%Matlab自带的ode45函数效果title('ode45函数效果')[T1,F1]=runge_kutta1(@test_fun,[1 1 3],0.25,0,15);%测试时改变test_fun 的函数维数，别忘记改变初始值的维数subplot(122)plot(T1,F1)%自编的龙格库塔函数效果title('自编的龙格库塔函数')用Runge-Kutta方法求一阶微分方程组初值问题的matlab通用程序2007-11-11 11:43题目：用经典Runge-Kutta方法求下列一阶微分方程组的近似解：y1' = 3y1 + 2y2 −(2x2 + 1)e2x, y1(0) = 1 e2x表示exp（2*x）y2 '= 4y1 + y2 + (x2 + 2x − 4)e2x, y2(0) = 1y3 '= 2y1 − y2 − xe3x, y3(0) = 1y4 '= y1 + x2ex, y4(0) = 1y5 '= y2 − e2x, y5(0) = 1其中初值条件y0为一个五维数组，包含了这五个方程在区间[0,1]左端点0的值，并假设N ＝10为区间等分数程序：function rk(A,x,h,y0)%A为字符串函数的元胞数组%x为x轴上的各点%h为点距%y0为初值i=1;y(i,:)=y0;m=length(A);b=x(length(x));while x(i)<ba=[x(i),y(i,:)];for l=1:mk1(l)=eval(A{l},a);enda=[x(i)+h/2,y(i,:)+h/2*k1];for l=1:lk2(l)=eval(A{l},a);enda=[x(i)+h/2,y(i,:)+h/2*k2];for l=1:mk3(l)=eval(A{l},a);enda=[x(i)+h,y(i,:)+h*k3];for l=1:mk4(l)=eval(A{l},a);endy(i+1,:)=y(i,:)+h/6*(k1+2*k2+2*k3+k4);i=i+1;endy输入及结果：>> y1='3*a(2)+2*a(3)-(2*a(1)^2+1)*exp(2*a(1))'; 解释：a(1)为x，a(2)、a(3)……为y1，y2……>> y2='4*a(2)+a(3)+(a(1)^2+2*a(1)-4)*exp(2*a(1))';>> y3='2*a(2)-a(3)-a(1)*exp(3*a(1))';>> y4='a(2)+a(1)^2*exp(a(1))';>> y5='a(3)-exp(2*a(1))';>> A=[{y1},{y2},{y3},{y4},{y5}]A =[1x38 char] [1x41 char] [1x28 char] [1x21 char] 'a(3)-exp(2*a(1))'>> rk(A,0:0.1:1,0.1,ones(1,5))y =1.0000 1.0000 1.0000 1.0000 1.00001.4692 1.1649 1.1312 1.1226 0.99632.1246 1.5112 1.3309 1.3031 0.99303.0680 2.1507 1.6105 1.5679 1.00784.4629 3.2638 1.9873 1.9573 1.07186.5725 5.1403 2.4884 2.5335 1.23769.8237 8.2476 3.1587 3.3940 1.593014.9117 13.3402 4.0745 4.6925 2.283722.9721 21.6384 5.3681 6.6746 3.549735.8640 35.1212 7.2699 9.7346 5.784356.6365 57.0045 10.1818 14.5095 9.6315matlab 解微分方程组dx/dt=x+y dy/dt=x-y2010-10-6 15:56提问者：刘の鱼|浏览次数：409次推荐答案2010-10-6 20:50不知道解得对不对程序：dsolve('Dx=x+y','Dy=x-y','t')解得：x=C1*exp(2^(1/2)*t)+C2*exp(-2^(1/2)*t)y=C1*2^(1/2)*exp(2^(1/2)*t)-C2*2^(1/2)*exp(-2^(1/2)*t)-C1*exp(2^(1/2)*t)-C2* exp(-2^(1/2)*t) >> dsolve('Dx=x+y','Dy=x-y')ans =y: [1x1 sym]x: [1x1 sym]>> disp(ans.x)C1/exp(2^(1/2)*t) + C2*exp(2^(1/2)*t) - (2^(1/2)*C1)/exp(2^(1/2)*t) +2^(1/2)*C2*exp(2^(1/2)*t)>> disp(ans.y)C1/exp(2^(1/2)*t) + C2*exp(2^(1/2)*t)参考资料：.cn/pc/index.php?id=hangdao。