干涉法测微小量-实验报告

合集下载

干涉法测微小量

实验八干涉法测微小量【实验目的】1. 理解牛顿环和尖劈干涉条纹的成因与等厚干涉的含义。

2. 学习用等厚干涉法测量曲率半径和薄膜厚度。

3. 学会使用读数显微镜。

【实验仪器】牛顿环仪、劈尖【仪器介绍】1、目镜接筒2、目镜3、锁紧螺钉4、调焦手轮5、标尺6、测微鼓轮7、锁紧手轮I &接头轴9、方轴10、锁紧手轮II 11、底座12、反光镜旋轮 13、压片 14、半反镜组 15、物镜组 16、镜筒17、刻尺 18、锁紧螺钉 19、棱镜室读数显微镜是测微螺旋和带十字叉丝的显微镜的组合体，它是一种既可作长度测量又可作观察之用的光学仪器。

本实验用来测量牛顿环的直径和劈尖厚度。

中包括读数显微镜的主要结构。

目镜（ 2）（3 ）固定于任一位置，棱镜室（19）可在转，物镜（15）用丝扣拧入镜筒内，镜筒（轮（4）完成调焦。

转动测微鼓轮（6）,显微镜沿燕尾导轨作纵向移动，利用锁紧手轮I （7）,将方轴（9）固定于接头轴十字孔中。

接头轴（ 8）可在底座（11）中旋转、升降，用锁紧手轮II （10）紧固。

根据使用要求不同方轴可插入接头轴另一个十字孔中，使镜筒处水平位置。

压片（13）用来固定被测件。

旋转反光镜旋轮（ 12）调节反光镜方位。

为便于做等厚干涉实验，本仪器还配备了半反镜（14）附件。

旋转测微鼓轮可以使显微镜筒横向水平移动，通过标尺和测微鼓轮的读数可以准确确定显微镜筒的水平横向位置。

标尺读数准线和测微鼓轮组成一个螺旋测微装置，当测微鼓轮旋转一周时，标尺读数准线沿标尺移动1mm ，而测微鼓轮的圆周上刻有 100个分度，故每分度便相当于0.01mm 。

如图16-2所示读书显微镜的读数应为 29.723mm 。

（注意要估读一位）1 —标尺；2-标尺读数准线；3 -测微鼓轮；4 -测微鼓轮读数准线。

读数显微镜、钠光灯。

如图 16-1 可用锁紧螺钉 3600方向上旋16）用调焦手2I 19 10 11图 16-1H 9 L8 171615 n J3 124【实验原理】图16-21、牛顿环们设任意两级暗环的直径为D K 1和D K 2，由（16-2）式可得出:牛顿环是牛顿1675年在制作天文望远镜时偶然将一个望远镜的物镜放在平玻璃上发现的。

干涉法测微小量-实验报告

干涉法测微小量-实验报告一、实验目的1、了解干涉法的基本原理。

2、熟悉干涉法测量微小量的方法。

3、掌握利用干涉法测量薄膜厚度的实验方法。

二、实验仪器干涉仪、白光源、磨镜机、膜层样品。

三、实验原理干涉仪是一种利用光的干涉现象来测量物体形状、膜厚度等的仪器。

（1）薄膜颜色法当光通过薄膜时，由于光的反射和透射作用，产生了干涉现象。

观察到的颜色与膜厚有关系，当膜厚满足一定的条件时，可以观察到非常明显的颜色条纹。

（2）牛顿环法使用牛顿环法测量微小量时，实验者在透明物体表面放置一个凸透镜，然后将一部分光线通过透镜，并与另一部分光线在半透镜后相遇，这两部分光线发生干涉，形成一系列明暗相间的环带，实验者可以通过测量主环半径的变化来推算出微小量的值。

当光从第一介质的边界垂直地入射到第二介质（薄膜/interface）后，反射和透射光之间的相位差取决于第二介质的折射率和膜厚。

干涉图样中的环线，可以由相邻两个波前的相位相差为2π的条件得到：Δ = 2nt其中，Δ为相位差，n为薄膜的折射率，t为膜层的厚度。

四、实验步骤1、用磨镜机将膜层样品磨成两面平行、厚度均匀的薄片。

2、设置干涉仪，调节反射镜和凸透镜位置，使使干涉图案清晰。

3、通过调节厚度标准，测量出膜层厚度与颜色之间的关系。

4、分别记录膜层样品在白光源和单色光源下的干涉图案和颜色，比较两种光源下测得的膜厚度数据。

5、通过测量主环半径的变化来推算出微小量的值。

五、实验注意事项1、干涉法测微小量是一种高精度的测试方法，实验者在实验过程中要小心谨慎操作。

2、干涉法测微小量需要使用精度高的仪器，实验者要注意保养和维护干涉仪的正常使用状态。

六、实验结果及分析样品编号透射颜色透射波长n 膜层厚度（nm）样品1 黄蓝色573nm 1.44 201.29样品2 绿紫色520nm 1.48 153.48样品3 黄色579nm 1.53 124.96样品4 绿色486nm 1.49 142.962、微小量的数据样品编号主环半径（m）微小量（m）样品1 0.0051 1.27 × 10-6样品2 0.0048 1.20 × 10-6样品3 0.0043 1.08 × 10-6样品4 0.0046 1.15 × 10-6从表格数据可以看出，随着膜层厚度增加，透射颜色发生变化，且主环半径也随之发生变化。

(实验报告)干涉法测微小量(已批阅).

（实验报告）干涉法测微小量（已批阅）.
干涉法测微小量是物理、化学等多种领域常用的测量技术，可广泛应用于检测微小量的物理、化学物质的构成成分及大小等特性。

本实验以物理学仪器—干涉仪，以了解其相关原理及测量方法，详细研究并妥善操作干涉仪，实现对微小量的准确测量。

实验现场，我们装备了多种仪器设备，其中有半导体激光、光纤、波导、干涉物镜、计算机等，?表示所测实验样品的长度，?表示该物体的物理实验现象及测量结果。

所测样品经过精确调整，激光整体成像稳定、清晰。

依据干涉仪的原理，在激光学范畴，当灰度图像准确拍摄完毕，即可无缝连接计算机，把模拟航班仪及其相关接口的输入端全部接受，真实表示所测实验样品的物理偏移量。

在量测的过程中，根据实验要求，逐渐变化激光的数量，由而伴随波数的变化，随时记录模拟仪和相关输入端的变化，把变化偏移量输入计算机，由计算机将接受的数据按照原理预定义好的算法进行分析，由此根据分析结果，乘以放大系数，便可计算出微小物体的长度?。

本实验让我清楚地认识了干涉仪的基本原理，熟悉了具体的操作过程，详细了解了对微小量的测量原理，以及量测实验样品物理偏移量的处理过程，进而求出实验物体的长度?。

另外，本实验也锻炼了我们熟练操作干涉仪及相关仪器设备、形成有效数据、熟练处理数据的实际能力，积累了大量经验，掌握了实用的实验技术。

干涉法测微小量

小结与讨论：
此实验中采取了那些措施，来避免或减少误差？
1. 弦长取代牛顿环直径
2. 消除空程误差：测量时只往同一方向转动螺尺
3. 取较高级次的环进行测量
4. 记录暗纹，不记录亮纹，使观察更加精确
R =
2
+
− 2
4（n + i − i）
=
2
+
− 2
4n
结果如下
2
25
− 52
37.474 2
R5 =
=
= 794.890mm
4n
80 × 5.893 × 10−4
2
2
30
− 10
42.6432
R10 =
=
= 904.520mm
4n
80 × 5.893 × 10−4
《大学物理实验》实验报告
实验名称：
干涉法测微小量
实验时间：
2020 年 12 月 13 日星期日
实验目的：
一、研究光的干涉现象，
二、测定透镜的曲率半径；
三、学习测量微小长度
四、学习读数显微镜的使用等
实验仪器
牛顿环仪、钠灯、读数显微镜
实验原理：
两相干波光程差可表示为δ = 2nhcos i′
R、r、h 三者的关系h
只要测得 Dm 和 Dn 并数出环纹序数之差，可以利用上式求出曲率半径 R
实验内容：
本实验的主要内容为利用干涉法测平凸透镜的曲率半径
（1）使显微镜十字叉丝交点和牛顿环中心重合，并使水平方向的叉丝和标尺平行（与显微
镜移动方向平行）
（2）转动显微镜微调鼓轮，使显微镜沿一个方向移动，同时数出十字叉丝移过的暗环数，

干涉法测微小量知识分享

干涉法测微小量干涉法测微小量段心蕊 PB05000826 （九号台）一、实验目的：学习、掌握利用光的干涉原理检验光学元件表面几何特征的方法。

二、实验原理：用牛顿环测平凸透镜的曲率半径如图所示，光束1、2干涉，全部光束在一起，产生牛顿环 1、2两束光的光程差为 22λδ+=∆第m 个暗环处 ...3,2,1,0,2)12(22=+=+=∆m m m λλδ2λδ⋅=⇒m m又222)(m m R r R δ-+=， R m <<δRr mm 22=⇒δλδλδmR r R r m m m m m =⇒⎪⎪⎭⎪⎪⎬⎫=⋅=2222 我们可由λ求R 或由R 求λ。

但由于r m 不易测准，且实验者无法看出暗环真正所处的级数，故测直径D m ， λmR D m 42= λR n m D n m )(42+=+ λn D D R mn m 422-=⇒+ 其中n 可以观察出来从而可以计算透镜的曲率半径R 。

三、实验仪器：显微镜、平凸透镜、显示器、玻璃片、钠光灯。

四、实验内容 1 观察牛顿环(1)将牛顿环仪按图所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方，木架上的透镜要正对着钠光灯窗口，调节玻璃片角度，使通过显微镜目镜观察时视场最亮。

(2)调节目镜，看清目镜视场的十字叉丝后，使显微镜筒下降到接近玻璃片，然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度及显微镜，使条纹更清楚。

2 测牛顿环直径(1)使显微镜的十字叉丝交点与牛顿环中心重合，并使水平方向的叉丝与标尺平行（与显微镜筒移动方向平行）。

(2)转动显微镜测微鼓轮，使显微镜筒沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第65环相切为止。

(3)反向转动鼓轮，当竖丝与第60环相切时，记录读数显微镜上的位置读数d 60，然后继续转动鼓轮，使竖丝依次与第50、40、30、20、10环相切，顺次记下读数d 50，d 40，d 30，d 20，d 10。

干涉法测量微小量

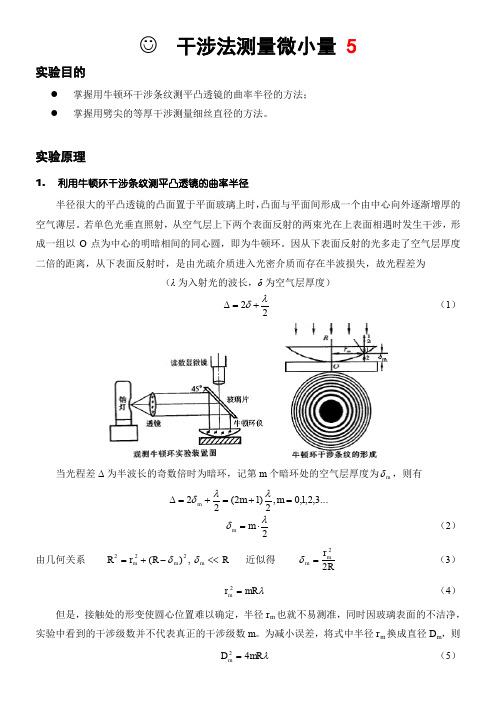
☺ 干涉法测量微小量 5实验目的● 掌握用牛顿环干涉条纹测平凸透镜的曲率半径的方法； ● 掌握用劈尖的等厚干涉测量细丝直径的方法。

实验原理1. 利用牛顿环干涉条纹测平凸透镜的曲率半径半径很大的平凸透镜的凸面置于平面玻璃上时，凸面与平面间形成一个由中心向外逐渐增厚的空气薄层。

若单色光垂直照射，从空气层上下两个表面反射的两束光在上表面相遇时发生干涉，形成一组以O 点为中心的明暗相间的同心圆，即为牛顿环。

因从下表面反射的光多走了空气层厚度二倍的距离，从下表面反射时，是由光疏介质进入光密介质而存在半波损失，故光程差为（λ为入射光的波长，δ为空气层厚度）22λδ+=∆ （1）当光程差Δ为半波长的奇数倍时为暗环，记第m 个暗环处的空气层厚度为m δ，则有...3,2,1,0,2)12(22=+=+=∆m m m λλδ2λδ⋅=m m （2）由几何关系222)(m mR r R δ-+=, R m <<δ近似得 Rr mm 22=δ（3）λmR r m =2 （4）但是，接触处的形变使圆心位置难以确定，半径r m 也就不易测准，同时因玻璃表面的不洁净，实验中看到的干涉级数并不代表真正的干涉级数m 。

为减小误差，将式中半径r m 换成直径D m ，则λmR D m 42= （5）对第m+n 个暗环有λR n m D n m )(42+=+ （6）故（7）所以，我们只需测D m 和D m+n ，就可利用上式计算曲率半径R 。

2. 劈尖的等厚干涉测细丝直径两玻璃片和细丝叠在一起如图所示，形成空气劈尖。

当用单色光垂直照射时，会产生一组明暗相间、平行于细丝的干涉条纹。

根据前面讨论知，在两玻璃片交线处，为零级暗条纹，第m 级暗纹处空气劈尖的厚度2λmd = （8）如果在细丝处呈现N 级条纹，则待测细丝直径实验室常用劈尖盒。

使用时切勿倒置木盒或将玻璃片倒出，以免细丝位置变动。

实验仪器单色光源，显微镜，牛顿环仪，待测细丝，平凸透镜。

干涉法测微小量实验报告

干涉法测微小量【实验目的】1.了解等厚干涉的应用2.掌握移测显微镜的使用方法【实验仪器】实验仪器:牛顿环法测曲率半径实验的主要仪器有:读数显微镜、Na光源、牛顿环仪用劈尖测细丝直径实验的主要仪器有:读数显微镜、Na光源、劈尖【实验原理】实验原理：实验内容一：牛顿环法测曲率半径图1如图所示，在平板玻璃面DCF上放一个曲率半径很大的平凸透镜ACB，C点为接触点，这样在ACB和DCF之间，形成一层厚度不均匀的空气薄膜，单色光从上方垂直入射到透镜上，透过透镜，近似垂直地入射于空气膜。

分别从膜的上下表面反射的两条光线来自同一条入射光线，它们满足相干条件并在膜的上表面相遇而产生干涉，干涉后的强度由相遇的两条光线的光程差决定，由图可见，二者的光程差△’等于膜厚度e的两倍，即△’ =2e此外，当光在空气膜的上表面反射时，是从光密媒质射向光疏媒质，反射光不发生相位突变，而在下表面反射时，则会发生相位突变，即在反射点处，反射光的相位与入射光的相位之间相差，与之对应的光程差为/2 ，所以相干的两条光线还具有/2的附加光程差，总的光程差为：(1)当△满足条件：(2)时，发生相长干涉，出现第K级亮纹。

而当：(3)时，发生相消干涉，出现第k级暗纹。

因为同一级条纹对应着相同的膜厚，所以干涉条纹是一组等厚度线。

可以想见，干涉条纹是一组以C点为中心的同心圆，这就是所谓的牛顿环。

如图所示，设第k级条纹的半径为rk ，对应的膜厚度为ek，则:(4)在实验中，R的大小为几米到十几米，而ek 的数量级为毫米，所以R >>ek，e k 2相对于2Rk是一个小量，可以忽略，所以上式可以简化为(5) 如果rk是第k级暗条纹的半径，由式(1)和(3)可得:(6) 代入式(5)得透镜曲率半径的计算公式(7) 对给定的装置，R为常数，暗纹半径(8) 和级数k的平方根成正比，即随着k的增大，条纹越来越细。

同理，如果rk是第k级明纹，则由式(1)和(2)得(9)代入式(5)，可以算出(10)由式(8)和(10)可见，只要测出暗纹半径（或明纹半径），数出对应的级数k，即可算出R。

干涉法测微小量实验报告

干涉法测微小量创建人:系统管理员总分:100实验目的学习掌握利用光的干涉原理检验光学元件表面集合特征的方法,用劈尖的等厚干涉测量细丝直径的方法,同时加深对光的波动性的认识。

实验仪器低频信号发生器、示波器、超声声速测定仪、频率计等实验原理1、用牛顿环测平凸透镜的曲率半径图1、牛顿环干涉条纹的形成当曲率很大的平凸透镜的凸面放在一平面玻璃上时,会产生一组以O为中心的明暗相接的同心圆环,称为牛顿环。

如图,1、2两束光的光成差22λδ+=∆,式中λ为入射光的波长,δ就是空气层厚度,空气折射率1n ≈。

如果第m 个暗环处空气厚度为m δ,则有故得到:2m m λδ⋅=2、劈尖的等厚干涉测细丝直径图2、劈尖干涉条纹的形成两片叠在一起的玻璃片,在它们的一端口夹一直径待测的细丝,于就是两片玻璃之间便形成一空气劈尖。

当用单色光垂直照射时,会产生干涉现象。

因为光程差相等的地方就是平行两玻璃片交线的直线,所以等厚干涉条纹就是一组明暗相间的、平行于交线的直线。

设入射光波长为λ,则得到第m 级暗纹处空气劈尖的的厚度2m λ⋅=d 。

由此可知,m=0时,d=0,即在两玻璃片交线处,为零级暗条纹。

如果在细丝处呈现m=N 级条纹,则待测细丝直径2λ⋅=N d 。

实验内容1、测平凸透镜的曲率半径(1)观察牛顿环1) 将牛顿环仪按图3所示放置在读数显微镜镜筒与入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。

图3、观测牛顿环实验装置图2) 调节目镜,瞧清目镜视场内的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。

(2)测牛顿环直径1) 使显微镜的十字叉丝交点与牛顿环中心重合,并使水平方向的叉丝与标尺平行(与显微镜筒移动方向平行)。

2) 转动显微镜测微鼓轮,使显微镜沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第35环相切为止。

干涉法测微小量

实验报告5数学系06级蔡园青 2007年5月25日 PB06001093 实验题目：干涉法测微小量实验目的：通过本次实验，学习、掌握利用光的干涉原理检验光学元件表面几何特征的方法，同时加深对光的波动性的认识。

实验原理：用牛顿环测平凸透镜的曲率半径当曲率半径很大的平凸透镜的凸面放在一平面玻璃上时，在透镜的凸面与平面之间形成一个从中心O 向四周逐渐增厚的空气层。

当单色光垂直照射下来时，从空气层上下两个表面反射的光束产生干涉。

等厚干涉条纹也是一组以O 点为中心的明暗相间的同心圆，称为牛顿环。

两束光的光程差为 22λδ+=∆ （1）式中λ为入射光的波长，δ是空气层厚度，空气折射率1≈n 。

当光程差Δ为半波长的奇数倍时为暗环，若第m 个暗环处的空气层厚度为m δ，则有2λδ⋅=m m （2）R m <<δ，可得 Rr mm 22=δ （3）式中r m 是第m 个暗环的半径。

由式（2）和式（3）可得λmR r m =2（4）我们将式（4）作一变换，将式中半径r m 换成直径D m ，展开整理后有λn D D R mn m 422-=+ （5）可见，如果我们测得第m 个暗环及第（m+n ）个暗环的直径D m 、D m+n ，就可由式（5）计算透镜的曲率半径R 。

实验器材：钠灯，牛顿环仪，读数显微镜。

实验内容：1．测平凸透镜的曲率半径（1）观察牛顿环 1）将牛顿环仪放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方，木架上的透镜要正对着钠光灯窗口，调节玻璃片角度，使通过显微镜目镜观察时视场最亮。

2）调节目镜，看清目镜视场的十字叉丝后，使显微镜筒下降到接近玻璃片，然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度及显微镜，使条纹更清楚。

（2）测牛顿环直径 1）使显微镜的十字叉丝交点与牛顿环中心重合，并使水平方向的叉丝与标尺平行（与显微镜筒移动方向平行）。

2）转动显微镜测微鼓轮，使显微镜筒沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第65环相切为止。

等厚干涉(干涉法测微小量)

姓名：；学号；班级；教师________；信箱号：______ 预约时间：第_____周、星期_____、第_____~ _____节；座位号：_______预习操作实验报告总分教师签字一、实验名称等厚干涉二、实验目的(1) 观察和研究等厚干涉的现象及其特点 .(2) 练习用干涉法测量透镜的曲率半径、微小厚度 ( 或直径 ).三、实验原理(基本原理概述、重要公式、简要推导过程、重要图形等；要求用自己的语言概括与总结，不可照抄教材)利用透明薄膜上、下两表面对入射光的依次反射，入射光的振幅将分解成有一定光程差的几个部分.这是一种获得相干光的重要途径，被多种干涉仪所采用若两束反射光在相遇时的光程差取决于产生反射光的薄膜厚度，则同一干涉条纹所对应的薄膜厚度相同.这就是所谓的等厚干涉。

（见右图）总的光程差为：(1)当△满足条件：(2)时，发生相长干涉，出现第K级亮纹。

而当：(3)时，发生相消干涉，出现第k级暗纹。

因为同一级条纹对应着相同的膜厚，所以干涉条纹是一组等厚度线。

可以想见，干涉条纹是一组以C点为中心的同心圆，这就是所谓的牛顿环。

如图所示，设第k级条纹的半径为rk，对应的膜厚度为ek ，则:(4)在实验中，R的大小为几米到十几米，而ek的数量级为毫米，所以R >>ek ，ek2相对于2Rk 是一个小量，可以忽略，所以上式可以简化为(5)如果rk是第k级暗条纹的半径，由式(1)和(3)可得:(6)代入式(5)得透镜曲率半径的计算公式(7)对给定的装置，R为常数，暗纹半径(8)和级数k的平方根成正比，即随着k的增大，条纹越来越细。

由于从劈尖的上下表面反射的两条光线来自同一条入射光线，它们满足相干条件并在劈尖的上表面相遇而产生干涉，干涉后的强度由相遇的两条光线的光程差决定，由图可见，二者的光程差等于劈尖厚度的两倍，即n = 0时，，即在两玻璃片交线处为零级暗条纹。

如果在细丝处呈现n = N级条纹，则待测细丝直径为(9)四、实验内容和步骤（要求用自己的语言概括与总结，不可照抄教材）1. 观察牛顿环。

干涉法测微小量(1)2022

实验题目：干涉法测微小量实验目的：用干涉法测平凸透镜曲率半径。

实验原理：1.用牛顿环测平凸透镜的曲率半径，公式及装置原理实验步骤：1.打开钠灯，等待直至颜色（波长）稳定2.放入凸透镜，把镜筒降至最低，逐渐升高直至目镜中能看到清晰牛顿环。

3.装入摄像头，从对侧65-65条纹间折返，每侧第10、20、30、40、50、60个条纹进行读数，读出6趟数据，分为3组。

4.整理实验器材。

22)12(22λδλλδm m mm =⇒+=+=∆ Rr R r R m m m m 2)(2222=⇒-+=δδ λλmR D mR r m m 422=⇒= λR n m D n m )(42+=+ λn D D R mn m 422-=+b 用逐差法可推导得：[]λ⨯⨯-+-+-=304)()()(31210240220250230260D D D D D D R代入各平均值得R ＝876.446mm 。

将上式两边求导得：λ⨯⨯⨯+++++=3043222222101020203030404050506060dD D dD D dD D dD D dD D dD D dR 两边取绝对值并改成不确定度符号：λ⨯⨯⨯+++++=3043222222101020203030404050506060D D D D D D R u D u D u D u D u D u D u写成标准差公式，为：()()()()()()λ⨯⨯⨯+++++=30432210102202023030240402505026060D D D D D D R u D u D u D u D u D u D u 故可算得U 0.68＝1.362mm U 0.95＝2.013mm U 0.99＝2.915mm实验结果：平凸透镜的曲率半径为 R ＝（876.446±1.362）mm P ＝0.69 R ＝（876.446±2.013）mm P ＝0.95 R ＝（876.446±2.915）mm P ＝0.99误差分析：1.凸透镜受重力发生变形，条纹宽度不均匀造成误差。

干涉法测微小量

干涉法测微小量实验一、实验简介：光的干涉现象表明了光的波动的性质，干涉现象在科学研究与计量技术中有着广泛的应用。

在干涉现象中，不论何种干涉，相邻干涉条纹的光程差的改变都等于相干光的波长，可见光的波长虽然很小，但干涉条纹间的距离或干涉条纹的数目是可以计量的。

因此，通过对干涉条纹数目或条纹移动数目的计量，可以得到以光的波长为单位的光程差。

利用光的等厚干涉可以测量光的波长，检验表面的平面度，球面度，光洁度，以及精确测量长度，角度和微小形变等。

二、实验原理：实验内容一：牛顿环法测曲率半径图1如图所示，在平板玻璃面DCF上放一个曲率半径很大的平凸透镜ACB，C点为接触点，这样在ACB和DCF之间，形成一层厚度不均匀的空气薄膜，单色光从上方垂直入射到透镜上，透过透镜，近似垂直地入射于空气膜。

分别从膜的上下表面反射的两条光线来自同一条入射光线，它们满足相干条件并在膜的上表面相遇而产生干涉，干涉后的强度由相遇的两条光线的光程差决定，由图可见，二者的光程差△’等于膜厚度e的两倍，即△’ =2e此外，当光在空气膜的上表面反射时，是从光密媒质射向光疏媒质，反射光不发生相位突变，而在下表面反射时，则会发生相位突变，即在反射点处，反射光的相位与入射光的相位之间相差π，与之对应的光程差为λ /2 ，所以相干的两条光线还具有λ /2的附加光程差，总的光程差为：(1) 当△满足条件：，（）(2) 时，发生相长干涉，出现第K级亮纹。

而当：，（）(3) 时，发生相消干涉，出现第k级暗纹。

因为同一级条纹对应着相同的膜厚，所以干涉条纹是一组等厚度线。

可以想见，干涉条纹是一组以C点为中心的同心圆，这就是所谓的牛顿环。

如图所示，设第k级条纹的半径为r k，对应的膜厚度为e k，则:(4)在实验中，R的大小为几米到十几米，而e k的数量级为毫米，所以R >>e k，e k2相对于2R k是一个小量，可以忽略，所以上式可以简化为(5)如果r k是第k级暗条纹的半径，由式(1)和(3)可得:(6)代入式(5)得透镜曲率半径的计算公式(7)对给定的装置，R为常数，暗纹半径(8)和级数k的平方根成正比，即随着k的增大，条纹越来越细。

干涉法测微小量-实验报告

干涉法测微小量创建人：系统管理员总分：100实验目的学习掌握利用光的干涉原理检验光学元件表面集合特征的方法，用劈尖的等厚干涉测量细丝直径的方法，同时加深对光的波动性的认识。

实验仪器低频信号发生器、示波器、超声声速测定仪、频率计等实验原理1、用牛顿环测平凸透镜的曲率半径图1.牛顿环干涉条纹的形成当曲率很大的平凸透镜的凸面放在一平面玻璃上时，会产生一组以O为中心的明暗相接的同心圆环，称为牛顿环。

如图，1、2两束光的光成差22λδ+=∆，式中λ为入射光的波长，δ是空气层厚度，空气折射率1n ≈。

如果第m 个暗环处空气厚度为m δ，则有故得到：2m m λδ⋅=2、劈尖的等厚干涉测细丝直径图2.劈尖干涉条纹的形成两片叠在一起的玻璃片，在它们的一端口夹一直径待测的细丝，于是两片玻璃之间便形成一空气劈尖。

当用单色光垂直照射时，会产生干涉现象。

因为光程差相等的地方是平行两玻璃片交线的直线，所以等厚干涉条纹是一组明暗相间的、平行于交线的直线。

设入射光波长为λ，则得到第m 级暗纹处空气劈尖的的厚度2m λ⋅=d 。

由此可知，m=0时，d=0，即在两玻璃片交线处，为零级暗条纹。

如果在细丝处呈现m=N 级条纹，则待测细丝直径2λ⋅=N d 。

实验内容1、测平凸透镜的曲率半径（1）观察牛顿环1）将牛顿环仪按图3所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方，木架上的透镜要正对着钠光灯窗口，调节玻璃片角度，使通过显微镜目镜观察时视场最亮。

图3.观测牛顿环实验装置图2）调节目镜，看清目镜视场内的十字叉丝后，使显微镜筒下降到接近玻璃片，然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度及显微镜，使条纹更清楚。

（2）测牛顿环直径1）使显微镜的十字叉丝交点与牛顿环中心重合，并使水平方向的叉丝与标尺平行（与显微镜筒移动方向平行）。

2）转动显微镜测微鼓轮，使显微镜沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第35环相切为止。

干涉法测微小量-实验报告

⼲涉法测微⼩量-实验报告⼲涉法测微⼩量创建⼈：系统管理员总分：100实验⽬的学习掌握利⽤光的⼲涉原理检验光学元件表⾯集合特征的⽅法，⽤劈尖的等厚⼲涉测量细丝直径的⽅法，同时加深对光的波动性的认识。

实验仪器低频信号发⽣器、⽰波器、超声声速测定仪、频率计等实验原理1、⽤⽜顿环测平凸透镜的曲率半径图1.⽜顿环⼲涉条纹的形成当曲率很⼤的平凸透镜的凸⾯放在⼀平⾯玻璃上时，会产⽣⼀组以O为中⼼的明暗相接的同⼼圆环，称为⽜顿环。

如图，1、2两束光的光成差22λδ+=?，式中λ为⼊射光的波长，δ是空⽓层厚度，空⽓折射率1n ≈。

如果第m 个暗环处空⽓厚度为m δ，则有故得到：2m m λδ?=2、劈尖的等厚⼲涉测细丝直径图2.劈尖⼲涉条纹的形成两⽚叠在⼀起的玻璃⽚，在它们的⼀端⼝夹⼀直径待测的细丝，于是两⽚玻璃之间便形成⼀空⽓劈尖。

当⽤单⾊光垂直照射时，会产⽣⼲涉现象。

因为光程差相等的地⽅是平⾏两玻璃⽚交线的直线，所以等厚⼲涉条纹是⼀组明暗相间的、平⾏于交线的直线。

设⼊射光波长为λ，则得到第m 级暗纹处空⽓劈尖的的厚度2m λ=d 。

由此可知，m=0时，d=0，即在两玻璃⽚交线处，为零级暗条纹。

如果在细丝处呈现m=N 级条纹，则待测细丝直径2λ=N d 。

实验内容1、测平凸透镜的曲率半径（1）观察⽜顿环1）将⽜顿环仪按图3所⽰放置在读数显微镜镜筒和⼊射光调节⽊架的玻璃⽚的下⽅，⽊架上的透镜要正对着钠光灯窗⼝，调节玻璃⽚⾓度，使通过显微镜⽬镜观察时视场最亮。

图3.观测⽜顿环实验装置图2）调节⽬镜，看清⽬镜视场内的⼗字叉丝后，使显微镜筒下降到接近玻璃⽚，然后缓慢上升，直到观察到⼲涉条纹，再微调玻璃⽚⾓度及显微镜，使条纹更清楚。

（2）测⽜顿环直径1）使显微镜的⼗字叉丝交点与⽜顿环中⼼重合，并使⽔平⽅向的叉丝与标尺平⾏（与显微镜筒移动⽅向平⾏）。

2）转动显微镜测微⿎轮，使显微镜沿⼀个⽅向移动，同时数出⼗字叉丝竖丝移过的暗环数，直到竖丝与第35环相切为⽌。

干涉法测量微小量

7.2.1 干涉法测微小量（本文内容选自高等教育《大学物理实验》）光的干涉现象表明了光的波动性质，干涉现象在科学研究与计量技术中有着广泛的应用。

在干涉现象中，不论是何种干涉，相邻干涉条纹的光程差的改变都等于相干光的波长，可见光的波长虽然很小，但干涉条纹间的距离或干涉条纹的数目却是可以计量的。

因此，通过对干涉条纹数目或条纹移动数目的计量，可得到以光的波长为单位的光程差。

利用光的等厚干涉现象可以测量光的波长，检验表面的平面度、球面度、光洁度，精确的测量长度、角度，测量微小形变以及研究工作内应力的分布等。

通过本次实验，学习、掌握利用光的干涉原理检验光学元件表面几何特征的方法，用劈尖的等厚干涉测量细丝直径的方法，同时加深对光的波动性的认识。

实验原理1．用牛顿环测平凸透镜的曲率半径当曲率半径很大的平凸透镜的凸面放在一平面玻璃上时，见图7.2.1-1，在透镜的凸面与平面之间形成一个从中心O 向四周逐渐增厚的空气层。

当单色光垂直照射下来时，从空气层上下两个表面反射的光束1和光束2在上表面相遇时产生干涉。

因为光程差相等的地方是以O 点为中心的同心圆，因此等厚干涉条纹也是一组以O 点为中心的明暗相间的同心圆，称为牛顿环。

由于从下表面反射的光多走了二倍空气层厚度的距离，以及从下表面反射时，是从光疏介质到光密介质而存在半波损失，故1、2两束光的光程差为22λδ+=∆ （1）式中λ为入射光的波长，δ是空气层厚度，空气折射率1≈n 。

当程差Δ为半波长的奇数倍时为暗环，若第m 个暗环处的空气层厚度为m δ，则有2λδ⋅=m m （2）由图7.2.1-1中的几何关系222)(m mR r R δ-+=，以及一般空气层厚度远小于所使用的平凸透镜的曲率半径R ，即R m <<δ，可得Rr m m 22=δ （3）式中r m 是第m 个暗环的半径。

由式（2）和式（3）可得λmR r m =2 （4）可见，我们若测得第m 个暗环的半径r m 便可由已知λ求R ，或者由已知R 求λ了。

干涉法测微小量

《干涉法测微小量》实验报告姓名学号学院专业班级一．实验目的学习掌握利用光的干涉原理检验光学元件表面集合特征的方法，用劈尖的等厚干涉测量细丝直径的方法，同时加深对光的波动性的认识二．实验仪器读数显微镜、钠光灯及电源、牛顿环仪、劈尖等三、实验原理1、用牛顿环测平凸透镜的曲率半径详见实验指导书2、劈尖的等厚干涉测细丝直径详见实验指导书四、实验步骤1. 观察牛顿环。

(1) 将牛顿环仪放置在读数显微镜镜筒和入射光调节架下方，调节玻璃片的角度，使通过显微镜目镜观察时视场最亮。

(2) 调节目镜，看清目镜视场的十字叉丝后，使显微镜镜筒下降到接近牛顿环仪然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度和显微镜，使条纹清晰。

2. 测牛顿环半径。

(1) 使显微镜十字叉丝交点和牛顿环中心重合，并使水平方向的叉丝和标尺平行（与显微镜移动方向平行）。

(2) 转动显微镜微调鼓轮，使显微镜沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第 45 环相切为止。

记录标尺读数。

(3) 反向转动鼓轮，当竖丝与第 40 环相切时，记录读数显微镜上的位置读数，然后继续转动鼓轮，使竖丝依次与第 35、30、25、20、15、10、5 环相切，顺次记下读数。

(4) 继续转动鼓轮,越过干涉圆环中心，记下竖丝依次与另一边的 5、10、15、20、25、30、35、40 环相切时的读数。

3．利用逐差法处理得到的数据，得到牛顿环半径 R。

4. 观察劈尖干涉条纹。

(1) 将劈尖放置在读数显微镜镜筒和入射光调节架下方，调节玻璃片的角度，使通过显微镜目镜观察时视场最亮。

(2) 调节目镜，看清目镜视场的十字叉丝后，使显微镜镜筒下降到接近劈尖然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度和显微镜，使条纹清晰。

5. 测量。

(1) 使显微镜的十字叉丝交点与劈尖中心重合，并使其与显微镜镜筒移动方向平行。

(2) 在劈尖玻璃面的三个不同部分，测出 20 条暗纹的总长度，测 3 个求平均值。