初一下册几何证明题(完整版)
七年级下几何证明题(精华版)-

几何证明题专项练习1、直接根据图示填空:(1)∠α=_________ (2)∠α=_________ (3)∠α=_________(4)∠α=_________ (5)∠α=_________ (6)∠α=_________α38°62°20°α°30°25°150°α(1) (2) (3)70°α°70°60°20°α20°135°45°α(4) (5) (6)2、填空完成推理过程: 如图,∵AB ∥EF ( 已知 )∴∠A + =1800( )∵DE ∥BC ( 已知 )∴∠DEF= ( )2.∠ADE= ( )3. 已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.4. 已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.3.5.已知AB ∥CD ,∠1=70°则∠2=_______,∠3=______,∠4=______5.4321A CDB 4.A CD E FBDEB CAEDBAC21FEDBACba34126. 已知:如图4, AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数6.7.8.7.直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.8. 如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.9.如图,AB ∥CD,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37º,求∠D 的度数.12.9.10.11.10.如图,已知:,,求的度数。
七年级下册数学期末考试几何大题证明必考题精选
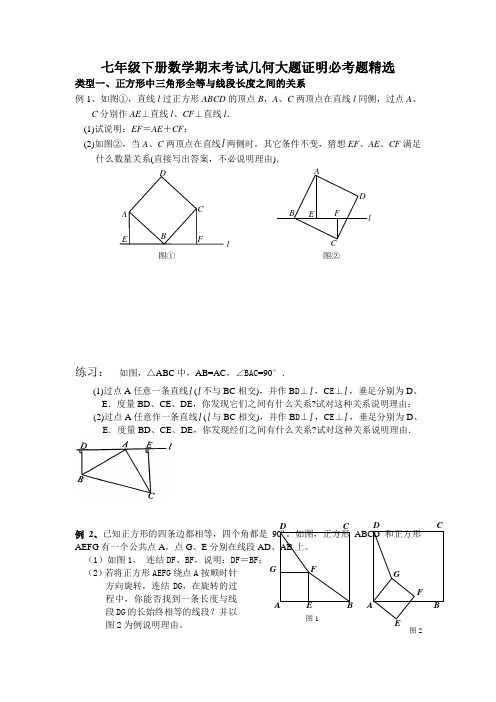
图①DA EC B Fl图②ABEF C lD 七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
(1)如图1, 连结DF 、BF ,说明:DF =BF ;(2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
A EB 图1D CG FA BD C GFE 图2练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上(1)BD 与CE 相等吗?请说明理由.(2)你能求出BD 与CE 的夹角∠BFC 的度数吗?(3)若将已知条件改为:四边形ABCD 与四边形AEFG 都是正方形,例3、正方形四边条边都相等,四个角都是90.如图,已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,点E 是直线MN 上一点,以AE 为边在直线MN 的上方作正方形AEFG .(1)如图1,当点E 在线段BC 上(不与点B 、C 重合)时: ①判断△ADG 与△ABE 是否全等,并说明理由;②过点F 作FH ⊥MN ,垂足为点H ,观察并猜测线段BE 与线段CH 的数量关系,并说明理由;(2)如图2,当点E 在射线CN 上(不与点C 重合)时: ①判断△ADG 与△ABE 是否全等,不需说明理由;F B②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度α,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C图 2FG D A 图 1F D A外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论. (4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o , R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21A B C D EP A B C DE P M(3) A B C D EP M (2) A B C D EM (P ) (1) A B C D E P M(5)C B APDEFC B E 又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中,h 1、h 2、h 3、h 之间的关系;⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的;例2、已知△ABC 是等边三角形,将一块含30角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存在,请指出这条线段,并证明;如果不存在,请说明理由.(B)CE F图1ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P ) (1)练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
(完整版)七年级数学几何证明题

七年级数学几何证明题1. 如图,在ABC中,D在AB上,且△ CAD^P A CBE都是等边三角形, 求证:(1)DE=AB(2)Z EDB=602. 如图,在A ABC中, AD平分/ BAC DE||AC,EF丄AD交BC延长线于F。
求证:/ FAC" B3. 已知,如图,在厶ABC中,AD,AE分别是△ ABC的高和角平分线,若/ B=30/ C=50°求:(1),求/ DAE的度数。
(2)试写出 / DAE与 / C - / B 有何关系?(不必证明)B D C4、一个零件的形状如图,按规定/ A=9Oo,/ C=25o,Z B=25o,检验已量得/运用三角形的有关知识说明零件不合格的理BDC=150,就判断这个零件不合格,由。
5、如图,已知DF // AC, / C=Z D,你能否判断CE // BD?试说明你的理由6、如图,△ ABC中,D在BC的延长线上,过D作DE丄AB于E,交AC于F.已知/ A=30 ° ,Z FCD=80° ,求/D。
7、如图,BE平分/ ABD , CF平分/ ACD , BE、CF交于G, 若/ BDC = 140。
,/ BGC = 110。
,则 / A ?C 8、如图,AD丄BC于D, EG丄BC于G,Z E =Z 1,求证AD 平分/ BAC9、如图,直线。
丘交厶ABC的边AB AC于D E,交BC延长线于F, 若/ B= 67°,/ ACB= 74°,/ AED= 48°,求/ BDF的度数•10、如图,将一副三角板叠放在一起,使直角的顶点重合于O,贝U/ AOC/ DOB11、如图,将两块直角三角尺的直角顶点C叠放在一起•(1)若/ DCE=35,求/ ACB的度数;(2)若/ ACB=140,求/ DCE的度数;(3)猜想:/ ACB与/ DCE有怎样的数量关系,并说明理由12、已知:直线AB与直线CD相交于点0,/ BOC= 45°,(1) 如图1,若EO丄AB,求/ DOE的度数;(2) 如图2,若EO平分/ AOC,求/ DOE的度数.13、已知AOB , P为OA上一点.(1)过点P画一条直线PQ,使PQ // OB ;(2)过点P画一条直线PM,使PM丄OA交0B于点M ;(3)若AOB 40 ,贝U PMO ?14、如图。
初一下数学证明经典例题及答案

如图,已知D是△ABC内一点,试说明AB+AC>BD+CD 证明:延长BD交AC于E在△ABC中,AB+AE>BE,即AB+AE>BD+DE……①在△DEC中,DE+EC>DC……②①+②,得(AB+AE)+(DE+EC)>(BD+DE)+CD 即AB+(AE+EC)+DE>(BD+DE)+CD即AB+AC+DE>BD+DE+CD∴AB+AC>BD+CD如图,△ABC中,D是BC的中点,求证:(1)AB+AC>2AD(2)若AB=5,AC=3,求AD的范围。
(1)延长AD到点G,使DG=AD.连接BG在△CDA和△BDE中AD=GD,∠ADC=∠GDB∵D是BC的中点∴CD=BD∴△CDA≌△BDG.∴BG=AC在△ABG中,AB+BG=AB+BCAG=2AD因为三角形两边和大于第三边,所以AB+BE>AG ∴AB+BC>2AD(2)AB-AC<2AD<AB+ACDC BAEAB CDG2<2AD <8 1<AD <4如图,AB=AD,AC=AE,∠BAD=∠CAE=90°,点F 为DE 的中点,求证:BC=2AF. 延长AF 到点G,使AF=DF.连接GD 在△AFE 和△DFG 中 AF=GF,∠AFE=∠DFG ∵点F 为DE 的中点 ∴DF=EF所以△AFE ≌△DFG. (SAS) GD=AE=AC;∠G=∠FAE.∴DG ∥AE.(内错角相等,两直线平行)则∠GDA+∠DAE=180°.(两直线平行,同旁内角互补) 又∵∠BAC+∠DAE=180°.∴∠GDA=∠BAC.(同角的补角相等). 又∵AD=AB.∴⊿ADG ≌⊿BAC(SAS) ∴AG=BC,即2AF=BC. ∴BC=2AF.如图,AD 是△ABC 的中线,点E 在BC 的延长线上,CE=AB, ∠BAC=∠BCA 求证:AE=2AD证明:在AD 的延长线上取点F,使AD =FD,连接CF ∵AD 是中线∴BD =CD,AD =FD,∠ADB =∠FDCECDBA∴△ABD≌△FCD (SAS)∴CF=AB,∠B=∠FCD∵∠ACF=∠BCA+∠BCE,∠ACE=∠BAC+∠B,∠BAC=∠BCA∴∠ACF=∠ACE∵CE=AB∴CE=CF∴△ACE≌△ACF (SAS)∴AE=AF∵AF=AD+FD=2AD∴AE=2AD如图,△ABC中,∠ABC=90°,AC=CE,BC=CD,∠ACE=∠BCD=90°,BC的延长线交DE于F。
七年级下册数学期末考试几何大题证明必考题
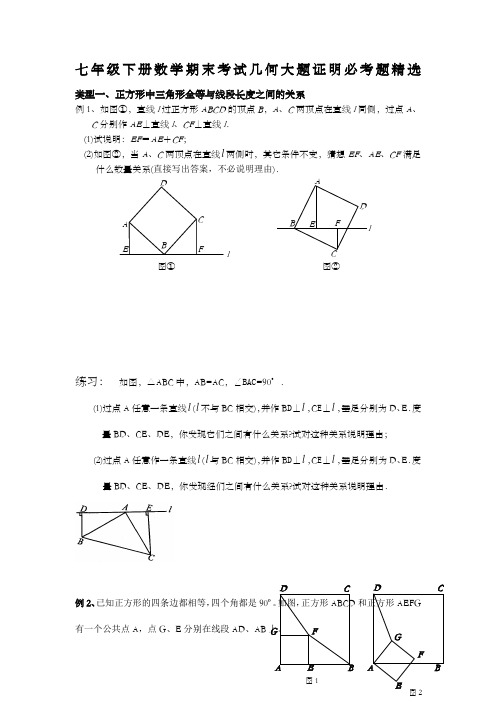
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
A E B 图1D CG FA BD CG FE图2(1)如图1, 连结DF 、BF ,说明:DF =BF ; (2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上画出示意图,并请求出这个大正方形的面积.附加:如图,△ABC 与△ADE 都是等边三角形,连结BD 、CE(1)BD 与CE 相等吗?请说明理由.A BCFDE GP32B(2)你能求出BD与CE的夹角∠BFC的度数吗?(3)若将已知条件改为:四边形ABCD与四边形AEFG都是正方形,连结BE、DG交点记为点M(如图).请直接写出线段BE和DGF例3、正方形四边条边都相等,四个角都是90o.如图,已知正方形ABCD在直线MN 的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.(1)如图1,当点E在线段BC上(不与点B、C重合)时:①判断△ADG与△ABE是否全等,并说明理由;②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;(2)如图2,当点E在射线CN上(不与点C重合)时:①判断△ADG与△ABE是否全等,不需说明理由;②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.图 2FG DA图 1FDA类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论.(4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o ,R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.CBAPDE2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的; (3)说明图(5)所得结论为什么是正确的.ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形,将一块含30o 角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立C图1吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
初一下册几何证明题(完整版)

初一下册几何证明题初一下册几何证明题第一篇:初一下册几何证明题初一下册几何证明题1.已知在三角形ab中,be,f分别是角平分线,d是ef中点,若d到三角形三边b,ab,a的距离分别为x,,z,求证:x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fq,do,en都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,=h,z=dj.所以x=+z。
在正五边形abde中,m、n分别是de、ea上的点,bm与n相交于点o,若∠bon=108°,请问结论bm=n是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中,ab=a,角a=58°,ab的垂直平分线交a与n,则角nb=3°因为ab=a,∠a=58°,所以∠b=61°,∠=61°。
七年级下册数学几何证明题

七年级下册数学几何证明题七年级下册数学几何证明题一、直线平分角在平面几何中,对于给定的角,如果有一条直线能够将这个角划分成两个相等的小角,我们称这条直线是该角的平分线。
接下来我们将证明两个定理和一个引理。
定理1:如果直线ab平分角BAC,则直线ab与弧BCB′的切点C相同。
引理:如果点D在圆弧BCB′上,且点D在角BAC的平分线ab上,则BD=DC。
定理2:如果点E在角BAC的平分线ab上,且BE=CE,则直线ab平分角BAC。
证明:首先,我们先证明引理。
根据圆的性质,半径与弦垂直且平分弦。
又因为BD=DC,所以BD和DC分别是圆弧BCB′的半径,从而BD⊥BC,DC⊥BC。
又因为点D在角BAC的平分线ab上,所以BD⊥BA,DC⊥CA。
综上所述,BD⊥BA,BD⊥BC,BD是角BAC的平分线上任意一点至圆弧BCB′的切线。
同理,DC是角BAC的平分线上任意一点至圆弧BCB′的切线。
这样,我们就证明了引理。
接下来,我们证明定理1。
假设直线ab平分角BAC,且ab与弧BCB′的切点为C′。
根据引理,如果D是角BAC的平分线上的一点,且D在圆弧BCB′上,则BD=DC。
所以,当切点C与切点C′不同时,就会导致BD≠DC,与引理矛盾。
所以,点C和点C′必须是同一个点,即直线ab与弧BCB′的切点C唯一。
综上所述,我们证明了定理1。
最后,我们证明定理2。
假设点E在角BAC的平分线ab上,且BE=CE。
根据定理1,直线ab与弧BCB′的切点C唯一。
假设BE和CE分别与圆弧BCB′交于点F和G。
根据弧与切线的性质,∠BCF≤90°,∠BCG≤90°。
又因为BE=CE,所以∠BEF=∠CEG。
综上所述,∠BCF=∠BEF=∠BAC,∠BCG=∠CEG=∠BAC。
所以,直线ab平分角BAC。
综上所述,我们证明了定理2。
二、垂直平分线在平面几何中,对于给定的线段,如果有一条直线能够将这个线段划分成两个相等的小线段,并且与这个线段垂直相交,我们称这条直线是该线段的垂直平分线。
(完整版)北师大七年级下几何证明入门专项练习

几何证明题专项训练11、( 1)∵∠ 1=∠ A(已知),∴∥,();( 2)∵∠ 3=∠4(已知),∴∥,();( 3)∵∠ 2=∠5(已知),∴∥,();( 4)∵∠ ADC+∠ C=180o(已知),∴∥,();2,如图,( 1)∵∠ ABD=∠ BDC(已知),∴∥,();( 2)∵∠ DBC=∠ ADB(已知),∴∥,();( 3)∵∠ CBE=∠ DCB(已知),∴∥,();( 4)∵∠ CBE=∠ A,(已知),∴∥,();( 5)∵∠ A+∠ ADC=180o(已知),∴∥,();( 6)∵∠ A+∠ ABC=180o(已知),∴∥,();3、如图,∠ 1=∠ 2, AC均分∠ DAB,试说明: DC∥ AB.4,如图,∠ ABC=∠ ADC, BF 和 DE分别均分∠ ABC和∠ ADC,∠1=∠ 2,试说明: DE∥ FB.5.如图 2-67,已知∠ 1= ∠2,求∠ 3+∠ 4 的度数.6、如图 2-56①∵ AB//CD (已知),∴∠ ABC=_______ ()______=______ (两直线平行,内错角相等),∴∠ BCD+______= 180()②∵∠ 3=∠ 4(已知),∴ ______∥ _____()③∵∠ FAD= ∠ FBC(已知),∴ _____∥()7、如图 2-57,直线 AB ,CD,EF 被直线 GH 所截,∠ 1= 70,∠ 2=110,∠3= 70.求证: AB//CD .证明:∵∠ 1= 70,∠ 3= 70(已知),∴∠ 1=∠ 3()∴ ____∥ _____()∵∠ 2=110,∠ 3= 70(),∴______+_____=____,∴_____//______,∴ AB//CD ().8.如图 2-58,①直线 DE ,AC 被第三条直线BA 所截,则∠ 1 和∠ 2 是 ________,假如∠ 1= ∠ 2,则 ___//___,其原因是().②∠ 3 和∠ 4 是直线 __________ 、 __________ ,被直线 ____________所截,所以 ____//____ .∠ 3____∠ 4,其原因是().9.如图 2-59,已知 AB//CD ,BE 均分∠ ABC , CE 均分∠ BCD ,求证∠ 1+∠ 2= 90 .证明:∵BE 均分∠ ABC (已知),∴∠ 2=_________()同理∠ 1=_______________,∴∠1)1+∠2= ____________ (2又∵ AB//CD (已知),∴∠ ABC+ ∠ BCD=_____ ()∴∠ 1+ ∠2= 90()10、如图 2-60,E、 F、 G 分别是 AB 、 AC 、BC 上一点.①假如∠ B= ∠ FGC,则 ____//____, 其原因是()②∠ BEG= ∠EGF,则 _____//____ ,其原因是()③假如∠ AEG+ ∠ EAF= 180,则 ____//____ ,其原因是()11.如图2-61,已知AB//CD , AB//DE ,求证:∠ B+ ∠D= ∠BCF+∠DCF.证明:∵ AB//CF(已知),∴∠ ______=∠ ________(两直线平行,内错角相等).∵ AB//CF ,AB//DE (已知),∴ CF//DE ()∴∠ _________=∠ _________()∴∠ B+ ∠ D=∠ BCF+ ∠ DCF(等式性质).EA CGBD 图 7 F几何证明题专项训练 21、如图,∠ B=∠ C, AB ∥ EF,试说明:∠BGF= ∠ C。
七年级下几何证明题(精选)

七年级下几何证明题(精选)第一篇:七年级下几何证明题(精选)七年级下几何证明题学了三角形的外角吗?(三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于和它不相邻的任何一个内角) 角ACD>角BAC>角AFE角ACD+角ACB=180度角BAC+角ABC+角ACB=180度所以角ACD=角BAC+角ABC所以角角ACD>角BAC同理:角BAC>角AFE所以角ACD>角BAC>角AFE解∶﹙1﹚连接AC∴五边形ACDEB的内角和为540°又∵∠ABE+∠BED+∠CDE=360°∴∠A+∠C=180°∴AB∥CD﹙2﹚过点D作AB的垂线DE∵∠CAD=∠BAD,∠C=∠AEDAD为公共边∴Rt△ACD≌Rt△AED∴AC=AE,CD=DE∵∠B=45°∠DEB=90°∴∠EDB=45°∴DE=BEAB=AE+BE=AC+CD﹙3﹚∵腰相等,顶角为120°∴两个底角为30°根据直角三角形中30°的角所对的边为斜边的一半∴腰长=2高=16﹙4﹚根据一条线段垂直平分线上的点到线段两个端点的距离相等∴该交点到三角形三个顶点的距离相等解∶﹙1﹚先连接AC∴五边形ACDEB的内角和为540°∵∠ABE+∠BED+∠CDE=360°∴∠A+∠C=180°∴就证明AB∥CD♂等鴏♀栐薳2010-05-3017:33(1)解:过E作FG∥AB∵FG∥AB∴∠ABE+∠FEB=180°又∵∠ABE+∠CDE+∠BED=360°∴∠FED+∠CDE=180°∴FG∥CD∴AB∥CD(2)解:作DE⊥AB于E∵AD平分∠CAB,CD垂直AC,DE垂直AB∴CD=DE,AC=AE又∵AC=CB,DE=EB,AC⊥CB,DE⊥EB∴∠ABC=∠EDB=45°∴DE=EB∴AB=AE+EB=AC+CD(3)16CM(4)3个顶点如图已知在四边形ABCD中,∠BAD为直角,AB=AD,G为AD 上一点,DE⊥BG交BG的延长线于E,DE的延长线与BA的延长线相交于点F。
(完整版)七年级下册数学全等三角形的经典证明
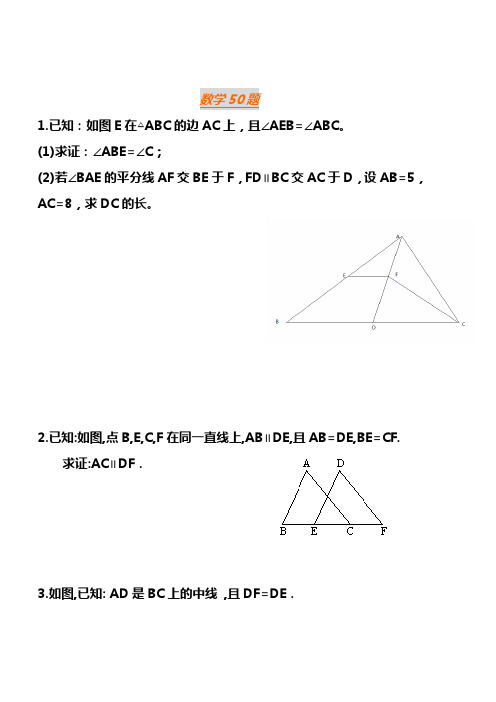
数学50题1.已知:如图E在△ABC的边AC上,且∠AEB=∠ABC。
(1)求证:∠ABE=∠C;(2)若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长。
2.已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.3.如图,已知: AD是BC上的中线,且DF=DE.求证:BE∥CF.4.如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF.求证:AC=EF.5.如图,在ΔABC中,AC=AB,AD是BC边上的中线。
求证:AD⊥BC,6.如图,已知AB=DE,BC=EF,AF=DC。
求证:∠EFD=∠BCAFGE DC BAAB C D EF AB CD7.如图,ΔABC 的两条高AD 、BE 相交于H ,且AD=BD ,试说明下列结论成立的理由。
(1)∠DBH=∠DAC ; (2)ΔBDH ≌ΔADC 。
8.已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
9.如图,在矩形ABCD 中,F 是BC 边上的一点,AF 的延长线交DC 的延长线于G ,DE ⊥AG 于E ,且DE =DC ,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论。
ABCDEH10.已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在BD 上,PM ⊥AD 于M ,•PN ⊥CD 于N ,判断PM 与PN 的关系.11.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .12.在△ABC 中,,AB=AC , 在AB 边上取点D ,在AC 延长线上了取点E ,使CE=BD , 连接DE 交BC 于点F ,求证DF=EF .P D AC M NF E DCB AB13.如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.求证:EG=EF;请你判断BE+CF与EF的大小关系,并说明理由。
七年级几何证明题训练(含答案)

1. 已知:如图11所示,∆ABC 中,∠=C 90于E ,且有AC AD CE ==。
求证:DE =122. 已知:如图 求证:BC =3. 已知:如图13所示,过∆ABC 的顶点A ,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ 。
设M 为BC 的中点。
求证:MP =MQ4. ∆ABC 中,∠=︒⊥BAC AD BC 90,于D ,求证:()AD AB AC BC <++14【试题答案】1. 证明:取AC ADAF CDAFC =∴⊥∴∠= 又∠+∠=︒∠+∠=︒14901390,∴∠=∠=∴≅∴=∴=4312AC CEACF CED ASA CF EDDE CD∆∆()2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截CB CE BCD ECD CD CD CBD CEDB EBAC B BAC E=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22又∠=∠+∠BAC ADE E∴∠=∠∴=∴==ADE E AD AEBC CE ,3. 证明:延长PM CQ AP BP BP CQ PBM ⊥∴∴∠=∠,// 又BM CM =,∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线AD BC AD AEBC AE AD⊥∴<∴=>,22()AB AC BCBC AB AC BC AD AB AC BC AD AB AC BC +>∴<++∴<++∴<++2414。
人教版七年级下几何证明题库-(已排版)

1.填空完成推理过程:如图,∵AB ∥EF ( 已知 )∴∠A + =1800( ) ∵DE ∥BC ( 已知 )∴∠DEF= ( ) ∠ADE= ( )2.已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.3. 已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.4.已知AB ∥CD ,∠1=70°则∠2=_______,∠3=______,∠4=______4321A CDB5. 已知:如图4, AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数6.直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.ACD E FBDEB CAH G21FEDC BA7.如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.8.如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37º,求∠D 的度数.9.如图,已知:21∠∠=, 50=D ∠,求B ∠的度数。
10.已知:如图,AB∥CD,∠B=400,∠E=300,求∠D的度数11.如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.ba341212.已知等腰三角形的周长是16cm .ABCDEE D C BAE DBAC21FEDBA C(1)若其中一边长为4cm ,求另外两边的长; (2)若其中一边长为6cm ,求另外两边长; (3)若三边长都是整数,求三角形各边的长.13.如图,AB//CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A=370,求∠D 的度数.14.AB//CD,EF ⊥AB 于点E ,EF 交CD 于点F ,已知∠1=600.求∠2的度数.15.叙述并证明“三角形的内角和定理”(要求根据下图写出已知、求证并证明)16.如图所示,把一张长方形纸片ABCD 沿EF 折叠,若∠EFG=50°,求∠DEG 的度数.17.如图所示,已知AB ∥CD,分别探索下列四个图形中∠P 与∠A,∠C 的关系,•请你对四个图形中的关系加以说NMG F E DC BA明.PDCBA P DCBAP DCB A PDCB A(1) (2) (3) (4)18.如图,AB ∥CD ,BF ∥CE ,则∠B 与∠C 有什么关系?请说明理由.19.如图,已知:DE ∥BC ,CD 是∠ACB 的平分线,∠B =70°,∠ACB =50°,求∠EDC 和∠BDC 的度数.20.如图,AB∥CD,∠NCM =90°,∠NCB =30°,CM 平分∠BCE ,求∠B 的大小.21.如图,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?ABCDEENMCD BANMFE DCBA22.如图,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.F E21DCBA23.如图,已知:CE =DF ,AC =BD ,∠1=∠2.求证:∠A =∠B .B24.如图,已知:AB //CD ,AB =CD ,求证:AC 与BD 互相平分.25.如图,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .2 ABECFDHG 126.如图,已知:在∆ABC 中,∠=︒C 90,AC =BC ,BD 平分∠CBA ,DE AB ⊥于E ,求证:AD +DE =BE .EABCD27.如图,已知:AB //CD ,求证:∠B +∠D +∠BED =360︒(至少用三种方法)EABCD28.直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.29.如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°.将求∠AGD 的过程填写完整. 因为EF ∥AD ,所以 ∠2 = . 又因为 ∠1 = ∠2,所以 ∠1 = ∠3. 所以AB ∥ .所以∠BAC + = 180°. 又因为∠BAC = 70°,所以∠AGD = .30.如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.AB CD E31.如图所示,AB ∥ED ,∠B =48°,∠D =42°, BC 垂直于CD 吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.2.如图,已知:DE ∥BC ,CD 是∠ACB 的平分线,∠B =70°, ∠ACB =50°,求∠EDC 和∠BDC 的度数.33.如图,AD ∥BC ,∠B=∠D ,求证:AB ∥CD 。
七年级下几何证明题集锦

第3题1、填空完成推理过程:[1] 如图,∵AB∥EF(已知)∴∠A + =1800()∵DE∥BC(已知)∴∠DEF= ()∠ADE= ()2.(6分) 已知:如图,∠ADE=∠B,∠DEC=115°.求∠C的度数.3.已知:如图,AD∥BC,∠D=100°,AC平分∠BCD,求∠DAC的度数.4.已知AB∥CD,∠1=70°则∠2=_______,∠3=______,∠4=______4321AC DB5. 已知:如图4,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求∠P的度数6、直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.4.(6分) 如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.ACDEFBD EB CAHG21FEDC BAE如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37º,求∠D 的度数.4、如图,已知:21∠∠=,ο50=D ∠,求B ∠的度数。
1. (本题10分)已知:如图,AB∥CD,∠B=400,∠E=300,求∠D的度数 1. 如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.ba3412已知等腰三角形的周长是16cm .(1)若其中一边长为4cm ,求另外两边的长; (2)若其中一边长为6cm ,求另外两边长; (3)若三边长都是整数,求三角形各边的长.如图,AB//CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A=370,ABCDEE DC BA21FEDBAC求∠D的度数.AB//CD,EF⊥AB于点E,EF交CD于点F,已知∠1=600.求∠2的度数.10.叙述并证明“三角形的内角和定理”(要求根据下图写出已知、求证并证明)1.如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,求∠DEG的度数.索发现:如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,•请你从所得的四个关系中任选一个加以说明.PDCBAPDCBAPDCBAPDCBA(1) (2) (3) (4)如图,AB∥CD,BF∥CE,则∠B与∠C有什么关系?请说明理由.18.如图,已知:DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.第17题图AB CD E19.如图AB∥CD,∠NCM =90°,∠NCB =30°,CM 平分∠BCE ,求∠B 的大小.如图5-24,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?NMFE DCBA如图5-25,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.F E21DCBA如图5-26,已知:CE =DF ,AC =BD ,∠1=∠2.求证:∠A =∠B .B如图5-27,已知:AB //CD ,AB =CD ,求证:AC 与BD 互相平分.ENMCDBA第19题图 图5-24图5-25图5-26OABCD如图5-27,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .2 ABECFDHG 1如图5-28,已知:在∆ABC 中,∠=︒C 90,AC =BC ,BD 平分∠CBA ,DE AB ⊥于E ,求证:AD +DE =BE .EABCD如图5-29,已知:AB //CD ,求证:∠B +∠D +∠BED =360︒(至少用三种方法)EABCD(5分) 直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.23.(6分) 如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°.将求∠AGD 的过程填写完整.因为EF ∥AD ,所以 ∠2 = . 又因为 ∠1 = ∠2,所以 ∠1 = ∠3. 所以AB ∥ .所以∠BAC + = 180°. 又因为∠BAC = 70°,所以∠AGD = .24.(6分) 如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.图5-26ABCDEH G21FEDC BA25.(6分) 如图所示,AB ∥ED ,∠B =48°,∠D =42°, BC 垂直于CD 吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.26. (6分) 如图,已知:DE ∥BC ,CD 是∠ACB 的平分线,∠B =70°, ∠ACB =50°,求∠EDC 和∠BDC 的度数.AD ∥BC ,AB ∥DC ,∠1=100º,求∠2,∠3的度数4、如图,已知:21∠∠=,ο50=D ∠,求B ∠的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一下册几何证明题初一下册几何证明题第一篇:初一下册几何证明题初一下册几何证明题1.已知在三角形ab中,be,f分别是角平分线,d是ef中点,若d到三角形三边b,ab,a的距离分别为x,,z,求证:x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fq,do,en都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,=h,z=dj.所以x=+z。
在正五边形abde中,m、n分别是de、ea上的点,bm与n相交于点o,若∠bon=108°,请问结论bm=n是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中,ab=a,角a=58°,ab的垂直平分线交a与n,则角nb=3°因为ab=a,∠a=58°,所以∠b=61°,∠=61°。
因为ab的垂直平分线交a于n,设交ab于点d,一个角相等,两个边相等。
所以,rt△adn全等于rt△bdn所以∠nbd=58°,所以∠nb=61°-58°=3°4.在正方形abd中,p,q分别为b,d边上的点。
且角paq=45°,求证:pq=pb+dq延长b到m,使bm=dq,连接ma∵mb=dqab=ad∠abm=∠d=rt∠∴三角形amb≌三角形aqd∴am=aq∠mab=∠daq∴∠map=∠mab+∠pab=45度=∠paq∵∠map=∠paqam=aqap为公共边∴三角形amp≌三角形aqp∴mp=pq∴mb+pb=pq∴pq=pb+dq5.正方形abd中,点m,n分别在ab,b上,且bm=bn,bp⊥m于点p,求证dp⊥np∵直角△bmp∽△bp∴pbp=mbb∵mb=bn正方形b=d∴pbp=bnd∵∠pb=∠pd∴△pbn∽△pd∴∠bpn=∠pd∵bp⊥m∴∠bpn+∠np=90°∴∠pd+∠np=90°∴dp⊥np。
第二篇:初一几何证明题初一《几何》复习题201X--6—29姓名:一.填空题1.过一点2.过一点,有且只有直线与这条直线平行;3.两条直线相交的,它们的交点叫做;4.直线外一点与直线上各点连接的中,最短;a b5.如果6.如图1,ab、d相交于o点,oe⊥d,∠1和∠2叫做,∠1和∠3叫做,∠1和∠4叫做,∠2和∠3叫做;a7.如图2,a⊥b,d⊥ab,b点到a的距离是a点到b的距离是,点到ab 的距离是d438.如图3,∠1=110°,∠2=75°,∠3=110°,∠4=;b二.判断题1.有一条公共边的两个角是邻补角;()2.不相交的两条直线叫做平行线;()3.垂直于同一直线的两条直线平行;()4.命题都是正确的;()5.命题都是由题设和结论两部分组成()6.一个角的邻补角有两个;()三.选择题1.下列命题中是真命题的是()a、相等的角是对顶角b、如果a⊥b,a⊥,那么b⊥、互为补角的两个角一定是邻补角d、如果a∥b,a⊥,那么b⊥下列语句中不是命题的是()a、过直线ab外一点作ab的平行线f b、任意两个奇数之和是偶数、同旁内角互补,则两直线平行d、两个角互为补角,与这两个角所在位置无关a3.如图4,已知∠1=∠2,若要∠3=∠4,则需()da、∠1=∠3b、∠2=∠3、∠1=∠4d、ab∥d4.将命题“同角的补角相等”改写成“如果,那么”的形式,正确的是()a.如果同角的补角,那么相等b.如果两个角是同一个角,那么它们的补角相等.如果有一个角,那么它们的补角相等d.如果两个角是同一个角的补角,那么它们相等四.解答下列各题:p1. 如图5,能表示点到直线(或线段)的距离的线段qa 有、、;abf 如图6,直线ab、d分别和ef相交,已知ab∥d,orebba平分∠be,∠bf=∠dfe,与∠d相等的角有∠d∠、∠、∠、∠等五个。
五.证明题e如图7,已知:be平分∠ab,∠1=∠3。
求证:de∥bbadb六.填空题1.过一点可以画条直线,过两点可以画2.在图8中,共有条线段,共有个锐角,个直角,∠a的余角是;3.ab=3.8m,延长线段ab到,使b=1m,再反向延长ab到d,使ad=3m,e是ad中点,f是d的中点,则ef=m ;4.35.56°=度分秒;105°45′15″—48°37′26 ″5.如图9,三角形ab中,d是b上一点,e是a上一点,ad与be交于f点,则图中共有e6.如图10,图中共有条射线,七.计算题bd1.互补的两个角的比是1:2,求这两个角各是多少度?a2.互余的两角的差为15°,小角的补角比大角的补角大多少?e bd1.如图11,aob是一条直线,od是∠bo的平分线,若∠ao=34°56′求∠bod的度数;d 八.画图题。
1 .已知∠α,画出它的余角和补角,并表示出来aob北已知∠α和∠β,画一个角,使它等于2∠α—∠β北偏西20 β3.仿照图12,作出表示下列方向的射线:西东⑴北偏东43°⑵南偏西37°⑶东北方向⑷ 西北方向九.证明题南两直线平行,内错角的平分线平行(要求:画出图形,写出已知、求证,并进行证明)已知:求证:证明:第三篇:初一几何证明题初一几何证明题一、1)d是三角形ab的b边上的点且d=ab,角adb=角bad,ae是三角形abd的中线,求证a=2ae。
在直角三角形ab中,角=90度,bd是角b的平分线,交a于d,e垂直ab于e,交bd于o,过o作fg平行ab,交b于f,交a于g。
求证d=ga。
延长ae至f,使ae=ef。
be=ed,对顶角。
证明abe全等于def。
=》ab=df,角b=角edf角adb=角bad=》ab=bd,d=ab=》d=df。
角ade=bad+b=adb+edf。
ad=ad=》三角形adf全等于ad=》a=af=2ae。
题干中可能有笔误地方:第一题右边的e点应为点,第二题求证的d不可能等于ga,是否是求证d=fa或d=o。
如上猜测准确,证法如下:第一题证明:设f是ab边上中点,连接ef角adb=角bad,则三角形abd为等腰三角形,ab=bd;∵ae是三角形abd的中线,f是ab边上中点。
∴ef为三角形abd对应da边的中位线,ef∥da,则∠fed=∠ad,且ef=12da。
∵∠fed=∠ad,且ef=12da,af=12ab=12d∴△afe∽△da∴ae:a=fe:da=af:d=1:2a=2ae得证第二题:证明:过d点作dh⊥ab交ab于h,连接oh,则∠dhb=90°;∵∠ab=90°=∠dhb,且bd是角b的平分线,则∠db=∠dbh,直角△db与直角△dbh有公共边db;∴△db≌△dbh,得∠db=∠hdb,d=hd;∵dh⊥ab,e⊥ab;∴dh∥e,得∠hdb=∠od=∠db,△do为等腰三角形,d=o=dh;四边形dho中o与dh两边平行且相等,则四边形dho为平行四边形,ho∥d且ho=d∵gf∥ab,四边形ahof 中,ah∥of,ho∥af,则四边形ahof为平行四边形,ho=fa∴d=fa得证有很多题1.已知在三角形ab中,be,f分别是角平分线,d是ef中点,若d到三角形三边b,ab,a的距离分别为x,,z,求证:x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fq,do,en都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,=h,z=dj.所以x=+z。
在正五边形abde中,m、n分别是de、ea上的点,bm与n相交于点o,若∠bon=108°,请问结论bm=n是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中,ab=a,角a=58°,ab的垂直平分线交a与n,则角nb=3°因为ab=a,∠a=58°,所以∠b=61°,∠=61°。
因为ab的垂直平分线交a于n,设交ab于点d,一个角相等,两个边相等。
所以,rt△adn全等于rt△bdn所以∠nbd=58°,所以∠nb=61°-58°=3°4.在正方形abd中,p,q分别为b,d边上的点。
且角paq=45°,求证:pq=pb+dq延长b到m,使bm=dq,连接ma∵mb=dqab=ad∠abm=∠d=rt∠∴三角形amb≌三角形aqd∴am=aq∠mab=∠daq∴∠map=∠mab+∠pab=45度=∠paq∵∠map=∠paqam=aqap为公共边∴三角形amp≌三角形aqp∴mp=pq∴mb+pb=pq∴pq=pb+dq5.正方形abd中,点m,n分别在ab,b上,且bm=bn,bp⊥m于点p,求证dp⊥np∵直角△bmp∽△bp∴pbp=mbb∵mb=bn正方形b=d∴pbp=bnd∵∠pb=∠pd∴△pbn∽△pd∴∠bpn=∠pd∵bp⊥m∴∠bpn+∠np=90°∴∠pd+∠np=90°∴dp⊥np。
