最短路径问题——和最小
最短路径知识点

l A 最短路径问题一、基本模型与方法问题1:“牵牛从点A 出发,到河边l 喝水,再到点B 处吃草,走哪条路径最短?”即在l 上找一点P ,使得PA+PB 和最小.(1)A ,B 两点在直线异侧时,连接AB 交l 于P ,则PA+PB 和最小.(2)A ,B 两点在直线同侧时,在l 上找一点P ,使得PA+PB 和最小.作B 点关l 的对标点B’,连接AB’交l 于点P ,即为所要找的P 点,使PA+PB 和最小.(3)变式讨论:在l 上找一P 点,使得△PAB 周长最小.问题2:在l 上找一点P ,使得|PA 一PB|最大(1)A ,B 两点在直线同侧时,连接AB 井延长交l 于P ,则|PA 一PB|最大(2)A ,B 两点在直线异侧时,作B 点关于l 的对称点B’,连接AB’并延长交l 于点P ,即为所要找的P 点,使|PA 一PB|最大.(3)当两定点A 、B 在直线l 同侧时,在直线l 上找一点P ,使得PA PB 最小. l A l A l l A问题3:(1)在直线l 1、l 2上分别求点M 、N ,使△PMN 周长最小做法:分别作点P 关于直线l 1、l 2的对称点P 1,P 2连接P 1,P 2与l 1、l 2交点即为M ,N(2)变式:在直线l 1、l 2上分别求点M 、N ,使四边形PMQN 周长最小.做法:分别作点P ,Q 关于直线l 1,l 2的对称点P’,Q’,连接P’,Q’ 与l 1,l 2交点即为M ,N问题4:点在锐角△AOB 内部,在OB 边上求作一点D ,在OA 边上求作一点C ,使PD+CD 最小做法:做点P 关于直线OB 的对称点P’,过P’向直线OA 作垂线与OB 的交点为所求点D ,垂足即为点C问题5:(1)直线l 1△l 2,并且l 1与l 2之间的距离为d ,点A 和点B 分别在直线l 1、l 2的两 侧,在直线l 1、l 2上分别求一点M 、N ,使AM+MN+AB 的和最小.作法:将点A 向下平移d 个单位到A 1,连结A 1B 交l 2于点N ,过N 作MN△”1,垂足为M ,连结AM ,则线段AM+MN+NB 的和最小,点M ,N 即为所求. l ABl 22O(2)直线l 的同侧有两点A ,B ,在直线l 上求两点C 、D ,使得AC+CD+DB 的和最小,且CD 的长为定值a ,点D 在点C 的右侧.作法:将点A 向右平移a 个单位到A 1,作点B 关于直线的对称点名B 1,连结A 1,B 1交直线l 于点D ,过点A 作AC//A 1D 交直线l 于点G ,连结BD ,则线段AC+CD+DB 的和最小. 点C 、D 即为所求二、基本题型训练(欢迎大家补充练习题并上传!)1. 如图,已知△ABC 为等腰直角三角形,AC =BC =4,∠BCD =15°,P 为CD 上的动点,则PA PB的最大值是多少?解答:l 21如图所示,作点A关于CD的对称点A′,连接A′C,连接A′B并延长交CD于点P,则点P就是PA PB-的值最大时的点,PA PB-=A′B.∵△ABC为等腰直角三角形,AC=BC等于4,∴∠ACB=90°.∵∠BCD=15°,∴∠ACD=75°.∵点A、A′关于CD对称,∴AA′⊥CD,AC=CA′,∵∠ACD=∠DCA′=75°,∴∠BCA′=60°.∵CA′=AC=BC=4,∴△A′BC是等边三角形,∴A′B=BC=4.∴PA PB-的最大值为4.2.。
二次函数压轴题最短路径问题
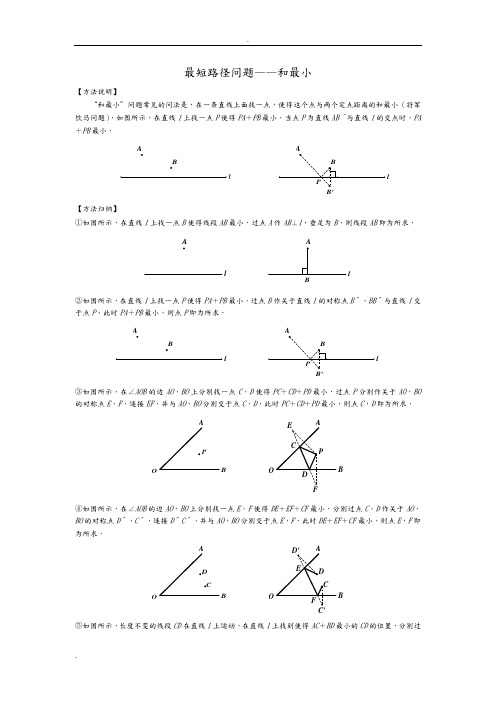
最短路径问题——和最小【方法说明】“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题).如图所示,在直线l 上找一点P 使得PA +PB 最小.当点P 为直线AB ′与直线l 的交点时,PA +PB 最小.lBA【方法归纳】①如图所示,在直线l 上找一点B 使得线段AB 最小.过点A 作AB ⊥l ,垂足为B ,则线段AB 即为所求.lAl②如图所示,在直线l 上找一点P 使得PA +PB 最小.过点B 作关于直线l 的对称点B ′,BB ′与直线l 交于点P ,此时PA +PB 最小,则点P 即为所求.lBAl③如图所示,在∠AOB 的边AO ,BO 上分别找一点C ,D 使得PC +CD +PD 最小.过点P 分别作关于AO ,BO 的对称点E ,F ,连接EF ,并与AO ,BO 分别交于点C ,D ,此时PC +CD +PD 最小,则点C ,D 即为所求.OBOB④如图所示,在∠AOB 的边AO ,BO 上分别找一点E ,F 使得DE +EF +CF 最小.分别过点C ,D 作关于AO ,BO 的对称点D ′,C ′,连接D ′C ′,并与AO ,BO 分别交于点E ,F ,此时DE +EF +CF 最小,则点E ,F 即为所求.BOB O⑤如图所示,长度不变的线段CD 在直线l 上运动,在直线l 上找到使得AC +BD 最小的CD 的位置.分别过点A ,D 作AA ′∥CD ,DA ′∥AC ,AA ′与DA ′交于点A ′,再作点B 关于直线l 的对称点B ′,连接A ′B ′与直线l 交于点D ′,此时点D ′即为所求.ll⑥如图所示,在平面直角坐标系中,点P 为抛物线(y =14x 2)上的一点,点A (0,1)在y 轴正半轴.点P在什么位置时PA +PB 最小?过点B 作直线l :y =-1的垂线段BH ′,BH ′与抛物线交于点P ′,此时PA +PB 最小,则点P 即为所求.1.(13)已知二次函数y =x 2-2mx +m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m =2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.【思路点拨】(1)由二次函数的图象经过坐标原点O (0,0),直接代入求出m 的值即可;(2)把m =2代入求出二次函数解析式,令x =0,求出y 的值,得出点C 的坐标;利用配方法或顶点坐标公式求出顶点坐标即可;(3)根据当P 、C 、D 共线时根据“两点之间,线段最短”得出PC +PD 最短,求出CD 的直线解析式,令y =0,求出x 的值,即可得出P 点的坐标. 【解题过程】解:(1)∵二次函数的图象经过坐标原点O (0,0),∴代入二次函数y =x 2-2mx +m 2-1,得出:m 2-1=0,解得:m =±1, ∴二次函数的解析式为:y =x 2-2x 或y =x 2+2x ;(2)∵m =2, ∴二次函数y =x 2-2mx +m 2-1得:y =x 2-4x +3=(x -2)2-1,∴抛物线的顶点为:D (2,-1),当x =0时,y =3,∴C 点坐标为:(0,3),∴C (0,3)、D (2,-1); (3)当P 、C 、D 共线时PC +PD 最短, 【方法一】∵C (0,3)、D (2,-1),设直线CD 的解析式为y =kx +3,代入得:2k +3=-1,∴k =-2,∴y =-2x +3, 当y =0时,-2x +3=0,解得x =32,∴PC +PD 最短时,P 点的坐标为:P (32,0).【方法二】过点D 作DE ⊥y 轴于点E , ∵PO ∥DE ,∴PO DE =CO CE ,∴PO 2=34,解得:PO =32,∴PC +PD 最短时,P 点的坐标为:P (32,0).2.(11)如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.【思路点拨】(1)把点A 的坐标代入求出b 的值,即可得出抛物线的解析式,通过配方法即可求出顶点D 的坐标; (2)观察发现△ABC 是直角三角形,可以通过勾股定理的逆定理证明.由抛物线的解析式,分别求出点B ,C 的坐标,再得出AB ,AC ,BC 的长度,易得AC 2+BC 2=AB 2,得出△ABC 是直角三角形;(3)作出点C 关于x 轴的对称点C ′,连接C 'D 交x 轴于点M ,根据“两点之间,线段最短”可知MC +MD 的值最小.求出直线C 'D 的解析式,即可得出点M 的坐标,进而求出m 的值. 【解题过程】解:(1)∵点A (-1,0)在抛物线y =12x 2+bx -2上,∴12×(-1 )2+b ×(-1)-2=0,解得b =-32,∴抛物线的解析式为y =12x 2-32x -2=12(x -32)2-258,∴顶点D 的坐标为 (32,-258).(2)当x =0时y =-2,∴C (0,-2),OC =2.当y =0时,12x 2-32x -2=0,∴x 1=-1,x 2=4,∴B (4,0),∴OA =1,OB =4,AB =5.∵AB 2=25,AC 2=OA 2+OC 2=5,BC 2=OC 2+OB 2=20,∴AC 2+BC 2=AB 2. ∴△ABC 是直角三角形.(3)作出点C 关于x 轴的对称点C ′,则C ′(0,2),OC ′=2,连接C ′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,MC +MD 的值最小. 【方法一】设直线C ′D 的解析式为y =kx +n ,则⎩⎨⎧n =232k +n =-258,解得:⎩⎨⎧n =2k =-4112.∴y =-4112x +2. ∴当y =0时,-4112x +2=0,x =2441.∴m =2441.【方法二】设抛物线的对称轴交x 轴于点E .∵ED ∥y 轴,∴∠OC ′M =∠EDM ,∠C ′OM =∠DEM ,∴△C ′OM ∽△DEM . ∴OM EM =OC ′ED ,∴m 32-m =2258,∴m =2441.3.(11)已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y=33x+3对称.(1)求A、B两点坐标,并证明点A在直线l上;(2)求二次函数解析式;(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.【思路点拨】(1)二次函数y=ax2+2ax﹣3a(a≠0)中只有一个未知参数a,令y=0,解出方程ax2+2ax﹣3a=0(a ≠0),即可得到点A,B的坐标.把点A的坐标代入直线l的解析式即可判断A是否在直线上;(2)根据点H、B关于过A点的直线l:y=33x+3对称,得出AH=AB=4,过顶点H作HC⊥AB交AB于C点,得AC=12AB=2,利用勾股定理求出HC的长,即可得出点H的坐标,代入二次函数解析式,求出a,即可得到二次函数解析式;(3)直线BK∥AH易得直线BK的解析式,联立直线l的解析式方程组,即可求出K的坐标.因为点H,B 关于直线AK对称,所以HN=BN,所以根据“两点之间,线段最短”得出HN+MN的最小值是MB.作点K关于直线AH的对称点Q,连接QK,交直线AH于E,所以QM=KM,易得BM+MK的最小值为BQ,即BQ的长是HN+NM+MK的最小值,求出QB的长即可.【解题过程】解:(1)依题意,得ax2+2ax﹣3a=0(a≠0),解得x1=﹣3,x2=1,∵B点在A点右侧,∴A点坐标为(﹣3,0),B点坐标为(1,0),∵直线l:y=33x+3,当x=﹣3时,y=33×(-3)+3=0,∴点A在直线l上.(2)∵点H、B关于过A点的直线l:y=33x+3对称,∴AH=AB=4,过顶点H作HC⊥AB交AB于C点,则AC=12AB=2,HC=23,∴顶点H(-1,23),代入二次函数解析式,解得a=-32,∴二次函数解析式为y=-32x2-3x+332,(3)直线AH 的解析式为y =3x +33,直线BK 的解析式为y =3x +33,由⎩⎪⎨⎪⎧y =33x +3y =3x -3,解得⎩⎨⎧x =3y =23,即K (3,23),则BK =4,∵点H 、B 关于直线AK 对称,∴HN +MN 的最小值是MB ,KD =KE =23,过点K 作直线AH 的对称点Q ,连接QK ,交直线AH 于E ,则QM =MK ,QE =EK =23,AE ⊥QK , ∴BM +MK 的最小值是BQ ,即BQ 的长是HN +NM +MK 的最小值, ∵BK ∥AH ,∴∠BKQ =∠HEQ =90°,由勾股定理得QB =8, ∴HN +NM +MK 的最小值为8.4.(14)如图,对称轴为直线x =2的抛物线经过A (-1,0),C (0,5)两点,与x 轴另一交点为B .已【思路点拨】(1)由对称轴为直线x =2,可以得出顶点横坐标为2,设二次函数的解析式为y =a (x -2)2+k ,再把点A ,B 的代入即可求出抛物线的解析式;(2)求四边形MEFP 的面积的最大值,要先表示出四边形MEFP 面积.直接求不好求,可以考虑用割补法来求,过点P 作PN ⊥y 轴于点N ,由S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME 即可得出;(3)四边形PMEF 的四条边中,线段PM ,EF 长度固定,当ME +PF 取最小值时,四边形PMEF 的周长取得最小值.将点M 向右平移1个单位长度(EF 的长度),得到点M 1(1,1),作点M 1关于x 轴的对称点M 2(1,-1),连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小. 【解题过程】解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5, ∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN •MN -12OM •OE=12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1 =-x 2+92x +92=-(x -94)2+15316∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316).(3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3). 四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值.如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1); 作点M 1关于x 轴的对称点M 2,则M 2(1,-1); 连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得: ⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF 周长最小.图1 图22.(14)如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了.(1)求点A ,B ,D 的坐标;(2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ的长最小时,求点P 的坐标,并直接写出点Q 的坐标.【思路点拨】(1)由顶点式直接得出点D 的坐标,再令y =0,得12(x -3)2-1=0解出方程,即可得出点A ,B 的坐标;(2)设HD 与AE 相交于点F ,可以发现△HEF 与△ADF 组成一个“8字型”.对顶角∠HFE =∠AFD ,只要∠FHE =∠FAD 即可.因为∠EHF =90°,只需证明∠EAD =90°即可.由勾股定理的逆定理即可得出△ADE 为直角三角形,得∠FHE =∠FAD =90°即可得出结论;(3)先画出图形.因为PQ 为⊙E 的切线,所以△PEQ 为直角三角形,半径EQ 长度不变,当斜边PE 最小时,PQ 的长度最小.设出点P 的坐标,然后表示出PE ,求出PE 的最小值,得到点P 的坐标,再求出点Q 的坐标即可. 【解题过程】解:(1)顶点D 的坐标为(3,-1).令y =0,得12(x -3)2-1=0,解得x 1=3+2,x 2=3-2.∵点A 在点B 的左侧,∴A 点坐标(3-2,0),B 点坐标(3+2,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,-1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72-(-1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90︒.∵∠MOE +∠COH =90︒,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90︒,∴△DCG ∽△EOM . ∴CG OM =DGEM ,即923=3EM .∴EM =2,即点E 坐标为(3,2),ED =3. 由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90︒.设AE 交CD 于点F .∴∠ADC +∠AFD =90︒.又∵∠AEO +∠HFE =90︒, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小.设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.∵y =12(x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)2-1=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1). 此时Q 点坐标为(3,1)或(195,135).6.(14)已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0). (1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ . (3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM .(ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值?若存在,求出点F 的坐标;若不存在,请说明理由.【思路点拨】(1)因为抛物线的对称轴是y 轴,所以b =0,再代入点(0,﹣1),(2,0)即可求出抛物线的解析式; (2)由(1)设出P 的坐标,分别表示出PE ,PQ 的长度,即可得出结论;(3)(i )因为BN ∥AM ,所以∠ABN +∠BAM =180°.由(2)的结论可得BO =BN ,AO =AM ,可得出∠BON =∠BNO ,∠AOM =∠AMO ,易得∠BON +∠AOM =90°再得到∠MON =90°即可;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,由(2)的结论根据矩形的性质可以得出结论. 【解题过程】解:(1)由题意,得⎩⎪⎨⎪⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎪⎨⎪⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1;(2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP =14a 2+1.在Rt △POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ;(3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°. ∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°,∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°, ∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,l∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O ,∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′, ∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点. ∵D (1,1),∴F 的横坐标为1,∴F (1,54).【举一反三】1.(12滨州)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.2.(13)在平面直角坐标系中,已知抛物线y =﹣12x 2+bx +c (b ,c 为常数)的顶点为P ,等腰直角三角形ABC 的顶点A 的坐标为(0,﹣1),C 的坐标为(4,3),直角顶点B 在第四象限.(1)如图,若该抛物线过A ,B 两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P 在直线AC 上滑动,且与AC 交于另一点Q .(i )若点M 在直线AC 下方,且为平移前(1)中的抛物线上的点,当以M 、P 、Q 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M 的坐标; (ii )取BC 的中点N ,连接NP ,BQ .试探究PQNP +BQ是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.3.(11眉山)如图,在直角坐标系中,已知点A(0,1),B(﹣4,4),将点B绕点A顺时针方向90°得到点C;顶点在坐标原点的拋物线经过点B.(1)求抛物线的解析式和点C的坐标;(2)抛物线上一动点P,设点P到x轴的距离为d1,点P到点A的距离为d2,试说明d2=d1+1;(3)在(2)的条件下,请探究当点P位于何处时,△PAC的周长有最小值,并求出△PAC的周长的最小值.【参考答案】1.解:(1)把A (﹣2,﹣4),O (0,0),B (2,0)三点的坐标代入y =ax 2+bx +c 中,得⎩⎨⎧4a -2b +c =-44a +2b +c =0c =0,解得a =﹣12,b =1,c =0,∴解析式为y =﹣12x 2+x . (2)由y =﹣12x 2+x =﹣12(x ﹣1)2+12,可得抛物线的对称轴为x =1,并且对称轴垂直平分线段OB ,∴OM =BM , ∴OM +AM =BM +AM ,连接AB 交直线x =1于M 点,则此时OM +AM 最小, 过点A 作AN ⊥x 轴于点N ,在Rt △ABN 中,AB =AN 2+BN 2=42+42=42, ∴OM +AM 最小值为42.2.解:(1)∵等腰直角三角形ABC 的顶点A 的坐标为(0,-1),C 的坐标为(4,3),∴点B 的坐标为(4,-1).∵抛物线过A (0,-1),B (4,-1)两点,∴ ⎩⎨⎧c =-1-12×16+4b +c =-1,解得:b =2,c =-1,∴抛物线的函数表达式为:y =-12x 2+2x -1.(2)(i )∵A (0,-1),C (4,3),∴直线AC 的解析式为:y =x -1.设平移前抛物线的顶点为P 0,则由(1)可得P 0的坐标为(2,1),且P 0在直线AC 上. ∵点P 在直线AC 上滑动,∴可设P 的坐标为(m ,m -1), 则平移后抛物线的函数表达式为:y =-12(x -m )2+m -1.解方程组:⎩⎨⎧y =x -1y =-12(x -m )2+(m -1),解得⎩⎨⎧x 1=m y 1=m -1, ⎩⎨⎧x 2=m -2y 2=m -3,∴P (m ,m -1),Q (m -2,m -3). 过点P 作PE ∥x 轴,过点Q 作QF ∥y 轴,则PE =m -(m -2)=2,QF =(m -1)-(m -3)=2.∴PQ =22=AP 0.若以M 、P 、Q 三点为顶点的等腰直角三角形,则可分为以下两种情况: ①当PQ 为直角边时:点M 到PQ 的距离为22(即为PQ 的长). 由A (0,-1),B (4,-1),P 0(2,1)可知,△ABP 0为等腰直角三角形,且BP 0⊥AC ,BP 0=22.如答图1,过点B 作直线l 1∥AC ,交抛物线y =-12x 2+2x -1于点M ,则M 为符合条件的点.∴可设直线l 1的解析式为:y =x +b 1,∵B (4,-1),∴-1=4+b 1,解得b ==-5,∴直线l 1的解析式为:y =x -5.解方程组 ⎩⎨⎧y =x -5y =-12x 2+2x -1,得:⎩⎨⎧x 1=4y 1=-1,⎩⎨⎧x 2=-2y 2=-7,∴M 1(4,-1),M 2(-2,-7).②当PQ 为斜边时:MP =MQ =2,可求得点M 到PQ 的距离为 2 . 如答图2,取AB 的中点F ,则点F 的坐标为(2,-1). 由A (0,-1),F (2,-1),P 0(2,1)可知:△AFP 0为等腰直角三角形,且点F 到直线AC 的距离为 2 .过点F 作直线l 2∥AC ,交抛物线y =-12x 2+2x -1于点M ,则M 为符合条件的点.∴可设直线l 2的解析式为:y =x +b 2,∵F (2,-1),∴-1=2+b 2,解得b 2=-3,∴直线l 2的解析式为:y =x -3.解方程组⎩⎨⎧y =x -3y =-12x 2+2x -1,得:⎩⎨⎧x 1=1+5y 1=-2+5,⎩⎨⎧x 1=1-5y 1=-2-5, ∴M 3(1+5,-2+5),M 4(1-5,-2-5). 综上所述,所有符合条件的点M 的坐标为:M 1(4,-1),M 2(-2,-7),M 3(1+5,-2+5),M 4(1-5,-2-5).(ii )PQNP +BQ存在最大值.理由如下:由i )知PQ =22为定值,则当NP +BQ 取最小值时,PQNP +BQ有最大值. 如答图2,取点B 关于AC 的对称点B ′,易得点B ′的坐标为(0,3),BQ =B ′Q . 连接QF ,FN ,QB ′,易得FN ∥PQ ,且FN =PQ ,∴四边形PQFN 为平行四边形.∴NP =FQ . ∴NP +BQ =FQ +B ′Q ≥FB ′=22+42=25.∴当B ′、Q 、F 三点共线时,NP +BQ 最小,最小值为25.∴PQ NP +BQ 的最大值为2225=105.F3.解:(1)设抛物线的解析式:y=ax2,∵拋物线经过点B(﹣4,4),∴4=a•42,解得a=14,所以抛物线的解析式为:y=14x2;过点B作BE⊥y轴于E,过点C作CD⊥y轴于D,如图,∵点B绕点A顺时针方向90°得到点C,∴Rt△BAE≌Rt△ACD,∴AD=BE=4,CD=AE=OE﹣OA=4﹣1=3,∴OD=AD+OA=5,∴C点坐标为(3,5);(2)设P点坐标为(a,b),过P作PF⊥y轴于F,PH⊥x轴于H,如图,∵点P在抛物线y=14x2上,∴b=14a2,∴d1=14a2,∵AF=OF﹣OA=PH﹣OA=d1﹣1=14a2﹣1,PF=a,在Rt△PAF中,PA=d2=AF2+PF2=(14a2-1)2+a2=14a2+1,∴d2=d1+1;(3)由(1)得AC=5,∴△PAC的周长=PC+PA+5=PC+PH+6,要使PC+PH最小,则C、P、H三点共线,∴此时P点的横坐标为3,把x=3代入y=14x2,得到y=94,即P点坐标为(3,94),此时PC+PH=5,∴△PAC的周长的最小值=5+6=11.。
最短路径问题 课件

知识点1:两点在直线异侧时的最短路径问题 【例1】 如图1-13-30-1,在直线l上找一点P,使得 PA+PB的和最小.
解:答图13-30-1,点P即为所求.
知识点2:两点在直线同侧时的最短路径问题 【例2】 如图1-13-30-3,已知直线l和l外两点A,B, 点A,B在l同侧,求作一点P,使点P在直线l上,并且 使PA+PB最短.
解:如答图13-30-6,作点A的对称点A′, 连接A′B,与直线l相交于点C,连接AC, 点C即为所求.
6. 如图1-13-30-9,正方形网格中每个小正方形边 长都是1.在直线l上找一点P,使PB+PC的值最小.
略.
7. 如图1-13-30-10,在平面直角坐标系中,点 A(4,4),B(2,-4).在y轴上求作一点P,使 PA+PB的值最小.(不写作法,保留作图痕迹)
略.
8. 如图1-13-30-11,∠XOY内有一点P,请在射线OX上 找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
解:如答图13-30-7,作点P关于OX对称的点 P1,关于OY对称的点P2,连接P1P2,交OX, OY于点M,N,则M,N两点即为所求.
9. 如图1-13-30-12,在△ABC中,AB=AC,AD是BC边 上的高,P是AB边上的一点,请在高AD上找一点E, 使得△PEB的周长最短.
解:作图略, 作点A关于直线l的对称点A′, 连接A′B与直线l交于点P, 则P点即为所求.
4. 如图1-13-30-7,直线l旁有两点A,B,在直线上 找一点CA,B两点的距离相等.
解:如答图13-30-5,点C,点D即为所求.
5. 如图1-13-30-8,l为某河流的南岸线,一天傍晚 某牧童在A处放牛,欲将牛牵到河边饮水后再回到家 B处,牧童想以最短的路程回家.请你在找中画出牛 饮水C的位置.
二次函数压轴题专题一 最短路径问题

二次函数压轴题专题一最短路径问题——和最小知识梳理最短路径就是无论在立体图形还是平面图形中,两点间的最短距离,常涉及以下 两个方面:1、两点之间,线段最短;2、垂线段最短。
常用思考的方式:1、把立体转化为平面;2、通过轴对称寻找对称点。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
例题导航例1:如图A 是锐角∠MON 内部任意一点,在∠MON 的两边OM ,ON 上各取一点B ,C ,组成三角形,使三角形周长最小.例:如图,A.B 两地在一条河的两岸,现要在河上建一座桥MN ,桥造在何处才能使从A 到B 的路径AMNB 最短?(假设河的两岸是平行的直线,桥要与河垂直) 解:1.将点B 沿垂直与河岸的方向平移一个河宽到E , 2.连接AE 交河对岸与点M,则点M 为建桥的位置,MN 为所建的桥。
证明:由平移的性质,得 BN ∥EM 且BN=EM, MN=CD, BD ∥CE, BD=CE, 所以A.B 两地的距:AM+MN+BN=AM+MN+EM=AE+MN, 若桥的位置建在CD 处,连接AC.CD.DB.CE, 则AB 两地的距离为:AC+CD+DB=AC+CD+CE=AC+CE+MN,在△ACE 中,∵AC+CE >AE, ∴AC+CE+MN >AE+MN,即AC+CD+DB >AM+MN+BN 所以桥的位置建在CD 处,AB 两地的路程最短。
例:如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,•要在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,•可使所修的渠道最短,试在图中确定该点。
作法:作点B 关于直线 a 的对称点点C,连接AC 交直线a 于点D ,则点D 为建抽水站的位置。
证明:在直线 a 上另外任取一点E ,连接AE.CE.BE.BD,··CDA BEa∵点B.C 关于直线 a 对称,点D.E 在直线 a 上,∴DB=DC,EB=EC, ∴AD+DB=AD+DC=AC, AE+EB=AE+EC在△ACE 中,AE+EC >AC, 即 AE+EC >AD+DB所以抽水站应建在河边的点D 处,常见问题归纳“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题).如图所示,在直线l 上找一点P 使得PA +PB 最小.当点P 为直线AB ′与直线l 的交点时,PA +PB 最小.【方法归纳】①如图所示,在直线l 上找一点B 使得线段AB 最小.过点A 作AB ⊥l ,垂足为B ,则线段AB 即为所求.②如图所示,在直线l 上找一点P 使得PA +PB 最小.过点B 作关于直线l 的对称点B ′,BB ′与直线l 交于点P ,此时PA +PB 最小,则点P 即为所求.③如图所示,在∠AOB 的边AO ,BO 上分别找一点C ,D 使得PC +CD +PD 最小.过点P 分别作关于AO ,BO 的对称点E ,F ,连接EF ,并与AO ,BO 分别交于点C ,D ,此时PC +CD +PD 最小,则点C ,D 即为所求.④如图所示,在∠AOB 的边AO ,BO 上分别找一点E ,F 使得DE +EF +CF 最小.分别过点C ,D 作关于AO ,BO 的对称点D ′,C ′,连接D ′C ′,并与AO ,BO 分别交于点E ,F ,此时DElBAllllBAOBOB+EF +CF 最小,则点E ,F 即为所求.⑤如图所示,长度不变的线段CD 在直线l 上运动,在直线l 上找到使得AC +BD 最小的CD 的位置.分别过点A ,D 作AA ′∥CD ,DA ′∥AC ,AA ′与DA ′交于点A ′,再作点B 关于直线l 的对称点B ′,连接A ′B ′与直线l 交于点D ′,此时点D ′即为所求.⑥如图所示,在平面直角坐标系中,点P 为抛物线(y =14x 2)上的一点,点A (0,1)在y轴正半轴.点P 在什么位置时PA +PB 最小?过点B 作直线l :y =-1的垂线段BH ′,BH ′与抛物线交于点P ′,此时PA +PB 最小,则点P 即为所求.二次函数中最短路径例题例1.(13广东)已知二次函数y =x 2-2mx +m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m =2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标; (3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BOB Oll练习1.(11菏泽)如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.练习2.(12滨州)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.例2.(14海南)如图,对称轴为直线x =2的抛物线经过A (-1,0),C (0,5)两点,与x 轴另一交点为B .已知M (0,1),E (a ,0),F (a +1,0),点P 是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a =1时,求四边形MEFP 的面积的最大值,并求此时点P 的坐标;(3)若△PCM 是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小?请说明理由.【思路点拨】 (1)由对称轴为直线x =2,可以得出顶点横坐标为2,设二次函数的解析式为y =a (x -2)2+k ,再把点A ,B 的代入即可求出抛物线的解析式;(2)求四边形MEFP 的面积的最大值,要先表示出四边形MEFP 面积.直接求不好求,可以考虑用割补法来求,过点P 作PN ⊥y 轴于点N ,由S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME 即可得出; (3)四边形PMEF 的四条边中,线段PM ,EF 长度固定,当ME +PF 取最小值时,四边形PMEF 的周长取得最小值.将点M 向右平移1个单位长度(EF 的长度),得到点M 1(1,1),作点M 1关于x 轴的对称点M 2(1,-1),连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小. 【解题过程】解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5,∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN•MN -12OM •OE =12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1=-x 2+92x +92 =-(x -94)2+15316 ∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316). (3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3).四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值. 如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1);作点M 1关于x 轴的对称点M 2,则M 2(1,-1);连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得:⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF 周长最小.图1 图2练习3.(11眉山)如图,在直角坐标系中,已知点A (0,1),B (﹣4,4),将点B 绕点A 顺时针方向90°得到点C ;顶点在坐标原点的拋物线经过点B . (1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为d 1,点P 到点A 的距离为d 2,试说明d 2=d 1+1;(3)在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出△PAC 的周长的最小值.例4.(14福州)如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了. (1)求点A ,B ,D 的坐标; (2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标.【思路点拨】(1)由顶点式直接得出点D 的坐标,再令y =0,得12(x -3)2-1=0解出方程,即可得出点A ,B 的坐标;(2)设HD 与AE 相交于点F ,可以发现△HEF 与△ADF 组成一个“8字型”.对顶角∠HFE =∠AFD ,只要∠FHE =∠FAD 即可.因为∠EHF =90°,只需证明∠EAD =90°即可.由勾股定理的逆定理即可得出△ADE 为直角三角形,得∠FHE =∠FAD =90°即可得出结论;(3)先画出图形.因为PQ 为⊙E 的切线,所以△PEQ 为直角三角形,半径EQ 长度不变,当斜边PE 最小时,PQ 的长度最小.设出点P 的坐标,然后表示出PE ,求出PE 的最小值,得到点P 的坐标,再求出点Q 的坐标即可.【解题过程】解:(1)顶点D 的坐标为(3,-1).令y =0,得12 (x -3)2-1=0,解得x 1=3+2,x 2=3-2.∵点A 在点B 的左侧,∴A 点坐标(3-2,0),B 点坐标(3+2,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,-1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72-(-1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90︒.∵∠MOE +∠COH =90︒,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90︒,∴△DCG ∽△EOM . ∴CG OM =DGEM ,即923=3EM .∴EM =2,即点E 坐标为(3,2),ED =3. 由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90︒.设AE 交CD 于点F .∴∠ADC +∠AFD =90︒.又∵∠AEO +∠HFE =90︒, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小.设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.∵y =12 (x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)21=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1).此时Q 点坐标为(3,1)或(195,135).例5.(14遂宁)已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ .(3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM . (ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值?若存在,求出点F 的坐标;若不存在,请说明理由.【解题过程】解:(1)由题意,得⎩⎨⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎨⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1; (2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP =14a 2+1.在Rt △POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ; (3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°.∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°,∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°, ∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O ,∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′,∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点.∵D (1,1),∴F 的横坐标为1,∴F (1,54).l。
最短路径问题梳理

按照路径最值问题的构成或解答方式分组。
模型组一
1 两点一线异侧和最小值问题 问题:两定点A、B位于直线l异侧,在直线l上找一点P,使PA+PB值最 小. 问题解决:
结论:根据两点之间线段最短,PA+PB的最小值即为线段AB长.
模型组一
2. 两点一线同侧和最小值问题 问题:两定点A、B位于直线l同侧,在直线l上找一点P,使得PA+PB值 最小. 问题解决:
(分析:PQ为定值,只需AP+QB的值最小,可通 过平移,使P、Q“接头”,转化为基本模型)
解:将点A沿着平行于l的方向,向右移至A´, 使AA´=PQ=a,连接A´B交直线l于点Q,在l上截取
PQ=a(P在Q左边),则线段PQ即为所求,此 时
AP+PQ+QB的最小值为A´B+PQ,即A´B+a
ห้องสมุดไป่ตู้
模型组三
解:作点A关于OM的对称点A′,过点A′作AQ⊥ON 于 点Q,A′Q交OM于点P,此时AP+PQ最小;
理由:由轴对称的性质知AP=A′P, 要使AP+PQ最小, 只需A′P+PQ最小,从而 转化为拓展模型1
模型组二
3. “胡不归”问题 基本模型:两定一动,动点在定直线上
问题:点A为直线l上一定点,点B为直线外一定点, P为直线l上一动点,要使 AP+BP最小.
模型组四
2.异侧差最小值问题
问题:两定点A、B位于直线l异侧,在直线l上找一点P,使得|PA-
PB|的值最小. 问题解决:
A▪
B▪
结论:根据垂直平分线上的点到线段两端点的距 离相等,当PA=PB时,|PA-PB|=0.
模型组四总结:
最短路径问题

A
O
N
3. 两定两动型最值
例:在∠MON的内部有点A和点B,在OM 上找一点C,在ON上找一点D,使得四边形 ABCD周长最短.
M
A
B
O
N
例:(造桥选址)将军每日需骑马从军营出发,去 河岸对侧的瞭望台观察敌情,已知河流的宽度为30 米,请问,在何地修浮桥,可使得将军每日的行程 最短?
A
C
D
B
4. 垂线段最短型
最短路径问题
1.两定一动型:两定点到一动 点的距离和最小
原理:两点之间线段最短。
例:在定直线l上找一个动点C,使动点C到两 个定点A与B的距离之和最小, 即CA+CB的和最小.
B A
l
2.两动一定型 例:在∠MON的内部有一点A,在OM上找 一点B,在ON上找一点C,使得△BAC周长 最短.
M
A
D
E
B
C
3.正方形ABCD的边长为8,M在DC上,且 DM=2,N是AC上的一动点,DN+MN的最小值 为————
课堂小结
通过本节课的学习,
你有哪些收获 ?作业CD NhomakorabeaA
B
典型例题
1.如图,在等边△ABC中,AB = 6,AD⊥BC, E是AC上的一点,M是AD上的一点,且AE = 2, 求EM+EC的最小值
A
A
E M
E
M
H
B
D
CB
D
C
2.正方形ABCD的面积为12, ABE是等边三角 形,点E在正方形ABCD内,在对角线AC上有一 点P,使PD+PE的和最小,则这个最小值是
例1:在∠MON的内部有一点A,在OM上找一点 B,在ON上找一点C,使得AB+BC最短.
最短路径与最小生成树的区别

最短路径与最小生成树的区别
在图论中,最短路径和最小生成树是两个重要的概念。
它们都是用来解决图中节点之间的距离问题,但是它们的解决方法和目的却有所不同。
最短路径问题是指在一个有向或无向加权图中,找到从一个节点到另一个节点最短的路径。
最短路径可以使用Dijkstra算法和Bellman-Ford算法来解决。
这类问题通常是求出从一个节点到其他节点的最短距离,通常用于网络路由、GPS导航等应用。
最小生成树问题是指在一个无向加权图中,找到一个生成树,使得该树中的所有边权之和最小。
最小生成树可以使用Prim算法和Kruskal算法来求解。
这类问题通常是在需要将图连接起来的场合,比如铺设电缆、通信网络等场合。
因此,最短路径问题和最小生成树问题虽然都与计算节点间距离有关,但是它们的解决方法和应用场景却有很大的差异。
在具体应用中,需要根据实际情况选择合适的算法和方法来解决问题。
- 1 -。
最短路径的十二个基本问题

两点之间线段最短. PA+PB 最小值为 A B'.
原理
分别作点 P 关于两直 线的对称点 P'和 P'', 在直线 l1 、l2 上分别求 连 P'P'',与两直线交 点 M、N,使△PMN 的 点即为 M,N. 周长最小.
两点之间线段最短. PM+MN+PN 的最小值为 线段 P'P''的长.
【十二个基本问题】
【问题 1】
作法
图形
原理
连 AB,与 l 交点即为
P.
在直线 l 上求一点 P,
使 PA+PB 值最小.
【问题 2】“将军饮马”
作法
作 B 关于 l 的对称点
B'连 A B',与 l 交点
在直线 l 上求一点 P,
即为 P.
使 PA+PB 值最小.
【问题 3】
作法
图形 图形
两点之间线段最短. PA+PB 最小值为 AB.
原理
将点 A 向下平移 MN 的
长度单位得 A',连 A'
B,交 n 于点 N,过 N 作
直线 m ∥ n ,在 m 、n , NM⊥ m 于 M.
上分别求点 M、N,使
MN⊥ m ,且 AM+MN+BN
的值最小.
【问题 6】
作法
图形
将点 A 向右平移 a 个
长度单位得 A',作 A'
关于 l 的对称点 A'',连 在直线 l 上求两点 M、N
对称点 B',连 A'B' l2 上一定点,在 l2 上求 交l2 于 M,交 l1 于 N.
点 M,在 l1 上求点 N,
使 AM+MN+NB 的 值 最
小.
最短路径问题初中数学模型

课后精练
【提示】过B作BF⊥OA于F,过D作DE⊥OA于E,过C 作CM⊥OA于M;证明△OBF∽△ODE,△ACM∽△ADE, 再根据相似三角形线段的比例关系,求解即可.
【答案】8
答案图
课后精练 11.在Rt△ABC中,∠ACB=90°,AC=8,BC= 6,点D是以点A为圆心4为半径的圆上一点,连接BD, 点M为BD中点,线段CM长度的最大值为______.
OC 交圆 O 于点 F,如图.
由题可得∠AED=∠AEB=90°,
∴点 E 在以 AB 中点 O 为圆心的圆上(在△ABC 内部).
由题意,得 AC=AB=4,半径 OE=OA=2,
∴由勾股定理,得 OC=2 5.
答案图
根据三角形三边的关系,得
CE≥OC-OE=2 5-2(取等号时非三角形),
∴当点 C,E,O 三点共线时,CE 最小,最小值为 2 5-2.
15
11 由相似三角形线段的比例关系表示出
A.4
B. 4
C.3
D. 4
HF,DH,再由S△CEF=S梯形HFCD+S△CDE-
S△EHF列关系式即可.
课后精练 5.如图,E是边长为4 cm的正方形ABCD的边AB上 一点,且AE=1 cm,P为对角线BD上的任意一点,则 AP+EP的最小值是___5___cm.
课堂精讲
例 2 如图,△ABC 中,∠BAC=60°,∠ABC=45°, AB=2 2,D 是线段 BC 上的一个动点,以 AD 为直径画⊙O 分别交 AB,AC 于点 E,F,连接 EF,则 EF 的最小值是________.
课堂精讲
【分析】由垂线段的性质可知,当 AD 为△ABC 的边 BC 上的高时,直径 AD 最短.如图,连接 OE,OF,过点 O 作 OH⊥EF,垂足为 H,
最短路径(将军饮马)问题(知识梳理与考点分类讲解)(人教版)(教师版) 24-25学年八年级数学上册

专题13.10最短路径(将军饮马)问题(知识梳理与考点分类讲解)第一部分【知识点归纳】【模型一:两定交点型】如图1,直线l和l的异侧两点A.B,在直线l上求作一点P,使PA+PB 最小;图1【模型二:两定一动型】如图2,直线l和l的同侧两点A.B,在直线l上求作一点P,使PA+PB 最小(同侧转化为异侧);图2【模型三:一定两动型】如图3,点P是∠MON内的一点,分别在OM,ON上作点A,B。
使△PAB的周长最小。
图3【模型四:两定两动型】如图4,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。
使四边形PAQB的周长最小。
图4【模型五:一定两动(垂线段最短)型】如图5,点A是∠MON外的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小。
图5【模型六:一定两动,找(作)对称点转化型】如图6,点A是∠MON内的一点,在射线ON 上作点P,使PA与点P到射线OM的距离之和最小。
图6【考点1】两定一动型;【考点2】一定两动(两点之间线段最短)型;【考点3】一定两动(垂线段最短)型;【考点4】两定两动型;【考点5】一定两动(等线段)转化型;.第二部分【题型展示与方法点拨】【考点1】两定一动型;【例1】(23-24八年级上·全国·课后作业)如图,在ABC ∆中,3,4AB AC ==,EF 垂直平分BC ,交AC 于点D ,则ABP 周长的最小值是()A .12B .6C .7D .8【答案】C 【分析】本题主要考查了,轴对称﹣最短路线问题的应用,解此题的关键是找出P 的位置.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,根据题意知点B 关于直线EF 的对称点为点C ,故当点P 与点D 重合时,AP BP +的值最小,即可得到ABP 周长最小.解:∵EF 垂直平分BC ,∴点B ,C 关于EF 对称.∴当点P 和点D 重合时,AP BP +的值最小.此时AP BP AC +=,∵3,4AB AC ==,ABP ∴ 周长的最小值是347AP BP AB AB AC ++=+=+=,故选:C .【变式】(23-24八年级上·广东广州·期中)如图,在ABC V 中,1216AB AC ==,,20BC =.将ABC V 沿射线BM 折叠,使点A 与BC 边上的点D 重合,E 为射线BM 上的一个动点,则CDE 周长的最小值.【答案】24【详解】设BM 与AC 的交点为点F ,连接AE ,DF 先根据折叠的性质可得12BD AB ==,DF AF =,DE AE =,BDF BAF ∠=∠,再根据两点之间线段最短可得当点E 与点F 重合时,CDE 周长最小,进而求解即可.解:如图,设BM 与AC 的交点为点F ,连接AE ,DF ,由折叠的性质得:12BD AB ==,DF AF =,DE AE =,BDF BAF ∠=∠,20128CD BC BD ∴=-=-=,CDE ∴ 周长8CD DE CE AE CE =++=++,要使CDE 周长最小,只需AE CE +最小,由两点之间线段最短可知,当点E 与点F 重合时,最小值为AC ,∴CDE 周长为:681624AC +=+=.故答案为:24.【点拨】本题考查了折叠的性质等知识点,熟练掌握折叠的性质是解题关键.【考点2】一定两动(两点之间线段最短)型;【例2】(23-24八年级上·湖北省直辖县级单位·期末)如图,45MON ∠=︒,P 为MON ∠内一点,A 为OM 上一点,B 为ON 上一点,当PAB 的周长取最小值时,APB ∠的度数为()A .45︒B .90︒C .100︒D .135︒【答案】B 【分析】本题主要考查了最短路线问题、四边形的内角和定理、轴对称的性质等知识点,掌握两点之间线段最短的知识画出图形是解题的关键.如图:作P 点关于OM ON 、的对称点A B ''、,连接A B '',此时PAB 的周长最小为A B '',求出A B ''即可.解:如图:作P 点关于OM ON 、的对称点A B ''、,然后连接A B '',∵点A '与点P 关于直线OM 对称,点B '与点P 关于ON 对称,∴A P OM B P ON A A AP B B BP ''''⊥⊥==,,,,∴A APA B BPB ''''∠=∠∠=∠,,∵A P OM B P ON ''⊥⊥,,∴180MON A PB ''∠+∠=︒,∴18045135A PB ''∠=︒-︒=︒,在A B P ''△中,由三角形的内角和定理可知:18013545A B ''∠+∠=︒-︒=︒,∴45A PA BPB ''∠+∠=︒,∴1354590APB ∠=︒-︒=︒.故选:B .【变式】(23-24八年级上·江苏无锡·期中)如图,45AOB ∠=︒,点M N 、分别在射线OA OB 、上,5MN =,15OMN S = ,点P 是直线MN 上的一个动点,点P 关于OA 的对称点为1P ,点P 关于OB 的对称点为2P ,连接1OP 、2OP 、12PP ,当点P 在直线MN 上运动时,则12OPP 面积的最小值是.【考点3】一定两动型(垂线段最短);【例3】(22-23八年级上·湖北武汉·期末)如图,在ABC V 中,3AB =,4BC =,5AC =,AB BC ⊥,点P 、Q 分别是边BC 、AC 上的动点,则AP PQ +的最小值等于()A .4B .245C .5D .275【答案】B 【分析】作A 过于BC 的对称点A ',过点A '作A Q AC '⊥,交AC 于点Q ,交BC 于点P ,根据对称可得:AP PQ A P PQ A Q ''+=+≥,得到当,,A P Q '三点共线时,AP PQ +最小,再根据垂线段最短,得到A Q AC '⊥时,A Q '最小,进行求解即可.解:作A 过于BC 的对称点A ',过点A '作A Q AC '⊥,交AC 于点Q ,交BC 于点P ,【变式】(23-24七年级下·陕西西安·阶段练习)如图,在Rt ABC △中,90ACB ∠=︒,3AC =,4BC =,5AB =,AD 是ABC V 的角平分线,若P Q 、分别是AD 和AC 边上的动点,则PC PQ +的最小值是.AD 是BAC ∠的平分线,1QAD Q AD∴∠=∠在AQD 与1AQ D 中【考点4】两定两动型;【例4】如图,已知24AOB ∠=︒,OP 平分AOB ∠,1OP =,C 在OA 上,D 在OB 上,E 在OP 上.当CP CD DE ++取最小值时,此时PCD ∠的度数为()A .36︒B .48︒C .60︒D .72︒【答案】D 【分析】作点P 关于OA 的对称点P',作点E 关于OB 的对称点'E ,连接'OP 、'PP 、'OE 、'EE 、''P E ,则由轴对称知识可知=''CP CD DE CP CD DE ++++,所以依据垂线段最短知:当''P C D E 、、、在一条直线上,且'''P E OE ⊥时,CP CD DE ++取最小值,根据直角三角形的两锐角互余及三角形外角的性质可以'P C PC =,'E D ED =,'1OP OP ==,=''CP CD DE CP CD DE ++++,'P OE ∠''P C D E 、、、在一条直线上,且''P E ''=9048=42OP E ∠︒-︒︒,'='''=7842CP P OP P OP E ∠∠-∠︒-︒=【答案】44βα-=︒【分析】本题考查轴对称—最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题.OQM OQM NQP '∴∠=∠=∠,OPQ ∠∴1(180)2PQN AOB α∠=︒-=∠+∠44βα∴-=︒,故答案为:44βα-=︒.【考点5】一定两动(等线段)转化型;【例5】(20-21八年级上·湖北鄂州·期中)如图,AD 为等腰△ABC 的高,其中∠ACB =50°,AC =BC ,E ,F 分别为线段AD ,AC 上的动点,且AE =CF ,当BF +CE 取最小值时,∠AFB 的度数为()A .75°B .90°C .95°D .105°【答案】C 【分析】先构造△CFH 全等于△AEC ,得到△BCH 是等腰直角三角形且FH=CE ,当FH+BF 最小时,即是BF+CE 最小时,此时求出∠AFB 的度数即可.解:如图,作CH ⊥BC ,且CH=BC ,连接HB ,交AC 于F ,此时△BCH 是等腰直角三角形且FH+BF 最小,∵AC=BC ,∴CH=AC ,∵∠HCB=90°,AD ⊥BC ,∴AD//CH ,∵∠ACB=50°,∴∠ACH=∠CAE=40°,∴△CFH ≌△AEC ,∴FH=CE ,∴FH+BF=CE+BF 最小,此时∠AFB=∠ACB+∠HBC=50°+45°=95°.故选:C .【点拨】本题考查全等三角形的性质和判定、等腰三角形的性质、最短路径问题,关键是作出辅助线,有一定难度.【变式】(23-24七年级下·四川宜宾·期末)在ABC V 中,80CAB ∠=︒,2AB =,3AC =,点E 是边AB 的中点,CAB ∠的角平分线交BC 于点D .作直线AD ,在直线AD 上有一点P ,连结PC 、PE ,则PC PE -的最大值是.∵CAB ∠的角平分线交∴FAP ∠∠=∵AP AP =,∴APF APE ≌∴PF PE =,第三部分【中考链接与拓展延伸】1、直通中考【例1】(2020·湖北·中考真题)如图,D 是等边三角形ABC 外一点.若8,6BD CD ==,连接AD ,则AD 的最大值与最小值的差为.【答案】12【分析】以CD 为边向外作等边三角形CDE ,连接BE ,可证得△ECB ≌△DCA 从而得到BE=AD ,再根据三角形的三边关系即可得出结论.解:如图1,以CD 为边向外作等边三角形CDE ,连接BE ,∵CE=CD ,CB=CA ,∠ECD=∠BCA=60°,∴∠ECB=∠DCA ,∴△ECB ≌△DCA (SAS ),∴BE=AD ,∵DE=CD=6,BD=8,∴8-6<BE<8+6,∴2<BE<14,∴2<AD<14.∴则AD 的最大值与最小值的差为12.故答案为:12【点拨】本题考查三角形全等与三角形的三边关系,解题关键在于添加辅助线构建全等三角形把AD 转化为BE 从而求解,是一道较好的中考题.【例2】(2020·新疆·中考真题)如图,在ABC V 中,90,60,4A B AB ∠=∠=︒=︒,若D 是BC 边上的动点,则2AD DC +的最小值为.在Rt DFC △中,30DCF ∠=︒,12DF DC ∴=,122()2AD DC AD DC +=+2()AD DF =+,∴当A ,D ,F 在同一直线上,即此时,60B ADB ∠=∠=︒,2、拓展延伸【例1】(23-24八年级上·江苏镇江·阶段练习)如图,AC 、BD 在AB 的同侧,点M 为线段AB 中点,2AC =,8BD =,8AB =,若120CMD ∠=︒,则CD 的最大值为()A .18B .16C .14D .12【答案】C 【分析】本题考查等边三角形的判定和性质,两点之间线段最短,解题的关键是学会添加常用辅助线,学会利用两点之间线段最短解决最值问题.如图,作点A 关于CM 的对称点A ',点B 关于DM 的对称点B ',证明'' A MB 为等边三角形,即可解决问题.解:如图,作点A 关于CM 的对称点A ',点B 关于DM 的对称点B ',∵120CMD ∠=︒,∴60∠+∠=︒AMC DMB ,∴60''∠+∠=︒CMA DMB ,∴60''∠=︒A MB ,∵MA MB MA MB ''===,∴'' A MB 为等边三角形∵14CD CA A B B D CA AM BD ''''<++=++=,∴CD 的最大值为14,故选:C .【例2】(22-23八年级上·湖北武汉·期末)如图,锐角ABC V 中,302A BC ∠=︒=,,ABC V 的面积是6,D 、E 、F 分别是三边上的动点,则DEF 周长的最小值是()A .3B .4C .6D .7∴AM AE AN ==,MF =∵BAC BAD DAC ∠=∠+∠∴MAN MAB BAD ∠=∠+∠∴(2MAN BAE EAC ∠=∠+∠。
《最短路径问题》课件

A A1
符合条件的路径,并标明桥的位置.
ll12
l3 B1 l4 B
课堂小结
最
短
A∙
路 径
造桥选址问题
M
问
A′
a b
题
N
∙B
即AM+NB+MN的值最小.
M′ a M
b
N′
N
∙B
新知探究 跟踪训练
如图,从A地到B地要经过一条小河(河的两岸平行), 现要在河上建一座桥(桥垂直于河的两岸),应如何 选择桥的位置才能使从A地到B地的路程最短?
A
B
解:(1)如图,过点A作AC垂直于河岸,且使得AC的 长等于河宽; (2)连接BC,与河岸GH相交于点N,且过点N作 MN⊥EF于点M,则MN即为所建桥的位置. A
点N,点A移动到点A′,则AA′=MN,AM+NB=A′N+NB.此
时问题转化为,当点N在直线b的什么位置时,A′N+ NB的值最小.A∙ M
a
A′
b
N
∙B
如图,连接A′,B,线段A′B最短.因此,线段A′B与直线 b的交点即为所求的点N的位置,即在此处造桥MN,所 得路径AMNB是最短的.
A∙ M
《最短路径问题》
知识回顾
1.两点一线型.
如图,点A,B分别是直线l异侧的两个点,在直线l上找
一点C,使得AC+BC的值最小,此时点C就是线段AB与
直线l的交点.
A
C
l
B
1.两点一线型.
如图,点A,B是直线l同侧的两
B
点,在直线l上找一点C使得
A
AC+BC的值最小,这时先作点B
最短路径问题(Dijkstra算法)和最小生成树(Kruskal算法和Prim算法)

t(j)=tmin;
end
end
end
ifk==n
break;
end
end
T;
c;
Prim算法程序:
function[T c] =Primf(a)
%a表示权值矩阵
%c表示生成树的权和
%T表示生成树的边集合
l=length(a);
a(a==0)=inf;
k=1:l;
listV(k)=0;
上机实验1、2
1.最短路径问题(Dijkstra算法)
2.最小生成树(Kruskal算法和Prim算法)
一、最短路径问题(Dijkstra算法)
实验问题描述:如图的交通网络,每条弧上的数字代表车辆在该路段行驶所需的时间,有向边表示单行道,无向边表示可双向行驶。若有一批货物要从1号顶点运往11号顶点,问运货车应沿哪条线路行驶,才能最快地到达目的地。
listV(1)=1;
e=1;
while(e<l)
min=inf;
fori=1:l
iflistV(i)==1
forj=1:l
iflistV(j)==0&min>a(i,j)
min=a(i,j);b=a(i,j);
s=i;d=j;
end
end
end
end
listV(d)=1;
distance(e)=b;
T =
3 4 1 2
4 5 3 5
c =
10
>> a=[0 5 3 7 inf;5 0 8 inf 4;3 8 0 1 6;7 inf 1 0 2;inf 4 6 2 0];
>> [T c] =Primf(a)
二次函数压轴题最短路径问题

最短路径问题一一和最小【方法说明】“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题)•如图所示,在直线 丨上找一点P 使得P%PB 最小•当点P 为直线AB 与直线丨的交点时,PA + PB 最小.B-r | P ,B'B4 P .B'③如图所示,在/ AOB 勺边AO B0上分别找一点 C D 使得PO C 戻PD 最小•过点P 分别作关于 AO BO 的对称点E ,F ,连接EF,并与AO B0分别交于点C, D,此时PO C 戻PD 最小,则点C D 即为所求.④如图所示,在/ AOB 勺边AO BO 上分别找一点 E F 使得D 可EF + CF 最小•分别过点 C , D 作关于AO BO 的对称点D ; C ;连接DC,并与AO BC 分别交于点E, F ,此时DE^EF + CF 最小,则点E, F 即为所求.⑤如图所示,长度不变的线段 CD 在直线丨上运动,在直线丨上找到使得AO BD 最小的CD 的位置•分别过 点A ,D 作AA// CD DA// AC AA 与 DA 交于点A ;再作点B 关于直线丨的对称点B',连接A'B 与直线丨交于【方法归纳】在直线丨上找一点B 使得线段AB 最小•过点A 作AB1丨,垂足为B,则线段AB 即为所求.在直线 ②如图所示,点P ,此时PA^ PB 最小,则点P 即为所求.丨上找一点P 使得PA^ PB 最小•过点B 作关于直线丨的对称点B',BB'与直线丨交于BFB点D ,此时点D 即为所求.1⑥如图所示,在平面直角坐标系中,点P 为抛物线(y = 4X 1 2)上的一点,点A ( 0, 1)在y 轴正半轴.点P在什么位置时PA+PB 最小?过点B 作直线I : y =— 1的垂线段BH, BH 与抛物线交于点 P ,此时PA+ PB最小,则点P 即为所求.【思路点拨】 (1)由二次函数的图象经过坐标原点 0(0,0),直接代入求出 m 的值即可;1 (13广东)已知二次函数 y = x2 — 2m 灶卅一1. (1)当二次函数的图象经过坐标原点 0(0, 0)时,求二次函数的解析式;(2) 如图,当m= 2时,该抛物线与y 轴交于点C ,顶点为D 求C 、D 两点的坐标;(3) 在(2)的条件下,x 轴上是否存在一点 P ,使得PO PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BBB'(2) 把m= 2代入求出二次函数解析式,令 X = o ,求出y 的值,得出点C 的坐标;利用配方法或顶点坐标 公式求岀顶点坐标即可; (3) 根据当P C 、D 共线时根据"两点之间,线段最短"得出PC +PD 最短,求出CD 的直线解析式,令y=0,求出x 的值,即可得出P 点的坐标. 【解题过程】解:(1)T 二次函数的图象经过坐标原点0(0,0),•••代入二次函数y = X 3 4 5-2m 对m — 1,得出:m — 1 = 0,解得:m=± 1, •••二次函数的解析式为:y =x 2— 2x 或y = X 2 + 2x ;(2) v m= 2, •二次函数 y = x 2 — 2m 灶 m - 1 得:y = x 2— 4x + 3=( x — 2) 2 — 1,•抛物线的顶点为:D (2,— 1),当 x = 0 时,y = 3,• C 点坐标为:(0, 3),• C (0, 3)、D( 2,— 1 ); (3) 当P 、C D 共线时PO PD 最短,【方法一】:C ( 0, 3)、D( 2,— 1),设直线CD 的解析式为y = kx + 3,代入得:2k + 3=— 1 ,• k =— 2, • y = — 2x + 3, 3 3当y = 0时,一2x + 3= 0,解得x = 2,二PO PD 最短时,P 点的坐标为:P ( 2,0). 【方法二】过点D 作DEL y 轴于点E ,3• PO PD 最短时,P 点的坐标为:P (2,0).12. (11菏泽)如图,抛物线 y = 2x 2 + bx - 2与x 轴交于A , B 两点,与y 轴交于C 点,且A (- 1, 0).3 求抛物线的解析式及顶点 D 的坐标;4 判断△ ABC 勺形状,证明你的结论;5 点M(m 0)是x 轴上的一个动点,当 M G MD 的值最小时,求 m 的值.v PO/ DEPO =CODE" CE P0=32 = 4,解得:3 P0=2,【思路点拨】(1)把点A 的坐标代入求出b 的值,即可得出抛物线的解析式,通过配方法即可求出顶点D 的坐标;(2) 观察发现A ABC 是直角三角形,可以通过勾股定理的逆定理证明. 由抛物线的解析式,分别求出点B , C 的坐标,再得出AB AC BC 的长度,易得AC + BC = AB ,得出△ ABC 是直角三角形; (3) 作出点C 关于x 轴的对称点C ;连接C D 交x 轴于点M 根据“两点之间,线段最短”可知 MO MD 的值最小•求岀直线 C D 的解析式,即可得岀点 M 的坐标,进而求岀 m 的值. 【解题过程】1 2 1 23解:(1) v 点 A (- 1, 0)在抛物线 y =於 + bx — 2 上, /• 2^ (- 1 ) + b x (- 1) — 2= 0,解得 b =- ,1 2 31 32 25 一3 25二抛物线的解析式为 y =—必—2= 2 (x — 2)— 8,二顶点D 的坐标为 (2,— 8)•(2)当 x = 0 时 y = — 2,「. C (0,— 2),OC= 2•, 亠 1 2 3当 y = 0 时,2X — q x — 2 = 0,二 X 1=— 1, X 2= 4,•: B (4, 0),「• OA= 1, OB= 4, AB= 5.V A B = 25, A C = oA + oC = 5, B C = OC + OB = 20,「. A C + B C = A B • •••△ ABO 直角三角形. (3) 作出点C 关于x 轴的对称点C',则C'(0, 2), OC = 2,连接C'D 交x 轴于点M 根据轴对称性及两点之间线段最短可知, MO MD 勺值最小.【方法一】设直线C'D 的解析式为y = kx +n ,则3丄=_ 25,解得:2k + n = — ~8 41 24 24.当 y = 0 时,一12x + 2 = 0, x = 41 • . n== 41 • 【方法二】设抛物线的对称轴交x 轴于点E.v ED/ y 轴,OCM=/ EDM /C‘OM= / DEM .△ C’Og DEM .OM =OC . = 2 . 24…EM = E D 3 = 25,n 41 •2 — m 百n = 2十4141 .. y = — —x + 2 k =— • y 12x 十 23. (11福州)已知,如图,二次函数 y = ax 2+ 2ax - 3a (a H))图象的顶点为 H,与x 轴交于A B 两点(B 在A 点右侧),点H B 关于直线丨:y=£x +冷3对称.(1 )求A 、B 两点坐标,并证明点 A 在直线丨上; (2) 求二次函数解析式;(3) 过点B 作直线BK// AH 交直线丨于K 点,M N 分别为直线AH 和直线丨上的两个动点,连接 HN NM MK 求HN^ NMF MK 和的最小值.【思路点拨】(1 )二次函数y = ax 2+ 2ax - 3a(a 旳)中只有一个未知参数 a ,令y = 0,解出方程ax 2 + 2ax - 3a = 0(a ^D ), 即可得到点A ,B 的坐标•把点A 的坐标代入直线丨的解析式即可判断 A 是否在直线上;(2) 根据点H B 关于过A 点的直线丨:y = jx + 3对称,得出AH= AB= 4,过顶点H 作HCL AB 交AB 于1C 点,得AC= 2AB= 2,利用勾股定理求出 HC 的长,即可得出点 H 的坐标,代入二次函数解析式,求出 a ,即可得到二次函数解析式;(3) 直线BK// AH 易得直线BK 的解析式,联立直线 丨的解析式方程组,即可求出 K 的坐标•因为点 H B 关于直线AK 对称,所以HN= BN 所以根据“两点之间,线段最短"得出 HN b MN 的最小值是MB 作点K 关 于直线AH 的对称点Q 连接QK 交直线AH 于 E ,所以Ql = KM 易得BW MK 的最小值为BQ 即BQ 的长是 HN F NMF MK 勺最小值,求出 QB 的长即可. 【解题过程】解:(1)依题意,得 ax' + 2ax - 3a = 0 ( a®,解得 X 1=- 3,X 2 = 1,v B 点在A 点右侧,A 点坐标为(-3,0),B 点坐标为(1,0),丁直线丨:y =3,当x =- 3时,y = X - 3) + 3 = 0,点A 在直线丨上.过顶点 H 作 HCLAB 交 AB 于 C 点,贝U AC= 2AB= 2, HC= 2 3, 顶点H ( — 1, 2寸3),代入二次函数解析式,解得 a =—芈 二次函数解析式为y = — 2^x 2 — ^ 3x + ~2^,(2) v 点H 、B 关于过A 点的直线丨:二 AH= AB= 4,(3)直线AH 的解析式为y = »:;3x + 3 3,直线BK 的解析式为y =-J 3x + 3寸3, 由y=老X 十护,解得x- 3即K ( 3, 2、0,则BK= 4,y - 3x - 3 y - 6 7 3T 点H B 关于直线 AK 对称,••• HW M N 勺最小值是 MB KD= KE - 2*3,过点K 作直线AH 的对称点 Q 连接QK 交直线AH 于巳_则QM= MK QE F EK= ^-3, AE 1QK 二B 冊 MK 勺最小值是 BQ 即BQ 的长是HN b NM- MK 勺最小值, v BK// AHBK —/HE(- 90° ° 由勾股定理得 QB= 8 , 二HN - NM- MK 勺最小值为8.当a -1时,求四边形 MEFP 勺面积的最大值,并求此时点 P 的坐标;若厶PCM!以点P 为顶点的等腰三角形,求 a 为何值时,四边形 PMEF 周长最小?请说明理由.(2) (3)4. (14海南) 如图,对称轴为直线x - 2的抛物线经过A (- 1 , 0), C(0 , 5)两点,与x 轴另一交点为 B-已知 M (0, 1),E (a , 0),F (a +1, 0),点P 是第一象限内的抛物线上的动点.(1) 求此抛物线的解析式;【思路点拨】(1 )由对称轴为直线x = 2,可以得出顶点横坐标为 2,设二次函数的解析式为 y = a (x -2) 2+ k ,再把点 A , B 的代入即可求出抛物线的解析式; (2) 求四边形MEF 的面积的最大值,要先表示出四边形MEF 面积•直接求不好求,可以考虑用割补法来求,过点P 作PN4L y 轴于点N,由S 四边形MEFP = S 梯形OFP — S ^PM — S OM 即可得出;(3) 四边形PMEF 勺四条边中,线段 PM EF 长度固定,当M H PF 取最小值时,四边形 PMEF 勺周长取得最 小值•将点M 向右平移1个单位长度(EF 的长度),得到点M (1,1),作点M 关于x 轴的对称点M (1, —1),连接PM ,与x 轴交于F 点,此时MB PF = PM 最小.【解题过程】解:(1 )v 对称轴为直线x = 2,.••设抛物线解析式为 y = a (x — 2) °+ k .2 2.y = —( x — 2) + 9= — x +4x + 5.(2)当 a = 1 时,E (1 , 0) , F ( 2, 0) , OE= 1 , OF= 2•设 P( x , — x 2 + 4x + 5), 如答图2,过点P 作PNL y 轴于点N,则PNhx , O = — x 2+ 4x + 5,.Mf = ONF OM= — x 2 + 4x + 4.1 1 1MEF= S梯形 OFP— S A PM — ® OM =2 ( PI H OF ?O — 2PN?M — 2OMOE1 1 1=2 (x + 2) (— x +4x + 5) — ?x ?( — x + 4x + 4) —1 X 19 153 9 153•••当x = 4时,四边形MEFP 勺面积有最大值为16,此时点P 坐标为(4, 16 .(3)v M( 0, 1), C (0, 5) ,△ PCM!以点P 为顶点的等腰三角形,•点 P 的纵坐标为3 . 令 y =— X 2 + 4X + 5 =3,解得 x = 2± 6.T 点 P 在第一象限,• P (2 + 6, 3). 四边形PMEF 勺四条边中,PM EF 长度固定, 因此只要MH PF 最小,则PMEF 勺周长将取得最小值.如答图3,将点M 向右平移1个单位长度(EF 的长度),得M (1, 1); 作点M 关于x 轴的对称点M ,则M (1,- 1);连接PM,与x 轴交于 F 点,此时 M 曰PF = PM 最小.设直线PM 的解析式为y = m>H n ,将P(2 + 6, 3) , M ( 1,- 1)代入得:将 A (— 1, 0), C (0, 5 )代入得:9a + k = 04a + k = 5,解得a =— 1 k = 9 S四边形9 =-(X -4)153 16(m +n =6—T n = 3,解得:m =呼6+ 5当y = 0时,解得x = 4,0). 丁 a +1 =•斗咛1时,四边形PME 周长最小.4 6+ 4 n =5 ,顶点为D 了.(1) 求点A B , D 的坐标;(2) 连接CD 过原点O 作O 吐CD 垂足为H, OE 与抛物线的对称轴交于点 E,连接AE AD 求证:/ AEO=Z ADC(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点 切点为Q,当PQ 的长最小时,求点 P 的坐标,并直接写岀点 Q 的坐标.【思路点拨】1(1) 由顶点式直接得出点 D 的坐标,再令y = 0,得2(x 3)2 1 = 0解出方程,即可得出点 A B 的坐标; (2) 设HD 与AE 相交于点F ,可以发现厶ADF 组成一个“ 8字型” •对顶角/ HFE=Z AFD 只要/ FHE=/FAD 即可•因为/ EHF= 90 °,只需证明/ EAD= 90°即可•由勾股定理的逆定理即可得出△ ADE 为 直角三角形,得/FHE=Z FAD= 90°即可得出结论;(3) 先画出图形.因为PQ 为。
(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.

13.4 课题学习最短路径问题1.最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′,证明AC+CB<AC′+C′B.如下:证明:由作图可知,点B和B′关于直线l对称,所以直线l是线段BB′的垂直平分线.因为点C与C′在直线l上,所以BC=B′C,BC′=B′C′.在△AB′C′中,AB′<AC′+B′C′,所以AC+B′C<AC′+B′C′,所以AC+BC<AC′+C′B.【例1】在图中直线l上找到一点M,使它到A,B两点的距离和最小.分析:先确定其中一个点关于直线l的对称点,然后连接对称点和另一个点,与直线l的交点M即为所求的点.解:如图所示:(1)作点B关于直线l的对称点B′;(2)连接AB′交直线l于点M.(3)则点M即为所求的点.点拨:运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上,然后用“两点之间线段最短”解决问题.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同.警误区利用轴对称解决最值问题应注意题目要求根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.解决这类最值问题时,要认真审题,不要只注意图形而忽略题意要求,审题不清导致答非所问.3.利用平移确定最短路径选址选址问题的关键是把各条线段转化到一条线段上.如果两点在一条直线的同侧时,过两点的直线与原直线的交点处构成线段的差最大,如果两点在一条直线的异侧时,过两点的直线与原直线的交点处构成的线段的和最小,都可以用三角形三边关系来推理说明,通常根据最大值或最小值的情况取其中一个点的对称点来解决.解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.在解决最短路径问题时,我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上,从而作出最短路径的方法来解决问题.【例2】如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村与B村供水.(1)若要使厂部到A,B村的距离相等,则应选择在哪建厂?(2)若要使厂部到A,B两村的水管最短,应建在什么地方?分析:(1)到A,B两点距离相等,可联想到“线段垂直平分线上的点到线段两端点的距离相等”,又要在河边,所以作AB的垂直平分线,与EF的交点即为符合条件的点.(2)要使厂部到A村、B村的距离之和最短,可联想到“两点之间线段最短”,作A(或B)点关于EF的对称点,连接对称点与B点,与EF的交点即为所求.解:(1)如图1,取线段AB的中点G,过中点G画AB的垂线,交EF于P,则P到A,B的距离相等.也可分别以A、B为圆心,以大于12AB 为半径画弧,两弧交于两点,过这两点作直线,与EF 的交点P 即为所求.(2)如图2,画出点A 关于河岸EF 的对称点A ′,连接A ′B 交EF 于P ,则P 到A ,B 的距离和最短.【例3】 如图,从A 地到B 地经过一条小河(河岸平行),今欲在河上建一座与两岸垂直的桥,应如何选择桥的位置才能使从A 地到B 地的路程最短?思路导引:从A 到B 要走的路线是A →M →N →B ,如图所示,而MN 是定值,于是要使路程最短,只要AM +BN 最短即可.此时两线段应在同一平行方向上,平移MN 到AC ,从C 到B 应是余下的路程,连接BC 的线段即为最短的,此时不难说明点N 即为建桥位置,MN 即为所建的桥.解:(1)如图2,过点A 作AC 垂直于河岸,且使AC 等于河宽.(2)连接BC与河岸的一边交于点N.(3)过点N作河岸的垂线交另一条河岸于点M.则MN为所建的桥的位置.4.生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知,求距离之和最小问题,就是运用等量代换的方式,把几条线段的和想办法转化在一条线段上,从而解决这个问题,运用轴对称性质,能将两条线段通过类似于镜面反射的方式转化成一条线段,如图,AO+BO=AC的长.所以作已知点关于某直线的对称点是解决这类问题的基本方法.【例4】(实际应用题)茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图a所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短?图a 图b解:如图b.(1)作C点关于OA的对称点C1,作D点关于OB的对称点D1,(2)连接C1D1,分别交OA,OB于P,Q,那么小明沿C→P→Q→D 的路线行走,所走的总路程最短.5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键.先做出其中一点关于对称轴的对称点,然后连接对称点和另一个点,所得直线与对称轴的交点,即为所求.根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值.破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法.【例5】如图所示,A,B两点在直线l的两侧,在l上找一点C,使点C到点A、B的距离之差最大.分析:此题的突破点是作点A(或B)关于直线l的对称点A′(或B′),作直线A′B(AB′)与直线l交于点C,把问题转化为三角形任意两边之差小于第三边来解决.解:如图所示,以直线l为对称轴,作点A关于直线l的对称点A′,A′B的连线交l于点C,则点C即为所求.理由:在直线l上任找一点C′(异于点C),连接CA,C′A,C′A′,C′B.因为点A,A′关于直线l对称,所以l为线段AA′的垂直平分线,则有CA=CA′,所以CA-CB=CA′-CB=A′B.又因为点C′在l上,所以C′A=C′A′.在△A′BC′中,C′A-C′B=C′A′-C′B<A′B,所以C′A′-C′B<CA-CB.点拨:根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路径问题——和最小【典型例题】1、已知二次函数y=x2-2mx+m2-1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P 点的坐标;若P点不存在,请说明理由.2、如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.3、已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y=33x+3对称.(1)求A、B两点坐标,并证明点A在直线l上;(2)求二次函数解析式;(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.5、如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了.(1)求点A ,B ,D 的坐标;(2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标.6、已知:直线l:y=﹣2,抛物线y=ax2+bx+c的对称轴是y轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P是抛物线上任意一点,过点P作直线l的垂线,垂足为Q,求证:PO=PQ.(3)请你参考(2)中结论解决下列问题:(i)如图②,过原点作任意直线AB,交抛物线y=ax2+bx+c于点A、B,分别过A、B两点作直线l的垂线,垂足分别是点M、N,连结ON、OM,求证:ON⊥OM.(ii)已知:如图③,点D(1,1),试探究在该抛物线上是否存在点F,使得FD+FO取得最小值?若存在,求出点F的坐标;若不存在,请说明理由.【举一反三】1.如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B (2,0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.2、在平面直角坐标系中,已知抛物线y =﹣12x 2+bx +c (b ,c 为常数)的顶点为P ,等腰直角三角形ABC 的顶点A 的坐标为(0,﹣1),C 的坐标为(4,3),直角顶点B 在第四象限. (1)如图,若该抛物线过A ,B 两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P 在直线AC 上滑动,且与AC 交于另一点Q .(i )若点M 在直线AC 下方,且为平移前(1)中的抛物线上的点,当以M 、P 、Q 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M 的坐标;(ii )取BC 的中点N ,连接NP ,BQ .试探究PQNP +BQ 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.3、如图,在直角坐标系中,已知点A(0,1),B(﹣4,4),将点B绕点A顺时针方向90°得到点C;顶点在坐标原点的拋物线经过点B.(1)求抛物线的解析式和点C的坐标;(2)抛物线上一动点P,设点P到x轴的距离为d1,点P到点A的距离为d2,试说明d2=d1+1;(3)在(2)的条件下,请探究当点P位于何处时,△P AC的周长有最小值,并求出△P AC 的周长的最小值.最短路径问题——和最小【典型例题】1、已知二次函数y =x 2-2mx +m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式;(2)如图,当m =2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标; (3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.解:(1)∵二次函数的图象经过坐标原点O (0,0),∴代入二次函数y =x 2-2mx +m 2-1,得出:m 2-1=0,解得:m =±1,∴二次函数的解析式为:y =x 2-2x 或y =x 2+2x ;(2)∵m =2, ∴二次函数y =x 2-2mx +m 2-1得:y =x 2-4x +3=(x -2)2-1,∴抛物线的顶点为:D (2,-1), 当x =0时,y =3,∴C 点坐标为:(0,3),∴C (0,3)、D (2,-1); (3)当P 、C 、D 共线时PC +PD 最短, 【方法一】∵C (0,3)、D (2,-1),设直线CD 的解析式为y =kx +3,代入得:2k +3=-1,∴k =-2,∴y =-2x +3, 当y =0时,-2x +3=0,解得x =32,∴PC +PD 最短时,P 点的坐标为:P (32,0).【方法二】过点D 作DE ⊥y 轴于点E ,∵PO ∥DE ,∴PO DE =CO CE ,∴PO 2=34,解得:PO =32,∴PC +PD 最短时,P 点的坐标为:P (32,0).2、如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.解:(1)∵点A (-1,0)在抛物线y =12x 2+bx -2上,∴12×(-1 )2+b ×(-1)-2=0,解得b =-32, ∴抛物线的解析式为y =12x 2-32x -2=12(x -32)2-258,∴顶点D 的坐标为 (32,-258).(2)当x =0时y =-2,∴C (0,-2),OC =2.当y =0时,12x 2-32x -2=0,∴x 1=-1,x 2=4,∴B (4,0),∴OA =1,OB =4,AB =5.∵AB 2=25,AC 2=OA 2+OC 2=5,BC 2=OC 2+OB 2=20,∴AC 2+BC 2=AB 2. ∴△ABC 是直角三角形.(3)作出点C 关于x 轴的对称点C ′,则C ′(0,2),OC ′=2,连接C ′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,MC +MD 的值最小.【方法一】设直线C ′D 的解析式为y =kx +n ,则⎩⎪⎨⎪⎧n =232k +n =-258,解得:⎩⎪⎨⎪⎧n =2k =-4112.∴y =-4112x +2. ∴当y =0时,-4112x +2=0,x =2441.∴m =2441.【方法二】设抛物线的对称轴交x 轴于点E .∵ED ∥y 轴,∴∠OC ′M =∠EDM ,∠C ′OM =∠DEM ,∴△C ′OM ∽△DEM .∴OM EM =OC ′ED ,∴m 32-m =2258,∴m =2441.3、已知,如图,二次函数y =ax 2+2ax ﹣3a (a ≠0)图象的顶点为H ,与x 轴交于A 、B 两点(B 在A 点右侧),点H 、B 关于直线l :y =33x +3对称. (1)求A 、B 两点坐标,并证明点A 在直线l 上; (2)求二次函数解析式; (3)过点B 作直线BK ∥AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连接HN 、NM 、MK ,求HN +NM +MK 和的最小值.解:(1)依题意,得ax 2+2ax ﹣3a =0(a ≠0),解得x 1=﹣3,x 2=1,∵B 点在A 点右侧,∴A 点坐标为(﹣3,0),B 点坐标为(1,0),∵直线l :y =33x +3,当x =﹣3时,y =33×(-3)+3=0,∴点A 在直线l 上.(2)∵点H 、B 关于过A 点的直线l :y =33x +3对称,∴AH =AB =4,过顶点H 作HC ⊥AB 交AB 于C 点,则AC =12AB =2,HC =23,∴顶点H (-1,23),代入二次函数解析式,解得a =-32,∴二次函数解析式为y =-32x 2-3x +332,(3)直线AH 的解析式为y =3x +33,直线BK 的解析式为y =3x +33,由⎩⎪⎨⎪⎧y =33x +3y =3x -3,解得⎩⎨⎧x =3y =23,即K (3,23),则BK =4,∵点H 、B 关于直线AK 对称,∴HN +MN 的最小值是MB ,KD =KE =23,过点K 作直线AH 的对称点Q ,连接QK ,交直线AH 于E ,则QM =MK ,QE =EK=23,AE ⊥QK ,∴BM +MK 的最小值是BQ ,即BQ 的长是HN +NM +MK 的最小值, ∵BK ∥AH ,∴∠BKQ =∠HEQ =90°,由勾股定理得QB =8, ∴HN +NM +MK 的最小值为8.4、如图,对称轴为直线x =2的抛物线经过A (-1,0),C (0,5)两点,与x 轴另一交点为B .已知M (0,1),E (a ,0),F (a +1,0),点P 是第一象限内的抛物线上的动点. (1)求此抛物线的解析式;(2)当a =1时,求四边形MEFP 的面积的最大值,并求此时点P 的坐标;(3)若△PCM 是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小?请说明理由. 解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5, ∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN •MN -12OM •OE=12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1 =-x 2+92x +92 =-(x -94)2+15316∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316).(3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3). 四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值. 如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1); 作点M 1关于x 轴的对称点M 2,则M 2(1,-1);连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得:⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF 周长最小.图1 图22、如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了.(1)求点A ,B ,D 的坐标;(2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标. 解:(1)顶点D 的坐标为(3,-1).令y =0,得12(x -3)2-1=0,解得x 1=3+2,x 2=3-2.∵点A 在点B 的左侧,∴A 点坐标(3-2,0),B 点坐标(3+2,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,-1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72-(-1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90︒.∵∠MOE +∠COH =90︒,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90︒,∴△DCG ∽△EOM .∴CG OM =DGEM ,即923=3EM.∴EM =2,即点E 坐标为(3,2),ED =3.由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90︒.设AE 交CD 于点F .∴∠ADC +∠AFD =90︒.又∵∠AEO +∠HFE =90︒, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小. 设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.∵y =12 (x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)2-1=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1).此时Q 点坐标为(3,1)或(195,135).6、已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ .(3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM . (ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值?若存在,求出点F 的坐标;若不存在,请说明理由.解:(1)由题意,得⎩⎨⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎨⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1;(2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP=14a 2+1. 在Rt △POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ;(3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°. ∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°, ∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°,∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ; (ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O , ∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′,∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点.∵D (1,1),∴F 的横坐标为1,∴F (1,54).【举一反三】1.如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值. .解:(1)把A (﹣2,﹣4),O (0,0),B (2,0)三点的坐标代入y =ax 2+bx +c 中,得⎩⎪⎨⎪⎧4a -2b +c =-44a +2b +c =0c =0,解得a =﹣12,b =1,c =0,∴解析式为y =﹣12x 2+x .(2)由y =﹣12x 2+x =﹣12(x ﹣1)2+12,可得抛物线的对称轴为x =1,并且对称轴垂直平分线段OB ,∴OM =BM ,∴OM +AM =BM +AM ,连接AB 交直线x =1于M 点,则此时OM +AM 最小,l过点A 作AN ⊥x 轴于点N ,在Rt △ABN 中,AB =AN 2+BN 2=42+42=42, ∴OM +AM 最小值为42.2、在平面直角坐标系中,已知抛物线y =﹣12x 2+bx +c (b ,c 为常数)的顶点为P ,等腰直角三角形ABC 的顶点A 的坐标为(0,﹣1),C 的坐标为(4,3),直角顶点B 在第四象限. (1)如图,若该抛物线过A ,B 两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P 在直线AC 上滑动,且与AC 交于另一点Q .(i )若点M 在直线AC 下方,且为平移前(1)中的抛物线上的点,当以M 、P 、Q 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M 的坐标;(ii )取BC 的中点N ,连接NP ,BQ .试探究PQNP +BQ 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由. .解:(1)∵等腰直角三角形ABC 的顶点A 的坐标为(0,-1),C 的坐标为(4,3),∴点B 的坐标为(4,-1).∵抛物线过A (0,-1),B (4,-1)两点,∴ ⎩⎪⎨⎪⎧c =-1-12×16+4b +c =-1,解得:b =2,c =-1,∴抛物线的函数表达式为:y =-12x 2+2x -1.(2)(i )∵A (0,-1),C (4,3),∴直线AC 的解析式为:y =x -1. 设平移前抛物线的顶点为P 0,则由(1)可得P 0的坐标为(2,1),且P 0在直线AC 上.∵点P 在直线AC 上滑动,∴可设P 的坐标为(m ,m -1),则平移后抛物线的函数表达式为:y =-12(x -m )2+m -1.解方程组:⎩⎪⎨⎪⎧y =x -1y =-12(x -m )2+(m -1),解得⎩⎨⎧x 1=m y 1=m -1, ⎩⎨⎧x 2=m -2y 2=m -3, ∴P (m ,m -1),Q (m -2,m -3).过点P 作PE ∥x 轴,过点Q 作QF ∥y 轴,则PE =m -(m -2)=2,QF =(m -1)-(m -3)=2.∴PQ =22=AP 0. 若以M 、P 、Q 三点为顶点的等腰直角三角形,则可分为以下两种情况: ①当PQ 为直角边时:点M 到PQ 的距离为22(即为PQ 的长). 由A (0,-1),B (4,-1),P 0(2,1)可知, △ABP 0为等腰直角三角形,且BP 0⊥AC ,BP 0=22.如答图1,过点B 作直线l 1∥AC ,交抛物线y =-12x 2+2x -1于点M ,则M 为符合条件的点.∴可设直线l 1的解析式为:y =x +b 1,∵B (4,-1),∴-1=4+b 1,解得b ==-5,∴直线l 1的解析式为:y =x -5.解方程组 ⎩⎪⎨⎪⎧y =x -5y =-12x 2+2x -1,得:⎩⎨⎧x 1=4y 1=-1,⎩⎨⎧x 2=-2y 2=-7,∴M 1(4,-1),M 2(-2,-7).②当PQ 为斜边时:MP =MQ =2,可求得点M 到PQ 的距离为 2 . 如答图2,取AB 的中点F ,则点F 的坐标为(2,-1). 由A (0,-1),F (2,-1),P 0(2,1)可知:△AFP 0为等腰直角三角形,且点F 到直线AC 的距离为 2 .过点F 作直线l 2∥AC ,交抛物线y =-12x 2+2x -1于点M ,则M 为符合条件的点.∴可设直线l 2的解析式为:y =x +b 2, ∵F (2,-1),∴-1=2+b 2,解得b 2=-3,∴直线l 2的解析式为:y =x -3.解方程组⎩⎪⎨⎪⎧y =x -3y =-12x 2+2x -1,得:⎩⎪⎨⎪⎧x 1=1+5y 1=-2+5,⎩⎪⎨⎪⎧x 1=1-5y 1=-2-5 ,∴M 3(1+5,-2+5),M 4(1-5,-2-5).综上所述,所有符合条件的点M 的坐标为:M 1(4,-1),M 2(-2,-7),M 3(1+5,-2+5),M 4(1-5,-2-5).(ii )PQNP +BQ 存在最大值.理由如下:由i )知PQ =22为定值,则当NP +BQ 取最小值时,PQNP +BQ有最大值.如答图2,取点B 关于AC 的对称点B ′,易得点B ′的坐标为(0,3),BQ =B ′Q . 连接QF ,FN ,QB ′,易得FN ∥PQ ,且FN =PQ ,∴四边形PQFN 为平行四边形.∴NP =FQ .∴NP +BQ =FQ +B ′Q ≥FB ′=22+42 =25.∴当B ′、Q 、F 三点共线时,NP +BQ 最小,最小值为25.∴PQ NP +BQ 的最大值为2225=105.F3、如图,在直角坐标系中,已知点A (0,1),B (﹣4,4),将点B 绕点A 顺时针方向90°得到点C ;顶点在坐标原点的拋物线经过点B . (1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为d 1,点P 到点A 的距离为d 2,试说明d 2=d 1+1;(3)在(2)的条件下,请探究当点P 位于何处时,△P AC 的周长有最小值,并求出△P AC 的周长的最小值.解:(1)设抛物线的解析式:y =ax 2,∵拋物线经过点B (﹣4,4),∴4=a •42,解得a =14,所以抛物线的解析式为:y =14x 2;过点B 作BE ⊥y 轴于E ,过点C 作CD ⊥y 轴于D ,如图, ∵点B 绕点A 顺时针方向90°得到点C ,∴Rt △BAE ≌Rt △ACD ,∴AD =BE =4,CD =AE =OE ﹣OA =4﹣1=3,∴OD =AD +OA =5,∴C 点坐标为(3,5);(2)设P 点坐标为(a ,b ),过P 作PF ⊥y 轴于F ,PH ⊥x 轴于H ,如图,∵点P 在抛物线y =14x 2上,∴b =14a 2,∴d 1=14a 2,∵AF =OF ﹣OA =PH ﹣OA =d 1﹣1=14a 2﹣1,PF =a ,在Rt △P AF 中,P A =d 2=AF 2+PF 2=(14a 2-1)2+a 2=14a 2+1,∴d 2=d 1+1;(3)由(1)得AC =5,∴△P AC 的周长=PC +P A +5=PC +PH +6,要使PC +PH 最小,则C 、P 、H 三点共线,∴此时P 点的横坐标为3,把x =3代入y =14x 2,得到y =94,即P 点坐标为(3,94),此时PC +PH =5,∴△P AC 的周长的最小值=5+6=11.。
