《圆周角和圆心角的关系》圆PPT课件(第1课时)
合集下载
北师大版九下《圆周角和圆心角的关系》课件

北师大版九下《圆周角和 圆心角的关系》ppt课件
这个课件将带你深入了解圆周角和圆心角的关系,以及它们在几何学中的应 用。准备好跟上了吗?让我们开始吧!
引言和背景
在几何学中,我们经常遇到与圆形相关的问题。掌握圆周角和圆心角的关系, 能够帮助我们解决这些问题,进一步理解和应用几何学的知识。
圆周角的定义
圆周角是指其两边都与圆的圆周相交,通常用度数或弧度来表示。圆周角是 一个重要的几何概念,它有着独特的性质和特点。
圆心角的定义
圆心角是指其两边都与圆的圆周相交,并且顶点位于圆的中心。圆心角是圆形的一个特殊角度,对于我们理解 圆形的性质非常重要。
圆周角和圆心角的关系
圆周角和圆心角之间存在着紧密的关联。它们的度数或弧度有一定的规律和 对应关系,我们可以通过推导和证明来进一步揭示它们之间的联系。
ቤተ መጻሕፍቲ ባይዱ
总结和应用
通过对圆周角和圆心角的学习,我们掌握了它们的定义、关系和应用。这些 知识将帮助我们更好地解决与圆形相关的几何问题,并且在实际生活中应用 几何学的原理和方法。
推导和证明
通过一些基本的几何性质,我们可以推导出圆周角和圆心角的具体关系。这个过程需要一些数学推理和运算, 但是它将帮助我们更深入地理解这两个角度之间的联系。
用例和示例
通过一些实际的案例和具体的示例,我们可以更好地理解圆周角和圆心角的 关系,并且看到它们在几何学中的应用。让我们一起来看几个有趣的例子吧!
这个课件将带你深入了解圆周角和圆心角的关系,以及它们在几何学中的应 用。准备好跟上了吗?让我们开始吧!
引言和背景
在几何学中,我们经常遇到与圆形相关的问题。掌握圆周角和圆心角的关系, 能够帮助我们解决这些问题,进一步理解和应用几何学的知识。
圆周角的定义
圆周角是指其两边都与圆的圆周相交,通常用度数或弧度来表示。圆周角是 一个重要的几何概念,它有着独特的性质和特点。
圆心角的定义
圆心角是指其两边都与圆的圆周相交,并且顶点位于圆的中心。圆心角是圆形的一个特殊角度,对于我们理解 圆形的性质非常重要。
圆周角和圆心角的关系
圆周角和圆心角之间存在着紧密的关联。它们的度数或弧度有一定的规律和 对应关系,我们可以通过推导和证明来进一步揭示它们之间的联系。
ቤተ መጻሕፍቲ ባይዱ
总结和应用
通过对圆周角和圆心角的学习,我们掌握了它们的定义、关系和应用。这些 知识将帮助我们更好地解决与圆形相关的几何问题,并且在实际生活中应用 几何学的原理和方法。
推导和证明
通过一些基本的几何性质,我们可以推导出圆周角和圆心角的具体关系。这个过程需要一些数学推理和运算, 但是它将帮助我们更深入地理解这两个角度之间的联系。
用例和示例
通过一些实际的案例和具体的示例,我们可以更好地理解圆周角和圆心角的 关系,并且看到它们在几何学中的应用。让我们一起来看几个有趣的例子吧!
《圆周角和圆心角的关系》圆PPT课件 (共14张PPT)

= 2∠COD,
1
一条弧所对的圆周角等于它所 对的圆心角的一半.
B
你能写出这个命题吗?
议一议
6
圆周角和圆心角的关系
• 如果圆心不在圆周角的一边上,结果会怎样? • 3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角 ∠ABC与圆心角∠AOC的大小关系会怎样? A
老师提示:能否也转化为1的情况?
A C
●
A
A C C B
●
O
B
●
O
OBLeabharlann 教师提示:注意圆心与圆周角的位置关系.
议一议
4
圆周角和圆心角的关系
• 1.首先考虑一种特殊情况: • 当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角 A ∠ABC与圆心角∠AOC的大小关系. C ∵∠AOC是△ABO的外角, 老师期望: ∴∠AOC=∠B+∠A. 你可要理 O ∵OA=OB, 解并掌握 ∴∠A=∠B. 这个模型. B ∴∠AOC=2∠B. 1 一条弧所对的圆周角等于它所 即 ∠ABC = ∠AOC. 对的圆心角的一半. 2 你能写出这个命题吗?
C
过点B作直径BD.由1可得:
∠ABD =
1 ∠AOD,∠CBD 2
B
●
O
∴
1 ∠ABC = ∠AOC. 2
= 2∠COD, 一条弧所对的圆周角等于它所 对的圆心角的一半.
1
你能写出这个命题吗?
议一议
7
圆周角定理
驶向胜利 的彼岸
• 综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是 • : 圆周角定理 一条弧所对的圆周角等于它所对的圆心 角的一半. 即 ∠ABC =
3.4+圆周角和圆心角的关系第1课时+圆周角定理课件2023-2024学年+北师大版九年级数学下册+

归纳新知
由上面的问题可以看出,∠ABC是圆上的一种新的 角,这种角我们称为圆周角.你能归纳出其完整定义吗?
定义:顶点在圆上,且角的两边分别与圆还有另
一个交点的角叫做圆周角.
A
C
圆心角和圆周角 有什么关系吗?
E
B D
归纳新知
A
C
E
B D
(1)在上图中,当球员在B,D,E处射门时,他所 处的位置对球门AC分别形成三个角∠ABC,∠ADC, ∠AEC.这三个角的大小有什么关系?
第3章 圆
3.4 圆周角和圆心角的关系
第1课时 圆周角定理
复习导课
请画出一个圆心角,并说明圆心角的特点.
O
A
B
特点:顶点在圆心,角的两边与圆相交.
复习导课
A
C
E
B D
图中∠ABC的顶点位置与圆心角的顶点位置有什么 不同?它的两边与圆有什么位置关系?
∠ABC的顶点在圆上,而圆心角的顶点在圆心; ∠ABC的两边与圆相交.
是△ABO的外角,
O
∴∠AOC=∠A+∠B.
∵OA=OB,∴∠A=∠B.
∴∠AOC=2∠A. 即 ABC = 1 AOC .
B
2
归纳新知
如果∠ABC的两边都不经过圆心,那么结果会怎样? 你能利用特殊结果把问题解决吗?
① 点 O 在 ∠ ABC 内 部 时 , 只要作出直径BD,将这个角转 化为上述情况的两个角的和即 可证出.
归纳新知
A
三个张角∠ABC,∠ADC 和∠AEC有什么关系呢?它们 会相等吗?
C O
E
B
D
∠ABC,∠ADC和∠AEC是同弧(弧AC)所对 的圆周角,根据我们所学的圆周角定理可知,它们 都等于圆心角∠AOC的一半,所以这几个圆周角相 等.即∠ ABC=∠ADC=∠AEC.
课件233圆周角和圆心角的关系.ppt
径。求证:AB ·AC = AE ·AD
分析:要证AB ·AC = AE ·AD
A
AC AD AE AB
O
△ADC∽ △ABE B
DC
或△ACE∽ △ADB E
题后思:1、证明题的思路寻找方法; 2、等积式的证明方法; 3、辅助线的思考方法。
讨论与思考 C
如图,CD是⊙O的直径,
弦AB⊥CD于E,那么你
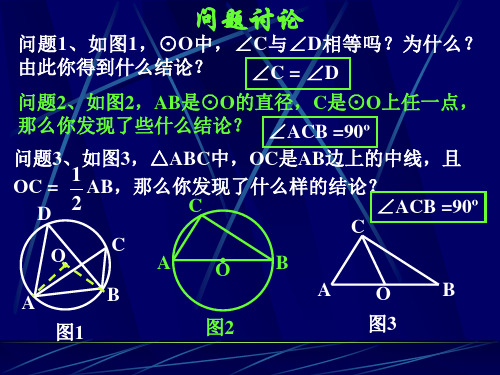
问题讨论
问题1、如图1,⊙O中,∠C与∠D相等吗?为什么? 由此你得到什么结论? ∠C = ∠D
问题2、如图2,AB是⊙O的直径,C是⊙O上任一点, 那么你发现了些什么结论? ∠ACB =90º
问题3、如图3,△ABC中,OC是AB边上的中线,且
OC = 1 AB,那么你发现了什么样的结论?
D2
C
∠ACB =90º C
O
能得到什么结论?
结论:Βιβλιοθήκη AEB(1)AE = BE,AC = BC,AD = BD D
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE ·CD,AD2 = DE ·DC
BE2 = AE2 = DE ·CE
小结与作业
1、本节课我们学习了哪些知识? 2、圆周角定理及其推论的用途你都知道了吗? 3、证明题思路的寻找方法如何? 4、证明等积式的一般思路你掌握了吗?
O
C A
O
B
A
B
AO
B
图1
图2
图3
自学与思考
1、圆周角定理的推论1、2、3的内容分别是什么? 你是怎样理解这些推论的?
2、从课本例2的学习中你认为证明等积式的一般思 路是怎样的?
圆周角和圆心角的关系课件第1课时北师大版九年级下册数学

A.40°
B.50°
C.60°
D.70°
合作探究
如图,已知圆心角∠AOB=100°,求圆周角∠ACB、
∠ADB的度数.
合作探究
解:设优弧ADB所对的圆心角为∠1,∵∠AOB=100°,
∴∠D= ∠AOB=50°,∠1=360°-∠AOB=260°,
∴∠ACB= ∠1=130°,
因此∠ACB、∠ADB的度数分别为130°、50°.
预习导学
1.如图,四个边长为1的小正方形拼成一个大正方形,A、B、
O是小正方形顶点,☉O的半径为1,P是☉O上的点,且位于右
上方的小正方形内,则∠APB等于( B )
A.30°
B.45°
C.60°
D.90°
预习导学
2.如图,AB、CD是☉O的两条弦,连接AD、BC.若∠BAD
=70°,则∠BCD的度数为( D )
合作探究
如图,点A、B、C都在圆O上,OC⊥OB,点A在劣弧
BC上,且OA=AB,求∠ABC的度数.
合作探究
解:∵OA=OB,OA=AB,
∴OA=OB=AB,
即△OAB是等边三角形,
∴∠AOB=60°.
∵OC⊥OB,
∴∠COB=90°,
∴∠COA=90°-60°=30°,
∴∠ABC=15°.
合作探究
圆内的部分是圆的两条弦
.
;(2)
两边在
预习导学
圆周角定理及其推论
1.同弧所对的圆周角等于它所对的圆心角的一半.
2.在
等.
同圆或等圆 中,同弧或等弧所对的 圆周角 相
预习导学
·导学建议·
在知识点二圆周角定理的得出和证明中,先把学生所画出
《圆心角和圆周角》PPT(第1课时)

圆心角和圆周角
第1课时
-.
知识回顾 1.圆是不是中心对称图形?对称中心是什么?
(圆是中心对称图形,圆心是它的对称中心)
2.将课前准备的两个圆形纸片重合在一起,绕圆心 转动其中一个圆,你发现什么现象?
(把圆绕圆心旋转任意一个角度,所得的图形与原图形 重合,即圆有旋转不变性)
获取新知 知识点一:圆心角的概念
4.如图,已知AB、CD为⊙O的两条弦,A⌒D=B⌒C.
求证:AB=CD. 证明:连接AO,BO,CO,DO ∵A⌒D=B⌒C
∴∠AOD=∠BOC ∴∠AOD+∠BOD=∠BOC+∠BOD 即∠AOB=∠COD
∴AB=CD
C B
O.
D A
课堂小结
圆心角
概念:顶点在圆心的角
弦、弧、圆心 角的关系定理
2.下列说法中,正确的是( C ) A.弦等所对的弧相等 B.弧相等所对的弦相等 C.在同圆中,圆心角相等,所对的弦相等 D.弦相等,所对的圆心角相等
3.如图,AB,CD是⊙O的两条弦. (1)∵∠AOB=∠COD,∴____A_⌒B_=_C_⌒D_,____A_B_=_C_D. (2)∵AB=CD,∴___∠_A_O__B_=__∠_C__O_D_,___A_⌒B_=_C_⌒D___. (3)∵AB⌒=C⌒D,∴___∠_A__O_B_=__∠__C_O_D_,__A__B_=_C_D_,.
弦AB与弦A'B'有怎样的数量关系?
(同圆)由圆的旋转不变性,我们发现: A
在⊙O中,如果∠AOB= ∠A'OB', 那么,A⌒B=A⌒'B',弦AB=弦A'B'
B C
·
O
第1课时
-.
知识回顾 1.圆是不是中心对称图形?对称中心是什么?
(圆是中心对称图形,圆心是它的对称中心)
2.将课前准备的两个圆形纸片重合在一起,绕圆心 转动其中一个圆,你发现什么现象?
(把圆绕圆心旋转任意一个角度,所得的图形与原图形 重合,即圆有旋转不变性)
获取新知 知识点一:圆心角的概念
4.如图,已知AB、CD为⊙O的两条弦,A⌒D=B⌒C.
求证:AB=CD. 证明:连接AO,BO,CO,DO ∵A⌒D=B⌒C
∴∠AOD=∠BOC ∴∠AOD+∠BOD=∠BOC+∠BOD 即∠AOB=∠COD
∴AB=CD
C B
O.
D A
课堂小结
圆心角
概念:顶点在圆心的角
弦、弧、圆心 角的关系定理
2.下列说法中,正确的是( C ) A.弦等所对的弧相等 B.弧相等所对的弦相等 C.在同圆中,圆心角相等,所对的弦相等 D.弦相等,所对的圆心角相等
3.如图,AB,CD是⊙O的两条弦. (1)∵∠AOB=∠COD,∴____A_⌒B_=_C_⌒D_,____A_B_=_C_D. (2)∵AB=CD,∴___∠_A_O__B_=__∠_C__O_D_,___A_⌒B_=_C_⌒D___. (3)∵AB⌒=C⌒D,∴___∠_A__O_B_=__∠__C_O_D_,__A__B_=_C_D_,.
弦AB与弦A'B'有怎样的数量关系?
(同圆)由圆的旋转不变性,我们发现: A
在⊙O中,如果∠AOB= ∠A'OB', 那么,A⌒B=A⌒'B',弦AB=弦A'B'
B C
·
O
《圆周角——圆周角和圆心角、弧的关系》PPT课件

解:PA+PB=PC.证明如下: 如图①,在 PC 上截取 PD=PA,连接 AD. ∵∠APC=60°,∴△PAD 是等边三角形. ∴PA=DA,∠PAD=60°. ∵∠CPB=60°,∴∠BAC=60°. ∴∠PAD=∠BAC. ∴∠PAB=∠DAC. 由(1)知 AB=AC,∴△PAB≌△DAC(SAS).∴PB=DC. ∵PD+DC=PC,∴PA+PB=PC.
则易得 PD= 3,PA=PB=PC=2 3. ∵PD⊥AB,PE⊥OC,∠AOC=90°, ∴四边形 PEOD 是矩形. ∴OE=PD= 3,PE=OD=3-1=2. ∴CE= PC2-PE2= 12-4=2 2. ∴OC=CE+OE=2 2+ 3. ∴点 C 的纵坐标为 2 2+ 3. 【答案】B
当点 P 为A︵B的中点时,E 与 F 重合,PE+CF=PC, 即 PC 为⊙O 的直径. ∴此时四边形 APBC 的面积最大. 易求得 AB= 3, ∴S 四边形 APBC=12× 3×2= 3.
同学们下课啦
授课老师:xxx
此页为防盗标记页(下载后可删)
教师课堂用语在学科专业方面重在进行“引”与“导”,通过点拨、搭桥等方式让学生豁然开朗,得出结论,而不是和盘托 出,灌输告知。一般可分为:启发类、赏识类、表扬类、提醒类、劝诫类、鼓励类、反思类。
答案显示
1.顶点_在__圆__上___,并且__两__边____都与圆相交,这样的角叫做圆 周角.
2.在⊙O 中,A,B 是圆上任意两点,则A︵B所对的圆心角有 ___1_____个,所对的圆周角有__无__数____个;弦 AB 所对的圆 心角有___1___个,所对的圆周角有__无__数____个.
1. 说得太好了,老师佩服你,为你感到骄傲! 2. 你的设计(方案、观点)富有想象力,极具创造性。 3. 我非常欣赏你的想法,请说具体点,好吗? 4. 某某同学的解题方法非常新颖,连老师都没想到,真厉害! 5. 让我们一起为某某喝彩!同学们在学习过程中,也要敢于猜想,善于猜想,这样才能有所发现,有所创造! 三、表扬类
圆周角和圆心角的关系ppt课件

50°,则∠EBC+∠ADC 的度数为 _______.
-18-
3.4 圆周角和圆心角的关系
解析:如解析图,连接 AB,DE,则∠ABE=∠ADE. ∵ 所对的圆心角的度数为 50°,∴∠ABE= ∠ADE =25°. ∵ 点 A,B,C,D 在 ⊙O 上 ,∴四边形 ABCD 是圆内接四边形, ∴∠ABC+∠ADC=180°, ∴∠ABE+∠EBC+∠ADC=180°, ∴∠EBC+∠ADC=180°-∠ABE=180°-25°=155°. 答案:155° 题型解法:本题考查了圆周角定理和圆内接四边形的 性质,作出辅助线构建圆内接四边形是解题的关键.
-10-
3.4 圆周角和圆心角的关系
■考点四 圆内接四边形
定义
四边形的四个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个 圆叫做四边形的外接圆
推论 圆内接四边形的对角互补
拓展 圆内接四边形的任何外角等于内对角
注意 并不是所有的四边形都存在外接圆,只有对角互补的四边形才存在外接圆
-11-
3.4 圆周角和圆心角的关系
A. 20° B. 40°
C. 50° D. 70°
-7-
3.4 圆周角和圆心角的关系
3. 如图,已知△ABC 的三个顶点都在同一圆上,且 AC=6,BC=8,AB=10, 则该圆的半径长是 ________.
(第 3 题图)
(第 4 题图)
4. 如图,AB=BC,∠ABC =120°,AD 为 ⊙O 的直径 ,AD=6,那么 AB 的
值为 ______.
-8-
3.4 圆周角和圆心角的关系
5. 如图,AB=AC,AB 是直径,求证:BC=2DE. (第 5 题图)
-18-
3.4 圆周角和圆心角的关系
解析:如解析图,连接 AB,DE,则∠ABE=∠ADE. ∵ 所对的圆心角的度数为 50°,∴∠ABE= ∠ADE =25°. ∵ 点 A,B,C,D 在 ⊙O 上 ,∴四边形 ABCD 是圆内接四边形, ∴∠ABC+∠ADC=180°, ∴∠ABE+∠EBC+∠ADC=180°, ∴∠EBC+∠ADC=180°-∠ABE=180°-25°=155°. 答案:155° 题型解法:本题考查了圆周角定理和圆内接四边形的 性质,作出辅助线构建圆内接四边形是解题的关键.
-10-
3.4 圆周角和圆心角的关系
■考点四 圆内接四边形
定义
四边形的四个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个 圆叫做四边形的外接圆
推论 圆内接四边形的对角互补
拓展 圆内接四边形的任何外角等于内对角
注意 并不是所有的四边形都存在外接圆,只有对角互补的四边形才存在外接圆
-11-
3.4 圆周角和圆心角的关系
A. 20° B. 40°
C. 50° D. 70°
-7-
3.4 圆周角和圆心角的关系
3. 如图,已知△ABC 的三个顶点都在同一圆上,且 AC=6,BC=8,AB=10, 则该圆的半径长是 ________.
(第 3 题图)
(第 4 题图)
4. 如图,AB=BC,∠ABC =120°,AD 为 ⊙O 的直径 ,AD=6,那么 AB 的
值为 ______.
-8-
3.4 圆周角和圆心角的关系
5. 如图,AB=AC,AB 是直径,求证:BC=2DE. (第 5 题图)
圆圆周角和圆心角的关系课件ppt

圆周角和圆心角的综合应用
总结词
定理、综合、应用、解题。
详细描述
圆周角和圆心角在几何学中有着广泛的应用,它们可以 单独使用,也可以综合使用来解决一些复杂的几何问题 。首先,我们可以利用圆周角和圆心角定理的综合应用 来解决一些几何问题。其次,我们可以通过一些解题方 法,如分析法、综合法和作图法等,来解决一些涉及圆 周角和圆心角的复杂问题。此外,我们还可以通过一些 实际问题的应用,来进一步理解圆周角和圆心角的重要 性和实际价值。
圆周角和圆心角的关系
在同圆或等圆中,相等的圆心角所对的圆周角也相等,但相等的圆周角所对的圆心角不一定相等。
运用圆周角和圆心角的关系解题的方法
利用圆心角和圆周角的关系,可以解决一些与圆有关的几何问题。在解题时,需要先找到所求问题的圆心角和圆周角,然 后利用其关系进行求解。
学习方法的总结
01
学习重点
本节课的重点是掌握圆周角和圆心角 的关系及其应用。
利用角的平分线性质定理可以证明,一个角平分线分一个角为两个相等的角,而同弧所对 的圆周角等于圆心角的一半。因此,同弧所对的圆周角相等。
应用
可以利用定理来解决一些有关圆的问题,如求角度、弧长、弦长等。同时,在圆的几何证 明题中,也可以利用定理来寻找突破口。
03
圆周角和圆心角的应用
圆周角在圆内的应用
圆周角和圆心角的关系定理
定理1
在同圆或等圆中,相等的圆心角所对的弧相等,所对的圆周 角也相等。
定理2
在同圆或等圆中,同弧所对的圆周角相等,都等于这条弧所 对的圆心角的一半。
定理的证明和应用
定理1的证明
利用圆的旋转对称性,可以通过将圆心角对折,使它与弧重合,从而得到弧所对的圆周角 也相等。
圆周角和圆心角的关系(第1课时)课件

第 三章 圆
第三章 圆
3.4 圆周角和圆心角的关系 (第1课时)
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理. 2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点) 3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
情景导入
如图,在足球射门的游戏中,球员射中球门的难易程度与 他所处的位置B对球门AC的张角(∠BAC)有关.当球员在B 、D、E三点射门时,他所处的位置对球门AC分别形成三个张 角∠BAC,∠BAC,∠BAC.这三个角的大小有什么关系?在 这三点射门的效果一样吗?
B
O
C
B
(2) 圆心角
O (3)
B
C
A(5)Biblioteka CO·B (6)
边AC没有与 圆相交
圆周角 A
合作探究
活动1: 圆周角与圆心角的关系
做一做: 如图,∠AOB=80°.
(1)请你画几个 A B 所对的圆周角?这几个圆
周角有什么关系?与同伴进行交流. (2)这些圆周角和圆心角∠AOB的大小有什么
关系?你是怎么发现的?与同伴进行交流.
求证: ∠C= 1 ∠AOB . 2
分析:根据圆周角和圆心角的位置关系,分三种情况讨论: (1)圆心O在圆周角∠C的一边上,如图(1); (2)圆心O在圆周角∠C的内部,如图(2); (3)圆心O在圆周角∠C的外部,如图(3).
证明:(1)当圆心O在圆周角∠C的一边上时,如图(1).
∵∠AOB是△ACO的外角,
∠1=∠4,∠2=∠7, ∠3=∠6,∠5=∠8,
△AEB∽△DEC △AED∽△BEC
课堂小结
1.圆周角定义: 顶点在圆上,并且两边都和 圆相交的角叫圆周角. 2.圆周角定理:一条弧所对的圆周角等于它 所对的圆心角的一半. 3.圆周角定理推论:同弧(或等弧)所对的圆周角相等 .
第三章 圆
3.4 圆周角和圆心角的关系 (第1课时)
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理. 2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点) 3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
情景导入
如图,在足球射门的游戏中,球员射中球门的难易程度与 他所处的位置B对球门AC的张角(∠BAC)有关.当球员在B 、D、E三点射门时,他所处的位置对球门AC分别形成三个张 角∠BAC,∠BAC,∠BAC.这三个角的大小有什么关系?在 这三点射门的效果一样吗?
B
O
C
B
(2) 圆心角
O (3)
B
C
A(5)Biblioteka CO·B (6)
边AC没有与 圆相交
圆周角 A
合作探究
活动1: 圆周角与圆心角的关系
做一做: 如图,∠AOB=80°.
(1)请你画几个 A B 所对的圆周角?这几个圆
周角有什么关系?与同伴进行交流. (2)这些圆周角和圆心角∠AOB的大小有什么
关系?你是怎么发现的?与同伴进行交流.
求证: ∠C= 1 ∠AOB . 2
分析:根据圆周角和圆心角的位置关系,分三种情况讨论: (1)圆心O在圆周角∠C的一边上,如图(1); (2)圆心O在圆周角∠C的内部,如图(2); (3)圆心O在圆周角∠C的外部,如图(3).
证明:(1)当圆心O在圆周角∠C的一边上时,如图(1).
∵∠AOB是△ACO的外角,
∠1=∠4,∠2=∠7, ∠3=∠6,∠5=∠8,
△AEB∽△DEC △AED∽△BEC
课堂小结
1.圆周角定义: 顶点在圆上,并且两边都和 圆相交的角叫圆周角. 2.圆周角定理:一条弧所对的圆周角等于它 所对的圆心角的一半. 3.圆周角定理推论:同弧(或等弧)所对的圆周角相等 .
