机车车辆串联橡胶垫的高圆弹簧刚度的计算分析
压力弹簧刚度计算

n
C Gd n
D Gd F c 334882===λ 上式中:
c :弹簧的刚度,(即你所说的弹性系数,中学物理叫倔强系数k ); F :弹簧所受的载荷;
λ:弹簧在受载荷F 时所产生的变形量;
G :弹簧材料的切变模量;(钢为8×104MPa ,青铜为4×104MPa ) d :弹簧丝直径;
D 2:弹簧直径;
n :弹簧有效圈数;
C :弹簧的旋绕比(又称为弹簧指数d
D C 2=) 由上式可知。
当其它条件相同时,C 值愈小的弹簧,刚度愈大,亦即弹簧愈硬;反之则愈软。
还应注意到,C 值愈小,弹簧内、外侧的应力差愈悬殊,卷制愈难,材料利用率也就愈低,并且在工作时将引起较大的扭应力。
所以在设计弹簧时,一般规定C ≥4,且当弹簧丝直径d 越小时,C 值越宜取大值。
其实上面这个公式是根据微段弹簧丝ds 受转矩后扭转d θ,从而产生微量变形d λ,再将d λ积分而得到圆弹簧丝螺旋弹簧在受载荷F 后所产生的变形量:
4328Gd n FD =λ。
(机械车辆工程专业论文)机车车辆中常用橡胶件的有限元分析

2.论述了非线性橡胶材料的混合有限单元法,以及ABAQUS软 件的非线性有限元法,详细比较了ABAQUS软件Standard和Explicit 两个求解器。橡胶的静态有限元分析,可以采用Standard求解器, 但是橡胶的动态有限元分析以及复杂的接触分析,则采用Explicit 求解器。
通过对机车车辆系统的分析较准确地得到产品在系统运行过程中的主要承受的载西南交通大学硕士研究生学位论文荷形式和载荷大小再运用有限元法建立与实际相符合的产品数值模型就可以准确计算出橡胶零件的应力或应变集中区域预测产品疲劳破坏的位置从而找出产品最薄弱环节为产品的结构优化提高疲劳性能奠定基础
西南交通大学 硕士学位论文 机车车辆中常用橡胶件的有限元分析 姓名:左亮 申请学位级别:硕士 专业:车辆工程 指导教师:肖绯雄
但是,由于橡胶材料的双重非线性和体积不可压缩性,使得橡 胶材料力学问题的理论计算十分困难,随着计算机的迅速发展和有 限单元法计算技术的发展,使得数值计算方法解决橡胶材料的力学 问题变得可能。
在橡胶制品的设计过程中,应用有限元仿真技术进行静、动态 性能的预测分析和设计改进,进而实现橡胶制品的优化设计,可以 有效提高橡胶件的设计质量,缩短产品开发周期,降低试制和实验 的消耗。本文在总结前人的橡胶制品有限元分析的基础上,应用有 限元仿真技术对机车车辆中常用的橡胶件进行有限元分析。本文的 主要研究内容大致可以归为以下几个方面:
the material modellings;summarized the rubber elastic element’S
压力弹簧刚度计算

上式中:
c:弹簧的刚度,(即你所说的弹性系数,中学物理叫倔强系数k);
F:弹簧所受的载荷;
λ:弹簧在受载荷F时所产生的变形量;
G:弹簧材料的切变模量;(钢为8×104MPa,青铜为4×104MPa)
d:弹簧丝直径;
D2:弹簧直径;
n:弹簧有效圈数;
C:弹簧的旋绕比(又称为弹簧指数)
由上式可知。
当其它条件相同时,C值愈小的弹簧,刚度愈大,亦即弹簧愈硬;反之则愈软。
还应注意到,C值愈小,弹簧内、外侧的应力差愈悬殊,卷制愈难,材料利用率也就愈低,并且在工作时将引起较大的扭应力。
所以在设计弹簧时,一般规定C≥4,且当弹簧丝直径d 越小时,C值越宜取大值。
其实上面这个公式是根据微段弹簧丝ds受转矩后扭转dθ,从而产生微量变形dλ,再将d λ积分而得到圆弹簧丝螺旋弹簧在受载荷F后所产生的变形量:。
弹簧刚度计算大全
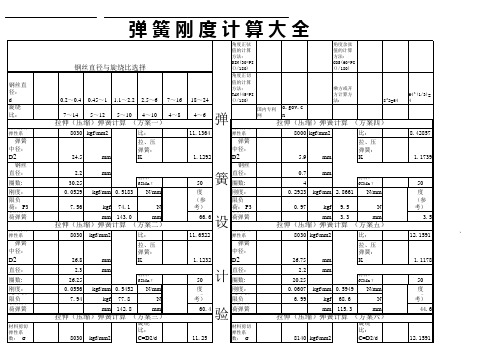
YII型 H
48.41 mm
C 5.7500
L型(不 加钩环 尺寸) H
24.00 mm
弹
簧
刚
度 :
P
`
0.0432 kgf/mm 0.4240 N/mm
允
许
极
限
负 荷
:
P
3
10.47 kgf 102.7
N
极
限 负
荷
弹
簧
总
变 形
量
:
f
3
242.2
mm
拼圈高 度
(参 考)
62.2
曲度系 数
K 1.2649
弹簧刚度计算大全
角度正弦 值的计算
角度余弦 值的计算
钢丝直径与旋绕比选择
方法: SIN(30*PI ()/180)
方法: COS(60*PI ()/180)
钢丝直 径:
d
0.2~0.4 0.45~1 1.1~2.2 2.5~6 7~16 18~24
角度正切 值的计算 方法: TAN(45*PI ()/180)
N
极
限
负
荷
弹 簧
总
变
形
量
:
f
3
4.2
mm
75
5
拼圈高 度
(参 考)
0
0
20
40
60
5.3
``
www.sip
乘方或开 方计算方 法:
8^2=64
64^(1/3)= 4
旋绕 比:
材料剪切 弹性系
7~14 5~12 5~10 4~10 4~8
拉伸(压缩)弹簧计算 (方旋绕案一)
8030 kgf/mm2
单桥复合悬架橡胶空心弹簧刚度分析和参数优化

单桥复合悬架橡胶空心弹簧刚度分析和参数优化单桥复合悬架是一种常见的车辆悬架结构,它是由多种材料和部件构成的复合系统,其中橡胶空心弹簧是其中重要的组成部分之一。
橡胶空心弹簧的刚度对于悬架的性能和行驶稳定性有着决定性的影响,因此对橡胶空心弹簧的刚度进行分析和参数优化十分必要。
首先,橡胶空心弹簧的刚度与其材料硬度、几何尺寸和壁厚等因素密切相关。
一般来说,橡胶弹簧的刚度与其材料硬度成正比,与截面积和弹簧高度的平方成反比,与弹簧的壁厚成正比。
因此,在进行橡胶空心弹簧刚度优化时,需要考虑这些因素的综合作用。
其次,橡胶空心弹簧的刚度对于悬架系统的动力特性和驾驶品质有着重要的影响。
如果弹簧刚度过大,容易出现车身反弹过度、颠簸感强等问题;如果弹簧刚度过小,则会影响悬架的稳定性和悬架系统的减震效果。
因此,进行橡胶空心弹簧刚度优化时,需要充分考虑悬架系统的整体性能和行驶稳定性。
最后,对于橡胶空心弹簧的刚度优化,需要结合实际使用情况和测试数据,采用试验方法和数值模拟分析进行验证和改进。
同时,对于不同类型和用途的车辆,需要根据其特定的工作条件和行驶环境进行个性化的橡胶空心弹簧刚度优化,以实现更高的悬架性能和行驶稳定性。
综上所述,橡胶空心弹簧刚度是单桥复合悬架中非常重要的组成部分,对于悬架的性能和行驶稳定性有着决定性的影响。
在优化橡胶空心弹簧刚度时,需要考虑材料硬度、几何尺寸、壁厚以及悬架系统的整体性能和行驶稳定性等因素,采用试验方法和数值模拟分析进行验证和改进,实现更高的悬架性能和行驶稳定性。
在进行橡胶空心弹簧刚度分析和参数优化时,还需要结合悬架系统的其他部分进行考虑。
例如,悬架系统中的减震器和悬挂连杆也会对弹簧刚度产生影响。
在悬架系统中,减震器主要起到缓冲和阻尼作用,能够有效减少车身的弹动和震动。
如果弹簧刚度过大,会使减震器的阻力不足导致无法有效地吸收冲击力,从而影响悬架的降震效果。
因此,在橡胶空心弹簧刚度优化时,需要支持适当考虑减震器的阻尼特性和悬挂连杆的长度和角度等因素,以达到更好的整体效果。
橡胶弹簧的刚度计算

E o 口 Eo
i k:( A: L1_ j 1 d - E 堕
o E t R 一
堂
由于 、r在弹簧总高度 0蓟 9 6 m 范围 内 .o 均 是 的分 段 函 数, 因 此 上 述 积 分 应 分 十 段
进 行 再 求 和 。 正 确 运 用 积 分 公 式 , 最 后 即 可 求得;
以 :4 0 E .2
式 中 为动荷 系数 。 与硬度Hs 的关系 为:
HS 5时 5
Hs 0时 6
取 12 .8
取 1. 4
2 .横 向( 方 向) 缃 剐度 计算 橡胶弹簧受横 向载荷 的变形通 常都 被看
作剪切变形,但是更为恰 当的力学 模型还应 是受横 向载荷 的悬臂梁 。根据 材料力 学的讨 论可知其 端部 挠度 为:
为;
K : — A E
r
其中 国 为拉压弹性模 量。与一般 的 金 属 材 料不同, 椽胺的 弹性 模量日一般不 是常量。 但 试验表 明, 在线应变 8 .6 .6 时,弹 ≤0 1 ~0 2
・
2 ・ 6
维普资讯
鉴 于对合式组合碟形橡胶弹 簧其横截 面积沿 轴线变化,故只 可写 出此弹簧沿轴向微分段
Hs 2时 7
可取 16 .6
对应上述 三种 硬度 的 皿 的计算值依序是・
3 .k /m ̄4 .k /m 8 .  ̄ /m 6 5g o 69 ge 31 o
前面得蓟 的橡胶 弹簧剐度 计算式 中的 皿 就应是动 表观弹性 模量 风 将得蓟 的
别 代 入 式
=4. 2 0 E = 0. 9 5 E
如 的 中 空 圆 柱形 橡 胶 弹 簧 串 联 而 成 。 串 联
减振器螺旋弹簧组串并联刚度计算与分析

减振器螺旋弹簧组串并联刚度计算与分析可帅;冯治国;李长虹;余世捷【摘要】基于有限元仿真提出了一种新的减振器弹簧组刚度计算方法,首先利用UG建模平台对减振器中弹簧组的两种常见的串并联方式进行简化三维建模,然后将建立好的弹簧组三维模型导入ANSYS中进行弹簧组串、并联有限元分析,分别得到两种弹簧组在不同作用力下位移的变化量,利用Matlab数据处理平台分别拟合出弹簧组理论曲线和有限元分析的位移与法向力的关系曲线,并分别计算出相对误差,将二者进行对比分析;最后采用相同的分析方法进行了整个减振器扭转刚度的计算与分析.研究表明,串、并联弹簧组均具有线性特征,为更复杂的弹簧组的使用提供可靠地理论依据和方法.【期刊名称】《机械设计与制造》【年(卷),期】2018(000)009【总页数】4页(P25-28)【关键词】螺旋弹簧组;刚度特性;三维建模;ANSYS;Matlab【作者】可帅;冯治国;李长虹;余世捷【作者单位】贵州大学机械工程学院,贵州贵阳 550025;贵州大学机械工程学院,贵州贵阳 550025;贵州大学机械工程学院,贵州贵阳 550025;贵州大学机械工程学院,贵州贵阳 550025【正文语种】中文【中图分类】TH161 引言汽车行驶的过程中,减振器中的弹簧起着缓冲和减震的作用,由于路况不同,弹簧要不断承受高频往复的运动,因此弹簧减振能力和质量的好坏,直接影响着车辆的平稳性和安全性。
在弹簧减振器中,把不同性能的弹簧按照一定的方式组成新的弹簧组系统,往往比单只弹簧的使用更加普遍。
弹簧组的使用提高了传统的单只长弹簧的侧向稳定性。
为改善货车小载荷下的运行品质,提高对扭曲线路的适应能力,货车转向架弹簧悬挂装置中两级刚度弹簧组早在上世纪50年代就在前苏联X-2型货车转向架上得到应用。
在国外一些国家的货车转向架上,两级刚度弹簧组都程度不同地得到了应用。
在解决管道热力学膨胀的问题中,国外科研人员采用多级弹簧串联使用,由多个弹簧来共同分担热位移的影响。
弹簧单圈刚度和弹簧刚度

弹簧单圈刚度和弹簧刚度弹簧单圈刚度和弹簧刚度是描述材料在受力作用下产生了多大的变形量的物理量。
弹簧单圈刚度是指单位长度(或单位横截面积)弹簧在一侧擅长一圈所产生的抗弯刚度,而弹簧刚度则是指单位长度(或单位横截面积)的杆状弹簧在受到拉伸或压缩时所产生的反作用力和变形之间的比值。
要理解弹簧单圈刚度和弹簧刚度的概念,我们需要了解一些基本的力学知识和弹性形变理论。
首先,我们来看一看弹簧单圈刚度。
弹簧单圈刚度是描述弹簧在承受扭转力时的抗弯刚度的一个指标。
在应用中,一般使用弹簧常数k来描述弹簧单圈刚度,其定义为单位长度(或单位横截面积)弹簧在一侧擅长一圈所产生的反作用力与弯曲角度(扭转角)之间的比值。
对于一个理想化的圆柱形均匀弹簧,弹簧单圈刚度可以用以下公式计算:k = G * A / L其中,k是弹簧单圈刚度,G是剪切模量,A是弹簧横截面积,L是弹簧长度。
从公式可以看出,弹簧单圈刚度是与弹簧材料的剪切模量、横截面积和长度有关的。
剪切模量反映了材料的刚度,横截面积反映了材料的几何形状和尺寸,长度反映了弹簧的整体大小。
因此,对于相同材料和相同横截面积的弹簧来说,长度越长,弹簧单圈刚度越小;而长度越短,弹簧单圈刚度越大。
接下来,我们来看一看弹簧刚度。
弹簧刚度是描述弹簧在受到拉伸或压缩时所产生的反作用力和变形之间的比值。
在应用中,一般使用弹簧常数k来描述弹簧刚度,其定义为单位长度(或单位横截面积)的杆状弹簧在受到拉伸或压缩时所产生的反作用力与变形量之间的比值。
对于一个理想化的杆状均匀弹簧,弹簧刚度可以用以下公式计算:k = E * A / L其中,k是弹簧刚度,E是杨氏模量,A是弹簧横截面积,L是弹簧长度。
从公式可以看出,弹簧刚度是与弹簧材料的杨氏模量、横截面积和长度有关的。
杨氏模量反映了材料的刚度,横截面积反映了材料的几何形状和尺寸,长度反映了弹簧的整体大小。
因此,对于相同材料和相同横截面积的弹簧来说,长度越长,弹簧刚度越小;而长度越短,弹簧刚度越大。
机车高圆簧刚度矩阵计算应用分析

!"#"$%&'()*$+&,+$-.()$)/011+.&$-.()(23-.22)"##4$-%.5(2 6+"57&(.+31%.)8#9#"/.):(&(;(-.<"#
,2&EOGI:OS$,2-=$4+*T 4>OS$U2*T&=OL=
!5GI7787HV:GI>OEG>80OSEO::<EOS$57=MIK:JM&E>7M7OS(OEW:<JEM?$1I:OSN=@"$$B"$1IEO>"
摘要高圆簧广泛应用于机车车辆中$其刚度作为车辆的主要悬挂参数$仿真时刚度矩阵的选择和简化处理
对计算结果有直接影响%在一般机车模型的动力学仿真中只考虑了高圆簧刚度矩阵@个对角元素$未考虑非对
角元素的影响%通过推导高圆簧的完整矩阵$并分别以弹簧振子和机车作为对象进行对比分析%计算结果表
明$仿真结果与理论分析结果吻合'高圆簧采用完整刚度矩阵的机车动力学性能优于高圆簧只采用对角元素的
第 卷第 !" # 年 #$"% #
期月
铁道学报
&'()*+, '-./01/2*+ )+2,3+45'120.4
6789!" *79# -:;<=><?#$"%
文章编号"$$"APB@$!#$"%"$#A$$CQA$Q
机车高圆簧刚度矩阵计算应用分析
李金城李芾杨阳丁军君
串联橡胶垫的高圆钢弹簧刚度与横向稳定性分析_周业明

度 ,同 时 也 可 以 有 效 降 低 圆 弹 簧 的 应 力 水 平 。 2 橡 胶 垫 的 有 限 元 分 析
橡胶垫刚度特性对于组合系统的横向刚度起着关 键性作用,但橡胶件的超弹性使其刚度具有强烈的 非 线 性特性而显得难以把握。为了验证有限元仿真的准确 性,首先以橡胶 垫 为 算 例,分 析 其 垂 向 压 缩 4 mm 时 的 垂向刚度,横向 位 移 12.5 mm 时 的 横 向 刚 度 以 及 翘 曲 0.2°时 的 弯 曲 刚 度。 图 2 为 施 加 垂 向 和 横 向 位 移 载 荷 后 橡 胶 垫 的 剪 切 变 形 情 况 ,图 3 为 分 析 橡 胶 垫 弯 曲 刚 度 时产生的翘曲变形。将有限元分析结果与公式法和试 验 数 据 相 比 较 以 判 断 其 可 靠 性 。 其 中 ,经 验 公 式 法 参 考 文献[1];试验 结 果 则 取 自 该 动 车 转 向 架 橡 胶 垫 静 强 度 试验报告。
;
{[ ( ) b= -
1 2
1 kL
-k1v
(cos2θ-
] } sin2θ)+k1Π P +h1 + H20cosθ ; [ ( ) ] c=- aP2 + H20sinθ P -kθθ 。
周 业 明 ,冯 永 华 ,马 利 军 (中国南车集团 青岛四方机车车辆股份有限公司,山东青岛 266111)
摘 要 为了精确计算串联橡胶垫的高圆钢弹簧各向刚度参数,现以出口斯里兰卡 内 燃 动 车 组 动 力 车 转 向 架 二 系 悬挂元件为例,运用有限元法对橡胶垫与高圆弹簧串 联 系 统 的 各 向 刚 度 进 行 分 析 ,将 该 分 析 结 果 与 公 式 法 计 算 结 果和试验数据进行对比,并且对串联系统的横向稳定性进行了试验研究。结果表 明 采 用 有 限 元 法 的 计 算 结 果 具 有 较高的精度。串联系统的倾覆稳定性的工作值小于临界值,且通过横向大位移稳 定 性 试 验 和 列 车 线 路 运 行 试 验 得 到了验证。 关 键 词 高 圆 弹 簧 ;橡 胶 垫 ;刚 度 ;稳 定 性 ;有 限 元 法 中图分类号:U270.331+ .4 文献标志码:A doi:10.3969/j.issn.1008-7842.2013.Z1.06
弹簧组刚度计算公式

弹簧组刚度计算公式弹簧是一种常见的机械元件,广泛应用于工业、汽车、航空航天等领域。
弹簧的主要作用是储存和释放能量,用于各种机械装置的控制和调节。
在设计和制造弹簧时,计算其刚度是非常重要的一步,因为刚度直接影响到弹簧的性能和工作效果。
本文将介绍弹簧组刚度的计算公式及其应用。
弹簧组刚度是指多个弹簧组合在一起后的整体刚度。
在实际工程中,常常需要将多个弹簧组合在一起,以满足特定的工作要求。
在这种情况下,需要计算弹簧组的整体刚度,以确保其能够正常工作并承受所需的载荷。
弹簧组刚度的计算公式可以通过以下步骤得到:1. 首先,需要计算每个弹簧的刚度。
弹簧的刚度通常用弹簧系数(K)来表示,即单位长度内的弹簧受力与变形之间的比值。
弹簧系数可以通过实验测定或理论计算得到。
2. 然后,将每个弹簧的刚度进行叠加,得到整个弹簧组的刚度。
如果弹簧组是串联排列的,则整体刚度为各个弹簧刚度的总和;如果弹簧组是并联排列的,则整体刚度需要根据并联弹簧的公式进行计算。
对于串联排列的弹簧组,整体刚度K_total可以通过以下公式计算得到:1/K_total = 1/K1 + 1/K2 + ... + 1/Kn。
其中,K1、K2、...、Kn分别为每个弹簧的刚度。
对于并联排列的弹簧组,整体刚度K_total可以通过以下公式计算得到:K_total = K1 + K2 + ... + Kn。
其中,K1、K2、...、Kn分别为每个弹簧的刚度。
通过以上公式,可以计算出弹簧组的整体刚度,从而为工程设计和制造提供参考依据。
在实际应用中,需要根据具体情况选择合适的弹簧组合方式,并进行刚度计算,以确保弹簧组能够满足工作要求。
除了上述的计算公式外,还需要注意以下几点:1. 弹簧的刚度受到材料、形状、工艺等因素的影响,因此在计算刚度时需要准确掌握弹簧的相关参数,并进行合理的估算和计算。
2. 弹簧在工作过程中会受到外部载荷的作用,因此在计算刚度时需要考虑弹簧的变形和受力情况,以确保计算结果准确可靠。
有关弹性刚度如何确定

有关弹性刚度如何确定000发短消息加为好友13#大中小发表于2006-9-215:15只看该作者简单的说就是结构杆件在力的作用下产生的位移,3*EcIc/L^3,这个公式是算支座下的支撑柱的刚度公式,一般我们做设计可以直接用这个算出值代入SFCAD,不过正规做法应该是计算出支座和柱的刚度串联。
而9楼说的支座加橡胶垫一般是用在大跨度或水平位移比较大的情况下,而且规范上有计算橡胶垫弹簧刚度的公式,一般的平板压力支座取0.3是粗算,最好还是计算柱的刚度,这个对结构还是影响很大的一般的平板压力支座取0.3,不知道0.3是怎么得来的?帖子152精华0威望25土木币3在线时间14小时注册时间2005-4-21查看详细资料TOPcivilfans列兵帖子43精华0威望25土木币9在线时间4小时注册时间2005-10-19发短消息加为好友14#大中小发表于2006-9-415:50只看该作者结构设计中的弹性刚度是指支撑体系发生单位位移所需要的外力,即将支撑结构体系看成一个三向弹簧,因此弹性刚度包括三个内容:竖向支撑刚度;两个水平方向的剪切侧移刚度。
楼上各位提到的公式"3*EcIc/L^3"仅是支撑结构为单柱时候的情况,如果支撑结构还有联系梁,则该公式失效,更不要说支撑结构为框架或其他复杂结构,就其原因,源于该公式来与结构力学的悬臂柱。
通常情况下,当下部支撑结构较复杂时,准确地做法应该是上下结构整体连算,一种可以替代的办法是考虑下部局部支撑结构联合计算,现有的计算软件完全能够做到这一点。
当然如果采取橡胶支座,则支撑刚度应该为橡胶和其他支撑结构对应刚度的串联弹簧刚度,不过这种情况下通常无需考虑下部其他支撑结构刚度,其原因各位可以用高等数学求极限的方法对串联弹簧等效刚度公式做一简单推导既可证明,推导的前提条件是橡胶刚度相对下部支撑结构刚度很小。
一般平板压力支座其自身的水平支撑刚度很难确定,竖向支撑可以近似按堪固考虑,但是水平刚度则不能简单按此处理,也不能近似按0.3考虑,通常,平板支座水平支撑刚度和压力有较大关系,以钢和混凝土支撑柱来说,钢和混凝土的摩查系数大约为0.2-0.3,在此条件下,水平滑移能力直接和压力相关,而压力对不同工程又是一个不确定值。
弹簧刚度计算
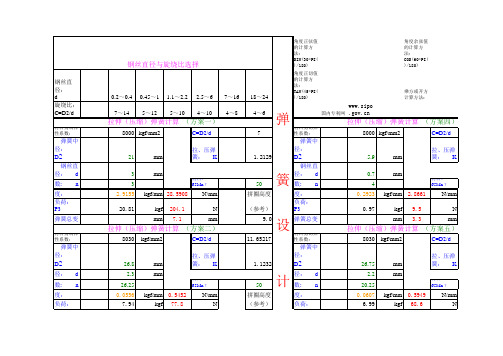
拉、压弹簧:
材料:65Mnτ (kgf/mm2)
材料:65Mnτ (kgf/mm2)
N/mm N mm 旋绕比:
N/mm N mm 旋绕比: C=D2/d K
允许极限负荷: P3
允许极限负荷: P3 极限负荷弹簧总变形量:
极限负荷弹簧总变形量:
拉伸(压缩)弹簧计算 (方案二)
材料剪切弹性系数: G
拉伸(压缩)弹簧计算 (方案五)
拉伸(压缩)弹簧计算 (方案六)
材料剪切弹性系数: G
8140 kgf/mm2 26.75 2.2 20.25 0.0615 6.99 f3 kgf/mm 0.6030 kgf 68.6 mm 113.7 mm mm
弹簧中径: 钢丝直径: 有效圈数: 弹簧刚度:
D2 d n P`
拉、压弹簧:
弹簧中径: 钢丝直径: 有效圈数: 弹簧刚度:
弹簧材料:60Si2Mn 弹簧材料:60Si2Mn 弹簧剪切弹性系数 弹簧指数: 曲度系数 钢丝直径 弹簧中径 工作圈数 总圈数 最小工作负荷 最大工作负荷 允许极限负荷 极限负荷单圈变形量 弹簧钢丝间距 弹簧刚度 最大工作负荷下间距 C=D2/d
第二步(验算弹簧工作圈数及有关参数) [τ ] 60.00 kgf/mm2 节距 τ 75.00 kgf/mm2 自由高度或长度: YI型 G 8030 kgf/mm2 C 5.7500 L型(不加钩环尺寸) K 1.2649 压缩弹簧稳定性指标: YI型 d 4.00 mm D2 23.00 mm L型(不加钩环尺寸) n 5.21 当b>3时,弹簧须套在心轴上使 n1 7.21 最小工作负荷下变形量 P1 26.60 kgf 最大工作负荷下变形量 P2 34.70 kgf 极限负荷下变形量 P3 64.79 kgf 最小工作负荷下高(长)度 f3 3.07 mm 最大工作负荷下高(长)度 δ 3.07 mm 极限负荷下高(长)度 P` 4.0500 kgf/mm 螺旋角 δ 1 1.42 mm ←δ 1(适用于压缩弹簧,指
普通弹簧刚度

普通弹簧刚度普通弹簧广泛应用于各种工程机械、设备和器具中,其刚度特性对整个系统的性能有着至关重要的影响。
本文将详细介绍普通弹簧刚度的定义、计算方法、影响因素以及在实际应用中的优势与局限,并提出提高普通弹簧刚度的方法与建议。
一、普通弹簧刚度的定义与意义普通弹簧刚度是指弹簧在单位变形下所承受的力。
它是一个衡量弹簧性能的重要参数,对于确保弹簧正常工作以及整个系统的稳定性具有显著意义。
刚度越大,弹簧在承受力时的变形就越小,表明弹簧的支撑能力越强。
二、普通弹簧刚度的计算方法普通弹簧刚度的计算公式为:刚度K = 力F / 变形ΔL其中,力F为弹簧所承受的力,变形ΔL为弹簧在受力时的伸长或压缩量。
三、影响普通弹簧刚度的主要因素1.弹簧的材料:材料的不同会影响弹簧的弹性模量,从而影响刚度。
2.弹簧的直径和长度:直径和长度的变化会改变弹簧的截面积,进而影响刚度。
3.弹簧的绕制方式:绕制方式的不同会影响弹簧的紧密程度,从而影响刚度。
4.外部环境:如温度、湿度等环境因素会影响弹簧的弹性性能,进而影响刚度。
四、普通弹簧刚度在实际应用中的优势与局限1.优势:普通弹簧具有较好的弹性性能,能够在一定范围内适应外部力的变化,保证系统的稳定性。
2.局限:普通弹簧的刚度相对较低,对于高刚度要求的场合可能不适用。
五、提高普通弹簧刚度的方法与建议1.选用高弹性模量的材料。
2.增加弹簧的直径和长度,以提高其刚度。
3.采用紧密绕制的方式,使弹簧具有更好的支撑能力。
4.在设计时,充分考虑弹簧的工作环境,选用合适的弹簧参数。
总之,普通弹簧刚度是一个关键的性能指标,对其深入了解和掌握有助于我们更好地应用弹簧产品。
串联弹簧刚度计算公式

串联弹簧刚度计算公式串联弹簧的刚度计算公式是指计算系统中多个弹簧串联时的总刚度。
由于弹簧的刚度是用来描述弹簧在受力时的压缩或伸长程度的指标,因此在串联时,需要考虑这些弹簧对系统整体刚度的影响。
串联弹簧的总刚度可以通过以下公式计算:1.弹簧力的平衡条件在计算串联弹簧的刚度之前,需要先确定弹簧力的平衡条件。
即系统中每个弹簧上的受力必须平衡。
对于串联弹簧而言,整个系统中的力平衡条件可以表示为:F=F1+F2+...+Fn其中,F为外力施加在系统上的力,F1,F2,...,Fn为每个弹簧上的力。
这个平衡条件是计算串联弹簧总刚度的基础。
2.弹簧的胡克定律接下来,我们需要使用弹簧的胡克定律来描述弹簧的力和位移之间的关系。
根据胡克定律,弹簧力F和弹簧位移x之间的关系可以表示为:F = kx其中,k为弹簧的刚度系数。
根据弹簧力和弹簧位移的关系,我们可以得到每个弹簧上的力Fi和位移xi之间的关系式:Fi = kixi其中,ki为第i个弹簧的刚度系数,xi为第i个弹簧的压缩或伸长位移。
3.弹簧总位移和总受力之间的关系接下来,我们需要确定整个系统中的位移和受力之间的关系。
根据平衡条件和胡克定律,我们可以得到位移和受力之间的关系式:F = k1x1 + k2x2 + ... + knxn其中,x1, x2, ..., xn为每个弹簧的压缩或伸长位移。
4.弹簧总刚度最后,我们可以通过比较总受力和总位移之间的关系,求解出串联弹簧的总刚度。
从上一步的关系式可以看出,总受力F和总位移x之间的关系是一个线性方程组。
我们可以将这个线性方程组写成矩阵形式:[F]=[K][x]其中,[F]和[x]为列向量,[K]为刚度矩阵。
刚度矩阵的每个元素为:[K] = [ k1 , k2 , ..., kn ]最终,我们可以将线性方程组求解,求得总刚度k_total:[F]=[K][x][F] = [ k_total , 0 , ..., 0][x][F] = k_total * [x]根据上述推导,我们可以得到串联弹簧的总刚度计算公式:k_total = k1 + k2 + ... + kn其中,k1, k2, ..., kn为每个弹簧的刚度系数。
串联弹簧刚度计算公式

串联弹簧刚度计算公式
弹簧串联同时应用,总劲度系数变小,弹簧并联同时应用,总劲度系数增大。
弹簧产生弹性形变时,弹力的大小F跟弹簧伸展(或宿短)的总长度x成正比,即F=kx,式中的k称之为弹簧的劲度系数,的单位是牛頓每米。
假如把弹簧串联或是是并联同时同时应用,这一个串联或是并联的总体的劲度系数,和一种弹簧的劲度系数中间有怎样的关联。
为了能简便考虑,让我们假定把完全一致的弹簧串联或并联。
设将两个劲度系数均为k的弹簧,串联同时成为一种总体应用,这一个总体的劲度系数是多少呢?因为F=kx,如果我们还是应用同样大小的力F去拉这一个弹簧,这一个总体将会伸展2x,那么这一个串联同时的弹簧总体,其劲度系数为1/2倍k,就是说串联同时应用的弹簧的劲度系数变小了。
设将两个劲度系数均为k的弹簧,并联同时成为一种总体应用。
同样的道理,如果我们还是应用同样大小的力F去拉这一个弹簧,两个弹簧分别分担了F的一半,这一个总体只能伸展1/2倍x,那么,这一个并联同时的弹簧总体,其劲度系数为2k,就是说并联同时应用的弹簧的劲度系数变为了原来的2倍,比一种弹簧的劲度系数大了。
弹簧串联公式计算
从公式计算而言,弹簧的刚度计算公式为:Gd^4/8/D^3/n。
弹簧串联时,作用力是作用在一个弹簧的端面上的,此时串联同时的
两个弹簧可以看成是一个弹簧的高度和圈数成倍数增加,此时弹簧刚度公式计算中除圈数成倍增加外,其化所有条件没有发生变化,那么此时刚度值是缩小的,由此可见弹簧串联时力度会变小。
弹簧并联公式计算
弹簧并联时,作用力是作用在两个并列的弹簧端面上的,此时并联同时的两个弹簧同时作用在一个物体时,此时弹簧是两个独立工作时,因此弹簧的力是成倍增加的。
橡胶弹簧动刚度

橡胶弹簧动刚度橡胶弹簧是一种常见的机械零件,其动刚度是一个重要的力学参数。
动刚度的大小决定了橡胶弹簧在受力时的变形程度和弹性回复能力。
本文将详细介绍橡胶弹簧动刚度的相关概念、计算方法以及影响动刚度的因素。
橡胶弹簧的动刚度是指在单位变形下所受的力。
一般来说,橡胶弹簧的动刚度可以通过斯贝尔公式来计算。
斯贝尔公式可以表示为:K = F / δ其中,K表示橡胶弹簧的动刚度,F表示橡胶弹簧所受的力,δ表示橡胶弹簧的变形量。
根据该公式,动刚度的大小与施加在橡胶弹簧上的力以及变形量是成正比的。
橡胶弹簧的动刚度与其材料的硬度和弹性有关。
一般情况下,橡胶弹簧的硬度越大,动刚度也就越大,弹性越小;相反,橡胶弹簧的硬度越小,动刚度也就越小,弹性越大。
因此,在实际应用中,可以通过选择不同硬度的橡胶材料来调节橡胶弹簧的动刚度,以满足不同的力学要求。
除了材料硬度,橡胶弹簧的几何形状也会对其动刚度产生影响。
弹簧的截面形状、长度以及螺旋角度等因素都会影响橡胶弹簧的刚度。
一般来说,橡胶弹簧的截面越大,长度越长,螺旋角度越小,动刚度也就越大。
而截面越小、长度越短、螺旋角度越大,动刚度也就越小。
因此,在设计橡胶弹簧时,需要根据实际需求选择合适的几何形状参数。
此外,温度也是影响橡胶弹簧动刚度的重要因素。
一般来说,橡胶材料在高温下会变得更加柔软,动刚度会降低。
而在低温下,橡胶材料会变得更加硬,动刚度会增大。
因此,在实际应用中,需要根据工作环境的温度来选择合适的橡胶材料以及相应的动刚度。
在工程实践中,橡胶弹簧的动刚度通常通过实验来测定。
一种常用的方法是采用拉伸试验机对橡胶弹簧进行加载,并测量变形量和所受力的关系。
通过绘制载荷-变形曲线,可以计算出橡胶弹簧的动刚度。
此外,还可以利用有限元分析等数值方法对橡胶弹簧的动刚度进行预测和优化。
综上所述,橡胶弹簧的动刚度是影响其力学性能的重要参数。
其大小与施加在橡胶弹簧上的力和变形量成正比,同时受到材料硬度、几何形状和温度等因素的影响。
机车高圆簧刚度矩阵计算应用分析

机车高圆簧刚度矩阵计算应用分析李金城;李芾;杨阳;丁军君【摘要】高圆簧广泛应用于机车车辆中,其刚度作为车辆的主要悬挂参数,仿真时刚度矩阵的选择和简化处理对计算结果有直接影响.在一般机车模型的动力学仿真中只考虑了高圆簧刚度矩阵6个对角元素,未考虑非对角元素的影响.通过推导高圆簧的完整矩阵,并分别以弹簧振子和机车作为对象进行对比分析.计算结果表明,仿真结果与理论分析结果吻合;高圆簧采用完整刚度矩阵的机车动力学性能优于高圆簧只采用对角元素的机车,其差异主要表现在与高圆簧轴向垂直的方向上,轴向性能基本一致;机车高圆簧只考虑矩阵对角元素时仿真结果较考虑完整刚度矩阵时偏于安全,但二者最大差值都未超过10%,可以用于机车模型的计算分析.【期刊名称】《铁道学报》【年(卷),期】2019(041)002【总页数】7页(P57-63)【关键词】机车高圆簧;刚度矩阵;性能差异;应用【作者】李金城;李芾;杨阳;丁军君【作者单位】西南交通大学机械工程学院 ,四川成都 610031;西南交通大学机械工程学院 ,四川成都 610031;西南交通大学机械工程学院 ,四川成都 610031;西南交通大学机械工程学院 ,四川成都 610031【正文语种】中文【中图分类】U260.2近年来随着列车运行速度的提高,对牵引机车的动力学性能提出了更高的要求。
为降低高圆弹簧工作应力,一般使用多组并联高圆簧作为机车的二系悬挂[1-2],如东风9和东风11型等内燃机车使用8组高圆簧,韶山7型和韶山8型等电力机车使用6组高圆簧[3-4]。
除机车外,高圆簧还广泛应用于三大件货车中。
高圆簧作为车辆主要悬挂部件之一,其刚度在进行车辆动力学仿真时需着重考虑,相同条件下采用不同刚度矩阵车辆运行性能仿真结果不同,在车辆模型的验证阶段,其刚度矩阵的选择及简化是否合理值得探讨与研究。
一般来说,在进行机车动力学仿真计算时,假设弹簧为一力元,考虑高圆簧的轴向刚度cl、抗剪刚度cs、抗弯刚度cφ及扭转刚度ca,由于弹簧的对称性,即认为此时只考虑了高圆簧刚度矩阵中的对角元素。
考虑橡胶垫复刚度的钢轨振动力学分析模型

考虑橡胶垫复刚度的钢轨振动力学分析模型
张明聚
【期刊名称】《石家庄铁道大学学报:自然科学版》
【年(卷),期】1991(000)001
【摘要】本文讨论了轨下橡胶垫的复刚度特性,建立了橡胶垫复刚度的等间距点支承无限长梁模型,并推导出该模型在稳态激振力作用下的解析解。
该模型是对轨道力学理论的一个补充。
【总页数】7页(P52-58)
【作者】张明聚
【作者单位】石家庄铁道学院铁道建筑系
【正文语种】中文
【中图分类】N
【相关文献】
1.橡胶垫参数及结构形式对高圆簧加橡胶垫的横向刚度的影响 [J], 蒋益平
2.具有非线性复刚度的复阻尼振动系统的摄动解 [J], 缪经良
3.转向架橡胶垫刚度对钢弹簧高频振动应力水平的影响分析 [J], 秦涛;张文涛;李茂春;喻佳文;黄江伟;张建全
4.扣件刚度对钢轨振动特性的影响研究 [J], 杭锦; 王金朝; 王志强
5.地铁线路扣件刚度对钢轨振动与波磨的影响 [J], 朱宁;杨新文;赵治均
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机车车辆串联橡胶垫的高圆弹簧刚度的计算分析孤夜狼 13车辆工程2班 20131310010204摘要:随着我国铁路进入高速重载的新时代,铁路列车运行的平稳性与安全性越来越重要。
轴箱弹簧是机车转向架的关键部件之一,其性能的稳定性直接影响机车运行的安全及平稳。
弹簧承载情况及工作环境十分复杂,所以,弹簧的强度、疲劳寿命具有非常大的随机性,是广大工程技术研究人员十分关注的问题。
因此,研究细化弹簧强度和精确计算串联橡胶垫的高圆钢弹簧刚度参数具有重要的理论及实际意义。
关键词:高圆弹簧;橡胶垫;刚度;稳定性Abstract : With China's railway enter a new era of speed and heavy duty,the smooth and security running of railway trains becomes more important.Spring is one of the key components in vehicle, the stability of which affect the safety and stabilization of vehicle operation. There is very large randomicity in strength and fatigue life of spring for the complicated status of load and work environment. For its importance of practical application, the problem catches many engineers to research.Keywords : flexicoil spring;rubber pad;stiffness;stability0、引言;近十年多来,中国的铁路发展迅猛,列车经过几次大提速,运行速度有了显著提高。
随着运行速度的提高,不可避免地加剧了机车车辆的振动和噪声,严重影响了列车的舒适性和安全性,因此对列车减振系统相应地提出了更高的要求。
由高圆钢制弹簧和橡胶垫串联组成的悬挂装置在铁道机车车辆中使用十分普遍,准确计算其各向刚度,特别是横向刚度值是保证机车车辆动力学性能的前提。
在机车车辆中大量使用螺旋弹簧,而螺旋弹簧的刚度显著影响机车车辆的运行稳定性、安全性和曲线通过性能。
到目前为止,有许多计算弹簧刚度的方法,但都无法在设计阶段取得试验数据,只能用其它相近弹簧的试验数据代替。
另外,弹簧本身就不是弹性直杆,弹性直杆不能解决弹簧两端的切口对刚度的影响,不能计算出精确的弹簧刚度。
在铁路机车车辆设计和方案论证阶段如果机车车辆悬挂系统的刚度参数不能准确确定,机车车辆系统动力学分析结果存在较大的分析误差,会给铁道车辆新产品开发带来困难及经济损失。
故其在很多方面扮演着相当重要的角色,对车辆的舒适性和安全性也起着相当重要的作用,因此其刚度的研究分析十分必要。
本文以高圆弹簧一端加橡胶和上下两端加橡胶垫两种不同结构型式进行计算强度,并分析两种结构的稳定性和影响因素。
1、高圆弹簧加橡胶垫的刚度高圆弹簧加橡胶垫的结构被广泛应用于新一代的内燃机车、电力机车及车辆上,作为二系悬挂装置。
橡胶垫的作用有两点:一是减小高圆弹簧的水平向刚度;二是显著降低高圆弹簧的应力水平。
橡胶垫的应用,既改善了高圆弹簧的水平刚度特性,还保证它的运用可靠性和耐久性。
在结构型式上,可以是高圆弹簧一端加橡胶垫,或上下两端加橡胶垫,所加橡胶垫可以是实心圆垫,也可以是中空圆垫。
一般圆垫为单层,也有用双层的。
1.1、高圆弹簧和橡胶元件1.1.1、高圆弹簧螺旋弹簧即扭转弹簧,是承受扭转变形的弹簧,它的工作部分也是密绕成螺旋形。
扭转弹簧的端部结构是加工成各种形状的扭臂,而不是勾环;扭转弹簧常用于机械中的平衡机构。
由高圆钢制造而成的弹簧叫做高圆弹簧,高圆弹簧和橡胶垫串联组成的悬挂装置在铁道机车车辆中使用十分普遍。
高圆弹簧如右图[1]所示:1.1.2、橡胶元件橡胶弹性元件由于具有典型的非线性刚度特性,同吋可以满足多向刚度的要求,在满足机车车辆动力学参数方面比金屈零件具有更强的优势,因此在机车车辆转向架中橡胶弹性元件得到了越来越多的应用。
机车牟辆在运行过程中会受到来自轮轨间强烈的瞬时冲击载荷,不仅会引起机车车辆的破坏,也会导致机车车辆的强烈的共振。
为衰减这些冲击和振动,满足机车本辆各利动力学指标(例如,稳性指标、脱轨系数、轮重减载率、轮轨冲等),在轮对和构架之间、转向架车体之间以及其他各种关节之间装有弹性元件(包括橡胶弹黄,各种橡胶关节,橡胶衬套,衬垫,止挡等)。
这些弹性元件存采用金属元件的,但更多的是采用橡胶弹性元件。
因为与金属元件相比,橡胶弹性元件在满足机市动力学性能方而有着非常显著的特点和不可替代的优势。
橡胶垫如右图[2]所示:1.2弹簧刚度分析根据弹簧刚度的定义可知,在上支承圈平面上施加单位轴向强迫位移,计算所得约束反力就是弹簧的轴向刚度[4]。
弹簧的刚度计算公式是由以下方法推到计算的到得:首先列出弹簧受载后的轴向变形,可根据材料力学的公式求(式1)式中:n---弹簧有效圈数;G---剪切弹性模数,弹簧钢 G=81.3GPa;d---簧条圆直径; D---弹簧平均直径。
利用上式可求出所需的弹簧工作圈数n,即:(式2)(1)若n<15时,则取n为0.5的倍数;(2)若n>15时,则取n为整数圈。
一般情况下n≥2,压缩弹簧的总圈数12nnn,2n为支撑圈数。
使弹簧产生单位变形量所需要的载荷,称为弹簧刚度k,即(式3)弹簧的刚度是表征弹簧的性能的主要参数之一。
刚度越大,弹簧变形所需要的力就越大。
影像弹簧刚度的因素很多,由上市可知,k与C的三次方成正比,即C值对k的影响很大,因此合理的选择C值能控制弹簧的弹力。
另外,k还与G、d、n有关,在调整弹簧刚度时,应综合考虑这些因素的影响。
将相应的参数代入式3 ,即可得本例圆柱压缩弹簧的刚度K 。
根据弹簧可知刚度是使弹簧产生单位变形所需要的载荷,因此可以在弹簧的一端施加一个单位受迫振动,即在弹簧的上盖板处施加一个单位位移。
在弹簧的下端可以查看其反作用力所得的反作用力即为弹簧刚度值。
图[3] 弹簧刚度计算过程框架图1.2.1高圆弹簧两端加橡胶垫的横向刚度计算如下图[4]:圆弹簧两端加橡胶垫的横向刚度计算示意图所示:设在工作过程中,其两端保持平行,则可以认为,圆弹簧横向变形对于中点C是对称的,即AC和EC对称。
同时假设圆弹簧的工作高度H不随横向位移fL的变化而变化,而是决定于载荷P′的大小,而且橡胶垫的工作高度h1只决定于垂向载荷P。
设下列代表符号:kL—圆弹簧的横向刚度(N/mm);kV—圆弹簧的垂向刚度(N/mm);H0—圆弹簧的自由高度(mm);kⅡ—橡胶垫的剪切刚度(N/mm);kθ—橡胶垫的弯曲刚度(N・mm/rad)。
由右图[4] 可列出下列方程B点处的力矩M′为:A点处的力矩M为:[图4]力的平衡方程式为:弹簧总成的横向挠度fL′为:各挠度近似地为:又圆弹簧工作高度:解各方程式,得:式中的:解方程式求得横向力Q及横向挠度fL′后, 便可计算得圆弹簧两端加橡胶垫后(或称圆弹簧总成)的横向刚度为:1.2.2高圆弹簧一端加橡胶垫的横向刚度计算圆弹簧一端加橡胶垫的横向刚度,用以下式计算:式中,kL,H—分别为圆弹簧的横向刚度及工作高度;kⅡ,h1—分别为橡胶垫的剪切刚度及工作高度;kθ—橡胶垫的弯曲刚度;P—垂向作用力。
2.高圆弹簧加橡胶垫的稳定性分析弹簧总成的横向稳定性主要与橡胶垫的高度和高圆弹簧所加橡胶垫的厚度,应合理选择,否则会引起弹簧总成的横向趋于不稳定。
但这是仅从橡胶垫的受压考虑,更全面的分析还应该计及高圆弹簧的特性。
如将高圆弹簧视作一受压柱体,则两端或一端的橡胶垫,是该柱体的约束条件。
对于高圆弹簧受压稳定,端部约束或是固定,或是铰接的。
高圆弹簧加橡胶垫在垂直力作用下的不稳定性,表现为弹簧总成的横向刚度为负值。
负刚度的物理意义是,弹簧总成在垂直力作用下,作横向位移时,需要有外力作用于弹簧总成的位移的相反方向,才能保持它的平衡。
在进行理论分析时,将高圆弹簧看作当量柱体,然后运用长柱体的稳定性理论推导它的计算公式。
即从欧拉公式出发,分析高圆弹簧加橡胶垫的临界载荷。
2.1高圆弹簧所加橡胶垫厚度的合理选择试验表明,圆形橡胶垫受压保持稳定的条件是其厚度(r是橡胶垫半径)说明橡胶垫厚度取得过大,接近失稳状态,因而使弹簧总成的实际横向刚度kL′远较计算值为低。
2.2高圆弹簧加橡胶垫的临界载荷的确定实际上,由于载荷的偏心和弹簧轴线偏离理想的直线,计算临界载荷时,应留有一定的裕度,即计入安全系数在内。
现以长度系数μ′=1.2μ来计算临界载荷。
应该说明的是,我们原参考国外资料,将安全系数取为1.25,即:μ′=1.25μ[52]。
后经试验表明,往往计算求得的数值,表明弹簧总成已经失稳,但实际试验时,还是稳定的。
表示计算过于安全,因此改取安全系数为1.2。
对于钢制圆截面弹簧,,建议以下式计算弹簧总成的临界挠度:式中:H0—高圆弹簧的自由高度(mm);D—高圆弹簧的簧圈平均直径(mm);μ—长度系数。
上式适用于高圆弹簧的两端具有各种约束条件,包括固定、铰接或弹性橡胶垫。
并适用于弹簧横向有约束或无约束的两种情况。
不论约束条件的不同和横向有无约束,都反映在长度系数μ的数值中。
μ的数值可由图[5]至图[8]查取,其中图[5]和图[7]分别为横向无约束及横向有约束的高圆弹簧一端加橡胶垫时与μ的曲线;而图[6]和图[8]分别为横向无约束及横向有约束的高圆弹簧两端加橡胶垫时的与μ的曲线。
[5]高圆弹簧一端加橡胶垫时与μ的关系曲线(横向无约束情况)[6]高圆弹簧两端加橡胶垫时与μ的关系曲线(横向无约束情况)[7]高圆弹簧一端加橡胶垫时与μ的关系曲线(横向有约束情况)[8]高圆弹簧两端加橡胶垫时与μ的关系曲线(横向有约束情况)在图[5]至图[8]中,kθ—橡胶垫的弯曲刚度(N・mm/rad);A—与高圆弹簧参数等有关的数,以下式表示:式中,E—弹簧的拉压弹性模数,E=21×104N/mm2;d—弹簧的簧条直径(mm);n e—弹簧的有效圈数;ν—泊松比,钢的ν=0.3;D—弹簧的簧圈平均直径(mm)。
为了保证弹簧总成的稳定工作,应使它的工作载荷P小于它的临界载荷(其中kV为高圆弹簧的垂向刚度,fcr′为临界挠度,由上式计算求得),即:一些高圆弹簧加橡胶垫的临界载荷数值:*该弹簧总成在工作载荷作用下未失稳。
3.总结根据经验公式法计算了橡胶垫与钢弹簧刚度参数以及高圆簧组合系统的垂向和横向刚度,结果表明橡胶垫对于垂向刚度的影响较小,而对于横向刚度有明显的改变。
