磁场高斯定理证明
磁场的高斯定理和安培环路定理

解:
Bp
发生变化. 发生变化.
I2 I1
∫
L
B dl 不发生变化 P
L
例如: 例如: I1 >0 L I2<0 I1 I2 I3 L I L
I3
∫
L
B dl = o ( I1 I 2 )
∫
L
B dl = o ( I1 + I 3 )
∫ B dl
l
= 4 0 I
二,安培环路定理
∑Ii
i =0
§8-4
稳恒磁场的高斯定理与 安培环路定理
一,稳恒磁场的高斯定理
由磁感应线的闭合性可知, 对任意闭合曲面, 由磁感应线的闭合性可知 , 对任意闭合曲面 , 穿入的磁感应线条数与穿出的磁感应线条数相同, 穿入的磁感应线条数与穿出的磁感应线条数相同 , 因此,通过任何闭合曲面的磁通量为零. 因此,通过任何闭合曲面的磁通量为零.
Φ = BS 2 = (6i + 3 j + 1.5k ) (0.15) i = 0.135Wb ( 2) z Φ = ∫∫ B dS = 0
S
O l
x
l
l
一长直导线通有电流I 距其d 例,一长直导线通有电流I,距其d处有 一长为a 宽为b的长方形, 一长为a,宽为b的长方形,求通过这个 长方形的磁通量. 长方形的磁通量.
n
闭合回路所包围的所有电流 的代数和. 的代数和. 所取的闭合路径上各点的磁 感强度值, 感强度值,是由闭合路径内 外所有的电流产生的. 外所有的电流产生的.即是 由空间所有的电流产生的. 由空间所有的电流产生的.
B
二,安培环路定理
定理的物理意义 由安培环路定理可以看出, 由安培环路定理可以看出,由于 磁场中的磁感强度的环流一般不 为零,所以磁场是非保守场 非保守场. 为零,所以磁场是非保守场.
12磁场的高斯定理和安培环路定理解读

穿过一面元的磁通量:
d m BdS BdS cos B dS 式中:dS dSn ˆ 称为面元矢量。 ˆ 为法线方向单位矢量。 n
4
2.穿过某一曲面的磁通量
m d m B dS
d m
B
BdS cos
dS
ˆ n
S
3.穿过闭合曲面的磁通量
m d m B dS
规定:取闭合面外法线方向为正向。 磁力线穿出闭合面为正通量, 磁力线穿入闭合面为负通量。
2
B
磁通量单位:韦伯,Wb
2
ˆ n
Байду номын сангаас
B
5
3.磁场中的高斯定理 定理表述:穿过任意闭合面的磁通量等于 0。
dB
dB ' dB' '
dl '
p
d
dl ' '
l
c
B
结果
o j
2
o
方向如图所示。
a
b
在无限大均匀平面电流的两侧的磁场都为 均匀磁场,并且大小相等,但方向相反。
15
例5 一矩形截面的空心环形螺线管,尺寸如图所示, 其上均匀绕有N匝线圈,线圈中通有电流I。试求: (1)环内距轴线为r 远处的磁感应强度;(2)通过 螺线管截面的磁通量。 I
解:在管内作环路半径为 r的圆环 ,
环路内电流代数和为: I NI
rR
o R1
2
当 r >> ( R2 – R1) 时N n 为沿轴向线圈密度;
0 NI B 2r 0 NI B 2r
磁场中高斯定理公式

磁场中高斯定理公式磁场中的高斯定理什么是磁场中的高斯定理?磁场中的高斯定理是一种描述磁场分布的物理定律,它与电场中的高斯定理类似。
磁场中的高斯定理告诉我们,通过任意闭合曲面的磁通量等于该闭合曲面内磁场的总极化矢量。
高斯定理的数学表达式磁场中的高斯定理可以用以下数学公式来表示:∮ B · dA = μ0 * Φ其中, - ∮ 表示对整个闭合曲面的积分运算; - B 表示磁场的磁感应强度; - dA 表示曲面上的微小面积元素; - μ0 表示真空中的磁导率,其值约为× 10^-6 H/m; - Φ 表示通过闭合曲面的磁通量。
如何理解高斯定理?为了更好地理解磁场中的高斯定理,我们来看一个例子。
假设有一个无限长直导线,通过这条导线的电流为I,我们想要计算该导线所产生的磁场在某表面上的磁通量。
我们可以选择一个以导线为轴线、面积为A的柱状闭合曲面,这个闭合曲面穿过导线并覆盖了所有的磁场线。
根据高斯定理,这个柱状闭合曲面上的磁通量等于该曲面内磁场的总极化矢量。
因为该闭合曲面只有一个入口和一个出口,而且导线内部的磁场线是圆形的,所以曲面上的磁场线数是一样的。
由于磁场线在柱状闭合曲面的投影面积都是相同的,所以曲面上的磁通量也是相同的。
根据高斯定理的数学表达式,磁场的磁通量等于磁感应强度与曲面上的微小面积元素的点积之和。
所以对于这个闭合曲面,磁通量可以表示为:Φ = B * A根据高斯定理的公式:∮ B · dA = μ0 * Φ我们可以得出:B * A = μ0 * Φ从而得出导线所产生的磁场的磁感应强度为:B = (μ0 * Φ) /A这个例子展示了如何使用高斯定理来计算闭合曲面中的磁通量。
通过选择合适的曲面和断面面积,我们可以方便地计算任何形状导线所产生的磁场的磁感应强度。
总结磁场中的高斯定理是一种描述磁场分布的重要定理。
它告诉我们,通过任意闭合曲面的磁通量等于该闭合曲面内磁场的总极化矢量。
磁场的高斯定理说明

磁场中的高斯定理说明磁场的性质:对一封闭曲面来说,一般取向外的指向为正法线的指向。
这样从闭合面穿出的磁通量为正,穿入的磁通量为负。
由于磁感线是闭合线,那么穿过任一封闭曲面的磁通量一定为零。
真空静电场的高斯定理:∮EdS=(∑Q)/ε0
稳恒磁场的高斯定理:∮BdS=0
这两个结论的不同揭示了静电场和磁场的一个差异:
静电场是有源场,它的电场线不会闭合,所以对一个封闭曲面的通量不一定为0;而稳恒磁场是无源场,它的磁场线是封闭的,有多少条磁场线穿出曲面,相应就有多少条磁场线穿进曲面,所以磁场对一个封闭曲面的通量恒为0。
用比较专业的场论术语来说,就是:静电场是有源场,散度一般不为0;稳恒磁场是无源场,散度恒为0。
静电场中的环路定理:∮Edl=0(l是L的小写,不是数字1)
稳恒磁场的安培环路定律:∮Bdl=(∑I)/μ0 (∑后面的是字母i的大写)
这两个不同的结论又反映了静电场和磁场的另一个差异:
静电场是无旋场,即它的旋度恒为0,所以静电场对环路积分结果为0;
稳恒磁场是有旋场,一般旋度不为零,所以磁场对环路的积分一般不等于0。
磁通量 磁场的高斯定理

B
B
0 I
dl
(5)多电流情况
I1
I2
I3
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
l
以上结果对任意形状 的闭合电流(伸向无限远 的电流)均成立.
n B dl 0 Ii i 1
安培环路定理
B
0 I
B
dB
I
.
dI
B
B
的方向与 I 成右螺旋
0 r R,
r R,
I
2π R 0 I B 2π r
B
0 Ir
2
0 I
2π R
B
R
o R
r
rR
0 I B 2r
区域:
rR
0 Ir B 2R 2
区域:
I
思考:具有一圆柱形空腔的无限长载流 圆柱,求空腔内的磁场?
B dl B (d l d l// )
L L
(4) 如果闭合曲线不在垂直 于导线的平面内:
B cos 90 dl B cos dl//
L L
I
0 Br d
L
dl
dl
dl
2
0
0 I r d 2 r
结果一样!
I
L 成右螺旋时,
二 安培环路定理的证明 (1)载流长直导线的情况
0 I l B dl 2π Rdl 0 I l B dl 2π R l dl B dl 0 I
l
0 I B 2πR
I
o
B
R
磁场的高斯定理
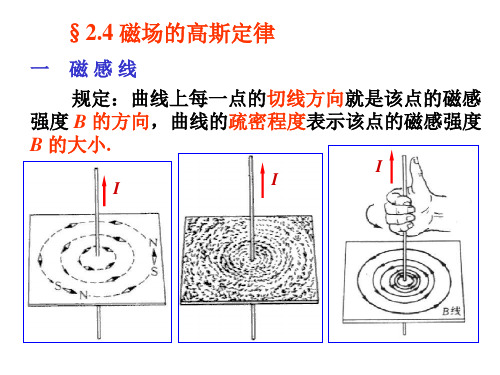
一 磁感线 规定:曲线上每一点的切线方向就是该点的磁感 规定:曲线上每一点的切线方向就是该点的磁感 切线方向 的方向,曲线的疏密程度 疏密程度表示该点的磁感强度 强度 B 的方向,曲线的疏密程度表示该点的磁感强度 B 的大小 的大小.
I I I
磁通量(Magnetic flux)v • 磁通量
单位 1Wb = 1T × 1m
2
v B
S
I
v B
v B
由电流与磁场的关系可知电流元的磁力线都是 圆心在电流元轴线上的同心圆。 圆心在电流元轴线上的同心圆。磁力线是无头无尾 的闭合曲线。 的闭合曲线。 r v v dB⋅ dS = 0 dB 是电流元的磁场
∫∫
S
载流导线的磁场
r r r r B = dB1 + dB2 + L + dBn + L
µ0 I
x
s⊥
θ
s
v B
θ v B
v dS
v en
B
磁通量: 磁通量:通过某一曲 面的磁感线数为通过此曲 面的磁通量. 面的磁通量
v θ B
s
Φ = BS cosθ = BS⊥ v v v v Φ = B ⋅ S = B ⋅ enS v v dΦ = B ⋅ dS dΦ = BdS cosθ v v Φ = ∫s B ⋅ dS
大学物理学》 《基础物理学》路果编著p345 《大学物理学》卢德馨编著线起始于正电荷,终止于负电荷。 电场线起始于正电荷,终止于负电荷。 磁感应线为无头无尾的闭合线。 磁感应线为无头无尾的闭合线。 原因: 原因:正、负电荷可单独存在,而磁单 负电荷可单独存在, 极子却不可单独存在 磁场是一种涡旋场
高斯定理证明

高斯定理证明
高斯定理是电磁学中的一个重要定理,也称为高斯第一定理、高斯-奥波尔兹定理或高斯-斯托克斯定理。
它是电场、磁场和流体动力学中的基本方程之一,描述电场、磁场和流体速度的场在一个闭合曲面上的性质。
高斯定理可以用来计算电场通过一个任意形状的闭合曲面的总通量,它的数学表达式为:
∮E · dA = 1/ε₀ · ∫∫∫ρ dV
其中:
- ∮E · dA表示电场E与曲面元dA的点乘积(即电场E沿曲面法向量方向的分量与曲面元面积的乘积)之和。
- ε₀为电场中的真空介电常数,其值为8.854×10⁻¹²
C²/(N·m²)。
- ∫∫∫ρ dV表示在闭合曲面内的电荷密度ρ乘以体积元dV 之和。
高斯定理的证明分为两个步骤:
1. 假设电场E是有限个点电荷的叠加,可以根据库仑定律得到电场E与闭合曲面上各点的点乘积之和等于电荷与外部点产生的共同电势的梯度在该点上的点乘积之和。
2. 利用极限的思想,将点电荷的数量无限逼近,使得点电荷产生的电场可以看作一个连续的场,通过对电场的积分可以得到闭合曲面上的总通量。
综上所述,高斯定理的证明基于库仑定律和极限的思想,将点电荷的叠加近似为连续的电场场源,通过对电场的积分计算闭合曲面上的总通量。
磁场的高斯定理

I π R2Bj
M m
IBR2
2π
0
sin
2 d
ISk I π R2k
y
B
J
I
x
R
Q o d K x
zP
磁介质
一 磁介质 磁化强度
1 磁介质
B B0 B'
磁介质中的
真空中的
介质磁化后的
总磁感强度
磁感强度
附加磁感强度
顺磁质 B B 0(铝、氧、锰等) 弱磁质
磁场的高斯定理
一 磁感线
切线方向—— 疏密程度——
B B
的方向; 的大小.
I
I
I
I
S
I
S
N
N
二 磁通量 磁场的高斯定
理
S B
B ΔN ΔS
磁通场过中的某磁点感处 线垂 数直 目等B矢于量该的点单B的位数面值积.上
B
磁通量:
en
通过某曲面的磁感
s
s
B
线数 匀强磁场下, 面
以Oy为轴,Idl
y
所受磁力矩大小
B
J
dM xdF IdlBxsin I
x
R
x R sin , dl Rd Q o d K x
dM IBR2 sin2 d
zP
dM IBR2 sin2 d
M IBπ R2
B Bi
M
m
B
I π R2Bk i
B
π 2
,M
M max
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
磁场高斯定理的证明
根据闭奥萨伐尔定律,单个电流元IdL产生的磁感应线是以 dL方向韦轴线的圆,如图,圆周上元磁场的数值处处相等:
在磁感应线穿入处取一面元dS1,穿出处取另一面元dS2,IdL产生的磁场通过两面元的磁感应通量分别为:
由于磁感应管呈严格的圆环状,其正截面处处相等,故,
所以,即。
所以高斯定理对单个电流元成立。
根据磁场叠加原理,任意载流回路产生的总磁场B是各电流元产生的元磁场dB的矢量和, 从而通过某一面元dS的总磁通量是各电流元产生元磁通的代数和。
至此,磁场的”高斯定理”得到了完全证明。
